| Issue |
A&A
Volume 558, October 2013
|
|
|---|---|---|
| Article Number | A118 | |
| Number of page(s) | 13 | |
| Section | Numerical methods and codes | |
| DOI | https://doi.org/10.1051/0004-6361/201321891 | |
| Published online | 15 October 2013 | |
MILCA, a modified internal linear combination algorithm to extract astrophysical emissions from multifrequency sky maps
1
Laboratoire de Physique Subatomique et de Cosmologie, Université Joseph
Fourier Grenoble I, CNRS/IN2P3, Institut National Polytechnique de
Grenoble,
53 rue des Martyrs,
38026
Grenoble Cedex,
France
e-mail:
ghurier@ias.u-psud.fr
2
Institut d’Astrophysique Spatiale, CNRS (UMR8617), Université
Paris-Sud 11, Bâtiment
121, 91405
Orsay,
France
3
Jet Propulsion Laboratory, California Institute of Technology,
4800 Oak Grove
Drive, Pasadena,
California,
USA
Received:
14
May
2013
Accepted:
23
July
2013
This analysis of current cosmic microwave background (CMB) experiments is based on the interpretation of multifrequency sky maps in terms of different astrophysical components and it requires specifically tailored, component separation algorithms. In this context, internal linear combination (ILC) methods have been extensively used to extract the CMB emission from the WMAP multifrequency data. We present here a modified internal linear component algorithm (MILCA) that generalizes the ILC approach to the case of multiple astrophysical components for which the electromagnetic spectrum is known. In addition, MILCA corrects for the intrinsic noise bias in the standard ILC approach and extends it to a hybrid space-frequency representation of the data. It also allows us to use external templates to minimize the contribution of extra components but still using only a linear combination of the input data. We applied MILCA to simulations of the Planck satellite data at the frequency bands from 100 GHz to 857 GHz. We explore the possibility of reconstructing the Galactic molecular CO emission and the thermal Sunyaev-Zeldovich effect from the Planck maps. We conclude that MILCA is able to accurately estimate those emissions, and it has been successfully used for this purpose within the Planck collaboration.
Key words: methods: data analysis / techniques: image processing / cosmic background radiation
© ESO, 2013
1. Introduction
Multifrequency comic microwave background (CMB) experiments, such as the WMAP (Bennett et al. 2003) and Planck (Planck Collaboration 2006) missions, observes a mixture of astrophysical emissions. Most of them follow different emission laws (e.g., CMB anisotropies, thermal Sunyaev-Zeldovich (tSZ) effect, Sunyaev & Zeldovich 1972, thermal dust, cosmic infrared background (CIB), synchrotron, molecular cloud emission, etc.). It is thus possible to separate the mixed astrophysical sources by taking advantage of the specific emission laws of each astrophysical component. The separation of astrophysical sources from a set of multichannel observations of the millimeter and submillimeter sky is an important step in the scientific exploitation of such data. In this context, several methods have been developed.
These component separation techniques can be separated into various categories depending on the degree and nature of the prior information used. For example, maximum likelihood techniques (e.g., Commander, Eriksen et al. 2008) and maximum of entropy methods (see e.g. Hobson et al. 1998; Stolyarov et al. 2002) assume that the electromagnetic spectrum of the different components is known or that it can be easily parametrized. By contrast, blind (or semi-blind) component separation methods such as, spectral matching ICA (Cardoso et al. 2008; Delabrouille et al. 2003), PolEMICA (Aumont & Macías-Pérez 2007), FastICA (Maino et al. 2002), CCA (Bonaldi et al. 2006), or GMCA (Bobin et al. 2008) exploit the spectral and spatial diversity of the components and need no a priori. In a different way, ILC (internal linear combination) techniques (Bennett et al. 2003; Eriksen et al. 2004; Remazeilles et al. 2011) aim to preserve an astrophysical component for which the electromagnetic spectrum is known, by minimizing the variance in the reconstructed signal.
Standard ILC methods are very popular because of their simplicity and robustness. However, as discussed by Vio & Andreani (2008), they are biased by the noise contribution to the variance of the final map. This bias reduces the efficiency of the algorithm in poor signal-to-noise conditions. Furthermore, they do not fully exploit the spatial and spectral diversity to minimize the contribution from other sky components for which the electromagnetic spectrum is poorly, or not at all, known.
The ILC methods also assume that the component of interest is statistically independent of the other ones. If the statistical independence assumption can be made for the CMB, it is not the case for all the astrophysical components of the millimeter and submillimeter sky. Indeed, galactic foregrounds, such as thermal dust, synchrotron, and molecular cloud emission, are highly correlated over the sky. Such correlations can also be observed for extragalactic components like tSZ and extragalactic point sources.
We present, in this article, the modified internal linear combination algorithm (MILCA) that generalizes standard ILC techniques to multiple constraints in order to reduce the level of contamination by other astrophysical emissions. We show that MILCA also corrects for the noise bias of the standard ILC solution and blindly minimizes the contribution from unknown or poorly constrained sky components.
The paper is organized as follows. In Sect. 2, we present our modeling the millimeter and submilimeter sky. Then, in Sect. 3, we address the problem of generalizing the ILC algorithm to multiple constraints. Section 4 discusses possible bias in the ILC algorithm. In Sect. 5, we propose modifications to the standard ILC estimator to minimize the instrumental noise and contamination from other astrophysical components. Finally, we apply MILCA to Planck simulated datasets, focusing on the extraction of the tSZ effect(Sect. 6) and molecular cloud emission (Sect. 7).
It is important to note that MILCA has already been used by the Planck collaboration to produce tSZ y-maps for validating the catalog of candidates (Planck Collaboration 2011d,i), for the extraction of the cluster pressure profiles (Planck Collaboration 2013b), for other physical analyses (Planck Collaboration 2013f,c) and for comparison with other experiments (Planck Collaboration 2013a). MILCA has also been used to produce tSZ maps in Planck Collaboration (2011d,i, 2013f,a,e,m,l).
MILCA has also been applied to the Planck bolometer maps at 100, 217, and 353 GHz in order to extract maps of the emission of the first three CO rotational transitions J = 1–0, J = 2–1, and J = 3–2 (Planck Collaboration 2013h). These maps were released by the Planck collaboration and have been extensively compared with external data in Planck Collaboration (2013h).
2. Simulation of the microwave sky seen by Planck
2.1. The Planck mission and the submillimeter sky
The Planck mission (Planck Collaboration 2011a, 2013g) is the third space mission, after the COBE (Smoot et al. 1992; Bennett et al. 1996) and the WMAP (Hinshaw et al. 2003, 2009; Bennett et al. 2003) missions, to be devoted to the study of the microwave and submm emissions, and especially to CMB. Planck, as other CMB experiments, observes the sky emission in different frequency bands. In particular, Planck has two instruments: the Low Frequency Instrument (LFI, Bersanelli et al. 2010; Mennella et al. 2011), which has three frequency bands centered at 30, 44, and 70 GHz, and the High Frequency Instrument (HFI, Lamarre et al. 2010; Planck Collaboration 2011b), which has six frequency bands centered at 100, 143, 217, 353, 545, and 857 GHz. The large number of detectors and their high sensitivity, make the Planck mission the first CMB experiment expected to be limited by our knowledge of the foreground emissions rather than by instrumental noise.
At the Planck frequencies, the main astrophysical emissions are the diffuse Galactic free-free, synchrotron, and thermal dust (Planck Collaboration 2006, 2011h) emissions; the anomalous microwave emission (AME, Planck Collaboration 2011g); the molecular Galactic emissions (mainly 12CO in the 100, 217, and 353 GHz bands, Planck Collaboration 2013h); the emission from Galactic and extragalactic point sources (radio and infrared sources, Planck Collaboration 2013d, 2011c); the CIB (Planck Collaboration 2011f); the zodiacal light emission (Planck Collaboration 2013i); and the thermal Sunyaev-Zeldovich effect (Sunyaev & Zeldovich 1972) in clusters of galaxies (Planck Collaboration 2011d, 2013m).
 |
Fig. 1 Simulation of the submillimeter sky for, from left to right and top to bottom; 100, 143, 217, 353, 545, and 857 GHz Planck channels. See Sect. 2 for more details. |
2.2. Simulations of the submillimeter sky
We have simulated the microwave and submillimeter sky observed by Planck using a set of template maps to reproduce astrophysical components. Within those components, we include CMB, diffuse Galactic emissions (synchrotron, free-free and thermal dust), Galactic CO emission, Galactic and extragalactic point sources, CIB and tSZ emissions. We did not include in the simulation the Anomalous Microwave Emission (AME) for which a template is not available and that we expect to be subdominant for the following analyses based on data from 100 to 857 GHz.
The CMB was simulated using a random correlated gaussian field as defined by the Planck best-fit CMB angular power spectrum (Planck Collaboration 2013j,k). The thermal dust emission was modeled using the reprocessed IRAS maps at 100 μm (IRIS, Miville-Deschênes & Lagache 2005) extrapolated to the Planck frequencies assuming a grey body emission law (e.g. Desert et al. 1990) with constant temperature, Tdust = 18 K and spectral index βdust = 1.8.
The synchrotron emission was simulated using the 408 MHz full-sky map from Haslam et al. (1981) corrected for free-free emission assuming an emission law with a spatially constant spectral index of −1.0 in terms of flux density (Davies et al. 1996). The Galactic free-free emission was modeled using the Hα full-sky map (Finkbeiner 2003) and an electron temperature of 7000 K as proposed by Dickinson et al. (2003) and a spatially constant spectral index of −0.1 in terms of flux density. The CO rotational transition line emission was modeled using the J = 1–0 CO survey from Dame et al. (2001). The CO transmission in Planck’s sky maps have been simulated assuming 10% fluctuations on the bandpass amplitude (Planck Collaboration 2013h).
We also add radio point sources using the sources in the NVSS catalog (Condon et al. 1998) and extrapolating their fluxes to the Planck frequencies assuming a random spectral index for each source derived from a Gaussian distribution with a mean of −0.5 and a standard deviation of 0.2 in terms of flux density (Planck Collaboration 2011e).
Extragalactic infrared (IR) astrophysical emissions can be decomposed into two categories, a poissonian contribution, composed by point sources, and a diffuse contribution, the clustered CIB. To model IR point sources, we used a randomly distributed sources with random spectral index for each source (with a mean of 2.8 and a standard deviation of 0.3 in terms of spectral density as found in Planck Collaboration 2011e). For the CIB emission, we assumed a random correlated gaussian distribution following the CIB power spectra as measured by Planck (Planck Collaboration 2011f) and constant correlation factors across multipoles. We do not account for the non-gaussianity of the CIB (see e.g. Lacasa et al. 2012) in our model.
The tSZ emission is produced by the hot and dense gas of electrons, such gas can be found in galaxy clusters or in the WHIM. In this study we only account for the emission from X-ray known galaxy clusters. To do so, the tSZ was simulated using a universal electron pressure profile from Arnaud et al. (2010) and physical parameters for clusters from the MCXC catalog (Piffaretti et al. 2011).
The simulations of the Planck frequency channels (from 100 to 857 GHz) we produced are presented in Fig. 1. It is important to note that the simulations presented in this paper are simplified as they do not account for spatial variations in the SED of the Galactic synchrotron and thermal dust emissions. However, these simplified simulations allow us to present the main characteristics of the MILCA procedure. A discussion of the application of MILCA to more realistic sky emission simulations constructed from the Planck sky model (PSM, Delabrouille et al. 2013), can be found in Planck Collaboration (2013l).
For each Planck channel, maps of the instrumental noise have been produced and added to the sky emission simulated maps, with the expected levels for the Planck mission (Planck Collaboration 2013g). The noise is assumed to be Gaussian and white but anisotropic as a consequence of the Planck scanning strategy (Planck Collaboration 2006).
3. Generalizing ILC method
The total emission observed at a given frequency channel map,
Ti, can be expressed as the superposition
of astrophysical components and instrumental noise 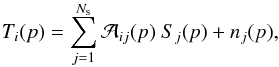 (1)where p
denotes the pixel number. Sj are the maps of
the Ns astrophysical components (CMB and foregrounds) in the
data and nj is the instrumental noise.
(1)where p
denotes the pixel number. Sj are the maps of
the Ns astrophysical components (CMB and foregrounds) in the
data and nj is the instrumental noise.
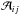 is the mixing matrix given by
is the mixing matrix given by 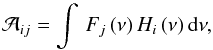 (2)with
Fj (ν) the spectral
dependence of the jth component and
Hi (ν) the spectral
response of the ith channel.
(2)with
Fj (ν) the spectral
dependence of the jth component and
Hi (ν) the spectral
response of the ith channel.
Assuming that the mixing matrix is constant across the sky or constant across a given set
of pixels, Eq. (1) can be written in a more
compact manner as 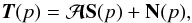 (3)where
T and N are vectors containing the total and
noise maps for the Nobs observation channels, S is
a matrix corresponding to the maps of the Ns astrophysical
components.
(3)where
T and N are vectors containing the total and
noise maps for the Nobs observation channels, S is
a matrix corresponding to the maps of the Ns astrophysical
components. 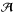 is the mixing matrix with dimensions
Nobs × Ns.
is the mixing matrix with dimensions
Nobs × Ns.
3.1. Internal Linear Combination algorithm
The Internal Linear Combination algorithm (Bennett et al.
2003) assumes that the astrophysical component to be reconstructed,
Sc, can be obtained as a linear combination of the input
observational maps 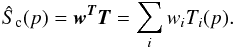 (4)The weights,
wT = (w1,...,wNobs),
of the linear combination are computed by minimizing the variance of the output map,
(4)The weights,
wT = (w1,...,wNobs),
of the linear combination are computed by minimizing the variance of the output map,
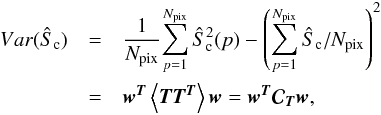 (5)under
constraints on the emission spectrum of Sc. The matrix
(5)under
constraints on the emission spectrum of Sc. The matrix
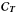 is the covariance matrix of the observed maps, T, averaged
across pixels.
is the covariance matrix of the observed maps, T, averaged
across pixels.
For the CMB and assuming that the maps are given in thermodynamic temperature units, the
constraint simply reads as (Bennett et al. 2003;
Eriksen et al. 2004)
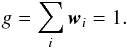 (6)More generally, for an
astrophysical component with emission spectrum,
fc, the
constraints can be written as
(6)More generally, for an
astrophysical component with emission spectrum,
fc, the
constraints can be written as 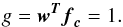 (7)We stress that
fc is related
to the mixing matrix,
(7)We stress that
fc is related
to the mixing matrix, 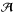 ,
by
,
by 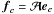 ,
where ec is an
Ns dimension vector for which all elements are set to zero
except the c-th element that is set to one.
,
where ec is an
Ns dimension vector for which all elements are set to zero
except the c-th element that is set to one.
Linear system solution
Weights can be computed solving a linear system using Lagrange multipliers,
λ, 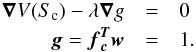 (8)The
final linear system can be expressed in the form
(8)The
final linear system can be expressed in the form 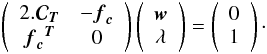 (9)Solving
the linear system we obtain
(9)Solving
the linear system we obtain 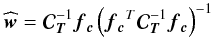 (10)and
then
(10)and
then 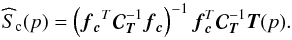 (11)In the case of the CMB
emission Eq. (11)reduces to
(11)In the case of the CMB
emission Eq. (11)reduces to 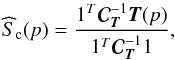 (12)where
1 = (1,...,1), as in Bennett et al. (2003) and Eriksen et al. (2004).
(12)where
1 = (1,...,1), as in Bennett et al. (2003) and Eriksen et al. (2004).
3.2. Multiple spectral constraints
In some particular cases, the emission spectra of various astrophysical components may be
known with sufficient accuracy. Thus, it is possible to use multiple constraints (i.e.,
g1,g2,...,gNnc)
for the minimization process to extract some astrophysical components and to reject some
others. In practice, we can write those constraints as 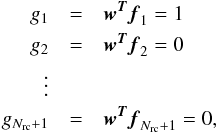 (13)where
Nrc are the number of rejected components.
(13)where
Nrc are the number of rejected components.
Remazeilles et al. (2011) have shown that two
components can be constrained and simultaneously recovered. We propose here a
generalization of this method to an arbitrarily large number of constraints. Defining
ℱ as a matrix with
Nobs × (1 + Nrc) elements
such that ![\begin{equation*} {\boldsymbol{\cal F}} = \begin{pmatrix} \fb_{1}[1] & \fb_{2}[1] & \cdots & \fb_{1+N_{\mathrm{rc}}}[1] \\ \vdots & \vdots &\ddots & \vdots \\ \fb_{1}[N_{\mathrm{obs}}] & \fb_{2}[N_{\mathrm{obs}}] & \cdots & \fb_{1+N_{\mathrm{rc}}}[N_{\mathrm{obs}}] \\ \end{pmatrix}, \end{equation*}](/articles/aa/full_html/2013/10/aa21891-13/aa21891-13-eq60.png) Equation (9) can be generalized to
Equation (9) can be generalized to 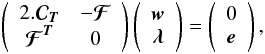 (14)where
λ = (λ(1),λ(2),··· ,λ(1 + Nrc))T
are the Lagrange multipliers and
e = (1,0,...,0)T.
The solution of the system can then be written as
(14)where
λ = (λ(1),λ(2),··· ,λ(1 + Nrc))T
are the Lagrange multipliers and
e = (1,0,...,0)T.
The solution of the system can then be written as 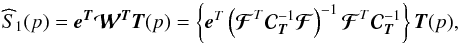 (15)with
(15)with
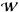 the (Nrc + 1) × Nobs dimension
matrix containing the weights extracting each constrained components. The first line of
this matrix contains the weights for the extraction of the components of interest,
the (Nrc + 1) × Nobs dimension
matrix containing the weights extracting each constrained components. The first line of
this matrix contains the weights for the extraction of the components of interest,
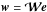 .
.
We stress that in the relation 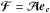 ,
ec is now a
Ns × (1 + Nrc) matrix.
,
ec is now a
Ns × (1 + Nrc) matrix.
4. Bias in the standard ILC estimator
The ILC estimator as presented above is biased. This bias can have several origins:
-
correlation between the “wanted” components and the otherastrophysical components;
-
differences between the true emission laws and the constraints used to minimize the variance. These differences can be produced by calibration uncertainties (Dick et al. 2010) or by discrepancies between the assumed emission laws and the actual ones;
-
noise-induced correlations.
4.1. Intrinsic bias
We first characterize the bias in the ILC estimator proposed in Eq. (10), neglecting the contribution of the
instrumental noise. In this situation, we can write the channel covariance matrix as
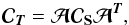 (16)with
(16)with
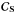 the Ns × Ns dimension
covariance matrix of the astrophysical components. The
the Ns × Ns dimension
covariance matrix of the astrophysical components. The
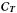 matrix has a dimension
Nobs × Nobs but has a rank:
min(Ns,Nobs),
by construction; as for
matrix has a dimension
Nobs × Nobs but has a rank:
min(Ns,Nobs),
by construction; as for 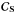 ,
it has a rank Ns. From here, three cases are possible for the
,
it has a rank Ns. From here, three cases are possible for the
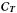 matrix inversion:
matrix inversion:
-
(1)
Ns > Nobs: there are more physical components than channels. It is not possible to describe
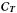 with an ns dimension sub-space. The
nt dimension subspace which describes the
with an ns dimension sub-space. The
nt dimension subspace which describes the
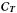 matrix thus has no physical meaning and consequently it is not possible to extract a
single component by a linear combination. The ILC approach will thus produce highly
biased estimation. A solution to this problem requires more information, such as
other channels of observations.
matrix thus has no physical meaning and consequently it is not possible to extract a
single component by a linear combination. The ILC approach will thus produce highly
biased estimation. A solution to this problem requires more information, such as
other channels of observations. -
(2)
Ns = Nobs: there are the same number of components than channels. In this case,
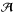 is a square matrix. There is no ambiguity in inverting
is a square matrix. There is no ambiguity in inverting
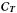 .
There exist an unbiased linear combination that allows us to extract
S1.
.
There exist an unbiased linear combination that allows us to extract
S1. -
(3)
Ns < Nobs: there are more channels than astrophysical components.
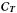 has a rank Ns lower than his dimension
Nobs. Consequently, this matrix is singular and cannot
be directly inverted. However, we can use the pseudo inverse as defined by the
singular value decomposition (SVD) of the matrix. We can thus write
has a rank Ns lower than his dimension
Nobs. Consequently, this matrix is singular and cannot
be directly inverted. However, we can use the pseudo inverse as defined by the
singular value decomposition (SVD) of the matrix. We can thus write
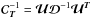 ,
with
,
with 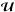 an orthogonal matrix and
an orthogonal matrix and 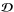 a diagonal matrix containing the singular values of
a diagonal matrix containing the singular values of
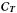 .
The
.
The  matrix is obtained by taking the inverse of all singular values different from zero,
and setting to zero the inverse of all singular values equal to zero. The
matrix is obtained by taking the inverse of all singular values different from zero,
and setting to zero the inverse of all singular values equal to zero. The
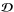 matrix is uniquely defined, however the
matrix is uniquely defined, however the 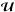 matrix is defined with
Nobs − Ns degrees of
freedom. There exist multiple linear combinations to extract the
S1 component.
matrix is defined with
Nobs − Ns degrees of
freedom. There exist multiple linear combinations to extract the
S1 component.
When the 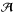 matrix is rectangular
(Ns < Nobs),
the notation
matrix is rectangular
(Ns < Nobs),
the notation 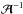 refers to the left inverse of the matrix (also defined with
Nobs − Ns degrees of freedom).
refers to the left inverse of the matrix (also defined with
Nobs − Ns degrees of freedom).
For each pixel, we can also define S′(p) and
S′′(p) two vectors of dimensions
Nrc + 1 and
Ns − Nrc − 1 respectively, that
contain the constrained and un-constrained components such that
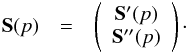 (17)For
simplicity hereafter, we do not explicitly write the pixel index, p.
(17)For
simplicity hereafter, we do not explicitly write the pixel index, p.
In the following, we will focus on the case
Ns ≤ Nobs. Using Eq. (16), we can express the estimator of
S1 as 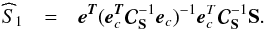 (18)To
simplify the following discussions, we choose to express
(18)To
simplify the following discussions, we choose to express
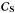 as a function of different sub-spaces
as a function of different sub-spaces 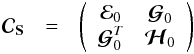 (19)with
ℰ0 the
(Nrc + 1) × (Nrc + 1)
dimension sub-space associated with the constrained components, ℋ0
the
(Ns − Nrc − 1) × (Ns − Nrc − 1)
dimension sub-space associated with the other components. The matrix
(19)with
ℰ0 the
(Nrc + 1) × (Nrc + 1)
dimension sub-space associated with the constrained components, ℋ0
the
(Ns − Nrc − 1) × (Ns − Nrc − 1)
dimension sub-space associated with the other components. The matrix
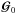 is a
(Nrc + 1) × (Ns − Nrc − 1)
sub-space of
is a
(Nrc + 1) × (Ns − Nrc − 1)
sub-space of 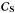 contains the correlation between the contained and un-constrained components.
contains the correlation between the contained and un-constrained components.
We can rewrite the estimator of S1, using a blocwise
inversion procedure 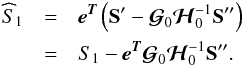 (20)We
note that the S1 component is effectively recovered. However,
we also notice the presence of a term of bias
(20)We
note that the S1 component is effectively recovered. However,
we also notice the presence of a term of bias 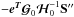 produced by
the correlation,
produced by
the correlation, 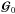 ,
between the reconstructed component and the un-constrained components. This term of bias
is composed by a linear combination of the un-constraints components and it is also
function of the inverse of the covariance matrix of the un-constrained component.
,
between the reconstructed component and the un-constrained components. This term of bias
is composed by a linear combination of the un-constraints components and it is also
function of the inverse of the covariance matrix of the un-constrained component.
This bias can be intuitively understood as the astrophysical emissions correlated with the “wanted” component, S1, can be used to minimize the variance by removing a fraction of the “wanted” emission. In order to reduce the bias induced by such correlations, it is possible to use prior information on the spatial distribution of the contaminating astrophysical components as discussed in Sect. 5.2.
4.2. Noise-induced bias
We now focus on the impact of the noise on the estimation of the “wanted” component,
S1. Adding noise, the
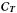 matrix can be simply written as
matrix can be simply written as 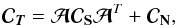 (21)where
(21)where
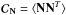 is the Nobs × Nobs dimension
covariance matrix of the instrumental noise averaged across pixels. This matrix is
diagonal if the noise between different observation channels is uncorrelated. This matrix
has a rank Nobs, consequently
is the Nobs × Nobs dimension
covariance matrix of the instrumental noise averaged across pixels. This matrix is
diagonal if the noise between different observation channels is uncorrelated. This matrix
has a rank Nobs, consequently
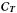 has also rank Nobs and can be inverted in any case. The
has also rank Nobs and can be inverted in any case. The
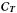 matrix can be projected in the space of the astrophysical components as
matrix can be projected in the space of the astrophysical components as 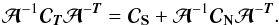 (22)Assuming that
(22)Assuming that
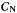 is a diagonal matrix (this is the case for the applications presented in this paper),
is a diagonal matrix (this is the case for the applications presented in this paper),
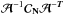 is not. The noise covariance matrix adds non-diagonal terms in
is not. The noise covariance matrix adds non-diagonal terms in
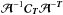 .
As discussed in Sect. 4.1, this term will add a bias
in the estimator of
.
As discussed in Sect. 4.1, this term will add a bias
in the estimator of 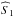 such that
such that 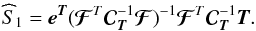 (23)Writing
(23)Writing
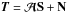 (signal plus noise terms) Eq. (23) reads
as
(signal plus noise terms) Eq. (23) reads
as 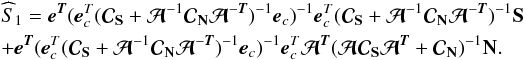 (24)We
observe two terms, one depending on the astrophysical signal and the second depending on
the noise contribution. To express clearly the extra-bias produced by noise, we rewrite
the matrix
(24)We
observe two terms, one depending on the astrophysical signal and the second depending on
the noise contribution. To express clearly the extra-bias produced by noise, we rewrite
the matrix 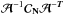 in the same form we used for
in the same form we used for 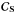 in Eq. (19)
in Eq. (19)
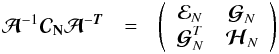 (25)and
(25)and
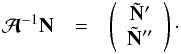 (26)We
can write the residual term in our estimator in the form
(26)We
can write the residual term in our estimator in the form ![\begin{eqnarray} R_{1} &= &\widehat S_{\mathrm{1}} - S_{\mathrm{1}} \nonumber \\ &= & \eb^{\Tb} \tilde{\Nb'} - \eb^{\Tb} ({\boldsymbol{\cal{G}}}_0 + {\boldsymbol{\cal{G}}}_N) ({\boldsymbol{\cal{H}}}_0 + {\boldsymbol{\cal{H}}}_N)^{-1} (\Sb'' + \tilde \Nb'') \nonumber \\ &=& \eb^{\Tb} \tilde{\Nb'} \!- \eb^{\Tb} ({\boldsymbol{\cal{G}}}_0 + {\boldsymbol{\cal{G}}}_N) {\boldsymbol{\cal{H}}}^{-1}_0 \left[\sum_{k=0}^{\infty} (-1)^{k} ({\boldsymbol{\cal{H}}}_0^{-1}{\boldsymbol{\cal{H}}}_N)^{k}\right] (\Sb'' \!+\! \tilde \Nb''). \label{biaswithnoise} \end{eqnarray}](/articles/aa/full_html/2013/10/aa21891-13/aa21891-13-eq121.png) (27)The
term
(27)The
term 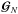 produces extra-bias. The additional bias introduced by the noise can be reduced if we have
an estimate of the noise covariance matrix,
produces extra-bias. The additional bias introduced by the noise can be reduced if we have
an estimate of the noise covariance matrix, 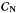 .
We will discuss the correction of this bias and its caveats in Sect. 5.
.
We will discuss the correction of this bias and its caveats in Sect. 5.
5. Modified internal linear combination algorithm (MILCA)
To reduce the bias presented in the previous section, we propose several modifications to the standard ILC estimator:
-
(1)
localization in pixel and spherical harmonic spaces to accountfor spatial spectral law variations;
-
(2)
modify the definition of the variance we minimize (by an action on the covariance matrix, which is equivalent to a modification of the Lagrangian of the problem), to account for noise-induced and astrophysical correlations;
-
(3)
add extra constraints as discussed in Sect. 3.2.
5.1. Localization in the pixel and spherical harmonic domains
Astrophysical components properties vary both spatially (pixel domain) and in frequency (spherical harmonic domain). For example, the CMB is homogeneous and isotropic over the sky and is dominant at a typical angular scale of about one degree. Galactic foregrounds are localized in the Galactic plane and at large angular scales with spectral laws that vary smoothly spatially. Extragalactic foregrounds are localized at small angular scales, with emission laws changing significantly from one object to another. Consequently, using a reconstruction localized both in space and frequency allows us to improve the ILC performance, by adapting the weights w to the local background. This point has intensively been discussed in the literature (see e.g. Basak & Delabrouille 2012; Bobin et al. 2013).
We choose here to filter the observations with
Nk filters in spherical harmonic space.
These filters are built from the difference between two Gaussian filters of the form
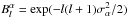 such that
such that
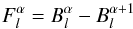 (28)where
(28)where
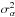 increases
with α. We also impose
increases
with α. We also impose 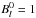 and
and
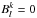 , in
order that the condition
, in
order that the condition 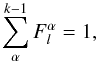 (29)is satisfied.
(29)is satisfied.
After filtering the observation channel maps, the weights w
are computed locally in predefined pixel regions. To ease the procedure these regions have
been built using the properties of the HEALPix pixelization NESTED
scheme (Górski et al. 2005). For each filter, these
regions are defined by HEALPix pixels at a given resolution
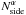 such that the size
of the pixel is 20 times greater than σα + 1
and
such that the size
of the pixel is 20 times greater than σα + 1
and 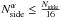 , where
Nside is the native resolution of observation channel maps.
, where
Nside is the native resolution of observation channel maps.
In order to ensure the continuity of the weights, w, at the
interface between two contiguous pixel regions at the resolution
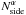 , the map of weights
at the native resolution Nside are convolved with a Gaussian
beam with a FWHM equal to the size of the HEALPix pixel at the
resolution
, the map of weights
at the native resolution Nside are convolved with a Gaussian
beam with a FWHM equal to the size of the HEALPix pixel at the
resolution 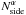 .
.
5.2. External template regularization of the ILC solution
In the following, we consider the possibility of using external templates to minimize the contribution of “unwanted” components, particularly those for which the electromagnetic spectrum is poorly known. For example, point-like sources and compact objects have varying electromagnetic spectra and therefore are difficult to handle with the standard ILC algorithm.
One of the main advantages of ILC methods is to only use information from a single
experiment in the linear combination. We present here an approach allowing us to use
external priors for the computation of the weights w but not
using the external templates themselves in the linear combination. To do so, we modify the
data covariance matrix 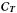 to include an extra term. Given “unwanted” astrophysical components, we first compute
their expected contribution to the data covariance matrix and then we exacerbate this
contribution to force the ILC algorithm to minimize them in the final estimate of
to include an extra term. Given “unwanted” astrophysical components, we first compute
their expected contribution to the data covariance matrix and then we exacerbate this
contribution to force the ILC algorithm to minimize them in the final estimate of
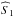 .
In practice, we write
.
In practice, we write 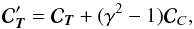 (30)where
(30)where
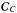 is a Nobs × Nobs dimension
matrix containing the contribution of the “unwanted” astrophysical components to the data
covariance matrix as estimated from external templates of these components. The
multiplicative factor γ takes only values higher than one and is adapted
depending on the accuracy of the estimated
is a Nobs × Nobs dimension
matrix containing the contribution of the “unwanted” astrophysical components to the data
covariance matrix as estimated from external templates of these components. The
multiplicative factor γ takes only values higher than one and is adapted
depending on the accuracy of the estimated 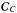 .
Writing
.
Writing 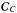 as
as 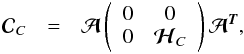 (31)we
can derive the following expression for the residuals
(31)we
can derive the following expression for the residuals ![\begin{eqnarray} R_{1} &= &\eb^{\Tb} \left[ \tilde{\Nb'}\! - ({\boldsymbol{\cal{G}}}_0 + {\boldsymbol{\cal{G}}}_N) \left({\boldsymbol{\cal{H}}}_0 + (\gamma^2\!-\!1){\boldsymbol{\cal{H}}}_C \!+\! {\boldsymbol{\cal{H}}}_N\right)^{-1} (\Sb'' \!+\! \tilde \Nb'') \right] \nonumber \\ &= &\eb^{\Tb} \left[ \tilde{\Nb'} - ({\boldsymbol{\cal{G}}}_0 + {\boldsymbol{\cal{G}}}_N) \left({\boldsymbol{\cal{H}}}_0' + {\boldsymbol{\cal{H}}}_N\right)^{-1} (\Sb'' + \tilde \Nb'') \right]. \label{biaswithnoise2} \end{eqnarray}](/articles/aa/full_html/2013/10/aa21891-13/aa21891-13-eq141.png) (32)As
we are not constraining all astrophysical components, the
ℋC matrix is in general singular.
Consequently, this matrix only modifies a sub-space of ℋ0.
(32)As
we are not constraining all astrophysical components, the
ℋC matrix is in general singular.
Consequently, this matrix only modifies a sub-space of ℋ0.
In Sect. 6.2, we present a practical application of this technique in order to reduce the CIB contamination in the reconstructed tSZ map. We observe that it leads to a reduction of the bias in the residuals proportional to the factor ≃γ2, but also to an increase in the noise.
5.3. Reducing the noise-induced bias
As discussed in Sect. 4.2, instrumental noise
produces a bias in the estimate of S1. To remove this bias,
Vio & Andreani (2008) proposed an
unbiased estimator that can be obtained by modifying the data covariance matrix as follows
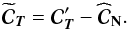 (33)If
the direct subtraction of the noise in T is not possible,
the estimation of the noise covariance matrix
(33)If
the direct subtraction of the noise in T is not possible,
the estimation of the noise covariance matrix 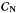 is possible. The estimate of the data covariance matrix in Eq. (33)allows us to obtain an estimate of
S1 equivalent to the one for the noiseless case, as
presented in Sect. 4.1. Consequently,
is possible. The estimate of the data covariance matrix in Eq. (33)allows us to obtain an estimate of
S1 equivalent to the one for the noiseless case, as
presented in Sect. 4.1. Consequently,
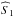 is only biased by the correlation between the “wanted”, S1,
and the other components. Indeed, we obtain the following expression for the residual
is only biased by the correlation between the “wanted”, S1,
and the other components. Indeed, we obtain the following expression for the residual
![\begin{equation} R_{1} = \widehat S_{\mathrm{1}} - S_{\mathrm{1}} = \eb^{\Tb} \left[ \tilde \Nb' - {\boldsymbol{\cal{G}}}_{0} {{\boldsymbol{\cal{H}}}'}_{0}^{-1} (\Sb''+\tilde \Nb'')\right]. \label{restilt} \end{equation}](/articles/aa/full_html/2013/10/aa21891-13/aa21891-13-eq147.png) (34)The excess of bias
introduced by the noise covariance matrix has been suppressed.
(34)The excess of bias
introduced by the noise covariance matrix has been suppressed.
However in this situation, we do no longer minimize the contribution of the noise to the
data covariance matrix 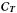 .
Furthermore, the
.
Furthermore, the 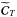 matrix is singular for
the case
Ns < Nobs.
This can lead to a significant increase in the instrumental noise on
S1. To balance this effect and minimize the noise
contribution, we add a regularization term to the ILC algorithm. We use the remaining
Nobs − Ns degrees of freedom in
the definition of the pseudo inverse for the
matrix is singular for
the case
Ns < Nobs.
This can lead to a significant increase in the instrumental noise on
S1. To balance this effect and minimize the noise
contribution, we add a regularization term to the ILC algorithm. We use the remaining
Nobs − Ns degrees of freedom in
the definition of the pseudo inverse for the 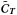 matrix.
matrix.
We start by clearly identifying the subspaces of 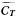 that are constrained by the ILC constraints and the variance minimization respectively.
The ILC constraints act on a Nrc + 1 dimension subspace, then
the minimization of the variance act on a
Ns − Nrc − 1 dimension subspace.
We still have an Nobs − Ns
dimension subspace to minimize the instrumental noise contribution.
that are constrained by the ILC constraints and the variance minimization respectively.
The ILC constraints act on a Nrc + 1 dimension subspace, then
the minimization of the variance act on a
Ns − Nrc − 1 dimension subspace.
We still have an Nobs − Ns
dimension subspace to minimize the instrumental noise contribution.
5.3.1. Constrained-components subspace
In order to isolate the subspace associated with the ILC constraints, we propose to
perform a transformation of the form 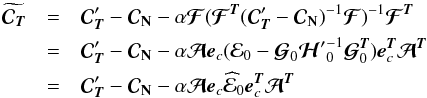 (35)with
α the fraction of variance from the constrained components to be
subtracted. For α = 1 the
(35)with
α the fraction of variance from the constrained components to be
subtracted. For α = 1 the 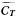 matrix has a rank Ns − Nrc − 1,
the
matrix has a rank Ns − Nrc − 1,
the 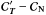 matrix having
a rank Ns. We subtract
matrix having
a rank Ns. We subtract
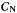 because we want to consider the variance of the astrophysical signal without noise.
because we want to consider the variance of the astrophysical signal without noise.
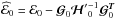 is the estimate of the covariance matrix of the constrained components for the standard
ILC algorithm. We observe the contribution of the intrinsic bias term
is the estimate of the covariance matrix of the constrained components for the standard
ILC algorithm. We observe the contribution of the intrinsic bias term
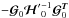 .
Indeed, the variance of the reconstructed component reads as
.
Indeed, the variance of the reconstructed component reads as
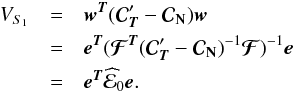 (36)Writing
the data covariance matrix as
(36)Writing
the data covariance matrix as 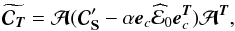 (37)and we derive
(37)and we derive
![\begin{eqnarray} \widehat S_{\mathrm{1}} = \eb^{\Tb} \left[ {\eb}_{\cb}^{\Tb} ({\Cb}_{\Sb}' - \alpha \eb_{c} \widehat {\cal{E}}_0 \eb_{c}^{\Tb})^{-1} {\eb}_{\cb} \right]^{-1}&& \nonumber\\ &&\times{\eb}_{\cb}^{\Tb}({\Cb}_{\Sb}'- \alpha \eb_{c}\widehat {\cal{E}}_0 \eb_{c}^{\Tb})^{-1}(\Sb + {\Ab}^{-1}\Nb), \end{eqnarray}](/articles/aa/full_html/2013/10/aa21891-13/aa21891-13-eq159.png) (38)the
(38)the
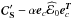 matrix can be rewritten in the following form
matrix can be rewritten in the following form
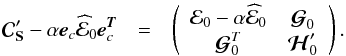 (39)Consequently,
the residual, R1, in Eq. (34)does not depend on ℰ0 and consequently do not depend
on the parameter α.
(39)Consequently,
the residual, R1, in Eq. (34)does not depend on ℰ0 and consequently do not depend
on the parameter α.
Indeed, the ℰ0 sub-space is constrained, its modification will not produce
any modification on 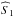 .
We can deduce that the weights w are invariant under this
transformation. So we select the value α = 1 for which
.
We can deduce that the weights w are invariant under this
transformation. So we select the value α = 1 for which
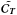 becomes Nrc + 1 singular.
becomes Nrc + 1 singular.
To estimate the value of
Ns − Nrc − 1 components, we
compute the number of eigenvalues of the 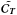 matrix which are significantly greater than 0. It is important to note that we also have
an estimate of Nobs − Ns giving
the remaining degrees of freedom that can be used to reduce the noise contribution in
matrix which are significantly greater than 0. It is important to note that we also have
an estimate of Nobs − Ns giving
the remaining degrees of freedom that can be used to reduce the noise contribution in
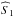 .
In the case
Ns < Nobs,
the pseudo inverse of
.
In the case
Ns < Nobs,
the pseudo inverse of 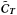 is
defined with Nobs − Ns degrees
of freedom as explained in the Sect. 4.2.
is
defined with Nobs − Ns degrees
of freedom as explained in the Sect. 4.2.
5.3.2. Minimizing the noise variance
To reduce the noise contribution in the final estimate of
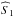 ,
we also minimize simultaneously the variance of the noise term
,
we also minimize simultaneously the variance of the noise term 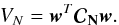 (40)This
can be performed by modifying the lowest eigenvalues of the
(40)This
can be performed by modifying the lowest eigenvalues of the
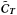 matrix,
assuming that they are not associated to astrophysical emissions. We search for the
value of the eigenvalues Dj of
matrix,
assuming that they are not associated to astrophysical emissions. We search for the
value of the eigenvalues Dj of
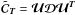 that
minimize VN. The minimization is performed
numerically and iteratively. It is important to notice that
VN might have several extrema.
Consequently, we use the first and second derivative of the variance to find the minimum
of VN.
that
minimize VN. The minimization is performed
numerically and iteratively. It is important to notice that
VN might have several extrema.
Consequently, we use the first and second derivative of the variance to find the minimum
of VN.
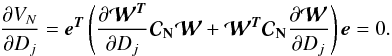 (41)The derivative of
the weight matrix
(41)The derivative of
the weight matrix 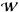 can be written as
can be written as ![\begin{equation} \frac{\partial^k {{\boldsymbol{\cal W}}}}{\partial D_{j}^k} = D_{j}^{-k} \left[ \left({{\boldsymbol{\cal W}}} {{\boldsymbol{\cal F}}}^{\Tb} - {\cal{I}} \right) \Ub {\cal{J}} \Ub^{\Tb} \right]^{k} {{\boldsymbol{\cal W}}}, \end{equation}](/articles/aa/full_html/2013/10/aa21891-13/aa21891-13-eq174.png) (42)with
(42)with
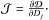
5.4. Uncertainty estimation and propagation
As the MILCA procedure is fully linear, it is possible to propagate analytically the statistical uncertainties induced by the instrumental noise. However, we use spatial and harmonic filters that are correlated (see Sect. 5.1). Consequently, the propagation of uncertainties is possible, but very costly. In the most generic case dealing with inhomogeneous correlated noise, noise propagation can be performed using Monte-Carlo simulations (see e.g. Planck Collaboration 2013b, for a description of such a procedure).
The estimation of foreground contamination is possible if we have templates and estimates of the SEDs. In this case, it is possible to propagate the template trough the same linear combination than the one applied to the data to provide an estimation of the contamination. Such approach has been used to estimate the contamination of the thermal dust, the CIB and point sources in the Planck Compton-y parameter maps in Planck Collaboration (2013l).
We stress that one of the advantages of using a linear combination approach is to be able to easily estimate uncertainties and biases in the reconstructed signal.
5.5. Summary of the main MILCA steps
The main steps of MILCA are the following:
-
(1)
Filter the original data to ensure space and frequencylocalization.
-
(2)
Use the Nrc + 1 constraints on the spectral emission laws of the known components.
-
(3)
Subtract the instrumental noise contribution to the covariance matrix.
-
(4)
Minimize of the variance of S1 in the sub-space associated to the Ns − Nrc − 1 non-constrained astrophysical components.
-
(5)
Use the extra Nobs − Ns degrees of freedom to reduce the instrumental noise contribution.
The final MILCA estimate of the “wanted” component reads as
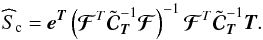 (43)For the case
Nrc + 1 = Ns, MILCA provides the
same result as a maximum likelihood approach
(43)For the case
Nrc + 1 = Ns, MILCA provides the
same result as a maximum likelihood approach 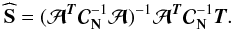 (44)The
w vector cannot be constrained using the minimization of
the variance of components. The last
Nobs − Ns degrees of freedom are
constrained by the minimization of the instrumental noise, as it is the case for a maximum
likelihood method.
(44)The
w vector cannot be constrained using the minimization of
the variance of components. The last
Nobs − Ns degrees of freedom are
constrained by the minimization of the instrumental noise, as it is the case for a maximum
likelihood method.
6. tSZ reconstruction with MILCA
We present here an application of the MILCA algorithm to the reconstruction of the tSZ effect. We first focus on the two main MILCA improvements to the ILC algorithm presented in Sect. 5. Then, we consider the extraction of a full-sky tSZ map using the Planck full-sky simulations presented in Sect. 2. We consider two constrained components, tSZ and CMB. Two degrees of freedom are used to minimize the variance of the unconstrained components and the remaining two are used to minimize the variance of the noise. The extraction of the tSZ effect has been performed at an effective resolution of 10 arcmin.
6.1. Noise variance minimization
As discussed in Sect. 5.3.2, it is possible to
reduce the noise contamination in the reconstructed map by modifying the lowest
eigenvalues, Dj, of
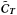 to
minimize VN. For illustration purposes, we
concentrate here on the lowest eigenvalue,
Dj, of
to
minimize VN. For illustration purposes, we
concentrate here on the lowest eigenvalue,
Dj, of
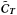 on
VN, that we vary over five orders of
magnitudes with respect to its original value. For each of these values, we compute the
noise level in the reconstructed tSZ y-map that is shown as a solid black
line in Fig. 2. In this case, the original value for
the lowest eigenvalue of
on
VN, that we vary over five orders of
magnitudes with respect to its original value. For each of these values, we compute the
noise level in the reconstructed tSZ y-map that is shown as a solid black
line in Fig. 2. In this case, the original value for
the lowest eigenvalue of 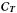 (vertical red line in Fig.2) leads to ten times
larger noise level than the optimal solution that minimize the noise variance.
(vertical red line in Fig.2) leads to ten times
larger noise level than the optimal solution that minimize the noise variance.
 |
Fig. 2 Variation of the noise level in the reconstructed y-map as a function of the value of the modified eigenvalue in the data covariance matrix. The black line shows the noise level in the y-map, the red vertical line indicates the original value of the eigenvalue before modification. |
Furthermore, for low values of Dj an
increase in the level of noise is observed since in this case
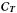 nearly singular. This produces high absolute values for w,
and thus a higher rms noise residual (computed following Eq. (40)). For high
Dj, we converge to a rank-reduction for
nearly singular. This produces high absolute values for w,
and thus a higher rms noise residual (computed following Eq. (40)). For high
Dj, we converge to a rank-reduction for
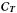 (Dj approaches ∞), and this solution leads
to a level of noise two times higher than the optimal MILCA solution.
(Dj approaches ∞), and this solution leads
to a level of noise two times higher than the optimal MILCA solution.
6.2. Minimization of the clustered CIB contamination using prior information
We discuss now how we can use MILCA to reduce the clustered CIB contamination in the reconstructed tSZ map. Reducing clustered CIB contamination is a major issue for tSZ analysis, because the CIB is, on the one hand, correlated with the tSZ emission (Addison et al. 2012) and on the other hand, it is a diffuse emission that cannot be masked in tSZ maps.
The clustered CIB component cannot be described with a single template and an SED; furthermore, it is only partially correlated from one frequency to another (Planck Collaboration 2011f). Indeed, the CIB is produced by the IR emission from extragalactic sources at different redshifts and their observed emission law is highly dependent on the redshift. Consequently, different frequency bands are not sensitive to the same sources, according to their redshifts.
We thus cannot apply constraints on the SED, in the ℱ matrix, in order to reduce the clustered CIB contamination. By contrast, we can use the approach proposed in Sect. 5.2 by modifying the data covariance matrix. The covariance matrix of the clustered CIB emission needs to account for the CIB SED and for partial correlation between frequencies and it can be inferred from models or from the data themselves.
In Fig. 3, we present the variation of the clustered CIB contamination and the reconstructed tSZ map noise level as a function of the parameter γ in Eq. (30). γ < 1 corresponds to the case where we do not account for the clustered CIB and it leads to strong clustered CIB contamination. As expected, the CIB contamination decreases with as γ increases. However, as the clustered CIB contamination decreases the noise level increases. A compromise between noise and clustered CIB contamination can be found for γ in the range between 3 and 30, with an optimal result for γ = 17, as we observe that the noise level is almost constant in this range and the clustered CIB contamination decreases with a slope ≃ γ2. It is important to notice that for γ = 1, the clustered CIB contamination is already reduced by one order of magnitude in variance with respect to the standard ILC algorithm. On the real data such a compromise can also be found using estimates of both the noise and clustered CIB covariance matrices. At high values of γ, we observe that the clustered CIB contamination becomes constant. This behavior is produced by the partial correlation of the clusterd CIB across frequencies. Indeed, as the CIB emission is not fully correlated between frequencies; it can not be totally removed.
6.3. Characterization of noise level and bias on fullsky simulations
We present in Fig. 4 the reconstructed tSZ map and the residual map in a small patch of 200 by 200 arcmin centered on the well-known pair of clusters A399-A401 (Planck Collaboration 2013e). This example illustrates the ability of MILCA to properly deal with complex tSZ systems like mergers.
 |
Fig. 3 Evolution of the clustered CIB contamination (black stars) and the noise level (red diamonds) as a function of γ. Both contributions (clustered CIB and noise) are presented in units of variance in the reconstructed tSZ Compton-y parameter map. |
 |
Fig. 4 Left panel: reconstruction of a tSZ y-map from simulated Planck data using the MILCA approach. Right panel: residual map after subtraction of the input tSZ signal. |
 |
Fig. 5 Top: histograms for the MILCA tSZ map (black), for the tSZ input map (red), for the noise (green) and the contamination by other components (in blue). Bottom: histograms for the residuals emission (black), for the noise (red), for the contamination by all other components (blue) and for the CIB component contribution (green). |
In a more quantitative way, we present in Fig. 5 the histogram of the reconstructed MILCA tSZ map for all pixels located inside a radius of 15 arcmin from the 1743 clusters of the MCXC catalog (Piffaretti et al. 2011). In the top panel, we present the main contributions to the reconstructed tSZ map: tSZ emission (black), noise (green), and other astrophysical components (blue). For comparison, we also plot the input tSZ signal (red). We observe that the reconstructed tSZ map is dominated by the tSZ signal. In the bottom panel, we represent the histogram of the residual map (same color scheme as before). The residual map is dominated by instrumental noise which contributes to the residual rms at a level of 1.7 × 10-6 (Compton parameter units), then, the CIB contributes to a level of 0.7 × 10-6, and all other components have a total contribution of about 1.0 × 10-6.
Notice in Fig. 5 that most of the residuals by other astrophysical components (in blue) appear as a negative bias, they are mainly produced by radio sources. Indeed, by contrast to the tSZ effect, which increases with frequency, radio source emission decreases with frequency. Consequently, when extracting the tSZ signal, radio emission generally appears as negative signal.
An extreme case of such a bias is discussed in Sect. 6.4. We also observe weak contamination by IR point sources which appear as positive bias in the reconstructed map. Other astrophysical emissions marginally contribute to the reconstructed signal.
An example of the application of MILCA to real Planck data is presented in Sect. 6.5.
6.4. Empirical extra constraints for tSZ extraction
We present an application of MILCA to an extreme case of radio-loud AGN contamination for a simulated Perseus-like cluster. This particular cluster is well known to be very extended over the sky and to host a radio-loud AGN (Brunzendorf & Meusinger 1999). The AGN emission makes the extraction of the tSZ signal for such kind of systems quite complex. However, as the tSZ signal is extended, it is possible to separate the two emissions (from the cluster and from the AGN).
 |
Fig. 6 Reconstructed y-map (top) and residuals (bottom) for the Planck simulated data using a standard ILC adapted to the tSZ effect (left panel) and using MILCA with three constrained components (right panel). |
Figure 6 presents the comparison between the tSZ y-maps (top) and residuals obtained from a standard ILC adapted to the tSZ effect (left panel) and MILCA (right panel) using three constraints to keep the tSZ signal but removing the CMB and the central radio-loud AGN contamination. We use an estimate of the AGN SED obtained directly from the data themselves. For the standard ILC case, we observe a strong contamination by the AGN emission (with an amplitude of −9 × 10-5 in Compton parameter units at the center of the AGN). In this case, the tSZ effect and the AGN radio emission are strongly spatially correlated over the sky. This leads to the bias discussed in Sect. 4.1, when a correlated component is used to clean the tSZ effect contribution. When considering an extra constraint, we are able to recover the tSZ signal with a much weaker bias from the AGN (an amplitude of about −0.5 × 10-6). This extra constraint presents however some drawbacks, such as an increase in the noise level (in this case by a factor of 1.5) and/or stronger bias from other astrophysical un-constrained components.
The ability of MILCA to reduce such contamination is directly related to the accuracy of
the estimated SED used for the extra constraint. In order to quantify this, we performed
simulations of the reconstruction but with an extra constraint applied on a noisy SED for
the AGN 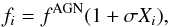 (45)where
fAGN is the AGN simulated SED,
Xi is a random variable following a
standard normal distribution and σ is the relative error on the AGN SED.
We performed 200 simulations of reconstruction for a grid of 100 values of
σ.
(45)where
fAGN is the AGN simulated SED,
Xi is a random variable following a
standard normal distribution and σ is the relative error on the AGN SED.
We performed 200 simulations of reconstruction for a grid of 100 values of
σ.
 |
Fig. 7 Top panel: bias induced in the MILCA reconstruction when using a noisy SED as extra constraint. Black points are the mean from the 200 simulations for each value of the relative error, the red line represents the best-fit for the bias term and the blue line is the expected value in an unbiased case. Bottom panel: extra noise induced in the MILCA reconstruction when using a noisy SED as extra constraint. Black points are computed from the 200 simulation for each value of the relative error and the red line represents the best-fit for the noise term. The contamination are presented in units of Compton parameter for the central pixel of the reconstructed map for which we expect the maximum contamination. |
A global bias is computed by averaging the 200 reconstructions and the noise rms is obtained from the standard deviation of the 200 reconstructions. Figure 7 shows the bias and the extra noise induced on the reconstruction by a noisy SED. The bias is proportional to the square of the relative error, σ, while the extra noise is directly proportional to σ. This relation allows us to propagate both bias and noise from the used SED to the final reconstructed map. We stress that the calibration of this relation depends on both the AGN amplitude and the local background of the cluster. Consequently, such estimation of the noise and bias induced by a noisy SED have to be computed for each specific case.
 |
Fig. 8 From left to right: tSZ reconstructed y-map with MILCA from Planck public data, with a tSZ effect adapted standard ILC and the difference between the 2 reconstructions. Each row represents the reconstructions for a particular cluster in a FOV of 4 × R500, with the dashed circle representing the R500 aperture. For each cluster the three maps are displayed with the same color scale. All maps are presented at a resolution of 7.18’ FWHM except the Virgo maps at 30’ FWHM. |
6.5. Extraction of the tSZ effect with MILCA on real data
For illustration in Fig. 8, we present tSZ effect reconstructed MILCA (left) maps using the Planck public data for very extended clusters over the sky (see also Planck Collaboration 2013m). We also present the comparison with a standard ILC reconstruction (middle). These figures illustrate the improvement provided by MILCA for the reconstruction of tSZ y-maps, not only on simulations, but also on real datasets.
For some clusters, such as A2199, Ophiucus, and A3627, MILCA and a standard ILC adapted to tSZ extraction produce very similar results. Indeed, for these clusters the foreground contamination is low and not correlated with the tSZ component.
However in the case of AGN contaminated clusters, such as Perseus and Virgo, we observe a clear contamination in the standard ILC maps that is significantly reduced in the MILCA maps. For the Perseus galaxy cluster, we observe similar results than the ones obtained on simulated datasets in Sect. 6.4. The use of an extra constraint allows MILCA to reduce the contamination by radio-loud AGNs, which are correlated to the tSZ effect in the cluster.
For the 3C 129.1 cluster, we observe in the standard ILC map, a strong contamination around the tSZ emission. This contamination is mainly produced by thermal dust residuals. This cluster is located in the Galactic plane. Consequently, there is a strong contamination by dust in this area. However, the MILCA maps are less contaminated by the thermal dust emission. This reduction of the contamination by thermal dust is mainly due to the correction of the noise-induced bias.
Finally for A0496, we observe a reduction of the contamination in MILCA map but we still observe contamination by an IR point source. This IR point source is very faint with respect to the thermal dust background. Consequently, it is difficult to extract the SED of this source, reducing the ability of MILCA to minimize the source contamination in the reconstructed tSZ map.
 |
Fig. 9 Reconstructed CO emission map (top) and residuals (bottom) for the CO-adapted ILC algorithm (left) and for MILCA (right). The maps are presented at a resolution of 30 arcmin to reduce the noise contribution in the maps. |
7. CO emission reconstruction using the Planck bolometer maps
We present an original application of MILCA for reconstruction of CO emission maps for the first three CO transitions J = 1–0, J = 2–1, and J = 3–2 using the spectral mismatch between the bolometers within a single Planck channel as discussed in Planck Collaboration (2013h). We discuss here the methodology and performance of the algorithm using the simulations of the Planck 100 GHz channel presented in Sect. 2. We consider four intensity maps constructed by combining the maps of two bolometers for each of the 4 PSB pairs.
Assuming bolometer maps are calibrated in CMB temperature units we can compute the bandpass mismatch for different astrophysical signals. For CMB, we expect no bandpass mismatch within the calibration uncertainties (below 1%). For other astrophysical components with a continuous emission spectrum, the variation of transmission in the different bolometers is very small (about 1% at 100 GHz). However, for molecular line associated emission, such as CO, the transmission variations from one bolometer to another can reach up to 20% (Planck Collaboration 2013h). We use this variation of transmission among bolometers to produce CO maps using MILCA. Formally speaking, bandpass mismatch can be accounted for by assuming a bolometer dependent mixing matrix (rather than one depending on observation frequency) and then component separation algorithms can be applied. However, there are several problems with this approach. First, spectral bandpass mismatch is very sensitive to the SED of the astrophysical component and it might be difficult to estimate for those astrophysical components for which the SED vary spatially. Second, the signal-to-noise ratio is low with respect to conventional problems based on channel maps. MILCA is well-adapted for this particular problem as it allows us on the one hand to only use the bandpass mismatch for those components for which is well known (mainly CMB and the “wanted” component) and on the other hand to minimize the noise contribution in the final recovered map.
We performed 10 000 simulations of the Planck bolometer maps using different simulated bandpasses based on the CO unit conversion coefficients values and uncertainties presented in Planck Collaboration (2013h). Figure 9 shows the comparison between the reconstructed CO emission at 100 GHz for an ILC algorithm spectrally adapted to CO (left) and for MILCA (right) for one these simulations. The top panel shows the reconstructed CO map and the bottom panel the residuals in K km s-1 units. We observe that the CO emission is well reconstructed with MILCA but in the inner Galactic plane where we observe some residual contamination. However, the ILC reconstructed map shows strong contamination by the CMB and the Galactic diffuse emission, and a higher noise level. In Table 1, we summarize the contamination in terms of contribution to the variance of the CO reconstructed map for MILCA and for the CO adapted ILC. We notice that MILCA allows us to produce CO maps with a level of contamination 5 times lower than a CO adapted ILC. At a resolution of 10 arcmin, the residual of the MILCA reconstructed CO map is dominated by the noise contribution, 6.06 K km s-1, other components contribute only for 0.31 K km s-1. For comparison, in the ILC CO map the noise contribution is about 7.55 K km s-1, and the contamination by other components reaches 5.53 K km s-1. We also notice that in the case of a MILCA reconstruction at 30 arcmin FWHM, the standard deviation of the map (9.35 K km s-1) is completely dominated by the CO emission (9.11 K km s-1) indicating the high level of purity of the map. For the ILC CO reconstructed map the standard deviation of the total map is 5.94 K km s-1, which is below the CO only contribution (9.11 K km s-1). This illustrates the strong bias in the ILC map for which the thermal dust emission is used to remove CO emission and then to reduce the total variance of the map.
Figure 10 presents the contamination level in the CO map for the 10 000 simulations for the ILC and the MILCA reconstructions. We represent on these figures the contamination by the CMB, the thermal dust + CIB, the tSZ effect and the synchrotron + free-free + radio point sources and by the noise.
For CMB, the contamination in MILCA map is equal to zero at the calibration uncertainties level, but in the ILC map we observe a strong contamination by the CMB, which amounts to 2.5 K km s-1 in average in terms of the standard deviation. This contamination is mainly due to the correlation between the CO emission and the thermal dust emission. Indeed, thermal dust emission has a continuous emission law over frequency, and has thus almost the same spectral response than the CMB in the difference bolometers. Consequently, we observe similar residuals for all contaminating astrophysical emission.
Contribution to the total standard deviation of the reconstructed CO emission map in units of K km s-1.
 |
Fig. 10 From left to right and top to bottom: contamination by other components in CO reconstruction for 10 000 simulations for CMB, tSZ, Dust + CIB, Synchrotron + Free-Free + Radio point sources, and Noise respectively. In black for a standard CO-adapted ILC and in red for MILCA. Each contamination are presented in terms of standard deviation in units of K km s-1. |
8. Conclusion
Component separation techniques are now a major ingredient in the scientific exploitation of multichannel and multicomponent datasets such as those of the CMB satellite experiments WMAP and Planck.
In this paper, we have presented the modified internal linear algorithm (MILCA) specially developed for the Planck data. MILCA generalizes the standard ILC algorithm, generally devoted to CMB emission extraction, to any astrophysical component with a known emission law. In practice, MILCA can be used to extract an arbitrary number of astrophysical emissions rejecting the contribution from others for which the emission law is also known. MILCA has been optimized in various ways in order to reduce significantly residuals from instrumental noise and other astrophysical components. For this purpose the separation is performed both in real and Fourier spaces. Moreover the data covariance matrix is modified and divided into multiple subspaces in order to avoid the confusion between instrumental noise and astrophysical components in the original data. Finally, we have also introduced the possibility of using external templates to improve the efficiency of the algorithm. Thanks to these improvements MILCA has been proved to be more efficient than standard ILC algorithms in a wide range of astrophysical problems. We have also demonstrate the efficiency of our modifications on the ILC estimator to reduce the instrumental noise and the “unwanted” astrophysical components.
We have applied MILCA to simulated Planck data, and have shown that it can be used to efficiently reconstruct the tSZ and CO emissions. We have proposed, with MILCA, an original way to used prior on the spatial distribution of contaminating components. Allowing to constraint emissions such as CIB, which can not be described with a single template and an SED.
In the tSZ case we have shown that MILCA can be used to reconstruct low signal-to-noise and highly non-Gaussian components in the Planck data. Indeed, MILCA has been used extensively by the Planck collaboration for tSZ and CO studies. For CO emission, we have presented a new component separation approach that takes advantage of the spectral bandpass mismatch between bolometers of the same Planck channel.
Acknowledgments
We thank Nabila Aghanim and François-Xavier Désert for useful discussions related to this work. We acknowledge the referee for useful comments that have improved the quality of the paper. Some of the results in this paper have been derived using the HEALPix package (Górski et al. 2005).
References
- Addison, G. E., Dunkley, J., & Spergel, D. N. 2012, MNRAS, 427, 1741 [NASA ADS] [CrossRef] [Google Scholar]
- Arnaud, M., Pratt, G. W., Piffaretti, R., et al. 2010, A&A, 517, A92 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Aumont, J., & Macías-Pérez, J.-F. 2007, MNRAS, 376, 739 [NASA ADS] [CrossRef] [Google Scholar]
- Basak, S., & Delabrouille, J. 2012, MNRAS, 419, 1163 [NASA ADS] [CrossRef] [Google Scholar]
- Bennett, C. L., Banday, A. J., Gorski, K. M., et al. 1996, ApJ, 464, L1 [NASA ADS] [CrossRef] [Google Scholar]
- Bennett, C. L., Halpern, M., Hinshaw, G., et al. 2003, ApJS, 148, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Bersanelli, M., Mandolesi, N., Butler, R. C., et al. 2010, A&A, 520, A4 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bobin, J., Moudden, Y., Starck, J.-L., Fadili, J., & Aghanim, N. 2008, Stat. Methodol., 5, 307 [NASA ADS] [CrossRef] [Google Scholar]
- Bobin, J., Starck, J.-L., Sureau, F., & Basak, S. 2013, A&A, 550, A73 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bonaldi, A., Bedini, L., Salerno, A., Baccigalupi, C., & de Zotti. 2006, MNRAS, 373, 271 [NASA ADS] [CrossRef] [Google Scholar]
- Brunzendorf, J., & Meusinger, H. 1999, A&AS, 139, 141 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Cardoso, J.-F., Le Jeune, M., Delabrouille, J., Betoule, M., & Patanchon, G. 2008, IEEE J. Select. Top. Signal Proc., 2, 735 [NASA ADS] [CrossRef] [Google Scholar]
- Condon, J. J., Cotton, W. D., Greisen, E. W., et al. 1998, AJ, 115, 1693 [NASA ADS] [CrossRef] [Google Scholar]
- Dame, T. M., Hartmann, D., & Thaddeus, P. 2001, ApJ, 547, 792 [NASA ADS] [CrossRef] [Google Scholar]
- Davies, R. D., Watson, R. A., & Gutierrez, C. M. 1996, MNRAS, 278, 925 [NASA ADS] [CrossRef] [Google Scholar]
- Delabrouille, J., Cardoso, J.-F., & Patanchon, G. 2003, MNRAS, 346, 1089 [NASA ADS] [CrossRef] [Google Scholar]
- Delabrouille, J., Betoule, M., Melin, J.-B., et al. 2013, A&A, 553, A96 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Desert, F.-X., Boulanger, F., & Puget, J. L. 1990, A&A, 237, 215 [NASA ADS] [Google Scholar]
- Dick, J., Remazeilles, M., & Delabrouille, J. 2010, MNRAS, 401, 1602 [NASA ADS] [CrossRef] [Google Scholar]
- Dickinson, C., Davies, R. D., & Davis, R. J. 2003, MNRAS, 341, 369 [Google Scholar]
- Eriksen, H. K., Banday, A. J., Górski, K. M., & Lilje, P. B. 2004, ApJ, 612, 633 [NASA ADS] [CrossRef] [Google Scholar]
- Eriksen, H. K., Jewell, J. B., Dickinson, C., et al. 2008, ApJ, 676, 10 [NASA ADS] [CrossRef] [Google Scholar]
- Finkbeiner, D. P. 2003, ApJS, 146, 407 [NASA ADS] [CrossRef] [Google Scholar]
- Górski, K. M., Hivon, E., Banday, A. J., et al. 2005, ApJ, 622, 759 [NASA ADS] [CrossRef] [Google Scholar]
- Haslam, C. G. T., Klein, U., Salter, C. J., et al. 1981, A&A, 100, 209 [NASA ADS] [Google Scholar]
- Hinshaw, G., Spergel, D. N., Verde, L., et al. 2003, ApJS, 148, 135 [NASA ADS] [CrossRef] [Google Scholar]
- Hinshaw, G., Weiland, J. L., Hill, R. S., et al. 2009, ApJS, 180, 225 [NASA ADS] [CrossRef] [Google Scholar]
- Hobson, M. P., Jones, A. W., Lasenby, A. N., & Bouchet, F. R. 1998, MNRAS, 300, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Lacasa, F., Aghanim, N., Kunz, M., & Frommert, M. 2012, MNRAS, 421, 1982 [NASA ADS] [CrossRef] [Google Scholar]
- Lamarre, J., Puget, J., Ade, P. A. R., et al. 2010, A&A, 520, A9 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Maino, D., Farusi, A., Baccigalupi, C., et al. 2002, MNRAS, 334, 53 [NASA ADS] [CrossRef] [Google Scholar]
- Mennella, A., Butler, R. C., Curto, A., et al. 2011, A&A, 536, A3 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Miville-Deschênes, M.-A., & Lagache, G. 2005, ApJS, 157, 302 [NASA ADS] [CrossRef] [Google Scholar]
- Piffaretti, R., Arnaud, M., Pratt, G. W., Pointecouteau, E., & Melin, J.-B. 2011, A&A, 534, A109 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Planck Collaboration 2006 [arXiv:astro-ph/0604069] [Google Scholar]
- Planck Collaboration 2011a, A&A, 536, A1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Planck Collaboration 2011b, A&A, 536, A4 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Planck Collaboration 2011c, A&A, 536, A7 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Planck Collaboration 2011d, A&A, 536, A8 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Planck Collaboration 2011e, A&A, 536, A13 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Planck Collaboration 2011f, A&A, 536, A18 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Planck Collaboration 2011g, A&A, 536, A20 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Planck Collaboration 2011h, A&A, 536, A21 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Planck Collaboration 2011i, A&A, 536, A26 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Planck Collaboration 2013a, A&A, 550, A128 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Planck Collaboration 2013b, A&A, 550, A131 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Planck Collaboration 2013c, A&A, 550, A132 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Planck Collaboration 2013d, A&A, 550, A133 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Planck Collaboration 2013e, A&A, 550, A134 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Planck Collaboration 2013f, A&A, 554, A140 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Planck Collaboration 2013g, A&A, submitted [arXiv:1303.5062] [Google Scholar]
- Planck Collaboration 2013h, A&A, submitted [arXiv:1303.5073] [Google Scholar]
- Planck Collaboration 2013i, A&A, submitted [arXiv:1303.5074] [Google Scholar]
- Planck Collaboration 2013j, A&A, submitted [arXiv:1303.5075] [Google Scholar]
- Planck Collaboration 2013k, A&A, submitted [arXiv:1303.5076] [Google Scholar]
- Planck Collaboration 2013l, A&A, submitted [arXiv:1303.5081] [Google Scholar]
- Planck Collaboration 2013m, A&A, submitted [arXiv:1303.5089] [Google Scholar]
- Remazeilles, M., Delabrouille, J., & Cardoso, J.-F. 2011, MNRAS, 410, 2481 [NASA ADS] [CrossRef] [Google Scholar]
- Smoot, G. F., Bennett, C. L., Kogut, A., et al. 1992, ApJ, 396, L1 [NASA ADS] [CrossRef] [Google Scholar]
- Stolyarov, V., Hobson, M. P., Ashdown, M. A. J., & Lasenby, A. N. 2002, MNRAS, 336, 97 [NASA ADS] [CrossRef] [Google Scholar]
- Sunyaev, R. A., & Zeldovich, Y. B. 1972, Comments Astrophys. Space Phys., 4, 173 [NASA ADS] [EDP Sciences] [Google Scholar]
- Vio, R., & Andreani, P. 2008, A&A, 487, 775 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
All Tables
Contribution to the total standard deviation of the reconstructed CO emission map in units of K km s-1.
All Figures
 |
Fig. 1 Simulation of the submillimeter sky for, from left to right and top to bottom; 100, 143, 217, 353, 545, and 857 GHz Planck channels. See Sect. 2 for more details. |
| In the text | |
 |
Fig. 2 Variation of the noise level in the reconstructed y-map as a function of the value of the modified eigenvalue in the data covariance matrix. The black line shows the noise level in the y-map, the red vertical line indicates the original value of the eigenvalue before modification. |
| In the text | |
 |
Fig. 3 Evolution of the clustered CIB contamination (black stars) and the noise level (red diamonds) as a function of γ. Both contributions (clustered CIB and noise) are presented in units of variance in the reconstructed tSZ Compton-y parameter map. |
| In the text | |
 |
Fig. 4 Left panel: reconstruction of a tSZ y-map from simulated Planck data using the MILCA approach. Right panel: residual map after subtraction of the input tSZ signal. |
| In the text | |
 |
Fig. 5 Top: histograms for the MILCA tSZ map (black), for the tSZ input map (red), for the noise (green) and the contamination by other components (in blue). Bottom: histograms for the residuals emission (black), for the noise (red), for the contamination by all other components (blue) and for the CIB component contribution (green). |
| In the text | |
 |
Fig. 6 Reconstructed y-map (top) and residuals (bottom) for the Planck simulated data using a standard ILC adapted to the tSZ effect (left panel) and using MILCA with three constrained components (right panel). |
| In the text | |
 |
Fig. 7 Top panel: bias induced in the MILCA reconstruction when using a noisy SED as extra constraint. Black points are the mean from the 200 simulations for each value of the relative error, the red line represents the best-fit for the bias term and the blue line is the expected value in an unbiased case. Bottom panel: extra noise induced in the MILCA reconstruction when using a noisy SED as extra constraint. Black points are computed from the 200 simulation for each value of the relative error and the red line represents the best-fit for the noise term. The contamination are presented in units of Compton parameter for the central pixel of the reconstructed map for which we expect the maximum contamination. |
| In the text | |
 |
Fig. 8 From left to right: tSZ reconstructed y-map with MILCA from Planck public data, with a tSZ effect adapted standard ILC and the difference between the 2 reconstructions. Each row represents the reconstructions for a particular cluster in a FOV of 4 × R500, with the dashed circle representing the R500 aperture. For each cluster the three maps are displayed with the same color scale. All maps are presented at a resolution of 7.18’ FWHM except the Virgo maps at 30’ FWHM. |
| In the text | |
 |
Fig. 9 Reconstructed CO emission map (top) and residuals (bottom) for the CO-adapted ILC algorithm (left) and for MILCA (right). The maps are presented at a resolution of 30 arcmin to reduce the noise contribution in the maps. |
| In the text | |
 |
Fig. 10 From left to right and top to bottom: contamination by other components in CO reconstruction for 10 000 simulations for CMB, tSZ, Dust + CIB, Synchrotron + Free-Free + Radio point sources, and Noise respectively. In black for a standard CO-adapted ILC and in red for MILCA. Each contamination are presented in terms of standard deviation in units of K km s-1. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


