| Issue |
A&A
Volume 558, October 2013
|
|
|---|---|---|
| Article Number | A55 | |
| Number of page(s) | 13 | |
| Section | Planets and planetary systems | |
| DOI | https://doi.org/10.1051/0004-6361/201321663 | |
| Published online | 03 October 2013 | |
HATS-2b: A transiting extrasolar planet orbiting a K-type star showing starspot activity⋆
1
Max Planck Institute for Astronomy, Königstuhl 17, 69117
Heidelberg,
Germany
e-mail: mohler@mpia.de
2
Astrophysics Group, School of Physics, University of
Exeter, Stocker Road, EX4
4QL, Exeter,
UK
3 Exoplanetary Science at UNSW, School
of Physics, University of New South Wales, 2052, Australia
4
Australian Centre for Astrobiology, University of New South
Wales, 2052
Kensington,
Australia
5 Department of Astrophysical Sciences,
Princeton University, NJ
08544, USA
6
Harvard-Smithonian Center for Astrophysics,
Cambridge, MA, USA
7
Research School of Astronomy and Astrophysics, Australian National
University, 2611
Canberra,
Australia
8
Departamento de Astronomía y Astrofísica, Pontificia Universidad
Católica de Chile, Av. Vicuña
Mackenna 4860, 7820436 Macul, Santiago, Chile
9
Niels Bohr Institute, University of Copenhagen,
2100
Copenhagen,
Denmark
10
Centre for Star and Planet Formation, Natural History Museum of
Denmark, University of Copenhagen, 1350
Copenhagen,
Denmark
11
Hungarian Astronomical Association, 1158
Budapest,
Hungary
12
ELTE Gothard–Lendület Research Group, 9700
Szombathely,
Hungary
Received: 8 April 2013
Accepted: 26 June 2013
We report the discovery of HATS-2b, the second transiting extrasolar planet detected by the HATSouth survey. HATS-2b is moving on a circular orbit around a V = 13.6 mag, K-type dwarf star (GSC 6665-00236), at a separation of 0.0230 ± 0.0003 AU and with a period of 1.3541 days. The planetary parameters have been robustly determined using a simultaneous fit of the HATSouth, MPG/ESO 2.2 m/GROND, Faulkes Telescope South/Spectral transit photometry, and MPG/ESO 2.2 m/FEROS, Euler 1.2 m/CORALIE, AAT 3.9 m/CYCLOPS radial-velocity measurements. HATS-2b has a mass of 1.37 ± 0.16 MJ, a radius of 1.14 ± 0.03 RJ, and an equilibrium temperature of 1567 ± 30 K. The host star has a mass of 0.88 ± 0.04 M⊙ and a radius of 0.89 ± 0.02 R⊙, and it shows starspot activity. We characterized the stellar activity by analyzing two photometric follow-up transit light curves taken with the GROND instrument, both obtained simultaneously in four optical bands (covering the wavelength range of 3860−9520 Å). The two light curves contain anomalies compatible with starspots on the photosphere of the host star along the same transit chord.
Key words: planetary systems / techniques: spectroscopic / stars: fundamental parameters / techniques: photometric / stars: individual: HATS-2 / stars: individual: GSC 6665-00236
Tables of the individual photometric measurements are only available at the CDS via anonymous ftp to cdsarc.u-strasbg.fr (130.79.128.5) or via http://cdsarc.u-strasbg.fr/viz-bin/qcat?J/A+A/558/A55
© ESO, 2013
1. Introduction
The first detection of a planet orbiting a main-sequence star (51 Peg; Mayor & Queloz 1995) started a new era of astronomy and planetary sciences. In the years since, the focus on exoplanetary discovery has steadily increased, resulting in more than 850 planets being detected in 677 planetary systems1. Statistical implications of the exoplanet discoveries, based on different detection methods, have also been presented (e.g., Mayor et al. 2011; Howard et al. 2012; Cassan et al. 2012; Fressin et al. 2013). Most of these planets have been detected by transit and radial velocity (RV) techniques. The former detects the decrease in a host star’s brightness caused by the transit of a planet in front of it, while the latter measures the Doppler shift of host-star light due to stellar motion around the star-planet barycenter. In the case of transiting extrasolar planets, the powerful combination of both methods permits a direct estimate of the mass and radius of the planetary companion and therefore of the planetary average density and surface gravity. Such information is fundamental for establishing the correct theoretical framework of planet formation and evolution (e.g., Liu et al. 2011; Mordasini et al. 2012a,b).
Thanks to the effectiveness of ground- and space-based transit surveys like TrES (Alonso et al. 2004), XO (McCullough et al. 2005), HATNet (e.g. Bakos et al. 2012; Hartman et al. 2012), HATSouth (Penev et al. 2013), WASP (e.g., Hellier et al. 2012; Smalley et al. 2012), QES (Alsubai et al. 2011; Bryan et al. 2012), KELT (Siverd et al. 2012), CoRoT (e.g., Rouan et al. 2012; Pätzold et al. 2012), and Kepler (Borucki et al. 2011a,b; Batalha et al. 2012), one third of the transiting exoplanets known today have been detected in the past two years. In some cases, extensive follow-up campaigns have been needed to determine the correct physical properties of several planetary systems (e.g., Southworth et al. 2011; Barros et al. 2011; Mancini et al. 2013) or have been used to discover other planets by measuring transit time variations (e.g., Rabus et al. 2009b; Steffen et al. 2013). With high-quality photometric observations, it is also possible to detect transit anomalies that are connected with physical phenomena, such as star spots (Pont et al. 2007; Rabus et al. 2009a; Désert et al. 2011; Tregloan-Reed et al. 2013), gravity darkening (Barnes 2009; Szabó et al. 2011), stellar pulsations (Collier Cameron et al. 2010), tidal distortion (Li et al. 2010; Leconte et al. 2011), and the presence of additional bodies (exomoons; Kipping et al. 2009; Tusnski & Valio 2011).
In this paper we report the detection of HATS-2b, the second confirmed exoplanet found by the HATSouth transit survey. HATSouth is the first global network of robotic wide-field telescopes, located at three sites in the southern hemisphere: Las Campanas Observatory (Chile), Siding Spring Observatory (Australia), and the H.E.S.S. (High Energy Stereoscopic System) site (Namibia). We refer the reader to Bakos et al. (2013), where the HATSouth instruments and operations are described in detail. HATS-2b is orbiting a K-type dwarf star and has characteristics similar to those of most hot-Jupiters detected so far. The photometric follow-up performed during two transits of this planet clearly reveals anomalies in the corresponding light curves, which are very likely related to the starspot activity of the host star.
2. Observations
2.1. Photometry
The star HATS-2 (GSC 6665-00236; V = 13.562 ± 0.016; J2000
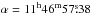 ,
, 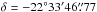 , proper motion
μα = −45.8 ± 1.1 mas/yr,
μδ = −1.3 ± 1.5 mas/yr; UCAC4
catalog, Zacharias et al. 2012) was identified as a
potential exoplanet host based on photometry from all the instruments of the HATSouth
facility (HS-1 to HS-6) between January 19 and August 10, 2010 (details are reported in
Table 1). The detection light curve is shown in
Fig. 1. This figure shows that the discovery data is
of sufficient quality to permit fitting a Mandel &
Agol (2002) limb-darkened transit model. A detailed overview of the observations,
the data reduction, and analysis is given in Bakos et al.
(2013).
, proper motion
μα = −45.8 ± 1.1 mas/yr,
μδ = −1.3 ± 1.5 mas/yr; UCAC4
catalog, Zacharias et al. 2012) was identified as a
potential exoplanet host based on photometry from all the instruments of the HATSouth
facility (HS-1 to HS-6) between January 19 and August 10, 2010 (details are reported in
Table 1). The detection light curve is shown in
Fig. 1. This figure shows that the discovery data is
of sufficient quality to permit fitting a Mandel &
Agol (2002) limb-darkened transit model. A detailed overview of the observations,
the data reduction, and analysis is given in Bakos et al.
(2013).
 |
Fig. 1 Top panel: unbinned instrumental r-band light curve of HATS-2 folded with the period P = 1.354133 days resulting from the global fit described in Sect. 3. Lower panel: zoom-in on the transit; the dark filled points show the light curve binned in phase using a bin size of 0.002. In both panels, the solid line shows the best-fit transit model (see Sect. 3.4). |
HATS-2 was afterwards photometrically followed up three times by two different instruments at two different telescopes. On UT 2011 June 25, the mid-transit and the egress were observed with the Spectral imaging camera, mounted at 2.0 m Faulkes Telescope South (FTS), situated at the Siding Spring Observatory (SSO) and operated as part of the Las Cumbres Observatory Global Telescope (LCOGT) network. The Spectral camera hosts a 4K × 4K array of 0.15′′ pixels, which is readout with 2 × 2 binning. We defocus the telescope to reduce the effect of imperfect flat-fielding and to allow for longer exposure times without saturating. We used an i-band filter and exposure times of 30 s, which with a 20 s readout time gave 50 s cadence photometry.
The data was calibrated with the automated LCOGT reduction pipeline, which includes flat-field correction and fitting of an astrometric solution. Photometry was performed on the reduced images using an automated pipeline based on aperture photometry with Source Extractor (Bertin & Arnouts 1996). The partial transit observed is shown in Fig. 2, and it permitted a refinement of the transit depth and ephemeris. The latter was particularly important for the subsequent follow-up observations performed with the MPG2/ESO 2.2 m telescope at the La Silla Observatory (LSO). Two full transits were covered on February 28 and June 1, 2012, using Gamma-Ray burst Optical/Near-infrared Detector (GROND), which is an imaging camera capable of simultaneous photometric observations in four optical (identical to Sloan g, r, i, z) passbands (Greiner et al. 2008). The main characteristics of the cameras and details of the data reduction are described in Penev et al. (2013). The GROND observations were performed with the telescope defocused and using relatively long exposure times (80−90 s, 150−200 s cadence). This way minimizes noise sources (e.g. flat-fielding errors, atmospheric variation or scintillation, variation in seeing, bad tracking, and Poisson noise) and delivers high-precision photometry for transit events (Alonso et al. 2008; Southworth et al. 2009). The light curves and their best-fitting models are shown in Fig. 2. Distortions in the GROND light curves are clearly visible, which we ascribe to stellar activity. These patterns are analyzed in detail in Sect. 4. Table 1 gives an overview of all the photometric observations for HATS-2.
Summary of photometric observations of HATS-2.
 |
Fig. 2 Phased transit light curves of HATS-2. The dates and instruments used for each event are indicated. The light curves are ordered according to the date and to the central wavelength of the filter used (Sloan g, r, i and z). Our best fit is shown by the solid lines (see Sect. 3.4). Residuals from the fits are displayed at the bottom, in the same order as the top curves. The GROND datapoints affected by anomalies are marked with red empty squares and were not considered in estimating the final values of the planetary-system parameters (see Sect. 4). |
2.2. Spectroscopy
HATS-2 was spectroscopically followed-up between May 2011 and April 2012 by five different instruments at five individual telescopes. The follow-up observations started in May 2011 with high signal-to-noise ratio (S/N) medium-resolution (λ/Δλ = 7000) reconnaissance observations performed at the ANU 2.3 m telescope located at SSO, with the image-slicing integral field spectrograph WiFeS (Dopita et al. 2007). The results show no RV variation with amplitude greater than 2 km s-1, and this excludes most false-positive scenarios involving eclipsing binaries. Furthermore, an initial determination of the stellar atmospheric parameters was possible (Teff, ⋆ = 4800 ± 300 K, log g⋆ = 4.4 ± 0.3), indicating that HATS-2 is a dwarf star. Within the same month, high-precision RV follow-up observations started with the fiber-fed echelle spectrograph CORALIE (Queloz et al. 2000) at the Swiss Leonard Euler 1.2 m telescope at LSO, followed by further high-precision RV measurements obtained with the fiber-fed optical echelle spectrograph FEROS (Kaufer & Pasquini 1998) at the MPG/ESO 2.2 m telescope at LSO. Using the spectral synthesis code SME (“Spectroscopy Made Easy”, Valenti & Piskunov 1996) on the FEROS spectra, it was possible to determine more accurate values for the stellar parameters (see Sect. 3.1). Further RV measurements were obtained with the CYCLOPS fiber-based integral field unit, feeding the cross-dispersed echelle spectrograph UCLES, mounted at the 3.9 m Anglo-Australian Telescope (AAT) at SSO, and with the fiber-fed echelle spectrograph FIES at the 2.5 m telescope at the Nordic Optical Telescope in La Palma. We refer to Penev et al. (2013) for a more detailed description of the observations, the data reduction, and the RV determination methods for each individual instrument that we utilized.
In total, 29 spectra were obtained, which are summarized in Table 2. Table 3 provides the high-precision RV and bisector span measurements. Figure 3 shows the combined high-precision RV measurements folded with the period of the transits. The error bars of the RV measurements include a component from astrophysical/instrumental jitter that was allowed to differ for the three instruments (Coralie: 74.0 m s-1, FEROS: 44.0 m s-1, CYCLOPS: 193.0 m s-1, see Sect. 3.3).
 |
Fig. 3 Top panel: high-precision RV measurements for HATS-2 from CORALIE (dark filled circles), FEROS (open triangles) and CYCLOPS (filled triangles) shown as a function of orbital phase, together with our best-fit model. Zero phase corresponds to the time of mid-transit. The center-of-mass velocity has been subtracted. Second panel: velocity O−C residuals from the best fit. The error bars include a component from astrophysical/instrumental jitter allowed to differ for the three instruments (see Sect. 3.3). Third panel: bisector spans (BS), with the mean value subtracted. Note the different vertical scales of the panels. |
Summary of spectroscopic observations of HATS-2. Observing mode: HPRV = high-precision RV measurements, RECON = reconnaissance observations.
3. Analysis
3.1. Stellar parameters
As already mentioned in Sect. 2.2, we estimated the stellar parameters (i.e., effective temperature Teff ⋆, metallicity [Fe/H], surface gravity log g and projected rotational velocity vsini) by applying SME to the high-resolution FEROS spectra. SME determines stellar and atomic parameters by fitting spectra from model atmospheres to observed spectra and estimates the parameter errors using the quality of the fit, expressed by the reduced χ2, as indicator. Whenever the S/N is not very high or the spectrum is contaminated by telluric absorption features, cosmics, or stellar emission lines, the reduced χ2 does not always converge to unity, which leads to small errors for the stellar parameter values. To estimate of error bars, we used SME to determine the stellar parameters of each FEROS spectrum and calculated the weighted mean and corresponding scatter (weighted by the S/N of individual spectra). The results for the spectroscopic stellar parameters, including the assumed values for micro- vmic and macroturbulence vmac of the SME analysis, are listed in Table 4.
By modeling the light curve alone, it is possible to determine the stellar mean density, which is closely related to the normalized semimajor axis a/R⋆ (Sect. 3.4), when assuming a circular orbit. Furthermore, adding RV measurements allows determination of these parameters for elliptical orbits as well.
To obtain the light curve model, quadratic limb-darkening coefficients are needed, which were determined using Claret (2004) and the initially determined stellar spectroscopic parameters. We used the Yonsei-Yale stellar evolution models (Yi et al. 2001; hereafter YY) to determine fundamental stellar parameters, such as the mass, radius, age, and luminosity. The light-curve-based stellar mean density and spectroscopy-based effective temperature and metallicity, coupled with isochrone analysis, together permit a more accurate stellar surface gravity determination. To allow uncertainties in the measured parameters to propagate into the stellar physical parameters, we assigned an effective temperature and metallicity, drawn from uncorrelated Gaussian distributions, to each stellar mean density in our Markov chain Monte Carlo (MCMC), and performed the isochrone look-up for each link in the MCMC. The newly determined value for log g⋆ = 4.50 ± 0.05 is consistent with the initial value of log g⋆ = 4.44 ± 0.12, so we refrained from re-analyzing the spectra fixing the surface gravity to the revised value.
Stellar parameters for HATS-2.
The spectroscopic, photometric, and derived stellar properties are listed in Table 4, whereas the adopted quadratic limb-darkening coefficients for the individual photometric filters are shown in Table 5.
To illustrate the position of HATS-2 in the H-R diagram, we plotted the normalized semi-major axis a/R⋆ versus effective temperature Teff ⋆. Figure 4 shows the values for HATS-2 with their 1-σ and 2-σ confidence ellipsoids, as well as YY-isochrones calculated for the determined metallicity of [Fe/H] = 0.15 and interpolated to values between 1 and 14 Gyr in 1 Gyr increments from our adopted model.
 |
Fig. 4 YY-isochrones from Yi et al. (2001) for the metallicity of [Fe/H] = 0.15. Isochrones are plotted for ages between 1 and 14 Gyr in steps of 1 Gyr (left to right). The ellipses mark the 1-σ and 2-σ confidence ellipsoids for the determined values of a/R⋆ and Teff ⋆. The isochrones plotted here have a fixed metallicity only for visualization purposes, and uncertainties on the metallicity are propagated into the uncertainties on the stellar mass and radius. |
3.2. Stellar rotation
We applied the Lomb-Scargle periodogram (Lomb 1976; Scargle 1982) to the HATSouth light curve for HATS-2 and found a significant peak at a period of P = 12.46 ± 0.02 d with a S/N measured in the periodogram of 87 and a formal false alarm probability of 10-98 calculated following Press et al. (1992). Figure 5 shows the normalized Lomb-Scargle periodogram of the HATSouth light curve. The peak-to-peak amplitude of the signal over the full 203 d spanned by the observations is 7.4 mmag. If we split the data into bins of duration 50 d, the amplitude in each bin varies from 3.6 mmag to 10.0 mmag. We interpret this signal as the result of starspots modulated by the rotation of the star. The stellar rotation period is thus ~12.5 d, or twice this value. As seen in many open clusters, an individual star often shows two minima per cycle so that the rotation period is double the value found from a periodogram analysis. Also owing to differential rotation and the unknown latitudinal distribution of spots on the star, the equatorial period may be as much as 10−20% shorter than the measured period. Both rotation periods (12.5 and 25 d) are consistent with the upper limit of P⋆ ,rot of 30.32 ± 10.13 d derived from the determined vsini and R⋆ (see Table 4). The rotation period of 12.46 d is comparable to that of similar-sized stars in the 1 Gyr open cluster NGC 6811 (Meibom et al. 2011), which shows a tight period-color sequence. The spin-down rate for sub-solar-mass stars is poorly constrained beyond 1 Gyr, but assuming a Skumanich (1972) spin-down of P ∝ t0.5, the expected rotation period reaches ~25 d at an age of 4 Gyr. Based on this, we estimate a gyrochronology age of either ~1 Gyr, or ~4 Gyr for HATS-2, depending on the ambiguous rotation period.
Orbital and planetary parameters for the HATS-2 system for different fitting scenarios, including the light curve distortions with free and fixed eccentricity e and excluding the light curve distortions with a fixed circular orbit.
 |
Fig. 5 Normalized Lomb-Scargle periodogram of the combined HATSouth light curve of HATS-2. Transits have been removed from the data before applying the periodogram. A strong signal with a period of 12.46 days is detected in the data. |
3.3. Excluding blend scenarios
To rule out the possibility that HATS-2 is actually a blended stellar system mimicking a transiting planet system, we conducted a detailed modeling of the light curves following the procedure described in Hartman et al. (2011). Based on this analysis we can reject hierarchical triple star systems with greater than 4.5σ confidence, and blends between a foreground star and a background eclipsing binary with ~4σ confidence. Moreover, the only nonplanetary blend scenarios that could plausibly fit the light curves (ones that cannot be rejected with greater than 5σ confidence) are ones that would have been easily rejected by the spectroscopic observations. (These would be obviously double-lined systems, also yielding several km s-1 RV and/or BS variations.) We thus conclude that the observed transit is caused by a planetary companion orbiting HATS-2.
3.4. Simultaneous analysis of photometry and radial velocity
Following Bakos et al. (2010) we corrected for systematic noise in the follow-up light curves by applying external parameter decorrelation and the trend-filtering algorithm (TFA) simultaneously with our fit. For the FTS light curve, we decorrelated against the hour angle of the observations (to second order), together with three parameters describing the profile shape (to first order), and we applied TFA. For the GROND light curves, we only decorrelated against the hour angle as the PSF model adopted for FTS is not applicable to GROND, and the number of neighboring stars that could be used in TFA is small. Following the procedure described in Bakos et al. (2010), the FTS and GROND photometric follow-up measurements (Table 1) were simultaneously fitted with the high-precision RV measurements (Table 3) and HATSouth photometry. The light curve parameters, RV parameters, and planetary parameters are listed in Table 5.
Table 5 also contains values for the radial velocity jitter for all three instruments used for high-precision RV measurements. They are added in quadrature to the RV results of the particular instrument. These values are determined such that χ2 per degree of freedom equals unity for each instrument when fitting a fiducial model. If χ2 per degree of freedom is less than unity for that instrument, then no jitter is added. The RV jitters are empirical numbers that are added to the measurements such that the actual scatter in the RV observations sets the posterior distributions on parameters like the RV semi-amplitude.
Allowing the orbital eccentricity to vary during the simultaneous fit, we included the uncertainty for this value in the other physical parameters. We found that the observations are consistent with a circular orbit (e = 0.071 ± 0.049) so we fixed the eccentricity to zero for the rest of this analysis. Table 5 shows that the derived parameters obtained by including the distorted regions of the light curves are consistent with those derived with these regions excluded, indicating that the starspots themselves do not affect the stellar or planet parameters in any significant way.
The RMS varies from 1 to 1.6 mmag for the complete light curves and 0.8 to 1.3 mmag when the spot-affected regions are excluded. We scaled the photometric uncertainties for each of the light curves such that χ2 per degree of freedom equals one about the best-fit model. We adopt the parameters obtained with the light curve distortions excluded in a fixed circular orbit.
4. Starspot analysis
Figure 6 shows the combined four-color GROND light curves for the two HATS-2 transit events that were observed with this imaging instrument. The slight difference in the transit depth among the datasets stems from the different wavelength range covered by each filter. In particular, the g, r, i, and z filters are sensitive to wavelength ranges of 3860−5340 Å, 5380−7060 Å, 7160−8150 Å, and 8260−9520 Å, respectively.
 |
Fig. 6 Combined four-color transit light curves of HATS-2 obtained with the GROND imaging system. Green dots are for the data taken in the g band, yellow upside-down triangles for the r band, red squares for the i band, and purple triangles for the z band. Top panel: transit observed on February 28, 2012. The bump observed just after the midtransit is interpreted as the covering of a “cold” starspot by the planet. Lower panel: transit observed on June 1, 2012. In addition to the bump occurred near the egress part of the light curve, a “hot” spot manifested in the g band, just before the start of the covering of the starspot. |
4.1. Starspots and plages
From an inspection of Fig. 6, it is easy to note several distortions in the light curves. Such anomalies cannot be removed by choosing different comparison stars for the differential photometry, and we interpret them as the consequence of the planet crossing irregularities on the stellar photosphere, such as starspots. It is well known that starspots are at a lower temperature than the rest of the photosphere. The flux ratio should therefore be lower in the blue than the red. We thus expect to see stronger starspot features in the bluest bands.
The data taken on February 28, 2012, are plotted in the top panel of Fig. 6, where the bump, which is clearly present just after midtransit in all four optical bands, is explained by a starspot covered by the planet. In particular, considering the error bars, the g, r, and i points in the starspot feature look as should be expected, whereas the feature in z is a bit peaked, especially the highest points at the peak of the bump at roughly BJD(TDB) 2 455 985.735. Before the planet crosses the starspot feature, it is also possible to note that the fluxes measured in the g and r bands are lower than those in the other two reddest bands, as if the planet were occulting a hotter zone of the stellar chromosphere. Actually, the most sensitive indicators of the chromospheric activity of a star in the visible spectrum are the emission lines of Ca II Hλ3968, Kλ3933, and Hαλ6563, which in our case fall on the transmission wings of the g and r GROND passbands. The characterization of the chromospheric activity by calculating the Ca activity indicator using FEROS spectra was not possible due to high noise in the spectra.
Within the transit observed on June 1, 2012, whose data are plotted in the lower panel of Fig. 6, we detected another starspot, which occurred near the transit-egress zone of the light curve. Again, before the planet crosses the starspot feature, we note another “hotspot” in the g band, which has its peak at roughly BJD(TDB) 2 456 079.681.
These hotspot distortions could be caused by differential color extinction or other time-correlated errors (e.g. red noise) of atmospheric origin. The g-band suffers most from the strength and variability of Earth-atmospheric extinction of all optical wavelengths covered by GROND, which is why the distortions in the g-band could have an atmospheric origin. Discrepancies in blue filters have been noted by other observers, and are often ascribed to systematic errors in ground-based photometry with these filters (e.g. Southworth et al. 2012). However, our group has observed more than 25 planetary transits with the GROND instrument to date, and in no other case have we seen similar features in the g-band alone. We consider it unlikely that a systematic error of this form would only appear near other spot features in the HATS-2 light curve, and therefore conclude that a more plausible scenario is that of a “plage”. A plage is a chromospheric region typically located near active starspots, usually forming before the starspots appear, and disappearing after the starspots vanish from a particular area (e.g. Carroll & Ostlie 1996). Accordingly, a plage occurs most often near a starspot region. As a matter of fact, in the GROND light curves, our plages are located just before each starspot. One can argue that the plage in the second transit is only visible in the g band, but this can be explained by temperature fluctuations in the chromosphere, which causes a lack of ionized hydrogen, and by the fact that the Ca II lines are much stronger than the Hα line for a K-type star like HATS-2. Another argument supporting this plage–starspot scenario is that, for these old stars, a solar-like relation between photospheric and chromospheric cycles is expected, with the photospheric brightness varying in phase with that of the chromosphere (Lockwood et al. 2007).
We note, however, that if these are plages they must be rather different from solar plages, which are essentially invisible in broad-band optical filters unless they are very close to the solar limb. Detecting a plage feature through a broad-band filter near the stellar center suggests a much higher temperature contrast and/or column density of chromospheric gas than in the solar case.
4.2. Modeling transits and starspots
We modeled the GROND transit light curves of HATS-2 with the PRISM3 and GEMC codes (Tregloan-Reed et al. 2013). The first code models a planetary transit over a spotted star, while the second is an optimization algorithm for finding the global best fit and associated uncertainties. With these codes, one can determine, besides the ratio of the radii Rp/R⋆, the sum of the fractional radii, rp + r⋆ = (Rp + R⋆)/a, the limb darkening coefficients, the transit midpoint T0, and the orbital inclination ip, as well as the photometric parameters of the spots, i.e., the projected longitude and the latitude of their centers (θ and φ, these are equal to the physical latitude and longitude only if the rotation axis of the star is perpendicular to the line of sight), the spot size rspot , and the spot contrast ρspot, which is basically the ratio of the surface brightness of the spot to that of the surrounding photosphere. Unfortunately, the current versions of PRISM and GEMC are set to fit only a single starspot (or hotspot), so we excluded the g-band dataset of the second transit from the analysis, because it contains a hotspot with high contrast ratio between stellar photosphere and spot, which strongly interferes with the best-fitting model for the light curve.
Given that the codes do not allow the datasets to be fitted simultaneously, we proceeded as follows. First, we modeled the seven datasets (1st transit: g, r, i, z; 2nd transit: r, i, z) of HATS-2 separately; this step allowed us to restrict the search space for each parameter. Then, we combined the four light curves of the first transit into a single dataset by taking the mean value at each point from the four bands at that point, and we fitted the corresponding light curve. This second step was necessary to find a common value for T0, ip, θ, and φ. Finally, we fit each light curve separately by fixing the starspot position, the midtime of transit T0, and the system inclination to the values found in the previous combined fit. While these parameters are the same for each band since they are physical parameters of the spot or the system and are therefore fixed during the analysis, other parameters, such as radius of the planet Rp, spot contrast ρspot, and temperature of the starspots Tspot, change according to the wavelength, hence according to the analyzed band, and are therefore free parameters during the fit.
The light curves and their best-fitting models are shown in Fig. 7, while the derived photometric parameters for each light curve are reported in Table 6, together with the results of the MCMC error analysis for each solution.
Photometric parameters derived from the GEMC fitting of the GROND transit light curves.
 |
Fig. 7 Phased GROND light curves of HATS-2b compared to the best GEMC fits. The light curves and the residuals are ordered according to the central wavelength of the filter used. Left panel: transit observed on February 28, 2012. Right panel: transit observed on June 1, 2012; due to to presence of the hotspot, the g band was not analysed with GEMC (see text). |
Comparing Table 5 with Table 6, we find that the fitted light curve parameters from the analysis described in Sect. 3.4 are consistent with the parameters that result from the GEMC+PRISM model, except for the inclination, which differs by more than 2σ. As already discussed in Sect. 3.4, the joint-fit analysis was performed both considering and without considering the points contaminated by the starspots, and the results are consistent with each other. Our conclusion is that the spots themselves do not systematically affect the stellar or planet parameters in a significant way, and the differences in the inclination between GEMC and our joint fit are most likely due to differences in the modeling.
4.3. Starspot discussion
The final value for the starspots’ angular radii comes from the weighted mean of the
results in each band and is rspot = 9.02° ± 0.30° for
the starspot in the first transit (spot #1) and
rspot = 19.16° ± 1.08° for the starspot in the second
transit (spot #2), with a reduced 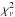 of 0.78 and 0.49 respectively, indicating
good agreement between the various light curves in each of the two transits. We note that
the error of the angular size of spot #2 is greater than for spot #1. While it may be that
spot #2 is larger, we caution that its position near the limb of the star makes its size
poorly constrained.
of 0.78 and 0.49 respectively, indicating
good agreement between the various light curves in each of the two transits. We note that
the error of the angular size of spot #2 is greater than for spot #1. While it may be that
spot #2 is larger, we caution that its position near the limb of the star makes its size
poorly constrained.
The above numbers translate to radii of 98 325 ± 3 876 Km and 208 856 ± 11 794 km, which are equivalent 2.5% and 11% of the stellar disk, respectively. Starspot sizes are in general estimated by Doppler-imaging reconstructions (i.e., Collier Cameron 1992; Vogt et al. 1999), and their range is 0.1% to 22% of a stellar hemisphere, the inferior value being the detection limit of this technique (Strassmeier 2009). Our measurements are thus perfectly reasonable for a common starspot or for a starspot assembly, and in agreement with what has been found in other K-type stars (e.g. TrES-1 (a K0V star) reveals a starspot of at least 42 000 km in radius, see Rabus et al. 2009a).
Starspots are also interesting in terms of how the contrast changes with passband. In
particular, we expect that when moving from ultraviolet (UV) to infrared (IR) wavelengths,
the spot becomes brighter relative to the photosphere. The contrast of starspot #2
decreases from r to z, even though this variation is
inside the 1σ error (see Table 6).
Considering that HATS-2 has an effective temperature
Teff ⋆ = 5227 ± 95 K and modeling
both the photosphere and the starspot as blackbodies (Rabus et al. 2009a; Sanchis-Ojeda & Winn
2011), we used Eq. (1) of Silva (2003) to
estimate the temperature of starspot #2 in each band:
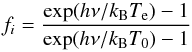 (1)with spot contrast
fi, the Planck constant
h, the frequency of the observation ν, the effective
surface temperature of the star Te, and spot temperature
T0. We obtained the following values:
Tspot#2,r = 4916 ± 105 K,
Tspot#2,i = 4895 ± 121 K, and
Tspot#2,z = 4856 ± 120 K. The
weighted mean is Tspot#2 = 4891.5 ± 66.2 K.
(1)with spot contrast
fi, the Planck constant
h, the frequency of the observation ν, the effective
surface temperature of the star Te, and spot temperature
T0. We obtained the following values:
Tspot#2,r = 4916 ± 105 K,
Tspot#2,i = 4895 ± 121 K, and
Tspot#2,z = 4856 ± 120 K. The
weighted mean is Tspot#2 = 4891.5 ± 66.2 K.
Unlike starspot #2, the spot contrasts for starspot #1 are inconsistent with expectations. The spot is too bright in r relative to the other bandpasses and too faint in z. If we estimate the starspot temperature in each band, we find Tspot#1,g = 4345 ± 97 K, Tspot#1,r = 4604 ± 109 K, Tspot#1,i = 4318 ± 128 K, and Tspot#1,z = 3595 ± 180 K. While the temperature in r agrees with those of g and i at the 1−2σ level, and slight differences could be explained by chromospheric contamination (filaments, spicules, etc.), the temperature in z seems physically inexplicable. This effect is essentially caused by the z points at the peak of the starspot, at phase ~0.004 (see Fig. 7), which are higher than the other points. However, one also has to consider that errorbars in this band are larger than those found in the other bands. This occurs because, since the GROND system design does not permit choosing different exposure times for each band, we are forced to optimize the observations for the r and i bands. Consequently, considering both the filter-transmission efficiency and the color and the magnitude of HATS-2, the S/N in these two bands is better than in z, for which we have larger uncertainty in the photometry. Taking these considerations into account, we estimated the final temperature of starspot #1, neglecting the z-band value and obtaining Tspot#1 = 4425 ± 63 K. In Fig. 8 the final values of the temperature contrast of the two starspots are compared with those of a sample of dwarf stars, which was reported by Berdyugina (2005). The derived contrast for the HATS-2 starspots is consistent with what is observed for other stars.
 |
Fig. 8 Spot temperature contrast with respect to the photospheric temperature in several dwarf stars. Gray square is from spot #2, black circle from spot #1, open circles from Berdyugina (2005), except TrES-1 (Rabus et al. 2009a) and HD189733 (Sing et al. 2011). The name of the star and its spectral type is also reported for most of them. Nameless targets do not have a name in the publication of Berdyugina (2005) as well. Note that some stars appear two times. |
As already observed by Strassmeier (2009), the temperature difference between photosphere and starspots is possibly not very different for stars with different spectral types. Moreover, in the case of a long lifetime, the same starspot could be seen at very different temperatures (Kang & Wilson 1989). It is then very difficult to find any clear correlation between starspot temperatures and the spectral classes of stars.
The achieved longitudes of the starspots agree with a visual inspection of the light curves. The latitude of starspot #1, 76.52° ± 1.94°, matches that of starspot #2 well, 80.6° ± 2.1°, the difference being within 1σ.
Multiple planetary transits across the same spot complex can be used to constrain the alignment between the orbital axis of the planet and the spin axis of the star (e.g., Sanchis-Ojeda et al. 2011). Unfortunately, from only two transits separated by 94 days we cannot tell whether the observed anomalies are due to the same complex. It is possible that they are. Following Solanki (2003) we estimate a typical lifetime of ~130 days for spots with the size seen here. Moreover, the rotation period of Prot = 31 ± 1 d that is inferred when assuming they are the same spot is consistent with the value of Prot = (30 ± 10 d)sini⋆ estimated from the spectroscopically determined, sky-projected equatorial rotation speed. If they are the same spot complex, then the sky-projected spin-orbit alignment is λ = 8° ± 8°, which is consistent with zero. We caution, however, that this value depends entirely on this assumption, which could easily be wrong. Continued photometric monitoring of HATS-2 or spectroscopic observations of the Rossiter-McLaughlin effect are needed to measure the spin-orbit alignment of this system.
To test whether the spot parameters inferred from modeling the transits are consistent with the amplitude of variations seen in the HATSouth photometry, we simulated a light curve using the Macula starspot model (Kipping 2012) and the model parameters determined from the first GROND r-band transit. We find that such a spot gives rise to periodic variations with peak-to-peak amplitudes of ~5 mmag, which is within the 3.6 to 10.0 mmag range of amplitudes observed in the HATSouth light curve. That the amplitude changes by a factor of ~3 over the course of the HATSouth observations indicates, however, that the spot(s) observed by HATSouth is(are) likely to be unrelated to the spot(s) observed with GROND.
 |
Fig. 9 Correlation diagrams for confirmed transit planets (exoplanet.eu, last updated January 10, 2013). From top to bottom: planetary radius Rp vs. stellar radius R⋆, planetary mass MP vs. planetary equilibrium temperature Teq,P, planetary radius Rp vs. planetary equilibrium temperature Teq,P, planetary radius Rp vs. stellar effective temperature Teff, ⋆ and planetary radius Rp vs. planetary mass MP. The positions of the HATS-2 and HATS-2b parameters are marked in red squares. Left panels give a general overview of the position of HATS-2 and HATS-2b in the population of known transit planets (black filled circles). Right panels illustrate a zoom-in; green diamonds represent known exoplanets that fall within the errorbars of the HATS-2 system parameters. Short cuts: HP = HAT-P, W = WASP, T = TrES. |
5. Conclusions
In this paper we have presented HATS-2b, the second planet discovered by the HATSouth survey. This survey is a global network of six identical telescopes located at three different sites in the southern hemisphere (Bakos et al. 2013). The parameters of the planetary system were estimated by an accurate joint fit of follow-up RV and photometric measurements. In particular, we found that HATS-2b has a mass of 1.369 ± 0.158MJ and a radius of 1.139 ± 0.025 RJ. To set this target in the context of other transit planet detections, we plotted four different types of correlation diagrams for the population of transiting planets (Fig. 9). We analyzed the location of determined parameters for HATS-2b and its host star HATS-2 in the following parameter spaces: planetary radius Rp vs. stellar radius R⋆, planetary mass MP vs. planetary equilibrium temperature Teq,P, planetary radius Rp vs. planetary equilibrium temperature Teq,P, planetary radius Rp vs. stellar effective temperature Teff, ⋆, and planetary radius Rp vs. planetary mass MP. As illustrated in Fig. 9, the analyzed parameter relations lie well within the global distribution of known exoplanets.
Within each correlation diagram, at least one well characterized exoplanet can be found, whose parameters are consistent with those of the HATS-2 system within the error bars. When looking at the correlation between planetary and stellar radius, the HATS-2 system is almost like the HAT-P-37 system (Bakos et al. 2012). Comparison of the planetary equilibrium temperature and planetary mass shows that HATS-2b is similar to TrES-2b (O’Donovan et al. 2006). The relation between planetary equilibrium temperature and planetary mass shows agreement with WASP-32b (Maxted et al. 2010), while the relation between stellar effective temperature and planetary radius points out that HATS-2b agrees well with WASP-45b (Anderson et al. 2012) within the error bars. The focus on the planetary parameter’s radius and mass reveals a similarity to the transiting planet TrES-2. Comparing the atmospheres of exoplanets with similar physical parameters will be especially important to pursue with, say, the future ECHO space mission (Tinetti et al. 2012).
Very interesting is the detection of anomalies in the two multi-band photometric-follow-up light curves obtained with the GROND imaging instrument. We recognize the anomalies as starspots covered by HATS-2b during the two transit events, and used PRISM and GEMC codes (Tregloan-Reed et al. 2013) to re-fit the transit light curves, measuring the parameters of the spots. Both the starspots appear to have associated hotspots, which appeared in the first transit in the g and r bands, and only in the g band in the second transit. These hotspots could be physically interpreted as chromospheric active regions known as plages, which can only be seen in GROND’s bluest bands. We estimated the size and the temperature of the two starspots and found values that agree with those found in other G-K dwarf stars.
Acknowledgments
Development of the HATSouth project was funded by NSF MRI grant NSF/AST-0723074, operations are supported by NASA grant NNX09AB29G, and follow-up observations receive partial support from grant NSF/AST-1108686. Data presented in this paper is based partly on observations obtained with the HATSouth Station at the Las Campanas Observatory of the Carnegie Institution of Washington. This work is based on observations collected at the MPG/ESO 2.2 m Telescope located at the ESO Observatory in La Silla (Chile), under program IDs P087.A-9014(A), P088.A-9008(A), P089.A-9008(A), 089.A-9006(A), and Chilean time P087.C-0508(A). Operations of this telescope are jointly performed by the Max Planck Gesellschaft and the European Southern Observatory. GROND has been built by the high-energy group of MPE in collaboration with the LSW Tautenburg and ESO, and is operating as a PI-instrument at the MPG/ESO 2.2 m telescope. We thank Timo Anguita and Régis Lachaume for their technical assistance during the observations at the MPG/ESO 2.2 m Telescope. A.J. acknowledges support from Fondecyt project 1130857, Anillo ACT-086, BASAL CATA PFB-06 and the Millenium Science Initiative, Chilean Ministry of Economy (Nucleus P10-022-F). V.S. acknowledges support form BASAL CATA PFB-06. R.B. and N.E. acknowledge support from Fondecyt project 1095213. N.N. acknowledges support from an STFC consolidated grant. M.R. acknowledges support from a FONDECYT postdoctoral fellowship N°3120097. L.M. thanks Jeremy Tregloan-Reed for his help for using of the PRISM and GEMC codes, and John Southworth and Valerio Bozza for useful discussions. This paper also uses observations obtained with facilities of the Las Cumbres Observatory Global Telescope. Work at the Australian National University is supported by ARC Laureate Fellowship Grant FL0992131. We acknowledge the use of the AAVSO Photometric All-Sky Survey (APASS), funded by the Robert Martin Ayers Sciences Fund, and the SIMBAD database, operated at the CDS, Strasbourg, France. Work at UNSW has been supported by ARC Australian Professorial Fellowship grant DP0774000, ARC LIEF grant LE0989347 and ARC Super Science Fellowships FS100100046.
References
- Alonso, R., Brown, T. M., Torres, G., et al. 2004, ApJ, 613, L153 [NASA ADS] [CrossRef] [Google Scholar]
- Alonso, R., Barieri, M., Rabus, M., et al. 2008, A&A, 487, L5 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Alsubai, K. A., Parley, N. R., Bramich, D. M., et al. 2011, MNRAS, 417, 709 [NASA ADS] [CrossRef] [Google Scholar]
- Anderson, D. R., Collier Cameron, A., Gillon, M., et al. 2012, MNRAS, 422, 1988 [NASA ADS] [CrossRef] [Google Scholar]
- Bakos, G. Á., Torres, G., Pál, A., et al. 2010, ApJ, 710, 1724 [NASA ADS] [CrossRef] [Google Scholar]
- Bakos, G. Á., Hartman, J. D., Torres, G., et al. 2012, AJ, 144, 19 [NASA ADS] [CrossRef] [Google Scholar]
- Bakos, G. Á., Csubry, Z., Penev, K., et al. 2013, PASP, 125, 154 [NASA ADS] [CrossRef] [Google Scholar]
- Barnes, J. W. 2009, ApJ, 705, 683 [Google Scholar]
- Barros, S. C. C., Pollacco, D. L., Gibson, N. P., et al. 2011, MNRAS, 416, 2593 [NASA ADS] [CrossRef] [Google Scholar]
- Batalha, N. M., Rowe, J. F., Bryson, S. T., et al. 2012, ApJS, 204, 24 [Google Scholar]
- Berdyugina, S. V. 2005, Liv. Rev. Sol. Phys., 2, 8 [Google Scholar]
- Bertin, E., & Anouts, S. 1996, A&AS, 117, 393 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Borucki, W. J., Koch, D. G., Basri, G., et al. 2011a, ApJ, 728, 117 [NASA ADS] [CrossRef] [Google Scholar]
- Borucki, W. J., Koch, D. G., Basri, G., et al. 2011b, ApJ, 736, 19 [NASA ADS] [CrossRef] [Google Scholar]
- Bryan, M. L., Alsubai, K. A., Latham, D. W., et al. 2012, ApJ, 750, 84 [NASA ADS] [CrossRef] [Google Scholar]
- Carroll, B. W., & Ostlie, D. A. 1996, An Introduction to Modern Astrophysics, Institute for Mathematics and Its Applications [Google Scholar]
- Cassan, A., Kubas, D., Beaulieu, J.-P., et al. 2012, Nature, 481, 167 [NASA ADS] [CrossRef] [Google Scholar]
- Claret, A. 2004, A&A, 428, 1001 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Collier Cameron, A. 1992, in Surface inhomogeneities on late-type stars, eds. P. B. Byrne, & D. J. Mullan (Berlin: Springer), 33 [Google Scholar]
- Collier Cameron, A., Guenther, E., Smalley, B., & Mcdonald, I. 2010, MNRAS, 407, 507 [NASA ADS] [CrossRef] [Google Scholar]
- Désert, J.-M., Charbonneau, D., Demory, B.-O., et al. 2011, ApJS, 197, 14 [NASA ADS] [CrossRef] [Google Scholar]
- Dopita, M., Hart, J., McGregor, P., et al. 2007, Ap&SS, 310, 255 [NASA ADS] [CrossRef] [Google Scholar]
- Fressin, F., Torres, G., Charbonneau, D., et al. 2013, ApJ, 766, 81 [NASA ADS] [CrossRef] [Google Scholar]
- Greiner, J., Bornemann, W., Clemens, C., et al. 2008, PASP, 120, 405 [NASA ADS] [CrossRef] [Google Scholar]
- Hansen, B. M. S., & Barman, T. 2007, ApJ, 671, 861 [NASA ADS] [CrossRef] [Google Scholar]
- Hartman, J. D., Bakos, G. Á., Torres, G., et al. 2011, ApJ, 742, 59 [NASA ADS] [CrossRef] [Google Scholar]
- Hartman, J. D., Bakos, G. Á., Béky, B., et al. 2012, AJ, 144, 139 [NASA ADS] [CrossRef] [Google Scholar]
- Hellier, C., Anderson, D. R., Collier Cameron, A., et al. 2012, MNRAS, 426, 739 [NASA ADS] [CrossRef] [Google Scholar]
- Howard, A. W., Marcy, G. W., Bryson, S. T., et al. 2012, ApJS, 201, 15 [NASA ADS] [CrossRef] [Google Scholar]
- Kang, Y. W., & Wilson, R. E. 1989, AJ, 97, 848 [NASA ADS] [CrossRef] [Google Scholar]
- Kaufer, A., & Pasquini, L. 1998, Proc. SPIE, 3355, 844 [NASA ADS] [CrossRef] [Google Scholar]
- Kipping, D. M. 2012, MNRAS, 427, 2487 [NASA ADS] [CrossRef] [Google Scholar]
- Kipping, D. M., Fossey, S. J., & Campanella, G. 2009, MNRAS, 400, 398 [NASA ADS] [CrossRef] [Google Scholar]
- Leconte, J., Lai, D., & Chabrier, G. 2011, A&A, 528, A41 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Li, S.-L., Miller, N., Lin, D. N. C., & Fortney, J. J. 2010, Nature, 463, 1054 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Liu, H., Zhou, J.-L., & Wang, S. 2011, ApJ, 732, 66 [NASA ADS] [CrossRef] [Google Scholar]
- Lockwood, G. W., Skiff, B. A., Henry, G. W., et al. 2007, ApJS, 171, 260 [NASA ADS] [CrossRef] [Google Scholar]
- Lomb, N. R. 1976, Ap&SS, 39, 447 [NASA ADS] [CrossRef] [Google Scholar]
- Mancini, L., Southworth, J., Ciceri, S., et al. 2013, A&A, 551, A11 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Mandel, K., & Agol, E. 2002, ApJ, 580, L171 [NASA ADS] [CrossRef] [Google Scholar]
- Maxted, P. F. L., Anderson, D. R., Collier Cameron, A., et al. 2010, PASP, 122, 1465 [NASA ADS] [CrossRef] [Google Scholar]
- Mayor, M., & Queloz, D. 1995, Nature, 378, 355 [NASA ADS] [CrossRef] [Google Scholar]
- Mayor, M., Marmier, M., Lovi, C., et al. 2011, A&A, submitted [arXiv:1109.2497] [Google Scholar]
- McCullough, P. R., Stys, J. E., Valenti, J. A., et al. 2005, PASP, 117, 783 [NASA ADS] [CrossRef] [Google Scholar]
- Meibom, A., Barnes, S. A., Latham, D. W., et al. 2011, ApJ, 733, L9 [NASA ADS] [CrossRef] [Google Scholar]
- Mordasini, C., Alibert, Y., Klahr, H., & Henning, T. 2012a, A&A, 547, A111 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Mordasini, C., Alibert, Y., Georgy, C., et al. 2012b, A&A, 547, A112 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- O’Donovan, F. T., Charbonneau, D., Mandushev, G., et al. 2006, ApJ, 651, L61 [NASA ADS] [CrossRef] [Google Scholar]
- Pätzold, M., Endl, M., Csizmadia, Sz., et al. 2012, A&A, 545, A6 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Penev, K., Bakos, G. Á., Bayliss, D., et al. 2013, AJ, 145, 5 [NASA ADS] [CrossRef] [Google Scholar]
- Pont, F., Gilliland, R. L., Moutou, C., et al. 2007, A&A, 476, 1347 [NASA ADS] [CrossRef] [EDP Sciences] [MathSciNet] [Google Scholar]
- Press, W. H., Teukolsky, S. A., Vetterling, W. T., & Flannery, B. P. 1992, Numerical recipes in FORTRAN. The art of scientific computing, 2nd edn. (Cambridge: Cambridge University Press) [Google Scholar]
- Queloz, D., Mayor, M., Weber, L., et al. 2000, A&A, 354, 99 [NASA ADS] [Google Scholar]
- Rabus, M., Alonso, R., Belmonte, J. A., et al. 2009a, A&A, 494, 391 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Rabus, M., Deeg, H. J., Alonso, R., et al. 2009b, A&A, 508, 1011 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Rouan, D., Parviainen, H., Moutou, C., et al. 2012, A&A, 537, A54 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Sanchis-Ojeda, R., & Winn, J. N. 2011, ApJ, 743, 61 [NASA ADS] [CrossRef] [Google Scholar]
- Sanchis-Ojeda, R., Winn, J. N., Holman, M. J., et al. 2011, ApJ, 733, 127 [NASA ADS] [CrossRef] [Google Scholar]
- Scargle, J. D. 1982, ApJ, 263, 835 [NASA ADS] [CrossRef] [Google Scholar]
- Silva, A. V. R. 2003, ApJ, 585, L147 [NASA ADS] [CrossRef] [Google Scholar]
- Sing, D. K., Pont, F., Aigrain, S., et al. 2011, MNRAS, 416, 1443 [NASA ADS] [CrossRef] [Google Scholar]
- Siverd, R. J., Beatty, T. G., Pepper, J., et al. 2012, ApJ, 761, 123 [Google Scholar]
- Skumanich, A. 1972, ApJ, 171, 565 [NASA ADS] [CrossRef] [Google Scholar]
- Smalley, B., Anderson, D. R., Collier-Cameron, A., et al. 2012, A&A, 547, A61 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Solanki, S. K. 2003, A&ARv, 11, 153 [Google Scholar]
- Southworth, J., Hinse, T. C., Jørgensen, U. G., et al. 2009, MNRAS, 396, 1023 [NASA ADS] [CrossRef] [Google Scholar]
- Southworth, J., Dominik, M., Jørgensen, U. G., et al., 2011, A&A, 527, A8 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Southworth, J., Mancini, L., Maxted, P. F. L., et al. 2012, MNRAS, 422, 3099 [NASA ADS] [CrossRef] [Google Scholar]
- Steffen, J. H., Fabrycky, D. C., Agol, E., et al. 2013, MNRAS, 428, 1077 [NASA ADS] [CrossRef] [Google Scholar]
- Strassmeier, K. G. 2009, A&AR, 17, 251 [Google Scholar]
- Szabó, Gy. M., Szabó, R., Benkõ, J. M., et al. 2011, ApJ, 736, L4 [NASA ADS] [CrossRef] [Google Scholar]
- Tinetti, G., Beaulieu, J. P., Henning, T., et al. 2012, Exp. Astron., 34, 311 [NASA ADS] [CrossRef] [Google Scholar]
- Tregloan-Reed, J., Southworth, J., & Tappert, C. 2013, MNRAS, 428, 3671 [NASA ADS] [CrossRef] [Google Scholar]
- Tusnski, L. R. M., & Valio, A. 2011, ApJ, 743, 97 [NASA ADS] [CrossRef] [Google Scholar]
- Valenti, J. A., & Piskunov, N. 1996, A&AS, 118, 595 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Vogt, S. S., Hatzes, A., Misch, A., & Kürster, M. 1999, ApJS, 121, 547 [NASA ADS] [CrossRef] [Google Scholar]
- Yi, S., Demarque, P., Kim, Y.-C., et al. 2001, ApJS, 136, 417 [NASA ADS] [CrossRef] [Google Scholar]
- Zacharias, N., Finch, C. T., Girard, T. M., et al. 2012, VizieR Online Data Catalog: I/322 [Google Scholar]
All Tables
Summary of spectroscopic observations of HATS-2. Observing mode: HPRV = high-precision RV measurements, RECON = reconnaissance observations.
Orbital and planetary parameters for the HATS-2 system for different fitting scenarios, including the light curve distortions with free and fixed eccentricity e and excluding the light curve distortions with a fixed circular orbit.
Photometric parameters derived from the GEMC fitting of the GROND transit light curves.
All Figures
 |
Fig. 1 Top panel: unbinned instrumental r-band light curve of HATS-2 folded with the period P = 1.354133 days resulting from the global fit described in Sect. 3. Lower panel: zoom-in on the transit; the dark filled points show the light curve binned in phase using a bin size of 0.002. In both panels, the solid line shows the best-fit transit model (see Sect. 3.4). |
| In the text | |
 |
Fig. 2 Phased transit light curves of HATS-2. The dates and instruments used for each event are indicated. The light curves are ordered according to the date and to the central wavelength of the filter used (Sloan g, r, i and z). Our best fit is shown by the solid lines (see Sect. 3.4). Residuals from the fits are displayed at the bottom, in the same order as the top curves. The GROND datapoints affected by anomalies are marked with red empty squares and were not considered in estimating the final values of the planetary-system parameters (see Sect. 4). |
| In the text | |
 |
Fig. 3 Top panel: high-precision RV measurements for HATS-2 from CORALIE (dark filled circles), FEROS (open triangles) and CYCLOPS (filled triangles) shown as a function of orbital phase, together with our best-fit model. Zero phase corresponds to the time of mid-transit. The center-of-mass velocity has been subtracted. Second panel: velocity O−C residuals from the best fit. The error bars include a component from astrophysical/instrumental jitter allowed to differ for the three instruments (see Sect. 3.3). Third panel: bisector spans (BS), with the mean value subtracted. Note the different vertical scales of the panels. |
| In the text | |
 |
Fig. 4 YY-isochrones from Yi et al. (2001) for the metallicity of [Fe/H] = 0.15. Isochrones are plotted for ages between 1 and 14 Gyr in steps of 1 Gyr (left to right). The ellipses mark the 1-σ and 2-σ confidence ellipsoids for the determined values of a/R⋆ and Teff ⋆. The isochrones plotted here have a fixed metallicity only for visualization purposes, and uncertainties on the metallicity are propagated into the uncertainties on the stellar mass and radius. |
| In the text | |
 |
Fig. 5 Normalized Lomb-Scargle periodogram of the combined HATSouth light curve of HATS-2. Transits have been removed from the data before applying the periodogram. A strong signal with a period of 12.46 days is detected in the data. |
| In the text | |
 |
Fig. 6 Combined four-color transit light curves of HATS-2 obtained with the GROND imaging system. Green dots are for the data taken in the g band, yellow upside-down triangles for the r band, red squares for the i band, and purple triangles for the z band. Top panel: transit observed on February 28, 2012. The bump observed just after the midtransit is interpreted as the covering of a “cold” starspot by the planet. Lower panel: transit observed on June 1, 2012. In addition to the bump occurred near the egress part of the light curve, a “hot” spot manifested in the g band, just before the start of the covering of the starspot. |
| In the text | |
 |
Fig. 7 Phased GROND light curves of HATS-2b compared to the best GEMC fits. The light curves and the residuals are ordered according to the central wavelength of the filter used. Left panel: transit observed on February 28, 2012. Right panel: transit observed on June 1, 2012; due to to presence of the hotspot, the g band was not analysed with GEMC (see text). |
| In the text | |
 |
Fig. 8 Spot temperature contrast with respect to the photospheric temperature in several dwarf stars. Gray square is from spot #2, black circle from spot #1, open circles from Berdyugina (2005), except TrES-1 (Rabus et al. 2009a) and HD189733 (Sing et al. 2011). The name of the star and its spectral type is also reported for most of them. Nameless targets do not have a name in the publication of Berdyugina (2005) as well. Note that some stars appear two times. |
| In the text | |
 |
Fig. 9 Correlation diagrams for confirmed transit planets (exoplanet.eu, last updated January 10, 2013). From top to bottom: planetary radius Rp vs. stellar radius R⋆, planetary mass MP vs. planetary equilibrium temperature Teq,P, planetary radius Rp vs. planetary equilibrium temperature Teq,P, planetary radius Rp vs. stellar effective temperature Teff, ⋆ and planetary radius Rp vs. planetary mass MP. The positions of the HATS-2 and HATS-2b parameters are marked in red squares. Left panels give a general overview of the position of HATS-2 and HATS-2b in the population of known transit planets (black filled circles). Right panels illustrate a zoom-in; green diamonds represent known exoplanets that fall within the errorbars of the HATS-2 system parameters. Short cuts: HP = HAT-P, W = WASP, T = TrES. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


