EDP Sciences logo
Subscriber Authentication Point
Search
Menu
Home All issues Volume 557 (September 2013) A&A, 557 (2013) A13 Full HTML
Free Access
Issue
A&A
Volume 557, September 2013
Article Number A13
Number of page(s) 7
Section Stellar structure and evolution
DOI https://doi.org/10.1051/0004-6361/201321642
Published online 13 August 2013

© ESO, 2013

1. Introduction

The fundamental quantity of a star is its mass because it determines the energy production, the evolution, and the final state; certainly there are other parameters like chemical composition and angular momentum that influence stellar evolution. At first glance, the easiest way to estimate stellar masses is by means of the mass-luminosity relation L ∝ Mα which is well established by both theory and observation. However, the exponent α itself is a function of mass: while α ~ 4 for solar-type stars it becomes smaller for stars of lower (<0.5 M⊙) and higher (>10 M⊙) mass. In practice, there are many other parameters that influence the mass-luminosity relation. All stars increase their luminosity with age and high-mass stars lose a considerable fraction of their mass during evolution. Observationally, the determination of the bolometric luminosity (Lbol) becomes more difficult for O- and early B-type stars because their high temperatures means that most of the light is radiated in the UV. Likewise, distance, reddening, and effective temperature (Teff) have to be known to calculate the absolute visual magnitude MV and to convert it into Lbol. For high-mass stars one can circumvent the mass-luminosity relation and determine Teff and Lbol by modelling the optical spectra and by placing the star in the Hertzsprung-Russel diagram (HRD). Finally, evolutionary models yield the stellar mass which is obviously based on many assumptions and whose error is dominated by the uncertainties of theoretical models.

In contrast, binary stars allow the determination of fundamental stellar parameters through a combination of photometry, astrometry, and spectroscopy and by applying basic physical laws. In the case of an eclipsing binary (hereafter EB), radii, distance, and, in favourable cases, Teff may also be determined from a combined analysis of light curves and radial velocity (hereafter RV) curves.

There is growing evidence that most high-mass stars occur as binaries and/or multiple systems (e.g. Preibisch et al. 1999; Mason et al. 2009; Sana & Evans 2011; Chini et al. 2012). Because properties such as binary fraction, period distribution, and mass-ratio distribution provide important constraints on models of star formation and dynamical evolution, precise knowledge of multiplicity characteristics, and how they change within this exceptional mass region are important to understanding the formation of high-mass stars. The currently discussed high-mass star formation scenarios involve i) the gravitational collapse of isolated massive cores and accretion discs (e.g. Myers 1991; Ward-Thompson 2002; Yorke & Sonnhalter 2002; Krumholz et al. 2005; Krumholz 2006); ii) competitive accretion in a clustered environment (Bonnell et al. 2003; Bonnell & Bate 2006; Bonnell 2008; Clark et al. 2008); and iii) stellar collisions in very dense clusters (Bonnell et al. 1998; Stahler et al. 2000; Vanbeveren et al. 2009).

Once a star has evolved to where it fills its Roche lobe, interaction with its companion through the transfer of mass is inevitable. The evolution of interacting binaries follows a significantly different path from that of single stars because of the mass flow outwards from one component, the mass gain by its companion, and the mass loss from the entire system. The evolution of massive stars in binary systems may lead to exotic phenomena such as stellar mergers, X-ray binaries, or gamma-ray bursts. As recently claimed by Sana et al. (2012), more than 70% of all high-mass stars will exchange mass with a companion, leading to a binary merger in one-third of the cases.

While great progress has been made so far in a statistical sense, the system parameters like period (P), eccentricity (e), and mass for individual high-mass binaries are less known. To date, substantial parts of the observational material for binaries and multiple systems among high-mass stars comes from high-resolution spectroscopic monitoring campaigns performed for clusters, for example Trumpler 14 and Trumpler 16 (Rauw et al. 2001a), Cr 228 (Levato et al. 1990), IC 2944 (Sana et al. 2011), IC 1805 (De Becker et al. 2006), NGC 6231 (Sana et al. 2008), NGC 6611 (Sana 2009), NGC 2244 (Mahy et al. 2009), NGC 6334, and NGC 6357 (Russeil et al. 2012), or OB associations, such as Monoceros OB2 (Mahy et al. 2009), Cyg OB (Mahy et al. 2013), and Cyg OB2 (Kiminki & Kobulnicky 2012; Kobulnicky et al. 2012).

Spectroscopic orbital parameters of individual binary systems have been reported for HD 166734 (O+O) (Conti et al. 1980), V382 Cyg (O+O), V448 Cyg (O+O), XZ Cep (O+O) (Harries et al. 1997), HD 93403 (O+O) (Rauw et al. 2000), HD 149404 (O+O) (Rauw et al. 2001b), HD 152248 (O+O) (Sana et al. 2001), HD 101131 (O+O) (Gies et al. 2002), HD 48099 (O+O) (Mahy et al. 2010), HD 152219 (O+B) (Sana et al. 2006), and HD 115071 (O+B) (Penny et al. 2002).

Photometric orbital parameters were reported, for example by Davidge & Forbes (1988), Balona (1992), Terrell et al. (2003), and Sana et al. (2006).

There are only a few dozen EBs known among the O-type stars in our galaxy, for example HD 167971 (O+O) (Davidge & Forbes 1988), V1182 Aqu (O+O) (Mayer et al. 2005), FO15 (O+O) (Niemela et al. 2006), and SZ Cam (O+B) (Lorenz et al. 1998). Additional O-type EBs are needed to increase the statistics on this exotic class of objects.

Currently, we are performing a photometric monitoring survey with the aim of detecting all eclipsing O-type binaries in the southern hemisphere from two brightness limited samples. Our targets comprise a complete sample of about 250 O-type stars (V < 8) taken from the Galactic O-Star (GOS) catalogue V.2.0 (Sota et al. 2008). Preliminary results indicate variability for about 24% of the objects (Chini et al. 2013). A second sample of fainter O stars comes from the Bochum Galactic disk Survey (Haas et al. 2012) where we are monitoring all stars with 10 < R,I < 15 in a strip of Δb =  ± 3° along the southern galactic plane.

In this paper we present a detailed photometric multi-epoch study of three selected O-type stars, HD 319702, CPD − 51° 8946, and PISMIS 24-1. We show the first light curve for Pismis 24-1, re-analyse the orbital period for CPD − 51° 8946, and finally present the orbital parameters for a new high-mass EB system HD 319702.

2. Data

2.1. Observations

The photometric observations were conducted between May and October 2011 using the robotic 15 cm VYSOS-6 telescope of the Universitätssternwarte Bochum, located near Cerro Armazones, the future location of the ESO Extreme Large Telescope (ELT) in Chile1. More information about the telescope and the instrument has been published by Haas et al. (2012). The images were obtained simultaneously through Sloan r and i filters at 6230 Å and 7616 Å; each star was observed typically for about 40 epochs.

2.2. Reduction

The images were processed by standard IRAF2 routines for image reduction, including bias, dark current, and flatfield correction. Additionally, astrometry and astrometric distortion were calculated and properly corrected using SCAMP (Bertin 2006) in combination with SExtractor (Bertin & Arnouts 1996). To improve the image quality further we resampled the frames of an original pixel size of 2.4′′  to a new pixel size of 0.8′′  using the routine SWARP (Bertin et al. 2002). More information about the data reduction can be found in Haas et al. (2012). Photometry was performed using an aperture radius of 4′′  maximizing the signal-to-noise ratio (S/N) and delivering the lowest absolute scatter for the fluxes.

The light curves in normalized flux units are calculated relative to nearby non-variable reference stars located in the same field. The absolute photometric calibration was obtained using the fluxes of about 20 standard stars from Landolt (2009). The standard star fields were observed during the same nights as the science targets. The photometry was corrected for airmass by using the extinction curve for the nearby site Cerro Paranal derived by Patat et al. (2011). The photometric errors are typically of the order of 0.05 mag at both wavelengths.

2.3. Light curve analysis

The photometric light curves were analysed assuming a standard Roche geometry based on the Wilson-Devinney code (Wilson & Devinney 1971; Wilson 1979, 1990). Because Kurucz model atmospheres assume local thermodynamic equilibrium (LTE) for calculating the emergent fluxes from a star, this approximation is insufficient to estimate the resulting light curves of high-mass stars where non-LTE effects alter the radiation field significantly from that of LTE. This is even more prominent in evolved stars like Pismis 24-1, which is one of the objects investigated in the present study. For a more thorough analysis of these systems, after follow-up spectroscopy has been obtained, we will use a code that allows for the input of model atmospheres that do not make the LTE assumption, such as the ELC code (Orosz & Hauschildt 2000).

For each model, the period P of the system and Teff of one component were fixed. In the following we refer to the temperatures of the primary and secondary component as T1 and T2, respectively. Periods were determined independently through the Lafler-Kinman algorithm (Lafler & Kinman 1965) which was subsequently generalized and called phase dispersion minimization (PDM) by Stellingwerf (1978). This method selects the period that yields the lowest dispersion of the phase light curve. The advantage of this algorithm compared to others (e.g. analysis of variance by Schwarzenberg-Czerny 1989, 1999; the Lomb-Scargle periodogram by Scargle 1982) is that it works reliably even in cases where there are only a moderate number of data points (~ 50).

Effective temperatures were adopted according to the spectral types of the stars. For cases where the mass ratio (q = M1/M2) of the stars was known, Teff was also fixed accordingly. The best model was determined through several fits to the light curves until the minimum of the χ2 was reached for each of the following free parameters adopted: the effective temperature of the secondary star, the Roche lobe filling factors, and the inclination i. Because our light curves did not reveal any sign of spots, any further physical analysis was excluded.

A standard gravity-darkening law (Teff ~ gβ) with coefficients β1 = β2 = 0.25 (von Zeipel 1924; Claret 2000; Djurašević et al. 2003) together with bolometric albedos A1 = A2 = 1.0 were assumed for early-type stars with radiative envelopes and hydrostatic equilibrium. We used a non-linear square-root limb-darkening law obtained at optical wavelengths (Diaz-Cordoves & Gimenez 1992) with limb darkening coefficients interpolated from the tables of van Hamme (1993) at the given bandpass.

3. Results

In the following, we introduce the three multiple high-mass systems and describe their properties as obtained from our light curve analysis.

thumbnail Fig. 1

Observed light curves of Pismis 24-1 with the best-fitting model obtained at l3 = 0.15 (yellow solid line) in the Sloan r (top) and Sloan i (middle) bands, folded onto the orbital period of 2.36 days. The error bar at the bottom of the plot represents the average measurement uncertainty for the data set. The blue and black solid lines correspond to the solutions obtained at l3 = 0.1 and l3 = 0.2, respectively. Bottom: 3D view of the system Pismis 24-1 at an orbital phase of 0.12.

3.1. Pismis 24-1

Pismis 24-1 is a triple system that belongs to the young open cluster Pismis 24 which resides within NGC 6357 in the Sagittarius spiral arm at a distance of 1.7 kpc (Fang et al. 2012). This well-studied region is known as a rich reservoir of young stars, containing several OB-type stars (Massey et al. 2001) and several shell-like H ii regions (Russeil et al. 2012).

As part of a multiplicity study at the high-mass end of the IMF, Pismis 24-1 (HDE 319718 A) has been investigated in depth by Maíz-Apellániz et al. (2007) by means of high-resolution images from the Hubble Space Telescope (HST). These observations resolved the system into two components, Pismis 24-1 SW and Pismis 24-1 NE, separated by 0.36′′ (see Fig. 1 of Maíz-Apellániz et al. 2007). Both components have similar absolute visual magnitudes (MV =  −6.28 for Pismis 24-1 SW and MV =  −6.41 for Pismis 24-1 NE) and similar intrinsic colours.

High-resolution spectroscopy (Maíz-Apellániz et al. 2007) yielded a spectral type O4 III(f+) for Pismis 24-1 SW and confirmed the spectral type O3.5 If* for Pismis 24-1 NE as determined previously by Walborn (2002). Radial velocity variations from + 20 to − 90 km s-1 for the absorption lines measured in eight spectra confirmed the variations reported previously by Lortet et al. (1984) and suggest that Pismis 24-1 NE is an unresolved spectroscopic binary. The estimated masses for Pismis 24-1 SW and Pismis 24-1 NE are 96 ± 10 M⊙ and 97 ± 10 M⊙ (Maíz-Apellániz et al. 2007).

Phil Massey and collaborators have detected optical variability in the unresolved Pismis 24-1 NE+SW system with a peak-to-peak amplitude of 0.07 mag and a period of 2.36088 days3; however, no light curve has been published to date. As a consequence, Pismis 24-1 is an excellent target to provide a decent light curve for this system and to test our photometric analysis. The PDM analysis of our 32 data points yields a period of P = 2.36 days which is in excellent agreement with the result reported by Maíz-Apellániz et al. (2007).

As already noted in Sect. 2, each final (reduced) image has a resolution of 0.8′′  which does not allow us to resolve both Pismis 24-1 NE+SW separately. In consequence, we expect that some amount of third light contribution could alter the properties of the system, reducing the depths of the eclipses resulting in temperature and inclination being underestimated. In order to estimate the third light contribution, we performed the analysis adopting l3 as a free parameter. The analysis yields reasonable solutions for 0.05 ≤ l3 ≤ 0.20 with the best-fitting model at l3 = 0.15. An acceptable solution can be found without considering the third light component (l3 = 0), however; the uncertainty in the inclination and the temperature is large. Figure 1 displays the observed Sloan r and Sloan i light curves together with the best-fitting model solution folded onto the orbital period. The light curves in both filters show nearly the same amplitude variations (~7%) and both partial eclipses with the same duration of 0.174 in phase. The primary and secondary minimum eclipses, which are separated symmetrically by 0.5 in phase, show similar depths ΔDp = ΔDp,min − ΔDmax = 8% and ΔDs = ΔDs,min − ΔDmax = 7%, where p and s refer to the primary and secondary minimum, and max denotes to the global maximum of the light curve (Sandquist & Shetrone 2003).

We fixed T1 = 42 000  K according to the spectral type O3.5 If* reported by Maíz-Apellániz et al. (2007) and used the observational Teff calibration by Martins et al. (2005) (his Table 6). Additionally, we assumed equal masses for both components (q = 1.0) as suggested by the spectroscopy (Maíz-Apellániz et al. 2007). The best-fitting model favours a detached configuration with an inclination i = 61.8° and requires that both components fill up their Roche lobes at about 79% and 81%, respectively. A 3D graphic representation of the Roche model of the system obtained at a orbital phase φ = 0.12 is shown in Fig. 1. Our calculations yield an effective temperature of T2 = 41 500  K for the secondary star which is consistent with its spectral type designation. The spectral type O3.5 If* corresponds to the combined light of the two stars, and so spectroscopic follow-up is required to classify the individual components. Likewise, the similarity of the depths in the primary and secondary minimum agrees well with the derived temperature. The observed symmetrical separation of the primary and secondary minimum eclipses suggests that the system has a circular orbit compatible with the current spectroscopic knowledge of the system. In consequence, we assumed zero eccentricity and synchronous rotation for which the model provides the best fit to the system. A summary of the relevant parameters and the best-fitting values are listed in Table 1.

Table 1

Pismis 24-1 orbital solution and system parameters.

Table 2

CPD − 51° 8946 orbital solution and system parameters.

3.2. CPD − 51° 8946

thumbnail Fig. 2

Observed (dots) and simulated (solid line) light curves in the r-Sloan (top) and i-Sloan (middle) bands, folded onto the orbital period (1.96 days) obtained from the PDM analysis. The error bar at the bottom of the plot represents the average measurement uncertainty for the data set. Bottom: The normalized V-band light curve obtained from the ASAS III catalogue folded with a period of 1.96 days.

The star CPD − 51° 8946 was classified as an OB-type star (Lynga 1964) and is part of a sample of about 700 OB stars observed by van Houten (2001) at the former Leiden Southern Station at Hartebeespoortdam, South Africa. The eclipsing nature of CPD − 51° 8946 was established by Pojmanski & Maciejewski (2004) using the data obtained from the ASAS III (All Sky Automated Survey) catalogue of variable stars. The authors determined a photometric period of 3.92 days and suggest an eclipsing detached binary configuration.

From 44 data points we obtain a photometric period of 1.96 days, which is exactly half the period reported by Pojmanski & Maciejewski (2004). To check this discrepancy, we performed a re-analysis of the light curves available from the ASAS photometric catalogue4 database. First, we considered whether the difference might have be caused by the selection of the ASAS photometric data points, which are identified with the letters A to D according to the quality of the data. Using only the high-quality data available (marked with A) the PDM analysis yields a period P = 1.96 days which is exactly the same value obtained from our light curves. Second, we considered whether the discrepancy might have been caused by the different algorithms used to calculate the period. However, using ~ 50 light curves obtained from the ASAS catalogue and performing a PDM analysis yields 100% agreement with the values reported by Pojmanski & Maciejewski (2004). Therefore, we assume that the entry in Table 2 from Pojmanski & Maciejewski (2004) must be incorrect.

Figure 2 shows the light curves together with the best-fitting model solution corresponding to Sloan r and i  filters. In addition, this figure shows the light curve obtained from the ASAS III catalogue with a period of 1.96 days. The light curves in both filters have similar amplitude variations of ~ 16%. The primary and secondary minimum have different depths ΔDp = 16% and ΔDs = 10%, which can be interpreted through the difference between the temperatures of the components. Both partial eclipses have the same duration (0.214 in phase) and their minima are separated symmetrically (0.5 in phase). In consequence, we estimated the parameters of the system by assuming a circular orbit and a synchronous rotation. The primary component fills up its Roche lobe at about 95% while the secondary at about 99%, favouring a semi-detached configuration with an orbital inclination i = 58.4°.

We fixed the effective temperature of the primary star T1 = 34 550 K according to the colour index B − V =  −0.32 obtained by van Houten (2001)5 corresponding to the spectral type O8.5 V, that was originally reported by Boehm-Vitense (1981) and re-analysed by Humphreys & McElroy (1984); this spectral designation is also consistent with recent investigations by Martins et al. (2005).

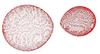thumbnail Fig. 3

Model of the system CPD − 51° 8946 viewed at orbital phase 0.214. The graphical 3D view shows when the secondary star fills up its Roche lobe. The model was obtained with the parameters estimated from the light curve analysis.

thumbnail Fig. 4

Observed (dots) and simulated (solid line) light curves in the Sloan r (top) and Sloan i (middle) bands, folded onto the orbital period (2.01 days) obtained from the PDM analysis. The error bar at the bottom of the plot represents the average measurement uncertainty for the data set. The graphical 3D view of the new detached binary system HD 319702 at an orbital phase 0.5 is displayed at the bottom.

The best fit to the light curve yields a mass ratio q = M1/M2 = 2.8 with a temperature of the secondary component T2 = 21 500 K corresponding to a spectral type B2 V (Boehm-Vitense 1981; Lefever et al. 2010; Nieva & Przybilla 2012). As displayed in Fig. 2, the 3D view of the Roche geometry of the system (φ = 0.63) shows a transitional evolutionary state of the system for which both stars are close to filling their Roche lobes. Most likely the future mass transfer will create a new contact binary system. A summary of the relevant parameters and the best-fitting values are listed in Table 2.

3.3. HD 319702

Located at a distance of 1.75 kpc (Russeil et al. 2010, 2012), HD 319702 is a member of the cluster NGC 6334. This region is considered one of the most active regions of high-mass star formation in our Galaxy (Tapia & Persi 2009; Russeil et al. 2012). The area contains evolved optical but also embedded compact H ii regions. This star was originally classified as a B1 Ib by Neckel (1978); later measurements converted the spectral type into O8 III(f) (Walborn 1982; Maíz-Apellániz et al. 2004; Pinheiro et al. 2010). So far there has been no hint of an eclipsing orbit.

As displayed in Fig. 4, the light curves constructed from 38 epochs show nearly identical amplitude variations with primary and secondary minimum eclipses at different depths (ΔDp = 11%, ΔDs = 8%). This behaviour is characteristic for an eclipsing binary with different effective temperatures; the primary minimum is due to the eclipse of the more luminous star by the less luminous companion. The eclipses are partial and symmetric with the same duration of 0.189 in phase. The primary and secondary minima are separated symmetrically by 0.5 in phase suggesting a circular orbit.

Our PDM analysis yields a period of P = 2.01 days. Again, we have assumed a zero eccentricity and synchronous rotation for which the model provides the best fit to the system. Based on the spectral type determination of the primary star we adopted a value of T1 = 34 000 K considering the observational Teff calibration by Martins et al. (2005) (their Table 5). We computed a set of orbital solutions where the best-fitting model favours an orbital inclination of 67.5° with a mass ratio of q = M1/M2 = 1.0. The system shows well-defined eclipses favouring a detached configuration, where both components fill up their Roche lobes at about 71%. The temperature of the secondary component is T2 = 25 200 K suggesting that this new system is most likely composed of an O8 III + a B0.5 V star if the calibration by Humphreys & McElroy (1984) is used for the secondary component. Considering the calibration reported by Boehm-Vitense (1981) and Harmanec (1988), the system would turn into O8 III + a B1 V. A summary of the relevant parameters and the best-fitting values are listed in Table 3.

Table 3

HD 319702 orbital solution and system parameters.

4. Summary and conclusions

We have presented optical photometric observations for three high-mass eclipsing binaries performed during a six-month monitoring campaign. A detailed analysis and modelling of the light curves was carried out within the framework of the Roche geometry. We find that all objects show light curve variations that occur on time-scales of less than three days and that the systems are well described by circular orbits (zero or negligible eccentricity). The individual results are:

  • Pismis 24-1 is a detached system with an orbital inclination of 61.8° and an orbital period of 2.36 days. We can confirm that the eclipsing binary system of Pismis 24-1 is composed of at least one O+O pair.

  • CPD − 51° 8946 is a semi-detached system with an orbital inclination of 58.4° and an orbital period of 1.96 days. This system is most likely composed of an O8.5 V and a B2 V star and develops towards a contact system.

  • HD 319702 is a new high-mass eclipsing binary system with detached configuration; its orbital inclination is 67.5° and the period is 2.01 days. The components are well described by the association of an O8 III and a B1 V star.

The current study has demonstrated that our photometric survey has the capability to detect O-type eclipsing binaries along the galactic plane in the brightness range 10 < R,I < 15; more EB candidates will be presented in the future. Follow-up spectroscopic RV studies of this sample are essential to determine the absolute parameters and to track the evolutionary state of individual systems. On the other hand, for the complete sample from the Galactic O-Star catalogue (V < 8) we are currently monitoring all SB2 candidates (Chini et al. 2012) to detect further O-type EBs among this sample and to obtain precise light curves (Barr Domínguez et al., in prep.). From the few results available so far, both in the literature and from our current study, it seems that the important mass ratio parameter q ~ 1. However, there might be an observational bias since O stars have very high luminosities that prevent fainter companions from being detected. So far there are only four known high-mass binaries where q > 2 with the exceptional maximum of q ~ 5.8: HD 37022 (O5), HD 53975 (B7 Iab), HD 199579 (O6 V), and HD 165246 (O8 V) (see Mayer et al. 2013 and references therein).

This strongly corroborates the view that high-mass binaries are generally created during the star formation process and are not a result of tidal capture. We expect that our study will substantially increase the number of known O-type EBs and that we can obtain a better census of the range of q = M1/M2 in the high-mass regime. Likewise, it will be interesting to see at which stellar primary mass q will significantly deviate from unity. For this reason we will extend our studies in the future also towards B-type binaries.

2

IRAF is distributed by the National Optical Astronomy Observatory, which is operated by the Association of Universities for Research in Astronomy (AURA) under cooperative agreement with the National Science Foundation.

3

Private communication between Maíz-Apellániz et al. (2007) and Phil Massey (2006).

5

Note that the colour index reported by van Houten was obtained in the Walraven photometric system. While the corresponding V filter is similar to the Johnson V passband in both peak and bandwith, the B filter has only half of the width of the Johnson B passband.

Acknowledgments

This publication is supported as a project of the Nordrhein-Westfälische Akademie der Wissenschaften und der Künste in the framework of the academic programme by the Federal Republic of Germany and the state Nordrhein-Westfalen. The observations at Cerro Armazones benefitted from the continuous support of the Universidad Católica del Norte and from the care of the guardians Hector Labra, Gerardo Pino, Roberto Munoz, and Francisco Arraya. This research has made use of the NASA/IPAC Extragalactic Database (NED) which is operated by the Jet Propulsion Laboratory, California Institute of Technology, under contract with the National Aeronautics and Space Administration. This research has made use of the SIMBAD database, operated at CDS, Strasbourg, France. We thank the anonymous referee for his contructive comments and careful review of the manuscript.

References

  1. Balona, L. A. 1992, MNRAS, 254, 404 [NASA ADS] [CrossRef] [Google Scholar]
  2. Bertin, E. 2006, Astronomical Data Analysis Software and Systems XV, 351, 112 [NASA ADS] [Google Scholar]
  3. Bertin, E., & Arnouts, S. 1996, A&AS, 117, 393 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  4. Bertin, E., Mellier, Y., Radovich, M., et al. 2002, Astronomical Data Analysis Software and Systems XI, 281, 228 [NASA ADS] [Google Scholar]
  5. Boehm-Vitense, E. 1981, ARA&A, 19, 295 [NASA ADS] [CrossRef] [Google Scholar]
  6. Bonnell, I. A. 2008, Pathways Through an Eclectic Universe, 390, 26 [NASA ADS] [Google Scholar]
  7. Bonnell, I. A., & Bate, M. R. 2006, MNRAS, 370, 488 [NASA ADS] [CrossRef] [Google Scholar]
  8. Bonnell, I. A., Bate, M. R., & Zinnecker, H. 1998, MNRAS, 298, 93 [NASA ADS] [CrossRef] [Google Scholar]
  9. Bonnell, I. A., Bate, M. R., & Vine, S. G. 2003, MNRAS, 343, 413 [NASA ADS] [CrossRef] [Google Scholar]
  10. Chini, R., Hoffmeister, V. H., Nasseri, A., Stahl, O., & Zinnecker, H. 2012, MNRAS, 424, 1925 [NASA ADS] [CrossRef] [Google Scholar]
  11. Chini, R., Barr, A., Buda, L. S., et al. 2013, Cent. Eur. Astrophys. Bull., 37, 295 [Google Scholar]
  12. Claret, A. 2000, A&A, 359, 289 [NASA ADS] [Google Scholar]
  13. Clark, P. C., Klessen, R. S., Bonnell, I. A., & Smith, R. J. 2008, Massive Star Formation: Observations Confront Theory, 387, 208 [NASA ADS] [Google Scholar]
  14. Conti, P. S., Ebbets, D., Massey, P., & Niemela, V. S. 1980, ApJ, 238, 184 [NASA ADS] [CrossRef] [Google Scholar]
  15. Davidge, T. J., & Forbes, D. 1988, MNRAS, 235, 797 [NASA ADS] [Google Scholar]
  16. De Becker, M., Rauw, G., Manfroid, J., & Eenens, P. 2006, A&A, 456, 1121 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  17. Diaz-Cordoves, J., & Gimenez, A. 1992, A&A, 259, 227 [NASA ADS] [Google Scholar]
  18. Djurašević, G., Rovithis-Livaniou, H., Rovithis, P., et al. 2003, A&A, 402, 667 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  19. Fang, M., van Boekel, R., King, R. R., et al. 2012, A&A, 539, A119 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  20. Gies, D. R., Penny, L. R., Mayer, P., Drechsel, H., & Lorenz, R. 2002, ApJ, 574, 957 [NASA ADS] [CrossRef] [Google Scholar]
  21. Haas, M., Hackstein, M., Ramolla, M., et al. 2012, Astron. Nachr., 333, 706 [NASA ADS] [Google Scholar]
  22. Harmanec, P. 1988, Bull. Astron. Inst. Czechoslovakia, 39, 329 [Google Scholar]
  23. Harries, T. J., Hilditch, R. W., & Hill, G. 1997, MNRAS, 285, 277 [NASA ADS] [CrossRef] [Google Scholar]
  24. Humphreys, R. M., & McElroy, D. B. 1984, ApJ, 284, 565 [NASA ADS] [CrossRef] [Google Scholar]
  25. Kiminki, D. C., & Kobulnicky, H. A. 2012, ApJ, 751, 4 [NASA ADS] [CrossRef] [Google Scholar]
  26. Kobulnicky, H. A., Smullen, R. A., Kiminki, D. C., et al. 2012, ApJ, 756, 50 [NASA ADS] [CrossRef] [Google Scholar]
  27. Krumholz, M. R. 2006 [arXiv:astro-ph/0607429] [Google Scholar]
  28. Krumholz, M. R., McKee, C. F., & Klein, R. I. 2005 [arXiv:astro-ph/0510412] [Google Scholar]
  29. Lafler, J., & Kinman, T. D. 1965, ApJS, 11, 216 [NASA ADS] [CrossRef] [Google Scholar]
  30. Landolt, A. U. 2009, AJ, 137, 4186 [NASA ADS] [CrossRef] [Google Scholar]
  31. Lefever, K., Puls, J., Morel, T., et al. 2010, A&A, 515, A74 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  32. Levato, H., Malaroda, S., Garcia, B., Morrell, N., & Solivella, G. 1990, ApJS, 72, 323 [NASA ADS] [CrossRef] [Google Scholar]
  33. Lorenz, R., Mayer, P., & Drechsel, H. 1998, A&A, 332, 909 [NASA ADS] [Google Scholar]
  34. Lortet, M. C., Testor, G., & Niemela, V. 1984, A&A, 140, 24 [NASA ADS] [Google Scholar]
  35. Lynga, G. 1964, Meddelanden fran Lunds Astronomiska Observatorium Serie II, 141, 1 [Google Scholar]
  36. Mahy, L., Nazé, Y., Rauw, G., et al. 2009, A&A, 502, 937 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  37. Mahy, L., Rauw, G., Martins, F., et al. 2010, ApJ, 708, 1537 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  38. Mahy, L., Rauw, G., De Becker, M., Eenens, P., & Flores, C. A. 2013, A&A, 550, A27 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  39. Maíz-Apellániz, J., Walborn, N. R., Galué, H. Á., & Wei, L. H. 2004, ApJS, 151, 103 [NASA ADS] [CrossRef] [Google Scholar]
  40. Maíz Apellániz, J., Walborn, N. R., Morrell, N. I., Niemela, V. S., & Nelan, E. P. 2007, ApJ, 660, 1480 [NASA ADS] [CrossRef] [Google Scholar]
  41. Martins, F., Schaerer, D., & Hillier, D. J. 2005, A&A, 436, 1049 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  42. Massey, P., DeGioia-Eastwood, K., & Waterhouse, E. 2001, AJ, 121, 1050 [NASA ADS] [CrossRef] [Google Scholar]
  43. Mason, B. D., Hartkopf, W. I., Gies, D. R., Henry, T. J., & Helsel, J. W. 2009, AJ, 137, 3358 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  44. Mayer, P., Drechsel, H., & Lorenz, R. 2005, ApJS, 161, 171 [NASA ADS] [CrossRef] [Google Scholar]
  45. Mayer, P., Harmanec, P., & Pavlovski, K. 2013, A&A, 550, A2 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  46. Myers, P. C. 1991, The Formation and Evolution of Star Clusters, 13, 73 [NASA ADS] [Google Scholar]
  47. Neckel, T. 1978, A&A, 69, 51 [NASA ADS] [Google Scholar]
  48. Niemela, V. S., Morrell, N. I., Fernández Lajús, E., et al. 2006, MNRAS, 367, 1450 [NASA ADS] [CrossRef] [Google Scholar]
  49. Nieva, M.-F., & Przybilla, N. 2012, A&A, 539, A143 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  50. Orosz, J. A., & Hauschildt, P. H. 2000, A&A, 364, 265 [NASA ADS] [Google Scholar]
  51. Patat, F., Moehler, S., O’Brien, K., et al. 2011, A&A, 527, A91 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  52. Penny, L. R., Gies, D. R., Wise, J. H., Stickland, D. J., & Lloyd, C. 2002, ApJ, 575, 1050 [NASA ADS] [CrossRef] [Google Scholar]
  53. Pinheiro, M. C., Copetti, M. V. F., & Oliveira, V. A. 2010, A&A, 521, A26 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  54. Pojmanski, G., & Maciejewski, G. 2004, Acta Astron., 54, 153 [NASA ADS] [CrossRef] [Google Scholar]
  55. Preibisch, T., Balega, Y., Hofmann, K.-H., Weigelt, G., & Zinnecker, H. 1999, New A, 4, 531 [Google Scholar]
  56. Rauw, G., Sana, H., Gosset, E., et al. 2000, A&A, 360, 1003 [NASA ADS] [Google Scholar]
  57. Rauw, G., Sana, H., Antokhin, I. I., et al. 2001a, MNRAS, 326, 1149 [NASA ADS] [CrossRef] [Google Scholar]
  58. Rauw, G., Nazé, Y., Carrier, F., et al. 2001b, A&A, 368, 212 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  59. Russeil, D., Zavagno, A., Motte, F., et al. 2010, A&A, 515, A55 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  60. Russeil, D., Zavagno, A., Adami, C., et al. 2012, A&A, 538, A142 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  61. Sana, H. 2009, A&A, 501, 291 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  62. Sana, H., & Evans, C. J. 2011, IAU Symp., 272, 474 [NASA ADS] [CrossRef] [Google Scholar]
  63. Sana, H., Rauw, G., & Gosset, E. 2001, A&A, 370, 121 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  64. Sana, H., Gosset, E., & Rauw, G. 2006, MNRAS, 371, 67 [NASA ADS] [CrossRef] [Google Scholar]
  65. Sana, H., Gosset, E., Nazé, Y., Rauw, G., & Linder, N. 2008, MNRAS, 386, 447 [NASA ADS] [CrossRef] [Google Scholar]
  66. Sana, H., James, G., & Gosset, E. 2011, MNRAS, 416, 817 [NASA ADS] [CrossRef] [Google Scholar]
  67. Sana, H., de Mink, S. E., de Koter, A., et al. 2012, Science, 337, 444 [Google Scholar]
  68. Sandquist, E. L., & Shetrone, M. D. 2003, AJ, 125, 2173 [NASA ADS] [CrossRef] [Google Scholar]
  69. Scargle, J. D. 1982, ApJ, 263, 835 [NASA ADS] [CrossRef] [Google Scholar]
  70. Schwarzenberg-Czerny, A. 1989, MNRAS, 241, 153 [NASA ADS] [CrossRef] [Google Scholar]
  71. Schwarzenberg-Czerny, A. 1999, ApJ, 516, 315 [NASA ADS] [CrossRef] [Google Scholar]
  72. Sota, A., Maíz-Apellániz, J., Walborn, N. R., & Shida, R. Y. 2008, Rev. Mex. Astron. Astrofis. Conf. Ser., 33, 56 [Google Scholar]
  73. Stahler, S. W., Palla, F., & Ho, P. T. P. 2000, Protostars and Planets IV, 327 [Google Scholar]
  74. Stellingwerf, R. F. 1978, ApJ, 224, 953 [NASA ADS] [CrossRef] [Google Scholar]
  75. Tapia, M., & Persi, P. 2009, Rev. Mex. Astron. Astrofis. Conf. Ser., 35, 78 [NASA ADS] [Google Scholar]
  76. Terrell, D., Munari, U., Zwitter, T., & Nelson, R. H. 2003, AJ, 126, 2988 [NASA ADS] [CrossRef] [Google Scholar]
  77. Vanbeveren, D., Belkus, H., van Bever, J., & Mennekens, N. 2009, Ap&SS, 324, 271 [NASA ADS] [CrossRef] [Google Scholar]
  78. van Hamme, W. 1993, AJ, 106, 2096 [NASA ADS] [CrossRef] [Google Scholar]
  79. van Houten, C. J. 2001, A&A, 369, 527 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  80. von Zeipel, H. 1924, MNRAS, 84, 702 [NASA ADS] [CrossRef] [Google Scholar]
  81. Walborn, N. R. 1982, AJ, 87, 1300 [NASA ADS] [CrossRef] [Google Scholar]
  82. Walborn, N. R. 2002, AJ, 124, 507 [NASA ADS] [CrossRef] [Google Scholar]
  83. Ward-Thompson, D. 2002, Science, 295, 76 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
  84. Wilson, R. E. 1979, ApJ, 234, 1054 [NASA ADS] [CrossRef] [Google Scholar]
  85. Wilson, R. E. 1990, ApJ, 356, 613 [NASA ADS] [CrossRef] [Google Scholar]
  86. Wilson, R. E., & Devinney, E. J. 1971, ApJ, 166, 605 [NASA ADS] [CrossRef] [Google Scholar]
  87. Yorke, H. W., & Sonnhalter, C. 2002, ApJ, 569, 846 [NASA ADS] [CrossRef] [Google Scholar]

All Tables

Table 1

Pismis 24-1 orbital solution and system parameters.

In the text
Table 2

CPD − 51° 8946 orbital solution and system parameters.

In the text
Table 3

HD 319702 orbital solution and system parameters.

In the text

All Figures

thumbnail Fig. 1

Observed light curves of Pismis 24-1 with the best-fitting model obtained at l3 = 0.15 (yellow solid line) in the Sloan r (top) and Sloan i (middle) bands, folded onto the orbital period of 2.36 days. The error bar at the bottom of the plot represents the average measurement uncertainty for the data set. The blue and black solid lines correspond to the solutions obtained at l3 = 0.1 and l3 = 0.2, respectively. Bottom: 3D view of the system Pismis 24-1 at an orbital phase of 0.12.
In the text
thumbnail Fig. 2

Observed (dots) and simulated (solid line) light curves in the r-Sloan (top) and i-Sloan (middle) bands, folded onto the orbital period (1.96 days) obtained from the PDM analysis. The error bar at the bottom of the plot represents the average measurement uncertainty for the data set. Bottom: The normalized V-band light curve obtained from the ASAS III catalogue folded with a period of 1.96 days.

In the text
thumbnail Fig. 3

Model of the system CPD − 51° 8946 viewed at orbital phase 0.214. The graphical 3D view shows when the secondary star fills up its Roche lobe. The model was obtained with the parameters estimated from the light curve analysis.

In the text
thumbnail Fig. 4

Observed (dots) and simulated (solid line) light curves in the Sloan r (top) and Sloan i (middle) bands, folded onto the orbital period (2.01 days) obtained from the PDM analysis. The error bar at the bottom of the plot represents the average measurement uncertainty for the data set. The graphical 3D view of the new detached binary system HD 319702 at an orbital phase 0.5 is displayed at the bottom.
In the text

Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.

Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.

Initial download of the metrics may take a while.