| Issue |
A&A
Volume 557, September 2013
|
|
|---|---|---|
| Article Number | A63 | |
| Number of page(s) | 24 | |
| Section | Galactic structure, stellar clusters and populations | |
| DOI | https://doi.org/10.1051/0004-6361/201220681 | |
| Published online | 30 August 2013 | |
Stellar and circumstellar properties of visual binaries in the Orion Nebula Cluster⋆,⋆⋆
1
Leibniz-Institut für Astrophysik Potsdam, An der Sternwarte 16, 14482
Potsdam, Germany
e-mail: sergeco@gmail.com
2
Institute for Astronomy, University of Hawaii,
34 Ohia Ku Street, Pukalani, HI
96768,
USA
3
Astronomy Department, University of California,
Berkeley, CA
94720-3411,
USA
4
UJF-Grenoble 1/CNRS-INSU, Institut de Planétologie et
d’Astrophysique de Grenoble, UMR 5274, 38041
Grenoble,
France
5
Institute for Astronomy, University of Hawaii,
640 N. Aohoku Place,
Hilo, HI
96720,
USA
6 NASA Astrobiology
Institute
7
Deutsches SOFIA Institut, Universität Stuttgart,
Pfaffenwaldring 29,
70569
Stuttgart,
Germany
8
SOFIA Science Center, NASA-Ames Research Center,
MS 232-12, Moffett Field, CA
94035,
USA
9
European Southern Observatory, Karl Schwartzschild Str. 2, 85748
Garching bei München,
Germany
10
Department of Astronomy & Astrophysics, University of
Toronto, 50 St. George Street,
Toronto, ON
M5S 3H4,
Canada
11
Max-Planck-Institut für Astronomie, Königstuhl 17, 69117
Heidelberg,
Germany
12
Landessternwarte, Zentrum für Astronomie der Universität
Heidelberg, Königstuhl, 69117
Heidelberg,
Germany
13
Universitäts-Sternwarte München,
Ludwig-Maximilians-Universität, Scheinerstr. 1, 81679
München,
Germany
14
Dunlap Institute for Astronomy and Astrophysics, University of
Toronto, 50 St. George Street,
Toronto M5S 3H4, Ontario, Canada
15
Department of Physics and Astronomy, UCLA,
Los Angeles, CA
90095-1547,
USA
16
Institute of Geophysics and Planetary Physics, UCLA,
Los Angeles, CA
90095-1565,
USA
Received: 31 October 2012
Accepted: 7 May 2013
Context. Our general understanding of multiple star and planet formation is primarily based on observations of young multiple systems in low density regions like Tau-Aur and Oph. Since many, if not most, of the stars are born in clusters, observational constraints from young binaries in those environments are fundamental for understanding both the formation of multiple systems and planets in multiple systems throughout the Galaxy.
Aims. We build upon the largest survey for young binaries in the Orion Nebula Cluster (ONC), which is based on Hubble Space Telescope observations to derive both stellar and circumstellar properties of newborn binary systems in this cluster environment.
Methods. We present adaptive optics spatially-resolved JHKL′-band photometry and K-band R ~ 5000 spectra for a sample of eight ONC binary systems from this database. We characterize the stellar properties of binary components and obtain a census of protoplanetary disks through K − L′ color excess. For a combined sample of ONC binaries including 7 additional systems with NIR spectroscopy from the literature, we derive mass ratio and relative age distributions. We compare the stellar and circumstellar properties of binaries in ONC with those in Tau-Aur and Oph from samples of binaries with stellar properties derived for each component from spectra and/or visual photometry and with a disk census obtained through K − L color excess.
Results. The mass ratio distribution of ONC binaries is found to be indistinguishable from that of Tau-Aur and, to some extent, to that of Oph in the separation range 85–560 AU and for primary mass in the range 0.15 to 0.8 M⊙. A trend toward a lower mass ratio with larger separation is suggested in ONC binaries, which is not seen in Tau-Aur binaries. The components of ONC binaries are found to be significantly more coeval than the overall ONC population and as coeval as components of binaries in Tau-Aur and Oph. There is a hint of a larger fraction of mixed pairs, i.e. systems with a disk around only one component, in wide ONC binaries in comparison to wide binaries in Tau-Aur and Oph within the same primary mass range that could be caused by hierarchical triples. The mass ratio distributions of mixed and unmixed pairs in the overall population of T Tauri binaries are shown to be different. Some of these trends require confirmation with observations of a larger sample of binary systems.
Key words: stars: pre-main sequence / binaries: close / techniques: high angular resolution
Based on observations obtained at the Gemini Observatory, which is operated by the Association of Universities for Research in Astronomy, Inc., under a cooperative agreement with the NSF on behalf of the Gemini partnership: the National Science Foundation (United States), the Science and Technology Facilities Council (United Kingdom), the National Research Council (Canada), CONICYT (Chile), the Australian Research Council (Australia), Ministério da Ciência e Tecnologia (Brazil), and SECYT (Argentina).
Appendices are available in electronic form at http://www.aanda.org
© ESO, 2013
Observed sample.
1. Introduction
The prevalence of double or higher order multiple systems among low-mass stars is now a well established fact for main sequence field stars (e.g., Duquennoy & Mayor 1991; Raghavan et al. 2010), and there is growing evidence that young stellar populations generally harbor as much as twice as many physical companions (Reipurth & Zinnecker 1993; Duchêne et al. 2007; Duchêne & Kraus 2013). Significant differences between star-forming regions have been documented (Duchêne 1999), and it remains unclear whether they stem from a different, more intense, dynamical evolution in dense clusters (like the Orion Nebula Cluster, ONC) or trace intrinsic variations in the output of the star formation process (Köhler et al. 2006; Reipurth et al. 2007).
In addition to the frequency of multiple systems (and its dependence on environment and primary mass) and to orbital characteristics like the separation distribution, stellar properties such as mass ratio and relative age distributions are able to give insight into the multiple star formation process (e.g. Hartigan et al. 1994; Brandner & Zinnecker 1997; Duchêne et al. 1999; Woitas et al. 2001; White & Ghez 2001; Hartigan & Kenyon 2003; Prato et al. 2003; Kraus & Hillenbrand 2009a; Kraus et al. 2011). The usefulness of such distributions to constrain formation models requires, however, determining the mass and age of young binary components in an unbiased way and with some accuracy, which implies the use of spectroscopy and multiwavelength photometry.
While our understanding of the physical processes responsible for the high degree of stellar multiplicity among young stars remains partial (e.g. Tohline 2002), this empirical fact has major consequences for theories of planet formation, which have been primarily developed in the context of isolated stars. Nevertheless, over 40 planet-hosting stars are members of multiple systems (Eggenberger & Udry 2010, and references therein), a substantial number when considering that binaries are usually excluded from planet surveys because of technical considerations. In fact, while there is marginal evidence that binaries tighter than ~200 AU are less likely to form planets (Eggenberger & Udry 2010), planet formation in such environments is not as rare as once thought. Instead, Duchêne (2010) has argued that planet formation follows a different path in tight binaries compared to wider binaries and single stars.
To better understand the processes of star and planet formation in binary systems, it is necessary to draw a complete picture of the stellar properties and of circumstellar disks in pre-main sequence (T Tauri) binary stars. Indeed, these disks are a ubiquitous outcome of star formation and serve as birthsite for planetary systems. In young binary systems, there is circumstantial evidence that the more massive primaries possess more massive and longer lived disks (e.g., Patience et al. 2008). Although it is tempting to relate this to the finding that extrasolar planets in multiple systems are almost exclusively found around primaries, strong selection effects prevent us from reaching a definitive conclusion.
While spatially unresolved studies, such as recent Spitzer surveys, have revealed intriguing trends (most notably the shorter disk lifetime for tighter binaries, Cieza et al. 2009, see also Kraus et al. 2012), it is critical to analyze the disk properties of individual components of multiple systems. A major reason is that all the studies using spatially unresolved disk indicators yield intrinsically biased comparisons between the frequency of disks in binaries and in singles, since they can only attest to the presence of at least one disk in a binary system. In addition, of particular interest are the so-called “mixed” systems, i.e. pairs of two T Tauri stars with only one of the two components hosting a circumstellar disk. The occurrence of these systems and any correlation with binary properties such as mass ratio and separation distributions may provide critical clues to the early phases of star formation, as well as the dissipation of disks and the prospects for planet formation in binary systems. Early studies found that such mixed systems are quite rare (e.g. Prato & Simon 1997; Duchêne et al. 1999; White & Ghez 2001; Hartigan & Kenyon 2003). However, recent analysis of a broader compilation of multiple systems revealed a much higher fraction of mixed systems (Monin et al. 2007). Most importantly, these authors concluded that there are substantial variations from one star-forming region to another in a way that cannot simply be explained by the age of the populations studied, again raising the possibility that star (and possibly planet) formation differs substantially from one cloud to the next.
Virtually all the studies about the physical properties of binaries have focused on nearby clouds, mostly Taurus-Auriga and Ophiuchus. However, it has become clear that clusters like the ONC are at least as likely a representative mode of star and planet formation (e.g. Lada & Lada 2003; Bressert et al. 2010). It is therefore important to revisit some of the “well-established” trends found in earlier studies in the light of a young dense cluster. The purpose of the present paper is to extend the previous studies about the stellar and circumstellar properties of pre-main sequence binaries to the ONC, the closest and prototypical young cluster. Specifically, we build on the hitherto largest ONC multiplicity survey by Reipurth et al. (2007, hereafter R07) using HST/ACS that has yielded the most complete census of binaries and higher-order multiples to date in the region.
 |
Fig. 1 K-band (two leftmost columns) and L′-band (two rightmost columns) NIRI imaging of the ONC binaries. The field of view is 2″ × 2″ and images are displayed with a logarithmic stretch. |
This paper is organized as follows: in Sect. 2 we present the sample of ONC binaries and describe the spectroscopic and photometric observations, while in Sect. 3 we derive the spatially-resolved photometry and check the relative astrometry. The stellar properties are derived in Sect. 4 and the circumstellar properties in Sect. 5. The results are used to investigate the distributions of mass ratio and of relative age in ONC binary components, as well as the occurrence of circumstellar disks. In Sect. 6 we discuss the properties of the mass ratio distribution and the presence of disks around wide binary components in the ONC and compare them to those in Tau-Aur and Oph.
Astrometric and photometric measurements.
2. Sample, observations and data reduction
2.1. Sample
Our sample of T Tauri binaries in the ONC were selected from the list of Reipurth et al.
(2007). The 8 binaries of the sample presented in
Table 1 are the optically brightest sources of
that list which can be observed with the Adaptive Optics (AO) system Altair on Gemini
North in natural guide star mode. The unresolved spectral types range from late-K to
early-M and the separations from 0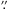 2 to
1
2 to
1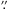 3, i.e. 85–560 AU at the distance of the
ONC of 415 pc (Menten et al. 2007). As a first step
towards building a relatively large sample of ONC binaries in order to obtain enough
statistics to study their stellar and disk properties, we complement our analysis with a
sample of 7 ONC binaries from a similar recent spatially-resolved spectro-photometric
study (Daemgen et al. 2012). These 7 additional
systems are among the brightest systems found in the small and localized NIR surveys of
Petr et al. (1998) and Köhler et al. (2006), some of them also detected in the optical R07
survey. All together our sample amounts to 15 T Tauri binaries, which represent a 10–15%
fraction of the known population of ONC binaries with separations between a few tens of AU
and ~500 AU.
3, i.e. 85–560 AU at the distance of the
ONC of 415 pc (Menten et al. 2007). As a first step
towards building a relatively large sample of ONC binaries in order to obtain enough
statistics to study their stellar and disk properties, we complement our analysis with a
sample of 7 ONC binaries from a similar recent spatially-resolved spectro-photometric
study (Daemgen et al. 2012). These 7 additional
systems are among the brightest systems found in the small and localized NIR surveys of
Petr et al. (1998) and Köhler et al. (2006), some of them also detected in the optical R07
survey. All together our sample amounts to 15 T Tauri binaries, which represent a 10–15%
fraction of the known population of ONC binaries with separations between a few tens of AU
and ~500 AU.
 |
Fig. 2 Sharper images of JW 248 Aa-Ab obtained after 100 iterations of the multiple LR deconvolution algorithm using JW 248 B as the PSF. |
2.2. Observations and data reduction
We obtained spatially-resolved J, H, K and L′-band photometry and R ~ 5000 K-band spectra for each individual component of the 8 close binaries listed in Table 1 using the Near IR Integral Field Spectrograph (NIFS) and the Near IR Imager (NIRI) at the Gemini North Telescope with both instruments fed by the AO system Altair (McGregor et al. 2002).
2.2.1. NIRI J, H, K and L′-band imaging
NIRI is a near-IR imager using a 1024 × 1024 Aladdin InSb array (Hodapp et al. 2003). The f/32 mode was used in all four filters
with a plate scale of 0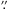 0218 pixel-1 and an
orientation of PA = 05 (Beck et al. 2004)
providing a field of view (FOV) of ~22″ × 22″. In L′ the faster
read-out mode required the use of a subarray reducing the FOV by half. Except for JW 63,
the observations in all filters were done consecutively in a single night. For JW 63,
the JHK observations were executed three days before the
L′ observations (see Table 1).
Observing conditions were for the most part photometric and with good seeing. The
on-source integration time ranged from 50 to 200 s in J, 43.8 to 200 s
in H, 15 to 200 s in K, and 333 to 804.8 s in
L′. The JHK photometric standards GSPC S840-F
(J = 11.365 ± 0.016, H = 11.099 ± 0.013,
K = 11.019 ± 0.009, MKO photometric system, Leggett et al. 2006) and HD 289907
(J = 9.857 ± 0.007, H = 9.818 ± 0.010,
K = 9.810 ± 0.010, MKO photometric system, Leggett et al. 2006) and the L′ photometric
standards HD 287736 (L′ = 8.559 ± 0.010, MKO photometric system,
Leggett et al. 2003) and HD 40335
(L′ = 6.441 ± 0.025, MKO photometric system, Leggett et al. 2003) were observed close in time (typically within
30 min) and airmass (within ≲0.2 airmass) to the targets. The difference in airmass
between targets and photometric standards is distributed with a mean and standard
deviation of 0.06 and 0.05, respectively, which is small enough to neglect extinction
correction. Due to an error in the preparation of the observations, GSPC S840-F was used
as L′ photometric standard for JW 709. In this case we estimated the
L′ magnitude of GSPC S840-F from its K magnitude.
Since the K − L′ color of this star should be no more
than 0.05 mag (from Bessell & Brett 1988) as
it is a G-type, around G5 (B − V = 0.69, Lasker et al.
1988), we set
L′ = 10.969 ± 0.050. Lamp flat and dark fields were also obtained.
0218 pixel-1 and an
orientation of PA = 05 (Beck et al. 2004)
providing a field of view (FOV) of ~22″ × 22″. In L′ the faster
read-out mode required the use of a subarray reducing the FOV by half. Except for JW 63,
the observations in all filters were done consecutively in a single night. For JW 63,
the JHK observations were executed three days before the
L′ observations (see Table 1).
Observing conditions were for the most part photometric and with good seeing. The
on-source integration time ranged from 50 to 200 s in J, 43.8 to 200 s
in H, 15 to 200 s in K, and 333 to 804.8 s in
L′. The JHK photometric standards GSPC S840-F
(J = 11.365 ± 0.016, H = 11.099 ± 0.013,
K = 11.019 ± 0.009, MKO photometric system, Leggett et al. 2006) and HD 289907
(J = 9.857 ± 0.007, H = 9.818 ± 0.010,
K = 9.810 ± 0.010, MKO photometric system, Leggett et al. 2006) and the L′ photometric
standards HD 287736 (L′ = 8.559 ± 0.010, MKO photometric system,
Leggett et al. 2003) and HD 40335
(L′ = 6.441 ± 0.025, MKO photometric system, Leggett et al. 2003) were observed close in time (typically within
30 min) and airmass (within ≲0.2 airmass) to the targets. The difference in airmass
between targets and photometric standards is distributed with a mean and standard
deviation of 0.06 and 0.05, respectively, which is small enough to neglect extinction
correction. Due to an error in the preparation of the observations, GSPC S840-F was used
as L′ photometric standard for JW 709. In this case we estimated the
L′ magnitude of GSPC S840-F from its K magnitude.
Since the K − L′ color of this star should be no more
than 0.05 mag (from Bessell & Brett 1988) as
it is a G-type, around G5 (B − V = 0.69, Lasker et al.
1988), we set
L′ = 10.969 ± 0.050. Lamp flat and dark fields were also obtained.
The data were reduced using the NIRI tasks in the Gemini IRAF package version 1.10. A
sky frame derived from the on-source raw frames was subtracted from the raw frames. The
frames were subsequently divided by the lamp flat field taken from the calibration unit
in JHK or by a sky flat field in L′ which was derived
from the on-source frames. The resulting images were then average-combined excluding the
bad pixels identified in the dark frames. The images of the binary systems in
K and L′-band are shown in Fig. 1. JW 248 A turned out to have a close
(~0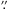 15 separation) faint (~3 mag
difference) visual companion. This companion is a discovery since it is not seen on the
HST-ACS images probably due to a large flux ratio in the visible between the primary and
the close companion candidate. Because of the relative faintness and closeness of the
companion in our AO images, we sharpened the images at each wavelength using multiple
Lucy-Richardson (LR) deconvolution of each single frame (e.g. Correia & Richichi
2000) with JW 248 B taken as the Point-Spread
Function – PSF (Fig. 2).
15 separation) faint (~3 mag
difference) visual companion. This companion is a discovery since it is not seen on the
HST-ACS images probably due to a large flux ratio in the visible between the primary and
the close companion candidate. Because of the relative faintness and closeness of the
companion in our AO images, we sharpened the images at each wavelength using multiple
Lucy-Richardson (LR) deconvolution of each single frame (e.g. Correia & Richichi
2000) with JW 248 B taken as the Point-Spread
Function – PSF (Fig. 2).
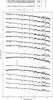 |
Fig. 3 K-band R ~ 5000 spatially-resolved NIFS spectra of the ONC binaries. Atomic and molecular features are labeled, as well as the main telluric correction residuals. |
2.2.2. NIFS R ~ 5000 K-band spectroscopy
NIFS is an image-slicing integral field unit (IFU). The NIFS field is 3″ × 3″ and the
individual IFU pixels are 0 1 × 0
1 × 0 04 on the sky. Seeing conditions were in
the range 0
04 on the sky. Seeing conditions were in
the range 0 3–1
3–1 0. The signal-to-noise was built up using
single exposure times of 60 s to 230 s per frame, 4 to 24 frames, and 50% of time
on-source, i.e. 10 to 20 min effective integration time per source. The instrument was
rotated along the PA of the binary in order to have the smallest pixel scale along the
binary separation.
0. The signal-to-noise was built up using
single exposure times of 60 s to 230 s per frame, 4 to 24 frames, and 50% of time
on-source, i.e. 10 to 20 min effective integration time per source. The instrument was
rotated along the PA of the binary in order to have the smallest pixel scale along the
binary separation.
The data were reduced using the NIFS tasks in the Gemini IRAF package version 1.10. For
each observation, a standard set of calibrations were acquired using the Gemini facility
calibration unit, GCAL (see details in Beck et al. 2008). The raw IFU frames were sky-subtracted using images of a nearby blank
sky field, flat-fielded, and cleaned out from residual bad pixels. A spatial
rectification was applied using a Ronchi calibration mask and the data were wavelength
calibrated with an arc exposure using Ar and Xe emission lamps taken shortly after the
observations. Telluric standards were observed and their data reduced following the same
procedure. Each target spectra were extracted through the data cubes with the IRAF task
nfextract using 0 1 and
0
1 and
0 25 radius circular apertures depending on
the binary separation. JW 248 Aa-Ab was not resolved and therefore considered as a
composite spectrum. This composite spectrum is assumed to be that of JW 248 Aa given the
faintness of JW 248 Ab. Telluric spectra were extracted using
0
25 radius circular apertures depending on
the binary separation. JW 248 Aa-Ab was not resolved and therefore considered as a
composite spectrum. This composite spectrum is assumed to be that of JW 248 Aa given the
faintness of JW 248 Ab. Telluric spectra were extracted using
0 25 radius apertures. The individual
spectra were median combined, the resulting spectrum of each target divided by the
corresponding telluric spectrum and multiplied by a blackbody spectrum of appropriate
temperature.
25 radius apertures. The individual
spectra were median combined, the resulting spectrum of each target divided by the
corresponding telluric spectrum and multiplied by a blackbody spectrum of appropriate
temperature.
HIP 22028 (A1V) and HIP 30594 (A0V) were used as telluric standard for JW 63, 128, 176, 391, 709 and JW 81, 248, 867, respectively. The spectra of HIP 22028 appeared to be time-variable, showing significant changes in continuum shape and occasionally emission-lines which cannot be attributed to atmospheric transmission variability. While the continuum of HIP 22028 for the observations corresponding to JW 63 and 709 were similar and well matched by a T = 9500 K blackbody, the continuum of HIP 22028 during the observations of JW 128, 176, and 391 changed locally dramatically by up to 20%. Moreover, emission-lines appeared which were also time-variable from one individual spectrum to another. The continuum of HIP 22028 was therefore fitted for JW 128, 176, and 391 with a 10th order Legendre polynomial with the IRAF task continuum and used in place of the blackbody spectrum to obtain the atmospheric transmission. We could also interpolate over the few strongest emission-lines. The Brackett gamma line of the telluric standards was removed using a Gaussian fit, except for JW 709 and 867 for which a linear interpolation gave better results (i.e. less residuals because the line profile is more peaked than a Gaussian). The resulting spectra are shown in Fig. 3 with the strongest atomic and molecular features labeled (compiled and cross-checked from several sources, notably Wallace & Hinkle 1996, 1997 and Hinkle et al. 1995).
3. Photometry and relative astrometry
Photometry and relative astrometry of the binary systems were performed using the tasks phot and mkapfile from the IRAF package APPHOT. The position of each system’s component is defined as the centroid of the brightness distribution within a box of 5 pixels width. At each wavelength, the error in the position measurement is the rms variation in our astrometric analysis with a minimum of 0.1 pixel. The final values of separation and position angle are the quadratic averages over the wavelengths, and the errors are the quadratic averages of the measurements errors which are added quadratically to the uncertainty in the plate scale and detector orientation. Since the plate scale of NIRI has not yet been characterized, we assumed a rather conservative plate scale uncertainty of 1%. Table 2 presents our resulting measurements.
 |
Fig. 4 Top: relative velocity of the binary components in RA and Dec between the positions from Reipurth et al. (2007, R07) reported in Table 1 and those measured in this study (our measured positions minus R07 positions). Bottom: relative velocity between Keck and Gemini measurements (Keck-Gemini), as well as between Keck and R07 measurements (Keck, R07) for JW 176, 391, and 709. The small relative motions between Keck and Gemini epochs are consistent with bound systems within the errors. |
We compared the separations and position angles with those measured in Reipurth et al. (2007) from HST-ACS images and reported in Table 1. The upper plot of Fig. 4 shows the relative velocity between the two measurements in RA and Dec. Uncertainties of the HST-ACS astrometry were considered quite conservatively and include a position measurement error of 5 mas (0.1 pixel) for each component and 15 mas in case the component is saturated. The detector scale and orientation uncertainties were assumed to be 2.45 mas (5% of plate scale) and 0.05°, respectively. The majority of the systems are consistent with no detectable relative motion between the two epochs, as expected for physical systems. As a comparison, the Keplerian velocity of a solar mass binary with a circular orbit in the plane of the sky would be in range of 1 to 3 km s-1 for this range of system separations (90 to 560 AU). JW 176, 391, and 709 are outliers at 2σ. The large relative velocities found for these systems could however be the result of the uncertainties from the measurements performed on the HST-ACS images due to small separations and large flux ratios and/or saturated components. In order to further explore this possibility, we obtained an additional epoch for these systems using AO-imaging with NIRC2 on Keck. The Keck observations were performed on 2011 Dec. 16 therefore providing a ~3.5 yr time baseline with respect to the Gemini observations, as well as a similar astrometric accuracy. Relative astrometry was extracted in the same way as for the Gemini measurements, considering plate scale and orientation uncertainties of 0.06% and 0.02°, respectively (Ghez et al. 2008). The derived astrometry is reported in Table 3 and the lower plot of Fig. 4 shows the relative velocity between these measurements and those from Gemini and HST-ACS data. The lack of significant relative motions between the Keck and the Gemini epochs indicates that the above outliers were indeed the result of biases in the HST images. While chance projection with a cluster member cannot in principle be excluded given the accuracy of these relative velocities and the velocity dispersion of the ONC (~2.5 mas yr-1 i.e. ~5 km s-1), we conclude that all systems are consistent with being bound systems within the uncertainties.
Additional astrometric measurements from Keck performed on 2011 Dec. 16.
Relative photometry of the individual binary components were performed with aperture radii
of 0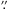 11 (5 pixels), except for JW 248 Aa and Ab
where they were 0
11 (5 pixels), except for JW 248 Aa and Ab
where they were 0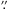 055 (2.5 pixels). The derived binary flux
ratios were combined with the aperture photometry of the entire systems to determine the
individual instrumental magnitudes. Aperture photometry was also employed for the
photometric standards. In both cases, small apertures were used and distinct aperture
corrections applied. The size of the apertures for the targets were the minimum radii to
encompass both components. For the standards, they were smaller and generally close to the
optimum aperture size (4–5 times FWHM). The convergence of the curves of growth determined
the values of the outer radius considered in the aperture corrections. The latter ranged
from ~1
055 (2.5 pixels). The derived binary flux
ratios were combined with the aperture photometry of the entire systems to determine the
individual instrumental magnitudes. Aperture photometry was also employed for the
photometric standards. In both cases, small apertures were used and distinct aperture
corrections applied. The size of the apertures for the targets were the minimum radii to
encompass both components. For the standards, they were smaller and generally close to the
optimum aperture size (4–5 times FWHM). The convergence of the curves of growth determined
the values of the outer radius considered in the aperture corrections. The latter ranged
from ~1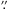 5 to
~5
5 to
~5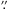 0, depending on the wavelength of
observation, the brightness of the source, the AO-correction, the presence of neighboring
sources, and the binary separation in the case of the targets. The final errors for the
component magnitudes take into account the errors in the instrumental magnitudes, the flux
ratios, the zero points, the aperture corrections, and the standard star magnitudes.
0, depending on the wavelength of
observation, the brightness of the source, the AO-correction, the presence of neighboring
sources, and the binary separation in the case of the targets. The final errors for the
component magnitudes take into account the errors in the instrumental magnitudes, the flux
ratios, the zero points, the aperture corrections, and the standard star magnitudes.
We compared our JHK magnitudes with those derived using a photometric calibration against the Two Micron All Sky Survey (2MASS) and converting our photometry from the MKO to the 2MASS photometric system with the color transformations from Carpenter et al. (20012). A 1σ scatter of 0.08, 0.05, and 0.06 mag was found in J, H, and K-band, respectively, which is consistent with the combined (2MASS and our) photometric errors. The largest deviations of ~0.2 mag may also be explained by photometric variability. JW 391 exhibits the maximum deviation in all JHK bands followed by JW 176 and 867 with ~0.15–0.10 mag in H and K. For all these systems active disk accretion is detected through the presence of Brγ emission and/or K − L color excess (Sect. 5) which could explain such photometric variability. It is interesting to note that the 2MASS magnitudes are found to be systematically fainter than our magnitudes by 0.07, 0.12, and 0.07 mag in J, H, and K-band, respectively. These differences cannot be explained by photometric variations but are most probably a result of photometric measurement methods. There are essentially no systematics in colors between our photometry and that derived from 2MASS except for JW 63 and JW 176 which are found to be clear outliers with HK2MASS − HK ~ 0.15 and JH2MASS − JH ~ −0.2, respectively. The JH − HK color–color diagram of the binary components (Fig. 5) shows the unusual location of these two systems. While a genuine color variation and/or contribution from scattered-light emission cannot be excluded, it is likely that this is due to a rapid variation in the sky transparency in H-band during the observation of these two systems.
 |
Fig. 5 Locus of the components of the ONC binaries in a J − H/H − K color–color diagram. Solid lines are the locus of photospheric dwarf and giant colors from Bessell & Brett (1988), while in dotted lines are shown the colors of young stellar photospheres of given spectral type in the range K4–L0 (Luhman et al. 2010). The dashed line is the CTTS locus from Meyer et al. (1997). The data point with large uncertainties is JW 248 Ab. All data are in the MKO photometric system. |
Astrometry of JW 248 Aa-Ab was performed on the deconvolved images. The values of separation and position angle were measured at each iteration of the LR algorithm in order to ensure convergence of these parameters which was observed to take place after typically 3000 iterations. The values and errors for each wavelength are the mean and rms of the values of the individual frames, and the final astrometry is the weigthed mean and standard deviation of the weighted mean of the astrometry over the JHK filters. In L′-band, only the co-added image was used. Because of possible biases introduced by the deconvolution process on the relative photometry, the flux ratio was estimated employing PSF-subtraction using the relative positions determined by the deconvolution. As before, the individual frames in JHK were used to derive the mean values and uncertainties. The JW 248 Aa-Ab pair is likely to be physically bound given the small separation and the low density of sources brighter than the brightness of the companion in the field. Using the 2MASS catalog in a field of 1.5 arcmin radius, and given the separation and magnitude of JW 248 Ab, the probability of a chance projection is ~2 × 10-4 in JHK. Although the H − K color is too blue but possibly contaminated by scattered-light emission (Fig. 5), the JHKL′ magnitudes and K − L′ color (1.07 ± 0.35) are suggestive of a late-M substellar source if bound.
 |
Fig. 6 Continuum-normalized spectra (upper panel) and non-continuum-normalized spectra (lower panel). The best-fit models (red) are also plotted and the derived spectral types, visual extinction AV, K-band IR-excess rK, and its blackbody temperature T reported. Atomic and molecular features are labeled, as well as the main uncorrected telluric features. |
4. Stellar properties
For each binary component we derived spectral type, visual extinction AV, infrared-excess in K-band rK, bolometric luminosity, mass, and age. Our method to derive spectral type, visual extinction, and infrared-excess is a composite of several methods and the results for each of them are shown in Table 4. The adopted values are reported in Table 5.
4.1. Spectral type, extinction, and infrared excess
The spectral typing made use of both a line ratio analysis of temperature-sensitive photospheric features and a spectral template fitting scheme which additionally provided K-band excess or veiling rK and visual extinction AV. rK is defined as the ratio of the infrared excess at 2.22 μm to the intrinsic stellar continuum flux. In addition, the spectral shape of the K-band excess is assumed to follow a blackbody function of temperature T. Our approach was the following. We obtained a first estimate of the spectral type, AV, rK and T by using a global template fitting scheme deriving these four parameters simultaneously. This gave us an idea about what to expect for these parameters. We then refined these first estimates by using line ratios, by deriving rK and T from continuum normalized template fitting with the spectral type fixed to its adopted value, and finally by obtaining AV from template fitting with the spectral type, rK and T fixed to their adopted values. We used this scheme in order to break the degeneracy that can occur when fitting all parameters simultaneously. Figure 6 shows the best-fit models together with the target spectra, with the spectra both continuum-normalized and not. Figure 7 focuses on two particular wavelength ranges with constraining photospheric features.
In the template fitting scheme the target spectrum was fit with a series of models of spectral type template stars which were veiled with infrared emission excess and reddened by extinction using a typical interstellar medium extinction law as defined in Prato et al. (2003). We used R ~ 2000 template spectra from the NASA IRTF SpeX stellar spectral library3 (Rayner et al. 2009). As the gravity of young low-mass stars is intermediate between that of giants and dwarfs due to their large radii, for each spectral type the spectral template used was a weighted average of dwarf and giant spectra with weights of 3/4 and 1/4, respectively. We used the locus of the binary components compared to that of the dwarf and giant templates on a Na 2.2076 μm + Ca 2.2634 μm versus CO(4–2) + CO(2–0) equivalent widths plot (Greene & Meyer 1995) as a guidance to define these weights (see Fig. A.1, upper left plot). Since K-band veiling could bias the use of such a plot as a gravity diagnostic, we restricted this procedure to the components with no obvious sign of IR-excess through K − L color, Brγ emission, and a posteriori rK determination. While extinction is in principle another source of bias for such a gravity tool, the effect on our low-extincted targets can be neglected. One should also note the remarkable locus of these intermediate-gravity templates with spectral type later than ~M5 on this plot. The library of spectral type template spectra was constructed with a resolution of 0.5 subclass by averaging adjacent spectra. The determination of the best-fit model was done using a χ2 minimization search. Wavelength ranges encompassing strong telluric correction residuals, as well as Brγ and the H2 2.12 micron features, were excluded from the χ2 computation. In the case of the continuum-normalized spectra, we found that excluding the CO lines from the χ2 computation gives more consistent results. This is presumably due to the strong sensitivity of the CO lines to gravity leading to small mismatches between the gravity of each target and the gravity assumed for the spectral templates. In both the template fitting scheme and the line ratio analysis, the binary component spectra were smoothed to the resolution of the spectral template library. In the template fitting scheme, the best-fit model in the minimum least-squares sense while fitting best the continuum shape was sometimes not giving a satisfactory fit to the relative strength of the photospheric features. In these cases the best-fit model was chosen by visual examination among the possible models closest to the χ2 minimum.
Determination of spectral type, extinction and K-band excess using different methods.
In the line ratio analysis we measured the equivalent width of the strongest photospheric features present in the spectra of the above specified template library and defined several diagnostic ratios of closeby features suitable for spectral typing, i.e. ratios exhibiting a monotonic behavior in a certain spectral type range. For the spectrum of each binary component we measured the same diagnostic ratios and derived a spectral type based on the relations previously determined from the spectral templates. The spectral type derived from the line ratio analysis is a weighted mean of the spectral types obtained from several line ratios (notably Mg 2.1066/Al 2.1169 μm, Mg 2.2814/Ca 2.2634 μm, and Si 2.1885/Ti 2.1903 μm), and its associated error the standard deviation of the weighted mean (see details in Appendix A). Fig. A.1 shows the behavior of some of these diagnostic line ratios. Even though the strong sensitivity to gravity of the ratio Mg 2.1066/Al 2.1169 μm, the locus of the targets on these plots are well matching those of the spectral templates, giving us confidence on the validity of those templates.
The adopted spectral type was chosen considering the results of the line ratio analysis and of the template fitting, both continuum normalized and not. While the continuum-normalized template fitting is relying mainly on the strength of all absorption features, the non-normalized template fitting is more sensitive to the shape of the continuum which is especially constraining for late (later than ~M2) spectral types based on the change of the spectra slope around 2.3 μm. Although the determination from both analyses are found to be in fair agreement, the spectral types from the non-normalized template fitting are found to be systematically later than those from the continuum-normalized template fitting and the line ratio analysis (see Table 4). The discrepancy between continuum slope and line strengths in our spectral templates is probably due to the intrinsic continuum slope of the spectrum of pre-main sequence (PMS) stars which are not simply the result of an average between giants and dwarfs but may be bluer, i.e. closer to the continuum of a giant for a given spectral type. In consequence, we gave in our analysis more weight to the spectral types derived from line ratio analysis and continuum-normalized template fitting. A spectral library of PMS stars would be very valuable in order to address this point. Figures 6 and 7 show that the quality of the fits degrades significantly for the latest type stars which is probably to be attributed to the templates. Besides the errors introduced by the templates, the values reported in Table 4 illustrate the uncertainties involved in the determination of the parameters and the risk of biased results when using only a simultaneous fitting method. We estimated a spectral typing error based on the values derived from the line ratio analysis with 0.5 subclass as a threshold. The uncertainties in rK and AV were estimated based on the spectral type errors. The rK values and uncertainties are the χ2 weighted means and standard deviations of the weighted mean of all rK values obtained from continuum-normalized template fitting with the spectral type varying within its uncertainties. Similarly, AV values and uncertainties were computed from the the χ2 weighted means and standard deviations of the weighted mean of all AV values derived from non-continuum-normalized template fitting within the spectral type ranges.
 |
Fig. 7 Continuum-normalized spectra with best-fit models around the Mg 2.1066 and Al 2.1169 μm features (upper panel) and around the Mg 2.2814 and Ca 2.2634 μm features (lower panel). |
Derived stellar properties.
The determination of AV and rK for each component based on the spectra was checked by estimating these quantities from photometry (Table 4). The extinction was derived for the components with disk signatures by dereddening to the CTTS locus (Meyer et al. 1997) and for the other components from the excess in J − H color given the adopted spectral type and using tabulated colors of young stellar photospheres from Luhman et al. (2010). The K-band excess rK was estimated from the H − K color excess using the same tabulated photospheric colors and the adopted value of extinction (e.g. Levine et al. 2006). This estimate is a lower-limit since the derivation assumes that rH = 0. All colors were converted to the CIT system and the extinction law used is that from Cohen et al. (1981). Uncertainties are the propagation of errors in colors, spectral type, and in the adopted AV value in the case of the derivation of rK. The values of AV derived from spectroscopy and from photometry agree at the 1.5σ level on average for all sources, with a better agreement for the WTTS components (1.2σ) compared to CTTS components (2.1σ). The K-band excesses estimated from spectroscopy and from photometry are consistent at the 1.7σ level on average.
4.2. Bolometric luminosity
The bolometric luminosity for each component was computed from the J-band magnitude and bolometric corrections from Kenyon & Hartmann (1995). We assumed a distance to the ONC of 415 pc as suggested from recent accurate trigonometric parallax measurements (Hirota et al. 2007; Sandstrom et al. 2007; Menten et al. 2007) and 10% relative error. The corresponding error in luminosity Δ log L is 0.09 dex which is the dominant source of error in derived luminosities. Minor source of errors are the uncertainties of 0.1 mag in the bolometric correction and those from the magnitudes (either J- or K-band) which translate in Δ log L of 0.04 dex and on average 0.01 dex. All errors were added quadratically.
 |
Fig. 8 H − R diagrams of the components of the T Tauri ONC binaries with the models of: (top) Baraffe et al. (1998), (middle) Palla & Stahler (1999), (bottom) Siess et al. (2000). |
It has been pointed out by Levine et al. (2006) that bolometric luminosities can be more accurately determined in the K-band than in the J-band when the extinction uncertainties are relatively large. However, in our case the luminosity uncertainties are on average only marginally smaller when using K-band magnitudes (⟨ Δ log L ⟩ = 0.110 dex) than with J-band (⟨ Δ log L ⟩ = 0.117 dex). The AV contribution to the error in log L is on average smaller in J-band (mean of 0.05 dex) than the sum of the AV and rk contributions in K-band (0.017 and 0.04 dex). In addition, the bolometric luminosities derived from K-band magnitudes are different to those derived from J-band by up to ±0.20 dex, but with a mean of only 0.02 dex. The reason is that, given the mean AV and rK values of our sample (0.75 ± 0.47 and 0.28 ± 0.12), the mean contribution to the luminosity from AV in J-band (+0.08 dex) is close to and opposite to the sum of the mean contributions from AV and rK in K-band (+0.03 and −0.11 dex). We further examined the difference in luminosity derived from J- and K-band as a function of AV and rK. When one splits the sample in two sub-samples of equal size, one with small rK values and the other one with large rK values, one obtains mean values of (log L)J − (log L)K of −0.03 and 0.07 dex, respectively. Therefore the correction for veiling could be introducing a bias on the luminosities. The same analysis performed on two sub-samples, one with high AV values and the other with low AV values, leads to a mean change in log L of 0.0 and 0.04 dex, respectively, which a priori excludes the possibility for a bias introduced by AV. Since the uncertainties of K-band derived luminosities are not significantly smaller than those of J-band derived luminosities, and given the possibility to be introducing a bias in K-band with the correction for veiling, we used here the J-band to compute bolometric luminosities.
4.3. Mass and age
The binaries of our sample are plotted in an H-R diagram together with the PMS evolutionary tracks of Baraffe et al. (1998 – B98), Palla & Stahler (1999 – PS99), and Siess et al. (2000 – S00) in Fig. 8. The spectral types were converted into effective temperatures using the intermediate-temperature scale from Luhman et al. (2003). We derived a mass and an age for each binary component using each set of PMS tracks (Table 5). To this purpose, we used interpolated values of the irregular grid of mass and age of the PMS tracks around the source loci. The estimated errors are the variations in mass and age computed from varying the effective temperature and luminosity within their uncertainties. For the B98 evolutionary models we used lmix/Hp = 1.0 and 1.9 at M/M⊙ ≤ 0.6 and M/M⊙ ≥ 0.6, respectively. The mass assigned to the sources falling above the 1 Myr isochrone of the B98 tracks was done by projecting down at constant temperature to the 1 Myr isochrone.
The mass of our sources estimated from the PS99 and S00 tracks are generally in good agreement, especially above ~0.4 M⊙. Below this value, S00 masses are slightly larger than PS99 masses by ~15%. Masses predicted by the B98 tracks are on average 20–30% larger than those derived from both S00 and PS99 tracks, in agreement with the results of Hillenbrand & White (2004). The mean age of all the components of our sample is of 0.87 ± 0.64 Myr and 1.25 ± 0.92 Myr for the PS99 and S00 tracks, respectively. Compared to the averaged values found for the whole ONC cluster from the same models (~2 Myr and ~3 Myr, respectively, Da Rio et al. 2010), our result shows that the optically-bright systems of our sample are among the youngest of the ONC binary population. The secondaries of JW 248 and 391 are close to being substellar with S00 masses of 0.13 ± 0.06 and 0.10 ± 0.02 M⊙, respectively.
Derived mass ratios and relative ages.
4.4. Mass ratio distribution
The differences in model-predicted masses are translating into mass ratios q = Msec/Mprim relatively mildly. Indeed, the mass ratio from different models are found to be quite unexpectedly in agreement (see Table 6). The uncertainties in mass ratio were estimated through a Monte-Carlo technique. Note that we took into account the fact that each component of a pair is at the same distance, therefore each realization in luminosity from each component of a pair was decomposed into a correlated term from the distance error and an uncorrelated term from the rest of the error contributors. The effect of such treatment is, however, relatively minor for the mass ratios as the tracks are mostly vertical.
In the following we will consider an extended sample of ONC binaries consisting of our sample of 8 binaries and 7 additional binaries for which spectral type and stellar luminosity for both components were derived in the spectroscopic and photometric study of Daemgen et al. (2012, hereafter D12). Figure 9 shows the distribution of mass ratio for this extended sample of ONC binaries. We compared this distribution with those for Tau-Aur wide binaries from White & Ghez (2001, hereafter WG01) and Hartigan & Kenyon (2003, hereafter HK03) and for Oph wide binaries from Prato et al. (2003, hereafter P03) spanning the separation range 85–560 AU and with primary masses in the range 0.15 to 0.8 M⊙, i.e. the separation range of the ONC sample and the range of primary mass encompassing most of the systems in these samples. For all systems of this plot the component masses, hence mass ratios, were uniformly derived from the three sets of PMS tracks. We used the spectral types and luminosities reported in WG01, HK03, P03, and D12 to derive the component mass of Tau-Aur, Oph, and ONC binaries, respectively (values reported in Tables B.1 and B.2). In our ONC sample, we excluded from the analysis the mass ratio derived from the B98 tracks for JW 248 and JW 391 because of the very uncertain estimate of their secondary masses. A Kolmogorov-Smirnov (K-S) test finds a high probability (≳40%) that all the distributions are drawn from the same parent population. Specifically, the probability of the K-S test between the ONC and Tau-Aur mass ratio distributions are 57, 43, and 55% for the B98, PS99, and S00 tracks, respectively. The corresponding values between ONC and Oph distributions are 55, 58, and 92%. Figure 9 also shows the best-fit power-law dN/dq ∝ qΓ to the q-distributions in ONC and Tau-Aur. In ONC and in the primary mass range 0.15–0.8 M⊙ we found Γ = 1.03 ± 0.66, 1.11 ± 0.37 and 0.57 ± 0.38 for the B98, PS99 and S00 tracks, respectively. Despite the large range of Γ encompassed by the different set of PMS tracks, the derived values are in agreement within the uncertainties. For each set of tracks the values of Γ in ONC are consistent with the corresponding values in Tau-Aur. Although statistics are small and selection biases may be present in our sample and in the comparison samples from Tau-Aur and Oph, this suggests that the mass ratio distribution of wide binaries with primary mass in the range 0.15 to 0.8 M⊙ are in agreement in these three regions.
 |
Fig. 9 Mass ratio distribution for the ONC binaries of our extended sample in comparison with the distribution derived for wide binaries in Tau-Aur and Oph with primary mass range 0.15 to 0.8 M⊙ using the B98, PS99, and S00 PMS tracks for systems with separations from 85 to 560 AU. Also shown are the best-fit power-laws dN/dq ∝ qΓ to the mass ratio distributions in ONC and Tau-Aur. The Tau-Aur distribution is offset along the x-axis for the purpose of clarity. |
4.5. Mass ratio vs. separation and distance from the Trapezium
In order to investigate the dependence of the mass ratio distribution on separation we compared the two distributions formed from systems with small and large separations. We used first a composite sample including all systems from ONC, Tau-Aur, and Oph with primary mass in the full mass range 0.15 to 3.0 M⊙ and computed the probability of the K-S test that both distributions are consistent with each other for a range of separation cut values. The upper-left panel of Fig. 10 shows that there is a minimum of the K-S probability at a separation cut between 200 and 280 AU for all set of tracks. A similar although less pronounced minimum at similar separations is seen when considering only systems with primary mass in the range 0.15 to 0.8 M⊙ (not shown). The other plots of Fig. 10 suggest that this feature is predominantly originating from the ONC and Oph samples and that systems from the comparative sample in Tau-Aur exhibit a mass ratio distribution essentially independent of separation. We conclude that there is a hint of a variation of the mass ratio distribution with separation in both Oph and ONC binaries which is not seen in Tau-Aur binaries.
While in the outer cluster regions starting at ~3–4 arcmin from the Trapezium the systems exhibit a mass ratio in the range 0.6–1.0, in the innermost cluster regions the smallest mass ratio systems of our sample are found (JW 248, JW 391, and [HC2000]73, see Fig. 14, upper plot). The presence of these low-mass ratio systems in the inner high stellar density regions of ONC is remarkable since dynamical interactions would tend to disrupt any weakly bound binaries. On the other hand, the formation of low-mass ratio systems is generally expected in a cluster environment for which gas and star motions are not correlated especially in the innermost regions (e.g. Bate 2001). In addition, in the lower plot of Fig. 14 it can be noted that among the systems at distances >4 arcmin there seems to be no trend toward a decreasing mass ratio with separation. This may suggest that the latter may be restricted to systems located in the inner parts of the cluster where dynamical interactions are more frequent.
 |
Fig. 10 K-S probability that the mass ration distribution of wide and close binaries derive from the same parent distribution as a function of the separation threshold. The sample is composed of systems from ONC, Tau-Aur, and Oph with primary mass range 0.15 to 3.0 M⊙ (upper-left), systems from Oph and ONC with primary mass range 0.15 to 3.0 M⊙ (upper-right), systems from Tau-Aur with primary mass range 0.15 to 3.0 M⊙ (lower-left), and systems from ONC with primary mass range 0.15 to 0.8 M⊙ (lower-right). Continuous line is for B98 tracks, dotted lines for PS99 tracks, and dashed line for S00 tracks. |
 |
Fig. 11 Distribution of the absolute difference in logarithmic age | Δ log τ | for the ONC binaries of our extended sample in comparison with the distribution derived for binaries in Tau-Aur and Oph using the PS99 (continous line) and S00 (dotted line) PMS tracks. The rms scatter in | Δ log τ | for both set of tracks are indicated by red lines. The rms of the | Δ log τ | distribution and its uncertainty are reported for each set of tracks and each sample. |
4.6. Relative age
The distribution of the absolute difference in logarithmic age | Δ log τ | = |log (ageprim) – log(agesec)| is shown in Fig. 11 for the extended sample of ONC binaries and is compared with that for the sample of Tau-Aur and Oph binaries. The values of relative age Δ log τ are reported in Table 6 for our ONC sample and in Table B.2 for the binaries from WG01, HK03, P03, and D12. The uncertainties in Δ log τ were estimated as in Sect. 4.4. In this case, the correlation of the luminosity errors due to the identical distance of each component of a pair resulted in a significant decrease of the relative age error. We excluded from our analysis the anomalous system JW 553. The secondary of this system is underluminous with ΔK ~ 3 mag with respect to the primary while both components have similar spectral types (see D12) suggesting a significant amount of flux from scattering due perhaps to a close to edge-on disk.
We found a consistent rms scatter in | Δ log τ | of the ONC distribution with values of 0.28 ± 0.09 and 0.30 ± 0.09 dex for the PS99 and S00 tracks, respectively. This means that the ages of the binary components are essentially within a factor two of each other. Compared to the sample of Tau-Aur and Oph binaries, the binaries in ONC are as coeval within the uncertainties. The distribution of absolute relative age | Δ log τ | in ONC and Tau-Aur are found to be consistent with K-S probabilities of 7.5% and 71% for the PS99 and S00 tracks, respectively. The corresponding probabilities between ONC and Oph are ~75%. We therefore conclude that the components of T Tauri binary stars in ONC are mostly as coeval as the components of T Tauri binaries in Tau-Aur and Oph. The rms scatter in | Δ log τ | of randomly paired single components of ONC binaries is 0.70 ± 0.08 and 0.73 ± 0.08 dex for the PS99 and S00 tracks, respectively. This is significantly larger than the standard deviation of the relative age of ONC binaries and this demonstrates that ONC binaries are more coeval than the overall ONC population. This matches with the conclusions of WG01 and Kraus & Hillenbrand (2009b) in Tau-Aur.
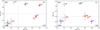 |
Fig. 12 K − L′ color (left) and K − L′ color excess (right) for the ONC binaries. The T Tauri type of each binary is named from the type of each component with C or W (CTTS or WTTS) indicating the presence or not of an inner disk. The dotted lines delimit the regions indicating the presence or not of an inner disk around each component, i.e. WW, CW, CC, and WC, with the first letter referring to the primary and the second to the secondary. Filled square symbols show systems with significant (>3σ) K-band excess rK which are all found in the primary only. Systems classified as Class II from Spitzer IRAC colors are plotted with large open diamonds. |
Derived accretion disk properties.
5. Circumstellar disks
5.1. Disk Census, fraction of mixed pairs
The left panel of Fig. 12 shows the observed K − L′ color of the secondary versus that of the primary for each ONC binary system. The T Tauri type of each binary is named from the type of each component with C or W (CTTS or WTTS) indicating the presence or not of an inner disk4. While K − L′ ≳ 0.4, which is roughly the photospheric K − L′ color of a M5 dwarf, suggests an IR-excess hence the presence of an inner disk, it is necessary to take into account reddening and spectral type to properly assess the presence or not of an inner circumstellar disk around each component. We therefore computed the K − L′ color excess of the individual components of ONC binary systems. The K − L′ color excess Δ(K − L′) is defined as the difference between the observed dereddened color and the photospheric color expected based on the spectral type. The photospheric K − L′ colors as a function of spectral type for M-dwarfs were derived from data of Leggett (1992) for M0-M4, and of Leggett et al. (2002) for M4-M9.5, converting the K-band data of Leggett (1992) from the CIT to MKO system. The resulting K − L′ scale is a 3rd order polynomial fit of the data and agrees well with the M-dwarf colors reported in Bessell & Brett (1988) for M0-M6 when converted to the MKO system. The uncertainties of Δ(K − L′) are those propagating photometric, spectral type, and reddening errors using a Monte-Carlo technique for the colors. The resulting excesses and their errors are listed in Table 7 and plotted in the right panel of Fig. 12. According to that analysis, JW 128 B, JW 176 A, JW 248 A, JW 391 A, and JW 867 A and B are consistent with having inner disks. Of these, JW 391 A, JW 867 A and B show Brγ emission. All the binary components with significant K-band excess rK exhibit K − L′ color excess (Fig. 12). The binary component JW 128 B shows K − L′ excess but no significant K-band veiling which indicates the presence of a disk with an inner hole. The systems with at least one component harboring an inner disk as revealed by the K − L′ color excess are the same systems classified as Class II from Spitzer IRAC colors (see Table 1 and Fig. 12).
From these measurements, JW 128, JW 176, JW 248, and JW 391 are mixed pairs, i.e. systems with a disk around only one component. In order to compute the fraction of mixed pairs and its uncertainties, we used a Monte-Carlo technique similar to that described in Liu et al. (2003) that take into account the color errors. This yields a fraction of mixed pairs of 42 ± 18%. When systems from D12 are also included, the fraction rises to 57 ± 12%. This can be compared to the fraction of 19 ± 7% found for binaries in Tau-Aur (Monin et al. 2007) or that of 21 ± 8% (5/24 systems) in the combined WG01 + HK03 sample. However, it can be noticed from the comparative samples in Tau-Aur and Oph that the fraction of mixed pairs is markedly larger in systems with a high-mass primary (see Table B.1). Restricting to wide binaries with separation >85 AU and to a common primary mass range of 0.15–0.8 M⊙ the fraction of mixed pairs is 20 ± 18% (1/5 systems) in both Tau-Aur and Oph comparative samples. Altogether there might be a hint that the fraction of mixed pairs is larger in ONC compared to Tau-Aur and Oph.
5.2. Accretion activity
Active accretion, revealed by the presence of Brγ emission, is another disk tracer although less reliable than K − L′ color excess. Indeed Brγ emission is seen in only a small fraction (~20%) of the components with K − L′ color excess. In Table 7 the accretion luminosity and mass accretion rate derived for these sources, as well as upper limits for the other components, are reported. The accretion luminosity is derived from the flux of the Brγ emission-line which is computed from the flux-scaled spectra, the distance, and the relation from Muzerolle et al. (1998, Eq. (2)). The spectra are flux-scaled using dereddened and de-veiled magnitudes previously converted to the 2MASS photometric system. The absolute calibration from 2MASS is used and the spectra are also multiplied by the transmission curve of the 2MASS Ks filter. Errors include uncertainties from the line flux measurement, errors from dereddening and de-veiling, and distance errors. The mass accretion rate is estimated from the accretion luminosity, stellar mass derived from B98 PMS tracks and stellar radius both reported in Table 5, using standard magnetospheric model (Gullbring et al. 1998, Eq. (8)). Mass accretion uncertainties include those from the accretion luminosity and the mass and radius uncertainties. Both derived accretion luminosities and mass accretion rates are found to be consistent with typical values for T Tauri stars (e.g. Muzerolle et al. 1998), as well as with sources of similar age and mass in ONC (Manara et al. 2012).
 |
Fig. 13 Mass ratio vs separation for binaries in ONC (this study), in Tau-Aur (WG01, HK03), and in Oph (P03) with T Tauri types (CTTS and WTTS) based on K − L color excess. For ONC systems, open symbols are systems taken from D12 with T Tauri types defined from a conjunction of rK, H − K color excess, and Brγ emission. Mass ratios derived from S00 tracks are plotted. |
5.3. Relation with mass ratio, separation, and component mass
The locus of the ONC mixed pairs in a mass ratio vs separation plot is shown in Fig. 13. For comparison the same samples of binaries with T Tauri types from Tau-Aur and Oph from WG01, HK03, and P03 as before are plotted. The T Tauri types are assigned from K − L color excess measured in this study, WG01, HK03, and in McCabe et al. (2006). For the ONC systems from D12 we assigned the T Tauri type based on a conjunction of rK, H − K color excess, and Brγ emission5. While such assignment is less secure than those based on K − L color excess, this gives us a rough estimate of the presence/absence of disks in this sample. Also, while including the D12 sample in the analysis of the presence of disks lowers the statistical uncertainties for ONC systems, it could introduce biases. For this reason, we will in the following mention also numbers without the D12 sample. We nevertheless note that such biases are likely to be small. If we compare the classification from D12 for the 8 sources of this study (therefore with K − L), only 2 out of the 16 components have their classification changed: JW 128 B (goes from W to C with the L band photometry) and JW 176 A (clear excess at L, not as marked in H − K). As found in the wide (≳100 AU) binaries from the Tau-Aur sample, and to a smaller extent from the Oph sample, mixed pairs in wide ONC binaries are present in both high- and low-mass ratio systems. This suggests that the disk dissipation timescale is independent of the system’s mass ratio for such wide binaries. Conversely, the mixed pairs in close (≲100 AU) binaries from Tau-Aur are mainly found in low mass ratio systems which is consistent with an early exhaustion of the secondary disk due to a smaller tidal truncation radius compared to the primary disk (Armitage et al. 1999). Overall the mass ratio distributions of mixed and unmixed pairs are found to be significantly different. A K-S test gives probabilities of 7%, 2.7%, and 0.05% that the two distributions are drawn from the same parent distribution for the B98, PS99, and S00 tracks. Similar values are found when the ONC systems are not included therefore confirming the result of Monin et al. (2007) and showing that ONC systems follow the same pattern. At separations ≳100 AU, the difference between these distributions are greatly reduced, especially for the B98 and PS99 tracks with K-S probabilities of 48%, 26%, and 0.6%. The mass ratio distribution of mixed pairs is therefore significantly different from that of unmixed pairs, especially at large separations.
Although the ONC and Oph samples are not covering the small separations, it seems that mixed pairs are mainly found at large separations which hints that early exhaustion due to disk truncation is not the main process for these systems to form. This is most apparent in the composite sample of binaries including all 3 regions but can also be seen within the limited separation range of ONC and Oph binaries. A K-S test on the separation distribution of mixed and unmixed pairs in the composite sample gives probabilities of 8%, 9%, and 3% that the two distributions are drawn from the same parent distribution for the B98, PS99, and S00 tracks. These probabilities are respectively 12%, 8%, and 14% when only considering ONC systems (including D12 systems). This is consistent with a more synchronized evolution of disks in close pairs and confirms the result based on accretion indicators from the ONC sample of D12.
The disk in mixed systems is mostly found around the primary for all binary samples. The only WC system identified from our sample (JW 128) is an equal-mass binary component, therefore the definition of the primary is arbitrary. The same applies for the equal-mass binary system JW 176. Finally, there seems to be a dependence of the presence of a disk on stellar mass. Including K − L measurement errors, the disk fraction of binary components with S00 masses >0.4 M⊙ is 65 ± 15% while it is 35 ± 20% for components with S00 masses <0.4 M⊙. It is unlikely that this can be explained exclusively by a lower sensitivity to disks around cooler components. While the amplitude of the K − L excess likely depends on the component mass, 4 out of the 6 components with S00 masses <0.4 M⊙ have a spectral type earlier than M4 and therefore assuming that the amplitude of IR-excess in binaries is similar to that in T Tauri singles, any K − L excess in these components should be detectable given our uncertainties (e.g. Kenyon & Hartmann 1995). For the coolest components, Liu et al. (2003) studied young brown dwarfs of M5.5-M9.5 type and found a K − L excess in the range ~0.15–0.4 which could have been missed in some of our cases. There is therefore a hint of mass dependence on the presence of disks such that higher mass components are more likely to harbor a disk.
5.4. Relation with distance from the Trapezium
We also investigated the relation between the presence of an inner disk and the distance of the system from the Trapezium. Although the plot of Fig. 14 shows no strong correlation, there is a trend toward a difference in the distance distribution of systems with and without disks such that systems with disks are found mainly in the inner regions at distance ≲7 arcmin from θ1 Ori C. Including the ONC systems T Tauri types from D12 leads to a K-S probability of 9% that the distance distribution of systems with disks (CC, CW, and WC) and without (WW) are drawn from the same distribution. While the explanation for such a difference is unclear, increasing further the sample size will tell us whether this trend is real or not.
 |
Fig. 14 Upper plot: mass ratio vs. the distance from θ1 Ori C with T Tauri types (CTTS and WTTS). Small symbols denote systems with separation <220 AU and large symbols separation >220 AU. Lower plot: mass ratio vs. binary separation with T Tauri types. Small symbols correspond to systems at a distance to θ1 Ori C < 4 arcmin and large symbols a distance >4 arcmin. As in Fig. 13 open symbols denote ONC systems from D12. Mass ratios derived from S00 tracks are plotted. |
6. Discussion
Given the small sample size and the presence of potential selection biases, one should be cautious in interpreting the results. Nevertheless, a few interesting trends, which need to be confirmed with a larger sample size, are identified. They can be compared qualitatively with theoretical expectations and with results from other environments.
6.1. A steep mass ratio distribution in ONC and Taurus?
In the most complete sample of multiple systems in Tau-Aur to date, Kraus et al. (2011) derived a mass ratio distribution in the primary mass range 0.25–0.7 M⊙ which is much flatter than that we obtained in both our Tau-Aur comparative sample and in our ONC sample. The exponent of the power-law they derived from their mass ratio distribution and using B98 tracks (Γ = 0.2 ± 0.4) is, however, still consistent with what we found here in our Tau-Aur comparison sample (see Sect. 4.4). An important difference between our study and that of Kraus et al. (2011) is that we used samples of binaries with stellar properties derived for each component from spectra (this study, HK03, P03, D12) and/or visual photometry (WG01). This has the advantage of taking into account differential extinction and veiling. When using flux ratio and system spectral type like it is done in many instances in Kraus et al. (2011) the mass ratio can be biased especially with flux ratios in K-band. Systems from our study, as well as from P03 and D12 studies, show that primaries are often significantly more veiled than their secondaries and that the visual extinction of primaries and secondaries are within a few magnitudes of each other. If the same holds for the systems in Tau-Aur then a method based on K-band flux ratios would lead to an overabundance of small mass ratio systems and therefore a flatter distribution. This could explain the fact that our Tau-Aur distribution is less flat than that derived in Kraus et al. (2011) in the same primary mass range, although a combination with selection effects cannot be excluded.
In order to check this assertion, we compared the mass ratio distribution for systems
with mass ratios derived from Kraus et al. (2011)
and in the primary mass range 0.15–0.8 M⊙ using the two
methods employed in this study. First, for systems with only K-band flux
ratio and system spectral type (39 out of the 89 pairs of the study), and second, for
systems with component spectral types taken from WG01 and HK03 and therefore in common
with our Tau-Aur comparative sample (15 systems). The distribution derived from flux ratio
is much flatter with Γ = 0.4 ± 0.5 than that using component spectral types for which
Γ = 1.1 ± 0.7. Although the systems with only flux ratio have on average smaller
separations than those with component spectral type (median of 20 mas vs 80 mas), this
difference in mass ratio distribution is presumably not a selection effect since Kraus et
al. (2011) did not find evidence for a variation of
mass ratio distribution with separation. It is also unlikely that the difference arises
from a better sensitivity to low mass ratio systems at small separations
(ΔK ~ 5 mag at λ/D, i.e. ~70 mas vs.
~2.5 mag at ~0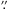 1 for speckle surveys in the 90s) since
most of the close new systems have ΔK < 2.5 mag. Nevertheless,
possible selection effects are that (1) the systems with only flux ratio are due to the
use of a more complete census of cloud members including sources not only selected from
Hα surveys but also from criteria such as IR-excess and lithium test,
and (2) the systems with component spectral types taken from WG01 and HK03 are not
representative of the Taurus binary population.
1 for speckle surveys in the 90s) since
most of the close new systems have ΔK < 2.5 mag. Nevertheless,
possible selection effects are that (1) the systems with only flux ratio are due to the
use of a more complete census of cloud members including sources not only selected from
Hα surveys but also from criteria such as IR-excess and lithium test,
and (2) the systems with component spectral types taken from WG01 and HK03 are not
representative of the Taurus binary population.
Our result is consistent with the study of mass ratio from Woitas et al. (2001). Although they are estimating masses from system spectral type and flux ratio, the latter are in J-band which a priori minimizes biases from IR-excess. While their sample is composed of binaries from several star-forming regions (Tau-Aur, Cha I, Lupus, Upper Scorpius) most systems are from Tau-Aur. Both the primary mass range and the separation range are similar to that of our samples. The power-law exponent we computed from the mass ratio distribution they derived with the B98 set of tracks is 0.8 ± 0.2, in agreement with what we found in the ONC and in the comparative Tau-Aur sample.
Although selection effects are a complex issue, we would like to understand to which extent those could affect our results. To do so, one has to consider the completeness of the multiplicity survey on which the binary sample is based (i.e. the observational technique and target list used) and how the observed binaries were selected from this sample. Since R07 searched for the multiplicity of all ONC members present in their Hα imaging survey which covered most of the cluster, their sample can be considered as volume-limited. A possible source of bias in the binary sample of R07 is the strong and localized nebulosity emission in Hα which could prevent from detecting faint companions although the survey is complete down to 5 mag flux difference. The sensitivity to faint companions is also lower in the optical than at NIR wavelengths due to the steeper stellar mass-luminosity relation. Thus, in comparison with the NIR multiplicity surveys in Tau-Aur and Oph, the R07 survey is presumably more incomplete for small (q ≲ 0.2) mass ratio binaries. The sample of ONC binaries for which we investigated the mass ratio distribution includes the optically brightest systems of the R07’s list6, i.e. the 8 binaries of this study. The additional 7 systems from D12 are among the brightest systems found in the NIR surveys of Petr et al. (1998) and Köhler et al. (2006). The natural question that arises is whether or not this selection of bright objects favors equal-mass systems. In order to check that, we compared the distribution of flux ratio in Hα for our extended sample with that of the binary population from R07. For the 10 systems present in R07 (all from this study and 2 from D12), the distribution of flux ratio in Hα presents a similar extension to the R07 distribution and is statistically indistinguishable with a K-S probability of 98%. Assuming that the flux ratio in Hα is indicative of the ratio of photospheric fluxes, this indicates that our extended ONC binary sample should not be significantly biased towards equal-mass systems. Since the selection of binaries in WG01 and HK03 is not based on flux ratios but on the at that time current binary census for WG01 and on T Tauri type and separation (CTTS and subarcsecond binaries) for HK03, a similar conclusion should be reached concerning the comparative sample we used in Tau-Aur. This suggests that selection biases are probably not a significant effect when analyzing the mass ratio distribution from the ONC and Tau-Aur samples. Whether selection criteria have led to a somewhat biased mass ratio distribution, studying a larger sample of ONC binaries is needed to reduce the statistical uncertainties, which are still too large to allow for decisive conclusions to be reached, relative both to other star-forming regions or to field stars.
6.2. The mass ratio distribution in ONC and in other environments
We found that the mass ratio distribution of wide (≳100 AU) low-mass binary stars appears to be independent of the environment when comparing ONC, Tau-Aur, and Oph distributions. Bate (2000, 2001) predicted that the decoupling of gas and stars would imply a flatter q-distribution in dense clusters than in isolated protostellar accretion for which the gas has a higher specific angular momentum. Accordingly, this would mean that the mass ratio distribution in ONC should be flatter than in Tau-Aur in contrast to what is observed. However, systems located in the outer cluster regions have been subject to little or no dynamical interactions compared to the inner cluster regions. If we only consider the systems closer than 3–4 arcmin from the Trapezium, then the q-distribution is much flatter. With a dividing distance set to 3.5 arcmin, the two q-distributions formed from S00 tracks and for systems in the primary mass range 0.15–0.8 M⊙ have Γ = 0.0 ± 0.2 and 0.3 ± 0.6 for the inner and outer regions, respectively. While these numbers are not yet statistically significant, it could be an indication for a variation of the mass ratio distribution with the distance to the cluster center.
There is an indication for a decreasing mass ratio with increasing separation in ONC binaries which would be consistent with theoretical predictions (Bate 2001, 2009). Further there are hints that this trend is only present for systems located in the inner regions of the cluster with a dividing distance at ≈4 arcmin. The mass ratio distribution of our comparison sample in Tau-Aur shows no significant variation with separation which is in agreement with the results from other studies (Woitas et al. 2001; Kraus et al. 2011). More generally, the trend with separation in the ONC is in contrast with the situation in the field and in other young associations and clusters (Reggiani & Meyer 2011) where no significant variation of the mass ratio distribution with binary separation was found.
In a more speculative way, the mass ratio distribution in the ONC could be composed of two regimes. A first regime for the systems in the inner cluster regions where dynamical interactions tend to favor the formation of low-mass ratio systems leading to a mass ratio distribution which is flatter than in Tau-Aur and is a decreasing function of the binary separation. A second regime in the outer regions of the cluster where the dynamical interactions are much reduced and is reminiscent of isolated star formation like in Tau-Aur, i.e. the mass ratio distribution tends to peak towards unity and is independent of separation.
6.3. Circumstellar disks around wide binary components
Two aspects can be considered regarding the evolution of disks in young binary components. First, one can compare the occurrence of circumstellar disks around wide binary components with that around apparently single stars for a given environment. Second, the relative evolution of disks around these binary components can be investigated as a function of environment as well.
A comparison of the fraction of disks in binary components (54 ± 13% and 52 ± 9% with D12 systems, including K − L measurement errors) with that in the population of single stars in ONC (80 ± 7%, Lada et al. 2000) would indicate that there is a significantly lower fraction of disks in binaries compared to singles. In order to remove any possibility for accelerated disk evolution due to disk truncation, we could further restrict to systems with separation >200 AU and would obtain 50 ± 20% and 56 ± 13% with D12 systems, including K-L measurement errors, i.e. the same result with a slightly lower statistical significance. However, since the survey of Lada et al. (2000) only covered the inner regions of the ONC (6 × 6 arcmin), we should take into account only systems located at a distance up to ~3 arcmin from θ1 Ori C. There are only 2 systems at such a distance in our sample (7 with D12 systems) and the corresponding fraction of disks in binary components becomes 72 ± 22% and 66 ± 14% with D12 systems, including K − L measurement errors, therefore not statistically different from that of singles. There is therefore no evidence for a difference in the frequency of disks, hence disk lifetime, around wide binary components and around singles in ONC.
The situation seems to be similar in Tau-Aur and Oph. In Tau-Aur there is a fraction of disks in binary components of 75 ± 13% (9 disks/12 components in systems with separation >200 AU) in the WG01 + HK03 sample. If one considers the Tau-Aur sample studied by McCabe et al. (2006) the fraction is 83 ± 9%, (15/18). These numbers agree with the disk fraction in Tau-Aur singles of 63 ± 9% derived from Spitzer measurements (Hernández et al. 2007; Hartmann et al. 2005). Kraus et al. (2012) reached a similar conclusion using a larger sample size and with binaries and singles identified at smaller spatial scales, although their result could have been biased by the use of unresolved disk indicators. This bias actually depends on the fraction of mixed pairs and their separation distribution. As already noted in D12, the effect could be substantial if mixed pairs are predominantly distributed at larger separations. In Oph the fraction of disks in binary components is 79 ± 11% (11/14 components in systems with separation ≳200 AU) from the sample of P03. Wilking et al. (2008) counted 93 Class II and 38 Class III objects among the L1688 cloud members based on Spitzer IRAC colors which implies a disk fraction of 71 ± 4%. Therefore, in both these star-forming regions the disk fraction of singles and of wide binary components are in agreement as it is found in the inner regions of the ONC cluster.
The frequency of disks around primaries and secondaries agree within the uncertainties with values of 67 ± 15% and 47 ± 16%, respectively, and 69 ± 11% and 38 ± 12% when D12 systems are included. In this frequency the systems with mass ratio unity JW 128 and JW 176 are counted both in primaries and secondaries. On the other hand there is a significant fraction of mixed pairs (see Sect. 5.1) and a hint that this fraction could be higher than the frequency of mixed pairs in wide binaries in Taur-Aur and Oph within the same primary mass range.
Mixed systems are more frequently found in wider pairs, their occurrence is mostly dependent of mass ratio (most strictly in Oph and more marginally in ONC), is increasing with primary mass, and the disk is generally found around the primary component. The fact that the presence of mixed pairs is relatively dependent of mass ratio is rather expected. It is reasonable to think that systems with exhausted secondary disks are systems with small mass ratio for which less material was accreted by the proto-secondary compared to the proto-primary hence leading to both low mass ratio and smaller secondary disk mass. In this framework, systems with similar stellar masses should have similar disk masses as well. A possible explanation for the presence of mixed pairs with high mass ratio could be that the disk around the secondary has an inner hole. McCabe et al. (2006) found that 14 ± 5% (7/51 binary components) of binary components have disks without K − L excess. We can therefore expect 2.6 binary components with disks without K − L excess in our sample which is similar to the 2 binary components (JW 128 A and JW 176 B) without K − L excess found in high mass ratio (q > 0.9) mixed-systems. Alternatively, these systems could be high-order hierarchical multiples (triples, quadruples) for which the close (presumably a few AU to a few tens of AU depending on eccentricity) yet undetected companion would tidally truncate one of the component disk leading to its earlier dissipation. Incidentally, ~25% of wide T Tauri binaries are found to be triples or quadruples (Correia et al. 2006), which is similar to the fraction of mixed pairs found in Taurus and Oph. The discovery of a hierarchical triple candidate in our small sample size (JW 248), for which the separation of the additional companion is however likely too large to lead to an early disk dissipation at a ~1 Myr age, strengthens the possibility that the origin of mixed pairs in ONC and perhaps also in Taurus and Oph could be in part due to hierarchical multiples.
In addition to the above considerations, it could be that, as for the mass ratio distribution, the systems in the inner regions are dominated by mixed pairs due to the fact that accretion is occurring mainly on the primary star and disk. As for the mass ratio, studies of protostellar accretion suggest that most of the accreted material should be accreted by the primaries in a cluster environment because of the small specific angular momentum of this material. Therefore, disks should be significantly less massive and long-lived around secondaries than around primaries. As for mass ratios, it would be expected that the effect is stronger in the inner cluster regions implying a larger number of mixed pairs in these regions and that mixed pairs occur primarily in low-mass ratio systems. This is what is found for the 2 systems at distance ≲3.5 arcmin from θ1 Ori C with known K − L colors, and for 4 out 7 systems in these regions when including systems from D12.
Finally, a high fraction of mixed pairs in dense clusters, and further the fact that the lone disk is usually found around the primary, would be consistent with a small fraction of extrasolar planets around the secondary component of binaries. Although the statistics of close hot Jupiter-like planets and Super-Earths around the components of mature binary stars is clearly biased against their detection around secondaries, the scarcity of planets around secondaries7 indicates that their frequency is probably rather small compared to that around primaries. This could be explained by the absence of the inner circumsecondary disk in mixed pairs at an evolutionary stage as early as a few Myr because the suggested short lifetime of these disks would a priori preclude the formation of planets.
7. Summary
We have derived the stellar and circumstellar properties for the components of 8 young low-mass wide binaries in the ONC through spatially-resolved K-band R ~ 5000 spectroscopy and near-IR JHKL′ photometry. The sample is complemented with 7 additional systems for which the stellar properties were recently derived using similar methods (Daemgen et al. 2012) and comparison is made with samples from Tau-Aur and Oph in order to investigate the dependence on the environment. The main results are as follows:
-
1.
The mass ratio distribution of ONC binaries isindistinguishable from that of Tau-Aur and to some extent fromthat of Oph. There is an indication for a variation of the mass ratiodistribution with separation for ONC binaries which is not seen inTau-Aur binaries. Such variation may be limited to systemslocated in the inner cluster regions.
-
2.
The components of ONC binaries are significantly more coeval than the overall ONC population and are found to be as coeval as components of binaries in Tau-Aur and Oph within the uncertainties.
-
3.
The presence of inner disks around wide ONC binary components is found to be less frequent than the presence of inner disks around ONC single stars. However, when considering only systems located in the inner cluster regions, the fractions of disks around wide binary components and singles are not statistically different in ONC, as it is found in Tau-Aur and Oph.
-
4.
There is a hint of a larger fraction of mixed pairs in wide ONC binaries in comparison to wide binaries in Tau-Aur and Oph within the same primary mass range. The mass ratio distribution of mixed and unmixed pairs are found to be significantly different for all systems of the three star-forming regions.
-
5.
Among the 8 ONC binaries of our sample we uncovered a new hierarchical triple candidate. This supports the idea that hierarchical triples could be a non-negligible cause for the large fraction of mixed pairs in the ONC.
Online material
Appendix A: Line ratio analysis
 |
Fig. A.1 Locus of the binary components in several equivalent width diagnostic plots. These plots are the Na 22076 μm + Ca 2.2634 μm versus CO(4–2) + CO(2–0) (upper right), Al 2.1169 μm versus Mg 2.1066 μm (upper left), Mg 2.2814/Ca 2.2634 μm versus Mg 2.1066/Al 2.1169 μm (lower left), and Si 2.1885/Ti 21903 μm versus Mg 2.1066/Al 2.1169 μm (lower right). The ONC binary components (in black) are labeled, as well as the spectral type of the dwarf (red), giant (turquoise), and intermediate-gravity (blue) spectral type templates. |
Determination of spectral type using several line ratios.
Appendix B: Comparative samples of T Tauri binaries
We used several samples of T Tauri binaries to study the dependency of the properties of T Tauri binaries on the environment. In order to minimize potential biases introduced by relative extinction and veiling, we prefer to use systems with a significant amount of observational data especially including spectroscopy and/or visual photometry. The considered samples are those from WG01 (20 systems) and HK03 (19 systems) in Tau-Aur, from P03 in Oph (8 systems), and from D12 in ONC (7 systems). We used the spectral types and luminosities reported in these studies to derive the component mass and age from
the B98, PS99, and S00 PMS tracks. For those 9 systems from WG01 found in HK03 we used the stellar parameters derived in HK03. Errors in spectral type were assumed to be ±1 subclass for WG01, HK03, and P03 and those reported in the case of D12. For HK03 systems uncertainties in log L were assumed to be 0.2 dex. The T Tauri types (C for CTTS and W for WTTS) were assigned from resolved IR-excess measurements, notably the K − L measurements from McCabe et al. (2006). For the D12 sample, we made use of criteria such as rK, H − K color excess, and Brγ emission. The component masses and ages are reported in Table B.1 and the system mass ratios and relative ages are shown in Table B.2.
Derived stellar properties of comparative samples of T Tauri binaries.
Derived mass ratios and relative ages.
Acknowledgments
We thank the referee for detailed and helpful comments on this paper. The authors wish to recognize and acknowledge the very significant cultural role and reverence that the summit of Mauna Kea has always had within the indigenous Hawaiian community. We are most fortunate to have the opportunity to conduct observations from this mountain. This material is based upon work supported by the National Aeronautics and Space Administration through the NASA Astrobiology Institute under Cooperative Agreement No. NNA09DA77A issued through the Office of Space Science. This research made use of data products from the Two Micron All Sky Survey and of the SIMBAD database, operated at CDS, Strasbourg, France.
References
- Armitage, P. J., Clarke, C. J., & Tout, C. A. 1999, MNRAS, 304, 425 [NASA ADS] [CrossRef] [Google Scholar]
- Bakos, G. Á., Noyes, R. W., Kovács, G., et al. 2007, ApJ, 656, 552 [NASA ADS] [CrossRef] [Google Scholar]
- Baraffe, I., Chabrier, G., Allard, F., et al. 1998, A&A, 337, 403 [B98] [NASA ADS] [Google Scholar]
- Bate, M. R. 2000, MNRAS, 314, 33 [NASA ADS] [CrossRef] [Google Scholar]
- Bate, M. R. 2001, in The Formation of Binary Stars, eds. H. Zinnecker, & R. D. Mathieu (San Francisco: ASP), IAU Symp., 200, 429 [Google Scholar]
- Bate, M. R. 2009, MNRAS, 392, 590 [NASA ADS] [CrossRef] [Google Scholar]
- Beck, T. L., Schaefer, G. H., Simon, M., et al. 2004, ApJ, 614, 235 [NASA ADS] [CrossRef] [Google Scholar]
- Beck, T. L., McGregor, P. J., Takami, M., & Pyo, T.-S. 2008, ApJ, 676, 472 [NASA ADS] [CrossRef] [Google Scholar]
- Bessel, M. S., & Brett, J. M. 1988, PASP, 100, 1134 [NASA ADS] [CrossRef] [Google Scholar]
- Brandner, W., & Zinnecker, H. 1997, A&A, 321, 220 [Google Scholar]
- Bressert, E., Bastian, N., Gutermuth, R., et al. 2010, MNRAS, 409, L54 [NASA ADS] [Google Scholar]
- Cieza, L. A., Padgett, D. L., Allen, L. E., et al. 2009, ApJ, 696, L84 [NASA ADS] [CrossRef] [Google Scholar]
- Cochran, W. D., Hatzes, A. P., Butler, R. P., & Marcy, G. W. 1997, ApJ, 483, 457 [NASA ADS] [CrossRef] [Google Scholar]
- Cohen, J. G., Persson, S. E., Elias, J. H., & Frogel, J. A. 1981, ApJ, 249, 481 [NASA ADS] [CrossRef] [Google Scholar]
- Correia, S., & Richichi, A. 2000, A&AS, 141, 301 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Correia, S., Zinnecker, H., Ratzka, Th., & Sterzik, M. 2006, A&A, 459, 909 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Daemgen, S., Correia, S., & Petr-Gotzens, M. 2012, A&A, 540, A46 [D12] [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Da Rio, N., Robberto, M., Soderblom, D. R., et al. 2010, ApJ, 722, 1092 [NASA ADS] [CrossRef] [Google Scholar]
- Delfosse, X., Bonfils, X., Forveille, T., et al. 2013, A&A, 553, A8 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Duchêne, G. 1999, A&A, 341, 547 [NASA ADS] [Google Scholar]
- Duchêne, G. 2010, ApJ, 709, L114 [NASA ADS] [CrossRef] [Google Scholar]
- Duchêne, G., & Kraus, A. 2013, ARA&A, in press [Google Scholar]
- Duchêne, G., Monin, J.-L., Bouvier, J., & Ménard, F. 1999, A&A, 351, 954 [NASA ADS] [Google Scholar]
- Duchêne, G., Delgado-Donate, E., Haisch, K. E., Jr., et al. 2007, in Protostars and Planets V, eds. B. Reipurth, D. Jewitt, & K. Keil (Tucson: Univ. Arizona Press), 379 [Google Scholar]
- Dumusque, X., Pepe, F., & Lovis, C. 2012, Nature, 491, 207 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Duquennoy, A., & Mayor, M. 1991, A&A, 248, 485 [NASA ADS] [Google Scholar]
- Eggenberger, A., & Udry, S. 2010, in Planets in Binary Star Systems, 1st edn. (Berlin: Springer), 366, 19 [Google Scholar]
- Getman, K. V., Feigelson, E. D., Grosso, N., et al. 2005, ApJS, 160, 353 [NASA ADS] [CrossRef] [Google Scholar]
- Ghez, A. M., Salim, S., Weinberg, N. N., et al. 2008, ApJ, 689, 1044 [NASA ADS] [CrossRef] [Google Scholar]
- Greene, T. P., & Meyer, M. R. 1995, ApJ, 450, 233 [NASA ADS] [CrossRef] [Google Scholar]
- Gullbring, E., Hartmann, L., Briceño, C., & Calvet, N. 1998, ApJ, 492, 323 [NASA ADS] [CrossRef] [Google Scholar]
- Hartigan, P., & Kenyon, S. J. 2003, ApJ, 583, 334 [HK03] [NASA ADS] [CrossRef] [Google Scholar]
- Hartigan, P., Strom, K. M., & Strom, S. E. 1994, ApJ, 427, 961 [NASA ADS] [CrossRef] [Google Scholar]
- Hartmann, L., Megeath, S. T., Allen, L., et al. 2005, ApJ, 629, 881 [NASA ADS] [CrossRef] [Google Scholar]
- Hernández, J., Hartmann, L., Megeath, T., et al. 2007, ApJ, 662, 1067 [NASA ADS] [CrossRef] [Google Scholar]
- Hillenbrand, L. A. 1997, AJ, 113, 1733 [NASA ADS] [CrossRef] [Google Scholar]
- Hillenbrand, L. A., & White, R. J. 2004, ApJ, 604, 741 [NASA ADS] [CrossRef] [Google Scholar]
- Hinkle, K., Wallace, L., & Livingston, W. 1995, PASP, 107, 1042 [NASA ADS] [CrossRef] [Google Scholar]
- Hirota, T., Bushimata, T., Choi, Y. K., et al. 2007, PASJ, 59, 897 [NASA ADS] [CrossRef] [Google Scholar]
- Hodapp, K.-W, Irwin, E. M., Yamada, H., et al. 2003, PASP, 115, 1388 [NASA ADS] [CrossRef] [Google Scholar]
- Jones, B. F., & Walker, M. F. 1988, AJ, 95, 1755 [NASA ADS] [CrossRef] [Google Scholar]
- Kenyon, S. J., & Hartmann, L. 1995, ApJS, 101, 117 [NASA ADS] [CrossRef] [Google Scholar]
- Köhler, R., Petr-Gotzens, M. G., McCaughrean, M. J., et al. 2006, A&A, 458, 461 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kraus, A. L., & Hillenbrand, L. A. 2009a, ApJ, 703, 1511 [NASA ADS] [CrossRef] [Google Scholar]
- Kraus, A. L., & Hillenbrand, L. A. 2009b, ApJ, 704, 531 [Google Scholar]
- Kraus, A. L., Ireland, M. J., Martinache, F., & Hillenbrand, L. 2011, ApJ, 731, 8 [NASA ADS] [CrossRef] [Google Scholar]
- Kraus, A. L., Ireland, M. J., Hillenbrand, L. A., & Martinache, F. 2012, ApJ, 745, 19 [NASA ADS] [CrossRef] [Google Scholar]
- Lada, C. J., & Lada, E. A. 2003, A&ARA, 41, 57 [Google Scholar]
- Lada, C. J., Muench, A. A., Haisch, K. E., Jr., et al. 2000, AJ, 120, 3162 [NASA ADS] [CrossRef] [Google Scholar]
- Lasker, B. M., Sturch, C. R., & Lopez, C. 1988, ApJS, 68, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Leggett, S. K. 1992, ApJS, 82, 351 [NASA ADS] [CrossRef] [Google Scholar]
- Leggett, S. K., Golimowski, D. A., & Fan, X. 2002, ApJ, 564, 452 [NASA ADS] [CrossRef] [Google Scholar]
- Leggett, S. K., Hawarden, T. G., Currie, M. J., et al. 2003, MNRAS, 345, 144 [NASA ADS] [CrossRef] [Google Scholar]
- Leggett, S. K., Currie, M. J., Warricatt, W. P., et al. 2006, MNRAS, 373, 781 [NASA ADS] [CrossRef] [Google Scholar]
- Levine, J. L., Steinhauer, A., Elston, R. J., & Lada, E. A. 2006, ApJ, 646, 1215 [NASA ADS] [CrossRef] [Google Scholar]
- Liu, M. C., Najita, J., & Tokunaga, A. T. 2003, ApJ, 585, 372 [NASA ADS] [CrossRef] [Google Scholar]
- Luhman, K. L., Stauffer, J. R., Muench, A. A., et al. 2003, ApJ, 593, 1093 [NASA ADS] [CrossRef] [Google Scholar]
- Luhman, K. L., Allen, P. R., Espaillat, C., et al. 2010, ApJS, 186, 111 [NASA ADS] [CrossRef] [Google Scholar]
- Manara, C. F., Robberto, M., Da Rio, N., et al. 2012, ApJ, 755, 154 [NASA ADS] [CrossRef] [Google Scholar]
- McCabe, C., Ghez, A. M., Prato, L., et al. 2006, ApJ, 636, 932 [NASA ADS] [CrossRef] [Google Scholar]
- McGregor, P., Hart, J., Conroy, P., et al. 2002, SPIE, 4841, 178 [Google Scholar]
- Menten, K. M., Reid, M. J., Forbrich, J., & Brunthaler, A. 2007, A&A, 474, 515 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Meyer, M. R., Calvet, N., & Hillenbrand, L. A. 1997, AJ, 114, 288 [NASA ADS] [CrossRef] [Google Scholar]
- Monin, J.-L., Clarke, C. J., Prato, L., et al. 2007, in Protostars and Planets V, eds. B. Reipurth, D. Jewitt, & K. Keil (Tucson: Univ. Arizona Press), 395 [Google Scholar]
- Morales-Calderón, M., Stauffer, J. R., Hillenbrand, L. A., et al. 2011, ApJ, 733, 50 [NASA ADS] [CrossRef] [Google Scholar]
- Mugrauer, M., Neuhäuser, R., & Mazeh, T. 2007, A&A, 469, 755 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Muzerolle, J., Hartmann, L., & Calvet, N. 1998, AJ, 116, 2965 [NASA ADS] [CrossRef] [Google Scholar]
- Palla, F., & Stahler, S. W. 1999, ApJ, 525, 772 [PS99] [NASA ADS] [CrossRef] [Google Scholar]
- Patience, J., Akeson, R. L., & Jensen, E. L. N. 2008, ApJ, 677, 616 [NASA ADS] [CrossRef] [Google Scholar]
- Petr, M. G., Foresto, V. C. D., Beckwith, S. V. W., et al. 1998, ApJ, 500, 825 [NASA ADS] [CrossRef] [Google Scholar]
- Prato, L., & Simon, M. 1997, ApJ, 474, 455 [NASA ADS] [CrossRef] [Google Scholar]
- Prato, L., Greene, T. P., & Simon, M. 2003, ApJ, 584, 853 [P03] [NASA ADS] [CrossRef] [Google Scholar]
- Raghavan, D., McAlister, H. A., Henry, T. J., et al. 2010, ApJS, 190, 1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Rayner, J. T., Cushing, M. C., & Vacca, W. D. 2009, ApJSS, 185, 289 [CrossRef] [Google Scholar]
- Reggiani, M. M., & Meyer, M. R. 2011, ApJ, 738, 60 [NASA ADS] [CrossRef] [Google Scholar]
- Reipurth, B., & Zinnecker, H. 1993, A&A, 278, 81 [NASA ADS] [Google Scholar]
- Reipurth, B., Guimarães, M. M., Connelley, M. S., & Bally, J. 2007, AJ, 134, 2272 [R07] [NASA ADS] [CrossRef] [Google Scholar]
- Sandstrom, K. M., Peek, J. E. G., Bower, et al. 2007, ApJ, 667, 1161 [NASA ADS] [CrossRef] [Google Scholar]
- Siess, L., Dufour, E., & Forestini, M. 2000, A&A, 358, 593 [S00] [NASA ADS] [Google Scholar]
- Tohline, J. E. 2002, ARA&A, 40, 349 [NASA ADS] [CrossRef] [Google Scholar]
- Wallace, L., & Hinkle, K. 1996, ApJS, 107, 312 [NASA ADS] [CrossRef] [Google Scholar]
- Wallace, L., & Hinkle, K. 1997, ApJSS, 111, 445 [NASA ADS] [CrossRef] [Google Scholar]
- White, R. J., & Ghez, A. M. 2001, ApJ, 556, 265 [WG01] [Google Scholar]
- Wilking, B. A., Gagné, M., & Allen, L. E. 2008, in Handbook of Star Forming Regions, ed. B. Reipurth, II, 351 [Google Scholar]
- Woitas, J., Leinert, Ch., & Köhler, R. 2001, A&A, 376, 982 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
All Tables
Determination of spectral type, extinction and K-band excess using different methods.
All Figures
 |
Fig. 1 K-band (two leftmost columns) and L′-band (two rightmost columns) NIRI imaging of the ONC binaries. The field of view is 2″ × 2″ and images are displayed with a logarithmic stretch. |
| In the text | |
 |
Fig. 2 Sharper images of JW 248 Aa-Ab obtained after 100 iterations of the multiple LR deconvolution algorithm using JW 248 B as the PSF. |
| In the text | |
 |
Fig. 3 K-band R ~ 5000 spatially-resolved NIFS spectra of the ONC binaries. Atomic and molecular features are labeled, as well as the main telluric correction residuals. |
| In the text | |
 |
Fig. 4 Top: relative velocity of the binary components in RA and Dec between the positions from Reipurth et al. (2007, R07) reported in Table 1 and those measured in this study (our measured positions minus R07 positions). Bottom: relative velocity between Keck and Gemini measurements (Keck-Gemini), as well as between Keck and R07 measurements (Keck, R07) for JW 176, 391, and 709. The small relative motions between Keck and Gemini epochs are consistent with bound systems within the errors. |
| In the text | |
 |
Fig. 5 Locus of the components of the ONC binaries in a J − H/H − K color–color diagram. Solid lines are the locus of photospheric dwarf and giant colors from Bessell & Brett (1988), while in dotted lines are shown the colors of young stellar photospheres of given spectral type in the range K4–L0 (Luhman et al. 2010). The dashed line is the CTTS locus from Meyer et al. (1997). The data point with large uncertainties is JW 248 Ab. All data are in the MKO photometric system. |
| In the text | |
 |
Fig. 6 Continuum-normalized spectra (upper panel) and non-continuum-normalized spectra (lower panel). The best-fit models (red) are also plotted and the derived spectral types, visual extinction AV, K-band IR-excess rK, and its blackbody temperature T reported. Atomic and molecular features are labeled, as well as the main uncorrected telluric features. |
| In the text | |
 |
Fig. 7 Continuum-normalized spectra with best-fit models around the Mg 2.1066 and Al 2.1169 μm features (upper panel) and around the Mg 2.2814 and Ca 2.2634 μm features (lower panel). |
| In the text | |
 |
Fig. 8 H − R diagrams of the components of the T Tauri ONC binaries with the models of: (top) Baraffe et al. (1998), (middle) Palla & Stahler (1999), (bottom) Siess et al. (2000). |
| In the text | |
 |
Fig. 9 Mass ratio distribution for the ONC binaries of our extended sample in comparison with the distribution derived for wide binaries in Tau-Aur and Oph with primary mass range 0.15 to 0.8 M⊙ using the B98, PS99, and S00 PMS tracks for systems with separations from 85 to 560 AU. Also shown are the best-fit power-laws dN/dq ∝ qΓ to the mass ratio distributions in ONC and Tau-Aur. The Tau-Aur distribution is offset along the x-axis for the purpose of clarity. |
| In the text | |
 |
Fig. 10 K-S probability that the mass ration distribution of wide and close binaries derive from the same parent distribution as a function of the separation threshold. The sample is composed of systems from ONC, Tau-Aur, and Oph with primary mass range 0.15 to 3.0 M⊙ (upper-left), systems from Oph and ONC with primary mass range 0.15 to 3.0 M⊙ (upper-right), systems from Tau-Aur with primary mass range 0.15 to 3.0 M⊙ (lower-left), and systems from ONC with primary mass range 0.15 to 0.8 M⊙ (lower-right). Continuous line is for B98 tracks, dotted lines for PS99 tracks, and dashed line for S00 tracks. |
| In the text | |
 |
Fig. 11 Distribution of the absolute difference in logarithmic age | Δ log τ | for the ONC binaries of our extended sample in comparison with the distribution derived for binaries in Tau-Aur and Oph using the PS99 (continous line) and S00 (dotted line) PMS tracks. The rms scatter in | Δ log τ | for both set of tracks are indicated by red lines. The rms of the | Δ log τ | distribution and its uncertainty are reported for each set of tracks and each sample. |
| In the text | |
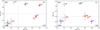 |
Fig. 12 K − L′ color (left) and K − L′ color excess (right) for the ONC binaries. The T Tauri type of each binary is named from the type of each component with C or W (CTTS or WTTS) indicating the presence or not of an inner disk. The dotted lines delimit the regions indicating the presence or not of an inner disk around each component, i.e. WW, CW, CC, and WC, with the first letter referring to the primary and the second to the secondary. Filled square symbols show systems with significant (>3σ) K-band excess rK which are all found in the primary only. Systems classified as Class II from Spitzer IRAC colors are plotted with large open diamonds. |
| In the text | |
 |
Fig. 13 Mass ratio vs separation for binaries in ONC (this study), in Tau-Aur (WG01, HK03), and in Oph (P03) with T Tauri types (CTTS and WTTS) based on K − L color excess. For ONC systems, open symbols are systems taken from D12 with T Tauri types defined from a conjunction of rK, H − K color excess, and Brγ emission. Mass ratios derived from S00 tracks are plotted. |
| In the text | |
 |
Fig. 14 Upper plot: mass ratio vs. the distance from θ1 Ori C with T Tauri types (CTTS and WTTS). Small symbols denote systems with separation <220 AU and large symbols separation >220 AU. Lower plot: mass ratio vs. binary separation with T Tauri types. Small symbols correspond to systems at a distance to θ1 Ori C < 4 arcmin and large symbols a distance >4 arcmin. As in Fig. 13 open symbols denote ONC systems from D12. Mass ratios derived from S00 tracks are plotted. |
| In the text | |
 |
Fig. A.1 Locus of the binary components in several equivalent width diagnostic plots. These plots are the Na 22076 μm + Ca 2.2634 μm versus CO(4–2) + CO(2–0) (upper right), Al 2.1169 μm versus Mg 2.1066 μm (upper left), Mg 2.2814/Ca 2.2634 μm versus Mg 2.1066/Al 2.1169 μm (lower left), and Si 2.1885/Ti 21903 μm versus Mg 2.1066/Al 2.1169 μm (lower right). The ONC binary components (in black) are labeled, as well as the spectral type of the dwarf (red), giant (turquoise), and intermediate-gravity (blue) spectral type templates. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


