| Issue |
A&A
Volume 557, September 2013
|
|
|---|---|---|
| Article Number | A82 | |
| Number of page(s) | 19 | |
| Section | Galactic structure, stellar clusters and populations | |
| DOI | https://doi.org/10.1051/0004-6361/201220338 | |
| Published online | 04 September 2013 | |
Ks- and Lp-band polarimetry on stellar and bow-shock sources in the Galactic center⋆,⋆⋆
1
I. Physikalisches Institut, Universität zu Köln,
Zülpicher Str. 77,
50937
Köln,
Germany
e-mail: buchholz@ph1.uni-koeln.de;eckart@ph1.uni-koeln.de;witzel@ph1.uni-koeln.de
2
Instituto de Astrofísica de Andalucía (CSIC),
Glorieta de la Astronomía
s/n, 18008
Granada,
Spain
e-mail: rainer@iaa.es
3
Max-Planck-Institut für Radioastronomie,
Auf dem Hügel 69,
53121
Bonn,
Germany
Received:
5
September
2012
Accepted:
10
June
2013
Context. Infrared observations of the Galactic center (GC) provide a unique opportunity to study stellar and bow-shock polarization effects in a dusty environment.
Aims. The goals of this work are to present new Ks- and Lp-band polarimetry on an unprecedented number of sources in the central parsec of the GC, thereby expanding our previous results in the H- and Ks-bands.
Methods. We use AO-assisted Ks- and Lp-band observations, obtained at the ESO VLT. High precision photometry and the new polarimetric calibration method for NACO allow us to map the polarization in a region of 8′′ × 25′′ (Ks) resp. 26′′ × 28′′ (Lp). These are the first polarimetric observations of the GC in the Lp-band in 30 years, with vastly improved spatial resolution compared to previous results. This allows resolved polarimetry on bright bow-shock sources in this area for the first time at this wavelength.
Results. We find foreground polarization to be largely parallel to the Galactic plane (Ks-band: 6.1% at 20°, Lp-band: 4.5% at 20°), in good agreement with our previous findings and with older results. The previously described Lp-band excess in the foregound polarization towards the GC could be confirmed here for a much larger number of sources. The bow-shock sources contained in the FOV seem to show a different relation between the polarization in the observed wavelength bands than what was determined for the foreground. This points to the different relevant polarization mechanisms. The resolved polarization patterns of IRS 5 and 10W match the findings we presented earlier for IRS 1W. Additionally, intrinsic Lp-band polarization was measured for IRS 1W and 21, as well as for other, less prominent mid-infrared-excess sources (IRS 2S, 2L, 5NE). The new data offer support for the presumed bow-shock nature of several of these sources (1W, 5, 5NE, 10W, 21) and for the model of bow-shock polarization presented in our last work.
Key words: Galaxy: center / polarization / dust, extinction / infrared: stars
Tables 1 and 2 are available in electronic form at http://www.aanda.org
A table containing the polarization parameters of the sources examined here is only available in electronic form at the CDS via anonymous ftp to cdsarc.u-strasbg.fr (130.79.128.5) or via http://cdsarc.u-strasbg.fr/viz-bin/qcat?J/A+A/557/A82
© ESO, 2013
1. Introduction
At a distance of ~8.0 kpc (Ghez et al. 2008; Gillessen et al. 2009), the center of the Milky Way is by far the closest galactic nucleus. In its central parsec, a nuclear stellar cluster (NSC) has been found with a ~4.0 × 106 M⊙ super-massive black hole at its dynamical center (Eckart et al. 2002; Schödel et al. 2002, 2003; Ghez et al. 2003, 2008; Gillessen et al. 2009). This cluster exhibits similar properties to the NSCs found at the dynamical and photometric centers of other galaxies (Böker 2010; Schödel 2011).
 |
Fig. 1 Ks-band image of the innermost 40.5′′ of the GC (ESO VLT NACO image, 2004, see Buchholz et al. 2009). The marked areas denote the polarimetric FOVs: white indicates Ks-band, green Lp-band and blue H-band. The H-band (H1, see Table 1 and the two southern Ks-band FOVs (K1, K2) have been presented in Buchholz et al. (2011), while the northern Ks-band (K3) and the Lp-band (L1) FOV are examined in this study. |
Near-infrared (NIR) polarimetric observations of this region have been conducted over the past 35 years (see Buchholz et al. 2011 for an overview). In general, the shorter wavelength bands (H and K) seem to be dominated by line-of-sight (LOS) effects, while localized effects become more important with longer wavelengths (see Capps & Knacke 1976; Knacke & Capps 1977; Kobayashi et al. 1980; Lebofsky et al. 1982). These first studies have already shown that the Galactic center (GC) is well suited to studying both interstellar polarization and intrinsically polarized sources.
More than a decade later, higher resolution observations (0.25′′) enabled Eckart et al. (1995) to increase the number of polarimetrically observed GC sources dramatically (160 sources in the central 13′′ × 13′′, only Ks-band). In a follow-up study, Ott et al. (1999) examined ~40 bright sources in the central 20′′ × 20′′ at 0.5′′ resolution. Both studies confirmed a largely uniform foreground polarization, but a more complex picture started to emerge as well: individual sources showed different polarization parameters, such as a significantly higher polarization degree (IRS 21).
These results illustrated that intrinsic polarization is not limited to longer wavelengths, but that it also plays a role in the Ks-band. Specifically, sources embedded in the Northern Arm and other bow-shock sources show signs of intrinsic polarization, with IRS 21 showing the strongest total Ks-band polarization of a bright GC source detected to date (Eckart et al. 1995; Ott et al. 1999, ~10–16% at 16°).
Using observations at even higher resolution, Buchholz et al. (2011) presented H- and Ks-band polarimetry on 163 (H) respectively 194 (Ks) sources in the central 3′′ × 19′′ (with an additional FOV in the Ks-band that was rotated by 45° containing 186 sources, see Fig. 1). That study indicated a possible additional large scale local contribution to the polarization, possibly caused by emission from aligned dust grains in the Northern Arm of the Minispiral. The new data we present here extend this study to the Lp-band, while also expanding the Ks-band FOV. Our new study contains the first polarimetric Lp-band observations of the GC in the last 30 years (with the last data at that wavelength taken by Lebofsky et al. 1982).
In general, three mechanisms can lead to NIR polarization in GC sources: emission by heated, non-spherical dust grains, scattering (on spherical and/or aligned non-spherical grains), and dichroic extinction by aligned dust grains. The observed LOS polarization can be explained by the third effect, while the first two cases can be regarded as intrinsic to the source, thereby allowing conclusions about the source itself and its immediate environment. If a source is enclosed in an optically thick dust shell, dichroic extinction can become important on a local scale as well (see e.g. Whitney & Wolff 2002).
Even 60 years after Davis & Greenstein (1951) suggested paramagnetic dissipation as the basic mechanism that could cause the observed, large scale grain alignment, the issue is still under discussion. In this process, the angular momentum of rapidly spinning grains is aligned with the magnetic field. This necessitates a sufficient grain magnetization and angular momentum, and it is still not clear what mechanisms can produce this (see e.g. Purcell et al. 1971; Lazarian 2003; Lazarian et al. 2007, for an overview of the proposed processes that are expected to be relevant in different environments). Therefore, it remains difficult to reach exact conclusions for dust parameters and magnetic field strength, but at least the magnetic field orientation can be determined. If the parameters change along the LOS, this further complicates the issue.
Using the polarization angle as a probe for the magnetic field orientation, Nishiyama et al. (2009, 2010) mapped magnetic fields in the innermost 20′ resp. 2° of the GC. These studies did not cover the central parsec due to insufficient resolution.
The GC cannot be observed at visual wavelengths due to the strong extinction caused by dust grains on the LOS (up to AV = 40−50 mag, depending on the assumed extinction law). This effects extends into the NIR as well, with a value around 3 mag in the Ks-band (e.g. Scoville et al. 2003; Schödel et al. 2010; Fritz et al. 2011). While the contribution to the total LOS extinction does not depend strongly on the geometry of individual grains, only elongated and aligned grains can contribute to the observed LOS polarization. This already implies that there is most likely no simple linear increase of polarization degree with rising extinction, especially since grain alignment does not have to be the same in every dust cloud along the LOS. Heiles (1987) and Jones (1989) proposed a model where grain alignment is influenced by a constant and a random component of the galactic magnetic field. The polarization caused by the former would “pile up”, while the contributions from the latter would cancel each other out along the LOS. This would lead to a decline of polarization efficiency (the relation between polarization degree and extinction) with rising extinction. Jones (1989) found that this takes the form of a power law relation with an exponent of β = −0.25. In our recent study, we were able to confirm this relation for the sources in the GC (see Buchholz et al. 2011). In that work as well as in our new study, we used a Ks-band extinction map of the central parsec recently presented by Schödel et al. (2010).
The wavelength dependency of the polarization degree is also complex in general, but in the NIR, a power law relation seems to apply (see Martin et al. 1990). That study also showed that the semi-empirical law applicable to polarization in the optical domain (Serkowski et al. 1975; Mathis 1986) is a poor approximation in the NIR. At longer wavelengths, the power law relation also seems to fail, with Lp-band polarization degrees exceeding the predicted values significantly. This effect even seems to increase towards the GC (Jones 1990). The exact cause for this effect is still unknown, partly due to the lack of polarimetric observations in the L/M-band in the last decades.
In Buchholz et al. (2011), we presented the first resolved polarimetric study of two extended and intrinsically polarized sources in the GC, IRS 1W and 21. Tanner et al. (2002, 2005) described IRS 21 as a bow-shock most likely created by a mass-losing Wolf-Rayet star. Separating the observed polarization into a foreground and a source intrinsic component, we were able to show that emission from aligned grains is probably the dominant mechanism that produces intrinsic polarization in both of these bow-shock sources.
The aims of this work are to present the first ~0.12′′ resolution Lp-band polarization measurements of GC sources, as well as Ks-band polarimetry on a large number of sources north of the FOV examined in our previous study. This allows us to study two additional sources embedded in the Northern Arm of the Minispiral (IRS 5 and 10W), as well as other extended and intrinsically polarized objects. Resolved Lp-band polarimetry could be obtained on all bright bow-shock sources in the central 26′′ × 28′′.
In Sect. 2, we present the photometric and calibration methods applied to the data. The results are presented in Sect. 3, followed by a summary and discussion of their implications in Sect. 4.
2. Observation and data reduction
2.1. Observation
The data presented here were obtained using the NAOS-CONICA (NACO, see Lenzen et al. 2003; Rousset et al. 2003) instrument at the ESO VLT unit telescope 4 on Paranal in March 2011 (program 086.C-0049A, see Table 1). The seeing varied during the observations, especially affecting the Ks-band dataset and the second night of Lp-band observations. Only Lp-band observations taken in the first night were used. Using the infrared wavefront sensor installed with NAOS, the bright super-giant IRS 7 located about 6′′ north of Sgr A* was used to close the feedback loop of the adaptive optics (AO) system. In the Ks-band, the sky background was determined by taking several dithered exposures of a dark cloud 713′′ west and 400′′ north of Sgr A*, a region largely devoid of stars. The Lp-band sky was estimated on a region located 60′′ west and 60′′ north of Sgr A*, switching between the sky and the target every other exposure.
We used the Wollaston prism available with NACO in combination with a rotatable half-wave plate for the polarization measurements. The two channels produced by the Wollaston prism (0° and 90°), combined with two orientations of the half-wave plate (0° and 22.5°), yielded four sub-images for each of several dither positions. Each sub-image covered a field-of-view of 3.2′′ × 13.6′′ (Ks-band), respectively 3.2′′ × 27.8′′ (Lp-band), due to the different optics that were used (see Table 1). 26 of these sub-images were used in the Lp-band, while the low data quality in the Ks-band forced us to discard 26 sub-images in the 0°/90° channel (leaving 21 out of 47 taken in total), as well as 23 out of 47 in the 45°/135° channel (leaving 25). In total, we were able to cover a field-of-view of 8′′ × 25′′ (Ks-band), respectively 26′′ × 28′′ (Lp-band). This corresponds to 0.30 pc × 0.96 pc and 0.96 pc × 1.04 pc, respectively (see Fig. 1). Per sub-image, the area covered corresponds to 0.12 pc × 0.51 pc (Ks-band) and 0.12 pc × 1.04 pc.
All images were corrected for dead/hot pixels, sky subtracted and flat-fielded. It is essential for a correct calibration that the flat-field observations are taken through the Wollaston, because the flat-field shows variations caused by different transmissivity of the channels as well as effects of the inclined mirrors behind the prism (see Witzel et al. 2011; Buchholz et al. 2011, for details on these effects).
Even after the sky-subtraction and flat-fielding, the March 2011 Lp-band images still contained significant patterns. These are not actual structures in the GC itself (as a comparison with previous Lp-band observations reveals, see e.g. Viehmann et al. 2005), but must have been introduced either by the detector itself or possibly by the sky correction. This can happen when the sky exposures contain sources themselves. Due to the high sky flux, these cannot be easily made out and masked, as it can be done in the Ks-band. Two distinct patterns occur in all images: a series of “stripes” along the east-west-axis and a “cloudy” structure in the east and west of the FOV. The latter occurs at the same position in each image, while the former is different for each exposure.
The east-west pattern was approximated by averaging over the x-axis of each image (excluding bright pixels, in order to avoid a bias from the stars). The resulting profile was subtracted from the image. This does not introduce a significant bias, since there are no large scale east-west structures expected in this FOV.
In order to remove the stationary pattern, a median image was computed from all individual exposures (excluding the stellar sources) for each polarization channel. This yielded a characteristic pattern for each channel, which was then subtracted from all images.
Before and after the removal of each pattern, each image was shifted to a background level centered around zero. This turned out to be necessary since the background level after sky subtraction varied on the order of 10–20 counts between individual images. With a highly variable sky (due to less-than-optimal observing conditions), this can be expected: the flux from the sky alone reaches 2000–3000 counts per pixel, so a change of 1% between sky and object exposure already produces an offset of 20–30 counts. Unfortunately, this means that the background flux cannot be measured and any information about the background polarization is lost.
Compared to the data presented in Buchholz et al. (2011), our new observations cover a much greater FOV, at the price of a lower depth. The low data quality of the Ks-band data further limits this study to the brighter sources in the field.
2.2. Photometry
2.2.1. Ks-band
Unlike the data contained in our previous study (Buchholz et al. 2011), where all individual images covered essentially the same FOV in the very center of the GC, the data taken in March 2011 sacrificed depth in order to achieve a much greater FOV. This made photometry on a combined image impractical, because the overlapping regions of the images were small, which in turn led to a variable depth over the field.
In addition, the observations suffered from a small isoplanatic angle. Therefore, the point spread function (PSF) changed visibly across the FOV. This effect varied in strength between the individual exposures. About half of the Ks-band exposures had to be discarded because the very low data quality did not allow reliable photometry. This introduced a further complication: about 50% of the individual images had to be discarded because of insufficient quality, and this left very few corresponding pairs of 0°/45° images (covering the same FOV and taken in sequence). The different data quality can also introduce offsets in total intensity between the exposures (due to variable AO performance), and this made it necessary to conduct the photometry on each exposure individually.
For this dataset (as well as for the Lp-band data, see below), using PSF-fitting or deconvolution-assisted photometry (Buchholz et al. 2009, 2011; Schödel 2010) proved impractical. The guide star IRS 7 was only covered in four of the selected exposures, and while this star would provide an excellent estimate of the PSF including the faint wings, the variation of the shape of the PSF between the different images did not allow only this PSF to be used for all other images as well. Local PSF extraction is complicated by the small number of suitable PSF stars in each exposure. The large residua that are produced by using a poorly fitting PSF in this case outweigh any advantage of these otherwise much more precise photometric methods.
We therefore determined that the best way to achieve reliable photometry on the individual images was aperture photometry, using manually placed apertures for all sources in the FOV. Due to the low depth of the observations, the issue of crowding is far less important than in our previous study (Buchholz et al. 2011), especially since precise photometry is not possible here for fainter sources (15–16 mag) anyway.
The apertures were created based on a mosaic image, by placing an aperture on each discernible source and adjusting its radius so that the whole PSF of each source was covered. Since only sources brighter than ~14 mag were used (see below), source crowding was not an issue, and contamination by the flux of neighboring or faint background sources can be assumed to be minimal. Brighter sources were covered by larger apertures, on the order of 1′′ for the two brightest sources in the field, IRS 7 (and IRS 3 in Lp-band). The apertures for the fainter sources were significantly smaller, on the order of 0.2′′.
 |
Fig. 2 Flux uncertainties for the 0 degree channel of the Ks-band dataset, plotted against the brightness of the sources in magnitudes. The uncertainties were determined from the flux variations in background apertures and can therefore only be regarded as a lower limit for the actual uncertainties. The other channels show a very similar uncertainty distribution. |
Using these apertures, aperture photometry was conducted on the sources present in each image. Only apertures fully contained in the respective FOV of each image were used (in order to avoid problems with sources not fully contained in the FOV). The background for each source was estimated using an average over four background apertures close to each source, which were placed in regions with no visible sources. This background flux was then subtracted from the flux measured for the source.
The resulting fluxes were used to calculate the Stokes Q and U parameters for each pair of 0°/90° and 45°/135° exposures (see Sect. 2.3). These values were then averaged to one Q and U value for each source. This eliminates the bulk of the offset in flux between individual exposures. No systematic offsets in the Q or U parameter were found between exposures.
The uncertainties of the measured fluxes were determined by calculating the FWHM of the
distribution of the fluxes in the background apertures. The value 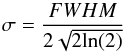 (1)was
adopted as the flux uncertainty per pixel. This led to a total flux uncertainty for a
given aperture of
(1)was
adopted as the flux uncertainty per pixel. This led to a total flux uncertainty for a
given aperture of 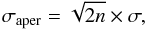 (2)with
n as the number of pixels contained in the aperture. These flux
uncertainties contributed one component to the uncertainties calculated for
Q and U (see below). Figure 2 shows these flux uncertainties in relation to the measured fluxes.
The uncertainty distribution shows a clear dependency on the flux, which can be expected
since this is basically a Poisson uncertainty. This only sets a lower limit for the
actual uncertainty of the measured Q and U parameters.
The main contribution to the uncertainties that were determined for these values stems
from the variation over several exposures (see below).
(2)with
n as the number of pixels contained in the aperture. These flux
uncertainties contributed one component to the uncertainties calculated for
Q and U (see below). Figure 2 shows these flux uncertainties in relation to the measured fluxes.
The uncertainty distribution shows a clear dependency on the flux, which can be expected
since this is basically a Poisson uncertainty. This only sets a lower limit for the
actual uncertainty of the measured Q and U parameters.
The main contribution to the uncertainties that were determined for these values stems
from the variation over several exposures (see below).
 |
Fig. 3 Ks-band magnitudes of the sources detected in the polarimetric dataset K3. Black: all sources. Green: sources with reliably measured polarization parameters. |
This technique was used to measure the fluxes of the 143 visible sources in the observed FOV of 8.6′′ × 25′′. Compared to the Ks-band data presented in Buchholz et al. (2011), the number of detected sources per arcsec2 is lower by a factor of ~6. This illustrates the much lower depth and worse data quality of the 2011 data.
In order to determine the depth of the new Ks-band observations, we used the Ks-band magnitudes provided for the observed sources in Schödel et al. (2010). Figure 3 shows the resulting Ks-band luminosity function. Accoridngly, we estimate the depth of the new observations as ~14 mag, which is shallower by 1.5 mag than the data used in Buchholz et al. (2011).
2.2.2. Lp-band
The Lp-band images varied much less in quality than the Ks-band dataset, and all exposures could be used for photometry. The small overlap between the individual images and the fact that most of the FOV was only covered by a single exposure made it necessary to conduct the photometry on the individual images. This was done in a similar way to the Ks-band dataset (see above): the sources in the FOV were covered by manually placed apertures, while the background was determined in a 2 pixel annulus around each aperture. Since the background was shifted to an average of zero for all images before (see Sect. 2.1), the residual background only contributed a small amount to the total flux measured in each aperture.
Unlike in the Ks-band dataset, each FOV was covered by two
corresponding 0° and 45° images. This allowed a direct comparison
of the total intensity measured for each source by adding up the fluxes in the
0° and 90° respectively the 45° and 135°
channels. For each image pair, the total intensities of all sources were added and a
relative calibration factor was determined:
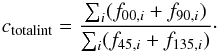 (3)All fluxes measured in
the 45° and 135° channels were multiplied with this factor in
order to ensure the same relative flux calibration in all corresponding images. Due to
the small overlaps between the images (the two northernmost FOVs showed no overlap at
all), a cross-calibration over the full FOV was not possible in this way. Therefore, the
measured fluxes were normalized to an average of one for each source before combining
them to a common list of all detected sources. This ensures that possible differences in
flux for sources detected in more than one exposure did not influence the polarization
determined for that source.
(3)All fluxes measured in
the 45° and 135° channels were multiplied with this factor in
order to ensure the same relative flux calibration in all corresponding images. Due to
the small overlaps between the images (the two northernmost FOVs showed no overlap at
all), a cross-calibration over the full FOV was not possible in this way. Therefore, the
measured fluxes were normalized to an average of one for each source before combining
them to a common list of all detected sources. This ensures that possible differences in
flux for sources detected in more than one exposure did not influence the polarization
determined for that source.
In order to determine the depth of the observations, we used the Lp-band magnitudes given for most of the observed sources in Schödel et al. (2010). The few remaining sources that were not contained in this catalogue were calibrated by comparing their measured fluxes with those of the sources with existing reference values in Schödel et al. (2010).
 |
Fig. 4 Flux uncertainties for the 0 degree channel of the Lp-band dataset, plotted against the brightness of the sources in magnitudes. The green points denote sources with reliable polarization parameters as was determined later in the analysis, while the black points indicate sources that were rated as unreliable. The uncertainties were determined from the flux variations in background apertures and can therefore only be regarded as lower limit for the actual uncertainties. The other channels show a very similar uncertainty distribution. |
The flux uncertainties per pixel were determined from the FWHM of the distribution of all background pixels of each image (see Eq. (1)), and this value was used to calculate a total flux uncertainty for each source (see Eq. (2)). Figure 4 shows these uncertainties in relation to the brightness of the sources, and they show the expected distribution of a Poisson uncertainty. Only sources with a relative flux uncertainty of less than 6% were used in the subsequent analysis. This effectively sets a lower brightness limit of ~10.5 mag (see Fig. 5) for a reliable determination of the polarization parameters.
2.3. Polarimetry
We determined the polarization degree and angle of each source by converting the measured normalized fluxes into normalized Stokes parameters:
 Since
NACO is not equipped with a
Since
NACO is not equipped with a  plate,
it was not possible to measure circular polarization. But since the circular polarization
of stellar sources in the GC is at best very small (Bailey
et al. 1984), we assume here that it can be neglected and set to 0 at our level
of accuracy. Note that this may not be the case for dusty sources where circular
polarization may result from multiple scattering if the local dust density is high enough.
Polarization degree and angle can then be determined in the following way:
plate,
it was not possible to measure circular polarization. But since the circular polarization
of stellar sources in the GC is at best very small (Bailey
et al. 1984), we assume here that it can be neglected and set to 0 at our level
of accuracy. Note that this may not be the case for dusty sources where circular
polarization may result from multiple scattering if the local dust density is high enough.
Polarization degree and angle can then be determined in the following way:
 Uncertainties
for Q and U (and subsequently p and
θ) were determined by error propagation of the measured flux
uncertainties. Since this just yields a lower limit for the true uncertainty, the standard
deviation of the Q and U parameters of the sources that
were found in more than one field was added quadratically to the uncertainties determined
from the flux uncertainties alone.
Uncertainties
for Q and U (and subsequently p and
θ) were determined by error propagation of the measured flux
uncertainties. Since this just yields a lower limit for the true uncertainty, the standard
deviation of the Q and U parameters of the sources that
were found in more than one field was added quadratically to the uncertainties determined
from the flux uncertainties alone.
 |
Fig. 5 Lp-band magnitudes of the sources detected in the polarimetric dataset L1. Black: all sources. Green: sources with reliably measured polarization parameters. |
In order to check whether or not the polarization of a source was determined reliably, we used a combination of several methods: in the Lp-band, we calculated the normalized fluxes that would be expected for the determined values of p and θ. The difference between these values and the measured fluxes was then compared to the photometric uncertainties of each data-point. The source was only classified as reliable if the root-mean-square of the deviations did not exceed the root-mean-square of the relative photometric uncertainties. In addition, sources with dp > p (the uncertainty of the polarization exceeding its value) were rated as unreliable. Due to the selection issues in the Ks-band, the first method was not applicable. Here, only the latter method was used, with sources with dp > p rated as unreliable measurements. The subsequent analysis is only based on the sources classified as reliable.
 |
Fig. 6 Ks-band polarization map of stars in the Galactic center. Only reliably measured polarization values are shown here. Black circles/red lines and blue circles/green lines: datasets presented in Buchholz et al. (2011). Red circles and black lines: new March 2011 Ks-band data. The diameter of the circles corresponds to the brightness of the source. Thin black lines in the background denote magnetic fields determined from mid-infrared (MIR) data (Aitken et al. 1998, based on a 1.5′′ beam). The brightest sources are also indicated. |
Using the analytical model for the polarimetric calibration of NACO developed by Witzel et al. (2011), we were able to reduce the systematic uncertainties produced by instrumental polarization and achieve a direct calibration for this larger FOV as well (compared to the FOV presented in Buchholz et al. 2011, thereby expanding our previous results). This method reduces the systematic uncertainties of polarization degrees and angles to ~1% and ~5°, so our final values are dominated by photometric uncertainties.
2.4. Correcting for foreground polarization
In the same way as in Buchholz et al. (2011), we
assume here that the total effect of the foreground polarization can be treated as a
linear polarizer with a certain orientation θfg and efficiency
pfg. This can be described by a Mueller matrix,
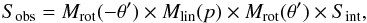 (8)with
Sobs as the observed total Stokes vector and
Sint as the Stokes vector of the intrinsic polarization. The
Mueller Matrix Mlin(p) describes a linear
polarizer, producing a maximum of polarization along the north-south-axis. This matrix has
to be rotated to the appropriate angle by multiplying it with
Mrot(θ′), a standard 4 × 4
rotation matrix. The angle
θ′ = 90° + θfg has to
be used in the rotation matrix, since we define the polarization angle θ
as the angle where we measure the flux maximum, while the angle of reference for the
Mueller matrix describing the linear polarizer is the angle where the maximum in
absorption occurs. The matrices are given in Buchholz et
al. (2011).
(8)with
Sobs as the observed total Stokes vector and
Sint as the Stokes vector of the intrinsic polarization. The
Mueller Matrix Mlin(p) describes a linear
polarizer, producing a maximum of polarization along the north-south-axis. This matrix has
to be rotated to the appropriate angle by multiplying it with
Mrot(θ′), a standard 4 × 4
rotation matrix. The angle
θ′ = 90° + θfg has to
be used in the rotation matrix, since we define the polarization angle θ
as the angle where we measure the flux maximum, while the angle of reference for the
Mueller matrix describing the linear polarizer is the angle where the maximum in
absorption occurs. The matrices are given in Buchholz et
al. (2011).
For each source to which the depolarization matrix was applied, the foreground polarization had to be estimated. The accuracy of this estimate controls the relevance of the resulting intrinsic polarization. We used the average of the polarization parameters of the surrounding point sources as an estimate for θfg and pfg.
The resulting matrix can then be inverted and multiplied with the calibrated observed Stokes vector of a source to remove the foreground polarization and leave only the intrinsic polarization. We applied this method to the extended sources, both to their total polarization and the polarization maps, in order to isolate their intrinsic polarization pattern (see Sect. 3.7). For each extended source, we indicated the point sources used as foreground references (see subsections in Sect. 3.7).
3. Results and discussion
3.1. Ks-band polarization
Despite the much wider FOV compared to Buchholz et al. (2011), the polarization parameters of only 126 sources could be measured reliably. This still represents an increase by a factor of 4 compared to the sources in the same FOV for which Eckart et al. (1995) determined the polarization (~30 sources in this area, while Ott et al. (1999) did not cover this region at all).
As in the deeper datasets, the polarization angles show the expected alignment with the Galactic plane (see Fig. 6). There may be a trend to larger polarization degrees towards the north compared to the southern center, but it is not as clear as the trend found in the Buchholz et al. (2011) data.
Fitting the distribution of the polarization angles with a single Gaussian yields a peak at 20° ± 7° (see Fig. 7, lower left frame). For comparison, the distribution was also fitted with a double Gaussian, which led to two peaks at 16° ± 1° and 22° ± 7°. This improves the reduced χ2 by a factor of 3, but the fact that the secondary peak lies within the FWHM of the primary peak reduces the confidence in this feature.
The polarization degrees seem to show lower values towards the southern-central part of the FOV, which would link up well with the results found in (Buchholz et al. 2011, see Fig. 6). Fitting the logarithms of the polarization degrees with a single Gaussian yields a peak at (6.1 ± 1.3)%, while using a double Gaussian resulted in a lower reduced χ2 (by a factor of 2), with peaks fitted at (5.7 ± 1.0)% and (8.0 ± 2.1)%.
 |
Fig. 7 Ks-band polarization degrees (plotted on logarithmic scale, upper left) and angles (lower left) of stars in the Galactic center. The red lines denotes fits with a single Gaussian distribution, while the green respectively blue lines denote the fit with a double Gaussian (green: sum, blue: individual Gaussians). Upper right: relative uncertainties of the polarization degrees. Lower right: absolute uncertainties of the polarization angles. |
The uncertainties of the polarization angle mostly stay below 15° (see Fig. 7, lower right frame), and this further limits the confidence in the second peak due to its small offset from the primary feature. The relative uncertainties of the polarization degree reach up to 50% (except a few outliers, see Fig. 7, upper right frame).
A complete list of all detected sources with reliably measured polarization parameters is included as online material (table A1). This list contains the position offsets from Sgr A* (RA, Dec), H-, Ks-, and Lp-band (see Sect. 3.2) polarization parameters of the sources observed in this work and in our previous publication, Buchholz et al. (2011).
3.2. Lp-band polarization
 |
Fig. 8 Lp-band polarization map of stars in the Galactic center. Only reliably measured polarization values are shown here. Red lines indicate the polarization vectors of sources classified as affected by intrinsic polarization according to Sect. 3.5 as well as the observed bow-shock sources, while green lines denote sources only exhibiting foreground polarization. |
The polarization of 84 sources in the Lp-band dataset could be determined reliably. Considering the size of the FOV, this number appears small compared to the H- and Ks-band data presented in Buchholz et al. (2011), but Lp-band polarimetry suffers from much larger difficulties than what is encountered at shorter wavelengths. Figure 8 shows that while there is an overall trend of polarization along the Galactic plane (as seen in the H- and Ks-band), there is a significant number of outliers with either strongly deviating polarization angles or much weaker/stronger polarization degrees than what is expected for pure foreground polarization. Considering the complex structures observed in the Lp-band in the central parsec (large-scale dust structures, bow-shocks, embedded sources), this is not surprising.
Despite these additional complications, the distribution of polarization angles (see Fig. 9, lower left frame) shows a clear peak at 20° ± 5° when fitted with a single Gaussian. A small secondary feature might be present at ~35°, and a fit with a double Gaussian indeed has a better reduced χ2 (by a factor of 2.5). But considering the small number of sources contained in this feature compared to the number of the other, more widely distributed outliers, this may not be a significant feature at all. In addition, the single Gaussian fits the distribution with sufficient accuracy, and it does not differ much from the first peak of the fitted double Gaussian.
 |
Fig. 9 Lp-band polarization degrees (plotted on logarithmic scale, upper left) and angles (lower left) of stars in the Galactic center. The red line denotes the fit with one Gaussian distribution, while green respectively blue lines denote the fit with a double Gaussian (green: sum, blue: individual Gaussians). Upper right: relative uncertainties of the polarization degrees. Lower right: absolute uncertainties of the polarization angles. |
In the same way, the distribution of the logarithms of the polarization degrees shows a slightly widened peak at (4.5 ± 1.4)% (see Fig. 9, upper left frame), which can also be fitted with a double Gaussian for a better reduced χ2 (by a factor of 5). This produces a secondary peak at ~6%, but again, this may not be significant, considering the width of this peak and the fact that it is within the FWHM of the fitted single peak. The single Gaussian provides a sufficient fit.
Figure 9, upper right frame, shows the relative uncertainties of the polarization degree. These uncertainties mostly stay below ~60%, a value significantly larger than what was found for the relative uncertainties of the other datasets (see Buchholz et al. 2011). This again indicates the problems of Lp-band polarimetry (difficult photometry combined with lower polarization degrees compared to the H/Ks-band). The uncertainties of the polarization angles (see Fig. 9, lower right frame) reach up to ~25°, which is also higher than what was found in the other datasets. The uncertainties of the polarization parameters further decrease the confidence in the significance of the small secondary features found in both distributions.
3.3. Comparison to previous results
Our own recent study (Buchholz et al. 2011) was the first that measured the NIR polarization of GC sources at this spatial resolution. The FOV of that work does not overlap with the new data, so a direct source-by-source comparison is not possible. The distributions of the polarization parameters show similar features, however: the distribution of the angles found here (see Fig. 7) does not differ much from what was found for datasets K1 and K2, and the fitted single Gaussian peaks agree within the uncertainties. The double Gaussian fit is also consistent with dataset K1: the two peaks fitted here match the values found for the peaks in dataset K1 within one respectively two sigma (peaks at 10°/16° respectively 26°/22°). On average, the polarization degrees are slightly higher than those found in our previous study (see Fig. 7, upper left frame), but the peak of the fitted single Gaussian still agrees with the value found in Buchholz et al. (2011) within the uncertainties. The peaks of the fitted double Gaussian are also consistent with the two peaks fitted in our last study, but the second feature found here is a lot less pronounced compared to the previously presented data.
A comparison to the values presented in Eckart et al. (1995) reveals considerable deviations: only 47% of the 32 sources found both in the older study and the new dataset show an agreement in polarization degree within 3σ or less. 63% of the sources show a 3σ agreement for the polarization angles. The FOV of this dataset and that of Ott et al. (1999) do not overlap, so no comparison was possible. It has to be noted, however, that the agreement with these older studies was significantly better for the sources contained in Buchholz et al. (2011).
In general, differences between these older studies and the new measurements can probably be attributed to the lower spatial resolution of the former. But the lower data quality of the observations presented in this work compared to the data used in our previous study most likely also reduces the agreement with the Eckart et al. (1995) values. Both older studies show average polarization angles generally parallel to the Galactic plane, on average at 25° respectively 30°. Similar results are found here for the much larger new sample of sources. The distribution of the polarization degrees determined from our new data peaks at higher values than the flux-weighted average polarization degree of the older studies, but that can be expected since the inclusion of IRS 7 with its polarization degree of only 3.6% in both older surveys lowered the flux weighted average that was calculated there considerably (see also the note on flux-weighted averaging in Buchholz et al. 2011).
There are only a few sources in the FOV of the presented dataset that can be compared directly to the K-band results of Knacke & Capps (1977): IRS 7 is bright and isolated enough to be detected as a single source even in the old data. IRS 3 would also be suitable for such a comparison, but this source is not fully contained (i.e. located on the edge of the FOV) in any of the 2011 images.
Knacke & Capps (1977) measured a polarization of (3.0 ± 0.3)% at 20° ± 5° for IRS 7, and the value found here matches that result quite well: (2.9 ± 1.0)% at 13° ± 10° have been measured based on the 2011 data, but it has to be cautioned that the saturation of the source might influence these results.
In the Lp-band, there are even less possibilities for a comparison: Lebofsky et al. (1982; 5.8′′ beam) and Knacke & Capps (1977; 7′′ beam) are the only studies to date that measured L-band polarization in the GC. Only two sources can be compared directly: Knacke & Capps (1977) measured the polarization of IRS 3 as (3.4 ± 1.0)% at 16° ± 8°, while they give values of (2.6 ± 0.3)% at 43° ± 5° for IRS 7. Lebofsky et al. (1982) do not provide values for IRS 3, but measured (3.2 ± 0.5)% polarization at 13° for IRS 7. The values found in our observations for these two sources, about 30 years and several instrument/telescope generations later, agree relatively well: the polarization of IRS 3 is measured as (3.7 ± 0.1)% at 16.0° ± 0.7°, which is in very good agreement with the Knacke & Capps (1977) value. IRS 7 exhibits a polarization of (3.6 ± 0.1)% at 20.9° ± 0.7°. This matches the Lebofsky et al. (1982) values better, while the measured angle deviates from Knacke & Capps (1977). The good agreement of these polarization parameters indicates that the recently developed calibration model of Witzel et al. (2011) is applicable to the Lp-band as well, though further observations of polarimetric standard sources in this wavelength band would be desirable to support this.
3.4. Detecting intrinsic polarization
The variation of the foreground polarization over the FOV (see e.g. Buchholz et al. 2011, and results presented above) makes it difficult to determine exactly whether a source is affected by additional intrinsic polarization. If only one wavelength band is available, the only possibility is a comparison of Q and U (or p and θ) for each source to the parameters found for the neighboring sources. In case of deviations that exceed a given theshold, the source can be classified as intrinsically polarized. This threshold can be determined from the width of the distributions of the parameters.
Another option exists where measurements in several wavelength bands are available as it
is the case for the sources common to Ks- and Lp-band
(as shown in Sect. 3.5). The relation between
Ks- and Lp-band polarization of a source can provide a
strong indication of intrinsic polarization: if 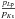 is significantly higher or lower than the value expected for foreground polarization
(~0.7–0.8 towards the GC, see Jones 1990) or if the
polarization angles deviate strongly between the two bands, the source can be regarded as
intrinsically polarized. The reason for this is that at least in the foreground component,
the same grains should be responsible for the polarization in all NIR (and optical) bands.
While different grain parameters and alignments could lead to different contributions at
the observed wavelengths, such influences will generally even our along the LOS, and a
purely foreground-polarized source should show the same polarization angle over these
wavelength bands. If it does not, another local component must be contributing.
is significantly higher or lower than the value expected for foreground polarization
(~0.7–0.8 towards the GC, see Jones 1990) or if the
polarization angles deviate strongly between the two bands, the source can be regarded as
intrinsically polarized. The reason for this is that at least in the foreground component,
the same grains should be responsible for the polarization in all NIR (and optical) bands.
While different grain parameters and alignments could lead to different contributions at
the observed wavelengths, such influences will generally even our along the LOS, and a
purely foreground-polarized source should show the same polarization angle over these
wavelength bands. If it does not, another local component must be contributing.
Table 2 lists the sources detected in both bands, classifying them as mainly foreground affected or as candidates for intrinsic polarization. This was determined based on the comparison between the two wavelength bands (see Sect. 3.5).
 |
Fig. 10 Left frame: relation of Lp- to Ks-band polarization degree (logarithmic plot). Right frame: difference between Lp- and Ks-band polarization angle. In both frames, the red columns represent suspected intrinsically polarized sources, while the black columns contain sources affected only by the foreground polarization. The green lines represent Gaussians fitted to the histograms. |
3.5. Relation between Ks- and Lp-band foreground polarization
For 37 sources, Ks-band and Lp-band polarization
parameters have been measured. This is less than half of the available
Lp-band sources, but that can be expected considering the respective
fields-of-view observed in both bands (see Fig. 1).
Of these common sources, 9 candidates for intrinsic polarization have been found based on
the methods described in Sect. 3.4. Table 2 shows the polarization parameters of the common
sources, as well as the classification of each source as intrinsically or foreground
polarized. Several bright likely intrinsically polarized sources are examined in more
detail in Sect. 3.7. Figure 10 shows the distribution of 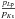 and the difference between the polarization angles. Most of the outlier values can be
assumed to be affected by intrinsic polarization (plotted in red), while the distribution
of the foreground-polarized sources shows clear peaks at 0.8 ± 0.3
(
and the difference between the polarization angles. Most of the outlier values can be
assumed to be affected by intrinsic polarization (plotted in red), while the distribution
of the foreground-polarized sources shows clear peaks at 0.8 ± 0.3
(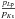 )
respectively − 2° ± 9°
(θLp − θks).
The latter value agrees with zero within the uncertainties, which is expected if indeed
the same grain population (or at least grains aligned in the same direction) is
responsible for the polarization at both wavelengths. The former exceeds the value
expected from theoretical and semi-empirical models: while the Serkowski et al. (1975) law does not work well in the NIR anyway (see
e.g. Martin et al. 1990), the model proposed by
Mathis (1986) and the power law relation
suggested by Martin et al. (1990) predict too small
values as well. Jones (1990) compared these
relations to data obtained on local sources and observations on three GC sources, IRS 7,
IRS 9 and GCS 9. The GC sources showed an even higher excess than the local sources
compared to the results of the models/relations, with
)
respectively − 2° ± 9°
(θLp − θks).
The latter value agrees with zero within the uncertainties, which is expected if indeed
the same grain population (or at least grains aligned in the same direction) is
responsible for the polarization at both wavelengths. The former exceeds the value
expected from theoretical and semi-empirical models: while the Serkowski et al. (1975) law does not work well in the NIR anyway (see
e.g. Martin et al. 1990), the model proposed by
Mathis (1986) and the power law relation
suggested by Martin et al. (1990) predict too small
values as well. Jones (1990) compared these
relations to data obtained on local sources and observations on three GC sources, IRS 7,
IRS 9 and GCS 9. The GC sources showed an even higher excess than the local sources
compared to the results of the models/relations, with
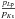 around 0.7. This is confirmed here for a much larger number of sources, while the cause
remains uncertain. Jones (1990) suggested
polarimetric observations at even longer wavelengths and spectropolarimetric observations
in the Lp-band as a possibility to shed some more light on this issue.
around 0.7. This is confirmed here for a much larger number of sources, while the cause
remains uncertain. Jones (1990) suggested
polarimetric observations at even longer wavelengths and spectropolarimetric observations
in the Lp-band as a possibility to shed some more light on this issue.
Nagata et al. (1994) conducted such
spectropolarimetric observations on several sources within 0.5° of the GC,
including IRS 7, finding a polarization excess over the whole 3 μm
window. They proposed that this excess might be a localized feature, and its source not
ubiquitous in the diffuse interstellar medium on galactic scales. It might prove
interesting to repeat such observations at higher resolution (the authors used an
8′′ aperture), comparing e.g. sources in the central parsec with those in
other areas close to the GC, such as the Arches and Quintuplet clusters. 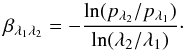 (9)In more recent
observations, Hatano et al. (2013) studied the
foreground polarization towards the GC (innermost 5.7 deg2), observing in the
J-, H-, and Ks-bands. They found a
significant flattening of the power-law wavelength dependence (see Eq. (9)) towards longer wavelengths, finding
power-law indices of βJH = 2.08 ± 0.02 and
βHKs = 1.76 ± 0.01. While polarimetric
J-band observations are not possible with NACO (the
J-band filter is mounted in the same filter wheel as the Wollaston
prism), we notice a similar flattening when we compare the H- and
Ks-band data of our last study (Buchholz
et al. 2011) with the Ks- and Lp-band data presented here: we
find βHKs = 2.4 ± 1.7 and
βKsLp = 0.40 ± 0.67.
Despite the large errors, we are able to confirm that the observed flattening of the
wavelength dependence extends well into the Lp-band. The only value that
is directly comparable (βHKs) agrees with the
value found by Hatano et al. (2013) within the
uncertainties, but it is quite a bit higher. It has to be considered of course that our
studies only cover a much smaller region of the sky, and that local effects may play a
significant role, as already stated in Buchholz et al.
(2011). But the observed trend supports the findings and conclusions of Hatano et al. (2013) towards this innermost region of
the GC as well, specifically that large aligned grains must exert a significant influence.
(9)In more recent
observations, Hatano et al. (2013) studied the
foreground polarization towards the GC (innermost 5.7 deg2), observing in the
J-, H-, and Ks-bands. They found a
significant flattening of the power-law wavelength dependence (see Eq. (9)) towards longer wavelengths, finding
power-law indices of βJH = 2.08 ± 0.02 and
βHKs = 1.76 ± 0.01. While polarimetric
J-band observations are not possible with NACO (the
J-band filter is mounted in the same filter wheel as the Wollaston
prism), we notice a similar flattening when we compare the H- and
Ks-band data of our last study (Buchholz
et al. 2011) with the Ks- and Lp-band data presented here: we
find βHKs = 2.4 ± 1.7 and
βKsLp = 0.40 ± 0.67.
Despite the large errors, we are able to confirm that the observed flattening of the
wavelength dependence extends well into the Lp-band. The only value that
is directly comparable (βHKs) agrees with the
value found by Hatano et al. (2013) within the
uncertainties, but it is quite a bit higher. It has to be considered of course that our
studies only cover a much smaller region of the sky, and that local effects may play a
significant role, as already stated in Buchholz et al.
(2011). But the observed trend supports the findings and conclusions of Hatano et al. (2013) towards this innermost region of
the GC as well, specifically that large aligned grains must exert a significant influence.
3.6. Correlation with extinction
 |
Fig. 11 Polarization efficiency in dataset K2 (Ks-band, upper frames) and dataset K3 (Ks-band, lower frames), compared to Ks-band extinction, plotted as point density, with typical uncertainties represented on the left. pK+ and pK− sources shown separately in left respectively right frames for both bands. Green lines represent the fitted power-law relation. For the polarization efficiency in dataset K1, see Buchholz et al. (2011), Fig. 16. |
We determined the extinction towards each source from the extinction map of the GC presented by Schödel et al. (2010). This was done in the same way as in Buchholz et al. (2011).
For the sources found in the K2 and K3 datasets, a clear separation into two distinct groups of sources based on the Ks-band polarization is not as evident as what was found in our previous study for the K1 dataset, but the polarization degrees still show a wide distribution compared to the individual peaks found in Buchholz et al. (2011) for the K1 data. In order to investigate if an offset in polarization efficiency (as found in the previous work) can be found here as well, a separation at 6% (K2) respectively 7.3% (K3) was introduced here (labeling the resulting sub-groups as pK+ and pK−) . These values were chosen based on Fig. 7 and Fig. 7 in Buchholz et al. (2011). We excluded sources with less than 3% polarization, since this low value indicates either a foreground source or intrinsic polarization perpendicular to the foreground (e.g. in IRS 1W and 10W, see Sect. 3.7). In both of these cases, no direct relation between the total polarization and the foreground extinction can be expected.
In all cases, the distributions can be fitted with a power law,
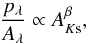 (10)yielding the
following power law indices:
(10)yielding the
following power law indices: 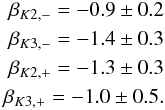 While
slightly steeper than the power law found for dataset K1 previously,
these new findings still agree with the results presented in Buchholz et al. (2011) and the conclusions drawn in that study.
Considering the shape of the point density plots (see Fig. 11), the uncertainties given for the power law indices might even be
underestimated. This effect is caused by the larger scatter in the polarization parameters
in these two datasets, which in turn results from the lower photometric quality.
While
slightly steeper than the power law found for dataset K1 previously,
these new findings still agree with the results presented in Buchholz et al. (2011) and the conclusions drawn in that study.
Considering the shape of the point density plots (see Fig. 11), the uncertainties given for the power law indices might even be
underestimated. This effect is caused by the larger scatter in the polarization parameters
in these two datasets, which in turn results from the lower photometric quality.
Compared to the pK− values, a significant offset in polarization efficiency is detected for the pK+ sources, while the underlying power law appears to be very similar. Again, this reproduces the findings in our previous study for the smaller FOV of dataset K1, and reinforces our conclusion that this might indicate a local contribution to the polarization, likely by dust in the central parsec itself. It has to be noted, however, that the offsets found for the K2 and K3 sources are smaller compared to the K1 sources, and this limits the confidence in this conclusion.
 |
Fig. 12 Polarization efficiency of the sources in all Ks-band datasets (K1, K2, K3) compared to Ks-band extinction, plotted as point density, with typical uncertainty represented on the left. pK+ and pK− sources shown separately in left respectively right frame. Green lines represent the fitted power-law relation. |
The distribution of the polarization efficiency combined for the three
Ks-band datasets is shown in Fig. 12. Fitting a power law to the polarization efficiency leads to
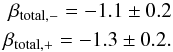 These
values agree with the results found for the individual datasets within the uncertainties.
A similar offset between the higher and lower polarized sources is also found here, but
there is a considerable overlap between the sub-groups. This stems from the different
selection criteria applied to the different datasets.
These
values agree with the results found for the individual datasets within the uncertainties.
A similar offset between the higher and lower polarized sources is also found here, but
there is a considerable overlap between the sub-groups. This stems from the different
selection criteria applied to the different datasets.
3.7. Bow-shock polarization
3.7.1. IRS 1W
In Buchholz et al. (2011), we determined the
H- and Ks-band polarization of IRS 1W as
![\begin{eqnarray} p_H^{\rm tot} &=& 5.2 \pm 0.5 \textnormal{ at } \theta_{H}^{\rm tot} = -12^{\circ} \pm 5^{\circ} \nonumber\\[1mm] p_H^{\rm int} &=& 6.9 \pm 0.5 \textnormal{ at } \theta_{H}^{\rm int} = -73^{\circ} \pm 5^{\circ} \nonumber\\[1mm] p_{K{\rm s}}^{\rm tot} &=& 1.8 \pm 0.5 \textnormal{ at } \theta_{K{\rm s}}^{\rm tot} = -37^{\circ} \pm 5^{\circ} \nonumber\\[1mm] p_{K{\rm s}}^{\rm int} &=& 7.8 \pm 0.5 \textnormal{ at } \theta_{K{\rm s}}^{\rm int} = -75^{\circ} \pm 5^{\circ} .\nonumber \end{eqnarray}](/articles/aa/full_html/2013/09/aa20338-12/aa20338-12-eq93.png) The
values found for the Lp-band confirm this trend: while a total
polarization of (4.9 ± 0.5)% at (− 62 ± 5)° is measured, applying a
depolarization matrix with p = 4%,θ = 25°
(estimated based on the IRS 1 and IRS 16 point sources) within yields an intrinsic
polarization of (8.9 ± 0.5)% at (− 63 ± 5)°. The polarization angle appears
consistent over the three bands, which suggests that the same process is responsible,
while the increase of the intrinsic polarization degree towards longer wavelengths
points to the higher influence of the extended dust component compared to that of the
central source.
The
values found for the Lp-band confirm this trend: while a total
polarization of (4.9 ± 0.5)% at (− 62 ± 5)° is measured, applying a
depolarization matrix with p = 4%,θ = 25°
(estimated based on the IRS 1 and IRS 16 point sources) within yields an intrinsic
polarization of (8.9 ± 0.5)% at (− 63 ± 5)°. The polarization angle appears
consistent over the three bands, which suggests that the same process is responsible,
while the increase of the intrinsic polarization degree towards longer wavelengths
points to the higher influence of the extended dust component compared to that of the
central source.
 |
Fig. 13 Map of the intrinsic Lp-band polarization of the extended source IRS 1W. The arrows indicate the proper motions of the central source, the motion of the Northern Arm material and the motion of both relative to each other. |
In order to investigate the polarization pattern in different regions of this extended source, the polarization was measured in small apertures in the deconvolved images, and the foreground polarization was subtracted using a Mueller matrix as described in Sect. 2.4. Figure 13 shows the polarization pattern in the Lp-band, and the similarity to both the H- and the Ks-band pattern (see Buchholz et al. 2011) is quite apparent, despite the much lower depth. The polarization increases in the tails of the bow-shock, while the apex shows signs of depolarization.
 |
Fig. 14 Map of the intrinsic Lp-band polarization of the extended source IRS 21. The arrows indicate the proper motions of the central source, the motion of the Northern Arm material and the motion of both relative to each other. |
3.7.2. IRS 21
In Buchholz et al. (2011), we measured the
Ks-band polarization of IRS 21 as
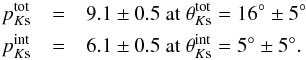 In
the Lp-band, IRS 21 shows a much stronger polarization compared to the
Ks-band. The total polarization amounts to (19.0 ± 0.5)% at
(24 ± 5)°, and subtracting the foreground polarization (see Sect. 3.7.1, estimated based on the IRS 1 and IRS 16 point
sources) reveals an intrinsic polarization of (15.0 ± 0.5)% at (24 ± 5)°.
In
the Lp-band, IRS 21 shows a much stronger polarization compared to the
Ks-band. The total polarization amounts to (19.0 ± 0.5)% at
(24 ± 5)°, and subtracting the foreground polarization (see Sect. 3.7.1, estimated based on the IRS 1 and IRS 16 point
sources) reveals an intrinsic polarization of (15.0 ± 0.5)% at (24 ± 5)°.
By comparison, the polarization pattern in the Lp-band (see Fig. 14) appears more uniform: polarization degrees on the order of 15% are detected in regions with significant flux, with very similar polarization angles of 20–25°. As in the Ks-band, no clear substructure (as it was found for IRS 1W) is apparent.
3.7.3. IRS 10W
 |
Fig. 15 Map of the intrinsic Lp-band polarization of the extended source IRS 10W. The arrows indicate the proper motions of the central source, the motion of the Northern Arm material and the motion of both relative to each other. |
IRS 10W is contained in the FOV of the 2011 Ks- and Lp-band data. No polarimetric H-band observations of this source are available.
The quality of this Ks-band dataset is insufficient for spatially resolved polarimetry, so only total values could be obtained: we measured the total polarization of IRS 10W as (2.1 ± 0.5)% at (6 ± 5)° in the Ks-band. Applying a depolarization matrix with the polarization of IRS 10E* used as the foreground value (this source is point-like and does not show signs of intrinsic polarization, with (5.4 ± 0.5)% at (28 ± 4)°) yielded an intrinsic polarization of (4.2 ± 0.5)% at (− 52 ± 5)°. In the Lp-band, we found similar values: the total polarization is measured as (0.9 ± 0.5)% at (− 61 ± 5)°, which yields an intrinsic polarization of (5.6 ± 0.5)% at (− 67 ± 5)°, assuming a foreground polarization of (4.7 ± 0.5)% at (22 ± 5)°, which was again estimated based on IRS 10E*.
IRS 10W does not show the clear bow-shock morphology that was found in the case of IRS 1W (see Fig. 15). Tanner et al. (2005) fitted this source with a bow-shock like shape, but the authors of that study themselves cautioned that the angle of the best-fit solution did not agree with the observed proper motions of the source and the dynamics of the Northern Arm. They instead suggested that the observed shape was produced by the additional influence of an outflow from IRS 10E*, a highly variable source about 2′′ to the south-east. The resolved Lp-band polarization (see Fig. 15) is also not consistent with a bow-shock with the apex towards the east. The pattern found here would agree well with a bow-shock oriented at about 30° east-of-north, which would be consistent with the source proper motions and the Northern Arm flow here. The polarization pattern is less symmetric than that found for IRS 1W, and the uncertainties are larger, but these findings seem to confirm the suggestion of Tanner et al. (2005) that the bright region in the south-east is indeed not the apex of the bow-shock.
The total polarization measured in the Ks- and Lp-band supports this argument as well. An intrinsic polarization angle perpendicular to the bow-shock angle would be expected, and therefore the observed angles of − 52° respectively − 67° would indicate a bow-shock angle of about 20–40°.
3.7.4. IRS 5
IRS 5 also shows a bow-shock shape in the Ks- and the Lp-bands (as found by e.g. Tanner et al. 2005), and the total polarization measured in both bands at least partly agrees with the observed morphology: in the Ks-band, the source shows a total polarization of (5.4 ± 0.5)% at (24 ± 5)°. Most sources in the vicinity seem to exhibit a stronger polarization (see Fig. 6) on the order of 7.5% at 24°, based on sources within ~5′′. This yields an intrinsic polarization of (2.1 ± 0.5)% at (− 62 ± 5)° for IRS 5. Note that this estimate depends critically on the accuracy of the foreground value.
 |
Fig. 16 Map of the intrinsic Lp-band polarization of the extended source IRS 5. The arrows indicate the proper motions of the central source, the motion of the Northern Arm material and the motion of both relative to each other. |
Looking at the Lp-band, the source also shows a deviation in polarization from the sources around it: we measured a value of (1.8 ± 0.5)% at (14 ± 5)°, and with a foreground polarization of 4% at 25° this leads to an intrinsic value of (2.5 ± 0.5)% at (− 57 ± 5)°. The angle we find here coincides with the Ks-band angle and with the expectations from the observed orientation of the bow-shock.
The resolved Lp-band polarization pattern (see Fig. 16) resembles that of IRS 1W closely, with stronger polarization found in the tails of the bow-shock, a decrease towards the apex and very uniform polarization angles. As for IRS 10W, the Ks-band data quality does not allow spatially resolved polarimetry. The observed pattern in the Lp-band agrees very well with the proper motions of the source and the streaming motion in the Northern Arm, as do the total intrinsic polarization parameters.
3.7.5. Comparing the bright bow-shock sources
In all four observed bright bow-shock sources, we find consistent polarization angles in all wavelength bands. In addition, there appears to be a similar relation between the Ks/Lp-band polarization degrees for all but one source, IRS 21. This increases the confidence in the respective foreground estimates (an incorrect foreground estimate can lead to a shift in the determined intrinsic polarization degree and angle, and this would generally affect the Lp- and Ks-band results differently due to the different total values).
For IRS 1W, we find that the intrinsic Lp-band polarization degree exceeds the Ks-band value by a factor of 1.1. IRS 5 shows a similar ratio (1.2), as does IRS 10W (1.3). By comparison, IRS 21 exhibits an increase from the Ks- to the Lp-band value by a factor of 2.5. Both values again differ from the foreground value, where a ratio of 0.8 is known from previous observations (Jones 1990) and was again confirmed here. How can this behavior be explained?
Buchholz et al. (2011) suggested emission from aligned grains as the dominant intrinsic polarization mechanism in the bow-shocks in the GC. This model is supported by the resolved Lp-band polarimetry patterns presented here. But can the competing processes of scattering (single or multiple) and local dichroic extinction play a role as well? For a given grain alignment, dichroic extinction would produce polarization perpendicular to emissive/single scattering polarization, while multiple scattering might simply reduce the observed intrinsic polarization (although multiple scattering on efficiently aligned elongated grains may have the same result as single scattering on these grains). The shape of IRS 21 suggests that the optical depth of the dust obscuring it is higher than what is found towards the Northern Arm bow-shocks, but is it sufficient for a significant contribution of multiple scattering and/or local dichroic extinction? While a detailed model of bow-shock polarization using measurements at more NIR/MIR wavelengths or even spectropolarimetry as input parameters would be desirable to clarify the extent and relative importance of these processes, a rough estimate may already be possible from the Ks- and Lp-band values alone.
The ratio 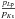 is much higher for IRS 21 compared to the IRS 1W-type sources (1W, 5, 10W). Moultaka et al. (2004) fitted the
Lp-band spectrum of IRS 21 with a 1200 K blackbody, which is hotter
than the value found for IRS 1W in the same study (~900 K). This alone would lead to a
higher emission at shorter wavelengths, and if dust emission is dominant for both
sources, why is the polarization of IRS 1W and IRS 21 almost the same in the
Ks-band, while the latter source has a much higher polarization in
the Lp-band? The answer might be that the optical depth respectively
dust extinction also has to be considered: a higher optical depth towards IRS 21 would
cause the light from the central source to be mostly absorbed at shorter wavelengths
(which produces polarization perpendicular to the emissive polarization) or affected by
multiple scattering (which depolarizes the light). Even if this contribution stays the
same in the Lp-band, the dust primarily emits at longer wavelengths, so
the highly polarized dust emission becomes more and more dominant towards the
Lp-band. The emissive polarization in the Ks-band is
in turn reduced by the absorption/multiple scattering component. For the IRS 1W-type
sources, these two processes would not play a significant role due to the much lower
optical depth towards the central source.
is much higher for IRS 21 compared to the IRS 1W-type sources (1W, 5, 10W). Moultaka et al. (2004) fitted the
Lp-band spectrum of IRS 21 with a 1200 K blackbody, which is hotter
than the value found for IRS 1W in the same study (~900 K). This alone would lead to a
higher emission at shorter wavelengths, and if dust emission is dominant for both
sources, why is the polarization of IRS 1W and IRS 21 almost the same in the
Ks-band, while the latter source has a much higher polarization in
the Lp-band? The answer might be that the optical depth respectively
dust extinction also has to be considered: a higher optical depth towards IRS 21 would
cause the light from the central source to be mostly absorbed at shorter wavelengths
(which produces polarization perpendicular to the emissive polarization) or affected by
multiple scattering (which depolarizes the light). Even if this contribution stays the
same in the Lp-band, the dust primarily emits at longer wavelengths, so
the highly polarized dust emission becomes more and more dominant towards the
Lp-band. The emissive polarization in the Ks-band is
in turn reduced by the absorption/multiple scattering component. For the IRS 1W-type
sources, these two processes would not play a significant role due to the much lower
optical depth towards the central source.
 |
Fig. 17 Left: Lp-band image of the MIR excess source IRS 5E before LR deconvolution. The arrows indicate the proper motions of the central source, the motion of the Northern Arm material and the motion of both relative to each other. The magenta line indicates the polarization. Right: The same source after LR deconvolution. The elongation of the source, the relative motion vector and the polarization all consistently indicate a bow-shock source. Contours indicate flux levels, in steps of 10% of the maximum flux. |
H-band polarimetry is only available for one bow-shock source, IRS 1W (see Buchholz et al. 2011). Combined with our new data, we find a HKsLp-relation of the polarization degrees of 0.9:1:1.1 (normalized to pKs). For the sources only affected by foreground polarization, we find a relation of 1.8:1:0.9 from comparing the peaks of the distributions of the polarization degrees of the individual datasets (with the caveat that these do not cover the same FOV). Considering the different mechanisms responsible for the polarization in the two cases and the different grain parameters (especially temperature, density and efficiency of alignment, also possibly the size distribution), it is not surprising that the relation found for the bow-shocks does not match the LOS behavior.
The intrinsic polarization degrees of the Northern Arm bow-shocks seems to exhibit another trend: from IRS 1W over IRS 10W to IRS 5, the intrinsic polarization degree decreases in the Ks- and the Lp-band. If we assume that the polarization is only caused by emission in these three sources, this effect might indicate a decline in grain alignment (which may in turn be caused by a lower magnetic field strength) towards the northern region of the Northern Arm. Viewed from the other side, this finding indicates that the field strength increases as the initially wide Northern Arm (Paumard et al. 2004) is compressed as it is funneled towards the center. This behavior appears consistent, but we must caution that this might be an overly simplified view since the polarization degree is not necessarily directly correlated with the field strength (see Aitken et al. 1998). In addition, the bow shocks should produce local disturbances in the magnetic field, which complicates any possible relation even more.
In order to further clarify these relations and to search for possible substructures in polarization in IRS 21, additional Lp-band observations with higher depth would be required, as well as Ks-band observations of the Northern Arm region with sufficient data quality for resolved polarimetry on IRS 5 and IRS 10W. Furthermore, deep Lp-band observations would allow direct measurements of the polarization of the Northern Arm dust features, as a supplement to the Aitken et al. (1998) MIR data.
3.7.6. IRS 5NE
In addition to the bright bow-shock sources observed in the GC, several other sources show a strong MIR excess. Among these, IRS 5NE (one of the sources east of IRS 5 that were examined in detail by Perger et al. 2008) shows a total Ks-band polarization of (7.4 ± 0.5)% at (13 ± 5)°. The polarization parameters agree with the expected foreground polarization (see Sect. 3.7.4). In the Lp-band, there appears to be a significant polarization excess, with a total polarization of (8.8 ± 0.5)% at (24 ± 5)° compared to a value of 4% at 25° in the vicinity. This leaves (4.8 ± 0.5)% at (23 ± 5)° of intrinsic polarization. While Perger et al. (2008) described this source as compact with no apparent bow-shock morphology or other extended component, they suggest that the very red color points to the influence of a dust envelope and that candidate sources include a dust-enshrouded low-luminosity AGB star or possibly a young stellar object still in its dust shell. They argue that IRS 5NE might also be a low luminosity variant of the brighter bow-shock sources in the central parsec.
With the higher resolution available here and after a Lucy-Richardson deconvolution, IRS 5NE appears clearly extended in the Lp-band (although no apparent bow-shock shape can be observed, see Fig. 17). The shape of the source would be marginally consistent with a bow-shock considering its proper motions and the local streaming motion of the Northern Arm (which seems to extend even further eastward than IRS 5 and 10, see Paumard et al. 2004). The intrinsic polarization also suggests a dusty source, and the polarization angle found here is almost perpendicular to the relative motion of the source through the surrounding material (Paumard et al. 2004; Perger et al. 2008) and the observed elongated feature. The source is too faint and the depth of the available data is too low for resolved polarimetry, but the findings mentioned above already make a good case for IRS 5NE being a bow-shock source, similar to IRS 1W and IRS 5.
3.7.7. IRS 2
The IRS 2 region, located south of IRS 13 (see e.g. map by Viehmann et al. 2005), is made up of three main bright sources: the extended sources IRS 2L in the north and IRS 2S in the south, and a more compact source between the two, here referred to as IRS 2C. Polarimetric data is only available in the Lp-band for these sources.
A total polarization of (7.1 ± 0.5)% at (− 60 ± 5)° is found for IRS 2L, and with an assumed foreground polarization of 4% at 25° based on neighboring sources within ~10′′, this source shows an intrinsic polarization of (11.1 ± 0.5)% at (− 62 ± 5)°. IRS 2S exhibits a weaker total polarization at a similar angle, with (3.2 ± 0.5)% at (− 49 ± 5)°. With the same foreground polarization, this leads to an intrinsic value of (6.9 ± 0.5)% at (− 58 ± 5)°. IRS 2C, located in projection directly between these two sources, shows only the foreground value and no signs of intrinsic polarization. This can easily be explained if this source simply lies in front of the dust feature that stretches from IRS 13 down to IRS 2, while the other two sources are embedded in this structure and affected by it. This is supported by the shape of the sources in Lp-band images, where IRS 2C appears point-like and the other two are visibly extended. The fact that both other sources show the same polarization angle but different polarization degrees may indicate a different dust column density towards these sources, and indeed it seems as if the dust structure they are embedded in becomes fainter towards the south (see e.g. Fig. 2 in Buchholz et al. 2011).
No direct measurements of the projected velocities of the local medium are available in this region (IRS 2 lies outside of the region where velocities were mapped by Paumard et al. 2004). These sources lie between the regions for which Zhao et al. (2009) determined local gas velocities. But if the local magnetic field (see Aitken et al. 1998) follows the velocity field as it is the case for the Northern Arm, this would indicate a local streaming motion with an angle of 20–30° to the north-south axis. If these sources are indeed embedded in a structure that is on an infalling orbit around the center (in a way similar to the Northern Arm), the local streaming motion should be towards the north-west. Figure 18 shows an assumed motion of the local medium (of ~120 km s-1, dashed blue line), and the resulting relative motion. If these were bow-shock sources, the polarization angle would be expected to be perpendicular to the relative motion, and this is clearly not the case here: for IRS 2L, the observed angle differs by about 45° from the expected value, while for IRS 2S, it is even perpendicular to what would be exptected for a bow-shock. In addition, the observed angles differ about 30° from the MIR angles determined for the extended emission by Aitken et al. (1998). These findings indicate that the observed polarization may be influenced significantly by the local extended dust distribution and the interaction of the central sources with the medium. Without examining the spatial polarization patterns and comparing them over different wavelength bands, it is not possible to determine whether these sources are bow-shocks or not.
 |
Fig. 18 Lp-band image of the MIR excess source IRS 2L (left) and IRS 2S (right) after LR deconvolution. The arrows indicate the proper motions of the central source, the (assumed) motion of the local medium and the (assumed) motion of both relative to each other. The magenta line indicates the polarization. |
4. Conclusions
We draw the following conclusions:
-
1.
Our new Ks-band observations do not show clear localized offsets in polarization degree and angle, compared to our previous study of the innermost 3′′ × 19′′ (Buchholz et al. 2011). These features may however be masked by the lower data quality, which leads to a wider distribution of both parameters.
-
2.
For the first time, Lp-band polarimetry was conducted with an 8 m telescope, yielding polarization parameters for 84 sources brighter than 11 mag in the central parsec. The results confirmed the findings by Jones (1990) of a deviation in the Lp-band from the NIR wavelength dependency of the foreground polarization based on a much larger number of sources.
-
3.
The correlation between the spatially variable extinction towards the central parsec and the polarization efficiency,
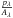 that was determined in Buchholz et al. (2011)
has been confirmed here. Separating the newly observed sources based on their
Ks-band polarization degree yields an offset in polarization
efficiency similar to what was found in our previous study. There may indeed be an
additional local component of the polarization here as well, but it cannot be
localized as clearly as in the Buchholz et al.
(2011) data.
that was determined in Buchholz et al. (2011)
has been confirmed here. Separating the newly observed sources based on their
Ks-band polarization degree yields an offset in polarization
efficiency similar to what was found in our previous study. There may indeed be an
additional local component of the polarization here as well, but it cannot be
localized as clearly as in the Buchholz et al.
(2011) data. -
4.
As already shown in e.g. Buchholz et al. (2011), intrinsic polarization takes place in several sources in the central parsec, not only at longer wavelengths as shown first by Knacke & Capps (1977), but also in the H- and Ks-band (e.g. Ott et al. 1999). Using the Müller calculus, the intrinsic component can be isolated for point sources and maps of extended features. The resulting total intrinsic polarization angles for several known extended sources such as IRS 1W, IRS 5, IRS 10W and IRS 21 agree very well with what can be expected from source morphology and relative motion of gas/dust in the Northern Arm and the sources themselves. Very similar intrinsic polarization degrees are measured for IRS 1W and IRS 21, with (7.8 ± 0.5)% at (− 75 ± 5)° for IRS 1W and (6.1 ± 0.5)% at (5 ± 5)° for IRS 21 (both Ks-band). Contrary to the wavelength dependency seen in the foreground polarization, the H-band polarization degree is slightly lower for IRS 1W compared to the Ks-band: (6.9 ± 0.5)% at (− 73 ± 5)°. The fact that the central source contributes a larger amount of flux in the H-band compared to the extended component, while the intrinsic polarization mostly stems from the bow-shock, explains this discrepancy. In the Lp-band, the intrinsic polarization degree of these two sources deviates considerably (while the angles are still very similar): IRS 21 shows a much stronger Lp-band polarization of (15 ± 0.5)% than IRS 1W with (8.9 ± 0.5)%. This may be an effect of a much higher dust density and therefore higher optical depth towards the former source.
-
5.
IRS 5 and IRS 10W show a relation between Ks- and Lp-band polarization similar to what was found for IRS 1W (at lower total polarization degrees). It seems that the intrinsic polarization degree in both bands declines from IRS 1W to IRS 5, with IRS 10W inbetween. This may point to a decrease in grain alignment (and therefore magnetic field strength?) from south to north along the Northern Arm, but drawing such conclusions based on only three data-points is risky at best. The resolved patterns also resemble that found for IRS 1W, and they also agree well with the observed proper motions and the streaming motion of the local medium, so it appears that the same mechanism is at work there.
-
6.
Of the remaining MIR excess sources contained in the observed FOV, only IRS 5NE, IRS 2L and IRS 2S seem to show significant intrinsic polarization (IRS 9, for instance, is apparently purely foreground-polarized). Considering the known proper motions of these sources and the known (or in case of the IRS 2 sources, assumed) streaming velocities of the local medium, the polarization of IRS 5NE would agree very well with a lower luminosity version of the bow-shocks observed in IRS 1W, 5 and 10 W, while no clear conclusions can be drawn for the IRS 2 sources. The latter may show an influence of local dust emission in addition to their own interaction with the medium.
Several effects appear to contribute to the observed polarization in the central parsec of the GC, in addition to the foreground polarization. While the latter is dominant in most sources in all three observed wavelength bands, large scale variations in foreground polarization angle and degree, as well as intrinsic effects play a very important role and may be used to further investigate the interstellar medium in the GC.
The recently achieved polarimetric calibration of NACO (Witzel et al. 2011) and the first successful polarimetric Lp-band observations in nearly 30 years offer the possibility to use these tools to further enhance the knowledge of the stellar population and the ISM in the vicinity of Sgr A*.
Online material
Details of the observations used for this work.
Polarization parameters of the sources detected in the Ks- and Lp-band.
Acknowledgments
We are grateful to all members of the NAOS/CONICA and the ESO PARANAL team. R. M. Buchholz acknowledges support by Renia GmbH. R. Schödel acknowledges support by the Ramón y Cajal programme of the Spanish Ministry of Economy and Competition, by grants AYA2010-17631 and AYA2009-13036 of the Spanish Ministry of Economy and Competition, and by grant P08-TIC-4075 of the Junta de Andalucía. Part of this work was supported by the COST Action MP0905: Black Holes in a violent Universe, the Deutsche Forschungsgemeinschaft (DFG) via the Cologne Bonn Graduate School (BCGS), and via grant SFB 956, as well as by the Max Planck Society and the University of Cologne through the International Max Planck Research School (IMPRS) for Astronomy and Astrophysics. We had fruitful discussions with members of the European Union funded COST Action MP0905: Black Holes in a violent Universe and the COST Action MP1104: Polarization as a tool to study the Solar System and beyond. We received funding from the European Union Seventh Framework Programme (FP7/2007-2013) under grant agreement No. 312789. We would also like to thank the anonymous referee for the helpful comments and suggestions.
References
- Aitken, D., Smith, C., Moore, T., & Roche, P. 1998, MNRAS, 299, 743 [NASA ADS] [CrossRef] [Google Scholar]
- Bailey, J., Hough, J. H., & Axon, D. J. 1984, MNRAS, 208, 661 [NASA ADS] [Google Scholar]
- Böker, T. 2010, IAU Symp. Proc., 266, 58 [NASA ADS] [Google Scholar]
- Buchholz, R. M., Schödel, R., & Eckart, A. 2009, A&A, 499, 483 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Buchholz, R. M., Witzel, G., Schödel, R., Eckart, A., Bremer, M., & Muzic, K. 2011, A&A, 534, A117 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Capps, R. W., & Knacke, R. F. 1976, ApJ, 210, 76 [NASA ADS] [CrossRef] [Google Scholar]
- Davis, L., & Greenstein, J., 1951, ApJ, 114, 206 [Google Scholar]
- Devillard, N., 1997, The Messenger 87, 19 [NASA ADS] [Google Scholar]
- Eckart, A., Genzel, R., Hofmann, R., Sams, B. J., & Tacconi-Garman, L. E. 1995, ApJ, 445, 23 [Google Scholar]
- Eckart, A., Genzel, R., Ott, T., & Schödel, R. 2002, MNRAS, 331, 917 [NASA ADS] [CrossRef] [Google Scholar]
- Fritz, T. K., Gillessen, S., Dodds-Eden, K., et al. 2011, ApJ, 737, 73 [NASA ADS] [CrossRef] [Google Scholar]
- Ghez, A. M., Duchêne, G., Matthews, K., et al. 2003, ApJ, 586, L127 [NASA ADS] [CrossRef] [Google Scholar]
- Ghez, A. M., Salim, S., Weinberg, N. N., et al. 2008, ApJ, 689, 1044 [NASA ADS] [CrossRef] [Google Scholar]
- Gillessen, S., Eisenhauer, F., Trippe, S., et al. 2009, ApJ, 692, 1075 [NASA ADS] [CrossRef] [Google Scholar]
- Hatano, H., Nishiyama, S., Kurita, M., et al. 2013, AJ, 145, 105 [NASA ADS] [CrossRef] [Google Scholar]
- Heiles, C. 1987, in Interstellar Processes, eds. D. Hollenbach, & H. Thronson (Boston: Reidel), 171 [Google Scholar]
- Jones, T. J. 1989, ApJ, 346, 728 [NASA ADS] [CrossRef] [Google Scholar]
- Jones, T. J. 1990, AJ, 99, 1894 [NASA ADS] [CrossRef] [Google Scholar]
- Knacke, R. F., & Capps, R. W. 1977, ApJ, 216, 271 [NASA ADS] [CrossRef] [Google Scholar]
- Kobayashi, Y., Kawara, K., Kozasa, T., Sato, S., & Okuda, H. 1980, Publ. Astron. Soc. Japan, 32, 291 [NASA ADS] [Google Scholar]
- Lazarian, A. 2003, J. Quant. Spectr. Radiat. Transf., 79, 881 [Google Scholar]
- Lazarian, A., & Hoang, T. 2007, MNRAS, 378, 910 [Google Scholar]
- Lebofsky, M. J., Rieke, G. H., Deshpande, M. R., & Kemp, J. C. 1982, ApJ, 263, 672 [NASA ADS] [CrossRef] [Google Scholar]
- Lenzen, R., Hartung, M., Brandner, W., et al. 2003, in SPIE Conf. Ser. 4841, eds. M. Iye, & A. F. M. Moorwood, 944 [Google Scholar]
- Martin, P. G., & Whittet, D. C. B. 1990, ApJ, 357, 113 [NASA ADS] [CrossRef] [Google Scholar]
- Mathis, J. S. 1986, ApJ, 308, 281 [NASA ADS] [CrossRef] [Google Scholar]
- Moultaka, J., Eckart, A., Viehmann, T., et al. 2004, A&A, 425, 529 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Nagata, T., Kobayashi, N., & Sato, S. 1994, ApJ, 423, L113 [NASA ADS] [CrossRef] [Google Scholar]
- Nishiyama, S., Tamura, M., Hatano, H., et al. 2009, ApJ, 690, 1648 [NASA ADS] [CrossRef] [Google Scholar]
- Nishiyama, S., Hatano, H., Tamura, M., et al. 2010, ApJ, 722, 23 [Google Scholar]
- Ott, T., Eckart, A., & Genzel, R. 1999, ApJ, 523, 248 [NASA ADS] [CrossRef] [Google Scholar]
- Paumard, T., Maillard, J.-P., & Morris, M. 2004, A&A, 426, 81 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Perger, M., Moultaka, J., Eckart, A., et al. 2008, A&A, 478, 127 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Purcell, E. M., & Spitzer, L. 1971, ApJ, 167, 31 [NASA ADS] [CrossRef] [Google Scholar]
- Reid, M. J., & Brunthaler, A. 2004, ApJ, 616, 872 [NASA ADS] [CrossRef] [Google Scholar]
- Rousset, G., Lacombe, F., Puget, P., et al. 2003, in SPIE Conf. Ser. 4839, eds. P. L. Wizinovich, & D. Bonaccini, 140 [Google Scholar]
- Schödel, R. 2010, A&A, 509, A58 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Schödel, R. 2011, in The Galactic Center: a Window to the Nuclear Environment of Disk Galaxies, ASP Proc. workshop 439, Shanghai, China, October 19–23, 2009, eds. M. Morris, Q. Wang, & F. Yuan (San Francisco: ASP), 222 [Google Scholar]
- Schödel, R., Ott, T., Genzel, R., et al. 2002, Nature, 419, 694 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Schödel, R., Ott, T., Genzel, R., et al. 2003, ApJ, 596, 1015 [NASA ADS] [CrossRef] [Google Scholar]
- Schödel, R., Najarro, F., Muzic, K., & Eckart, A. 2010, A&A, 511, A18 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Scoville, N. Z., Stolovy, S. R., Rieke, M., Christopher, M., & Yusef-Zadeh, F. 2003, ApJ, 594, 294 [Google Scholar]
- Serkowski, K., Mathewson, D. S., & Ford, V. L., 1975, ApJ, 196, 261 [NASA ADS] [CrossRef] [Google Scholar]
- Tanner, A., Ghez, A. M., Morris, M., et al. 2002, ApJ, 575, 860 [NASA ADS] [CrossRef] [Google Scholar]
- Tanner, A., Ghez, A. M., Morris, M., & Christou, J. C. 2005, ApJ, 624, 742 [NASA ADS] [CrossRef] [Google Scholar]
- Viehmann, T., Eckart, A., Schödel, R., et al. 2005, A&A, 433, 117 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Whitney, B. A., & Wolff, M. J. 2002, ApJ, 574, 205 [NASA ADS] [CrossRef] [Google Scholar]
- Witzel, G., Eckart, A., Buchholz, R. M., et al. 2011, A&A, 525, A130 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Zhao, J.-H., Morris, M. R., Goss, W. M., & An, T. 2009, ApJ, 699, 186 [NASA ADS] [CrossRef] [Google Scholar]
All Tables
All Figures
 |
Fig. 1 Ks-band image of the innermost 40.5′′ of the GC (ESO VLT NACO image, 2004, see Buchholz et al. 2009). The marked areas denote the polarimetric FOVs: white indicates Ks-band, green Lp-band and blue H-band. The H-band (H1, see Table 1 and the two southern Ks-band FOVs (K1, K2) have been presented in Buchholz et al. (2011), while the northern Ks-band (K3) and the Lp-band (L1) FOV are examined in this study. |
| In the text | |
 |
Fig. 2 Flux uncertainties for the 0 degree channel of the Ks-band dataset, plotted against the brightness of the sources in magnitudes. The uncertainties were determined from the flux variations in background apertures and can therefore only be regarded as a lower limit for the actual uncertainties. The other channels show a very similar uncertainty distribution. |
| In the text | |
 |
Fig. 3 Ks-band magnitudes of the sources detected in the polarimetric dataset K3. Black: all sources. Green: sources with reliably measured polarization parameters. |
| In the text | |
 |
Fig. 4 Flux uncertainties for the 0 degree channel of the Lp-band dataset, plotted against the brightness of the sources in magnitudes. The green points denote sources with reliable polarization parameters as was determined later in the analysis, while the black points indicate sources that were rated as unreliable. The uncertainties were determined from the flux variations in background apertures and can therefore only be regarded as lower limit for the actual uncertainties. The other channels show a very similar uncertainty distribution. |
| In the text | |
 |
Fig. 5 Lp-band magnitudes of the sources detected in the polarimetric dataset L1. Black: all sources. Green: sources with reliably measured polarization parameters. |
| In the text | |
 |
Fig. 6 Ks-band polarization map of stars in the Galactic center. Only reliably measured polarization values are shown here. Black circles/red lines and blue circles/green lines: datasets presented in Buchholz et al. (2011). Red circles and black lines: new March 2011 Ks-band data. The diameter of the circles corresponds to the brightness of the source. Thin black lines in the background denote magnetic fields determined from mid-infrared (MIR) data (Aitken et al. 1998, based on a 1.5′′ beam). The brightest sources are also indicated. |
| In the text | |
 |
Fig. 7 Ks-band polarization degrees (plotted on logarithmic scale, upper left) and angles (lower left) of stars in the Galactic center. The red lines denotes fits with a single Gaussian distribution, while the green respectively blue lines denote the fit with a double Gaussian (green: sum, blue: individual Gaussians). Upper right: relative uncertainties of the polarization degrees. Lower right: absolute uncertainties of the polarization angles. |
| In the text | |
 |
Fig. 8 Lp-band polarization map of stars in the Galactic center. Only reliably measured polarization values are shown here. Red lines indicate the polarization vectors of sources classified as affected by intrinsic polarization according to Sect. 3.5 as well as the observed bow-shock sources, while green lines denote sources only exhibiting foreground polarization. |
| In the text | |
 |
Fig. 9 Lp-band polarization degrees (plotted on logarithmic scale, upper left) and angles (lower left) of stars in the Galactic center. The red line denotes the fit with one Gaussian distribution, while green respectively blue lines denote the fit with a double Gaussian (green: sum, blue: individual Gaussians). Upper right: relative uncertainties of the polarization degrees. Lower right: absolute uncertainties of the polarization angles. |
| In the text | |
 |
Fig. 10 Left frame: relation of Lp- to Ks-band polarization degree (logarithmic plot). Right frame: difference between Lp- and Ks-band polarization angle. In both frames, the red columns represent suspected intrinsically polarized sources, while the black columns contain sources affected only by the foreground polarization. The green lines represent Gaussians fitted to the histograms. |
| In the text | |
 |
Fig. 11 Polarization efficiency in dataset K2 (Ks-band, upper frames) and dataset K3 (Ks-band, lower frames), compared to Ks-band extinction, plotted as point density, with typical uncertainties represented on the left. pK+ and pK− sources shown separately in left respectively right frames for both bands. Green lines represent the fitted power-law relation. For the polarization efficiency in dataset K1, see Buchholz et al. (2011), Fig. 16. |
| In the text | |
 |
Fig. 12 Polarization efficiency of the sources in all Ks-band datasets (K1, K2, K3) compared to Ks-band extinction, plotted as point density, with typical uncertainty represented on the left. pK+ and pK− sources shown separately in left respectively right frame. Green lines represent the fitted power-law relation. |
| In the text | |
 |
Fig. 13 Map of the intrinsic Lp-band polarization of the extended source IRS 1W. The arrows indicate the proper motions of the central source, the motion of the Northern Arm material and the motion of both relative to each other. |
| In the text | |
 |
Fig. 14 Map of the intrinsic Lp-band polarization of the extended source IRS 21. The arrows indicate the proper motions of the central source, the motion of the Northern Arm material and the motion of both relative to each other. |
| In the text | |
 |
Fig. 15 Map of the intrinsic Lp-band polarization of the extended source IRS 10W. The arrows indicate the proper motions of the central source, the motion of the Northern Arm material and the motion of both relative to each other. |
| In the text | |
 |
Fig. 16 Map of the intrinsic Lp-band polarization of the extended source IRS 5. The arrows indicate the proper motions of the central source, the motion of the Northern Arm material and the motion of both relative to each other. |
| In the text | |
 |
Fig. 17 Left: Lp-band image of the MIR excess source IRS 5E before LR deconvolution. The arrows indicate the proper motions of the central source, the motion of the Northern Arm material and the motion of both relative to each other. The magenta line indicates the polarization. Right: The same source after LR deconvolution. The elongation of the source, the relative motion vector and the polarization all consistently indicate a bow-shock source. Contours indicate flux levels, in steps of 10% of the maximum flux. |
| In the text | |
 |
Fig. 18 Lp-band image of the MIR excess source IRS 2L (left) and IRS 2S (right) after LR deconvolution. The arrows indicate the proper motions of the central source, the (assumed) motion of the local medium and the (assumed) motion of both relative to each other. The magenta line indicates the polarization. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


