| Issue |
A&A
Volume 556, August 2013
|
|
|---|---|---|
| Article Number | A116 | |
| Number of page(s) | 11 | |
| Section | Numerical methods and codes | |
| DOI | https://doi.org/10.1051/0004-6361/201321837 | |
| Published online | 06 August 2013 | |
Observing extended sources with the Herschel SPIRE Fourier Transform Spectrometer
1
Laboratoire AIM, CEA/DSM − CNRS − Irfu/Service d’Astrophysique, CEA
Saclay,
91191
Gif-sur-Yvette,
France
e-mail:
ronin.wu@cea.fr
2
RAL Space, Rutherford Appleton Laboratory,
Didcot
OX11 0QX,
UK
3
Institute for Space Imaging Science, Department of Physics
& Astronomy, University of Lethbridge, Lethbridge, AB T1K3M4, Canada
4
Centro de Astrobiología (CSIC/INTA), Ctra. de Torrejón a Ajalvir,
km 4, 28850 Torrejón de Ardoz, Madrid, Spain
5
Cambridge University, Cavendish Laboratory and the Kavli Institute
for Cosmology, CB3
0 HA Cambridge,
UK
6
University College London, Department of Physics and
Astronomy, WC1E
6 BT London,
UK
7
Blue Sky Spectroscopy, 9/740 4 Ave S, Lethbridge, Alberta, T1J
0N9, Canada
8
Cardiff University, The Parade, Cardiff, UK
9
Laboratoire d’Astrophysique de Marseille − LAM, Université
d’Aix-Marseille & CNRS, UMR 7326, 38 rue F. Joliot-Curie, 13388
Marseille Cedex 13,
France
10
Center for Astrophysics and Space Astronomy, 389-UCB, University
of Colorado, CO
80303
Boulder,
USA
11
Physics Department, Imperial College London, SW7 2, AZ South Kensington Campus,
UK
12
NASA Herschel Science Centre, IPAC, Pasadena, California, USA
13
Department of Physical Sciences, The Open
University, MK7
6 AA Milton Keynes,
UK
14
European Space Astronomy Centre, Herschel Science Centre, ESA,
28691
Villanueva de la Cañada,
Spain
Received:
5
May
2013
Accepted:
25
June
2013
The Spectral and Photometric Imaging Receiver (SPIRE) on the European Space Agency’s Herschel Space Observatory utilizes a pioneering design for its imaging spectrometer in the form of a Fourier Transform Spectrometer (FTS). The standard FTS data reduction and calibration schemes are aimed at objects with either a spatial extent that is much larger than the beam size or a source that can be approximated as a point source within the beam. However, when sources are of intermediate spatial extent, neither of these calibrations schemes is appropriate and both the spatial response of the instrument and the source’s light profile must be taken into account and the coupling between them explicitly derived. To that end, we derive the necessary corrections using an observed spectrum of a fully extended source with the beam profile and considering the source’s light profile. We apply the derived correction to several observations of planets and compare the corrected spectra with their spectral models to study the beam coupling efficiency of the instrument in the case of partially extended sources. We find that we can apply these correction factors for sources with angular sizes up to θD ~ 17′′. We demonstrate how the angular size of an extended source can be estimated using the difference between the subspectra observed at the overlap bandwidth of the two frequency channels in the spectrometer, at 959 < ν < 989 GHz. Using this technique on an observation of Saturn, we estimate a size of 17.2′′, which is 3% larger than its true size on the day of observation. Finally, we show the results of the correction applied on observations of a nearby galaxy, M82, and the compact core of a Galactic molecular cloud, Sgr B2.
Key words: instrumentation: spectrographs / methods: analytical / methods: data analysis / techniques: spectroscopic
© ESO, 2013
1. Introduction
Accurate calibration of astronomical observations is normally achieved by using standard sources whose flux density is well known from other telescopes, or is well modeled, or both. However, this limits the applicability of the calibration to those sources that have the same spatial extent within the telescope beam as the standards. A correction using simple filling factors is often applied on real astronomical objects that have a non-negligible size with respect to the telescope beam. This paper addresses the problem of sources that are partially extended with respect to the beam of the Herschel SPIRE instrument.
The Spectral and Photometric Imaging Receiver (SPIRE) is one of three focal plane instruments on board the ESA Herschel Space Observatory (Pilbratt et al. 2010). It contains an imaging photometric camera and an imaging Fourier Transform Spectrometer (FTS). Both subinstruments use arrays of bolometric detectors operating at ~300 mK (Turner et al. 2001) with feedhorn focal plane optics giving sparse spatial sampling over an extended field of view (Dohlen et al. 2000). The FTS is composed of two bolometer arrays with overlapping bands. The SPIRE Long Wavelength Array (SLW) covers 447 < ν < 990 GHz, and the SPIRE Short Wavelength Array (SSW) covers 958 < ν < 1546 GHz. The SLW and SSW contain 19 and 37 hexagonally packed detectors separated by 51′′ and 33′′ respectively. The FTS can observe requested targets in single-pointed or raster mode with sparse, intermediate, or full sampling by moving the SPIRE internal beam steering mirror to 1, 4, or, 16 jiggle positions. The three available sampling mode settings result in observations with spatial points separated by approximately 2, 1, and, 1/2 beams, respectively. A more detailed description of the instrument design can be found in Griffin et al. (2010) and more details of the observing modes in the SPIRE observer’s manual (2011).
The standard SPIRE FTS pipeline provides data calibrated with two extreme geometrical assumptions: either uniformly extended emission over a region that is much larger than the beam, or truly point-like emission centered on the optical axis. This calibration scheme was initially presented in Swinyard et al. (2010) and the FTS pipeline described in Fulton et al. (2010). More recent updates are described in the SPIRE observer’s manual (2011) and Swinyard et al. (in prep.). However, neither of these assumptions fits with real astronomical sources, which often have a complex morphology between the two assumed cases.
In this paper, we calculate a correction for extended sources based on a model of their distribution, and knowledge of the beam profile shape for single-pointed sparsely sampled observations. In Sect. 2, we summarize the current understanding of the FTS beam profile and its dependence on frequency. In Sect. 3, we summarize the important points of the FTS pipeline calibration scheme. We then calculate the efficiency factors needed to correct the standard calibration for a semi-extended source in Sect. 4 and test this with two real observations in Sect. 5. A discussion of this work is presented in Sect. 6. For the convenience of description, in the following context, we refer to a uniformly distributed extended source as an “extended source”, and an extended source with spatially dependent distribution as a “semi-extended source”.
2. Beam profile
The SPIRE FTS detector arrays use feedhorns to couple radiation to the bolometric sensors (Turner et al. 2001). Each feedhorn consists of a conical concentrator in front of a circular section waveguide designed to act as a spatial filter, allowing only certain electromagnetic modes to propagate along the waveguide. In most radio and submillimeter instruments, the waveguides are sized such that only a single electromagnetic mode is propagated and the resulting spatial response is a well controlled beam that is mathematically described well by a Gaussian profile (Martin & Bowen 1993). However, the requirement that the SPIRE FTS cover a large instantaneous bandwidth necessitated the use of multimoded feedhorns, whose spatial response is determined by the superposition of a finite number of modes that are enabled at specific frequencies. The frequencies at which the higher order modes are enabled are determined by the diameter of the waveguide (Chattopadhyay et al. 2003; Murphy & Padman 1991).
One can, in principle, derive the instrument beam pattern by time reversed propagation of the known feedhorn modes through the SPIRE optical system. However, modeling a complex system like the SPIRE FTS, consisting of 18 mirrors, 2 beam splitters, several filters, a dichroic, a lens and an undersized pupil stop, is impractical. Moreover, some clipping of the divergent beam in the two arms of the FTS is inevitable since the location of the intermediate pupil image changes as the spectrometer is scanned (Caldwell et al. 2000). Thus, the efficiency with which each electromagnetic mode couples to the incoming radiation pattern from a source of finite size is not amenable to direct calculation, being dependent on the source distribution. The frequency dependent coupling between a source of a given size and the FTS beam is therefore best determined experimentally using sources of known spatial distribution and flux. This technique has been employed by Makiwa et al. (2013) who used spectral scans of Neptune as the planet was raster scanned across the entrance aperture. The resulting map covered an angular extent equivalent to the third dark Airy ring at 1500 GHz and approximately the first dark Airy ring for frequencies below 510 GHz.
 |
Fig. 1 SPIRE FTS spectral beam size as measured by Makiwa et al. (2013). The shaded region shows 3σ errors. The frequencies at which the waveguide modes are enabled and the number of modes expected to be present (from theory) in each range is also shown, along with the expected size due to single–mode diffraction (dashed blue line). The inset plot shows the shape of the profile at 3 sample frequencies from SLW (420, 699, 990 GHz) and one frequency from SSW (1269 GHz). The horizontal axis of the inset plot is in the unit of arcsec. |
When designing submillimeter instruments it is common practice to consider the beam as a superposition of a set of discrete orthonormal modes, which are best represented by Hermite-Gaussian (HG) functions (Martin & Bowen 1993). Figure 1 shows the frequency dependent beam profile derived by Makiwa et al. (2013) using HG decomposition, and, for comparison, the FWHM expected from basic diffraction (based on an Airy pattern with effective mirror diameter 3.287 m). Also indicated in Fig. 1 is the number of modes expected to be present given the waveguide diameters. It is clear that, where the waveguide is single-moded (i.e., at frequencies below ~580 GHz in the SLW band and below ~1205 GHz in the SSW band), the instrument is essentially diffraction limited. As further modes propagate in the feedhorn their superposition leads to larger beam sizes relative to the optical diffraction limit. Within the noise limits of the available Neptune data, the SSW band is best represented by a Gaussian function, whereas the SLW band requires the first three radially symmetric HG functions (Makiwa et al. 2013). These authors also provide the recipe for constructing full radially symmetric beam profiles at any frequency.
3. Extended and point source calibration of the FTS
In this section, we briefly summarize the standard pipeline calibration scheme for the FTS. The instrument measures an interferogram pattern when observing a given astronomical source, in units of detector voltage. The interferogram is then converted to a spectrum in units of volts per GHz (V GHz-1) via a Fourier transform (Fulton et al. 2010). The resulting spectrum, in voltage density, is represented by Vobs.
The standard pipeline processes all non-mapping observations from voltage density to physical units in two stages. Firstly, the Herschel telescope is used as a calibrator to convert voltage density to surface brightness, Iext, which is appropriate for sources uniformly extended in the beam, and provides the “Level-1” product. Secondly, a point-source calibration is applied, derived using the planet Uranus, and convert Iext to flux density, Fpoint, providing the “Level-2” product. The observer is then able to choose which of Level-1 or Level-2, if either, matches the reality of their source.
3.1. Level-1: extended-source calibration
As described above, the Level-1 spectrum output by the FTS pipeline is calibrated
assuming that the source is uniformly extended within the beam. The calibration is based
on observations of a dark region of sky, i.e., where the detectors should only be
receiving thermal radiation from the Herschel telescope and SPIRE
instrument. Models of the telescope and instrument emission are constructed using onboard
temperature sensors and the telescope mirror emissivity as measured on the ground (Fischer et al. 2004), as described in the SPIRE observer’s manual (2011). The spectral response
applicable to extended sources is then defined as, 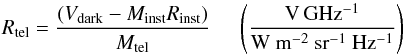 (1)where
Rtel is referred to as the telescope relative spectral
response function (RSRF), although it also contains the absolute conversion from
V GHz-1 to surface brightness in units of flux density per steradian.
W m-2 sr-1 Hz-1. Vdark,
which has the unit of V GHz-1, is the voltage density when observing the dark
sky. Minst and Mtel, which have
the unit of W m-2 sr-1 Hz-1, are the intensities,
calculated from the measured temperatures, of the instrument and the telescope.
Rinst is the instrument RSRF (the spectral response to the
instrument is different to that of the main beam). The observed source voltage density,
Vobs, is then converted to surface brightness,
Iext, using,
(1)where
Rtel is referred to as the telescope relative spectral
response function (RSRF), although it also contains the absolute conversion from
V GHz-1 to surface brightness in units of flux density per steradian.
W m-2 sr-1 Hz-1. Vdark,
which has the unit of V GHz-1, is the voltage density when observing the dark
sky. Minst and Mtel, which have
the unit of W m-2 sr-1 Hz-1, are the intensities,
calculated from the measured temperatures, of the instrument and the telescope.
Rinst is the instrument RSRF (the spectral response to the
instrument is different to that of the main beam). The observed source voltage density,
Vobs, is then converted to surface brightness,
Iext, using, 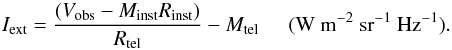 (2)This calibration is
only suitable for a uniformly extended source, which means that the solid angle of the
source light distribution profile is assumed to be much larger than the that of the FTS
beam at any given frequency, ν, i.e.
Ωsource(ν) ≫ Ωbeam(ν). For
point-like sources, the Level-1 data are not meaningful, but act as an intermediate step
to the Level-2 data.
(2)This calibration is
only suitable for a uniformly extended source, which means that the solid angle of the
source light distribution profile is assumed to be much larger than the that of the FTS
beam at any given frequency, ν, i.e.
Ωsource(ν) ≫ Ωbeam(ν). For
point-like sources, the Level-1 data are not meaningful, but act as an intermediate step
to the Level-2 data.
 |
Fig. 2 Spectra for a point source (CRL 618, left), semi-extended source (M83, center) and fully extended source (Orion Bar, right) after extended calibration (top row) and point source calibration (bottom row). The spectra have been smoothed. The flux density and brightness are in normalized units. |
3.2. Level-2: point-source calibration
In the second step of the pipeline, Iext is converted into flux density, in units of Jy, with a point-source calibration based on observations of Uranus. This calibration uses a point-source conversion factor, Cpoint,
![\begin{eqnarray} \label{eq2a} C_{\mathrm{point}} &=& \frac{M_{\mathrm{uranus}}}{I_{\mathrm{uranus}}}\hspace{0.5cm}(\mathrm{sr}),\\[0.5mm] \label{eq2b} F_{\rm point}& =& I_{\rm ext}\ C_{\rm point}\hspace{0.5cm}(\mathrm{Jy}) \end{eqnarray}](/articles/aa/full_html/2013/08/aa21837-13/aa21837-13-eq30.png) where
Muranus is the modeled flux density spectrum of Uranus as
described in Orton et al. (in prep.), and Iuranus is the
Level-1 data from the observation of Uranus. The model is corrected to take the finite
size of the planet on the day of observation into account, giving a true point source
calibration (assuming good telescope pointing). The resulting flux density (in Jy),
Fpoint, forms Level-2 data in the pipeline. This calibration
is only suitable when the observed source is point-like, i.e.,
Ωsource(ν) ≪ Ωbeam(ν).
where
Muranus is the modeled flux density spectrum of Uranus as
described in Orton et al. (in prep.), and Iuranus is the
Level-1 data from the observation of Uranus. The model is corrected to take the finite
size of the planet on the day of observation into account, giving a true point source
calibration (assuming good telescope pointing). The resulting flux density (in Jy),
Fpoint, forms Level-2 data in the pipeline. This calibration
is only suitable when the observed source is point-like, i.e.,
Ωsource(ν) ≪ Ωbeam(ν).
4. Correction for the semi-extended source distribution
While the standard pipeline process for analyzing SPIRE FTS data accommodates either point-like or fully extended sources (see Sect. 3), in practice, most astronomical sources fall between these two extreme cases. The effects of improperly applied calibration can become pronounced in the overlap region of the two bands of SPIRE FTS because the SLW beam diameter is a factor of ~2 larger than that of SSW (see Fig. 1). Figure 2 illustrates the resulting spectra of point and extended calibrated data for sources of increasing angular size (point-like, semi-extended and fully extended). When the calibration is inappropriate for the extent of the source, a noticeable difference in the measured flux and slope of the spectrum is observed at the overlapping region of the two bands. This is caused by the abrupt change in the effective beam size at those frequencies (see Sect. 2). For example, Fig. 2f shows the case in which a single-pointed, sparsely sampled observation of a uniformly extended source has been calibrated as a point source. It can be clearly seen that the resulting spectra show a distorted shape with a large step between the two bands, in which the SSW spectrum is underestimated. By comparison, the extended-source calibrated spectra are smooth and have no step between the bands, as shown in Fig. 2c). Similarly, the spectrum of a true point source would appear smooth when point-source calibrated (e.g., Fig. 2d), but distorted when extended-source calibrated (e.g. Fig. 2a).
An appropriately calibrated spectrum should contain no discontinuity between the SSW and SLW bands. Thus, the difference in intensity in the overlap region of the two bands, in both point-source and extended-source calibrated data, provides a simple method of estimating the source intensity distribution. This is particularly important for sparsely sampled SPIRE FTS observations, because in the absence of corresponding higher spatial resolution maps, the intensity jump may be the only indication of angular extent of the observed object.
The remainder of this section describes a method for correcting a SPIRE FTS spectrum based on an assumed source intensity distribution.
The goal of calibrating the FTS observation of a semi-extended source is to recover the
total flux density (in Jy) from the source signal that has reached the bolometers. In order
to achieve this, a conversion factor for a given source should be calculated, similar to Eq.
(3), as follows, 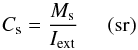 (5)where
Ms is the true integrated flux density of the
source. Once Cs has been determined, it is possible to obtain
the flux density by multiplying Iext (from Eq. (2)) by Cs, or by
multiplying the point-source calibrated data, Fpoint (from Eq.
(4)), by a factor
(5)where
Ms is the true integrated flux density of the
source. Once Cs has been determined, it is possible to obtain
the flux density by multiplying Iext (from Eq. (2)) by Cs, or by
multiplying the point-source calibrated data, Fpoint (from Eq.
(4)), by a factor
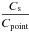 .
.
Cs is impossible to measure, because determining the true flux
density, Ms, is, after all, the purpose of the observation that
is being calibrated. However, Cs can be constructed by assuming
a dimensionless source light distribution,
Dν(Ψ), and an understanding of the beam
profile, Pν(Ψ).
Dν(Ψ) and
Pν(Ψ) define the solid angles of the
source, Ωsource, and of the beam, Ωbeam, with the following
relationship,  If
Dν(Ψ) provides a good representation of the
source spatial profile, a relationship between Ms and
Dν(Ψ) can be established,
If
Dν(Ψ) provides a good representation of the
source spatial profile, a relationship between Ms and
Dν(Ψ) can be established, 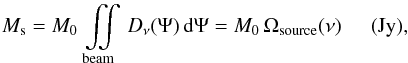 (8)where
M0 is a measure of the average surface brightness
of the source and has the unit of
W m-2 sr-1 Hz-1.
(8)where
M0 is a measure of the average surface brightness
of the source and has the unit of
W m-2 sr-1 Hz-1.
 |
Fig. 3 Diagram demonstrating how signals from a source, Ms, change before reaching the bolometer. |
4.1. Correction for the source-distribution
The propagation of the source model spectrum through the telescope and instrument is
summarized in Fig. 3. The efficiency with which the
source couples to the telescope is defined by the forward coupling
efficiency (see Ulich & Haas
1976; Kutner & Ulich 1981),
ηf, 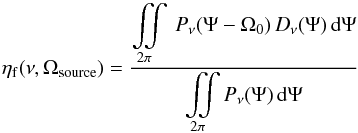 (9)where
Ω0 accounts for any offset of the source from the center of the beam (the
position of the source inside the beam clearly affects how the source distribution couples
to the beam profile).
(9)where
Ω0 accounts for any offset of the source from the center of the beam (the
position of the source inside the beam clearly affects how the source distribution couples
to the beam profile).
We introduce an empirically derived factor, the correction efficiency
(ηc), to deal with additional effects that are not already
taken into account by Eq. (9). Firstly, the
efficiency with which the reconstructed beam profile is coupled to the source distribution
is not known. Secondly, the efficiency with which Eq. (8) represents the true source is not known, and finally the beam
profile was only measured over a finite solid angle and so the reconstruction does not
take account of the response far from the optical axis. For a point source, we expect
ηc(ν,Ωpoint) = 1, i.e., the
measured beam profile, Pν(Ψ), is sufficient
to represent the effective solid angle covered by the source. For semi-extended sources,
in principle, ηc(ν,Ωsource) could
be determined by decomposing the source distribution using the same technique discussed in
Sect. 2. For computational efficiency, we only treat
the total source and beam separately in this work. As presented in Eq. (2), Iext is the
observed voltage density (see Fig. 3) calibrated with
observations of dark sky. That is, instead of applying an ηc
proper for the observed source, an ηc suitable for an
observation of dark sky is applied to Iext. With the
ηc factor taken into account,
Iext can be formulated as, 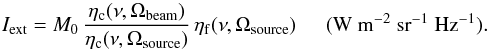 (10)Equation (5) can then be re-written as,
(10)Equation (5) can then be re-written as, 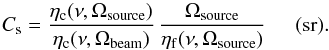 (11)In the two extreme
cases, i.e., when the source is uniformly extended or point-like, Eq. (11) should be consistent with the calibration
data from the FTS pipeline:
(11)In the two extreme
cases, i.e., when the source is uniformly extended or point-like, Eq. (11) should be consistent with the calibration
data from the FTS pipeline:
Case i: Ωsource(ν) ≫ Ωbeam(ν)
In this extreme case, the source can be locally regarded as uniformly extended at the
scale of the FTS beam, so Dν(Ψ) = 1. This
means that
ηc(ν,Ωsource) = ηc(ν,Ωbeam),
and ηf is reduced to 1. If one would like to recover the
total flux of the source, Eq. (11) can be
expressed as, 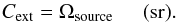 (12)
(12)
In Eq. (12), Ωsource for a uniformly extended source will be determined by the reference solid angle (Ωbeam), within which the source can be regarded as uniformly extended.
Case ii: Ωsource(ν) ≪ Ωbeam(ν)
In the case of a point source,
Ωsource ~ δΩ ≪ Ωbeam. Since the beam profile
has a value of unity at the center, 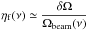 .
Based on Eq. (11),
Cpoint can be written as
.
Based on Eq. (11),
Cpoint can be written as 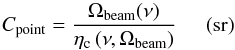 (13)where, as previously
mentioned, ηc for a point source has been set to unity in
Eq. (13).
(13)where, as previously
mentioned, ηc for a point source has been set to unity in
Eq. (13).
The final correction for intermediate cases, based on Eq. (11), can be applied to either the
extended-source calibrated (Iext) or point-source calibrated
(Fpoint) data with the following equations, ![\begin{equation} \label{source_correction} F_{\mathrm{s}}=\left\{ \begin{array}{l} \displaystyle{\,I_{\mathrm{ext}}\, \frac{\eta_{\mathrm{c}}(\nu,\Omega_{\mathrm{source}})}{\eta_{\mathrm{c}}(\nu,\Omega_{\mathrm{beam}})}\,\frac{\Omega_{\mathrm{source}}}{\eta_{\mathrm{f}}(\nu,\Omega_{\mathrm{source}})}}\hspace{0.5cm}(\mathrm{Jy}) \\[8mm] \displaystyle{\,F_{\mathrm{point}}\,\eta_{\mathrm{c}}(\nu,\Omega_{\mathrm{source}})\,\frac{\Omega_{\mathrm{source}}} {\eta_{\mathrm{f}}(\nu,\Omega_{\mathrm{source}})\,\Omega_{\mathrm{beam}}(\nu)}}\hspace{0.5cm}(\mathrm{Jy}). \end{array}\right. \end{equation}](/articles/aa/full_html/2013/08/aa21837-13/aa21837-13-eq65.png) (14)For
most astronomical objects, the light distribution changes little in the bandwidth of the
FTS as seen in the SPIRE photometry measurements. Therefore, for the purpose of the
correction, Dν(Ψ) is assumed to be
independent of frequency. This general assumption may not be suitable for the
distribution of the spectral lines that often originate in regions of the source with
spatial extents that can vary greatly from line to line, from species to species, and
from line to continuum. The correction derived in this section, as given in Eq. (14), gives the total flux density from the
source as defined by Dν(Ψ). If this covers
a large solid angle, it may actually be desirable to limit the flux density to that
which is within a reference beam. In order to define a consistent spectrum, the
reference beam should be constant in frequency across the band. It could, for example,
be set to a Gaussian that approximates the beam of another telescope. The effect of a
reference beam modifies the solid angle of the source in the numerator of Eq. (14) to be,
(14)For
most astronomical objects, the light distribution changes little in the bandwidth of the
FTS as seen in the SPIRE photometry measurements. Therefore, for the purpose of the
correction, Dν(Ψ) is assumed to be
independent of frequency. This general assumption may not be suitable for the
distribution of the spectral lines that often originate in regions of the source with
spatial extents that can vary greatly from line to line, from species to species, and
from line to continuum. The correction derived in this section, as given in Eq. (14), gives the total flux density from the
source as defined by Dν(Ψ). If this covers
a large solid angle, it may actually be desirable to limit the flux density to that
which is within a reference beam. In order to define a consistent spectrum, the
reference beam should be constant in frequency across the band. It could, for example,
be set to a Gaussian that approximates the beam of another telescope. The effect of a
reference beam modifies the solid angle of the source in the numerator of Eq. (14) to be, 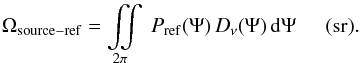 (15)
(15)
4.2. Determination of the correction efficiency
To understand how ηc is affected by different source sizes,
observations of several planets, with well defined source size and spectral flux density,
were examined. Table 1 presents the sources and
observations used. Assuming their light distribution is well described by a circular
top-hat model, the model spectrum for each planet was divided by the source-distribution
corrected spectrum from Eq. (14) to
calculate ηc as a function of frequency,
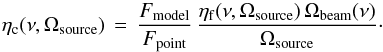 (16)The derivation of the
model of Saturn is described in detail in Fletcher et al.
(2012). This model was scaled to the observation of Saturn on 2011−07−25 (OD 803)
based on the distance to the planet at the time of the observation. The contribution of
Saturn’s rings was found to be negligible (<1%) for the data
observed in 2010 (ObsID 1342198279, Fletcher et al.
2012). On the day of the Saturn observation used in this work (ObsID 1342224754),
the planet phase angle, as simulated by the NASA JPL Solar System Simulator1, is only 0.4° smaller, and the position
angle of the rings is slightly larger than in 2010. However, within the other
uncertainties of the measurement, the contribution of the rings can still be considered as
negligible. The models of Uranus and Neptune are described in Swinyard et al. (in prep.).
A high spectral resolution model of Mars was constructed based on the thermophysical model
of Rudy et al. (1987), updated to use the thermal
inertia and albedo maps (0.125 degree resolution) derived from the Mars Global Surveyor
Thermal Emission Spectrometer (5.1−150 μm) observations (Putzig & Mellon 2007). These new maps were
binned to 1 degree resolution. A dielectric constant of 2.25 was used for latitudes
between 60 degrees South and 60 degrees North. As in the original Rudy model, surface
absorption was ignored in the polar regions and a dielectric constant of 1.5 in the
CO2 frost layer was assumed. Disk-averaged brightness temperatures were
computed over the SPIRE frequency range and converted to flux densities for the times of
the observations. This model was then photometrically matched to the continuum model of
Lellouch (available on the internet2) for the time of
the Mars observation on 2011−10−16 (OD 383).
(16)The derivation of the
model of Saturn is described in detail in Fletcher et al.
(2012). This model was scaled to the observation of Saturn on 2011−07−25 (OD 803)
based on the distance to the planet at the time of the observation. The contribution of
Saturn’s rings was found to be negligible (<1%) for the data
observed in 2010 (ObsID 1342198279, Fletcher et al.
2012). On the day of the Saturn observation used in this work (ObsID 1342224754),
the planet phase angle, as simulated by the NASA JPL Solar System Simulator1, is only 0.4° smaller, and the position
angle of the rings is slightly larger than in 2010. However, within the other
uncertainties of the measurement, the contribution of the rings can still be considered as
negligible. The models of Uranus and Neptune are described in Swinyard et al. (in prep.).
A high spectral resolution model of Mars was constructed based on the thermophysical model
of Rudy et al. (1987), updated to use the thermal
inertia and albedo maps (0.125 degree resolution) derived from the Mars Global Surveyor
Thermal Emission Spectrometer (5.1−150 μm) observations (Putzig & Mellon 2007). These new maps were
binned to 1 degree resolution. A dielectric constant of 2.25 was used for latitudes
between 60 degrees South and 60 degrees North. As in the original Rudy model, surface
absorption was ignored in the polar regions and a dielectric constant of 1.5 in the
CO2 frost layer was assumed. Disk-averaged brightness temperatures were
computed over the SPIRE frequency range and converted to flux densities for the times of
the observations. This model was then photometrically matched to the continuum model of
Lellouch (available on the internet2) for the time of
the Mars observation on 2011−10−16 (OD 383).
Properties of the sources used to derive the correction efficiency.
 |
Fig. 4 Correction efficiency ηc(ν,Ωsource) for the sources listed in Table 1 and dark sky (gray). The plot shows the variation of ηc with the frequency for each source. The blue dotted lines indicate the efficiency predicted by the optics model. The black dashed lines indicate a smoothed efficiency function of an extended source. The ratio between the two is indicated by the red dash dot lines. The two black stars are the far field efficiency measured from prototype arrays in the lab (Chattopadhyay et al. 2003). |
Figure 4 shows ηc as a function of frequency for the listed sources. The average values of ηc for Neptune, Uranus, Mars, and, Saturn, are 0.94, 0.98, 0.98, and, 1.02, respectively for SLWC3, and, 0.94, 0.98, 0.99, and, 0.99, respectively for SSWD4. The results indicate that for the sources with angular size up to 16.7′′ (the size of Saturn on OD803), which is slightly larger than the smallest FWHM, 16.55′′ of the FTS beam, the correction efficiency is nearly 1. Due to the difficulty of selecting well–studied sources with angular sizes between Saturn and an extended source, Fig. 4 also contains the results for a fully extended source (e.g., an observation of dark sky). In this case, Fmodel was calculated following Eq. (12), such that ηc = Ωbeam/Cpoint – i.e., the data from the observation itself cancels and the plot shows the limiting case for a fully extended source (gray curve in Fig. 4). This result shows that the correction works at least on the sources that are as large as or smaller than the smallest FWHM of the SPIRE FTS.
In Fig. 4, the apparent difference indicated by the correction efficiency between coupling to an extended source and a point like source illustrated here has several possible causes. The most obvious one is loss of flux due to diffraction of the beam as it passes through the optics of the telescope and instrument. Whilst the number of optical elements within the system precludes developing a detailed physical model, the diffraction loss versus frequency for a point source on axis can be obtained from a simple physical optics model using Fourier transforms. The pupil mask within SPIRE is designed to limit the detector spatial response with an edge taper of 8 dB, and there is additional obscuration from the secondary mirror and the secondary mirror supports (Caldwell et al. 2000). A simple representation of this system was used to make a first order Fourier transform optical model. The results of the model are shown in Fig. 4 together with ηc for an extended source, and the residual, which is the ratio between a smoothed version of ηc for an extended source and the diffraction model results. The residual is seen to be essentially linear with the detailed shape of the efficiency curve replicated by the diffraction losses. This suggests that diffraction is responsible for part of the difference in coupling efficiency and some other factor accounts for the residual. One plausible explanation for the residual losses is a difference in the coupling efficiency of a point and extended sources within the feedhorns and bolometers. This is supported by comparing the residual linear efficiency curve to the results of the measurement of the far field coupling efficiency of the feedhorns and bolometers themselves (indicated by the black stars in Fig. 4). These measurements were taken in the absence of any fore optics and are reported in Chattopadhyay et al. (2003). The dependence on frequency looks similar between the residual and the Chattopadhyay et al. (2003) results indicating that the possible cause of the apparently low correction efficiency for extended sources is due to a combination of diffraction losses and a difference in the response of the feed horns and bolometers to a source fully filling the aperture and that to a point source.
 |
Fig. 5 Diagram showing how the best-fit θD varies with S/N for Saturn. Gray indicates the instances where the best-fit θD is below 16.7′′, which is the true angular size of Saturn for the observation. Black indicates where the best-fit θD is above 16.7′′. |
4.3. Determine source size using Saturn
The SLW and SSW bands overlap in the region of 959 < ν < 989 GHz. As already shown in Fig. 1, the FWHM of SLW in this frequency range is approximately twice that of SSW. If the correction described by Eq. (14) is applied using the fitted SPIRE profiles (Makiwa et al. 2013), the spectra from SLW and SSW should match in the overlap bandwidth. The Saturn observation, of which the true intensity distribution is well known, can be used to estimate the sensitivity of the correction to source size, to give an indication of the uncertainties in the method. The diameter of Saturn’s disk on OD803 was 16.7′′ and the observed spectrum has an averaged signal-to-noise ratio (S/N) of ~630 in the overlapping frequency range. This makes it a perfect reference case with a well-constrained source distribution and high S/N.
The error of estimation was propagated based on a series of simulated observations
generated from the observed fluxes (fo) and errors
(ϵo) using a Monte-Carlo method. For each simulated
observation, the observed errors were multiplied by a fixed number which varied between 1
and 600 to generate simulated errors (ϵs). The simulated flux
density (fs) was then randomly generated to
be in the range,
(fo − ϵs) < fs < (fo + ϵs).
For each simulated observation, a 2D circular top–hat model of the planet size was created
with a range of diameters,
3′′ < θD < 23′′.
These were then used in Eq. (14) and the
best-fit angular size selected by minimizing the χ2 parameter
for the overlap region, 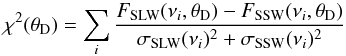 (17)where
FSLW(νi,θD)
and
FSSW(νi,θD)
are the flux densities of Saturn corrected with Eq. (14) on a simulated spectrum;
σSLW(νi) and
σSSW(νi) are
the simulated errors for SLW and SSW, respectively.
(17)where
FSLW(νi,θD)
and
FSSW(νi,θD)
are the flux densities of Saturn corrected with Eq. (14) on a simulated spectrum;
σSLW(νi) and
σSSW(νi) are
the simulated errors for SLW and SSW, respectively.
 |
Fig. 6 Spectrum of Saturn corrected by a top-hat disk model with 17.2′′ in its angular size. Gray indicates the values between two spectra corrected with a Gaussian profile with θD = 12′′ and a Sersic profile with θD = 4′′. |
Considering only the statistical errors, the best-fit θD is 17.2′′, which is about 3% larger than the true value of 16.7′′, and the reduced χ2 is 60.62. The large value of reduced χ2 reflects that the statistical errors under-represent the total errors of the spectrum in Eq. (17). Figure 5 shows how the best-fit θD varies with the simulated S/N. The best-fit θD is systematically smaller than the true size when S/N < 35 (in gray) and converges to 17.2′′ with increasing S/N above S/N = 35 (in black). The best-fit θD is closest to 16.7” at the simulated S/N ~ 35 with a reduced χ2 ~ 0.18. At S/N ~ 80, the reduced χ2 = 1.01 for θD = 17.0. This means that beyond S/N ~ 100, where the best-fit θD starts to converge, increase of S/N does not affect the estimated source size, and the estimation is only applicable when the observation has at least S/N ~ 30. Figure 6 shows the FTS spectrum of Saturn corrected by a top-hat intensity distribution with θD = 17.2′′, the best fit found with the least χ2 analysis at the overlap bandwidth. With consideration of only the source distribution (ηc = 1 has been adopted throughout the derivation) the distribution–corrected spectrum shows good agreement with the model spectrum.
The above analysis indicates that the determined angular size has ≲3% deviation from the true size when the observed spectrum has S/N > 10. The large reduced χ2 implies that there are errors that were unaccounted for in the analysis. Based on the fact that the reduced χ2 = 1.01 at S/N ~ 80, the total error of observation should be ~1.2%, instead of ~0.1% as originally indicated by the S/N of the observation. The increase of error can be due to under-estimated errors from the pipeline and/or the over-simplified model for the light distribution of Saturn. It should also be noted that the above derivation assumes a Gaussian distribution of the errors.
 |
Fig. 7 Demonstration of how the angular size of source affects the flux difference at the overlap bandwidth for a top-hat (green), a Gaussian (red), and, a Sersic n = 1 (blue) profile. The two vertical dashed lines indicate the largest and the smallest beam FWHM of the FTS at 42′′ and 16.55′′. The horizontal dashed line indicates the percentage difference of the fluxes if a source uniformly fills the beams without taking ηc in account, while the gray band indicates the same value but accounts for the uncertainty introduced by ηc. |
The determination of source size using the overlap bandwidth is carried out by minimizing differences between the fluxes measured in SSW and SLW. Figure 7 shows the relationship between the percentage difference in the overlap bandwidth and the angular size of the source light profile (FWHM when applicable). The figure shows profiles described by a top–hat, Sersic profile with n = 1, and, Gaussian model, with the naive assumption that ηc = 1 throughout. At large angular size, the percentage difference approaches 68% (indicated by the horizontal dashed line), which can be well explained by the ratio of the beam solid angles of SSW and SLW in the overlap bandwidth region (approximately a ratio of 0.32). The horizontal gray shaded band in Fig. 7 shows the effect of taking ηc for a fully extended source (the gray curve in Fig. 4) into account in the overlap region. The flux percentage differences of the three example profiles intersect with the gray band at sizes approximately equal to or slightly larger than the largest FWHM of the SLW beam (gray vertical line). The intersect values of 42′′ (Sersic profile, n = 1), 48′′ (top-hat profile), and, 50′′ (Gaussian profile) mark the limit beyond which a source should be considered an extended source. Based on this result, we recommend adopting ηc = 1 for sources with a size that is between the FWHM of the SSW and SLW beams in the overlap bandwidth region (20′′ < θD < 42′′), but caution should be exercised when interpreting the results with real observations in this range.
In the case of the Saturn observation used in Fig. 6, the median percentage difference in the overlap bandwidth is ~26.3%. This value corresponds to a θD of 12′′ for a Gaussian profile and of 4′′ for a Sersic profile with n = 1. To examine how the assumption of a source profile affects the corrected spectrum, the same observation of Saturn was corrected with a Gaussian profile with θD = 12′′ and a Sersic profile with θD = 4′′. Gray in Fig. 6 indicates the range between the Gaussian corrected profile (upper boundary) and Sersic corrected profile (lower boundary). The median difference is insignificant (~1%) for SLW but rises to ~7% for SSW due to the decrease in the beam size. For the SLW beam, either of the assumed profiles is enclosed in the beam, so the difference between the corrected spectra is not significant. For the SSW beam, since the source has a size that is similar to the beam FWHM, the assumed θD = 12′′ Gaussian profile predicts a more extended source than the θD = 17.2′′ top-hat profile. Thus the spectrum is overcorrected to account for the extension of the Gaussian profile. On the other hand, a θD = 4′′ Sersic profile proposes a more compact source which results in a spectrum that is under corrected.
 |
Fig. 8 M82 FTS spectrum corrected with the method developed in this work. a) Spectrum of M82 observed by the FTS on 2010−11−08 (OD 543). Red and blue indicate the spectra observed by the SLWC3 and SSWD4, respectively. The dashed line shows the spectrum calibrated by the point-source calibration mode. The solid line shows the spectrum corrected by the method presented in this work with a best-fit source re = 11′′ (see Eq. (18).) b) Comparison of the CO SLEDs from the starburst core of M82. Red indicates the fluxes derived from the central detector spectrum (SLWC3 and SSWD4), corrected for the source distribution and convolved to a Gaussian beam of FWHM = 42′′ (red). Cyan is the same spectrum corrected by a source-beam coupling factor derived from the SPIRE photometry 250 μm map with appropriate profiles to produce the continuum light distribution seen with the FTS (cyan, Kamenetzky et al. 2012). |
5. Benchmarking and testing
In this section, the correction algorithm derived in Sect. 4 is applied to observations of the nearby galaxy M82 and the compact core of the molecular cloud, Sgr B2. We adopt ηc = 1 in this section.
5.1. M82
M82 is a nearly edge-on starburst galaxy at 3.4 Mpc distance from the Milky-way (Dalcanton et al. 2009). The FTS observed M82 in fully sampled mode on the 2010−11−08 (OD 543; ObsID 1342208388). Details of results from the fully sampled map of M82 can be found in Kamenetzky et al. (2012). Here, we apply the correction to the spectrum of M82 taken with the central FTS detectors, SLWC3 and SSWD4, at J2000 coordinates, (α,δ) = (9h55m52.6s, + 69d40m48.02s) and compare it to the beam size corrected data taken at the same coordinates with the central detectors (Kamenetzky et al. 2012).
The signal-to-noise ratio of the FTS spectrum of M82 is ~200. Assuming the intensity
distribution at the core of M82 can be described as a 2D circular exponential profile,
 (18)we correct the spectrum
of SLWC3 and SSWD4 by matching the fluxes at
959 < ν < 989 GHz with
varying scale radius
(8′′ < re < 14′′).
(18)we correct the spectrum
of SLWC3 and SSWD4 by matching the fluxes at
959 < ν < 989 GHz with
varying scale radius
(8′′ < re < 14′′).
The best-fit re determined by minimizing χ2, defined in Eq. (17), is ~11′′, which corresponds to θD ~ 15′′ in FWHM. Compared to the SCUBA observation of M82 (Leeuw & Robson 2009) at 450 μm, the estimated distribution only roughly describes the double-peaked star–forming nucleus of M82. However, more detailed mathematical description of the intensity profile will introduce additional variables into the correction. Because the goal of this work is to correct the spectrum based on the limited information one can derive from the FTS observation, we retain the simple exponential profile. A comparison between our semi-extended corrected spectrum and the point-source calibrated spectrum is shown in Fig. 8a. Since the emission lines from 12CO at J = 4−3 to J = 13−12 are among the most important features in the FTS spectrum, the 12CO spectral line energy distribution (SLED) is plotted in Fig. 8b. In this figure, our semi-extended corrected SLED is compared with the results from Kamenetzky et al. (2012), where the spectrum was corrected by applying a source-beam coupling factor derived by convolving the M82 SPIRE photometer 250 μm map with appropriate profiles to produce the continuum light distribution seen with the FTS (Panuzzo et al. 2010). In Fig. 8b, the CO line fluxes from the semi-extended corrected data were measured from the unapodized spectrum with a sinc function superposed on a parabola at a 20 GHz range centered at the redshifted frequency of each CO line. The measured line fluxes were multiplied by a factor of 0.55, which is the ratio of a simulated exponential profile with re = 11′′ after and before convolution by a Gaussian beam profile with FWHM = 42′′ at its central 9.5′′ × 9.5′′ region.
As shown in Fig. 8b, the semi-extended corrected line fluxes (red) and the line fluxes measured and corrected by using the photometry map as a reference (cyan) agree with each other within their error bars, even though the semi-extended corrected spectrum is based on a simplified circular exponential profile. It is interesting to note that the line fluxes for J = 8−7, close to 959 < ν < 989 GHz, from the two spectra overlap in Fig. 8b. For transitions higher than J = 8−7, the semi-extended corrected line fluxes are higher than the line fluxes measured and corrected by using the photometry map as a reference, and for transitions between lower excitation levels than J = 8−7, the semi-extended corrected line fluxes are slightly lower. This is due to the assumed circular exponential profile with re = 11′′ has a different distribution than the photometry map.
5.2. Sgr B2
Sagittarius B2 (Sgr B2) is a giant molecular cloud at a distance of ~8.3 ± 0.4 Kpc (Kerr & Lynden Bell 1986; Ghez et al. 2008; Gillessen et al. 2009; Reid et al. 2009), and located in the Central Molecular Zone at ~120 pc from the Galactic Center (Lis & Goldsmith 1990). It contains three main compact cores, Sgr B2(N), Sgr B2(M) and Sgr B2(S) distributed from north to south, associated with massive star formation. The FTS observed Sgr B2 on 2011−02−27 (OD 655, ObsID 1342214843) in single pointing observations towards the (N) and (M) positions. Full details of these spectra are presented and analyzed by Etxaluze et al. (2013).
Figure 9 shows the unapodized spectra at the position of Sgr B2(M) calibrated as a point source (dashed) and after the application of our semi-extended correction. Assuming a Gaussian emission profile, the best continuum matching for the spectral continuum levels in the overlap region between SSW and SLW is obtained with FWHM = 30′′ (this is equivalent to a radius of ~0.62 pc). For the purpose of comparing the integrated line fluxes at the same spatial resolution, the resulting spectrum is convolved to a Gaussian beam with FWHM ~ 43′′, equivalent to a radius of ~0.8 pc.
 |
Fig. 9 Correction of the Sgr B2(M) FTS spectrum. The dashed spectrum shows the point source calibration of the Sgr B2(M) spectrum. The solid line represents the Sgr B2(M) spectrum corrected with the semi-extended correction. |
The Sgr B2(M) spectral continuum, once corrected, provides a good measurement of the dust spectral energy distribution (SED) and allows us to estimate the luminosity, the mass and the molecular hydrogen column density of the source. These results obtained with the semi-extended corrected spectrum can then be compared with the results of previous studies.
The total integrated continuum intensity inside the beam with FWHM = 43′′ provides a luminosity of LFIR = (5 ± 1) × 106L⊙, which is in good agreement with that measured by Goldsmith et al. (1992): 6.3 × 106 L⊙. The far-infrared luminosity requires several young O-type stars as power sources, which are deeply embedded in the star forming cores (Jones et al. 2008).
The dust mass and the molecular hydrogen column density of the core is calculated as
(Deharveng et al. 2009; Hildebrand 1983): 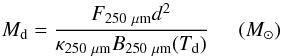 (19)where
F250 μm is the total intensity at 250
μm, d is the distance (~8.5 kpc),
B250 μm(Td)
is the blackbody intensity at 250 μm for a dust temperature
Td ~ 36.5 K (Etxaluze et al.
2013), and κ250 μm = 5.17
cm2 g-1 is the dust opacity (Li
& Draine 2001). The H2 column density is given as:
(19)where
F250 μm is the total intensity at 250
μm, d is the distance (~8.5 kpc),
B250 μm(Td)
is the blackbody intensity at 250 μm for a dust temperature
Td ~ 36.5 K (Etxaluze et al.
2013), and κ250 μm = 5.17
cm2 g-1 is the dust opacity (Li
& Draine 2001). The H2 column density is given as:
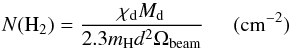 (20)where we assumed a
gas-to-dust ratio χd = 100, mH is
the mass of a hydrogen atom and Ωbeam is the beam solid angle. The
H2 column density derived is
N(H2) ~ 5 × 1024 cm-2. The total mass
of the core is: Md = 2300 M⊙.
This mass is lower than the total masses determined by Qin
et al. (2011): ~3300 M⊙, and higher than the mass
calculated by Gaume & Claussen (1990):
~1050 M⊙. The derived physical quantities indicate that the
corrected spectrum is generally in agreement with results obtained in previous studies of
Sgr B2(M). If using an uncorrected spectrum, despite the apparent discontinuity at the
overlap bandwidth, which makes fitting a blackbody continuum to the spectrum difficult,
the derived value of Md would be
~900 M⊙. This value is lower than the previously measured
dust mass in Sgr B2(M), leading to a possible underestimation of the dust mass in Sgr
B2(M).
(20)where we assumed a
gas-to-dust ratio χd = 100, mH is
the mass of a hydrogen atom and Ωbeam is the beam solid angle. The
H2 column density derived is
N(H2) ~ 5 × 1024 cm-2. The total mass
of the core is: Md = 2300 M⊙.
This mass is lower than the total masses determined by Qin
et al. (2011): ~3300 M⊙, and higher than the mass
calculated by Gaume & Claussen (1990):
~1050 M⊙. The derived physical quantities indicate that the
corrected spectrum is generally in agreement with results obtained in previous studies of
Sgr B2(M). If using an uncorrected spectrum, despite the apparent discontinuity at the
overlap bandwidth, which makes fitting a blackbody continuum to the spectrum difficult,
the derived value of Md would be
~900 M⊙. This value is lower than the previously measured
dust mass in Sgr B2(M), leading to a possible underestimation of the dust mass in Sgr
B2(M).
6. Conclusion
In this paper, we have shown that care must be exercised in the interpretation of spectral images produced by the SPIRE FTS as the spectra depend on both the frequency dependent beam and on the intrinsic source structure. While the beam profile can be determined from spectral scans of a point source, the effect of the source structure is less easy to model. However, since the beam profile in the overlap frequency range between the two bands employed by the SPIRE FTS is significantly different, this range provides a useful diagnostic on the source intensity distribution. For example, an abrupt change in the measured spectral intensity from one band to the other can often be directly related to the angular extent of the source.
An empirical method to correct for the effects induced by the discontinuity in beam size and shape for single-pointing sparse-sampling observations (Sect. 4, Eq. (14)) has been presented. Alternatively, if a sufficiently simple analytic description of the source structure exists, a crude measure of the source extent can be derived from the SPIRE FTS observation by minimizing the intensity difference between the two bands. This work has now been included as an interactive tool in version 11 of the Herschel interactive processing environment (HIPE; Ott 2010) that is used for Herschel data processing.
Two examples have been presented which illustrate both the power of the technique and its limitations. Fundamentally, the tailored matching of the intensity in the overlap between the two bands can provide information on the angular extent of the source emitting continuum photons at those frequencies (959 < ν < 989 GHz). However, caution should be exercised in extrapolating this source structure to the interpretation of the remaining spectrum. This extrapolation may be valid in some cases, but, in general, the physical distribution of individual components depends on local conditions, e.g., density, temperatures of dust and gas, and chemical balance.
One of the primary advantages of Fourier transform spectrometers is their ability to provide intermediate spectral resolution over a relatively broad spectral range. In general, however, the spectral range is too large to be covered by feedhorn coupled detectors operating in single mode, as is the case for most heterodyne spectrometers, e.g., Herschel HIFI (De Graauw et al. 2010). The result is that the beam profile for an FTS exhibits a complex dependency on frequency as additional modes, propagated by the waveguides, couple to the instrument and ultimately form the beam on the sky. Complete solutions to Maxwell’s equations for incident radiation propagating through an instrument tend to be extremely challenging and although “quasi-optical” approaches have been developed to simulate complex instruments (O’Sullivan et al. 2009), in practice the frequency dependent beam profile must be determined from spectral observations of a point source (Makiwa et al. 2013).
While it is in principle possible to illuminate a detector array using reflective camera optics, which provides a well-defined beam profile (i.e., without the use of feedhorns; as is done for example with FTS-2 (Naylor & Gom 2003), the Fourier spectrometer developed for use with the SCUBA-2 camera Holland 2006), it is difficult to control stray light in such direct imaging applications. While stray light is less of a concern for ground based instruments, whose sensitivity is limited by the photon flux from the warm telescope and atmosphere, control of stray light is of critical importance in cryogenic far-infrared space astronomy missions currently being proposed (Swinyard et al. 2009). To exploit the sensitivity of state-of-the-art detectors on these missions stray light must be controlled using feedhorn coupled detectors. The SAFARI instrument (Roelfsema et al. 2012) under development for the SPICA mission is an imaging FTS employing feedhorns and will encounter a similar frequency dependent beam profile and require a similar analysis for semi-extended sources as that described in this paper.
Acknowledgments
SPIRE has been developed by a consortium of institutes led by Cardiff University (UK) and including Univ. Lethbridge (Canada); NAOC (China); CEA, LAM (France); IFSI, Univ. Padua (Italy); IAC (Spain); Stockholm Observatory (Sweden); Imperial College London, RAL, UCL-MSSL, UKATC, Univ. Sussex (UK); and Caltech, JPL, NHSC, Univ. Colorado (USA). This development has been supported by national funding agencies: CSA (Canada); NAOC (China); CEA, CNES, CNRS (France); ASI (Italy); MCINN (Spain); SNSB (Sweden); STFC (UK); and NASA (USA). R.W. would like to thank Dr. J. Bock, F. Galliano, S. Hony, J. Kamenetzky, and, C. Wilson for their helpful discussions and comments on this work. M.E. thanks ASTROMADRID for funding support through the grant S2009ESP-1496, the Spanish MINECO (grant AYA2009-07304) and the Spanish Consolider-Ingenio program, ASTROMOL: CSD2009-00038. G.M., D.N. and M.v.d.W. acknowledge support from NSERC.
References
- Arvidsson, K., Kerton, C. R., Alexander, M. J., Kobulnicky, H. A., & Uzpen, B. 2010, AJ, 140, 462 [NASA ADS] [CrossRef] [Google Scholar]
- Caldwell, M. E., Swinyard, B. M., Richards, A. G., & Dohlen, K. 2000, Proc. SPIE, 4013, 210 [NASA ADS] [CrossRef] [Google Scholar]
- Chattopadhyay, G., Glenn, J., Bock, J., et al. 2003, IEEE Trans. MTT, 51, 2139 [NASA ADS] [CrossRef] [Google Scholar]
- Dalcanton, J. J., Williams, B. F., Seth, A. C., et al. 2009, ApJS, 183, 67 [NASA ADS] [CrossRef] [Google Scholar]
- De Graauw, T., Helmich, F., Phillips, T., et al. 2010, A&A, 518, L6 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Deharveng, L., Zavagno, A., Schuller, F., et al. 2009, A&A, 496, 177 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Dohlen, K., Origne, A., Pouliquen, D., & Swinyard, B. M. 2000, in SPIE Conf. Ser. 4013, eds. J. B. Breckinridge, & P. Jakobsen, 119 [Google Scholar]
- Etxaluze, M., Goicoechea, J. R., Cernicharo, J., et al. 2013, A&A, in press DOI: 10.1051/0004-6361/201321258 [Google Scholar]
- Ferlet, M., Laurent, G., Swinyard, B., et al. 2008, Proc. SPIE, 7010 [Google Scholar]
- Fischer, J., Klaassen, T., Hovenier, N., et al. 2004, Appl. Opt., 43, 3765 [NASA ADS] [CrossRef] [Google Scholar]
- Fletcher, L. N., Swinyard, B., Salji, C., et al. 2012, A&A, 539, A44 [Google Scholar]
- Fulton, T. R., Baluteau, J.-P., Bendo, G., et al. 2010, Proc. SPIE, 7731 [Google Scholar]
- Gaume, R. A., & Claussen, M. J. 1990, ApJ, 351, 538 [NASA ADS] [CrossRef] [Google Scholar]
- Ghez, A. M., Salim, S., Weinberg, N. N., et al. 2008, ApJ, 689, 1044 [NASA ADS] [CrossRef] [Google Scholar]
- Gillessen, S., Eisenhauer, F., Trippe, S., et al. 2009, ApJ, 692, 1075 [NASA ADS] [CrossRef] [Google Scholar]
- Goldsmith, P. F., Lis, D. C., Lester, D. F., & Harvey, P. M. 1992, ApJ, 389, 338 [NASA ADS] [CrossRef] [Google Scholar]
- Griffin, M. J., Bock, J. J., & Gear, W. K. 2002, Appl. Opt., 41, 6543 [Google Scholar]
- Griffin, M. J., Abergel, A., Abreu, A., et al. 2010, A&A, 518, L3 [Google Scholar]
- Habart, E., Dartois, E., Abergel, A., et al. 2010, A&A, 518, L116 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hildebrand, R. H. 1983, QJRAS, 24, 267 [NASA ADS] [Google Scholar]
- Holland, W., Macintosh, M., Fairley, A., et al. 2006, Proc. SPIE, 6275, 62751E [CrossRef] [Google Scholar]
- Jones, P. A., Burton, M. G., Cunningham, M. R., et al. 2008, MNRAS, 386, 117 [NASA ADS] [CrossRef] [Google Scholar]
- Kamenetzky, J., Glenn, J., Rangwala, N., et al. 2012, ApJ, 753, 70 [NASA ADS] [CrossRef] [Google Scholar]
- Kerr, F. J., & Lyn den Bell, D. 1986, MNRAS, 221, 1023 [NASA ADS] [CrossRef] [Google Scholar]
- Kutner, M. R., & Ulich, B. L. 1981, ApJ, 250, 341 [NASA ADS] [CrossRef] [Google Scholar]
- Leeuw, L. L., & Robson, E. I. 2009, ApJ, 137, 517 [Google Scholar]
- Li, A., & Draine, B. T. 2001, ApJ, 554, 778 [Google Scholar]
- Lis, D. C., & Goldsmith, P. F. 1990, ApJ, 356, 195 [NASA ADS] [CrossRef] [Google Scholar]
- Makiwa, G., Naylor, D. A., Ferlet, M., et al. 2013, Appl. Opt., 52, 3864 [NASA ADS] [CrossRef] [Google Scholar]
- Martin, D. H., & Bowen, J. W. 1993, IEEE Trans. MTT, 41, 1676 [NASA ADS] [CrossRef] [Google Scholar]
- Murphy, J. A., & Padman, R. 1991, Infrared Physics, 31, 291 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Naylor, D. A., & Gom, B. G. 2003, Proc. SPIE, 5159, 91 [NASA ADS] [CrossRef] [Google Scholar]
- O’Sullivan, C., Murphy, J. A., Gradziel, M. L., et al. 2009, Proc. of SPIE, 7215, 72150P [CrossRef] [Google Scholar]
- Ott, S. 2010, Astronomical Data Analysis Software and Systems XIX, 434, 139 [NASA ADS] [Google Scholar]
- Panuzzo, P., Rangwala, N., Rykala, A., et al. 2010, A&A, 518, L37 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Pilbratt, G. L., Riedinger, J. R., Passvogel, T., et al. 2010, A&A, 518, L1 [CrossRef] [EDP Sciences] [Google Scholar]
- Putzig, N. E., & Mellon, M. T. 2007, Icarus, 191, 68 [NASA ADS] [CrossRef] [Google Scholar]
- Qin, S. L., Schilke, P., Rolffs, R., et al. 2011, A&A, 530, L9 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Reid, M. J., Menten, K. M., Zheng, X. W., Brunthaler, A., & Xu, Y. 2009, ApJ, 705, 1548 [NASA ADS] [CrossRef] [Google Scholar]
- Roelfsema, P., Giard, M., Najarro, F., et al. 2012, Proc. SPIE, 8442, 84420 [CrossRef] [Google Scholar]
- Rudy, D. J., Muhleman, D. O., Berge, G. L., Jakosky, B. M., & Christensen, P. R. 1987, Icarus, 71, 159 [NASA ADS] [CrossRef] [Google Scholar]
- Swinyard, B., Nakagawa, T., Merken, P., et al. 2009, Exp. Astron., 23, 193 [NASA ADS] [CrossRef] [Google Scholar]
- Swinyard, B. M., Ade, P., Baluteau, J.-P., et al. 2010, A&A, 518, L4 [Google Scholar]
- Turner, A. D., Bock, J. J., Beeman, J. W., et al. 2001, Appl. Opt., 40, 4921 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Ulich, B. L., & Haas, R. W. 1976, ApJS, 30, 247 [NASA ADS] [CrossRef] [Google Scholar]
- SPIRE observer’s manual 2011, HERSCHEL-HSC-DOC-0798, accessed from http://herschel.esac.esa.int/Documentation.shtml [Google Scholar]
All Tables
All Figures
 |
Fig. 1 SPIRE FTS spectral beam size as measured by Makiwa et al. (2013). The shaded region shows 3σ errors. The frequencies at which the waveguide modes are enabled and the number of modes expected to be present (from theory) in each range is also shown, along with the expected size due to single–mode diffraction (dashed blue line). The inset plot shows the shape of the profile at 3 sample frequencies from SLW (420, 699, 990 GHz) and one frequency from SSW (1269 GHz). The horizontal axis of the inset plot is in the unit of arcsec. |
| In the text | |
 |
Fig. 2 Spectra for a point source (CRL 618, left), semi-extended source (M83, center) and fully extended source (Orion Bar, right) after extended calibration (top row) and point source calibration (bottom row). The spectra have been smoothed. The flux density and brightness are in normalized units. |
| In the text | |
 |
Fig. 3 Diagram demonstrating how signals from a source, Ms, change before reaching the bolometer. |
| In the text | |
 |
Fig. 4 Correction efficiency ηc(ν,Ωsource) for the sources listed in Table 1 and dark sky (gray). The plot shows the variation of ηc with the frequency for each source. The blue dotted lines indicate the efficiency predicted by the optics model. The black dashed lines indicate a smoothed efficiency function of an extended source. The ratio between the two is indicated by the red dash dot lines. The two black stars are the far field efficiency measured from prototype arrays in the lab (Chattopadhyay et al. 2003). |
| In the text | |
 |
Fig. 5 Diagram showing how the best-fit θD varies with S/N for Saturn. Gray indicates the instances where the best-fit θD is below 16.7′′, which is the true angular size of Saturn for the observation. Black indicates where the best-fit θD is above 16.7′′. |
| In the text | |
 |
Fig. 6 Spectrum of Saturn corrected by a top-hat disk model with 17.2′′ in its angular size. Gray indicates the values between two spectra corrected with a Gaussian profile with θD = 12′′ and a Sersic profile with θD = 4′′. |
| In the text | |
 |
Fig. 7 Demonstration of how the angular size of source affects the flux difference at the overlap bandwidth for a top-hat (green), a Gaussian (red), and, a Sersic n = 1 (blue) profile. The two vertical dashed lines indicate the largest and the smallest beam FWHM of the FTS at 42′′ and 16.55′′. The horizontal dashed line indicates the percentage difference of the fluxes if a source uniformly fills the beams without taking ηc in account, while the gray band indicates the same value but accounts for the uncertainty introduced by ηc. |
| In the text | |
 |
Fig. 8 M82 FTS spectrum corrected with the method developed in this work. a) Spectrum of M82 observed by the FTS on 2010−11−08 (OD 543). Red and blue indicate the spectra observed by the SLWC3 and SSWD4, respectively. The dashed line shows the spectrum calibrated by the point-source calibration mode. The solid line shows the spectrum corrected by the method presented in this work with a best-fit source re = 11′′ (see Eq. (18).) b) Comparison of the CO SLEDs from the starburst core of M82. Red indicates the fluxes derived from the central detector spectrum (SLWC3 and SSWD4), corrected for the source distribution and convolved to a Gaussian beam of FWHM = 42′′ (red). Cyan is the same spectrum corrected by a source-beam coupling factor derived from the SPIRE photometry 250 μm map with appropriate profiles to produce the continuum light distribution seen with the FTS (cyan, Kamenetzky et al. 2012). |
| In the text | |
 |
Fig. 9 Correction of the Sgr B2(M) FTS spectrum. The dashed spectrum shows the point source calibration of the Sgr B2(M) spectrum. The solid line represents the Sgr B2(M) spectrum corrected with the semi-extended correction. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


