| Issue |
A&A
Volume 556, August 2013
|
|
|---|---|---|
| Article Number | A14 | |
| Number of page(s) | 15 | |
| Section | Stellar structure and evolution | |
| DOI | https://doi.org/10.1051/0004-6361/201321076 | |
| Published online | 17 July 2013 | |
X-ray emission regimes and rotation sequences in M 35 ⋆
An updated model of stellar activity evolution on the main sequence
European Space Agency, ESTEC − Postbus 299,
2200 AG
Noordwijk,
The Netherlands
e-mail:
pgondoin@rssd.esa.int
Received:
10
January
2013
Accepted:
27
May
2013
Context. Late-type stars in young open clusters show two kinds of dependence of their X-ray emission on rotation. They also tend to group into two main sub-populations that lie on narrow sequences in diagrams where their rotation periods are plotted against their (B − V) colour indices. A correlation between these two regimes of X-ray emission and the rotation sequences has been recently observed in the M 34 open cluster. Sun-like M 34 stars also show a drop of their X-ray to bolometric luminosity ratio by about one order of magnitude at a Rossby number of about 0.3.
Aims. The present study looks for similar connections between X-ray activity and rotation in an other open cluster. The aim is to consolidate a model of X-ray activity evolution on the main sequence and to provide observational constraints on dynamo processes in the interiors of late-type stars.
Methods. The paper compares XMM-Newton measurements of X-ray stellar emission in M 35 with X-ray luminosity distributions derived from rotation period measurements assuming either an X-ray regime transition at a critical Rossby number or a correlation between X-ray emission regimes and rotation sequences.
Results. This second hypothesis could account for the low number of M 35 stars detected in X-rays. A model of X-ray activity evolution is proposed based on the correlation. One major output is that the transition from saturated to non-saturated X-ray emission occurs at Rossby numbers between about 0.13 and 0.4 for each star depending on its mass and initial period of rotation on the ZAMS. This prediction agrees with observations of stellar X-ray emission in M 34. It explains the large range of X-ray luminosities observed among Sun-like stars in young open clusters.
Conclusions. I conclude that the correlation between X-ray emission regimes and rotation sequences could be a fundamental property of the early evolution of stellar magnetic activity on the main sequence. I argue that the angular momentum redistribution mechanism(s) responsible for the transition between rotation sequences could result in a changing mixture of dynamo processes occurring side by side, possibly including a turbulent dynamo at high rotation rate and an interface-type dynamo whose efficiency decreases progressively at later stage of stellar evolution when rotation dies away.
Key words: open clusters and associations: general / stars: activity / stars: coronae / stars: evolution / stars: rotation / magnetic fields
© ESO, 2013
1. Introduction
One major topic of stellar activity is to explain how phenomena seen on the Sun and stars, and especially magnetic phenomena, depend on stellar parameters such as rotation rate, mass, and age. One magnetic field diagnostic for cool stars is coronal X-ray emission. In particular, the relationship between the coronal radiative flux density and the average surface magnetic flux density is nearly linear for solar active regions and for entire stars (e.g. Fisher et al. 1998; Schrijver & Zwaan 2000) over 12 orders of magnitude in absolute magnetic flux (Pevtsov et al. 2003). The X-ray emission from late-type stars in open clusters exhibits two kinds of dependences on stellar rotation (e.g. Patten & Simon 1996; Randich 2000; Feigelson et al. 2003; Pizzolato et al. 2003). Fast rotators show a relatively constant X-ray to bolometric luminosity ratio at the so-called (LX/Lbol) ≈ 10-3 saturation level. Slower rotators show a decline of their X-ray emission with decreasing rotation rate. The physical significance of the transition between these two regimes is a matter of debate (e.g. Jardine & Unruh 1999).
The rotation periods of late-type stars can be accurately derived from the modulation of their brightness by starspots (e.g. Lanza et al. 2009; Fröhlich et al. 2009; Silva-Valio et al. 2010; Gondoin et al. 2012). Photometric monitoring programs have produced a large number of measurements of this kind in young open clusters (e.g. Prosser et al. 1995; Krishnamurthi et al. 1998; Irwin et al. 2007; Collier Cameron et al. 2009; Hartman et al. 2009, 2010). Based on these data, Barnes (2003a) found that young stars tend to group into two main sub-populations that lie on narrow sequences in diagrams where the measured rotation periods of the members of a stellar cluster are plotted against their B − V colour indices. One sequence, called the I sequence, consists of stars that form a diagonal band of increasing period with increasing B − V colour. In young clusters, another sequence of ultra-fast rotators called the C sequence is also observed splitting away from the I sequence towards shorter rotation periods. Some stars lie in the intervening gap between the I and C sequences.
Possible connections between these rotation sequences and the X-ray emission regimes have been addressed by Barnes (2003b) and Wright et al. (2011). In a recent paper, Gondoin (2012; hereafter G12) reported a correlation between the saturated and non-saturated regime of X-ray emission and the C and I rotation sequences that have been observed in M 34 from extensive rotation periods surveys (Irwin et al. 2006; James et al. 2010; Meibom et al. 2011). Messier 34 sample stars also show a steep transition in X-ray to bolometric luminosity ratio between the C-sequence and gap stars that emit close to the 10-3 saturation level, and the I-sequence stars, whose LX/Lbol ratio is significantly lower for similar values of the Rossby number.
Based on M 34 X-ray observation, G12 proposed a time evolution model of X-ray activity on the main sequence. This model assumes that the transition from the saturated to the non-saturated regime of X-ray emission occurs as the rotation rates of young stars decrease and their Rossby numbers reach a critical value Rosat ~ 0.3. Gondoin (2012) argues that the drop of (LX/Lbol) by one order of magnitude observed in M 34 around this Rossby number is indicative of a change in dynamo regime, possibly between a turbulent dynamo and an interface-type dynamo.
The present study is looking for similar correlations between stellar activity and rotation in a different open cluster. Its aim is to consolidate the evolution model of stellar X-ray activity on the main sequence proposed by G12. The study compares X-ray stellar emissions measured in M 35 with X-ray luminosity distributions derived from rotation period measurements assuming either a transition between X-ray emission regimes at a critical Rossby number or a correlation between X-ray emission regimes and rotational sequences. The objective is to provide observational constraints on evolution scenarios of dynamo processes in the interiors of cool stars.
The M 35 open cluster has been the subject of an extensive photometric time-series survey by Meibom et al. (2009; hereafter M09) who reported rotation periods for 441 stars within a field centred on the cluster. Messier 35 was also observed in 2008 with the XMM-Newton space observatory. The present paper reports on the results of a study of X-ray coronal emission as a function of stellar rotation in this rich Galactic cluster. Messier 35 (NGC 2168; α = 06h08m54s, δ = 24°20′; l = 186.59°, b = + 02.19°) contains at least 1000 stars brighter than V = 22 (Kalirai et al. 2003) with a well-populated main sequence down to stars with masses of 0.2 M⊙. Its metallicity is lower than solar with [Fe/H] values between −0.18 and −0.21 (McNamara et al. 2011).
Estimates of M 35 distance range from 725 pc (Sun & Lee 1992) to 912 pc (Kalirai et al. 2003). McNamara et al. (2011) found a cluster distance of 762 ± 145 pc when combining the cluster’s internal proper motion dispersion with a radial velocity dispersion of 0.65 ± 0.1 km s-1 found by Geller et al. (2010). Using isochrone fits to the cluster main sequence, this distance suggests that M 35 has an age of about 133 Myr. Although this age is consistent with that typically found for M 35, McNamara et al. (2011) noted that the formal error in the dynamical distance of ±19% can accommodate ages between 65 Myr and 201 Myr. Meibom et al. (2009) obtained gyro-ages from 134 Myr to 161 Myr using the gyrochronology technique (Barnes 2007).
The X-ray and rotation datasets and the compilation of the stellar samples are described in Sect. 2. The properties of the sample stars are reported in Sect. 3. Measurements of X-ray stellar emission in M 35 are compared in Sect. 4 with different distributions of X-ray luminosities inferred from rotation period measurements. An updated model of X-ray activity evolution on the main sequence is derived in Sect. 5 and compared with observational data. The study results are discussed in Sect. 6 and are summarised in Sect. 7.
 |
Fig. 1 Combined EPIC MOS and PN image of the M 35 open cluster in the 0.5 to 4.5 keV X-ray band. |
2. Compilation of the sample
2.1. Observational data
Messier 35 was observed with the XMM-Newton space observatory (Jansen et al. 2001) on 20 September 2008. The observations were conducted with the EPIC pn (Strüder et al. 2001) and MOS cameras (Turner et al. 2001) located at the prime focus of the grazing incidence telescopes (Gondoin et al. 2000). The exposure times were 7 ks and 8.6 ks, respectively (see Fig. 1). A medium aluminum filter was used in front of the cameras to reject visible light from the stars. Seventy-one X-ray sources were detected that are listed in the XMM-Newton Serendipitous Source Catalog (Watson et al. 2009).
The X-ray data were complemented with a list of stellar rotation periods derived by M09 from an extensive photometric survey of M 35. The list contains 441 stars with known rotation periods located in a 40 × 40 arcmin2 field centred on the cluster. Within this list, 259 sources are located in the field of view of the EPIC cameras, of which 46 are classified by M09 as photometric non-members of the cluster. The remaining list of 213 sources was correlated with a list of 1151 stars with radial velocity measurements established by Geller et al. (2010). This list includes main-sequence stars over a 13.0 ≤ V ≤ 16.5 mag range located within 30 arcmin from the M 35 cluster centre. For stars with more than three measurements, Geller et al. (2010) derived membership probabilities and identified radial velocity variables. Out of the 213 photometric members of M 35 within the EPIC field of view, 17 stars were identified as radial velocity non-members or, more often, as binaries and were discarded. The remaining sample of 196 stars form a reference sample of M 35 members with known rotation periods that were located in the field of view of the EPIC cameras during the XMM-Newton observation of September 2008 and that are not identified as binaries.
The XMM-Newton X-ray source list was correlated with the M09 list of
stars. In order to estimate the optimal radius of cross correlation, I used the approach
outlined by Jeffries et al. (1997). The cumulative
distribution of the number of detected sources was generated as a function of the
cross-correlation radius (see Fig. 2). It was fitted by the function
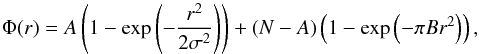 (1)where
N, A, σ, and B stand
for the total number of cross-correlated X-ray sources (N = 71), the
number of true correlations, the uncertainty on the X-ray source positions, and the
surface density of optical sources, respectively. The first term in the above expression
describes the cumulative distribution of true correlations, whereas the second term yields
the cumulative number of spurious correlations. The values A = 19,
σ = 1.3 arcsec, and B = 1.7 × 10-4
arcsec-2 were obtained from the best fit to the cumulative distribution (see
Fig. 2). The optimal correlation radius, i.e. the
radius that includes the bulk of the true correlations while simultaneously limiting
contamination by spurious correlations, is found to be 4 arcsec. For this radius, 19
correlations are found, and less than one is expected to be spurious. Table 1 lists their XMM-Newton catalog
identifiers and X-ray fluxes in the 0.5−4.5 keV band. It also provides their rotational
periods, V0 magnitudes corrected for extinction, and
(B − V)0 colour indices corrected for
reddening.
(1)where
N, A, σ, and B stand
for the total number of cross-correlated X-ray sources (N = 71), the
number of true correlations, the uncertainty on the X-ray source positions, and the
surface density of optical sources, respectively. The first term in the above expression
describes the cumulative distribution of true correlations, whereas the second term yields
the cumulative number of spurious correlations. The values A = 19,
σ = 1.3 arcsec, and B = 1.7 × 10-4
arcsec-2 were obtained from the best fit to the cumulative distribution (see
Fig. 2). The optimal correlation radius, i.e. the
radius that includes the bulk of the true correlations while simultaneously limiting
contamination by spurious correlations, is found to be 4 arcsec. For this radius, 19
correlations are found, and less than one is expected to be spurious. Table 1 lists their XMM-Newton catalog
identifiers and X-ray fluxes in the 0.5−4.5 keV band. It also provides their rotational
periods, V0 magnitudes corrected for extinction, and
(B − V)0 colour indices corrected for
reddening.
 |
Fig. 2 Cumulative number of correlations between X-ray sources and M 35 stars with known rotation periods. The dashed and dotted curves correspond to the best fitting expressions for the real and spurious correlations. The continuous curve yields the sum of these terms. |
 |
Fig. 3 Colour magnitude diagram of M 35 stars with known rotation periods that were located in the field of view of the EPIC camera during the XMM-Newton observation of September 2008. Filled circles identify the stars that were detected in X-rays. Stars identified as binaries have been excluded. |
X-ray fluxes, rotation periods, and photometric indices of X-ray emitting stars in M 35.
X-ray fluxes are normally derived from source count rates using energy conversion factors (ECF). In the XMM-Newton catalog, these factors are calculated from a broadband source spectrum caracterised by a power law with a photon index Γ = 1.7 and an absorption column density NH = 3 × 1020 cm-2 (Watson et al. 2009).
In the 0.5−4.5 keV band, this model provides ECF values very similar to those obtained from emission models of optically thin plasma with temperatures T ~ 4 × 107 K and absorbing hydrogen column density NH ~ 1021 cm-2. These models are representative of plasma emission spectra expected from active coronae in M 35. Indeed, the absorbing hydrogen column density towards M 35 is estimated to (0.8−1.1) × 1021 cm-2 from the reddening correction EB − V = 0.17−0.22 of McNamara et al. (2011). In the 0.5−4.5 keV range, ECF calculations using the Portable, Interactive, Multi-Mission Simulator (PIMMS; Mukai 1993) lead to X-ray flux estimates at most a factor of 2 lower for optically thin plasmas with cooler temperatures (T ~ 4 × 106 K) of less active stars and lower absorbing hydrogen column density (0.8 × 1021 cm-2) . The ECF calculation is barely affected by the less-than-solar metallicity of M 35. The X-ray fluxes provided in the 2XMMi-DR3 catalog are thus reasonable estimates.
2.2. Samples properties
Among the 19 correlations between the XMM-Newton X-ray source list and the M09 list of stars, one is classified by M09 as a photometric non-member. Five stars are classified as binaries and three stars are classified as radial velocity non-members by Geller et al. (2010; see Table 1). Thus, X-ray emission was detected from only 10 stars out of the 196 M 35 members with known rotational periods that were located in the field of view of the EPIC cameras during the September 2008 XMM-Newton observations and that have not been identified as binaries. This group of 10 stars is referred to hereafter as the X-ray sample. Their X-ray fluxes were converted into stellar X-ray luminosities assuming a distance of 762 pc (McNamara et al. 2011). Figure 3 shows their positions in a V0 vs. (B − V)0 colour magnitude diagram. The positions of the 196 stars in the parent sample are provided for comparison.
I used the effective temperature and bolometric correction vs. B − V colour index of Flower (1996) to derive the effective temperatures and bolometric luminosities of the X-ray sample stars. Their X-ray luminosities, effective temperatures, rotation periods, and Rossby numbers (see Sect. 3) are given in Table 2. Bolometric luminosities and X-ray to bolometric luminosity ratios are also provided. The last column of Table 2 shows the M09 classification of each star as a member of the convective sequence (C), the interface sequence (I), or the gap (g) (see Sect. 3).
 |
Fig. 4 Histograms showing bolometric luminosity (left), effective temperature (middle), and rotation period (right) of the parent sample and of the X-ray sample (bold line) of M 35 stars. |
X-ray luminosities in the 0.5−4.5 keV band, bolometric luminosities, X-ray to bolometric luminosity ratios, effective temperatures, rotation periods, and Rossby numbers of M 35 cluster members stars not identified as binaries.
The brightest star of the X-ray sample has a magnitude V0 = 13.94 and a colour index (B − V)0 = 0.66 (see Fig. 3) corresponding to an effective temperature of approximately 5700 K (Flower 1996) and a G2 V spectral type. The faintest star of the X-ray sample has a magnitude V = 18.54 and a colour index (B − V)0 = 1.36 corresponding to an effective temperature of approximately 4200 K (Flower 1996) and a M0 V spectral type. For comparison, the (B − V)0 colour indices of stars in the parent sample are included between 0.25 and 1.47 corresponding to effective temperatures in the range 4000 to 7500 K and to spectral types between M 2 and F0 on the main sequence.
The X-ray sample stars span a relatively narrow domain of X-ray luminosities with values between 5.2 × 1029 and 17 × 1029 erg s-1. The lowest value provides an estimate of the sensitivity of the M 35 XMM-Newton observation in September 2008. This detection limit is high compared with the typical range of X-ray luminosities on the main sequence and is due to the large distance of the cluster and the short exposures of the observation.
The X-ray to bolometric luminosity ratios of the X-ray sample stars are between 0.14 × 10-3 and 0.96 × 10-3 with the exception of two objects, 2XMMJ60913.7+241545 and 2XMMJ60908.6+242947. Their LX/Lbol ratios exceed the so-called saturation limit by a factor of more than 5. This suggests unusual states of X-ray emission possibly associated with an intense flaring activity. This hypothesis is corroborated by their positions at (B − V)0 = 1.08 and (B − V)0 = 1.36 (corresponding to Teff ≈ 4700 K and 4200 K, respectively) in a region of the colour magnitude diagram where no other M 35 star is detected in X-rays (see Fig. 3).
Rotation period, effective temperature and Rossby number histograms of the X-ray and parent samples are shown in Fig. 4. The effective temperatures of the parent sample range between 4000 and 7500 K while those of the X-ray sample are included between 4200 and 5700 K. Only cool dwarfs with an outer convective zone exhibit magnetic activity and hot coronae. The number of such stars in clusters increases with decreasing mass and effective temperature. On the contrary, their detection probability decreases towards low masses and effective temperatures since their X-ray luminosities, which are proportional to their bolometric luminosities, decrease eventually reaching the sensitivity limit of the observation. The effective temperature histogram of the X-ray sample is thus expected to reach a maximum, which is indeed observed around 5000 K (see Fig. 4, middle). Stars with Lbol > LX,lim/RX,sat, where RX,sat is the X-ray to bolometric luminosity ratio at saturation (see Sect. 4) and LX,lim is the X-ray luminosity detection threshold, should have effective temperatures greater than 4400 K corresponding to spectral types earlier than K5.
The rotation periods (see Fig. 4, right) of the parent sample stars range from 0.237 to 15.373 days, but most of the stars rotate faster than 10.5 days. The histogram shows a bimodal distribution with 60 stars rotating faster than 1.5 days and 132 stars having periods of rotation between 1.5 and 10 days. In the short period domain, the distribution exhibits a sharp peak below 1.5 day. In the long period domain, the distribution has a broad maximum around a period of about 6 days. This bimodal distribution was noted by M09 (see their Fig. 6) in their initial sample of 310 stars with determined rotation periods. These stars represented about 12% of the photometric cluster population within the brightness and areal limit of their photometric survey. Since the photometric measurement protocol of M09 was sensitive to a range of periods extending from a 0.08 day pseudo-Nyquist limit up to 23 days, these authors suggested that the 10 days cut-off represent a physical upper limit of the rotation period distribution among F, G, and K dwarfs in M 35. The rotation period histogram of the X-ray sample stars (see Fig. 4, right) indicates that only the fastest rotators were detected in X-rays. Their rotation periods are between 0.56 and 3.72 days and nine of them (out of ten) rotate faster than 1.3 days (see Table 2).
 |
Fig. 5 X-ray luminosity range of M 35 sample stars (crosses) with masses between 0.8 M⊙ and 1.2 M⊙ compared with median luminosities of stars with similar masses in the α Per, Pleiades, M 34, and the Hyades. The vertical error bars indicate the 25% and 75% quartiles of the distributions (Micela 2002). The various lines represent X-ray luminosity evolution models (see Sect. 5) of solar mass stars with initial rotation periods on the ZAMS ranging from 0.2 to 3.4 days. |
Out of the ten X-ray sample stars listed in Table 2, eight have effective temperatures between 4900 and 5700 K which correspond to stellar masses in the range 0.8 to 1.1 M⊙. Their X-ray luminosities are between 5.4 × 1029 erg s-1 and 17 × 1029 erg s-1. Stars with similar masses and a similar age usually show larger spread in X-ray luminosities. Spreads of more than one order of magnitude have been observed in many open clusters including the Pleiades, the Hyades (e.g. Stern et al. 1995; Micela et al. 1996), and NGC 752 (Giardino et al. 2008). This suggests that the narrow range of X-ray luminosities observed among M 35 stars is not an intrinsic property of the cluster but results from the low sensitivity of the XMM-Newton observation in September 2008. The M 35 parent sample includes 116 stars with 4800 K < Teff < 5800 K (see Fig. 4) of which only a small fraction was detected in X-rays.
Figure 5 compares the X-ray luminosities of Sun-like stars in M 35 with those of similar stars in α Per (Randich et al. 1996), in the Pleiades (Micela et al. 1999), in M 34 (G12), in the Hyades (Stern et al. 1995), and among nearby field stars (Schmitt 1997), including the Sun (Peres 2001). The data points are median values of the distributions reported for most of the clusters by Micela (2002). They represent stars within the 0.8−1.2 M⊙ mass range. The size of the vertical bars are determined by the 25% and 75% quartiles of the X-ray luminosity distribution in each cluster. These quartiles correspond to X-ray luminosities of 1.6 × 1029 erg s-1 and 6.4 × 1029 erg s-1, respectively, in the M 34 open cluster (G12) whose age (~240 Myr) is comparable to that of M 35 (~150 Myr). Figure 5 shows that the measured X-ray luminosities of Sun-like stars in M 35 are higher than in the Pleiades (~125 Myr) and in M 34. This is not expected since M 35 evolves at an age between these two clusters. The effect results from a bias of the X-ray luminosity measurements in M 35 towards high values due to the large distance of the cluster and the limited sensitivity of the observation.
 |
Fig. 6 Rotation periods vs. (B − V) colour indices of the M 35 sample stars. The solid line represents the I sequence defined by Barnes (2007). The dashed line represents the C sequence determined by M09. M 35 stars of the parent sample represented as blue circles belong to the I sequence. M 35 parent stars represented as red squares belong to the C sequence. Grey triangles represent M 35 gap stars. Filled symbols represent stars detected as X-ray emitters. |
3. Rossby numbers and rotation sequences in M 35
Durney & Latour (1978) argued that the activity level of main-sequence stars should be a function of the rotation period Prot divided by a convective turnover time scale τc. The Rossby number (Ro = Prot/τc) is an important indicator in hydromagnetic dynamo theory that measures the extent to which rotation can induce both helicity and differential rotation, which are considered essential for a solar-type dynamo. The dependence of the X-ray luminosity relative to the bolometric luminosity on the Rossby number was confirmed for F5 through M5 main-sequence stars using both clusters and field stars (e.g. Patten & Simon 1996; Randich et al. 2000).
While the rotation period can be directly measured, τc is
sometimes derived from the mixing-length theory (e.g. Kim & Demarque 1996) and is
usually determined empirically (Noyes et al. 1984; Stepien 1994; Gilliland 1985; Pizzolato
et al. 2001). The determination provided by Noyes et al. (1984) is the most used in the
literature, but is based on only a few points redder than
B − V = 1.0. Pizzolato et al. (2003) provided improved values using a sample with a greater coverage of
low-mass stars. Based on these consolidated values, Wright et al. (2011) suggested that the stellar mass is the relevant physical parameter
that determines the convective turnover time. They provided empirical values of the
convective turnover time as a function of (B − V) colour
bins. Their conversion table is valid over a range
0.09 < M/M⊙ <
1.36 (see Wright et al. 2011; their Table 2 with β = −2.7). It can be
parameterised as 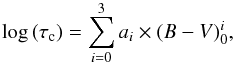 (2)where
ao = 1.191,
a1 = −0.804, a2 = 1.020, and
a3 = −0.145. I calculated the Rossby numbers of the X-ray
and parent sample stars using this parameterisation combined with the rotation period
measurements of M09.
(2)where
ao = 1.191,
a1 = −0.804, a2 = 1.020, and
a3 = −0.145. I calculated the Rossby numbers of the X-ray
and parent sample stars using this parameterisation combined with the rotation period
measurements of M09.
 |
Fig. 7 Right: X-ray to bolometric luminosity ratios of M 35 sample stars vs. Rossby numbers. Left: X-ray luminosities of M 35 sample stars vs. rotation periods. The thin black lines in both graphs represent models of X-ray activity evolution of 0.8 M⊙ stars with initial rotation periods on the ZAMS ranging from 0.12 to 3.4 days (see Sect. 5). |
In agreement with the paradigm advanced by Barnes (2003a), M09 found that M 35 stars group into two main sub-populations that lie on
narrow sequences in a colour-period diagram (see Fig. 6). One sequence, called the I sequence, consists of stars with increasing period
with increasing B − V colour. Another sequence, called the
C sequence, includes ultra-fast rotators with periods lower than about 1.5 days. Some stars,
called gap stars, lie in the gap between these two sequences. The M 35 colour-period diagram
(see Fig. 6) displays functional forms of the M 35
rotation isochrones of the I and C sequences. These were first introduced by Barnes (2003a). For the I sequence, I used the form subsequently
modified by Barnes (2007) in line with the
gyrochronology analysis of M 35 performed by M09. The equations of these isochrones are
![\begin{equation} P_{\rm C} = 0.2 \exp\left(t/100[(B-V)_{\rm 0}+0.1-t/3000]^3\right) \end{equation}](/articles/aa/full_html/2013/08/aa21076-13/aa21076-13-eq89.png) (3)and
(3)and
![\begin{equation} P_{\rm I} = \left[a \times ((B-V)_{\rm 0} - b)^c\right] \times t^n, \end{equation}](/articles/aa/full_html/2013/08/aa21076-13/aa21076-13-eq90.png) (4)where
a = 0.77, b = 0.40, and c = 0.60 are the
coefficients from a least-squares fit of PI to the M 35 I
sequence using n = 0.52 and t = 134 Myr (M09). The value
n = 0.52 had been previously determined by demanding solar rotation at
solar age using the I sequence from multiple young open clusters (Barnes 2007). The CgI
classification of the X-ray sample stars is given in the last column of Table 2.
(4)where
a = 0.77, b = 0.40, and c = 0.60 are the
coefficients from a least-squares fit of PI to the M 35 I
sequence using n = 0.52 and t = 134 Myr (M09). The value
n = 0.52 had been previously determined by demanding solar rotation at
solar age using the I sequence from multiple young open clusters (Barnes 2007). The CgI
classification of the X-ray sample stars is given in the last column of Table 2.
The X-ray luminosities and X-ray to bolometric luminosity ratios of the X-ray sample stars are displayed in Fig. 7 vs. their rotation periods and Rossby numbers. Figure 7 distinguishes members of the I sequence, of the C sequence, and of the gap. Although most of the M 35 stars detected in X-rays belong to the C sequence, their distribution in these diagrams looks consistent with the existence of a correlation between X-ray activity regimes and rotation sequences. Indeed, M 35 members of the C sequence detected in X-ray have short rotation periods (Prot < 1.3 days), small Rossby numbers (Ro ≤ 0.10), and X-ray to bolometric luminosity ratios close to the 10-3 saturation level. In contrast, the unique M 35 member of the I sequence detected in X-rays has a larger rotation period (3.72 d), a larger Rossby number (0.29), and an X-ray to bolometric luminosity ratio significantly smaller than the saturation limit. No gap star has been detected.
The connection between X-ray emission regimes and Rossby numbers on one side and between X-ray emission regimes and rotation sequences on the other side suggests that the classification in rotation sequences is equivalent to a classification in Rossby numbers. The rotation period, effective temperature, and Rossby number histograms of the M 35 parent sample are shown in Fig. 8 differentiating stars on the C or I rotation sequences and in the gap. Stars belonging to C and I sequences and to the gap spread over a large range of effective temperature (see Fig. 8, middle). The rotation period histogram (Fig. 8, right) shows that the C sequence includes the fastest rotators, which is in line with its definition. The C and I rotation sequences correspond to the two components of the bimodal distribution in rotation periods observed in the parent sample (Fig. 4, right).
The Rossby number histogram (Fig. 8, left) shows a clear separation between the C sequence at Ro < 0.12 and the I sequence at Ro > 0.16. The gap stars occupy an intermediate position. Their distribution in Rossby numbers overlaps the C sequence at low Ro and the I sequence at large Ro. The rotation sequence classification thus differs from a classification in term of Ro domains. The Rossby number alone does not permit the C- and I-sequence stars to be distinguished from the gap stars. In the M 34 open cluster, G12 reported a correlation between the saturated and non-saturated regimes of X-ray emission and the rotation sequence classification, but proposed a time evolution model of stellar activity where the X-ray luminosity of a star is essentially determined by its Rossby number. The comparison between rotation sequences and Rossby numbers in M 35 suggests that this model may not be appropriate for all stars.
 |
Fig. 8 Histograms of the Rossby number (left), effective temperature (middle) and rotation period (right) of the M 35 parent sample. The red continuous line represents stars belonging to the C sequence. The black dotted line represents gap stars. The blue dashed line represents stars belonging to the I sequence. |
4. X-ray luminosity distributions in M 35
In order to verify this statement, I calculated X-ray luminosity distributions of the
parent sample of M 35 stars assuming
LX/Lbol = RX,sat
in the saturated regime of X-ray emission and
LX/Lbol = Cst × (P/τc)β
in the non-saturated regime (Pizzolato et al. 2003).
In these activity-rotation relationships, Rosat is the Rossby number below which
X-ray emission is saturated, and RX,sat is the
X-ray to bolometric luminosity ratio at saturation. The dependence of X-ray luminosity on
mass is provided by the bolometric luminosity and convective turnover time. I used
RX,sat = 0.74 × 10-3 and
β = −2.7 in agreement with the Wright et al. (2011) study of a large stellar sample that includes members of IC 2602
(~30 Myr), IC 2391 (~30 Myr), NGC 2547 (~40 Myr), α Persei (~50 Myr), the
Pleiades (~125 Myr), NGC 2516 (~150 Myr), Praesepe (~580 Myr), the Hyades (~625 Myr), and
field stars. The proportionality coefficient Cst was estimated
using solar data as 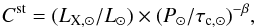 (5)with
log (LX, ⊙/L⊙) = −6.24
(Judge et al. 2003),
P⊙ = 26.09 days (Donahue et al. 1996), and τc, ⊙ = 14.45 days (Wright
et al. 2011).
(5)with
log (LX, ⊙/L⊙) = −6.24
(Judge et al. 2003),
P⊙ = 26.09 days (Donahue et al. 1996), and τc, ⊙ = 14.45 days (Wright
et al. 2011).
I considered two models of X-ray luminosity distributions in M 35 using two different
hypotheses. In the first model, X-ray luminosity distributions are derived assuming that the
transition from the saturated to the non-saturated regime of X-ray emission occurs at a
critical Rossby number Rosat = 0.3 in line with G12 observation of Sun-like stars
in M 34. The model simulates a drop of the X-ray to bolometric luminosity ratio by about one
order of magnitude at Rosat = 0.3. Hereafter, it is referred to the steep
transition model and can be expressed mathematically as
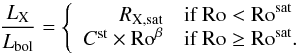 (6)In
the second model, X-ray luminosity distributions are derived assuming a strict correlation
between rotation sequences and X-ray emission regimes, also in agreement with the G12
analysis of M 34 data. In this model, stars on the C sequence and in the gap emits X-rays at
the saturation level while I-sequence stars exhibit a power-law dependence of the X-ray to
bolometric luminosity ratio as a function of the Rossby number. This model is called
hereafter the CgI model. It is different from the previous model since stars with
0.13 < Ro < 0.4 can have different X-ray
luminosities if they belong to the I sequence or to the gap. This model can be expressed as
(6)In
the second model, X-ray luminosity distributions are derived assuming a strict correlation
between rotation sequences and X-ray emission regimes, also in agreement with the G12
analysis of M 34 data. In this model, stars on the C sequence and in the gap emits X-rays at
the saturation level while I-sequence stars exhibit a power-law dependence of the X-ray to
bolometric luminosity ratio as a function of the Rossby number. This model is called
hereafter the CgI model. It is different from the previous model since stars with
0.13 < Ro < 0.4 can have different X-ray
luminosities if they belong to the I sequence or to the gap. This model can be expressed as
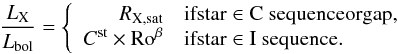 (7)Distributions
of X-ray luminosities could also be simulated using a critical Rossby number value
Rosat = 0.13 (see Wright et al. 2011).
The mathematical formulation of this model would be identical to that of the first model but
would use Rosat = 0.13 instead of 0.3. A critical Rossby number value
Rosat = 0.13 leads to a continuous transition from the saturated to the
non-saturated regime of X-ray emission (see Fig. 2 in
Wright et al. 2011). This contrasts with the sharp
decrease of the X-ray to bolometric luminosity ratio by about one order of magnitude at
Rosat = 0.3 in the steep transition model (see Fig. 11, right, in G12). I did not consider such a smooth transition model in
the present study since it does not explain the observation of saturated X-ray emission from
M 34 gap stars with 0.13 < Ro < 0.4 (see
G12). The steep transition model only affects the activity-rotation relationship derived by
Wright et al. (2011) in a narrow range of Rossby
numbers between 0.13 and 0.4. It remains consistent with the
LX/Lbol vs. Ro
plot of statistical data derived from measurements of rotation periods and X-ray
luminosities on main sequence stars in many open clusters (see Fig. 2 in Wright et al. 2011).
(7)Distributions
of X-ray luminosities could also be simulated using a critical Rossby number value
Rosat = 0.13 (see Wright et al. 2011).
The mathematical formulation of this model would be identical to that of the first model but
would use Rosat = 0.13 instead of 0.3. A critical Rossby number value
Rosat = 0.13 leads to a continuous transition from the saturated to the
non-saturated regime of X-ray emission (see Fig. 2 in
Wright et al. 2011). This contrasts with the sharp
decrease of the X-ray to bolometric luminosity ratio by about one order of magnitude at
Rosat = 0.3 in the steep transition model (see Fig. 11, right, in G12). I did not consider such a smooth transition model in
the present study since it does not explain the observation of saturated X-ray emission from
M 34 gap stars with 0.13 < Ro < 0.4 (see
G12). The steep transition model only affects the activity-rotation relationship derived by
Wright et al. (2011) in a narrow range of Rossby
numbers between 0.13 and 0.4. It remains consistent with the
LX/Lbol vs. Ro
plot of statistical data derived from measurements of rotation periods and X-ray
luminosities on main sequence stars in many open clusters (see Fig. 2 in Wright et al. 2011).
 |
Fig. 9 Cumulative histograms averaged over 10 000 simulations of X-ray luminosity distributions derived using the CgI model (continuous line) and the steep transition model (dashed line). The distributions of stellar X-ray luminosities around their average values are assumed to be Gaussian with a relative standard deviation of 0.5 (lefthand graph). Relative standard deviations of 1.3 for the C-sequence and the gap stars and of 4.0 for the I sequence are assumed in the righthand graph. The error bars correspond to a ±2σ accuracy. The bold line represents the cumulative histogram of measured X-ray luminosities in M 35. |
The X-ray luminosities of active stars may vary on timescales of hours, days, or years because of flares, rotational modulation by active regions, or activity cycles, for example. To take into account these stochastic effects, I ran Montecarlo simulations of X-ray luminosities for the 196 reference sample stars assuming Gaussian distributions around the average values defined by the X-ray activity vs. rotation relationships. Figure 9 shows the average values and error bars of the cumulative histograms of 10 000 simulated distributions of the CgI model and of the steep transition model. They assume a Gaussian distribution of X-ray luminosities. A relative standard deviation of 0.5 corresponding to a moderate X-ray variability is assumed in the left panel of Fig. 9. This relative standard deviation corresponds to the X-ray luminosity dispersion of M 35 C-sequence stars relative to the average X-ray saturation level excluding the two objects, 2XMMJ60913.7+241545 and 2XMMJ60908.6+242947, possibly in a flaring state. The right panel of Fig. 9 shows the result of 10 000 simulations with Gaussian distribution of X-ray luminosities assuming a relative standard deviation of 1.3 for the C-sequence and the gap stars and of 4.0 for the I sequence. These values correspond to a much higher variability of the stellar X-ray emission. They have been derived from the X-ray luminosity dispersion of all M 35 C-sequence stars relative to the average X-ray saturation level and from the X-ray luminosity dispersion of the M 34 I-sequence stars relative to the X-ray luminosity vs. the Ro power-law model, respectively. This assumes that the dispersion of measured X-ray luminosities is entirely due to the stochastic variability of intrinsic stellar X-ray emission. The dispersion of data points due to measurement errors or non-stochastic star-to-star X-ray luminosity differences, for example, are assumed to be negligible.
Figure 9 compares the simulated X-ray luminosity distributions of the parent sample with the measured distribution in M 35 (see Table 2). The detection threshold of the September 2008 XMM-Newton observations appears in the cumulative histogram of the measured distribution as a plateau below LX = 5 × 1029 erg s-1. According to the CgI and steep transition models, the X-ray luminosity distribution of the M 35 parent sample should extend down to about 1028 erg s-1. The large difference between this value and the detection threshold accounts for the small number of M 35 stars that have been detected in X-rays compared with the size of the parent sample.
In the moderate X-ray variability case (Fig. 9, left), the simulated distributions of X-ray luminosities derived from the steep transition model at Rosat = 0.30 show a larger number of stars than observed at high X-ray luminosities (LX > 1030 erg s-1). The distributions derived from the CgI model are closer to the measured distribution. An explanation for the difference in numbers of X-ray luminous stars between the CgI and the steep transition model is given by the Rossby number histogram (see left panel of Fig. 8). This histogram indicates that about 20 stars of the I sequence have a Rossby number lower than 0.3. According to the steep transition model, these stars emit X-rays at the saturation level. The CgI model assumes that they emit in the non-saturated regime of X-ray emission which leads to a lower number of X-ray luminous stars and is in closer agreement with the observation.
In the high X-ray variability case (Fig. 9, right), the X-ray luminosity distributions associated with the CgI and steep transition models become indistinguishable. The effect of the high X-ray variability is not only to increase the error bars on the simulated distributions but also to reduce the average number of X-ray bright stars in the steep transition model and to increase it in the CgI model. The associated distributions both differ significantly from the measured distribution.
The error bars in Fig. 9 correspond to the ±2σ deviation in the 10 000 Montecarlo simulations of X-ray distributions performed according to the CgI or to the steep transition model. They indicate that the difference between these two models would be significant in a moderate X-ray variability case. According to the steep transition model, the number of stars with luminosity higher than 1030 erg s-1 is greater than 15 while the CgI model indicates that this number should be greater than 6 at 95% confidence level. Four stars with LX > 1030 erg s-1 have actually been detected in the field of view of the EPIC cameras because of the decreasing detection probability of X-ray sources as their X-ray luminosities approach the 5 × 1029 erg s-1 detection threshold of the September 2008 XMM-Newton observations. On the other hand, the high X-ray variability case accounts for the large dispersion in X-ray luminosity of M 35 C-sequence stars and especially of M 34 I-sequence stars. However, in that case the CgI and the steep transition models indicate that the number of stars with luminosity higher than 1030 erg s-1 should be greater than 12 and 13, respectively, at 95% confidence level, while only four such stars have been detected.
 |
Fig. 10 Relationships between the convective turnover time and the rotation period Psat at which a transition occurs between the saturated and non-saturated regimes of X-ray emission. The convective turnover time is expressed in the scale of Wright et al. (2011). Relationships are shown for stars with initial periods of rotation on the ZAMS ranging from 0.12 to 3.4 days. These relations have been derived assuming a correlation between X-ray emission regimes and rotation sequences using the I and C sequence parameterisation of Barnes (2010). They are compared with the linear relation (continuous thick line) that assumes a transition between X-ray emission regime at a critical Rossby number Rosat = 0.30 (G12). The linear relation corresponding to a continuous transition from saturated to non-saturated regime X-ray emission at Rosat = 0.13 is shown as a thick dashed line. |
5. X-ray activity evolution on the main sequence
5.1. Transition between X-ray emission regimes
The steep transition model at Rosat = 0.3 (see Eq. (6)) provides a good description of the X-ray luminosities of main-sequence stars with low (Ro < 0.13) and high (Ro > 0.4) Rossby numbers. This model may not be adequate to describe the evolution of stellar activity in the range 0.13 < Ro < 0.4, i.e. at the transition between the saturated and non-saturated regime of X-ray emission. Section 4 suggests that the CgI model based on a correlation between X-ray emission regimes and rotation sequences could be used instead, although neither this model nor the steep transition model are able to account for a stochastic time variability of the stellar X-ray emission with an amplitude large enough to explain the dispersion of X-ray luminosity measurements.
In line with Eq. (7), the CgI model can be formulated as
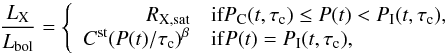 (8)where
PC and PI are the isochrone
equations whose empirical derivations as a function of the
B − V colour index are given in Eq. (3) and (4). Using
arguments based on angular momentum loss from fast and slow rotators, Barnes & Kim
(2010) suggested that the C and I isochrones can be expressed as a function of the
convective turnover time and a constant of integration P0,
(8)where
PC and PI are the isochrone
equations whose empirical derivations as a function of the
B − V colour index are given in Eq. (3) and (4). Using
arguments based on angular momentum loss from fast and slow rotators, Barnes & Kim
(2010) suggested that the C and I isochrones can be expressed as a function of the
convective turnover time and a constant of integration P0,
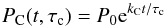 (9)and
(9)and
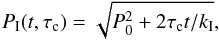 (10)where the constants
kc = 0.646 days Myr-1,
kI = 452 Myr day-1, and
τc,B = 34.884 days have been calibrated
on the Sun, with input from open cluster rotation observations demanding that the rotation
of the star start off with an initial period of 1.1 days and be 26.09 days at an age of
4570 Myr (Barnes 2010);
P0 represents the initial period of rotation on the ZAMS and
Eqs. (9) and (10) are only valid on the ZAMS, i.e. for t ≥ 0.
(10)where the constants
kc = 0.646 days Myr-1,
kI = 452 Myr day-1, and
τc,B = 34.884 days have been calibrated
on the Sun, with input from open cluster rotation observations demanding that the rotation
of the star start off with an initial period of 1.1 days and be 26.09 days at an age of
4570 Myr (Barnes 2010);
P0 represents the initial period of rotation on the ZAMS and
Eqs. (9) and (10) are only valid on the ZAMS, i.e. for t ≥ 0.
Since stellar rotation decays with age, stars evolve from the C to the I rotation sequence. For any given star, there is a rotation period Psat above which the star evolves on the I rotation sequence in a regime of non-saturated X-ray emission. If Psat > P0, the transition on the I rotation sequence occurs at a time tsat > 0 on the main sequence such that Psat(τc) = PC(tsat, τc) = PI(tsat, τc). If Psat < P0, the transition occurs during the pre-main-sequence phase of the star’s evolution.
A numerical solution to the equation Psat(τc) = PC(tsat, τc) = PI(tsat, τc) is given in Fig. 10 as a function of τc for 0.12 d <P0 < 3.4 d. It is compared with the linear relation Psat/ τc = 0.30 that corresponds to the steep transition model. Figure 10 shows that this model is a good approximation of the CgI model at low convective turnover time, i.e. for solar mass stars. At lower masses, the two models can differ significantly depending on the star convective turnover time and initial period of rotation on the ZAMS.
 |
Fig. 11 Simulations (thin lines) of the X-ray luminosity vs. rotation period (left) and of the X-ray to bolometric luminosity ratio vs. Rossby number (right) for stars with masses between 0.4 and 1.2 M⊙ having an initial period of rotation of 1.1 days on the ZAMS. Red squares, blue circles, and grey triangles represent measurements of M 34 stars (see Gondoin 2012) located respectively on the C sequence, on the I sequence, and in the gap between these two sequences. |
Remarkably, the smooth transition model at Rosat = 0.13 forms a lower envelope to the family of curves Psat(τc) shown on Fig. 10. It corresponds to the limit Psat(τc) = P0. Any star with P0 > 0.13 τc reaches the ZAMS on the I sequence in a non-saturated regime of X-ray emission. Only the fastest rotators with P0 < 0.13 τc are on the C rotation sequence or in the gap and emit X-rays in the saturation regime during the early phase of evolution on the main sequence.
The equation of the lower envelope for which Psat tends
towards P0 is
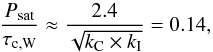 (11)where the turnover time
τc,W used by Wright et al. (2011) is
rescaled by a factor of
(τc,B/τc,W)⊙ ≈ 2.4
to correct for the different value of the Sun convective turnover time used by Barnes
(2010).
(11)where the turnover time
τc,W used by Wright et al. (2011) is
rescaled by a factor of
(τc,B/τc,W)⊙ ≈ 2.4
to correct for the different value of the Sun convective turnover time used by Barnes
(2010).
5.2. Updated model of X-ray activity evolution
Barnes (2010) noted that an infinite family of functions have the two asymptotic
behaviours described by Eq. (9) and (10). He proposed one particularly simple solution
recognising that another more complicated case may be found to be more physically
meaningful in time. This solution leads to the formulation of the rotation period
evolution on the main-sequence star as a function of τc and
P0, 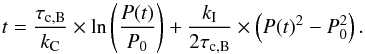 (12)Combining this
expression with a new formulation of the CgI model (see Eq. (8)) using
Psat(τc) provides a time
evolution model of the stellar X-ray emission on the main sequence that can be expressed
as
(12)Combining this
expression with a new formulation of the CgI model (see Eq. (8)) using
Psat(τc) provides a time
evolution model of the stellar X-ray emission on the main sequence that can be expressed
as 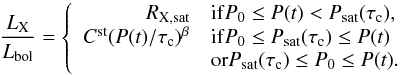 (13)The
dependence of the X-ray luminosity on stellar mass in Eq. (13) is implicitly contained in
the bolometric luminosity and in the convective turnover time. The bolometric luminosity
is related to stellar mass on the main sequence by the expression (e.g., Duric 2003)
(13)The
dependence of the X-ray luminosity on stellar mass in Eq. (13) is implicitly contained in
the bolometric luminosity and in the convective turnover time. The bolometric luminosity
is related to stellar mass on the main sequence by the expression (e.g., Duric 2003)
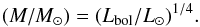 (14)A parameterisation of the
convective turnover time as a function of stellar mass is proposed by Wright et al. (2011)
as
(14)A parameterisation of the
convective turnover time as a function of stellar mass is proposed by Wright et al. (2011)
as 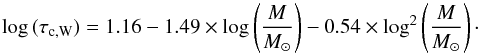 (15)One graphical
representation of the CgI model is shown in Fig. 7
(right). It displays the X-ray to bolometric luminosity ratio as a function of Rossby
number for 0.8 M⊙ stars with initial periods of rotation on
the ZAMS ranging from 0.12 to 3.4 days. Another representation is given in Fig. 11 (right) that plots
LX/Lbol vs.
Ro for stars with 0.4 ≤ M/M⊙ ≤ 1.2 and
P0 = 1.1 days on the ZAMS. A major change of the CgI model
compared with the steep transition model proposed by G12 is that the transition from
saturated to non-saturated X-ray emission does not occur for all stars at the same
critical Rossby number Rosat = 0.3. For each single star, it occurs at a Ro
value that depends on the mass of the star and on its initial period of rotation on the
ZAMS. For instance, the transition from saturated to non-saturated X-ray emission occurs
at 0.14 < Ro < 0.41 for 0.8
M⊙ stars with 0.12 d
< P0 < 2.8 d
(see Fig. 7). A 0.8 M⊙
star with P0 > 2.8 days reaches the
main sequence on the I sequence emitting X-ray in the non-saturated regime. Main-sequence
stars with 0.4 ≤ M/M⊙ ≤ 1.2 and
P0 = 1.1 days evolve from the saturated to the non-saturated
regime of X-ray emission at Rossby numbers between 0.32 and 0.19 (see Fig. 11, right). The CgI model thus suggests that stars with
0.14 < Ro < 0.41 exhibit a large range of
X-ray luminosities. This could explain the large dispersion of X-ray to bolometric
luminosity ratios among the I-sequence stars of the M 34 open cluster (see Fig. 11, right).
(15)One graphical
representation of the CgI model is shown in Fig. 7
(right). It displays the X-ray to bolometric luminosity ratio as a function of Rossby
number for 0.8 M⊙ stars with initial periods of rotation on
the ZAMS ranging from 0.12 to 3.4 days. Another representation is given in Fig. 11 (right) that plots
LX/Lbol vs.
Ro for stars with 0.4 ≤ M/M⊙ ≤ 1.2 and
P0 = 1.1 days on the ZAMS. A major change of the CgI model
compared with the steep transition model proposed by G12 is that the transition from
saturated to non-saturated X-ray emission does not occur for all stars at the same
critical Rossby number Rosat = 0.3. For each single star, it occurs at a Ro
value that depends on the mass of the star and on its initial period of rotation on the
ZAMS. For instance, the transition from saturated to non-saturated X-ray emission occurs
at 0.14 < Ro < 0.41 for 0.8
M⊙ stars with 0.12 d
< P0 < 2.8 d
(see Fig. 7). A 0.8 M⊙
star with P0 > 2.8 days reaches the
main sequence on the I sequence emitting X-ray in the non-saturated regime. Main-sequence
stars with 0.4 ≤ M/M⊙ ≤ 1.2 and
P0 = 1.1 days evolve from the saturated to the non-saturated
regime of X-ray emission at Rossby numbers between 0.32 and 0.19 (see Fig. 11, right). The CgI model thus suggests that stars with
0.14 < Ro < 0.41 exhibit a large range of
X-ray luminosities. This could explain the large dispersion of X-ray to bolometric
luminosity ratios among the I-sequence stars of the M 34 open cluster (see Fig. 11, right).
The CgI model of X-ray luminosity evolution reproduces features observed by Pizzolato et al. (2003) in their study on the relationship between coronal X-ray emission and stellar rotation in late-type main-sequence stars. In particular, Fig. 11 (left) shows that (i) the expression of the X-ray activity-rotation relationship in terms of LX vs. Prot, instead of LX/Lbol vs. Ro, considerably increases the scatter of data points because of the introduction of an additional mass dependence (ii) the X-ray luminosity saturation level increases with stellar mass because of the strong mass dependence of the bolometric luminosity and (iii) the rotation period at which the transition between X-ray emission regimes occurs increases with decreasing stellar mass. In addition, for a given initial rotation period on the ZAMS, lower mass stars evolve from the saturated to the non-saturated regime of X-ray emission at later ages. According to the model, the transition occurs at an age after arrival on the ZAMS of about 100 Myr for Sun-like stars with P0 = 1.1 days and after about 900 Myr for 0.4 M⊙ stars with the same initial period of rotation on the ZAMS (see Fig. 12).
5.3. Comparison with observational data
The effective temperature histogram of M 35 stars (see Fig. 4, middle) peaks at temperatures of about 5000 K that correspond to early K stars with masses of about 0.8 M⊙. Figure 7 compares the simulated evolution of the X-ray emission from such stars with the positions of M 35 stars in LX vs. P and LX/Lbol vs. Ro diagrams. All X-ray sample stars located on the C sequence emits at the saturation level in agreement with the model except two stars, 2XMMJ60913.7+241545 and 2XMMJ60908.6+242947, whose abnormal emission has been discussed previously (see Sect. 2.2). Another star, 2XMMJ60900.5+241159, exhibits an exceptionally low X-ray to bolometric luminosity ratio (LX/Lbol ≈ 10-4) in view of its Rossby number (Ro = 0.05). Its location above the main-sequence in the colour-magnitude diagram (see Fig. 3) suggests that this object is a binary system.
Only one M 35 star has been detected in X-ray that belongs to the I sequence. No M 35 star has been detected in X-rays that belongs to the gap between the C and I rotation sequences (see Fig. 7). The M 34 open cluster provides additional stars detected in X-rays that have been classified as members of the C, g and I rotation sequences (see G12). Figure 11 (right) compares their locations in an LX/Lbol vs. Ro diagram with X-ray evolutionary tracks of stars with 0.4 ≤ M/M⊙ ≤ 1.2 and P0 = 1.1 day. One interesting output of the model is that the hypothesis of a correlation between rotation sequences and X-ray emission regimes leads to a transition from the saturated to the non-saturated regime of X-ray emission in a range of Rossby number between 0.32 and 0.19 for stars with 0.4 ≤ M/M⊙ ≤ 1.2 and P0 = 1.1 day. The LX/Lbol vs. Ro diagram in Fig. 11 (right) shows that gap stars in M 34 are indeed located in this domain.
 |
Fig. 12 Simulated evolution of the X-ray luminosity of main-sequence stars with masses between 0.4 and 1.2 M⊙ that have an initial period of rotation of 1.1 days on the ZAMS. |
Using the CgI model, I calculated the time evolution of the X-ray luminosities of Sun-like stars with a range of initial rotation periods observed in young stellar clusters. These stars are assumed to reach the ZAMS at an age of 35 Myrs, approximately equal to the Kelvin-Helmholtz timescale of a solar mass star. Figure 5 compares the evolutionary track of their X-ray emissions with the measured X-ray luminosities of Sun-like stars in various open clusters (see Sect. 2.3). The model shows, in agreement with the measurements, a large dispersion of X-ray luminosities among young Sun-like stars. This large dispersion in the early phase of evolution on the main sequence occurs because fast rotating Sun-like stars emit X-ray in the saturated regime while slower rotators with similar masses already operate in the non-saturated regime of X-ray emission.
Regarding the slow rotators, the model indicates that Sun-like stars with initial periods of rotation on the ZAMS greater than about two days have an X-ray luminosity lower than about 5 × 1029 erg s-1 at the age of M 35. This explains why they were not detected in X-rays during the XMM-Newton observation of September 2008. Figure 5 also shows that Sun-like stars with P0 of ~1 day are transiting from the saturated to the non-saturated regime of X-ray emission approximately at the age of M 35. Sun-like stars rotating more slowly have already reached the I sequence and emit X-ray in the non-saturated regime. Solar mass stars rotating more quickly experience a transition to the non-saturated regime of X-ray emission at a later age. The transition does not occur later than about 400 Myr for stars that reach the ZAMS with a rotation close to break-up.
6. Discussion
In the present study, I calculated the Rossby numbers of a reference sample of M 35 stars located in the field of view of the EPIC cameras during the XMM-Newton observation of September 2008. The calculation uses a conversion table of the convective turnover time vs. B − V index established by Wright et al. (2011) and M09 measurements of stellar rotation periods derived from an extensive photometric survey of the M 35 open cluster. I simulated X-ray luminosity distributions of this reference sample using well known activity-rotation relationships in the saturated and non-saturated regime of X-ray emission (see e.g. Wright et al. 2011).
A first set of X-ray luminosity distributions was obtained assuming that the transition from saturated to non-saturated X-ray emission occurs at a critical Rossby number Rosat = 0.3 in line with an evolution model of X-ray activity on the main sequence proposed by G12 based on a study of the M 34 open cluster. This study also revealed a strong correlation between the saturated and non-saturated regimes of X-ray emission and the C and I rotation sequences observed in M 34 (Irwin et al. 2006; James et al. 2010; Meibom et al. 2011). Using the CgI sequence classification of M 35 stars by M09, a second set of X-ray luminosity distributions was calculated assuming that C-sequence and gap stars emit X-rays at the RX,sat saturation level and that I-sequence stars emit X-rays in the non-saturated regime.
A comparison with XMM-Newton observations suggests that only this second group of distributions could account for the low number of M 35 stars detected in X-rays. I conclude that the correlation between X-ray emission regimes and rotation sequences could be a fundamental property of the magnetic activity evolution on the main sequence. The evolution model of X-ray activity proposed by G12 was updated taking this correlation into account. Its formulation was derived from mathematical expressions of the I and C isochrones as a function of convective turnover time and initial period of rotation on the ZAMS proposed by Barnes & Kim (2010). One major prediction of the model is that the transition from the saturated to the non-saturated regime of X-ray emission occurs in a range of Rossby numbers depending on stellar mass and initial period of rotation on the ZAMS. This Rossby number domain is between 0.14 and 0.4 for 0.8 M⊙ stars with 0.12 d < P0 < 2.8 and between 0.32 and 0.19 for stars with 0.4 ≤ M/M⊙ ≤ 1.2 and P0 = 1.1 day. Remarkably, this model prediction is in agreement with observations of stellar X-ray emission in the M 34 open cluster. It could explain the large dispersion of X-ray to bolometric luminosity ratios among its I sequence stars. The model also accounts for the large range of X-ray luminosities observed among Sun-like stars in young open clusters.
The X-ray to bolometric luminosity ratio is an indicator of dynamo efficiency in late-type stars. Indeed, the bolometric luminosity is a close upper limit of the total outer convective flux since almost all the energy is transported by convection in the top layers of their convection zone (e.g. Böhm-Vitense 1992). The coronal X-ray radiative flux density is proportional to the average surface magnetic flux density (Fisher et al. 1998). Hence, the LX/Lbol ratio is a lower limit of the ratio between the surface magnetic flux and the outer convective flux. A steep decrease of this ratio around Rossby numbers Ro ≈ 0.14−0.4 is thus indicative of a significant drop in dynamo efficiency. The present study suggests that the transition between X-ray emission regimes in M 35 is also correlated with the rapid change in the rate of stellar angular momentum loss that is indicated by the transition from the C to the I rotation sequence. The good agreement between the proposed X-ray emission evolution model and X-ray luminosity distributions in young open clusters suggests that this correlation between X-ray emission regimes and rotation sequences is a fundamental property of the early magnetic activity evolution of young stars.
Rotational braking by stellar winds is a commonly accepted explanation for the decay of stellar rotation with age. Parker (1958), who proposed the existence of the solar wind, already noted that this wind would cause a retardation of solar rotation on a long time scale. It was soon recognised that this phenomenon also applied to other stars and the associated angular momentum loss was linked to the existence of a surface convection zone (Schatzman 1962). Models were developed to understand angular momentum loss from magnetised stellar winds (e.g. Weber & Davis 1967; Mestel 1968; Kawaler 1988).
 |
Fig. 13 Left: age tsat on the main sequence at which stars change from a saturated to a non-saturated regime of X-ray emission as a function of convective turnover time. Right: time delay tsat − tgap between the epoch of X-ray emission regime transition and the epoch of maximum rotational deceleration. |
Observations of young open clusters showed that late-type stars are formed with a large spread in angular momentum. Stauffer & Hartmann (1987) noted that these stars spin down very rapidly once on the main sequence. This suggested that angular momentum loss mechanisms were highly efficient (Kawaler 1988). In addition, observational data indicated that G-type stars spin down more quickly than K-type stars which rotate faster than G-type stars in the Pleiades and which have experienced spin-down by the age of the Hyades. This led Stauffer & Hartmann (1987) to conclude that only the convective envelope initially undergoes spin-down by magnetic braking. Indeed, if the magnetic field lines that sling charged particles from the wind into space are rooted in the photosphere, the envelope rotation should be decelerated by the wind torque more efficiently in higher mass stars since their thinner convective envelopes contain a smaller fraction of the overall stellar moment of inertia and angular momentum. This statement assumes that the convective envelope experiences spin-down separately from the radiative core. While the envelope rotation is decelerated by the wind torque, the conservation of angular momentum keeps the radiative core in rapid rotation. The star will thus develop a strong gradient in angular velocity at the base of the convection zone that may trigger various instabilities (e.g. Endal & Sofia 1981).
This expectation is not supported by measurements of internal solar rotation (Brown et al. 1989). According to the above interpretation, the difference in the angular velocity between the Sun’s radiative core and its convective envelope must thus have been erased by some mechanism of angular momentum redistribution. Several processes have been proposed including angular momentum transport by viscously-driven large scale flows (e.g. Spiegel & Zahn 1992), by internal gravity waves generated by turbulent eddies in the convective envelope (Zahn et al. 1997), or by magnetic torquing (e.g. Mestel & Weiss 1987; Charbonneau & MacGregor 1993).
Rotation-induced turbulent diffusion (Pinsonneault et al. 1989) and wind-driven meridional circulation (Zahn 1992) fail to extract sufficient angular momentum from the radiative interior (Chaboyer et al. 1995). Estimates of the timescale for core-envelope coupling in solar-type stars range from about 1 Myr for the fastest rotators up to 10−100 Myr (e.g. Keppens et al. 1995; Alain 1998) and 0.5 Gyr (Irwin et al. 2007) for slowly rotating stars. Models of rotational evolution of solar-type stars with angular momentum transport described as a purely diffusive process show that these coupling time intervals correspond to large diffusion coefficients that would lead to rates of surface Li destruction strongly exceeding the trend observed in the Sun and its twins (Denissenkov et al. 2010). Also, the natural action of internal gravity waves produces large-scale oscillations in the solar rotation as a function of depth (Denissenkov et al. 2008), which is in marked contrast to the nearly uniform rotation in the outer region of the Sun’s radiative core.
Mechanisms for angular momentum transport employing magnetic fields (Charbonneau & MacGregor 1992, 1993; Spruit 1999, 2002) seem to be better candidates. A strong gradient in angular velocity between the radiative core and the convective envelope is an essential ingredient for the generation of magnetic field at the base of the convection zone and magnetic fields are quite effective at transporting angular momentum (Spruit 2002). In line with the above discussion, Barnes (2003a) proposed that the C sequence is due to the coupling of the stellar wind to just the convective zone that is decoupled from the radiative zone, while the I sequence is due to the coupling of the wind with the entire star. The transition across the gap between these two rotation sequences would therefore be associated with a coupling between the radiative and the convective zone. Barnes (2003b) suggested that stars on the convective sequence generate a convective or turbulent dynamo similar to that described by Durney et al. (1993). He proposed that the shear between the fast spinning radiative interior and the convective envelope would eventually generate an interface dynamo that results in the transition onto the I sequence.
According to the current picture of such an interface dynamo, large scale toroidal magnetic fields responsible for the formation of active regions are stored and amplified at the base of the convection zone (e.g. Gilman 2000; Charbonneau 2010). These toroidal fields ultimately become unstable to magnetic buoyancy and rise through the convection zone. Some eventually break through the surface to form active regions. Others are shredded by the convection and used to create poloidal fields, thereby completing the dynamo cycle. Solar cycle dynamo models suggest that the toroidal magnetic field at the base of the solar convection zone is of the order of 40−50 kG with typical rise time of the order of a couple of years (Weber et al. 2011). The emergence of new active regions will increase the X-ray stellar emission at the epoch of transition onto the I sequence if this transition is the result of an angular momentum redistribution associated with the generation of an interface dynamo.
In contrast, the transition from the C to the I rotation sequence appears to be associated with a sharp decrease of the X-ray to bolometric luminosity ratio. This suggests a quenching of the dynamo regime responsible for the high X-ray activity level of rapidly rotating young stars with low Rossby numbers. Although not directly applicable to stars, numerical simulations (Käpylä et al. 2009) indicate that large-scale dynamos are excited in rapidly rotating convection, i.e. in the absence of shear, provided that rotation is rapid enough. Such turbulent dynamos probably operate in stars less massive than about 0.35 solar masses that are fully convective, and so cannot possess a transition region like the solar tachocline (Durney et al. 1993; Küher & Rüdiger 1999; Chabrier & Küher 2006). A recent study of the magnetic activity-rotation for a large sample of field M dwarfs with known rotational periods (West et al. 2012) show a trend of decreasing activity with increased rotation period for all M dwarf spectral types.
The evolution model of X-ray activity developed in the present study (see Sect. 5.2) provides an estimate of the age tsat at which a star changes from the saturated to the non-saturated regime of X-ray emission. This age is plotted in Fig. 13 (left) as a function of mass for a range of initial rotation periods on the ZAMS typical of those observed in young open clusters. It can be compared with the age tgap (see Eq. (26) in Barnes 2010) taken by a star to evolve through its C rotation phase, and to reach the nominal rotational gap g marking the onset of the I-rotation phase. The comparison shows that tsat ≫ tgap. The transition from saturated to non-saturated X-ray emission thus occurs well after the stellar evolution through the rotational gap between the C and I sequences, which corresponds to a maximum of the rotation deceleration. If the associated redistribution of angular momentum is the result of a nascent interface dynamo, the model suggests that during the time interval between the rotation sequence transition and the X-ray regime transition two different dynamo regimes operate simultaneously within the interior of Sun-like stars.
According to the above scenario, the angular momentum redistribution mechanism responsible for the transition from the C to the I rotation sequence results in a changing mixture of two dynamo processes occurring side by side, i.e. a boundary-layer interface dynamo and a convective envelope turbulent dynamo. This last process dominates in rapidly rotating young stars. As the shear between the fast spinning radiative interior and the convective envelope increases, another process strengthens in which dynamo action occurs in the boundary region between the radiative core and the convective envelope. This dynamo process relies on differential rotation, but also induces important redistributions of angular momentum. As the rotation of the convective envelope decays, the turbulent dynamo is quenched and the interface dynamo becomes dominant, decreasing progressively at later stages of evolution when rotation dies away.
7. Summary
Late-type stars in open clusters exhibit two kinds of dependences of their X-ray emission on stellar rotation. While fast rotators have a relatively constant X-ray to bolometric luminosity ratio, slower rotators show a decline of their X-ray emission with decreasing rotation rate. In a previous paper, I reported a correlation between these regimes of X-ray emission and the rotation sequences that have been observed in the M 34 open cluster from extensive rotation period surveys. I also noted that M 34 Sun-like stars show a steep transition of their X-ray to bolometric luminosity ratio by about one order of magnitude at a critical Rossby number of about 0.3. The purpose of the present study was to verify whether such connections between X-ray activity and rotation also exist in other open clusters.
The M 35 cluster has an age comparable to that of M 34 and was also the subject of an intensive rotation period survey. Its large distance limits the detection of its stellar X-ray emission with XMM-Newton to the brightest sources. I thus compared the distribution of stellar X-ray luminosities in M 35 with models derived from rotation period measurements assuming either an X-ray regime transition at a critical Rossby number or a correlation between X-ray emission regimes and rotation sequences. The study suggests that this second hypothesis could account for the low number of M 35 stars detected in X-rays.
A time evolution model of X-ray activity evolution initially based on M 34 observations (see G12) was thus updated based on this correlation. An important prediction of the model is that the transition from saturated to non-saturated X-ray emission occurs at Rossby numbers between 0.13 and 0.4 depending on each individual star’s mass and initial period of rotation on the ZAMS. This result is in agreement with observations of stellar X-ray emission in M 34. The model also explains the large range of X-ray luminosities observed among Sun-like stars in young open clusters. It indicates that, in the early phase of evolution on the main sequence, fast rotating Sun-like stars emit X-ray in the saturated regime while slower rotators with similar masses already operate in a non-saturated regime of X-ray emission.
The good agreement between the model and the observations suggests that the correlation between X-ray emission regimes and rotation sequences is a fundamental property of the early evolution of stellar magnetic activity on the main sequence. I argue that the angular momentum redistribution mechanism(s) responsible for the transition between rotation sequences could result in a changing mixture of dynamo processes occurring side by side, possibly including a turbulent dynamo dominant at high rotation rate and an interface-type dynamo whose efficiency decreases progressively at a later stage of stellar evolution when rotation dies away.
Acknowledgments
I am grateful to the anonymous referee for the helpful comments that allowed me to improve the paper.
References
- Allain, S. 1998 A&A, 333, 629 [Google Scholar]
- Barnes, S. A. 2003a, ApJ, 586, 464 [NASA ADS] [CrossRef] [Google Scholar]
- Barnes, S. A. 2003b, ApJ, 586, L145 [NASA ADS] [CrossRef] [Google Scholar]
- Barnes, S. A. 2007, ApJ, 669, 1167 [NASA ADS] [CrossRef] [Google Scholar]
- Barnes, S. A. 2010, ApJ, 722, 222 [NASA ADS] [CrossRef] [Google Scholar]
- Barnes, S. A., & Kim, Y.-C. 2010, ApJ, 721, 675 [NASA ADS] [CrossRef] [Google Scholar]
- Boehm-Vitense, E. 1992, Introduction to stellar astrophysics − Stellar structure and evolution (Cambridge University Press), 3 [Google Scholar]
- Brown, T. M., Christensen-Dalsgaard, J., Dziembowski, W. A., et al. 1989, ApJ, 343, 526 [NASA ADS] [CrossRef] [Google Scholar]
- Chaboyer, B., Demarque, P., & Pinsonneault, M. H. 1995, ApJ, 441, 876 [NASA ADS] [CrossRef] [Google Scholar]
- Chabrier, G., & Küher, M. 2006, A&A, 446, 1027 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Charbonneau, P. 2010, Liv. Rev. Sol. Phys., 7, 3 [Google Scholar]
- Charbonneau, P., & MacGregor, K. B. 1992, ApJ, 387, 639 [NASA ADS] [CrossRef] [Google Scholar]
- Charbonneau, P., & MacGregor, K. B. 1993, ApJ, 417, 762 [NASA ADS] [CrossRef] [Google Scholar]
- Collier Cameron, A., Davidson, V. A., Hebb, L., et al. 2009, MNRAS, 400, 451 [NASA ADS] [CrossRef] [Google Scholar]
- Denissenkov, P. A. 2010, ApJ, 719, 28 [NASA ADS] [CrossRef] [Google Scholar]
- Denissenkov, P. A., Pinsonneault, & MacGregor, K. B. 2008, ApJ, 684, 757 [NASA ADS] [CrossRef] [Google Scholar]
- Denissenkov, P. A., Pinsonneault, M., Terndrup, D. M., & Newsham, G. 2010, ApJ, 716, 1269 [NASA ADS] [CrossRef] [Google Scholar]
- Donahue, R. A., Saar, S. H., & Baliunas, S. L. 1996, ApJ, 466, 384 [NASA ADS] [CrossRef] [Google Scholar]
- Duric, N. 2003, Advanced Astrophysics (Cambridge University Press) [Google Scholar]
- Durney, B. R., & Latour, J. 1978, Geophys. Astrophys. Fluid Dyn., 9, 241 [NASA ADS] [CrossRef] [Google Scholar]
- Durney, B. R., De Young, D. S., & Roxburgh, I. W. 1993, Sol. Phys., 145, 207 [NASA ADS] [CrossRef] [Google Scholar]
- Endal, A. S., & Sofia, S. 1981, ApJ, 243, 625 [NASA ADS] [CrossRef] [Google Scholar]
- Feigelson, E. D., Gaffney, J. A., Garmire, G., Hillenbrand, L. A., & Townsley, L. 2003, ApJ, 584, 911 [NASA ADS] [CrossRef] [Google Scholar]
- Fisher, G., Longcope, D., Metcalf, T., et al. 1998, ApJ, 508, 885 [NASA ADS] [CrossRef] [Google Scholar]
- Flower, P. J. 1996, ApJ, 469, 335 [Google Scholar]
- Fröhlich, H.-E., Küker, M., Hatzes, A. P., & Strassmeier, K. G. 2009, A&A, 506, 263 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Geller, A., Mathieu, R., Braden, E., et al. 2010, AJ, 139, 1383 [NASA ADS] [CrossRef] [Google Scholar]
- Giardino, G., Pillitteri, I., Favata, F., & Micela, G. 2008, A&A, 490, 113 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gilliland, R. L. 1985, ApJ, 299, 286 [NASA ADS] [CrossRef] [Google Scholar]
- Gilman, P. A. 2000, Sol. Phys., 192, 27 [NASA ADS] [CrossRef] [Google Scholar]
- Gondoin, P. 2012, A&A, 546, A117 (G12) [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gondoin, P., Aschenbach, B., Erd, C., et al. 2000, SPIE Proc., 4140, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Gondoin, P., Gandolfi, D., Fridlund, M., et al. 2012, A&A, 548, A15 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hartman, J. D., Gaudi, B. S., Pinsonneault, M. H., et al. 2001, ApJ, 691, 342 [Google Scholar]
- Hartman, J. D., Bakos, G. A., Kovacs, G, & Noyes, R. W. 2010, MNRAS, 408, 475 [NASA ADS] [CrossRef] [Google Scholar]
- Irwin, J., Aigrain, S., Hodgkin, S., et al. 2006, MNRAS, 370, 954 [NASA ADS] [Google Scholar]
- Irwin, J., Hodgkin, S., Aigrain, S., et al. 2007, MNRAS, 377, 741 [NASA ADS] [CrossRef] [Google Scholar]
- James, D. J., Barnes, S. A., Meibom, S., et al. 2010, A&A, 515, A100 (J10) [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Jansen, F., Lumb, D., Altieri, B., et al. 2001, A&A, 365, L1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Jardine, M., & Unruh, Y. C. 1999, A&A, 346, 883 [NASA ADS] [Google Scholar]
- Jeffries, R. D., Thurston, M. R., & Pye, J. P. 1997, MNRAS, 287, 350 [NASA ADS] [CrossRef] [Google Scholar]
- Judge, P. G., Solomon, S. C., & Ayres, T. R. 2003, ApJ, 593, 534 [NASA ADS] [CrossRef] [Google Scholar]
- Kalirai, J. S., Fahlman, G. G., Richer, H. B., & Ventura, P. 2003, AJ, 333, 236 [Google Scholar]
- Käpylä, P. J., Korpi, M. J., & Brandenburg, A. 2009, ApJ, 697, 1153 [NASA ADS] [CrossRef] [Google Scholar]
- Kawaler, S. D. 1988, ApJ, 333, 236 [NASA ADS] [CrossRef] [Google Scholar]
- Keppens, R., MacGregor, K. B., & Charbonneau, P. 1995, A&A, 294, 469 [NASA ADS] [Google Scholar]
- Kim, Y., & Demarque, P. 1996, ApJ, 457, 340 [NASA ADS] [CrossRef] [Google Scholar]
- Krishnamurthi, A., Terndrup, D. M., Pinsonneault, M. H., et al. 1998, ApJ, 493, 914 [NASA ADS] [CrossRef] [Google Scholar]
- Küher, M., & Rüdiger, G. 1999, A&A, 346, 922 [NASA ADS] [Google Scholar]
- Lanza, A. F., Pagano, I., Leto, G., et al. 2009, A&A, 493, 193 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- McNamara, B. J., Harrison, T. E., McArthur, B. E., & Benedict, G. F. 2011, AJ, 142, 53 [NASA ADS] [CrossRef] [Google Scholar]
- Meibom, S., Mathieu, R. D., & Stassun, K. G. 2009, ApJ, 695, 679 (M09) [NASA ADS] [CrossRef] [Google Scholar]
- Meibom, S., Matthieu, R. D., Stassun, K. G., et al. 2011, ApJ, 733, 115 [NASA ADS] [CrossRef] [Google Scholar]
- Mestel, L. 1968, MNRAS, 138, 359 [NASA ADS] [CrossRef] [Google Scholar]
- Mestel, L., & Weiss, N. O. 1987, MNRAS, 226, 123 [NASA ADS] [CrossRef] [Google Scholar]
- Micela, G. 2002, Stellar Coronae in the Chandra and XMM-Newton Era, ASP Conf. Proc., 277, 263 [Google Scholar]
- Micela, G., Sciortino, S., Serio, S. et al. 1985, ApJ, 292, 172 [NASA ADS] [CrossRef] [Google Scholar]
- Micela, G., Sciortino, S., Kashyap, V. et al. 1996, ApJS, 102, 75 [NASA ADS] [CrossRef] [Google Scholar]
- Micela, G., Sciortino, S., Harnden, F. R. Jr., et al. 1999, A&A, 341, 751 [NASA ADS] [Google Scholar]
- Mukai, K. 1993, Legacy 3, 21-31 [Google Scholar]
- Noyes, R. W., Hartmann, L. W., Baliunas, S. L., et al. 1984, ApJ, 279, 763 [NASA ADS] [CrossRef] [Google Scholar]
- Pallavicini, R., Golub, L., Rosner, R., et al. 1981, ApJ, 248, 279 [NASA ADS] [CrossRef] [Google Scholar]
- Parker, E. N. 1958, ApJ, 128, 664 [Google Scholar]
- Patten, B. M., & Simon, T. 1996, ApJS, 106, 489 [NASA ADS] [CrossRef] [Google Scholar]
- Peres, G. 2001, in X-ray Astronomy 2000, ASP Conf. Ser., 234, 41 [NASA ADS] [Google Scholar]
- Pevtsov, A. A., Fisher, G. H., Acton, L. W., et al. 2003, ApJ, 598, 1387 [NASA ADS] [CrossRef] [Google Scholar]
- Pinsonneault, M. H., Kawaler Steven, D., Sofia, S., & Demarque, P. 1989, ApJ, 338, 424 [NASA ADS] [CrossRef] [Google Scholar]
- Pizzolato, N., Ventura, P., D’Antona, F., et al. 2001, A&A, 373, 597 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Pizzolato, N., Maggio, A., Micela, G., Sciortino, S., & Ventura, P. 2003, A&A, 397, 147 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Prosser, C. F., Shretone, M. D., Dasgupta, A. et al. 1995, PASP, 107, 211 [NASA ADS] [CrossRef] [Google Scholar]
- Randich, S. 2000, in Stellar Clusters and Association: Convection, Rotation and Dynamos, ASP Conf. Ser., 198, 401 [Google Scholar]
- Randich, S., Schmitt, J. H. M. M., Prosser, C. F., & Stauffer, J. R. 1996, A&A, 305, 785 [NASA ADS] [Google Scholar]
- Schatzman, E. 1962, Ann. Astrophys., 25, 18 [Google Scholar]
- Schmitt, J. H. M. M. 1997, A&A, 318, 215 [NASA ADS] [Google Scholar]
- Schrijver, C. J., & Zwaan, C. 2000, in Solar and Stellar Magnetic Activity (Cambridge University Press) [Google Scholar]
- Silva-Valio, A., Lanza, A. F., Alonso, R., & Barge, P. 2010, A&A, 510, A25 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Spiegel, E. A., & Zahn, J.-P. 1992, A&A, 265, 106 [NASA ADS] [Google Scholar]
- Spruit, H. C. 1999, A&A, 349, 189 [NASA ADS] [Google Scholar]
- Spruit, H. C. 2002, A&A, 381, 923 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Stauffer, J. R., & Hartmann, L. W. 1987, ApJ, 318, 337 [NASA ADS] [CrossRef] [Google Scholar]
- Stepien, K. 1994, A&A, 292, 191 [NASA ADS] [Google Scholar]
- Stern, R. A., Schmitt, J. H. M. M., & Kahabka, P. T. 1995, ApJ, 448, 683 [Google Scholar]
- Strüder, L., Briel, U., Dennerl, K., et al. 2001, A&A, 365, L18 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Sung, H., & Lee, S.-W. 1992, J. Korean Astron. Soc., 25, 91 [NASA ADS] [Google Scholar]
- Turner, M. J. L. T., Abbey, A., Arnaud, M., et al. 2001, A&A, 365, L18 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Watson, M. G., Schröder, A. C., Fyfe, D., et al. 2009, A&A, 493, 339 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Weber, E. J., & Davis, L., Jr.1967, ApJ, 148, 217 [NASA ADS] [CrossRef] [Google Scholar]
- Weber, M. A., Fan, Y., & Miesch, M. S. 2011, ApJ, 741, 11 [NASA ADS] [CrossRef] [Google Scholar]
- West, A. A., Weisenburger, K. L., Irwin, J., et al. 2012, AAS meeting, 219, 313.02 [Google Scholar]
- Wright, N. J., Drake, J. J., Mamajek, E. E., & Henry, G. W. 2011, ApJ, 743, 48 [NASA ADS] [CrossRef] [Google Scholar]
- Zahn, J.-P. 1992, A&A, 265, 115 [NASA ADS] [Google Scholar]
- Zahn, J.-P., Talon, S., & Matias, J. 1992, A&A, 322, 320 [Google Scholar]
All Tables
X-ray fluxes, rotation periods, and photometric indices of X-ray emitting stars in M 35.
X-ray luminosities in the 0.5−4.5 keV band, bolometric luminosities, X-ray to bolometric luminosity ratios, effective temperatures, rotation periods, and Rossby numbers of M 35 cluster members stars not identified as binaries.
All Figures
 |
Fig. 1 Combined EPIC MOS and PN image of the M 35 open cluster in the 0.5 to 4.5 keV X-ray band. |
| In the text | |
 |
Fig. 2 Cumulative number of correlations between X-ray sources and M 35 stars with known rotation periods. The dashed and dotted curves correspond to the best fitting expressions for the real and spurious correlations. The continuous curve yields the sum of these terms. |
| In the text | |
 |
Fig. 3 Colour magnitude diagram of M 35 stars with known rotation periods that were located in the field of view of the EPIC camera during the XMM-Newton observation of September 2008. Filled circles identify the stars that were detected in X-rays. Stars identified as binaries have been excluded. |
| In the text | |
 |
Fig. 4 Histograms showing bolometric luminosity (left), effective temperature (middle), and rotation period (right) of the parent sample and of the X-ray sample (bold line) of M 35 stars. |
| In the text | |
 |
Fig. 5 X-ray luminosity range of M 35 sample stars (crosses) with masses between 0.8 M⊙ and 1.2 M⊙ compared with median luminosities of stars with similar masses in the α Per, Pleiades, M 34, and the Hyades. The vertical error bars indicate the 25% and 75% quartiles of the distributions (Micela 2002). The various lines represent X-ray luminosity evolution models (see Sect. 5) of solar mass stars with initial rotation periods on the ZAMS ranging from 0.2 to 3.4 days. |
| In the text | |
 |
Fig. 6 Rotation periods vs. (B − V) colour indices of the M 35 sample stars. The solid line represents the I sequence defined by Barnes (2007). The dashed line represents the C sequence determined by M09. M 35 stars of the parent sample represented as blue circles belong to the I sequence. M 35 parent stars represented as red squares belong to the C sequence. Grey triangles represent M 35 gap stars. Filled symbols represent stars detected as X-ray emitters. |
| In the text | |
 |
Fig. 7 Right: X-ray to bolometric luminosity ratios of M 35 sample stars vs. Rossby numbers. Left: X-ray luminosities of M 35 sample stars vs. rotation periods. The thin black lines in both graphs represent models of X-ray activity evolution of 0.8 M⊙ stars with initial rotation periods on the ZAMS ranging from 0.12 to 3.4 days (see Sect. 5). |
| In the text | |
 |
Fig. 8 Histograms of the Rossby number (left), effective temperature (middle) and rotation period (right) of the M 35 parent sample. The red continuous line represents stars belonging to the C sequence. The black dotted line represents gap stars. The blue dashed line represents stars belonging to the I sequence. |
| In the text | |
 |
Fig. 9 Cumulative histograms averaged over 10 000 simulations of X-ray luminosity distributions derived using the CgI model (continuous line) and the steep transition model (dashed line). The distributions of stellar X-ray luminosities around their average values are assumed to be Gaussian with a relative standard deviation of 0.5 (lefthand graph). Relative standard deviations of 1.3 for the C-sequence and the gap stars and of 4.0 for the I sequence are assumed in the righthand graph. The error bars correspond to a ±2σ accuracy. The bold line represents the cumulative histogram of measured X-ray luminosities in M 35. |
| In the text | |
 |
Fig. 10 Relationships between the convective turnover time and the rotation period Psat at which a transition occurs between the saturated and non-saturated regimes of X-ray emission. The convective turnover time is expressed in the scale of Wright et al. (2011). Relationships are shown for stars with initial periods of rotation on the ZAMS ranging from 0.12 to 3.4 days. These relations have been derived assuming a correlation between X-ray emission regimes and rotation sequences using the I and C sequence parameterisation of Barnes (2010). They are compared with the linear relation (continuous thick line) that assumes a transition between X-ray emission regime at a critical Rossby number Rosat = 0.30 (G12). The linear relation corresponding to a continuous transition from saturated to non-saturated regime X-ray emission at Rosat = 0.13 is shown as a thick dashed line. |
| In the text | |
 |
Fig. 11 Simulations (thin lines) of the X-ray luminosity vs. rotation period (left) and of the X-ray to bolometric luminosity ratio vs. Rossby number (right) for stars with masses between 0.4 and 1.2 M⊙ having an initial period of rotation of 1.1 days on the ZAMS. Red squares, blue circles, and grey triangles represent measurements of M 34 stars (see Gondoin 2012) located respectively on the C sequence, on the I sequence, and in the gap between these two sequences. |
| In the text | |
 |
Fig. 12 Simulated evolution of the X-ray luminosity of main-sequence stars with masses between 0.4 and 1.2 M⊙ that have an initial period of rotation of 1.1 days on the ZAMS. |
| In the text | |
 |
Fig. 13 Left: age tsat on the main sequence at which stars change from a saturated to a non-saturated regime of X-ray emission as a function of convective turnover time. Right: time delay tsat − tgap between the epoch of X-ray emission regime transition and the epoch of maximum rotational deceleration. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


