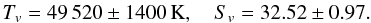| Issue |
A&A
Volume 555, July 2013
|
|
|---|---|---|
| Article Number | A119 | |
| Number of page(s) | 11 | |
| Section | Interstellar and circumstellar matter | |
| DOI | https://doi.org/10.1051/0004-6361/201321807 | |
| Published online | 11 July 2013 | |
Seed particle formation for silicate dust condensation by SiO nucleation⋆
1
Universität Heidelberg, Zentrum für Astronomie, Institut für Theoretische
Astrophysik,
Albert-Ueberle-Str. 2,
69120
Heidelberg,
Germany
e-mail:
gail@uni-heidelberg.de
2
Universität Heidelberg, Kirchhoff-Institut für Physik,
Im Neuenheimer Feld
227, 69120
Heidelberg,
Germany
Received:
30
April
2013
Accepted:
16
May
2013
Context. Dust formation in stellar outflows is initiated by the formation of some seed particles that form the growth centres for macroscopic dust grains. The nature of the seed particles for silicate dust in stellar outflows with an oxygen-rich element mixture is still an open question. Clustering of the abundant SiO molecules has been discussed several times as a possible mechanism and investigated both theoretically and by laboratory experiments. The initial results seemed to indicate, however, that condensation temperatures obtained by model calculations based on this mechanism are significant lower than what is really observed, which renders SiO nucleation unlikely.
Aims. This negative result strongly rests on experimental data on the vapour pressure of SiO. The case for SiO nucleation may be not as bad as it previously seemed and needs to be discussed again because new determinations of the vapour pressure of SiO molecules over solid SiO have shown the older data on SiO vapour pressure to be seriously in error. Here we aim to check again the possibility that SiO nucleation triggers the cosmic silicate dust formation in light of improved new data.
Methods. First we present results of our measurements of vapour pressure of solid SiO. Second, we use the improved vapour pressure data to recalibrate existing experimental data on SiO nucleation from the literature. Third, we use the recalibrated data on SiO nucleation in a simple model program for dust-driven winds to determine the condensation temperature of silicate in stellar outflows from AGB stars.
Results. Our measurements extend the temperature range of measurements for the vapour pressure to lower temperatures and pressures than ever before. This improves the reliability of the required extrapolation from the temperature range where laboratory data can be obtained to the temperature range where circumstellar dust condensation is observed. We determine an analytical fit for the nucleation rate of SiO from recalibrated literature data and show that the onset of nucleation under circumstellar conditions commences at a higher temperature than was previously found. This brings calculated condensation temperatures of silicate dust much closer to the observed condensation temperatures derived from analysis of infrared spectra from dust-enshrouded M stars. Calculated condensation temperatures are still by about 100 K lower than observed ones, but this may be due to the greenhouse effect of silicate dust temperatures, which is not considered in our model calculation.
Conclusions. The assumption that the onset of dust formation in late-type stars with oxygen-rich element mixtures is triggered by the cluster formation of SiO is compatible with dust condensation temperatures derived from infrared observations.
Key words: stars: AGB and post-AGB / stars: winds, outflows / circumstellar matter / astrochemistry / methods: laboratory
Appendix A is available in electronic form at http://www.aanda.org
© ESO, 2013
1. Introduction
Outflow of matter in the stellar winds of highly evolved stars is observed to be accompanied by copious dust formation. As long as the element mixture in the outflow remains oxygen-rich, the dominating dust components are magnesium-iron-silicates (see Molster et al. 2010,for a review of observations). Since the outflowing gas from the star is free of condensation seeds, the first step in the sequence of events ultimately ending with the growth of silicate dust grains in the cooling outflow has to be the formation of seed particles. Because SiO is one of the most abundant of all the gas-phase species of refractory elements that could be involved in the process, it has been discussed several times whether it is cluster formation by this species that is at the basis of all the processes (Donn et al. 1981; Nuth & Donn 1982, 1983; Gail & Sedlmayr 1986, 1998a,b, Ali & Castleman 2005; Nuth & Ferguson 2006; Reber et al. 2006; Paquette et al. 2011; Goumans & Bromley 2012) and that this ultimately leads to the condensation of silicate dust particles.
The reason that formation of large complexes of SiO molecules or of solid SiO is thought to be an important intermediate step in the formation of silicate dust is as follows: there are no molecular species with a composition that corresponds to the chemical formula of silicate compounds as free gas-phase species (at least not in detectable amounts). It is necessary, therefore, that the initial stages of the condensation of silicates involve some different kind of material. It has been thought since the early 1980s that condensation of SiO is the most obvious initial step in silicate formation (e.g. Nuth & Donn 1982; Gail & Sedlmayr 1986) because of the high abundance of SiO molecules in the gas phase in oxygen-rich environments and, in particular, because a rather stable condensed phase exists with chemical composition SiO. It is assumed that initially silicon monoxide particles form which then serve as seed particles for growth of silicates. There is even the possibility that in a number of cases the silicon-monoxide seed particles finally grow to a dust species of their own (Wetzel et al. 2013).
Some dedicated laboratory experiments have been performed to study the nucleation and condensation of SiO (Nuth & Donn 1982). It turned out that the results suggest an onset of condensation at much too low a temperature to be compatible with observed condensation temperatures in circumstellar dust shells. Theoretical calculations (Gail & Sedlmayr 1986) based on the results of Nuth & Donn (1982) show that nucleation of SiO should not commence before temperature has dropped below ≈600 K, while observed condensation temperatures in circumstellar dust shells are typically of the order of 900 K or sometimes even higher. Alternatives to seed formation by SiO are nucleation of oxides of, e.g., Al or Ti (Gail & Sedlmayr 1998a,b; Jeong et al. 1998). Such mechanisms, however, raise serious problems. Because of the low elemental abundances of Al or Ti, seed particle formation at mass-loss rates as low as 10-7 M⊙ a-1 would occur at a prohibitively low rate, while it is observed that even at such low mass-loss rates at least some dust can be formed. The proposed alternatives to SiO nucleation were therefore not successful.
It therefore seems worthwhile to investigate the case of SiO nucleation again and to look for possibilities for circumventing the difficulties with this mechanism that in the past led to a rejection of the SiO-nucleation hypothesis. Nuth & Ferguson (2006) and Ferguson & Nuth (2008) addressed the problem of the vapour pressure of SiO and found this to be considerably lower than previous measurements (Schick 1960) had suggested. This would allow condensation of SiO to occur at higher temperatures than previously thought. They argued on this basis (Nuth & Ferguson 2006) that SiO could be the first species to nucleate in the outflow from a star with oxygen-rich element mixture if the effects of non-TE level population of SiO molecules are also accounted for (Nuth & Donn 1981). But even then condensation temperatures do not fit observations very well.
We also performed a new determination of the vapour pressure of SiO (Wetzel et al. 2012) and used the result to re-evaluate the old experimental results of Nuth & Donn (1982) on SiO nucleation using our new data for SiO vapour pressure. We will show that the experimentally determined nucleation rates after correcting for the former strongly overestimated vapour pressure of SiO are significantly higher than those derived by using the old vapour-pressure data of Schick (1960). Extrapolated to circumstellar conditions, these corrected experimental data predict much higher condensation temperatures than previously.
Additionally we argue that the previous model calculations of circumstellar dust condensation have not properly taken into account that the “dust condensation temperature” derived from analysing infrared (IR) spectra is the temperature of lattice vibrations of the dust particles in the region of onset of massive dust growth in the shell, while the nucleation process is governed by the gas temperature. We show that both temperatures may be significantly different. Both effects cooperate to remove the hitherto suspected strong discrepancy between calculated nucleation temperatures and observed dust temperatures. This again makes clustering of SiO the hottest candidate for the production of seed particles for silicate dust condensation.
Another way to tackle the problem is to study the chemistry of the gas phase and the kinetics of cluster formation on the basis of reaction kinetics (cf. Reber et al. 2006; Goumans & Bromley 2012). This is not considered here but will be the subject of a forthcoming paper.
2. Vapour pressure of SiO
Experimentally obtained vapour-pressure data for SiO are discussed in this section, including a brief description of our experimental setup that is based on the Knudsen method (Knudsen 1909). Fundamentally, the mass-loss rate and vapour pressure are measured by a quartz crystal micro balance and the Knudsen cell is heated by electron bombardment with an electron beam evaporator. All experimental results, as well as detailed information regarding the experimental conditions and the samples, are defined in Wetzel et al. (2012).
2.1. Knudsen method
The vapour pressure can be determined by measuring the mass-loss rate of a Knudsen cell,
(dm/dt)K, at a
well-defined temperature T. The Knudsen cell is a small container with a
small orifice, AO, that is partially filled with an
experimental sample. The vapour pressure inside the cell and the mass-loss rate are
related by 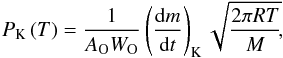 (1)where
WO is the Clausing factor of the orifice, R
the ideal gas constant and M the molecular mass (Margrave 1967). The Clausing factor is the probability that a particle
passes the orifice and can be calculated for cylindrical tubes from its geometry (Clausing 1932). The equilibrium vapour pressure can be
expressed by the Whitman- Motzfeld equation
(1)where
WO is the Clausing factor of the orifice, R
the ideal gas constant and M the molecular mass (Margrave 1967). The Clausing factor is the probability that a particle
passes the orifice and can be calculated for cylindrical tubes from its geometry (Clausing 1932). The equilibrium vapour pressure can be
expressed by the Whitman- Motzfeld equation ![\begin{equation} \label{eq:whitmann} P\left(T\right) = \left[1 + \frac{A_\mathrm{O} W_\mathrm{O}}{A} \left( \frac{1}{\alpha\left(T\right)} + \frac{1}{W_\mathrm{Cell}} -2 \right)\right] P_\mathrm{K}, \end{equation}](/articles/aa/full_html/2013/07/aa21807-13/aa21807-13-eq10.png) (2)where
(2)where
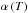 is the vaporization coefficient, A the cross-sectional area of the cell,
and WCell the Clausing factor of the cell (Whitman 1952; Motzfeldt
1955). Both unknown quantities in Eq. (2), which are the equilibrium vapour pressure and the vaporization coefficient,
can be derived from two measurements with different orifice sizes.
is the vaporization coefficient, A the cross-sectional area of the cell,
and WCell the Clausing factor of the cell (Whitman 1952; Motzfeldt
1955). Both unknown quantities in Eq. (2), which are the equilibrium vapour pressure and the vaporization coefficient,
can be derived from two measurements with different orifice sizes.
2.2. Experimental setup
Here we briefly describe our experimental setup (for more details see Wetzel et al. 2012). A basic schematic drawing of the experimental setup is shown in Fig. 1. The quartz crystal micro-balance that is placed at a distance d from the Knudsen cell measures the mass changes due to condensing particles during the molecular effusion from the Knudsen cell. The angular dependence of the beam profile can be calculated from the equations given in Clausing (1930) and Dayton (1956) that directly relate the signal detected from the quartz crystal micro-balance to the mass loss of the Knudsen cell. The temperature is determined by a temperature calibration that gives a relation between the temperature in the cell and the heating power controlled during the measurements. The reliability and performance quality of this experimental approach has been verified by a precise reproduction of the vapour pressure of copper (Wetzel et al. 2012).
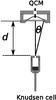 |
Fig. 1 Schematic drawing of the experimental setup for the Knudsen method. The quartz crystal microbalance (QCM) is placed at a distance d from the Knudsen cell and measures the mass rate of the condensing particles during effusion from the cell. |
 |
Fig. 2 Vaporization coefficient of solid SiO derived from the experimental measurements of the mass-loss rate obtained for two orifice diameters of the Knudsen cell. The full line is the approximation according to Eq. (3). |
2.3. Experimental results
Two orifices with different diameter (0.50 mm and 0.79 mm) of the Knudsen cell were
employed in order to determine the vapour pressure, as well as the vaporization
coefficient of SiO. Figure 2 shows the vaporization
coefficient of SiO derived from the experimental outcomes as a function of temperature.
The results can be approximated by an Arrhenius law, 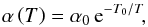 (3)with
(3)with
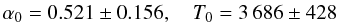 for the
temperature range between 1275 K and 1525 K. This shows that the kinetics of vaporization
involves a modest activation energy barrier.
for the
temperature range between 1275 K and 1525 K. This shows that the kinetics of vaporization
involves a modest activation energy barrier.
 |
Fig. 3 Equilibrium vapour pressure of solid SiO derived from the experimental measurements of the mass-loss rate obtained for two orifice diameters of the Knudsen cell (filled circles). The full line is the analytic approximation according to Eq. (4). |
The equilibrium vapour pressure of SiO over solid silicon monoxide was calculated by
using the vaporization coefficient described by Eq. (3). The equilibrium vapour pressure is plotted in Fig. 3 as a function of inverse temperature. From a best fit
to the experimental data points, the vapour pressure of SiO molecule over solid silicon
monoxide in units of dyn cm-2 is approximated by 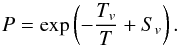 (4)with
(4)with
3. Stability limits
Dust is formed in space in a variety of environments either in a continuous fashion as in stellar winds or brown dwarf atmospheres or as short events in stellar ejecta following explosive events, such as in supernovae or in novae. The elemental composition of dust-forming matter may also be very diverse in different kinds of objects. Here we consider dust formation from oxygen-rich material with a standard cosmic element mixture (cf., e.g., Lodders et al. 2009). The most abundant dust materials that are expected to form from the most abundant refractory elements in such an element mixture, i.e. from Si, Mg, and Fe, are magnesium-rich silicates and metallic iron (cf., e.g., Gail 2010). From the somewhat less abundant, but even more refractory elements Al and Ca, the minerals corundum (or hibonite), spinel, gehlenite, and diopside are formed. The upper stability limits or the field of stability in the p-T-plane of these compounds are shown in Fig. 4. They are calculated for chemical equilibrium states between the gas phase and condensed phases.
 |
Fig. 4 Stability limit of solid SiO for the new data from our laboratory measurements for data from Ferguson & Nuth (2008) and for the old data of Schick (1960). Also shown are stability limits for the most abundant refractory compounds formed from an oxygen-rich element mixture with cosmic standard element abundances. The dashed line corresponds to the p-T-trajectory of a dust-driven stellar wind. |
As a new feature, we show the upper stability limit of SiO according to our new
measurements of the vapour pressure of SiO molecules over solid SiO. This curve in the
p-T-plane is constructed from the relation
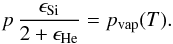 (5)Here p
is the gas pressure, pvap the vapour pressure of SiO molecules
over solid SiO according to Eq. (4), and
ϵSi and ϵHe are the element
abundances of Si and He with respect to H. The left-hand side corresponds to the pressure of
SiO molecules in the gas phase in an element mixture with cosmic composition. Here we made
use of the fact that H is completely associated to H2 and almost all Si is bound
in SiO 1 in the pressure and temperature regime of
interest.
(5)Here p
is the gas pressure, pvap the vapour pressure of SiO molecules
over solid SiO according to Eq. (4), and
ϵSi and ϵHe are the element
abundances of Si and He with respect to H. The left-hand side corresponds to the pressure of
SiO molecules in the gas phase in an element mixture with cosmic composition. Here we made
use of the fact that H is completely associated to H2 and almost all Si is bound
in SiO 1 in the pressure and temperature regime of
interest.
For comparison we also show in Fig. 4 the stability
limits (i) for solid SiO resulting from the vapour pressure data reported by Ferguson & Nuth (2008), i.e. calculated from Eq.
(4), but with coefficients
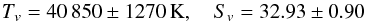 (6)(in units
dyn cm-2) and (ii) from the old vapour pressure data for solid SiO of Schick (1960)
(6)(in units
dyn cm-2) and (ii) from the old vapour pressure data for solid SiO of Schick (1960)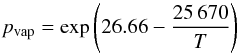 (7)(in
units dyn cm-2). From Fig. 4 it is
immediately obvious that the condensation temperatures following from the data of Schick (1960) are unrealistically low.
(7)(in
units dyn cm-2). From Fig. 4 it is
immediately obvious that the condensation temperatures following from the data of Schick (1960) are unrealistically low.
For our new data, as well as for the recent data of Ferguson & Nuth (2008), the stability limit of solid SiO is still at a lower temperature than the upper stability limits of the more refractory silicates and the Ca-Al-compounds, but with the strongly reduced vapour pressure determined by our measurements and those of Ferguson & Nuth (2008), it is not as unfavourably low for condensation under circumstellar conditions as was suggested by the old data of Schick (1960). The strong upward shift of the stability limit according to the new data again makes SiO a candidate for the seed particle formation in M stars. First steps to investigate this have already performed by Nuth & Ferguson (2006) and Paquette & Nuth (2011). Here we follow a different approach.
4. Application to SiO nucleation
The details of the reaction mechanisms standing behind the nucleation of SiO are not yet known, but some experimental results have been obtained by Nuth & Donn (1982) that give insight into the conditions under which SiO nucleation occurs. It seems worthwhile to look at how these results change if corrected for the much reduced vapour pressure of SiO.
4.1. Re-evaluation of the Nuth & Donn data
In their laboratory experiment Nuth & Donn (1982) evaporated solid SiO from a crucible into a hydrogen atmosphere in order to prepare a gas mixture that only contains SiO and H2 molecules. In this case, any observed condensation necessarily starts with cluster formation from SiO molecules2.
They determined the temperature and the partial pressure of SiO at which an onset of smoke formation can be observed. This was quantified by taking the instant at which the extinction of a light beam with wavelength λ = 200 nm traversing the condensation zone reached a level of 1%, as the instant where avalanche nucleation commences. Unfortunately the rate of nucleation J at the onset of detectable smoke formation could only be estimated crudely. It was argued that the value of J at this instant is between 108 and 1010 particles cm-3 s-1.
The results were presented as a set of values of temperature T and
supersaturation ratio 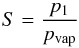 (8)with
p1 the partial pressure of SiO in the condensation zone, and
pvap the vapour pressure of SiO molecules over solid SiO at
temperature T. The vapour pressure was calculated by Nuth & Donn (1982) from the formula given by
Schick (1960), Eq. (7). The partial pressure p1 or particle
densities
n1 = p1/kT
of SiO molecules in the gas phase in the condensation zone was calculated (i) from the
vapour pressure of SiO in the crucible at the temperature of the crucible and (ii) from
the dilution as the vapour diffused away from the crucible to the condensation zone. The
pressure in the condensation zone was estimated to be one tenth of the vapour pressure at
the crucible.
(8)with
p1 the partial pressure of SiO in the condensation zone, and
pvap the vapour pressure of SiO molecules over solid SiO at
temperature T. The vapour pressure was calculated by Nuth & Donn (1982) from the formula given by
Schick (1960), Eq. (7). The partial pressure p1 or particle
densities
n1 = p1/kT
of SiO molecules in the gas phase in the condensation zone was calculated (i) from the
vapour pressure of SiO in the crucible at the temperature of the crucible and (ii) from
the dilution as the vapour diffused away from the crucible to the condensation zone. The
pressure in the condensation zone was estimated to be one tenth of the vapour pressure at
the crucible.
 |
Fig. 5 Supersaturation at onset of avalanche nucleation from the experiment of Nuth & Donn (1982), re-evaluated with the new vapour pressure data for SiO. Black dots: data for the nucleation experiments conducted at pH2 = 50 Torr. Crosses: data for experiments conducted at pH2 = 35 Torr. Open sqares: supersaturation based on old vapour pressure data, as given by Nuth & Donn (1982), for the same set of experiments. |
For a new evaluation of the experimental results of Nuth & Donn (1982), we read values for S and T from their Fig. 3. We can convert these data for S at given T to a new set of data based on the improved vapour pressure formula for SiO in the following way: first we calculate a vapour pressure pvap from the temperature T by means of Eq. (7) and the corresponding pressure p1 from the value of S. Considering that this is assumed to equal one tenth of pvap calculated with the crucible temperature Tc we reconstruct from Eq. (7) the temperature Tc. Then we calculate with this temperature a new value for p1 at the crucible by means of Eq. (4) and take one tenth of this as the corrected value for p1 in the condensation zone. From the same equation we calculate a new value of pvap(T) in the condensation zone, and from this and the corrected value of p1 a new value for S. This defines a new set of values for S at given T that correspond to the fixed value of Jav = 109 ± 1 particles cm-3 s-1 in the experiments of Nuth & Donn (1982), but now based on the improved vapour pressure of solid SiO.
The results are shown in Fig. 5 for the two series of measurements with a total pressure of pH2 = 35 Torr and pH2 = 50 Torr. This looks very much the same as the corresponding Fig. 3 of Nuth & Donn (1982), except that the new values for S are more than a factor of a thousand higher than those calculated with the old vapour pressure formula (7).
4.2. Fit for the nucleation rate
Next we follow the same procedure as Nuth & Donn
(1982) and check that the results can be fitted with the formula resulting from
the Zeldovich theory of homogeneous nucleation (Zeldovich
1943) that gives the following result for the nucleation rate 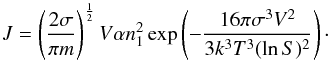 (9)Here σ
is the surface energy of the condensed phase, V the volume of the SiO
molecule in the solid, A and m the atomic weight and
mass of the SiO molecule, α the sticking coefficient at the size of the
critical cluster, and
n1 = p1/kT
the particle density of SiO molecules in the gas phase.
(9)Here σ
is the surface energy of the condensed phase, V the volume of the SiO
molecule in the solid, A and m the atomic weight and
mass of the SiO molecule, α the sticking coefficient at the size of the
critical cluster, and
n1 = p1/kT
the particle density of SiO molecules in the gas phase.
 |
Fig. 6 Plot of |
Equation (9) predicts that for a constant
nucleation rate Jav as in the measurements of Nuth & Donn (1982), a linear relationship
should exist between lnn1 and
T3lnS of the form 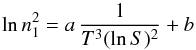 (10)with constants
a and b given by
(10)with constants
a and b given by  This
relationship rests on assumptions that may hold for macroscopic particles but are hard to
justify for molecular-sized particles. Nevertheless, one can speculate that the dependency
of the classical nucleation rate on the basic macroscopic parameters T,
S, and n1 is essentially correct, except
that the constants in this equation cannot be derived meaningfully within the framework of
a macroscopic theory. This means that we assume that the nucleation rate
J is given by
This
relationship rests on assumptions that may hold for macroscopic particles but are hard to
justify for molecular-sized particles. Nevertheless, one can speculate that the dependency
of the classical nucleation rate on the basic macroscopic parameters T,
S, and n1 is essentially correct, except
that the constants in this equation cannot be derived meaningfully within the framework of
a macroscopic theory. This means that we assume that the nucleation rate
J is given by 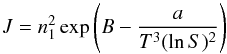 (13)with
constants a and
(13)with
constants a and 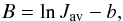 (14)to be empirically
determined.
(14)to be empirically
determined.
One can check this hypothesis by fitting the experimental results of Nuth & Donn (1982) for
n1 and S for given T by
the linear relation (10). The result is
shown in Fig. 6 where
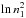 is plotted against
[T3(lnS)2] -1 for
the experimental data corrected for the new values for the vapour pressure. Figure 6 is completely analogous to Fig. 4 of Nuth & Donn (1982) except that the data are
different. The scatter of the data is rather large and the range of values regrettably
rather narrow, but a linear dependency of
is plotted against
[T3(lnS)2] -1 for
the experimental data corrected for the new values for the vapour pressure. Figure 6 is completely analogous to Fig. 4 of Nuth & Donn (1982) except that the data are
different. The scatter of the data is rather large and the range of values regrettably
rather narrow, but a linear dependency of 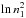 on
[T3(lnS)2] -1 seems
to exist. The least square fitting gave the following results for the coefficients of the
linear relation for the corrected data
on
[T3(lnS)2] -1 seems
to exist. The least square fitting gave the following results for the coefficients of the
linear relation for the corrected data
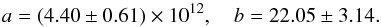 (15)From this, we obtain
the following analytical approximation to the experimental data on the nucleation rate by
SiO
(15)From this, we obtain
the following analytical approximation to the experimental data on the nucleation rate by
SiO 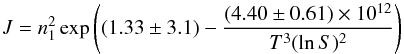 (16)in
units cm-3 s-1. This may be used as a purely empirical fit formula
to nucleation rates, the analytical form of which is motivated by theoretical
considerations and the constants of which are determined from the results of laboratory
experiment.
(16)in
units cm-3 s-1. This may be used as a purely empirical fit formula
to nucleation rates, the analytical form of which is motivated by theoretical
considerations and the constants of which are determined from the results of laboratory
experiment.
 |
Fig. 7 Lines of constant nucleation rate per H-nucleus according to the numerical fit to the experimental data. The red lines correspond to values of J/NH from 10-34 s-1 (top) to 10-10 (bottom) in steps of 102. The shaded area indicates the range of pressures typically encountered at the inner edge of dust shells. The thick dashed (blue) line corresponds to the critical nucleation rate of J/NH = 10-20 particles cm-3 s-1 where massive dust nucleation commences under circumstellar conditions. The uppermost (green) line corresponds to the stability limit if solid SiO is in equilibrium with a gas with standard cosmic elemental abundances. The line denoted as “wind” corresponds to the p-T-trajectory of a wind model. The circles correspond to the data points of the laboratory experiments, if the pressure of SiO in the condensation zone is converted into an equivalent pressure of a gas with cosmic elemental composition. |
4.3. Circumstellar SiO-nucleation
We assume that the nucleation rate calculated from Eq. (16) remains applicable over a wider range of condensation conditions than that for which the experiments were performed because the coefficients in this expression are essentially determined by molecular and solid phase-properties and not so much by the pressure-temperature conditions of the laboratory experiments. We use this to calculate nucleation rates based on clustering of SiO molecules for astrophysical problems.
Figure 7 shows lines of constant nucleation rate in the p-T-plane per H-atom, J′ = J/NH, calculated in this way for an oxygen-rich element mixture. Here NH is the particle density of H nuclei if all hydrogen atoms are present as free atoms. The particle density of SiO molecules is assumed to be given by n1 = ϵSiNH, and the supersaturation ratio S is calculated by using our fit-formula, Eq. (4), for the vapour pressure of SiO.
If we have a typical number of dust grains of the order of 3 × 10-13 per hydrogen nucleus and assume that these are formed in about one year, then the formation rate would be about 10-20 seed particles per H nucleus per second. This is the black line in Fig. 7, which marks the critical pressure-temperature combination where massive dust particle formation occurs. For typical pressures between 10-10 bar at mass-loss rates of 10-6 M⊙ a-1 and 10-8 bar at mass-loss rates of 10-4 M⊙ a-1, the critical rate corresponds to temperatures roughly between 720 K and 850 K. This range of gas temperatures for the onset of massive dust formation is predicted by the empirical nucleation rate (16).
For comparison, Fig. 7 also shows the
p-T combinations that correspond to the data points of
Nuth & Donn (1982). Their pressure of SiO
in the condensation zone is converted to the total pressure in an element mixture with
cosmic abundances via 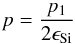 (17)with
Si abundance ϵSi and neglecting He. This gives an impression
of the extrapolation that is required if the results are applied to circumstellar
nucleation.
(17)with
Si abundance ϵSi and neglecting He. This gives an impression
of the extrapolation that is required if the results are applied to circumstellar
nucleation.
5. Models for dust-driven winds
As a simple first application of the new nucleation rate, some models for dust formation in outflows from M stars are calculated. The aim of this is to check which condensation temperatures of dust result if the nucleation rate for SiO is applied to circumstellar dust condensation. It is assumed that the condensation of silicate dust is triggered by the nucleation of SiO clusters from the gas phase and that these seed particles later grow to magnesium-iron silicate dust grains by collecting more SiO molecules and Mg and Fe atoms from the gas phase, while reaction with H2O provides the required additional oxygen atoms for building the SiO4 tetrahedrons of the silicate compounds.
In a stellar outflow more than one dust component may be formed in oxygen-rich matter (e.g. Gail & Sedlmayr 1998a). If some components are already formed at higher temperatures than the silicates (corundum for instance) and if their opacity suffices to drive the outflow velocities to supersonic values, then the gas density has strongly decreased by expansion if the temperature drops below the stability limits of silicates. In that case silicate dust probably precipitates on top of the seed particles formed at higher temperatures, so separate nucleation by SiO is probably not important. If, however, the subsonic-supersonic transition in the flow is due to silicate dust condensation, then the whole process is governed by the nucleation of silicates. Then we have to deal with dust-driven winds. Here we perform some sample calculations for dust-driven, spherically symmetric and stationary wind models of giant stars. Other possible cases where seed particles with different origins are present will not be considered.
5.1. Model assumptions
The wind models including dust formation and growth are calculated by the methods outlined in Gail et al. (1984) and Gail & Sedlmayr (1985, 1987). In those papers, the condensation of graphite dust in C stars was considered, but the modifications required for calculating silicate dust condensation for M stars are simple and straightforward. We do not repeat, therefore, a description of the details of the method but only give remarks on a few points that change in the case of M stars.
Since it is assumed that the condensation of silicate dust is triggered by nucleation of SiO clusters from the gas phase, the nucleation rate is assumed to be given by Eq. (16). The final growth of macroscopic dust grains is assumed to result in the formation of amorphous silicates with an iron-rich composition. That such material is formed in most circumstellar dust shells around M stars is known from analysis of their IR spectra (see Molster et al. 2010; Habing 1996, for reviews). Additionally it has been known for a few years from laboratory analysis of the composition of silicate grains from AGB stars (Vollmer et al. 2009; Nguyen et al. 2010; Bose et al. 2010) that amorphous silicate dust grains from AGB stars have widely varying iron content, where iron-poor grains are rare. This is an important point because the extinction properties of the silicates in the near IR, hence, the possibility of driving a wind by radiation pressure on silicate dust strongly depends on the iron content of the silicates. It has not always been adequately considered in the literature that real amorphous silicate grains are not iron-poor, except for the crystalline component.
A compilation of the equations required for calculating the silicate dust and other dust components in M stars is given in Ferrarotti & Gail (2006). Here for simplicity we consider only a single amorphous silicate dust component. Furthermore we assume that this has the composition MgFeSiO4; i.e., we do not include a calculation of the mixing ratio between the two end members of the solid solution in the present model calculation. A composition like the assumed one will be the outcome of non-equilibrium condensation in a rapidly cooling environment because of nearly equal abundances of Si, Mg, and Fe in the standard cosmic element mixture (see, e.g., Lodders et al. 2009). Such a composition is also compatible with the results of the laboratory analysis of dust grains from AGB stars, though the observed scatter in composition is large (Bose et al. 2010).
The basic net chemical reaction for the silicate condensation is assumed to be
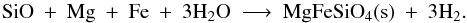 For
calculating the growth rate of dust grains (see Ferrarotti
& Gail 2006), one needs the abundances of the gas phase species in this
reaction equation. The composition of the gas phase is treated in a simple way. In
oxygen-rich matter the Si in the gas phase almost exlusively forms SiO, all O not bound in
SiO and CO forms H2O, while Mg and Fe are mainly present as free atoms. We
simpy describe this as the gas phase composition and do not explicitly calculate its
chemical composition.
For
calculating the growth rate of dust grains (see Ferrarotti
& Gail 2006), one needs the abundances of the gas phase species in this
reaction equation. The composition of the gas phase is treated in a simple way. In
oxygen-rich matter the Si in the gas phase almost exlusively forms SiO, all O not bound in
SiO and CO forms H2O, while Mg and Fe are mainly present as free atoms. We
simpy describe this as the gas phase composition and do not explicitly calculate its
chemical composition.
The dust opacity is calculated with the complex index of refraction of the dirty silicate model of Ossenkopf et al. (1992,their set 1), which is well suited to modelling the IR emission from the dust shells of M stars. The absorption and scattering efficiencies Cλ are calculated in the small-particle limit for spherical grains. From analysing the silicate dust grains from AGB stars identified im primitive meteorites, one knows that the large majority of the grains have diameters significantly less than 1 μm (Vollmer et al. 2009; Nguyen et al. 2010; Bose et al. 2010), which justifies the use of this approximation from the red to the far IR spectral region, though at the shortward border of the wavelength region where absorption and scattering of stellar photons transmit the momentum to the dust grains (mainly the range 0.5 ≲ λ ≲ 3 μm), one comes to the limit of validity of this approximation. Investigation of silicate grains from AGB stars (Vollmer et al. 2009; Nguyen et al. 2010) show the grains to be somewhat elongated, though deviations from sphericity seem to be small for most particles. Therefore we assume for simplicity spherical grains for calculating the dust opacities. (In any case, using a distribution of shapes, like CDE, does not significantly change the model.)
For calculating the radiation pressure on the dusty gas one needs the flux average
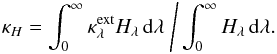 (18)of the
mass-extinction coefficient
(18)of the
mass-extinction coefficient 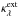 for the
dust-gas mixture. Here 4πHν
is the spectral energy flux density of the radiation field. From radiative transfer
calculations of circumstellar dust shells we found that this average can be well
approximated by (for details see Appendix A)
for the
dust-gas mixture. Here 4πHν
is the spectral energy flux density of the radiation field. From radiative transfer
calculations of circumstellar dust shells we found that this average can be well
approximated by (for details see Appendix A)
![\begin{equation} \kappa_H=\kappa_{\rm P}^{\rm ext}(T_*)\,{\rm e}^{-\tau_*}+\left[\kappa_{\rm P}^{\rm ext}(T_{\rm ph})+(1-f)\kappa_{\rm R}^{\rm ext}(T_{\rm d})\right]\left(1-{\rm e}^{-\tau_*}\right) \label{ApproxKapH} \end{equation}](/articles/aa/full_html/2013/07/aa21807-13/aa21807-13-eq104.png) (19)where
(19)where
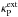 is the
Planck-average,
is the
Planck-average, 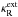 the
Rosseland-average of the extinction coefficient, T∗ the
effective temperature of the star, Tph the dust temperature at
the inner edge of the dust shell, Td the dust temperature in
the shell, and τ∗ is the optical depth calculated from the
inner edge of the dust shell outwards using
the
Rosseland-average of the extinction coefficient, T∗ the
effective temperature of the star, Tph the dust temperature at
the inner edge of the dust shell, Td the dust temperature in
the shell, and τ∗ is the optical depth calculated from the
inner edge of the dust shell outwards using 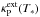 as opacity. The Eddington
factor f can be taken for example from the approxiation of Lucy (1976) (see also Gail & Sedlmayr 1987, for details).
as opacity. The Eddington
factor f can be taken for example from the approxiation of Lucy (1976) (see also Gail & Sedlmayr 1987, for details).
 |
Fig. 8 Some results for a wind model with Ṁ = 5 × 10-6 M⊙ yr-1. a) Variation in the degree of condensation of Si into silicate dust with radial distance from the mass centre. b) Radial variation with distance of outflow velocity v (solid line), sonic velocity cT (dashed line), and escape velocity from star (dotted line). c) Variation in p and T along the wind (solid line) and lines of constant nucleation rate (dashed lines). The crosses denote the pressure and temperature at the inner edge of the dust shell for the models of Table 1. |
5.2. Model calculations
With these assumptions some models are calculated for dust-driven winds of oxygen-rich AGB stars. The assumption of stationarity can hardly be justfied for AGB stars because they are variables. The outerflowing gas is subject to shock waves triggered by the pulsation of the underlying star and the whole structure is far from being stationary. One can only speculate that stationary models describe long-term average properties of such outflows, which is justified, at least in part, by the success of radiative transfer models based on r−n density distributions. These can be used to model IR spectra from dust shells. In any case, the purpose of our present calculation is to see whether the new empirical nucleation rate results in condensation temperatures of silicate dust that mainly agree with what one derives from analysis of IR spectra.
Models are calculated for the higher end (Ṁ ≳ 1 × 10-6 M⊙ yr-1) of the observed range of mass-loss rates for such stars (Ṁ ≳ 1 × 10-8 M⊙ yr-1) because the present model does not consider the drift of dust grains relative to the gas. This is not important for higher mass-loss rates because drift velocities are less than the thermal verlocity of the growth species in this case, such that the collision rate of dust grains with growth species is not significantly increased by drift. For low mass-loss rates, however, particle drift dramatically enhances dust growth and so must be considered.
Table 1 shows the stellar parameters chosen for the calculations and some results. Figure 8 shows some details of the model with a mass-loss rate of Ṁ = 5 × 10-6 M⊙ yr-1. Its general structure is representative of all our models. One feature of interest is the rather strong increase in the degree of condensation (Fig. 8a), which means that dust appears rather suddenly, and the dust shell has a reasonably well-defined inner boundary. The wind trajectory shown in Fig. 8c shows how an outflowing gas parcel first cools and reduces pressure by expansion, then intrudes into the region of the increasing nucleation of seed particles for silicate dust growth, upon which the resulting strong acceleration results in a rapid blow-out of the gas parcel into low-pressure regions where, finally, growth ceases because of strong gas expansion.
Of particular interest in our context are the typical temperatures at the onset of condensation, because this defines the hottest temperatures of dust grains that may contribute to the IR spectrum from the dust shell. We take the position of the sonic point, where the wind velocity v equals the sonic velocity cT (see Fig. 8b) as the position of the inner boundary of the dust shell. The distance of this point is given in Table 1 and also the temperature at this radius. At this point substantial condensation has already occurred in order that radiation pressure on the dust component increases to the level that it locally surmounts the gravitational pull by the star. Additional substantial condensation, however, is requiered to enhance radiation pressure for ultimately lifting the matter out of the deep gravitational potential well of the star (see Fig. 8b). The degree of condensation at the sonic point and the final degree of condensation far in the outflow are shown in Table 1.
The table also shows the pressure and temperature at the inner boundary of the dust shell for the models. This outlines the typical range of “condensation temperatures” where avalanche nucleation and dust growth have just begun. The dust grains at the inner border of the dust shell are the hottest dust grains that exist for the considered dust species because of their proximity to the star. Their temperature may be derived from observations of IR spectra, and this temperature can in turn be compared with the theoretical results following from our approximation for the nucleation rate.
 |
Fig. 9 Temperature at the inner edge of dust shells of AGB stars in the Small and Large Magellanic clouds with estimated errors of the temperature determination (data from Groenewegen et al. 2009). This corresponds to the temperature where massive silicate dust condensation commences in the outflow. The data are plotted against the derived mass-loss rate. Dotted line with open circles denotes the temperature at the sonic point of the models from Table 1. |
6. Comparison with observations
We do not present radiative transfer models for dust shells but use data from the literature for dust temperatures at the inner edges of dust shells. In such models of dust shells, it is usually assumed that (i) the dust is formed at some condensation temperature Tc in the outflow; and (ii) the density distribution of dust outwards from this point is proportional to r-2. The mean intensity, Jν, is then calculated from a solution of the radiative transfer problem with the inner boundary condition that we have a star of given luminosity L∗ and effective temperature T∗. The dust opacity is calculated from optical constants of materials thought to be analogues of circumstellar dust materials. For M-stars different kinds of silicates and sometimes Al-Ca-bearing minerals are considered in the calculations. The run of temperature in the shell and its inner radius are determined self-consistently from radiative equilibrium between emission and absorption by the dust grains and the solution of the radiative transfer problem.
The kind of dust material used for the modelling, the temperature Tc, the corresponding inner radius Rc, and the dust density at Rc are then varied to obtain an optimum fit with observed IR spectra from circumstellar shells. If the outflow velocity is known from, say, the width of CO lines, one can determine a dust mass-loss rate from the dust density and a total mass-loss rate with an assumed gas/dust ratio.
It is generally assumed that the temperature Tc derived this way reflects the dust temperature at the inner edge of the dust shell, where efficient dust formation commences. For this reason, this temperature is called the condensation temperature of the dust. It is to be observed that this temperature corresponds to the lattice temperature in radiative equilibrium of particles, which have grown to such a size that their extinction properties have changed to solid-like behaviour. This does not imply any information on the gas temperature in that region.
From the numerous such studies published in the literature we consider here a set of data for late-type M-stars on the AGB from the Small and Large Magellanic Clouds derived by Groenewegen et al. (2009), because this is a very homogeneous data set both with respect to the acquisition of spectra and the model data derived for all stars with the same method and the same set of opacity data. The condensation temperatures Tc are shown in Fig. 9. Here only data for those objects are used for which the dust temperature at the inner edge could uniquely be determined by the model fit. The figure suggests that there are two different groups of objects with different condensation temperatures. For one group, the typical temperatures are around 880 K ± 100 K. These are the “condensation temperatures” of silicate dust that have to be explained by theoretical calculations of dust formation.
Then there seems to be a second group of objects with condensation temperatures between 1100 K and 1200 K. They could correspond to objects with an observable production of Ca-Al-bearing dust species which are thermally more stable than silicates. We neglect such objects because they may represent physically distinct objects.
Figure 9 shows the temperature at the inner inner edge of dust shells in our theoretical models, based on the approximation for the nucleation rate from Sect. 4. At first glance the theoretical condensation temperatures seem to fall short of what is followed from radiative transfer models for observed dust shells by about 100 to 200 K. This cannot result from the big uncertainties connected with the conversion of the experimental data of Nuth & Donn (1982) into the apprimate formula (16) because the nucleation rate depends very steeply on temperature, as can be seen in Fig. 7. Variations in J even over many decades correspond to relativly small temperature changes. The discepancy is too big to result from such errors.
 |
Fig. 10 Dust temperature and grey temperature in optically thin dust shells for a star radiating like a black body with temperature Teff = 2700 K, calculated for silicate dust with opacities from Ossenkopf et al. (1992). |
A more likely origin for the difference in condensation temperature is the approximation
that the model does not distinguish between the gas temperature that rules nucleation and
dust temperature which rules the emission of IR radiation by dust. Generally, both
temperatures are significantly different, in particular if dust shells, are optically thin
(τR ≲ 1). For optically thin to moderately optically thick
dust shells, the local mean radiation intensity is dominated by the stellar contribution.
The dust temperature in radiative equilibrium is then given by the well known relation
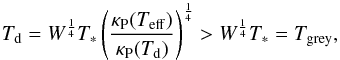 (20)with the geometrical
diluton factor
(20)with the geometrical
diluton factor 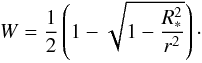 (21)Here
R∗ is the stellar radius, r the radial
distance to the stellar centre, T∗ the effective temperature of
the star, and Tgrey the temperature of a grey absorber. The
variation in the Planck-average
(21)Here
R∗ is the stellar radius, r the radial
distance to the stellar centre, T∗ the effective temperature of
the star, and Tgrey the temperature of a grey absorber. The
variation in the Planck-average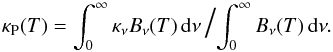 (22)of the dust
absorption coefficient with temperature has a significant influence on the dust temperature.
(22)of the dust
absorption coefficient with temperature has a significant influence on the dust temperature.
Figure 10 shows the dust temperature of silicate dust material in radiative equilibrium at different distances from a central star with effective temperature Teff = 2700 K, determined according to Eq. (20), using optical data from Ossenkopf et al. (1992). Additionally, the temperature of a material with grey absorption is shown, for which the monochromatic absorption is independent of wavelength. For silicates the dust temperature is higher than for a grey body because their Planck-averaged absorption coefficient is higher for the effective temperature of the stellar radiation field than for the much lower dust temperatures. Since the gas temperature tends to be close to the grey temperature except behind shocks (cf. Schirrmacher et al. 2003), this behaviour can easely explain the remaining difference between the condensation temperature in our models and the observed condensation temperatures. As a result, the laboratory determined nucleation rate for SiO (Nuth & Donn 1982), corrected for the the strong reduction of vapour pressure of SiO required by recent measurements (Wetzel et al. 2012; Nuth & Ferguson 2006), seems to be able to explain the dust condensation in circumstellar dust shells of AGB stars.
Unfortunately, we presently cannot definitely fix the difference between gas and dust temperature unless the model calculation exlicitly considers a different gas and dust temperature. These more elaborate model calculations will be published elsewhere.
7. Concluding remarks
We have re-analysed the long-standing problem of nucleation of silicate dust grains in circumstellar dust shells around oxygen-rich evolved stars. Though it has already been proposed at an early stage that this is due to clustering of the abundant SiO molecules (Donn et al. 1981; Nuth & Donn 1982), serious problems remained with this hypothesis. The nucleation process was studied by dedicated laboratory expriments by Nuth & Donn (1982, 1983), but the results, if applied to ciurcumstellar conditions, seemed to predict condensation temperatures that are much too low (Gail & Sedlmayr 1986) compared to the dust temperatures at the inner edge of dust shells derived from IR spectra.
New determinations of the vapour pressure of SiO by Nuth & Ferguson (2006) and Ferguson & Nuth (2008) and that are reported in this paper (see also Wetzel et al. 2012) show that former determinations were grossly in error. Our new measurements yield vapour pressures that are even somewhat lower than obtained by Ferguson & Nuth (2008).
Nuth & Ferguson (2006) have already shown that the case for SiO nucleation may be not as unfavourable as was thought in the past. They use their vapour pressure data to calculate more realistic supersaturation values S and using the approximation given in Nuth & Donn (1982) they determine the nucleation rate J. They showed that condensation temperatures were increased by a lot if the new vapour pressure data are used. But still a significant gap to observed values remains which they try to explain by non-LTE effects in the population of energy levels in SiO (cf. also Nuth & Donn 1981).
Here we completely re-evaluated the experimentally determined data for the SiO nucleation of Nuth & Donn (1982) with our new vapour-pressure data and derived a fit-formula for the nucleation rate. This can be used in model calculations for stellar outflows. Some explorative calculations were done by calculating stationary dust-driven wind models in a simple approximation. The resulting temperatures at the inner edge of the dust shells were compared to data for the dust condensation temperature derived from analysing IR spectra. It was found that model results based on the new approximation for the nucleation rate are now close to what one observes. We argue that the remaining small gap is due to the difference between gas temperature (responsible for nucleation) and dust temperature (responsible for IR emission), which was not considered in our simple models.
Our result suggests that, indeed, in circumstellar dust shells around M stars silicate dust formation may start with nucleation
of SiO. This holds only for those cases where not some different kind of seed particles, which formed well before SiO nucleation becomes possible (e.g. corundum grains), served as growth centres for the silicate grains. Observed condensation temperatures suggest that both cases seem to occur in circumstellar shells.
The problem of silicate nucleation can, however, not be considered as completely solved, because our model calculations assumed stationary outflows, which are at best a rather crude approximation for winds of AGB stars, because all such stars are variables. Time-dependent model calculations accounting for the shock structure in the winds and accounting for the difference between gas and dust temperature are required before definite conclusions can be draw.
Online material
Appendix A: Approximation for flux-averaged extinction
In a study of radiative transfer models in circumstellar dust shells (Gail et al., in prep.), it was found that the flux-averaged extinction coefficient can be approximated rather well by the expression given in Eq. (19). This approximation is based on the following considerations.
-
1.
At the inner edge of the dust shell the radiation field is dominatedby stellar radiation. The spectral distribution of the flux,4πHλ, can be approximated by a black body with the effective temperature of the star. The flux-averaged extinction coefficient can be approximated by the Planck-averaged extinction coefficient
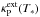 in this case.
in this case. -
2.
Moving from the inside into the shell, the stellar contribution to the radiation field diminishes as exp(−τ∗), where τ∗ is the optical depth calculated from the inner edge with
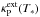 . At the same time,
the contribution of the local dust emission to the total flux increases
proportional to 1−exp(−τ∗).
. At the same time,
the contribution of the local dust emission to the total flux increases
proportional to 1−exp(−τ∗). -
3.
As long as the optical depth of the shell is not very high, the spectral flux distribution from dust emission can be approximated by a black body radiation field with temperature corresponding to the inner edge of the dust shell, Tph. This results in a contribution
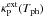 to the
flux-averaged extinction coefficient.
to the
flux-averaged extinction coefficient. -
4.
If the shell becomes very thick optically, the flux-averaged extinction coefficient should approach the Rosseland mean of the local radiation field,
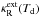 . The approach to
the optically thick case can be modelled by the factor 1−f with
the Eddington factor f, which is f ≈ 1 in an
optically thin shell, and approaches f ≈ 1/3
for optically thick shells.
. The approach to
the optically thick case can be modelled by the factor 1−f with
the Eddington factor f, which is f ≈ 1 in an
optically thin shell, and approaches f ≈ 1/3
for optically thick shells.
As a demonstration of the accuracy of the approximation, Fig. A.1 compares the result for κH based on a full calculation of radiative transfer, as outlined in Wetzel et al. (2013), using a powerlaw variation κλ ∝ λ-1 as a simple model case. An inspection of the figure shows that the approximation for κH is fairly accurate.
 |
Fig. A.1 Approximation of the flux-averaged extinction coefficient κH in models for a dust shell with a powerlaw wavelength variation of the extinction coefficient for different mass-loss rates (in units M⊙ a-1). Solid line: Result of a complete model calculation of radiative transfer. Dashed line: approximation according to Eq. (19). |
For this reason we do not consider the results of Nuth & Donn (1983) for the more complex Si-O-Mg system.
Acknowledgments
This work was supported in part by Forschergruppe 759’ and special research progamme SPP 1385, which both are financed by the “Deutsche Forschungsgemeinschaft (DFG)”.
References
- Ali, A., & Castleman, Jr., A. W. 2005, in IAU Symp., 235, 107 [Google Scholar]
- Bose, M., Floss, C., & Stadermann, F. J. 2010, ApJ, 714, 1624 [NASA ADS] [CrossRef] [Google Scholar]
- Clausing, P. 1930, Z. Phys., 66, 471 [Google Scholar]
- Clausing, P. 1932, Ann. Phys., 404, 961 [CrossRef] [Google Scholar]
- Dayton, B. B. 1956, Vacuum Symposium Transactions, 5 [Google Scholar]
- Donn, B., Hecht, J., Khanna, R., et al. 1981, Surface Science, 106, 576 [NASA ADS] [CrossRef] [Google Scholar]
- Ferguson, F. T., & Nuth, III, J. A. 2008, J. Chem. Eng. Data, 53, 2824 [CrossRef] [Google Scholar]
- Ferrarotti, A. S., & Gail, H.-P. 2006, A&A, 447, 553 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gail, H.-P. 2010, in Astromineralogy, 2nd edn., ed. T. Hennig (Heidelberg: Springer), 55 [Google Scholar]
- Gail, H.-P., & Sedlmayr, E. 1985, A&A, 148, 183 [Google Scholar]
- Gail, H.-P., & Sedlmayr, E. 1986, A&A, 166, 225 [NASA ADS] [Google Scholar]
- Gail, H.-P., & Sedlmayr, E. 1987, A&A, 171, 197 [NASA ADS] [Google Scholar]
- Gail, H.-P., & Sedlmayr, E. 1998a, in The Molecular Astrophysics of Stars and Galaxies, eds. T. W. Hartquist, & D. A. Williams (Oxford: Oxford University Press), 285 [Google Scholar]
- Gail, H.-P., & Sedlmayr, E. 1998b, Faraday Discussion, 109, 303 [Google Scholar]
- Gail, H.-P., Keller, R., & Sedlmayr, E. 1984, A&A, 133, 320 [NASA ADS] [Google Scholar]
- Goumans, T. P. M., & Bromley, S. T. 2012, MNRAS, 420, 3344 [NASA ADS] [Google Scholar]
- Groenewegen, M. A. T., Sloan, G. C., Soszyński, I., & Petersen, E. A. 2009, A&A, 506, 1277 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Habing, H. J. 1996, A&ARv, 7, 97 [NASA ADS] [CrossRef] [Google Scholar]
- Jeong, K. S., Winters, J. M., Fleischer, A. J., & Sedlmayr, E. 1998, in A Half Century of Stellar Pulsation Interpretation, eds. P. A. Bradley, & J. A. Guzik, ASP Conf. Ser., 135, 335 [Google Scholar]
- Knudsen, M. 1909, Ann. Phys., 333, 75 [CrossRef] [Google Scholar]
- Lodders, K., Palme, H., & Gail, H.-P. 2009, in Landolt-Börnstein, New Series, Group IV, ed. J. E. Trümper (Berlin: Springer), 4, 560 [Google Scholar]
- Lucy, L. B. 1976, ApJ, 205, 482 [NASA ADS] [CrossRef] [Google Scholar]
- Margrave, J. L. 1967, The Characterization of High-Temperature Vapours (John Wiley and Sons) [Google Scholar]
- Molster, F. J., Waters, L. B. F. M., & Kemper, F. 2010, in Lect. Notes Phys. (Berlin: Springer Verlag), ed. T. Henning, 815, 143 [Google Scholar]
- Motzfeldt, K. 1955, J. Phys. Chem., 59, 139 [CrossRef] [Google Scholar]
- Nguyen, A. N., Nittler, L. R., Stadermann, F. J., Stroud, R. M., & Alexander, M. O. 2010, ApJ, 719, 166 [NASA ADS] [CrossRef] [Google Scholar]
- Nuth, J. A., & Donn, B. 1981, ApJ, 247, 925 [NASA ADS] [CrossRef] [Google Scholar]
- Nuth, J. A., & Donn, B. 1983, J. Chem. Phys., 78, 1618 [NASA ADS] [CrossRef] [Google Scholar]
- Nuth, J. A. III, & Donn, B. 1982, J. Chem. Phys., 77, 2639 [NASA ADS] [CrossRef] [Google Scholar]
- Nuth, J. A. III, & Ferguson, F. T. 2006, ApJ, 649, 1178 [NASA ADS] [CrossRef] [Google Scholar]
- Ossenkopf, V., Henning, T., & Mathis, J. S. 1992, A&A, 261, 567 [NASA ADS] [Google Scholar]
- Paquette, J. A., & Nuth, III, J. A. 2011, ApJ, 737, L6 [NASA ADS] [CrossRef] [Google Scholar]
- Paquette, J. A., Ferguson, F. T., & Nuth, III, J. A. 2011, ApJ, 732, 62 [NASA ADS] [CrossRef] [Google Scholar]
- Reber, A. C., Clayborne, P. A., Reveles, J. U., et al. 2006, Nano Lett., 6, 1190 [NASA ADS] [CrossRef] [Google Scholar]
- Schick, H. L. 1960, Chem. Rev., 60, 331 [CrossRef] [Google Scholar]
- Schirrmacher, V., Woitke, P., & Sedlmayr, E. 2003, A&A, 404, 267 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Vollmer, C., Brenker, F. E., Hoppe, P., & Stroud, R. M. 2009, ApJ, 700, 774 [NASA ADS] [CrossRef] [Google Scholar]
- Wetzel, S., Pucci, A., & Gail, H.-P. 2012, J. Chem. Eng. Data, 57, 1594 [CrossRef] [Google Scholar]
- Wetzel, S., Klevenz, M., Gail, H.-P., Pucci, A., & Trieloff, M. 2013, A&A, 553, A92 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Whitman, C. I. 1952, J. Chem. Phys., 20, 161 [NASA ADS] [CrossRef] [Google Scholar]
- Zeldovich, Y. B. 1943, Acta Physicochim., 18, 1 [Google Scholar]
All Tables
All Figures
 |
Fig. 1 Schematic drawing of the experimental setup for the Knudsen method. The quartz crystal microbalance (QCM) is placed at a distance d from the Knudsen cell and measures the mass rate of the condensing particles during effusion from the cell. |
| In the text | |
 |
Fig. 2 Vaporization coefficient of solid SiO derived from the experimental measurements of the mass-loss rate obtained for two orifice diameters of the Knudsen cell. The full line is the approximation according to Eq. (3). |
| In the text | |
 |
Fig. 3 Equilibrium vapour pressure of solid SiO derived from the experimental measurements of the mass-loss rate obtained for two orifice diameters of the Knudsen cell (filled circles). The full line is the analytic approximation according to Eq. (4). |
| In the text | |
 |
Fig. 4 Stability limit of solid SiO for the new data from our laboratory measurements for data from Ferguson & Nuth (2008) and for the old data of Schick (1960). Also shown are stability limits for the most abundant refractory compounds formed from an oxygen-rich element mixture with cosmic standard element abundances. The dashed line corresponds to the p-T-trajectory of a dust-driven stellar wind. |
| In the text | |
 |
Fig. 5 Supersaturation at onset of avalanche nucleation from the experiment of Nuth & Donn (1982), re-evaluated with the new vapour pressure data for SiO. Black dots: data for the nucleation experiments conducted at pH2 = 50 Torr. Crosses: data for experiments conducted at pH2 = 35 Torr. Open sqares: supersaturation based on old vapour pressure data, as given by Nuth & Donn (1982), for the same set of experiments. |
| In the text | |
 |
Fig. 6 Plot of |
| In the text | |
 |
Fig. 7 Lines of constant nucleation rate per H-nucleus according to the numerical fit to the experimental data. The red lines correspond to values of J/NH from 10-34 s-1 (top) to 10-10 (bottom) in steps of 102. The shaded area indicates the range of pressures typically encountered at the inner edge of dust shells. The thick dashed (blue) line corresponds to the critical nucleation rate of J/NH = 10-20 particles cm-3 s-1 where massive dust nucleation commences under circumstellar conditions. The uppermost (green) line corresponds to the stability limit if solid SiO is in equilibrium with a gas with standard cosmic elemental abundances. The line denoted as “wind” corresponds to the p-T-trajectory of a wind model. The circles correspond to the data points of the laboratory experiments, if the pressure of SiO in the condensation zone is converted into an equivalent pressure of a gas with cosmic elemental composition. |
| In the text | |
 |
Fig. 8 Some results for a wind model with Ṁ = 5 × 10-6 M⊙ yr-1. a) Variation in the degree of condensation of Si into silicate dust with radial distance from the mass centre. b) Radial variation with distance of outflow velocity v (solid line), sonic velocity cT (dashed line), and escape velocity from star (dotted line). c) Variation in p and T along the wind (solid line) and lines of constant nucleation rate (dashed lines). The crosses denote the pressure and temperature at the inner edge of the dust shell for the models of Table 1. |
| In the text | |
 |
Fig. 9 Temperature at the inner edge of dust shells of AGB stars in the Small and Large Magellanic clouds with estimated errors of the temperature determination (data from Groenewegen et al. 2009). This corresponds to the temperature where massive silicate dust condensation commences in the outflow. The data are plotted against the derived mass-loss rate. Dotted line with open circles denotes the temperature at the sonic point of the models from Table 1. |
| In the text | |
 |
Fig. 10 Dust temperature and grey temperature in optically thin dust shells for a star radiating like a black body with temperature Teff = 2700 K, calculated for silicate dust with opacities from Ossenkopf et al. (1992). |
| In the text | |
 |
Fig. A.1 Approximation of the flux-averaged extinction coefficient κH in models for a dust shell with a powerlaw wavelength variation of the extinction coefficient for different mass-loss rates (in units M⊙ a-1). Solid line: Result of a complete model calculation of radiative transfer. Dashed line: approximation according to Eq. (19). |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.