| Issue |
A&A
Volume 555, July 2013
|
|
|---|---|---|
| Article Number | A119 | |
| Number of page(s) | 11 | |
| Section | Interstellar and circumstellar matter | |
| DOI | https://doi.org/10.1051/0004-6361/201321807 | |
| Published online | 11 July 2013 | |
Online material
Appendix A: Approximation for flux-averaged extinction
In a study of radiative transfer models in circumstellar dust shells (Gail et al., in prep.), it was found that the flux-averaged extinction coefficient can be approximated rather well by the expression given in Eq. (19). This approximation is based on the following considerations.
-
1.
At the inner edge of the dust shell the radiation field is dominatedby stellar radiation. The spectral distribution of the flux,4πHλ, can be approximated by a black body with the effective temperature of the star. The flux-averaged extinction coefficient can be approximated by the Planck-averaged extinction coefficient
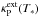 in this case.
in this case. -
2.
Moving from the inside into the shell, the stellar contribution to the radiation field diminishes as exp(−τ∗), where τ∗ is the optical depth calculated from the inner edge with
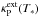 . At the same time,
the contribution of the local dust emission to the total flux increases
proportional to 1−exp(−τ∗).
. At the same time,
the contribution of the local dust emission to the total flux increases
proportional to 1−exp(−τ∗). -
3.
As long as the optical depth of the shell is not very high, the spectral flux distribution from dust emission can be approximated by a black body radiation field with temperature corresponding to the inner edge of the dust shell, Tph. This results in a contribution
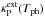 to the
flux-averaged extinction coefficient.
to the
flux-averaged extinction coefficient. -
4.
If the shell becomes very thick optically, the flux-averaged extinction coefficient should approach the Rosseland mean of the local radiation field,
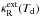 . The approach to
the optically thick case can be modelled by the factor 1−f with
the Eddington factor f, which is f ≈ 1 in an
optically thin shell, and approaches f ≈ 1/3
for optically thick shells.
. The approach to
the optically thick case can be modelled by the factor 1−f with
the Eddington factor f, which is f ≈ 1 in an
optically thin shell, and approaches f ≈ 1/3
for optically thick shells.
As a demonstration of the accuracy of the approximation, Fig. A.1 compares the result for κH based on a full calculation of radiative transfer, as outlined in Wetzel et al. (2013), using a powerlaw variation κλ ∝ λ-1 as a simple model case. An inspection of the figure shows that the approximation for κH is fairly accurate.
 |
Fig. A.1
Approximation of the flux-averaged extinction coefficient κH in models for a dust shell with a powerlaw wavelength variation of the extinction coefficient for different mass-loss rates (in units M⊙ a-1). Solid line: Result of a complete model calculation of radiative transfer. Dashed line: approximation according to Eq. (19). |
| Open with DEXTER | |
© ESO, 2013
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


