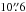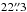| Issue |
A&A
Volume 555, July 2013
|
|
|---|---|---|
| Article Number | A41 | |
| Number of page(s) | 11 | |
| Section | Interstellar and circumstellar matter | |
| DOI | https://doi.org/10.1051/0004-6361/201321481 | |
| Published online | 26 June 2013 | |
Dynamics, CO depletion, and deuterium fractionation of the dense condensations within the fragmented prestellar core Orion B9–SMM 6⋆
1
Department of PhysicsUniversity of Helsinki,
PO Box 64
00014
Helsinki
Finland
e-mail:
oskari.miettinen@helsinki.fi
2
Department of Astronomy, Yale University,
New Haven, CT
06511,
USA
e-mail:
stella.offner@yale.edu
Received:
15
March
2013
Accepted:
22
May
2013
Context. Low-mass prestellar cores are rarely found to be fragmented into smaller condensations, but studying any substructure, where present, is essential for understanding the origin of multiple stellar systems.
Aims. We attempt to better understand the kinematics and dynamics of the subfragments inside the prestellar core SMM 6 in Orion B9. Another goal of the present study is to constrain the evolutionary stage of the condensations by investigating the levels of CO depletion and deuterium fractionation.
Methods. We used the APEX telescope to observe the molecular lines C17O(2−1), N2H+(3−2), and N2D+(3−2) towards the condensations. We used the line data in conjunction with our previous SABOCA 350-μm dust continuum map of the source.
Results. The condensations are characterised by subsonic internal non-thermal motions (σNT ≃ 0.5cs), and most of them appear to be gravitationally bound. The dispersion of the N2H+ velocity centroids among the condensations is very low (0.02 km s-1). The CO depletion factors we derive, fD = 0.8 ± 0.4−3.6 ± 1.5, do not suggest any significant CO freeze-out, but this may be due to the canonical CO abundance we adopt. The fractional abundances of N2H+ and N2D+ with respect to H2 are found to be ~0.9−2.3 × 10-9 and ~4.9−9.9 × 10-10, respectively. The deuterium fractionation of N2H+ lies in the range 0.30 ± 0.07−0.43 ± 0.09.
Conclusions. The detected substructure inside SMM 6 is most likely the result of cylindrical Jeans-type gravitational fragmentation. We estimate the timescale for this fragmentation to be ~1.8 × 105 yr. The condensations are unlikely to be able to interact with one another and coalesce before local gravitational collapse ensues. Moreover, significant mass growth of the condensations via competitive-like accretion from the parent core seems unfeasible. The high level of molecular deuteration in the condensations suggests that gas-phase CO should be strongly depleted. It also points towards an advanced stage of chemical evolution. The subfragments of SMM 6 might therefore be near the onset of gravitational collapse, but whether they can form protostellar or substellar objects (brown dwarfs) depends on the local star formation efficiency and remains to be clarified.
Key words: astrochemistry / stars: formation / ISM: individual objects: Orion B9-SMM 6 / ISM: kinematics and dynamics / ISM: molecules
This publication is based on data acquired with the Atacama Pathfinder EXperiment (APEX) under programmes 079.F-9313(A), 084.F-9312(A), and 090.F-9313(A). APEX is a collaboration between the Max-Planck-Institut für Radioastronomie, the European Southern Observatory, and the Onsala Space Observatory.
© ESO, 2013
1. Introduction
Fragmentation of interstellar molecular clouds appears to occur in a hierarchical fashion. Recent Herschel observations have clearly demonstrated that on the scales of several parsecs to ~10 pc the cloud structures are highly filamentary in shape (e.g., André et al. 2010; Arzoumanian et al. 2011; Hill et al. 2011; Palmeirim et al. 2013). The origin of large-scale filaments is still unclear, but they often (if not always) show substructures along their long axes. Substructures on scales of ~0.5–1 pc are typically called clumps, which may contain significant gas substructures and would likely form a cluster of stars. Gas fragments ≲0.1 pc, which are expected to form a single star or bound multiple system, are called cores.
The dense cores formed in the course of hierarchical fragmentation represent the size scale on which protostellar collapse and the formation of low-mass (~0.1–2 M⊙) stars take place. Initially starless cores that are bound by their self-gravity are called prestellar cores (Ward-Thompson et al. 1994). These are ideal laboratories for studying the genuine initial physical and chemical conditions of star formation. Because many stars are found in binary or higher order multiple systems (e.g., Raghavan et al. 2010; Kraus & Hillenbrand 2012; Duchêne & Kraus 2013), core fragmentation into still smaller subunits is expected to occur at some point in their evolution, possibly during the prestellar phase. In the present work, we use the term condensation for such subfragments with sizes of ~0.01 pc (e.g., André et al. 2007, hereafter ABMP07). Since condensations are fairly low mass and are usually found within a gravitationally bound core, they probably represent the precursors of individual stars that will eventually comprise a multiple-star system.
Core fragmentation is of prime importance when studying the origin of core mass function and its connection to the stellar initial mass function (IMF). From a theoretical point of view, the formation of multiple stellar systems is far from well-understood (e.g., Tohline 2002; Goodwin et al. 2007). For example, the initial phase and characteristic timescale of the fragmentation process still need to be established. Observationally, it is unclear how common the fragmentation of low-mass cores actually is, particularly in the case of starless or prestellar cores.
Some of the earliest instances of core substructure were discovered by Lemme et al. (1995). They mapped the starless core L1498 in the C-bearing molecules C18O and CS using the IRAM 30-m telescope with 12″−25″ resolution. The core was resolved into many small-scale condensations with diameters of about 0.02 pc and masses about 0.01 M⊙. The subfragments were found to be gravitationally unbound, and the authors suggested that they are just transient structures (see also Kuiper et al. 1996). Langer et al. (1995) used high-resolution (6″−9″) interferometric observations to map the TMC-1 core D. Similiarly to L1498, the core was found to be composed of several condensations with sizes of 0.007–0.021 pc and masses of ~0.01 M⊙. These sources were also found to be gravitationally unbound and unable to form even proto-brown dwarfs unless the condensations were to merge and form more massive structures. Langer et al. (1995) suggested that a pure Jeans-type gravitational instability could not be responsible for the core fragmentation. However, the substructure was identified from molecular-line maps (the C-bearing species CCS and CS). Therefore, it is possible that the subfragments represent small-scale chemical inhomogeneities of the parent core (cf. Takakuwa et al. 1998).
Kamazaki et al. (2001) detected the first subfragments inside prestellar cores in dust emission. They carried out high-resolution NMA observations of 2- and 3-mm dust continuum emission towards two prestellar cores in the ρ Oph A region, namely SM1 and SM1N. Both cores appeared to contain condensations of 600–1100 AU in size with masses in the range 0.054–0.14 M⊙. Interestingly, as opposed to the above mentioned studies, the condensations found by Kamazaki et al. (2001) were determined to be gravitationally bound entities. We note that one of the condensations within SM1, with a mass of 0.14 M⊙, was suggested by the authors to already be in the early protostellar phase. Kamazaki et al. (2001) also concluded that the substructures were the result of gravitational fragmentation of the parent cores. Takakuwa et al. (2003) studied two prestellar cores in the TMC-1C region with high-resolution molecular-line observations, and found ~2500 AU -size condensations with masses of ~0.02 M⊙ inside the cores. These substellar-mass fragments were found to be gravitationally unbound but with dissipation timescales long enough to allow the fragments to coalesce with one another and form more massive objects.
More recently, Kirk et al. (2009) studied the prestellar core L183 (L134N) with
high-resolution (13″ × 10″ or ~0.006 pc ~1200 AU) BIMA interferometric observations, and
found it to be composed of three condensations of ~0.005–0.01 pc in radii. They concluded
that the observed substructure was the result of the fragmentation of a rotating and
collapsing prestellar core. On the other hand, Schnee et al.
(2010) found that none of their 11 starless cores in Perseus break into smaller
components at 5″ resolution or on the ~103 AU scale (see also Miettinen & Offner 2013 for Ori B9–SMM 1). Chen & Arce (2010), using SMA observations at
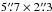 resolution (~0.003 pc or ~620
AU), discovered three condensations inside the prestellar core R CrA SMM 1A. The projected
separation between the 0.1–0.2 M⊙ mass condensations was found
to be between 1000 and 2100 AU. The observed spacings are comparable to the local Jeans
length, and the authors suggested that the condensations were formed through the
fragmentation of an elongated prestellar core during the isothermal phase of evolution
(i.e., when the radiative cooling is able to compensate for the heating by compression).
Nakamura et al. (2012) used the SMA with a few
arcsec (a few hundred AU) resolution to observe the prestellar cores SM1 and B2-N5 in
ρ Ophiuchus (cf. Kamazaki et al.
2001). These cores were resolved into three and four condensations, respectively,
with masses of ~0.01–0.1 M⊙ and sizes of a few hundred AU. The
masses were determined to be high enough for the condensations to be gravitationally bound.
Nakamura et al. (2012) proposed that the origin of
the substructures could be explained by turbulent fragmentation (e.g., Fisher 2004; Offner et al. 2010).
resolution (~0.003 pc or ~620
AU), discovered three condensations inside the prestellar core R CrA SMM 1A. The projected
separation between the 0.1–0.2 M⊙ mass condensations was found
to be between 1000 and 2100 AU. The observed spacings are comparable to the local Jeans
length, and the authors suggested that the condensations were formed through the
fragmentation of an elongated prestellar core during the isothermal phase of evolution
(i.e., when the radiative cooling is able to compensate for the heating by compression).
Nakamura et al. (2012) used the SMA with a few
arcsec (a few hundred AU) resolution to observe the prestellar cores SM1 and B2-N5 in
ρ Ophiuchus (cf. Kamazaki et al.
2001). These cores were resolved into three and four condensations, respectively,
with masses of ~0.01–0.1 M⊙ and sizes of a few hundred AU. The
masses were determined to be high enough for the condensations to be gravitationally bound.
Nakamura et al. (2012) proposed that the origin of
the substructures could be explained by turbulent fragmentation (e.g., Fisher 2004; Offner et al. 2010).
The target source of the present study is the prestellar core SMM 6 in the Orion B9 star-forming region. It was originally discovered by Miettinen et al. (2009, hereafter, Paper I) from the LABOCA 870-μm mapping of Orion B9. The core was found to be elongated in shape and not harbouring any embedded infrared point source, and we suggested that it is likely to be prestellar due its high density. Based on the NH3 observations with the Effelsberg 100-m telescope, Miettinen et al. (2010, henceforth, Paper II) derived the gas kinetic temperature of Tkin = 11.0 ± 0.4 K towards a selected position in SMM 6. The one-dimensional non-thermal velocity dispersion was derived to be 0.1 km s-1, which is subsonic by a factor of two. Employing the new temperature value with the assumption that Tkin equals the dust temperature (Tdust), the mass of SMM 6 was estimated to be 8.2 ± 1.1 M⊙. The virial-parameter analysis of the source suggested that it is gravitationally bound and near virial equilibrium, supporting our earlier speculation that it is in the prestellar phase of evolution1. Miettinen et al. (2012, hereafter, Paper III) presented further molecular-line observations towards the NH3 target position in SMM 6. The CO depletion factor was estimated to be 4.2 ± 1.3, and the N2D+/N2H+ column density ratio was found to be ~0.6 ± 0.1, indicating a high degree of deuterium fractionation. In Paper III, we also presented the results of our SABOCA 350-μm imaging of dense cores in Orion B9. SMM 6, determined to be a thermally supercritical cylindrical object, was resolved into three to four very low-mass (revised masses are ~0.2–0.6 M⊙; see Appendix A) condensations projectively separated by ~0.06 pc or ~1.2 × 104 AU (see Fig. 1)2. The origin of this substructure can be explained in terms of thermal Jeans-type fragmentation. It seems likely that SMM 6 has undergone a similar fragmentation process as R CrA SMM 1A described above. In Table 1, we list the SABOCA 350-μm peak positions of the SMM 6’s condensations along with their main physical properties.
The 350-μm condensations within SMM 6.
Recent Herschel data show that SMM 6 belongs to a northeast-southwest oriented filamentary structure (see Fig. 2). Miettinen (2012b) found that there is a sharp velocity gradient in the parent filament (across its short axis), and suggested that it might represent a shock front resulting from the feedback from the nearby expanding H ii region NGC 2024 (~4 pc southwest of Orion B9). The formation of dense cores in Orion B9, including SMM 6, might have been triggered by this feedback. As highlighted in Fig. 2, the ring-like cloud structure consisting partly of SMM 6 could be a manifestation of such a dynamic environment.
 |
Fig. 1 SABOCA 350-μm image of the fragmented prestellar core SMM 6 in Orion
B9. The image is displayed with power-law scaling, and the colour bar indicates the
surface-brightness scale in Jy beam-1. The overlaid green SABOCA contours
are plotted at three times the noise level (3σ = 180 mJy
beam-1). The white contours show the Herschel/SPIRE
250-μm dust continuum emission (18″ resolution); these contours are
plotted at 3.0 and 3.5 Jy beam-1. The green plus sign indicates the target
position of our previous molecular-line observations, while the other plus signs mark
the target positions of the present study (i.e., the 350-μm peaks). A
scale bar indicating the 0.05 pc projected length is shown in the top left, with the
assumption of a 450 pc line-of-sight distance. The three circles in the upper left
corner show the effective FWHM of the SABOCA beam
( |
In Paper III, we noticed that our LABOCA map employed in Papers I and II was misaligned, and therefore we had to adjust its pointing using the Spitzer and SABOCA source positions (see footnote 2 in Paper III and Miettinen & Offner 2013). The target positions of our previous molecular-line observations were chosen to be the peak positions of the LABOCA map before adjusting the pointing, and therefore they are slightly offset from the 870-μm maxima. In the case of SMM 6, our previous line observations probed the core edge (as shown by the green plus sign in Fig. 1). To better understand the physics and chemistry of SMM 6, particularly the properties of its substructure, we performed follow-up molecular-line observations towards the condensations. In the present paper, we examine the kinematics and dynamics of these subfragments and their chemical properties, namely CO depletion and molecular deuteration of N2H+. The latter parameter has the potential to constrain the evolutionary stage of the condensations (e.g., Crapsi et al. 2005; Friesen et al. 2013). The present work is one of the first studies of the dynamics of subfragments within a prestellar core. The observations and data reduction are described in Sect. 2. Section 3 presents the observational results, while analysis and its results are presented in Sect. 4 and Appendix A. We discuss the results in Sect. 5 and in Sect. 6, we summarise the paper and draw our main conclusions.
 |
Fig. 2 Herschel/SPIRE 250-μm far-infrared image towards the Orion B9 star-forming filament. The image is shown with a square-root scaling to improve the contrast between bright and faint features. The image is overlaid with black contours of SABOCA 350-μm emission. The SABOCA contours start at 3σ and increase at this interval (Paper III). The SABOCA data towards the IRAS 05399/SMM 1 -system with a 1σ noise level of 80 mJy beam-1 are taken from Miettinen & Offner (2013). Selected cores are labelled. The ring-like structure comprising partly of SMM 6 is highlighted with a white dashed circle of radius or ~0.3 pc. A scale bar indicating the 0.3 pc projected length is shown in the bottom left corner. |
2. Observations and data reduction
We used the APEX (Atacama Pathfinder EXperiment; Güsten et al. 2006) 12-m telescope in Chile to observe the spectral-line transitions C17O(2−1), N2H+(3−2), and N2D+(3−2) towards the 350-μm peaks of the dense condensations within SMM 6. The N2H+ observations were carried out on 25 September 2012, while those of C17O and N2D+ were performed on the 27th of the month. The strongest 350-μm condensation SMM 6a was observed again in C17O on 28 September because the previous day’s weather was poor when the source was observed.
The observed transitions, their selected spectroscopic properties, and observational parameters are summarised in Table 2. The critical densities, ncrit = Aul/Cul, listed in Col. (4) of Table 2, were calculated at T = 10 K using the Einstein A −coefficients from the Leiden Atomic and Molecular Database (LAMDA; Schöier et al. 2005)3 (C17O) and Pagani et al. (2009) (N2H+ and N2D+). The collisional-rate data (Cul) were taken from LAMDA (C17O) and the Caltech Submillimeter Wave Astrophysics website4 (N2H+ and N2D+). The latter are based on data from BASECOL (Dubernet et al. 2013)5.
As a front end for the C17O(2−1) and N2D+(3−2) observations, we used the APEX-1 receiver of the Swedish Heterodyne Facility Instrument (SHeFI; Belitsky et al. 2007; Vassilev et al. 2008a,b). APEX-1 operates in single-sideband (SSB) mode using sideband separation mixers, and it has a sideband rejection ratio >10 dB. For the N2H+(3−2) observations the front end used was APEX-2, which has similar characteristics as APEX-1. The backend for all observations was the RPG eXtended bandwidth Fast Fourier Transfrom Spectrometer (XFFTS; cf. Klein et al. 2012) with an instantaneous bandwidth of 2.5 GHz and 32 768 spectral channels.
Observed spectral-line transitions and observational parameters.
The observations were performed in the wobbler-switching mode with a 100″ azimuthal throw
(symmetric offsets) and a chopping rate of 0.5 Hz. The telescope focus and pointing were
optimised and checked at regular intervals on the planet Jupiter, and the variable stars W
Orionis, RAFGL865 (V1259 Ori), o Ceti (Mira A), and R Leporis (Hind’s
Crimson Star). The pointing was found to be accurate to ~3″. Calibration was made by means
of the chopper-wheel technique and the output intensity scale given by the system is
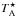 , i.e., the
antenna temperature corrected for the atmospheric attenuation. The observed intensities were
converted to the main-beam brightness temperature scale by
, i.e., the
antenna temperature corrected for the atmospheric attenuation. The observed intensities were
converted to the main-beam brightness temperature scale by
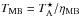 , where
ηMB is the main-beam efficiency. The absolute calibration
uncertainty is estimated to be about 10%.
, where
ηMB is the main-beam efficiency. The absolute calibration
uncertainty is estimated to be about 10%.
 |
Fig. 3 Hanning-smoothed C17O(2−1), N2H+(3−2), and N2D+(3−2) spectra. Hyperfine-structure fits to the lines are overlaid in green. In each panel, the vertical red dashed line indicates the radial velocity of the C17O(2−1) line. Note that towards SMM 6c, two velocity components of C17O(2−1) and N2H+(3−2) (at ~2.3 and ~9.4 km s-1) are detected. |
Spectral-line parameters.
The spectra were reduced using the CLASS90 programme of the GILDAS software package6. The individual spectra were averaged and the resulting spectra were Hanning-smoothed to improve the signal-to-noise ratio. Linear (first-order) baselines were determined from velocity ranges without line-emission features, and then subtracted from the spectra. The resulting 1σ rms noise levels at the smoothed resolutions are listed in the last column of Table 2.
The J = 2−1 transition of C17O contains nine hyperfine (hf)
components that are spread over ~2.4 km s-1. We fitted this hf structure using
“method hfs” of CLASS90 to derive the LSR velocity (vLSR) of the
emission, and FWHM linewidth (Δv). The hf line fitting can also be used to derive the line
optical thickness by comparing the relative intensities of the hf components. However, in
all spectra the hf components are mostly blended together and thus the total optical
thickness could not be reliably determined from the sum of the peak optical thicknesses of
the components. For the rest frequencies of the hf components, we used the values from Ladd
et al. (1998, Table 6 therein). The adopted central
frequency, 224 714.199 MHz, refers to the strongest hf component
JF = 29/2 → 17/2
which has a relative intensity of 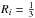 .
.
The J = 3−2 transition of both N2H+ and
N2D+ is split up into 38 hf components spread over about 5.7 and 6.9
km s-1, respectively. To fit these hf structures, we used the rest frequencies
from Pagani et al. (2009, Tables 4 and 10 therein).
The adopted central frequencies of N2H+(3−2) and
N2D+(3−2), 279 511.832 and 231 321.912 MHz, are those of the
JF1F = 345 → 234
hf component which has a relative intensity of 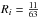 . Also in
these cases, the hf components are blended and thus the optical thickness could not be
reliably determined through hf fitting.
. Also in
these cases, the hf components are blended and thus the optical thickness could not be
reliably determined through hf fitting.
3. Observational results
3.1. Spectra
The Hanning-smoothed spectra are presented in Fig. 3. The lines are clearly detected towards all condensations. The hf structure of
the C17O(2−1) line is partially resolved in SMM 6b–d (note the hf satellites
on the low-velocity side of the strongest component), but not sufficiently well to derive
the line optical thickness. Towards SMM 6c, the C17O and
N2H+ lines exhibit two well-separated velocity components: besides
the lines at the systemic velocity ~9.4 km s-1, there are weak lines at a lower
velocity (~2.3 km s-1). There is also a hint of low-velocity C17O
emission in the spectra towards SMM 6a and 6b. The low-velocity line emission has already
been detected towards other Orion B9 cores in Papers I–III and by Miettinen (2012b). We note that some of the spectra show small
artificial “absorption”-like features, most notably the C17O spectra towards
SMM 6a and 6b. These are caused by emission in the OFF-source reference position
(OFF-beam); for example, there is C17O emission in the velocity range ~1–2 km
s-1 towards the OFF-position of SMM 6b. We also note that the nearby
condensations SMM 6c and 6d are encompassed by the  beams. Therefore, line emission
from one of the sources is (partly) caught in the beam when observing towards the dust
peak of the other and may thus affect the line profiles to some degree.
beams. Therefore, line emission
from one of the sources is (partly) caught in the beam when observing towards the dust
peak of the other and may thus affect the line profiles to some degree.
3.2. Spectral-line parameters
The spectral-line parameters are listed in Table 3. The values of vLSR and Δv were derived through fitting the hf
structure. The quoted uncertainties are formal 1σ fitting errors. The
fact that the lines are only marginally resolved at best means that the quoted Δv values
represent only an upper limit to the intrinsic linewidth. The peak intensities
(TMB) were derived by fitting a single Gaussian to the
profile of the strongest line. The integrated line intensities
(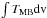 ) listed in Col. (6) of Table
3 were computed over the velocity range given in
square brackets in the corresponding column. This way, we were able to take the
non-Gaussian shape of the lines into account. The uncertainties in the peak and integrated
intensities represent the quadrature sums of the fitting errors and the 10% calibration
uncertainties. In the last two columns of Table 3,
we list the estimated peak line optical-thicknesses (τ0) and
assumed excitation temperatures (Tex), which are described in
Sect. 4.5.
) listed in Col. (6) of Table
3 were computed over the velocity range given in
square brackets in the corresponding column. This way, we were able to take the
non-Gaussian shape of the lines into account. The uncertainties in the peak and integrated
intensities represent the quadrature sums of the fitting errors and the 10% calibration
uncertainties. In the last two columns of Table 3,
we list the estimated peak line optical-thicknesses (τ0) and
assumed excitation temperatures (Tex), which are described in
Sect. 4.5.
4. Analysis and results
4.1. Revisiting the core fragmentation
Because the mass of the parent core is revised in the present work (Appendix A), we also re-analyse its fragmentation here.
The line mass of SMM 6 is found to be
Mline ≃ 27 ± 6 M⊙
pc-1. For an infinite, unmagnetised, isothermal cylinder, instability
(collapse to line singularity) occurs if its Mline exceeds the
critical equilibrium value of (e.g., Ostriker 1964;
Inutsuka & Miyama 1992) 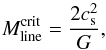 (1)where
cs is the isothermal sound speed and G the
gravitational constant. Using the gas temperature
Tkin = 11.0 ± 0.4 K to calculate the sound speed
(0.196 ± 0.004 km s-1), we derive the value
(1)where
cs is the isothermal sound speed and G the
gravitational constant. Using the gas temperature
Tkin = 11.0 ± 0.4 K to calculate the sound speed
(0.196 ± 0.004 km s-1), we derive the value
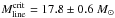 pc-1.
If the ~0.1 km s-1 non-thermal velocity dispersion derived in Paper II is taken
into account, the effective sound speed
pc-1.
If the ~0.1 km s-1 non-thermal velocity dispersion derived in Paper II is taken
into account, the effective sound speed 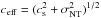 increases the value of
increases the value of 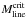 to
~22.5 ± 0.8 M⊙ pc-1. SMM 6 therefore appears to
be (slightly) supercritical, in accordance with the detected substructure along the
filament.
to
~22.5 ± 0.8 M⊙ pc-1. SMM 6 therefore appears to
be (slightly) supercritical, in accordance with the detected substructure along the
filament.
The projected spacing between the condensations is ~29″ or ~0.06 pc, where the sources 6c
and 6d are treated as a single fragment. In case the cylinder has
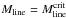 , as is
roughly the case for SMM 6, the Jeans length along the long axis is (Larson 1985; Hartmann 2002)
, as is
roughly the case for SMM 6, the Jeans length along the long axis is (Larson 1985; Hartmann 2002)
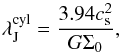 (2)where Σ0 =
μH2mHN(H2)
is the central surface density with μH2 = 2.82
being the mean molecular weight per H2 molecule (when the He/H abundance ratio
is about 0.1; see Appendix A) and mH the mass of a hydrogen
atom. If the central column density is adopted to be the average value derived towards the
condensations, ~2.1 ± 0.2 × 1022 cm-2 (Col. (6) of Table 1),
(2)where Σ0 =
μH2mHN(H2)
is the central surface density with μH2 = 2.82
being the mean molecular weight per H2 molecule (when the He/H abundance ratio
is about 0.1; see Appendix A) and mH the mass of a hydrogen
atom. If the central column density is adopted to be the average value derived towards the
condensations, ~2.1 ± 0.2 × 1022 cm-2 (Col. (6) of Table 1), 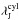 is
≃0.07 ± 0.01 pc – very close to the observed interval of the condensations. We note that
due to projection effects we are measuring only a lower limit to the separations.
is
≃0.07 ± 0.01 pc – very close to the observed interval of the condensations. We note that
due to projection effects we are measuring only a lower limit to the separations.
If the finite length and diameter of the cylindrical cloud are
L and D, respectively, the number of fragments forming
due to gravitational instability is expected to be (e.g., Bastien et al. 1991; Wiseman & Ho
1998) 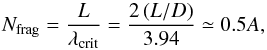 (3)where
λcrit = 1.97D is the wavelength of the most
unstable perturbation, and A the cylinder’s aspect ratio. The average
width of the SMM 6 filament is about
(3)where
λcrit = 1.97D is the wavelength of the most
unstable perturbation, and A the cylinder’s aspect ratio. The average
width of the SMM 6 filament is about 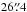 or
D = 2R = 0.06 pc, so A is about 4.
One would therefore expect to have two subfragments, i.e., half the number we observe. The
discrepancy could be caused by projection effects (the true length of the filament is
longer), and the fact that the source is not a perfect cylinder but is bent or curved as
shown in Fig. 2 and it narrows towards the southeast
(i.e., D is changing along the filament). The number of detected
subfragments could also be an imprint of internal turbulent motions, i.e., turbulent
fragmentation (cf. Nakamura et al. 2012). Note that
λcrit is about 0.12 pc when computed using the average width
0.06 pc, i.e., a factor of 1.7 larger than
or
D = 2R = 0.06 pc, so A is about 4.
One would therefore expect to have two subfragments, i.e., half the number we observe. The
discrepancy could be caused by projection effects (the true length of the filament is
longer), and the fact that the source is not a perfect cylinder but is bent or curved as
shown in Fig. 2 and it narrows towards the southeast
(i.e., D is changing along the filament). The number of detected
subfragments could also be an imprint of internal turbulent motions, i.e., turbulent
fragmentation (cf. Nakamura et al. 2012). Note that
λcrit is about 0.12 pc when computed using the average width
0.06 pc, i.e., a factor of 1.7 larger than 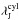 .
.
We conclude that SMM 6 has likely fragmented into subcondensations as a result of
cylindrical Jeans-type gravitational instability. Considering a filament of radius
R, the fragmentation timescale is then expected to be comparable to the
radial crossing time,
τcross = R/σ,
where σ refers to the total velocity dispersion. If we use the average
FWHM linewidth of the C17O lines detected here,
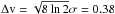 km
s-1, the τcross for the SMM 6 filament is
~1.8 × 105 yr.
km
s-1, the τcross for the SMM 6 filament is
~1.8 × 105 yr.
One-dimensional non-thermal velocity dispersions, virial masses, and virial parameters of the condensations.
4.2. Gas velocity dispersion and virial state of the condensations
To study the gas kinematics of the high-density portion of the condensations, we employed the N2H+(3−2) transition due to its high critical density. We computed the non-thermal portion of the line-of-sight velocity dispersion, σNT, using Eq. (9) of Paper II. It was assumed that Tkin = 10 K, and the error in σNT was calculated from that of the FWHM linewidth. As shown in Col. (2) of Table 4, σNT = 0.1 km s-1 for each source. Because the isothermal sound speed at 10 K is cs = 0.19 km s-1, the σNT/cs ratios are ~0.5 ± 0.1, i.e., the condensations are characterised by subsonic internal non-thermal (turbulent) motions. The true values of σNT could be even lower because the N2H+(3−2) lines are not spectrally resolved, enabling us to derive only upper limits to the linewidths and velocity dispersions.
To examine the dynamical state of the condensations, we calculated their virial masses by
employing the N2H+(3−2) linewidths and using the formula where the
effects of external pressure, rotation, and magnetic field are ignored (cf. Eq. (12) of
Paper II): 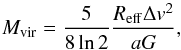 (4)where the dimensionless
parameter a measures the effect of a non-uniform density distribution on
the gravitational energy and is given by
a = (1−p/3)/(1−2p/5),
where p is the power-law index of the density profile
(n ∝ r− p; Bertoldi & McKee 1992). Following ABMP07, we
assume that the density structure of the sources is that of a centrally condensed
isothermal sphere with
n(r) ∝ r-2
(a = 5/3). The resulting values are listed in Col.
(3) of Table 4 with uncertainties propagated from
the linewidth errors. We note that if the condensations have inner density profiles
shallower than ~r-2, the virial masses will be higher. For
example, if the density power-law index is p = 1 or
a = 10/9, the Mvir
values are larger by a factor of 1.5 compared to those with p = 2.
(4)where the dimensionless
parameter a measures the effect of a non-uniform density distribution on
the gravitational energy and is given by
a = (1−p/3)/(1−2p/5),
where p is the power-law index of the density profile
(n ∝ r− p; Bertoldi & McKee 1992). Following ABMP07, we
assume that the density structure of the sources is that of a centrally condensed
isothermal sphere with
n(r) ∝ r-2
(a = 5/3). The resulting values are listed in Col.
(3) of Table 4 with uncertainties propagated from
the linewidth errors. We note that if the condensations have inner density profiles
shallower than ~r-2, the virial masses will be higher. For
example, if the density power-law index is p = 1 or
a = 10/9, the Mvir
values are larger by a factor of 1.5 compared to those with p = 2.
The virial parameters of the condensations were calculated following the definition by Bertoldi & McKee (1992), i.e., αvir = Mvir/M. The values are given in Col. (4) of Table 4 with the uncertainties derived by propagating the errors in both mass estimates. The uncertainties in αvir are quite large, but gravitational boundedness with αvir < 2 seems possible at least for SMM 6a and 6c, d. If the intrinsic N2H+(3−2) linewidths are smaller, the αvir values would also become smaller enhancing the importance of the condensations’ self-gravity.
4.3. Relative motions and interactions between the condensations
The centroid velocity difference between C17O and N2H+
for each condensation is small, only 0.045 km s-1 on average. This suggests
that the condensations are not moving much with respect to the lower-density envelope
(e.g., Kirk et al. 2007, 2010). The observed radial velocity data can also be used to study the
(possible) motions of the condensations relative to one another (e.g., ABMP07). The
average line-of-sight or radial velocity of the N2H+(3−2) lines is
9.43 km s-1 and the dispersion of the velocity centroids is
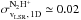 km s-1
(⟨ vLSR ⟩ = 9.48 km s-1 and
km s-1
(⟨ vLSR ⟩ = 9.48 km s-1 and
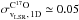 km s-1 for the
optically thin C17O lines). The latter value is taken to represent the
one-dimensional dispersion of the velocities of the high-density condensations (Peng et al. 1998; ABMP07). If the condensation
velocities perpendicular to the line of sight are the same as their radial velocities, the
three-dimensional dispersion of the velocities would be
km s-1 for the
optically thin C17O lines). The latter value is taken to represent the
one-dimensional dispersion of the velocities of the high-density condensations (Peng et al. 1998; ABMP07). If the condensation
velocities perpendicular to the line of sight are the same as their radial velocities, the
three-dimensional dispersion of the velocities would be
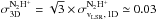 km s-1. If the
orientation of the SMM 6 filament is not exactly perpendicular to our
line of sight, and if the condensations would be moving along the
filament, one would expect to see an imprint of these motions in the radial velocity data.
The vLSR values would be expected to change monotonically if the movement of
condensations along the parent filament (in either direction) is taking place. However,
such a systematic trend is not observed.
km s-1. If the
orientation of the SMM 6 filament is not exactly perpendicular to our
line of sight, and if the condensations would be moving along the
filament, one would expect to see an imprint of these motions in the radial velocity data.
The vLSR values would be expected to change monotonically if the movement of
condensations along the parent filament (in either direction) is taking place. However,
such a systematic trend is not observed.
As mentioned in Appendix A the length of SMM 6 along its long axis is
L = 0.22 pc. Using the above value of
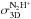 ,
a typical timescale for the condensations to cross the long axis of the parent core
becomes
,
a typical timescale for the condensations to cross the long axis of the parent core
becomes 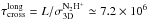 yr. On the other hand,
the average width of the filament, D = 2R = 0.06 pc,
suggests a radial crossing time of
yr. On the other hand,
the average width of the filament, D = 2R = 0.06 pc,
suggests a radial crossing time of 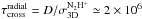 yr. Because the
projected separation between the condensations is also ≃0.06 pc (when SMM 6c and 6d are
treated as a one fragment), the time required for one condensation to encounter and
interact with another condensation is expected to be ~2 Myr (e.g., Takakuwa et al. 2003). We note that there are two effects that can
affect the rate of collision between condensations: i) gas drag caused by
the surrounding medium; and ii) gravitational focusing (ABMP07). While
the former is likely to make the real collision timescale longer, the latter could enhance
the collision rate. Moreover, gas gradients (density, velocity) in the parent filament
(cf. Kirk et al. 2013) could modify the time
required for the condensations to encounter and interact with one another.
yr. Because the
projected separation between the condensations is also ≃0.06 pc (when SMM 6c and 6d are
treated as a one fragment), the time required for one condensation to encounter and
interact with another condensation is expected to be ~2 Myr (e.g., Takakuwa et al. 2003). We note that there are two effects that can
affect the rate of collision between condensations: i) gas drag caused by
the surrounding medium; and ii) gravitational focusing (ABMP07). While
the former is likely to make the real collision timescale longer, the latter could enhance
the collision rate. Moreover, gas gradients (density, velocity) in the parent filament
(cf. Kirk et al. 2013) could modify the time
required for the condensations to encounter and interact with one another.
If the representative density of the condensations is a few × 105 cm-3, their free-fall time is only τff ~ 7 × 104 yr. Therefore, it seems unlikely that the condensations have time to interact with one another before collapsing into protostars or proto-brown dwarfs unless their lifetime is a few tens of τff, which seems unlikely (see, e.g., ABMP07, and references therein). Within the errors, it is in principle possible that the condensations are not gravitationally bound. For unbound condensations, one should also consider the dissipation timescale, τdiss = 2 Reff/ceff (e.g., Takakuwa et al. 2003). For the average condensation effective radius, 0.017 pc, and average ceff calculated from the N2H+(3−2) lines, 0.215 km s-1, τdiss becomes ~1.5 × 105 yr. The typical dissipation speed of the condensations would therefore be an order of magnitude shorter than the coalescence timescale.
4.4. Mass accretion onto the condensations
Some numerical simulations suggest that protostars can gain mass via competitive
accretion, i.e., accretion from a shared reservoir of material (Bonnell et al. 2001; Bonnell &
Bate 2006). Even though competitive accretion models apply to protostars that
accrete the available gas while moving around within the protocluster potential well, we
can still obtain a rough estimate of the accretion rate onto the starless condensations if
competitive-like accretion is occurring (cf. ABMP07). The mass accretion rate is given by
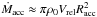 , where
ρ0 is the gas density of the background medium,
Vrel is the relative velocity of the subfragments with
respect to the ambient medium, and Racc is the accretion
radius (see Eq. (3) of ABMP07). The revised volume-average density of SMM 6 is about
~1.6 × 104 cm-3, the value we adopt for the background gas
density. We assume that Vrel is equal to
, where
ρ0 is the gas density of the background medium,
Vrel is the relative velocity of the subfragments with
respect to the ambient medium, and Racc is the accretion
radius (see Eq. (3) of ABMP07). The revised volume-average density of SMM 6 is about
~1.6 × 104 cm-3, the value we adopt for the background gas
density. We assume that Vrel is equal to
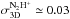 km s-1. 7 As concluded by ABMP07,
Racc is typically comparable to the condensation radius, and
therefore we estimate it to be the average effective radius of the condensations, i.e.,
0.017 pc. We thus derive the value
Ṁacc ~ 2.6 × 10-8 M⊙
yr-1. For comparison, the characteristic mass infall rate for a singular
isothermal sphere undergoing gravitational collapse,
~
km s-1. 7 As concluded by ABMP07,
Racc is typically comparable to the condensation radius, and
therefore we estimate it to be the average effective radius of the condensations, i.e.,
0.017 pc. We thus derive the value
Ṁacc ~ 2.6 × 10-8 M⊙
yr-1. For comparison, the characteristic mass infall rate for a singular
isothermal sphere undergoing gravitational collapse,
~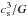 (Shu 1977), is
~1.5 × 10-6 M⊙ yr-1 at 10 K – about
60 times higher than the above Ṁacc value. Local gravitational
instability of the individual condensations is therefore likely to be more important than
competitive-like accretion (ABMP07). However, given the total mass of the parent core,
5.9 ± 1.3 M⊙, there is a considerable mass reservoir for
(some of) the condensations to increase their mass via accretion, although by how much
remains unclear. High-resolution spectral-line imaging of the whole core would be
necessary to study whether there are infall motions towards the condensations and to
estimate how much additional mass they could accrete (cf. Hacar & Tafalla 2011).
(Shu 1977), is
~1.5 × 10-6 M⊙ yr-1 at 10 K – about
60 times higher than the above Ṁacc value. Local gravitational
instability of the individual condensations is therefore likely to be more important than
competitive-like accretion (ABMP07). However, given the total mass of the parent core,
5.9 ± 1.3 M⊙, there is a considerable mass reservoir for
(some of) the condensations to increase their mass via accretion, although by how much
remains unclear. High-resolution spectral-line imaging of the whole core would be
necessary to study whether there are infall motions towards the condensations and to
estimate how much additional mass they could accrete (cf. Hacar & Tafalla 2011).
4.5. Molecular column densities and fractional abundances
Molecular column densities, fractional abundances with respect to H2, CO depletion factors, and the deuteration degrees.
To properly determine the column density of the molecules, we must first determine the optical thickness of the transition. The optical thickness of a spectral line can be derived from the radiative transfer equation, provided the line intensity and excitation temperature are known (as mentioned in Sect. 2, the optical thickness could not be derived through fitting the hf structure). We used the line peak intensities (TMB) to calculate the peak optical thicknesses, τ0 (see, e.g., Eq. (A.3) in Miettinen 2012a). The C17O(2−1) transition was assumed to be thermalised at the adopted gas temperature of the condensations, i.e., we set Tex = 10 K. This assumption is supported by the results obtained in Paper III [Tex(C17O) ≃ Tkin]. For the J = 3−2 transition of N2H+ and N2D+, we adopted the value Tex = 5 K. This is the typical value derived for the J = 3−2 line or lower-J lines of N2H+ and N2D+ (e.g., Caselli et al. 2002; Crapsi et al. 2005; Papers II–III; Friesen et al. 2013). Finally, the background temperature was assumed to be equal to the cosmic background radiation temperature of 2.725 K. The derived τ0 values are listed in Col. (7) of Table 3, with the uncertainties propagated from those in TMB.
The beam-averaged C17O column densities, N(C17O), were derived following the standard LTE analysis outlined, e.g., in the paper by Miettinen (2012a, Appendix A.3 therein). Because the τ0 values of the C17O lines are so small, even the total optical thicknesses are τtot ≪ 1 (as seen in a number of other studies; e.g., Ladd et al. 1998; Fuller & Ladd 2002). The N(C17O) values were therefore computed from the integrated line intensities under the assumption of optically thin line emission. In the two cases where the detected line does not cover all the hf components (SMM 6a and 2nd velocity component towards SMM 6c), the column density was scaled by the inverse of the relative line strength within the detected line. The errors in N(C17O) were propagated from those associated with the integrated intensity.
Because the strongest hf component of the J = 3−2 transition of N2H+ and N2D+ has a relative strength of only 11/63 = 0.1746, the τtot values inferred from τ0 are clearly above unity in most cases, i.e., the lines are optically thick (as is often the case for these lines; e.g., Crapsi et al. 2004; Fontani et al. 2006). The beam-averaged column densities of N2H+ and N2D+ were therefore computed from the FWHM linewidths and τtot (see, e.g., Eq. (10) in Paper II). The column density uncertainties were derived from those of Δv and τtot. If we are overestimating the true linewidths, the corresponding column densities would represent upper limits in this sense. We also checked our derivation of the column density by examining some additional optically thin hf satellites. The N2H+ line towards SMM 6a offered the best opportunity to do this because in this case five hf lines lying 1.5–2.4 km s-1 from the strongest component were clearly detected (Fig. 3). The integrated intensity of the satellite group is 0.05 ± 0.04 K km s-1 and its overall relatively strength is about 0.035. These can be converted into a total N(N2H+) of 1.5 ± 1.2 × 1013 cm-2, which is 0.6 ± 0.5 times the value derived from τtot. The results are in reasonable agreement within the error.
The fractional abundances of the molecules were calculated by dividing their column densities by the H2 column density. For this purpose, the N(H2) values were derived from the SABOCA map smoothed to the corresponding resolution of the line observations. The abundance errors were derived by propagating the errors in the column densities of the observed species and H2 molecules. The derived column densities and abundances are listed in Table 5.
4.6. CO depletion and deuterium fractionation
To investigate the amount of CO depletion in the condensations, we calculated the CO
depletion factors following the analysis presented in Sect. 4.5 of Paper III. In summary,
the canonical (or undepleted) CO abundance was adopted to be 9.5 × 10-5 (Frerking et al. 1982). With the additional assumptions
about the oxygen-isotopic ratios, namely
[16O]/[18O] = 500 and
[18O]/[17O] = 3.52, the canonical
C17O abundance was set to 5.4 × 10-8. This value was then divided
by the observed C17O abundance, which gives the CO depletion factor,
fD (the eighth column of Table 5). The fD uncertainty was propagated from
that in the observed abundance but it probably underestimates the true uncertainty by a
factor of 2–3 because of the uncertainties in the assumptions used (e.g., canonical
abundance, oxygen-isotopic ratios, etc.). For instance, Lacy et al. (1994) found the best-fitting CO abundance of
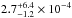 towards NGC 2024 in Orion B. Adopting this value would almost triple our
fD values. A lower limit to the condensation’s age can be
estimated to be comparable to its CO depletion timescale. Following the analysis presented
in Miettinen (2012a, Sect. 5.5 therein), at a
characteristic density of a few times 105 cm-3, the depletion time
is τdep ~ 2.2 × 104 yr.
towards NGC 2024 in Orion B. Adopting this value would almost triple our
fD values. A lower limit to the condensation’s age can be
estimated to be comparable to its CO depletion timescale. Following the analysis presented
in Miettinen (2012a, Sect. 5.5 therein), at a
characteristic density of a few times 105 cm-3, the depletion time
is τdep ~ 2.2 × 104 yr.
Towards each condensation, the N2H+ and N2D+ lines have similar radial velocities and linewidths. Therefore, the two lines are probably tracing the same gas. It is therefore reasonable to calculate the degree of deuterium fractionation by dividing the column density of the deuterated isotopologue N2D+ by its normal hydrogen-bearing form N2H+. The error was derived from the errors in the corresponding column densities. The results are shown in the last column of Table 5.
5. Discussion
5.1. Substructure within Ori B9–SMM 6
The studied core SMM 6 is one of the rare examples of a prestellar core that is fragmented into smaller condensations. Even though the theoretical predictions of the cylindrical fragmentation are not exactly similar to the observed characteristics, it still seems likely that the core has fragmented as a result of Jeans-type gravitational instability. In particular, the projected separation between the fragments is very close to the local thermal Jeans length. The radial crossing time of the filamentary parent core suggests that its fragmentation timescale is ~0.18 Myr.
The estimated masses of the condensations are ~0.2–0.6 M⊙ with a typical uncertainty of ~0.1 M⊙. The condensations are characterised by subsonic non-thermal motions with σNT ≃ 0.5cs assuming that the characteristic gas temperature is 10 K. The calculated condenstation virial parameters have relatively large errors, but it seems likely that they are self-gravitating. The minimum mass for a main-sequence star is M⋆ = 0.08 M⊙, below which the stellar temperature is not high enough to ignite proton-proton nuclear fusion. If the star formation efficiency for individual condensations is comparable to that of dense cores, ϵcore = M⋆/Mcore ~ 30−50% (e.g., Matzner & McKee 2000; Goodwin et al. 2008; André et al. 2009), they might be able to collapse to form stars without any additional mass accretion. At least for the most massive fragment, SMM 6a, this seems possible. The lowest mass fragments could also form substellar-mass objects or brown dwarfs (0.012 < M/M⊙ < 0.08; e.g., Mollière & Mordasini 2012). Examples of brown dwarfs that were likely formed or are currently forming via direct collapse include the wide (800 AU) binary brown dwarf system FU Tau A/B (Luhman et al. 2009) and the pre-brown dwarf condensation Oph B-11 discovered by André et al. (2012). Some of the very low luminosity objects, such as L1148-IRS, could also be the precursors of isolated brown dwarfs (Kauffmann et al. 2011). Brown dwarfs may also form (and subsequently be ejected) through disk fragmentation (see, e.g., Stamatellos & Whitworth 2009). In theory, the minimum mass of an object capable of forming through gas fragmentation is set by the opacity limit for radiative cooling and is in the range ~0.001–0.004 M⊙, that is to say, fragmentation could even form planetary-mass objects (e.g., Whitworth & Stamatellos 2006).
The dispersion of the condensation velocity centroids is smaller than the one-dimensional velocity dispersion of the parent core gas by a factor of 11 (0.02 vs. 0.22 km s-1, where the latter is derived from cs at 11 K and 0.1 km s-1 non-thermal contribution). Synthetic observations (e.g., N2H+) of simulated environments (decaying and driven turbulence) by Offner et al. (2008) also show that on the scale of cores, the dispersion of the velocity centroids is small (cf. Offner et al. 2009). Indeed, the motions of the condensations relative to one another appear to be so slow that they have no time to coalesce or gather together before evolving individually into protostars or proto-brown dwarfs. Moreover, despite the relatively large mass reservoir (~6 M⊙) surrounding the condensations, they are unlikely to be able to increase their mass via competitive-like accretion. Instead, the fragments’ internal self-gravity could induce inward motions and accretion of additional mass – a scenario that could be tested by future high-resolution observations.
5.2. CO depletion and deuterium fractionation in the condensations
The gas phase depletion factors of CO derived towards the condensations are in the range fD = 0.8 ± 0.4−3.6 ± 1.5. Therefore, there is no evidence of significant CO depletion. There are a few examples of high-density (~105 cm-3) cores where CO depletion is not prominent, namely L1495B, L1521B, and L1521E (Tafalla & Santiago 2004; Hirota et al. 2004). Deuterium fractionation in these Taurus cores is also found to be low (Hirota et al. 2004, and references therein), and they are considered to be both chemically and dynamically young.
However, as mentioned in Sect. 4.6, the undepleted CO abundance in Orion B9 might well be
higher than what we have adopted in the analysis. For this reason, we might be
underestimating the fD values by a factor of about three
(Lacy et al. 1994). Also, we have observed the
J = 2−1 rotational transition of C17O, the line whose 10-K
critical density is 2.1 × 104 cm-3. Apart from the condensations, we
might therefore be tracing lower density gas along the line of sight where CO is not
significantly depleted (e.g., Fontani et al. 2012).
The 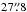 resolution of our
C17O observations also provides us with only beam-averaged
fD values. The above factors are likely to explain the
fD value less than unity derived for SMM 6d. Indeed, the
temperatures and densities of the condensations are likely to be so low and high,
respectively, that significant CO freeze-out is expected (e.g., Léger 1983; Rawlings et al.
1992). For example, Tafalla et al. (2004) estimated that the density at which CO
disappears from the gas phase is only 7.8 × 104 cm-3 and
2.5 × 104 cm-3 for the starless cores L1498 and L1517B in Taurus,
respectively. Moreover, for our condensations the CO freeze-out timescale is estimated to
be shorter than the free-fall time by a factor of about four (see Bergin & Tafalla 2007) and about eight times shorter than the
fragmentation timescale (τcross).
resolution of our
C17O observations also provides us with only beam-averaged
fD values. The above factors are likely to explain the
fD value less than unity derived for SMM 6d. Indeed, the
temperatures and densities of the condensations are likely to be so low and high,
respectively, that significant CO freeze-out is expected (e.g., Léger 1983; Rawlings et al.
1992). For example, Tafalla et al. (2004) estimated that the density at which CO
disappears from the gas phase is only 7.8 × 104 cm-3 and
2.5 × 104 cm-3 for the starless cores L1498 and L1517B in Taurus,
respectively. Moreover, for our condensations the CO freeze-out timescale is estimated to
be shorter than the free-fall time by a factor of about four (see Bergin & Tafalla 2007) and about eight times shorter than the
fragmentation timescale (τcross).
For comparison, Caselli et al. (1999) found that CO is depleted by a factor of ~10 at the dust peak of the prestellar core L1544. Similarly, Savva et al. (2003) found that, relative to the canonical abundances from Frerking et al. (1982), CO is depleted by a factor of ~10 in a sample of nine dense cores in Orion B. More recently, Christie et al. (2012) derived the mean (median) CO depletion factor of 19 (10) towards starless cores in the NGC 2024 region of Orion B. We note that in Paper III, where we also employed APEX/C17O(2−1) observations, we derived the value fD = 4.2 ± 1.3 towards a position lying 11″ north of the 350-μm peak of SMM 6a (where we now obtain the value 3.6 ± 1.5). One would expect to see stronger depletion towards the denser dust peak, but there are two reasons that explain this discrepancy: i) the C17O column densities in Paper III were derived through non-LTE RADEX analysis (van der Tak et al. 2007); and ii) the H2 column densities were computed from the LABOCA 870-μm peak flux densities assuming a thick ice mantle dust model of OH94 and a dust-to-gas ratio of 1/100 (see Appendix A).
When CO molecules freeze out on the surface of dust grains, the rate of gas-phase deuterium fractionation increases (e.g., Dalgarno & Lepp 1984). The reason for this is that the main destruction path of H2D+, namely H2D+ + CO → HCO+ or DCO+, is no longer effective, enabling H2D+ to donate its deuteron to other species (e.g., H2D+ + N2 → N2H+ or N2D+). The levels of N2D+/N2H+ deuteration we derive here, 0.30 ± 0.07−0.43 ± 0.09, are relatively high compared to those found in other studies of starless cores. For example, Crapsi et al. (2005) found N2D+/N2H+ column density ratios in the range <0.02−0.44 ± 0.08 for their sample of starless/prestellar cores. Friesen et al. (2013) derived the values ≲0.02−0.20 ± 0.04 towards starless and protostellar cores in Perseus with no significant difference between the two types of objects. Through radiative transfer modelling of the starless core L183, Pagani et al. (2007) derived a deuteration level of 0.70 ± 0.12 at the CO-depleted core centre, exceeding the highest value found in the present study. As for fD, a high value of deuteration (0.60 ± 0.08) was derived in Paper III towards the edge of SMM 6. Again, the column density calculations were based on RADEX analysis (N2H+) and LTE modelling with CLASS/Weeds (N2D+), and are therefore not directly comparable with the present results.
The deuterium fractionation of N2H+ and the amount of CO depletion are found to be positively correlated in starless/prestellar cores and the envelopes of Class 0 protostars (e.g., Crapsi et al. 2004, 2005; Emprechtinger et al. 2009). This is not evident among our condensations. In fact, the most CO-depleted fragment, SMM 6a, shows the lowest level of deuteration. Our source sample is, however, very small, and within the error bars the values of fD and N(N2D+)/N(N2H+) are comparable to each other, suggesting that they are in a similar stage of chemical and dynamical evolution. This conforms to the scenario where the condensations were formed simultaneously via core fragmentation. The high levels of molecular D/H ratio suggest that they are highly evolved, and possibly at the onset of protostellar collapse. This seems to contradict the low depletion factors in the condensations, but as discussed above we are very likely underestimating the fD values.
6. Summary and conclusions
We have used the APEX telescope to observe the molecular-line transitions C17O(2−1), N2H+(3−2), and N2D+(3−2) towards the low-mass condensations inside the prestellar core Ori B9–SMM 6 which were discovered by our previous SABOCA 350-μm imaging of the core (Paper III). The present work is one of the first studies of the dynamics of subfragments within a prestellar core.
The condensations were likely formed as a result of Jeans-type fragmentation of the parent core. Based on the C17O velocity dispersion data, we estimate that the fragmentation timescale of the filamentary parent core is ~1.8 × 105 yr. The condensations show only subsonic internal non-thermal motions (σNT = 0.1 km s-1 if Tkin = 10 K), and most of them are likely to be gravitationally bound. The condensation-to-condensation kinematics was investigated by employing the velocity information provided by the high-density tracer N2H+(3−2). The estimated timescale required for the condensations to coalesce is a few Myr, which is much longer than their free-fall timescale. It is therefore unlikely that the subfragments will have time to coalesce before collapsing into protostars or proto-brown dwarfs, or fragment even further down to planetary-mass objects. Significant accretion in a competitive fashion between the condensations from the parent core’s mass reservoir is also unlikely. The reason for this is that the condensations’ self-gravity is expected to lead to a much higher (by a factor of ~60) mass infall rate than what is provided by competitive-like process.
The present molecular data were also used to study the amount of CO depletion and deuterium fractionation in the condensations. The CO depletion factors we derive, fD = 0.8 ± 0.4−3.6 ± 1.5, do not suggest any significant CO freeze-out. However, these values are based on the canonical CO abundance of 9.5 × 10-5 relative to H2, whereas in Orion B this value can be considerably higher (by a factor of ~3). Therefore, at least an intermediate level of CO depletion seems possible in the condensations. The CO depletion timescale for the condensations (~2.2 × 104 yr) is shorter than the fragmentation timescale (by a factor of ~8) and the free-fall time of the condensations (~7 × 104 yr). Higher-resolution observations would undoubtedly reveal more CO-depleted condensation interiors. The derived N2H+ and N2D+ column densities lie in the range 0.7−2.5 × 1013 and 2.5−7.6 × 1012 cm-2, and the corresponding fractional abundances are ~0.9−2.3 × 10-9 and ~4.9−9.9 × 10-10, respectively. The deuterium fractionation of N2H+, or the N2D+/N2H+ column density ratio, lies in the range 0.30 ± 0.07−0.43 ± 0.09. This is a stronger level of deuteration than is typically observed in starless/prestellar cores and should require significant gas-phase depletion of CO. The very high molecular deuteration observed towards the condensations suggests that they are in an advanced stage of chemical evolution and possibly on the verge of gravitational collapse. The actual fate of the subfragments, i.e., whether they can collapse into protostellar or substellar objects, remains to be elucidated. The lowest-mass condensations within SMM 6 could be the precursor sites of brown dwarf formation.
http://www.submm.caltech.edu/~tab/molecular_data/ collisional_rates.html
Grenoble Image and Line Data Analysis Software is provided and actively developed by IRAM, and is available at http://www.iram.fr/IRAMFR/GILDAS
ABMP07 assumed that the velocity distribution of their sample of condensations was given
by the Maxwell-Boltzmann distribution, and adopted Vrel for
the average relative speed of a condensation (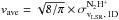 in our notation). The Maxwell-Boltzmann distribution is not expected to apply to our small
number of subfragments, but we note that the value of
in our notation). The Maxwell-Boltzmann distribution is not expected to apply to our small
number of subfragments, but we note that the value of
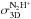 is very close to vave.
is very close to vave.
Acknowledgments
We are grateful to the staff at the APEX telescope for performing the service-mode heterodyne observations presented in this paper. We also appreciate the positive comments and insight of the anonymous referee. O.M. acknowledges the Academy of Finland for the financial support through grant 132291. S.S.R.O. acknowledges support from NASA through Hubble Fellowship grant HF-51311. This research has made use of NASA’s Astrophysics Data System and the NASA/IPAC Infrared Science Archive, which is operated by the JPL, California Institute of Technology, under contract with the NASA. SPIRE has been developed by a consortium of institutes led by Cardiff Univ. (UK) and including: Univ. Lethbridge (Canada); NAOC (China); CEA, LAM (France); IFSI, Univ. Padua (Italy); IAC (Spain); Stockholm Observatory (Sweden); Imperial College London, RAL, UCLMSSL, UKATC, Univ. Sussex (UK); and Caltech, JPL, NHSC, Univ. Colorado (USA). This development has been supported by national funding agencies: CSA (Canada); NAOC (China); CEA, CNES, CNRS (France); ASI (Italy); MCINN (Spain); SNSB (Sweden); STFC, UKSA (UK); and NASA (USA).
References
- André, P., Belloche, A., Motte, F., & Peretto, N. 2007, A&A, 472, 519 (ABMP07) [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- André, P., Basu, S., & Inutsuka, S. 2009, in Structure Formation in Astrophysics, ed. G. Chabrier (Cambridge Univ. Press), 254 [Google Scholar]
- André, P., Men’shchikov, A., Bontemps, S., et al. 2010, A&A, 518, L102 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- André, P., Ward-Thompson, D., & Greaves, J. 2012, Science, 337, 69 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Arzoumanian, D., André, P., Didelon, P., et al. 2011, A&A, 529, L6 [Google Scholar]
- Bastien, P., Arcoragi, J.-P., Benz, W., et al. 1991, ApJ, 378, 255 [NASA ADS] [CrossRef] [Google Scholar]
- Belitsky, V., Lapkin, I., Vassilev, V., et al. 2007, in Proc. of joint 32nd International Conference on Infrared Millimeter Waves and 15th International Conference on Terahertz Electronics, September 3–7, 2007, City Hall, Cardiff, Wales, UK, 326 [Google Scholar]
- Bergin, E. A., & Tafalla, M. 2007, ARA&A, 45, 339 [NASA ADS] [CrossRef] [Google Scholar]
- Bertoldi, F., & McKee, C. F. 1992, ApJ, 395, 140 [NASA ADS] [CrossRef] [Google Scholar]
- Bonnell, I. A., & Bate, M. R. 2006, MNRAS, 370, 488 [NASA ADS] [CrossRef] [Google Scholar]
- Bonnell, I. A., Bate, M. R., Clarke, C. J., & Pringle, J. E. 2001, MNRAS, 323, 785 [NASA ADS] [CrossRef] [Google Scholar]
- Caselli, P., Walmsley, C. M., Tafalla, M., et al. 1999, ApJ, 523, L165 [NASA ADS] [CrossRef] [Google Scholar]
- Caselli, P., Benson, P. J., Myers, P. C., & Tafalla, M. 2002, ApJ, 572, 238 [NASA ADS] [CrossRef] [Google Scholar]
- Chen, X., & Arce, H. G. 2010, ApJ, 720, L169 [NASA ADS] [CrossRef] [Google Scholar]
- Christie, H., Viti, S., Yates, J., et al. 2012, MNRAS, 422, 968 [NASA ADS] [CrossRef] [Google Scholar]
- Crapsi, A., Caselli, P., Walmsley, C. M., et al. 2004, A&A, 420, 957 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Crapsi, A., Caselli, P., Walmsley, C. M., et al. 2005, ApJ, 619, 379 [Google Scholar]
- Dalgarno, A., & Lepp, S. 1984, ApJ, 287, L47 [NASA ADS] [CrossRef] [Google Scholar]
- Draine, B. T. 2011, Physics of the Interstellar and Intergalactic Medium (Princeton University Press) [Google Scholar]
- Dubernet, M. L., Alexander, M. H., Ba, Y. A., et al. 2013, A&A, 553, A50 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Duchêne, G., & Kraus, A. L. 2013, ARA&A, submitted [arXiv:1303.3028] [Google Scholar]
- Emprechtinger, M., Caselli, P., Volgenau, N. H., et al. 2009, A&A, 493, 89 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Fisher, R. T. 2004, ApJ, 600, 769 [NASA ADS] [CrossRef] [Google Scholar]
- Fontani, F., Caselli, P., Crapsi, A., et al. 2006, A&A, 460, 709 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Fontani, F., Giannetti, A., Beltrán, M. T., et al. 2012, MNRAS, 423, 2342 [NASA ADS] [CrossRef] [Google Scholar]
- Frerking, M. A., Langer, W. D., & Wilson, R. W. 1982, ApJ, 262, 590 [NASA ADS] [CrossRef] [Google Scholar]
- Friesen, R. K., Kirk, H. M., & Shirley, Y. L. 2013, ApJ, 765, 59 [NASA ADS] [CrossRef] [Google Scholar]
- Fuller, G. A., & Ladd, E. F. 2002, ApJ, 573, 699 [NASA ADS] [CrossRef] [Google Scholar]
- Goodwin, S. P., Kroupa, P., Goodman, A., & Burkert, A. 2007, in Protostars and Planets V, eds. B. Reipurth, D. Jewitt, & K. Keil (Tucson: Univ. of Arizona Press), 133 [Google Scholar]
- Goodwin, S. P., Nutter, D., Kroupa, P., et al. 2008, A&A, 477, 823 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Güsten, R., Nyman, L. Å., Schilke, P., et al. 2006, A&A, 454, L13 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hacar, A., & Tafalla, M. 2011, A&A, 533, A34 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hartmann, L. 2002, ApJ, 578, 914 [NASA ADS] [CrossRef] [Google Scholar]
- Hill, T., Motte, F., Didelon, P., et al. 2011, A&A, 533, A94 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hirota, T., Maezawa, H., & Yamamoto, S. 2004, ApJ, 617, 399 [NASA ADS] [CrossRef] [Google Scholar]
- Inutsuka, S.-I., & Miyama, S. M. 1992, ApJ, 388, 392 [NASA ADS] [CrossRef] [Google Scholar]
- Kamazaki, T., Saito, M., Hirano, N., & Kawabe, R. 2001, ApJ, 548, 278 [NASA ADS] [CrossRef] [Google Scholar]
- Kauffmann, J., Bertoldi, F., Bourke, T. L., et al. 2008, A&A, 487, 993 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kauffmann, J., Bertoldi, F., Bourke, T. L., et al. 2011, MNRAS, 416, 2341 [NASA ADS] [CrossRef] [Google Scholar]
- Kirk, H., Johnstone, D., & Tafalla, M. 2007, ApJ, 668, 1042 [NASA ADS] [CrossRef] [Google Scholar]
- Kirk, J. M., Crutcher, R. M., & Ward-Thompson, D. 2009, ApJ, 701, 1044 [NASA ADS] [CrossRef] [Google Scholar]
- Kirk, H., Pineda, J. E., Johnstone, D., & Goodman, A. 2010, ApJ, 723, 457 [NASA ADS] [CrossRef] [Google Scholar]
- Kirk, H., Myers, P. C., Bourke, T. L., et al. 2013, ApJ, 766, 115 [NASA ADS] [CrossRef] [Google Scholar]
- Klein, B., Hochgürtel, S., Krämer, I., et al. 2012, A&A, 542, L3 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kraus, A. L., & Hillenbrand, L. A. 2012, ApJ, 757, 141 [NASA ADS] [CrossRef] [Google Scholar]
- Kuiper, T. B. H., Langer, W. D., & Velusamy, T. 1996, ApJ, 468, 761 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Lacy, J. H., Knacke, R., Geballe, T. R., & Tokunaga, A. T. 1994, ApJ, 428, L69 [NASA ADS] [CrossRef] [Google Scholar]
- Ladd, E. F., Fuller, G. A., & Deane, J. R. 1998, ApJ, 495, 871 [NASA ADS] [CrossRef] [Google Scholar]
- Langer, W. D., Velusamy, T., Kuiper, T. B. H., et al. 1995, ApJ, 453, 293 [NASA ADS] [CrossRef] [Google Scholar]
- Larson, R. B. 1985, MNRAS, 214, 379 [NASA ADS] [Google Scholar]
- Léger, A. 1983, A&A, 123, 271 [NASA ADS] [Google Scholar]
- Lemme, C., Walmsley, C. M., Wilson, T. L., & Muders, D. 1995, A&A, 302, 509 [NASA ADS] [Google Scholar]
- Luhman, K. L., Mamajek, E. E., Allen, P. R., et al. 2009, ApJ, 691, 1265 [NASA ADS] [CrossRef] [Google Scholar]
- Matzner, C. D., & McKee, C. F. 2000, ApJ, 545, 364 [NASA ADS] [CrossRef] [Google Scholar]
- Miettinen, O. 2012a, A&A, 540, A104 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Miettinen, O. 2012b, A&A, 545, A3 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Miettinen, O., & Offner, S. S. R. 2013, A&A, 553, A88 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Miettinen, O., Harju, J., Haikala, L. K., Kainulainen, J., & Johansson, L. E. B. 2009, A&A, 500, 845 (Paper I) [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Miettinen, O., Harju, J., Haikala, L. K., & Juvela, M. 2010, A&A, 524, A91 (Paper II) [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Miettinen, O., Harju, J., Haikala, L. K., & Juvela, M. 2012, A&A, 538, A137 (Paper III) [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Mollière, P., & Mordasini, C. 2012, A&A, 547, A105 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Nakamura, F., Takakuwa, S., & Kawabe, R. 2012, ApJ, 758, L25 [NASA ADS] [CrossRef] [Google Scholar]
- Offner, S. S. R., Krumholz, M. R., Klein, R. I., & McKee, C. F. 2008, AJ, 136, 404 [NASA ADS] [CrossRef] [Google Scholar]
- Offner, S. S. R., Hansen, C. E., & Krumholz, M. R. 2009, ApJ, 704, L124 [NASA ADS] [CrossRef] [Google Scholar]
- Offner, S. S. R., Kratter, K. M., Matzner, C. D., Krumholz, M. R., & Klein, R. I. 2010, ApJ, 725, 1485 [NASA ADS] [CrossRef] [Google Scholar]
- Ossenkopf, V., & Henning, T. 1994, A&A, 291, 943 (OH94) [NASA ADS] [Google Scholar]
- Ostriker, J. 1964, ApJ, 140, 1056 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- Pagani, L., Bacmann, A., Cabrit, S., & Vastel, C. 2007, A&A, 467, 179 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Pagani, L., Daniel, F., & Dubernet, M.-L. 2009, A&A, 494, 719 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Palmeirim, P., André, P., Kirk, J., et al. 2013, A&A, 550, A38 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Peng, R., Langer, W. D., Velusamy, T., et al. 1998, ApJ, 497, 842 [NASA ADS] [CrossRef] [Google Scholar]
- Raghavan, D., McAlister, H. A., Henry, T. J., et al. 2010, ApJS, 190, 1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Rawlings, J. M. C., Hartquist, T. W., Menten, K. M., & Williams, D. A. 1992, MNRAS, 255, 471 [NASA ADS] [CrossRef] [Google Scholar]
- Savva, D., Little, L. T., Phillips, R. R., & Gibb, A. G. 2003, MNRAS, 343, 259 [NASA ADS] [CrossRef] [Google Scholar]
- Schöier, F. L., van der Tak, F. F. S., van Dishoeck, E. F., & Black, J. H. 2005, A&A, 432, 369 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Schnee, S., Enoch, M., Johnstone, D., et al. 2010, ApJ, 718, 306 [NASA ADS] [CrossRef] [Google Scholar]
- Shu, F. H. 1977, ApJ, 214, 488 [NASA ADS] [CrossRef] [Google Scholar]
- Stamatellos, D., & Whitworth, A. P. 2003, A&A, 407, 941 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Stamatellos, D., & Whitworth, A. P. 2009, MNRAS, 392, 413 [Google Scholar]
- Tafalla, M., & Santiago, J. 2004, A&A, 414, L53 [Google Scholar]
- Tafalla, M., Myers, P. C., Caselli, P., & Walmsley, C. M. 2004, A&A, 416, 191 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Takakuwa, S., Mikami, H., & Saito, M. 1998, ApJ, 501, 723 [NASA ADS] [CrossRef] [Google Scholar]
- Takakuwa, S., Kamazaki, T., Saito, M., & Hirano, N. 2003, ApJ, 584, 818 [NASA ADS] [CrossRef] [Google Scholar]
- Tohline, J. E. 2002, ARA&A, 40, 349 [NASA ADS] [CrossRef] [Google Scholar]
- van der Tak, F. F. S., Black, J. H., Schöier, F. L., et al. 2007, A&A, 468, 627 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Vassilev, V., Meledin, D., Lapkin, I., et al. 2008a, A&A, 490, 1157 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Vassilev, V., Henke, D., Lapkin, I., et al. 2008b, IEEE Microwave and Wireless Components Letters, 18, 55 [Google Scholar]
- Ward-Thompson, D., Scott, P. F., Hills, R. E., & André, P. 1994, MNRAS, 268, 276 [NASA ADS] [CrossRef] [Google Scholar]
- Whitworth, A. P., & Stamatellos, D. 2006, A&A, 458, 817 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Williams, J. P., de Geus, E. J., & Blitz, L. 1994, ApJ, 428, 693 [NASA ADS] [CrossRef] [Google Scholar]
- Wiseman, J. J., & Ho, P. T. P. 1998, ApJ, 502, 676 [NASA ADS] [CrossRef] [Google Scholar]
Appendix A: Revision of core/condensation properties presented in Paper III
In Paper III, the condensation masses and densities were estimated assuming that Tdust equaled the Tkin derived towards the selected position near the edge of SMM 6, i.e., 11.0 ± 0.4 K. However, all the subcondensations except SMM 6a lie outside the 40″ beam of the NH3 measurements used to derive Tkin. Moreover, Tdust is expected to be lower in the embedded small condensations because they are better shielded from the external dust heating radiation field. On these grounds, we revise the temperature-dependent condensation properties by assuming that Tdust = 10 K. This seems a reasonable choice given that the gas temperature is about 11 K at the core edge.
In addition, it was previously assumed that the 350-μm dust mass absorption (or emission) coefficient, i.e., the dust opacity per unit dust mass, was κ350 μm = 10 cm2 g-1. This value was interpolated from the widely used Ossenkopf & Henning (1994, hereafter OH94) model describing graphite-silicate dust grains that have coagulated and accreted thick ice mantles over a period of 105 yr at a gas density of nH = 105 cm-3. If we assume that grains have thin ice mantles, which might be more appropriate here (e.g., Stamatellos & Whitworth 2003 and references therein)8, κ350 μm is decreased to 7.84 cm2 g-1. In Paper III, the dust-to-gas ratio was assumed to be 1/100. However, this value refers to the canonical dust-to-hydrogen mass ratio, Mdust/MH (e.g., Draine 2011; Table 23.1 therein). If we assume solar composition, i.e., the mass fractions for hydrogen, helium, and heavier elements are X = 0.71, Y = 0.27, and Z = 0.02, respectively, the ratio of total mass (H+He+metals) to hydrogen mass is 1/X ≃ 1.41. The total dust-to-gas mass ratio is therefore Mdust/Mgas = Mdust/(1.41MH) = 1/141. We note that for the assumed gas composition, the mean molecular weight per free particle is μp = 2.37 and that per H2 molecule is μH2 ≃ 2.82 (Kauffmann et al. 2008; Appendix A.1 therein).
The masses (M), peak beam-averaged H2 column densities [N(H2)], and averaged H2 number densities [⟨ n(H2) ⟩] were computed using the standard optically thin dust emission formulation (see, e.g., Eqs. (2) and (3) in Paper I, and Eq. (1) in Paper III). The results are given in Table 1. The uncertainties in M and N(H2) were propagated from the uncertainties in the integrated flux density and the peak surface brightness, respectively. We note that the uncertainty in dust opacity, which is likely a factor ≳2, is the major source of error in the mass and column density estimate. The error in ⟨ n(H2) ⟩ was propagated from that of M.
We note that the total mass of the SMM 6 core was previously determined from the LABOCA 870-μm emission adopting the thick ice mantle model of OH94, in which case κ870 μm ≃ 1.7 cm2 g-1. If we employ the above thin ice mantle model, κ870 μm is 1.38 cm2 g-1. Moreover, the 870-μm flux density of the source, when integrated inside the 0.09 Jy beam-1 or 3σ contour of the re-reduced LABOCA map (see Miettinen & Offner 2013), is S870 μm = 1.03 ± 0.22 Jy. For Tdust = 11.0 ± 0.4 K and Mdust/Mgas = 1/141, these revisions yield a mass of 5.9 ± 1.3 M⊙, a factor of 1.4 lower than reported previously (see Paper II). The discrepancy mostly stems from the larger area previously used to compute S870 μm. The virial parameter of the core from Paper II is accordingly revised to αvir = 1.1 ± 0.2, which still satisfies the gravitational boundedness condition of αvir < 2 and is very close to virial equilibrium (αvir = 1). Therefore, the source can be considered a candidate prestellar core (cf. Sect. 4.2).
The projected length of the SMM 6 filament along its long axis, as measured from the Herschel 250-μm emission shown in Fig. 1, is about or L = 0.22 pc. This corresponds to the extent of the 3σ LABOCA 870-μm emission (Paper III; Fig. 9 therein). The corresponding mass per unit length, or line mass, is Mline ≃ 27 ± 6 M⊙ pc-1.
All Tables
One-dimensional non-thermal velocity dispersions, virial masses, and virial parameters of the condensations.
Molecular column densities, fractional abundances with respect to H2, CO depletion factors, and the deuteration degrees.
All Figures
 |
Fig. 1 SABOCA 350-μm image of the fragmented prestellar core SMM 6 in Orion
B9. The image is displayed with power-law scaling, and the colour bar indicates the
surface-brightness scale in Jy beam-1. The overlaid green SABOCA contours
are plotted at three times the noise level (3σ = 180 mJy
beam-1). The white contours show the Herschel/SPIRE
250-μm dust continuum emission (18″ resolution); these contours are
plotted at 3.0 and 3.5 Jy beam-1. The green plus sign indicates the target
position of our previous molecular-line observations, while the other plus signs mark
the target positions of the present study (i.e., the 350-μm peaks). A
scale bar indicating the 0.05 pc projected length is shown in the top left, with the
assumption of a 450 pc line-of-sight distance. The three circles in the upper left
corner show the effective FWHM of the SABOCA beam
( |
| In the text | |
 |
Fig. 2 Herschel/SPIRE 250-μm far-infrared image towards the Orion B9 star-forming filament. The image is shown with a square-root scaling to improve the contrast between bright and faint features. The image is overlaid with black contours of SABOCA 350-μm emission. The SABOCA contours start at 3σ and increase at this interval (Paper III). The SABOCA data towards the IRAS 05399/SMM 1 -system with a 1σ noise level of 80 mJy beam-1 are taken from Miettinen & Offner (2013). Selected cores are labelled. The ring-like structure comprising partly of SMM 6 is highlighted with a white dashed circle of radius or ~0.3 pc. A scale bar indicating the 0.3 pc projected length is shown in the bottom left corner. |
| In the text | |
 |
Fig. 3 Hanning-smoothed C17O(2−1), N2H+(3−2), and N2D+(3−2) spectra. Hyperfine-structure fits to the lines are overlaid in green. In each panel, the vertical red dashed line indicates the radial velocity of the C17O(2−1) line. Note that towards SMM 6c, two velocity components of C17O(2−1) and N2H+(3−2) (at ~2.3 and ~9.4 km s-1) are detected. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.