| Issue |
A&A
Volume 555, July 2013
|
|
|---|---|---|
| Article Number | A103 | |
| Number of page(s) | 14 | |
| Section | Interstellar and circumstellar matter | |
| DOI | https://doi.org/10.1051/0004-6361/201220190 | |
| Published online | 08 July 2013 | |
Multiwavelength interferometric observations and modeling of circumstellar disks⋆,⋆⋆
1
Max-Planck-Institut für Astronomie,
Königstuhl 17,
69117
Heidelberg,
Germany
2
Ludwig-Maximilians-Universität, Universitäts-Sternwarte München,
Scheinerstraße 1,
81679
München,
Germany
3
Universität zu Köln, I. Physikalisches Institut,
Zülpicher Straße
77, 50937
Köln,
Germany
4
Universität Kiel, Institut für Theoretische Physik und
Astrophysik, Leibnizstraße
15, 24098
Kiel,
Germany
5
MTA Research Center for Astronomy and Earth Sciences, Konkoly
Thege Miklós Astronomical Institute, 1525
Budapest,
Hungary
Received:
8
August
2012
Accepted:
4
April
2013
Aims. We investigate the structure of the innermost region of three circumstellar disks around pre-main sequence stars HD 142666, AS 205 N, and AS 205 S. We determine the inner radii of the dust disks and, in particular, search for transition objects where dust has been depleted and inner disk gaps have formed at radii of a few tenths of AU up to several AU.
Methods. We performed interferometric observations with IOTA, AMBER, and MIDI in the infrared wavelength ranges 1.6−2.5 μm and 8−13 μm with projected baseline lengths between 25 m and 102 m. The data analysis was based on radiative transfer simulations in 3D models of young stellar objects (YSOs) to reproduce the spectral energy distribution and the interferometric visibilities simultaneously. Accretion effects and disk gaps could be considered in the modeling approach. Results from previous studies restricted the parameter space.
Results. The objects of this study were spatially resolved in the infrared wavelength range using the interferometers. Based on these observations, a disk gap could be found for the source HD 142666 that classifies it as transition object. There is a disk hole up to a radius of Rin = 0.30 AU and a (dust-free) ring between 0.35 AU and 0.80 AU in the disk of HD 142666. The classification of AS 205 as a system of classical T Tauri stars could be confirmed using the canonical model approach, i.e., there are no hints of disk gaps in our observations.
Key words: infrared: stars / accretion, accretion disks / protoplanetary disks / instrumentation: interferometers / stars: general / radiative transfer
Based on observations made with telescopes of the European Organisation for Astronomical Research in the southern Hemisphere (ESO) at the Paranal Observatory, Chile, under the programs 073.A-9014, 075.C-0014, 075.C-0064, 075.C-0253, 077.C-0750, 079.C-0101, and 079.C-0595.
Appendix A is available in electronic form at http://www.aanda.org
© ESO, 2013
1. Introduction
Observations of the innermost region of circumstellar disks, i.e., at a distance of a few tenths of AU from the central star, are motivated by the outcomes of theoretical investigations that predict planet formation there. The ambient conditions in this region, such as high direct stellar radiation, high dust particle densities, and long-lived vortices, can favor planet formation (Klahr & Bodenheimer 2003; Wünsch et al. 2005; Johansen et al. 2007). Close to the star, the dust temperature reaches values up to the sublimation temperature of ~1500 K resulting in near-infrared (NIR) and mid-infrared (MIR) radiation excess. First, highly resolved, i.e., interferometric observations of young stellar objects (YSOs) in the NIR wavelength range (Millan-Gabet et al. 2001) and the subsequent successful modeling of these measurements using simple rings have motivated the idea of a compact, potentially puffed-up rim at the inner dust disk (Dullemond et al. 2001) where dust at the inner edge of the disk is strongly heated by direct stellar irradiation. However, further interferometric measurements have suggested a more complex disk model where accretion and/or an optically thin envelope close to the inner edge are additionally implemented (Schegerer et al. 2008).
The viscous evolution of the disk, i.e., accretion and spreading (Lynden-Bell & Pringle 1974; Hartmann et al. 1998; Armitage et al. 1999), photoevaporation (Hollenbach et al. 1994; Clarke et al. 2001; Alexander et al. 2006a,b), dust evolution (Monnier & Millan-Gabet 2002), and planet formation (Youdin & Shu 2002) strongly affect the inner disk structure. The inner dust disk radius Rin is initially determined by the sublimation temperature of dust in the case of disks with ages up to several million years. For T Tauri stars, the primary inner disk radius Rin is in the range of 0.1 AU. But if the viscous accretion inflow rate falls below the photoevaporation rate, the dust density strongly reduces in the inner disk regions where the inner disk radius can increase or a nearly dust-free inner ring can form on a time scale of 105 years (Clarke et al. 2001; see Dullemond et al. 2006, for a review). Tidal forces, which can be caused by a stellar companion or a newly formed planet, can accelerate the formation of disk gaps (Bouwman et al. 2006; Bryden et al. 1999). Spectrophotometric measurements of YSOs show a strong decrease in infrared radiative excess with age (Haisch et al. 2001; Carpenter et al. 2005; Sicilia-Aguilar et al. 2006, 2009) which is assumed to be caused by the depletion of small dust particles (Weinberger et al. 1999; Grady et al. 2001). Classical T Tauri stars (CTTS) usually fulfill the photometric conditions K − N > 2 mag and K − L > 0.4 mag (Kenyon & Hartmann 1995). But there are some YSOs where K − N > 2 mag and K − L < 0.4 mag. McCabe et al. (2003) assume that the latter color relation could be a hint of a transition disk object (TO) where an inner disk gap has been formed. To derive further indicators for the classification of YSOs as CTTS and TO, various infrared color relations of huge samples of pre-main sequence stars from different star-forming regions have been studied (e.g., Sicilia-Aguilar et al. 2006, 2009). These studies conclude that objects with no significant infrared excess at λ < 6 μm (but with excess at longer wavelengths) can be classified as TO. However, as pointed out by Ercolano et al. (2009), the missing excess in the NIR wavelength range is a necessary but not sufficient condition for a TO, for late-type stars in particular.
Observations that spatially resolve the inner disk region can directly identify a TO. In fact, Brown et al. (2008) spatially resolved a 40 AU radius inner gap in the circumstellar disk around LkHα 330 in the far-infrared (FIR) wavelength range with the Submillimeter Array. There are more spatially resolved observations of correspondingly large gaps in circumstellar disks (e.g., Guilloteau et al. 2008; Sauter et al. 2009). However, the spatial resolution of the innermost disk region, where the formation of disk gaps is assumed to start, is possible by interferometric observations in the MIR and NIR wavelength range. Considering the spectral energy distribution (SED) and interferometric observations in the MIR wavelength range, Ratzka et al. (2007) found a depletion of the innermost disk regions from warm dust grains, i.e., an increase in the inner disk radius of the TO TW Hya, which supplements the model of Calvet et al. (2002). Akeson et al. (2011) have recently presented a three-component model of this transition object.
In this study, we present high-resolution interferometric, multiwavelength observations of three YSOs using the Infrared Optical Telescope Array (IOTA), the Astronomical Multi-BEam combineR (AMBER), and the MID-infrared Interferometer instrument (MIDI). The interferometric visibilities V that were obtained from these observations allow study of the spatial distribution of dust with temperatures between several 100 K (MIDI) and <1500 K (IOTA, AMBER) supposedly at the innermost regions of protoplanetary disks. In Sect. 2, we describe our interferometric observations and the subsequent data reduction. Computer models of YSOs where the Monte Carlo method is used can explain the observations (Sect. 3). We additionally consider previous studies concerning stellar and accretion parameters, as well as photometric measurements, to get a coherent model of the YSOs. The results of our interferometric observations and modeling efforts are presented in Sect. 4. The uniqueness of our results is discussed in more detail in Sect. 5. There, we also discuss a more advanced modeling approach. We conclude the study in Sect. 6.
2. Interferometric observations and data reduction
 |
Fig. 1 Crosses in the SEDs (first column) represent measured photometric data obtained from the literature (Appendix A). The solid and the dashed curves represent the SED obtained from computer models, as well as its initial stellar flux, respectively. The dark and light gray bars in the figures of the second column result from H band images at λ = 1.65 μm of the models of HD 142666, while the crosses with the vertical error bars represent the measurements with IOTA. The bar width represents the interval that constrains the NIR visibilities V(λ) for different PAs but the same inclination of the model. Numbers added to the crosses are the position angles of the corresponding interferometric baseline. The measured MIR, spectrally dispersed visibilities (3rd and 4th columns) are represented by solid lines with error bars. The modeled visibilities (gray bars) were derived from model images at wavelengths of 8.5 μm, 9.5 μm, 10.6 μm, 11.5 μm, and 12.5 μm. The bar width represents the interval that constrains the MIR visibilities V(λ) for different PAs but the same inclination of the model. The upper row shows the effect after increasing the inner disk radius by a factor of five, from Rin = 0.1 AU (light gray; initial model i) to Rin = 0.5 AU (dark gray, model ii). The second row shows the result after increasing the profile parameters from β = 1.0 to β = 1.1 (model iii). The mass accretion rate is increased to Ṁ = 7 × 10-8 M⊙a-1 in model (iv) displayed in the third row while the mass density at the inner edge is decreased by a factor of fρ = 0.01 in the model (v) shown in the fourth row. In the sixth row, a dust-free disk gap is also cut in model (vi) after the density has decreased (model v). Model of row (vii) is identical to model (vi) but without decreasing the density as in model (v). The light gray bars also presented in all rows show the initial model (i) for comparison. |
Object properties derived in previous measurements (flags refer to the references).
2.1. Object sample
The objects of our study are HD 142666 and AS 205 which belong to the ρ Ophiuchi star formation region. Selected object parameters known from literature are compiled in Table 1 and in Appendix A. Considering the spectral type, the A7 III source HD 142666 is a Herbig Ae/Be object while the other two sources are T Tauri objects. HD 142666 is assumed not to have any stellar companion (e.g., Fukagawa et al. 2010). Considering our interferometric measurements, a sinusoidal visibility spectrum could not be found that would be characteristic of a close (stellar) companion in both systems. AS 205 is a triple system (Eisner et al. 2005; Koresko et al. 1997). In this study, we also present the interferometric observation of the main southern (S) companion of AS 2051.
2.2. Observations with IOTA
IOTA at the Smithsonian F. L. Whipples Observatory on Mount Hopkins, Arizona, belonged to the first Michelson interferometers observing in the NIR wavelength range (Carleton et al. 1994; Traub 1998, 2003) and was operated until 2006 (Schloerb et al. 2006). IOTA consisted of three 0.45 m-Cassegrain telescopes that could be shifted on an L-shaped 15 m × 35 m-track, allowing a flexible modification of the baseline lengths. An angular resolution of five milli-arcseconds (mas) at a maximum baseline length of B = 38 m could theoretically be reached with IOTA. Not only the visibilities and the corresponding differential phases, but also the closure phase could be measured with IOTA. The closure phase, unaffected by atmopheric effects, is a prerequisite for determining asymmetries in the measured brightness distribution, so essential for image reconstruction (e.g., Jennison 1958; Leinert 1992). However, numerous interferometric observations are necessary for an acceptable image (Kraus et al. 2005). Therefore, the closure phase is not discussed any further in this study.
Atmospheric effects were compensated by a piezo-actuated tip-tilt tertiary mirror. After the compensation of the optical path difference by a sequence of light reflections in an evacuated tank, two beams were combined using the IONIC 3 Beam Combiner (Berger et al. 2003). A single exposure consisted of 200 to 300 readouts in four minutes. Photometric measurements and exposures of dark current concluded the observation sequence. The observation of a main-sequence star with known diameter (calibrator) before and after the observation sequence allowed the determination of the modulation transfer function (MTF) of the interferometer by linear interpolation. Also, atmospheric and instrumental background were eliminated by the calibration measurements.
In June 2006, the bright YSO HD 142666 could be observed with IOTA at a maximum projected baseline length of ~27 m. The H band visibility within the wavelength interval of (1.65 ± 0.15) μm was measured. For data calibration, we observed the main-sequence stars HD 134758, HD 143033, and HD 139663 with the uniform disk (UD) diameters (1.42 ± 0.02) mas, (1.36 ± 0.02) mas, and (1.99 ± 0.02) mas, respectively, in H band (Merand et al. 2005; Bordé et al. 2002). The projected baseline lengths as well as the position angles during our interferometric observations with IOTA are listed in Table 2. The visibilities are shown in Fig. 1.
Journal of IOTA observations of HD 142666.
The IOTA Data Reduction Software (IDRS) was used. It offers two alternative methods of determining the visibility V (IDRS v0.7 and v0.8; Kraus et al. 2005). A first approach uses the linear relation between the measured power spectrum and the visibility (Jackson 1983). In this standard approach, data sets with low signal-to-noise ratios can be added easily. Gaussian-shaped, narrow signal profiles in the power spectrum result from data sets with low noise. Fitting linear functions to the tails of the Gaussian-shaped profiles allows background noise to be subtracted. Furthermore, a lower and an upper limit are defined to eliminate noise with low and high spatial frequencies. The signal profiles that were measured in this study are broad as a result of a low signal-to-noise ratio. Therefore, the error bars of the visibilities that we obtained for HD 142666 with IOTA are high.
Another approach is based on the continous wavelet transform (CWT). It results from a convolution of the interference signal with a Morlet function from which the power spectrum can be determined. Atmospheric perturbances, instrumental vibrations, as well as background noise, can effectively be eliminated with the CWT method (Kraus et al. 2005), in particular for data sets of faint objects. The CWT was used to confirm the results obtained from the standard method described above.
2.3. Observations with AMBER
The system AS 205 was observed with AMBER (Petrov et al. 2005; see Table 3), and it operates at the Very Large Telescope Interferometer (VLTI). The combination of three telescopes with AMBER allows the closure phase to be determined. Analogous to our measurements with IOTA, the closure phase is not discussed further in this study. In contrast to observations with IOTA, AMBER allows the observations to be spectrally resolved in H and K band (1.6 μm−2.5 μm).
For our observations with AMBER, we used the Unit Telescopes UT 2, UT 3, and UT 4. This telescope combination not only includes two almost perpendicular baselines, but also offers an appropriate angular resolution. The baseline UT 2-UT 4 reached a baseline length of 89 m, which corresponds to a resolution of 1.9 mas at a wavelength of 1.6 μm corresponding to 0.22 AU and 0.30 AU at the distance of the sources HD 142666 and AS 205, respectively. Correspondingly, the angular resolution of the shortest baseline UT2-UT3 with a maximum baseline length of 47 m reaches 3.5 mas, which corresponds to 0.40 AU and 0.56 AU. The resolution of AMBER on this baseline is thus a factor 2–3 higher than the resolution that can be reached by MIDI in the MIR wavelength range with the longest baseline used (see Sect. 2.4). This allowed us to continuously trace the circumstellar disks from the hot inner regions to the warm parts at distances of several AU from the central star. We chose the low-resolution prism mode with a spectral resolving power of λ/Δλ ≈ 35, which is similar to the resolving power provided by MIDI in prism mode, and it allows good spectral coverage. For the observation of the weak source AS 205 S, only measurements in K band were possible, since IRIS (VLTI InfraRed Image Sensor; Gitton et al. 2004) was operated in the H band to stabilize the beams.
Journal of AMBER observations.
Observations with AMBER start with exposures that are used for the wavelength calibration
and the calibration of the offsets between the interferometric and the photometric
channels. In a second step, the so-called pixel-to-visibility matrix
MV2P is determined. This matrix is the MTF between visibility
V and measured interferogram I, i.e., 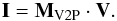 (1)The
quantity I represents here the interferogram measured on the detector after
the total flux is subtracted. The total flux is obtained from the photometric channels.
The scientific measurements with AMBER consist of several thousands of exposures. A single
exposure takes 25 ms. For a calibrated visibility, a standard star with known diameter,
i.e., with known visibility is observed. Standard stars were chosen from the CalVin
list2. We used the standard stars HD 143033 and
HD 143900 with the UD diameters (1.36 ± 0.02) mas and (1.25 ± 0.02) mas, respectively.
Additional measurements are necessary for determining of the detector background and the
sky background.
(1)The
quantity I represents here the interferogram measured on the detector after
the total flux is subtracted. The total flux is obtained from the photometric channels.
The scientific measurements with AMBER consist of several thousands of exposures. A single
exposure takes 25 ms. For a calibrated visibility, a standard star with known diameter,
i.e., with known visibility is observed. Standard stars were chosen from the CalVin
list2. We used the standard stars HD 143033 and
HD 143900 with the UD diameters (1.36 ± 0.02) mas and (1.25 ± 0.02) mas, respectively.
Additional measurements are necessary for determining of the detector background and the
sky background.
The AMBER Data Reduction Software amdlib v3.0.3 was used to reduce the data3. This recent release of the software is based on a new algorithm with an improved data and noise model (Chelli et al. 2009). The standard procedure described in the user manual was followed. For the frame selection, the following criteria were chosen. The piston, i.e., the mean optical path length difference of the incoming wavefronts, was limited to 8.0 μm (Hummel 2008). Furthermore, only 20% of the frames with the highest signal-to-noise ratio were taken into account to avoid degrading the fringe signal. This percentage is slightly more constraining than the value used in different previous studies using AMBER (e.g., Weigelt et al. 2007).
Subsamples of the data from several thousand single exposure frames were created by comparing the resulting visibilities with those derived from the complete data sets. Obvious outliers in the subsample set were discarded. If the overall data quality is low, the selection of the highest signal-to-noise ratios could lead to significantly different results for the complete data set and the subsamples were finally selected as different frames. During our observations, a second calibrator was available. We used this calibrator for a consistency test, i.e., to cross-check the results.
The visibilities presented in this paper were derived by averaging the calibrated subsamples. The error bars that are presented in Sect. 4 represent the corresponding standard deviation. The journal of our observations with AMBER is provided in Table 3.
Journal of MIDI observations of HD 142666.
2.4. Observations with MIDI
The studied YSOs have also been observed with MIDI at the VLTI (Leinert et al. 2003a), see Tables 4 and 5. Operating in N-band (8–13 μm), MIDI combines two telescopes and offers – as in our case – a spectral resolving power of λ/Δλ ≈ 30 using the prism mode.
To determine the MTF of the instrument, different calibrators that were taken from the “MIDI Calibrator Catalogue” 4 were observed before or after the observation of the scientific object. Five of these calibrators, HD 95272, HD 102461, HD 133774, HD 139127, and HD 178345, were used for absolute flux calibration5. Observations of both scientifc target and calibrator consist of 8000 exposures. A single exposure takes 18 ms. For descriptions of MIDI and its operation, see Leinert et al. (2003a,b), and Morel et al. (2004). The results of our MIDI observations of the objects HD 142666, AS 205 N, and AS 205 S, as well as a basic data analysis, have already been published in Schegerer (2008).
For data reduction, we used a custom software called MIA+EWS6. The data reduction steps are described in a tutorial on the cited web page, as well as in Leinert et al. (2004) and Ratzka et al. (2005). The visibilities shown in this paper were derived by using all calibrators that were observed during one night with the same baseline and instrument setup as the scientific targets, which show no peculiarities. The correction of the calibration that is required due to the diameters of the calibrators is considered in the software package. But this correction has a negligible effect on the calibration. The error bars in the visibility curves represent the standard deviation when using the ensemble of calibrator measurements. We discarded a measurement whenever the result that was obtained from the MIA software package differs from the results obtained from the EWS software package.
The journals of our observations with MIDI are provided in Tables 4 and 5. Depending on the baseline that was used, an angular resolution between 8.6 mas and 17 mas corresponding to 0.98 AU–1.9 AU and 1.4 AU–2.7 AU at the distances of the sources HD 142666 and AS 205, respectively, was reached in our observations with MIDI.
Journal of MIDI observations of AS 205 N and AS 205 S.
For the determination of spatially unresolved spectra, the dedicated software package MIA+EWS was used. It extracts and calibrates raw spectra. The calibration was done by comparing the measured spectrum with the measured spectrum of spectrophotometric calibrators (Table 6).
Photometric datasets used to derive the spectra.
3. Modeling approach
3.1. Canonical disk model
For a detailed analysis, we used the radiative-transfer code MC3D which is based on a
Monte Carlo method (Wolf et al. 1999) and which
was developed by Schegerer et al. (2008) to the
form used here. A predefined, parameterized model of a passive disk is the basic element
of our modeling approach. The approach of Shakura & Sunyaev (1973) was used where the density distribution is given as ![\begin{eqnarray} \label{eq:shakura} \hfill{} \rho(r,z)=\rho_{0} \left( \frac{R_{\star}}{r} \right)^{\alpha} \exp \left[ - \frac{1}{2} \left( \frac{z}{h(r)} \right)^{2} \right]\cdot \hfill{} \end{eqnarray}](/articles/aa/full_html/2013/07/aa20190-12/aa20190-12-eq105.png) (2)The
quantity ρ0 allows scaling the total disk mass
Mdisk. The quantities r and
z are the radii measured from the disk center and the vertical distance
from the disk midplane, respectively, while the quantity
R⋆ is the stellar radius. The function
h(r) represents the scaleheight7
(2)The
quantity ρ0 allows scaling the total disk mass
Mdisk. The quantities r and
z are the radii measured from the disk center and the vertical distance
from the disk midplane, respectively, while the quantity
R⋆ is the stellar radius. The function
h(r) represents the scaleheight7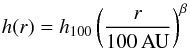 (3)with
h100 = h(r=100 AU).
Determining the shape of the disk profile, the parameters β and
h100 are called profile parameters in this study. In our
approach the exponents α and β satisfy the relation
(3)with
h100 = h(r=100 AU).
Determining the shape of the disk profile, the parameters β and
h100 are called profile parameters in this study. In our
approach the exponents α and β satisfy the relation
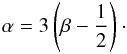 (4)The
latter relation results from the coupling of surface density and temperature of the disk
based on the assumption of a disk in hydrostatic equilibrium (Shakura & Sunyaev
1973). We note that this approach is only correct
for geometrically thin disks, where z ≪ r. However,
since the scaleheight h(r) is at least one order of
magnitude smaller than the corresponding radius r, this approximation
should be justified for those parts of the disk where infrared emission has its maximum.
The error in the density of regions
(4)The
latter relation results from the coupling of surface density and temperature of the disk
based on the assumption of a disk in hydrostatic equilibrium (Shakura & Sunyaev
1973). We note that this approach is only correct
for geometrically thin disks, where z ≪ r. However,
since the scaleheight h(r) is at least one order of
magnitude smaller than the corresponding radius r, this approximation
should be justified for those parts of the disk where infrared emission has its maximum.
The error in the density of regions 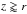 is z5/r7 for
Taylor’s series. A rounded puffed-up inner rim was not considered as an analytical
supplement to our modeling approach (Natta et al. 2001; Isella & Natta 2005).
is z5/r7 for
Taylor’s series. A rounded puffed-up inner rim was not considered as an analytical
supplement to our modeling approach (Natta et al. 2001; Isella & Natta 2005).
The infrared excess that is emitted from YSOs originates in heated dust and scattered light in the circumstellar environment (Vinkovic 2012). Assuming compact, homogeneous, spherical dust grains, their optical properties such as scattering and extinction cross sections were determined by Mie scattering theory from the measured complex refractive index of the specific material (Wolf & Voshchinnikov 2004). A dust mixture of a “astronomical silicate” and graphite was assumed with relative abundances of 62.5% and 37.5%, respectively (Draine & Malhotra 1993). We used a two-layer disk model to take dust settling into account. The disk interior, which is optically thick in N band, contains dust grains with a maximum particle size of amax = 1 mm. A size of amax = 1 mm was found for several T Tauri stars with millimeter observations using the Very Large Array (Rodmann et al. 2006). The optical depth was measured for constant radii, from the disk atmosphere vertically to the disk midplane. The surface regions consisted of interstellar, unevolved dust with amax = 0.25 μm as found in the interstellar medium (Mathis et al. 1977; MRN dust composition).
Accretion effects were taken into account. As extensively described in Schegerer et al. (2008), the potential energy of a particle on its way towards the star is partly released in the disk midplane (Lynden-Bell & Pringle 1974; Pringle 1981). Considering the “magnetically mediated” modeling approach (e.g., Uchida & Shibata 1984; Bertout et al. 1988; Calvet & Gullbring 1998), more than half of the potential energy of the accreting particles is released in a boundary region above the stellar surface. The accretion rate Ṁ, which determines the total accretion luminosity Lacc, was not an independent model parameter, but its value was constrained by the results of previous measurements. Correspondingly, the stellar mass M⋆, the effective stellar temperature T⋆, and the stellar luminosity L⋆, which were derived in previous studies, were fixed parameters in the modeling. Because the SED and the infrared emission, in particular, only marginally depend on the disk outer radius Rout, this disk parameter was fixed to Rout = 100 AU. Fitted model parameters of our approach were the scaleheight h100, the flaring parameter β, and the inclination i of the circumstellar disk8. By considering a stellar temperature T⋆, the quadratic distance law, a mean dust sublimation temperature of 1500 K, and the specific absorption coefficients κ of the adopted dust set, the temperature of single dust grains at any distance from the central star can be determined. The resulting radius Rsub where dust sublimates was the initial value of Rin. However, this approach is an approximation for optically thick media since the buildup factor is not considered.
By means of manual modifications of the parameters, we searched for the model that most successfully reproduces the measured SED, NIR, and MIR visibilities simultaneously. A manual modification was necessary because a disk model with a specific SED and images9 at different wavelengths takes several hours to compute. Therefore, in our search for the best-fit model, the uniqueness of our final models cannot be proven10. We verified whether the modeling results can be improved by varying the model parameters using the following changes:
ΔMdisk = 0.5 Mdisk, ΔRin = 0.05 AU, Δβ = 0.1, and Δh100 = 1 AU.
The step widths can be considered as the precision to which the local minimum in the χ2-surface can be determined. The determination of the modeling errors would require a fit of a polynomial to the χ2-surface of the simulation grid of the independent parameters. For inclination i, only an upper value could be determined. Depending on the flaring of the disk, the sight of the observer onto the star and the innermost disk regions get worse for an increasing inclination, resulting in a decrease in the visible (and infrared) flux from the source.
3.2. Extended disk model for TOs
As a result of photoevaporation, as well as planet formation and planet motion, the mass density at the inner disk regions decreases and disk gaps can be formed. To reproduce the SED that was obtained from the 8 Myr-T Tauri object RECX 5 using the InfraRed Spectrograph (IRS) onboard the Spitzer Space Telescope, Bouwman et al. (2010) decreased the mass density in the disk model by a constant factor of 100 up to a disk radius of r < 33 AU. This clearing of the disk around the TO RECX 5 was assumed to be a consequence of the formation of a planet. In our approach, we generally assumed the canonical disk model, even for more evolved T Tauri stars and TOs in particular. We found, however, that this conventional approach cannot reproduce all the observations obtained from the source HD 142666. Therefore, a modification of the conventional approach was subsequently necessary for this source.
Depletion of small dust grains at smaller disk radii is characteristic of evolved T Tauri
stars, and TOs in particular. To simulate dust depletion in disks, the primary disk
density ρ(r,z) (Eq. (2)) was multiplied with an exponential function,
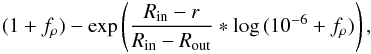 (5)that
decreases the density at the inner disk edge Rin by a factor
fρ with
fρ < 1. The
density is not decreased for fρ = 1. This
exponential function, which is strictly increasing, is unity at
r = Rout, and it guarantees a smooth
transition to the primary disk model in contrast to the approach of Bouwman et al. (2010). For the density reduction factor, only the two
different values fρ = 0.1 and
fρ = 0.01 were used.
(5)that
decreases the density at the inner disk edge Rin by a factor
fρ with
fρ < 1. The
density is not decreased for fρ = 1. This
exponential function, which is strictly increasing, is unity at
r = Rout, and it guarantees a smooth
transition to the primary disk model in contrast to the approach of Bouwman et al. (2010). For the density reduction factor, only the two
different values fρ = 0.1 and
fρ = 0.01 were used.
Considering the theoretical effects of photoevaporation or planet formation, another characteristic of TOs is the depletion of small dust grains within a defined disk region, resulting in the formation of an inner hole or ring with (negligibly) low dust density. A dust-free inner hole was implemented by increasing the inner disk radius Rin. A dust-free ring with sharp boundaries, Rgapin and Rgapout, could also be cut from the model. The remaining disk structure was not affected by the gap.
The gap parameters were varied using the following step widths:
ΔRgapin = 0.05 AU, ΔRgapout = 0.05 AU.
4. Observations and modeling results
All scientific targets could be resolved spatially with IOTA or AMBER in the NIR range and MIDI in the MIR range. Because of technical failures and/or bad weather conditions during the measurements, the observations of AS 205 S with AMBER failed. Furthermore, some single observations with AMBER or MIDI at specific baselines and PAs, which are flagged in Tables 4 and 5, are also not considered in the data analysis for the same reason.
Table 7 presents the parameters resulting from our effort to model the YSOs. The ratio between the stellar and disk model flux at 1.6 μm is also listed. The H-band visibilities depend on the ratio between the stellar and disk flux, as well as on the disk geometry. The excess at 1.6 μm was calculated by subtracting the observed flux from the value for the assumed stellar photosphere. A negative ratio results from a high inclination of the sdisk. Flared, outer disk regions screen the infrared flux from the center. Along with the observations, we present and discuss the modeling results for each object of our sample in the following. Previous observations, including photometric measurements, are mentioned in Appendix A. The measured and modeled SED, as well as NIR and MIR visibilities of the objects in this study, are presented in Figs. 1–3.
4.1. HD 142666
Figure 1 shows the SED of HD 142666, the spectrally unresolved but spatially resolved NIR visibilities from IOTA, as well as the spectrally and spatially resolved MIR visibility spectra from MIDI. With IOTA, an angular resolution of 6.3 mas (0.72 AU at 114 pc) could be reached. The HAeBe object was observed with MIDI in the context of guaranteed time observations where a spatial resolution of 1.1 AU and 0.98 AU for λ = 8−13 μm could be reached using the projected baselines B = 89 m and B = 102 m, respectively. The low MIR visibility spectra correspond to a strongly spatially resolved circumstellar disk in the MIR range.
 |
Fig. 2 SED, NIR, and MIR visibilities spectra for the different projected baselines that result from the measurements and our model of AS 205 N. |
 |
Fig. 3 SED and spectrally dispersed MIR visibility for a projected baseline length of B=52 m that result from the measurements and our model of AS 205 S. |
We used different disk parameter sets and different approaches for disk models until we could finally fit all the data obtained. The models (i−iv; Table 7) show the modeling results that consider the classical approach of Eq. (2) and accretion, while the disk densities were decreased in models (v−vi) using the modifications described in Sect. 3.2.
-
(i)
Considering the stellar properties, we initially assumed aninner disk radius of Rin = 0.1 AU. After scanning the parameter space of the canonical approach of Shakura & Sunyaev (1973), no model could be found that reproduces the SED, MIR visibility, and NIR visibilities of this source, simultaneously. While the NIR visibilities are consistent with the dust sublimation radius, the 10 μm emission appears to arise from a region that is more extended than predicted by assuming a smooth radial profile of the dust density and temperature distribution.
-
(ii)
The low MIR visibility spectra favor an inner radius Rin > 0.1 AU. For an increasing inner radius, the NIR and MIR flux distribution shift to larger radii resulting in a decrease in the corresponding visibilities. However, a decrease in the NIR visibilities does not solely reproduce the IOTA data. The NIR photometric flux, which has its origin mainly at the inner disk edge (Fig. 4), generally decreases for an increasing inner disk radius Rin, and the fit of the photometric measurements in the NIR range gets worse. As the disk mass is kept constant, there are more particles that emit in the MIR wavelength range at >0.1 AU and the MIR photometric flux increases. The upper row of Fig. 1 shows the modifications of the simulation results if the inner disk radius is increased by a factor of 5 from Rin = 0.1 AU in model (i) to Rin = 0.5 AU in model (ii).
-
(iii)
To shift the MIR flux distribution to larger disk radii and, thus, to decrease the MIR visibility spectra in the model, we increased the profile parameters h100 and β resulting in disk flaring where outer disk regions are more strongly illuminated and heated by the central star. Another effect of disk flaring is the increase in the far-infared (FIR) flux by orders of magnitude. Outer disk regions are still too cold to contibute sufficiently to the NIR flux, so the NIR visibility only slightly decreases. Considering Eqs. (2) and (4), the mass density of the inner disk regions also decreases, resulting in too low NIR flux with respect to the photometric measurements. The second row of Fig. 1 shows the model (iii) where the profile parameter β has been increased from β = 1.0 to β = 1.1, while all the other parameters were kept constant.
-
(iv)
Assuming an inner disk radius Rin > 0.1 AU to reproduce the MIR visibilities, an increase in the NIR flux and NIR visibility can result from an increase in the accretion rate Ṁ in model (ii). But in contrast to the effect on the SED, a modification of the accretion rate only slightly increases the NIR visibility in the model with Rin = 0.5 AU. Furthermore, considering the high age of the object of 6.3 million years and the measurements of Garcia-Lopez et al. (2006) where an accretion rate of Ṁ = 1 × 10-8 M⊙ yr-1 was determined by analyzing the FWHM of the Brγ line, a large accretion rate can be excluded. Apart from the accretion rate, any further (infrared) source in the disk region that cannot be resolved with IOTA, such as a close stellar/planetary companion or hypothetical inner rim wall that is puffed up by the strong irradiation of the central star, could increase the NIR flux and NIR visibility in disks with larger inner radii. A puffed up inner rim wall, however, also results in a higher concentration of warm dust. Consequently, the MIR visibility does not decrease since it is necessary for a better fit. Furthermore, the stellar temperature and luminosity of HD 142666 are similar to the corresponding properties of the YSO RY Tau. In an extensive study using a self-consistent disk model, Schegerer et al. (2008) have shown that there are not hints of a puffed upper rim wall for this YSO. Finally, we also implemented an optical and geometrically thin disk for Rsub < r < Rin with a dust grain radii
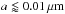 .
Eisner et al. (2006) succeed in reproducing
the SED and NIR visibilities of the TO TW Hya, assuming such an optically thin
structure in the inner hole of the disk. However, not all of the photometric and
interferometric data could be reproduced by assuming such an inner thin disk.
.
Eisner et al. (2006) succeed in reproducing
the SED and NIR visibilities of the TO TW Hya, assuming such an optically thin
structure in the inner hole of the disk. However, not all of the photometric and
interferometric data could be reproduced by assuming such an inner thin disk. -
(v)
To shift the MIR flux distribution to larger disk radii and decrease the MIR visibility, the disk density was exponentially reduced according to Sect. 3.2 using fρ = 0.01. Another effect is the increase in the infrared flux. But such a modification in model (v) is not sufficient to fit the MIR visibilities (fourth row in Fig. 1).
-
(vi)
Therefore, in addition to the latter modification in model (v), we increased the inner disk radius to Rin = 0.3 and cut a dust-free ring from the disk between Rgapin = 0.35 AU and Rgapout = 0.8 AU in model (vi). The remaining dust ring between 0.3 AU and 0.35 AU is large enough to provide enough NIR flux and to reproduce the NIR visibility. In contrast, the dust-free ring causes a shift in the MIR flux distribution towards larger disk radii, resulting in a decrease in the corresponding visibilities. The model flux at 1.6 μm deviates by 19% from the measured H band flux.
-
(vii)
In disk model (vii), there is an identical disk gap to the one in model (vi). But the density was not decreased. Here, the MIR visibility is decreased, but not enough to reproduce the observations. Furthermore, the NIR visibility decreased too strongly.
4.2. AS 205 N
There are previous flux measurements in the NIR and MIR wavelength ranges that can be exclusively ascribed to the northern component (Eisner et al. 2005; Prato et al. 2003). Apart from a recent observation at a wavelength of 860 μm (Andrews et al. (2011), we assumed that all other previous photometric measurements could not spatially resolve each single component of the system. Cohen & Kuhi (1979) could measure the visual flux of each component, but they missed ascribing the photometric values to each single component. Since AS 205 N is an active and variable source (Johns-Krull et al. 2000; Eisner et al. 2005), it depends on the variability of the visual fluxes if the measurements of Cohen & Kuhi can be correctly assigned. The spectral flux in this wavelength regime and the visibilities have to be measured simultaneously.
 |
Fig. 4 Flux distributions at wavelengths of 1.65 μm, 3.5 μm, and 12.5 μm (dashed, solid, and dotted-dashed line, respectively) that are derived from a model that fits the measurements best. These distributions are normalized to the maximum of the 3.5 μm flux distribution. |
The canonical disk model was used for modeling this source. We found that an advanced disk model with a larger inner disk radius and lower dust density in the inner disk region, respectively, cannot reproduce the observations, in particular the photometric measurements. The successful data reproduction using the canonical modeling approach confirms the primordial, unevolved character of the disk, which is consistent with the young age of the source of 1 Myr (Prato et al. 2003). However, there is an ambiguity in the profile parameters β and h100. Models with values β ∈ [1.0,1.1] and h100 ∈ [19,21] reproduce the measurements just as well.
The visibility that was measured with the 89 m-baseline is ~30% lower than the modeled value. The SED that results from our best model for AS 205 N differs by about 40% from the photometric measurements of Prato et al. (2003) in the NIR wavelength range (Fig. 2). Considering a deviation by 6%, the modeled SED agrees with the fluxes that were measured by Eisner et al. (2005). This disagreement with Prato et al. and the agreement with the Eisner et al. probably point to an intrinsic variability of the source in the NIR. However, the stellar luminosity of L⋆ = 1.3 L⊙ that was derived by Eisner et al. (2005) is about a factor of ~7 lower than other previous results (Prato et al. 2003; Liu et al. 1996) and cannot be confirmed by our model. In contrast, the accretion rate of Ṁ = 7 × 10-7 M⊙ yr-1 that is used in our model corresponds to the estimation of Eisner et al. (2005) and Johns-Krull et al. (2000: Ṁ = 6.7 × 10-7 M⊙ yr-1). The accretion luminosity is about Lacc ≈ 6 L⊙. Therefore, AS 205 N is a T Tauri object with one of the highest accretion rates in comparison to other T Tauri stars (Ratzka et al. 2007; Schegerer et al. 2008, 2009).
Although we assume an accretion rate of Ṁ = 7 × 10-7 M⊙ yr-1, we have found that a model with the same profile parameters as listed in Table 7 but with an accretion rate that is lower by a factor 3−4 assuming a larger inner disk radius of Rin = 0.15 AU at the same time can also simultaneously fit the SED, MIR, and NIR visibilities. A lower accretion rate of Ṁ < 7 × 10-7 M⊙ yr-1 results in less NIR and MIR radiation and a larger inner disk radius of Rin = 0.15 AU (instead of Rin = 0.10 AU) induces a temperature decrease of ΔT ≈ 150 K on average in the innermost disk regions and a shift of the thermal emission peak to longer wavelengths. Our modeling approach thus allows models with different modeling parameters to fit the whole data set. This ambiguity can be avoided by considering the results of the previous, independent measurements of the accretion rate.
4.3. AS 205 S
Apart from a recent submillimeter observation by Andrews et al. (2011), the photometric fluxes in the visual, FIR, and millimeter ranges have to be ascribed to AS 205 N and AS 205 S. Moreover, the visual extinction of the southern component, which is a binary itself, could not be derived unambiguously. While Prato et al. (2003) assume AV = (2.1 ± 1.0) mag, Eisner et al. (2005) and McCabe et al. (2006) derived higher values of AV = (3.6 ± 1.0) mag and AV = 2.41 mag, respectively. Although the measurements approximately agree with each other within the error bars, a standard deviation of σ = 1.0 mag makes a subsequent allocation of the photometric, spatially resolved fluxes in the visual range impossible.
The flux in L band, which results from the model of AS 205 S differs by about 26% from the fluxes measured by Prato et al. (2003, Fig. 3). It is possible that photometric variability in the NIR is also responsible for this difference between the measurements and the model of the southern component. The accretion luminosity of this component is Lacc = 0.32 L⊙. The interferometric measurements on the baselines of B = 56 m and B = 85 m (Table 5) were discarded because of the bad weather conditions during the observations. According to Eisner et al. (2005), even AS 205 S is a binary. The separation of both components is 1.3 AU at a position angle of PA = 101°. Such a binary system was not considered in our models for AS 205 S because a sinusoidal visibility curve that is characteristic of a close binary system could not be identified (Schegerer et al. 2008).
5. Discussion
Our comprehensive modeling approach is complex. There are some deficiencies that should be listed.
-
The main limitation of our observations is the limited uvcoverage, which makes the data analysis model dependent. Thephysical quantity that can be best constrained is the radial extent ofthe NIR and MIR disk emission. The goal of this paper was toconstrain this quantity for the sources under investigation.Studying SED and visibility, the inclination and the position angleof the disks cannot be derived precisely. Only a few visibility pointsare not sufficient to derive these values. With respect to the SEDonly an upper limit of the inclination can be determined. This limitcorresponds to the angle where the disk allows the observations ofinner disk regions (and the central star).
-
There are small, local deviations between measured and modeled data. The modeling approach of Shakura & Sunyaev (1973) assumes a rotationally symmetric structure. Deviations between modeled and measured visibilities at fixed baseline lengths but different PAs, for instance, could be caused by local asymmetric structures. In fact, such structural asymmetries could be evoked, e.g., by large-scale eddies (Klahr et al. 2003), which have already been observed in large-scale images of YSOs (Fukagawa et al. 2004; Lagage et al. 2006).
-
For HD 142666, we found a model for this putative TO by assuming a smooth transition to the canonical disk approach. Although this approach was confirmed by our interferometric observations, there are different possible approaches that are supposed to reproduce the measurements as well (e.g., Bouwman et al. 2010).
-
A latent ambiguity in our modeling approach cannot be ruled out (Sect. 4.2).
-
The discontinuous boundaries at the inner disk edge, as well as the edges of a potential ring gap, that can be implemented in our advanced disk model are a simplification.
-
A wide variety of outer disk radii 80 AU < Rout < 250 AU can reproduce the measured data of all objects of this study. Because of the intrinsic ambiguity of the SED (Men’shchikov & Henning 1994; Thamm et al. 1994), large photometric errors, and missing spatially resolved observations in the FIR range, an unambiguous determination of the model parameter Rout is not possible.
-
The modeled SED can deviate from the measured SED. We assume a dust mixture of “astronomical silicate” and graphite with the canonical MRN grain-size distribution. But previous studies of the silicate feature and the water ice feature have already shown strong modifications of the composition in circumstellar disks (Bouwman et al. 2001, 2008; Przygodda et al. 2003; Schegerer & Wolf 2010). The modification of the dust composition depends on properties of the central star and the evolutionary status of the source (van Boekel et al. 2005; Schegerer et al. 2006), as well as on the distance from the star (van Boekel et al. 2004; Schegerer et al. 2008) and from the midplane (Rodmann et al. 2006). However, the analysis of dust features only allows investigations of the relative occurrence of silicate grains with sizes between ~0.1 μm and ~2 μm assuming nonporous grains. Therefore, an individual dust composition is not considered in our modeling approach, although the dust composition affects the disk structure as shown by Monnier & Millan-Gabet (2002).
Different modeling approaches have been used for the objects of this study. This is discussed in detail in the following.
5.1. HD 142666
Extensive modifications of the parameter of the canonical model, i.e., the inner disk radius Rin, the profile parameters β and h100, and the accretion rate Ṁ, respectively, failed to reproduce all the observations. Therefore, the modeling of the source HD 142666 required an extension of the canonical approach of Shakura & Sunyaev (1973, Eq. (2)). In our approach for HD 142666, we reduced the dust density at the inner disk edge by multiplying of the canonical disk with the factor fρ = 0.01. This factor smoothly increased up to unity at Rout. Additionally, we increased the inner disk radius from 0.1 AU to 0.3 AU and cut a dust-free ring from the disk between Rgapin = 0.35 AU and Rgapout = 0.8 AU. There are several different approaches in advanced disk models that potentially reproduce the whole data set that we obtained. However, an increased inner disk radius and a disk gap is putatively necessary for a successful fit. While the increased inner disk radius decreases the infrared flux and the NIR visibility, a low MIR visibility results from the disk gap. For a constant disk mass, the NIR flux even increases after cutting the gap from the disk. A larger sublimation radius or a disk gap, alone, cannot explain the infrared visibilities and the SED of this source. Higher accretion rates, an inner optical and geometrically thin disk, a more flared disk, or a puffed-up inner rim can all be excluded.
The disk gaps in HD 142666 classify this source as TO. This result contrasts with previous studies where TOs were classified as sources with specific color relations (McCabe et al. 2003; Alexander et al. 2006b) or a significant lack of infrared excess at λ < 6 μm, solely (Table 8). The last two characteristics are not even fulfilled by HD 142666. Recently, several such “unexpected” transition disks have been discovered through direct imaging on the millimeter wave dust emission in more outer disk regions (e.g., Andrews et al. 2011). All these objects have normal SED but cavities larger than 10 AU, as measured in the millimeter wavelength range.
We assume that this clearing of the disk can be a consequence of planet formation where adjacent regions are strongly affected by tidal forces (Calvet et al. 2002; Rice et al. 2003; Quillen et al. 2004). However, this modeling result also confirms the outcome of the theoretical study of Takeuchi et al. (2003), in principle, where disk evolution has been modeled combining viscous evolution, photoevaporation, and the differential radial motion of dust grains and gas. In this study, the formation of a dust ring in the disk of HAeBe stars is predicted without assuming planet formation but as a natural consequence of photoevaporation and grain migration. HAeBe stars strongly suffer from a photoevaporative mass loss from the disk. The outer disk regions are slowly eroded, the inner hole grows, and the dust becomes concentrated close to the inner disk edge. We have to note, however, that Takeuchi et al. (2003) studied more massive (M⋆ = 2.5 M⊙) and more luminous (L⋆ = 30 L⊙) HAeBe objects where a dust ring appears at radii on the order of 10 AU.
For the case that a young planet has formed the disk gap, we studied its theoretical effects on our interferometric observations. In fact, a planetary companion of the main source evokes a specific sinusoidal visibility curve whose amplitude and frequency depend on the separation asep, the position angle of the companion with respect to the position angle of the interferometric baseline aPA, and the brightness ratio arat (Ratzka et al. 2009). We assume a brightness ratio of 100:1 between the main source and a potential planetary companion, the primordial visibility curve without companion would change by ΔV = 0.02, only. Considering a standard deviation of 0.07 on average (Sect. 4.1), such a modification would be too weak to be noticed using the interferometers available in this study. The brightness ratio should be arat < 25:1, at least, to be directly found by our interferometric measurements.
5.2. AS 205
The SED and the MIR visibilities of AS 205 have been investigated and modeled in Schegerer (2008) and Schegerer et al. (2009). Only a few, small modifications of these previous disk models, which are canonical models, were enough to fit the NIR visibility spectra of these sources, as well. We conclude that the inner disk structure (>0.1 AU up to several 1 AUs) is strongly determined by SED and MIR visibility spectra. In fact, considering Fig. 4, the regions where MIR and NIR flux arise overlap. However, the spatial resolution of MIDI is probably too low to uniquely determine the parameter Rin, in particular for less evolved objects. For the northern and the southern components of AS 205, the inner disk radius is assumed to be the sublimation radius that was determined by the properties of the star and the dust.
K − L color index ranges of the objects of our sample.
6. Summary and outlook
In this study, we observed three well-known YSOs using the interferometers IOTA and AMBER in the NIR wavelength range and MIDI in the MIR wavelength range. A maximum spatial resolution of 0.3AU and 0.9AU could be reached, respectively, allowing study of the innermost disk regions and of the inner disk edge in particular. The visibility V, i.e., the outcome from our interferometric observations, is a complex function of the dust density distribution, dust properties, and stellar properties of the source. Thus, a proper quantitative analysis was only possible by comparison with radiative transfer simulations for circumstellar disk models, which we performed with our radiative transfer code MC3D. We created large samples of models of YSOs and mimicked the interferometric observational data to compare the results with our observations. We considered photometric data and object properties from the literature to obtain a unique disk model that reproduces all the data. AS 205 N and AS 205 S could be modeled using the canonical approach of Shakura & Sunyaev (1973) for viscous disks.
Here, we considered accretion effects, as well as a two-layer disk model with the classical MRN dust composition in the surface layer. Several model parameters were constrained by literature values, such as stellar properties, the distance of the object, and its accretion rate. Five (free) parameters were modified in the canonical approach. Since no parameter set could be found that model all the observations that are available for HD 142666, this modeling approach was extended. The disk density at the inner disk edge was multiplied with an exponential function of radius r that reduces the mass density at the inner disk edge Rin by a constant fρ < 1 and converges to unity at the outer disk radius Rout. Additionally, a dust-free ring was cut from the disk. Thus, the advanced approach where three extra parameters (fρ, Rgapin, Rgapout)s are available allows the putative properties of a TO to be modeled, i.e., disk gaps and a low dust density.
Considering the simplifications in our modeling approach (Sect. 5), the models cannot reproduce all the data perfectly. However, the following basic results can be derived from our modeling approach:
-
The canonical modeling approach failed to reproduce all thedata obtained from high spatially resolved observations ofHD 142666, which is a YSO at an advancedevolutionary stage. An advanced modeling approach was anecessary criterion for a TO.
-
The HAeBe star HD 142666 could be successfully modeled by implementing an inner disk hole where the inner disk radius (Rin = 0.20 AU) is equal to the initial sublimation radius Rsub. The initial sublimation radius was approximated after assuming the stellar temperature and an optically thin disk with MRN dust composition. A dust-free ring between Rgapin = 0.35 AU and Rgapout = 0.80 AU had to be cut from the disk, leaving a dust ring between Rin = 0.3 AU and Rgapin = 0.35 AU with reduced mass density.
-
If we classify a TO as a YSO with a disk gap, the object HD 142666 is a TO. This finding is based on our interferometric observations, while the SED or the color relations are not appropriate for a final classification. Table 8 lists the color K − L for the objects of this study, but a criterion that separates CTTS from TOs could not be found.
-
The canonical disk model satisfied the observations for the binary system AS 205 where the components AS 205 N and AS 205 S were separately modeled. The implementation of accretion effects were necessary for a successful reproduction of the observations. The presence of accretion could be a necessary hint that the transmit to a TO has not happened yet. A disk gap or lower dust densities than the canonical model provides can be excluded as the sources of this system.
-
This study has shown that the SED and the MIR visibilities are generally not sufficient to determine the inner disk radius of more evolved YSOs, although the inner disk edge close to the sublimation radius emits MIR radiation (Fig. 4). NIR visibilities obtained from long enough interferometric baselines can avoid such an ambiguity.
-
For both components of the CTTS-system AS 205, the NIR visibility data could confirm the model that we previously derived for both sources considering their SED and MIR visibilities alone. For these sources, the inner disk radius Rin is the sublimation radius Rsub that we formerly approximated.
Apart from our findings, the following questions arise from this study:
-
Is the small dust ring betweenRin = 0.30AU and Rgapin = 0.35 AU in HD 142666 a region that favors planet formation?
-
Do disk gaps (inner disk hole, dust-free ring) result from photoevaporation or can they be attributed to the action of planet formation/motion of young planets? In fact, inner disk gaps such as an inner disk hole in T Tauri objects and an inner hole and dust-free ring in HAeBe stars are an outcome of the theoretical study of Takeuchi et al. (2003), which only assumes viscous motion and photoevaporation. However, Takeuchi et al. (2003) studied more massive sources and predicted dust gaps at larger disk radii (r > 1 AU) than we found. An inner disk hole has also been found and confirmed for the nearby TO TW Hya with an age of 8−10 million years (Calvet et al. 2002; Ratzka et al. 2007). But Setiawan et al. (2008) report the detection of a planetary companion with a mass of 9.8 ± 3.3 MJupiter around TW Hya in an orbit with radius r = 0.04 AU. The authors of that study supposed that this planet is responsible for clearing the inner disk through the accretion of gas and dust, and they conclude that disk evolution and planet formation are probably directly connected. However, the actual existence of the planet orbiting TW Hya is still being discussed.
Online material
Appendix A: Previous measurements
HD 142666, that is also known as V 1026 Sco, was classified as Herbig Ae/Be-star by Gregorio-Hetem et al. (1992). It has a spectral type of A 7 III (e.g., Blondel et al. 2006). The source belongs to the star formation region R 1 in Scorpius (Vieira et al. 2003). According to Meeus et al. (2001), HD 142666 is a group-II object whose disk is flat. The object is a photometrically variable UX Ori star (Natta et al. 1997), i.e., dust clouds with a size in the range of the stellar diameter move into the line of sight of the observer from time to time. The extinction then increases and the stellar light can be reddened depending on the absorbing material. Considering polarimetric measurements (Hales et al. 2006) and the high variability of the flux in the NIR and visual wavelength range (ΔV = 1.2; Meeus et al. 1998), the disk is assumed to be inclined. The approximate age of the object is 10 million years (Natta et al. 1997). Millimeter measurements indicate this age, as well. The low decrease in the millimeter flux towards longer wavelengths could be a hint of cm-sized dust grains (Natta et al. 2004). Brγ measurements showed that the circumstellar disk around HD 142666 is still active with an accretion rate of Ṁ = 1 × 10-8 M⊙ yr-1 (Garcia-Lopez et al. 2006).
Photometric fluxes of HD 142666.
AS 205, also known as V866 Scorpii, is a member of the Upper Scorpius association, West from the ρ Ophiuc star forming region (Reipurth & Zinnecker 1993). As formerly observed by Herbig & Rao (1974), AS 205 has an infrared companion at a position angle of PA = 211° and at an angular distance of 1.32″, i.e., at a projected distance of 210 AU (Prato et al. 2003).
Observations in the I and NIR bands could spatially resolve both components with the northern component as the brighter source (Reipurth & Zinnecker 1993; Liu et al. 1996). Visual and NIR Speckle-interferometric observations (Koresko 2002) as well as spectrally highly resolving measurements (Eisner et al. 2005), have shown that the southern component is a close binary system (angular distance 8.5″, position angle PA = 101° ± 1°), as well. Both components of this system have similar brightnesses in the R and I bands and similar stellar properties (L⋆ = 0.44 L⊙ and 0.44 L⊙; M⋆ = 0.74 M⊙ and 0.54 M⊙; AV = 3.9 mag and 3.4 mag, respectively; Eisner et al. 2005). Although the age of the entire system is still discussed, it is assumed that all the components have simultaneously formed by fragmentation from the same region of the molecular cloud. The northern and southern components show hints of accretion (Cohen & Kuhi 1979; Prato et al. 1997; Eisner et al. 2005). Johns-Krull et al. (2000) have derived an accretion rate of Ṁ = 6.7 × 10-7 M⊙ yr-1 from the profile of the C IV line of the northern component. Considering the high activity and variability of the source which has been known for 30 years already, Welin (1976) assumed that AS 205 is a good candidate for future FU Ori variability outbursts.
Photometric measurements of AS 205.
Acknowledgments
A. A. Schegerer and S. Wolf were supported by the German Research Foundation (DFG) through the Emmy-Noether grant WO 857/2 (“The evolution of circumstellar dust disks to planetary systems”). Financial support from the Hungarian OTKA grant NN102014 and K101393 is acknowledged.
References
- Akeson, R. L., Millan-Gabet, R., Ciardi, D. R., et al. 2011, ApJ, 728, 96 [NASA ADS] [CrossRef] [Google Scholar]
- Alexander, R. D., Clarke, C. J., & Pringle, J. E. 2006a, MNRAS, 369, 216 [NASA ADS] [CrossRef] [Google Scholar]
- Alexander, R. D., Clarke, C. J., & Pringle, J. E. 2006b, MNRAS, 369, 229 [NASA ADS] [CrossRef] [Google Scholar]
- Andrews, S. M., Wilner, D. J., Hughes, A. M., Chunhua, Q., & Dullemond, C. P. 2009, ApJ, 700, 1502 [NASA ADS] [CrossRef] [Google Scholar]
- Armitage, P. J., Clarke, C. J., & Tout, C. A. 1999, MNRAS, 304, 425 [NASA ADS] [CrossRef] [Google Scholar]
- Berger, J.-P., Haguenauer, P., Kern, P. Y., et al. 2003, Proc. SPIE, 4838, 1099 [NASA ADS] [CrossRef] [Google Scholar]
- Bertout, C., Basri, G., & Bouvier, J. 1988, ApJ, 330, 350 [NASA ADS] [CrossRef] [Google Scholar]
- Blondel, P. F. C., Djie, H. R. E., & Tjin, A. 2006, A&A, 456, 1045 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bordé, P., Coudé du Foresto, V., Chagnon, G., & Perrin, G. 2002, A&A, 393, 183 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bouwman, J., Meeus, G., de Koter, A., et al. 2001, A&A, 375, 950 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bouwman, J., Lawson, W. A., Dominik, C., et al. 2006, ApJ, 653, 57 [Google Scholar]
- Bouwman, J., Henning, Th., Hillenbrand, L. A., et al. 2008, ApJ, 683, 479 [NASA ADS] [CrossRef] [Google Scholar]
- Bouwman, J., Lawson, W. A., Juhász, A., et al. 2010, ApJ, 723, L243 [NASA ADS] [CrossRef] [Google Scholar]
- Brown, J. M., Blake, G. A., Qi, C., Dullemond, C. P., & Wilner, D. J. 2008, ApJ, 675, 109 [Google Scholar]
- Bryden, G., Chen, X., Lin, D. N. C., Nelson, R. P., & Papaloizou, J. C. B. 1999, AJ, 514, 344 [NASA ADS] [CrossRef] [Google Scholar]
- Calvet, N., & Gullbring, E. 1998, ApJ, 509, 802 [NASA ADS] [CrossRef] [Google Scholar]
- Calvet, N., D’Alessio, P., Hartmann, L., et al. 2002, ApJ, 568, 1008 [NASA ADS] [CrossRef] [Google Scholar]
- Carleton, N. P., Traub, W. A., Lacasse, M. G., et al. 1994, Proc. SPIE, 2200, 152 [NASA ADS] [CrossRef] [Google Scholar]
- Carpenter, J. M., Wolf, S., Schreyer, K., Launhardt, R., & Henning, Th. 2005, AJ, 129, 1049 [Google Scholar]
- Chelli, A., Utrera, O. H., & Duvert, G. 2009, A&A, 502, 705 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Clarke, C. J., Gendrin, A., & Sotomayor, M. 2001, MNRAS, 328, 485 [NASA ADS] [CrossRef] [Google Scholar]
- Cohen, M., & Kuhi, L. V. 1979, ApJS, 41, 743 [NASA ADS] [CrossRef] [Google Scholar]
- Cutri, R. M., Skrutskie, M. F., van Dyk, S., et al. 2003, in 2MASS All Sky Catalog of point sources [Google Scholar]
- Draine, B. T., & Malhotra, S. 1993, ApJ, 414, 632 [NASA ADS] [CrossRef] [Google Scholar]
- Dullemond, C. P., Dominik, C., & Natta, A. 2001, ApJ, 560, 967 [NASA ADS] [Google Scholar]
- Dullemond, C. P., Hollenbach, D., Kamp, I., & D’Alessio, P. 2006, Protostars and Planets V, eds. B. Reipurth, D. Jewitt, & K. Keil [Google Scholar]
- Eisner, J. A., Hillenbrand, L. A., White, R. J., et al. 2005, ApJ, 623, 952 [NASA ADS] [CrossRef] [Google Scholar]
- Eisner, J. A., Chiang, E. I., & Hillenbrand, L. A. 2006, ApJ, 637, 133 [Google Scholar]
- Ercolano, B., Clarke, C. J., & Robitaille, T. P. 2009, MNRAS, 394, 141 [Google Scholar]
- Fukagawa, M., Hayashi, M., Tamura, M., et al. 2004, ApJ, 605, 53 [Google Scholar]
- Fukagawa, M., Tamura, M., Itoh, Y., et al. 2010, PASJ, 62, 347 [NASA ADS] [Google Scholar]
- Garcia-Lopez, R., Natta, A., Testi, L., & Habart, E. 2006, A&A, 459, 837 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gitton, P. B., Lèvêque, B., Samuel, A., Avila, G., & Phan Duc, T. 2004, Proc. SPIE, 5491, 944 [NASA ADS] [CrossRef] [Google Scholar]
- Grady, C. A., Polomski, E. F., Henning, Th., et al. 2001, AJ, 122, 3396 [NASA ADS] [CrossRef] [Google Scholar]
- Gregorio-Hetem, J., Lepine, J. R. D., Quast, G. R., Torres, C. A. O., & de La Reza, R. 1992, AJ, 103, 549 [NASA ADS] [CrossRef] [Google Scholar]
- Guilloteau, S., Dutrey, A., Petry, J., & Gueth, F. 2008, A&A, 478, 31 [Google Scholar]
- Jackson, J. D. 1983, in Klassische Elektrodynamik (Walter de Gruyter) [Google Scholar]
- Jennison, R. C. 1958, MNRAS, 118, 276 [NASA ADS] [CrossRef] [Google Scholar]
- Jensen, E. L. N., Mathieu, R. D., & Fuller, G. A. 1996, ApJ, 458, 312 [Google Scholar]
- Johansen, A., Oishi, J. S., McLow, M.-M., et al. 2007, Nature, 448, 1022 [Google Scholar]
- Johns-Krull, C. M., Valenti, J. A., & Linsky, J. L. 2000, ApJ, 539, 815 [NASA ADS] [CrossRef] [Google Scholar]
- Haisch, K. E., Lada, E. A., & Lada, C. J. 2001, ApJ, 553, 153 [Google Scholar]
- Hales, A. S., Gledhill, T. M., Barlow, M. J., & Lowe, K. T. E. 2006, MNRAS, 365, 1348 [NASA ADS] [CrossRef] [Google Scholar]
- Hartmann, L., Calvet, N., Gullbring, E., & D’Alessio, P. 1998, ApJ, 495, 385 [NASA ADS] [CrossRef] [Google Scholar]
- Hollenbach, D., Johnstone, D., Lizano, S., & Shu, F. 1994, ApJ, 428, 654 [NASA ADS] [CrossRef] [Google Scholar]
- Houk, N., Evans, A., & Sowell, J. R. 1988, BAAS, 20, 695 [NASA ADS] [Google Scholar]
- Hummel, C. A. 2008, Proc. SPIE, 7013, 136 [NASA ADS] [Google Scholar]
- IRAS Explanatory Supplement to the Catalogs and Atlasses 1985, eds. C. Beichmann, G., Neugebauer, H. J. Habing, P. E. Clegg, & T. J. Chester, NASA RP-1190, 1 [Google Scholar]
- Isella, A., & Natta, A. 2005, A&A, 438, 899 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kenyon, S. J., & Hartmann, L. 1995, ApJS, 101, 117 [NASA ADS] [CrossRef] [Google Scholar]
- Klahr, H., & Bodenheimer, P. 2003, ApJ, 582, 869 [NASA ADS] [CrossRef] [Google Scholar]
- Koresko, C. D. 2002, AJ, 124, 1082 [NASA ADS] [CrossRef] [Google Scholar]
- Koresko, C. D., Herbst, T. M., & Leinert, Ch. 1997, ApJ, 480, 741 [NASA ADS] [CrossRef] [Google Scholar]
- Kraus, S., Schloerb, F. P., Traub, W. A., et al. 2005, AJ, 130, 246 [NASA ADS] [CrossRef] [Google Scholar]
- Lagache, P.-O., Doucet, C., Pantin, E., et al. 2006, Sci, 314, 621 [Google Scholar]
- Leinert, Ch. 1992, in Star Formation and Techniques in Infrared and mm-Wave Astronomy, LNP, eds. T. P. Ray, & S. V. W. Beckwith (Berlin: Springer), 431, 215 [Google Scholar]
- Leinert, Ch., Graser, U., Przygodda, F., et al. 2003a, Ap&SS, 286, 73 [NASA ADS] [CrossRef] [Google Scholar]
- Leinert, Ch., Graser, U., Waters, L. B. F. M., et al. 2003b, Proc. SPIE, 4839, 893 [Google Scholar]
- Leinert, Ch., van Boekel, R., Waters, L. B. F. M., et al. 2004, A&A, 423, 537 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Liu, M. C., Graham, J. R., Ghez, A. M., et al. 1996, ApJ, 461, 334 [NASA ADS] [CrossRef] [Google Scholar]
- Lynden-Bell, D., & Pringle, J. E. 1974, MNRAS, 168, 603 [NASA ADS] [CrossRef] [Google Scholar]
- Mathis, J. S., Rumpl, W., & Nordsieck, K. H. 1977, ApJ, 217, 425 [NASA ADS] [CrossRef] [Google Scholar]
- McCabe, C., Duchêne, G., & Ghez, A. M. 2003, ApJ, 588, 113 [Google Scholar]
- McCabe, C., Ghez, A. M., Prato, L., et al. 2006, ApJ, 636, 932 [NASA ADS] [CrossRef] [Google Scholar]
- Meeus, G., Waelkens, C., & Malfait, K. 1998, A&A, 329, 131 [NASA ADS] [Google Scholar]
- Meeus, G., Waters, L. B. F. M., Bouwman, J., et al. 2001, A&A, 365, 476 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Men’shchikov, A. B., & Henning, Th. 1994, Proc. 10th IAP Astrophys. Meet., eds. R. Ferlet, & A. Vidal-Madjar (Éditions Frontières), 381 [Google Scholar]
- Mérand, A., Bordé, P., & Coudé Du Foresto, V. 2005, A&A, 433,1155 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Millan-Gabet, R., Schloerb, F. P., & Traub, W. 2001, ApJ, 546, 358 [NASA ADS] [CrossRef] [Google Scholar]
- Monnier, J. D., & Millan-Gabet, R. 2002, ApJ, 579, 694 [NASA ADS] [CrossRef] [Google Scholar]
- Morel, S., Ballester, P., Bauvir, B., et al. 2004, Proc. SPIE, 5491, 1666 [Google Scholar]
- Natta, A., Grinin, V. P., Mannings, V., & Ungerechts, H. 1997, ApJ, 491, 885 [NASA ADS] [CrossRef] [Google Scholar]
- Natta, A., Prusti, T., Neri, R., et al. 2001, A&A, 371, 186 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Natta, A., Testi, L., Neri, R., Shephard, D. S., & Wilner, D. J. 2004, A&A, 416, 179 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Natta, A., Testi, L., & Randich, S. 2006, A&A, 447, 609 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Petrov, R. G., Millour, F., Chesneau, O., et al. 2005 [arXiv:astro-ph/0509208] [Google Scholar]
- Pottasch, S. R., & Parthasarathy, M. 1988, A&A, 192, 182 [NASA ADS] [Google Scholar]
- Prato, L., Greene, T. P., & Simon, M. 2003, ApJ, 584, 853 [NASA ADS] [CrossRef] [Google Scholar]
- Preibisch, Th., Brown, A. G. A., Bridges, T., Günther, E., & Zinnecker, H. 2002, ApJ, 124, 404 [Google Scholar]
- Pringle, J. E. 1981, ARA&A, 19, 137 [NASA ADS] [CrossRef] [Google Scholar]
- Przygodda, F., van Boekel, R., Ábráham, P., et al., 2003, A&A, 412, 43 [Google Scholar]
- Quillen, A. C., Blackman, E. G., Frank, A., & Varnière, P. 2004, ApJ, 612, 137 [Google Scholar]
- Ratzka, Th. 2005, Ph.D. Thesis, Ruprecht-Karls-Universität Heidelberg, Germany [Google Scholar]
- Ratzka, Th., Leinert, Ch., Henning, Th., et al. 2007, A&A, 471, 173 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ratzka, Th., Schegerer, A. A., Leinert, Ch., et al. 2009, A&A, 502, 623 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Rice, W. K. M., Wood, K., Armitage, P. J., Whitney, B. A., & Bjorkman, J. E. 2003, MNRAS, 342, 79 [NASA ADS] [CrossRef] [Google Scholar]
- Rodmann, J., Henning, Th., Chandler, C. J., Mundy, L. G., & Wilner, D. J. 2006, A&A, 446, 211 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Sandell, G., Weintraub, D. A., & Hamidouche, M. 2011, ApJ, 727, 26 [NASA ADS] [CrossRef] [Google Scholar]
- Sauter, J., Wolf, S., Launhardt, R., et al. 2009, A&A, 505, 1167 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Schegerer, A., Wolf, S., Voshchinnikov, N. V., Przygodda, F., & Kessler-Silacci, J. E. 2006, A&A, 456, 535 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Schegerer, A. A. 2008, in Junge Planetensysteme (Vdm Verlag Dr. Müller) [Google Scholar]
- Schegerer, A. A., & Wolf, S. 2010, A&A, 517, 87 [Google Scholar]
- Schegerer, A. A., Wolf, S., Ratzka, Th., & Leinert, Ch. 2008, A&A, 478, 779 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Schegerer, A. A., Wolf, S., Hummel, C. A., Quanz, S. P., & Richichi, A. 2009, A&A, 502, 367 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Schloerb, F. P., Berger, J.-P., Carleton, N. P., et al. 2006, SPIE, 6268, 18 [NASA ADS] [Google Scholar]
- Setiawan, J., Henning, Th., Launhardt, R., et al. 2008, Nature, 451, 38 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Shakura, N. I., & Sunyaev, R. A. 1973, AAP, 24, 337 [Google Scholar]
- Sicilia-Aguilar, A., Hartmann, L., Fürész, G., et al. 2006, AJ, 132, 2135 [NASA ADS] [CrossRef] [Google Scholar]
- Sicilia-Aguilar, A., Bouwman, J., Juhász, A., et al. 2009, ApJ, 701, 1188 [NASA ADS] [CrossRef] [Google Scholar]
- Sylvester, R. J., Skinner, C. J., Barlow, M. J., & Mannings, V. 1996, MNRAS, 279, 915 [NASA ADS] [CrossRef] [Google Scholar]
- Takeuchi, T., & Lin, D. N. C. 2003, ApJ, 593, 524 [NASA ADS] [CrossRef] [Google Scholar]
- Thamm, E., Steinacker, J., & Henning, Th. 1994, A&A, 287, 493 [NASA ADS] [Google Scholar]
- Traub, W. A. 1998, Proc. SPIE, 3350, 848 [NASA ADS] [CrossRef] [Google Scholar]
- Traub, W. A., Ahearn, A., Carleton, N. P., et al. 2003, Proc. SPIE, 4838, 45 [Google Scholar]
- Uchida, Y., & Shibata, K. 1984, PASJ, 36, 105 [NASA ADS] [Google Scholar]
- Valenti, J. A., & Fischer, D. A. 2005, ApJS, 159, 141 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- van Boekel, R., Min, M., Leinert, Ch., et al. 2004, Nature, 432, 479 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- van Boekel, R., Min, M., Waters, L. B. F. M., et al. 2005, A&A, 437, 189 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Vieira, S. L. A., Corradi, W. J. B., Alencar, S. H. P., et al. 2003, AJ, 126, 2971 [NASA ADS] [CrossRef] [Google Scholar]
- Vinkovic, D. 2012, MNRAS, 420, 1541 [NASA ADS] [CrossRef] [Google Scholar]
- Weigelt, G., Kraus, S., Driebe, T., et al. 2007, A&A, 464, 87 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Weinberger, A. J., Becklin, E. E., Schneider, G., et al. 1999, ApJ, 525, 53 [Google Scholar]
- Wolf, S., & Voshchinnikov, N. V. 2004, Comput. Phys. Commun., 162, 113 [NASA ADS] [CrossRef] [Google Scholar]
- Wolf, S., Henning, Th., & Stecklum, B. 1999, A&A, 349, 839 [Google Scholar]
- Wünsch, R., Klahr, H., & Różyczka, M. 2005, MNRAS, 362, 361 [NASA ADS] [CrossRef] [Google Scholar]
- Youdin, A. N., & Shu, F. H. 2002, ApJ, 580, 494 [NASA ADS] [CrossRef] [Google Scholar]
- Zacharias, N., Monet, D. G., Levine, S. E., et al. 2005, AAS, 205, 4815 [Google Scholar]
All Tables
Object properties derived in previous measurements (flags refer to the references).
All Figures
 |
Fig. 1 Crosses in the SEDs (first column) represent measured photometric data obtained from the literature (Appendix A). The solid and the dashed curves represent the SED obtained from computer models, as well as its initial stellar flux, respectively. The dark and light gray bars in the figures of the second column result from H band images at λ = 1.65 μm of the models of HD 142666, while the crosses with the vertical error bars represent the measurements with IOTA. The bar width represents the interval that constrains the NIR visibilities V(λ) for different PAs but the same inclination of the model. Numbers added to the crosses are the position angles of the corresponding interferometric baseline. The measured MIR, spectrally dispersed visibilities (3rd and 4th columns) are represented by solid lines with error bars. The modeled visibilities (gray bars) were derived from model images at wavelengths of 8.5 μm, 9.5 μm, 10.6 μm, 11.5 μm, and 12.5 μm. The bar width represents the interval that constrains the MIR visibilities V(λ) for different PAs but the same inclination of the model. The upper row shows the effect after increasing the inner disk radius by a factor of five, from Rin = 0.1 AU (light gray; initial model i) to Rin = 0.5 AU (dark gray, model ii). The second row shows the result after increasing the profile parameters from β = 1.0 to β = 1.1 (model iii). The mass accretion rate is increased to Ṁ = 7 × 10-8 M⊙a-1 in model (iv) displayed in the third row while the mass density at the inner edge is decreased by a factor of fρ = 0.01 in the model (v) shown in the fourth row. In the sixth row, a dust-free disk gap is also cut in model (vi) after the density has decreased (model v). Model of row (vii) is identical to model (vi) but without decreasing the density as in model (v). The light gray bars also presented in all rows show the initial model (i) for comparison. |
| In the text | |
 |
Fig. 2 SED, NIR, and MIR visibilities spectra for the different projected baselines that result from the measurements and our model of AS 205 N. |
| In the text | |
 |
Fig. 3 SED and spectrally dispersed MIR visibility for a projected baseline length of B=52 m that result from the measurements and our model of AS 205 S. |
| In the text | |
 |
Fig. 4 Flux distributions at wavelengths of 1.65 μm, 3.5 μm, and 12.5 μm (dashed, solid, and dotted-dashed line, respectively) that are derived from a model that fits the measurements best. These distributions are normalized to the maximum of the 3.5 μm flux distribution. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


