| Issue |
A&A
Volume 554, June 2013
|
|
|---|---|---|
| Article Number | A102 | |
| Number of page(s) | 11 | |
| Section | Cosmology (including clusters of galaxies) | |
| DOI | https://doi.org/10.1051/0004-6361/201321403 | |
| Published online | 12 June 2013 | |
Polarization of cluster radio halos with upcoming radio interferometers
1 INAF – Osservatorio Astronomico di Cagliari, Strada 54, Loc. Poggio dei Pini, 09012 Capoterra (Ca), Italy
e-mail: fgovoni@ira.inaf.it
2 Center for Astrophysics and Space Science, University of California at San Diego, 92093 La Jolla (CA), USA
3 Theoretical Division, Los Alamos National Laboratory, 87544 Los Alamos (NM), USA
4 INAF – Istituto di Radioastronomia, Via P.Gobetti 101, 40129 Bologna, Italy
5 Dipartimento di Fisica e Astronomia, Università degli Studi di Bologna, Via Ranzani 1, 40127 Bologna, Italy
Received: 4 March 2013
Accepted: 19 March 2013
Context. Synchrotron radio halos at the center of merging galaxy clusters provide the most spectacular and direct evidence of the presence of relativistic particles and magnetic fields associated with the intracluster medium. The study of polarized emission from radio halos has been shown to be extremely important to constrain the properties of intracluster magnetic fields. However, detecting this polarized signal is a very hard task with the current radio facilities.
Aims. We investigate whether future radio observatories, such as the Square Kilometer Array (SKA), its precursors and its pathfinders, will be able to detect the polarized emission of radio halos in galaxy clusters.
Methods. On the basis of cosmological magnetohydrodynamical simulations with initial magnetic fields injected by active galactic nuclei, we predict the expected radio halo polarized signal at 1.4 GHz. We compare these expectations with the limits of current radio facilities and explore the potential of the upcoming radio interferometers to investigate intracluster magnetic fields through the detection of polarized emission from radio halos.
Results. The resolution and sensitivity values that are expected to be obtained in future sky surveys performed at 1.4 GHz using the SKA precursors and pathfinders (like APERTIF and ASKAP) are very promising for the detection of the polarized emission of the most powerful (L1.4 GHz > 1025 Watt/Hz) radio halos. Furthermore, the JVLA have the potential to already detect polarized emission from strong radio halos, at a relatively low resolution. However, the possibility of detecting the polarized signal in fainter radio halos (L1.4 GHz ≃ 1024 Watt/Hz) at high resolution requires a sensitivity reachable only with SKA.
Key words: galaxies: clusters: general / magnetic fields / large-scale structure of Universe
© ESO, 2013
1. Introduction
According to the hierarchical scenario of structure formation, galaxy groups and sub-clusters merge together into more massive clusters releasing amounts of gravitational energy as high as 1064 erg. Shocks and turbulence associated with cluster merger events are thought to heat thermal gas, to accelerate relativistic particles, and to compress and amplify magnetic fields in the intracluster medium (e.g. Roettiger et al. 1999).
Sensitive radio observations have revealed diffuse emission from the central regions of many merging galaxy clusters. These radio sources, which extend over volumes of ~1 Mpc3, are called radio halos. They are diffuse, low-surface-brightness (≃1 μJy arcsec-2 at 1.4 GHz), and steep-spectrum1 (α > 1) synchrotron sources with no obvious optical counterparts. Radio halos demonstrate the existence of relativistic electrons and magnetic fields spread in the intracluster medium. Most of what we know about intracluster magnetic fields derives from studies of these large-scale cluster diffuse radio sources and from Faraday rotation measures of polarized radio galaxies located inside or behind galaxy clusters (see Feretti et al. 2012, for a recent review).
Under the assumption that radio halos are on the minimum energy condition, and hence their magnetic energy density is comparable to the energy density in relativistic electrons, it is found that the volume-averaged magnetic field is of the order of ~0.1−1 μG and the total magnetic energy is as high as 1061 erg. By comparing the rotation measures observed in seven radio sources, which are projected or belonging to the Coma cluster with simulations, Bonafede et al. (2010) found a cluster magnetic field of a few μG. Similar results have been obtained by Bonafede et al. (2011a) by studying the trend of the fractional polarization of radio sources in a large sample of clusters.
Important information on the intracluster magnetic field structure can be derived from the analysis of detailed radio halo images. The total intensity and the polarization intensity radio halo surface-brightness fluctuations are strictly related to the magnetic field power spectrum (Tribble 1991; Murgia et al. 2004). For example, radio halos with a lack of polarization and a smooth, regular surface brightness may indicate that the cluster magnetic field is tangled on scales smaller than the resolution of the radio images, while a disturbed radio morphology and the presence of polarization patches could be related to a magnetic field ordered on scales larger than the observing beam. Thus, observations of radio halos have been used to study the structure of the cluster-wide magnetic fields by comparing observations with mock halos from turbulent magnetic fields by construction (Murgia et al. 2004; Govoni et al. 2006; Vacca et al. 2010). In a study of the magnetic field power spectrum in the galaxy cluster A665, which contains a Mpc-scale radio halo, the modeling performed by Vacca et al. (2010) suggests that radio halos can be intrinsically polarized, although radio halos are usually found to be unpolarized. However, detecting this polarized signal is a very hard task with the current radio interferometers because of their faintness. Polarized emission from radio halos have been observed only in bright filaments of the clusters A2255 (Govoni et al. 2005; Pizzo et al. 2011) and MACS J0717+3745 (Bonafede et al. 2009).
Cosmological simulations have been playing an important part in studying the intracluster magnetic field evolution of galaxy clusters (e.g. Dolag et al. 1999, 2002, 2005; Brüggen et al. 2005; Dubois & Teyssier 2008; Xu et al. 2009; Bonafede et al. 2011b). Although the existence of cluster-wide magnetic fields is now well-established, their origin, which is ultimately important for understanding the evolution of the intracluster medium during the course of cluster formation, is still unclear (Widrow 2002; Dolag et al. 2008). Magnetohydrodynamical simulations of cluster formation have been performed with different initial magnetic fields, which have included random or uniform fields from high redshifts (Dolag et al. 2002; Dubois & Teyssier 2008; Dubois et al. 2009), or from the outflows of normal galaxies (Donnert et al. 2009) or from active galaxies (Xu et al. 2009, 2010, 2011, 2012). The cluster magnetic fields of all these simulations are roughly in agreement at low redshifts. These simulations predict μG level magnetic field strengths in the cluster centers and a decrease of the magnetic field strengths with radius in the outer regions. These simulations provide a variety of merger configurations for evolving galaxy clusters, which can be used to interpret observed radio and X-ray features of particular systems (e.g. Donnert et al. 2010; Bonafede et al. 2012).
Recently, Xu et al. (2012) used cosmological magnetohydrodynamical cluster simulations with initial magnetic fields injected by active galactic nuclei to generate synthetic Faraday rotation measures and total intensity radio-halo images. The resulting Faraday rotation measures are consistent with the observed values of radio sources in clusters. Additionally, by giving a reasonable energy spectrum for the synchrotron electrons and by assuming the energy equipartition between magnetic fields and non-thermal electrons, the resulting radio halos have global properties in line with the observations. The synthetic Faraday rotation measure and total intensity radio halo images presented by Xu et al. (2012) show that the cluster wide magnetic fields that originate from active galaxies and are then amplified by the intracluster turbulence match on the first order with the magnetic field strength and structure which are observed in galaxy clusters.
In this work, we make a step forward by predicting the expected radio halo polarized signal at 1.4 GHz on the basis of the cosmological magnetohydrodynamical simulations by Xu et al. (2012). These simulations provide radio halo images that are compatible with data, as far as the total intensity signal is considered. We now investigate using the software FARADAY (Murgia et al. 2004) the synthetic radio halo polarization, and we compare these expectations with the current observational upper limits. Furthermore, we explore the possibility of detecting the polarized signal with the next generation of radio interferometers. Our base of knowledge on cluster magnetic fields will be greatly enhanced by radio observatories, such as the SKA2, its precursors, and its pathfinders which will provide the necessary sensitivity to study the details of total intensity and polarization of radio halos at GHz frequencies in a large number of galaxy clusters.
This paper is organized as follows. In Sect. 2, we present the expected polarized signal of mock radio halos. In Sect. 3, we show that this faint polarized emission is undetectable if observed with the comparatively shallow sensitivity and low resolution of current radio interferometers. In Sect. 4, we use our magnetohydrodynamical simulations to explore the potential of the forthcoming large radio telescopes to constrain cluster magnetic fields through the detection of polarized emission from cluster radio halos. Finally, we draw the conclusions in Sect. 5.
The intrinsic parameters quoted in this paper are computed for a ΛCDM cosmology with H0 = 73 km s-1 Mpc-1, Ωm = 0.27, and ΩΛ = 0.73.
2. Simulated radio halo polarized emission
 |
Fig. 1 Example of full resolution (10.7 kpc/pixel) radio halo in the simulated galaxy cluster R1a. Left and right panels refer to the total intensity and polarized surface brightness images, respectively. The bottom panels show the azimuthally averaged radio-halo brightness profiles of the total intensity I (green dots), polarized intensity P (red squares), and fractional polarization FPOL (blue triangles). The profiles have been calculated in concentric annuli, as shown in the inset panel. |
The combined effects of the central magnetic field strength and the radial decline in the simulations performed by Xu et al. (2012) can produce a volume-averaged magnetic field that matches the equipartition magnetic field estimates for observed radio halos and, at the same time, is able to explain the observed values of Faraday rotation measures of radio sources in clusters.
In this work, we use the magnetohydrodynamical cluster simulations by Xu et al. (2011, 2012) to investigate the polarized surface brightness of mock radio halos. Following Murgia et al. (2004), we generate synthetic radio halo images by illuminating the cosmological magnetic fields with a population of relativistic electrons. The synthetic images are calculated on a grid of (512)3 points with a spatial resolution of 10.7 kpc and a field of view of 5.48 Mpc. At each point, on the computational grid, we calculate the total intensity and the intrinsic linear polarization emissivity at 1.4 GHz, by convolving the emission spectrum of a single relativistic electron with the particle energy distribution of an isotropic population of relativistic electrons: N(γ,θ) = K0γ− δ(sinθ)/2, where γ is the electron’s Lorentz factor, and θ is the pitch angle between the electron’s velocity and the local direction of the magnetic field. To be consistent with the radio halo total intensity images presented by Xu et al. (2012), we adopt the same distribution for the relativistic particles (whose parameters are summarized in Table 1), and we assume equipartition between the magnetic field (uB) and the relativistic electron (uel) energy density at every location in the intracluster medium.
The Stokes parameters Q and U, the polarized intensity P = (Q2 + U2)1/2, and polarization plane Ψ = 0.5tan-1 (U/Q) images, have been calculated by taking into account that the polarization plane of the radio signal is subject to the Faraday rotation as it traverses the magnetized intracluster medium. Therefore, the integration of the polarized emissivity along the line of sight has been performed as a vectorial sum in which the intrinsic polarization angle of the radiation coming from the simulation cells located at a depth L is rotated by an amount: 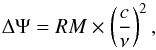 (1)where the rotation measure RM is given by
(1)where the rotation measure RM is given by ![\begin{equation} RM_{\rm~[rad/m^2]}=812\int_{0}^{L_{\rm [kpc]}}n_{\rm e~[cm^{-3}]}B_{\parallel~[\mu \rm G]}{\rm d}l. \label{rm2} \end{equation}](/articles/aa/full_html/2013/06/aa21403-13/aa21403-13-eq39.png) (2)Here, B∥ is the magnetic field along the line-of-sight. This effect leads to the so-called internal depolarization of the radio signal.
(2)Here, B∥ is the magnetic field along the line-of-sight. This effect leads to the so-called internal depolarization of the radio signal.
We present the results for some simulated clusters taken from the sample by Xu et al. (2011). In particular, we focus on three clusters (labeled with R1a, R2, and R6) that are characterized by virial masses ranging from 9.897 × 1013 to 1.252 × 1015M⊙ and that have different final magnetic field strengths. Their properties are summarized in Table 2. These clusters have been obtained by performing a self-consistent adaptive mesh refinement MHD simulation with initial magnetic fields injected by a single active galactic nucleus (AGN) using ENZO (Collins et al. 2010).
Properties of simulated galaxy clusters.
 |
Fig. 2 Left: radio power at 1.4 GHz versus the cluster X-ray luminosity in the 0.1−2.4 keV band. Full dots are observed clusters taken from the recent compilations by Feretti et al. (2012) and Govoni et al. (2012); green triangles are the simulated clusters R1a, R2, and R6 from Xu et al. (2012). In these simulations LX and L1.4 GHz have been calculated within a circle of 1 Mpc in radius. Right: azimuthally averaged radio-halo brightness profiles of the total intensity I (green dots), polarized intensity P (red squares), and fractional polarization FPOL = (blue triangles) of the clusters R1a (solid lines), R2 (dashed lines), and R6 (dotted lines). |
In Fig. 1, we show the results for the simulated cluster R1a, which is among the most massive and most luminous systems in the simulated cluster sample by Xu et al. (2011). The magnetic field strength at the cluster center is ≃2.5 μG. The full resolution images presented in Fig. 1 were performed at 1.4 GHz (with a bandwidth of 25 MHz) and are mapped as they would appear on the sky at a redshift3z = 0.2 (the current known average distance of the radio halos, Feretti et al. 2012). The left panel refers to the total intensity I image, while the right panel refers to the polarized intensity P image. It is not only possible to appreciate the full extension of the radio halo emission both in total intensity and polarization but also the fine details of its filamentary structure. The total intensity surface brightness averaged in a circle of 500 kpc in radius was determined to be ⟨ I ⟩ ≃ 1.51 × 10-6 Jy/arcsec2 while the polarization intensity surface brightness averaged in the same area was determined to be ⟨ P ⟩ ≃ 2.75 × 10-7 Jy/arcsec2. Thus, the fractional polarization (FPOL = P/I) for this simulation was found to be on average ⟨ FPOL ⟩ ≃ 18%.
The bottom panel of Fig. 1 shows the azimuthally averaged radio-halo brightness profiles of I, P, and FPOL. Each point represents the intensity, which is azimuthally averaged in concentric annuli of 50″ width centered on the cluster center. The observed intensity profiles are traced up to a projected distance from the cluster center of 1.5 Mpc. At this distance from the cluster center, the fractional polarization is as high as 45%. The internal depolarization is stronger where the cluster RM is higher and where the magnetic field is more disordered. According to Eq. (2), the central regions of a cluster, where the magnetic field strength and the gas density are higher, result in a higher RM. Therefore, the cluster center is expected to have a lower fractional polarization. Indeed, the fractional polarization decreases down to FPOL ≃ 15% near to the cluster center.
If we want to compare R1a with other radio halos that are known in the literature, it is important to note that this system (L1.4 GHz = 2.4 × 1025 Watt/Hz), may represent the most luminous radio halos that are known so far. In the simulated cluster sample by Xu et al. (2011), other mock halos like R2 and R6 may be helpful in the comparison with fainter radio halos. The radio halo in R2 results in a power at 1.4 GHz of L1.4 GHz = 1.8 × 1024 Watt/Hz; thus, R2 represents intermediate power radio halos. Finally, the radio halo in the cluster R6 (L1.4 GHz = 3.1 × 1022 Watt/Hz) is fainter than the halos that are known so far. The radio power calculated at 1.4 GHz versus the cluster X-ray luminosity are shown in the left panel of Fig. 2. Full dots refer to the data published in the literature (Feretti et al. 2012; Govoni et al. 2012, and references therein), while green triangles refer to the simulated clusters R1a, R2, R6. The synthetic radio halos lies perfectly in the relation between radio power versus X-ray luminosity (L1.4 GHz – LX). We note that in the L1.4 GHz – LX relation a few observed galaxy clusters are over-luminous in radio with respect to the clusters X-ray luminosity. Xu et al. (2012) found that a simulated cluster with multiple injection sources seems to fit in the relation with the few outliers that are known in the literature.
The I, P, and FPOL brightness profiles of R1a are compared with those of R2 and R6 in the right panel of Fig. 2. At the center of R2, the I and P surface brightnesses are about an order of magnitude fainter than in R1a, and the brightness profiles are steeper than in R1a. The I and P brightness profiles of R6 are even fainter and steeper than in R2. This behavior has been observed for real halos by Murgia et al. (2009). In agreement with the fractional polarization profile of R1a, the clusters R2 and R6 also show a smaller FPOL close to the cluster center and a higher value at an increasing distance from the cluster centers. The decrease of fractional polarization near the cluster center is due to internal depolarization. Since the internal depolarization is strictly related to the cluster magnetic field strength, magnetic filed topology, and gas density, this trend is expected to change from cluster to cluster. We consistently found less internal depolarization in the clusters characterized by a lower magnetic field strength.
Although radio halos are affected by internal depolarization, which is stronger where the RM is higher (i.e. in more magnetized and denser clusters) and where the magnetic field structure is more tangled, a significant polarization level is still expected as far as radio halos are observed at arbitrary high resolution and sensitivity.
3. Polarization of cluster radio halos with current radio interferometers
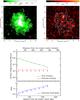 |
Fig. 3 Example of radio halo in the simulated galaxy cluster R1a. Left and right panels refer to the total intensity and polarized surface brightness images, respectively. The images have been convolved to a resolution of 50′′. The white contour levels refer to the total intensity image at 50′′ resolution. Contour levels start at 0.3 mJy/beam (3-σ) and increase by a factor of 2. The bottom panels show the azimuthally averaged radio-halo brightness profiles of the total intensity I (green dots), polarized intensity P (red squares), and fractional polarization FPOL (blue triangles). The upper limits are at 3-σ level. |
The best images of radio halos available so far have been obtained with sensitive interferometers like the Very Large Array (e.g. Clarke & Ensslin 2006; Giovannini et al. 2009; Vacca et al. 2011), the Australia Telescope Compact Array (e.g. Liang et al. 2000), the Westerbork Synthesis Radio Telescope (e.g. Pizzo & de Bruyn 2009; Brown & Rudnick 2011; van Weeren et al. 2012), and the Giant Metrewave Radio Telescope (e.g. Venturi et al. 2007; 2008; Bonafede et al. 2012). Experience shows that observations with a resolution of ~45–50″ are the best suited to detecting and to imaging halo type sources. Although many radio halos have been imaged well in total intensity, their polarized signals are still very difficult to be detected, and so far, only a few radio halos have been imaged in polarization (Govoni et al. 2005; Pizzo et al. 2011; Bonafede et al. 2009).
We use the mock radio halos presented in Sect. 2 to investigate how instrumental effects in primis resolution and sensitivity are related to the difficulties in detecting polarized emission from radio halos. In particular, we investigate the polarized signal of the powerful radio halo R1a when observed with the sensitivity and resolution of the current radio interferometers.
3.1. Sensitivity and resolution effects on radio halos
A limited sensitivity imposes a threshold on the minimum detectable surface brightness, both in total intensity and in polarization. At the same time, the low resolution needed to detect the faint radio halo signal prevents the detection of the small-scale fluctuations of the surface brightness causing a suppression of the polarized intensity. In fact, observing an extended source which is not uniformly polarized with a resolution larger than the angular scale of coherent polarization patches leads to a decrease of the polarization signal. The beam thus smoothes out the polarization of the source, and the measured polarization will be less than the true source polarization. This effect is called beam depolarization.
To investigate how the radio halo R1a would appear when observed with a set-up typically used in many of the pointed interferometric observations of radio halos reported in the literature, we convolved the full resolution I, Q, and U images with a Gaussian beam of 50′′, and we added a noise of 0.1 mJy/beam in the I image and a noise of 0.05 mJy/beam in the Q and U images. These are typical resolution and sensitivity values achieved for a two-hour time-on-source observation with the VLA at 1.4 GHz in D configuration. Finally, the convolved Q and U images were transformed back to P. The polarized intensity image P has been corrected for the positive bias.
The resulting radio halo images in total intensity I and polarized intensity P are shown on the left and on the right of Fig. 3, respectively. Most of the fine details of the halo structure, as seen in the full resolution images, are not visible anymore. In total intensity, the radio halo appears smoother but still quite well detected. On the contrary, in polarized intensity, most of the halo emission falls below the noise level and the only few surviving localized spots are hardly detectable.
In the bottom panels of Fig. 3, we show the azimuthally averaged radio-halo brightness profiles of I, P, and FPOL. Each data point represents the average brightness in concentric annuli of a beam width centered on the cluster center. The total intensity brightness profile is above the 3-σI up to about 1.2 Mpc from the cluster center, while the polarized intensity falls below the 3-σP noise level everywhere along the profile. Thus, the combination of a relatively shallow sensitivity and the beam depolarization has a strong effect in determining the observable polarization properties of radio halos. Even for a powerful radio halo like R1a with a typical observing setup (two-hour of a VLA observation in D configuration), we do not expect to detect polarization because of the current observational upper limits (e.g. Bacchi et al. 2003).
We checked that the radio halo is still visible for R2 (see also Xu et al. 2012) in total intensity but it is below the threshold of the minimum detectable polarization. R6 is not detectable either in total intensity or in polarization.
Therefore, our simulations suggest that detecting this polarized signal is a very hard task with the current radio facilities, although radio halos can be intrinsically polarized We need observations at a high resolution to reduce the beam depolarization of radio halos but, at the same time, at high resolution we need to increase the sensitivity to detect their low surface brightness.
3.2. Resolution effects on radio halos
In Sect. 3.1 we point out that the sensitivity and the beam depolarization are two major effects that limit the possibility to detect the polarized signal from a radio halo. To understand the weight of these two limitations, we focus on the effect of the beam alone, by neglecting the sensitivity of the observation. We know the “true” polarization (see Sect. 2) of mock radio halos; thus, we can easily investigate how their fractional polarization decreases by increasing the observing beam resolution.
We consider the cluster R1a and we convolve the full resolution I, Q, and U images at different resolutions with a Gaussian beam of 10″, 30″, 50″, and 100″, without adding any noise. Finally, the convolved Q and U images are transformed back to P.
In the top panels of Fig. 4, we show the resulting fractional polarization images of the radio halo R1a, as expected at different resolutions. In the bottom panel of Fig. 4, we show the azimuthally averaged radio-halo brightness profiles of the fractional polarization FPOL images at different resolution. Each point represents the fractional polarization azimuthally averaged in concentric annuli of 50″ width centered on the cluster center. The profiles at different resolutions are compared with the “true” polarization (at full resolution) shown in Fig. 1. At a fixed distance from the cluster center, different observing beams clearly affect the fractional polarization. In particular, the fractional polarization for larger beams is drastically reduced. For example, at a distance of about 1.5 Mpc from the cluster center the fractional polarization of 45% present at full resolution is reduced to about 36% when the radio halo is observed with a beam of 10″ and reaches a value of 15% if observed at a resolution of 100″. The plot clearly shows that the beam depolarization also affects the trend of the polarized emission of radio halos as a function of the projected distance from the cluster center. By increasing the observing beam, the depolarization is higher at the cluster center. This effect can be explained by the fact that the polarization vectors are intrinsically more disordered near the cluster center than in the external part, and thus the beam depolarization is higher. For example, the depolarization (DP = FPOLint/FPOLext) between the internal (≃100 kpc from the cluster center) and the external (≃1.5 Mpc from the cluster center) part of the halo in the full resolution image is DP ≃ 0.37, but the fractional polarization is further reduced at the cluster center for lower resolution observation. The depolarization is DP ≃ 0.18 at a resolution of 10″, DP ≃ 0.11 at 30″, DP ≃ 0.08 at 50″, and finally, DP ≃ 0.06 at 100″ resolution.
It is important to note that processes related to merger events could change the magnetic field structure in galaxy clusters and may amplify the magnetic field strength. Both the magnetic field topology and the magnetic field strength affect the fractional polarization in radio halos. The observed trend of the fractional polarization versus the projected distance found for these mock radio halos can be used for comparison with future observations to constrain the cluster magnetic field properties. Indeed, both the strength and the morphology (i.e. the power spectrum) of cluster magnetic fields affect the polarization properties of radio halos, and the consequent internal depolarization (Sect. 2) and beam depolarization investigated here. Thanks to these simulations, we are able to separate the contribution of the intrinsic internal depolarization from that of the extrinsic beam depolarization.
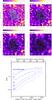 |
Fig. 4 Top: fractional polarization (FPOL = P/I) images of the radio halo, R1a, as expected at a resolution of 10″, 30″, 50″, and 100″. Contour levels refer to the corresponding total intensity emission which are convolved at the same resolution. Bottom: the azimuthally averaged radio-halo brightness profile of the fractional polarization at full resolution (solid line) is compared with the profiles at a resolution of 10″ (long dashed line), 30″ (short dashed line), 50″ (dot dashed line), and 100″ (dotted line). |
4. Polarization of cluster radio halos with upcoming radio interferometers
Tight constraints on the magnetic field power spectrum of the galaxy clusters could be potentially obtained by detecting the radio halo polarization fluctuations and not just total intensity fluctuations (Vacca et al. 2010). In fact, the fractional polarization is a very robust indicator of the intracluster magnetic field power spectrum because it only marginally depends on the energy spectrum of the synchrotron electrons and on the equipartition assumption. Therefore, it would be very important to improve the sensitivity and angular resolution (as discussed in the Sect. 3) of the future observations to detect polarized signal in as many radio halos as possible.
A new era of the study of the intracluster magnetic field will begin with upcoming radio interferometers. The high-sensitivity, low-instrumental polarization contribution, large-bandwidth, and large field of view of future instruments will allow high accuracy investigations of the intracluster magnetic fields in the central regions of the galaxy clusters and in the outskirts, where the magnetic fields are weaker.
On the basis of the cosmological magnetohydrodynamical simulations with initial magnetic fields that are injected by single active galactic nuclei (Xu et al. 2012), we explore the potential of the upcoming radio interferometers to detect the polarized emission from radio halos. In Sect. 4.1, we investigate how radio halos will appear at 1.4 GHz when observed with a bandwidth of 300 MHz. Future sky surveys performed with SKA precursors and pathfinders are planned at this frequency and bandwidth. In Sect. 4.2, we investigate pointed observations performed at 1.4 GHz with a bandwidth of 1 GHz. This wide bandwidth is provided for the SKA and is already available for the Jansky Very Large Array (JVLA).
If observations are carried out within a wide frequency band, the polarized vector may rotates by a large amount within the band, and the polarized signal can be affected by a strong bandwidth depolarization. The high sensitivity provided by the incoming radio instrumentation will make possible to observe the polarized signal in narrow frequency channels over large bandwidths, and hence to exploit the RM synthesis (Brentjens & de Bruyn 2005; Pizzo et al. 2011; Macquart et al. 2012) at its best. Pizzo et al. (2011) showed that this powerful technique is very effective method to study the polarized emission of both the discrete sources and the diffuse emission in a comprehensive way. In the simulations presented in the following, we apply the RM-synthesis to recover polarized signal reduced by the bandwidth depolarization. The details of the RM-synthesis procedure are given in a forthcoming paper (Murgia et al., in prep.).
4.1. Sky surveys with SKA precursors and pathfinders
In preparation for SKA, several next-generation radio telescopes and upgrades are being constructed around the world. Among them, JVLA (USA), APERTIF (The Netherlands), ASKAP (Australia), and Meerkat (South Africa) are very good candidates to explore the polarization properties of cluster diffuse emission at GHz frequencies. Deep total intensity and polarization sky surveys have been planned for many of these telescopes and in the following we investigate the potential of some of these surveys in detecting polarized emission from radio halos.
The survey WODAN (Westerbork Observations of the Deep APERTIF Northern-Sky; Röttgering et al. 2011) will use APERTIF to explore the northern sky (declination >+ 30deg) at 1.4 GHz with a large bandwidth of 300 MHz. This survey will provide a spatial resolution of ≃15″ and a sensitivity of about 10 μJy/beam. Similar performances will be reached in the southern sky with ASKAP through the total intensity survey EMU (Evolutionary Map of the Universe; Norris et al. 2011) and the polarization survey POSSUM (POlarization Sky Survey of the Universe’s Magnetism). These surveys, their scientific goals, and the technical challenges, which have been addressed to maximize the scientific results, have been recently described by Norris et al. (2013). All these surveys will play an important role for the study of non-thermal cluster physics. In this context, Cassano et al. (2012) derive the expected number of radio halos at 1.4 GHz to explore the potential of the EMU and WODAN surveys. By restricting the clusters to a redshift z < 0.6, they show that these surveys have the potential to detect up to 200 new radio halos.
We investigate here how the total intensity and the polarized emission of radio halos with different size and radio power will appear in radio observations, whose resolution and sensitivity are in line with those expected for these future sky surveys.
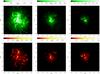 |
Fig. 5 Mock radio halos taken from the simulations of R1a (left), R2 (middle) and R6 (right) by Xu et al. (2012). Total intensity (top) and polarized (bottom) surface brightness images are smoothed to a resolution of 15″. |
The top panels of Fig. 5 show the total intensity images of the simulated clusters R1a, R2, and R6 smoothed to a resolution of 15′′. The bottom panels of Fig. 5 show the polarized images of the R1a, R2, and R6 simulated clusters smoothed to a resolution of 15″, after that the RM-synthesis is applied. For each cluster, we produced Q and U image cubes that were 300 channels by 1 MHz each, and the RM-synthesis was applied to the cubes. This technique derotates the Q and U vectors for each pixel in each frequency channel image to compensate for a certain assumed rotation measure. An RM-synthesis cube was formed and the polarized signal was recovered by integrating over the Faraday depth space.
Figure 5 shows that the fine details of the radio halos at this resolution are imaged well and the polarized surface brightness emission follow the structure of the total intensity. Accordingly with the different properties of the hosting clusters, the three mock halos appear on the sky with different surface brightness and angular extension. R1a, the most massive and the higher magnetized, is the brightest and the most extended of the three systems.
In agreement with observations (e.g Govoni et al. 2001; Orrù et al. 2007; Murgia et al. 2009), the brightness profiles of these mock radio halos smoothly decrease with distance from the cluster center. Therefore, the outermost low brightness regions of the halos become difficult to detect when the sensitivity limit is introduced and the entire radio halo may be missed if its surface brightness is below the sensitivity threshold of the observation. Since the surface brightness is typically higher in powerful radio halos, the detection of polarized emission will be easier in powerful radio halos. In the top panels of Fig. 6, the same clusters are shown as they would appear when a noise level (1-σ) of 10 μJy/beam is considered. This value is approximately the confusion limit at this resolution (Condon 1974).
In the bottom panels of Fig. 6, the same clusters are shown as they would appear in polarization when a noise level is considered. Determining the sensitivity in polarization is not easy since the expected polarization confusion limit is not obvious. For the Q and U images, we assume as a reference a 1-σ sensitivity value which is half the quoted value for the total intensity sensitivity (i.e. 5 μJy/beam in Q and U), being the sensitivity in polarization typically better than in total intensity.
Figure 6 clearly shows that this observing setup is very promising for detecting the polarized emission of the most powerful (>1025 Watt/Hz) radio halos. Therefore, surveys, like WODAN with APERTIF, and POSSUM with ASKAP, may be useful possibilities to investigate the morphology of bright radio halos, both in total intensity and polarization, at 1.4 GHz. Indeed, our results suggest that the future surveys have enough sensitivity to detect the polarization emission up to the outermost low brightness regions of the most powerful radio halos. On the other hand, radio halos of intermediate power with L1.4 GHz ≃ 1024 Watt/Hz, like R2, will be imaged at high resolution in total intensity, but their polarization will still be hardly detectable. Finally, the fainter radio halos, like R6, will definitely need a higher brightness sensitivity to be detected both in total intensity and in polarization.
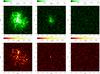 |
Fig. 6 Mock radio halos taken from the simulations of R1a (left), R2 (middle) and R6 (right) by Xu et al. (2012). Total intensity (top) and polarized (bottom) surface brightness images are shown as they would appear when observed at 1.4 GHz with a bandwidth of 300 MHz, at a resolution of 15′′, a noise level (1-σ) of 10 μJy/beam in I, and 5 μJy/beam in Q and U. These resolutions and sensitivity values are in line with that expected in future sky surveys at 1.4 GHz performed with SKA precursors and pathfinders. |
4.2. Pointed observations with SKA, its precursors, and its pathfinders
One of the main difficulties in the study of radio halos is their faintness, which complicates their detection and complicates their study with the current resources. A huge sensitivity to extended low-surface brightness emission is needed for a proper study of the radio halos both in total intensity and in polarization.
The SKA will provide an unprecedented improvement in collecting area, thus providing the necessary sensitivity to study the low-surface brightness radio halo emission at an angular resolution much higher than the study previously done. The simulations presented in this work offer the possibility of testing whether these improvements are suitable for detecting the faint polarized emission originating in the intracluster magnetic field filamentary structures.
We consider how the total intensity and the polarized surface brightness of the mock halos of R1a, R2, and R6 would appear as seen at different resolutions. In practice, we produce a set of images (similar to those shown in Fig. 5) at 1.4 GHz with a bandwidth of 1 GHz by varying the beam size in the range from 3″ (the full resolution of our simulations) to 100″. We then analyze the expected fluctuations of the radio brightness in the central region of the simulated halos and compare them with the sensitivity expected for observations performed with SKA (see e.g. The Square Kilometer Array Design Reference Mission). In Figs. 7, 8, we show the results of this analysis.
Since we are comparing radio halos of different luminosities (see Fig. 2), we need to rescale the region of interest according to the radio halo size. As shown by Murgia et. al (2009), the e-folding radius re of the surface brightness radial profile can be used as a reference for the radio halo size. Following the procedures described in Murgia et. al (2009), we obtained re = 101′′, 56′′, and 30′′ for R1a, R2, and R6, respectively by fitting the simulated radial profiles with an exponential. Thus, we include in the statistics only those regions of the halo to within 3re from the cluster center, for a proper comparison. For each cluster, we plot the average brightness as a solid thin line and we use a shaded region to show the maximum and minimum brightness fluctuations calculated to within 3re from the cluster center at that resolution. The simulated surface brightnesses are compared with the sensitivity and the resolution of wide band instruments to explore their potential in detecting the total intensity and polarized emission of halos at different radio power.
In Fig. 7, we present the expected total intensity emission of the mock radio halos R1a (top), R2 (middle), and R6 (bottom) as a function of the angular resolution. We calculated, up to a resolution of 40″, the sensitivity achievable with SKA Phase-1 and SKA Phase-2 at 1.4 GHz for 1 h of integration time and a bandwidth of 1 GHz. The solid thick lines indicate the 3-σ sensitivity limit which is obtained by taking into account both the sensitivity reached for an 1 h of exposure time and the confusion limit. The sensitivity of the SKA Phase-2 at the few arcsec resolution is an order of magnitude better than that of the SKA Phase-1. At a resolution higher than ≃10″ the confusion limit is dominant, therefore, the sensitivity of the SKA Phase-1 and Phase-2 are the same. We compare these limits with the expectations of the JVLA, which represent the state-of-the-art instrument to investigate radio halos. In the resolution range between 15″ to 45″, the JVLA too is dominated by the confusion noise for 1 h of integration time. On the other hand, the UV coverage of the JVLA does not permit to image the large angular structure of radio halos at higher resolution.
For a given resolution, we compare the average surface brightness of the mock radio halos R1a, R2, and R6 with the minimum (3-σ) surface brightness that is detectable with the SKA (Phase-1 and Phase-2) and the JVLA. Operationally, we consider that the halo emission is fully detectable only if the average surface brightness exceeds the 3-σ sensitivity limit of the instruments. However, it is possible also to have partial detections if a few isolated patches have enough signal-to-noise to “emerge” above the sensitivity limit threshold.
Figure 7 shows that observations performed with the SKA (Phase-1 and Phase-2) have the potential of detecting the total intensity emission in R1a-like and R2-like radio halos. Similar results can also be obtained with the JVLA and with sky surveys that are planned with the SKA precursor and pathfinders (see Sect. 4.1), but the SKA will provide unprecedented capabilities for imaging these radio halos at arcsecond resolution, where the confusion noise is negligible. On the other hand, SKA will miss the fainter R6-like halos.
In Fig. 8, we present the expected polarized emission of the mock radio halos R1a (top), R2 (middle), and R6 (bottom) as a function of the angular resolution. The analysis of polarization data performed with instruments having a bandwidth of 1 GHz requires the RM-synthesis; therefore, this technique is applied to the simulations in polarization. We tentatively represent with solid thick lines a 3-σ limit expected with the SKA (Phase-1 and Phase-2) and the JVLA. Determining the sensitivity in polarization is not easy, since the expected polarization confusion limit is not obvious. Therefore, we assume that the confusion limit is negligible in polarization, and we consider a putative polarization sensitivity calculated as half the sensitivity expected in total intensity. Under the above assumptions, the SKA Phase-2 will improve the sensitivity to about one order of magnitude with respect the SKA Phase-1 and to about two orders of magnitude with respect to the JVLA.
 |
Fig. 7 Total intensity surface brightness as a function of the beam size (3″–100″) for the mock radio halos R1a (top), R2 (middle), and R6 (bottom). For each radio halo, the surface brightness is calculated within a circle of 3re in radius. The solid thin green line shows the average brightness, while the shaded region shows the maximum and minimum brightness fluctuations. The simulated surface brightness is compared with the sensitivity of wide band instruments (SKA Phase-1, SKA Phase-2, JVLA) to explore their potential in detecting the total intensity emission of halos at different radio power. The sensitivity refers to the 3-σ limit. |
Figure 8 shows that the sensitivity reachable with the SKA will detect the polarized emission in radio halos of high (R1a-like) and intermediate (R2-like) luminosity. Therefore, the detection of high-resolution polarized emission in radio halos with a luminosity of L1.4 GHz = 1 − 2 × 1024 Watt/Hz requires a sensitivity reachable only with the SKA. For fainter halos (R6-like), the partial detection of the polarized emission could be also possible, albeit very difficult even for the SKA Phase-2. It is interesting to note that on the basis of our modeling, the JVLA can already detect polarized emission from strong radio halos at a relatively low resolution. Indeed, this is a prediction of what we will be able to test in the near future because of the wide-band polarized observations scheduled with the JVLA at 1.4 GHz for a sample of radio halos.
As a last point, we briefly address the scatter of the radio halo brightness at a given resolution. The scatter of the simulated surface brightness represented by the shaded region is very interesting in its own. This intrinsic variation is due to two distinct effects. One is the general dimming of the radio halo surface brightness with its radius and the other is the point-to-point scatter due to the filamentary structure of the intracluster magnetic field. The brightness dispersion increases by increasing the resolution because the filamentary structure of the halo is progressively resolved. Therefore, the SKA will not only be able to detect the radio halo emission but also to measure the intrinsic scatter of both the total intensity and the polarized surface brightness. Determining the amplitude of this scatter is important, since this quantity is strictly related to the power spectrum of the intracluster magnetic field fluctuations (Murgia et al. 2004; Govoni et al. 2006; Vacca et al. 2010).
 |
Fig. 8 Polarized intensity surface brightness as a function of the beam size (3″–100″) for the mock radio halos R1a (top), R2 (middle), and R6 (bottom). For each radio halo, the surface brightness is calculated within a circle of 3re in radius. The solid thin red line shows the average brightness, while the shaded region shows the maximum and minimum brightness fluctuations. The simulated surface brightness is compared with the sensitivity of wide band instruments (SKA Phase-1, SKA Phase-2, JVLA) to explore their potential in detecting the polarized intensity emission of halos at different radio power. The sensitivity refers to the 3-σ limit. |
5. Conclusion
In this work, we use the cosmological magnetohydrodynamical simulations by Xu et al. (2012) to predict the expected surface brightness distribution of radio halos both in total intensity and in polarization. Under the equipartition assumption and a reasonable shape for the relativistic electron energy spectrum, we produce synthetic radio halo images at a frequency of 1.4 GHz for three simulated halos of representative total radio luminosity.
We first show that, simulated radio halos are intrinsically polarized at full-resolution. The fractional polarization at the cluster center is ≃15–35% with values varying from cluster to cluster and increasing with the distance from the cluster center. However, the polarized signal is undetectable if observed with the comparatively shallow sensitivity and low resolution of current radio interferometers.
We then use our modeling to investigate the potential of the increased sensitivity and the resolution of the forthcoming large radio telescopes. We find that surveys planned with the SKA precursors will be in principle able to detect the polarized emission in the most luminous halos known, while the halos of intermediate and faint luminosity will still be hardly detectable. Furthermore, we find that the JVLA have the potential to already detect polarized emission from strong radio halos.
For radio halos of strong and intermediate luminosity, we expect a polarized signal of about 2–0.5 μJy/beam at 1.4 GHz with a resolution of 3″. The SKA, the most ambitious radio telescope ever planned, could have the sufficient sensitivity to fully detect the polarized emission of these radio halos at high resolution. For fainter halos, the partial detection of the polarized emission could also be possible, albeit very difficult even for the SKA.
Furthermore, the SKA will be capable of measuring the intrinsic scatter of both the total intensity and the polarized surface brightness fluctuations. Determining the amplitude of this scatter is important, since this quantity is strictly related to the power spectrum of the intracluster magnetic field fluctuations (Murgia et al. 2004; Govoni et al. 2006; Vacca et al. 2010).
Acknowledgments
The authors thank Joseph Lazio for useful discussions. This research was supported by PRIN-INAF2009 and by the project L.R. 7 Agosto 2007, N.7: “Promozione della Ricerca Scientifica e dell’innovazione Tecnologica in Sardegna”, Progetti di ricerca fondamentale o di base annualitá 2012. H.X. and H.L. were supported by the LDRD and IGPP programs at LANL and by the DOE/Office of Fusion Energy Science through CMSO. Computing resources for cluster simulations were supplied by LANL on Institutional Computing Resource. ENZO is developed at the Laboratory for Computational Astrophysics, UCSD, with partial support from NSF grants AST-0708960 and AST-0808184 to M.L.N.
References
- Bacchi, M., Feretti, L., Giovannini, G., & Govoni, F. 2003, A&A, 400, 465 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bonafede, A., Feretti, L, Giovannini, G., et al. 2009, A&A, 503, 707 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bonafede, A., Feretti, L., Murgia, M., et al. 2010, A&A, 513, A30 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bonafede, A., Govoni, F., Feretti, L., et al. 2011a, A&A, 530, A24 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bonafede, A., Dolag, K., Stasyszyn, F., Murante, G., & Borgani, S. 2011b, MNRAS, 418, 2234 [NASA ADS] [CrossRef] [Google Scholar]
- Bonafede, A., Brüggen, M., van Weeren, R., et al. 2012, MNRAS, 426, 40 [NASA ADS] [CrossRef] [Google Scholar]
- Brentjens, M. A., & de Bruyn, A. G. 2005, A&A, 441, 1217 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Brown, S., & Rudnick, L. 2011, MNRAS, 412, 2 [NASA ADS] [CrossRef] [Google Scholar]
- Brüggen, M., Ruszkowski, M., Simionescu, A., Hoeft, M., & Dalla Vecchia, C. 2005, ApJ, 631, L21 [NASA ADS] [CrossRef] [Google Scholar]
- Cassano, R., Brunetti, G., Norris, R. P., et al. 2012, A&A, 548, A100 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Clarke, T. E., & Ensslin, T. A. 2006, AJ, 131, 2900 [Google Scholar]
- Collins, D. C., Xu, H., Norman, M. L., et al. 2010, ApJS, 186, 308 [NASA ADS] [CrossRef] [Google Scholar]
- Condon, J. J. 1974, ApJ, 188, 279 [NASA ADS] [CrossRef] [Google Scholar]
- Dolag, K., Bartelmann, M., & Lesch, H. 1999, A&A, 348, 351 [NASA ADS] [Google Scholar]
- Dolag, K., Bartelmann, M., & Lesch, H. 2002, A&A, 387, 383 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Dolag, K., Grasso, D., Springel, V., & Tkachev, I. 2005, J. Cosmol. Astropart. Phys., 1, 9 [Google Scholar]
- Dolag, K., Bykov, A. M., & Diaferio, A. 2008, Space Sci. Rev., 134, 311 [NASA ADS] [CrossRef] [Google Scholar]
- Donnert, J., Dolag, K., Lesch, H., & Müller, E. 2009, MNRAS, 392, 1008 [NASA ADS] [CrossRef] [Google Scholar]
- Donnert, J., Dolag, K., Brunetti, G., Cassano, R., & Bonafede, A. 2010, MNRAS, 401, 47 [NASA ADS] [CrossRef] [Google Scholar]
- Dubois, Y., & Teyssier, R. 2008, A&A, 482, L13 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Dubois, Y., Devriendt, J., Slyz, A., & Silk, J. 2009, MNRAS, 399, L49 [NASA ADS] [Google Scholar]
- Feretti, L., Giovannini, G., Govoni, F., & Murgia, M. 2012, A&ARv, 20, 54 [Google Scholar]
- Giovannini, G., Bonafede, A., Feretti, L., et al. 2009, A&A, 507, 1257 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Govoni, F., Enßlin, T. A., Feretti, L., & Giovannini, G. 2001, A&A, 369, 441 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Govoni, F., Murgia, M., Feretti, L., et al. 2005, A&A, 430, L5 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Govoni, F., Murgia, M., Feretti, L., et al. 2006, A&A, 460, 425 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Govoni, F., Ferrari, C., Feretti, L., et al. 2012, A&A, 545, A74 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Liang, H., Hunstead, R. W., Birkinshaw, M., & Andreani, P. 2000, ApJ, 544, 686 [NASA ADS] [CrossRef] [Google Scholar]
- Macquart, J.-P., Ekers, R. D., Feain, I., & Johnston-Hollitt, M. 2012, ApJ, 750, 139 [NASA ADS] [CrossRef] [Google Scholar]
- Murgia, M., Govoni, F., Feretti, L., et al. 2004, A&A, 424, 429 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Murgia, M., Govoni, F., Markevitch, M., et al. 2009, A&A, 499, 679 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Norris, R. P., Hopkins, A. M., Afonso, J., et al. 2011, PASA, 28, 215 [NASA ADS] [CrossRef] [Google Scholar]
- Norris, R. P., Afonso, J., Bacon, D., et al. 2013, PASA, 30, e020 [NASA ADS] [CrossRef] [Google Scholar]
- Orrù, E., Murgia, M., Feretti, L., et al. 2007, A&A, 467, 943 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Pizzo, R. F., & de Bruyn, A. G. 2009, A&A, 507, 639 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Pizzo, R. F., de Bruyn, A. G., Bernardi, G., & Brentjens, M. A. 2011, A&A, 525, A104 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Roettiger, K., Stone, J. M., & Burns, J. O. 1999, ApJ, 518, 594 [NASA ADS] [CrossRef] [Google Scholar]
- Röttgering, H., Afonso, J., Barthel, P., et al. 2011, A&A, 32, 557 [Google Scholar]
- SKA Science Working Group 2011, The Square Kilometer Array Design Reference Mission: SKA Phase 1 [Google Scholar]
- Tribble, P. C. 1991, MNRAS, 253, 147 [NASA ADS] [Google Scholar]
- Vacca, V., Murgia, M., Govoni, F., et al. 2010, A&A, 514, A71 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Vacca, V., Govoni, F., Murgia, M., et al. 2011, A&A, 535, A82 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- van Weeren, R. J., Bonafede, A., Ebeling, H., et al. 2012, MNRAS, 425, L36 [NASA ADS] [CrossRef] [Google Scholar]
- Venturi, T., Giacintucci, S., Brunetti, G., et al. 2007, A&A, 463, 937 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Venturi, T., Giacintucci, S., Dallacasa, D., et al. 2008, A&A, 484, 327 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Widrow, L. M. 2002, Rev. Mod. Phys., 74, 775 [NASA ADS] [CrossRef] [Google Scholar]
- Xu, H., Li, H., Collins, D. C., Li, S., & Norman, M. L. 2009, ApJ, 698, L14 [NASA ADS] [CrossRef] [Google Scholar]
- Xu, H., Li, H., Collins, D. C., Li, S., & Norman, M. L. 2010, ApJ, 725, 2152 [NASA ADS] [CrossRef] [Google Scholar]
- Xu, H., Li, H., Collins, D. C., Li, S., & Norman, M. L. 2011, ApJ, 739, 77 [NASA ADS] [CrossRef] [Google Scholar]
- Xu, H., Govoni, F., Murgia, M., et al. 2012, ApJ, 759, 40 [NASA ADS] [CrossRef] [Google Scholar]
All Tables
All Figures
 |
Fig. 1 Example of full resolution (10.7 kpc/pixel) radio halo in the simulated galaxy cluster R1a. Left and right panels refer to the total intensity and polarized surface brightness images, respectively. The bottom panels show the azimuthally averaged radio-halo brightness profiles of the total intensity I (green dots), polarized intensity P (red squares), and fractional polarization FPOL (blue triangles). The profiles have been calculated in concentric annuli, as shown in the inset panel. |
| In the text | |
 |
Fig. 2 Left: radio power at 1.4 GHz versus the cluster X-ray luminosity in the 0.1−2.4 keV band. Full dots are observed clusters taken from the recent compilations by Feretti et al. (2012) and Govoni et al. (2012); green triangles are the simulated clusters R1a, R2, and R6 from Xu et al. (2012). In these simulations LX and L1.4 GHz have been calculated within a circle of 1 Mpc in radius. Right: azimuthally averaged radio-halo brightness profiles of the total intensity I (green dots), polarized intensity P (red squares), and fractional polarization FPOL = (blue triangles) of the clusters R1a (solid lines), R2 (dashed lines), and R6 (dotted lines). |
| In the text | |
 |
Fig. 3 Example of radio halo in the simulated galaxy cluster R1a. Left and right panels refer to the total intensity and polarized surface brightness images, respectively. The images have been convolved to a resolution of 50′′. The white contour levels refer to the total intensity image at 50′′ resolution. Contour levels start at 0.3 mJy/beam (3-σ) and increase by a factor of 2. The bottom panels show the azimuthally averaged radio-halo brightness profiles of the total intensity I (green dots), polarized intensity P (red squares), and fractional polarization FPOL (blue triangles). The upper limits are at 3-σ level. |
| In the text | |
 |
Fig. 4 Top: fractional polarization (FPOL = P/I) images of the radio halo, R1a, as expected at a resolution of 10″, 30″, 50″, and 100″. Contour levels refer to the corresponding total intensity emission which are convolved at the same resolution. Bottom: the azimuthally averaged radio-halo brightness profile of the fractional polarization at full resolution (solid line) is compared with the profiles at a resolution of 10″ (long dashed line), 30″ (short dashed line), 50″ (dot dashed line), and 100″ (dotted line). |
| In the text | |
 |
Fig. 5 Mock radio halos taken from the simulations of R1a (left), R2 (middle) and R6 (right) by Xu et al. (2012). Total intensity (top) and polarized (bottom) surface brightness images are smoothed to a resolution of 15″. |
| In the text | |
 |
Fig. 6 Mock radio halos taken from the simulations of R1a (left), R2 (middle) and R6 (right) by Xu et al. (2012). Total intensity (top) and polarized (bottom) surface brightness images are shown as they would appear when observed at 1.4 GHz with a bandwidth of 300 MHz, at a resolution of 15′′, a noise level (1-σ) of 10 μJy/beam in I, and 5 μJy/beam in Q and U. These resolutions and sensitivity values are in line with that expected in future sky surveys at 1.4 GHz performed with SKA precursors and pathfinders. |
| In the text | |
 |
Fig. 7 Total intensity surface brightness as a function of the beam size (3″–100″) for the mock radio halos R1a (top), R2 (middle), and R6 (bottom). For each radio halo, the surface brightness is calculated within a circle of 3re in radius. The solid thin green line shows the average brightness, while the shaded region shows the maximum and minimum brightness fluctuations. The simulated surface brightness is compared with the sensitivity of wide band instruments (SKA Phase-1, SKA Phase-2, JVLA) to explore their potential in detecting the total intensity emission of halos at different radio power. The sensitivity refers to the 3-σ limit. |
| In the text | |
 |
Fig. 8 Polarized intensity surface brightness as a function of the beam size (3″–100″) for the mock radio halos R1a (top), R2 (middle), and R6 (bottom). For each radio halo, the surface brightness is calculated within a circle of 3re in radius. The solid thin red line shows the average brightness, while the shaded region shows the maximum and minimum brightness fluctuations. The simulated surface brightness is compared with the sensitivity of wide band instruments (SKA Phase-1, SKA Phase-2, JVLA) to explore their potential in detecting the polarized intensity emission of halos at different radio power. The sensitivity refers to the 3-σ limit. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


