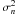| Issue |
A&A
Volume 554, June 2013
|
|
|---|---|---|
| Article Number | A26 | |
| Number of page(s) | 9 | |
| Section | Numerical methods and codes | |
| DOI | https://doi.org/10.1051/0004-6361/201321236 | |
| Published online | 30 May 2013 | |
NIFTY – Numerical Information Field Theory⋆
A versatile PYTHON library for signal inference
1
Max Planck Institute für Astrophysik,
Karl-Schwarzschild-Straße 1,
85748
Garching,
Germany
e-mail: mselig@mpa-garching.mpg.de
2
Ludwig-Maximilians − Universität München,
Geschwister-Scholl-Platz
1, 80539
München,
Germany
3
Technische Universität München, Arcisstraße 21, 80333
München,
Germany
Received:
5
February
2013
Accepted:
12
April
2013
NIFTy (Numerical Information Field Theory) is a software package designed to enable the development of signal inference algorithms that operate regardless of the underlying spatial grid and its resolution. Its object-oriented framework is written in Python, although it accesses libraries written in Cython, C++, and C for efficiency. NIFTy offers a toolkit that abstracts discretized representations of continuous spaces, fields in these spaces, and operators acting on fields into classes. Thereby, the correct normalization of operations on fields is taken care of automatically without concerning the user. This allows for an abstract formulation and programming of inference algorithms, including those derived within information field theory. Thus, NIFTy permits its user to rapidly prototype algorithms in 1D, and then apply the developed code in higher-dimensional settings of real world problems. The set of spaces on which NIFTy operates comprises point sets, n-dimensional regular grids, spherical spaces, their harmonic counterparts, and product spaces constructed as combinations of those. The functionality and diversity of the package is demonstrated by a Wiener filter code example that successfully runs without modification regardless of the space on which the inference problem is defined.
Key words: methods: data analysis / methods: numerical / methods: statistical / techniques: image processing
NIFTy homepage http://www.mpa-garching.mpg.de/ift/nifty/; Excerpts of this paper are part of the NIFTy source code and documentation.
© ESO, 2013
1. Introduction
In many signal inference problems, one tries to reconstruct a continuous signal field from a finite set of experimental data. The finiteness of data sets is due to their incompleteness, resolution, and the sheer duration of the experiment. A further complication is the inevitability of experimental noise, which can arise from various origins. Numerous methodological approaches to such inference problems are known in modern information theory founded by Cox (1946), Shannon (1948), and Wiener (1949).
Signal inference methods are commonly formulated in an abstract, mathematical way to be applicable in various scenarios; i.e., the method itself is independent, or at least partially independent, of resolution, geometry, physical size, or even dimensionality of the inference problem. It then is up to the user to apply the appropriate method correctly to the problem at hand.
In practice, signal inference problems are solved numerically, rather than analytically. Numerical algorithms should try to preserve as much of the universality of the underlying inference method as possible, given the limitations of a computer environment, so that the code is reuseable. For example, an inference algorithm developed in astrophysics that reconstructs the photon flux on the sky from high energy photon counts might also serve the purpose of reconstructing two- or three-dimensional medical images obtained from tomographical X-rays. The desire for multi-purpose, problem-independent inference algorithms is one motivation for the NIFTy package presented here. Another is to facilitate the implementation of problem specific algorithms by providing many of the essential operations in a convenient way.
NIFTy stands for “Numerical Information Field Theory”. It is a software package written in Python12, however, it also incorporates Cython3 (Behnel et al. 2009; Seljebotn 2009), C++, and C libraries for efficient computing.
The purpose of the NIFTy library is to provide a toolkit that enables users to implement their algorithms as abstractly as they are formulated mathematically. NIFTy’s field of application is kept broad and not bound to one specific methodology. The implementation of maximum entropy (Jaynes 1957, 1989), likelihood-free, maximum likelihood, or full Bayesian inference methods (Bayes 1763; Laplace 1795/1951; Cox 1946) are feasible, as well as the implementation of posterior sampling procedures based on Markov chain Monte Carlo procedures (Metropolis & Ulam 1949; Metropolis et al. 1953).
Although NIFTy is versatile, the original intention was the implementation of inference algorithms that are formulated methodically in the language of information field theory (IFT)4. The idea of IFT is to apply information theory to the problem of signal field inference, where “field” is the physicist’s term for a continuous function over a continuous space. The recovery of a field that has an infinite number of degrees of freedom from finite data can be achieved by exploiting the spatial continuity of fields and their internal correlation structures. The framework of IFT is detailed in the work by Enßlin et al. (2009) where the focus lies on a field theoretical approach to inference problems based on Feynman diagrams. An alternative approach using entropic matching based on the formalism of the Gibbs free energy can be found in the work by Enßlin & Weig (2010). IFT based methods have been developed to reconstruct signal fields without a priori knowledge of signal and noise correlation structures (Enßlin & Frommert 2011; Oppermann et al. 2011). Furthermore, IFT has been applied to a number of problems in astrophysics, namely to recover the large scale structure in the cosmic matter distribution using galaxy counts (Kitaura et al. 2009; Jasche & Kitaura 2010; Jasche et al. 2010a,b; Weig & Enßlin 2010), and to reconstruct the Faraday rotation of the Milky Way (Oppermann et al. 2012). A more abstract application has been shown to improve stochastic estimates such as the calculation of matrix diagonals by sample averages (Selig et al. 2012).
One natural requirement of signal inference algorithms is their independence of the choice of a particular grid and a specific resolution, so that the code is easily transferable to problems that are similar in terms of the necessary inference methodology but might differ in terms of geometry or dimensionality. In response to this requirement, NIFTy comprises several commonly used pixelization schemes and their corresponding harmonic bases in an object-oriented framework. Furthermore, NIFTy preserves the continuous limit by taking care of the correct normalization of operations like scalar products, matrix-vector multiplications, and grid transformations; i.e., all operations involving position integrals over continuous domains.
The remainder of this paper is structured as follows. In Sect. 2 an introduction to signal inference is given, with the focus on the representation of continuous information fields in the discrete computer environment. Section 3 provides an overview of the class hierarchy and features of the NIFTy package. The implementation of a Wiener filter algorithm demonstrates the basic functionality of NIFTy in Sect. 4. We conclude in Sect. 5.
2. Concepts of signal inference
2.1. Fundamental problem
Many signal inference problems can be reduced to a single model equation, 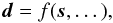 (1)where
the data set d is the outcome of some function
f being applied to a set of unknowns5. Some of the unknowns are of interest and form the signal
s, whereas the remaining are considered as nuisance
parameters. The goal of any inference algorithm is to obtain an approximation for the
signal that is “best” supported by the data. Which criteria define this “best” is answered
differently by different inference methodologies.
(1)where
the data set d is the outcome of some function
f being applied to a set of unknowns5. Some of the unknowns are of interest and form the signal
s, whereas the remaining are considered as nuisance
parameters. The goal of any inference algorithm is to obtain an approximation for the
signal that is “best” supported by the data. Which criteria define this “best” is answered
differently by different inference methodologies.
There is in general no chance of a direct inversion of Eq. (1). Any realistic measurement involves random processes summarized as noise and, even for deterministic or noiseless measurement processes, the number of degrees of freedom of a signal typically outnumbers those of a finite data set measured from it, because the signal of interest might be a continuous field; e.g., some physical flux or density distribution.
In order to clarify the concept of measuring a continuous signal field, let us consider a
linear measurement by some response R with additive and
signal independent noise n, 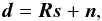 (2)which
reads for the individual data points,
(2)which
reads for the individual data points, 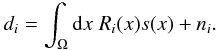 (3)Here
we introduced the discrete index
i ∈ { 1,...,N } ⊂ N
and the continuous position x ∈ Ω of some abstract position space Ω. For
example, in the context of image reconstruction, i could label the
N image pixels and x would describe real space
positions.
(3)Here
we introduced the discrete index
i ∈ { 1,...,N } ⊂ N
and the continuous position x ∈ Ω of some abstract position space Ω. For
example, in the context of image reconstruction, i could label the
N image pixels and x would describe real space
positions.
The model given by Eq. (2)already poses a full inference problem since it involves an additive random process and a non-invertible signal response. As a consequence, there are many possible field configurations in the signal phase space that could explain a given data set. The approach used to single out the “best” estimate of the signal field from the data at hand is up to the choice of inference methodology. However, the implementation of any derived inference algorithm needs a proper discretization scheme for the fields defined on Ω. Since one might want to extend the domain of application of a successful algorithm, it is worthwhile to keep the implementation flexible with respect to the characteristics of Ω.
Overview of derivatives of the NIFTy space class, the corresponding grids, and conjugate space classes.
2.2. Discretized continuum
The representation of fields that are mathematically defined on a continuous space in a finite computer environment is a common necessity. The goal hereby is to preserve the continuum limit in the calculus in order to ensure a resolution independent discretization.
Any partition of the continuous position space Ω (with volume V) into a
set of Q disjoint, proper subsets Ωq (with
volumes Vq) defines a pixelization,
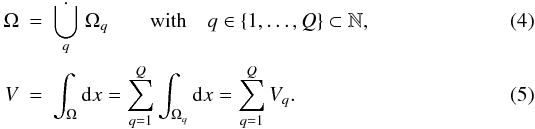 Here
the number Q characterizes the resolution of the pixelization, and the
continuum limit is described by Q → ∞ and
Vq → 0 for all
q ∈ { 1,...,Q }
simultaneously. Moreover, Eq. (5)defines a
discretization of continuous integrals,
∫Ωdx → ∑ qVq.
Here
the number Q characterizes the resolution of the pixelization, and the
continuum limit is described by Q → ∞ and
Vq → 0 for all
q ∈ { 1,...,Q }
simultaneously. Moreover, Eq. (5)defines a
discretization of continuous integrals,
∫Ωdx → ∑ qVq.
Any valid discretization scheme for a field s can be
described by a mapping, 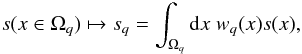 (6)if
the weighting function wq(x)
is chosen appropriately. In order for the discretized version of the field to converge to
the actual field in the continuum limit, the weighting functions need to be normalized in
each subset; i.e., ∀q:
(6)if
the weighting function wq(x)
is chosen appropriately. In order for the discretized version of the field to converge to
the actual field in the continuum limit, the weighting functions need to be normalized in
each subset; i.e., ∀q: 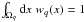 . Choosing such a weighting
function that is constant with respect to x yields
. Choosing such a weighting
function that is constant with respect to x yields 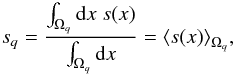 (7)which
corresponds to a discretization of the field by spatial averaging. Another common and
equally valid choice is
wq(x) = δ(x − xq),
which distinguishes some position
xq ∈ Ωq, and
evaluates the continuous field at this position,
(7)which
corresponds to a discretization of the field by spatial averaging. Another common and
equally valid choice is
wq(x) = δ(x − xq),
which distinguishes some position
xq ∈ Ωq, and
evaluates the continuous field at this position,
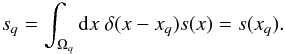 (8)In
practice, one often makes use of the spatially averaged pixel position,
xq = ⟨x⟩Ωq;
cf. Eq. (7). If the resolution is high
enough to resolve all features of the signal field s, both
of these discretization schemes approximate each other,
⟨s(x)⟩Ωq ≈ s(⟨x⟩Ωq),
since they approximate the continuum limit by construction6.
(8)In
practice, one often makes use of the spatially averaged pixel position,
xq = ⟨x⟩Ωq;
cf. Eq. (7). If the resolution is high
enough to resolve all features of the signal field s, both
of these discretization schemes approximate each other,
⟨s(x)⟩Ωq ≈ s(⟨x⟩Ωq),
since they approximate the continuum limit by construction6.
All operations involving position integrals can be normalized in accordance with Eqs.
(5)and (7). For example, the scalar product between two fields
s and u is defined as
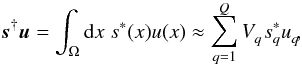 (9)where
† denotes adjunction and ∗ complex conjugation. Since the approximation in Eq. (9)becomes an equality in the continuum limit,
the scalar product is independent of the pixelization scheme and resolution, if the latter
is sufficiently high.
(9)where
† denotes adjunction and ∗ complex conjugation. Since the approximation in Eq. (9)becomes an equality in the continuum limit,
the scalar product is independent of the pixelization scheme and resolution, if the latter
is sufficiently high.
The above line of argumentation analogously applies to the discretization of operators.
For a linear operator A acting on some field
s as
As = ∫ΩdyA(x,y)s(y),
a matrix representation discretized in analogy to Eq. (7)is given by 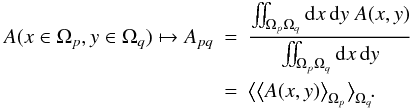 (10)Consequential
subtleties regarding operators are addressed in Appendix A.
(10)Consequential
subtleties regarding operators are addressed in Appendix A.
The proper discretization of spaces, fields, and operators, as well as the normalization of position integrals, is essential for the conservation of the continuum limit. Their consistent implementation in NIFTy allows a pixelization independent coding of algorithms.
Selection of instance methods of the NIFTy field class.
3. Class and feature overview
The NIFTy library features three main classes: spaces that represent certain grids, fields that are defined on spaces, and operators that apply to fields. In the following, we will introduce the concept of these classes and comment on further NIFTy features such as operator probing.
3.1. Spaces
The space class is an abstract class from which all other specific space subclasses are derived. Each subclass represents a grid type and replaces some of the inherited methods with its own methods that are unique to the respective grid. This framework ensures an abstract handling of spaces independent of the underlying geometrical grid and the grid’s resolution.
An instance of a space subclass represents a geometrical space approximated by a specific grid in the computer environment. Therefore, each subclass needs to capture all structural and dimensional specifics of the grid and all computationally relevant quantities such as the data type of associated field values. These parameters are stored as properties of an instance of the class at its initialization, and they do not need to be accessed explicitly by the user thereafter. This prevents the writing of grid or resolution dependent code.
Spatial symmetries of a system can be exploited by corresponding coordinate transformations. Often, transformations from one basis to its harmonic counterpart can greatly reduce the computational complexity of algorithms. The harmonic basis is defined by the eigenbasis of the Laplace operator; e.g., for a flat position space it is the Fourier basis7. This conjugation of bases is implemented in NIFTy by distinguishing conjugate space classes, which can be obtained by the instance method get_codomain (and checked for by check_codomain). Moreover, transformations between conjugate spaces are performed automatically if required.
Thus far, NIFTy has six classes that are derived from the abstract space class. These subclasses are described here, and an overview can be found in Table 1.
-
The point_space class merely embodies a geometricallyunstructured list of points. This simplest possible kind of grid hasonly one parameter, the total number of points. This space isthought to be used as a default data space and neither has aconjugate space nor matches any continuum limit.
-
The rg_space class comprises all regular Euclidean grids of arbitrary dimension and periodic boundary conditions. Such a grid is described by the number of grid points per dimension, the edge lengths of one n-dimensional pixel and a few flags specifying the origin of ordinates, internal symmetry, and basis type; i.e., whether the grid represents a position or Fourier basis. The conjugate space of a rg_space is another rg_space that is obtained by a fast Fourier transformation of the position basis yielding a Fourier basis or vice versa by an inverse fast Fourier transformation.
-
The spherical harmonics basis is represented by the lm_space class which is defined by the maximum of the angular and azimuthal quantum numbers, ℓ and m, where mmax ≤ ℓmax and equality is the default. It serves as the harmonic basis for the instance of both the gl_space and the hp_space class.
-
The gl_space class describes a Gauss-Legendre grid on an
 sphere, where the pixels are centered at the roots of Gauss-Legendre polynomials. A
grid representation is defined by the number of latitudinal and longitudinal bins,
nlat and nlon.
sphere, where the pixels are centered at the roots of Gauss-Legendre polynomials. A
grid representation is defined by the number of latitudinal and longitudinal bins,
nlat and nlon. -
The hierarchical equal area isolatitude pixelization of an
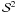 sphere (abbreviated as HEALPix8) is
represented by the hp_space class. The grid is characterized by twelve basis pixels
and the nside parameter that specifies how often each of
them is quartered.
sphere (abbreviated as HEALPix8) is
represented by the hp_space class. The grid is characterized by twelve basis pixels
and the nside parameter that specifies how often each of
them is quartered. -
The nested_space class is designed to comprise all possible product spaces constructed out of those described above. Therefore, it is defined by an ordered list of space instances that are meant to be multiplied by an outer product. Conjugation of this space is conducted separately for each subspace. For example, a 2D regular grid can be cast to a nesting of two 1D regular grids that would then allow for separate Fourier transformations along one of the two axes.
3.2. Fields
The second fundamental NIFTy class is the field class whose purpose is to represent discretized fields. Each field instance has not only a property referencing an array of field values, but also domain and target properties. The domain needs to be stated during initialization to clarify in which space the field is defined. Optionally, one can specify a target space as codomain for transformations; by default the conjugate space of the domain is used as the target space.
In this way, a field is not only implemented as a simple array, but as a class instance carrying an array of values and information about the geometry of its domain. Calling field methods then invokes the appropriate methods of the respective space without any additional input from the user. For example, the scalar product, computed by field.dot, applies the correct weighting with volume factors as addressed in Sect. 2.2 and performs basis transformations if the two fields to be scalar-multiplied are defined on different but conjugate domains9. The same is true for all other methods applicable to fields; see Table 2 for a selection of those instance methods.
Furthermore, NIFTy overloads standard operations for fields in order to support a transparent implementation of algorithms. Thus, it is possible to combine field instances by +, −, ∗, /,... and to apply trigonometric, exponential, and logarithmic functions componentwise to fields in their current domain.
3.3. Operators
Overview of derivatives of the NIFTy operator class.
Up to this point, we abstracted fields and their domains leaving us with a toolkit capable of performing normalizations, field-field operations, and harmonic transformations. Now, we introduce the generic operator class from which other, concrete operators can be derived.
In order to have a blueprint for operators capable of handling fields, any application of operators is split into a general and a concrete part. The general part comprises the correct involvement of normalizations and transformations, necessary for any operator type, while the concrete part is unique for each operator subclass. In analogy to the field class, any operator instance has a set of properties that specify its domain and target as well as some additional flags.
For example, the application of an operator A to a field s is coded as A(s), or equivalently A.times(s). The instance method times then invokes _briefing, _multiply and _debriefing consecutively. The briefing and debriefing are generic methods in which in- and output are checked; e.g., the input field might be transformed automatically during the briefing to match the operators domain. The _multiply method, being the concrete part, is the only contribution coded by the user. This can be done both explicitly by multiplication with a complete matrix or implicitly by a computer routine.
There are a number of basic operators that often appear in inference algorithms and are therefore preimplemented in NIFTy. An overview of preimplemented derivatives of the operator class can be found in Table 3.
3.4. Operator probing
While properties of a linear operator, such as its diagonal, are directely accessible in case of an explicitly given matrix, there is no direct approach for implicitly stated operators. Even a brute force approach to calculate the diagonal elements one by one may be prohibited in such cases by the high dimensionality of the problem.
That is why the NIFTy library features a generic probing class. The basic idea
of probing (Hutchinson 1989) is to approximate
properties of implicit operators that are only accessible at a high computational expense
by using sample averages. Individual samples are generated by a random process constructed
to project the quantity of interest. For example, an approximation of the trace or
diagonal of a linear operator A (neglecting the
discretization subtleties) can be obtained by ![\begin{eqnarray} & & \mathrm{tr}[\bb{A}] \approx \left< \bb{\xi}^{\dagger} \bb{A} \bb{\xi} \right>_{\{\bb{\xi}\}} = \sum_{pq} A_{pq} \left< \xi_p \xi_q \right>_{\{\bb{\xi}\}} \rightarrow \sum_{p} A_{pp} , \\ \label{eq:diag} && \Big( \mathrm{diag}[\bb{A}] \Big)_p \approx \left( \left< \bb{\xi} \ast \bb{A} \bb{\xi} \right>_{\{\bb{\xi}\}} \right)_p = \sum_q A_{pq} \left< \xi_p \xi_q \right>_{\{\bb{\xi}\}} \rightarrow A_{pp} , \end{eqnarray}](/articles/aa/full_html/2013/06/aa21236-13/aa21236-13-eq59.png) where
⟨ · ⟩ { ξ } is the sample average of a
sample of random fields ξ with the property
where
⟨ · ⟩ { ξ } is the sample average of a
sample of random fields ξ with the property
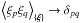 for
| { ξ }|→ ∞ and ∗ denotes componentwise
multiplication, cf. (Selig et al. 2012, and
references therein). One of many possible choices for the random values of
ξ are equally probable values of ± 1 as originally
suggested by Hutchinson (1989). Since the residual
error of the approximation decreases with the number of used samples, one obtains the
exact result in the limit of infinitely many samples. In practice, however, one has to
find a tradeoff between acceptable numerical accuracy and affordable computational cost.
for
| { ξ }|→ ∞ and ∗ denotes componentwise
multiplication, cf. (Selig et al. 2012, and
references therein). One of many possible choices for the random values of
ξ are equally probable values of ± 1 as originally
suggested by Hutchinson (1989). Since the residual
error of the approximation decreases with the number of used samples, one obtains the
exact result in the limit of infinitely many samples. In practice, however, one has to
find a tradeoff between acceptable numerical accuracy and affordable computational cost.
The NIFTy probing class allows for the implementation of arbitrary probing schemes. Because each sample can be computed independently, all probing operations take advantage of parallel processing for reasons of efficiency, by default. There are two derivatives of the probing class implemented in NIFTy, the trace_probing and diagonal_probing subclasses, which enable the probing of traces and diagonals of operators, respectively.
An extension to improve the probing of continuous operators by exploiting their internal correlation structure as suggested in the work by Selig et al. (2012) is planned for a future version of NIFTy.
3.5. Parallelization
The parallelization of computational tasks is supported. NIFTy itself uses a shared memory parallelization provided by the Python standard library multiprocessing10 for probing. If parallelization within NIFTy is not desired or needed, it can be turned off by the global setting flag about.multiprocessing.
Nested parallelization is not supported by Python; i.e., the user has to decide between the useage of parallel processing either within NIFTy or within dependent libraries such as HEALPix.
4. Demonstration
 |
Fig. 1 Illustration of the Wiener filter code example showing (left to
right) a Gaussian random signal a), d), g), the data including noise
(b,e,h), and the reconstructed map (c,f,i). The additive Gaussian white noise has a
variance |
An established and widely used inference algorithm is the Wiener filter (Wiener 1949) whose implementation in NIFTy shall serve as a demonstration example.
The underlying inference problem is the reconstruction of a signal,
s, from a data set, d, that
is the outcome of a measurement process (2),
where the signal response, Rs,
is linear in the signal and the noise, n, is additive. The
statistical properties of signal and noise are both assumed to be Gaussian,
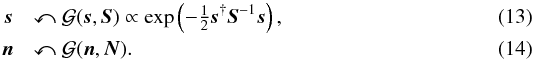 Here,
the signal and noise covariances, S and
N, are known a priori. The a posteriori solution for this
inference problem can be found in the expectation value for the signal
m = ⟨s⟩(s|d)
weighted by the posterior
P(s|d) .
This map can be calculated with the Wiener filter equation,
Here,
the signal and noise covariances, S and
N, are known a priori. The a posteriori solution for this
inference problem can be found in the expectation value for the signal
m = ⟨s⟩(s|d)
weighted by the posterior
P(s|d) .
This map can be calculated with the Wiener filter equation, 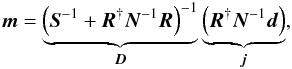 (15)which
is linear in the data. In the IFT framework, this scenario corresponds to a free theory as
discussed in the work by Enßlin et al. (2009), where a
derivation of Eq. (15)can be found. In
analogy to quantum field theory, the posterior covariance, D,
is referred to as the information propagator and the data dependent term,
j, as the information source.
(15)which
is linear in the data. In the IFT framework, this scenario corresponds to a free theory as
discussed in the work by Enßlin et al. (2009), where a
derivation of Eq. (15)can be found. In
analogy to quantum field theory, the posterior covariance, D,
is referred to as the information propagator and the data dependent term,
j, as the information source.
 |
Fig. 2 Illustration of the performance of the Wiener filter code given in Appendix C showing computation time against the size of the data set (ranging from 512 to 256 × 256 × 256 data points) for different signal spaces (see legend). The markers show the average runtime of multiple runs, and the error bars indicate their variation. (Related markers are solely connected to guide the eye.) |
The NIFTy based implementation is given in App. C, where a unit response and noise covariance are used11. This implementation is not only easily readable, but it also solves for m regardless of the chosen signal space; i.e., regardless of the underlying grid and its resolution. The functionality of the code for different signal spaces is illustrated in Fig. 1. The performance of this implementation is exemplified in Fig. 2 for different signal spaces and sizes of data sets. A qualitative power law behavior is apparent, but the quantitative performance depends strongly on the used machine.
The confidence in the quality of the reconstruction can be expressed in terms of a
1σ-confidence interval that is related to the diagonal of
D as follows,
![\begin{eqnarray} \sigma^{(\bb{m})} = \sqrt{\mathrm{diag}[\bb{D}]} . \end{eqnarray}](/articles/aa/full_html/2013/06/aa21236-13/aa21236-13-eq84.png) (16)The
operator D defined in Eq. (15)may involve inversions in different bases and thus is accessible
explicitly only with major computational effort. However, its diagonal can be approximated
efficiently by applying operator probing (12). Figure 3 illustrates the 1D reconstruction
results in order to visualize the estimates obtained with probing and to emphasize the
importance of a posteriori uncertainties.
(16)The
operator D defined in Eq. (15)may involve inversions in different bases and thus is accessible
explicitly only with major computational effort. However, its diagonal can be approximated
efficiently by applying operator probing (12). Figure 3 illustrates the 1D reconstruction
results in order to visualize the estimates obtained with probing and to emphasize the
importance of a posteriori uncertainties.
 |
Fig. 3 Illustration of the 1D reconstruction results. Panel a) summarizes the results from Fig. 1 by showing the original signal (red dashed line), the reconstructed map (green solid line), and the 1σ-confidence interval (gray contour) obtained from the square root of the diagonal of the posterior covariance D that has been computed using probing; cf. Eq. (12). Panel b) shows the 1D data set from Fig. 1 with a blinded region in the interval [0.5,0.7] . Panel c) shows again the original signal (red, dashed line), the map reconstructed from the partially blinded data (green solid line), and the corresponding 1σ-interval (gray contour) which is significantly enlarged in the blinded region indicating the uncertainty of the interpolation therein. |
 |
Fig. 4 Application of a Wiener filter to the classic “Moon Surface” image on a 2D regular grid with 256 × 256 pixels showing (top, left to right) the original “Moon Surface” signal a), the data including noise b), and the reconstructed map c). The response operator involves a convolution with a Gaussian kernel d) and a masking e). The additive noise is Gaussian white noise with an inhomogeneous standard deviation f) that approximates an overall signal-to-noise ratio ⟨σs⟩Ω/⟨σn⟩Ω of roughly 1. (All figures have been created by NIFTy using the field.plot method.) |
The Wiener filter code example given in Appendix C can easily be modified to handle more complex inference problems. In Fig. 4, this is demonstrated for the image reconstruction problem of the classic “Moon Surface” image12. During the data generation (2), the signal is convolved with a Gaussian kernel, multiplied with some structured mask, and finally, contaminated by inhomogeneous Gaussian noise. Despite these complications, the Wiener filter is able to recover most of the original signal field.
NIFTy can also be applied to non-linear inference problems, as has been demonstrated in the reconstruction of log-normal fields with a priori unknown covariance and spectral smoothness (Oppermann et al. 2013). Further applications reconstructing three-dimensional maps from column densities (Greiner et al., in prep.) and non-Gaussianity parameters from the cosmic microwave background (Dorn et al., in prep.) are currently in preparation.
5. Conclusions and summary
The NIFTy library enables the programming of grid and resolution independent algorithms. In particular for signal inference algorithms, where a continuous signal field is to be recovered, this freedom is desirable. This is achieved with an object-oriented infrastructure that comprises, among others, abstract classes for spaces, fields, and operators. NIFTy supports a consistent discretization scheme that preserves the continuum limit. Proper normalizations are applied automatically, which makes considerations by the user concerning this matter (almost) superfluous. NIFTy offers a straightforward transition from formulas to implemented algorithms thereby speeding up the development cycle. Inference algorithms that have been coded using NIFTy are reusable for similar inference problems even though the underlying geometrical space may differ.
The application areas of NIFTy are widespread and include inference algorithms derived within both information field theory and other frameworks. The successful application of a Wiener filter to non-trivial inference problems illustrates the flexibility of NIFTy. The very same code runs successfully whether the signal domain is an n-dimensional regular or a spherical grid. Moreover, NIFTy has already been applied to the reconstruction of Gaussian and log-normal fields (Oppermann et al. 2013).
The NIFTy source code and online documentation is publicly available on the project homepage13.
Python homepage http://www.python.org/
Cython homepage http://cython.org/
IFT homepage http://www.mpa-garching.mpg.de/ift/
HEALPix homepage http://sourceforge.net/projects/healpix/
Python documentation http://docs.python.org/2/library/multiprocessing.html
The Wiener filter demonstration is also part of the NIFTy package; see nifty/demos/demo_excaliwir.py for an extended version.
Source taken from the USC-SIPI image database at http://sipi.usc.edu/database/
NIFTy homepage http://www.mpa-garching.mpg.de/ift/nifty/
NumPy and SciPy homepage http://numpy.scipy.org/
GFFT homepage https://github.com/mrbell/gfft
HEALPy homepage https://github.com/healpy/healpy
LibSHARP homepage http://sourceforge.net/projects/libsharp/
libsharp-wrapper homepage https://github.com/mselig/libsharp-wrapper
Acknowledgments
We thank Philipp Wullstein, the NIFTy alpha tester Sebastian Dorn, and an anonymous referee for the insightful discussions and productive comments. Michael Bell is supported by the DFG Forschergruppe 1254 Magnetisation of Interstellar and Intergalactic Media: The Prospects of Low-Frequency Radio Observations. Martin Reinecke is supported by the German Aeronautics Center and Space Agency (DLR), under program 50-OP-0901, funded by the Federal Ministry of Economics and Technology. Some of the results in this paper have been derived using the HEALPix package (Górski et al. 2005). This research has made use of NASA’s Astrophysics Data System.
References
- Bayes, T. 1763, Phil. Trans. Roy. Soc., 35, 370 [Google Scholar]
- Behnel, S., Bradshaw, R. W., & Seljebotn, D. S. 2009, in Proc. 8th Python in Science Conference, Pasadena, CA USA, 4 [Google Scholar]
- Cox, R. T. 1946, Am. J. Phys., 14, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Enßlin, T. A., & Frommert, M. 2011, Phys. Rev. D, 83, 105014 [NASA ADS] [CrossRef] [Google Scholar]
- Enßlin, T. A., & Weig, C. 2010, Phys. Rev. E, 82, 051112 [NASA ADS] [CrossRef] [Google Scholar]
- Enßlin, T. A., Frommert, M., & Kitaura, F. S. 2009, Phys. Rev. D, 80, 105005 [NASA ADS] [CrossRef] [Google Scholar]
- Górski, K. M., Hivon, E., Banday, A. J., et al. 2005, ApJ, 622, 759 [NASA ADS] [CrossRef] [Google Scholar]
- Hutchinson, M. F. 1989, Commun. Stat. − Simul. Comput., 18, 1059 [Google Scholar]
- Jasche, J., & Kitaura, F. S. 2010, MNRAS, 407, 29 [NASA ADS] [CrossRef] [Google Scholar]
- Jasche, J., Kitaura, F. S., Li, C., & Enßlin, T. A. 2010a, MNRAS, 409, 355 [NASA ADS] [CrossRef] [Google Scholar]
- Jasche, J., Kitaura, F. S., Wandelt, B. D., & Enßlin, T. A. 2010b, MNRAS, 406, 60 [NASA ADS] [CrossRef] [Google Scholar]
- Jaynes, E. T. 1957, Phys. Rev., 106, 620 [Google Scholar]
- Jaynes, E. T. 1989, in Maximum Entropy and Bayesian Methods, ed. J. Skilling (Dordrecht: Kluwer) [Google Scholar]
- Kitaura, F. S., Jasche, J., Li, C., et al. 2009, MNRAS, 400, 183 [NASA ADS] [CrossRef] [Google Scholar]
- Laplace, P. S. 1795/1951, A philosophical essay on probabilities (New York: Dover) [Google Scholar]
- Metropolis, N., & Ulam, S. 1949, J. Am. Stat. Assoc., 44, 335 [Google Scholar]
- Metropolis, N., Rosenbluth, A. W., Rosenbluth, M. N., Teller, A. H., & Teller, E. 1953, J. Chem. Phys., 21, 1087 [NASA ADS] [CrossRef] [Google Scholar]
- Oliphant, T. 2006, A Guide to NumPy (Trelgol Publishing) [Google Scholar]
- Oppermann, N., Robbers, G., & Enßlin, T. A. 2011, Phys. Rev. E, 84, 041118 [NASA ADS] [CrossRef] [Google Scholar]
- Oppermann, N., Junklewitz, H., Robbers, G., et al. 2012, A&A, 542, A93 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Oppermann, N., Selig, M., Bell, M. R., & Enßlin, T. A. 2013, Phys. Rev. E, 87, 032136 [NASA ADS] [CrossRef] [Google Scholar]
- Reinecke, M. 2011, A&A, 526, A108 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Reinecke, M., & Seljebotn, D. S. 2013 [arXiv:1303.4945] [Google Scholar]
- Selig, M., Oppermann, N., & Enßlin, T. A. 2012, Phys. Rev. E, 85, 021134 [NASA ADS] [CrossRef] [Google Scholar]
- Seljebotn, D. S. 2009, in Proc. 8th Python in Science Conference, Pasadena, CA USA, 15 [Google Scholar]
- Shannon, C. E. 1948, Bell Syst. Tech. J., 27, 379 [Google Scholar]
- Weig, C., & Enßlin, T. A. 2010, MNRAS, 409, 1393 [NASA ADS] [CrossRef] [Google Scholar]
- Wiener, N. 1949, Extrapolation, Interpolation and Smoothing of Stationary Time Series, with Engineering Applications (New York: Technology Press and Wiley), note: Originally issued in Feb. 1942 as a classified Nat. Defense Res. Council Rep. [Google Scholar]
Appendix A: Remark on matrices
The discretization of an operator that is defined on a continuum is a necessity for its
computational implementation and is analogous to the discretization of fields; cf.
Sect. 2.2. However, the involvement of volume
weights can cause some confusion concerning the interpretation of the corresponding matrix
elements. For example, the discretization of the continuous identity operator, which
equals a δ-distribution
δ(x − y), yields a weighted
Kronecker-Delta δpq,
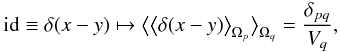 (A.1)where
x ∈ Ωp and
y ∈ Ωq. Say a field
ξ is drawn from a zero-mean Gaussian with a covariance
that equals the identity,
(A.1)where
x ∈ Ωp and
y ∈ Ωq. Say a field
ξ is drawn from a zero-mean Gaussian with a covariance
that equals the identity, 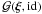 .
The intuitive assumption that the field values of ξ have a
variance of 1 is not true. The variance is given by
.
The intuitive assumption that the field values of ξ have a
variance of 1 is not true. The variance is given by
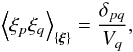 (A.2)and
scales with the inverse of the volume Vq.
Moreover, the identity operator is the result of the multiplication of any operator with
its inverse,
id = A-1A. It is
trivial to show that, if
A(x,y) → Apq
and
(A.2)and
scales with the inverse of the volume Vq.
Moreover, the identity operator is the result of the multiplication of any operator with
its inverse,
id = A-1A. It is
trivial to show that, if
A(x,y) → Apq
and 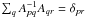 , the inverse of
A maps as follows,
, the inverse of
A maps as follows,
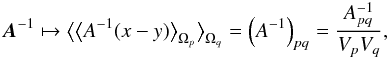 (A.3)where
(A.3)where
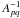 in comparison to (A-1)pq is
inversely weighted with the volumes Vp and
Vq.
in comparison to (A-1)pq is
inversely weighted with the volumes Vp and
Vq.
Since all those weightings are implemented in NIFTy, users need to concern themself with these subtleties only if they intend to extend the functionality of NIFTy.
Appendix B: Libraries
NIFTy depends on a number of other libraries which are listed here for completeness and in order to give credit to the authors.
-
NumPy, SciPy14 (Oliphant 2006), andseveral other Python standard libraries.
-
GFFT15 for generalized fast Fourier transformations on regular and irregular grids; of which the latter are currently considered for implementation in a future version of NIFTy.
-
HEALPy16 and HEALPix (Górski et al. 2005) for spherical harmonic transformations on the HEALPix grid which are based on the LibPSHT (Reinecke 2011) library or its recent successor LibSHARP17 (Reinecke & Seljebotn 2013), respectively.
-
Another Python wrapper18 for the performant LibSHARP library supporting further spherical pixelizations and the corresponding transformations.
These libraries have been selected because they have either been established as standards or they are performant and fairly general.
The addition of alternative numerical libraries is most easily done by the indroduction of new derivatives of the space class. Replacements of libraries that are already used in NIFTy are possible, but require detailed code knowledge.
Appendix C: Wiener filter code example
from nifty import * # version 0.3.0
from scipy.sparse.linalg import LinearOperator as lo
from scipy.sparse.linalg import cg
class propagator(operator): # define propagator class
_matvec = (lambda self, x: self.inverse_times(x).val.flatten())
def _multiply(self, x):
# some numerical invertion technique; here, conjugate gradient
A = lo(shape=tuple(self.dim()), matvec=self._matvec, dtype=self.domain.datatype)
b = x.val.flatten()
x_, info = cg(A, b, M=None)
return x_
def _inverse_multiply(self, x):
S, N, R = self.para
return S.inverse_times(x) + R.adjoint_times(N.inverse_times(R.times(x)))
# some signal space; e.g., a one-dimensional regular grid
s_space = rg_space(512, zerocenter=False, dist=0.002) # define signal space
# or rg_space([256, 256])
# or hp_space(128)
k_space = s_space.get_codomain() # get conjugate space
kindex, rho = k_space.get_power_index(irreducible=True)
# some power spectrum
power = [42 / (kk + 1) ** 3 for kk in kindex]
S = power_operator(k_space, spec=power) # define signal covariance
s = S.get_random_field(domain=s_space) # generate signal
R = response_operator(s_space, sigma=0.0, mask=1.0, assign=None) # define response
d_space = R.target # get data space
# some noise variance; e.g., 1
N = diagonal_operator(d_space, diag=1, bare=True) # define noise covariance
n = N.get_random_field(domain=d_space) # generate noise
d = R(s) + n # compute data
j = R.adjoint_times(N.inverse_times(d)) # define source
D = propagator(s_space, sym=True, imp=True, para=[S, N, R]) # define propagator
m = D(j) # reconstruct map
s.plot(title="signal") # plot signal
d.cast_domain(s_space)
d.plot(title="data", vmin=s.val.min(), vmax=s.val.max()) # plot data
m.plot(title="reconstructed map", vmin=s.val.min(), vmax=s.val.max()) # plot map
All Tables
Overview of derivatives of the NIFTy space class, the corresponding grids, and conjugate space classes.
All Figures
 |
Fig. 1 Illustration of the Wiener filter code example showing (left to
right) a Gaussian random signal a), d), g), the data including noise
(b,e,h), and the reconstructed map (c,f,i). The additive Gaussian white noise has a
variance |
| In the text | |
 |
Fig. 2 Illustration of the performance of the Wiener filter code given in Appendix C showing computation time against the size of the data set (ranging from 512 to 256 × 256 × 256 data points) for different signal spaces (see legend). The markers show the average runtime of multiple runs, and the error bars indicate their variation. (Related markers are solely connected to guide the eye.) |
| In the text | |
 |
Fig. 3 Illustration of the 1D reconstruction results. Panel a) summarizes the results from Fig. 1 by showing the original signal (red dashed line), the reconstructed map (green solid line), and the 1σ-confidence interval (gray contour) obtained from the square root of the diagonal of the posterior covariance D that has been computed using probing; cf. Eq. (12). Panel b) shows the 1D data set from Fig. 1 with a blinded region in the interval [0.5,0.7] . Panel c) shows again the original signal (red, dashed line), the map reconstructed from the partially blinded data (green solid line), and the corresponding 1σ-interval (gray contour) which is significantly enlarged in the blinded region indicating the uncertainty of the interpolation therein. |
| In the text | |
 |
Fig. 4 Application of a Wiener filter to the classic “Moon Surface” image on a 2D regular grid with 256 × 256 pixels showing (top, left to right) the original “Moon Surface” signal a), the data including noise b), and the reconstructed map c). The response operator involves a convolution with a Gaussian kernel d) and a masking e). The additive noise is Gaussian white noise with an inhomogeneous standard deviation f) that approximates an overall signal-to-noise ratio ⟨σs⟩Ω/⟨σn⟩Ω of roughly 1. (All figures have been created by NIFTy using the field.plot method.) |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.