| Issue |
A&A
Volume 554, June 2013
|
|
|---|---|---|
| Article Number | A62 | |
| Number of page(s) | 12 | |
| Section | Galactic structure, stellar clusters and populations | |
| DOI | https://doi.org/10.1051/0004-6361/201219676 | |
| Published online | 04 June 2013 | |
Constraining the Galactic millisecond pulsar population using Fermi Large Area Telescope
Institut de Recherche en Astrophysique et Planétologie, UPS/CNRS, 31028 Toulouse Cedex 4, France
e-mail: tristan.gregoire@irap.omp.eu
Received: 24 May 2012
Accepted: 11 March 2013
Context. The Fermi Large Area Telescope (Fermi-LAT) has recently revealed a large population of gamma-ray emitting millisecond pulsars (MSPs) in our Galaxy.
Aims. We aim to infer the properties of the Galactic population of gamma-ray emitting MSPs from the samples detected by the Fermi-LAT.
Methods. We developed a Monte Carlo model to predict the spatial and gamma-ray luminosity distribution of the Galactic MSP population. Based on the estimated detection sensitivity of Fermi-LAT, we split the model population into detectable and undetectable samples of MSPs. Using a maximum likelihood method, we compared the detectable sample to a set of 36 MSPs detected by Fermi-LAT, and we derived the parameters of the spatial distribution and the total number of gamma-ray emitting MSPs in the Galaxy. The corresponding undetectable sample provided us with an estimate for the expected diffuse emission from unresolved MSPs in the Milky Way. We also applied our method to an extended sample of 66 MSPs that combines firmly detected MSPs and γ-ray sources that show characteristics reminiscent of MSPs.
Results. Using the sample of 36 MSPs detected by Fermi-LAT, our analysis suggests the existence of 9000−11 000 γ-ray emitting MSPs in the Galaxy. The maximum likelihood analysis suggests an exponential radial scale length of ~4 kpc and an exponential vertical scale height of ~1 kpc for the underlying MSP population. The unresolved population of Galactic γ-ray emitting MSPs is predicted to contribute a flux of ~2 × 10-6 ph cm-2 s-1 sr-1 to the Galactic diffuse emission observed from the central radian above 100 MeV. This value corresponds to ~1% of the total observed γ-ray flux from that region. For latitudes |b| ≥ 40° the expected average intensity amounts to ~2 × 10-8 ph cm-2 s-1 sr-1 above 100 MeV, which corresponds to 0.2% of the high-latitude background intensity. Using the extended sample increases the estimated number of γ-ray emitting MSPs in the Galaxy to ~22 000 and slightly reduces the scale parameters of the spatial distribution. The results are robust with respect to systematic uncertainties in the estimated Fermi-LAT detection sensitivity.
Conclusions. For the first time our analysis provides γ-ray based constraints on the Galactic population of MSPs. The radial scale length and vertical scale height of the population is consistent with estimates based on radio data. Our analysis suggests that MSPs do not provide any significant contribution to the isotropic diffuse γ-ray background emission.
Key words: pulsars: general / gamma rays: diffuse background
© ESO, 2013
1. Introduction
Pulsars are highly magnetized and rapidly spinning neutron stars, obeying a beam of radiation that periodically intersects the Earth. Pulsars were first discovered in the radio band by Hewish et al. (1968), but they are observed today throughout the electromagnetic spectrum, which covers visible light, radio waves, X-rays and gamma-rays. Several classes of pulsars are distinguishable, characterized by their spin period and period derivative. The period derivative relates to the spin down power, characteristic pulsar age, and surface magnetic field. Ironically, the most rapidly spinning pulsars that reach spin periods of less than a few tens of milliseconds are also the oldest pulsars. These so-called millisecond pulsars (MSPs) are commonly interpreted as the result of a mass-transfer period in a close binary system, where the spin of an old neutron star has been drastically increased by the transfer of angular momentum (Alpar et al. 1982).
Radio observations have so far unveiled a population of 137 Galactic field MSPs, while the Galactic population of MSPs has been estimated to ~30 000 (Cordes & Chernoff 1997; Lyne et al. 1998; Lorimer 2005). Improving our knowledge of the Galactic MSP population provides important clues to understanding the MSP progenity. In this work, we try to constrain the Galactic MSP population using γ-ray observations of MSPs. Before the launch of the Fermi satellite, only circumstantial evidence of pulsed γ-rays from one MSP had been found (Kuiper et al. 2000). Now, the Large Area Telescope (LAT) aboard Fermi has been established them as a new and important population of Galactic γ-ray sources (Abdo et al. 2009a). So far, more than 40 MSPs have been detected by Fermi-LAT, which corresponds to ~30% of the Galactic field MSP population. Moreover, the search for radio pulsations towards the direction of still unidentified γ-ray sources that obey spectral characteristics of typical γ-ray pulsars has turned out to be extremely efficient to unveil yet unknown MSPs (e.g. Cognard et al. 2011; Ransom et al. 2011; Kerr et al. 2012).
We make use of this new sample of Galactic field γ-ray MSPs to constrain the total number and spatial distribution of γ-ray emitting MSPs within our Galaxy. In Sect. 2, we describe the sample of γ-ray emitting MSPs used in this study. In Sect. 3, we introduce a population model of Galactic MSPs that we use to constrain the population parameters in Sect. 4. The results are discussed in Sect. 5, and we conclude in Sect. 6.
List of 36 MSPs seen by the Fermi-LAT and used in this study.
2. MSP sample used in this study
The sample of γ-ray MSPs used in this work is based on the first catalogue of Fermi-LAT sources (1FGL; Abdo et al. 2010c). Among the 1451 sources found in the 1FGL catalogue, 821 had been associated to known sources at other wavelengths, while 630 sources remained unassociated. By the time the 1FGL catalogue was published, 9 sources in the catalogue were identified as MSPs through their observed γ-ray pulsations. All γ-ray MSPs detected in 1FGL show similar spectral shapes, exhibiting hard power laws with exponential cut-offs near a few GeV. A non-negligible fraction of the unassociated sources exhibited similar spectral features, and dedicated searches for pulsations using radio searches of the corresponding 1FGL error boxes have led to the discovery of 27 still unknown Galactic field MSPs.
This result established a new strategy of discovering Galactic MSPs: the Fermi-LAT telescope indicates potential locations of Galactic MSPs that are then investigated using radio observations to reveal the pulsar’s pulsations. Although these studies are still limited by the sensitivity of the radio telescopes to unveil the radio pulsations, they are probably less biased than the pure radio surveys, because Fermi-LAT scans the entire sky rather homogeneously. It can thus be expected that the Fermi-LAT sample of Galactic MSPs is mainly limited by the actual sensitivity of the γ-ray observations. In total, 36 γ-ray MSPs have been firmly identified in the 1FGL catalogue. We use this sample in this paper and summarize their 1FGL names, together with the source positions and relevant references in Table 1.
Nevertheless, we also recognize the possibility that this sample is not totally free of any radio bias, as the identification of the MSPs still relies on the detection of the pulsar at radio frequencies. We thus also consider an extended sample of 66 objects in this work that is comprised of identified γ-ray MSPs and unassociated 1FGL sources, which are located outside the Galactic plane with spectral and temporal characteristics reminiscent of Galactic MSPs. As probably not all sources in this sample are indeed MSPs, we may consider this sample as an upper limit to the true sample of Galactic γ-ray emitting MSPs detectable by Fermi-LAT during the first 11 months of observation that served as the basis for the 1FGL source catalogue.
3. MSP population model
3.1. General approach
With characteristic ages of the order of 109 yr, MSPs are members of the old stellar population, which can be described by a relatively smooth Galactic density distribution with a vertical scale height of several 100 pc (Robin et al. 2003). Dynamic modelling of the MSP evolution in the Galactic gravitational potential suggests radial and vertical scale heights of R0 ≈ 4.2 kpc and z0 ≈ 0.5 kpc, assuming exponential spatial distributions of the form 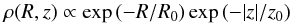 (1)where R is the distance from the Galactic centre and z is the vertical scale height measured from the Galactic plane (Story et al. 2007). Other authors model the radial distribution of MSPs using a Gaussian density profile
(1)where R is the distance from the Galactic centre and z is the vertical scale height measured from the Galactic plane (Story et al. 2007). Other authors model the radial distribution of MSPs using a Gaussian density profile 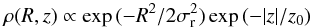 (2)with σr ≈ 5 kpc and z0 ≈ 1 kpc (Faucher-Giguère & Loeb 2010). We test both equations in the present work, but we already note in advance that our results are fairly insensitive to the selected radial law. We do not attempt to model a possible contribution from Galactic bulge MSPs, because Fermi-LAT observations currently probe only the nearby MSP population; thus, the bulge contribution essentially remains unconstrained.
(2)with σr ≈ 5 kpc and z0 ≈ 1 kpc (Faucher-Giguère & Loeb 2010). We test both equations in the present work, but we already note in advance that our results are fairly insensitive to the selected radial law. We do not attempt to model a possible contribution from Galactic bulge MSPs, because Fermi-LAT observations currently probe only the nearby MSP population; thus, the bulge contribution essentially remains unconstrained.
The first step in our MSP population modelling procedure is that we draw random locations of pulsars from the density laws Eqs. (1) or (2). By definition, the spatial distributions are axisymmetric with respect to the Galactic centre, and for randomly drawn pairs of R and z, we randomly assign an azimuth angle by drawing from a uniform distribution between 0 and 2π. We then transform these Galactocentric coordinates into Galactic longitude l, latitude b, and distance d from the Sun by assuming that the Sun is placed at 8.5 kpc from the Galactic centre and 20 pc above the Galactic plane (Reed 2006).
As a second step, we assign for each pulsar a period P and a period derivative Ṗ using either the approach proposed by Faucher-Giguère & Loeb (2010, hereafter FG), or the approach developed by Story et al. (2007, hereafter ST; see Sect. 3.2). We do not explicitly take orientation or light beam effects into account, but we assume that each MSP obeys a mean luminosity drawn from a luminosity distribution function that only depends on P and Ṗ (see Sect. 3.3).
Finally, we then determine the γ-ray flux Fγ on Earth from the assigned luminosity using 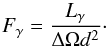 (3)where we take ΔΩ = 4π.
(3)where we take ΔΩ = 4π.
This procedure provides us with a list of positions and fluxes for a population of MSPs that is then used for further analysis (Sect. 4). We typically draw samples of NMC = 107 pulsars in the Galaxy to reduce the impact of statistical fluctuations on our final results. We then split the sample into two subsamples. The first subsample contains all pulsars for which Fγ > Fsensitivity, where Fsensitivity is the detection sensitivity of Fermi-LAT at the specific sky position of the pulsar. We call this subsample the detectable MSP population. The second subsample contains all pulsars with fluxes below the sensitivity limit, making up the subsample of undetectable MSPs.
We use the detectable MSP population as a reference for comparison to the observed γ-ray MSP population, to draw conclusions about the spatial parameters R0/σr and z0 and the total number NMSP of γ-ray emitting MSPs in our Galaxy (cf. Sect. 4). The subsample of undetectable MSPs is used to study the Galactic diffuse emission that will arise from the large population of pulsars falling below the detection threshold (cf. Sect. 5).
 |
Fig. 1 Simulated P − Ṗ distribution of the detectable sample (filled symbols) and an according undetectable sample (open symbols) using the approaches of Faucher-Giguère & Loeb (2010) (red squares) and of Story et al. (2007) (blue circles). We use [σr = 5, z0 = 1] kpc and [R0 = 4.2, z0 = 0.5] kpc respectively for Faucher-Giguère & Loeb and Story et al. approaches. For comparison we show the observed distribution of Fermi-LAT MSPs as green triangles. The P − Ṗ distribution of all pulsars from the ATNF catalogue (Manchester et al. 2005, http://www.atnf.csiro.au/research/pulsar/psrcat) is shown as black dots. We also show lines of constant spin-down power Ė (dashed), constant characteristic age (dashed-dotted), and constant magnetic field (dotted). The area excluded by the deathline implemented in Faucher-Giguère & Loeb’s model is indicated by the blue filled area. The inset presents a zoom into the MSP region of the P − Ṗ diagram. |
 |
Fig. 2 HEALPix maps (Nside = 64) for R0 = 4.2 kpc and σz = 500 pc using the Story et al. (2007) luminosity model. The panels show the entire simulated MSP population (top left), the undetectable (top right) and detectable (bottom left) samples, and the smoothed detectable sample (bottom right). |
3.2. MSP period and period derivative
3.2.1. Faucher-Giguère & Loeb (2010)
Our first method to assign P and Ṗ to individual pulsars has been inspired from the work of Faucher-Giguère & Loeb (2010). We randomly draw P from the empirically determined power law distribution N(P) ∝ P-1 (Cordes & Chernoff 1997) under the constraint P ≥ 1.5 ms. We also randomly draw a value for the magnetic field B from the distribution 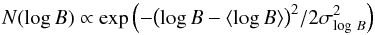 (4)with ⟨ log B ⟩ = 8 and σlog B = 0.3. Using both quantities, we then use the conventional formula for magnetic dipol braking, which is expressed as B = 3.2 × 1019(PṖ)1/2 G (Lyne 2000), to derive Ṗ for each pulsar. We then introduce a “deathline” defined by B/P2 = 0.17 × 1012 G s-2 and only retain pulsars that lie above this deathline in the P − Ṗ diagram. We note that the exponent of N(P) and the spread of the magnetic field σlog B that we have chosen differ slightly from the values adopted by Faucher-Giguère & Loeb (2010; they use N(P) ∝ P-2 and σlog B = 0.2), because we found that our values produce a slightly better match to the observed P − Ṗ distribution.
(4)with ⟨ log B ⟩ = 8 and σlog B = 0.3. Using both quantities, we then use the conventional formula for magnetic dipol braking, which is expressed as B = 3.2 × 1019(PṖ)1/2 G (Lyne 2000), to derive Ṗ for each pulsar. We then introduce a “deathline” defined by B/P2 = 0.17 × 1012 G s-2 and only retain pulsars that lie above this deathline in the P − Ṗ diagram. We note that the exponent of N(P) and the spread of the magnetic field σlog B that we have chosen differ slightly from the values adopted by Faucher-Giguère & Loeb (2010; they use N(P) ∝ P-2 and σlog B = 0.2), because we found that our values produce a slightly better match to the observed P − Ṗ distribution.
Figure 1 shows the simulated P − Ṗ distribution of a sample of detectable (red filled squares) and undetectable (red open squares) pulsars. For the shake of comparison to the observed sample of 36 MSPs, we limit here the total number of simulated pulsars to the first N pulsars that comprise 36 detectable MSPs. Apparently, the approach of Faucher-Giguère & Loeb (2010) produces a non-negligible population of undetectable MSPs with characteristics ages largely exceeding the age of the Universe. Although these pulsars are classified as undetectable by Fermi-LAT, they contribute to some extent to the diffuse γ-ray emission of the Galaxy, and they affect our estimate of the total number of γ-ray emitting MSPs that are present in the Milky Way.
3.2.2. Story et al. (2007)
Our second method to assign P and Ṗ to individual pulsars has been based on the work of Story et al. (2007). As a first step, we draw a random magnetic field from within the interval [Bmin,Bmax] = [0.1,10] × 108 G using the distribution 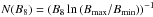 , where B8 is the magnetic field in units of 108 G. Story et al. (2007) use a larger range of [1,104] × 108 G in their simulations, but we found that setting the range to [0.1,10] × 108 G improves the match between the observed and predicted P − Ṗ distribution. The initial spin period of MSPs is then determined using
, where B8 is the magnetic field in units of 108 G. Story et al. (2007) use a larger range of [1,104] × 108 G in their simulations, but we found that setting the range to [0.1,10] × 108 G improves the match between the observed and predicted P − Ṗ distribution. The initial spin period of MSPs is then determined using 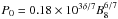 , where δ is a dithering parameter introduced to take variations in the accretion rate of the MSP progenitors into account. Similar to Story et al. (2007), we draw δ from a ramp distribution that increases by a factor of 4 between 0 and 2.8.
, where δ is a dithering parameter introduced to take variations in the accretion rate of the MSP progenitors into account. Similar to Story et al. (2007), we draw δ from a ramp distribution that increases by a factor of 4 between 0 and 2.8.
We then draw an age τ for each MSP using a uniform age distribution within [0,12] Gyr, and based on this age and assuming a constant dipole magnetic field, we spin-down the initial spin period to the current spin-period using 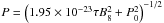 , We then estimate the derivative period, using
, We then estimate the derivative period, using 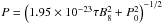 .
.
Finally, we force the initial period P0 to be greater than 1.3 ms and we take electron-positron pair production into account that occurs for strong fields and/or long spin periods (Alpar et al. 1982) by requiring B12P-2 ≥ 1, which is typical of a pair production model (no cut-off has been considered by Story et al. 2007).
The resulting P − Ṗ distribution is shown in Fig. 1, using filled blue circles for the detectable and open blue circles for the undetectable MSPs. Although the match is not perfect, the simulated distribution of detectable MSPs follows the observed distribution better than the distribution based on Faucher-Giguère & Loeb’s approach. In particular, the problem of generating MSPs with characteristic ages in excess of the age of the Universe is avoided by construction.
3.3. Luminosity function
We use the empirical law 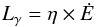 (5)to estimate the γ-ray luminosity from the spin-down luminosity Ė = 4π2IṖ/P3 of the MSPs, where I is the moment of inertia (assumed to be equal to 1045 g cm2), P the spin period, Ṗ the period derivative of the pulsar and η a proportionality factor. The use of Eq. (5) is motivated by the fact that the observed γ-ray luminosities for the Fermi-LAT MSPs follow a rough proportionality with Ė. This relation is illustrated in Fig. 3, which shows the γ-ray luminosity measured by Fermi-LAT for the 36 MSPs used in this work as a function of Ė. The luminosities Lγ have been derived from the γ-ray fluxes Fγ, which were observed by Fermi-LAT using Eq. (3) and were consistent with ΔΩ = 4π. For clarity, the displayed error bars reflect only the uncertainties in the estimation of the γ-ray flux and do not include uncertainties in pulsar distance. Uncertainties in distance are substantial and dominate the overall error budget, which may explain a significant fraction of the observed dispersion. Orientation effects for individual pulsars also play very likely an important role.
(5)to estimate the γ-ray luminosity from the spin-down luminosity Ė = 4π2IṖ/P3 of the MSPs, where I is the moment of inertia (assumed to be equal to 1045 g cm2), P the spin period, Ṗ the period derivative of the pulsar and η a proportionality factor. The use of Eq. (5) is motivated by the fact that the observed γ-ray luminosities for the Fermi-LAT MSPs follow a rough proportionality with Ė. This relation is illustrated in Fig. 3, which shows the γ-ray luminosity measured by Fermi-LAT for the 36 MSPs used in this work as a function of Ė. The luminosities Lγ have been derived from the γ-ray fluxes Fγ, which were observed by Fermi-LAT using Eq. (3) and were consistent with ΔΩ = 4π. For clarity, the displayed error bars reflect only the uncertainties in the estimation of the γ-ray flux and do not include uncertainties in pulsar distance. Uncertainties in distance are substantial and dominate the overall error budget, which may explain a significant fraction of the observed dispersion. Orientation effects for individual pulsars also play very likely an important role.
We show the luminosity laws (Eq. (5)) for η = 0.1,0.2,0.3, and 1.0 as dashed lines. We also show the relation 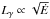 that has been advocated by some authors in the past (e.g. Faucher-Giguère & Loeb 2010). Notably, η = 0.2 presents a reasonable average value, and we adopt this value for our study. However, we explore the impact of this choice by varying η between 0.05 (which is the value used by Faucher-Giguère & Loeb 2010) and 0.3 (see Sect. 4.5.3).
that has been advocated by some authors in the past (e.g. Faucher-Giguère & Loeb 2010). Notably, η = 0.2 presents a reasonable average value, and we adopt this value for our study. However, we explore the impact of this choice by varying η between 0.05 (which is the value used by Faucher-Giguère & Loeb 2010) and 0.3 (see Sect. 4.5.3).
4. Constraining the Galactic MSP population
4.1. Maximum likelihood method
We now use our MSP population model to derive constraints on the Galactic population of γ-ray emitting MSPs. We use a maximum likelihood ratio method to compare the distribution of MSPs observed by Fermi-LAT to our model. For this purpose, we decompose the sky using a HEALPix1 pixelization with Nside = 64 (see Górski et al. 2005), and denote by ni the number of MSPs observed by the Fermi-LAT within a given pixel. The estimated number of detectable MSPs predicted by our model for each pixel is given by ei. The absolute numbers ei relate to the total number NMC of pulsars that have been simulated and need to be adjusted by a scaling factor α to match the data. The total number of γ-ray emitting MSPs in our Galaxy is then directly given by 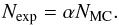 (6)
(6)
 |
Fig. 3 Observed γ-ray luminosity Lγ versus spin down power Ė for the 36 Fermi-LAT MSPs used in this study. The dashed lines indicate empirical laws used to predict the γ-ray luminosity of individual MSPs (see text). |
The adjustment of α is done by maximizing the log likelihood (Cash 1979) ![\begin{equation} \ln \, (\mathcal{L}) = \sum \limits_{{i=0}}^{N_{\rm pix}} \left[ n_i \ln \, (\alpha e_i) - \alpha e_i - \ln \, (n_i!) \right] . \label{eqn:lkhd} \end{equation}](/articles/aa/full_html/2013/06/aa19676-12/aa19676-12-eq95.png) (7)We also use Eq. (7) to determine the spatial parameters σr/R0 and z0 that best reproduce the distribution of MSPs observed by Fermi-LAT. For this purpose, we compute ln (ℒ) on a grid spanned by σr and z0 for the Gaussian density profile (Eq. (2)) or R0 and z0 for the exponential density profile (Eq. (1)). We then use Wilks theorem (Wilks 1938), which states that 2Δln (ℒ) follows a
(7)We also use Eq. (7) to determine the spatial parameters σr/R0 and z0 that best reproduce the distribution of MSPs observed by Fermi-LAT. For this purpose, we compute ln (ℒ) on a grid spanned by σr and z0 for the Gaussian density profile (Eq. (2)) or R0 and z0 for the exponential density profile (Eq. (1)). We then use Wilks theorem (Wilks 1938), which states that 2Δln (ℒ) follows a 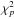 law with p degrees of freedom, to derive confidence contours in both parameters. For our case (p = 2), a value of 2Δln (ℒ) equal to 2.30, 6.16, and 11.83 corresponds to 1, 2, and 3σ confidence levels respectively.
law with p degrees of freedom, to derive confidence contours in both parameters. For our case (p = 2), a value of 2Δln (ℒ) equal to 2.30, 6.16, and 11.83 corresponds to 1, 2, and 3σ confidence levels respectively.
Instead of directly using the contours from the grid, we adjust ellipses to the 2Δln (ℒ) values as a function of radial and vertical scaling parameters by using a moment method (Teague 1980). This approach makes our results robust against statistical fluctuations that arise from the limited number of pulsars drawn in our population model. We then use these ellipses to derive statistical uncertainties in both scaling parameters.
Figure 2 shows HEALPix maps of a population of NMC = 107 MSPs. All pulsars (top left), the undetectable pulsars (top right), and the detectable pulsars (bottom left) are presented. The number of (detectable) MSPs becomes rather sparse with increasing Galactic latitude, and eventually, some of the pixels in the HEALPix map for the estimate (ei) may become zero, which makes Eq. (7) undefined. We thus applied a modest smoothing to our map of detectable MSPs using an adaptive Gaussian filter. For each pixel in our HEALPix map, we adjusted the smoothing kernel of the Gaussian, so that at least 50 MSPs are covered by the kernel. This drastically reduces the statistical noise in our HEALPix maps, and avoids any empty pixel in our analysis. The result of this smoothing operation in illustrated in the bottom right panel of Fig. 2.
4.2. Sensitivity map
An essential ingredient for the separation of the detectable from the undetectable population of Galactic MSPs is the sensitivity map of the Fermi-LAT shown in Fig. 4. This sensitivity map is an estimate of the minimum flux that a point source needs to pass to be detected by the telescope and to be integrated in the Fermi-LAT source catalogue. Our sample of MSPs used in this work were all detected during the first year of Fermi-LAT operations, and are all included in the 1FGL source catalogue (Abdo et al. 2010c). We thus use the corresponding sensitivity map that was published with the 1FGL catalogue. Instrument and pipeline responses are implicitly included in this estimation, and some assumptions about the spectral shape of the sources (power law with index 2.2), instrumental backgrounds, and astrophysical backgrounds have been made (see Appendix A of Abdo et al. 2010c). We discuss the dependency of our results on the sensitivity map in a dedicated Sect. 4.5.
 |
Fig. 4 Sensitivity map of the Fermi-LAT for detection of 1FGL point sources, which are given in Galactic coordinates and Aitoff projection (Abdo et al. 2010c). |
 |
Fig. 5 Log-likelihood as a function of radial scale length (R0 or σr) and vertical scale height (z0) for four MSP population models (see text). Contours show the 1, 2, and 3σ confidence ellipses that have been computed from the log-likelihood maps (colours). All maps show the same dynamic range in log-likelihood. |
4.3. Results
The results of the maximum likelihood analysis are illustrated in Fig. 5 and summarized in Table 2. For both P − Ṗ modelling approaches (designated by ST for Story et al. 2007; and FG for Faucher-Giguère & Loeb 2010), we explored the exponential density profile (Eq. (1); models ST1 and FG1) and the Gaussian density profile (Eq. (2); models ST2 and FG2). For all of those models, a value of NMC = 107 pulsars have been simulated.
Results of the maximum likelihood analysis.
Figure 5 shows the log-likelihood function ln (ℒ) as a function of the radial (R0 or σr) and vertical (z0) scale parameters for all models. All panels of the figure have been adjusted to the same dynamic range. Solid, dashed, and dotted ellipses show 1, 2, and 3σ confidence levels, respectively, and the colours depict the log-likelihood values. From the minimum and maximum values reached by the 2σ confidence ellipses and the centroid, mean values and statistical uncertainties are derived for the scale parameters and are summarized in Table 2. From the value of the scaling factor α at the ellipse centroid, the expected number Nexp of gamma-ray emitting MSPs in our Galaxy is derived using Eq. (6). Uncertainties of Nexp are determined by finding the values of αmin and αmax for which the log-likelihood function (Eq. (7)) decreases by a value of 2 with respect to the maximum (corresponding to a 2σ confidence interval).
By comparing models ST1 to FG1 and models ST2 to FG2, it becomes obvious that the choice of the P − Ṗ model has some impact on the results, which leads to higher values for the scaling parameters for FG with respect to ST. The detectable pulsars predicted by the FG model have an average luminosity that is larger than those predicted by the ST model, which is readily seen in their P − Ṗ distribution shown in Fig. 1. Detectable FG pulsars are thus seen at greater distances. For a given set of scale parameters their spatial distributions more concentrated towards the Galactic plane and the inner Galaxy with respect to the ST model. Consequently, larger scale parameters are required for the FG pulsars to fit to the observed spatial distribution of MSPs.
In summary, the ST models suggest a vertical scale height z0 of ~1 kpc, while the FG models predict a larger scale height of ~1.8 kpc. For the radial exponential scale length R0, the ST1 model suggests a value of ~4 kpc, while the FG1 model predicts ~10 kpc. Using a Gaussian radial profile leads to σr values of ~6 kpc for ST2 and ~13 kpc for FG2.
In addition to the spatial parameters, our analysis also predicts the total number Nexp of MSPs in our Galaxy that are potentially detectable in γ-rays. Because the FG pulsars are on average brighter, a higher fraction of the Galaxy becomes detectable with that model. Because the normalization of the model is given by the constraint that the number of pulsars in the detectable volume is equal to 36, a larger volume implies a smaller scaling factor α. Consequently, Nexp is lower for the FG model (~4000) than for the ST model (~10 000).
Our model also allows the prediction of the total γ-ray intensity received at Earth from MSPs that do not pass the detection threshold, hence forming a diffuse background from unresolved sources (Bhattacharya & Srinivasan 1991). We estimate this intensity SΩ by summing the individual fluxes above 100 MeV of all undetectable MSPs in a given region Ω divided by the solid area of the region, i.e. 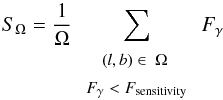 (8)In Table 2, the expected average intensities above 100 MeV from the central Galactic radian (S| b | ≤ 10°, | l | ≤ 30°, integrated over | l | ≤ 30° and | b | ≤ 10°) and high Galactic latitudes (S| b | ≥ 40°, integrated over | b | ≥ 40°) are shown.
(8)In Table 2, the expected average intensities above 100 MeV from the central Galactic radian (S| b | ≤ 10°, | l | ≤ 30°, integrated over | l | ≤ 30° and | b | ≤ 10°) and high Galactic latitudes (S| b | ≥ 40°, integrated over | b | ≥ 40°) are shown.
The diffuse fluxes follow the same trend as the expected number of MSPs in the Galaxy, with the ST model predicting larger fluxes than the FG models. Using the ST models, the expected diffuse flux from the Galactic central radial is estimated to ~2 × 10-6 ph cm-2 s-1 sr-1, while this flux is only about ~0.8 × 10-6 ph cm-2 s-1 sr-1 for the FG models. This result corresponds to a total of 1% or less of the Galactic γ-ray flux that is observed by Fermi-LAT from that area (Ackermann et al. 2012). At high Galactic latitudes, the ST models predict a value of ~2.0 × 10-8 ph cm-2 s-1 sr-1 for an average γ-ray intensity above 100 MeV due to unresolved MSPs, while the FG models predict a value of ~1.5 × 10-8 ph cm-2 s-1 sr-1. This intensity corresponds to an approximate value of a few permil of the extragalactic background intensity (Abdo et al. 2010d).
 |
Fig. 6 Log-likelihood as a function of radial scale length (R0 or σr) and vertical scale height (z0) for the model ST1. The panels show (from top left to bottom right) the results for 36 MSPs a), 66 MSP candidates b), 36 mock MSPs c), and 66 mock MSPs d). Contours show the 1, 2, and 3σ confidence ellipses that have been computed from the log-likelihood maps (colours). All maps show the same dynamic range in log-likelihood. |
4.4. Extended MSP sample
So far, we applied our analysis to the sample of 36 MSPs that have been detected in the 1FGL catalogue and for which γ-ray pulsations have been significantly detected. Through searches with radio telescopes for pulsations from the error regions of yet unassociated Fermi-LAT sources that obey spectral and temporal characteristics that are reminiscent of MSPs, many of the MSPs in our sample have only been identified as such after the publication of the catalogue. Further unassociated sources in 1FGL show similar characteristics. Based on the classification analysis of unassociated sources made by Ackermann et al. (2012), we extend our sample by including unassociated 1FGL sources that were classified in this work as potential pulsars and exclude all sources that are either flagged as dubious (flag c) or that are situated closer than | b | ≤ 10° to the Galactic plane. This list provides 38 additional sources that eventually could be γ-ray emitting MSPs. Adding to this list of the known MSPs, where we also excluded all objects situated closer than | b | ≤ 10° to the Galactic plane for consistency, we obtain a final list of 66 potential γ-ray emitting MSPs, as seen in the 1FGL catalogue.
Figure 6b shows the resulting log-likelihood distribution when using this sample instead of the 36 MSPs that were used. We excluded in this analysis all HEALPix pixels with pixel centres of | b | ≤ 10°. We only show here results for model ST1. For reference, we also show the log-likelihood distribution obtained for the 36 MSPs for model ST1 in Fig. 6a.
With the additional MSP candidates, the Galactic scaling parameters are now much better constrained. Our model predicts a radial scale length of R0 ~ 3 kpc, a vertical scale height of z0 ~ 0.6 kpc, and a total number of Nexp ~ 22 000 γ-ray emitting MSPs in the Milky Way. This number is about a factor of ~2 larger than our estimate that is based on the 36 confirmed MSPs, which directly reflects the larger number of MSPs in the extended sample. As the extended sample includes all objects of the 1FGL catalogue, which shows the spectral and temporal characteristics of MSPs, it may include some sources that simply mimic MSPs, and in this sense, the results obtained for the extended sample may be interpreted as upper limits. However, some unassociated sources in 1FGL may be too faint to exhibit a significant spectral curvature, which is required in the extended sample. The true number of MSPs in the 1FGL catalogue may thus still be a bit larger.
Using the extended sample, the unresolved average background intensity above 100 MeV from the Galactic central radian is now estimated to be S| b | ≤ 10°, | l | ≤ 30° ~ 6 × 10-6 ph cm-2 s-1 sr-1 (about 2% of the observed Galactic diffuse flux in that region), and the average intensity above 100 MeV at high Galactic latitudes is predicted to be S| b | ≥ 40° ~ 2 × 10-8 ph cm-2 s-1 sr-1 (about 0.4% of the observed intensity).
4.5. Possible biases
4.5.1. Statistical variations
Ideally, our results should be driven by the particular sample of observed MSPs (or MSP candidates) that we have at hand, and the confidence contours should reflect the statistical uncertainties that arise from the limited number of objects. We now use mock catalogues of observed MSPs to investigate how statistical variations impact our results, and to search for possible biases in our analysis.
As a first test, we produce mock MSP catalogues using the bootstrap method (Efron 1979). In this method, we create mock catalogues by randomly selecting 36 objects from the 36 observed MSPs, which allows individual MSPs to be selected multiple times. This result leads to a resampling of the list of observed MSP that should be a statistical variation of the original sample. We created ten bootstrap samples, and for each sample, we perform a maximum likelihood analysis from which we determine the confidence ellipses in the scaling parameters. We find that the scaling parameters vary substantially between each individual bootstrap samples and remain compatible within the statistical uncertainties with the values found for the observed MSP sample. We thus conclude that the particular shape of the log-likelihood contours is primarily driven by the statistics of the sample.
Alternatively to the bootstrap analysis, we also performed the maximum likelihood analysis on subsets of only 30 MSPs that were drawn randomly from the original list of 36 objects. The results of the subset analysis were qualitatively comparable to the bootstrap analysis, which confirm that the confidence contours are driven by the statistical variations.
Results with increased sample and simulated samples.
As a third test, we also performed the maximum likelihood analysis on mock samples composed of 36 MSPs which were generated randomly from our population model. In total, we performed 20 mock analyses. We show one result in Fig. 6c for illustration. The parameter values obtained for this simulation are given in the third column of Table 3. The results for this specific mock sample are reasonably close to the results obtained using the observed 36 MSPs (cf. Fig. 6a), which illustrate that at least one out of 20 samples (i.e. 5%) produces confidence contours that are compatible with those of the observed MSPs. We also note that the 2σ confidence contours enclose the true values of R0 = 4.2 kpc and z0 = 500 pc that were used in the simulation, which confirms that our parameter estimates are reliable. This finding is important, because it demonstrates that our analysis procedure does not introduce any bias in the scaling parameters of the Galactic MSP density distribution. In particular, the observed MSP sample seems to indicate a larger vertical scale height than the 500 pc that have been chosen for the simulation, suggesting that the Galactic latitude distribution of γ-ray emitting MSPs may eventually be broader than previously assumed (Story et al. 2007).
Finally, we also performed 20 mock simulations for a population of 66 observed MSPs. We show one result in Fig. 6d. The corresponding parameter values are quoted in the fifth column of Table 3. These simulations collerate the results found earlier for 36 MSPs, and confirm that the uncertainties in the analysis are compatible because of only statistical uncertainties.
4.5.2. Impact of sensitivity map
As mentioned earlier (cf. Sect. 4.2), the sensitivity map is an important ingredient in our analysis that is used to discern detectable from undetectable MSPs in our simulations and that has an impact on the parameters of the Galactic MSP population. For our study, we use the sensitivity map published for the 1FGL catalogue, which is based on the hypothesis that all sources have a power law spectral shape with an spectral index of Γ = 2.2.
 |
Fig. 7 Fermi-LAT MSPs flux above 100 MeV (FMSP) against the sensitivity (Fsensitivity). Solid and dashed lines show FMSP = Fsensitivity and FMSP = 1.4 × Fsensitivity respectively. |
Figure 7 shows the flux above 100 MeV of the 36 MSPs used for analysis versus the sensitivity value at the respective locations. Ideally, all MSPs should fall above the solid line, which indicates an MSP flux identical to the sensitivity value. We find one object (1FGL J1600.7−3055) that violates this constraint, but detailed inspection of this object reveals an unusually hard spectral power law index (Γ = 1.8) for this source. Due to the decreasing size of the point spread function with increasing energy, hard spectrum sources are in fact easier to detect by Fermi-LAT. The corresponding sensitivity should thus be smaller for such hard spectrum sources brings the measured flux in agreement with the expected instrument performances.
 |
Fig. 8 Dependecy of R0, z0 and Nexp on the assumed γ-ray efficiency η of MSPs (see Eq. (5)) for model ST1. Error bars are 2σ confidence. |
The ratio between flux FMSP and sensitivity Fsensitivity for a given source should approximately scale with the ratio between source significance (σ) and chosen significance limit (σ0), i.e. 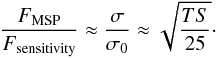 (9)For the 1FGL catalogue, source significance is measured using the Test Statistics (Abdo et al. 2010a), which roughly scales with the square of the source significance. The threshold for source detection has been set to TS = 25 for 1FGL. We can use these relations to verify how well the actual sensitivity map matches the measured flux values. For this purpose, we multiply Fsensitivity using an arbitrary scaling factor s and determine the value that minimizes the function:
(9)For the 1FGL catalogue, source significance is measured using the Test Statistics (Abdo et al. 2010a), which roughly scales with the square of the source significance. The threshold for source detection has been set to TS = 25 for 1FGL. We can use these relations to verify how well the actual sensitivity map matches the measured flux values. For this purpose, we multiply Fsensitivity using an arbitrary scaling factor s and determine the value that minimizes the function: 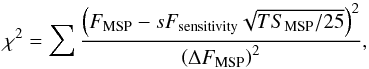 (10)where ΔFMSP is the measured statistical uncertainty in the source flux and TSMSP is the Test Statistics of the MSPs. A best scaling factor of s ≈ 1.4 results, which is shown in Fig. 7 as a dashed line. Using an 1FGL sensitivity map scaled by a factor of 1.4 reduces the radial scale length R0 from 4 kpc to 3 kpc and the vertical scale height z0 from 1.0 kpc to 0.6 kpc, while the expected number of γ-ray emitting MSPs in the Galaxy increases from 11 000 to 18 000. In general, increasing the sensitivity values (i.e. reducing the assumed Fermi-LAT detection sensitivity) shuffles more MSPs from the detectable sample into the undetectable sample, which leads to larger scale factors α in the maximum likelihood analysis. Consequently, the total number Nexp of gamma-ray emitting MSPs in the Galaxy and the diffuse flux estimates are increased.
(10)where ΔFMSP is the measured statistical uncertainty in the source flux and TSMSP is the Test Statistics of the MSPs. A best scaling factor of s ≈ 1.4 results, which is shown in Fig. 7 as a dashed line. Using an 1FGL sensitivity map scaled by a factor of 1.4 reduces the radial scale length R0 from 4 kpc to 3 kpc and the vertical scale height z0 from 1.0 kpc to 0.6 kpc, while the expected number of γ-ray emitting MSPs in the Galaxy increases from 11 000 to 18 000. In general, increasing the sensitivity values (i.e. reducing the assumed Fermi-LAT detection sensitivity) shuffles more MSPs from the detectable sample into the undetectable sample, which leads to larger scale factors α in the maximum likelihood analysis. Consequently, the total number Nexp of gamma-ray emitting MSPs in the Galaxy and the diffuse flux estimates are increased.
For the first Fermi-LAT pulsar catalogue, Abdo et al. (2010c) presents a sensitivity map that is specifically computed for sources with pulsar-like spectra and assumes an exponentially cut off power law with spectral index Γ = 1.4 and cut off energy Ec = 2.2 GeV. We scale this sensitivity from the 6 months of data used by Abdo et al. (2010c) to the 11 months of data used for 1FGL by dividing the map by 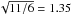 . Using this sensitivity map, instead of the 1FGL sensitivity map, provides the same radial scale length R0 = 4 kpc and reduces the vertical scale height z0 from 1.0 kpc to 0.8 kpc, while the expected number of γ-ray emitting MSPs in the Galaxy increases from 11 000 to 16 000.
. Using this sensitivity map, instead of the 1FGL sensitivity map, provides the same radial scale length R0 = 4 kpc and reduces the vertical scale height z0 from 1.0 kpc to 0.8 kpc, while the expected number of γ-ray emitting MSPs in the Galaxy increases from 11 000 to 16 000.
The sensitivity map thus has a non-negligible impact on our analysis, but given the still larger statistical uncertainties, the precise prescription and scaling of the sensitivity map does not significantly affect our conclusions.
4.5.3. Luminosity law
Another source of uncertainty is related to our specific choice for the luminosity function. In particular, the precise value η for the γ-ray efficiency of MSPs is rather poorly constrained by the present data as illustrated in Fig. 3. We thus explore how changes in η affect our analysis results and present the variation of R0, z0 and Nexp for the ST1 model for efficiencies of η = 0.05,0.1,0.2, and 0.3 in Fig. 8.
The first trend is that R0 and z0 increase with increasing γ-ray efficiency. We have already explained the reason behind this effect in Sect. 4.3, when comparing the results for the ST model to those for the FG model. Notably, a larger η leads to a larger volume of the Galaxy that becomes detectable and to a spatial distribution for the detectable MSPs that is more concentrated towards the Galactic plane and the central Galactic radian. To match the observed MSP distribution, the scale parameters thus need to be increased with respect to those obtained for lower efficiencies. The variation over the explored range of η amounts to be about a factor of 2, which is smaller than the statistical uncertainties.
The second trend is that Nexp strongly declines with an increasing value of η. This effect also has already been observed in the comparison of the ST model and the FG model results and is explained by the increase in the Galactic volume that is explored by Fermi-LAT, which has an increasing η for a given sensitivity limit. Here the effect is significant, that is, the choice of the η value dominates the statistical uncertainties of the MSP sample. Fortunately, the η dependency weakens for an increasing γ-ray efficiency, and the change in Nexp becomes rather low above ≳20%. Figure 3 illustrates that the average η values are found in the range 0.2 − 0.3, and that the values as low as 0.1 or even 0.05 appear to be excluded, unless the distance estimates to MSPs are heavily biased. Our estimates determined based on the value of η = 0.2 are thus relatively solid and likely constrain the true value of Nexp from the high side, since the higher values of η are consistent with the Fermi-LAT data.
5. Discussion
The comparison of the spatial distribution of the 36 MSPs detected in the 1FGL catalogue to a population model provides first constraints on the spatial distribution of Galactic MSPs, which are based solely on γ-ray data. Although the statistical uncertainties still remain large, the analysis suggests radial scale lengths of R0 ~ 4 kpc for an exponential law and ~6 kpc for a Gaussian law, when the modelling approach of Story et al. (2007) is used. The vertical scale height for this model is around z0 ~ 1 kpc. The alternative approach of Faucher-Giguère & Loeb (2010) suggests higher values; yet, this approach leads to a P − Ṗ distribution that seems incompatible with the Fermi-LAT data, and that predicts pulsars with characteristic ages in excess of the age of the Universe. We thus concentrate in the remainder of this section on the results obtained using the ST models.
Adding unassociated 1FGL sources with spectral and temporal characteristics reminiscent of MSPs to the sample reduces the statistical uncertainties, which suggests an exponential radial scale length of R0 ~ 3 kpc and an exponential vertical scale height of z0 ~ 0.6 kpc. These values are in the range of expectations for Galactic MSPs (Story et al. 2007).
It should be noted that the estimation of the vertical scale height could be biased due to inaccurate modelling of the Fermi-LAT sensitivity variations close to the Galactic plane. The sensitivity map only reflects the statistical limitations in the point source detection process, while inaccurate modelling of the Galactic diffuse emission necessarily adds a systematic uncertainty that is not quantified. It is, however, assuring that exclusion of the complex Galactic plane region does not alter our maximum likelihood results, which demonstrates that our results are robust with respect to analysis details.
Another interesting estimate resulting from our analysis is the expected number Nexp of γ-ray emitting MSPs in the Galaxy. It should be emphasized that the total number of MSPs in the Galaxy may indeed be larger than Nexp, because a fraction of the MSPs may not be γ-ray emitters or may have a γ-ray beam that does not intersect with the line of sight towards Earth. Using the more plausible P − Ṗ prescription of Story et al. (2007), our model estimates Nexp to be 9000 − 11 000 with a typical statistical uncertainty of ±4000 (2σ confidence). Althouhg there are more γ-ray emitting MSPs in the 1FGL catalogue, our extended sample of 66 MSPs raises Nexp to 22 000 ± 14 000. Increasing the assumed γ-ray efficiency η above the value of 0.2 in this study decreases this number. Radio estimates of the Galactic MSP population that have been derived by extrapolating the local density to the entire Galaxy (Cordes & Chernoff 1997; Lyne et al. 1998; Lorimer 2005), fall in the interval between ~30 000 and ~200 000 objects, which is only marginally compatible with our estimates. Clearly, our γ-ray estimate based on the Fermi-LAT detection of MSPs favours lower numbers.
By assuming a typical lifetime of 10 Gyr for MSPs (Camilo et al. 1994), we can translate our estimated number of 9000 − 11 000 Galactic γ-ray emitting MSPs into a birthrate of (0.9 − 1.1) × 10-6 yr-1. This value is 3 times less than the conventional MSP birthrates derived from radio observations (Cordes & Chernoff 1997; Lyne et al. 1998; Lorimer 2005; Ferrario & Wickramasinghe 2007; Story et al. 2007). On the other hand, birthrates of low-mass X-ray binaries (LMXB), which are suggested to be the progenitors of MSP (Alpar et al. 1982), are estimated to be ~10-7 − 10-6 yr-1 (Kulkarni & Narayan 1988; Cote & Pylyser 1989; Lorimer 1995), and the discrepancy with respect to the estimated radio MSP birthrates is commonly referred to as the “birthrate problem”. Our birthrate estimate is still at the high side of LMXB birthrate estimates, yet marginally compatible with the range of proposed values.
Faucher-Giguère & Loeb (2010) suggested that ~10 − 20% of the high-latitude γ-ray background detected by Fermi-LAT could originate from unresolved MSPs. Our analysis suggests an average intensity above 100 MeV that amounts to less than one percent of the high-latitude γ-ray background emission, and leads us to conclude that MSPs do probably not provide any significant contribution to the isotropic diffuse γ-ray background.
In contrast, a few percent of the Galactic diffuse emission towards the inner central radian may be attributed to unresolved MSPs, although it remains questionable whether such a component can reliably be extracted from the dominating cosmic-ray induced components. Possibly, the characteristic spectral shape (an exponentially cut-off power law with a hard spectral index of Γ ~ 1.4 and a cut-off energy of a few GeV) of MSP could be used to disentangle the components. Additional help may come from the relative large vertical scale height of MSPs, which exceeds those of the gas related cosmic-ray induced components (pion decay, Bremsstrahlung). Conversely, the Inverse Compton component is expected to reach towards higher latitudes, which makes a spatial distinction between MSP and cosmic-ray induced γ-ray emission challenging.
6. Conclusion
Based on a Monte Carlo model, we derive constraints on the Galactic MSP population based solely on γ-ray detections of MSPs for the first time. We use a maximum likelihood method to determine the radial scale length, vertical scale height, and total size of the Galactic γ-ray emitting MSP population. We apply our model to a sample of 36 MSPs that are detected in the 1FGL catalogue, and to an increased list of 66 objects comprised of confirmed MSPs and MSP candidates.
The spatial parameters are consistent with previous estimates based on radio observations. The estimated size of the Galactic MSP population is lower than the estimates obtained from radio observations, which alleviates the MSP birthrate problem. The contribution of unresolved MSPs to the isotropic diffuse background emission at high Galactic latitudes is estimated to be negligible. Towards the central Galactic radian, unresolved MSPs may contribute up to a few percent of the total emission. It remains to be seen, however, whether this contribution can be reliably disentangled from the other dominating emission components.
Our analysis still suffers from relatively large statistical uncertainties, because of the limited number of MSPs detected so far in γ-rays. Using an extended sample that also includes unassociated 1FGL catalogue sources with spectral and temporal characteristics reminiscent of MSPs leads to a substantial reduction of the uncertainties. Assuming that the number of detected MSPs by Fermi-LAT simply scales with the decrease of sensitivity that arises from a continuous survey of the sky, we expect that ~80 MSPs should be detected by Fermi-LAT after 5 years of observations. This number should increase to ~110 MSPs after 10 years. As shown from the analysis of our extended sample, such a large number of γ-ray detections will provide us with unprecedented constraints on the Galactic MSP distribution.
Acknowledgments
Some of the results in this paper have been derived using the HEALPix (K.M. Górski et al. 2005, ApJ, 622, 759) package.
References
- Abdo, A. A., Ackermann, M., Ajello, M., et al. 2009a, Science, 325, 848 [NASA ADS] [CrossRef] [Google Scholar]
- Abdo, A. A., Ackermann, M., Atwood, W. B., et al. 2009b, ApJ, 699, 1171 [NASA ADS] [CrossRef] [Google Scholar]
- Abdo, A. A., Ackermann, M., Ajello, M., et al. 2010a, ApJS, 188, 405 [NASA ADS] [CrossRef] [Google Scholar]
- Abdo, A. A., Ackermann, M., Ajello, M., et al. 2010b, ApJ, 712, 957 [NASA ADS] [CrossRef] [Google Scholar]
- Abdo, A. A., Ackermann, M., Ajello, M., et al. 2010c, ApJS, 187, 460 [NASA ADS] [CrossRef] [Google Scholar]
- Abdo, A. A., Ackermann, M., Ajello, M., et al. 2010d, Phys. Rev. Lett., 104, 101101 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Ackermann, M., Ajello, M., Atwood, W. B., et al. 2012, ApJ, 750, 3 [NASA ADS] [CrossRef] [Google Scholar]
- Alpar, M. A., Cheng, A. F., Ruderman, M. A., & Shaham, J. 1982, Nature, 300, 728 [NASA ADS] [CrossRef] [Google Scholar]
- Bhattacharya, D., & Srinivasan, G. 1991, A&A, 12, 17 [Google Scholar]
- Camilo, F., Thorsett, S. E., & Kulkarni, S. R. 1994, ApJ, 421, L15 [NASA ADS] [CrossRef] [Google Scholar]
- Cash, W. 1979, ApJ, 228, 939 [NASA ADS] [CrossRef] [Google Scholar]
- Cognard, I., Guillemot, L., Johnson, T. J., et al. 2011, ApJ, 732, 47 [NASA ADS] [CrossRef] [Google Scholar]
- Cordes, J. M., & Chernoff, D. F. 1997, ApJ, 482, 971 [NASA ADS] [CrossRef] [Google Scholar]
- Cote, J., & Pylyser, E. H. P. 1989, A&A, 218, 131 [NASA ADS] [Google Scholar]
- Efron, B. 1979, Ann. Stat., 7, 1 [Google Scholar]
- Faucher-Giguère, C.-A., & Loeb, A. 2010, J. Cosmol. Astropart. Phys., 2010, 005 [CrossRef] [Google Scholar]
- Ferrario, L., & Wickramasinghe, D. 2007, MNRAS, 375, 1009 [NASA ADS] [CrossRef] [Google Scholar]
- Górski, K. M., Hivon, E., Banday, A. J., et al. 2005, ApJ, 622, 759 [NASA ADS] [CrossRef] [Google Scholar]
- Guillemot, L. 2010, in Radio Pulsars: An astrophysical key to unlock the secret of the Universe [Google Scholar]
- Guillemot, L., Freire, P. C. C., Cognard, I., et al. 2012a, MNRAS, 422, 1294 [NASA ADS] [CrossRef] [Google Scholar]
- Guillemot, L. J., Johnson, T., Venter, C., et al. 2012b, ApJ, 744, 33 [NASA ADS] [CrossRef] [Google Scholar]
- Hessels, J. W. T., Roberts, M. S. E., McLaughlin, M. A., et al. 2010, in Radio Pulsars: An astrophysical key to unlock the secret of the Universe [Google Scholar]
- Hewish, A., Bell, S. J., Pilkington, J. D. H., Scott, P. F., & Collins, R. A. 1968, Nature, 217, 709 [NASA ADS] [CrossRef] [Google Scholar]
- Keith, M. J., Johnston, S., Ray, P. S., et al. 2011, MNRAS, 414, 1292 [NASA ADS] [CrossRef] [Google Scholar]
- Keith, M. J., Johnston, S., Bailes, M., et al. 2012, MNRAS, 419, 1752 [NASA ADS] [CrossRef] [Google Scholar]
- Kerr, M., Camilo, F., Johnson, T. J., et al. 2012, ApJ, 748, L2 [NASA ADS] [CrossRef] [Google Scholar]
- Kuiper, L., Hermsen, W., Verbunt, F., et al. 2000, A&A, 359, 615 [NASA ADS] [Google Scholar]
- Kulkarni, S. R., & Narayan, R. 1988, ApJ, 335, 755 [NASA ADS] [CrossRef] [Google Scholar]
- Lorimer, D. R. 1995, MNRAS, 274, 300 [NASA ADS] [Google Scholar]
- Lorimer, D. R. 2005, Liv. Rev. Rel., 8, 7 [Google Scholar]
- Lyne, A. G. 2000, Philos. Trans. Roy. Soc. A: Mathematical, Physical and Engineering Sciences, 358, 831 [CrossRef] [Google Scholar]
- Lyne, A. G., Manchester, R. N., Lorimer, D. R., et al. 1998, MNRAS, 295, 743 [NASA ADS] [CrossRef] [Google Scholar]
- Manchester, R. N., Hobbs, G. B., Teoh, A., & Hobbs, M. 2005, ApJ, 129, 1993 [Google Scholar]
- Parent, D. 2010, in Radio Pulsars: An astrophysical key to unlock the secret of the Universe [Google Scholar]
- Ransom, S. M., Ray, P. S., Camilo, F., et al. 2011, ApJ, L727, 16 [Google Scholar]
- Ray, P. S., Abdo, A. A., Parent, D., et al. 2011, in Radio Searches of Fermi LAT Source and Blind Search Pulsars: The Fermi Pulsar Search Consortium, The Fermi Symposium [Google Scholar]
- Reed, B. C. 2006, Roy. Astron. Soc. Canada, 1 [Google Scholar]
- Robin, A. C., Reylé, C., Derrière, S., & Picaud, S. 2003, A&A, 409, 523 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Story, S. A., Gonthier, P. L., & Harding, A. K. 2007, ApJ, 671, 713 [NASA ADS] [CrossRef] [Google Scholar]
- Teague, M. R. 1980, J. Opt. Soc. Am., 70, 920 [NASA ADS] [CrossRef] [Google Scholar]
- Wilks, S. S. 1938, Ann. Math. Stat., 9, 60 [Google Scholar]
All Tables
All Figures
 |
Fig. 1 Simulated P − Ṗ distribution of the detectable sample (filled symbols) and an according undetectable sample (open symbols) using the approaches of Faucher-Giguère & Loeb (2010) (red squares) and of Story et al. (2007) (blue circles). We use [σr = 5, z0 = 1] kpc and [R0 = 4.2, z0 = 0.5] kpc respectively for Faucher-Giguère & Loeb and Story et al. approaches. For comparison we show the observed distribution of Fermi-LAT MSPs as green triangles. The P − Ṗ distribution of all pulsars from the ATNF catalogue (Manchester et al. 2005, http://www.atnf.csiro.au/research/pulsar/psrcat) is shown as black dots. We also show lines of constant spin-down power Ė (dashed), constant characteristic age (dashed-dotted), and constant magnetic field (dotted). The area excluded by the deathline implemented in Faucher-Giguère & Loeb’s model is indicated by the blue filled area. The inset presents a zoom into the MSP region of the P − Ṗ diagram. |
| In the text | |
 |
Fig. 2 HEALPix maps (Nside = 64) for R0 = 4.2 kpc and σz = 500 pc using the Story et al. (2007) luminosity model. The panels show the entire simulated MSP population (top left), the undetectable (top right) and detectable (bottom left) samples, and the smoothed detectable sample (bottom right). |
| In the text | |
 |
Fig. 3 Observed γ-ray luminosity Lγ versus spin down power Ė for the 36 Fermi-LAT MSPs used in this study. The dashed lines indicate empirical laws used to predict the γ-ray luminosity of individual MSPs (see text). |
| In the text | |
 |
Fig. 4 Sensitivity map of the Fermi-LAT for detection of 1FGL point sources, which are given in Galactic coordinates and Aitoff projection (Abdo et al. 2010c). |
| In the text | |
 |
Fig. 5 Log-likelihood as a function of radial scale length (R0 or σr) and vertical scale height (z0) for four MSP population models (see text). Contours show the 1, 2, and 3σ confidence ellipses that have been computed from the log-likelihood maps (colours). All maps show the same dynamic range in log-likelihood. |
| In the text | |
 |
Fig. 6 Log-likelihood as a function of radial scale length (R0 or σr) and vertical scale height (z0) for the model ST1. The panels show (from top left to bottom right) the results for 36 MSPs a), 66 MSP candidates b), 36 mock MSPs c), and 66 mock MSPs d). Contours show the 1, 2, and 3σ confidence ellipses that have been computed from the log-likelihood maps (colours). All maps show the same dynamic range in log-likelihood. |
| In the text | |
 |
Fig. 7 Fermi-LAT MSPs flux above 100 MeV (FMSP) against the sensitivity (Fsensitivity). Solid and dashed lines show FMSP = Fsensitivity and FMSP = 1.4 × Fsensitivity respectively. |
| In the text | |
 |
Fig. 8 Dependecy of R0, z0 and Nexp on the assumed γ-ray efficiency η of MSPs (see Eq. (5)) for model ST1. Error bars are 2σ confidence. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


