EDP Sciences logo
Subscriber Authentication Point
Search
Menu
Home All issues Volume 553 (May 2013) A&A, 553 (2013) A75 Full HTML
Free Access
Issue
A&A
Volume 553, May 2013
Article Number A75
Number of page(s) 7
Section Interstellar and circumstellar matter
DOI https://doi.org/10.1051/0004-6361/201220967
Published online 07 May 2013

© ESO, 2013

1. Introduction

Despite the low elemental deuterium abundance in the local interstellar gas (1–2  ×  10-5; Linsky et al. 2006), numerous deuterated molecules have been detected with enhanced D/H ratios in the environments of low-mass star-forming regions. The doubly deuterated form of water, D2O, has been in particular detected in the solar-type protostar IRAS 16293-2422 (hereafter IRAS 16293), which is well known for its high deuterium fractionation: the fundamental 11,0–10,1 para–D2O transition at 317 GHz was detected by Butner et al. (2007) using the James Clerk Maxwell Telescope (JCMT), whereas the fundamental 11,1–00,0 ortho–D2O transition at 607 GHz was discovered with the Heterodyne Instrument for Far-Infrared (HIFI) instrument onboard the Herschel Space Observatory by Vastel et al. (2010). The observed line profile at 317 GHz shows a component in emission in addition to a deep and narrow absorption. The emission component has been attributed to heavy water in the hot corino of this source, where the grain ices are sublimated and released into the gas phase (Ceccarelli et al. 2000; Bottinelli et al. 2004). The absorption component, whose linewidth is 0.5 km s-1, is seen in both transitions at the velocity of 4.2 km s-1. It probably originates in the foreground gas (molecular cloud and cold envelope), which is studied through the fundamental HDO transition at 465 and 894 GHz (Coutens et al. 2012). Both transitions present deep absorption features at the same velocity as the D2O component. The OD molecule, a key species in the formation of deuterated water on grains, also shows a deep absorbing component (Parise et al. 2012) and most certainly arises from the same region as water and its deuterated forms. Besides, numerous absorption lines of several nitrogen molecules (NH, ND, NH2, and NH3) are detected towards the IRAS 16293 source (Bacmann et al. 2010; Hily-Blant et al. 2010), suggesting an origin of these species in a cold environment. Coutens et al. (2012) used the spherical Monte Carlo radiative transfer code RATRAN (Hogerheijde & van der Tak 2000) to reproduce the line profiles of the two HDO fundamental transitions as well as eleven other detected lines by assuming an abundance jump at 100 K (Fraser et al. 2001). From the emission line profiles, the derived HDO inner abundance (T ≥ 100 K) is about 1.7  ×  10-7, whereas the HDO outer abundance (T < 100 K) is estimated at about 8  ×  10-11. A water-rich absorbing layer is, however, required in front of the envelope to reproduce the HDO absorption components observed at 465 and 894 GHz. This layer may result from the photodesorption of the ices at the edges of the molecular cloud, as predicted by chemical models (e.g., Hollenbach et al. 2009).

A non-LTE (local thermal equilibrium) modeling has been performed by Vastel et al. (2010) to estimate the ortho-to-para D2O ratio in the cold (<30 K) dense (<5  ×  106 cm-3) cloud surrounding the IRAS 16293 protostar, adopting the density and temperature profiles of the envelope (Crimier et al. 2010). Vastel et al. (2010) considered the first two levels of each D2O form and used the computed collisional rates for the two fundamental deexcitation transitions of ortho– and para–D2O with para–H2 in the 10–30 K range (Scribano et al. 2010). Their computation yields an ortho-to-para ratio of 1.1  ±  0.4 at a 1σ level of uncertainty with the corresponding column densities N(ortho) = (8.7 ± 2.1) × 1011 cm-2 and N(para) = (7.8 ± 2.6) × 1011 cm-2. This ratio is lower than 2.6 at a 3σ level of uncertainty, taking into account the statistical error as well as the overall calibration budget for the HIFI band 1b. The comparison between the upper value of the measured D2O ortho-to-para ratio and the thermal equilibrium value shows that they are consistent with a gas at a temperature higher than about 15 K and, therefore, with the assumed absorbing gas location.

The present paper aims at determining the D2O abundance distribution throughout the whole protostellar envelope of IRAS 16293, from the hot corino to the foreground water-rich absorbing layer (see Fig. 2 in Coutens et al. 2012). Using the previous results obtained in a similar way by Coutens et al. (2012) for HDO and H2O, the derived D2O/H2O and HDO/H2O ratios are then discussed and compared with a grain-surface chemical model (Cazaux et al. 2011). The paper is organized as follows. First, we describe the observations as well as their reduction in Sect. 2. Then we present the modeling and the results in Sect. 3. Finally, we discuss the results in Sect. 4 and conclude in Sect. 5.

2. Observations

In the framework of the Chemical HErschel Surveys of Star forming regions (CHESS) key program (Ceccarelli et al. 2010), we observed the solar-type protostar IRAS 16293 with the Herschel/HIFI instrument (Pilbratt et al. 2010; de Graauw et al. 2010). The targeted coordinates were α2000 = 16h32m2275, δ2000 = −24°28′34.2″, a position at equal distance from the binary components A and B. A full spectral coverage of bands 1b and 3b was performed on 2010 March 2 and 2010 March 19 respectively, using the HIFI spectral scan double beam switch (DBS) mode with optimization of the continuum. The fundamental ortho–D2O 11,1–00,0 transition lies in this frequency coverage at 607.349 GHz whereas the para–D2O 21,2–11,0 transition lies at 897.947 GHz. The HIFI Wide Band Spectrometer (WBS) was used, providing a spectral resolution of 1.1 MHz (~0.55 km s-1 at 600 GHz and  ~0.37 km s-1 at 900 GHz) over an instantaneous bandwidth of 4  ×  1 GHz. The ortho–D2O 11,1–00,0 transition was re-observed in February 2011 with the High Resolution Spectrometer (HRS) to benefit from a higher spectral resolution (~0.06 km s-1). We consequently use these new observations hereafter. At 610 GHz (900 GHz), the beam size is about 35″ (24″ resp.) and the measured main beam efficiency is 0.75 (0.74 resp.), whereas the forward efficiency is 0.96 in both cases (Roelfsema et al. 2012). The DBS reference positions were situated approximately 3′ east and west of the source.

The data reduction of the para–D2O 21,2–11,0 transition at 898 GHz was performed similarly to the HDO and H218O lines studied by Coutens et al. (2012). This transition was observed eight times (four in lower sideband and four in upper sideband) for each polarization in the selected observing mode. To produce the final spectra, the observations that were processed using the standard HIFI pipeline up to level 2 with the ESA-supported package Herschel interactive processing environment (HIPE) 5.1 (Ott 2010) were exported to the GILDAS/CLASS1 software. We then baseline subtracted and averaged the H and V polarizations at the line frequency, weighting them by the observed noise for each spectra. We verified for all spectra that no emission from other species was present in the image band. This transition had not been discovered when Vastel et al. (2010) published their results with an early version (3.01) of the HIPE software, using the sideband deconvolution method on all bands. The present data reduction, which uses the selected spectra re-aligned on one single transition and averaged after an accurate baseline subtraction and rms weighting, leads to a lower noise level than the one obtained with the standard HIPE deconvolution routine, and allows us to present the first tentative detection of a high-energy level transition of deuterated water (see Fig. 2). For the pointed HRS data at 607 GHz, the observations of the H and V polarizations were processed with the ESA-supported package HIPE 8.0 (Ott 2010) up to level 2 and then exported to the GILDAS/CLASS software for the baselines to be subtracted and the two polarizations averaged. HIFI operates as a double sideband (DSB) receiver. From the in-orbit performances of the instrument (Roelfsema et al. 2012), a sideband ratio of unity is assumed for the observed D2O transitions seen in absorption against the continuum (bands 1b and 3b). The continuum values observed over the frequency range of the whole bands are closely fitted by straight lines. The continuum derived from the polynomial fit at the considered frequency and divided by two to obtain the single sideband (SSB) continuum was added to the spectra.

Table 1

Derived parameters of the absorbing components of the ortho– and para–D2O fundamental lines.

The parameters of the lines, taking into account the ortho– and para–D2O forms (within the CASSIS software2) separated from the Cologne Database for Molecular Spectroscopy (Müller et al. 2005; Brünken et al. 2007), are reported in Table 1. The fundamental ortho–D2O transition at 607.349 GHz is clearly detected in absorption against the strong continuum (~0.3 K). We present here the first tentative detection of the para–D2O 21,2–10,1 transition at 897.95 GHz, seemingly in absorption against the continuum (~0.75 K). In the same table, we also report the parameters of the para–D2O 11,0–10,1 fundamental line previously observed at 316.800 GHz with the JCMT by Butner et al. (2007). We used the line decomposition in three Gaussian components derived by Vastel et al. (2010): two of them are attributed to the broad emission component and the deep absorbing line of D2O, whereas an additional component emitted at 10.1 km s-1 is likely due to the 70–60+ CH3OD line at 316.795 GHz. This latter component was subtracted in Fig. 2. The 20,2–11,1 ortho transition at 468.25 GHz (see Fig. 1) has not been observed, and we consequently only provide a prediction with the modeling.

Observations were recently carried out with the Atacama Pathfinder EXperiment (APEX) telescope between 270 and 330 GHz to complete The IRAS16293-2422 Millimeter And Submillimeter Spectral Survey (TIMASSS; Caux et al. 2011). While the para–D2O fundamental 11,0–10,1 line at 317 GHz is also detected in this survey, it shows a much lower signal-to-noise ratio than the one observed with JCMT (Butner et al. 2007). This observation is nevertheless useful due to the accurate continuum at this frequency (0.235 K in 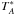). The beam efficiency is 0.73 and the forward efficiency 0.97.

thumbnail Fig. 1

Energy levels for the lowest rotational transitions of ortho– and para–D2O.

Table 2

HDO/H2O, D2O/HDO, and D2O/H2O abundance ratios estimated towards the protostar IRAS 16293.

thumbnail Fig. 2

In black: D2O transitions observed with HIFI and JCMT. The CH3OD (70–60+) transition at 316.795074 GHz contaminating the para−D2O (11,0 − 10,1) line profile has been subtracted for a direct comparison with the D2O best-fit model. In red: best-fit model obtained when adding an absorbing layer with N(para–D2O) = 1.1 × 1012 cm-2 and N(ortho–D2O) = 1.4 × 1012 cm-2. The resulting inner abundance is 7  ×  10-10 and the outer abundance is 5  ×  10-12.

3. Modeling

In order to determine the D2O/HDO and D2O/H2O ratios within the different components of this source (hot corino, colder envelope, and external absorption layer), we developed the same modeling as performed in Coutens et al. (2012) for the HDO and H218O species with the RATRAN radiative transfer code (Hogerheijde & van der Tak 2000). We employed the ortho– and para–D2O collisional coefficients calculated with ortho– and para–H2 by Faure et al. (2012) in the 5–100 K range. We assumed that the ortho-to-para D2O ratio is 2:1, compatible with the results from Vastel et al. (2010). Using the same parameters for the modeling (see details in Coutens et al. 2012), we realized that the continuum modeled at 317 GHz (0.38 K) is not consistent with the continuum observed by Butner et al. (2007) at 0.85 K. To determine whether this divergence comes from the modeling or from the observations, we used the recent APEX observations. The SSB continuum observed with APEX is 0.31 K (Tmb). Our modeling predicts a 0.29 K continuum value at the same frequency. From the comparison between transitions from overlapping frequency ranges, we can estimate the calibration to be 20%. The value estimated from the modeling is therefore consistent with the APEX continuum value, and in the following we will use the 0.38 K predicted by our modeling for the continuum of the 317 GHz transition observed with JCMT.

With the source structure (hot corino + colder envelope) derived by Crimier et al. (2010), the modeling is not able to reproduce any absorption feature for the D2O fundamental transitions. The overall absorption can only be reproduced by the external absorbing layer, which was discovered by Coutens et al. (2012) in their efforts to reproduce the absorption components seen on the HDO fundamental transitions. Assuming an H2 density of  ~103–104 cm-3, a kinetic temperature of  ~10–30 K and a b-Doppler parameter of 0.3 km s-1 (turbulence), the ortho–D2O (respectively para–D2O) column density in this layer is about 1.4  ×  1012 cm-2 (respectively 1.1  ×  1012 cm-2). Our modeling predicts that the 21,2–10,1 para–D2O transition is expected in absorption as well, tracing the external absorbing layer. The tentatively detected absorbing component at 898 GHz is consequently in perfect agreement with the modeling (see Fig. 2). The kinetic temperature (~10–30 K) has a limited influence on the absorbing transitions, but hydrogen density seems to have more influence. With a 105 cm-3 density, the absorption depth is less pronounced for the fundamental 11,0–10,1 and 11,1–00,0 transitions at 317 and 607 GHz, requiring a higher D2O column density. However, the higher energy para–D2O transition absorption is overestimated compared to the observations, suggesting a lower H2 density. From the above estimations, the D2O ortho-to-para ratio is, in the absorbing layer, about 1.3, close to the value determined by Vastel et al. (2010). However, taking into account the observation and modeling uncertainties, we cannot exclude that the measured value might be consistent with the 2:1 value at equilibrium. The quoted column densities are slightly higher (less than a factor 2) than those estimated by Vastel et al. (2010), but within their 3σ uncertainties. If this absorbing layer is produced by photodesorption at AV ~ 1–4 mag as predicted by Hollenbach et al. (2009), the D2O abundance in this layer should be about 6.6  ×  10-10–2.7 × 10-9, using the relation between the H2 column density and the visual extinction, N(H2)/AV = 9.4 × 1020 cm-2 mag-1 (Frerking et al. 1982).

To estimate the D2O abundances in the hot corino (Xin) and the outer envelope (Xout) of IRAS 16293, we ran a grid of models that take into account the structure of Crimier et al. (2010) as well as the foregound absorbing layer previously defined. The best-fit modeling is then obtained for an internal abundance Xin = 7 × 10-10 and an external abundance Xout = 5 × 10-12 from the χ2 minimization (see Fig. 3) computed on the line profiles according to the following formalism: 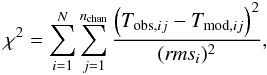(1)with N the number of lines i, nchan the number of channels j for each line, Tobs,ij and Tmod,ij the intensity observed and predicted by the RATRAN non-LTE modeling respectively in the channel j of the line i and rmsi the rms of the line i. Here, the reduced χ2 is equal to 2.5. At 2σ, the inner and outer abundances ranges are Xin =  [9 × 10-11–1.1 × 10-9] and Xout =  [8    ×    10-13 − 1.1 × 10-11]. Only upper limits can, however, be given at 3σ, with Xin ≤ 1.3 × 10-9 and Xout ≤ 1.3 × 10-11. The best-fit modeling is shown in Fig. 2.

To check the influence on the ortho-to-para ratio assumed for D2O in the protostellar envelope (i.e., the equilibrium value of 2:1), we ran another grid of models with an ortho-to-para D2O ratio equal to 1.3 in the envelope, i.e., the same as estimated in the absorbing layer. The results in both cases are quite in agreement and do not allow us to conclude with an ortho-to-para ratio different from the equilibrium value 2:1. In addition, we checked that the para–D2O emission line predicted at 317 GHz was consistent with the line observed with APEX. Regarding the 20,2–11,1 ortho transition at 468 GHz, we predict that the line only shows an emission component with an intensity about 0.1 K (Tmb) if observed with APEX.

thumbnail Fig. 3

χ2 contours at 1σ, 2σ, and 3σ obtained when adding an absorption layer with a para–D2O column density of 1.1  ×  1012 cm-2 and ortho–D2O column density of 1.4  ×  1012 cm-2. The best-fit model is represented by the symbol “+”.

4. Discussion

4.1. Ortho-to-para D2O ratio

At the thermal equilibrium, the ortho-to-para ratio of D2O is higher or equal to 2, depending on temperature (see Fig. 4 in Vastel et al. 2010). If the ortho-to-para D2O ratio estimated at  ~1.3 in the absorbing layer really deviates from the 2:1 value as already suggested by Vastel et al. (2010), this could mean that some nuclear spin exchanges occur in the gas phase or at the grain surface. Indeed, the ortho-to-para ratio should be initially set during the molecule formation at a value reflecting the grain temperature (≥ 2). Some spin exchange mechanisms would be consequently required to decrease the ortho-to-para ratio. These mechanisms are, however, poorly known. We can imagine some exchange mechanisms at the grain surface with interaction between electronic or nuclear spins. Unfortunately, the theoretical and laboratory measurements (Limbach et al. 2006; Pardanaud et al. 2007) are difficult to carry out. In the gas phase, no fast radiative transition is possible between ortho and para species, except via proton exchange with ions. For example, to modify the ortho-to-para ratio of water, collisions with H+ and H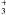 are required. For D2O, the following reaction could consequently occur via D exchange between D2O and H2D+: o-D2O + H2D+  ↔ p-D2O + H2D+. However, this reaction could also lead to other products for which the branching ratios are unknown: D2O + H2D+  ↔ HD2O+ + HD D2O + H2D+  ↔ D3O+ + H2. never been studied experimentally or theoretically, but could be exothermic like the H2O + H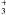 reaction (Woon & Herbst 2009). The nuclear spin conversion could also be possible thanks to an exchange with D+.

4.2. Water deuterium fractionation

As already noticed in Coutens et al. (2012), the HDO/H2O ratios determined in the hot corino and in the external absorbing layer are similar (~2–5%), although the corresponding densities are very different, a few 108 cm-3 in the hot corino region and, typical of a molecular cloud, probably 103–104 cm-3 in the external layer. Water shows a different behavior from other tracers as methanol (CH3OH) and formaldehyde (H2CO), whose deuteration increases with the density. Indeed, the deuteration of these heavier molecules that need CO ices to form is correlated with the CO depletion (linked to the molecular hydrogen density: Caselli et al. 1999; Bacmann et al. 2002) in prestellar cores (Bacmann et al. 2003, 2007). In contrast, the water fractionation ratio does not seem to vary with density. As discussed in Coutens et al. (2012), it is therefore possible that water was formed at low densities in the early stages of the star formation before the protostellar collapse.

thumbnail Fig. 4

Deuterium fractionation of water predicted by the grain surface chemical model (see text) assuming 3 initial dust temperatures Tdust = 12 K (dashed lines), 15 K (dotted lines) and 20 K (solid lines) and densities n = 103 (lower panel), 104 (middle panel) and 5 × 104 cm-3 (upper panel). The HDO/H2O and D2O/H2O ratios determined at 3σ in the hot corino are indicated in pink with a red line for the best-fit value. The ratios of the absorbing layer are shown with a blue line.

To understand how the deuterium fractionation of water depends on the initial conditions of the cloud in which ices are forming, we used in the present study a grain surface chemical model (Cazaux et al. 2011), in which we considered the formation of ices by accreting species from the gas phase. The icy mantles then grow until 99% of CO and O from the gas are depleted onto dust. We set the initial densities of O and CO in the gas similar to densities of O and CO in translucent clouds, i.e., n(O) ~ n(CO)  ~1.5  ×  10-4nH (Hollenbach et al. 2009). The gas phase species accrete on the dust and the chemical evolution of ices can be followed with time until most of O and CO are depleted from the gas phase (t ~ 1–5 × 105 years, depending on the density of the medium). During the formation of ices, O and CO gas phase abundances are decreasing while the abundances of gas phase H2, H and D are kept constant. The density of the cloud sets the gas phase D/H ratio through ion-molecule chemistry (deuteration of H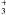 sets the gas D/H ratio, as described in Roberts et al. 2002). Therefore, a translucent cloud with an initial density of 103, 104, and 5  ×  104 cm-3 results in a D/H ratio in the gas phase of 5  ×  10-3, 5  ×  10-2, and 10-2 respectively (Cazaux et al. 2011). Consequently, we assume these three initial values for the density (103, 104, and 5  ×  104 cm-3) as well as three different temperatures (12, 15, and 20 K). The HDO/H2O as well as the D2O/H2O ratios obtained during the formation of ices are presented in Fig. 4. Both ratios are strongly sensitive to the dust temperature. Indeed, at low temperatures, H2 is much more abundant than H on the dust grains, and the successive hydrogenations of O with H2 dominate the formation of H2O. The reaction O(3P) + H2 is energetically not accessible at low temperatures since the reaction has a barrier of 0.57 eV and is endo-ergic with an energy of 0.1 eV for H2(v = 0) (Weck et al. 2006). However, this reaction becomes exo-ergic for v > 0 and the barrier decreases to  ~0.4 eV for v = 1 (Sultanov & Balakrishnan 2005). The reaction O(3P) + H2(v = 1) proceeds through tunneling at low temperatures, as shown by Weck et al. (2006). In our model, we consider only the reaction of H2 vibrationally excited with O(3P). For a population in equilibrium at a temperature Tdust, the fraction of molecules in the J = 1 state is  ~exp(−150/Tdust) ~ 3 × 10-6 − 5.5 × 10-4 in the range of Tdust considered in this study (12−20 K). The reaction through tunneling between H2(v = 1) and O(3P) dominates at very low temperatures when the dust is saturated with H2 molecules and the oxygen atoms present on the surface repetitively collide with H2. On the other hand, HDO forms through addition of atomic deuterium. These different formation routes imply that the HDO/H2O ratio scales with D/H2 ratio present in the gas, while the D2O/H2O scales with (D/H2)2. The reaction between O and H, however, dominates at 12 K at short timescale because of the relatively high initial H/H2 ratio (~10-4). However, the H/H2 ratio decreases with time, since H atoms are quickly converted into OH and H2, and the reaction O + H2 dominates (for t ~ 104 years at nH = 103 cm-3 and for t ~ 105 years at nH = 104 cm-3). If the grain is warm, the H2 molecules evaporate and the formation of H2O is insured by successive hydrogenation with H atoms. Since the formation of HDO involves atomic deuterium, the HDO/H2O ratio becomes comparable to the D/H ratio and the D2O/H2O ratio comparable to (D/H)2. Therefore, the variation of the deuterium fractionation with the initial dust temperature is due to the different routes to form water molecules. In their modeling, Cazaux et al. (2011) found that the deuterium fractionation of the water ice mantle is not altered by the cloud collapse, pointing to the fact that the deuterium fractionation of water must have been set during the formation of ices.

The HDO/H2O and D2O/H2O observed ratios suggest that the ices present in IRAS 16293 and desorbing in the hot corino were made in a warm (~15–20 K) and dense (~104−5    ×  104 cm-3) translucent cloud. Recently, Taquet et al. (2013) modeled the formation of deuterated water ice in cold conditions with a pseudo time-dependent multilayer approach (see Taquet et al. 2013, for a full description of the model). They showed that the relatively high deuterium fractionation of water could be attributed to the formation of water ices in dark phases (either at nH ~ 104 cm-3 at low temperatures,  ~10 K, and high visual extinction, larger than 4 mag, or for higher densities,  ~105 cm-3, at higher temperatures), where the D/H ratio starts to efficiently increase. Although the chemical models diverge on the deuteration processes which are enhanced for warm dust in one case (Cazaux et al. 2011) and for cold dust in the other case (Taquet et al. 2013), our results agree that the high deuterium fractionation originates from a dense medium (both models need dense medium for high D/H ratio).

In the extended absorbing layer, which is possibly due to photodesorption mechanisms, the observed D2O/H2O ratio appears much larger compared to the hot corino value, in contrast to the HDO/H2O ratio. It is also higher than all the chemical predictions. If the D2O/H2O ratio observed in the gas phase of this layer really reflects the D2O/H2O ratio at the grain surface, it would consequently suggest that water formed in a denser (≳5  ×  104 cm-3) region with warm (~20 K) gas. A high density (105–106 cm-3) is also required for the chemical modeling by Taquet et al. (2013). However, these results disagree with our observational constraints obtained from the density of this absorbing layer (<105 cm-3, see Sect. 3). Nevertheless, we cannot exclude that, in this external layer, water can also be formed by gas phase mechanisms through ion-molecule reactions. This could also be one of the possible explanations of the difference between the D2O/H2O ratios determined in the hot corino and in the absorbing layer. Other reasons can be mentioned to explain the discrepancy of the water deuterium fractionation between the hot corino and the absorbing layer. During the heating of the grain surfaces, an isotope exchange between water molecules may also occur at 150 K (Smith et al. 1997; Dulieu et al. 2010), leading to a decrease of the D2O abundance in the hot corino region. Also, in the hot corino, large columns of H2O, HDO, and D2O could self-shield these molecules. Since H2O is more abundant than its deuterated forms, it should self-shield first, reducing its photodissociation. Then if important columns of HDO and D2O can be reached, these molecules will be shielded. This implies a stratification of molecules and should favor the amount of water compared to its deuterated forms in environments where lots of water is present in the gas phase.

Recently, Persson et al. (2013) used interferometric (SMA and ALMA) observations of one HDO transition (226 GHz) and two H218O transitions (203 and 692 GHz) to determine the water deuterium fractionation in the hot corino of IRAS 16293. Water is only emitted by the core A and not by its binary component B. With their different method, Persson et al. (2013) derive a fractionation ratio about a factor of 10 lower than ours (Coutens et al. 2012). The origin of the divergence between these results is not clear, but could arise from the uncertain inner structure of the source. Indeed, a recent publication by Pineda et al. (2012) mentions that ALMA observations towards the source A would be consistent with the rotation of a disk, which is close to being edge-on. None of the two studies assume such a complex structure in their modeling, maybe implying the divergence between the estimated HDO/H2O ratios. Compared with the predictions of the chemical model by Cazaux et al. (2011), the ratio determined by Persson et al. (2013) would require a low initial dust temperature (around 12 K), in contrast to our results. But doubly deuterated water has never been detected with interferometers, making it not possible to check whether the D2O/H2O ratio is also in agreement with an origin on cold dust grains and provide more constraints on the initial density. Consequently, complementary D2O observations at high spatial resolution would be necessary to assess precisely the conditions in which ices are forming with a method based on interferometric data as in Persson et al. (2013).

5. Conclusions

Thanks to the numerous HDO and H218O transitions observed with the HIFI instrument on board the Herschel Observatory, we were able (Coutens et al. 2012) to constrain the abundances of these species from the hot corino throughout the envelope of the IRAS 16293 protostar to the external absorbing layer. In the present study, we have used the same non-LTE radiative transfer modeling to constrain the D2O abundances, employing the previous detections of the para and ortho fundamental transitions (Butner et al. 2007; Vastel et al. 2010) as well as the tentative detection of the higher energy para–D2O 21,2–10,1 transition at 898 GHz in Herschel/HIFI band 3b. To estimate the abundances, we used the full set of D2O collisional rate coefficients computed with ortho– and para–H2 (Faure et al. 2012), which were not available for the original detections. The results are presented in Table 2. The best-fit inner abundance Xin(D2O) is about 7  ×  10-10, whereas the best-fit outer abundance Xout(D2O) is about 5  ×  10-12. The absorbing D2O components cannot be reproduced without taking into account the external absorbing layer. The column density in this layer is about 2.5  ×  1012 cm-2, leading to an abundance ranging from 6.6  ×  10-10 to 2.7  ×  10-9 if the lines are produced in a photodesorption layer at AV ~ 1−4 mag. We then compared the HDO/H2O and D2O/H2O observed ratios with the predictions of a grain surface chemical model (Cazaux et al. 2011), in which we considered the formation of ices by accreting species from the gas phase. Our estimations of the HDO/H2O and D2O/H2O ratios suggest that the ices present in IRAS 16293 and desorbing in the hot corino were made in a warm (~15–20 K) and dense (104–5 × 104 cm-3) translucent cloud. The observed D2O/H2O ratio appears much larger in the absorbing layer than in the hot corino, and we explored tentative explanations.

2

Developed by IRAP-UPS/CNRS: http://cassis.irap.omp.eu

Acknowledgments

HIFI was designed and built by a consortium of institutes and university departments from across Europe, Canada, and the United States under the leadership of SRON Netherlands Institute for Space Research, Groningen, The Netherlands and with major contributions from Germany, France and the US. Consortium members are: Canada: CSA, U. Waterloo; France: IRAP (formerly CESR), LAB, LERMA, IRAM; Germany: KOSMA, MPIfR, MPS; Ireland, NUI Maynooth; Italy: ASI, IFSI-INAF, Osservatorio Astrofisico di Arcetri-INAF; Netherlands: SRON, TUD; Poland: CAMK, CBK; Spain: Observatorio Astronómico Nacional (IGN), Centro de Astrobiología (CSIC-INTA). Sweden: Chalmers University of Technology – MC2, RSS & GARD; Onsala Space Observatory; Swedish National Space Board, Stockholm University – Stockholm Observatory; Switzerland: ETH Zurich, FHNW; USA: Caltech, JPL, NHSC. We thank the CNES (Centre National d’Études Spatiales) for its financial support. V.W. thanks the French National Program PCMI for the partial funding of her research.

References

  1. Bacmann, A., Lefloch, B., Ceccarelli, C., et al. 2002, A&A, 389, L6 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  2. Bacmann, A., Lefloch, B., Ceccarelli, C., et al. 2003, ApJ, 585, L55 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  3. Bacmann, A., Lefloch, B., Parise, B., Ceccarelli, C., & Steinacker, J. 2007, in Molecules in Space and Laboratory [Google Scholar]
  4. Bacmann, A., Caux, E., Hily-Blant, P., et al. 2010, A&A, 521, L42 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  5. Bottinelli, S., Ceccarelli, C., Neri, R., et al. 2004, ApJ, 617, L69 [NASA ADS] [CrossRef] [Google Scholar]
  6. Brünken, S., Müller, H. S. P., Endres, C., et al. 2007, Phys. Chem. Chem. Phys., 9, 2103 [CrossRef] [PubMed] [Google Scholar]
  7. Butner, H. M., Charnley, S. B., Ceccarelli, C., et al. 2007, ApJ, 659, L137 [NASA ADS] [CrossRef] [Google Scholar]
  8. Caselli, P., Walmsley, C. M., Tafalla, M., Dore, L., & Myers, P. C. 1999, ApJ, 523, L165 [NASA ADS] [CrossRef] [Google Scholar]
  9. Caux, E., Kahane, C., Castets, A., et al. 2011, A&A, 532, A23 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  10. Cazaux, S., Caselli, P., & Spaans, M. 2011, ApJ, 741, L34 [NASA ADS] [CrossRef] [Google Scholar]
  11. Ceccarelli, C., Castets, A., Caux, E., et al. 2000, A&A, 355, 1129 [NASA ADS] [Google Scholar]
  12. Ceccarelli, C., Bacmann, A., Boogert, A., et al. 2010, A&A, 521, L22 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  13. Coutens, A., Vastel, C., Caux, E., et al. 2012, A&A, 539, A132 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  14. Crimier, N., Ceccarelli, C., Maret, S., et al. 2010, A&A, 519, A65 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  15. Daniel, F., Dubernet, M.-L., & Grosjean, A. 2011, A&A, 536, A76 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  16. de Graauw, T., Helmich, F. P., Phillips, T. G., et al. 2010, A&A, 518, L6 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  17. Dulieu, F., Amiaud, L., Congiu, E., et al. 2010, A&A, 512, A30 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  18. Faure, A., Wiesenfeld, L., Scribano, Y., & Ceccarelli, C. 2012, MNRAS, 420, 699 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
  19. Fraser, H. J., Collings, M. P., McCoustra, M. R. S., & Williams, D. A. 2001, MNRAS, 327, 1165 [NASA ADS] [CrossRef] [Google Scholar]
  20. Frerking, M. A., Langer, W. D., & Wilson, R. W. 1982, ApJ, 262, 590 [NASA ADS] [CrossRef] [Google Scholar]
  21. Hily-Blant, P., Maret, S., Bacmann, A., et al. 2010, A&A, 521, L52 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  22. Hogerheijde, M. R., & van der Tak, F. F. S. 2000, A&A, 362, 697 [NASA ADS] [Google Scholar]
  23. Hollenbach, D., Kaufman, M. J., Bergin, E. A., & Melnick, G. J. 2009, ApJ, 690, 1497 [CrossRef] [Google Scholar]
  24. Limbach, H.-H., Buntkowsky, G., Matthes, J., et al. 2006, Chem. Phys. Chem., 7, 551 [CrossRef] [PubMed] [Google Scholar]
  25. Linsky, J. L., Draine, B. T., Moos, H. W., et al. 2006, ApJ, 647, 1106 [NASA ADS] [CrossRef] [Google Scholar]
  26. Müller, H. S. P., Schlöder, F., Stutzki, J., & Winnewisser, G. 2005, J. Mol. Struct., 742, 215 [NASA ADS] [CrossRef] [Google Scholar]
  27. Ott, S. 2010, in Astronomical Data Analysis Software and Systems XIX, eds. Y. Mizumoto, K.-I. Morita, & M. Ohishi, ASP Conf. Ser., 434, 139 [Google Scholar]
  28. Pardanaud, C., Michaut, X., Fillion, J.-H., Vasserot, A.-M., & Abouaf-Marguin, L. 2007, in Molecules in Space and Laboratory [Google Scholar]
  29. Parise, B., Du, F., Liu, F.-C., et al. 2012, A&A, 542, L5 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  30. Persson, M. V., Jørgensen, J. K., & van Dishoeck, E. F. 2013, A&A, 549, L3 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  31. Pilbratt, G. L., Riedinger, J. R., Passvogel, T., et al. 2010, A&A, 518, L1 [CrossRef] [EDP Sciences] [Google Scholar]
  32. Pineda, J. E., Maury, A. J., Fuller, G. A., et al. 2012, A&A, 544, L7 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  33. Roberts, H., Herbst, E., & Millar, T. J. 2002, MNRAS, 336, 283 [NASA ADS] [CrossRef] [Google Scholar]
  34. Roelfsema, P. R., Helmich, F. P., Teyssier, D., et al. 2012, A&A, 537, A17 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  35. Scribano, Y., Faure, A., & Wiesenfeld, L. 2010, J. Chem. Phys., 133, 1105 [Google Scholar]
  36. Smith, S. R., Huang, C., & Kay, B. D. 1997, J. Phys. Chem. B, 101, 6123 [CrossRef] [Google Scholar]
  37. Sultanov, R. A., & Balakrishnan, N. 2005, ApJ, 629, 305 [NASA ADS] [CrossRef] [Google Scholar]
  38. Taquet, V., Peters, P. S., Kahane, C., et al. 2013, A&A, 550, A127 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  39. Vastel, C., Ceccarelli, C., Caux, E., et al. 2010, A&A, 521, L31 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  40. Weck, P. F., Balakrishnan, N., Brandão, J., Rosa, C., & Wang, W. 2006, J. Chem. Phys., 124, 4308 [Google Scholar]
  41. Woon, D. E., & Herbst, E. 2009, ApJS, 185, 273 [NASA ADS] [CrossRef] [Google Scholar]

All Tables

Table 1

Derived parameters of the absorbing components of the ortho– and para–D2O fundamental lines.

In the text
Table 2

HDO/H2O, D2O/HDO, and D2O/H2O abundance ratios estimated towards the protostar IRAS 16293.

In the text

All Figures

thumbnail Fig. 1

Energy levels for the lowest rotational transitions of ortho– and para–D2O.
In the text
thumbnail Fig. 2

In black: D2O transitions observed with HIFI and JCMT. The CH3OD (70–60+) transition at 316.795074 GHz contaminating the para−D2O (11,0 − 10,1) line profile has been subtracted for a direct comparison with the D2O best-fit model. In red: best-fit model obtained when adding an absorbing layer with N(para–D2O) = 1.1 × 1012 cm-2 and N(ortho–D2O) = 1.4 × 1012 cm-2. The resulting inner abundance is 7  ×  10-10 and the outer abundance is 5  ×  10-12.

In the text
thumbnail Fig. 3

χ2 contours at 1σ, 2σ, and 3σ obtained when adding an absorption layer with a para–D2O column density of 1.1  ×  1012 cm-2 and ortho–D2O column density of 1.4  ×  1012 cm-2. The best-fit model is represented by the symbol “+”.
In the text
thumbnail Fig. 4

Deuterium fractionation of water predicted by the grain surface chemical model (see text) assuming 3 initial dust temperatures Tdust = 12 K (dashed lines), 15 K (dotted lines) and 20 K (solid lines) and densities n = 103 (lower panel), 104 (middle panel) and 5 × 104 cm-3 (upper panel). The HDO/H2O and D2O/H2O ratios determined at 3σ in the hot corino are indicated in pink with a red line for the best-fit value. The ratios of the absorbing layer are shown with a blue line.
In the text

Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.

Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.

Initial download of the metrics may take a while.