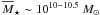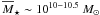| Issue |
A&A
Volume 553, May 2013
|
|
|---|---|---|
| Article Number | A78 | |
| Number of page(s) | 24 | |
| Section | Extragalactic astronomy | |
| DOI | https://doi.org/10.1051/0004-6361/201220286 | |
| Published online | 07 May 2013 | |
MASSIV: Mass Assembly Survey with SINFONI in VVDS⋆,⋆⋆
V. The major merger rate of star-forming galaxies at 0.9 < z < 1.8 from IFS-based close pairs
1
Aix-Marseille Université, CNRS, LAM (Laboratoire d’Astrophysique de
Marseille) UMR 7326,
13388
Marseille,
France
2
Centro de Estudios de Física del Cosmos de Aragón, Plaza San Juan
1, planta 2, 44001
Teruel,
Spain
e-mail: clsj@cefca.es
3
Institut de Recherche en Astrophysique et Planétologie (IRAP),
CNRS, 14 avenue Édouard
Belin, 31400
Toulouse,
France
4
IRAP, Université de Toulouse, UPS-OMP, Toulouse, France
5
IASF – INAF, via Bassini 15, 20133
Milano,
Italy
6
ESO, Karl-Schwarzschild-Str.2, 85748
Garching b. München,
Germany
7
INAF – IASFBO, via P. Gobetti 101, 40129
Bologna,
Italy
Received:
24
August
2012
Accepted:
10
March
2013
Context. The contribution of the merging process to the early phase of galaxy assembly at z > 1 and, in particular, to the build-up of the red sequence, still needs to be accurately assessed.
Aims. We aim to measure the major merger rate of star-forming galaxies at 0.9 < z < 1.8, using close pairs identified from integral field spectroscopy (IFS).
Methods. We use the velocity field maps obtained with SINFONI/VLT on the MASSIV sample, selected from the star-forming population in the VVDS. We identify physical pairs of galaxies from the measurement of the relative velocity and the projected separation (rp) of the galaxies in the pair. Using the well constrained selection function of the MASSIV sample, we derive at a mean redshift up to z = 1.54 the gas-rich major merger fraction (luminosity ratio μ = L2/L1 ≥ 1/4), and the gas-rich major merger rate using merger time scales from cosmological simulations.
Results. We find a high gas-rich major merger fraction of
20.8+15.2-6.8%,
20.1+8.0-5.1%,
and 22.0+13.7-7.3%
for close pairs with
rp ≤ 20 h-1 kpc in redshift
ranges
z = [0.94,1.06] , [1.2,1.5),
and [1.5,1.8), respectively. This translates into a gas-rich major
merger rate of 0.116+0.084-0.038 Gyr-1,
0.147+0.058-0.037 Gyr-1,
and 0.127+0.079-0.042 Gyr-1
at z = 1.03,1.32, and 1.54, respectively. Combining our
results with previous studies at z < 1, the
gas-rich major merger rate evolves as
(1 + z)n, with
n = 3.95 ± 0.12, up to z = 1.5. From these results we
infer that ~35% of the star-forming galaxies with stellar masses
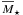 =
1010 - 1010.5 M⊙ have undergone a
major merger since z ~ 1.5. We develop a simple model that shows that,
assuming that all gas-rich major mergers lead to early-type galaxies, the combined effect
of gas-rich and dry mergers is able to explain most of the evolution in the number density
of massive early-type galaxies since z ~ 1.5, with our measured gas-rich
merger rate accounting for about two-thirds of this evolution.
=
1010 - 1010.5 M⊙ have undergone a
major merger since z ~ 1.5. We develop a simple model that shows that,
assuming that all gas-rich major mergers lead to early-type galaxies, the combined effect
of gas-rich and dry mergers is able to explain most of the evolution in the number density
of massive early-type galaxies since z ~ 1.5, with our measured gas-rich
merger rate accounting for about two-thirds of this evolution.
Conclusions. Merging of star-forming galaxies is frequent at around the peak in star formation activity. Our results show that gas-rich mergers make an important contribution to the growth of massive galaxies since z ~ 1.5, particularly on the build-up of the red sequence.
Key words: galaxies: evolution / galaxies: interactions / galaxies: formation
This work is based mainly on observations collected at the European Southern Observatory (ESO) Very Large Telescope (VLT), Paranal, Chile, as part of the Programs 179.A-0823, 177.A-0837, 78.A-0177, 75.A-0318, and 70.A-9007. This work also benefits from data products produced at TERAPIX and the Canadian Astronomy Data Centre as part of the Canada-France-Hawaii Telescope Legacy Survey, a collaborative project of NRC and CNRS.
Appendices are available in electronic form at http://www.aanda.org
© ESO, 2013
1. Introduction
Understanding the mechanisms involved in the mass assembly of galaxies and their relative role over cosmic time is an important open topic in modern astrophysics. In particular, the evolution of the red sequence, which includes passive galaxies dominated by old stellar populations and an early-type (E/S0) morphology, imposes fundamental constraints on the formation and evolution models.
The stellar mass density in the red sequence has increased by a factor of ~10 in the 2.5 Gyr between z = 2 and z = 1, but only by a factor of ~2 in the last 7–8 Gyr of cosmic history (e.g., Arnouts et al. 2007; Vergani et al. 2008; Ilbert et al. 2010). Major mergers, the merger of two galaxies with similar stellar masses, is an efficient mechanism for creating new passive, early-type galaxies (e.g., Naab et al. 2006; Rothberg & Joseph 2006a,b; Hopkins et al. 2008; Rothberg & Fischer 2010; Bournaud et al. 2011). Thus, the knowledge of the merger rate at z > 1 is important input when estimating the relative contribution of merging and cold-gas accretion (e.g., Dekel & Birnboim 2006) in the early assembly of galaxies and, in particular, the role of merging in the build-up of the red sequence.
The evolution of the merger rate since z ~ 1 is now well constrained by direct observations. The early measurements using photometric pairs (Patton et al. 1997; Le Fèvre et al. 2000) or post-merger morphological signatures (Conselice 2003; Jogee et al. 2009) have been superseded by spectroscopic measurements confirming physical pairs from the redshift measurement of both components of a major merger with a luminosity/mass ratio μ ≥ 1/4 (e.g., Lin et al. 2008; de Ravel et al. 2009, 2011), as well as for minor mergers down to μ = 1/10 (López-Sanjuan et al. 2011). With a parametrization of the merger rate’s evolution following ∝ (1 + z)n, it is observed that the major merger rate’s evolution depends on the luminosity and on the mass of the galaxy sample (e.g., de Ravel et al. 2009), where massive galaxies with M⋆ > 1011 M⊙ have a higher merger rate, but with little redshift evolution (n ~ 0–2), while lower mass galaxies with M⋆ = 109−1011 M⊙ have a lower merging rate but with stronger redshift evolution (n ~ 3–4). This mass dependency seems to explain some of the apparent discrepancy of merger rate measurements made from observations targeting different mass samples.
Beyond z ~ 1, direct measurements of the merger rate are still limited. Previous attempts to measure the major merger rate at z > 1 have focused on the identification of merger remnants from morphological signatures (Conselice et al. 2008, 2011b; Bluck et al. 2012), on the study of projected close pairs (Ryan et al. 2008; Bluck et al. 2009; Williams et al. 2011; Man et al. 2012; Mármol-Queraltó et al. 2012; Law et al. 2012), or on indirect estimations (Cameron & Pettitt 2012; Puech et al. 2012). These studies find a high merger rate to z ~ 2–3 but with a large scatter between different measurements. However, these results are up to now solely based on photometric measurements which are increasingly hard to correct for contamination along the line of sight as redshift increases. Another complication stems from the morphological evolution of galaxies, with show more irregular morphologies at high redshifts, and a wavelength dependency with more multi-component objects present when observed in the rest-frame UV (Law et al. 2007), with some of these components possibly related to strong star-forming regions rather than to different dynamical components.
To improve on this situation, it is necessary to obtain spectroscopic confirmation of the physical nature of the photometric pairs at z ≳ 1. In the last years, NIR integral field spectrographs (IFSs), like SINFONI on the VLT or OSIRIS on the Keck, have opened the possibility for a systematic study of the dynamical field around high redshift galaxies in the optical rest-frame. Some examples are the MASSIV1 (Mass Assembly Survey with SINFONI in VVDS, Contini et al. 2012) survey at 0.9 < z < 1.8, the SINS2 (Spectroscopic Imaging survey in the Near-infrared with SINFONI, Förster Schreiber et al. 2009) survey at z ~ 2, or the Keck-OSIRIS (Law et al. 2009), the AMAZE (Assessing the Mass-Abundance redshift –Z– Evolution, Maiolino et al. 2008) and the LSD (Lyman-break galaxies Stellar populations and Dynamics, Mannucci et al. 2009) surveys at z ~ 3.
The MASSIV survey has been designed to target the peak of the star-formation rate at 0.9 < z < 1.8, filling the gap between higher redshift (z ~ 2) IFS surveys with those at z < 1, e.g., IMAGES (Intermediate MAss Galaxy Evolution Sequence, Yang et al. 2008). The MASSIV survey has targeted 84 star-forming galaxies at 0.9 < z < 1.8 with SINFONI, drawn from the VVDS3 (VIMOS VLT Deep Survey, Le Fèvre et al. 2005) survey. MASSIV has been used as a unique opportunity to study in detail the dynamical state of 0.9 < z < 1.8 galaxies (Epinat et al. 2012), their metallicity gradients (Queyrel et al. 2012), or the evolution of the fundamental mass-size-velocity relations since z ~ 1.2 (Vergani et al. 2012).
In this paper, using the MASSIV survey, we present for the fist time a measurement of the gas-rich major merger rate of star-forming galaxies from kinematical close pairs at 0.9 < z < 1.8. Thanks to the large field-of-view of IFS we have access to the complete surrounding volume of the galaxies when searching for close kinematical companions. In addition, the well-defined selection of sources from the VVDS and the well controlled selection function of MASSIV observations ensures the study of a representative population of star-forming galaxies at these redshifts (see Contini et al. 2012, for details). This all together enables the measurement of average volume quantities like the merger fraction and rate.
The paper is organised as follows: in Sect. 2 we summarise the MASSIV data set used to identify merging pairs, and in Sect. 3 we develop the methodology to measure the merger fraction from IFS data. We report the gas-rich major merger fraction in MASSIV in Sect. 4, and derive the gas-rich major merger rate in Sect. 5. We discuss the implication of our results in Sect. 6. Finally, we present our conclusions in Sect. 7. We use H0 = 100h km s-1 Mpc-1, h = 0.7, Ωm = 0.3, and ΩΛ = 0.7 throughout this paper. All magnitudes refer to the AB system. The stellar masses assume a Salpeter (1955) initial mass function (IMF).
2. The MASSIV data set
The galaxy sample studied in this paper is the final release of the MASSIV project (ESO Large Programme 179.A-0823; PI.: T. Contini). A full description of the sample can be found in Contini et al. (2012). We briefly summarise some properties of this sample of 84 galaxies below. The galaxies were selected from the VVDS in the RA = 2 h area of the deep (IAB ≤ 24; Le Fèvre et al. 2005) and ultradeep (IAB ≤ 24.75; Le Fèvre et al., in prep.) surveys, and in the RA = 14 h and RA = 22 h areas of the wide survey (IAB ≤ 22.5; Garilli et al. 2008).
The MASSIV sources are a subsample of the VVDS star-forming population at z > 0.9. The star-forming selection was performed on the measured intensity of [O ii]λ3727 emission line in the VIMOS spectrum (see Lamareille et al. 2009; Vergani et al. 2008) or, for the cases where the [O ii]λ3727 emission line was out of the VIMOS spectral range (i.e., for z ≳ 1.5 galaxies), on the UV flux based on their observed photometric UBVRIK spectral energy distribution and/or UV rest-frame spectrum. The star formation criteria ensure that rest-frame optical emission lines Hα and [N ii]λ6584, or in a few cases [O iii]λ5007, will be bright enough to be observed with SINFONI in the near-infrared (NIR) J (sources at z < 1.1) and H (sources at z > 1.1) bands. In addition, to ensure that the Hα emission line will be detected with SINFONI with a sufficient signal-to-noise (S/N) ratio in a reasonable exposure time, an additional selection in the [O ii]λ3727 equivalent width of 0.9 < z < 1.5 sources is imposed. The final selection of parent VVDS star-forming galaxies in the [O ii]λ3727 flux vs. equivalent width plane at 0.9 < z < 1.5 is shown in Fig. 1.
The 84 MASSIV sources were randomly selected from the star-forming population in the VVDS and also fulfil two important observational constraints, (i) the observed wavelength of Hα line falls 9 Å away from strong OH night-sky lines, in order to avoid heavy contamination of the galaxy spectrum by sky-subtraction residuals. And (ii) a bright star (R < 18 mag) is close enough to the target to observe it at higher spatial resolution with the adaptive optics (AO) system of SINFONI.
The most stringent selection criterion used to build the MASSIV sample is certainly the requirement of a minimum [O ii]λ3727 equivalent width. This sensitivity limit is likely to translate into an overall bias towards younger and more actively star-forming systems. To check for this possible effect, Contini et al. (2012) compare the properties of the MASSIV sample with those of the global VVDS sample, which is purely apparent magnitude-selected without any colour selection and thus representative of the overall star-forming population of galaxies at high redshifts. They conclude that the final MASSIV sample provides a good representation of “normal” star-forming galaxies at 0.9 < z < 1.8 in the stellar mass regime M⋆ = 109−1011 M⊙, with a median star formation rate SFR ~ 30 M⊙ yr-1 and a detection limit of ~ 5 M⊙ yr-1.
The observations have been performed between April 2007 and January 2011. Most (85%) of the galaxies in the sample have been observed in a seeing-limited mode (with a spatial sampling of 0.125 arcsec/pixel). However, eleven galaxies have been acquired with AO assisted with a laser guide star (AO/LGS, seven with 0.05 and four with 0.125 arcsec/pixel spatial sampling). The data reduction was performed with the ESO SINFONI pipeline (version 2.0.0), using the standard master calibration files provided by ESO. The absolute astrometry for the SINFONI data cubes was derived from nearby bright stars also used for point spread function (PSF) measurements. Custom IDL and Python scripts have been used to flux calibrate, align, and combine all the individual exposures. For each galaxy a non sky-subtracted cube was also created, mainly to estimate the effective spectral resolution. For more details on data reduction, we refer to Epinat et al. (2012).
We use the Hα emission line (or [O iii]λ5007 in a few cases) in the SINFONI data cubes to derive the kinematical maps (flux, velocity field and velocity dispersion map) of the MASSIV galaxies. To estimate their dynamical properties, we assume that the ionised gas rotates in a thin disc with two regimes for the rotation velocity, a solid body shape in the innermost regions and a plateau in the outskirts. Using a χ2 minimization we produce seeing-corrected velocity and dispersion maps of galaxies with geometrical inputs weighted for the S/N ratio of each pixel. We estimate the geometrical parameters used in the fitting model on the i-band best-seeing CFHTLS Megacam images for all galaxies (Goranova et al. 2009), except for VVDS-Wide 14 h galaxies that were covered with the CFHT-12K/CFHT camera (Le Fèvre et al. 2004). We use the GALFIT software (Peng et al. 2002) that convolves a PSF with a model galaxy image based on the initial parameter estimates fitting a Sérsic (1968) profile. Residual maps from the fitting were used to optimise the results. At the end of the fitting procedure, GALFIT converges into a final set of parameters such as the centre, the position angle, and the axial ratio. The i-band images were also used to correct for SINFONI astrometry, using the relative position of the PSF star. The morphology and kinematics maps of the 50 first-epoch galaxies are presented in Epinat et al. (2012) together with a more extensive discussion on the model fitting procedure. The 34 second-epoch galaxies, already included in the present work, will be presented in a future paper.
 |
Fig. 1 MASSIV selection in the [O ii]λ3727 flux [10-17 erg s-1 cm-2] vs. equivalent width [Å] plane (see Contini et al. 2012, for details). Red squares are the VVDS sources at 0.94 < z < 1.5 with individual [O ii]λ3727 line measurement in the VVDS-Wide 14 h (top-left), VVDS-Wide 22 h (top-right), VVDS-Deep (bottom-left), and VVDS-Ultradeep surveys (bottom-right). The dashed lines mark the selection of MASSIV star-forming galaxies. White dots are those VVDS sources that fulfil the MASSIV selection. Green pentagons are the MASSIV galaxies observed with SINFONI/VLT. (A colour version of this plot is available at the electronic edition.) |
We obtain the stellar mass of MASSIV galaxies from a spectral energy distribution (SED) fit to the photometric and spectroscopic data with Bruzual & Charlot (2003) stellar population synthesis models using the GOSSIP2 Spectral Energy Distribution tool (Franzetti et al. 2008). We assume a Salpeter (1955) IMF, and a set of delayed exponential star formation histories with galaxy ages in the range from 0.1 to 15 Gyr. As input for the SED fitting, in addition to the VVDS spectra, we use the multi-band photometric observations available in the VVDS fields (see Contini et al. 2012, for further details). Following Walcher et al. (2008) we adopt the probability distribution function to obtain the stellar mass.
In all, the final 84 MASSIV galaxies are representative of the normal star-forming (SFR ≳ 5M⊙ yr-1) population of M⋆ = 109−1011 M⊙ galaxies at 0.9 < z < 1.8.
3. Measuring the merger fraction from IFS data
We define as a close pair two galaxies with a projected separation in the sky plane
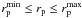 and a rest-frame
relative velocity along the line of sight
Δv ≤ Δvmax. We used
Δvmax = 500 km s-1 and
and a rest-frame
relative velocity along the line of sight
Δv ≤ Δvmax. We used
Δvmax = 500 km s-1 and
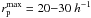 kpc
(see Sect. 3.3, for details), while setting
kpc
(see Sect. 3.3, for details), while setting
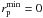 . We therefore searched for close
companions in the kinematical maps of the MASSIV sources, analysing and classifying the
sample using the velocity field and the velocity dispersion map (see Epinat et al. 2012, for details about the classification). Note that
spectroscopic redshifts from the VVDS sources outside MASSIV are not used in this close pair
search and only those sources detected in the SINFONI data cubes are taken into account. We
find 20 close pair candidates in the MASSIV data cubes, and we study these systems in detail
to select major (luminosity difference between both components
μ = L2/L1 ≥ 1/4)
close pairs (Sect. 4).
. We therefore searched for close
companions in the kinematical maps of the MASSIV sources, analysing and classifying the
sample using the velocity field and the velocity dispersion map (see Epinat et al. 2012, for details about the classification). Note that
spectroscopic redshifts from the VVDS sources outside MASSIV are not used in this close pair
search and only those sources detected in the SINFONI data cubes are taken into account. We
find 20 close pair candidates in the MASSIV data cubes, and we study these systems in detail
to select major (luminosity difference between both components
μ = L2/L1 ≥ 1/4)
close pairs (Sect. 4).
If there was Np major close pairs in our sample, the major
merger fraction is 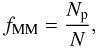 (1)where N is
the number of principal galaxies targeted for the survey. We named principal galaxy the
source in the pair closest to the kinematical centre of the targeted system, even if it is
not the brightest/more massive galaxy in the pair. In addition, we assume that all our close
pairs are gas-rich: as shown by Vergani et al.
(2012), the gas fraction of the MASSIV sources is above 10%, with a median value of
~30%. The simple definition in Eq. (1) is
only valid for volume-limited samples. While our sample is not only luminosity-limited but
spectroscopically defined, we must take into account the different selection effects, both
in the VVDS parent samples and in MASSIV, in our computation of the merger fraction.
(1)where N is
the number of principal galaxies targeted for the survey. We named principal galaxy the
source in the pair closest to the kinematical centre of the targeted system, even if it is
not the brightest/more massive galaxy in the pair. In addition, we assume that all our close
pairs are gas-rich: as shown by Vergani et al.
(2012), the gas fraction of the MASSIV sources is above 10%, with a median value of
~30%. The simple definition in Eq. (1) is
only valid for volume-limited samples. While our sample is not only luminosity-limited but
spectroscopically defined, we must take into account the different selection effects, both
in the VVDS parent samples and in MASSIV, in our computation of the merger fraction.
3.1. Accounting for selection effects in the VVDS
Since a fraction of the total number of potential targets in the VVDS fields have been
spectroscopically observed and since the redshifts are not measured with 100% accuracy, we
must correct for the VVDS target sampling rate (TSR) and the spectroscopic sucess rate
(SSR), computed as a function of redshift and source magnitude. The SSR has been assumed
independent of galaxy type, as demonstrated up to z ~ 1 in Zucca et al. (2006). Every VVDS source has a redshift
confidence flag (see Le Fèvre et al. 2005, for
details), that can be flag = 4 (redshift 99% secure), flag = 3 (97% secure), flag = 2 (87%
secure), flag = 9 (redshift from a single emission line, 90% secure), flag = 1 (50%
secure), or flag = 0 (no redshift information). As several VVDS-Deep galaxies with flag =
2 have been re-observed in the VVDS-Ultradeep survey, providing a robust measurement of
their redshift, this offers the opportunity to estimate the reliability of VVDS-Deep
flag = 2 sources. We thus define a weight w29 to take this
into account. We also define the weight w29 for flag = 9
sources by comparison with the latest photometric redshifts in the VVDS-Deep field (see
Cucciati et al. 2010, for details about the
latest photometric data set in the 2 h field). By definition, the
w29 weight is equal to 1 for flag = 3 and 4 sources in
VVDS-Deep, and for all sources in VVDS-Wide and VVDS-Ultradeep. We derived the
spectroscopic completeness weight for each galaxy i in the VVDS catalogue
as 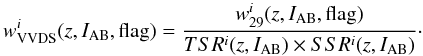 (2)The TSR, SSR and
w29 on VVDS-Deep and VVDS-Ultradeep were measured in
previous works (Ilbert et al. 2006; Cucciati et al. 2012). We assume
TSR = 0.22 in VVDS-Wide fields (Garilli
et al. 2008), and we detail the computation of the SSR in VVDS-Wide fields in
Appendix A.
(2)The TSR, SSR and
w29 on VVDS-Deep and VVDS-Ultradeep were measured in
previous works (Ilbert et al. 2006; Cucciati et al. 2012). We assume
TSR = 0.22 in VVDS-Wide fields (Garilli
et al. 2008), and we detail the computation of the SSR in VVDS-Wide fields in
Appendix A.
3.2. Accounting for selection effects in the MASSIV survey
The MASSIV sources were randomly drawn from the star-forming population in the VVDS (Sect. 2). We correct for three basic selection effects in MASSIV.
-
The selection weight, wsel. We define this weight as the fraction of star-forming galaxies that fulfil the MASSIV selection in the [O ii]λ3727 flux [10-17 erg s-1 cm-2] vs. equivalent width [Å] plane at z < 1.5 (Fig. 1). The weight wsel tells us how representative the MASSIV selection of the global star-forming population in each of the VVDS surveys (Wide, Deep and Ultradeep) is, and gives more importance to the more representative samples. The VVDS-Deep and Ultradeep have wsel ~ 0.67 at z < 1.5, while the VVDS-Wide fields have wsel ~ 0.53 in the same redshift range. We assume wsel = 1 at z ≥ 1.5, where the selection is based on colour/spectral properties and all the star-forming galaxies in the VVDS are thus pre-selected;
-
the MASSIV IFS rate (MIR) is defined as the fraction of galaxies that fulfil the MASSIV selection and which were finally observed with SINFONI (Fig. 1). The MIR ranges from 0.43 for VVDS-Ultradeep to 0.05 for VVDS-Deep;
-
the MASSIV success rate (MSR) is the fraction of observed sources with a reliable kinematical classification. This fraction is always high, MSR ≳ 0.8.
Finally, the MASSIV weight is 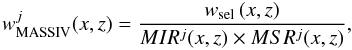 (3)where the index
j spans for the MASSIV sources and x refers to the
VVDS survey (Wide at 14 h, Wide at 22 h, Deep or Ultradeep) to which the source belongs.
(3)where the index
j spans for the MASSIV sources and x refers to the
VVDS survey (Wide at 14 h, Wide at 22 h, Deep or Ultradeep) to which the source belongs.
 |
Fig. 2 Typical field-of-view of a MASSIV source. We show the flux of the source 220397579 in the five channels of its reduced, flux calibrated, data cube centred on the position of the Hα emission line (scale in the right). The pixel spatial scale is 0.125″, that at the redshift of the source (z = 1.0379) corresponds to ~1 kpc. The source is at the centre of the image (black cross), while the white circle delimits the 20 h-1 kpc area around the source. In this particular case, 99% of this area is covered with MASSIV data and the two negatives of the source (black regions) are also excluded. |
3.3. Area correction
Thanks to the large field-of-view of SINFONI, we have access to the complete surrounding
volume of the principal galaxy when searching for close companions. This is a major
advantage with respect to long-slit spectroscopic surveys, in which the observed number of
close pairs is proportional to TSR2,
diminishing the statistics. However, the final reduced MASSIV data cubes cover a finite
area in the sky plane. To deal with this, we define the area weight as
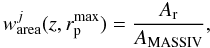 (4)where
Ar is the area subtended in the sky plane by a circle of
radius
(4)where
Ar is the area subtended in the sky plane by a circle of
radius 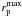 at the redshift
of the source j, and AMASSIV is the area of
the same circle covered by the reduced SINFONI mosaic (Fig. 2). We state that the optimum search radius is
at the redshift
of the source j, and AMASSIV is the area of
the same circle covered by the reduced SINFONI mosaic (Fig. 2). We state that the optimum search radius is
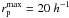 kpc.
This choice of
kpc.
This choice of 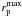 minimises the
area correction, with warea ~ 1 in all cases. In addition, the
two negatives of the main source produced by the offset observing procedure and that
appear in the extremes of the reduced SINFONI mosaic are then excluded from the search
area.
minimises the
area correction, with warea ~ 1 in all cases. In addition, the
two negatives of the main source produced by the offset observing procedure and that
appear in the extremes of the reduced SINFONI mosaic are then excluded from the search
area.
Finally, the corrected gas-rich major merger fraction is
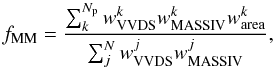 (5)where the index
j and k spans respectively for all MASSIV galaxies and
for the MASSIV galaxies with a major close companion. The error budget in the major merger
fraction is dominated by the low statistics. We use the Bayesian approach from Cameron (2011) to measure the statistical error in the
raw major merger fraction, i.e., in
Np/N, then scale it with
the weighting scheme above.
(5)where the index
j and k spans respectively for all MASSIV galaxies and
for the MASSIV galaxies with a major close companion. The error budget in the major merger
fraction is dominated by the low statistics. We use the Bayesian approach from Cameron (2011) to measure the statistical error in the
raw major merger fraction, i.e., in
Np/N, then scale it with
the weighting scheme above.
Close pair candidates at 0.9 < z < 1.8 in the MASSIV sample.
4. Mergers classification and the gas-rich major merger fraction in MASSIV
In this section we measure, for the first time, the major merger fraction at 0.9 < z < 1.8 from spectroscopically-confirmed close pairs. The MASSIV observational strategy defines three natural redshift bins (Sect. 2). The low redshift MASSIV sources were observed in the J band, while the higher redshift ones in the H band. This translates to a gap in the redshift distribution at z ~ 1.1. In addition, the selection function of MASSIV targets changes at z = 1.5, providing another redshift boundary. We take advantage of these natural separations in the data to estimate the gas-rich major merger fraction in three redshift ranges, zr,1 = [0.94,1.06] , zr,2 = [1.2,1.5), and zr,3 = [1.5,1.8). We restrict our study to those galaxies with IAB ≤ 23.9 to ensure completeness in the detection of close pairs (see Appendix C, for details).
We follow the steps described bellow to split the close pairs candidates in the MASSIV data cubes into major and no major mergers:
-
1.
As described in Epinatet al. (2012), we had performed aclassification of the MASSIV sources based on the shape of thevelocity field (regular or irregular) and the close environment(isolated or not-isolated). From this classification, we hadpre-selected as close pair candidates the non-isolated sourcesand those identified as mergers from the velocity field(see Epinatet al. 2012, for more details). Weidentified 20 close pair candidates (Table 1).
-
2.
To study in detail these close pair candidates we used the deepest i-band images in the VVDS fields: CFTH12K (14 h field, exposure time of texp = 3.6 ks, Le Fèvre et al. 2004), CFHTLS-Wide (22 h field, texp = 4–10 ks, Goranova et al. 2009), and CFTHLS-Deep (02 h field, texp ~ 300 ks, Goranova et al. 2009). We run SExtractor on the systems with well separated sources, and GALFIT (with two Sérsic components) on the blended ones, to estimate the luminosity difference in the i band between both sources, Δmi = mi,2 − mi,1. We took Δmi ≤ 1.5 (factor four or less in luminosity) to identify major mergers. The observed i band corresponds to ~300–350 nm rest-frame in the redshift range of our sample. We stress that for the blended sources, we run GALFIT v3.0 (Peng et al. 2010) without imposing any constraint to the parameters of the fit and we only used the information from the kinematical maps to set the initial positions of the sources. We present the residual maps of these blended sources in Appendix B.
-
3.
We confronted the images and the two component fits from GALFIT with the velocity field and the velocity dispersion map of the sources. We compared the distribution of Hα emission and the geometry of the velocity field to the rest-frame UV continuum (or rest-frame visible when NIR images are available). The presence of two components with position and geometry concordant in the velocity field and in the continuum images, is a strong indication of the reality of the pair.
-
4.
We run SExtractor in the residual image from GALFIT with the principal source subtracted to obtain a second estimation of mi,2, while with the companion source subtracted to estimate mi,1. Then we compared the Δmi derived from the GALFIT modeling with that from these SExtractor estimations. We found good agreement between both measurements (difference of ~0.2 mag or less). The major merger classification did not change from the initial estimate.
-
5.
Finally, we also explored ΔmKs for well separated galaxies and for one blended source (020294045). We used the Ks-band images from UKIDSS-DXS survey (22 h field, Dye et al. 2006) and WIRDS (2 h field, Bielby et al. 2012). The observed Ks band corresponds to ~0.8–1 μm rest-frame in the redshift range of our sample, and is a better tracer of the stellar mass content of the galaxies. After this second check there is not change in the major merger classification, except for one close pair (source 910186191), supporting the previous i-band results.
We converged to the steps above after exploring different possibilities. The stellar mass ratio between the two galaxies in a close pair is the best parameter to classify such system as a major merger. However, the estimation of the stellar mass in the blended sources and in some well separated pairs is not feasible due to spatial resolution and photometric depth limitations. We concluded that the luminosity difference in the i band is an homogeneous criterion applicable to the whole MASSIV sample and have additional benefits (i) the observed i band corresponds to the UV continuum of the source, which is related with the star formation of the galaxy and thus with its Hα emission. Hence, both pieces of information should provide a consistent picture about the system under study. (ii) The MASSIV PSF is 0.5−0.8″, similar to the typical seeing in the i band, ~0.74″, minimising spatial resolution differences. (iii) The 3σ detection magnitude of the CFTLHS i-band images in the 2 h field is ~26 (AB). Thanks to this depth we are able to detect the outskirts of the fainter MASSIV galaxies, making feasible the decomposition of the blended sources. We tried the two components fit in redder bands, but the lower S/N lead in general to poor constraints. And (iv) the VVDS parent samples are i-band magnitude selected, so the completeness of the MASSIV close pair sample is well defined in the i band (see Appendix C, for further details). In conclusion, even if Δmi is not the optimal parameter to select major merger systems, it is the best practical one with the current data sets.
In the next sections we present the decomposition and the classification of the 20 close pair candidates in the MASSIV data cubes (Table 1).
 |
Fig. 3 The i-band image (left panel, scale in ADU in the right), the velocity field (central panel, scale in km s-1 in the right), and the velocity dispersion map (right panel, scale in km s-1 in the right) of the MASSIV source 020294045 (major merger). On each map, North is up and East is left. The level contours mark the isophotes of the two components obtained with GALFIT in the i-band image. The principal galaxy (red/white) is the one closer to the kinematical centre of the system and sets the origin in right ascension (α) and declination (δ), while the companion (blue/black) is the secondary component. The outer contour marks the 3.43 ADU (7σsky) isophote. The next contours mark brighter isophotes in 1.96 ADU (4σsky) steps. The luminosity difference between both components in the i band, Δmi, as well as the CFHTLS exposure time, texp, are shown in the left panel. The redshift of the source and the on-source SINFONI exposure time, tSINFONI, are shown in the central panel. (A colour version of this plot is available at the electronic edition.) |
 |
Fig. 4 The same as Fig. 3, but for the Ks-band image (left panel) of the MASSIV source 020294045 (major merger). The outer contour marks the 6.76 ADU (2σsky) isophote, while brighter isophotes increase in 5.07 ADU (1.5σsky) steps. The flux difference between both components in the Ks band, ΔmKs, as well as the WIRDS exposure time, texp, are show in the left panel. (A colour version of this plot is available at the electronic edition.) |
 |
Fig. 5 The same as Fig. 3, but for the MASSIV source 020386743 (no major merger). The outer contour marks the 1.41 ADU (2σsky) isophote, while brighter isophotes increase in 1.76 ADU (2.5σsky) steps up to 10 ADU to avoid crowded figures. (A colour version of this plot is available at the electronic edition.) |
 |
Fig. 6 The same as Fig. 3, but for the MASSIV source 020461235 (no major merger). The outer contour marks the 1.31 ADU (3σsky) isophote, while brighter isophotes increase in 1.75 ADU (4σsky) steps up to 7 ADU to avoid crowded figures. (A colour version of this plot is available at the electronic edition.) |
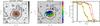 |
Fig. 7 Left and central panels are the same as in Fig. 3, but for the MASSIV source 140096645 (no major merger). The level contours mark the isophotes of the original i-band image. The Hα companion source is not detected in the i band. The outer contour marks the 2.64 ADU (1σsky) isophote, while brighter isophotes increase in 7.94 ADU (3σsky) steps up to 45 ADU to avoid crowded figures. The right panel shows the detection fraction of fake galaxies injected in the i-band image as a function of the magnitude of the companion source mi,2. The size of the dots marks the detection curves for extended, normal and compact galaxies (see text for details). The vertical line marks the limiting magnitude for major companion (Δmi = 1.5). (A colour version of this plot is available at the electronic edition.) |
4.1. Close pair candidates at 0.94 ≤ z ≤ 1.06
The weighted mean redshift of the first redshift bin is
 . We
have identified 6 close pairs over 18 sources in this redshift range:
. We
have identified 6 close pairs over 18 sources in this redshift range:
-
020294045 (Fig. 3). Major merger. The veloc-ity map suggests two projected components. The companionis toward the north and presents a steep velocity gradient com-pared with the principal galaxy. The GALFIT model with twocomponents in the i band reproduces both the position of thetwo kinematical components in the velocity map and the highvelocity dispersion in the overlapping region between bothcomponents. The luminosity difference is Δmi = 0.4. The separation be-tween the sources is 2.9 h-1 kpc andtheir relative velocity is Δv ~ 180 km s-1.Despite the close separation lead into significant overlap, thissystem also gives a satisfactory fit in the WIRDS Ks-band image(Fig. 4). In this case ΔmKs = 0.3, confirming that this system is amajor merger.
-
020386743 (Fig. 5). No major merger. The velocity map suggests two projected components. The companion is toward the north and presents a different velocity than the northern part of the principal galaxy. The GALFIT model with two components suggests that we are only detecting the western part of the companion galaxy, with the eastern part being too faint. This is also consistent with the velocity dispersion map, which shows a regular pattern in the overlapping region. The separation between the sources is 3.7 h-1 kpc and the luminosity difference is Δmi = 1.8. Hence, we do not classify the system as a major merger.
-
020461235 (Fig. 6). No major merger. The velocity map suggests two projected components. The companion is toward the south-west and presents a nearly constant velocity, in contrast with the velocity gradient of the principal galaxy. The GALFIT model with two components suggests that the companion is highly distorted, perhaps because the system is in an advanced merger stage (i.e., after first pericenter passage or pre-coalescence). The luminosity difference from the GALFIT model is Δmi = 1.7, while from the residual maps is Δmi = 1.9. This difference strongly suggests that this system is not a major merger. The separation between the components is 2.8 h-1 kpc.
-
140096645 (Fig. 7). No major merger. A small companion is identified in the velocity map about 1.2 arcsec away from the principal galaxy. There is no continuum detection in the i-band image in the position of the Hα companion, although there is a ~1σsky excess emission. To estimate if the non-detected companion could be bright/massive enough to lead to a major merger, we injected fake companion sources in the i-band image and studied their detection fraction as a function of the fake companion luminosity mi,2. The fake sources were modelled with a Sérsic function and convolved with a typical PSF of the 14 h field using GALFIT. For each fake source we assumed a random inclination and position angle, a Sérsic index ns = 1, i.e., an exponential disc (we checked that the detection curve is similar assuming either ns = 0.5 or ns = 2), and an effective radius re given by the re − M⋆ relation in MASSIV, log re = 0.36 + 0.37 [log (M⋆/M⊙) − 10] (see also Vergani et al. 2012). To estimate the stellar mass of the fake companion, we took Δmi as a proxy of the mass ratio between the principal galaxy, for which the stellar mass is known, and the companion. Then, we applied Poissonian noise to the model and injected it in the expected position of the possible companion. We measured, for different luminosities mi,2, which fraction of the 500 injected fake sources were detected. We repeated the previous steps for fake sources with 2re (extended sources) and 0.5re (compact sources), spanning all the possible sizes of the real sources. We show the result of this experiment in the right panel of Fig. 7.

Fig. 8 The same as Fig. 3, but for the MASSIV source 220397579 (major merger). The level contours mark the isophotes of the original i-band image. The outer contour marks the 5.36 ADU (3σsky) isophote, while brighter isophotes increase in 2.68 ADU (1.5σsky) steps. (A colour version of this plot is available at the electronic edition.)

Fig. 9 The same as Fig. 3, but for the MASSIV source 220544394 (major merger). The outer contour marks the 4.31 ADU (2σsky) isophote, while brighter isophotes increase in 3.23 ADU (1.5σsky) steps. (A colour version of this plot is available at the electronic edition.)

Fig. 10 The same as Fig. 8, but for the MASSIV source 020167131 (major merger). The outer contour marks the 3.43 ADU (10σsky isophote, while brighter isophotes increase in 2.74 ADU (8σsky) steps. (A colour version of this plot is available at the electronic edition.)
We find that even for extended sources, we are ~90% complete at mi,2 ~ 24, while the limiting magnitude for a major companion is
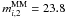 (vertical line in the
right panel of Fig. 7). Because of the small
probability of non detection of a major companion, we classify this system as no
major merger.
(vertical line in the
right panel of Fig. 7). Because of the small
probability of non detection of a major companion, we classify this system as no
major merger. -
220397579 (Fig. 8). Major merger. The velocity map shows two different components with a separation of rp = 14.4 h-1 kpc and a relative velocity of Δv ~ 340 km s-1. The companion is toward the north-west. The luminosity difference is Δmi = 0.4, suggesting a major merger. The difference in the Ks band is ΔmKs = −1.4. The negative sign implies that the companion is more luminous than the principal, which is brighter in the NUV rest-frame and in Hα. This is consistent with the measured integrated metallicity of these sources, that is higher for the companion (Queyrel et al. 2012). The suggested picture is that the system comprises a nearly face-on principal galaxy with intense star formation and low dust reddening, and a nearly edge-on companion galaxy with either a low level of star formation or strong dust reddening. We classify the system as a major merger.
-
220544394 (Fig. 9). Major merger. The velocity map shows two different components with a separation of rp = 7.1 h-1 kpc and a relative velocity of Δv ~ 50 km s-1, that are also well recovered by the GALFIT model with two components. The companion is toward the north, while the luminosity difference is Δmi = 1.3. We classify the system as a major merger.
 at
at  .
.
 |
Fig. 11 The same as Fig. 7, but for the MASSIV source 020218856 (no major merger). The Hα companion galaxy is not detected in the i band. The outer contour marks the 0.34 ADU (1σsky) isophote, while brighter isophotes increase in 1.01 ADU (3σsky) steps. (A colour version of this plot is available at the electronic edition.) |
 |
Fig. 12 The same as Fig. 7, but for the MASSIV source 020240675 (no major merger). The Hα companion galaxy is not detected in the i band. The outer contour marks the 0.36 ADU (1σsky) isophote, while brighter isophotes increase in 1.08 ADU (3σsky) steps up to 8 ADU to avoid crowded figures. (A colour version of this plot is available at the electronic edition.) |
4.2. Close pair candidates at 1.2 ≤ z < 1.5
The weighted mean redshift of the second redshift bin is
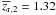 .
This is a redshift range where there is no measurement of the major merger fraction from
spectroscopic close pairs yet. In this framework, MASSIV provides a unique opportunity to
measure the major merger fraction at this crucial epoch of galaxy evolution. We identify
11 close pair candidates over 30 galaxies in this redshift bin:
.
This is a redshift range where there is no measurement of the major merger fraction from
spectroscopic close pairs yet. In this framework, MASSIV provides a unique opportunity to
measure the major merger fraction at this crucial epoch of galaxy evolution. We identify
11 close pair candidates over 30 galaxies in this redshift bin:
-
020167131 (Fig. 10). Major merger. The velocity map shows two different components with a separation of rp = 15.2 h-1 kpc and a relative velocity of Δv ~ 130 km s-1. The line targeted in this case is [O iii] λ5007, which explains the low signal. The companion galaxy is toward the south-east, while the luminosity differences are Δmi = 0.2 and ΔmKs = 0.1. We classify the system as a major merger.
-
020218856 (Fig. 11). No major merger. A faint companion is detected in the velocity map about 1.6 arcsec from the principal galaxy. There is no continuum detection of this companion at the depth of the i-band image. We followed the same steps than for the source 140096645 to estimate the detection probability of companion galaxies, finding that we are 100% complete up to mi,2 = 26. We note that the curves for extended, normal and compact galaxies are similar, reflecting that the size of the PSF is larger than the assumed size of the fake sources. Because a major companion should be brighter than
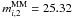 (vertical line in the
left panel of Fig. 11), and the non detection
in the continuum means that the companion should have
Δmi ≳ 2, we do not classify the
system as a major merger.
(vertical line in the
left panel of Fig. 11), and the non detection
in the continuum means that the companion should have
Δmi ≳ 2, we do not classify the
system as a major merger. -
020240675 (Fig. 12). No major merger. A faint companion is detected in the velocity map about 2.4 arcsec from the principal galaxy. There is no continuum detection of this companion at the depth of the i-band image. We followed the same steps than for the source 020218856 to estimate the detection curves of companion galaxies. We find similar completeness curves. Because a major companion should be brighter than
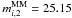 (vertical line in the
left panel of Fig. 12), and the non detection
in the continuum means that the companion should have
Δmi ≳ 2.5, we do not classify the
system as a major merger.
(vertical line in the
left panel of Fig. 12), and the non detection
in the continuum means that the companion should have
Δmi ≳ 2.5, we do not classify the
system as a major merger. -
020283083 (Fig. 13). Major merger. The velocity map suggests two projected components separated by 3.8 h-1 kpc and ~5 km s-1, with an extended region in the north-west. The GALFIT model with two components reproduces the shape of the velocity map and suggests that the extended region is due to the companion galaxy. The luminosity difference from the models is Δmi = 0.7. Thus, we classify this system as a major merger.

Fig. 13 The same as Fig. 3, but for the MASSIV source 020283083 (major merger). The outer contour marks the 2.12 ADU (4σsky) isophote, while brighter isophotes increase in 1.06 ADU (2σsky) steps. (A colour version of this plot is available at the electronic edition.)
-
020283830 (Fig. 14). No major merger. The velocity map shows two different components with a separation of rp = 8.5 h-1 kpc and a relative velocity of Δv ~ 500 km s-1. The companion only presents six detected pixels in the Hα map, already suggesting a minor companion. We used GALFIT to model the system, finding Δmi = 1.9. However, the model of the companion provided by GALFIT is a point-like source, thus overestimating the luminosity of the extended companion. The measurement with SExtractor in the image with the principal galaxy subtracted suggests Δmi = 2.1. Since the companion is fainter than the major merger limit, we do not classify the system as a major merger.
-
020465775 (Fig. 15). Major merger. The velocity map suggests two projected components. The GALFIT model with two components finds that the companion galaxy is toward the north-west of the principal galaxy, at rp = 3.6 h-1 kpc and Δv ~ 40 km s-1. The Hα emission of this system is located in the central part of the galaxies, since the i-band models match the velocity map at 9σsky level, i.e., we do not detect emission from the outer parts of the galaxies. The position of the companion explains the abnormal velocity pattern and the high velocity dispersion peak in the maps. The luminosity difference of the system is Δmi = 0.7, so we classify it as a major merger.
-
220376206 (Fig. 16). No major merger. The velocity map shows two different components with a separation of rp = 13.4 h-1 kpc and a relative velocity of Δv ~ 400 km s-1. The companion, located toward the north, presents ten detected pixels and its velocity is inconsistent with that expected from the velocity field of the principal galaxy. We find Δmi = 2.4, so the system is not a major merger.
-
220544103 (Fig. 17). Major merger. The velocity map suggests two projected components. The southern component presents a large velocity gradient and defines the kinematical centre of the system, while the northern component is more extended and has a nearly flat velocity field. The GALFIT model with two components recovers the configuration in the velocity map and suggests that the southern component is edge-on, while the northern component is nearly face-on, thus explaining the observed high and null velocity gradients. The separation between the components is rp = 5 h-1 kpc, while their relative velocity is Δv ~ 75 km s-1. From the GALFIT models we estimate Δmi = −1.1, and we classify the system as a major merger.

Fig. 16 The same as Fig. 3, but for the MASSIV source 220376206 (no major merger). The outer contour marks the 3.39 ADU (3σsky) isophote, while brighter isophotes increase in 2.26 ADU (2σsky) steps. (A colour version of this plot is available at the electronic edition.)

Fig. 17 The same as Fig. 3, but for the MASSIV source 220544103 (major merger). The outer contour marks the 3.32 ADU (2σsky) isophote, while brighter isophotes increase in 3.32 ADU (2σsky) steps. (A colour version of this plot is available at the electronic edition.)

Fig. 18 The same as Fig. 3, but for the MASSIV source 910154631 (major merger). The outer contour marks the 1.9 ADU (6σsky) isophote, while brighter isophotes increase in 0.8 ADU (2.5σsky) steps. (A colour version of this plot is available at the electronic edition.)

Fig. 19 The same as Fig. 8, but for the MASSIV source 910296626 (major merger). The outer contour marks the 3.32 ADU (10σsky) isophote, while brighter isophotes increase in 2.56 ADU (8σsky) steps. (A colour version of this plot is available at the electronic edition.)

Fig. 20 The same as Fig. 8, but for the MASSIV source 910337228 (major merger). The outer contour marks the 1.73 ADU (4σsky) isophote, while brighter isophotes increase in 1.30 ADU (3σsky) steps. (A colour version of this plot is available at the electronic edition.)

Fig. 21 The same as Fig. 8, but for the MASSIV source 020116027 (major merger). The principal galaxy is that in the south-east. The outer contour marks the 2.02 ADU (3.5σsky) isophote, while brighter isophotes increase in 1.16 ADU (2σsky) steps. (A colour version of this plot is available at the electronic edition.)

Fig. 22 The same as Fig. 3, but for the MASSIV source 910186191 (major merger). The outer contour marks the 2.83 ADU (8σsky) isophote, while brighter isophotes increase in 2.83 ADU (8σsky) steps. (A colour version of this plot is available at the electronic edition.)

Fig. 23 The same as Fig. 3, but for the MASSIV source 910274060 (major merger). The outer contour marks the 1.20 ADU (3σsky) isophote, while brighter isophotes increase in 1.00 ADU (2.5σsky) steps. The grey dot in the central figure marks the centre of the system given by the kinematical model, while the red/blue dot marks the photometric centre of the principal/companion galaxy given by the two-component model of the source. The long bars mark the position angle of the previous models. The short bar marks the photometric position angle given by the one-component model of the source. (A colour version of this plot is available at the electronic edition.)
-
910154631 (Fig. 18). Major merger. The velocity map suggests two projected components, with the companion toward the north-west. The i-band image shows another two well separated sources close to the MASSIV target. These sources are not detected in Hα. To avoid contamination from these sources in the i-band photometry, we performed a four component fitting, with two components for the MASSIV target and one component for each nearby source. The GALFIT model finds the second component of the MASSIV target at the expected position, but we only detect the southern half of the i-band source in Hα. We explored the reduced data cube of the source, and we find (i) there are two clear velocity gradients in the cube, reinforcing the presence of two different components and (ii) there is an OH sky-line in the channels in which we expect the northern part of the companion, explaining the non detection in the maps. In addition, the higher velocity dispersion of the MASSIV target occurs in the expected overlapping region between both components. We conclude that this is a close pair system with rp = 4.2 h-1 kpc, Δv ~ 130 km s-1 and Δmi = 0.8. Thus, we classify the system as a major merger.
-
910296626 (Fig. 19). Major merger. The velocity map shows two different components with a separation of rp = 12.1 h-1 kpc and a relative velocity of Δv ~ 165 km s-1. The companion is located toward the north-east. We find Δmi = −0.1 and ΔmKs = −0.2, so the system is a major merger.
-
910337228 (Fig. 20). Major merger. The velocity map shows two different components with a separation of rp = 9.5 h-1 kpc and a relative velocity of Δv ~ 220 km s-1. The companion is toward the west and has Δmi = 1.4. Thus, we classify the system as a major merger.
In summary for this redshift range, we classify 7 of the 11 close pair candidates as
major mergers. This translates to a gas-rich major merger fraction of
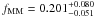 at
at 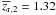 .
.
4.3. Close pair candidates at 1.5 ≤ z < 1.8
The weighted mean redshift of the third redshift bin is
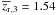 .
This is a redshift range where there is no measurement of the merger fraction from
spectroscopic close pairs yet. We identify 3 close pair candidates over 12 galaxies:
.
This is a redshift range where there is no measurement of the merger fraction from
spectroscopic close pairs yet. We identify 3 close pair candidates over 12 galaxies:
-
020116027 (Fig. 21). Major merger. The velocity map shows two different components with a separation of rp = 26.8 h-1 kpc and a relative velocity of Δv ~ 100 km s-1. The companion is toward the north-west. The luminosity difference is Δmi = 0.7, suggesting a major merger. The difference in the Ks band is ΔmKs = 0.5, confirming the previous major merger classification.
-
910186191 (Fig. 22). Major merger. The velocity map shows two different components with a separation of rp = 12.7 h-1 kpc and a relative velocity of Δv ~ 450 km s-1. The MASSIV target is only detected in 6 pixels because there is an OH sky-line in the position of Hα at its redshift. The companion, located toward the west, is well detected. We find Δmi = −0.2, this is, the companion is slightly brighter than the principal galaxy. However, the MASSIV target is barely detected in the Ks band, with ΔmKs = −2.4, suggesting a low mass system. This is the only system in which the classification in the two bands is different. Fortunately, both sources are VVDS targets, and we have an estimation of their stellar masses from SED fitting. The difference in stellar mass is μ ~ 1/3, so we classify the system as a major merger.
-
910274060 (Fig. 23). Major merger. The velocity map is consistent with one single component. However, the position angle (PA) from the i-band photometry, PA = 105° (North has PA = 0° and East has PA = 90°), is nearly perpendicular to that from the kinematical modelling, PA = 33°. This suggests a complex system, so we performed the GALFIT modelling with two sources. We recover well two sources, one in the north and the other in the south. The photometric PAs of these two sources, provided by the GALFIT fitting, are now in better agreement with the kinematical one (PA1 = 75°, PA2 = 41°), supporting that this is a close pair system. The separation between the components is 3.4 h-1 kpc, with Δv ~ 10 km s-1, and the luminosity difference is Δmi = 0.2. Thus, we classify the system as a major merger.
 .
Note that in this range our merger candidates have
.
Note that in this range our merger candidates have  kpc to improve the statistics. Applying Eq. (7) we estimate
kpc to improve the statistics. Applying Eq. (7) we estimate  for
for  kpc
at
kpc
at 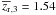 .
.
Our results alone, summarised in Table 2, suggest
a constant major merger fraction of fMM ~ 0.21 at
0.9 < z < 1.8 for
 kpc
close pairs (Fig. 24). This merger fraction at
z > 1 is higher by an order of magnitude than
in the local universe, where fMM ~ 0.01–0.03 (Patton et al. 2000; De
Propris et al. 2007; Patton & Atfield
2008; Domingue et al. 2009; Darg et al. 2010; Xu
et al. 2012). This is the first main result of the present paper. We compare our
major merger fractions with others in the literature in Sect. 6.1.
kpc
close pairs (Fig. 24). This merger fraction at
z > 1 is higher by an order of magnitude than
in the local universe, where fMM ~ 0.01–0.03 (Patton et al. 2000; De
Propris et al. 2007; Patton & Atfield
2008; Domingue et al. 2009; Darg et al. 2010; Xu
et al. 2012). This is the first main result of the present paper. We compare our
major merger fractions with others in the literature in Sect. 6.1.
Gas-rich major merger fraction and rate of star-forming galaxies at 0.9 < z < 1.8 in the MASSIV sample.
5. The gas-rich major merger rate in MASSIV
In this section we estimate the gas-rich major merger rate
(RMM), defined as the number of mergers per galaxy and Gyr, of
star-forming galaxies at
0.9 < z < 1.8. We remind
here the steps to transform a merger fraction to a merger rate. Following de Ravel et al. (2009), we define the major merger rate
as 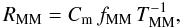 (6)where the factor
Cm is the fraction of the observed close pairs that finally
merge in a typical time scale TMM. The typical merger time scale
can be estimated by cosmological and N-body simulations. In our case, we
compute the major merger time scale from the cosmological simulations of Kitzbichler & White (2008), based on the
Millennium simulation (Springel et al. 2005). This
major merger time scale refers to major mergers (μ ≥ 1/4
in stellar mass), and depends mainly on
(6)where the factor
Cm is the fraction of the observed close pairs that finally
merge in a typical time scale TMM. The typical merger time scale
can be estimated by cosmological and N-body simulations. In our case, we
compute the major merger time scale from the cosmological simulations of Kitzbichler & White (2008), based on the
Millennium simulation (Springel et al. 2005). This
major merger time scale refers to major mergers (μ ≥ 1/4
in stellar mass), and depends mainly on  and on the
stellar mass of the principal galaxy, with a weak dependence on redshift in our range of
interest (see de Ravel et al. 2009, for details). We
measured the median-weighted stellar mass from MASSIV sources in each of the three redshift
bins under study, and estimated the merger time scale for these stellar masses. These time
scales already include the factor Cm (see Patton & Atfield 2008; Bundy
et al. 2009; Lin et al. 2010; López-Sanjuan et al. 2011), so we take
Cm = 1 in the following. In addition, López-Sanjuan et al. (2011) show that the time scales from Kitzbichler & White (2008) are equivalent to that
from the N-body/hydrodynamical simulations by Lotz et al. (2008). However, we stress that these merger time scales have
an additional factor of two uncertainty in their normalization (e.g., Hopkins et al. 2010; Lotz et al.
2011). We summarise the stellar masses, the merger time scales and the gas-rich
major merger rates in Table 2. As for the merger
faction, MASSIV data suggests a nearly constant major merger rate at
0.9 < z < 1.8,
RMM ~ 0.12 Gyr-1 (Fig. 25). We study in detail the evolution of the major merger rate at
z ≲ 1.5 in Sect. 6.2.
and on the
stellar mass of the principal galaxy, with a weak dependence on redshift in our range of
interest (see de Ravel et al. 2009, for details). We
measured the median-weighted stellar mass from MASSIV sources in each of the three redshift
bins under study, and estimated the merger time scale for these stellar masses. These time
scales already include the factor Cm (see Patton & Atfield 2008; Bundy
et al. 2009; Lin et al. 2010; López-Sanjuan et al. 2011), so we take
Cm = 1 in the following. In addition, López-Sanjuan et al. (2011) show that the time scales from Kitzbichler & White (2008) are equivalent to that
from the N-body/hydrodynamical simulations by Lotz et al. (2008). However, we stress that these merger time scales have
an additional factor of two uncertainty in their normalization (e.g., Hopkins et al. 2010; Lotz et al.
2011). We summarise the stellar masses, the merger time scales and the gas-rich
major merger rates in Table 2. As for the merger
faction, MASSIV data suggests a nearly constant major merger rate at
0.9 < z < 1.8,
RMM ~ 0.12 Gyr-1 (Fig. 25). We study in detail the evolution of the major merger rate at
z ≲ 1.5 in Sect. 6.2.
 |
Fig. 24 Gas-rich major merger fraction of |
6. The redshift evolution of the gas-rich major merger fraction and rate up to z ~1.5
In this section we use the MASSIV results at z > 1 to expand the study of the gas-rich major merger fraction (Sect. 6.1) and rate (Sect. 6.2) from spectroscopic close pairs to the redshift desert. Then, we explore the importance of gas-rich major mergers in the assembly of the red sequence since z ~ 1.5 in Sects. 6.3 and 6.4.
6.1. The redshift evolution of the gas-rich major merger fraction
In this section we compare the merger fraction from MASSIV with those from previous
works. Because the merger fraction evolution depends on mass (e.g., de Ravel et al. 2009, 2011),
luminosity (e.g., de Ravel et al. 2009; López-Sanjuan et al. 2010a) and colour (e.g., Lin et al. 2008; Chou
et al. 2011), we focus on samples with  (Salpeter 1955 IMF) to minimise systematics. In
addition, this mass regime is greatly dominated by gas-rich (wet) mergers, as those that
we observe in MASSIV, at least at z ≳ 0.2 (Lin et al. 2008; de Ravel et al.
2009; Chou et al. 2011).
(Salpeter 1955 IMF) to minimise systematics. In
addition, this mass regime is greatly dominated by gas-rich (wet) mergers, as those that
we observe in MASSIV, at least at z ≳ 0.2 (Lin et al. 2008; de Ravel et al.
2009; Chou et al. 2011).
We define the major (μ ≥ 1/4) merger fraction
normalised to  kpc
as
kpc
as 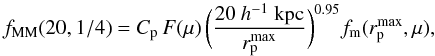 (7)where the factor
(7)where the factor
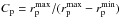 accounts for the missing close
companions at small radii in those studies with
accounts for the missing close
companions at small radii in those studies with 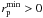 (e.g.,
Bell et al. 2006) and the factor
F(μ) translates the merger fraction for a given
μ to the major merger fraction. The merger fraction depends on
μ as
fm(≥ μ) ∝ μs
(e.g., López-Sanjuan et al. 2011), that implies
F(μ) = (4μ)−s.
We take s = −0.9 ± 0.4, a value derived from the observational
estimations of López-Sanjuan et al. (2011, 2012) and Xu et al.
(2012). The search radius dependence of the major merger fraction,
(e.g.,
Bell et al. 2006) and the factor
F(μ) translates the merger fraction for a given
μ to the major merger fraction. The merger fraction depends on
μ as
fm(≥ μ) ∝ μs
(e.g., López-Sanjuan et al. 2011), that implies
F(μ) = (4μ)−s.
We take s = −0.9 ± 0.4, a value derived from the observational
estimations of López-Sanjuan et al. (2011, 2012) and Xu et al.
(2012). The search radius dependence of the major merger fraction,
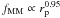 , is the
observational one found by López-Sanjuan et al.
(2011) in the VVDS. With Eq. (7)
we avoid systematic differences due to the close pair definition when comparing different
works.
, is the
observational one found by López-Sanjuan et al.
(2011) in the VVDS. With Eq. (7)
we avoid systematic differences due to the close pair definition when comparing different
works.
de Ravel et al. (2009) study the major merger
fraction of
M⋆ ≥ 109.75 M⊙
(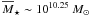 ) galaxies in
VVDS-Deep by spectroscopic close pairs, while López-Sanjuan et al. (2011) provide the major merger fraction of blue
(star-forming) galaxies with
) galaxies in
VVDS-Deep by spectroscopic close pairs, while López-Sanjuan et al. (2011) provide the major merger fraction of blue
(star-forming) galaxies with 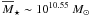 in the same sample.
In both studies
in the same sample.
In both studies 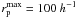 kpc.
Lin et al. (2008) report the number of companions
of −21 ≤ MB + 1.3z ≤ −19
galaxies (
kpc.
Lin et al. (2008) report the number of companions
of −21 ≤ MB + 1.3z ≤ −19
galaxies (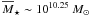 ) with
10 h-1 kpc
≤ rp ≤ 30 h-1 kpc in three
DEEP2 redshift survey (Davis et al. 2003) fields.
Their principal and companion sample are the same, so they miss major companions near to
the selection boundary. Thus, we apply an extra factor 1.74 to Eq. (7) to account for these missing companions (see
Lin et al. 2004, for details). Xu et al. (2012) measure the fraction of galaxies in
close pairs with μ ≥ 1/2.5 in the COSMOS4 (Cosmological Evolution Survey, Scoville et al. 2007) and SDSS5
(Sloan Digital Sky Survey, Abazajian et al. 2009)
surveys for
) with
10 h-1 kpc
≤ rp ≤ 30 h-1 kpc in three
DEEP2 redshift survey (Davis et al. 2003) fields.
Their principal and companion sample are the same, so they miss major companions near to
the selection boundary. Thus, we apply an extra factor 1.74 to Eq. (7) to account for these missing companions (see
Lin et al. 2004, for details). Xu et al. (2012) measure the fraction of galaxies in
close pairs with μ ≥ 1/2.5 in the COSMOS4 (Cosmological Evolution Survey, Scoville et al. 2007) and SDSS5
(Sloan Digital Sky Survey, Abazajian et al. 2009)
surveys for 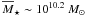 galaxies. We applied
a factor 0.5 to pass from their number of galaxies in close pairs to the number of close
pair systems in the sample (Xu, priv. comm.), and a factor
F(1/2.5) = 1.5 ± 0.3 to obtain the major merger
fraction. All these published (gas-rich) major merger fractions are shown as a function of
redshift in Fig. 24, together with the values
derived from MASSIV.
galaxies. We applied
a factor 0.5 to pass from their number of galaxies in close pairs to the number of close
pair systems in the sample (Xu, priv. comm.), and a factor
F(1/2.5) = 1.5 ± 0.3 to obtain the major merger
fraction. All these published (gas-rich) major merger fractions are shown as a function of
redshift in Fig. 24, together with the values
derived from MASSIV.
We parametrise the redshift evolution of the (gas-rich) major merger fraction with a
power-law, 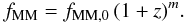 (8)The least-squares fit
to all the data in Fig. 24 yields
fMM,0 = (6.6 ± 0.6) × 10-3 and
m = 3.91 ± 0.16. We find good agreement between all works, with the
MASSIV point at z ~ 1 being higher than expected from the fit, but
consistent within errors with the measurement of Lin
et al. (2008) at that redshift. In the next section we show that this difference
disappears when the stellar mass of the samples is taken into account, emphasizing the
importance of comparing results from similar parent samples.
(8)The least-squares fit
to all the data in Fig. 24 yields
fMM,0 = (6.6 ± 0.6) × 10-3 and
m = 3.91 ± 0.16. We find good agreement between all works, with the
MASSIV point at z ~ 1 being higher than expected from the fit, but
consistent within errors with the measurement of Lin
et al. (2008) at that redshift. In the next section we show that this difference
disappears when the stellar mass of the samples is taken into account, emphasizing the
importance of comparing results from similar parent samples.
 |
Fig. 25 Gas-rich major merger rate of |
6.2. The redshift evolution of the gas-rich major merger rate
We use Eq. (6) to translate the original
(i.e., without any normalization in 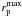 ) major
merger fractions reported in previous section into merger rates. We show them in
Fig. 25. The good agreement between different
works is remarkable, reinforcing the idea that the merger time scales used account
properly for the dependence of the merger fraction both on
) major
merger fractions reported in previous section into merger rates. We show them in
Fig. 25. The good agreement between different
works is remarkable, reinforcing the idea that the merger time scales used account
properly for the dependence of the merger fraction both on
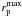 and on stellar
mass.
and on stellar
mass.
We also show the major merger rate from morphological criteria derived by López-Sanjuan et al. (2009b). They measure the gas-rich
merger fraction of 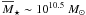 galaxies from
asymmetries (A) in the GOODS6 (Giavalisco et al. 2004) South field and take into
account the effect of observational errors in z and A,
that lead to overestimations in the major merger fraction by a factor of two-three (López-Sanjuan et al. 2009a,b), using maximum likelihood techniques developed in López-Sanjuan et al. (2008). Other studies find good
agreement between the asymmetry-based major merger rates from López-Sanjuan et al. (2009b) and those from close pair statistics
(López-Sanjuan et al. 2010a; Lotz et al. 2011; de
Ravel et al. 2011), confirming the robustness of their methodology.
galaxies from
asymmetries (A) in the GOODS6 (Giavalisco et al. 2004) South field and take into
account the effect of observational errors in z and A,
that lead to overestimations in the major merger fraction by a factor of two-three (López-Sanjuan et al. 2009a,b), using maximum likelihood techniques developed in López-Sanjuan et al. (2008). Other studies find good
agreement between the asymmetry-based major merger rates from López-Sanjuan et al. (2009b) and those from close pair statistics
(López-Sanjuan et al. 2010a; Lotz et al. 2011; de
Ravel et al. 2011), confirming the robustness of their methodology.
We also parametrise the redshift evolution of the (gas-rich) major merger rate with a
power-law, 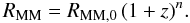 (9)The least-squares fit
to all the data in Fig. 25 yields
RMM,0 = (4.8 ± 0.3) × 10-3
Gyr-1 and n = 3.95 ± 0.12. The agreement between different
works points out the importance of comparing results from similar parent samples to avoid
systematics (see also Lotz et al. 2011, for an
extensive discussion on this topic). We also point out that the merger rate and the merger
fraction of star-forming galaxies show a similar evolution with redshift.
(9)The least-squares fit
to all the data in Fig. 25 yields
RMM,0 = (4.8 ± 0.3) × 10-3
Gyr-1 and n = 3.95 ± 0.12. The agreement between different
works points out the importance of comparing results from similar parent samples to avoid
systematics (see also Lotz et al. 2011, for an
extensive discussion on this topic). We also point out that the merger rate and the merger
fraction of star-forming galaxies show a similar evolution with redshift.
The second main result in this paper is that the major merger rate is well described by a power-law function up to z ~ 1.5. However, we note that our MASSIV data seem to indicate a flattening of the merger rate’s evolution beyond z ~ 1. Previous studies from morphological criteria (e.g., Conselice 2003; Conselice et al. 2008) and from photometric pairs (Ryan et al. 2008) suggest that the power-law parametrization is not longer valid at z ≳ 1.5, where a lower merger fraction than expected from the low-z evolution is measured, possibly indicating a maximum in the major merger rate at z ~ 2 (e.g., Conselice 2006; Ryan et al. 2008; López-Sanjuan et al. 2009b). Our new measurements agree with this picture and measurements from spectroscopic close pairs beyond z ~ 1.5 are needed to test the early evolution of the merger fraction.
The power-law index n = 3.95 ± 0.12 is higher than several previous
measurements in the literature (e.g., Bridge et al.
2010; Lotz et al. 2011), as well as our
major merger fraction evolution, m = 3.91 ± 0.16. However, our results
refer to 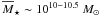 star-forming
galaxies, and it is known that the merger fraction and rate evolve faster for blue,
star-forming galaxies than for the red and global populations (e.g., Lin et al. 2008; de Ravel et al.
2009; Chou et al. 2011; López-Sanjuan et al. 2011).
star-forming
galaxies, and it is known that the merger fraction and rate evolve faster for blue,
star-forming galaxies than for the red and global populations (e.g., Lin et al. 2008; de Ravel et al.
2009; Chou et al. 2011; López-Sanjuan et al. 2011).
6.3. Number of gas-rich mergers since z = 1.5
We can obtain the average number of gas-rich major mergers per star-forming galaxy
between z2 and
z1 < z2
as 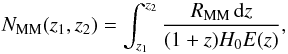 (10)where
(10)where
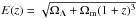 in a flat universe. Using the merger rate parametrisation in Eq. (9), we obtain
NMM(0,1.5) = 0.35 ± 0.04. Interestingly,
half of this merging activity happens at z > 1,
with NMM(1,1.5) = 0.18 ± 0.02 and
NMM(0,1) = 0.17 ± 0.02. Because the cosmic
time lapse in these redshift intervals is 1.55 Gyr and 7.7 Gyr, respectively, the average
merger activity was higher at
1 < z < 1.5 than at
1 < z by a factor of five. In the next section
we further explore the consequences of this very different major merger activity above and
below z ~ 1 for the assembly of the red sequence.
in a flat universe. Using the merger rate parametrisation in Eq. (9), we obtain
NMM(0,1.5) = 0.35 ± 0.04. Interestingly,
half of this merging activity happens at z > 1,
with NMM(1,1.5) = 0.18 ± 0.02 and
NMM(0,1) = 0.17 ± 0.02. Because the cosmic
time lapse in these redshift intervals is 1.55 Gyr and 7.7 Gyr, respectively, the average
merger activity was higher at
1 < z < 1.5 than at
1 < z by a factor of five. In the next section
we further explore the consequences of this very different major merger activity above and
below z ~ 1 for the assembly of the red sequence.
6.4. Testing the major merger origin of massive early-type galaxies
The number density of massive (M⋆ ≳ 1011 M⊙) early-type galaxies (E/S0, ETGs in the following) has increased with cosmic time since z ~ 3 (e.g., Pozzetti et al. 2010; Buitrago et al. 2013), with ETGs being the dominant population among massive galaxies only since z ~ 1 (Vergani et al. 2008; Buitrago et al. 2013; van der Wel et al. 2011; van Dokkum et al. 2011). Gas-rich major mergers have been proposed as an efficient mechanism to transform star-forming late-type galaxies into red ETGs (e.g., Naab et al. 2006; Rothberg & Joseph 2006a,b; Hopkins et al. 2008; Rothberg & Fischer 2010; Bournaud et al. 2011), so the comparison between the observed number density evolution of ETGs (ρETG) and the major merger history of star-forming galaxies imposes important constraints on the role of mergers in galaxy evolution.
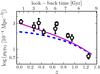 |
Fig. 26 Number density evolution of massive (M⋆ ≥ 1011.25 M⊙) ETGs (E/S0) as a function of redshift from Buitrago et al. (2013, pentagons) and Pozzetti et al. (2010, squares). The dashed line is the expected number density evolution due to gas-rich (wet) major mergers from our model. The solid line is the expected number density evolution due to wet major and dry mergers (both major and minor) from our model. Mergers are common enough to drive the number density evolution of massive ETGs since z ~ 1.3. (A colour version of this plot is available at the electronic edition.) |
In their work, Robaina et al. (2010) and Man et al. (2012) integrate the observed major merger rate over cosmic time and predict the evolution of the number density of massive galaxies assuming that all the merger remnants are new massive galaxies. They suggest that major mergers are common enough to explain the number density evolution of massive galaxies (ETGs + spirals) at z < 1 and z < 3, respectively. Eliche-Moral et al. (2010) model the evolution of the luminosity function backwards in time for bright galaxies, selected according to their colours (red/blue/total) and their morphologies. They find that the observed luminosity functions’ evolution can be naturally explained by the observed gas-rich and dry major merger rates, and that 50–60% of massive ETGs in the local universe were formed by major mergers at 0.8 < z < 1, with a small number evolution since z = 0.8.
In this section we implement a model to explore the role of mergers in the number density evolution of massive ETGs since z ~ 1.3. As reference values, we use the number densities of massive (M⋆ ≥ 1011.25 M⊙) ETGs provided by Buitrago et al. (2013). They perform a consistent morphological study by visual inspection between z = 0 and z = 3, combining the SDSS, POWIR (Palomar Observatory Wide-Field Infrared, Conselice et al. 2007) and GNS7 (GOODS NICMOS survey, Conselice et al. 2011a) surveys. We also use the number densities of massive spheroidal galaxies with M⋆ ≥ 1011.25 M⊙, selected by automatic indices in the zCOSMOS8 (Lilly et al. 2007) survey, provided by Pozzetti et al. (2010). We show these number densities in Fig. 26.
 |
Fig. 27 Number density distribution from the different functions in Eq. (11) at z = 1. The solid line is the stellar mass function (Φ) multiplied by the major merger rate (RMM). The dashed line includes the major merger efficiency function (EMM). The dotted line includes the fraction of late-type galaxies (fLTG) and provides the final function that we integrate over stellar mass and cosmic time to obtain ρwet. The vertical dashed line marks the limiting stellar mass that define massive galaxies, M⋆, lim = 1011.25 M⊙, while the dotted lines mark the stellar masses M ⋆ ,1 = 1010.15 M⊙ and M ⋆ ,2 = 1011.05 M⊙ when fsf = 0 (see text for details). (A colour version of this plot is available at the electronic edition.) |
In our model we assume that, after the final coalescence of the merging galaxies, a cosmic time Δt = 0.5 Gyr is necessary for the merger remnant to be classified as an ETG (see Eliche-Moral et al. 2010, for a detailed summary of this topic). This implies that the new ETGs which appeared between zmax and zmin came from the merger activity in the range z ∈ [z1, z2), where z1 = zmin + Δz, z2 = zmax + Δz, and Δz is the redshift interval that spans Δt in each case. Therefore, we take zmax = 1.3 as the upper redshift in our model because that implies z2 ~ 1.5, the redshift limit of the present merger rate study (see Sect. 6.2).
The number density of new ETGs with stellar mass
M⋆ ≥ M⋆, lim
from gas-rich major merger events appeared in the range
zmin ≤ z < zmax
is 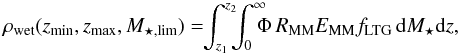 (11)where the different
elements in the integral are (Fig. 27):
(11)where the different
elements in the integral are (Fig. 27):
-
the global mass function, parametrised with a Schechter function
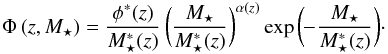 (12)We assumed the
Schechter function parameters from Pérez-González
et al. (2008) and used their parametrisation with redshift provided by
López-Sanjuan et al. (2010a),
(12)We assumed the
Schechter function parameters from Pérez-González
et al. (2008) and used their parametrisation with redshift provided by
López-Sanjuan et al. (2010a),
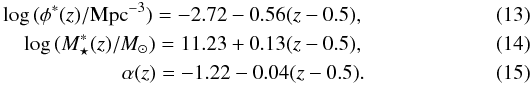
-
The gas-rich major merger rate, RMM(z), as measured in Sect. 6.2. We assumed that it is independent of the stellar mass.
-
The merger efficiency function, E(z,M⋆, M⋆, lim, μmax, μmin). This function provides the probability that a gas-rich merger with a mass ratio μmin < μ ≤ μmax produces an early-type remnant more massive than M⋆, lim. The merger efficiency function takes several effects into account:
-
The stellar mass difference μ needed to reach M⋆, lim for a given M⋆. Forexample, and regarding major mergers with μ ≥ 1/4, the μmax = 1 mergers ofgalaxies with M⋆ ≥ 1010.7 M⊙ will provide a massive remnant with M⋆ ≥ M⋆, lim = 1011 M⊙, while for μmin = 1/4only galaxies with M⋆ ≥ 1010.9 M⊙ can be progenitors of massive ETGs. Thus,mergers below M⋆, lim/(1 + μmin) do not contribute to the assembly of massiveETG, while all mergers above M⋆, lim/(1 + μmax) contribute. Between μmin and μmax, weused the dependence of the merger fraction on the mass ratio μ, fMM ∝ μs(e.g., López-Sanjuanet al. 2011), to estimate theeffective merger rate at M⋆ = M⋆, lim/(1 + μ).
-
The extra stellar mass in the final remnant due to the star formation during the merger, fsf. This extra stellar mass simply decreases the limiting mass for a given μ described in the previous item by a factor (1 + fsf)-1.
-
The fraction of remnants of a gas-rich major merger that are ETGs. We express this fraction as 1 − fdisc, where fdisc is the fraction of remnants that rebuild a disc component and are classified as late-type galaxies after the merger (see Sect. 6.4.2, for further details).
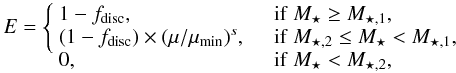 (16)where
(16)where
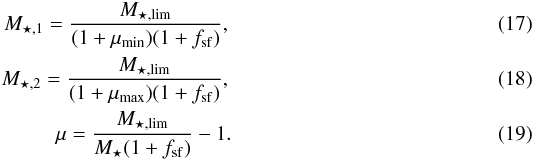 For
convenience, we define the major merger efficiency in Eq. (11) as
EMM ≡ E(z,M⋆, M⋆, lim, μmax = 1, μmin = 1/4).
We assumed that fdisc = 0, i.e., all the merger remnants
are ETGs (see Sect. 6.4.2), and that
s = −0.9 as in Sect 6.1.
To estimate fsf we used the parametrisation of the gas
fraction as a function of stellar mass and cosmic time provided by Rodrigues et al. (2012),
For
convenience, we define the major merger efficiency in Eq. (11) as
EMM ≡ E(z,M⋆, M⋆, lim, μmax = 1, μmin = 1/4).
We assumed that fdisc = 0, i.e., all the merger remnants
are ETGs (see Sect. 6.4.2), and that
s = −0.9 as in Sect 6.1.
To estimate fsf we used the parametrisation of the gas
fraction as a function of stellar mass and cosmic time provided by Rodrigues et al. (2012), ![\begin{equation} f_{\rm gas}(z,M_{\star}) = \frac{M_{\rm gas}}{M_{\star} + M_{\rm gas}} = \frac{1}{1 + [M_{\star}/10^{A(t)}]^{\,B(t)}},\label{fgas} \end{equation}](/articles/aa/full_html/2013/05/aa20286-12/aa20286-12-eq354.png) (20)where
t is the cosmic time between redshift z and the
present,
(20)where
t is the cosmic time between redshift z and the
present, 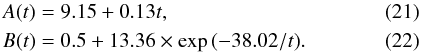 A(t)represents
the stellar mass at a given time for which the gas fraction is equal to 50%. The
parameter increases linearly with lookback time.
B(t) corresponds to the slope of the function.
Then, we assumed the prescriptions in Hopkins et al.
(2009) to estimate the amount of the initial gas mass that is transformed
into stars during the merger,
fburst = fgas(1 − fgas)2μ/(1 + μ).
Finally,
A(t)represents
the stellar mass at a given time for which the gas fraction is equal to 50%. The
parameter increases linearly with lookback time.
B(t) corresponds to the slope of the function.
Then, we assumed the prescriptions in Hopkins et al.
(2009) to estimate the amount of the initial gas mass that is transformed
into stars during the merger,
fburst = fgas(1 − fgas)2μ/(1 + μ).
Finally, 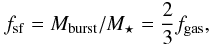 (23)where the factor
2/3 is the efficiency for μ = 1/2 mergers, which
is the typical major merger mass ratio (López-Sanjuan et al. 2011, 2012).
(23)where the factor
2/3 is the efficiency for μ = 1/2 mergers, which
is the typical major merger mass ratio (López-Sanjuan et al. 2011, 2012).

Fig. 28 Fraction of late-type galaxies as a function of redshift (top panel) and stellar mass at z ~ 0 (bottom panel). The redshift data points are from Buitrago et al. (2013), and the stellar mass ones from Bernardi et al. (2010) in the SDSS. The line in both panels is the best least-squares linear fit to the data. (A colour version of this plot is available at the electronic edition)
-
-
The fraction of late-type galaxies (spirals and irregulars), fLTG(z,M⋆), is the number of potential gas-rich merger progenitors over the total population. We parametrise this fraction as
![\begin{equation} f_{\rm LTG}(z,M_{\star}) = 0.56 + 0.16z - 0.58[\log\, (M_{\star}/M_{\odot}) - 11].\label{fltgzmass} \end{equation}](/articles/aa/full_html/2013/05/aa20286-12/aa20286-12-eq364.png) (24)We estimated
the redshift dependence from the fLTG reported by Buitrago et al. (2013) at
z < 3 (Fig. 28, top panel), and the mass dependence from the late-type
fractions in the SDSS presented in Bernardi et al.
(2010, Fig. 28. We assumed
fLTG = 1 when Eq. (24) is higher than one, and fLTG = 0
when it is negative.
(24)We estimated
the redshift dependence from the fLTG reported by Buitrago et al. (2013) at
z < 3 (Fig. 28, top panel), and the mass dependence from the late-type
fractions in the SDSS presented in Bernardi et al.
(2010, Fig. 28. We assumed
fLTG = 1 when Eq. (24) is higher than one, and fLTG = 0
when it is negative.
Finally, we define the fraction of new massive ETGs due to gas-rich (wet) mergers as
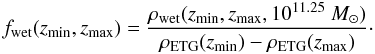 (25)Our merger model
finds fwet(0,1.3) ~ 50%, while this fraction
increases up to fwet(z,1.3) ≳ 90% when we
focus on the high-z regime, z ≳ 0.8 (dashed line in
Fig. 26). This indicates that gas-rich major
mergers are common enough at z ≳ 0.8 to explain the observed increase in
the number density of massive ETGs. However, at z ≲ 0.8 only one third of
the evolution can be accounted by these mergers,
fwet(0,0.8) ~ 40%. That supports the idea
that gas-rich major merging is the main process involved in the assembly of the red
sequence at z ≳ 1 (e.g., Ilbert et al.
2010; López-Sanjuan et al. 2010b; Eliche-Moral et al. 2010; Prieto et al. 2013).
(25)Our merger model
finds fwet(0,1.3) ~ 50%, while this fraction
increases up to fwet(z,1.3) ≳ 90% when we
focus on the high-z regime, z ≳ 0.8 (dashed line in
Fig. 26). This indicates that gas-rich major
mergers are common enough at z ≳ 0.8 to explain the observed increase in
the number density of massive ETGs. However, at z ≲ 0.8 only one third of
the evolution can be accounted by these mergers,
fwet(0,0.8) ~ 40%. That supports the idea
that gas-rich major merging is the main process involved in the assembly of the red
sequence at z ≳ 1 (e.g., Ilbert et al.
2010; López-Sanjuan et al. 2010b; Eliche-Moral et al. 2010; Prieto et al. 2013).
In addition to wet mergers, dry mergers can also increase the number density of massive
ETGs. In this case they promote ETGs with
M⋆ < 1011.25 M⊙
to the massive regime. We estimate the contribution of both major and minor dry mergers as
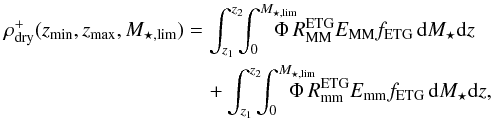 (26)where
(26)where
 (
( ) is the major
(minor) merger rate of massive ETGs galaxies from López-Sanjuan et al. (2012),
fETG = 1 − fLTG, the minor
merger efficiency function is defined as
Emm ≡ E(z,M⋆, M⋆, lim, μmax = 1/4, μmin = 1/10),
and we assumed fsf = 0 in both major and minor merger
efficiency functions. Note that the integration in mass space only reach
M⋆, lim and that the
merger rates from López-Sanjuan et al. (2012)
include also mixed mergers (ETGs – LTGs). However, dry mergers between two already massive
ETGs decrease the number density ρETG. We
take this into account with the following function,
) is the major
(minor) merger rate of massive ETGs galaxies from López-Sanjuan et al. (2012),
fETG = 1 − fLTG, the minor
merger efficiency function is defined as
Emm ≡ E(z,M⋆, M⋆, lim, μmax = 1/4, μmin = 1/10),
and we assumed fsf = 0 in both major and minor merger
efficiency functions. Note that the integration in mass space only reach
M⋆, lim and that the
merger rates from López-Sanjuan et al. (2012)
include also mixed mergers (ETGs – LTGs). However, dry mergers between two already massive
ETGs decrease the number density ρETG. We
take this into account with the following function,
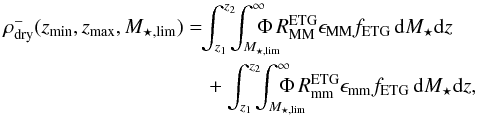 (27)where
in this case the merger efficiency function has the form
(27)where
in this case the merger efficiency function has the form
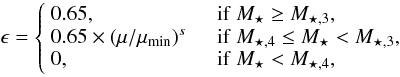 (28)where
(28)where
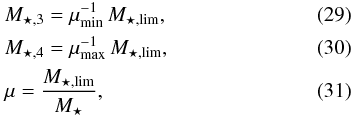 and
the factor 0.65 is the fraction of companions of massive galaxies that are already
early-type/red galaxies (López-Sanjuan et al. 2012;
Newman et al. 2012). As previously, we define the
major merger efficiency as
ϵMM ≡ ϵ(z,M⋆, M⋆, lim, μmax = 1, μmin = 1/4)
and the minor merger efficiency as
ϵmm ≡ ϵ(z,M⋆, M⋆, lim, μmax = 1/4, μmin = 1/10).
and
the factor 0.65 is the fraction of companions of massive galaxies that are already
early-type/red galaxies (López-Sanjuan et al. 2012;
Newman et al. 2012). As previously, we define the
major merger efficiency as
ϵMM ≡ ϵ(z,M⋆, M⋆, lim, μmax = 1, μmin = 1/4)
and the minor merger efficiency as
ϵmm ≡ ϵ(z,M⋆, M⋆, lim, μmax = 1/4, μmin = 1/10).
Analogous to the wet merger case, we define
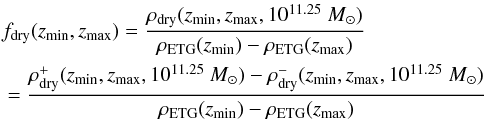 (32)to
explore the role of dry mergers in massive ETGs assembly since z = 1.3.
We find fdry(0,1.3) ~ 40%. As shown in
Fig. 26, dry mergers are more important at recent
cosmic times due to the increase in the number density of ETGs, in contrast with the
diminishing importance of gas-rich mergers. For example, we have
fdry(0.8,1.3) ~ 15%, while
fdry(0,0.8) ~ 45%.
(32)to
explore the role of dry mergers in massive ETGs assembly since z = 1.3.
We find fdry(0,1.3) ~ 40%. As shown in
Fig. 26, dry mergers are more important at recent
cosmic times due to the increase in the number density of ETGs, in contrast with the
diminishing importance of gas-rich mergers. For example, we have
fdry(0.8,1.3) ~ 15%, while
fdry(0,0.8) ~ 45%.
The combined effect of gas-rich and dry mergers, ftot = fwet + fdry, is able to explain most of the evolution in ρETG since z = 1.3, with ftot(0,1.3) ~ 90%. Thus, our model suggests merging as the main process in the assembly of massive ETGs since z = 1.3. Two thirds of the number density evolution is due to gas-rich major mergers, while one third is coming from major and minor dry mergers.
The measurement of the merger rate at z ≳ 1.5 is needed to fully constraint the role of gas-rich major mergers in the early assembly of the red sequence, as well as the possible contribution of cold gas accretion in this mass assembly.
6.4.1. Fast and slow rotators in the local universe
The results from the SAURON project (de Zeeuw et al. 2002) propose a kinematical classification of morphological ETGs into fast and slow rotators (Emsellem et al. 2007). Recently, the ATLAS3D,9 (Cappellari et al. 2011) survey has observed a representative sample of 260 nearby ETGs, finding that the fraction of slow rotators increases with the dynamical mass (Emsellem et al. 2011). The cosmological simulation analysed by Khochfar et al. (2011) suggests that the main difference between fast and slow rotators is their average number of major mergers, with fast rotators having undergone one major merger, while slow rotators have undergone two. We use this fact and the merging model developed in the previous section, to predict the fraction of slow rotators in the local universe, fslow. We simply assumed that wet major mergers produce fast rotators (first major merger event), dry major mergers produce slow rotators (second major merger event), and dry minor mergers do not change the kinematical state of ETGs. In addition, we took all the ETGs at z = 1.3 as fast rotators.
With the previous assumptions, we expect fslow ~ 60%, in good agreement with the ATLAS3D result of fslow ~ 47–75% for ETGs with a dynamical mass Mdyn ≥ 1011.25 M⊙ (Emsellem et al. 2011). Thus, our model also reproduces the local fraction of slow/fast rotators of massive ETGs galaxies, reinforcing the conclusions of the previous section.
6.4.2. Uncertainties in the model
The model presented in previous sections has set most of its parameters from observational results. However, there are two unconstrained parameters that could affect our conclusions. The first parameter is fdisc, the fraction of gas-rich major mergers whose remnant rebuild a disc component and do not contribute to the increase in ρETG. We assumed fdisc = 0, and in the following we justify this selection. Hopkins et al. (2009) find that a high gas fraction prevents the destruction of the disc component after a major merger in their N-body/hydrodynamical simulations (but see Bournaud et al. 2011 for a different point of view). These simulations suggest that disc rebuild could be an efficient process when the gas fraction is fgas ≳ 50%. However, we have focused in the massive end of the galaxy population, where the gas fractions are lower. Thanks to Eq. (20), we can estimate the gas fraction of the gas-rich mergers in our model. We find fgas ≲ 30%, justifying the assumed fdisc = 0. At lower masses than explored in the present section, the gas fraction is higher, and disc rebuild could be an important process in the formation of bulge-dominated spirals (e.g., Huertas-Company et al. 2010; Puech et al. 2012). However, we cannot discard positive values of fdisc for massive galaxies, as we see below.
The second parameter is the assumed merger time scale, which typically has a factor of two uncertainty in their normalization (e.g., Hopkins et al. 2010). The TMM from Kitzbichler & White (2008) are typically longer than others in the literature (e.g., Patton & Atfield 2008; Lin et al. 2010) or similar to those from N-body/hydrodynamical simulations (Lotz et al. 2010b,a). Thus, we expect, if anything, a shorter TMM, which implies a larger number density of ETGs due to mergers. Nevertheless, the good description of the ρETG evolution with our merger model strongly suggests that mergers are indeed the main process in massive ETGs assembly. Thus, a lower TMM (i.e., a higher merger rate that translates to an excess of ETGs) could be compensated by a positive value of fdisc, that reduces the number density of ETGs due to mergers.
Future observational studies will be important to better constraint the parameters of our model, and further theoretical efforts are needed to understand the uncertainties in the assumed parameters.
7. Summary and conclusions
Using SINFONI/VLT 3D spectroscopy, we have been able to measure, for the first time with spectroscopically-confirmed close pairs, the gas-rich major merger fraction and merger rate at around the peak in star formation activity at 0.9 < z < 1.8, from the MASSIV sample of star-forming galaxies with a stellar mass range M⋆ = 109−1011 M⊙. In this redshift range we identify 20 close pairs, and classify 13 as major mergers based on a separation rp ≤ 20 h-1 − 30 h-1 kpc and a relative velocity Δv ≤ 500 km s-1.
We find that the gas-rich major merger fraction is high,
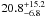 %,
%,
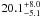 %,
and
%,
and 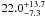 %
for rp ≤ 20 h-1 kpc close pairs in
redshift ranges
z = [0.94,1.06] , [1.2,1.5),
and [1.5,1.8), respectively. When compared to measurements at redshifts
z < 1, the evolution of the (gas-rich) merger
fraction can be parametrised as
fMM = 0.0066 × (1 + z)m
with m = 3.91 ± 0.16. We note that the evolution between
z = 1 and z ~ 1.5 seems to flatten out compared to lower
redshifts.
%
for rp ≤ 20 h-1 kpc close pairs in
redshift ranges
z = [0.94,1.06] , [1.2,1.5),
and [1.5,1.8), respectively. When compared to measurements at redshifts
z < 1, the evolution of the (gas-rich) merger
fraction can be parametrised as
fMM = 0.0066 × (1 + z)m
with m = 3.91 ± 0.16. We note that the evolution between
z = 1 and z ~ 1.5 seems to flatten out compared to lower
redshifts.
The merger rate has been derived using merger time scales from the literature: we find that
the gas-rich merger rate is 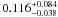 Gyr-1,
Gyr-1,
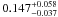 Gyr-1,
and
Gyr-1,
and 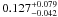 Gyr-1
at z = 1.03,1.32, and 1.54, respectively, for merger time
scales of TMM ~ 1.5 Gyr. We then find that the (gas-rich) merger
rate’s evolution for galaxies with stellar mass
Gyr-1
at z = 1.03,1.32, and 1.54, respectively, for merger time
scales of TMM ~ 1.5 Gyr. We then find that the (gas-rich) merger
rate’s evolution for galaxies with stellar mass 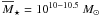 over
z = [0,1.5] scales as
(1 + z)n with
n = 3.95 ± 0.12.
over
z = [0,1.5] scales as
(1 + z)n with
n = 3.95 ± 0.12.
Using these measurements, we developed a simple model to estimate the contribution of
gas-rich major mergers to the growth of galaxies on the red sequence. We infer that ~ 35%
of the star-forming galaxies with stellar mass 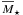 have undergone a major
merger since z ~ 1.5. The number of major merger events was about 5 times
higher at 1 < z < 1.5
compared to z < 1. Assuming that each gas-rich
major merger produces a new early-type galaxy, we infer that the number of gas-rich major
mergers is large enough at z > 1 to explain the
increase in the number density of massive ETGs, supporting a picture where gas-rich (wet)
merging is the main process building-up the red sequence. While gas-rich mergers become
rarer towards lower redshifts, the number of dry mergers is steadily increasing, and the
combination of these two processes accounts for most, if not all, of the increase in the
number density of massive ETGs since z ~ 1.3. Two-thirds of this number
density evolution is due to wet major mergers, while one-third is coming from major and
minor dry mergers. These results add further evidence to a picture where merging is a major
process driving mass assembly into the massive red sequence galaxies.
have undergone a major
merger since z ~ 1.5. The number of major merger events was about 5 times
higher at 1 < z < 1.5
compared to z < 1. Assuming that each gas-rich
major merger produces a new early-type galaxy, we infer that the number of gas-rich major
mergers is large enough at z > 1 to explain the
increase in the number density of massive ETGs, supporting a picture where gas-rich (wet)
merging is the main process building-up the red sequence. While gas-rich mergers become
rarer towards lower redshifts, the number of dry mergers is steadily increasing, and the
combination of these two processes accounts for most, if not all, of the increase in the
number density of massive ETGs since z ~ 1.3. Two-thirds of this number
density evolution is due to wet major mergers, while one-third is coming from major and
minor dry mergers. These results add further evidence to a picture where merging is a major
process driving mass assembly into the massive red sequence galaxies.
We note that minor merging is definitely present in the MASSIV sample (see Sect. 4). However, due to incompleteness in detecting these faint companions, we are not able to assess a minor merger rate at these epochs from our data. In the global picture of red sequence assembly, we emphasise that a simple extrapolation of the minor merger rate measured up to z ~ 1 by López-Sanjuan et al. (2011), would indicate that from z ~ 1.5 to the present, minor mergers with 1/10 ≤ μ < 1/4 are not common enough to significantly move spiral galaxies into the red sequence.
To get a complete picture of the life-time effect of major merging on massive galaxies, accurate measurements of the merger fraction and merger rate are needed beyond z ~ 2. Spectroscopic surveys will remain an important element to provide secure identification of merging systems at these early epochs.
Online material
Appendix A: Spectroscopic success rate in the VVDS-Wide fields
We computed the spectroscopic success rate (SSR) in the VVDS-Wide 14 h and 22 h fields
for a given redshift range by following the prescriptions in Ilbert et al. (2006): we compared the number of galaxies with flag =
4, 3 and 2 over the total number of galaxies (those with flag = 4, 3, 2, 1 and 0).
Because flag = 1 galaxies have a 50% reliability and no redshift information is
available for flag = 0 galaxies, we took advantage of the latest photometric redshifts
from CFHTLS survey to estimate the number of galaxies with flag = 1 and 0 that belong to
the redhsift range of interest. With the previous steps we estimate the SSR in the 22 h
field as 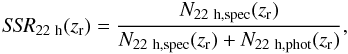 (A.1)where
N22 h,spec(zr)
is the number of galaxies with flag = 4, 3 and 2 in the redshift range
zr, and
N22 h,phot(zr)
is the number of galaxies with flag = 1 and 0, and with a photometric redshift in the
same redshift range. As the available imaging data in the 14 h eld is not as deep as the
CFHTLS, we show in the following that we can assume that the SSR in the 14 h field
follows the same distribution as in the 22 h field, for which CFHTLS photometry is
available.
(A.1)where
N22 h,spec(zr)
is the number of galaxies with flag = 4, 3 and 2 in the redshift range
zr, and
N22 h,phot(zr)
is the number of galaxies with flag = 1 and 0, and with a photometric redshift in the
same redshift range. As the available imaging data in the 14 h eld is not as deep as the
CFHTLS, we show in the following that we can assume that the SSR in the 14 h field
follows the same distribution as in the 22 h field, for which CFHTLS photometry is
available.
First we checked the properties of the stars in these two VVDS-Wide fields. The fraction of stars in the 22 h (14 h) field is 66% (51%) for flag = 4 sources, 38% (26%) for flag = 3 sources, 24% (23%) for flag = 2 sources, and 11% (12%) for flag = 1 sources. So the fraction of stars is similar in both fields for flag = 2 and 1 sources, while higher in the 22 h field for flag = 4 and 3. We checked that the normalised distributions of the VVDS-Wide stars as a function of their observed IAB-band magnitude in both fields are similar for each flag. We note that stars with high confidence flag are brighter than the low confidence ones, as expected. The fraction of bright stars (IAB ≤ 21) in the 22 h (14 h) field is 75% (67%) for flag = 4 stars, 49% (43%) for flag = 3 stars, 30% (29%) for flag = 2 stars, and 19% (16%) for flag = 1 stars. These fractions suggest that there is a higher density of bright stars in the 22 h area than in the 14 h one, that translates in a higher fraction of stars for flag = 4 and 3 sources, while faint stars have similar densities in both fields, leading to a similar fraction of stars with flag = 2 and 1. Because of this, we assumed that the fraction of stars among flag = 0 sources, that we estimate in the 22 h field from the CFHTLS photometry, is similar in 22 h and 14 h fields.
The distribution of galaxies at z ≥ 0.9, the redshift range in which
we are interested on, are also similar in both fields. Because of this, we assumed that
the photometric distribution of galaxies with flag = 1 and 0 is similar in both fields,
and we use those in 22 h field to estimate
N14 h,phot and the SSR in the 14 h
field: 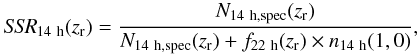 (A.2)where
n14 h(1,0) is the total number of
sources (galaxies and stars) with flag = 1 and 0 in the 14 h field, and
f22 h(zr) = N22 h,phot(zr)/n22 h(1,0)
is the fraction of sources with a photometric redshift in the redshift range
zr over the total population of sources with flag = 1 and
0 in the 22 h field.
(A.2)where
n14 h(1,0) is the total number of
sources (galaxies and stars) with flag = 1 and 0 in the 14 h field, and
f22 h(zr) = N22 h,phot(zr)/n22 h(1,0)
is the fraction of sources with a photometric redshift in the redshift range
zr over the total population of sources with flag = 1 and
0 in the 22 h field.
Appendix B: GALFIT residual images of blended MASSIV close pairs
 |
Fig. B.1 Original i-band image (left panels) and residual images from the GALFIT fit with one (central panels) and two components (right panels) of those MASSIV close pair candidates with overlapping components in the kinematical maps. The grey scale has been chosen to enhance the light residuals in the images. The solid contour marks the targeted MASSIV source to guide the eye. The ID of the showed MASSIV source is labelled in each left panel. |
In this Appendix we detail the modelling in the i band of those MASSIV close pair candidates with overlapping components in the kinematical maps. We used GALFIT v3.0 (Peng et al. 2010) to model the light distribution with two independent Sérsic components. We set the initial positions of the sources using the information from the kinematical maps, and we did not impose any constraint on the other initial parameters of the fit (i.e., luminosity, effective radius, Sérsic index, position angle and inclination). Because of the minimisation process preformed by GALFIT in the fitting, the best model with two components should not be unique and the convergence to a given solution should depend on the initial values of the parameters defined by the user. We checked, by exploring randomly the space of initial values, that the number of good solutions is at most two. Where two good solutions exist, the one that better reproduces both the velocity field and the velocity dispersion map is preferred. To illustrate the need of a second component to describe the blended close pair systems in MASSIV, we show in Fig. B.1 the original image in the i band and the residual image from GALFIT with one and two components. In all the cases the residual map from the one component fit suggests that a second component is present. This Figure also demonstrates that both the seeing (~0.7″) and the depth of the i-band images used in the present study are good enough to characterise sources with two overlapping components.
Appendix C: Completeness of the close pair sample
Throughout the present paper we have assumed that the close pair systems detected in the MASSIV sample are representative for galaxies with IAB ≤ 23.9. The MASSIV sample comprises galaxies fainter than this luminosity limit, and in this Appendix we justify the boundary applied in our analysis.
The VVDS parent samples of the MASSIV sample are randomly selected in the IAB band (Le Fèvre et al. 2005). Because of this, we studied the distribution of MASSIV sources as a function of the IAB-band magnitude to obtain clues about the completeness of the MASSIV sample in our close pair study. We show the cumulative distribution of all MASSIV sources and of those with a close companion (both major and no major) in the top panel of Fig. C.1. Obviously, we are able to detect single MASSIV galaxies at fainter magnitudes than the close pairs (IAB = 24.4 vs. 23.8) because in the latter case we have to detect both the principal source and the companion galaxy, which is usually fainter.
Lets assume for a moment that the detection curve of the MASSIV sources is a step function that is 1 for IAB ≤ IAB,lim and 0 for fainter magnitudes. In this ideal case, IAB,lim is defined by the fainter galaxy (close pair) detected. Thus, we should only be able to detect close pairs at IAB ≤ 23.8, and the measured merger fraction in the total MASSIV sample (IAB ≤ 24.4) will be lower than the real merger fraction because of the missing faint close pairs with IAB > 23.8. Of course, the detection curve in the MASSIV sample is more complicated than a step function, and could depend on redshift, geometry, luminosity, etc. Instead of trying to estimate the detection curve for MASSIV sources and for close companions to recover statistically the missing close pairs (see Patton et al. 2000; de Ravel et al. 2009, for examples of this kind of correction), we define the IAB-band magnitude up to which the detected close pairs are representative of the total MASSIV sample, named IAB,comp, and in our study we only keep those sources brighter than IAB,comp to ensure reliable merger fractions.
The MASSIV sample is a representative subsample of the global star-forming population (Contini et al. 2012), and we expect the MASSIV galaxy pairs to be also a random sample of this global population. Therefore, the distributions in the IAB band of the total and the close pair MASSIV sources should be similar when the close pairs detection was slightly affected by incompleteness issues. Following this idea, we performed a Kolmogorov-Smirnov (KS) test over the total and close pair MASSIV galaxies with IAB ≤ IAB,lim, and explored different values of IAB,lim, from 23.0 to 24.5. Then, the completeness magnitude IAB,comp was defined by the minimum in the KS estimator D, i.e., where both distributions have the lower probability to be different. This exercise provides the curve in the bottom panel of Fig. C.1, that states IAB,comp = 23.9. We repeated this procedure with the major merger sample, and we obtain a similar distribution of D values, reinforcing our choice.
In summary, in the estimation of the merger fraction we only use those MASSIV galaxies with IAB ≤ IAB,comp = 23.9. This ensures that the close pair sample is a random subsample of the total MASSIV one, and we avoid any bias related with the shallower detection curve of close pairs compared with that of the total MASSIV sample.
 |
Fig. C.1 Top: cumulative distribution in the apparent IAB magnitude of the total MASSIV sample (green line), the close pair sample (red line) and the total MASSIV sample with IAB ≤ 23.9 (blue line). Middle: the same than before, but the red line shows the distribution of the major merger sample. Bottom: Kolmogorov-Smirnov estimator D of the total MASSIV sample distribution against the close pair (blue solid line) and the major merger (red dashed line) distributions. We computed D for those galaxies brighter than a given IAB magnitude. The solid (dashed) horizontal line marks the minimum in the D distribution for close pairs (major mergers). The vertical solid line marks the IAB magnitude at the minimum value of D, IAB,comp = 23.9. |
Acknowledgments
We dedicate this paper to the memory of our six IAC colleagues and friends who met with a fatal accident in Piedra de los Cochinos, Tenerife, in February 2007, with a special thanks to Maurizio Panniello, whose teachings of python were so important for this paper.
We thank the comments and suggestions of the anonymous referee, and L. Pozzetti and F. Buitrago for kindly provide their number densities. This work has been supported by funding from ANR-07-BLAN-0228 and ERC-2010-AdG-268107-EARLY and partially supported by the CNRS-INSU and its Programme National Cosmologie-Galaxies (France) and by the French ANR grant ANR-07-JCJC-0009.
References
- Abazajian, K. N., Adelman-McCarthy, J. K., Agüeros, M. A., et al. 2009, ApJS, 182, 543 [NASA ADS] [CrossRef] [Google Scholar]
- Arnouts, S., Walcher, C. J., Le Fèvre, O., et al. 2007, A&A, 476, 137 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bell, E. F., Phleps, S., Somerville, R. S., et al. 2006, ApJ, 652, 270 [NASA ADS] [CrossRef] [Google Scholar]
- Bernardi, M., Shankar, F., Hyde, J. B., et al. 2010, MNRAS, 404, 2087 [NASA ADS] [Google Scholar]
- Bielby, R., Hudelot, P., McCracken, H. J., et al. 2012, A&A, 545, A23 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bluck, A. F. L., Conselice, C. J., Bouwens, R. J., et al. 2009, MNRAS, 394, L51 [NASA ADS] [CrossRef] [Google Scholar]
- Bluck, A. F. L., Conselice, C. J., Buitrago, F., et al. 2012, ApJ, 747, 34 [NASA ADS] [CrossRef] [Google Scholar]
- Bournaud, F., Chapon, D., Teyssier, R., et al. 2011, ApJ, 730, 4 [NASA ADS] [CrossRef] [Google Scholar]
- Bridge, C. R., Carlberg, R. G., & Sullivan, M. 2010, ApJ, 709, 1067 [NASA ADS] [CrossRef] [Google Scholar]
- Bruzual, G., & Charlot, S. 2003, MNRAS, 344, 1000 [NASA ADS] [CrossRef] [Google Scholar]
- Buitrago, F., Trujillo, I., Conselice, C. J., & Häußler, B. 2013, MNRAS, 428, 1460 [NASA ADS] [CrossRef] [Google Scholar]
- Bundy, K., Fukugita, M., Ellis, R. S., et al. 2009, ApJ, 697, 1369 [NASA ADS] [CrossRef] [Google Scholar]
- Cameron, E. 2011, PASA, 28, 128 [NASA ADS] [CrossRef] [Google Scholar]
- Cameron, E., & Pettitt, A. N. 2012, MNRAS, 425, 44 [NASA ADS] [CrossRef] [Google Scholar]
- Cappellari, M., Emsellem, E., Krajnović, D., et al. 2011, MNRAS, 413, 813 [NASA ADS] [CrossRef] [Google Scholar]
- Chou, R. C. Y., Bridge, C. R., & Abraham, R. G. 2011, AJ, 141, 87 [NASA ADS] [CrossRef] [Google Scholar]
- Conselice, C. J. 2003, ApJS, 147, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Conselice, C. J. 2006, ApJ, 638, 686 [NASA ADS] [CrossRef] [Google Scholar]
- Conselice, C. J., Bundy, K., Trujillo, I., et al. 2007, MNRAS, 381, 962 [NASA ADS] [CrossRef] [Google Scholar]
- Conselice, C. J., Rajgor, S., & Myers, R. 2008, MNRAS, 386, 909 [NASA ADS] [CrossRef] [Google Scholar]
- Conselice, C. J., Bluck, A. F. L., Buitrago, F., et al. 2011a, MNRAS, 413, 80 [NASA ADS] [CrossRef] [Google Scholar]
- Conselice, C. J., Bluck, A. F. L., Ravindranath, S., et al. 2011b, MNRAS, 417, 2770 [NASA ADS] [CrossRef] [Google Scholar]
- Contini, T., Garilli, B., Le Fèvre, O., et al. 2012, A&A, 539, A91 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Cucciati, O., Marinoni, C., Iovino, A., et al. 2010, A&A, 520, A42 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Cucciati, O., Tresse, L., Ilbert, O., et al. 2012, A&A, 539, A31 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Darg, D. W., Kaviraj, S., Lintott, C. J., et al. 2010, MNRAS, 401, 1043 [NASA ADS] [CrossRef] [Google Scholar]
- Davis, M., Faber, S. M., Newman, J., et al. 2003, in SPIE Conf. Ser. 4834, ed. P. Guhathakurta, 161 [Google Scholar]
- De Propris, R., Conselice, C. J., Liske, J., et al. 2007, ApJ, 666, 212 [NASA ADS] [CrossRef] [Google Scholar]
- de Ravel, L., Le Fèvre, O., Tresse, L., et al. 2009, A&A, 498, 379 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- de Ravel, L., Kampczyk, P., Le Fèvre, O., et al. 2011, A&A, submitted [arXiv:1104.5470] [Google Scholar]
- de Zeeuw, P. T., Bureau, M., Emsellem, E., et al. 2002, MNRAS, 329, 513 [NASA ADS] [CrossRef] [Google Scholar]
- Dekel, A., & Birnboim, Y. 2006, MNRAS, 368, 2 [NASA ADS] [CrossRef] [Google Scholar]
- Domingue, D. L., Xu, C. K., Jarrett, T. H., & Cheng, Y. 2009, ApJ, 695, 1559 [NASA ADS] [CrossRef] [Google Scholar]
- Dye, S., Warren, S. J., Hambly, N. C., et al. 2006, MNRAS, 372, 1227 [NASA ADS] [CrossRef] [Google Scholar]
- Eliche-Moral, M. C., Prieto, M., Gallego, J., et al. 2010, A&A, 519, A55 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Emsellem, E., Cappellari, M., Krajnović, D., et al. 2007, MNRAS, 379, 401 [NASA ADS] [CrossRef] [Google Scholar]
- Emsellem, E., Cappellari, M., Krajnović, D., et al. 2011, MNRAS, 414, 888 [NASA ADS] [CrossRef] [Google Scholar]
- Epinat, B., Tasca, L., Amram, P., et al. 2012, A&A, 539, A92 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- FörsterSchreiber, N. M., Genzel, R., Bouché, N., et al. 2009, ApJ, 706, 1364 [NASA ADS] [CrossRef] [Google Scholar]
- Franzetti, P., Scodeggio, M., Garilli, B., Fumana, M., & Paioro, L. 2008, in Astronomical Data Analysis Software and Systems XVII, eds. R. W. Argyle, P. S. Bunclark, & J. R. Lewis, ASP Conf. Ser., 394, 642 [Google Scholar]
- Garilli, B., Le Fèvre, O., Guzzo, L., et al. 2008, A&A, 486, 683 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Giavalisco, M., Ferguson, H. C., Koekemoer, A. M., et al. 2004, ApJ, 600, L93 [NASA ADS] [CrossRef] [Google Scholar]
- Goranova, Y., Hudelot, P., Magnard, F., et al. 2009, the CFHTLS T0006 Release [Google Scholar]
- Hopkins, P. F., Hernquist, L., Cox, T. J., Dutta, S. N., & Rothberg, B. 2008, ApJ, 679, 156 [NASA ADS] [CrossRef] [Google Scholar]
- Hopkins, P. F., Cox, T. J., Younger, J. D., & Hernquist, L. 2009, ApJ, 691, 1168 [Google Scholar]
- Hopkins, P. F., Croton, D., Bundy, K., et al. 2010, ApJ, 724, 915 [NASA ADS] [CrossRef] [Google Scholar]
- Huertas-Company, M., Aguerri, J. A. L., Tresse, L., et al. 2010, A&A, 515, A3 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ilbert, O., Lauger, S., Tresse, L., et al. 2006, A&A, 453, 809 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ilbert, O., Salvato, M., Le Floc’h, E., et al. 2010, ApJ, 709, 644 [NASA ADS] [CrossRef] [Google Scholar]
- Jogee, S., Miller, S. H., Penner, K., et al. 2009, ApJ, 697, 1971 [NASA ADS] [CrossRef] [Google Scholar]
- Khochfar, S., Emsellem, E., Serra, P., et al. 2011, MNRAS, 417, 845 [NASA ADS] [CrossRef] [Google Scholar]
- Kitzbichler, M. G., & White, S. D. M. 2008, MNRAS, 1300 [Google Scholar]
- Law, D. R., Steidel, C. C., Erb, D. K., et al. 2007, ApJ, 656, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Law, D. R., Steidel, C. C., Erb, D. K., et al. 2009, ApJ, 697, 2057 [NASA ADS] [CrossRef] [Google Scholar]
- Law, D. R., Steidel, C. C., Shapley, A. E., et al. 2012, ApJ, 745, 85 [NASA ADS] [CrossRef] [Google Scholar]
- Le Fèvre, O., Abraham, R., Lilly, S. J., et al. 2000, MNRAS, 311, 565 [NASA ADS] [CrossRef] [Google Scholar]
- Le Fèvre, O., Vettolani, G., Paltani, S., et al. 2004, A&A, 428, 1043 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Le Fèvre, O., Vettolani, G., Garilli, B., et al. 2005, A&A, 439, 845 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lilly, S. J., Le Fèvre, O., Renzini, A., et al. 2007, ApJS, 172, 70 [NASA ADS] [CrossRef] [Google Scholar]
- Lin, L., Koo, D. C., Willmer, C. N. A., et al. 2004, ApJ, 617, L9 [NASA ADS] [CrossRef] [Google Scholar]
- Lin, L., Patton, D. R., Koo, D. C., et al. 2008, ApJ, 681, 232 [NASA ADS] [CrossRef] [Google Scholar]
- Lin, L., Cooper, M. C., Jian, H., et al. 2010, ApJ, 718, 1158 [NASA ADS] [CrossRef] [Google Scholar]
- López-Sanjuan, C., García-Dabó, C. E., & Balcells, M. 2008, PASP, 120, 571 [NASA ADS] [CrossRef] [Google Scholar]
- López-Sanjuan, C., Balcells, M., García-Dabó, C. E., et al. 2009a, ApJ, 694, 643 [Google Scholar]
- López-Sanjuan, C., Balcells, M., Pérez-González, P. G., et al. 2009b, A&A, 501, 505 [Google Scholar]
- López-Sanjuan, C., Balcells, M., Pérez-González, P. G., et al. 2010a, A&A, 518, A20 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- López-Sanjuan, C., Balcells, M., Pérez-González, P. G., et al. 2010b, ApJ, 710, 1170 [NASA ADS] [CrossRef] [Google Scholar]
- López-Sanjuan, C., Le Fèvre, O., de Ravel, L., et al. 2011, A&A, 530, A20 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- López-Sanjuan, C., Le Fèvre, O., Ilbert, O., et al. 2012, A&A, 548, A7 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lotz, J. M., Jonsson, P., Cox, T. J., & Primack, J. R. 2008, MNRAS, 391, 1137 [NASA ADS] [CrossRef] [Google Scholar]
- Lotz, J. M., Jonsson, P., Cox, T. J., & Primack, J. R. 2010a, MNRAS, 404, 590 [NASA ADS] [CrossRef] [Google Scholar]
- Lotz, J. M., Jonsson, P., Cox, T. J., & Primack, J. R. 2010b, MNRAS, 404, 575 [NASA ADS] [CrossRef] [Google Scholar]
- Lotz, J. M., Jonsson, P., Cox, T. J., et al. 2011, ApJ, 742, 103 [NASA ADS] [CrossRef] [Google Scholar]
- Maiolino, R., Nagao, T., Grazian, A., et al. 2008, A&A, 488, 463 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Man, A. W. S., Toft, S., Zirm, A. W., Wuyts, S., & van der Wel, A. 2012, ApJ, 744, 85 [NASA ADS] [CrossRef] [Google Scholar]
- Mannucci, F., Cresci, G., Maiolino, R., et al. 2009, MNRAS, 398, 1915 [NASA ADS] [CrossRef] [Google Scholar]
- Mármol-Queraltó, E., Trujillo, I., Pérez-González, P. G., Varela, J., & Barro, G. 2012, MNRAS, 422, 2187 [NASA ADS] [CrossRef] [Google Scholar]
- Naab, T., Jesseit, R., & Burkert, A. 2006, MNRAS, 372, 839 [NASA ADS] [CrossRef] [Google Scholar]
- Newman, A. B., Ellis, R. S., Bundy, K., & Treu, T. 2012, ApJ, 746, 162 [NASA ADS] [CrossRef] [Google Scholar]
- Patton, D. R., & Atfield, J. E. 2008, ApJ, 685, 235 [NASA ADS] [CrossRef] [Google Scholar]
- Patton, D. R., Pritchet, C. J., Yee, H. K. C., Ellingson, E., & Carlberg, R. G. 1997, ApJ, 475, 29 [NASA ADS] [CrossRef] [Google Scholar]
- Patton, D. R., Carlberg, R. G., Marzke, R. O., et al. 2000, ApJ, 536, 153 [NASA ADS] [CrossRef] [Google Scholar]
- Peng, C. Y., Ho, L. C., Impey, C. D., & Rix, H.-W. 2002, AJ, 124, 266 [NASA ADS] [CrossRef] [Google Scholar]
- Peng, C. Y., Ho, L. C., Impey, C. D., & Rix, H.-W. 2010, AJ, 139, 2097 [NASA ADS] [CrossRef] [Google Scholar]
- Pérez-González, P. G., Rieke, G. H., Villar, V., et al. 2008, ApJ, 675, 234 [NASA ADS] [CrossRef] [Google Scholar]
- Pozzetti, L., Bolzonella, M., Zucca, E., et al. 2010, A&A, 523, A13 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Prieto, M., Eliche-Moral, M. C., Balcells, M., et al. 2013, MNRAS, 428, 999 [NASA ADS] [CrossRef] [Google Scholar]
- Puech, M., Hammer, F., Hopkins, P. F., et al. 2012, ApJ, 753, 128 [NASA ADS] [CrossRef] [Google Scholar]
- Queyrel, J., Contini, T., Kissler-Patig, M., et al. 2012, A&A, 539, A93 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Robaina, A. R., Bell, E. F., van der Wel, A., et al. 2010, ApJ, 719, 844 [NASA ADS] [CrossRef] [Google Scholar]
- Rodrigues, M., Puech, M., Hammer, F., Rothberg, B., & Flores, H. 2012, MNRAS, 421, 2888 [NASA ADS] [CrossRef] [Google Scholar]
- Rothberg, B., & Fischer, J. 2010, ApJ, 712, 318 [NASA ADS] [CrossRef] [Google Scholar]
- Rothberg, B., & Joseph, R. D. 2006a, AJ, 131, 185 [NASA ADS] [CrossRef] [Google Scholar]
- Rothberg, B., & Joseph, R. D. 2006b, AJ, 132, 976 [NASA ADS] [CrossRef] [Google Scholar]
- Ryan, Jr., R. E., Cohen, S. H., Windhorst, R. A., & Silk, J. 2008, ApJ, 678, 751 [NASA ADS] [CrossRef] [Google Scholar]
- Salpeter, E. E. 1955, ApJ, 121, 161 [Google Scholar]
- Scoville, N., Aussel, H., Brusa, M., et al. 2007, ApJS, 172, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Sérsic, J. L. 1968, Atlas de galaxias australes (Cordoba, Argentina: Observatorio Astronomico, 1968) [Google Scholar]
- Springel, V., White, S. D. M., Jenkins, A., et al. 2005, Nature, 435, 629 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- van der Wel, A., Rix, H.-W., Wuyts, S., et al. 2011, ApJ, 730, 38 [NASA ADS] [CrossRef] [Google Scholar]
- van Dokkum, P. G., Brammer, G., Fumagalli, M., et al. 2011, ApJ, 743, L15 [NASA ADS] [CrossRef] [Google Scholar]
- Vergani, D., Scodeggio, M., Pozzetti, L., et al. 2008, A&A, 487, 89 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Vergani, D., Epinat, B., Contini, T., et al. 2012, A&A, 546, A118 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Walcher, C. J., Lamareille, F., Vergani, D., et al. 2008, A&A, 491, 713 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Williams, R. J., Quadri, R. F., & Franx, M. 2011, ApJ, 738, L25 [NASA ADS] [CrossRef] [Google Scholar]
- Xu, C. K., Zhao, Y., Scoville, N., et al. 2012, ApJ, 747, 85 [NASA ADS] [CrossRef] [Google Scholar]
- Yang, Y., Flores, H., Hammer, F., et al. 2008, A&A, 477, 789 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Zucca, E., Ilbert, O., Bardelli, S., et al. 2006, A&A, 455, 879 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
All Tables
Gas-rich major merger fraction and rate of star-forming galaxies at 0.9 < z < 1.8 in the MASSIV sample.
All Figures
 |
Fig. 1 MASSIV selection in the [O ii]λ3727 flux [10-17 erg s-1 cm-2] vs. equivalent width [Å] plane (see Contini et al. 2012, for details). Red squares are the VVDS sources at 0.94 < z < 1.5 with individual [O ii]λ3727 line measurement in the VVDS-Wide 14 h (top-left), VVDS-Wide 22 h (top-right), VVDS-Deep (bottom-left), and VVDS-Ultradeep surveys (bottom-right). The dashed lines mark the selection of MASSIV star-forming galaxies. White dots are those VVDS sources that fulfil the MASSIV selection. Green pentagons are the MASSIV galaxies observed with SINFONI/VLT. (A colour version of this plot is available at the electronic edition.) |
| In the text | |
 |
Fig. 2 Typical field-of-view of a MASSIV source. We show the flux of the source 220397579 in the five channels of its reduced, flux calibrated, data cube centred on the position of the Hα emission line (scale in the right). The pixel spatial scale is 0.125″, that at the redshift of the source (z = 1.0379) corresponds to ~1 kpc. The source is at the centre of the image (black cross), while the white circle delimits the 20 h-1 kpc area around the source. In this particular case, 99% of this area is covered with MASSIV data and the two negatives of the source (black regions) are also excluded. |
| In the text | |
 |
Fig. 3 The i-band image (left panel, scale in ADU in the right), the velocity field (central panel, scale in km s-1 in the right), and the velocity dispersion map (right panel, scale in km s-1 in the right) of the MASSIV source 020294045 (major merger). On each map, North is up and East is left. The level contours mark the isophotes of the two components obtained with GALFIT in the i-band image. The principal galaxy (red/white) is the one closer to the kinematical centre of the system and sets the origin in right ascension (α) and declination (δ), while the companion (blue/black) is the secondary component. The outer contour marks the 3.43 ADU (7σsky) isophote. The next contours mark brighter isophotes in 1.96 ADU (4σsky) steps. The luminosity difference between both components in the i band, Δmi, as well as the CFHTLS exposure time, texp, are shown in the left panel. The redshift of the source and the on-source SINFONI exposure time, tSINFONI, are shown in the central panel. (A colour version of this plot is available at the electronic edition.) |
| In the text | |
 |
Fig. 4 The same as Fig. 3, but for the Ks-band image (left panel) of the MASSIV source 020294045 (major merger). The outer contour marks the 6.76 ADU (2σsky) isophote, while brighter isophotes increase in 5.07 ADU (1.5σsky) steps. The flux difference between both components in the Ks band, ΔmKs, as well as the WIRDS exposure time, texp, are show in the left panel. (A colour version of this plot is available at the electronic edition.) |
| In the text | |
 |
Fig. 5 The same as Fig. 3, but for the MASSIV source 020386743 (no major merger). The outer contour marks the 1.41 ADU (2σsky) isophote, while brighter isophotes increase in 1.76 ADU (2.5σsky) steps up to 10 ADU to avoid crowded figures. (A colour version of this plot is available at the electronic edition.) |
| In the text | |
 |
Fig. 6 The same as Fig. 3, but for the MASSIV source 020461235 (no major merger). The outer contour marks the 1.31 ADU (3σsky) isophote, while brighter isophotes increase in 1.75 ADU (4σsky) steps up to 7 ADU to avoid crowded figures. (A colour version of this plot is available at the electronic edition.) |
| In the text | |
 |
Fig. 7 Left and central panels are the same as in Fig. 3, but for the MASSIV source 140096645 (no major merger). The level contours mark the isophotes of the original i-band image. The Hα companion source is not detected in the i band. The outer contour marks the 2.64 ADU (1σsky) isophote, while brighter isophotes increase in 7.94 ADU (3σsky) steps up to 45 ADU to avoid crowded figures. The right panel shows the detection fraction of fake galaxies injected in the i-band image as a function of the magnitude of the companion source mi,2. The size of the dots marks the detection curves for extended, normal and compact galaxies (see text for details). The vertical line marks the limiting magnitude for major companion (Δmi = 1.5). (A colour version of this plot is available at the electronic edition.) |
| In the text | |
 |
Fig. 8 The same as Fig. 3, but for the MASSIV source 220397579 (major merger). The level contours mark the isophotes of the original i-band image. The outer contour marks the 5.36 ADU (3σsky) isophote, while brighter isophotes increase in 2.68 ADU (1.5σsky) steps. (A colour version of this plot is available at the electronic edition.) |
| In the text | |
 |
Fig. 9 The same as Fig. 3, but for the MASSIV source 220544394 (major merger). The outer contour marks the 4.31 ADU (2σsky) isophote, while brighter isophotes increase in 3.23 ADU (1.5σsky) steps. (A colour version of this plot is available at the electronic edition.) |
| In the text | |
 |
Fig. 10 The same as Fig. 8, but for the MASSIV source 020167131 (major merger). The outer contour marks the 3.43 ADU (10σsky isophote, while brighter isophotes increase in 2.74 ADU (8σsky) steps. (A colour version of this plot is available at the electronic edition.) |
| In the text | |
 |
Fig. 11 The same as Fig. 7, but for the MASSIV source 020218856 (no major merger). The Hα companion galaxy is not detected in the i band. The outer contour marks the 0.34 ADU (1σsky) isophote, while brighter isophotes increase in 1.01 ADU (3σsky) steps. (A colour version of this plot is available at the electronic edition.) |
| In the text | |
 |
Fig. 12 The same as Fig. 7, but for the MASSIV source 020240675 (no major merger). The Hα companion galaxy is not detected in the i band. The outer contour marks the 0.36 ADU (1σsky) isophote, while brighter isophotes increase in 1.08 ADU (3σsky) steps up to 8 ADU to avoid crowded figures. (A colour version of this plot is available at the electronic edition.) |
| In the text | |
 |
Fig. 13 The same as Fig. 3, but for the MASSIV source 020283083 (major merger). The outer contour marks the 2.12 ADU (4σsky) isophote, while brighter isophotes increase in 1.06 ADU (2σsky) steps. (A colour version of this plot is available at the electronic edition.) |
| In the text | |
 |
Fig. 14 The same as Fig. 3, but for the MASSIV source 020283830 (no major merger). The outer contour marks the 1.14 ADU (3.5σsky) isophote, while brighter isophotes increase in 0.75 ADU (2.3σsky) steps. (A colour version of this plot is available at the electronic edition.) |
| In the text | |
 |
Fig. 15 The same as Fig. 3, but for the MASSIV source 020465775 (major merger). The outer contour marks the 2.92 ADU (9σsky) isophote, while brighter isophotes increase in 0.97 ADU (3σsky) steps. (A colour version of this plot is available at the electronic edition.) |
| In the text | |
 |
Fig. 16 The same as Fig. 3, but for the MASSIV source 220376206 (no major merger). The outer contour marks the 3.39 ADU (3σsky) isophote, while brighter isophotes increase in 2.26 ADU (2σsky) steps. (A colour version of this plot is available at the electronic edition.) |
| In the text | |
 |
Fig. 17 The same as Fig. 3, but for the MASSIV source 220544103 (major merger). The outer contour marks the 3.32 ADU (2σsky) isophote, while brighter isophotes increase in 3.32 ADU (2σsky) steps. (A colour version of this plot is available at the electronic edition.) |
| In the text | |
 |
Fig. 18 The same as Fig. 3, but for the MASSIV source 910154631 (major merger). The outer contour marks the 1.9 ADU (6σsky) isophote, while brighter isophotes increase in 0.8 ADU (2.5σsky) steps. (A colour version of this plot is available at the electronic edition.) |
| In the text | |
 |
Fig. 19 The same as Fig. 8, but for the MASSIV source 910296626 (major merger). The outer contour marks the 3.32 ADU (10σsky) isophote, while brighter isophotes increase in 2.56 ADU (8σsky) steps. (A colour version of this plot is available at the electronic edition.) |
| In the text | |
 |
Fig. 20 The same as Fig. 8, but for the MASSIV source 910337228 (major merger). The outer contour marks the 1.73 ADU (4σsky) isophote, while brighter isophotes increase in 1.30 ADU (3σsky) steps. (A colour version of this plot is available at the electronic edition.) |
| In the text | |
 |
Fig. 21 The same as Fig. 8, but for the MASSIV source 020116027 (major merger). The principal galaxy is that in the south-east. The outer contour marks the 2.02 ADU (3.5σsky) isophote, while brighter isophotes increase in 1.16 ADU (2σsky) steps. (A colour version of this plot is available at the electronic edition.) |
| In the text | |
 |
Fig. 22 The same as Fig. 3, but for the MASSIV source 910186191 (major merger). The outer contour marks the 2.83 ADU (8σsky) isophote, while brighter isophotes increase in 2.83 ADU (8σsky) steps. (A colour version of this plot is available at the electronic edition.) |
| In the text | |
 |
Fig. 23 The same as Fig. 3, but for the MASSIV source 910274060 (major merger). The outer contour marks the 1.20 ADU (3σsky) isophote, while brighter isophotes increase in 1.00 ADU (2.5σsky) steps. The grey dot in the central figure marks the centre of the system given by the kinematical model, while the red/blue dot marks the photometric centre of the principal/companion galaxy given by the two-component model of the source. The long bars mark the position angle of the previous models. The short bar marks the photometric position angle given by the one-component model of the source. (A colour version of this plot is available at the electronic edition.) |
| In the text | |
 |
Fig. 24 Gas-rich major merger fraction of |
| In the text | |
 |
Fig. 25 Gas-rich major merger rate of |
| In the text | |
 |
Fig. 26 Number density evolution of massive (M⋆ ≥ 1011.25 M⊙) ETGs (E/S0) as a function of redshift from Buitrago et al. (2013, pentagons) and Pozzetti et al. (2010, squares). The dashed line is the expected number density evolution due to gas-rich (wet) major mergers from our model. The solid line is the expected number density evolution due to wet major and dry mergers (both major and minor) from our model. Mergers are common enough to drive the number density evolution of massive ETGs since z ~ 1.3. (A colour version of this plot is available at the electronic edition.) |
| In the text | |
 |
Fig. 27 Number density distribution from the different functions in Eq. (11) at z = 1. The solid line is the stellar mass function (Φ) multiplied by the major merger rate (RMM). The dashed line includes the major merger efficiency function (EMM). The dotted line includes the fraction of late-type galaxies (fLTG) and provides the final function that we integrate over stellar mass and cosmic time to obtain ρwet. The vertical dashed line marks the limiting stellar mass that define massive galaxies, M⋆, lim = 1011.25 M⊙, while the dotted lines mark the stellar masses M ⋆ ,1 = 1010.15 M⊙ and M ⋆ ,2 = 1011.05 M⊙ when fsf = 0 (see text for details). (A colour version of this plot is available at the electronic edition.) |
| In the text | |
 |
Fig. 28 Fraction of late-type galaxies as a function of redshift (top panel) and stellar mass at z ~ 0 (bottom panel). The redshift data points are from Buitrago et al. (2013), and the stellar mass ones from Bernardi et al. (2010) in the SDSS. The line in both panels is the best least-squares linear fit to the data. (A colour version of this plot is available at the electronic edition) |
| In the text | |
 |
Fig. B.1 Original i-band image (left panels) and residual images from the GALFIT fit with one (central panels) and two components (right panels) of those MASSIV close pair candidates with overlapping components in the kinematical maps. The grey scale has been chosen to enhance the light residuals in the images. The solid contour marks the targeted MASSIV source to guide the eye. The ID of the showed MASSIV source is labelled in each left panel. |
| In the text | |
 |
Fig. C.1 Top: cumulative distribution in the apparent IAB magnitude of the total MASSIV sample (green line), the close pair sample (red line) and the total MASSIV sample with IAB ≤ 23.9 (blue line). Middle: the same than before, but the red line shows the distribution of the major merger sample. Bottom: Kolmogorov-Smirnov estimator D of the total MASSIV sample distribution against the close pair (blue solid line) and the major merger (red dashed line) distributions. We computed D for those galaxies brighter than a given IAB magnitude. The solid (dashed) horizontal line marks the minimum in the D distribution for close pairs (major mergers). The vertical solid line marks the IAB magnitude at the minimum value of D, IAB,comp = 23.9. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.