| Issue |
A&A
Volume 552, April 2013
|
|
|---|---|---|
| Article Number | A63 | |
| Number of page(s) | 12 | |
| Section | Stellar structure and evolution | |
| DOI | https://doi.org/10.1051/0004-6361/201220230 | |
| Published online | 26 March 2013 | |
Fundamental stellar and accretion disc parameters of the eclipsing binary DQ Velorum⋆
1 Universidad de Concepción, Departamento de Astronomía, Concepción, Casilla 36 D, Chile
e-mail: dbarria@astro-udec.cl; rmennick@astro-udec.cl
2 European Southern Observatory, Vitacura, Santiago, Chile
e-mail: lschmidt@eso.org; mvuckovi@eso.org
3 Astronomical Observatory, PO Box 74, 11060 Belgrade, Serbia
e-mail: gdjurasevic@aob.rs
4 Isaac Newton Institute of Chile, Yugoslavia Branch, Casilla 8-9, Correo 9, Santiago, Chile
5 Instytut Astronomiczny Uniwersytetu Wroclawskiego, 51-622 Wrocław, Poland
e-mail: zibi@astro-udec.cl; michalska.gabi@gmail.com
6 Astronomical Institute, Wrocław University, 51-622 Wrocław, Poland
e-mail: eniem@astro.uni.wroc.pl
Received: 14 August 2012
Accepted: 25 January 2013
Context. To add to the growing collection of well-studied double periodic variables (DPVs) we have carried out the first spectroscopic and photometric analysis of the eclipsing binary DQ Velorum to obtain its main physical stellar and orbital parameters.
Aims. Combining spectroscopic and photometric observations that cover several orbital cycles allows us to estimate the stellar properties of the binary components and the orbital parameters. We also searched for circumstellar material around the more massive star.
Methods. We separated DQ Velorum composite spectra and measured radial velocities with an iterative method for double spectroscopic binaries. We obtained the radial velocity curves and calculated the spectroscopic mass ratio. We compared our single-lined spectra with a grid of synthetic spectra and estimated the temperature of the stars. We modeled the V-band light curve with a fitting method based on the simplex algorithm, which includes an accretion disc. To constrain the main stellar parameters we fixed the mass ratio and donor temperature to the values obtained by our spectroscopic analysis.
Results. We obtain a spectroscopic mass ratio q = 0.31 ± 0.03 together with donor and gainer masses Md = 2.2 ± 0.2 M⊙, Mg = 7.3 ± 0.3 M⊙, the radii Rd = 8.4 ± 0.2 R⊙, Rg = 3.6 ± 0.2 R⊙ and temperatures Td = 9400 ± 100 K, Tg = 18 500 ± 500 K for the stellar components. We find that DQ Vel is a semi-detached system consisting of a B3V gainer and an A1III donor star plus an extended accretion disc around the gainer. The disc is filling 89% of the gainer Roche lobe with a temperature of 6580 ± 300 K at the outer radius. It has a concave shape that is thicker at its edge (de = 0.6 ± 0.1 R⊙) than at its centre (dc = 0.3 ± 0.1 R⊙). We find a significant sub-orbital frequency of 0.19 d-1 in the residuals of the V-band light curve, which we interpret as a pulsation of an slowly pulsating B-type (SPB) of a gainer star. We also estimate the distance to the binary (d ~ 3.1 kpc) using the absolute radii, apparent magnitudes, and effective temperatures of the components found in our study.
Key words: binaries: eclipsing / stars: fundamental parameters / stars: early-type / circumstellar matter / stars: oscillations
Table 1 is available in electronic form at http://www.aanda.org
© ESO, 2013
1. Introduction
Discovered by Hoffmeister (1949), DQ Velorum (TYC 8175-333-1, ASAS J093034-5011.9) is a Galactic eclipsing binary of Algol-type with an orbital period of 6.08337 d (Hoffmeister 1949). Considering that DQ Vel is a bright system (V ~ 10.7), it is still poorly analysed in detail.
A study of the system using photographic plates was made by van Houten (1950), who determined the following ephemeris for the primary minimum: 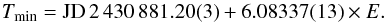 (1)Milone (1986), using UVB photometry, indicated that DQ Vel shows a β Lyrae-like light curve and investigated the O’Connell effect on the system (O’Connell 1951), studying the differential light between maxima of the light curves. He concluded that the O’Connell effect is positive and stronger in the U band. He also used low-resolution spectra obtained at the Cerro Tololo inter-american observatory with the image-tube spectrograph at the Yale 1-m telescope to obtain an estimate of the spectral type as A3V. However, no attempt was made to measure the radial velocities.
(1)Milone (1986), using UVB photometry, indicated that DQ Vel shows a β Lyrae-like light curve and investigated the O’Connell effect on the system (O’Connell 1951), studying the differential light between maxima of the light curves. He concluded that the O’Connell effect is positive and stronger in the U band. He also used low-resolution spectra obtained at the Cerro Tololo inter-american observatory with the image-tube spectrograph at the Yale 1-m telescope to obtain an estimate of the spectral type as A3V. However, no attempt was made to measure the radial velocities.
More recently, Michalska et al. (2010) discovered an additional long-term variability of 188.9 d using ASAS photometric data. This places the system in the new group of variable stars called double periodic variables (hereafter DPVs). This group of interacting binaries is characterised by two photometric variabilities linked one to each other with a period ratio of about 33 (Mennickent et al. 2003; Mennickent & Kołaczkowski 2010). The short-term variability corresponds to the orbital motion of the binary while the long-term variability is still not completely understood. DPVs have been interpreted as semi-detached binaries showing cycles of mass loss into the interstellar medium (Mennickent et al. 2008, 2012b).
To study these interesting objects, an intense observational effort is being carried out to find DPVs both in the Galaxy and the Magellanic Clouds using the microlensing surveys OGLE and MACHO (Mennickent et al. 2005; Poleski et al. 2010), as well as in the ASAS project. At present, there are more than 150 DPVs discovered in the Magellanic Clouds and 11 systems (including DQ Vel) in the Milky Way (Mennickent et al. 2012a). Results of multiwavelength spectroscopy and/or photometry have made it possible to study DPVs in more detail, such as AU Mon (Desmet et al. 2010; Djurašević et al. 2010), V393 Sco (Mennickent et al. 2010, 2012a), and LP Ara (Mennickent et al. 2011).
Here, we present the first optical spectroscopic analysis of DQ Vel using 46 high-resolution spectra that cover several orbital cycles. Our analysis includes the separated components with a determination of their radial velocity curves, an estimation of the spectroscopic mass ratio, stellar and system parameters, and the spectral type of the two components.
To constrain the main stellar parameters we also include in our analysis V-band light curves obtained from the public ASAS archive and VIJK photometric data obtained by Michalska et al. (2010) at the REM 0.6-m telescope at La Silla.
2. Observations
To investigate the fundamental properties of DQ Vel we collected a series of high-resolution optical spectra between April 2008–2011. Most of the spectra were taken with the 1.2 m Leonard Euler Swiss telescope at the La Silla Observatory using the CORALIE echelle fiber-fed spectrograph. In our analysis we also included five spectra obtained in June 2008 and May 2009 from the 2.5 m Irénée du Pont telescope echelle spectrograph at the Las Campanas Observatory as well as two spectra taken with the echelle spectrograph FEROS mounted at the ESO/MPI 2.2 m telescope at La Silla. A detailed summary of our spectroscopic observations is given in Table 1. The orbital phases φo were calculated using the ephemeris obtained by Michalska et al. (2010); they are detailed in Sect. 3.3. The echelle spectrograph at Du Pont has a wavelength coverage from ~3700 to 7000 Å. The instrument resolution is 45 000 for one arc-sec slit. These data were reduced with the standard procedures of de-biasing, flat-fielding, background subtraction, extraction of one-dimensional spectra, wavelength calibration, cosmic spike removal and continuum normalisation using the Image Reduction and Analysis Facility IRAF1. The reduced spectra were then subjected to barycentric corrections.
The high-resolution FEROS spectrograph (R ~ 48 000) has a slightly broader spectral range than CORALIE, from 3500 to 9200 Å (Kaufer et al. 1999, 2000). The FEROS data presented here were previously reduced by the FEROS Data Reduction System (DRS), which includes barycentric corrections and the standard procedures mentioned above except for continuum normalisation, which was made using the continuum task of IRAF.
The CORALIE spectrograph was developed to measure precise stellar radial velocities. The maximum spectral resolution of about 100 000. The instrument has an automatic reduction software (Baranne et al. 1996) that provides fully calibrated images and computes barycentric velocities. Just as with the FEROS spectrograph, CORALIE uses a simultaneous Thorium lamp spectrum during the science exposures, which allows a regular wavelength calibration. Here we used the CORALIE spectra reduced with this automatic pipeline. Cosmic spikes were removed manually. It should be noted here that we found a small-amplitude (lower than 1% of the total flux) continuum modulation, most likely produced by an imperfect automatic extraction of the orders. To attenuate or remove this modulation we subdivided each CORALIE spectrum into different wavelength intervals. For each interval we applied the continuum task using the spline3 function with a corresponding order (different in each interval), to create a “continuum normalised” interval. We repeated this procedure for all spectra using the same wavelength intervals, same function, and same orders as used for the first spectrum. Finally, we combined the corresponding intervals of each spectrum to create a final normalised spectrum. Although the data quality significantly improved, there still remain some residuals, which were further attenuated by applying a high-frequency Fourier filter to the spectra during the cross-correlation process, as will be explained in Sect. 3.1.
Our photometric analysis includes a V-band light curve obtained from the public ASAS database2. The observations include 583 frames taken in different epochs during November 2000–2009. Typical errors on these data are less than 0.06 mag. The VIJK photometric data used here were obtained with the REM 0.6 m telescope at La Silla, which were previously reported by Michalska et al. (2010), who decoupled the short- and long-term variabilities using the Fourier decomposition technique. The observational campaign included 1051 frames in the V − I bands and 345 frames in the J − K bands. Details of the photometric data are presented in Table 2.
Detailed photometric data used in this paper. First column is the observing window and N is the number of frames.
3. Results
3.1. Spectral separation and radial velocity curves
To investigate if DQ Vel is a single or double line spectroscopic binary we analysed the 46 spectra listed in Table 1. We detected known absorption lines and calculated their corresponding Doppler shifts. Excluding the intense and broader Balmer lines that seem to contain several components, we selected the stronger and unblended lines: HeI 4387.929 Å, MgII 4481.126 Å, FeI 4957.596 Å, HeI 5875.614 Å, the silicon doblet SiII 6347.103 Å/6371.359 Å, and HeI 6678.151 Å. We directly measured each line position fitting a Gaussian profile using the IRAF task splot and calculated their corresponding radial velocities. We measured each line at least four times to obtain an estimate of the error. We found that all selected HeI lines seem to belong to the more massive star (hereafter gainer) while the metal lines apparently belong to the less massive star (hereafter donor). Averaging the Doppler shifts measured for each line, we calculated mean radial velocities (RVs) for the gainer and donor star in each spectrum. The resulting RV measurements are plotted in Fig. 1. Preliminar inspection of these RV curves shows a defined sinusoidal curve for the donor star. The orbit seems to be circular; if eccentricity is present, its value is negligible within the errors.
 |
Fig. 1 Mean RVs obtained by direct measurement. Donor velocities were obtained averaging the Doppler shifts for the MgII 4481 Å, FeI 4957 Å, SiII 6347 Å, and SiII 6371 Å lines. HeI lines were used to calculate gainer velocities. |
We observed more scatter on the gainer velocities. We attributed this to the fact that the helium lines are broader than the donor’s metal lines, which results in a higher uncertainty on the determination of the line centre. Possible causes for the broadening of the helium lines and/or for the large scatter observed on the gainer RVs are either a hot rapidly rotating star, as expected for a gainer that is accreting angular momentum together with the material, or line profiles blended by the contribution of a non-symmetrical pseudo-photosphere or disc. Yet another cause could be that the gainer is a pulsating star (see Sect. 3.5). Using the last calculated RVs, we decided to separate the individual spectra to obtain more precise RVs. We used a simple iterative method originally proposed by Marchenko et al. (1998), which was used more recently by González & Levato (2006), who applied this method for the orbital analysis of the binary HD143511. In general terms, this method is able to separate both components, providing two higher signal-to-noise (S/N) single-line spectra templates, which can be used to calculate individual RVs, for instance through a cross-correlation process (Griffin 1967; Hill 1993). The Fourier cross-correlation process (hereafter CCR) convolves two functions (spectra against the template) using a Fourier transform algorithm to find the so-called cross-correlation function (CCF). Considering that ~80% of our data are from the CORALIE spectrograph and that the accuracy of a relative velocity measured with the CCR process increases using a narrow CCF (Hilditch 2001), we applied separating and CCR processes only to the CORALIE data. The main reason for this is that lines on the template spectrum and the observed spectra will have similar shapes and widths, which decreases the broadening of the CCF.
 |
Fig. 2 Separated spectra of DQ Vel. The composite spectrum (top) at φo = 0.8110 is used here as a reference from the list in Table 1. Final S/N for the decomposed spectra are 97 (middle) and 267 (bottom) for the donor and gainer star. The spectra were offset for clarity. |
Using previously calculated CORALIE RVs, we shifted all spectra to the donor rest-frame and combined these to create a first-guess spectral template for the donor star. This template is an orbital-cycle averaged single-line spectrum. This procedure attenuates the spectral features of the remaining component (gainer). Subtracting this donor template from all spectra and shifting the resulting spectra to the gainer rest-frame, we combined the data again to obtain an orbital-cycle-averaged template for the gainer star. We repeated this procedure until the residuals of one component contribution disappeared from the template spectra of the other. According to González & Levato (2006), no more than 5–7 iterations are necessary considering that with each iteration the residuals are reduced by a factor 1/n, where n is the number of observed spectra. Figure 2 shows a portion of our separated spectra after six iterations.
We applied a 1D Fourier CCR process to the observed spectra and previously obtained templates using the IRAF fxcor task. For binaries this task works as follows: we select the template of one component (which is by construction at rest in the barycentric frame), and convolve it with each of the observed spectra in which the spectral lines move according to the relative motion of the binary. The maximum of the CCF will be, in this case, the shifted velocity of the spectrum relative to the template. The process is then repeated using the other template. In this way, we obtain the relative velocities of each spectrum with respect to the donor and gainer templates.
During the CCR process and to finally remove the weak modulation found on the CORALIE spectra, we applied a Hanning-type filter to the template and the observed spectra after the data were transformed and prior to correlation. This Hanning-filter function is used to attenuate the Fourier components over a specific wavenumber range to remove remaining high-frequency noise that was not removed by the continuum subtraction.
Calculated RVs for DQ Velorum using 1D CCR.
From the donor template, we calculated RVs independently in two spectral ranges at 4500–4800 Å and 4900–5600 Å, where we found more spectral lines from the donor star. A third measurement was made in both spectral ranges simultaneously. Final RVs were obtained by taking the mean between these three measurements. We applied the same procedure using the gainer template in the 4350–4750 Å and 4900–5300 Å ranges. Table 3 shows our final RVs determined from the CCR process and their corresponding rms errors.
In Table 4 we show the RVs for the remaining spectra that were not included in the CCR process.
RVs for Du Pont/echelle and MPI/FEROS spectra not included in the CCR process.
To use all available RV measurements, we decided to obtain the mean RV value in orbital phase bins of 0.05. We fitted the RV curves with a sinus function. Best fits and circular-orbit solutions are shown in Fig. 3 and Table 5. The different γ obtained for the gainer suggests that their lines are influenced by circumstellar material.
 |
Fig. 3 RV curves and best sinus fit for DQ Vel components. Each RV was measured from Table 3 and Table 4 taking the mean value in orbital phase bins of 0.05. |
Circular-orbit solutions obtained for the best sinus fits.
Based on these results, we determined the projected semi-major axes and minimum masses for donor and gainer star using the expressions by Hilditch (2001) for a circular orbit:
![\begin{eqnarray} && a_\mathrm{d,g} \sin i = \left(1.9758 \times 10^{-2}\right) K_\mathrm{d,g} P_\mathrm{o}\, [R_{\odot}] \\[2mm] && a_\mathrm{d} \sin i = 22.288 \pm 0.596 \, [R_{\odot}] \end{eqnarray}](/articles/aa/full_html/2013/04/aa20230-12/aa20230-12-eq148.png)
![\begin{eqnarray} && a_\mathrm{g} \sin i = 6.917 \pm 0.665 \, [R_{\odot}] \\[2mm] && m_\mathrm{d,g} \sin^{3} i = (1.0361 \times 10^{-7})(K_\mathrm{d}+K_\mathrm{g})^{2} K_\mathrm{g,d} P_\mathrm{o}\, [M_{\odot}] \\[2mm] && m_\mathrm{d} \sin^{3} i = 2.141 \pm 0.244\, [M_{\odot}] \\[2mm] && m_\mathrm{g} \sin^{3} i = 6.901 \pm 0.460\, [M_{\odot}], \end{eqnarray}](/articles/aa/full_html/2013/04/aa20230-12/aa20230-12-eq149.png) where ad and ag are the donor and gainer semi-major axes measured in solar radii (R⊙), md and mg are the donor and gainer masses measured in solar masses (M⊙), Kd and Kg are the semi-amplitudes of the RV curves expressed in km s-1, Po is the orbital period in days, and i the orbital inclination of the system.
where ad and ag are the donor and gainer semi-major axes measured in solar radii (R⊙), md and mg are the donor and gainer masses measured in solar masses (M⊙), Kd and Kg are the semi-amplitudes of the RV curves expressed in km s-1, Po is the orbital period in days, and i the orbital inclination of the system.
It can be shown that independently of the orbital inclination, Eq. (5) yields 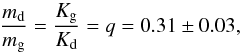 (8)which represents the spectroscopic mass ratio q of the system. Note that for this q value we assumed that the observed RV variations of the gainer’s lines represent the motion of the gainer.
(8)which represents the spectroscopic mass ratio q of the system. Note that for this q value we assumed that the observed RV variations of the gainer’s lines represent the motion of the gainer.
If we consider that the donor star fills its Roche lobe, we can approximate the donor radius (Rd) to the size of the donor Roche lobe according to Eggleton (1983): 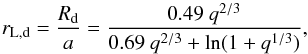 (9)where a is the semimajor axis of the relative orbit.
(9)where a is the semimajor axis of the relative orbit.
For q = 0.31 ± 0.03, we obtain 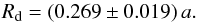 (10)For an eclipsing binary with an orbital inclination 70° ≤ i ≤ 90° we can estimate a donor radius between (7.856 ± 0.604) R⊙ ≤ Rd ≤ (8.366 ± 0.643) R⊙, which indicates an oversized star based on the previous mass value.
(10)For an eclipsing binary with an orbital inclination 70° ≤ i ≤ 90° we can estimate a donor radius between (7.856 ± 0.604) R⊙ ≤ Rd ≤ (8.366 ± 0.643) R⊙, which indicates an oversized star based on the previous mass value.
We can also determine the maximum value for the equatorial rotational velocity of the donor assuming it is rotating synchronously: 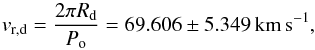 (11)for which we used the maximum donor radius obtained above.
(11)for which we used the maximum donor radius obtained above.
3.2. Spectral type classification and analysis of spectral features
The donor star template shows several absorption metal lines including FeI − II, MgI − II, TiII, CrII, and SiII. Some lines like FeII 4233.2 Å, FeI 4383.5 Å, MgI 5167.3 Å, MgII 5528.4 Å, and SiII 5688.8 Å were not clearly identified in the original spectra. We compared our donor template with a grid of synthetic spectra in the region 5200–5350 Å which is deprived of hydrogen and helium lines but has several metal lines. To determine the grid of synthetic fluxes we used atmospheric models computed with the line-blanketed LTE ATLAS9 code (Kurucz 1993), which treats line opacity with opacity distribution functions (ODFs). The Kurucz models are constructed assuming plane-parallel geometry and hydrostatic and radiative equilibrium of the gas. The synthetic spectra were computed with the SYNTHE code (Kurucz 1993). Both codes, ATLAS9 and SYNTHE, were ported under GNU Linux by Sbordone (2005) and are available online3. The atomic data were taken from Castelli & Hubrig (2004)4. The theoretical models were obtained for effective temperatures from 6000 to 10 000 K with steps of 100 K and for surface gravities from 2.0 to 4.5 dex with steps of 0.1 dex. Solar and 0.5 dex higher metallicities were taken into account. The grid of synthetic spectra was calculated for five different rotation velocities, vrsini = 0, 25, 50, 75 and 100 km s-1. We subtracted the donor template from every grid spectrum and analysed the residuals of the resulting spectra. The best model is obtained for an A-type star with Td = 9400 K, log gd = 3.1, vr sini = 75 km s-1 and solar metallicity. To obtain a more restricted value for the rotational velocity, we decided to interpolate between the different values of rotation velocities generated in the grid of synthetic spectra. We selected four synthetic spectra from the grid with T = 9400 K, log g = 3.1 and velocities of 25, 50, 75, and 100 km s-1. We measured the full width at half maximum (fwhm) for the isolated and unblended metal lines MgI 4703.0 Å, MgII 4481.3 Å, TiII 4780.0/4805.1 Å, and SiII 6371.3 Å. We plot in Fig. 4 the fwhm-vrsini calibration curves. We calculated the fwhm for the same spectral lines in the donor template and determined a mean velocity of vr,dsini = 65 ± 4 km s-1, which agrees with our previous result of Eq. (11).
 |
Fig. 4 Calibration curves for measured fwhm (Å) of MgI 4703.0 Å, MgII 4481.3 Å, TiII 4780.0/4805.1 Å, and SiII 6371.3 Å lines plotted against vr sin i. |
A first inspection of spectral features in the gainer template suggests a B-type star with marked Balmer and helium lines like HeI 4026/4471/4921/5015/5875/6678 Å and also a few and weak metal lines such as FeII 4303/5169/5276 Å, MgII 4481 Å, and SiII 4133 Å. We also observed asymmetric profiles in the helium and Balmer lines after the separation, as shown in Fig. 7.
 |
Fig. 5 Donor light contribution with respect to the total light calculated from the light curve model. Each curve shows the donor contribution for a specific spectral range around a spectral line. The selected spectral lines (and ranges) are from top to the bottom: HeI 6678 Å, Hα, HeI 5875 Å, Hβ, HeI 4471 Å, and Hγ. L1 and L2 are the stellar fluxes and Ld is the disc contribution. |
 |
Fig. 6 Selected donor-subtracted Hα (left) and Hβ (right) profiles along the orbital period. Orbital phases are shown on the right side of the left plot. Same values were used in the right panel. |
 |
Fig. 7 Asymmetric helium and Balmer profiles found in the gainer template after separating the spectra. |
In the current DPV scenario, the donor star fills its Roche lobe and transfers mass to a rapidly rotating gainer star via gas stream. Therefore, the analysis of the gainer spectra requieres special attention to check for the possible presence of circumstellar material. To study the spectral-orbital behaviour of the gainer, we decided to remove the donor contribution from the original spectra using the previously found donor template. To derive the contribution of the donor to the total light along the orbital phase, we modeled the light curve in the V-band with the previously calculated donor temperature and mass ratio and assumed that the donor light adds to the total light. Under these assumptions, the total light includes two stellar components (L1 and L2) plus a circumstellar disc component (Ld). More details about the photometric model are explained in Sect. 3.4. We calculated the donor factor contribution to the total light for specific spectral lines. These factors were determined taking into account the orbital changes in the proyected area of the donor as well as the wavelength dependence on the different colour terms of donor and gainer (see Fig. 5). From each observed spectrum, we subtracted the donor template multiplied by the corresponding factor for the specific wavelength range. The resulting spectra were normalised to the new continuum level. Selected donor-subtracted Hα and Hβ profiles are shown in Fig. 6. The two profiles are composed of a central absorption surrounded by weak blue/red asymmetric wings, whose velocities reach up to about ~350 km s-1 and are phased with the gainer’s RVs. Similar behaviour was found in Hγ profiles. We detected a weakness of central absorption during the orbital phases φo = 0.1−0.2 and φo = 0.6−0.7 also observed in the helium lines and probably associated to a filling emission from a higher local temperature interaction regions such as hot or bright spots, visible during those orbital phases.
To gain some insight into the gainer temperature we calculated equivalent widths (hereafter EW) for the HeI 4471 Å and MgII 4481 Å lines for all donor-subtracted spectra. Mennickent at al. (2012b) determined the EWs ratios R = EW4471/EW4481 for B-type stars using a grid of synthetic spectra (log g = 4.0, vturb = 2 km s-1 and solar metallicity) and plotted it against temperatures. These results were used to determine the temperature of the gainer. Similarly, we calculated R in all donor-subtracted spectra and used the mean value to estimate a temperature Tg ~ (15 000 ± 1000) K for the gainer star. We show the variability of EW4471 and R along the orbital phase in Fig. 8.
 |
Fig. 8 EW4471 (bottom) and R = EW4471/EW4481 (top) plotted against orbital phase. |
 |
Fig. 9 Separated VIJK orbital light curves during one season in 2008 phased with the orbital period. |
3.3. Orbital and long light curves
We separated multiperiodic V, I, J, and K light curves with a Fourier decomposition technique (for more details see Demircan 1979; Mennickent et al. 2012a) and found two main Fourier components of frequencies f1 and f2, the sum of which (including their most important harmonics) is the best representation of the light curves. f1 is higher and associated with a period of 6.083299 d, which represents the orbital variability of the binary (see Fig. 9). We find the following orbital cycle ephemeris for the light curve minimum: 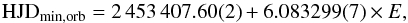 (12)which agrees with the ephemeris from van Houten (1950).
(12)which agrees with the ephemeris from van Houten (1950).
The frequency f2 is related to a period of 188.7 d and is represented by a smooth variability whose amplitude in V-band is ~2% with respect to the total luminosity (see Fig. 10). The ephemeris for the maximum of the long-term variability is best represent by 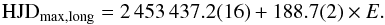 (13)A visual inspection of the orbital light curves shows an eclipsing variable with well-defined eclipses and noticeable proximity effects. Clearly, at least one of the components is tidally distorted. Differences in the depths of the minima suggest different surfaces temperatures. The deepest primary minimum on the V-band indicates that the bluer, hotter, and smaller gainer star is being eclipsed. Its light contribution is even less dominant on the infrared bands, supporting our previous results from the spectroscopic studies.
(13)A visual inspection of the orbital light curves shows an eclipsing variable with well-defined eclipses and noticeable proximity effects. Clearly, at least one of the components is tidally distorted. Differences in the depths of the minima suggest different surfaces temperatures. The deepest primary minimum on the V-band indicates that the bluer, hotter, and smaller gainer star is being eclipsed. Its light contribution is even less dominant on the infrared bands, supporting our previous results from the spectroscopic studies.
 |
Fig. 10 DQ Vel ASAS V-band light curve after separating the short-term (top) and long-term (bottom) variability. |
3.4. Light curve modelling
To derive the main physical parameters for the stellar components we fitted the V-band light curve with the inverse-problem-solving method based on the simplex algorithm. Main binary elements used in the model and the light-curve-fitting procedure are described in Djurašević (1992, 1996). We assumed a semi-detached configuration with the donor filling its Roche lobe. After unsuccessful attempts to model the system without a disc, we finally adopted a configuration that included an optically thick accretion disc around the gainer star. The disc is characterised by its radially dependent temperature Tdisc(r), its radius Rdisc, its thickness at edge de and at centre dc, and by assuming that it is in physical and thermal contact with the gainer. The temperature distribution of the disc is given by ![\begin{equation} T_\mathrm{disc}(r)= T_\mathrm{disc_{e}}+(T_\mathrm{g}-T_\mathrm{disc_{e}})\left[1-\frac{r-R_\mathrm{g}}{R_\mathrm{disc}-R_\mathrm{g}}\right]^{a_\mathrm{T}}, \end{equation}](/articles/aa/full_html/2013/04/aa20230-12/aa20230-12-eq226.png) (14)where Tdisce is the temperature of the disc at the edge, aT is the temperature exponent, and (Tg,Rg) represent the temperature and radius of the gainer star.
(14)where Tdisce is the temperature of the disc at the edge, aT is the temperature exponent, and (Tg,Rg) represent the temperature and radius of the gainer star.
The model also includes two active regions, hot spot (hs) and bright spot (bs), with higher local temperatures, which are located at the edge of the disc. Including these regions significantly improved the fit. They are represented by their temperatures (Ths,bs), angular dimensions (θhs,bs), and longitudes (λhs,bs), which are free parameters in the model. The longitudes λhs,bs are measured clockwise in the range 0 − 360 degrees and are viewed from the direction of the +z-axis, which is orthogonal to the orbital plane. More details about the disc model are described in Mennickent et al. (2012a).
 |
Fig. 11 Panels from top to bottom: observed (LCO) and synthetic (LCC) light-curves of DQ Vel obtained by analysing photometric observations; final O–C residuals between the observed and optimum synthetic light curves; fluxes of donor, gainer and of the accretion disc, normalised to the donor flux at phase 0.25; the views of the optimal model at orbital phases 0.25, 0.50 and 0.75, obtained with parameters estimated by the light curve analysis. |
 |
Fig. 12 Location of DQ Vel including the errors of stellar components on the H-R diagram. Some stellar pulsation instability regions are indicated. The evolutionary tracks were taken from Bressan et al. (1993) for z = 0.02. |
To restrict the number of free parameteres we fixed the donor temperature Td = 9400 K and mass ratio q = 0.31, whose values were reliably derived from the previous spectroscopic analysis (Sects. 3.1 and 3.2). We also fixed the gravity-darkening and albedo coefficients of the components to the values βd,g = 0.25 and Ad,g = 1.0 according to the von Zeipel law for radiative shells (von Zeipel 1924). Considering that the donor star fills its Roche lobe, we assumed this star to rotate synchronously with a rotation coefficient fd = 1.0. We modeled the ASAS V-band light curve with the gainer star in synchronous-rotation regime (fg = 1.0) and also in a critical-rotation scenario with a non-synchronous rotation coefficient fg = 12.8. We observed no significant difference in the two fitting results, revealing a minor effect of the gainer rotational velocity on the system parameters. The V-band light curve fitting with the gainer in synchronous rotation is shown in Fig. 11. Table 6 shows the final parameters of the fitting. The main physical properties of the gainer star such as mass (Mg = 7.3 ± 0.3 M⊙), radius (3.6 ± 0.2 R⊙), and gravity (log gg = 4.2 ± 0.1) agree with our previous spectroscopic result for the spectral classification (B-type star). However, we find a temperature value for the gainer Tg = 18 500 ± 500 K different from the previously obtained Tg = 15 000 ± 1000 K using the equivalent width ratio between the spectral features R = EW4471/EW4481. This difference is probably associated with the disc contribution to the spectra.
As was mentioned before, the best-fit model for DQ Vel includes an optically thick disc around the gainer star. From Fig. 11, we estimate a disc contribution of about 7% of the total light at quadrature phases. It has a concave shape with higher thickness at its edge than at its centre and is extended. It fills (89 ± 3)% of the critical gainer Roche lobe radius with a temperature of 6580 ± 300 K at the outer radius, as shown in Table 6. According to the model, the hot spot – where the material coming from the donor impacts the disc – is located at longitude 329.1° ± 7.0° and has a temperature of Ths = 9500 ± 750 K, which is close to the donor temperature found previously. This is probably the reason why we do not observe emission from the hot spot on the composite spectra. Because the disc is extended, the distance between L1 and the outer radius of the disc is short and not sufficient to produce a substantial acceleration of the gas stream and thus reach a higher temperature at this region.
3.5. Possible pulsations of the B-type gainer star
As suggested in Sect. 3.1, the scatter in the gainer RVs might be associated with pulsations of the B-type gainer star. The main reason to consider this scenario is the location of the gainer in the H-R diagram, as shown in Fig. 12. According to its mass and luminosity, the gainer is located well within the instability region of slowly pulsating B-stars (SPBs). These pulsators are typically B2 to B9 stars of intermediate mass between 3 to 7 M⊙. SPBs show multiperiodic light variations of the order of days produced by high-order g-modes. The typical photometric amplitude variations are lower than 0.1 mag while the radial velocity variations can reach up to 15 km s-1 (De Cat 2002; De Cat & Aerts 2002).
To find possible stellar pulsations, we carried out a Fourier frequency analysis on the gainer RVs and also on the O-C residuals of the V-band light curve after subtracting the orbital and long variabilities (see second panel in Fig. 11).
The Fourier frequency analysis was performed with the software Period045, which is based on a discrete Fourier transform algorithm and is applied to the spectral analysis of unevenly sampled data.
We computed the Fourier transform (hereafter FT) for the gainer RVs data set. We found a significant peak of 0.16 d-1, which corresponds to the binary orbital frequency. In addition, several marginal peaks appear at higher frequencies, but the sampling of our scarce data set is not sufficient to unambiguously determine any periodicities above the noise level.
Analysis results of the DQ Vel V-band light-curve.
 |
Fig. 13 Top panel: FT of the 516 data points obtained from the (O–C) DQ Vel photometric data. Middle upper panel: FT of the residuals after prewhitening the original data by the first significant frequency (f1). Middle lower panel: FT of the residuals prewhitened by the two significant frequencies f1 and f2 listed in Table 7. The white solid line corresponds to σnoise and the dotted line corresponds to 4σnoise. Bottom panel: spectral window for the whole data set. |
Using the larger sample of 516 data points obtained after subtracting the orbital and long variability from the V-band light curve, we calculated the FT for this data set. In the top and bottom panels of Fig. 13 we show the FT for the whole sample and its corresponding spectral window up to the Nyquist frequency (fN ≈ 0.25 d-1). To distinguish the significance of a frequency peak we used a 4σnoise criterion, which resulted in a 99.9% confidence limit (Kuschnig et al. 1997). To determine the σnoise in the Fourier spectrum we calculated the noise level by averaging the amplitudes around each frequency along the whole frequency domain. As shown in Fig. 13, the solid white line in the FT corresponds to this mean noise level. The dotted line indicates a significance threshold of four times the σnoise. After determining the highest frequency peak above 4σnoise in the FT of the original data set, we prewhitened the data, removing the sinusoid corresponding to this frequency. Then, we calculated the FT of the residuals and found the next highest peak. We repeated this procedure until no new peaks with significance above 4σnoise could be detected. In Table 7 we list the seven detected frequency signals. According to their S/N, only two frequencies (f1 and f2) are considered significant. In the middle upper panel of Fig. 13 we show the FT of the residuals after removing f1. Their corresponding σnoise and 4σnoise levels are shown. In the middle lower panel the prewhitened FT after removing f1 and f2 is displayed. No new significant peaks appear in the power spectrum after removing f1 and f2. The frequencies f1 = 0.005 d-1 and f3 = 0.166 d-1 correspond to the long and orbital photometric variabilities, which are still present in the data. The origin of the significant frequency f2 = 0.194 d-1 corresponding to a period of 5.14 d is unknown and could be interpreted as a pulsation of the SPB type.
Significant and marginal frequencies detected in the Fourier spectrum of the (O–C) DQ Vel photometric data.
We independently computed a simple Monte Carlo simulation to check the significance of f2. To do this, we generated 1000 samples of synthetic random data with a Gaussian distribution. For each sample, we generated an amount of points equal to the original number of 516 O–C data points and used the same time sampling. Then, we calculated the FT for each data set in the same frequency range as in the previous analysis, and found the amplitude of the highest frequency peak. In 99.9% of cases we do not find any amplitude peak higher than 17 mma. This is an additional independent test indicating the significance of the f2 detection.
3.6. Distance to DQ Vel
It is well known that eclipsing double-lined binaries can be used as standard candles to calculate accurate distances for Local Group galaxies (Kang et al. 2007; Clausen 2004). The most often used method for Milky Way binaries allows one to derive the distance modulus for either component of a binary (Clausen 2004). In the V-band we have 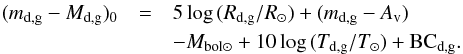 (15)The absolute radii of stars and effective temperatures together with the visual apparent magnitudes of the components (md,mg), interstellar absorption (Av), and bolometric corrections (BC) are needed. Considering the apparent magnitudes on the light curves including the disc contribution, we determined the apparent magnitudes for the donor and gainer star using the V-band light curve and the theoretical fluxes from the photometric model (Fig. 11). From this last we measured the total flux of the system (ft) and the individual contributions (fd, fg, fdisc), where ft = fd + fg + fdisc in the cuadrature phases φo = 0.25 and also φo = 0.75. The total flux at these orbital phases is related to the highest observed apparent magnitude of the system in the light curve mt(V) = 10.977. Thus, the apparent magnitude of the donor md can be obtained from
(15)The absolute radii of stars and effective temperatures together with the visual apparent magnitudes of the components (md,mg), interstellar absorption (Av), and bolometric corrections (BC) are needed. Considering the apparent magnitudes on the light curves including the disc contribution, we determined the apparent magnitudes for the donor and gainer star using the V-band light curve and the theoretical fluxes from the photometric model (Fig. 11). From this last we measured the total flux of the system (ft) and the individual contributions (fd, fg, fdisc), where ft = fd + fg + fdisc in the cuadrature phases φo = 0.25 and also φo = 0.75. The total flux at these orbital phases is related to the highest observed apparent magnitude of the system in the light curve mt(V) = 10.977. Thus, the apparent magnitude of the donor md can be obtained from
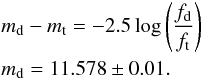 (16)The same procedure was applied to the gainer star to obtain mg = 12.097 ± 0.01. The bolometric corrections were obtained from the calibrations by Flower (1996) using log Tg = 4.267; BCg = ( − 1.76 ± 0.16) for the gainer and log Td = 3.973 and BCd = ( − 0.13 ± 0.05) for the donor. We determined the interstellar absorption Av = 1.02 ± 0.02 using the algorithm from Cardelli et al. (1989) that is available online6.
(16)The same procedure was applied to the gainer star to obtain mg = 12.097 ± 0.01. The bolometric corrections were obtained from the calibrations by Flower (1996) using log Tg = 4.267; BCg = ( − 1.76 ± 0.16) for the gainer and log Td = 3.973 and BCd = ( − 0.13 ± 0.05) for the donor. We determined the interstellar absorption Av = 1.02 ± 0.02 using the algorithm from Cardelli et al. (1989) that is available online6.
Equation (15) yields
![\begin{eqnarray} && (m_\mathrm{g}-M_\mathrm{g})_{0}=12.46\pm0.23 \\[2mm] &&(m_\mathrm{d}-M_\mathrm{d})_{0}=12.47\pm0.09. \end{eqnarray}](/articles/aa/full_html/2013/04/aa20230-12/aa20230-12-eq350.png) Finally, we estimated the average distance from donor and gainer distance modulus:
Finally, we estimated the average distance from donor and gainer distance modulus: 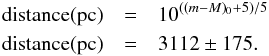 (19)
(19)
3.7. Comparison with V393 Scorpii
During recent years a comprehensive study of the DPV system V393 Sco has been carried out by Mennickent et al. (2010, 2012a,b) to study the nature and evolution of the system. The studies include photometry (VIJK bandpasses and V-ASAS light curves) and high-resolution spectroscopy in the optical, near-infrared, and ultraviolet wavelength ranges. V393 Sco is a galactic (d = 523 pc) bright DPV composed of an A-type donor (Td = 8600 ± 600 K) and a B-type gainer (Tg = 16 600 ± 500 K) surrounded by a massive disc. The system shows a complex variability of spectral features along the orbital and long cycles including intense double-peaked emission in optical Balmer lines.
Comparison of the main stellar and disc parameters for DQ Vel and V393 Sco.
We noted strong similarities of the physical properties of V393 Sco and DQ Vel, as can be seen in Table 8. Physical parameters of the stellar components such as masses, radii, temperatures, gravities, and also orbital parameters (binary separation and inclination) are similar. However, a detailed comparison showed significant differences in the optical spectral features of the two systems. We suggest that these differences are associated with the physical properties of the accretion discs and thus with the mass transfer rates. As shown in Table 8, the disc in DQ Vel seems to be more extended and colder than that of V393 Sco. Moreover, the hot and bright spots in V393 Sco are hotter than in DQ Vel. From the geometric point of view, DQ Vel’s disc is concave and thick at the outer border, in contrast to the modelled disc in V393 Sco, which is convex and probably has most of its mass concentrated close to the gainer. We suggest that the main differences of the discs are related to different evolutionary stages. The high mass-transfer rate of V393 Sco would form a massive accretion disc and lead the gainer to rotate critically. DQ Vel instead could be an older system in a state of lower mass transfer where the gainer had time to slow down, allowing the formation of an extended disc. A detailed analysis of the evolutionary stage of DQ Vel remains to be conducted in the future.
4. Summary
Our analysis of VIJK (REM-telescope) and V (ASAS) photometric data togheter with the study of 46 optical high-resolution echelle spectra along several orbital cycles allowed us to estimate the main physical properties for the components of the DPV system DQ Vel.
We separated the composite spectra using the Doppler shifts of known spectral lines to obtain two single-lined templates, which were used to derive the RV curves through a Fourier cross-correlation process, and obtained the spectroscopic mass ratio (q = 0.31 ± 0.03) of the system. A comparison of the templates with a grid of synthetic spectra enabled us to estimate the effective temperature Td = 9400 ± 100 K for the donor star. We calculated the fractional light contribution of the donor star to subtract it from the spectra and thus analyse the gainer spectral features. The donor-subtracted spectra along the orbital cycle show a variability of the Balmer and helium profiles, suggesting the presence of circumstellar material. The spectroscopic mass ratio and donor temperature were used to carry out a V-band light curve fitting and to obtain the main binary elements such as the masses Mg = 7.3 ± 0.3 M⊙ and Md = 2.2 ± 0.2 M⊙, and the radii Rg = 3.6 ± 0.2 R⊙ and Rd = 8.4 ± 0.2 R⊙ for gainer and donor star together with the orbital separation (aorb = 29.7 ± 0.3 R⊙) and the inclination angle (i° = 82.5 ± 0.2) of the system. The best model suggest a semi-detached system comprising an A1III donor star (Td = 9400 ± 100 K) and a B3V gainer star (Tg = 18 500 ± 500 K) with an extended accretion disc around the gainer. The model includes two active regions (hot and bright spots) located at the outer edge of the disc. The temperatures and radii of the stellar components together with the individual apparent magnitudes determined from the light curve were used to estimate the distance to DQ Vel (d = 3.112 kpc).
Based on the position of the gainer on the HR diagram, which is well within the SPB instability strip, we interprete this periodicity of 5.14 d as a pulsation of an SPB type formed in the gainer.
Similarities on the stellar parameters for DQ Vel and the DPV system V393 Sco were found during this study. However, we observed differences on the geometrical and physical properties of the two accretion discs, and we suggest that they are related to different evolutionary stages. We are currently working on a detailed analysis of the evolutionary stage of DQ Vel and aim to present our results in a forthcoming publication.
Online material
IRAF (http://iraf.noao.edu/) is distributed by the National Optical Astronomy Observatories and operated by the Association of Universities for Research in Astronomy Inc., under cooperative agreement with the National Science Foundation.
Acknowledgments
R.M. acknowledges support by Fondecyt grant 1110347 and from the BASAL Centro de Astrofísica y Tecnologias Afines (CATA) PFB–06/2007. G.D. gratefully acknowledges the financial support of the Ministry of Education and Science of the Republic of Serbia through the project 176004, “Stellar physics”. D.B. acknowledges support by the Chilean CONICYT PhD grant and the European Southern Observatory grant.
References
- Baranne, A., Queloz, D., Mayor, M., et al. 1996, A&AS, 119, 373 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bressan, A., Fagotto, F., Bertelli, G., & Chiosi, C. 1993, A&AS, 100, 647 [NASA ADS] [Google Scholar]
- Cardelli, J., Clayton, G., & Mathis, J. 1989, ApJ, 345, 245 [NASA ADS] [CrossRef] [Google Scholar]
- Castelli, F., & Hubrig, S. 2004, A&A, 425, 263 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Clausen, J. V. 2004, New Astron. Rev., 48, 679 [Google Scholar]
- De Cat, P. 2002, ASPC, 259, 196 [Google Scholar]
- De Cat, P., & Aerts, C. 2002, ESA SP, 485, 257 [NASA ADS] [Google Scholar]
- Demircan, O. 1979, Ap&SS, 61, 499 [NASA ADS] [CrossRef] [Google Scholar]
- Desmet, M., Frémat, Y., Baudin, F., et al. 2010, MNRAS, 401, 418 [NASA ADS] [CrossRef] [Google Scholar]
- Djurašević, G. 1992, Ap&SS, 196, 267 [NASA ADS] [CrossRef] [Google Scholar]
- Djurašević, G. 1996, Ap&SS, 240, 317 [NASA ADS] [CrossRef] [Google Scholar]
- Djurašević, G., Latković, O., Vince, I., & Cséki, A. 2010, MNRAS, 409, 329 [NASA ADS] [CrossRef] [Google Scholar]
- Eggleton, P. 1983, ApJ, 268, 368 [NASA ADS] [CrossRef] [Google Scholar]
- Flower, P. 1996, ApJ, 469, 355 [NASA ADS] [CrossRef] [Google Scholar]
- González, J. F., & Levato, H. 2006, A&A, 448, 283 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Griffin, R. F. 1967, ApJ, 148, 465 [NASA ADS] [CrossRef] [Google Scholar]
- Hilditch, R. W. 2001, An Introduction to Close Binary Stars (Cambridge University Press) [Google Scholar]
- Hill, G. 1993, ASPC, 38, 127 [Google Scholar]
- Hoffmeister, C. 1949, Astr. Abh. Ergänz. Astron. Nach., 12, A24 [Google Scholar]
- Kang, Y.-W., Hong, K.-S., & Lee, J. 2007, ASPC, 362, 19 [NASA ADS] [Google Scholar]
- Kaufer, A., Stahl, O., Tubbesing, S., et al. 1999, Msngr, 95, 8 [Google Scholar]
- Kaufer, A., Stahl, O., Tubbesing, S., et al. 2000, SPIE, 4008, 459 [NASA ADS] [Google Scholar]
- Kurucz, R. 1993, CD-ROM, 18 [Google Scholar]
- Kuschnig, R., Weiss, W., Gruber, R., Bely, P. Y., & Jenkner, H. 1997, A&A, 328, 544 [NASA ADS] [Google Scholar]
- Marchenko, S., Moffat, A., & Eenens, P. 1998, PASP, 110, 1416 [NASA ADS] [CrossRef] [Google Scholar]
- Mennickent, R., & Kołaczkowski, Z. 2010, ASPC, 435, 283 [NASA ADS] [Google Scholar]
- Mennickent, R., Pietrzyński, G., Díaz, M., & Gieren, W. 2003, A&A, 399, L47 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Mennickent, R., Cidale, L., Díaz, M., et al. 2005, MNRAS, 357, 1219 [NASA ADS] [CrossRef] [Google Scholar]
- Mennickent, R., Kołaczkowski, Z., Michalska, G., et al. 2008, MNRAS, 389, 1605 [Google Scholar]
- Mennickent, R., Kołaczkowski, Z., Graczyk, D., & Ojeda, J. 2010, MNRAS, 405, 1947 [NASA ADS] [Google Scholar]
- Mennickent, R., Graczyk, D., Kołaczkowski, Z., et al. 2011, IAUS, 272, 527 [NASA ADS] [Google Scholar]
- Mennickent, R., Djurašević, G., Kołaczkowski, Z., & Michalska, G. 2012a, MNRAS, 421, 862 [NASA ADS] [Google Scholar]
- Mennickent, R., Kolaczkowski, Z., Niemczura, E., et al. 2012b, MNRAS, 427, 607 [NASA ADS] [CrossRef] [Google Scholar]
- Michalska, G., Mennickent, R., Kołaczkowski, Z., & Djurašević., G. 2010, ASPC, 435, 357 [NASA ADS] [Google Scholar]
- Milone, E. F. 1986, ApJS, 61, 455 [NASA ADS] [CrossRef] [Google Scholar]
- O’Connell, D. 1951, PRCO, 2, 85 [Google Scholar]
- Poleski, R., Soszyński, I., Udalski, A., et al. 2010, Acta Astronom., 60, 179 [Google Scholar]
- Sbordone, L. 2005, MSAIS, 8, 61 [NASA ADS] [Google Scholar]
- van Houten, C. J. 1950, AnLei, 20, 223 [NASA ADS] [Google Scholar]
- von Zeipel, H. 1924, MNRAS, 84, 702 [NASA ADS] [CrossRef] [Google Scholar]
All Tables
Detailed photometric data used in this paper. First column is the observing window and N is the number of frames.
Significant and marginal frequencies detected in the Fourier spectrum of the (O–C) DQ Vel photometric data.
All Figures
 |
Fig. 1 Mean RVs obtained by direct measurement. Donor velocities were obtained averaging the Doppler shifts for the MgII 4481 Å, FeI 4957 Å, SiII 6347 Å, and SiII 6371 Å lines. HeI lines were used to calculate gainer velocities. |
| In the text | |
 |
Fig. 2 Separated spectra of DQ Vel. The composite spectrum (top) at φo = 0.8110 is used here as a reference from the list in Table 1. Final S/N for the decomposed spectra are 97 (middle) and 267 (bottom) for the donor and gainer star. The spectra were offset for clarity. |
| In the text | |
 |
Fig. 3 RV curves and best sinus fit for DQ Vel components. Each RV was measured from Table 3 and Table 4 taking the mean value in orbital phase bins of 0.05. |
| In the text | |
 |
Fig. 4 Calibration curves for measured fwhm (Å) of MgI 4703.0 Å, MgII 4481.3 Å, TiII 4780.0/4805.1 Å, and SiII 6371.3 Å lines plotted against vr sin i. |
| In the text | |
 |
Fig. 5 Donor light contribution with respect to the total light calculated from the light curve model. Each curve shows the donor contribution for a specific spectral range around a spectral line. The selected spectral lines (and ranges) are from top to the bottom: HeI 6678 Å, Hα, HeI 5875 Å, Hβ, HeI 4471 Å, and Hγ. L1 and L2 are the stellar fluxes and Ld is the disc contribution. |
| In the text | |
 |
Fig. 6 Selected donor-subtracted Hα (left) and Hβ (right) profiles along the orbital period. Orbital phases are shown on the right side of the left plot. Same values were used in the right panel. |
| In the text | |
 |
Fig. 7 Asymmetric helium and Balmer profiles found in the gainer template after separating the spectra. |
| In the text | |
 |
Fig. 8 EW4471 (bottom) and R = EW4471/EW4481 (top) plotted against orbital phase. |
| In the text | |
 |
Fig. 9 Separated VIJK orbital light curves during one season in 2008 phased with the orbital period. |
| In the text | |
 |
Fig. 10 DQ Vel ASAS V-band light curve after separating the short-term (top) and long-term (bottom) variability. |
| In the text | |
 |
Fig. 11 Panels from top to bottom: observed (LCO) and synthetic (LCC) light-curves of DQ Vel obtained by analysing photometric observations; final O–C residuals between the observed and optimum synthetic light curves; fluxes of donor, gainer and of the accretion disc, normalised to the donor flux at phase 0.25; the views of the optimal model at orbital phases 0.25, 0.50 and 0.75, obtained with parameters estimated by the light curve analysis. |
| In the text | |
 |
Fig. 12 Location of DQ Vel including the errors of stellar components on the H-R diagram. Some stellar pulsation instability regions are indicated. The evolutionary tracks were taken from Bressan et al. (1993) for z = 0.02. |
| In the text | |
 |
Fig. 13 Top panel: FT of the 516 data points obtained from the (O–C) DQ Vel photometric data. Middle upper panel: FT of the residuals after prewhitening the original data by the first significant frequency (f1). Middle lower panel: FT of the residuals prewhitened by the two significant frequencies f1 and f2 listed in Table 7. The white solid line corresponds to σnoise and the dotted line corresponds to 4σnoise. Bottom panel: spectral window for the whole data set. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


