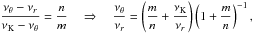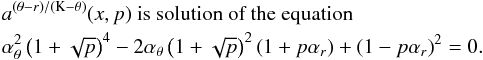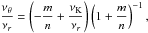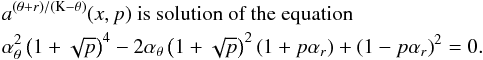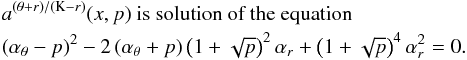| Issue |
A&A
Volume 552, April 2013
|
|
|---|---|---|
| Article Number | A10 | |
| Number of page(s) | 41 | |
| Section | Astrophysical processes | |
| DOI | https://doi.org/10.1051/0004-6361/201219724 | |
| Published online | 14 March 2013 | |
Multi-resonance orbital model of high-frequency quasi-periodic oscillations: possible high-precision determination of black hole and neutron star spin⋆
Institute of Physics, Faculty of Philosophy and Science, Silesian University in Opava, Bezručovo nám. 13, 74601 Opava, Czech Republic
e-mail: andrea.kotrlova@fpf.slu.cz
Received: 31 May 2012
Accepted: 8 January 2013
Context. Using known frequencies of the twin-peak high-frequency quasiperiodic oscillations (HF QPOs) and known mass of the central black hole, the black-hole dimensionless spin a can be determined by assuming a concrete version of the resonance model. However, a wide range of observationally limited values of the black hole mass implies low precision of the spin estimates.
Aims. We discuss the possibility of higher precision for the black hole spin a measurements in the framework of a multi-resonance model inspired by observations of more than two HF QPOs in the black hole systems, which are expected to occur at two (or more) different radii of the accretion disc. This framework is also applied in a modified form to the neutron star systems.
Methods. We determine the spin and mass dependence of the twin-peak frequencies with a general rational ratio n:m, assuming a non-linear resonance of oscillations with the epicyclic and Keplerian frequencies or their combinations. In the multi-resonant model, the twin-peak resonances are combined properly to give the observed frequency set. For the black hole systems we focus on the special case of duplex frequencies, when the top, bottom, or mixed frequency is common at two different radii where the resonances occur giving triple frequency sets.
Results. The sets of triple frequency ratios and the related spin a are given. The resonances are considered up to n = 5 since excitation of higher order resonances is improbable. The strong resonance model for “magic” values of the black hole spin means that two (or more) versions of resonance could occur at the same radius, allowing cooperative effects between the resonances. For neutron star systems we introduce a resonant switch model that assumes switching of oscillatory modes at resonant points.
Conclusions. In the case of doubled twin-peak HF QPOs excited at two different radii with common top, bottom, or mixed frequency, the black hole spin a is given by the triple frequency ratio set. The spin is determined precisely, but not uniquely, because the same frequency set could correspond to more than one concrete spin a. The black hole mass is given by the magnitude of the observed frequencies. The resonant switch model puts relevant limits on the mass and spin of neutron stars, and we expect a strong increase in the fitting procedure precision when different twin oscillatory modes are applied to data in the vicinity of different resonant points. We expect the multi-resonance model to be applicable to data from the planned LOFT or similar X-ray satellite observatory.
Key words: Accretion, accretion disks / X-rays: binaries / black hole physics / stars: neutron
Appendices are available in electronic form at http://www.aanda.org
© ESO, 2013
1. Introduction
In the black hole systems observed in both Galactic and extragalactic sources, strong gravity effects play a crucial role in three phenomena related to the accretion disc that is the emitting source: the spectral continuum, spectral profiled lines, and oscillations of the disc. Moreover, it is clear that strong gravity should also play an important role in the binary systems containing neutron (quark) stars. Quasiperiodic oscillations (QPOs) of X-ray brightness had been observed at low-(Hz) and high-(kHz) frequencies in many Galactic low mass X-ray binaries (LMXBs) containing neutron stars (see, e.g., van der Klis 2000, 2006; Barret et al. 2005b; Belloni et al. 2005, 2007b; Wang et al. 2013) or black holes (see, e.g., McClintock & Remillard 2004; Remillard 2005; Remillard & McClintock 2006). Some of the high-frequency (HF) QPOs are in the kHz range and often come in pairs of the upper and lower frequencies (νU, νL) of twin peaks1 in the Fourier power spectra. Since the peaks of high frequencies are close to the orbital frequency of the marginally stable circular orbit, representing the inner edge of Keplerian discs orbiting black holes (or neutron stars), the strong gravity effects must be relevant in explaining HF QPOs (Török et al. 2005).
Before the twin-peak HF QPOs were discovered in microquasars (first by Strohmayer 2001) and the 3:2 ratio pointed out, Kluźniak & Abramowicz (2001) suggested that these QPOs should have rational ratios, because of the resonances in oscillations of nearly Keplerian accretion discs; see also Aliev & Galtsov (1981). It seems that the resonance hypothesis is now well supported by observations and that, in particular, the 3:2 ratio (2νU = 3νL) is seen most often in twin-peak QPOs in the LMXBs containing black holes (microquasars). In addition, there is even some evidence of the same 3:2 ratio in the X-ray spectra of the Galaxy centre’s black hole in Sgr A∗ (Abramowicz et al. 2004; Aschenbach 2004; Török 2005), the galactic nuclei MCG-6-30-15 and NGC 4051 (Lachowicz et al. 2006), and other active galactic nuclei (Middleton et al. 2011, 2009).
There is a crucial difference between the HF QPOs in black hole and neutron star systems. In black hole systems, the peaks of HF QPOs are detected at (nearly) constant frequencies that are characteristic of a given source across long times and various observations. When more frequencies are detected (simultaneously or in various observations), they come in ratios of small numbers, usually in the 3:2 ratio (Remillard & McClintock 2006). In neutron star systems, the HF QPOs often appear as twin QPOs consisting from two simultaneously observed peaks with distinct actual frequencies that substantially change over time (in one observational sequence); moreover, sometimes only one of the frequencies is observed and has evolved (Belloni et al. 2007a; Boutelier et al. 2010). Most of the twin QPOs in the so-called atoll sources (van der Klis 2006) have been detected at lower frequencies, 600 − 800 Hz vs. upper frequencies 900 − 1200 Hz, demonstrating a clustering of the twin HF QPOs frequency ratio around 3:2 and thus indicating some analogy to the black hole case (Abramowicz et al. 2003a; Belloni et al. 2007a; Török et al. 2008a,b,c; Boutelier et al. 2010). The amplitudes of twin HF QPOs in neutron star systems are usually much stronger, and their coherence times are much longer than those of black hole sources (see, e.g., Remillard & McClintock 2006; Barret et al. 2005b, 2006). It is probable that a 3:2 resonance also plays a significant role in the LMXBs containing neutron stars. However, the evidence is much more complicated, since the frequency ratio is concentrated around 3:2, but has much wider range than in the hole systems (Belloni et al. 2005; Török et al. 2005, 2008c; Abramowicz et al. 2005a; Török 2009; Boutelier et al. 2010). It remains controversial whether the peak in distribution of the twin-peak frequency ratios νU/νL at 3:2 is physical (Montero & Zanotti 2012).
It has also been suggested that the multi-peaked distribution in the frequency ratios meant that more than one resonance could be realized if a resonant mechanism is involved in generating the neutron star (Belloni et al. 2005; Stuchlík et al. 2011b) and black hole (Stuchlík & Török 2005) HF QPOs. For a given neutron star source, the upper and lower HF QPO frequencies can be traced over the whole observed range, but the probability of detecting both QPOs simultaneously increases when the frequency ratio is close to the ratio of small natural numbers, namely 3:2, 4:3, 5:4, in the case of the atoll sources (Török 2009; Boutelier et al. 2010) or the ratios that are close to 2:1, and 3:1 in the Z-source Circinus X-1 (Boutloukos et al. 2006; Török et al. 2010). The analysis of root-mean-squared-amplitude evolution in a group of six atoll sources (4U 1636−53, 4U 1608−52, 4U 0614−09, 4U 1728−34, 4U 1820−30, 4U 1735−44) shows that the upper and lower HF QPO amplitudes equal each other and alter their dominance, while passing rational frequency ratios corresponding to the datapoint clustering (Török 2009). Such an “energy switch effect” can be explained well in the framework of non-linear resonant orbital models as shown in Horák et al. (2009).
In the orbital resonance models of HF QPOs, the resonance conditions applied to the frequency ratio of oscillations entering the resonances imply specific radii of accretion discs where the resonances can occur. For any specific version of the orbital resonance models, the resonant radii at thin, Keplerian accretion discs (Török et al. 2005) are given by the frequency ratio and the parameters of the central black hole or neutron star (mass M, spin a, and quadrupole moment q in the case of neutron stars)2. The frequencies of disc oscillation modes can be expressed in terms of the geodetical orbital and epicyclic frequencies of the test particle motion for both Keplerian discs and slender tori when gravitation is the relevant restoring force (Abramowicz et al. 2003b; Šrámková et al. 2007). For non-slender tori, corrections to the epicyclic frequencies have to be introduced, depending on the thickness of the tori, with differences to the epicyclic frequencies approaching tens of percent (Blaes et al. 2007; Šrámková 2005; Straub & Šrámková 2009).
When the pressure gradients in thick tori become important as the restoring force, the radial oscillation frequency strongly differs from the radial geodetical epicyclic frequency (Rezzolla et al. 2003b,a; Montero et al. 2004), similar to the model of oscillating string loops where the string tension due to magnetic field is the main restoring force (Stuchlík & Kološ 2012b,a; Jacobson & Sotiriou 2009; Semenov et al. 2004; Spruit 1981).
We focus our attention mainly on the black hole systems. According to the resonance hypothesis (Kluźniak & Abramowicz 2001), the two modes in resonance should have eigenfrequencies νr (equal to the radial epicyclic frequency) and νv (equal to the vertical epicyclic frequency νθ, or to the Keplerian frequency νK; see also Abramowicz et al. 2004; Török et al. 2005). While models based on the parametric resonance identify the two observed frequencies of the twin peak (νU, νL) directly with the eigenfrequencies of resonant oscillations, models based on the forced resonance allow combinational (beat) frequencies of the modes to be observed. Both parametric and forced resonance models make clear and precise predictions about the values of observed frequencies in connection with the spin and mass of the observed object, at least in the case of black holes – see Török et al. (2005) where the black hole specific (dimensionless) internal angular momentum (spin) is predicted by a few possible models for microquasars with observed twin-peak HF QPOs.
Although the observed frequencies are consistent with several (but not all) resonance models, the most probable and natural explanation for the presence of a 3:2 ratio is the 3:2 parametric (or internal) resonance (Abramowicz et al. 2004; Török et al. 2005). However, in all the cases under consideration, a relatively wide range of observationally allowed black hole masses implies rather unprecise determination of the black hole spin (Török et al. 2005). Therefore, it is useful to look for some possibilities how to make the spin estimate more precise (Stuchlík & Török 2005; Stuchlík et al. 2008b).
Of course, the spin estimates based on various versions of the resonance model have to be compared with the spin estimates based on the accretion disc spectral continuum fitting (McClintock et al. 2011, 2006; Done & Davis 2008; Done et al. 2007; Middleton et al. 2006; Shafee et al. 2006) and profiled spectral lines (Laor 1991; Bao & Stuchlík 1992; Karas et al. 1992; Dovčiak et al. 2004; Fabian & Miniutti 2005; Zakharov 2003; Čadež et al. 2003; Fanton et al. 1997; Čadež & Calvani 2005; Zakharov & Repin 2006; Schee & Stuchlík 2009a,b; Miller et al. 2009). In the case of Sgr A∗ the orbital precession of some stars moving in close vicinity of the central black hole could also give an interesting restriction on the black hole spin (Kraniotis 2005, 2007).
In some sources, more than two high-frequency peaks are observed. The microquasar GRS 1915+105 reveals high-frequency QPOs appearing at four frequencies with the lower and upper pairs in the ratio close to 3:2 or 5:3 (Remillard & McClintock 2006), and even a fifth frequency was reported (Belloni et al. 2001). An additional sixth frequency was mentioned (Strohmayer 2001), although not confirmed. In Sgr A∗, three frequencies were reported with ratios close to 3:2:1 (Aschenbach 2004; Aschenbach et al. 2004; Török 2005). In the source NGC 5408 X-1, oscillations with three frequencies of ratios close to 6:4:3 were observed (Strohmayer et al. 2007). In the galactic nuclei MCG-6-30-15 and NGC 4051, two pairs of QPOs were reported with the ratios close to 3:2 and 2:1, respectively (Lachowicz et al. 2006).
In the microquasar GRS 1915+105, a near-extreme Kerr black hole with a ~ 1 is expected according to the spectral continuum fitting (McClintock et al. 2006), and all five (six) frequencies of QPOs can be explained in the framework of the extended resonance model with the hump-induced oscillations (Stuchlík et al. 2007c). In the extended resonance model, forced resonances of the epicyclic oscillations are assumed with the oscillations induced by the humpy orbital velocity profile (related to the locally non-rotating frames, Bardeen et al. 1972) that occurs in Keplerian discs orbiting Kerr black holes with a > 0.9953 (Aschenbach 2006, 2004; Stuchlík et al. 2005, 2007b,c, 2011a). In the extended “humpy” resonance model, all the oscillations in resonance are related to the exclusively defined “humpy radius” with extremal orbital velocity gradient within the humpy profile (Stuchlík et al. 2007b). However, this model can only be relevant for near-extreme Kerr black holes with spins of a > 0.9953. Some concrete implications of a rapid spin in GRS 1915+105 for other frequently quoted QPO models are discussed in Török et al. (2011).
When more than two resonant frequencies or, precisely, more than one resonant point corresponding to two resonant eigenfrequencies of the system are observed, a multi-resonant model of HF QPOs is necessary in order to understand the behaviour of a concrete system generating such HF QPOs. There are different types of the multi-resonant model based on oscillations with the orbital frequencies νK, νθ, and νr, all of which allow higher precision in determining the black hole parameters in comparison with situations where only one resonant point is observed.
First, for special “magic” values of the black hole spin, the resonance points share the same radius in the disc that enables cooperative phenomena between resonances of different origin. Of special interest is the case of so-called strong resonant phenomena allowing direct resonances of oscillations having frequency ratio νK:νθ:νr = s:t:u (with s,t,u being small natural numbers) at the radius given by the frequency ratio; for each triple frequency set ratio, the black hole spin a is given uniquely (Stuchlík et al. 2008b).
Second, two resonance points occur at two different radii. Generally, a set of four frequencies is observed. However, a common frequency appears for special values of the black hole spin, which is related to the types of resonances involved and the frequency ratio. Then the ratio of the three observed frequencies determines the black hole spin uniquely, if the resonance conditions at the resonant points are given. Here, we concentrate our attention on these situations.
Third, one fixed type of resonance is enhanced at different radii, with different frequency ratios. This type is probably relevant in neutron star atoll and Z systems, where it is shown that the observed datapoint clusters concentrated around frequency ratios 3:2, 4:3, 5:4 could be approximated for a variety of models, e.g., the relativistic precession model (Stella & Vietri 1999, 1998) or the so-called total precession model, where the Keplerian oscillations of frequency νK are in resonance with the total precession oscillations of frequency νT = νθ − νr (Stuchlík et al. 2007d). However, we observe a bad quality of data fitting by the HF QPO models in neutron star LMXBs (Török et al. 2010, 2012; Boutelier et al. 2010). Therefore, we introduce a new, resonant switch model that could be applied to some neutron star LMXBs exploring observational data spanning two resonant points. Such a model could improve data fitting without using a non-geodesic corrections to the orbital and epicyclic frequencies.
In general, for two resonant points observed, we can expect the oscillations to be excited at two different radii of the accretion disc and to enter the resonance in the framework of different versions of the resonance model. In such situations we are making the black hole spin estimate within two properly chosen versions of the resonance model, thus in principle obtaining a more precise determination of the spin in comparison with situations where only one resonant point is observed. In special cases where a common upper, lower, or mixed frequency is observed in the two frequency pairs (i.e., only three different frequencies are observed), the triple frequency set is precisely given independently of the black hole mass for appropriately fixed values of the black hole spin (Stuchlík & Török 2005). Then, the spin is in principle determined precisely (within the precision of the frequency measurements), but not uniquely, because the same frequency set could occur for different values of the spin within different versions of the resonance model. It is clear that in such situations the black hole spin estimates coming from the spectral continuum fitting and the line profile models have to be relevant for determining the proper versions of the resonant model3. The recently discussed method based on the frequency shift interval of radiation emitted from matter excited at the resonant radii can also be very efficient in restricting the spin of the black hole or some other compact object (Murphy et al. 2009; Stuchlík & Schee 2010). When the black hole spin is found, the black hole mass can be determined from the magnitude of the observed frequencies. We expect the multi-resonance model of HF QPOs to be applicable to both black hole and neutron star systems for precise data obtained by the planned LOFT (Feroci et al. 2012) or a similar X-ray satellite observatory.
2. Digest of orbital resonance model
The standard orbital resonance model (Abramowicz & Kluźniak 2001; Török et al. 2005; Aliev & Galtsov 1981) assumes non-linear resonance between oscillation modes of an accretion disc orbiting a central object, here considered to be a rotating Kerr black hole (or a neutron star with exterior described by the Kerr geometry – see Török et al. 2010 for details)4. The accretion disc can be a thin disc with Keplerian angular velocity profile (Novikov & Thorne 1973) or a thick toroidal disc with angular velocity profile given by the distribution of the specific angular momentum of the fluid (Kozłowski et al. 1978; Abramowicz et al. 1978; Stuchlík et al. 2000). The frequency of the oscillations is related to the Keplerian frequency (orbital frequency of tori) or to the radial and vertical epicyclic frequencies of the circular test particle motion. The epicyclic frequencies can be relevant both for the thin, Keplerian discs with quasicircular geodetical motion (Kato et al. 1998; Nowak & Lehr 1998; Abramowicz et al. 2003b; Kluźniak et al. 2007; Kato 2001b, 2004b; Wagoner 1999) and for slender toroidal discs (Schnittman & Rezzolla 2006; Rezzolla 2004a,b; Rezzolla et al. 2003b). However, with the thickness of an oscillating toroid growing, the eigenfrequencies of its radial and vertical oscillations deviate from the epicyclic test particle frequencies (Šrámková 2005; Blaes et al. 2007; Straub & Šrámková 2009). Here we focus our attention on the Keplerian thin discs.
A variety of different versions of the orbital resonance model exists that could be classified according to the following criteria:
-
a)
the type of the resonance(parametric or forced),
-
b)
the presence of beat, combinational frequencies,
-
c)
the type of oscillations entering the resonance.
Thus, according to the basical criterion a), two main groups of orbital resonance model versions exist, differing by the type of the resonance. In both of them, the epicyclic frequencies of the equatorial test particle circular motion play a crucial role (Török et al. 2005).
2.1. Parametric internal resonance
The internal resonance model is based on the idea of parametric resonance between vertical and radial epicyclic oscillations with the frequencies νθ = ωθ/2π and νr = ωr/2π. The parametric resonance is described by the Mathieu equation (Landau & Lifshitz 1976) ![\begin{equation} \label{Mathieu} \delta \ddot \theta + \omega_{\theta}^2\,[ 1 + h \cos (\omega_{r} t) ]\, \delta \theta = 0. \end{equation}](/articles/aa/full_html/2013/04/aa19724-12/aa19724-12-eq28.png) (1)Theory behind the Mathieu equation implies that a parametric resonance is excited when
(1)Theory behind the Mathieu equation implies that a parametric resonance is excited when 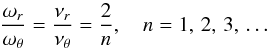 (2)and is strongest for the lowest possible value of n (Landau & Lifshitz 1976). Because there is νr < νθ near black holes, the low possible value for the parametric resonance in the so-called epicyclic resonance model is n = 3, which means that 2νθ = 3νr. This explains observed 3:2 ratio, assuming νU = νθ and νL = νr. The internal resonance corresponds to a system with conserved energy, as shown, e.g., in Horák et al. (2009).
(2)and is strongest for the lowest possible value of n (Landau & Lifshitz 1976). Because there is νr < νθ near black holes, the low possible value for the parametric resonance in the so-called epicyclic resonance model is n = 3, which means that 2νθ = 3νr. This explains observed 3:2 ratio, assuming νU = νθ and νL = νr. The internal resonance corresponds to a system with conserved energy, as shown, e.g., in Horák et al. (2009).
2.2. Forced resonance
Models based on the forced resonance come from the idea of a forced non-linear oscillator, when the relation of the latitudinal (vertical) and radial oscillations is given by the formulae
![\begin{eqnarray} &&\delta \ddot \theta + \omega_{\theta}^2\delta \theta + \left[{\mathrm{non~linear~terms~in}}~\delta \theta \right] = g (r)\cos (\omega_0\,t),\\[3mm] &&\delta \ddot r + \omega_{{r}}^2\delta r + \left[{\mathrm{non~linear~terms~in}}~\delta \theta, \delta r \right] = h (r)\cos (\omega_0\,t), \end{eqnarray}](/articles/aa/full_html/2013/04/aa19724-12/aa19724-12-eq36.png) with
with 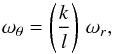 (5)where k,l are small natural numbers and ω0 is the frequency of the external force5. The non-linear terms allow combinational (beat) frequencies in resonant solutions for δθ(t) and δr(t) (see, e.g., Landau & Lifshitz 1976), which in the simplest case give
(5)where k,l are small natural numbers and ω0 is the frequency of the external force5. The non-linear terms allow combinational (beat) frequencies in resonant solutions for δθ(t) and δr(t) (see, e.g., Landau & Lifshitz 1976), which in the simplest case give  (6)Such resonances can produce the observable frequencies in the 3:2 ratio, as well as in other rational ratios. (One of the cases that give 3:2 observed ratio is also the “direct” case of k:l = 3:2 corresponding to the same frequencies and radius as in the case of 3:2 parametric resonance.) Therefore, we consider direct and simple combinational resonances.
(6)Such resonances can produce the observable frequencies in the 3:2 ratio, as well as in other rational ratios. (One of the cases that give 3:2 observed ratio is also the “direct” case of k:l = 3:2 corresponding to the same frequencies and radius as in the case of 3:2 parametric resonance.) Therefore, we consider direct and simple combinational resonances.
The “Keplerian” resonance model assumes parametric or forced resonances between oscillations with radial epicyclic frequency νr and Keplerian orbital frequency νK. Of course, there are many additional possibilities for composing the resonance conditions. We systematically treat the possibilities in the following.
For the parametric and direct forced resonances, the resonance conditions related to the frequency ratio of oscillations are common, however, physical details, such as the time evolution of the resonance, the dependence of the resonance strength and the resonant frequency width on the order of the resonance, are different (see Landau & Lifshitz 1976; Nayfeh & Mook 1979; Stuchlík et al. 2008b). Here we concentrate on the frequency-ratio resonant conditions, leaving the physical details aside for investigation in the concrete situations expected to be discovered in future thanks to development of the observational techniques (e.g., the proposed LOFT observatory, Feroci et al. 2012).
3. Determination of the black hole spin from the resonance model
It is well known that the formulae for the vertical epicyclic frequency νθ and the radial epicyclic frequency νr of the geodetical motion take in the gravitational field of a rotating Kerr black hole (with the mass M and spin a) the form  (7)(e.g., Aliev & Galtsov 1981; Kato et al. 1998; Stella & Vietri 1998; Török & Stuchlík 2005) where the Keplerian frequency νK and related epicyclic frequencies are given by the formulae
(7)(e.g., Aliev & Galtsov 1981; Kato et al. 1998; Stella & Vietri 1998; Török & Stuchlík 2005) where the Keplerian frequency νK and related epicyclic frequencies are given by the formulae 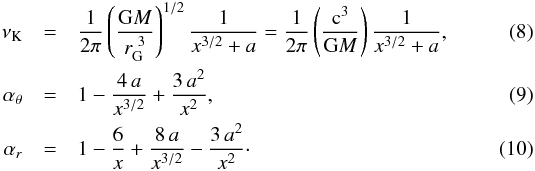 Here x = r/(GM/c2) is the dimensionless radius, expressed in terms of the gravitational radius of the black hole, and a is the dimensionless spin.
Here x = r/(GM/c2) is the dimensionless radius, expressed in terms of the gravitational radius of the black hole, and a is the dimensionless spin.
It is known that the Keplerian frequency νK(x,a) is a monotonically decreasing function of the radial coordinate for any value of the black hole spin. On the other hand, the radial epicyclic frequency has the global maximum for any Kerr black hole. However, the vertical epicyclic frequency is also not monotonic if the spin is sufficiently high (see, e.g., Kato et al. 1998; Perez et al. 1997)6.
For the Kerr black-hole spacetimes, the locations ℛr (a), ℛθ (a) of maxima of the epicyclic frequencies νr, νθ are implicitly given by the conditions (Török & Stuchlík 2005) 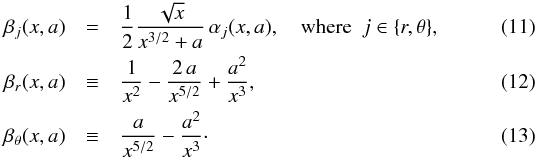 For any black hole spin, the extrema of the radial epicyclic frequency ℛr (a) must be located above the marginally stable orbit. On the other hand, the latitudinal extrema ℛθ (a) are located above the photon (marginally bound or marginally stable) circular orbit only if the limits on the black hole spin a > 0.748 (0.852, 0.952) are satisfied (Török & Stuchlík 2005). In the Keplerian discs, with the inner boundary xin ~ xms, the limiting value a = 0.952 is relevant.
For any black hole spin, the extrema of the radial epicyclic frequency ℛr (a) must be located above the marginally stable orbit. On the other hand, the latitudinal extrema ℛθ (a) are located above the photon (marginally bound or marginally stable) circular orbit only if the limits on the black hole spin a > 0.748 (0.852, 0.952) are satisfied (Török & Stuchlík 2005). In the Keplerian discs, with the inner boundary xin ~ xms, the limiting value a = 0.952 is relevant.
For a particular resonance with frequency ratio n:m, the equation  (14)determines the dimensionless resonance radius xn:m as a function of the spin a in the case of direct resonances. This can be easily extended to the resonances with combinational frequencies, as discussed in detail later.
(14)determines the dimensionless resonance radius xn:m as a function of the spin a in the case of direct resonances. This can be easily extended to the resonances with combinational frequencies, as discussed in detail later.
The known mass of the central black hole, the observed twin-peak frequencies (νU, νL), the Eqs. (7)−(14) and a concrete type of resonance, assumed to be direct or to have the combinational frequencies, enable to determine the black hole spin. This procedure was first applied to the microquasar GRO 1655–40 by Abramowicz & Kluźniak (2001), to the other three microquasars (Török et al. 2005), and also to the Galaxy centre black hole Sgr A∗ (Török 2005).
More complex resonant phenomena in HF QPOs have to be expected in the field of Kerr superspinars (naked singularities), as shown in Török & Stuchlík (2005) and Stuchlík & Schee (2012b). In the superspinar (or naked singularity) backgrounds, the optical effects also demonstrate considerable differences as compared with those generated in the field of black holes (Stuchlík & Schee 2010, 2012a,b; Virbhadra & Ellis 2002; Virbhadra & Keeton 2008; Takahashi & Harada 2010).
4. Multiple resonances and resonance conditions
The very probable interpretation of twin-peak frequencies observed in microquasars is the 3:2 parametric resonance of epicyclic oscillations; however, generally it is possible that more than one resonance could be excited in the disc simultaneously (or at different times) under different internal conditions. Indeed, observations of the HF QPOs in the microquasar GRS 1915+105 (Remillard 2005), in extragalactic sources NGC 4051, MCG-6-30-15 (Lachowicz et al. 2006), NGC 5408 X-1 (Strohmayer et al. 2007), and the Galaxy centre Sgr A∗ (Aschenbach et al. 2004) show a variety of QPOs with frequency ratios differing from (or additional to) the 3:2 ratio.
The resonances could be parametric or forced and have different versions according to the epicyclic (Keplerian) frequencies entering the resonance directly, or in some combinational form. In principle, for any case of the orbital resonance model version, one can determine both the spin and mass of the black hole just from the eventually observed set of frequencies. However, the obvious difficulty would be to identify the right combination of resonances and its relation to the observed frequency set. Within the range of black hole mass allowed by observations, each set of twin-peak frequencies puts a limit on the black hole spin. The resonance model versions are consistent with observations if the allowed spin ranges overlap. Two or more twin peaks (resonant oscillations) then generally make the spin measurement more precise.
 |
Fig. 1 Spin resonance functions aνU/νL(x,p) for the direct resonances D1 – D3 and the frequency ratios n:m = 5:4 (black solid line), 4:3 (black dashed line), 3:2 (black dotted line), 5:3 (red solid line), 2:1 (red dashed line), 5:2 (red dotted line), 3:1 (blue solid line), 4:1 (blue dashed line), 5:1 (blue dotted line). Black thick line represents ams(x), which implicitly determines the radius of the marginally stable orbit xms giving a natural restriction on the validity of the resonance model versions involving radial epicyclic oscillations. In the case D3, the black points determine turning points of the functions aνU/νL(x,p) joining two separate branches of the solution of the resonance condition equation. Of course, only those parts of the resonance functions with x > xms(a) are acceptable. |
Here we consider a special case of two different resonances, determined by a doubled ratio of natural numbers n:m and n′:m′. The resonances occur at the corresponding radii of the disc xn:m, xn′:m′ that can be determined from the observed set of frequencies using the relevant orbital resonance models. Thus, the generic relations n:m, n′:m′ put restrictions on the spin of the central black hole. We consider general frequency ratios of small integers, with the order of the resonances n + m ≤ 9 (n′ + m′ ≤ 9); only for n ≤ 5 are the resonant phenomena realistic (see Landau & Lifshitz 1976; Nayfeh & Mook 1979, for details). In some sources (e.g., NGC 5408 X-1), the ratio 4:3 occurs for the strongest QPOs (Strohmayer et al. 2007), supporting the necessity of considering the general ratios at both radii. In special cases, the resonant radii could coincide, i.e., xn:m = xn′:m′. Then we can expect strongest resonances due to possible direct interactions of the relevant oscillatory modes (see, e.g., Nayfeh & Mook 1979; Stuchlík et al. 2008b).
We first discuss how the frequency ratio of twin oscillation modes in a resonance implies the resonance conditions, i.e., dependence of the radius of the accretion disc where the resonance occurs on the spin parameter a of the Kerr geometry and the frequency ratio n:m.
4.1. Resonance conditions
We study radial coordinates determining positions where the rational frequency ratios occur for all possible versions of the resonance between the radial and vertical epicyclic and the Keplerian oscillations (νK > νθ > νr for 1 ≥ a ≥ 0), taking both the direct and simple combinational resonances into account. For all possible resonances of the epicyclic and Keplerian oscillations, the resonance condition is given in terms of the frequency ratio parameter 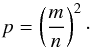 (15)All the resonant conditions that implicitly determine the resonant radius xn:m(a,p) must be related to the radius of the innermost stable circular geodesic xms(a) giving the inner edge of Keplerian discs. Therefore, for all the relevant resonance radii, we require xn:m(a,p) ≥ xms(a), where xms(a) is implicitly given by (Bardeen et al. 1972)
(15)All the resonant conditions that implicitly determine the resonant radius xn:m(a,p) must be related to the radius of the innermost stable circular geodesic xms(a) giving the inner edge of Keplerian discs. Therefore, for all the relevant resonance radii, we require xn:m(a,p) ≥ xms(a), where xms(a) is implicitly given by (Bardeen et al. 1972) 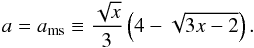 (16)The results are summarized in such a way as to relate the black hole spin a and the dimensionless resonance radius xn:m(a,p) determined for the corresponding resonance model version and the frequency ratio parameter p. The resonance functions are denoted as aνU/νL(x,p).
(16)The results are summarized in such a way as to relate the black hole spin a and the dimensionless resonance radius xn:m(a,p) determined for the corresponding resonance model version and the frequency ratio parameter p. The resonance functions are denoted as aνU/νL(x,p).
4.1.1. Direct resonances
We consider first the direct resonances concerning the epicyclic and Keplerian orbital frequencies giving the resonance conditions that have to be fulfilled:
The results are illustrated in Fig. 1. In cases D1 and D2, the resonance lines aνU/νL(x,p) are monotonous functions of x and do not cross the stability line ams(x). They are given by a single branch of the solutions of the resonance conditions. In case D3, the resonance lines cross the stability line and in some cases are determined by two branches of the resonance condition solutions, joined at a turning point. The solutions are acceptable at the stability domain, i.e., for 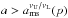 , where
, where 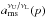 denotes crossing of the resonance line aνU/νL(x,p) with ams(x) and is called “stability point” of the resonance function.
denotes crossing of the resonance line aνU/νL(x,p) with ams(x) and is called “stability point” of the resonance function.
4.1.2. Simple combinational resonances
We study the simple combinational resonances in Appendix A for combinations of frequency pairs, and in Appendix B for combinations of all three frequencies νK, νθ, νr.
4.1.3. Double-beat combinational resonances
Resonances of beat frequencies (four frequencies combined from νK, νθ, νr) constitute family of 13 cases. The behavior of the resonance functions is similar to the case of the simple combinational resonances. The double-beat combinational resonances are treated in Appendix C.
4.2. Warped disc oscillations
In the framework of the warped disc oscillations models (Kato 2004b; Wagoner 1999), where the frequencies of the disc oscillations are given by combinations of the (multiples of the) Keplerian and epicyclic frequencies, resonant phenomena could be relevant too. Usually, the inertial-acoustic and g-mode oscillations and their resonances are relevant (Kato 2007). We give as an example the frequency relation νL = νK − νr; νU = 2νK − νθ which can be considered as an acceptable model of HF QPOs in some atoll sources (e.g., 4U 1636−53, Barret et al. 2005b) and typical Z-source Circinus X-1 (Boutloukos et al. 2006; Török et al. 2010).
Assuming 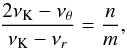 (20)we find that the resonance points are determined by the resonance condition
(20)we find that the resonance points are determined by the resonance condition 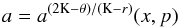 (21)where the resonance function a(2K − θ)/(K − r)(x,p) is given by the equation
(21)where the resonance function a(2K − θ)/(K − r)(x,p) is given by the equation 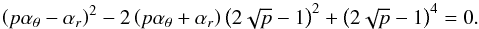 (22)Results of solutions of (22) are given in Fig. C.2 in Appendix C7.
(22)Results of solutions of (22) are given in Fig. C.2 in Appendix C7.
5. Characteristic frequency sets with a duplex frequency
In some specific situations, for some specific values of the black hole spin, two twin-peak QPOs observed at the radii xn:m and xn′:m′ have the bottom, top, or mixed (the bottom at the inner radius and the top in the outer radius, or vice versa) frequencies identical. Such situations can be characterized by sets of three frequencies (upper νU, middle νM and lower νL frequency) with ratio νU:νM:νL = s:t:u, given by the n:m and n′:m′ ratios, the relevant versions of the resonance, and the type of the duplex (common) frequency.
When only direct resonances of the epicyclic oscillations are allowed, the first case with “bottom identity” can be realized when two resonances have a common radial epicyclic frequency, while the second case with “top identity” can be realized when two resonances have a common vertical epicyclic frequency. These two possibilities only are in principle allowed by the non-monotonicity of the epicyclic frequencies (7) discussed in detail by Török & Stuchlík (2005). When the Keplerian oscillations and the combinational frequencies are allowed, all the mixed, bottom, and top identities are possible.
From the point of view of the observational consequences, it is important to know for which frequency ratios n:m the resonant frequency νθ(a,n:m), which is considered as a function of the black hole spin a for a given frequency ratio n:m, has a non-monotonic character. A detailed analysis (Török & Stuchlík 2005) shows that νθ(a,n:m) has a local maximum for n:m > 11:5; i.e., in physically relevant situations (n, m small enough for the resonance), it occurs for the ratios νθ:νr = 5:2, 3:1, 4:1, 5:1. This means that while the “bottom identity” could happen for any black hole spin a, the “top identity” can only arise for a ~ 1 if only the epicyclic oscillations are considered.
The typical cases of the frequency triple sets with bottom, top, and both types of mixed identities containing duplex frequencies are illustrated in Fig. 2. Another interesting exceptional case occurs, e.g., for the spin a = 0.958, when two oscillations of frequencies with the same magnitude (and ratio) are in resonance at two different radii, see Fig. 2h.
 |
Fig. 2 Typical cases of the frequency triples with top a), b), bottom c), d), and both types of mixed identities e), f), g). Also shown is the interesting exceptional case where two oscillations of frequencies with the same magnitude and the same ratio are in resonance at two different radii h). |
We use the following system of notation throughout this paper: T(X)(Y), B(X)(Y), and M(X) (Y) where T stands for top, B for bottom, and M for mixed identity. The (X)(Y) corresponds to the given types of the doubled resonances (X) and (Y) with identical top, bottom, or mixed frequencies (for the case of mixed identity (X) always denotes the resonance with the top frequency and (Y) the resonance with the identical bottom frequency). The concrete types of resonances (X)(Y) can be easily deduced from the notation presented in Appendix D (Tables D.1 and D.5).
 |
Fig. 3 Determination of black hole spin for several cases of doubled resonances. The functions |
5.1. Triple frequency sets and black hole spin
We consider a simple situation with the “top identity” of the upper frequencies in two resonances between the radial and vertical epicyclic oscillations at the radii xp,xp′ with p1/2 = m:n, p′1/2 = m′:n′. The condition νθ(a,xp) = νθ(a,xp′) is then transformed to the relation 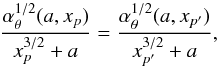 (23)which uniquely determines the black hole spin a. When two different resonances are combined, we proceed in the same manner. For example, the case of “bottom identity” in the resonance between the radial and vertical epicyclic oscillations at xp and the resonance between the Keplerian oscillations with νK and total precession oscillations with νT = νθ − νr at xp′ implies the condition
(23)which uniquely determines the black hole spin a. When two different resonances are combined, we proceed in the same manner. For example, the case of “bottom identity” in the resonance between the radial and vertical epicyclic oscillations at xp and the resonance between the Keplerian oscillations with νK and total precession oscillations with νT = νθ − νr at xp′ implies the condition 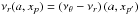 that leads to the relation
that leads to the relation 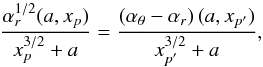 (24)which uniquely determines the spin a, since in Eq. (17) (and (B.2)), the radii xp and xp′ are related to the spin a by the resonance conditions for aθ/r(x,p) and aK/(θ − r)(x,p′), respectively.
(24)which uniquely determines the spin a, since in Eq. (17) (and (B.2)), the radii xp and xp′ are related to the spin a by the resonance conditions for aθ/r(x,p) and aK/(θ − r)(x,p′), respectively.
Therefore, for given types of the doubled resonances, the ratios n:m and n′:m′ determine the ratio in the triple frequency set s:t:u. The black hole spin a is given by the types of the two resonances and the ratios p, p′, quite independently of the black hole mass M.
Since the radial and vertical epicyclic frequencies and the Keplerian frequency have the same dependence on the black hole mass M, the above arguments hold in the same way for any kind of the three frequency sets, for any of the bottom, top, or mixed frequency identity with any two resonances containing any combination of the frequencies νK,νθ,νr. Therefore, the triple frequency sets with the “duplex” frequencies can be used to determine the black hole spin with very high precision, independently of the uncertainties in determining the black hole mass M: the parameter M can be addressed by the magnitude of the measured frequencies. However, the relation between the black hole spin and the triple frequency ratios is not unique in general. For a given frequency ratio set, several values of a are allowed, and some other methods of the spin measurement (spectral continuum fitting, profiled spectral lines) must be involved.
The triple frequency set ratios are directly given by the versions of resonance that occur in the two twin-peak QPOs under consideration, while the relevant spin a can be easily determined by seeking common points of the relevant frequency functions for a fixed mass M. The schemes for treating the situations with duplex frequencies are given in Figs. 2 and 3.
The method of finding the spin a is illustrated in Fig. 3 for several cases of resonances. We can see from Fig. 3 that there are no solutions for the cases T33, T44, and B33, but for T11, T34, and M13 there are some specific values of the black hole spin when the top (or mixed) frequencies are identical and give the characteristic triple frequency ratio sets. The complete results of detailed analysis are given in Appendix D (Tables D.2−D.4). We give schemes of the direct resonances (D1−D3) and some of the triple combinational resonances (CT1, CT2) that cannot be deduced from the direct resonances.
For the simple combinational resonances containing only two of the three relevant frequencies, the results can be easily determined from the direct resonances, because at a given radius xp, where a direct resonance occurs, the combinational resonances of the two relevant frequencies occur, and the relevant ratio of the combinational resonances is given by the relations expressed explicitly for the direct resonance. In all of the simple combinational resonances occurring at the same radius as the corresponding direct resonance, the related black hole spin a remains unchanged, and only the triple of the frequency ratios is different and is determined by the relations for the combinational frequencies.
In presenting the final results for the direct and simple combinational resonances in the tables in Appendix D, we have considered all the ratios with n,m = 1,2,3,4. Of course, owing to the theory (Landau & Lifshitz 1976), the highest resonance order that should be considered here is n + m = 9, corresponding to the highest order resonances with n:m = 5:4 that are observed in some black hole systems (see Remillard & McClintock 2006; Strohmayer et al. 2007) and in some neutron star systems (see Belloni et al. 2005, 2007b; Barret et al. 2005b; Török 2009; Stuchlík et al. 2011b). However, such tables are too extended to be presented here, and that is the reason we restrict ourselves to the limited range of n,m = 1,2,3,4. The complete tables with n,m = 1,2,3,4,5 can be found for some important cases in Stuchlík et al. (2007a).
In the case of the doubled combinational (and warped disc) frequency ratios, we restrict our attention to triple frequency sets that contain their combinations with the most frequently expected direct resonance of the radial and vertical epicyclic oscillations and to the ratios involving n,m = 1,2,3,4. The results are presented in Appendix D (Tables D.6−D.8). The other combinations can be constructed in an analogous manner. An explicit form of tables representing all the possible combinations of doubled beat frequencies is very extended, and that is why we do not present them explicitly. Using our results they could be constructed in a straightforward way. The resonance “guide” book can be thus completed easily.
5.2. Strong resonant radii and related black hole spin
The presented results show that usually the triple frequency sets fixing the black hole spin a occur at two different radii. However, there are important cases when the triple frequencies occur at the same (shared) radius. Then one could expect an intuitively higher probability that the resonant phenomena will arise, especially in the cases of ratios of very low integers 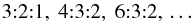 (25)because a causally related cooperation of the resonances at the given radius should come into play. A crucial role is expected for direct resonances of oscillations with all three orbital frequencies characterized by a triple frequency ratio set (s, t, u being small natural numbers)
(25)because a causally related cooperation of the resonances at the given radius should come into play. A crucial role is expected for direct resonances of oscillations with all three orbital frequencies characterized by a triple frequency ratio set (s, t, u being small natural numbers) 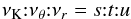 (26)when strong resonant phenomena are possible (Stuchlík et al. 2008b). Assuming two resonances with ratios νK:νθ = s:t and νK:νr = s:u sharing the same radius x, we can determine the radius giving s:t:u ratio from the equation (Stuchlík et al. 2008b)
(26)when strong resonant phenomena are possible (Stuchlík et al. 2008b). Assuming two resonances with ratios νK:νθ = s:t and νK:νr = s:u sharing the same radius x, we can determine the radius giving s:t:u ratio from the equation (Stuchlík et al. 2008b)
![\begin{eqnarray} &&x\left(s/u,t/u\right)\equiv 6\left(s/u\right)^2{X}^{-1} ,\\ &&X=6 \left(s/u\right)^2\pm 2 \sqrt{2} \sqrt{\left(t/u-1\right) \left(t/u+1\right) \left[3 \left(s/u\right)^2-\left(t/u\right)^2-2 \right]}\nonumber\\ &&\hspace*{10mm}- \left[\left(t/u\right)^2+5\right] , \end{eqnarray}](/articles/aa/full_html/2013/04/aa19724-12/aa19724-12-eq145.png) and the related black hole “magic” spin is given by
and the related black hole “magic” spin is given by ![\begin{equation} a\left(x\left(s/u,t/u\right),u/s\right)\equiv\frac{\sqrt{x}}{3}\left(4\pm\sqrt{-2+3x\left[1-\left(u/s\right)^2\right]}\,\right). \end{equation}](/articles/aa/full_html/2013/04/aa19724-12/aa19724-12-eq146.png) (29)A detailed discussion of the black holes that admit strong resonant phenomena is for small integers (s ≤ 5) given in Stuchlík et al. (2008b). All the results (denoted by an asterisk) are contained in Appendix D (Tables D.2−D.4 and D.6−D.8). Since x(s,t,u) can be considered as a two-parameter (s/u,t/u) family of solutions for the shared resonant radii, we are able to give the results of finding the strong resonance radii and the corresponding spin in Fig. 4. The radius and spin at these points are xA = 2.395, aA = 0.983; xB = 2.880, aB = 0.866; xC = 2.083, aC = 0.962; xD = 3.240, aD = 0.775; xE = 3.407, aE = 0.882.
(29)A detailed discussion of the black holes that admit strong resonant phenomena is for small integers (s ≤ 5) given in Stuchlík et al. (2008b). All the results (denoted by an asterisk) are contained in Appendix D (Tables D.2−D.4 and D.6−D.8). Since x(s,t,u) can be considered as a two-parameter (s/u,t/u) family of solutions for the shared resonant radii, we are able to give the results of finding the strong resonance radii and the corresponding spin in Fig. 4. The radius and spin at these points are xA = 2.395, aA = 0.983; xB = 2.880, aB = 0.866; xC = 2.083, aC = 0.962; xD = 3.240, aD = 0.775; xE = 3.407, aE = 0.882.
Of special interest seems to be the case of the “magic” spin a = 0.983, when the Keplerian and epicyclic frequencies are in the ratio νK:νθ:νr = 3:2:1 at the common radius x3:2:1 = 2.3947 (see Fig. 5a). In fact, this case involves rather extended structure of resonances with νK:νr = 3:1, νK:νθ = 3:2, νθ:νr = 2:1. Also the simple combinational frequencies could be in this small integer ratio (Stuchlík et al. 2008b). The strongest possible resonances occur when the beat frequencies enter the resonance satisfying the conditions 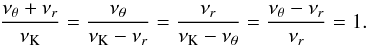 (30)It should be stressed that beside the case of strong resonances between oscillations with νK, νθ, νr sharing the same radius, the characteristic set 3:2:1 could also appear because of resonances at different radii (see Fig. 5b). All the relevant versions of the multi-resonant model with 3:2:1 frequency ratio set are given in Appendix E by Table E.1.
(30)It should be stressed that beside the case of strong resonances between oscillations with νK, νθ, νr sharing the same radius, the characteristic set 3:2:1 could also appear because of resonances at different radii (see Fig. 5b). All the relevant versions of the multi-resonant model with 3:2:1 frequency ratio set are given in Appendix E by Table E.1.
 |
Fig. 4 Function x(s/u,t/u) determining the triple frequency ratio set s:t:u at the properly given radius of a black hole with a “magic” spin. The points represent the ratio: s:t:u = 3:2:1 A), 4:3:1 B), 5:3:1 C), 5:4:1 D), 5:4:2 E). |
6. Resonant switch model
In the case of LMXB systems containing neutron or quark stars, we propose a new model of twin-peak HF QPOs. It is based on the idea that the twin oscillatory modes with changing frequencies that create sequences of the lower and upper HF QPOs switch at a resonant point – we call it resonant switch (RS) model. We assume the resonant point occurs at a radius of the oscillating disc where frequencies of the twin oscillatory modes become commensurable. We expect that at the resonant point non-linear resonant phenomena will cause excitation of a new oscillatory mode (or two new oscillatory modes) and dumping (vanishing) of one of the previously acting modes (or both the previously acting modes), i.e., switching from one pair of the oscillatory modes to the other pair of them that will be acting up to the next relevant resonant point.
The observational X-ray data obtained for both the atoll and Z-sources indicate the feasibility of the RS model in some of the observed sources. In the atoll sources (e.g., in 4U 1636−53), the twin-peak HF QPOs span a wide range of frequencies crossing the frequency ratios 3:2, 4:3 and finishing at 5:4, just near the inner edge of the accretion disc (Boutelier et al. 2010; Török 2009). In the case of the 4U 1636−53 source, the behaviour of these observed oscillations, reflected by the energy switch effect occurring at the related frequency ratios (Török 2009), indicates the resonant effects at disc radii where the frequencies are in the ratios 3:2 and 5:4. The energy switch effect, reflecting the change of the dominance of the lower frequency oscillations to dominance of the upper frequency oscillations while the resonant point is crossed, can be naturally explained in the framework of non-linear resonant phenomena (Horák et al. 2009). Therefore, it is probably reasonable to assume that the frequencies of oscillations at the energy reverse point determine the eigenfrequencies of the oscillations at the resonance point.
The energy switch effect allows the frequencies to be determined at the resonant points that can then be used to determine (or significantly restrict) parameters of the central neutron (quark) star for various models of the HF QPOs. A similar, but slightly modified, situation occurs for Z-sources. In the case of the typical Z-source Circinus X-1, we again observe a wide range of HF QPO frequencies, but these are crossing frequency ratios 2:1 and 3:1 which are substantially higher than in the atoll sources, indicating that the QPOs occur at different parts of the accretion discs in comparison with the atoll sources. We expect that in the atoll sources HF QPOs occur in the innermost parts of the disc (we can even assume that the resonant point with frequency ratio 5:4 represents the inner boundary of the disc, Stuchlík et al. 2011b), while in the Z-sources we expect HF QPOs generated at more distant parts of the disc, lying behind the radius where the maximum of the radial epicyclic frequency occurs (Török et al. 2010). We can determine the resonant points (and their observational extension) by both (i) the switch energy effect, i.e., due to the frequency where the difference in amplitude of the lower and upper frequency oscillations vanishes, and (ii) the region of observational data in the resonant frequency ratio. We have checked that these methods agree in the case of the 4U 1636−53 source.
In the (simplest version of) RS model, we assume two resonant points at the disc radii rout and rin, with observed frequencies 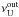 ,
, 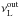 and
and 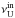 ,
, 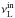 , being in commensurable ratios pout = nout:mout and pin = nin:min. These resonant frequencies are determined by the energy switch method (Török 2009; Horák et al. 2009). The observations put the restrictions
, being in commensurable ratios pout = nout:mout and pin = nin:min. These resonant frequencies are determined by the energy switch method (Török 2009; Horák et al. 2009). The observations put the restrictions 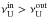 and pin < pout. In the region covering the resonant point at rout we assume the twin oscillatory modes with the upper (lower) frequency determined by the function
and pin < pout. In the region covering the resonant point at rout we assume the twin oscillatory modes with the upper (lower) frequency determined by the function 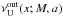 (
(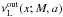 ). In the region of the inner resonant point we assume (generally) different oscillatory modes with the upper and inner frequency functions
). In the region of the inner resonant point we assume (generally) different oscillatory modes with the upper and inner frequency functions 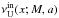 and
and 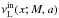 . We assume all the frequency functions to be given by combinations of the orbital and epicyclic frequencies of the geodesic motion in the Kerr backgrounds, and such a simplification is correct with high precision for neutron (quark) stars with high mass. The rotating neutron stars are described quite well by the Hartle–Thorne geometry characterized by three parameters: mass M, internal angular momentum J, and quadrupole moment Q (Hartle & Thorne 1968). It is convenient to use dimensionless parameters a = J/M2 (spin – denoted j in Török et al. 2010) and q = QM/J2 (dimensionless quadrupole moment). In the special case where q ~ 1, the Hartle–Thorne geometry reduces to the Kerr geometry that is very convenient for relativistic calculations in a strong gravitational field regime because of the simplicity of relevant formulae. It has been shown that near-maximum-mass neutron (quark) star Hartle–Thorne models, constructed for any given realistic equation of state, imply q ~ 1, and the simple Kerr geometry is quite correctly applicable in such situations instead of the complicated Hartle–Thorne geometry (Török et al. 2010). High neutron star masses can be expected in the LMXBs because their mass grows owing to the accretion.
. We assume all the frequency functions to be given by combinations of the orbital and epicyclic frequencies of the geodesic motion in the Kerr backgrounds, and such a simplification is correct with high precision for neutron (quark) stars with high mass. The rotating neutron stars are described quite well by the Hartle–Thorne geometry characterized by three parameters: mass M, internal angular momentum J, and quadrupole moment Q (Hartle & Thorne 1968). It is convenient to use dimensionless parameters a = J/M2 (spin – denoted j in Török et al. 2010) and q = QM/J2 (dimensionless quadrupole moment). In the special case where q ~ 1, the Hartle–Thorne geometry reduces to the Kerr geometry that is very convenient for relativistic calculations in a strong gravitational field regime because of the simplicity of relevant formulae. It has been shown that near-maximum-mass neutron (quark) star Hartle–Thorne models, constructed for any given realistic equation of state, imply q ~ 1, and the simple Kerr geometry is quite correctly applicable in such situations instead of the complicated Hartle–Thorne geometry (Török et al. 2010). High neutron star masses can be expected in the LMXBs because their mass grows owing to the accretion.
 |
Fig. 5 Left: case of a “magic” spin, where the strongest resonances could occur at the same radius. For completeness we present the relevant simple combinational frequencies νθ − νr, νθ + νr, νK − νθ, νK − νr (grey dashed lines). The “magic” spin am = 0.983 represents the only case where the combinational and direct orbital frequencies coincide at the shared resonance radius. Right: another example of the characteristic frequency ratio set 3:2:1 that appears at different radii. |
The frequency functions have to meet the observationally given resonant frequencies. In the framework of the simple RS model this requirement enables determination of the parameters of the Kerr background describing the exterior of the neutron (quark) star. The “shooting” of the frequency functions to the resonant points, giving the neutron star parameters, can be realized efficiently in two steps. First, we can apply our method based on the frequency ratio’s independence of the mass parameter M. Therefore, the conditions
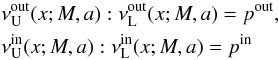 (31)imply the relations for the spin a in terms of the dimensionless radius x and the resonant frequency ratio p. We can express them in the form aout(x,pout) and ain(x,pin) as determined in Sect. 4 for a concrete version of the twin oscillatory modes, or in an inverse form xout(a,pout) and xin(a,pin). At the resonant radii, the conditions
(31)imply the relations for the spin a in terms of the dimensionless radius x and the resonant frequency ratio p. We can express them in the form aout(x,pout) and ain(x,pin) as determined in Sect. 4 for a concrete version of the twin oscillatory modes, or in an inverse form xout(a,pout) and xin(a,pin). At the resonant radii, the conditions 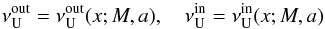 (32)are satisfied along the functions
(32)are satisfied along the functions 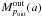 and
and 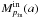 , which are obtained by using the functions aout(x,pout) and ain(x,pin). The parameters of the neutron (quark) star are then given by the condition
, which are obtained by using the functions aout(x,pout) and ain(x,pin). The parameters of the neutron (quark) star are then given by the condition 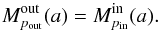 (33)Usually, condition (33) determines M and a uniquely, if the resonant frequencies are determined precisely. If an error occurs in determining the resonant frequencies, as expected naturally, our method gives corresponding intervals of the acceptable values of the mass and spin parameter of the neutron (quark) star.
(33)Usually, condition (33) determines M and a uniquely, if the resonant frequencies are determined precisely. If an error occurs in determining the resonant frequencies, as expected naturally, our method gives corresponding intervals of the acceptable values of the mass and spin parameter of the neutron (quark) star.
Predictions of the RS model have to be tested in three ways:
-
a)
by the range of values of the massand spin parameters of the central neutron (quark)star allowed by theoretical models of the neutron(quark) star structure,
-
b)
by the fitting of the twin-peak HF QPO data sequences around the resonant points by the twin oscillation modes used near the resonant points,
-
c)
by the observational limits on mass and spin given by different phenomena observed in X-rays coming from the source, e.g., by the profiled spectral lines.
The method of finding the M(a) relation in the framework of the RS model can be directly used for the black hole systems that provide four QPO frequencies at two resonant points located at two different radii. Of course, for black holes the four frequencies are exactly determined from precise observations, and there are generally no restrictions on the models applied to the two resonant points since we expect no relation between the two resonances, contrary to the RS model related to the systems containing a neutron star.
7. Discussion
We discuss the applicability and precision of the multi-resonance model in black hole or neutron star systems. As an illustration we offer a detailed discussion of the HF QPO phenomena for triple frequency set with ratio 3:2:1 in terms of the multi-resonance model, including estimates of the error in determining the black hole spin. The RS model for neutron star systems exhibiting two resonant points is tested for data from the atoll source 4U 1636−53.
7.1. Black holes
The relation between the tripled frequency ratios and the black hole spin is presented in Appendix D, which gives all the possible cases of the bottom, top, and mixed frequency identities. Of course, there is potentially a real difficulty in choosing the proper combination of the resonance model versions in analysing the frequency data from concrete sources. Then all the relevant data on HF QPOs have to be used, and the results have to be compared with results from the other methods of measuring black hole spin, e.g., those based on the spectral continuum and profiled spectral lines.
 |
Fig. 6 Error in determining the “magic” spin am = 0.983043 allowing νK:νθ:νr = 3:2:1 at the same radius. The interval of allowed values of the black hole spin a ∈ ⟨ am − Δ;am + Δ ⟩ related to the 2% error in frequency measurements is for T23: a ∈ ⟨ 0.973038;0.992436 ⟩; for M13: a ∈ ⟨ 0.970599;0.995125 ⟩; for T34: a ∈ ⟨ 0.981643;0.984157 ⟩; for B14: a ∈ ⟨ 0.981436;0.984253 ⟩. For the case of B12, only the 0.5% measurement error gives a reasonable restriction on black hole spin: a ∈ ⟨ 0.969714;0.993428 ⟩ (for 2% measurement error there is a ∈ ⟨ 0.91012;1.01155 ⟩). |
The method of triple frequency sets must be treated very carefully because of uncertainties in the frequency measurement in HF QPOs (Remillard & McClintock 2006). In fact, in some versions of the multi-resonance model, even a relatively high precision of the frequency measurements could imply rather high scatter in the estimated black hole spin. The triple frequency set method could be expected to work quite efficiently in the case of ratios of small integers, such as 3:2:1, 4:3:2, etc. The other possible frequency sets have to be taken seriously, but analysis must be very careful for high integers in the triple frequency sets. It is increasingly difficult to distinguish different triple frequency sets when the order of the resonance increases, since the uncertainties of the frequency measurements are relatively high. Nevertheless, we can expect that data from a new generation of X-ray satellites, especially from the LOFT project aimed at extremely precise timing measurements (Feroci et al. 2012), could improve the situation due to an expected strong increase in the frequency measurement precision.
We expect that analysis of each concrete source will need an appropriate combination of different methods. Clearly, a detailed analysis of assumed resonance phenomena, both parametric and forced, and their excitation by both external and internal causes must be taken into consideration. In particular, the expected resonance strength and allowed range of resonant frequencies must be treated very carefully (Stuchlík et al. 2008b; Nayfeh & Mook 1979). When the equations of motion for non-linear oscillations are solved by successive approximations, higher harmonics and combinational frequencies occur in oscillating systems corresponding to higher approximations. As the degree of approximation increases, the strength of the resonances and the resonant frequency width decrease rapidly as shown by Landau & Lifshitz (1976) and Nayfeh & Mook (1979).
The most promising example of the triple frequency ratios arising in a single radius (or in its close vicinity) occurs for the “magic” black hole spin a = 0.983, when at the radius x3:2:1 = 2.395, the frequency ratio is νK:νθ:νr = 3:2:1. Then the resonant phenomena should be strongest, and all the resonances, including those with beat frequencies, could cooperate efficiently even for frequencies scattered from the exact resonant eigenfrequencies. For the triple frequency ratio set 3:2:1, all the allowed combinations of the oscillatory modes are given in Appendix E (Table E.1) and demonstrate a significant complexity.
It is necessary for us to compare the results of the multi-resonance model to the results of the other methods of black hole spin measurements, namely those related to the optical phenomena in the vicinity of the black hole (Schee & Stuchlík 2009a; Bin-Nun 2010a,b; Horváth & Gergely 2012). For Sgr A∗, considered to be a candidate for the test object of the resonant phenomena with frequency ratio 3:2:1 (Aschenbach 2004; Török 2005), the relativistic precession of the nearby star orbits is also very promising (Kraniotis 2005, 2007).
It is quite instructive to determine how the frequency measurement precision could influence the black hole spin estimates in this very special case8. We give the range of the black hole spin for which the 3:2:1 resonant phenomena could be relevant because of the precision of frequency measurements that is usually reported in the period of 0.5 − 2% (Remillard & McClintock 2006). The scatter of the black hole spin related to the frequency measurement errors is shown in Fig. 6. We illustrate the situation for some representative versions of oscillatory modes in resonance, namely T23, T34, B12, B14, M13. We can see that, except for the case of B12, all the cases give a strong restriction on the spin even for the two percent error in the frequency measurements. On the other hand, for B12, only the 0.5% measurement error gives a reasonable restriction on a, while even for 1% error, values of a > 1 are allowed. Clearly, if the relevant frequency curves cross in a large (small) relative angle, the spin is determined with high (low) precision. The same rule is relevant in analysing any resonance triple frequency set. In the case of T23, the detailed results are illustrated in the Table 1. We can see that the one percent error in frequency measurement implies an error of 0.005 in spin determination, while a three percent frequency error implies a 0.015 error in spin determination. In the latter case, the interval of allowed values for the spin reads as 0.9678 < am < 0.9969, and the upper limit enters the region of applicability of the extended resonance model (Stuchlík et al. 2007b). The LOFT project promises high enough precision for extended application of our multi-resonance model. The assumed precision of the LOFT measurements of HF QPOs is expected to be at least one order higher than for recent satellites (Feroci et al. 2012), implying precision of the spin determination at the level of 0.001 (see Table 1).
In the framework of the multi-resonance model, a detailed guide book of triple frequency sets and related black hole spins has been developed (see Appendix D). However, this is only an introductory book based solely on the frequency ratios of the observed oscillations. Additional case-dependent information has to be related to the multi-resonance model in order to restrict variants of the oscillatory modes in resonance or to falsify all of them. The most important information is connected to the amplitude of the oscillatory modes, simultaneity of their appearance, their time dependence, and frequency scatter.
Properties of the observed oscillations are related to the magnitude of the accretion flow (see, e.g., Ford et al. 2000). The multi-resonance model is unaffected by the flow magnitude if the gravitation remains the main restoring force of the oscillations. In those cases where the restoring forces of non-gravitational origin becomes relevant, the model has to be modified.
7.2. Neutron stars
In LMXB systems containing neutron (quark) stars, the simple resonance model assuming resonance of oscillations with radial νr and vertical νθ epicyclic frequencies can be excluded with high probability, or requires substantial non-geodesic corrections to the formulae of the epicyclic frequencies (Urbanec et al. 2010b; Abramowicz et al. 2011). The evolution of the lower and upper HF QPOs frequencies (across a single measurement sequence) in such sources suggests (very rough) agreement of the data distribution with the relativistic precession (RP), hot spot model (Stella & Vietri 1999, 1998). In rough agreement with the data are also other models based on the assumption of the oscillatory motion of hot spots or accretion disc oscillations, such as the total precession model (Stuchlík et al. 2007d), the tidal disruption model (Čadež et al. 2008; Kostić et al. 2009; Germanà et al. 2009), or the warped disc oscillations model (Kato 2001a, 2004b,a, 2007, 2008, 2009). In all of these models the frequency difference νU − νL decreases with increase in the magnitude of the lower and upper frequencies in accord with trends given by the observational data (Barret et al. 2005a; Belloni et al. 2007a; Boutelier et al. 2010). An alternative explanation of HF QPOs in neutron star systems provides the sonic-point and spin-resonance models (Lamb & Miller 2001, 2003), higher-order nonlinearity model (Mukhopadhyay 2009), shock-wave model (Chakrabarti et al. 2009; Debnath et al. 2010), Rayleigh–Taylor gravity wave model (Osherovich & Titarchuk 1999; Titarchuk 2003; Titarchuk & Shaposhnikov 2008), MHD Alfvén wave oscillation model (Zhang 2004; Zhang et al. 2006, 2007; Shi 2011), and MHD model (Shi & Li 2009).
The νU − νL frequency relation, given by a variety of the relevant frequency-relation models mentioned above, can be fitted to the observational data for some properly chosen neutron star sources. Rather surprisingly, the fitting procedure applied implies a mass-spin relation M(a) = M0 [1 + k(a + a2)] for both the sources rather than concrete values of the neutron star parameters M and a. Both the parameters M0 and k depend on the source and the combination of the twin oscillatory modes (for details see Török et al. 2010, 2012). The quality of the fitting procedure is very poor for the atoll source 4U 1636−53 as demonstrated in Török et al. (2012). Similar, very bad fitting of observational data with the frequency relation models has been found in Lin et al. (2011) for the atoll source 4U 1636−53 and Sco X-1. This disagreement of the data distribution with their fitting by the frequency-relation models is based on the assumption of the geodesic character of the oscillatory frequencies. It implied some attempts to find a non-geodesic correction reflecting additional physical ingredients (such as an influence of the magnetic field) that could make the fitting procedure much better (Török et al. 2012).
For the RP model, a strong improvement can be reached by a small shift in the geodetical radial epicyclic frequency and a related small change in the marginally stable orbit location (Török et al. 2010, 2012). The non-geodesic corrections to the radial epicyclic frequencies can be generated on the level of tens of percent for oscillating non-slender tori (Šrámková 2005; Blaes et al. 2007; Straub & Šrámková 2009), or can do so by assuming a slightly charged internal part of the accretion disc interacting with the external dipole magnetic field of the neutron star when very strong effects can be obtained, on the level of hundred percent or higher (Bakala et al. 2010, 2012; Pachon et al. 2012). We can consider several diverse possibilities to explain the behaviour of charged accretion discs. First, the disc can be treated as a “dielectric” structure, with the effective charge fixed to the moving matter, as discussed in Kovář et al. (2011). Second, there might be an inverse possibility, when the electric charge happens to be concentrated in a hot spot of a solitonic character that could be a cosmic object similar to the well known and poorly understood “ball lightning”. Third, an interesting new and open possibility is represented by oscillations of coronal structures distributed in the vicinity of the off-equatorial circular orbits of charged particles discovered and discussed in Kovář et al. (2008, 2010), Stuchlík et al. (2009), and Kopáček et al. (2010). Preliminary studies indicate that the non-geodesic corrections make the fits much better, however they do introduce additional free parameters into the HF QPOs models. Therefore, it is useful to also test the possibility of improving the fitting procedure by using proper combinations of the models that assume purely geodesic origin of the observed frequencies. Our multi-resonant approach can be applied to the neutron star systems thanks to the possible occurrence of one or two resonant points along the observed twin-peak HF QPOs (Belloni et al. 2007b; Török et al. 2008c,a,b; Török 2009; Boutelier et al. 2010).
The twin-peak frequencies are widely scattered, but concentrated in the vicinity of the resonance point with the frequency ratio close to 3:2 in most of the atoll sources. The scatter of the twin-peak frequencies around this 3:2 resonant point is correlated and approximated by the linear fits νU = AνL + B, and an anticorrelation of the parameters A, B was predicted by the resonance theory and indicated from observational data related to twelve atoll neutron star X-ray binary systems (Abramowicz et al. 2005a,b). However, analysis of the neutron star source 4U 1636−53 indicates resonance at two resonance points with frequency ratios 3:2 and 5:4 (Török et al. 2008c,a,b; Török 2009); moreover, two resonance points with the same frequency ratios are demonstrated by analysis of the source 4U 1608−52 (Török 2009). This means that the HF QPO frequency linear fits and the anticorrelation data (Abramowicz et al. 2005b) only related to the 3:2 frequency ratio are contaminated with the data connected to the 5:4 resonance point in the case of at least these two sources.
Recent observational data obtained for the atoll sources indicate convincingly that the resonance points are located very close to the innermost stable circular geodesics (ISCO) of the spacetime, which are usually assumed to represent the inner edge of the accretion disc (Barret et al. 2006, 2005b,c). Therefore, it is quite natural to expect that the resonant oscillations could be excited by inhomogeneities on the surface of the neutron star, and these inhomogeneities strongly influence the innermost parts of the accretion disc (Stuchlík et al. 2008a). In fact, the twin-peak QPOs’ amplitude analysis of four atoll sources (4U 1636−53, 4U 1608−52, 4U 1820−30, and 4U 1735−44) demonstrates a cut-off of HF QPOs at the resonant radii corresponding to the frequency ratios 5:4 or 4:3 and indicating thus a possibility that in such sources the accretion discs are strongly influenced by resonant phenomena and that the inner edge is shifted from the ISCO to the corresponding resonant radius (Stuchlík et al. 2011b).
A non-standard way to improve the data fitting can be realized in the neutron star systems demonstrating two resonant points in HF QPOs when assumption of a unique frequency relation applicable along the full twin-peak HF QPOs frequency range can be abandoned thanks to the RS model.
7.3. Resonant switch model applied to the atoll source 4U 1636–53
We tested our RS model in the case of the atoll 4U 1636−53 source that seems to be the best possibility owing to the character of the observational data clearly demonstrating two “resonant points” where the energy switch effect occurs. Using the results of Török (2009), the resonant frequencies determined by the energy switch effect are given in the outer resonant point with frequency ratio νU/νL = 3/2 by the frequency intervals 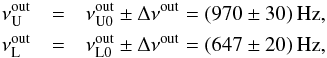 (34)and at the inner resonant point with frequency ratio νU/νL = 5/4 there is
(34)and at the inner resonant point with frequency ratio νU/νL = 5/4 there is 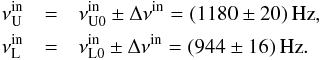 (35)The resonant points determined by using the energy switch effect accord with observational data points crossing the lines of constant frequency ratios 3:2 and 5:4 as given in the standard papers (Barret et al. 2005b; Belloni et al. 2007a).
(35)The resonant points determined by using the energy switch effect accord with observational data points crossing the lines of constant frequency ratios 3:2 and 5:4 as given in the standard papers (Barret et al. 2005b; Belloni et al. 2007a).
 |
Fig. 7 Intervals of acceptable values of mass and spin of the neutron star in the atoll source 4U 1636−53 predicted by the resonant switch model for the combination of RP–TD models (left) and RP–TP models (right) using the scatter of the resonant frequencies at each of the two resonant points where RP ≡ νK:(νK − νr) = 5:4, TD ≡ (νK + νr):νK = 3:2 and TP ≡ νθ:(νθ − νr) = 3:2. |
We tested the RS model determining the parameters M and a of the neutron (quark) star at the 4U 1636−53 source for the standard relativistic precession (RP) model (Stella & Vietri 1999) combined with the tidal distortion (TD) model (Kostić et al. 2009), and the total precession (TP) model (Stuchlík et al. 2007d). In the case of the RP model, the frequency ratio of two oscillatory modes reads as 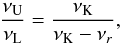 (36)for the TD model we have to consider the frequency ratio
(36)for the TD model we have to consider the frequency ratio 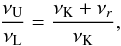 (37)while in the case of the TP model there is
(37)while in the case of the TP model there is 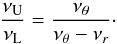 (38)
(38)
7.3.1. Combination of the RP and TD models
For the combination of RP and TD models, the RP model has to be related to the inner resonant point, while the TD model has to be related to the outer resonant point. We applied the method of determining the neutron star parameters M and a presented in the Sect. 6, and the results are presented in Fig. 7. For the frequency scatter at the resonant points, given by relations (34) and (35), the range of allowed values for the mass and spin of the neutron star is given by 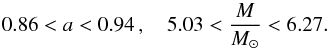 (39)The central point of the frequency ranges implies that the central estimates of the neutron star parameters are a = 0.91 and M = 5.67 M⊙.
(39)The central point of the frequency ranges implies that the central estimates of the neutron star parameters are a = 0.91 and M = 5.67 M⊙.
Clearly, for the combination of the RP and TD oscillatory modes, the RS model implies parameters of the neutron star that are totally out of the ranges accepted by the recent theory of the structure of the neutron stars both for their spin and mass. It is well known that the neutron star mass surely cannot exceed the critical value of M ~ 3 M⊙ (Rhoades & Ruffini 1974) and the models based on the realistic equations of state give maximal masses going up to Mmax ~ 2.8 M⊙ (Postnikov et al. 2010). In fact, the extremal maximum Mmax ~ 2.8 M⊙ is predicted by the field theory (Müller & Serot 1996). The limit of Mmax ~ 2.5 M⊙ is predicted by the Dirac–Brueckner–Hartree–Fock approach in some special cases (Müther et al. 1987), in the variational approaches (Akmal & Pandharipande 1997; Akmal et al. 1998), and in other approaches (Urbanec et al. 2010a) allow for Mmax ~ 2.25 M⊙. For the maximum spin of neutron stars, the limit a < amax ~ 0.7 has been demonstrated recently by Lo & Lin (2011), independently of the equation of state; on the other hand, they have shown the possible existence of quark stars with spin slightly exceeding the black hole limit a = 1. Therefore, the RP–TD combination can be excluded as a realistic explanation of the observed data in the atoll source 4U 1636−53 because of the high values of the predicted neutron star parameters.
7.3.2. Combination of the RP and TP models
For the combination of RP and TP models, the RP model has to be related to the inner resonant point, while the TP model has to be related to the outer resonant point. The method of determining the neutron star parameters M and a implies the results presented in Fig. 7. The range of allowed values of the mass and spin of the neutron star is given by 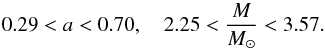 (40)The central point of the frequency ranges implies that the central estimates of the neutron star parameters are a = 0.54 and M = 2.91 M⊙.
(40)The central point of the frequency ranges implies that the central estimates of the neutron star parameters are a = 0.54 and M = 2.91 M⊙.
The RP–TP combination of the oscillatory modes in the RS model implies parameters of the neutron star that are quite acceptable at the lower end of the allowed ranges of spin and mass. Owing to the rotational frequency of the central neutron star in the atoll source 4U 1636−53, observed to be fNS = 580 Hz (or fNS = 290 Hz), the spin estimated by the Hartle–Thorne models of rotating neutron stars puts limits in the range 0.2 < a < 0.4 on near-extreme masses predicted by models with realistic equations of state (Urbanec et al., in prep.). The related restriction on the neutron star mass reads as M < 2.4 M⊙. The physical explanation of the RP–TP special model could be very simple. A hot spot is oscillating in both vertical and radial directions, and its radiation is modified by the frequencies νθ and νθ − νr; approaching the 3:2 resonant point, oscillations in the vertical direction are successively damped by non-linear (e.g., tidal) effects and the radial oscillations are enforced. Then the Keplerian and the radial epicyclic frequencies become important. This model requires a detailed description that is planned in future.
The RP–TP combination of the RS model should be explicitly tested by a fitting procedure realized for the observed twin HF QPO sequences related to the resonant points. We plan to make such a test in a future work. Of course, we shall also test all the possible combinations of the RS model and estimate allowed values of the spin and mass of the neutron stars for these combinations.
8. Conclusions
The multi-resonance model of HF QPOs assumes that both internal parametric resonance and/or forced resonance can occur in accretion discs rotating around black holes or neutron stars and that the resonant non-linear phenomena can influence oscillations with the vertical and radial epicyclic frequency and/or with the orbital (Keplerian) frequency and their simple combinations. It is possible that the resonances occur for different internal reasons, at different radii within the accretion discs, and two pairs (or more complex combinations) of the resonant frequencies could be exhibited in general situations. For simplicity, we considered two pairs of the resonant frequencies, or their special reductions, but more complex situations can be treated in an analogous way. The spin and mass of the black hole can then be found with higher precision than for individual twin peaks, but it could be rather difficult to identify any relevant combination of the resonances.
For special values of the black hole spin, the bottom (top) epicyclic frequencies could be equal at different radii, since there are local extrema of the radial profiles for both the epicyclic frequencies in the Kerr black hole spacetimes. If Keplerian frequency or beat frequencies can also enter the resonance phenomena, top, bottom, or mixed coinciding frequencies in various versions of resonance are possible. In such situations, the ratio of the triples of the resonant frequencies is directly related to the black hole spin, independently of the black hole mass. The related possibility of directly measuring the black hole spin is very important because of relatively high uncertainties in observational estimates of the black hole mass that are necessary for determining the black hole spin in general resonant phenomena (Török et al. 2005, 2011), or in black hole spin determinations based on the measurements of profiled spectral lines (Laor 1991; Karas et al. 1992; Dovčiak et al. 2004; Fabian & Miniutti 2005; Zakharov 2003; Zakharov & Repin 2006; Zakharov et al. 2012; Fanton et al. 1997; Čadež et al. 2003; Čadež & Calvani 2005).
The multi-resonance model of HF QPOs represents a promising approach to understanding the observational data from LMXBs containing both black holes and neutron stars and data from discs orbiting black holes in the ULX sources or in active galactic nuclei. We focussed our attention on the properties of the frequency patterns implied by various versions of the resonance orbital model, but not going into physical details because they are clearly case dependent.
The special triple frequency set method determines the black hole spin with high precision and is quite independent of the measurement of the black hole mass, but it could work only accidentally for special values of the spin. Nevertheless, it is worth making a detailed scan of all the observational data for the LMXB black hole systems or supermassive black holes in active galactic nuclei in order to look for some candidate systems, since any successful determination of the spin could help very much in determining other physical parameters of the system and in understanding a wide scale of astrophysical phenomena. The prepared new space X-ray mission LOFT (Feroci et al. 2012) proposes a sensitivity of the observational instruments that is high enough to obtain data that could be both extended and precise enough to apply the triple frequency set method in a realistic way.
In Appendix D we present a detailed guide to all the possible triple frequency sets and related values of the black hole spin a, shown for all possible double combinations of both the direct and simple combinational resonances with the order of individual resonances limited by n ≤ 49. It is clear that comparison of observational data with the guide tables must be done extremely carefully, since different resonances can give the same triple frequency ratio set and black hole spin. It is worth noting that the triple frequency set resonant model can be approximately used also in situations where two resonant points are detected with two of the four frequencies involved in the resonances close to each other, and the black hole spin then can be estimated independently of the black hole mass.
The efficiency of the black hole spin determination by using the triple frequency set ratios grows strongly with the growing precision of the frequency measurements. We believe that the precision of the planned LOFT mission will be high enough to enable application of the multi-resonance methods for an order of resonance up to n = 5.
In the LMXB neutron star sources exhibiting a possible two resonant points in the data of twin-peak HF QPOs, the RS model can be relevant, since based on the switching of the twin oscillatory modes at the outer resonant point. Of course, the neutron star parameters given by the RS model have to accord with those determined by fitting all the observed data by the frequency relations corresponding to the oscillatory modes in action.
We expect differences between the black hole and neutron star resonant phenomena to be attributed to the presence of the neutron star surface and related inhomogeneities influencing the HF QPOs in the vicinity of the star surface. A switch of the frequency relations reflecting twin-peak HF QPOs in neutron star systems from one pair to some other pair is not necessarily caused by the resonant phenomena, but could be excited, e.g., by the influence of the neutron star magnetic field or by something else.
We can conclude that the multi-resonant model of HF QPOs based on the orbital motion is able to explain a wide range of HF QPO phenomena observed in both black hole and neutron star X-ray binary systems, around the supermassive galactic centre (Sgr A∗) black hole or in some other black hole systems in the centre of active galactic nuclei, and in the intermediate (NGC 5408 X-1) black hole systems.
A lot of observational and theoretical research is necessary for deeper understanding of the resonant phenomena indicated in the black hole and neutron (quark) star systems, and we hope that the multi-resonant model will turn out to be very useful in future research in connection with the observational data provided by the LOFT X-ray satellite or some similar X-ray observatory.
Online material
Appendix A: Simple combinational resonances of frequency pairs
The simple combinational resonances correspond to frequency relations of a single orbital (epicyclic) frequency να and a simple combinational (beat) frequency of another frequency νβ with the frequency να, assuming να > νβ. Considering the pair (α,β) in the combinations of (θ,r), (K,r), (K,θ) and introducing the new frequency ratio parameters 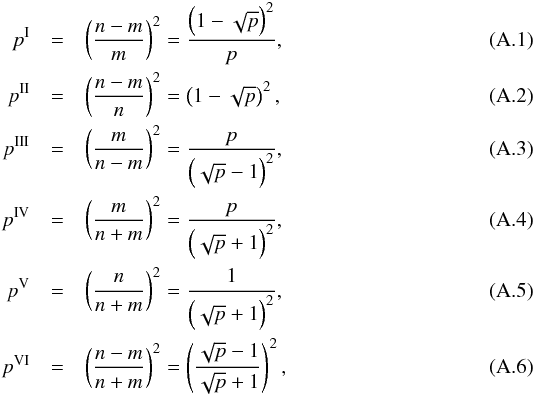 we arrive at the following resonance conditions expressed in the general form:
we arrive at the following resonance conditions expressed in the general form:
- CS.1.
- CS.2.
- CS.3.
- CS.4.
- CS.5.
- CS.6.
Simple combinational resonances of the type CS occur at the same radii as the direct resonances D1, D2, D3. Therefore, it is enough to relate the ratios of the simple combinational and direct resonances. For example, the frequency ratio να:νβ = 5:4 implies (να + νβ):να = 9:5, να:(να − νβ) = 5:1, etc.
Appendix B: Simple combinational resonances of three frequencies νK, νθ, νr
We consider resonances of oscillations with one simple frequency of the orbital frequencies and a simple combination (beat) of the other two frequencies:
We consider resonances of oscillations with one simple frequency of the orbital frequencies and a simple combination (beat) of the other two frequencies:
-
CT1.
νU = νK, νL = νθ − νr. The resonance function aK/(θ − r)(x,p) is given by
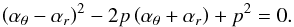 (B.1)In the explicit form the solution reads as
(B.1)In the explicit form the solution reads as ![\appendix \setcounter{section}{2} \begin{eqnarray} \label{aCT1} && \lefteqn{a=a^{\mathrm{K}/(\theta-{r})}(x,p) \equiv \sqrt{x}+\frac{1}{2\cdot 3^{5/6}}}\\ && \times\left[\sqrt{\frac{A^{2/3}+B}{A^{1/3}}}-\sqrt{A^{1/3} \left(\frac{4 \sqrt{3} p x^{5/2}}{\sqrt{A+A^{1/3} B}}-1\right)-\frac{B}{A^{1/3}}}\,\right], \nonumber \end{eqnarray}](/articles/aa/full_html/2013/04/aa19724-12/aa19724-12-eq321.png) (B.2)where
(B.2)where ![\appendix \setcounter{section}{2} \begin{eqnarray} \lefteqn{A=6 p^2 x^5+\sqrt{36 p^4 x^{10}-B^3},}\\ \lefteqn{B=3^{1/3} p x^3 \left[4+(p-4) x\right].} \end{eqnarray}](/articles/aa/full_html/2013/04/aa19724-12/aa19724-12-eq322.png)
-
CT2.
νU = νθ, νL = νK − νr. The resonance function aθ/(K − r)(x,p) is given by
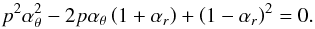 (B.5)
(B.5) -
CT3.
νU = νr, νL = νK − νθ. The resonance function ar/(K − θ)(x,p) is given by
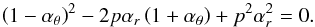 (B.6)
(B.6) -
CT4.
νU = νθ + νr, νL = νK. The resonance function a(θ + r)/K(x,p) is given by
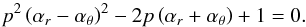 (B.7)The condition m < n < 2m has to be satisfied.
(B.7)The condition m < n < 2m has to be satisfied. -
CT5.
νU = νK + νr, νL = νθ. The resonance function a(K + r)/θ(x,p) is given by
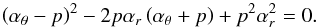 (B.8)
(B.8) -
CT6.
νU = νK + νθ, νL = νr. The resonance function a(K + θ)/r(x,p) is given by
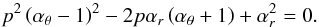 (B.9)The condition n > 2m has to be satisfied.
(B.9)The condition n > 2m has to be satisfied.
Except for the case CT1, we give the resonance functions in an implicit graphical form, because the functions are too complex and too long to be written explicitly. The implicit resonance functions are given in Fig. B.1.
The implicit resonance conditions are polynomials of the fourth order in the spin a in all six cases. Only one of the possible solutions of the resonance condition is physically relevant. Now the resonance functions exhibit more complex behaviour in comparison with the direct resonance functions. Along with those that are monotonous and do not cross the stability line, we have found monotonous functions crossing the stability line at the stability points 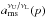 and non-monotonous functions crossing the stability line. In some cases the non-monotonous resonance lines appear to be (seemingly) discontinuous because of entering the region with spin a > 1, corresponding to naked-singularity spacetimes.
and non-monotonous functions crossing the stability line. In some cases the non-monotonous resonance lines appear to be (seemingly) discontinuous because of entering the region with spin a > 1, corresponding to naked-singularity spacetimes.
 |
Fig. B.1 Spin resonance functions aνU/νL(x,p) for the simple combinational resonances CT1 – CT6 and the frequency ratios n:m = 5:4 (black solid line), 4:3 (black dashed line), 3:2 (black dotted line), 5:3 (red solid line), 2:1 (red dashed line), 5:2 (red dotted line), 3:1 (blue solid line), 4:1 (blue dashed line), 5:1 (blue dotted line). Black thick line represents ams(x), which implicitly determines the radius of the marginally stable orbit xms. |
Appendix C: Double-beat combinational resonances
We introduce 13 types of the double-beat combinational resonances: 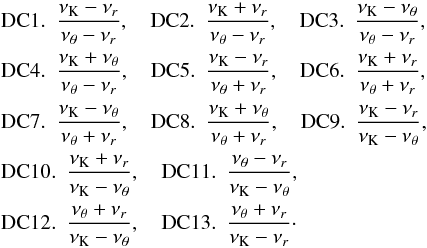 We present the implicit graphical form of the solution of the resonance conditions related to the double-beat combinational resonances DC1−DC13. We also give the overview of the allowed ranges of the direct and combinational resonances limited by the stability points that are explicitly given and by the local extrema of the resonance functions in Table C.1.
We present the implicit graphical form of the solution of the resonance conditions related to the double-beat combinational resonances DC1−DC13. We also give the overview of the allowed ranges of the direct and combinational resonances limited by the stability points that are explicitly given and by the local extrema of the resonance functions in Table C.1.
The results obtained for the relevant resonance functions are given in Figs. C.1 and C.2. In order to keep the discussion straightforward, we assume the frequency ratio n/m > 1 in all 13 cases. Therefore, we treat the frequency relations allowing for ratios higher and lower than 1 as separate (inverse) cases. For each relation of the beat frequencies, we give the relation between νθ/νr and νK/νr in terms of the ratio n/m that uniquely determines the spin “resonance” function aνU/νL(x,p). Then we determine “resonance equations” relating the functions αθ(x,a), αr(x,a) to the frequency ratio p that are used for numerical determination of the spin “resonance” functions; however, the “resonance equations” do not give unique results and usually determine two spin “resonance” functions that must be separated during the numerical procedure. The separation is given by the stability line, i.e., the function ams(x) giving the marginally stable orbits. The resonance conditions are given in the following form.
 |
Fig. C.1 Spin resonance functions aνU/νL(x,p) for the double combinational resonances of the types DC1 – DC4, DC11 and the frequency ratios n:m = 5:4 (black solid line), 4:3 (black dashed line), 3:2 (black dotted line), 5:3 (red solid line), 2:1 (red dashed line), 5:2 (red dotted line), 3:1 (blue solid line), 4:1 (blue dashed line), 5:1 (blue dotted line). The grey lines represent the solutions of the same resonance equations that are relevant for the corresponding types of resonances (DC5−DC8, DC12). The related solutions are separated by the line of marginally stable orbits ams(x) (black thick line), they have a common stability point |
 |
Fig. C.2 Spin resonance functions aνU/νL(x,p) for the double combinational resonances of the types DC9, DC10, DC13 and the warped disc oscillation model (WD) for the frequency ratios n:m = 5:4 (black solid line), 4:3 (black dashed line), 3:2 (black dotted line), 5:3 (red solid line), 2:1 (red dashed line), 5:2 (red dotted line), 3:1 (blue solid line), 4:1 (blue dashed line), 5:1 (blue dotted line). Black thick line represents ams(x), which implicitly determines the radius of the marginally stable orbit xms. The grey lines are related to the resonance DC10 – for details see Fig. C.1. |
Allowed ranges of the Kerr geometry spin for the direct orbital resonance model D3 and the combinational resonances of the types CT1, CT5, DC1, DC2, DC5, DC6 for given frequency ratio n:m.
Generally, the resonant radii corresponding to specific spin “resonance” functions are determined by the related “resonance equations” representing fourth-order polynomials in terms of the black hole spin. The “resonance equations” are identical in the following twin cases: DC1 ≡ DC6, DC2 ≡ DC5, DC3 ≡ DC7, DC4 ≡ DC8, DC9 ≡ DC10, DC11 ≡ DC12. The resonant radii are then determined by different branches of the “resonance equations” solutions, separated by the line of the marginally stable orbits ams(x). Only the case of DC13 is an exception, where the resonant lines do not touch the marginally stable line. Some of the “resonance equations” are related because of the definition of the frequency ratio (p → 1/p), namely DC3 ↔ DC11, DC5 ↔ DC13, DC7 ↔ DC12. Furthermore, there are additional interesting connections between the resonance lines of the classes DC1 (DC6) and DC9 (DC10) (see Figs. C.1 and C.2) expressed by the relations  The corresponding frequency ratios n:m and k:l are given in Table C.2.
The corresponding frequency ratios n:m and k:l are given in Table C.2.
We can see from Figs. 1, B.1−C.2 that some of the considered orbital model versions do not work for the whole range of the Kerr black hole (neutron star) spin a. For example, for the direct orbital resonance model D3 (νK:νθ) there are minimal values of spin 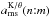 for the given frequency ratio n:m that determines the stability point for considered resonance functions (see Fig. 1). Such stability points
for the given frequency ratio n:m that determines the stability point for considered resonance functions (see Fig. 1). Such stability points 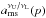 also represent limiting (minimum or maximum) values of spin for related combinational resonances of the types CT1, CT5, DC1, DC2, DC5, and DC6. Another limit on spin allowed for resonance of a given type and frequency ratio occurs in the case of non-monotonic resonance functions aνU/νL(x,p) by their local minimum
also represent limiting (minimum or maximum) values of spin for related combinational resonances of the types CT1, CT5, DC1, DC2, DC5, and DC6. Another limit on spin allowed for resonance of a given type and frequency ratio occurs in the case of non-monotonic resonance functions aνU/νL(x,p) by their local minimum 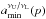 (see, e.g., Fig. C.1). The limiting values of
(see, e.g., Fig. C.1). The limiting values of
the spin, and related allowed spin ranges for given frequency ratio n:m, are presented for given types of resonance in Table C.1.
When two twin-peak QPOs are observed with frequency ratios n:m and n′:m′, respectively, we have to find two versions of resonance that could explain both the ratios and magnitudes of the observed frequencies and, for a given range of allowed mass in the source, they must predict the same black hole spin a, or more precisely, overlapping intervals of the spin. Therefore, it is clear that, generally, two observed twin-peak QPOs could make the spin estimates more precise. Two different resonances are necessary when two twin peaks are observed with the same ratios but different magnitudes.
Appendix D: Detailed table guide across all the possible triple frequency ratio sets and related values of the black hole spin a
In Tables D.2−D.4 and D.6−D.8 we present the cases with no solution as empty. An asterisk denotes the special values of the black hole spin when the triple frequencies occur at the same (shared) radius.
Notation system of double combinations of both the direct (D1−D3) and some of the simple triple combinational resonances (CT1 and CT2) with identical top (T), bottom (B), and both types of mixed (M) frequencies.
Top identity – characteristic triple frequency ratio sets and related values of the black hole spin.
Bottom identity – characteristic triple frequency ratio sets and related values of the black hole spin.
Mixed identity – characteristic triple frequency ratio sets and related values of the black hole spin.
Notation system of double combinations of the direct resonance D1 and all double combinational resonances (DC1 – DC13) with identical top (T), bottom (B), and both types of mixed (M) frequencies.
Top identity – characteristic triple frequency ratio sets and related values of the black hole spin.
Bottom identity – characteristic triple frequency ratio sets and related values of the black hole spin.
Mixed identity – characteristic triple frequency ratio sets and related values of the black hole spin.
Appendix E: Detailed table guide for the triple frequency 3:2:1
Relevant versions of the multi-resonant model with assumed observed characteristic frequency ratio set νU:νM:νL = 3:2:1. The radius of marginally stable orbit xms and corresponding resonant radii x1 and x2 are given.
For toroidal discs (Rezzolla et al. 2001, 2003b; Blaes et al. 2007; Straub & Šrámková 2009; Montero & Zanotti 2012) or slightly charged discs around magnetic neutron stars (Bakala et al. 2010, 2012; Pachon et al. 2012; Kovář et al. 2008), additional parameters must enter the resonance conditions.
Very promising seems to be modelling of the energy dependencies of high-frequency QPO, i.e., the QPO spectra generated at the QPO radius (Życki et al. 2007), as they could be credited by the multi-resonant models giving exact values of the black hole spin and the QPO radii.
We consider here only the Kerr spacetime as the standard description for rotating black holes, although alternatives have been discussed in the same context (see Kotrlová et al. 2008; Stuchlík & Kotrlová 2009; Aliev & Talazan 2009; Rahimov et al. 2011; Aliev et al. 2013; Horváth & Gergely 2012).
For example, the gravitational perturbation forces are discussed in Stuchlík & Hledík (2005) and Stuchlík et al. (2008a) for the case of a neutron star with “mountains” and of a binary partner of the neutron star or a black hole.
In the model of p-mode (axisymmetric) oscillations of thick tori with the fundamental frequency and its first overtone, both the frequencies decrease monotonically with increasing dimension of the oscillating torus (Rezzolla et al. 2003b,a). In the model of oscillating string loops, the radial profiles of the radial and vertical frequencies cross each other near the black hole horizon (Stuchlík & Kološ 2012b). In both these models the resonant phenomena could be irrelevant, as for the model of shock waves (Mondal & Chakrabarti 2006; Mondal et al. 2009; Mondal & Choi 2013).
In the realistic models of warped disc oscillations that could be used to explain QPOs observed in the black hole systems, and due to precession of the disc also in the neutron star systems (Kato 2007), the higher-harmonic oscillations are usually considered up to the third order being thus allowed up to the frequencies 3νK − νr, etc.
Tables limited by n ≤ 5 are much too extended to be published here; however, in relevant cases they can be found in Stuchlík et al. (2007a).
Acknowledgments
We would like to express our gratitude to the Czech grants MSM 4781305903, GAČR 202/09/0772, GAČR 205/09/H033 and the internal grants of the Silesian University Opava FPF SGS/1,2/2010. The authors further acknowledge the project Supporting Integration with the International Theoretical and Observational Research Network in Relativistic Astrophysics of Compact Objects, reg. no. CZ.1.07/2.3.00/20.0071, supported by Operational Programme Education for Competitiveness funded by Structural Funds of the European Union and the state budget of the Czech Republic.
References
- Abramowicz, M. A., & Kluźniak, W. 2001, A&A, 374, L19 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Abramowicz, M. A., Jaroszyński, M., & Sikora, M. 1978, A&A, 63, 221 [NASA ADS] [Google Scholar]
- Abramowicz, M. A., Bulik, T., Bursa, M., & Kluźniak, W. 2003a, A&A, 404, L21 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Abramowicz, M. A., Karas, V., Kluźniak, W., Lee, W., & Rebusco, P. 2003b, PASJ, 55, 467 [NASA ADS] [CrossRef] [Google Scholar]
- Abramowicz, M. A., Kluźniak, W., McClintock, J. E., & Remillard, R. A. 2004, ApJ, 609, L63 [NASA ADS] [CrossRef] [Google Scholar]
- Abramowicz, M. A., Barret, D., Bursa, M., et al. 2005a, in Proc. of RAGtime 6/7: Workshops on black holes and neutron stars, Opava, 16−18/18−20 September 2004/2005, eds. S. Hledík, & Z. Stuchlík (Opava: Silesian University in Opava), 1 [Google Scholar]
- Abramowicz, M. A., Barret, D., Bursa, M., et al. 2005b, Astron. Nachr., 326, 864 [Google Scholar]
- Abramowicz, M. A., Kluźniak, W., & Yu, W. 2011, Acta Astron., 61, 319 [NASA ADS] [Google Scholar]
- Akmal, A., & Pandharipande, V. R. 1997, Phys. Rev. C, 56, 2261 [NASA ADS] [CrossRef] [Google Scholar]
- Akmal, A., Pandharipande, V. R., & Ravenhall, D. G. 1998, Phys. Rev. C, 58, 1804 [NASA ADS] [CrossRef] [Google Scholar]
- Aliev, A. N., & Galtsov, D. V. 1981, Gen. Relativity Gravitation, 13, 899 [Google Scholar]
- Aliev, A. N., & Talazan, P. 2009, Phys. Rev. D, 80, 044023 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- Aliev, A. N., Esmer, G. D., & Talazan, P. 2013, Class. Quant. Grav., 30, 045010 [Google Scholar]
- Aschenbach, B. 2004, A&A, 425, 1075 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Aschenbach, B. 2006, Chinese J. Astron. Astrophys., 6, 221 [Google Scholar]
- Aschenbach, B., Grosso, N., Porquet, D., & Predehl, P. 2004, A&A, 417, 71 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bakala, P., Šrámková, E., Stuchlík, Z., & Török, G. 2010, Class. Quant. Grav., 27, 045001 [Google Scholar]
- Bakala, P., Urbanec, M., Šrámková, E., Stuchlík, Z., & Török, G. 2012, Class. Quant. Grav., 29, 065012 [Google Scholar]
- Bao, G., & Stuchlík, Z. 1992, ApJ, 400, 163 [Google Scholar]
- Bardeen, J. M., Press, W. H., & Teukolsky, S. A. 1972, ApJ, 178, 347 [NASA ADS] [CrossRef] [Google Scholar]
- Barret, D., Kluźniak, W., Olive, J., Paltani, S., & Skinner, G. K. 2005a, MNRAS, 357, 1288 [NASA ADS] [CrossRef] [Google Scholar]
- Barret, D., Olive, J.-F., & Miller, M. C. 2005b, MNRAS, 361, 855 [NASA ADS] [CrossRef] [Google Scholar]
- Barret, D., Olive, J.-F., & Miller, M. C. 2005c, Astron. Nachr., 326, 808 [NASA ADS] [CrossRef] [Google Scholar]
- Barret, D., Olive, J., & Miller, M. C. 2006, MNRAS, 370, 1140 [NASA ADS] [CrossRef] [Google Scholar]
- Belloni, T., Méndez, M., & Sánchez-Fernández, C. 2001, A&A, 372, 551 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Belloni, T., Méndez, M., & Homan, J. 2005, A&A, 437, 209 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Belloni, T., Homan, J., Motta, S., Ratti, E., & Méndez, M. 2007a, MNRAS, 379, 247 [NASA ADS] [CrossRef] [Google Scholar]
- Belloni, T., Méndez, M., & Homan, J. 2007b, MNRAS, 376, 1133 [NASA ADS] [CrossRef] [Google Scholar]
- Bin-Nun, A. Y. 2010a, Phys. Rev. D, 82, 064009 [NASA ADS] [CrossRef] [Google Scholar]
- Bin-Nun, A. Y. 2010b, Phys. Rev. D, 81, 123011 [NASA ADS] [CrossRef] [Google Scholar]
- Blaes, O. M., Šrámková, E., Abramowicz, M. A., Kluźniak, W., & Torkelsson, U. 2007, ApJ, 665, 642 [NASA ADS] [CrossRef] [Google Scholar]
- Boutelier, M., Barret, D., Lin, Y., & Török, G. 2010, MNRAS, 401, 1290 [NASA ADS] [CrossRef] [Google Scholar]
- Boutloukos, S., van der Klis, M., Altamirano, D., et al. 2006, ApJ, 653, 1435 [NASA ADS] [CrossRef] [Google Scholar]
- Čadež, A., & Calvani, M. 2005, MNRAS, 363, 177 [NASA ADS] [CrossRef] [Google Scholar]
- Čadež, A., Calvani, M., & Fanton, C. 2003, Mem. Soc. Astron. It., 74, 446 [NASA ADS] [Google Scholar]
- Čadež, A., Calvani, M., & Kostić, U. 2008, A&A, 487, 527 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Chakrabarti, S. K., Debnath, D., Pal, P. S., et al. 2009, submitted [arXiv:0903.1482] [Google Scholar]
- Debnath, D., Chakrabarti, S. K., & Nandi, A. 2010, A&A, 520, A98 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Done, C., & Davis, S. W. 2008, ApJ, 683, 89 [NASA ADS] [Google Scholar]
- Done, C., Gierliński, M., & Kubota, A. 2007, A&ARv, 15, 1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Dovčiak, M., Karas, V., Martocchia, A., Matt, G., & Yaqoob, T. 2004, in Proc. of RAGtime 4/5: Workshops on black holes and neutron stars, Opava, 14–16/13–15 October 2002/2003, eds. S. Hledík, & Z. Stuchlík (Opava: Silesian University in Opava), 33 [Google Scholar]
- Fabian, A. C., & Miniutti, G. 2005, Kerr Spacetime: Rotating Black Holes in General Relativity (Cambridge: Cambridge University Press), eprint [arXiv:astro-ph/0507409] is a part of this book [Google Scholar]
- Fanton, C., Calvani, M., de Felice, F., & Čadež, A. 1997, PASJ, 49, 159 [NASA ADS] [CrossRef] [Google Scholar]
- Feroci, M., Stella, L., van der Klis, M., et al. 2012, EXA, 34, 415 [Google Scholar]
- Ford, E. C., van der Klis, M., Méndez, M., et al. 2000, ApJ, 537, 368 [NASA ADS] [CrossRef] [Google Scholar]
- Germanà, C., Kostić, U., Čadež, A., & Calvani, M. 2009, in AIP Conf. Ser. 1126 SIMBOL-X: Focusing on the Hard X-Ray Universe: Proc. of the 2nd International Simbol-X Symposium, eds. J. Rodriguez, & P. Ferrando, 367 [Google Scholar]
- Hartle, J. B., & Thorne, K. 1968, ApJ, 153, 807 [NASA ADS] [CrossRef] [Google Scholar]
- Horák, J., Abramowicz, M. A., Kluźniak, W., Rebusco, P., & Török, G. 2009, A&A, 499, 535 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Horváth, Z., & Gergely, L. Á. 2012, submitted [arXiv:1203.6576] [Google Scholar]
- Jacobson, T., & Sotiriou, T. P. 2009, Phys. Rev. D, 79, 065029 [NASA ADS] [CrossRef] [Google Scholar]
- Karas, V., Vokrouhlický, D., & Polnarev, A. G. 1992, MNRAS, 259, 569 [NASA ADS] [CrossRef] [Google Scholar]
- Kato, S. 2001a, PASJ, 53, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Kato, S. 2001b, PASJ, 53, L37 [Google Scholar]
- Kato, S. 2004a, PASJ, 56, L25 [NASA ADS] [CrossRef] [Google Scholar]
- Kato, S. 2004b, PASJ, 56, 905 [NASA ADS] [Google Scholar]
- Kato, S. 2007, PASJ, 59, 451 [NASA ADS] [Google Scholar]
- Kato, S. 2008, PASJ, 60, 111 [NASA ADS] [Google Scholar]
- Kato, S. 2009, PASJ, 61, 1237 [NASA ADS] [Google Scholar]
- Kato, S., Fukue, J., & Mineshige, S. 1998, in Black-hole accretion disks, eds. S. Kato, J. Fukue, & S. Mineshige (Kyoto, Japan: Kyoto University Press) [Google Scholar]
- Kluźniak, W., & Abramowicz, M. A. 2001, unpublished [arXiv:astro-ph/0105057] [Google Scholar]
- Kluźniak, W., Abramowicz, M. A., Bursa, M., & Török, G. 2007, in Rev. Mex. Astron. Astrofis. (Serie de Conferencias), 27, 18 [Google Scholar]
- Kopáček, O., Karas, V., Kovář, J., & Stuchlík, Z. 2010, ApJ, 722, 1240 [NASA ADS] [CrossRef] [Google Scholar]
- Kostić, U., Čadež, A., Calvani, M., & Gomboc, A. 2009, A&A, 496, 307 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kotrlová, A., Stuchlík, Z., & Török, G. 2008, Class. Quant. Grav., 25, 225016 [Google Scholar]
- Kovář, J., Stuchlík, Z., & Karas, V. 2008, Class. Quant. Grav., 25, 095011 [NASA ADS] [CrossRef] [Google Scholar]
- Kovář, J., Kopáček, O., Karas, V., & Stuchlík, Z. 2010, Class. Quant. Grav., 27, 135006 [Google Scholar]
- Kovář, J., Slaný, P., Stuchlík, Z., et al. 2011, Phys. Rev. D, 84, 084002 [NASA ADS] [CrossRef] [Google Scholar]
- Kozłowski, M., Jaroszyński, M., & Abramowicz, M. A. 1978, A&A, 63, 209 [NASA ADS] [Google Scholar]
- Kraniotis, G. V. 2005, Class. Quant. Grav., 22, 4391 [NASA ADS] [CrossRef] [Google Scholar]
- Kraniotis, G. V. 2007, Class. Quant. Grav., 24, 1775 [NASA ADS] [CrossRef] [Google Scholar]
- Lachowicz, P., Czerny, B., & Abramowicz, M. A. 2006, MNRAS, submitted [arXiv:astro-ph/0607594] [Google Scholar]
- Lamb, F. K., & Miller, M. C. 2001, ApJ, 554, 1210 [NASA ADS] [CrossRef] [Google Scholar]
- Lamb, F. K., & Miller, M. C. 2003, submitted [arXiv:astro-ph/0308179] [Google Scholar]
- Landau, L. D., & Lifshitz, E. M. 1976, Course of Theoretical Physics, I, Mechanics, 3rd edn. (Oxford: Elsevier Butterworth-Heinemann) [Google Scholar]
- Laor, A. 1991, ApJ, 376, 90 [NASA ADS] [CrossRef] [Google Scholar]
- Lin, Y.-F., Boutelier, M., Barret, D., & Zhang, S.-N. 2011, ApJ, 726, 74 [NASA ADS] [CrossRef] [Google Scholar]
- Lo, K.-W., & Lin, L.-M. 2011, ApJ, 728, 12 [NASA ADS] [CrossRef] [Google Scholar]
- McClintock, J. E., & Remillard, R. A. 2004, in Compact Stellar X-Ray Sources, eds. W. H. G. Lewin, & M. van der Klis (Cambridge: Cambridge University Press) [Google Scholar]
- McClintock, J. E., Shafee, R., Narayan, R., et al. 2006, ApJ, 652, 518 [NASA ADS] [CrossRef] [Google Scholar]
- McClintock, J. E., Narayan, R., Davis, S. W., et al. 2011, Class. Quant. Grav., 28, 114009 [NASA ADS] [CrossRef] [Google Scholar]
- Middleton, M., Done, C., Gierliński, M., & Davis, S. W. 2006, MNRAS, 373, 1004 [NASA ADS] [CrossRef] [Google Scholar]
- Middleton, M., Done, C., Ward, M., Gierliński, M., & Schurch, N. 2009, MNRAS, 394, 250 [NASA ADS] [CrossRef] [Google Scholar]
- Middleton, M., Uttley, P., & Done, C. 2011, MNRAS, 417, 250 [NASA ADS] [CrossRef] [Google Scholar]
- Miller, J. M., Reynolds, C. S., Fabian, A. C., Miniutti, G., & Gallo, L. C. 2009, ApJ, 697, 900 [NASA ADS] [CrossRef] [Google Scholar]
- Mondal, S., & Chakrabarti, S. K. 2006, MNRAS, 371, 1418 [NASA ADS] [CrossRef] [Google Scholar]
- Mondal, S., & Choi, C. S. 2013, New A, 19, 109 [NASA ADS] [CrossRef] [Google Scholar]
- Mondal, S., Basu, P., & Chakrabarti, S. K. 2009, MNRAS, 396, 1038 [NASA ADS] [CrossRef] [Google Scholar]
- Montero, P. J., & Zanotti, O. 2012, MNRAS, 419, 1507 [NASA ADS] [CrossRef] [Google Scholar]
- Montero, P. J., Rezzolla, L., & Yoshida, S. 2004, MNRAS, 354, 1040 [NASA ADS] [CrossRef] [Google Scholar]
- Mukhopadhyay, B. 2009, ApJ, 694, 387 [NASA ADS] [CrossRef] [Google Scholar]
- Müller, H., & Serot, B. D. 1996, Nucl. Phys. A, 606, 508 [NASA ADS] [CrossRef] [Google Scholar]
- Murphy, K. D., Yaqoob, T., Karas, V., & Dovčiak, M. 2009, ApJ, 701, 635 [NASA ADS] [CrossRef] [Google Scholar]
- Müther, H., Prakash, M., & Ainsworth, T. L. 1987, Phys. Lett. B, 199, 469 [NASA ADS] [CrossRef] [Google Scholar]
- Nayfeh, A. H., & Mook, D. T. 1979, Nonlinear Oscillations (New York: Wiley-interscience) [Google Scholar]
- Novikov, I. D., & Thorne, K. S. 1973, in Black Holes, eds. C. D. Witt, & B. S. D. Witt (New York–London–Paris: Gordon and Breach), 343 [Google Scholar]
- Nowak, M. A., & Lehr, D. E. 1998, in Theory of Black Hole Accretion Disks, eds. M. A. Abramowicz, G. Björnsson, & J. E. Pringle (Cambridge: Cambridge University Press), 233 [Google Scholar]
- Osherovich, V., & Titarchuk, L. 1999, ApJ, 522, L113 [NASA ADS] [CrossRef] [Google Scholar]
- Pachon, L. A., Rueda, J. A., & Valenzuela-Toledo, C. A. 2012, ApJ, 756, 82 [NASA ADS] [CrossRef] [Google Scholar]
- Perez, C. A., Silbertgleit, A. S., Wagoner, R. V., & Lehr, D. E. 1997, ApJ, 476, 589 [NASA ADS] [CrossRef] [Google Scholar]
- Postnikov, S., Prakash, M., & Lattimer, J. M. 2010, Phys. Rev. D, 82, 024016 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- Rahimov, O. G., Abdujabbarov, A. A., & Ahmedov, B. J. 2011, Ap&SS, 335, 499 [NASA ADS] [CrossRef] [Google Scholar]
- Remillard, R. A. 2005, Astron. Nachr., 326, 804 [NASA ADS] [CrossRef] [Google Scholar]
- Remillard, R. A., & McClintock, J. E. 2006, ARA&A, 44, 49 [NASA ADS] [CrossRef] [Google Scholar]
- Rezzolla, L. 2004a, in X-ray Timing 2003: Rossi and Beyond, eds. P. Karet, F. K. Lamb, & J. H. Swank (Melville: NY: American Institute of Physics), 714, 36 [Google Scholar]
- Rezzolla, L. 2004b, in Proc. of RAGtime 4/5: Workshops on black holes and neutron stars, Opava, 14–16/13–15 October 2002/03, eds. S. Hledík, & Z. Stuchlík (Opava: Silesian University in Opava), 151 [Google Scholar]
- Rezzolla, L., Ahmedov, B. J., & Miller, J. C. 2001, MNRAS, 322, 723, ibid. (2003), 338, 816 [NASA ADS] [CrossRef] [Google Scholar]
- Rezzolla, L., Yoshida, S., Maccarone, T. J., & Zanotti, O. 2003a, MNRAS, 344, L37 [NASA ADS] [CrossRef] [Google Scholar]
- Rezzolla, L., Yoshida, S., & Zanotti, O. 2003b, MNRAS, 344, 978 [NASA ADS] [CrossRef] [Google Scholar]
- Rhoades, C. E., & Ruffini, R. 1974, Phys. Rev. Lett., 32, 324 [Google Scholar]
- Schee, J., & Stuchlík, Z. 2009a, Internat. J. Modern Phys. D, 18, 983 [Google Scholar]
- Schee, J., & Stuchlík, Z. 2009b, Gen. Relativity Gravitation, 41, 1795 [NASA ADS] [CrossRef] [Google Scholar]
- Schnittman, J. D., & Rezzolla, L. 2006, ApJ, 637, L113 [NASA ADS] [CrossRef] [Google Scholar]
- Semenov, V., Dyadechkin, S., & Punsly, B. 2004, Science, 305, 978 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Shafee, R., McClintock, J. E., Narayan, R., et al. 2006, ApJ, 636, L113 [NASA ADS] [CrossRef] [Google Scholar]
- Shi, C. 2011, RAA, 11, 1327 [NASA ADS] [Google Scholar]
- Shi, C., & Li, X.-D. 2009, MNRAS, 392, 264 [NASA ADS] [CrossRef] [Google Scholar]
- Spruit, H. C. 1981, A&A, 102, 129 [NASA ADS] [Google Scholar]
- Šrámková, E. 2005, Astron. Nachr., 326, 835 [NASA ADS] [CrossRef] [Google Scholar]
- Šrámková, E., Torkelsson, U., & Abramowicz, M. A. 2007, A&A, 467, 641 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Stella, L., & Vietri, M. 1998, ApJ, 492, L59 [NASA ADS] [CrossRef] [Google Scholar]
- Stella, L., & Vietri, M. 1999, Phys. Rev. Lett., 82, 17 [NASA ADS] [CrossRef] [Google Scholar]
- Straub, O., & Šrámková, E. 2009, Class. Quant. Grav., 26, 055011 [Google Scholar]
- Strohmayer, T. E. 2001, ApJ, 552, L49 [NASA ADS] [CrossRef] [Google Scholar]
- Strohmayer, T. E., Mushotzky, R. F., Winter, L., et al. 2007, ApJ, 660, 580 [NASA ADS] [CrossRef] [Google Scholar]
- Stuchlík, Z., & Hledík, S. 2005, in Proc. of RAGtime 6/7: Workshops on black holes and neutron stars, Opava, 16–18/18–20 September 2004/2005, eds. S. Hledík, & Z. Stuchlík (Opava: Silesian University in Opava), 189 [Google Scholar]
- Stuchlík, Z., & Kološ, M. 2012a, Phys. Rev. D, 85, 065022 [NASA ADS] [CrossRef] [Google Scholar]
- Stuchlík, Z., & Kološ, M. 2012b, J. Cosmology Astropart. Phys., 10, 8 [NASA ADS] [CrossRef] [Google Scholar]
- Stuchlík, Z., & Kotrlová, A. 2009, Gen. Relativity Gravitation, 41, 1305 [Google Scholar]
- Stuchlík, Z., & Schee, J. 2010, Class. Quant. Grav., 27, 215017 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- Stuchlík, Z., & Schee, J. 2012a, Class. Quant. Grav., 29, 025008 [NASA ADS] [CrossRef] [Google Scholar]
- Stuchlík, Z., & Schee, J. 2012b, Class. Quant. Grav., 29, 065002 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- Stuchlík, Z., & Török, G. 2005, in Proc. of RAGtime 6/7: Workshops on black holes and neutron stars, Opava, 16–18/18–20 September 2004/2005, eds. S. Hledík, & Z. Stuchlík (Opava: Silesian University in Opava), 253 [Google Scholar]
- Stuchlík, Z., Slaný, P., & Hledík, S. 2000, A&A, 363, 425 [NASA ADS] [Google Scholar]
- Stuchlík, Z., Slaný, P., Török, G., & Abramowicz, M. A. 2005, Phys. Rev. D, 71, 024037 [NASA ADS] [CrossRef] [Google Scholar]
- Stuchlík, Z., Kotrlová, A., & Török, G. 2007a, in Proc. of RAGtime 8/9: Workshops on black holes and neutron stars, Opava, Hradec nad Moravicí, 15–19/19–21 September 2006/2007, eds. S. Hledík, & Z. Stuchlík (Opava: Silesian University in Opava), 363 [Google Scholar]
- Stuchlík, Z., Slaný, P., & Török, G. 2007b, A&A, 463, 807 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Stuchlík, Z., Slaný, P., & Török, G. 2007c, A&A, 470, 401 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Stuchlík, Z., Török, G., & Bakala, P. 2007d, submitted [arXiv:0704.2318] [Google Scholar]
- Stuchlík, Z., Konar, S., Miller, J. C., & Hledík, S. 2008a, A&A, 489, 963 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Stuchlík, Z., Kotrlová, A., & Török, G. 2008b, Acta Astron., 58, 441 [NASA ADS] [Google Scholar]
- Stuchlík, Z., Kovář, J., & Karas, V. 2009, in IAU Symp., 259, 125 [Google Scholar]
- Stuchlík, Z., Blaschke, M., & Slaný, P. 2011a, Class. Quant. Grav., 28, 175002 [NASA ADS] [CrossRef] [Google Scholar]
- Stuchlík, Z., Kotrlová, A., & Török, G. 2011b, A&A, 525, A82 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Takahashi, R., & Harada, T. 2010, Class. Quant. Grav., 27, 075003 [NASA ADS] [CrossRef] [Google Scholar]
- Titarchuk, L. 2003, ApJ, 591, 354 [NASA ADS] [CrossRef] [Google Scholar]
- Titarchuk, L., & Shaposhnikov, N. 2008, ApJ, 678, 1230 [NASA ADS] [CrossRef] [Google Scholar]
- Török, G. 2005, A&A, 440, 1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Török, G. 2009, A&A, 497, 661 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Török, G., & Stuchlík, Z. 2005, A&A, 437, 775 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Török, G., Abramowicz, M. A., Kluźniak, W., & Stuchlík, Z. 2005, A&A, 436, 1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Török, G., Abramowicz, M. A., Bakala, P., et al. 2008a, Acta Astron., 58, 15 [NASA ADS] [Google Scholar]
- Török, G., Bakala, P., Stuchlík, Z., & Čech, P. 2008b, Acta Astron., 58, 1 [NASA ADS] [Google Scholar]
- Török, G., Bursa, M., Horák, J., et al. 2008c, Acta Astron., 58, 113 [NASA ADS] [Google Scholar]
- Török, G., Bakala, P., Šrámková, E., Stuchlík, Z., & Urbanec, M. 2010, ApJ, 714, 748 [NASA ADS] [CrossRef] [Google Scholar]
- Török, G., Kotrlová, A., Šrámková, E., & Stuchlík, Z. 2011, A&A, 531, A59 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Török, G., Bakala, P., Šrámková, E., et al. 2012, ApJ, 760, 138 [NASA ADS] [CrossRef] [Google Scholar]
- Urbanec, M., Běták, E., & Stuchlík, Z. 2010a, Acta Astron., 60, 149 [NASA ADS] [Google Scholar]
- Urbanec, M., Török, G., Šrámková, E., et al. 2010b, A&A, 522, 7 [Google Scholar]
- van der Klis, M. 2000, ARA&A, 38, 717 [NASA ADS] [CrossRef] [Google Scholar]
- van der Klis, M. 2006, in Compact Stellar X-Ray Sources, eds. W. H. G. Lewin, & M. van der Klis (Cambridge: Cambridge University Press), 39 [Google Scholar]
- Virbhadra, K. S., & Ellis, G. F. 2002, Phys. Rev. D, 65, 103004 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- Virbhadra, K. S., & Keeton, C. R. 2008, Phys. Rev. D, 77, 124014 [NASA ADS] [CrossRef] [Google Scholar]
- Wagoner, R. V. 1999, Phys. Rep., 311, 259 [NASA ADS] [CrossRef] [Google Scholar]
- Wang, D. H., Chen, L., Zhang, C. M., Lei, Y. J., & Qu, J. L. 2013, submitted [arXiv:1301.5478] [Google Scholar]
- Zakharov, A. F. 2003, Pub. Astronomical Observatory of Belgrade, 76, 147 [Google Scholar]
- Zakharov, A. F., & Repin, S. V. 2006, New A, 11, 405 [Google Scholar]
- Zakharov, A. F., Paolis, F. D., Ingrosso, G., & Nucita, A. A. 2012, New A Rev., 56, 64 [Google Scholar]
- Zhang, C. 2004, A&A, 423, 401 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Zhang, C. M., Yin, H. X., Zhao, Y. H., Zhang, F., & Song, L. M. 2006, MNRAS, 366, 1373 [NASA ADS] [CrossRef] [Google Scholar]
- Zhang, C., Yin, H. X., Kojima, Y., et al. 2007, MNRAS, 374, 232 [Google Scholar]
- Życki, P. T., Niedźwiecki, A., & Sobolewska, M. A. 2007, MNRAS, 379, 123 [NASA ADS] [CrossRef] [Google Scholar]
All Tables
Allowed ranges of the Kerr geometry spin for the direct orbital resonance model D3 and the combinational resonances of the types CT1, CT5, DC1, DC2, DC5, DC6 for given frequency ratio n:m.
Notation system of double combinations of both the direct (D1−D3) and some of the simple triple combinational resonances (CT1 and CT2) with identical top (T), bottom (B), and both types of mixed (M) frequencies.
Top identity – characteristic triple frequency ratio sets and related values of the black hole spin.
Bottom identity – characteristic triple frequency ratio sets and related values of the black hole spin.
Mixed identity – characteristic triple frequency ratio sets and related values of the black hole spin.
Notation system of double combinations of the direct resonance D1 and all double combinational resonances (DC1 – DC13) with identical top (T), bottom (B), and both types of mixed (M) frequencies.
Top identity – characteristic triple frequency ratio sets and related values of the black hole spin.
Bottom identity – characteristic triple frequency ratio sets and related values of the black hole spin.
Mixed identity – characteristic triple frequency ratio sets and related values of the black hole spin.
Relevant versions of the multi-resonant model with assumed observed characteristic frequency ratio set νU:νM:νL = 3:2:1. The radius of marginally stable orbit xms and corresponding resonant radii x1 and x2 are given.
All Figures
 |
Fig. 1 Spin resonance functions aνU/νL(x,p) for the direct resonances D1 – D3 and the frequency ratios n:m = 5:4 (black solid line), 4:3 (black dashed line), 3:2 (black dotted line), 5:3 (red solid line), 2:1 (red dashed line), 5:2 (red dotted line), 3:1 (blue solid line), 4:1 (blue dashed line), 5:1 (blue dotted line). Black thick line represents ams(x), which implicitly determines the radius of the marginally stable orbit xms giving a natural restriction on the validity of the resonance model versions involving radial epicyclic oscillations. In the case D3, the black points determine turning points of the functions aνU/νL(x,p) joining two separate branches of the solution of the resonance condition equation. Of course, only those parts of the resonance functions with x > xms(a) are acceptable. |
| In the text | |
 |
Fig. 2 Typical cases of the frequency triples with top a), b), bottom c), d), and both types of mixed identities e), f), g). Also shown is the interesting exceptional case where two oscillations of frequencies with the same magnitude and the same ratio are in resonance at two different radii h). |
| In the text | |
 |
Fig. 3 Determination of black hole spin for several cases of doubled resonances. The functions |
| In the text | |
 |
Fig. 4 Function x(s/u,t/u) determining the triple frequency ratio set s:t:u at the properly given radius of a black hole with a “magic” spin. The points represent the ratio: s:t:u = 3:2:1 A), 4:3:1 B), 5:3:1 C), 5:4:1 D), 5:4:2 E). |
| In the text | |
 |
Fig. 5 Left: case of a “magic” spin, where the strongest resonances could occur at the same radius. For completeness we present the relevant simple combinational frequencies νθ − νr, νθ + νr, νK − νθ, νK − νr (grey dashed lines). The “magic” spin am = 0.983 represents the only case where the combinational and direct orbital frequencies coincide at the shared resonance radius. Right: another example of the characteristic frequency ratio set 3:2:1 that appears at different radii. |
| In the text | |
 |
Fig. 6 Error in determining the “magic” spin am = 0.983043 allowing νK:νθ:νr = 3:2:1 at the same radius. The interval of allowed values of the black hole spin a ∈ ⟨ am − Δ;am + Δ ⟩ related to the 2% error in frequency measurements is for T23: a ∈ ⟨ 0.973038;0.992436 ⟩; for M13: a ∈ ⟨ 0.970599;0.995125 ⟩; for T34: a ∈ ⟨ 0.981643;0.984157 ⟩; for B14: a ∈ ⟨ 0.981436;0.984253 ⟩. For the case of B12, only the 0.5% measurement error gives a reasonable restriction on black hole spin: a ∈ ⟨ 0.969714;0.993428 ⟩ (for 2% measurement error there is a ∈ ⟨ 0.91012;1.01155 ⟩). |
| In the text | |
 |
Fig. 7 Intervals of acceptable values of mass and spin of the neutron star in the atoll source 4U 1636−53 predicted by the resonant switch model for the combination of RP–TD models (left) and RP–TP models (right) using the scatter of the resonant frequencies at each of the two resonant points where RP ≡ νK:(νK − νr) = 5:4, TD ≡ (νK + νr):νK = 3:2 and TP ≡ νθ:(νθ − νr) = 3:2. |
| In the text | |
 |
Fig. B.1 Spin resonance functions aνU/νL(x,p) for the simple combinational resonances CT1 – CT6 and the frequency ratios n:m = 5:4 (black solid line), 4:3 (black dashed line), 3:2 (black dotted line), 5:3 (red solid line), 2:1 (red dashed line), 5:2 (red dotted line), 3:1 (blue solid line), 4:1 (blue dashed line), 5:1 (blue dotted line). Black thick line represents ams(x), which implicitly determines the radius of the marginally stable orbit xms. |
| In the text | |
 |
Fig. C.1 Spin resonance functions aνU/νL(x,p) for the double combinational resonances of the types DC1 – DC4, DC11 and the frequency ratios n:m = 5:4 (black solid line), 4:3 (black dashed line), 3:2 (black dotted line), 5:3 (red solid line), 2:1 (red dashed line), 5:2 (red dotted line), 3:1 (blue solid line), 4:1 (blue dashed line), 5:1 (blue dotted line). The grey lines represent the solutions of the same resonance equations that are relevant for the corresponding types of resonances (DC5−DC8, DC12). The related solutions are separated by the line of marginally stable orbits ams(x) (black thick line), they have a common stability point |
| In the text | |
 |
Fig. C.2 Spin resonance functions aνU/νL(x,p) for the double combinational resonances of the types DC9, DC10, DC13 and the warped disc oscillation model (WD) for the frequency ratios n:m = 5:4 (black solid line), 4:3 (black dashed line), 3:2 (black dotted line), 5:3 (red solid line), 2:1 (red dashed line), 5:2 (red dotted line), 3:1 (blue solid line), 4:1 (blue dashed line), 5:1 (blue dotted line). Black thick line represents ams(x), which implicitly determines the radius of the marginally stable orbit xms. The grey lines are related to the resonance DC10 – for details see Fig. C.1. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.



![\begin{eqnarray} \label{aD1} a&=&a^{\theta/{r}}(x,p)\equiv\frac{\sqrt{x}}{3(p+1)}\Bigg\{2(p+2)\nonumber\\ && -\sqrt{(1-p)\left[3x(p+1)-2(2p+1)\right]}\Bigg\}, \end{eqnarray}](/articles/aa/full_html/2013/04/aa19724-12/aa19724-12-eq82.png)
![\begin{equation} \label{aD2} a=a^{\mathrm{K}/{r}}(x,p)\equiv\frac{\sqrt{x}}{3}\left[4-\sqrt{3x(1-p)-2}\right] , \end{equation}](/articles/aa/full_html/2013/04/aa19724-12/aa19724-12-eq84.png)
![\begin{equation} \label{aD3} a=a^{\mathrm{K}/\theta}(x,p)\equiv\frac{\sqrt{x}}{3}\left[2\pm\sqrt{4-3x(1-p)}\right] . \end{equation}](/articles/aa/full_html/2013/04/aa19724-12/aa19724-12-eq86.png)
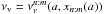
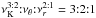
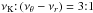
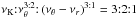
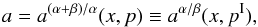
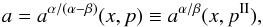

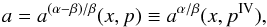
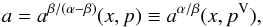
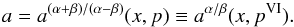
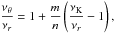
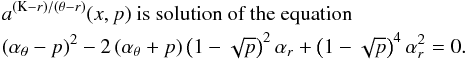
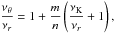
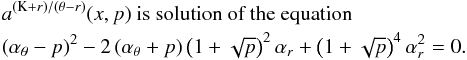
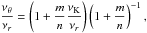
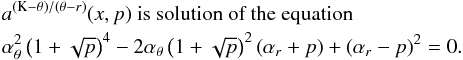
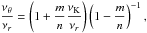
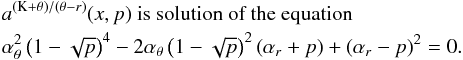
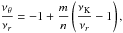
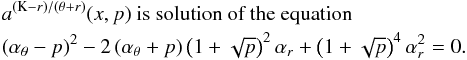
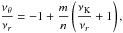
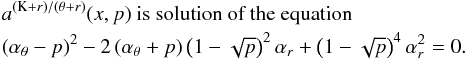
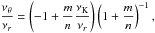
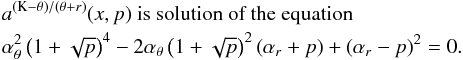
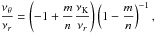
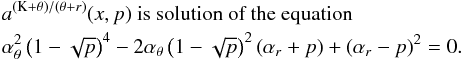
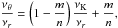
![\appendix \setcounter{section}{3} \begin{eqnarray} \lefteqn{a^{\left(\mathrm{K}-{r}\right)/\left(\mathrm{K}-\theta\right)}(x,p) \mbox{ is solution of the~equation}}\nonumber\\ \lefteqn{ \left[\alpha_{\theta}-\left(1-\sqrt{p}\right)^2\right]^2-2p\left[\alpha_{\theta}+\left(1-\sqrt{p}\right)^2\right] \alpha_{{r}}+p^2\alpha_{{r}}^2=0.}\nonumber \end{eqnarray}](/articles/aa/full_html/2013/04/aa19724-12/aa19724-12-eq366.png)
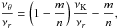
![\appendix \setcounter{section}{3} \begin{eqnarray} \lefteqn{a^{\left(\mathrm{K}+{r}\right)/\left(\mathrm{K}-\theta\right)}(x,p) \mbox{ is solution of the~equation}}\nonumber\\ \lefteqn{ \left[\alpha_{\theta}-\left(1-\sqrt{p}\right)^2\right]^2- 2p\left[\alpha_{\theta}+\left(1-\sqrt{p}\right)^2\right] \alpha_{{r}}+p^2\alpha_{{r}}^2=0.}\nonumber \end{eqnarray}](/articles/aa/full_html/2013/04/aa19724-12/aa19724-12-eq368.png)