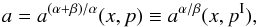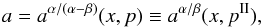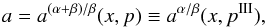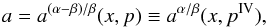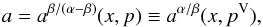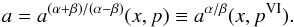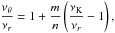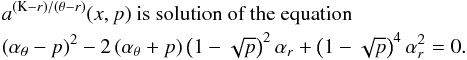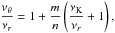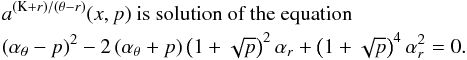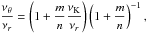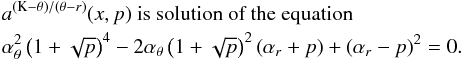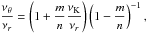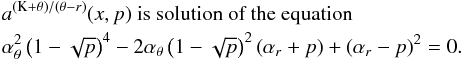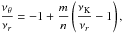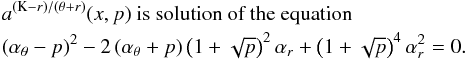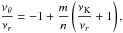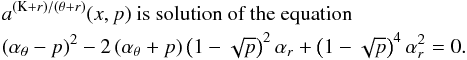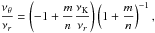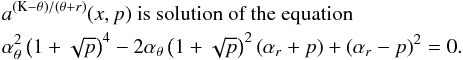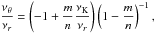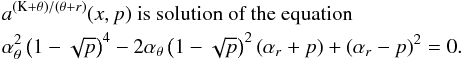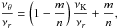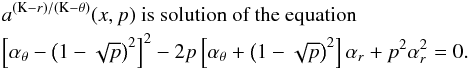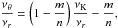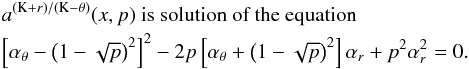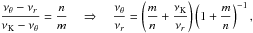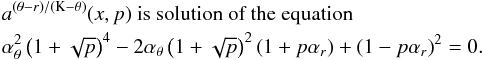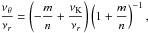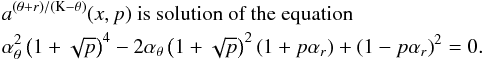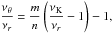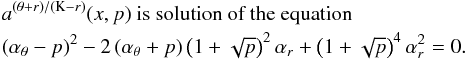| Issue |
A&A
Volume 552, April 2013
|
|
|---|---|---|
| Article Number | A10 | |
| Number of page(s) | 41 | |
| Section | Astrophysical processes | |
| DOI | https://doi.org/10.1051/0004-6361/201219724 | |
| Published online | 14 March 2013 | |
Online material
Appendix A: Simple combinational resonances of frequency pairs
The simple combinational resonances correspond to frequency relations of a single orbital (epicyclic) frequency να and a simple combinational (beat) frequency of another frequency νβ with the frequency να, assuming να > νβ. Considering the pair (α,β) in the combinations of (θ,r), (K,r), (K,θ) and introducing the new frequency ratio parameters 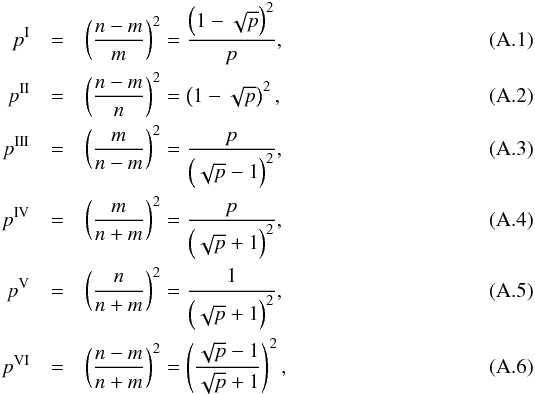 we arrive at the following resonance conditions expressed in the general form:
we arrive at the following resonance conditions expressed in the general form:
- CS.1.
- CS.2.
- CS.3.
- CS.4.
- CS.5.
- CS.6.
Simple combinational resonances of the type CS occur at the same radii as the direct resonances D1, D2, D3. Therefore, it is enough to relate the ratios of the simple combinational and direct resonances. For example, the frequency ratio να:νβ = 5:4 implies (να + νβ):να = 9:5, να:(να − νβ) = 5:1, etc.
Appendix B: Simple combinational resonances of three frequencies νK, νθ, νr
We consider resonances of oscillations with one simple frequency of the orbital frequencies and a simple combination (beat) of the other two frequencies:
We consider resonances of oscillations with one simple frequency of the orbital frequencies and a simple combination (beat) of the other two frequencies:
-
CT1.
νU = νK, νL = νθ − νr. The resonance function aK/(θ − r)(x,p) is given by
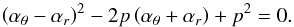 (B.1)In the explicit form the solution reads as
(B.1)In the explicit form the solution reads as 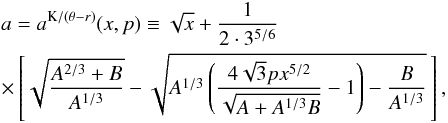 (B.2)where
(B.2)where 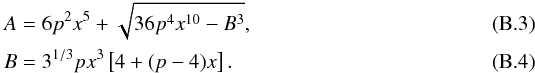
-
CT2.
νU = νθ, νL = νK − νr. The resonance function aθ/(K − r)(x,p) is given by
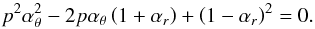 (B.5)
(B.5) -
CT3.
νU = νr, νL = νK − νθ. The resonance function ar/(K − θ)(x,p) is given by
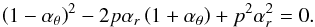 (B.6)
(B.6) -
CT4.
νU = νθ + νr, νL = νK. The resonance function a(θ + r)/K(x,p) is given by
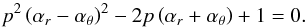 (B.7)The condition m < n < 2m has to be satisfied.
(B.7)The condition m < n < 2m has to be satisfied. -
CT5.
νU = νK + νr, νL = νθ. The resonance function a(K + r)/θ(x,p) is given by
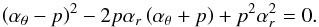 (B.8)
(B.8) -
CT6.
νU = νK + νθ, νL = νr. The resonance function a(K + θ)/r(x,p) is given by
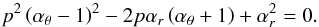 (B.9)The condition n > 2m has to be satisfied.
(B.9)The condition n > 2m has to be satisfied.
Except for the case CT1, we give the resonance functions in an implicit graphical form, because the functions are too complex and too long to be written explicitly. The implicit resonance functions are given in Fig. B.1.
The implicit resonance conditions are polynomials of the fourth order in the spin a in all six cases. Only one of the possible solutions of the resonance condition is physically relevant. Now the resonance functions exhibit more complex behaviour in comparison with the direct resonance functions. Along with those that are monotonous and do not cross the stability line, we have found monotonous functions crossing the stability line at the stability points  and non-monotonous functions crossing the stability line. In some cases the non-monotonous resonance lines appear to be (seemingly) discontinuous because of entering the region with spin a > 1, corresponding to naked-singularity spacetimes.
and non-monotonous functions crossing the stability line. In some cases the non-monotonous resonance lines appear to be (seemingly) discontinuous because of entering the region with spin a > 1, corresponding to naked-singularity spacetimes.
 |
Fig. B.1
Spin resonance functions aνU/νL(x,p) for the simple combinational resonances CT1 – CT6 and the frequency ratios n:m = 5:4 (black solid line), 4:3 (black dashed line), 3:2 (black dotted line), 5:3 (red solid line), 2:1 (red dashed line), 5:2 (red dotted line), 3:1 (blue solid line), 4:1 (blue dashed line), 5:1 (blue dotted line). Black thick line represents ams(x), which implicitly determines the radius of the marginally stable orbit xms. |
| Open with DEXTER | |
Appendix C: Double-beat combinational resonances
We introduce 13 types of the double-beat combinational resonances: 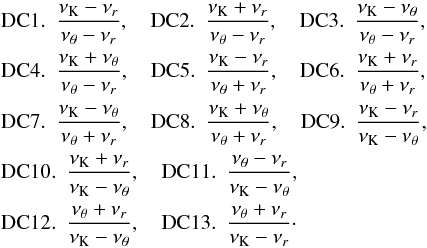 We present the implicit graphical form of the solution of the resonance conditions related to the double-beat combinational resonances DC1−DC13. We also give the overview of the allowed ranges of the direct and combinational resonances limited by the stability points that are explicitly given and by the local extrema of the resonance functions in Table C.1.
We present the implicit graphical form of the solution of the resonance conditions related to the double-beat combinational resonances DC1−DC13. We also give the overview of the allowed ranges of the direct and combinational resonances limited by the stability points that are explicitly given and by the local extrema of the resonance functions in Table C.1.
The results obtained for the relevant resonance functions are given in Figs. C.1 and C.2. In order to keep the discussion straightforward, we assume the frequency ratio n/m > 1 in all 13 cases. Therefore, we treat the frequency relations allowing for ratios higher and lower than 1 as separate (inverse) cases. For each relation of the beat frequencies, we give the relation between νθ/νr and νK/νr in terms of the ratio n/m that uniquely determines the spin “resonance” function aνU/νL(x,p). Then we determine “resonance equations” relating the functions αθ(x,a), αr(x,a) to the frequency ratio p that are used for numerical determination of the spin “resonance” functions; however, the “resonance equations” do not give unique results and usually determine two spin “resonance” functions that must be separated during the numerical procedure. The separation is given by the stability line, i.e., the function ams(x) giving the marginally stable orbits. The resonance conditions are given in the following form.
 |
Fig. C.1
Spin resonance functions aνU/νL(x,p) for the double combinational resonances of the types DC1 – DC4, DC11 and the frequency ratios n:m = 5:4 (black solid line), 4:3 (black dashed line), 3:2 (black dotted line), 5:3 (red solid line), 2:1 (red dashed line), 5:2 (red dotted line), 3:1 (blue solid line), 4:1 (blue dashed line), 5:1 (blue dotted line). The grey lines represent the solutions of the same resonance equations that are relevant for the corresponding types of resonances (DC5−DC8, DC12). The related solutions are separated by the line of marginally stable orbits ams(x) (black thick line), they have a common stability point |
| Open with DEXTER | |
 |
Fig. C.2
Spin resonance functions aνU/νL(x,p) for the double combinational resonances of the types DC9, DC10, DC13 and the warped disc oscillation model (WD) for the frequency ratios n:m = 5:4 (black solid line), 4:3 (black dashed line), 3:2 (black dotted line), 5:3 (red solid line), 2:1 (red dashed line), 5:2 (red dotted line), 3:1 (blue solid line), 4:1 (blue dashed line), 5:1 (blue dotted line). Black thick line represents ams(x), which implicitly determines the radius of the marginally stable orbit xms. The grey lines are related to the resonance DC10 – for details see Fig. C.1. |
| Open with DEXTER | |
Allowed ranges of the Kerr geometry spin for the direct orbital resonance model D3 and the combinational resonances of the types CT1, CT5, DC1, DC2, DC5, DC6 for given frequency ratio n:m.
Generally, the resonant radii corresponding to specific spin “resonance” functions are determined by the related “resonance equations” representing fourth-order polynomials in terms of the black hole spin. The “resonance equations” are identical in the following twin cases: DC1 ≡ DC6, DC2 ≡ DC5, DC3 ≡ DC7, DC4 ≡ DC8, DC9 ≡ DC10, DC11 ≡ DC12. The resonant radii are then determined by different branches of the “resonance equations” solutions, separated by the line of the marginally stable orbits ams(x). Only the case of DC13 is an exception, where the resonant lines do not touch the marginally stable line. Some of the “resonance equations” are related because of the definition of the frequency ratio (p → 1/p), namely DC3 ↔ DC11, DC5 ↔ DC13, DC7 ↔ DC12. Furthermore, there are additional interesting connections between the resonance lines of the classes DC1 (DC6) and DC9 (DC10) (see Figs. C.1 and C.2) expressed by the relations 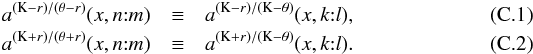 The corresponding frequency ratios n:m and k:l are given in Table C.2.
The corresponding frequency ratios n:m and k:l are given in Table C.2.
We can see from Figs. 1, B.1−C.2 that some of the considered orbital model versions do not work for the whole range of the Kerr black hole (neutron star) spin a. For example, for the direct orbital resonance model D3 (νK:νθ) there are minimal values of spin 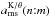 for the given frequency ratio n:m that determines the stability point for considered resonance functions (see Fig. 1). Such stability points
for the given frequency ratio n:m that determines the stability point for considered resonance functions (see Fig. 1). Such stability points 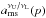 also represent limiting (minimum or maximum) values of spin for related combinational resonances of the types CT1, CT5, DC1, DC2, DC5, and DC6. Another limit on spin allowed for resonance of a given type and frequency ratio occurs in the case of non-monotonic resonance functions aνU/νL(x,p) by their local minimum
also represent limiting (minimum or maximum) values of spin for related combinational resonances of the types CT1, CT5, DC1, DC2, DC5, and DC6. Another limit on spin allowed for resonance of a given type and frequency ratio occurs in the case of non-monotonic resonance functions aνU/νL(x,p) by their local minimum 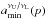 (see, e.g., Fig. C.1). The limiting values of
(see, e.g., Fig. C.1). The limiting values of
the spin, and related allowed spin ranges for given frequency ratio n:m, are presented for given types of resonance in Table C.1.
When two twin-peak QPOs are observed with frequency ratios n:m and n′:m′, respectively, we have to find two versions of resonance that could explain both the ratios and magnitudes of the observed frequencies and, for a given range of allowed mass in the source, they must predict the same black hole spin a, or more precisely, overlapping intervals of the spin. Therefore, it is clear that, generally, two observed twin-peak QPOs could make the spin estimates more precise. Two different resonances are necessary when two twin peaks are observed with the same ratios but different magnitudes.
Appendix D: Detailed table guide across all the possible triple frequency ratio sets and related values of the black hole spin a
In Tables D.2−D.4 and D.6−D.8 we present the cases with no solution as empty. An asterisk denotes the special values of the black hole spin when the triple frequencies occur at the same (shared) radius.
Notation system of double combinations of both the direct (D1−D3) and some of the simple triple combinational resonances (CT1 and CT2) with identical top (T), bottom (B), and both types of mixed (M) frequencies.
Top identity – characteristic triple frequency ratio sets and related values of the black hole spin.
Bottom identity – characteristic triple frequency ratio sets and related values of the black hole spin.
Mixed identity – characteristic triple frequency ratio sets and related values of the black hole spin.
Notation system of double combinations of the direct resonance D1 and all double combinational resonances (DC1 – DC13) with identical top (T), bottom (B), and both types of mixed (M) frequencies.
Top identity – characteristic triple frequency ratio sets and related values of the black hole spin.
Bottom identity – characteristic triple frequency ratio sets and related values of the black hole spin.
Mixed identity – characteristic triple frequency ratio sets and related values of the black hole spin.
Appendix E: Detailed table guide for the triple frequency 3:2:1
Relevant versions of the multi-resonant model with assumed observed characteristic frequency ratio set νU:νM:νL = 3:2:1. The radius of marginally stable orbit xms and corresponding resonant radii x1 and x2 are given.
© ESO, 2013
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.