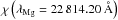| Issue |
A&A
Volume 550, February 2013
|
|
|---|---|---|
| Article Number | A104 | |
| Number of page(s) | 8 | |
| Section | Stellar atmospheres | |
| DOI | https://doi.org/10.1051/0004-6361/201220521 | |
| Published online | 04 February 2013 | |
3D radiative transfer effects in parametrized starspots
1
Hamburger Sternwarte, Gojenbergsweg 112,
21029
Hamburg,
Germany
e-mail: aberkner@hs.uni-hamburg.de; yeti@hs.uni-hamburg.de
2
Homer L. Dodge Department of Physics and Astronomy, University of
Oklahoma, 440 W Brooks, Rm
100, Norman,
OK
73019-2061,
USA
e-mail: baron@ou.edu
Received: 9 October 2012
Accepted: 20 December 2012
Aims. We use our 3D radiative transfer framework to investigate how the presence of a parametrized starspot affects radiative transfer in stellar atmospheres in general, and molecular CO lines in a stellar spectrum, in particular.
Methods. The equation of state is solved for a given temperature structure including a simple parametrized spot model and the 3D scattering problem for line transfer is solved via an operator splitting technique. The formal solution is based on a full characteristics solution. We have used both a LTE model and a test model with a 2 level atom, simulating a single spectral line in NLTE.
Results. We present the resulting CO band spectra showing both surface resolved and an integrated total emergent flux for the star and compare the umbral, penumbral, and quiet spectrum for a solar type star, which clearly shows the presence of spots as an increased CO line-depth. Furthermore, we show that the opacity structure of the spot has a significantly different angular variation than the quiet plane parallel star and its visible shape is strongly influenced by scattering, where strong scattering disconnects the lateral intensity profile from the temperature profile of the spot.
Conclusions. Even a simple, small scale parametrized model shows significant 3D effects, in both the resolved and in the surface integrated spectrum. The 3D model allows for a much more detailed treatment than simple mixing of spectra with different effective temperatures.
Key words: radiative transfer / stars: atmospheres / scattering / starspots
© ESO, 2013
1. Introduction
While spots on the solar surface can be observed directly, the same is not possible for starspots. However, it is possible to determine the existence of spots on a star indirectly as variations in brightness (Kron 1947) or by using line-depth-ratios to detect changes in the temperature structure of a star (Catalano et al. 2002a,b). The latter method is based upon the fact that the chemical composition of the stellar atmosphere inside the spot is different due to the reduced temperatures. For instance, molecules like carbon monoxide (CO), titanium oxide (TiO) and water (H2O) can only form in regions where the temperature is sufficiently low, so that the molecules do not dissolve. Since typical temperatures in spots are, in case of the sun, lower by up to 2000 K, we expect that the molecular concentration in the stellar atmosphere will increase, and, therefore, the depth of molecular lines will be affected accordingly.
Modern computing capabilities allow for full 3D simulation of spots, as well as other effects beyond a spherical symmetric or plane parallel temperature structure of stellar atmospheres. Sunspots have been simulated in MHD, for example, by Rempel et al. (2009) to determine their magnetic structure.
In the case of starspots, we are limited by the fact that it is impossible to obtain an inverse solution for a distinctive pattern of spots on a stellar surface due to the infinite number of free parameters that a full 3D grid of a star would require. However, spot models can be included into spectral synthesis, so that the presence of spots and possibly their number should be obtainable by comparison.
Hauschildt & Baron (2006, hereafter Paper I, Baron & Hauschildt (2007, hereafter Paper II, Hauschildt & Baron (2008, hereafter Paper III and Hauschildt & Baron (2008, hereafter Paper VI describe the Phoenix/3D simulation code for atmospheres, which solves the equation of state, as well as radiative transfer problem with scattering in 3D, for a given temperature structure. We have used this simulation code, as well as a 2 level atom NLTE code based upon the same 3D radiative transfer solver, on a parametrized model of a starspot embedded in a plane parallel atmosphere structure as a test case to investigate the feasibility of such a method. We focus on molecular CO lines, since CO is an important diagnostic in cool stars.
We present the results of our model calculations focusing on the effects that the reduced temperature of the starspot has on the CO concentration within the atmosphere and thus, on the opacities and the 3D radiative transfer. We have simulated both the effects on the emergent total flux of the observable spectrum of the star, as well as the resolved intensity of the spot and its angular variation, which can be used to test any given spot model against solar spots. Surface resolved models could also benefit techniques in which planetary transits are used to actually resolve stellar surfaces and detect features like starspots indirectly in this way (Huber et al. 2010).
2. Method
The problem of 3D radiative transfer is solved by a full characteristic method for the formal solution and non local operator splitting for the scattering problem. The method has been described in detail in Papers I, II, III and VI, and shall not be repeated at length here. Instead, we will focus on the implementation of a parametrized starspot model into the existing framework.
The starspot model is implemented into a plane parallel atmosphere structure with periodic boundary conditions in the x and y directions, as was introduced in Paper III. In this case, we use a Cartesian grid with 653 equally sized voxels, where each voxel has a size of Δx = Δy = Δz = 22.38 km. The plane parallel structure is based upon a model for a solar type star with Teff = 5700 K, log (g) = 4.5 and solar abundances (Asplund et al. 2005), which is the same model that was used in Paper VI.
The presence of the starspot is considered as a local temperature anomaly. We choose to use a monolithic model since a so called spaghetti model could not be parametrized as easily (Rempel & Schlichenmaier 2011). For this work we have used a conical shape for the spot, in which the temperature of the plane parallel structure is reduced depending on the distance to the center of the umbra and the depth 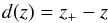 (1)beneath the outward surface of the grid, where z+ is the z-coordinate of the upper boundary of the grid. The temperature difference between neighbouring voxels is kept low enough that no discontinuities occur. The cone is the most simple circularly symmetric shape which allows for a smooth transition between inside and outside in both radial and horizontal direction, assuming that the spot has to decrease in diameter with depth.
(1)beneath the outward surface of the grid, where z+ is the z-coordinate of the upper boundary of the grid. The temperature difference between neighbouring voxels is kept low enough that no discontinuities occur. The cone is the most simple circularly symmetric shape which allows for a smooth transition between inside and outside in both radial and horizontal direction, assuming that the spot has to decrease in diameter with depth.
The adopted shape of the model allows us to control the starspot with as few as four free parameters and avoids huge temperature gradients in adjacent voxels. Our parametrization produces a simplified single trunk starspot with a cylindrically symmetric temperature profile.
The temperature for each voxel is parametrized as:
where Tpp is the unmodified temperature of the plane parallel atmosphere model, rnorm normalizes rspot(z) so that rspot(z) → rspot,max for d(z) → 0, and the parameters control the temperature difference in the center of the spot (ΔTCore), the vertical temperature profile (dspot), the lateral temperature profile (rspot,max) and the maximum depth of the model (dmax).
In this case, the following parameters where used to produce a small spot structure, which allowed for a high spatial resolution: 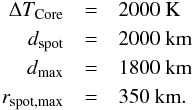 This represents a rather small spot compared to spots on the solar surface. The small size was chosen to limit the computational demands of the simulation without having to use a very low spatial resolution. However, the small scale of the spot is only relevant for those results, that are strongly influenced by the lateral opacity structure of the spot, which is primarily the case for the angular variation of the resolved intensity. In case of the surface resolved intensity for cos(ϑ) = 1 and the surface integrated fluxes the radial size of the spot is of limited influence.
This represents a rather small spot compared to spots on the solar surface. The small size was chosen to limit the computational demands of the simulation without having to use a very low spatial resolution. However, the small scale of the spot is only relevant for those results, that are strongly influenced by the lateral opacity structure of the spot, which is primarily the case for the angular variation of the resolved intensity. In case of the surface resolved intensity for cos(ϑ) = 1 and the surface integrated fluxes the radial size of the spot is of limited influence.
Since we are simulating a static temperature structure and are only interested in the effects a starspot will have on the outgoing spectrum and the feasibility of including starspots into our 3D radiative transfer simulation, this simple model will be sufficient for this work.
The resulting plane parallel grid with the anomaly is then used as an input for the ACES equation of state (Barman, in prep.) to obtain the chemical composition for the spot area.
2.1. Integrated spectra
Calculating the entire star would mean calculating a great number of voxels with the plane parallel settings of the quiet star, since a single sunspot, while possibly quite large, is still small compared to the entire surface area. Furthermore, integrating over the stellar surface removes any information on the position of a single voxel, so, even if it were theoretically possible to place multiple identical spots into a huge plane parallel grid to simulate a star with a certain level of coverage, this would be a waste of computational resources.
Instead, we opted to simulate a grid with a single spot and periodic boundary conditions, then virtually add a number of quiet surface voxels into the integration to produce the desired level of coverage. For this calculation, every voxel with an outward intensity of less then 99.9% of the undisturbed rim of the grid has been assumed to be part of the spot. The quiet voxels where taken from a simulation that consisted of a plane parallel grid without modifications. The outgoing total flux is then normalized to compensate for the different size of the integration area.
To illustrate the use of a three dimensional solution of the radiative transfer problem, we compare the integrated spectra with spectra from 1D calculations, where the presence of spots has been roughly included by mixing synthetic spectra from 1D calculations for Teff = 5700 K and Teff = 3700 K, both based upon the solar model the plane parallel structure was created from, which is the simplest form of simulating spots with 1D models.
Using a mixed model has the disadvantage of reducing the total power output of the star. Therefore the mixed model was corrected by introducing a correction factor calculated from the reduction in total luminosity caused by the inclusion of the low temperature model. 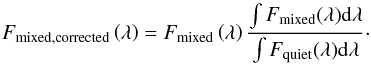 (2)
(2)
2.2. Angular variations
To obtain the limb variations for the simulated spot, we calculate a formal solution with the aforementioned full characteristics solution for a specific line of sight with the source function obtained by solving the radiative transfer problem via operator splitting. At this time, the source function S is known for the entire grid, so that obtaining arbitrary angles of view is comparably easy.
2.3. Scattering
As a first step toward a multi level NLTE treatment of 3D radiative transfer, similar to the work of Schweitzer et al. (2000) in 1D, we have used a two-level solver, as previously discussed in Paper II, with complete redistribution line scattering.
Starting from the same spot model used for the LTE tests, we have calculated the radiative transfer solution for a single absorption line plus continuum. The scattering was set explicitly using a thermalization parameter εline in the source function 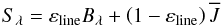 (3)for radiative transfer with total redistribution scattering and calculated for different values of εline, where Bλ is the planck function and
(3)for radiative transfer with total redistribution scattering and calculated for different values of εline, where Bλ is the planck function and 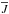 the mean intensity integrated over the line profile. In this way, it was possible to investigate the influence of scattering directly.
the mean intensity integrated over the line profile. In this way, it was possible to investigate the influence of scattering directly.
Since scattering connects spatially distant parts of the stellar atmosphere, we expect to see a difference in the lateral intensity profile of the spot structure.
 |
Fig. 1 Vertical cut through the voxel grid aligned right through the center of the umbra. The left half of the plot has been color coded logarithmically with the electron temperature Telec of the atmosphere, while the right half of the plot shows the resulting LTE CO concentration. |
 |
Fig. 2 Vertical cut through the voxel grid aligned through the center of the umbra. The left half shows opacities χ(λCO = 44 674.59 Å), while the right half shows the opacities χ(λcont = 44 676.00 Å). The opacities have been color coded logarithmically. The dark horizontal lines mark the level of optical depth τλ = 1 for both wavelength and μ = 1. |
 |
Fig. 3 Vertical cut through the voxel grid aligned through the center of the umbra. The left half shows temperature for comparison, while the right half shows the opacities |
3. Results
Figure 1 shows the temperature structure that was used and the resulting CO concentration obtained with the EOS solver. The CO concentration closely follows the temperature at different depths, so that it is highest in the core of the spot beneath the visual umbra. Further outward, the number density of CO molecules is still higher than outside of the spot, though not as high as directly in its center. In relative numbers, the relative increase in CO compared to the outside region, is high both in the spot center, at the surface level, as well as at the bottom of the model – regions that were originally devoid of significant CO concentration (below 0.1 ppm).
The number densities yield the wavelength dependant opacities 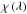 , which are necessary to solve the radiative transfer problem. Figure 2 shows the opacity for a CO line with a line center of λCO = 44 674.59 Å and a Gaussian line profile compared to a continuum point dominated by radiation from a region at the lower boundary of the spot and, thus, is not affected as strongly, as can be seen from the black lines in Fig. 2, which mark the optical depth level of τλ = 1 for the respective wavelength and μ = 1, indicating the region that produces the line and the continuum. As can be seen, the different opacities inside the spot change the depth of τλ = 1 for any characteristic traversing the spot, so that it is dominated by radiation from a shallower depth, compared to the outside region at CO line wavelength and by a slightly deeper level at continuum wavelength. We can even see that the exact shape of the anomaly has a strong influence on the shape of the τλ = 1 level.
, which are necessary to solve the radiative transfer problem. Figure 2 shows the opacity for a CO line with a line center of λCO = 44 674.59 Å and a Gaussian line profile compared to a continuum point dominated by radiation from a region at the lower boundary of the spot and, thus, is not affected as strongly, as can be seen from the black lines in Fig. 2, which mark the optical depth level of τλ = 1 for the respective wavelength and μ = 1, indicating the region that produces the line and the continuum. As can be seen, the different opacities inside the spot change the depth of τλ = 1 for any characteristic traversing the spot, so that it is dominated by radiation from a shallower depth, compared to the outside region at CO line wavelength and by a slightly deeper level at continuum wavelength. We can even see that the exact shape of the anomaly has a strong influence on the shape of the τλ = 1 level.
 |
Fig. 4 Intensity spectrum for a surface resolved starspot and μ = 1.0. Shown is the umbra (blue), represented by the spectrum for the central voxel of the spots surface, the penumbra (green), represented by a voxel at half of the spots radius from the center of the grid and the undisturbed surface (black), represented by a voxel at the far rim of the grid. The left panel shows several lines of a CO band spectrum, while the right panel shows a wavelength region including a Mg I doublet line. |
In this way, opacity is the dominant factor for the reduced brightness at CO line wavelength, while temperature has a more indirect role, since the opacity is, of course, temperature dependent.
For the continuum on the other hand, we see a reduced intensity, even if the opacity is slightly decreased within the spot, due to the reduced temperature. This is the case both for the continuum and certain lines that show reduced opacity under the influence of the spot as well. An example for a line that is influenced in this way would be Mg I, which is formed at a deeper level of the atmosphere, as can be seen in Fig. 3 which shows opacity and τ(λMg) = 1 for the Mg I doublet line at λMg = 22 814.2 Å. The intensity is reduced for all wavelength points by the simple fact that the temperatures T(x,y,z) along the outgoing characteristics are lower, and therefore the temperature dependent source functions S(x,y,z) are smaller as well.
This is clearly visible in Fig. 4a, which shows the transition of the surface resolved spectrum from the quiet region outside the spot, through the penumbral region, and into the heart of the umbra. As expected, we see that the CO lines have a higher contrast compared to the quiet surface, than the continuum. This is especially true for the two overlapping lines around 44 664 Å, where the opacities for two close lines are both increased, so that the increase in total opacity is even stronger and the depth to which we can see is further reduced. The same effect is shown for the Mg I doublet line at λMg = 22 814.2 Å in Fig. 4b.
3.1. Horizontal energy flows
 |
Fig. 5 Illustration of horizontal energy flow for the upper region z = 45 of the spot model at CO line wavelength λ = λline. The graphic shows the flow lines of x and y components of the flux vector F. The length of an arrow is proportional to the field vector magnitude ∥ (Fx,Fy) ∥ following the direction of (Fx,Fy), the field vectors shown have been selected randomly. The 3D radiative transport equation is solved for nϑ = nφ = 64 solid angle points. The normalized x and y coordinates are shown on the x and y axes, respectively. |
 |
Fig. 6 Illustration of horizontal energy flow for the bottom region z = 10 of the spot model at CO line wavelength λ = λline. The graphic shows the flow lines of x and y components of the flux vector F. The length of an arrow is proportional to the field vector magnitude ∥ (Fx,Fy) ∥ following the direction of (Fx,Fy), the field vectors shown have been selected randomly. The 3D radiative transport equation is solved for nϑ = nφ = 64 solid angle points. The normalized x and y coordinates are shown on the x and y axes, respectively. |
 |
Fig. 7 Part of CO band spectrum for the plane parallel 1D model without spot (black), the mixed 5700/3700 K 1D spot model with (green) and without (blue) correction for luminosity and the 3D spot model (red). The model is for a solar type star with 20% spot coverage. The flux has been normalized to the quiet continuum level to allow comparison of the two different sized models. |
In Figs. 5 and 6 we present the horizontal radiation flow from the region outside the spot into the starspot. In a plane parallel setting the flux would be parallel to the z direction, as can be seen in Fig. 6 at the edges of the grid, far from the spot. We can see that with the lowered temperature of the spot present, there is a redirection of flux into the spot following the temperature gradient and therefore a horizontal component of the flux. In the upper region (Fig. 5) this horizontal flow affects the whole grid since the spot is large. Close to the lower boundary, the energy flow is redirected primarily inside the spot and close to its rim, while there is no horizontal flow in the quiet region of the grid. Since the temperature gradient at this level is steeper due to the smaller size of the spot model, the horizontal flow increased more rapidly.
3.2. Effect on outgoing flux spectrum
 |
Fig. 8 Wavelength dependent change to outward flux Fz due to a spot coverage of 20% for the 3D spot model (a) and 1D model with corrected luminosity (b). Several molecular lines of CO are shown. |
We have already shown how the presence of the spot has an influence on the CO molecular lines in our simulation. The previous results were obtained for the surface resolved intensity spectrum, which cannot be observed for stars directly with current methods. Therefore, we will now use the aforementioned integration method to obtain total outgoing flux spectra for an entire stellar disk, which can be measured for unresolved stars.
Figures 7 shows the total emergent flux for the same spectral region of a solar type star. In this case, the flux has been integrated over the surface of the star with the assumption, that 20% of its surface are covered by spot structures. In Fig. 7a the spectrum of the star with spots is compared to the quiet 3D solution for the same stellar model. As expected, the CO lines have increased more strongly than the continuum, as can be seen in Fig. 8a, where the relative change to the outward flux Fz is shown for the same wavelength region. The CO doublet line at about 44 664 Å shows the strongest change, since it is most affected by the changed opacity structure.
Figure 7b shows the same 3D model for a star with 20% spot coverage, this time compared to a 1D model, where the same amount of starspot coverage was considered by using a 1D model with a lower effective temperature. As can be seen, the mixed 1D model shows a reduction in flux for the entire spectrum and not just for the CO molecular lines. The CO lines do not show any increase in line depth compared to the 3D model.
The difference between both models is caused by the fact, that the simple 1D mixed model does not account for any kind of penumbra transition between the inside and the outside region. In the 3D model, 20% coverage includes the penumbra of the spot, due to the fact, that any voxel cell that does not show the quiet outward flux is considered as part of the spot. The 1D spot with 20% coverage would suggest, that 20% of the stellar surface is covered by the umbrae of spots, which explains the increased darkening. Furthermore, the inclusion of the lower temperature model reduces the total luminosity of the star. If we include a correction for the reduction in luminosity, the corrected 1D model produces results that are closer to the 3D model in general, as can be seen from the green line in Fig. 7b. However, the corrected model does not reproduce the changes to the strong CO lines and predicts an increase in continuum flux, as is evident from 8b.
With the simple assumptions we have made for this model, the reduction in line flux should be linear in the grade of coverage, this can be seen in Fig. 9 for spot coverage up to 50%.
 |
Fig. 9 Maximum change in CO line flux for a solar type star with different levels of spot coverage. |
3.3. Center-to-limb variations
 |
Fig. 10 Variation of the perceived Intensity Iλ from the center to the limb of a resolved stellar disk. Shown is the limb variation law for the quiet, plane parallel atmosphere model, as well as the intensity of the darkest part of the spot model (red) for the CO line at λ = λCO. The intensity has been normalized to quiet line intensity at the center of the stellar disk. |
 |
Fig. 11 Variation of the perceived intensity Iλ from the center to the limb of a resolved stellar disk. Shown is the limb variation law for the quiet, plane parallel atmosphere model, as well as the intensity of the darkest part of the spot model (orange) for the CO line at λ = λCO, for a different set of model parameters (ΔTCore = 2000 K, dspot = 1000 km, dmax = 900 km, rspot,max = 250 km). The intensity has been normalized to quiet line intensity at the center of the stellar disk. |
 |
Fig. 12 Variation of the perceived intensity Iλ from the center to the limb of a resolved stellar disk. The limb variation law for the quiet, plane parallel atmosphere model, as well as the intensity of the darkest part of the spot model (blue) for the Mg I line at λ = λMg are shown. The intensity has been normalized to quiet line intensity at μ = 1. |
Calculating the formal solution for different angles of view ϑ for the surface resolved stellar disk shows that the spot has a different limb variation compared to the quiet atmosphere, as it apparently grows brighter, the closer it is seen at the rim of the stellar disk. Figures 10−12 show the intensity of the darkest point of the umbra, compared to the quiet intensity of the star as we approach the stellar limb for different wavelengths λ and, in case of Fig. 11, a different set of model parameters (ΔTCore = 2000 K, dspot = 1000 km, dmax = 900 km, rspot,max = 250 km). Up to about cos(ϑ) = 0.2, the spot steadily loses contrast in all three cases. This is due to the fact that each characteristic traverses different parts of the sub surface structure of the spot and, at high angles, the outside region on the other side of the spot shines through.
The cause for this kind of limb brightening is that the optical depth τ along a characteristic is, in any full 3D calculation, dependent on each of the voxels traversed by the characteristic. We have already seen that the opacity within the spot region differs strongly from the quiet region outside the spot, so that the optical depth for a direct line of sight changes and is a major reason for the reduced line intensity in the spot. At lower cos(ϑ), the actual physical spot is projected to a larger surface area, so that we can see deeper into the spot and part of its subsurface structure.
This effect is strongly dependant on the opacity structure of the spot for each wavelength, which as we have seen before, varies between lines of different species. So that while we see limb brightening as demonstrated for strongly affected lines, we can see from comparison between Figs. 10 and 12, that lines that are not affected as strongly show a different kind of angular variation.
The additional spot model used in Fig. 11 is both smaller in radial size and has a reduced depth. At μ = 1.0 the contrast between the model and the quiet surface is reduced, primarily due to the reduced depth. The spot has a lower volume, therefore, the region with increased opacity is smaller, so that the overall effect is reduced. However, we see a different kind of limb brightening compared to the earlier model. While the deep spot shows a more or less constant rate of limb brightening, the contrast of this model decreases primarily between cos(ϑ) = { 1.0,0.6 }. This different form of angular variation is obviously caused by the fact, that the smaller model has steeper temperature gradients, since the total ΔT is the same, and, therefore, the opacity structure is different.
Notice that beyond cos(ϑ) = 0.2, the effect reverses in both cases and the contrast of the spots umbrae seems to be almost constant. However, this is not a real effect but a consequence of the periodic boundary conditions. Since any characteristic leaving the grid at the positive and negative x or y boundary is wrapped around to the opposite side of the grid, we actually simulate a semi infinite slab with an infinite number starspots in both directions. At low cos(ϑ) this means that we do not see just one spot, but several, and at angles close to cos(ϑ) = 0 an almost infinite number of spots. This affects characteristics at cos(ϑ) → 0 strongly, but does not occur at characteristics that are perpendicular or almost perpendicular to the surface, since they will see the spot only once.
 |
Fig. 13 Lateral intensity profiles through the center of the umbra, calculated for a two level absorption line with complete redistribution scattering of εline = {100,10-1,10-2,10-4}. |
3.4. Scattering
Figure 13 shows the lateral intensity profile for the spot for different values of the line scattering coefficient εline. The lateral profile changes substantially with increased importance of scattering in the atmosphere. Without scattering, the lateral profile of the spot is clearly directly dependant on the temperature structure of the spot, the more important scattering is, the farther we depart from this dependency.
Scattering connects different parts of the stellar atmosphere and provides an additional exchange between hotter and cooler regions, redirecting energy into the spot. This results in a lateral profile where we have a large umbral core of nearly constant intensity, though the intensity in the umbra is not reduced by as much as without scattering. On the other hand, the penumbral flanks of the lateral profile are pushed outward, so that the outer regions of the spot now show a larger contrast to the quiet surface.
In this way, the total area darkened is somewhat larger than before, while the maximal contrast is reduced. This not only extends the visible spot beyond the physical boundary of the region with reduced temperature, but it also means that this is one effect that can not be adequately simulated without a full 3D treatment of the radiative transfer, since it shows that different parts of the spot structure can not be seen independently, as they influence each other directly and interact with the surroundings.
4. Conclusions
For the influence of spots on radiative transfer in general, we have identified two primary effects. The lowered temperature directly reduces the source function within the spot and, thus, the emission from the spot. This is dominant for wavelength bands without strongly temperature sensitive spectral lines, because the change to the relevant species for these wavelength regimes and therefore the change to wavelength dependent opacity is minimal. Indirectly, the reduced temperature allows for a change in chemical composition of the atmosphere, in this case an increased density of molecules forming below certain temperatures. The increased presence of a species, and the change in temperature influence the opacity within the spot. In the case of affected molecular line wavelength, the opacity is increased by about an order of magnitude. The increased opacity in this case changes the relation between physical depth and optical depth, so that we see shallower and even cooler regions of the star. This is the reason behind the increase in line depth for molecular lines like CO and other temperature sensitive lines.
The small spot structures we have simulated in this work result in an increase in line depth of about 1.5% for a moderate amount of spot coverage. This number is of course dependent on the model used and can be expected to vary strongly with different spot models. We conclude that with the models of the necessary accuracy, accounting for spot coverage in synthetic spectra is absolutely feasible. In future work, we will expand the size of the model to include larger spots and compare the results to observational data.
We have shown that even a comparatively simple parametrized 3D starspot model shows significant differences from the 1D assumption of two models of different temperatures that are combined. The 3D approach is better suited to determine the influence of strongly temperature sensitive molecular lines like the CO spectra we have modeled in this work. This is mainly due to the fact that mixing models for just 2 different temperatures not only ignores any penumbra transition and does not allow for horizontal radiation flow in radiative transfer, but also assumes a different stellar structure for the entire atmosphere inside the spot, namely that of a cooler stellar model. Using a correction to compensate for reduced luminosity can partly reduce the problems of the 1D mixed model, but cannot consistently reproduce the changes in line depth and continuum at the same time. Furthermore, to include the penumbral region, at least one additional temperature would
have to be included. Nevertheless, it is more accurate, to improve parametrized 3D models or use 3D MHD models, since both allow for subsurface structure of spots and account for horizontal energy flows, which have proven to be significant in our models, without need for complex corrections that would require additional assumptions to be made.
The surface resolved intensities we obtained reproduce the known behaviour of starspots to increase the apparent brightness while approaching the stellar rim. We have shown that the angular variation of the intensity is both wavelength dependent and depends on the actual subsurface temperature and opacity structure of the model and is very sensitive to changes. Different vertical profiles and different sizes of the model produce different types of limb brightening. At different stellar angles cos(ϑ) different parts of the subsurface structure become dominant. This could be used in light-curve analyses of planetary transits, but the primary purpose of this method is to obtain data for comparison with resolved sunspots, which will enable us to test both parametrized models as those used already and full hydrodynamical models once available.
As a last step, we have investigated the influence of scattering in starspots. Our calculations have shown that scattering has to be considered carefully, since it redistributes energy from hotter to cooler regions differently and thus has a strong influence on radiative transfer within the boundaries of the cooler star spot and on the other hand for the surrounding quiet atmosphere. This is another reason why the interaction between different parts of the spot can’t be neglected.
In the future, we plan to extend our current models to a multi level NLTE treatment of CO, to study NLTE effects in inhomogeneous structures like starspots with greater detail.
Acknowledgments
This research used resources of the Höchstleistungs Rechenzentrum Nord (HLRN), the Hamburger Sternwarte Delta Opteron cluster and IBM AIX p690s, and the National Energy Research Scientific Computing Center (NERSC), which is supported by the Office of Science of the US Department of Energy under Contract No. DE-AC02-05CH11231. We thank all these institutions for a generous allocation of computer time.
References
- Asplund, M., Grevesse, N., & Sauval, A. J. 2005, in Cosmic Abundances as Records of Stellar Evolution and Nucleosynthesis, eds. T. G. Barnes III, & F. N. Bash, ASP Conf. Ser., 336, 25 [Google Scholar]
- Baron, E., & Hauschildt, P. H. 2007, A&A, 468, 255 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Catalano, S., Biazzo, K., Frasca, A., & Marilli, E. 2002a, A&A, 394, 1009 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Catalano, S., Biazzo, K., Frasca, A., et al. 2002b, Astron. Nachr., 323, 260 [NASA ADS] [CrossRef] [Google Scholar]
- Hauschildt, P. H., & Baron, E. 2006, A&A, 451, 273 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hauschildt, P. H., & Baron, E. 2008, A&A, 490, 873 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hauschildt, P. H., & Baron, E. 2010, A&A, 509, A36 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Huber, K. F., Czesla, S., Wolter, U., & Schmitt, J. H. M. M. 2010, A&A, 514, A39 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kron, G. 1947, PASP, 59, 261 [NASA ADS] [CrossRef] [Google Scholar]
- Rempel, M., & Schlichenmaier, R. 2011, Liv. Rev. Sol. Phys., 8, 3 [Google Scholar]
- Rempel, M., Schüssler, M., & Knölker, M. 2009, A&A, 691, 640 [Google Scholar]
- Schweitzer, A., Hauschildt, P. H., & Baron, E. 2000, ApJ, 541, 1004 [NASA ADS] [CrossRef] [Google Scholar]
All Figures
 |
Fig. 1 Vertical cut through the voxel grid aligned right through the center of the umbra. The left half of the plot has been color coded logarithmically with the electron temperature Telec of the atmosphere, while the right half of the plot shows the resulting LTE CO concentration. |
| In the text | |
 |
Fig. 2 Vertical cut through the voxel grid aligned through the center of the umbra. The left half shows opacities χ(λCO = 44 674.59 Å), while the right half shows the opacities χ(λcont = 44 676.00 Å). The opacities have been color coded logarithmically. The dark horizontal lines mark the level of optical depth τλ = 1 for both wavelength and μ = 1. |
| In the text | |
 |
Fig. 3 Vertical cut through the voxel grid aligned through the center of the umbra. The left half shows temperature for comparison, while the right half shows the opacities |
| In the text | |
 |
Fig. 4 Intensity spectrum for a surface resolved starspot and μ = 1.0. Shown is the umbra (blue), represented by the spectrum for the central voxel of the spots surface, the penumbra (green), represented by a voxel at half of the spots radius from the center of the grid and the undisturbed surface (black), represented by a voxel at the far rim of the grid. The left panel shows several lines of a CO band spectrum, while the right panel shows a wavelength region including a Mg I doublet line. |
| In the text | |
 |
Fig. 5 Illustration of horizontal energy flow for the upper region z = 45 of the spot model at CO line wavelength λ = λline. The graphic shows the flow lines of x and y components of the flux vector F. The length of an arrow is proportional to the field vector magnitude ∥ (Fx,Fy) ∥ following the direction of (Fx,Fy), the field vectors shown have been selected randomly. The 3D radiative transport equation is solved for nϑ = nφ = 64 solid angle points. The normalized x and y coordinates are shown on the x and y axes, respectively. |
| In the text | |
 |
Fig. 6 Illustration of horizontal energy flow for the bottom region z = 10 of the spot model at CO line wavelength λ = λline. The graphic shows the flow lines of x and y components of the flux vector F. The length of an arrow is proportional to the field vector magnitude ∥ (Fx,Fy) ∥ following the direction of (Fx,Fy), the field vectors shown have been selected randomly. The 3D radiative transport equation is solved for nϑ = nφ = 64 solid angle points. The normalized x and y coordinates are shown on the x and y axes, respectively. |
| In the text | |
 |
Fig. 7 Part of CO band spectrum for the plane parallel 1D model without spot (black), the mixed 5700/3700 K 1D spot model with (green) and without (blue) correction for luminosity and the 3D spot model (red). The model is for a solar type star with 20% spot coverage. The flux has been normalized to the quiet continuum level to allow comparison of the two different sized models. |
| In the text | |
 |
Fig. 8 Wavelength dependent change to outward flux Fz due to a spot coverage of 20% for the 3D spot model (a) and 1D model with corrected luminosity (b). Several molecular lines of CO are shown. |
| In the text | |
 |
Fig. 9 Maximum change in CO line flux for a solar type star with different levels of spot coverage. |
| In the text | |
 |
Fig. 10 Variation of the perceived Intensity Iλ from the center to the limb of a resolved stellar disk. Shown is the limb variation law for the quiet, plane parallel atmosphere model, as well as the intensity of the darkest part of the spot model (red) for the CO line at λ = λCO. The intensity has been normalized to quiet line intensity at the center of the stellar disk. |
| In the text | |
 |
Fig. 11 Variation of the perceived intensity Iλ from the center to the limb of a resolved stellar disk. Shown is the limb variation law for the quiet, plane parallel atmosphere model, as well as the intensity of the darkest part of the spot model (orange) for the CO line at λ = λCO, for a different set of model parameters (ΔTCore = 2000 K, dspot = 1000 km, dmax = 900 km, rspot,max = 250 km). The intensity has been normalized to quiet line intensity at the center of the stellar disk. |
| In the text | |
 |
Fig. 12 Variation of the perceived intensity Iλ from the center to the limb of a resolved stellar disk. The limb variation law for the quiet, plane parallel atmosphere model, as well as the intensity of the darkest part of the spot model (blue) for the Mg I line at λ = λMg are shown. The intensity has been normalized to quiet line intensity at μ = 1. |
| In the text | |
 |
Fig. 13 Lateral intensity profiles through the center of the umbra, calculated for a two level absorption line with complete redistribution scattering of εline = {100,10-1,10-2,10-4}. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.



![\begin{eqnarray*} &&T_{\rm elec}\left(x,y,z\right) = T_{\rm pp}\left(z\right) - \Delta T_{\rm Core} \\ & &\qquad\qquad \qquad \times \exp\left(- \left(\frac{\sqrt{x^2 + y^2}}{r_{\rm spot}(z)}\right)^2 \right) \exp \left(-\frac{d(z)}{d_{\rm spot}} \right) \\ && r_{\rm spot}(z) = \left\{ \begin{array}{l l} \frac{r_{\rm spot,max}}{r_{\rm norm}} \sqrt{- \log\left(\frac{d(z)}{d_{\rm max}}\right)} & ~~~~~~~~~~~~~~~~ \mbox{if} ~~ d(z) > 0\\[2mm] r_{\rm spot,max} & ~~~~~~~~~~~~~~~~ \mbox{if} ~~ d(z) = 0 \end{array}\right. \\ && r_{\rm norm} = \sqrt{- \log\left(\frac{\Delta z}{d_{\rm max}}\right)} \end{eqnarray*}](/articles/aa/full_html/2013/02/aa20521-12/aa20521-12-eq11.png)