| Issue |
A&A
Volume 549, January 2013
|
|
|---|---|---|
| Article Number | A135 | |
| Number of page(s) | 8 | |
| Section | Interstellar and circumstellar matter | |
| DOI | https://doi.org/10.1051/0004-6361/201220658 | |
| Published online | 15 January 2013 | |
The mid-infrared extinction law in the darkest cores of the Pipe Nebula⋆
1
European Southern Observatory, Karl-Schwarzschild-Str. 2, 85748
Garching bei München,
Germany
e-mail: jascenso@eso.org
2
Harvard-Smithsonian Center for Astrophysics, 60 Garden
Street, Cambridge,
MA
02138,
USA
3
University of Vienna, Türkenschanzstrasse 17, 1180
Vienna,
Austria
4
Instituto de Astronomía, Unidad Académica de Ensenada, Universidad
Autónoma de México, 22860
Ensenada,
México
5
University of Milan, Department of Physics,
via Celoria 16, 20133
Milan,
Italy
Received: 29 October 2012
Accepted: 27 November 2012
Context. The properties of dust grains, in particular their size distribution, are expected to differ from the interstellar medium to the high-density regions within molecular clouds.
Aims. We measure the mid-infrared extinction law produced by dense material in molecular cloud cores. Since the extinction at these wavelengths is caused by dust, the extinction law in cores should depart from what is found in low-density environments if the dust grains have different properties.
Methods. We used the unbiased LINES method to measure the slope of the reddening vectors in color-color diagrams. We derived the mid-infrared extinction law toward the dense cores B59 and FeSt 1-457 in the Pipe Nebula over a range of visual extinction between 10 and 50 mag, using a combination of Spitzer/IRAC and ESO NTT/VLT data.
Results. The mid-infrared extinction law in both cores departs significantly from a power law between 3.6 and 8 μm, suggesting that these cores contain dust with a considerable fraction of large dust grains. We find no evidence of any dependence in the extinction law with column density up to 50 mag of visual extinction in these cores, and no evidence of any variation between our result and those for other clouds at lower column densities reported elsewhere in the literature. This suggests either that large grains are present even in low column density regions or that the existing dust models need to be revised at mid-infrared wavelengths. We find a small but significant difference in the extinction law of the two cores, which we tentatively associate with the onset of star formation in B59.
Key words: radiation mechanisms: general / methods: observational / techniques: photometric / stars: formation / ISM: clouds / infrared: ISM
© ESO, 2013
1. Introduction
Dust plays a crucial role in many of the chemical and physical processes that take place in the interstellar medium. It plays an especially important role in molecular clouds and in the formation of stars. At low densities, dust grains are the catalysts for the formation of molecules that then cool the clouds radiatively (e.g., Draine 2011; Whitworth et al. 1998). At high densities the molecules begin to deplete from the gas phase, and dust becomes the dominant coolant, lowering the gas temperature enough that fragmentation of cores into stars may occur (Larson 2005; Whitworth et al. 1998). Nevertheless, the properties of the dust grains, including their composition and size distribution, and the way they evolve in different environments are not accurately known.
As the density increases, dust grains are believed to grow by coalescence through grain-grain inelastic collisions and by the accretion of ice mantles, as molecules freeze out onto their surfaces (e.g., Ossenkopf 1993; Whittet et al. 1988). The ice mantles are typically very thin (Draine 1985) and so do not increase the grain size significantly by themselves, but they do promote further growth by making the grains “stickier” in collisions (e.g., Ormel et al. 2009). The size distribution of dust grains is therefore expected to vary from the low-density interstellar medium to the cold, dense environment of cores as the small grains and PAHs (polycyclic aromatic hydrocarbons) disappear and populate the larger grain-size side of the distribution.
The impact of grain growth on star formation is not clear, but there are indications that it may play a part. Larson (2005) suggests that the grain size distribution is not relevant to the control of temperature at the highest densities (>10-18 g cm-3), but that it can be important at intermediate densities where it can still affect the collision rate between the gas and dust. This defines the density at which gas and dust become thermally coupled, which according to the author ultimately determines the characteristic stellar mass. Omukai (2000), on the other hand, suggests that different grain size distributions can produce different minimum temperatures, again influencing the fragmentation properties of the cloud, although, according to Larson (2005), their models produce unrealistically low temperatures considering the radiative heating by ambient far-infrared radiation.
The extinction law is often used as a proxy for the size distribution and composition of dust grains, traditionally in the optical and ultra-violet (e.g., Draine 2011; Savage & Mathis 1979) and more recently also in the near- and mid-infrared. The optical and ultraviolet have been successfully used for decades to study the low-density interstellar medium, revealing an extinction law that can be described as a function of a single parameter, the total-to-selective extinction ratio, RV = AV/E(B − V) (Cardelli et al. 1989; Olofsson & Olofsson 2010). In the near-infrared (NIR) the extinction law is considered invariant and well described by a power law (Aλ ∝ λ− α) of index α in the range 1.6 − 1.85 (Becklin et al. 1978; Cardelli et al. 1989; Clayton & Mathis 1988; Koornneef 1982; Landini et al. 1984; Martin & Whittet 1990; Nishiyama et al. 2006; Olofsson & Olofsson 2010; Rosenthal et al. 2000; Whittet et al. 1988), and in the mid-infrared (MIR, 3−8 μm in this paper), the wavelength range of interest for the present study, the extinction law is not yet well-characterized or understood. Steinacker et al. (2010) propose another tool for probing the grain size distribution of dust using scattering of light rather than absorption. They used the “coreshine” method to infer the presence of large (up to 1 μm) grains in dense molecular cores.
In this paper we compare the infrared extinction law in two dense cores of the Pipe Nebula: FeSt 1-457, which is quiescent, and B59, which contains a small young cluster (Covey et al. 2010; Forbrich et al. 2009). The Pipe Nebula is one of the closest molecular clouds to the Sun (d = 130 pc, Lombardi et al. 2006) and it has been studied extensively over the few past years. The first systematic study of the cloud belongs to Onishi et al. (1999), who present CO observations of a large part of the cloud and estimate the total 12CO mass to be on the order of 104M⊙. Lombardi et al. (2006) refine the distance to the cloud and present a high-resolution extinction map based on 2MASS data covering 8° × 6°, later improved by Román-Zúñiga et al. (2010) using deep infrared data. Alves et al. (2007) identify and characterize 159 cores within the Pipe based on the extinction map, ranging from 3.0 to 24.3 visual magnitudes of extinction, and with corresponding masses between 0.5 to 28 M⊙, and use this information to derive the Pipe’s dense core mass function. Muench et al. (2007) establish most of these cores as actual dense structures, rather than the superposition of less dense material, using observations of the J = 1 − 0 transition of C18O, further analyzing the cores’s kinematical structure. Rathborne et al. (2008) go on to validate the association of the cores with dense gas using molecular line observations of NH3 (1,1), NH3 (2, 2), CCS (21 − 10), and HC5N (9, 8). Using the C18O radio data and the data from the extinction map, Rathborne et al. (2009) produce a refined sample of cores and confirm the previously found core mass function. Frau et al. (2010) and Frau et al. (2012) study the size, density, and chemistry of a few cores in the Pipe using radio data, proposing an evolutionary scenario for the chemistry in the cloud. The magnetic fields of the Pipe were studied by Alves et al. (2008) using optical polarimetry. They divide the cloud in three zones according to the properties of the magnetic field: B59, the densest core in the cloud, the long “stem”, and finally the “bowl”, with the strongest magnetic field (15% polarization). They estimate the mass-to-flux ratio to be approximately supercritical toward B59 and subcritical inside the bowl. Finally, Peretto et al. (2012) and Gritschneder & Lin (2012) address the formation of the cloud based on Herschel data and analytical calculations. The extinction law in the Pipe was first studied in the NIR by Lombardi et al. (2006), who find an average normal extinction law for the whole cloud using 2MASS data. Román-Zúñiga et al. (2007) study the extinction law of the B59 core in particular and find it to be flat in the 3.6 − 8.0 μm regime, while confirming a normal law in the NIR.
In this paper we readdress the extinction law of B59 using the LINES method presented in Ascenso et al. (2012, hereafter referred to as Paper I), and determine the extinction law of another dense core in the Pipe, FeSt 1-457. This core is located in the opposite extreme of the nebula from B59, and has no signs of active star formation. Aguti et al. (2007) suggest the core is gravitationally bound in a quasi-stable state near hydrostatic equilibrium, while the outer layers of the core are proposed to be oscillating.
Studying the extinction law in the context of the dust properties in two cores of the same cloud has the clear advantage that the chemical composition and in general the environment and conditions external to the cloud must be the same. The differences between the two cores can therefore be isolated and studied in detail.
In Sect. 2 we present the data used for this study, and in Sect. 3 we derive the extinction laws. In Sect. 4 we discuss the results in the context of previous studies and models, and we present our conclusions in Sect. 5.
2. Observations
This section describes the data used to derive the extinction law in B59 (J2000, 17h11m21s, − 27°26′10′′) and FeSt 1-457 (J2000, 17h35m47s − 25°33′09′′) in the Pipe Nebula molecular cloud. The data used here will be made available in the context of a forthcoming paper.
2.1. B59
We used the dataset for B59 of Román-Zúñiga et al. (2007). The NIR data were obtained with ESO NTT/SOFI and ESO VLT/ISAAC in the H (1.6 μm) and Ks (2.2 μm) bands. The J band (1.2 μm) was only partially observed, and the catalog was therefore complemented with 2MASS1 data for better coverage. This added 162 sources with respect to the original catalog of Román-Zúñiga et al. (2007). Unfortunately, because 2MASS is too shallow, there are still no sources with J band information in the center of the core.
The MIR (Spitzer/IRAC) dataset was the exact same as in Román-Zúñiga et al. (2007): the publicly available catalog, part of the Cores to Disks Legacy Project (Evans et al. 2003).
2.2. FeSt 1-457
2.2.1. NIR data
The main observations for FeSt 1-457 were made with the ISAAC and the SOFI NIR imagers, mounted, respectively, at the 8.2 m UT3 unit of the ESO/VLT, and at the 3.5 m ESO/NTT. The FeSt 1-457 observing runs were completed in March 1999 (SOFI, program ID 62.I-0866) and July 2000 (ISAAC, program ID 65.I-0083). All the data are currently available in the ESO archives. SOFI has a field of view (FOV) of 5′ × 5′ with plate scale of 0.288 arcsec pixel-1, almost seven times the angular resolution of 2MASS, and higher sensitivity: achieved limits are estimated to be about 4−5 mag deeper than 2MASS in each band. Such characteristics can resolve the densely crowded Galactic bulge field in the background of the Pipe Nebula and penetrate in regions with up to about 50 mag of visual extinction. The field of view of SOFI is wide enough to completely contain some of the larger dense regions in the Pipe Nebula (R ~ 0.1 − 0.15 pc), with the exception of the central core in Barnard 59. The ISAAC observations were intended to fully resolve the centers of the most dense and obscured regions. These observations have a resolution of 0.144 arcsec pixel-1 with a field of view a quarter of the size of that of SOFI.
2.2.2. MIR data
The Spitzer/IRAC2 dataset for FeSt 1-457 is from the Cycle I GTO observations and from the Cycle II GO Pipe Cloud Survey. The data were available in the archive as processed by the Spitzer Science Center team using pipeline version S18.7 that already includes artifact correction. Each field was observed with long (10.4 s) and short (0.4 s) exposure times. The source detection and photometry were done using the MOPEX3 pipeline software APEX multiframe on the artifact-corrected images. The main difficulty in this step was the extreme crowding caused by the position of the Pipe Nebula against the Galactic bulge. The crowding was severe in all fields except toward the very center of the core where the extinction eliminates most of the (background) sources. Apart from the technical problems that arise when the software attempts to fit several point response functions (PRFs) to many “clustered” sources at once, the crowding ultimately produced uncertainties in the photometry of sources with bright neighbors. Unlike the typical photometric error, estimated by the pipeline during the detection and fitting procedure, these errors are difficult to quantify on an individual basis. Since the crowding is a function of wavelength, Channel 1 (3.6 μm) being the most crowded due to its higher sensitivity, these uncertainties will be larger for the shorter wavelength bands. The source extraction and photometry were done independently for the long and short exposures.
Only the objects with the best quality photometry were selected. The quality criteria were a relative flux error below 10%, and a χ2 of the PRF fit per degree of freedom below 25, which ensured a clean sample. After the error cuts, the long and short exposure catalogs for the same channel were merged such that, for the stars common to both, those with the smaller signal-to noise ratio were discarded. The final catalogs for the different channels containing only the sources obeying these criteria were then merged with the NIR data.
2.3. Control field
No dedicated control field was taken for this study. Instead we used an extinction-free nearby field close to the core B72, the same that was used by Román-Zúñiga et al. (2007) in their work. For this field the near-IR observations were from the same ESO/SOFI survey as described in Sect. 2.2.1, and the MIR data were from the Spitzer/IRAC catalog of the Cores to Disk (c2d) Legacy project (Evans et al. 2003). The measured photometric dispersion for background sources is comparable to the uncertainties in the (λ − Ks) colors. This indicates that the intrinsic color dispersion in the Galactic bulge background field of the Pipe Nebula is small enough that our photometric accuracy cannot resolve it. Because these data were not meant as control fields for the present study, they are shallower than the science observations.
3. The extinction law in B59 and FeSt
3.1. LINES determination of Aλ/AKs
 |
Fig. 1 (Ks − λ) vs. (H − Ks) color-color diagrams for B59, for λ = 3.6 μm (top left), λ = 4.5 μm (top right), λ = 5.8 μm (bottom left), and λ = 8.0 μm (bottom right). The solid lines illustrate the reddening vectors for each band: the slopes are the LINES estimates, and the intercepts are such that the lines pass through the median of the distributions. |
Slopes E(Ks − λ)/E(H − Ks) and the extinction law Aλ/AKs as a function of wavelength for B59 and FeSt.
The data described above was used to construct (Ks − λ) vs. (H − Ks) color-color diagrams, where λ is 3.6, 4.5, 5.0 and 8.0 μm for the IRAC bands. Since the observed stars are mostly giants behind the FeSt and B59 cores, their position in the color-color diagrams is dictated by the loci of their intrinsic colors, by their photometric error, that scatters the points randomly in the diagram, and by the extinction caused by the cores, that moves the points along the reddening vector. The latter is the dominant effect, as can be seen in Figs. 1 and 2, and it is the slope β of these vectors in the different color-color diagrams that we wish to measure in order to derive the extinction laws. LINES (LINear regression with Errors and Scatter) has been validated in Paper I as the best and most unbiased method to do this.
The LINES method determines the slope of a linear distribution of points with errors in both directions, possibly correlated, and with an intrinsic distribution that may not itself be linear. In the case of the reddening vector in a color-color diagram, the intrinsic scatter is the locus of the stellar population that is being reddened by the cloud, and we wish to disentangle this scatter from the pure contribution of the extinction. The intrinsic distribution of the points is sampled by a control field expected to sample the same stellar population. As described in Sect. 2.3 our control field was observed with a different setup from the science field, producing a shallower dataset. However, since the background population of the Pipe Nebula is dominated by giant stars which have a very narrow range in infrared colors, the control field, albeit shallow, represents the intrinsic scatter in the science field appropriately.
The slope βλ
(=E(Ks − λ)/E(H − Ks))
of the reddening vector is calculated as 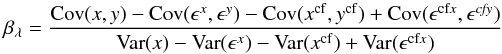 (1)where x and
y are the (H − Ks) and the
(Ks − λ) colors, respectively, and
Cov(x,y),
Cov(ϵx,ϵy),
Var(x), and Var(ϵx) are
the covariance of the (x,y) distribution, the covariance of the
(x,y) errors, the variance of the x distribution, and
the variance of the errors in x, respectively; the symbols marked with
cf are the same but refer to the control field. The uncertainty in
βλ is estimated using the bootstrap method
corrected by a factor of 1.25 as described in detail in Paper I.
(1)where x and
y are the (H − Ks) and the
(Ks − λ) colors, respectively, and
Cov(x,y),
Cov(ϵx,ϵy),
Var(x), and Var(ϵx) are
the covariance of the (x,y) distribution, the covariance of the
(x,y) errors, the variance of the x distribution, and
the variance of the errors in x, respectively; the symbols marked with
cf are the same but refer to the control field. The uncertainty in
βλ is estimated using the bootstrap method
corrected by a factor of 1.25 as described in detail in Paper I.
Figures 1 and 2 show the best LINES fits to the color-color diagrams of B59 and FeSt, respectively. The fit is naturally weighed more heavily toward the low-extinction end, since it contains most of the datapoints. The apparent deviation between the fit line and the data points at high extinction is not considered to be statistically relevant (see Sect. 3.3).
The extinction law
Aλ/AKs
is derived from βλ as 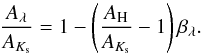 (2)The uncertainty in the ratios
Aλ/AKs
is calculated by error propagation from the uncertainty in
βλ. We assume a ratio
AH/AKs
of 1.55 following Indebetouw et al. (2005) since we
cannot determine it accurately from our data. The choice of this anchor point is crucial
for the comparison between different observations and between observations and models,
since different values will produce different extinction laws. We chose this value over
others in the literature (for example, most recently, Nishiyama et al. (2009) found
AH/AKs = 1.62
toward the Galactic center) because it is the most widely used in previous studies and
therefore allows for the most direct comparison. Also, using this value,
βJ translates into a value of
AJ/AKs
in very close agreement with the models considered here (see Fig. 3). All these models agree on the value of
AJ/AKs
even though they refer to different grain size distributions, so this agreement lends
support to our assumption. Regardless, our results can be easily adapted to another
definition should it prove to be more appropriate (see also Sect. 4.3).
(2)The uncertainty in the ratios
Aλ/AKs
is calculated by error propagation from the uncertainty in
βλ. We assume a ratio
AH/AKs
of 1.55 following Indebetouw et al. (2005) since we
cannot determine it accurately from our data. The choice of this anchor point is crucial
for the comparison between different observations and between observations and models,
since different values will produce different extinction laws. We chose this value over
others in the literature (for example, most recently, Nishiyama et al. (2009) found
AH/AKs = 1.62
toward the Galactic center) because it is the most widely used in previous studies and
therefore allows for the most direct comparison. Also, using this value,
βJ translates into a value of
AJ/AKs
in very close agreement with the models considered here (see Fig. 3). All these models agree on the value of
AJ/AKs
even though they refer to different grain size distributions, so this agreement lends
support to our assumption. Regardless, our results can be easily adapted to another
definition should it prove to be more appropriate (see also Sect. 4.3).
3.2. The extinction law in B59 and FeSt
 |
Fig. 3 Extinction law for FeSt (blue line) and B59 (red line). Also shown are the Draine (2003a,b) models for RV = 3.1 (solid line) and RV = 5.5 (dotted line), and the Weingartner & Draine (2001) models for RV = 5.5, case B (dashed line). |
The derived slopes βλ and the corresponding extinction law Aλ/AKs from 1.2 to 8.0 μm are given in Table 1 for B59 and FeSt, and graphically in Fig. 3. Also shown in the figure are the models from Weingartner & Draine (2001, hereafter referred to as WD01).
In the NIR only the J band relative extinction can be assessed, since AKs/AKs = 1 and we fixed AH/AKs = 1.55 (see Sect. 3.1). Our derived AJ/AKs for both B59 and FeSt are in perfect agreement with the dust grain models, and are also indistinguishable from other measurements in the literature for this wavelength (see Sect. 4.1). This agreement supports our assumption of AH/AKs = 1.55.
 |
Fig. 4 βlow and βhigh for B59 as a function of (H − Ks)limit for each IRAC band, [3.6], [4.5], [5.8], [8.0] from left to right, showing no evidence of a break in the extinction law with column density. The scale of the y-axes is the same for all panels. |
 |
Fig. 5 βlow and βhigh for FeSt as a function of (H − Ks)limit for each IRAC band, [3.6], [4.5], [5.8], [8.0] from left to right, showing no evidence of a break in the extinction law with column density. The scale of the y-axes is the same for all panels. |
 |
Fig. 6 Extinction law for FeSt (blue filled squares) and B59 (red filled squares), in comparison with the extinction laws from the literature, shown for each IRAC band separately for clarity. The scale of the y-axes is the same for all panels. From left to right, Aλ/AKs for the IRAC bands [3.6], [4.5], [5.8], and [8.0] is shown for each reference in the literature. For the works not based on IRAC data the plotted values were the closest match in wavelength. The dark circles refer to extinction laws derived toward lines of sight containing dense regions, the light circles toward the diffuse medium, the open circles toward low (column) density lines of sight in the direction of star forming regions, and the star symbols toward regions dominated by outflows. Also shown are the Aλ/AKs values from the Draine (2003a,b) models for RV = 3.1 (solid line) and RV = 5.5 (dotted line), and the Weingartner & Draine (2001) models for RV = 5.5, case B (dashed line) for the corresponding wavelengths. All extinction laws are normalized to AH/AKs = 1.55. The references are as follows: (1) Lutz (1999); (2) Bertoldi et al. (1999) and Bertoldi et al. (1999); (3–5) Indebetouw et al. (2005) for RCW49; l = 284°; l = 42°; (6–10) Flaherty et al. (2007) for 2024/2023; 2068/2071; Serpens; Orion; Ophiuchus; (11–12) McClure (2009) for AKs < 1 mag; AKs > 1 mag; (13–16) Zasowski et al. (2009) for 10° < |l| < 15°; 30° < |l| < 40°; 50° < |l| < 60°; | l| > 90°; (17) Nishiyama et al. (2009); (18–21) Chapman et al. (2009) for 0 < AKs ≤ 0.5; 0.5 < AKs ≤ 1; 1 < AKs ≤ 2; AKs ≥ 2 mag; (22-25) Chapman & Mundy (2009) for 0 < AKs ≤ 0.5; 0.5 < AKs ≤ 1; AKs > 1 mag; regions with outflows; (26) Gao et al. (2009); (27) Fritz et al. (2011); (28–29) Olofsson & Olofsson (2011) for low and high column densities; (30–31) Cambrésy et al. (2011) for AV < 15 mag; AV > 20 mag; (32–33) This work for B59 and FeSt. |
In the IRAC bands, from 3.6 to 8.0 μm, both cores show a very flat extinction law, in particular flatter than the RV = 5.5 “case B” model of WD01.
3.3. The extinction law as a function of column density
We analyzed the behavior of the extinction law as a function of extinction to see whether we found a change that could be attributed to grain growth at any specific column density threshold. Figures 4 and 5 show that the datapoints at high extinctions depart slightly from the LINES fit, suggesting a change of behavior at some column density. In Paper I we showed that the LINES method is robust enough to detect such a change. Using the (H − Ks) color, we divided the sample in low-extinction ((H − K) less than a value (H − K)limit), and high-extinction ((H − K) > (H − K)limit) subsamples, and determined the best fits to the reddening vector in the two groups using LINES, obtaining two slopes βlow and βhigh for each (H − K)limit. This was done for increasing values of (H − K)limit in steps of 0.1 mag. Figures 4 and 5 show the results for B59 and FeSt, respectively. According to the tests with synthetic data from Paper I, a break in the extinction law would show as a significant difference between the black (low extinction) and the red (high extinction) curves, which is not observed. Based on this analysis we conclude that the departure of the datapoints at high extinction from the LINES fit observed in the color-color diagrams is not statistically significant. We do not find any change of the extinction law with column density for either core.
4. Discussion
4.1. Comparison with previous work: a universal MIR extinction law?
In the NIR the extinction law is well described by a power law (Aλ ∝ λ−α) with indexes tightly ranging from 1.6 to 1.85. This constancy has led authors to use the NIR as anchor to normalize the extinction law in the MIR. Although early studies reported that the MIR extinction law continued as a power law from the NIR (Landini et al. 1984; Martin & Whittet 1990; Whittet et al. 1988), most recent studies find that it departs from the power law around 3 μm and becomes flat (also referred to as gray) at least until the silicate feature around 9.7 μm.
Figure 6 summarizes the extinction laws determined by previous works, and shows that most regions have flat extinction laws. Each panel shows Aλ/AKs for each of the IRAC bands ([3.6], [4.5], [5.8], and [8.0]) as a function of the corresponding reference in the literature. For the same reference, a gray or flat extinction law will show approximately the same value in all panels, whereas an extrapolation of the NIR power law will show as a decrease from the left- to the right-hand panels. Lutz et al. (1996) and Lutz (1999, Ref. #1) first found a flat MIR extinction law toward the Galactic center using spectroscopy of hydrogen recombination lines. Viehmann et al. (2005) later measured a consistently flat extinction at 4.66 μm toward the same region, and Nishiyama et al. (2009, Ref. #17) and Fritz et al. (2011, Ref. #27) independently confirmed a flat MIR extinction law toward that line of sight. Based on Spitzer photometry, Indebetouw et al. (2005) found a flat MIR extinction law toward other lines of sight crossing both dense (Ref. #3) and diffuse (Ref. #4–5) media. A number of other studies using Spitzer followed, namely Flaherty et al. (2007, Ref. #6–10), Chapman et al. (2009, Ref. #18–21) and McClure (2009, Ref. #11−, who found gray extinction laws for star forming regions and molecular clouds, and Román-Zúñiga et al. (2007), Chapman & Mundy (2009, Ref. #22–25) and Olofsson & Olofsson (2011, Ref. #28), who found gray extinction laws for cloud cores. Specifically targeting low density lines of sight, Zasowski et al. (2009, Ref. #14–16) found flat MIR extinction laws over a very wide portion of the Galactic midplane. The extinction laws of FeSt (red, Ref. #32) and B59 (blue filled circles, Ref. #33) follow the same flat trend in the IRAC bands. The column densities probed by our data (AV up to 50 mag) are among the highest ever studied in this context, and correspond to high local volume densities as attested by the presence of high-density tracer molecules (Frau et al. 2010, 2012; Rathborne et al. 2008). Still, despite the difference in density, the extinction laws of these cores are unremarkable with respect to less dense environments.
Some authors (Chapman et al. (2009, Ref. #18–21), McClure (2009, Ref. #11–12), Olofsson & Olofsson (2011, Ref. #28−, and Cambrésy et al. (2011, Ref. #30–31)) surveyed lines of sight of different column densities within single regions and found a slight flattening trend toward higher densities, but only the first find significantly steep laws in absolute terms. In contrast, other studies have looked for but failed to find any significant variation of the extinction law with increasing density (Chapman & Mundy 2009, Ref #22–24), as do we for B59 and FeSt (Sect. 3.3), even though we probe a large range in extinction.
There are only three exceptions in the recent literature where the observed MIR extinction laws are steep enough to follow the power-law extrapolation from the NIR: Chapman et al. (2009, Ref. # 18), toward the low column density (AKs < 0.5 mag) regions of Perseus, Ophiuchus and Serpens; Bertoldi et al. (1999) and Rosenthal et al. (2000, Ref. #2), toward the outflow region of the Orion OMC-1; and Chapman & Mundy (2009, Ref. #25), also in the direction of outflows. These differences are interesting and require further study but represent a small minority of the studies in the literature.
From the data collected so far, there is no clear indication that the MIR extinction law varies notably from region to region, or that it varies as a function of density, since diffuse and dense regions alike show flat extinction laws. The MIR extinction law does not seem to depend (uniquely) on density, at least within the (column) density regimes probed by current observations.
4.2. Comparison with models: implications for grain sizes
As mentioned briefly in the Introduction, the extinction can be used to study the grain size distribution of the interstellar dust. The extinction law in the optical and ultraviolet has been reported to change from region to region, presumably due to the size distribution of the grains causing the extinction (e.g., Savage & Mathis 1979; Whittet 2003), with a correlation between larger grains and higher densities4 interpreted as evidence of grain growth (Cardelli et al. 1989). The extinction law at these wavelengths is however only sensitive to grain sizes less than ~0.2 μm (Draine 2011). To probe the size distribution of larger grains, the infrared extinction law must be used instead.
The observed flat MIR extinction laws are best described by the case B, RV of 5.5 model of Weingartner & Draine (2001). Case B refers to a grain size distribution that includes a significant fraction of large (up to 10 μm) grains, whereas their case A model includes grains with maximum sizes of ~1 μm and produces a steep MIR extinction law5. Therefore, flat extinction laws are believed to be produced by dust containing significant fractions of large grains. Figure 6 shows that the case B, RV of 5.5 model of WD01 adequately describes the observed extinction laws at 3.6 μm and 4.5 μm but that it does not produce a gray enough extinction law to match most observations at 5.8 μm and 8.0 μm. Since most of these observations are based on broad-band data, this may indicate that there are narrow, unresolved emission features contributing to the extinction law at these wavelengths. Alternatively, it may mean that the grain size distribution corresponding to these models still does not contain enough large grains, or large enough grains to explain the observations.
As mentioned before, grains are believed to grow at the high densities and low temperatures of shielded molecular clouds, where the formation of ice mantles and grain-grain collisions are most favored. However, observations show that the extinction law is not (uniquely) dependent on density (see Fig. 6 and Sect. 4.1), so either other factors determine the shape of the MIR extinction law, or large grains can form and exist at relatively low densities. Even though the case A, RV = 3.1 model of WD01 (later renormalized by Draine 2003a,b) without large grains has been considered to be the appropriate model for the diffuse interstellar medium, it is actually hardly ever observed in the MIR.
The extinction laws of B59 and FeSt are also comparable to, and actually flatter than the case B, RV = 5.5 model of WD01 (Fig. 3), suggesting that these cores contain a significant fraction of large grains if the models are taken at face value. Unlike Cambrésy et al. (2011), who find a flattening of the extinction law at a threahold of AV = 20 mag, we do not find any such change in the extinction laws of B59 or FeSt (Sect. 3.3) even though our data cover a large enough range of extinction and our method has been shown to be able to detect it (Paper I), further suggesting that large grains are present already in the low-density edges of these cores. However, this is somewhat inconsistent with the results of Aguti et al. (2007), who find depletion of C18O toward FeSt at relatively low extinctions (AV = 12 mag). If the accretion of ice mantles by grains as molecular species condense onto their surfaces increases their sizes and promotes their growth, the depletion of molecules should be regarded as indirect evidence of grain growth. For completeness, Frau et al. (2012) suggest that there is no depletion in B59, although their arguments are solely based on a high abundance of CS6.
It is clear from this study and from the literature that we still do not have a consistent understanding of the extinction law and/or of the dust grain properties in the different environments.
4.3. Comparison between the two cores
In detail, the MIR extinction laws of FeSt and B59 are not identical: the extinction law of FeSt is grayer than that of B59 at the 5- to 12-σ level depending on the wavelength. This is true as long as our assumption that the NIR extinction law is the same for the two lines of sight applies. When converting the reddening laws (the color excess ratios βλ, Sect. 3.1) to extinction laws (Aλ/AKs), we assumed AH/AKs = 1.55 following Indebetouw et al. (2005), which corresponds to a NIR extinction law being a power law with index 1.65 (Aλ ∝ λ-1.65). This value is adopted by many studies of the extinction law as universal but in fact different values have been measured toward different lines of sight. The values in the literature range between 1.85 and 1.65 (see references in the Introduction), and there is no understanding of how it changes from region to region. It is therefore possible that B59 and FeSt have different extinction laws in the NIR. In particular, if the index of the NIR extinction law for FeSt is the adopted 1.65, but that for B59 is instead 1.90, the two extinction laws are indistinguishable within the errors. However, as mentioned in Sect. 3.2, we measure very similar AJ/AKs values for the two cores, supporting the assumption of similar NIR extinction laws for the two cores. In the following we take this assumption as correct and discuss the implications of the MIR extinction laws for the two cores being different, as shown in Fig. 3.
We also assume, for the sake of argument and based on the models of WD01, Draine (2003a) and Draine (2003b), that the flatter the extinction law, the larger the grains causing the extinction. In this context, FeSt should have larger grains (or a larger fraction of large grains) than B59, since it has the flattest extinction law. The depletion of C18O at relatively low extinctions observed in FeSt in contrast to the lack of depletion in B59 further suports the presence of larger grains in FeSt.
Why are the grains smaller in B59 than in FeSt? Since the two cores belong to the same cloud it is reasonable to assume that they have the same chemical composition, so we do not expect that different metallicities are the source of the different extinction laws. Our data probe approximately the same range of column densities for both lines of sight, and both FeSt and B59 are dense cores, so the column density is likely to represent approximately the same physical density. If this is the case, then the difference in grain size distribution for the two cores cannot be explained by density arguments either. If density is not the dominant factor, it may be that the different internal conditions of FeSt and B59 are causing the difference in extinction laws. In fact, the most obvious difference between the two cores is that FeSt is quiescent, whereas B59 contains ~20 young stellar objects (Brooke et al. 2007; Covey et al. 2010; Forbrich et al. 2009) and at least two molecular outflows (Duarte-Cabral et al. 2012; Onishi et al. 1999; Riaz et al. 2009; Román-Zúñiga et al. 2010). The young stars necessarily increase the temperature of the core, at least locally, and their winds and outflows inject mechanical energy and turbulence into the intra-core medium. It would therefore not be unexpected that the newly formed stars have some bearing in the reprocessing of the dust grains. If star formation is instrumental in the destruction of large grains, then the extinction law in B59 would be steeper than that of FeSt, as is observed. This would be consistent with the other observation of steep extinction laws toward other, more exposed outflow regions (Bertoldi et al. 1999; Chapman & Mundy 2009; Rosenthal et al. 2000).
We note that Alves et al. (2008) find a magnetic field strength toward FeSt around 65 μG, almost 4 times higher than that toward B59, corresponding to degrees of polarization reaching 15% in the region of FeSt and around 1% for B59. However, the strength of the magnetic field is related to the alignment of the grains, and therefore is not very revealing to the understanding of the grain size distribution. Also, since this study was done with R-band observations, it characterizes the magnetic field of the lower-density regions (AV < 5 mag) of the cloud, so the ambient magnetic field instead of that of the cores
5. Conclusions
We applied the unbiased LINES method (Ascenso et al. 2012) to determine the extinction law from photometric data from 1.2 to 8.0 μm toward the two densest cores in the Pipe Nebula, B59 and FeSt 1-457.
We find a flat or gray extinction law for both cores. The comparison with models suggests that the dust in these cores contains a significant fraction of large grains. Despite the wide range of column density probed in this study (up to 50 mag of visual extinction) with respect to most previous studies, the extinction laws we derive are not remarkably different from others toward other lines of sight. In particular a review of the literature indicates that the MIR extinction law is gray already at low column densities, suggesting that either large grains are present in low column density regions and in the diffuse medium, or that the existing dust models need to be revised at MIR wavelengths. The implications for the theories of grain growth, that generally require high densities for the formation of large grains, are not discussed in this paper but should be addressed appropriately in the future.
Although the extinction laws are gray for the two cores, that of FeSt is grayer than that of B59. Taken at face value this suggests that FeSt has larger grains, or a larger fraction of large grains, than does B59. We hypothesize that this reflects the internal differences in the two cores, in particular with the presence of young stars and outflows in B59 and lack thereof in FeSt. We propose that the grains have already started to be reprocessed in B59 by the increase in temperature and turbulence caused by the young stars.
We find no evidence of a flattening of the extinction law as a function of column density, and conclude that the low-density (AV ≲ 10 mag) edges of the cores already contain large grains.
Acknowledgments
The authors thank D. Lutz and N. Chapman for kindly providing the electronic versions of their extinction laws. The research leading to these results has received funding from the European Community’s Seventh Framework Programme (/FP7/2007-2013/) under grant agreement No. 229517. Support for this work was also provided by NASA through an award issued by JPL/Caltech, contract 1279166. CRZ acknowledges support from Program CONACYT 152160, México.
References
- Aguti, E. D., Lada, C. J., Bergin, E. A., Alves, J. F., & Birkinshaw, M. 2007, ApJ, 665, 457 [NASA ADS] [CrossRef] [Google Scholar]
- Alves, J., Lombardi, M., & Lada, C. J. 2007, A&A, 462, L17 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Alves, F. O., Franco, G. A. P., & Girart, J. M. 2008, A&A, 486, L13 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ascenso, J., Lombardi, M., Lada, C. J., & Alves, J. 2012, A&A, 540, A139 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Becklin, E. E., Neugebauer, G., Willner, S. P., & Matthews, K. 1978, ApJ, 220, 831 [NASA ADS] [CrossRef] [Google Scholar]
- Bertoldi, F., Timmermann, R., Rosenthal, D., Drapatz, S., & Wright, C. M. 1999, ApJ, 346, 267 [Google Scholar]
- Brooke, T. Y., Huard, T. L., Bourke, T. L., et al. 2007, ApJ, 655, 364 [NASA ADS] [CrossRef] [Google Scholar]
- Cambrésy, L., Rho, J., Marshall, D. J., & Reach, W. T. 2011, A&A, 527, A141 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Cardelli, J. A., Clayton, G. C., & Mathis, J. S. 1989, ApJ, 345, 245 [NASA ADS] [CrossRef] [Google Scholar]
- Chapman, N. L., & Mundy, L. G. 2009, ApJ, 699, 1866 [NASA ADS] [CrossRef] [Google Scholar]
- Chapman, N. L., Mundy, L. G., Lai, S., & Evans, N. J. 2009, ApJ, 690, 496 [NASA ADS] [CrossRef] [Google Scholar]
- Clayton, G. C., & Mathis, J. S. 1988, ApJ, 327, 911 [NASA ADS] [CrossRef] [Google Scholar]
- Covey, K. R., Lada, C. J., Román-Zúñiga, C., et al. 2010, ApJ, 722, 971 [NASA ADS] [CrossRef] [Google Scholar]
- Draine, B. T. 1985, in Protostars and Planets II, eds. D. C. Black, & M. S. Matthews, 621 [Google Scholar]
- Draine, B. T. 2003a, ApJ, 598, 1017 [NASA ADS] [CrossRef] [Google Scholar]
- Draine, B. T. 2003b, ApJ, 598, 1026 [NASA ADS] [CrossRef] [Google Scholar]
- Draine, B. T. 2011, Physics of the Interstellar and Intergalactic Medium [Google Scholar]
- Duarte-Cabral, A., Chrysostomou, A., Peretto, N., et al. 2012, A&A, 543, A140 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Evans, II, N. J., Allen, L. E., Blake, G. A., et al. 2003, PASP, 115, 965 [NASA ADS] [CrossRef] [Google Scholar]
- Flaherty, K. M., Pipher, J. L., Megeath, S. T., et al. 2007, ApJ, 663, 1069 [CrossRef] [Google Scholar]
- Forbrich, J., Lada, C. J., Muench, A. A., Alves, J., & Lombardi, M. 2009, ApJ, 704, 292 [NASA ADS] [CrossRef] [Google Scholar]
- Frau, P., Girart, J. M., Beltrán, M. T., et al. 2010, ApJ, 723, 1665 [NASA ADS] [CrossRef] [Google Scholar]
- Frau, P., Girart, J. M., Beltrán, M. T., et al. 2012, ApJ, 759, 3 [NASA ADS] [CrossRef] [Google Scholar]
- Fritz, T. K., Gillessen, S., Dodds-Eden, K., et al. 2011, ApJ, 737, 73 [NASA ADS] [CrossRef] [Google Scholar]
- Gao, J., Jiang, B. W., & Li, A. 2009, ApJ, 707, 89 [NASA ADS] [CrossRef] [Google Scholar]
- Gritschneder, M., & Lin, D. N. C. 2012, ApJ, 754, L13 [NASA ADS] [CrossRef] [Google Scholar]
- Indebetouw, R., Mathis, J. S., Babler, B. L., et al. 2005, ApJ, 619, 931 [NASA ADS] [CrossRef] [Google Scholar]
- Koornneef, J. 1982, ApJ, 107, 247 [Google Scholar]
- Landini, M., Natta, A., Salinari, P., Oliva, E., & Moorwood, A. F. M. 1984, ApJ, 134, 284 [Google Scholar]
- Larson, R. B. 2005, MNRAS, 359, 211 [NASA ADS] [CrossRef] [Google Scholar]
- Lombardi, M., Alves, J., & Lada, C. J. 2006, A&A, 454, 781 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lutz, D. 1999, in The Universe as Seen by ISO, eds. P. Cox, & M. Kessler, ESA SP, 427, 623 [Google Scholar]
- Lutz, D., Feuchtgruber, H., Genzel, R., et al. 1996, A&A, 315, L269 [NASA ADS] [Google Scholar]
- Martin, P. G., & Whittet, D. C. B. 1990, ApJ, 357, 113 [NASA ADS] [CrossRef] [Google Scholar]
- McClure, M. 2009, ApJ, 693, L81 [NASA ADS] [CrossRef] [Google Scholar]
- Muench, A. A., Lada, C. J., Rathborne, J. M., Alves, J. F., & Lombardi, M. 2007, ApJ, 671, 1820 [NASA ADS] [CrossRef] [Google Scholar]
- Nishiyama, S., Nagata, T., Kusakabe, N., et al. 2006, ApJ, 638, 839 [NASA ADS] [CrossRef] [Google Scholar]
- Nishiyama, S., Tamura, M., Hatano, H., et al. 2009, ApJ, 696, 1407 [NASA ADS] [CrossRef] [Google Scholar]
- Olofsson, S., & Olofsson, G. 2010, A&A, 522, A84 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Olofsson, S., & Olofsson, G. 2011, A&A, 534, A127 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Omukai, K. 2000, ApJ, 534, 809 [NASA ADS] [CrossRef] [Google Scholar]
- Onishi, T., Kawamura, A., Abe, R., et al. 1999, PASJ, 51, 871 [Google Scholar]
- Ormel, C. W., Paszun, D., Dominik, C., & Tielens, A. G. G. M. 2009, A&A, 502, 845 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ossenkopf, V. 1993, A&A, 280, 617 [NASA ADS] [Google Scholar]
- Peretto, N., André, P., Könyves, V., et al. 2012, A&A, 541, A63 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Rathborne, J. M., Lada, C. J., Muench, A. A., Alves, J. F., & Lombardi, M. 2008, ApJS, 174, 396 [NASA ADS] [CrossRef] [Google Scholar]
- Rathborne, J. M., Lada, C. J., Muench, A. A., et al. 2009, ApJ, 699, 742 [NASA ADS] [CrossRef] [Google Scholar]
- Riaz, B., Martin, E. L., Bouy, H., & Tata, R. 2009, ApJ, 700, 1541 [NASA ADS] [CrossRef] [Google Scholar]
- Román-Zúñiga, C. G., Lada, C. J., Muench, A., & Alves, J. F. 2007, ApJ, 664, 357 [NASA ADS] [CrossRef] [Google Scholar]
- Román-Zúñiga, C. G., Alves, J. F., Lada, C. J., & Lombardi, M. 2010, ApJ, 725, 2232 [NASA ADS] [CrossRef] [Google Scholar]
- Rosenthal, D., Bertoldi, F., & Drapatz, S. 2000, A&A, 356, 705 [NASA ADS] [Google Scholar]
- Savage, B. D., & Mathis, J. S. 1979, ARA&A, 17, 73 [NASA ADS] [CrossRef] [Google Scholar]
- Steinacker, J., Pagani, L., Bacmann, A., & Guieu, S. 2010, A&A, 511, A9 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Viehmann, T., Eckart, A., Sch del, R., et al. 2005, ApJ, 433, 117 [Google Scholar]
- Weingartner, J. C., & Draine, B. T. 2001, ApJ, 548, 296 [NASA ADS] [CrossRef] [Google Scholar]
- Whittet, D. C. B. 2003, Dust in the galactic environment [Google Scholar]
- Whittet, D. C. B., Bode, M. F., Longmore, A. J., et al. 1988, MNRAS, 233, 321 [NASA ADS] [CrossRef] [Google Scholar]
- Whitworth, A. P., Boffin, H. M. J., & Francis, N. 1998, MNRAS, 299, 554 [NASA ADS] [CrossRef] [Google Scholar]
- Zasowski, G., Majewski, S. R., Indebetouw, R., et al. 2009, ApJ, 707, 510 [NASA ADS] [CrossRef] [Google Scholar]
All Tables
Slopes E(Ks − λ)/E(H − Ks) and the extinction law Aλ/AKs as a function of wavelength for B59 and FeSt.
All Figures
 |
Fig. 1 (Ks − λ) vs. (H − Ks) color-color diagrams for B59, for λ = 3.6 μm (top left), λ = 4.5 μm (top right), λ = 5.8 μm (bottom left), and λ = 8.0 μm (bottom right). The solid lines illustrate the reddening vectors for each band: the slopes are the LINES estimates, and the intercepts are such that the lines pass through the median of the distributions. |
| In the text | |
 |
Fig. 2 Same as Fig. 1 but for FeSt. |
| In the text | |
 |
Fig. 3 Extinction law for FeSt (blue line) and B59 (red line). Also shown are the Draine (2003a,b) models for RV = 3.1 (solid line) and RV = 5.5 (dotted line), and the Weingartner & Draine (2001) models for RV = 5.5, case B (dashed line). |
| In the text | |
 |
Fig. 4 βlow and βhigh for B59 as a function of (H − Ks)limit for each IRAC band, [3.6], [4.5], [5.8], [8.0] from left to right, showing no evidence of a break in the extinction law with column density. The scale of the y-axes is the same for all panels. |
| In the text | |
 |
Fig. 5 βlow and βhigh for FeSt as a function of (H − Ks)limit for each IRAC band, [3.6], [4.5], [5.8], [8.0] from left to right, showing no evidence of a break in the extinction law with column density. The scale of the y-axes is the same for all panels. |
| In the text | |
 |
Fig. 6 Extinction law for FeSt (blue filled squares) and B59 (red filled squares), in comparison with the extinction laws from the literature, shown for each IRAC band separately for clarity. The scale of the y-axes is the same for all panels. From left to right, Aλ/AKs for the IRAC bands [3.6], [4.5], [5.8], and [8.0] is shown for each reference in the literature. For the works not based on IRAC data the plotted values were the closest match in wavelength. The dark circles refer to extinction laws derived toward lines of sight containing dense regions, the light circles toward the diffuse medium, the open circles toward low (column) density lines of sight in the direction of star forming regions, and the star symbols toward regions dominated by outflows. Also shown are the Aλ/AKs values from the Draine (2003a,b) models for RV = 3.1 (solid line) and RV = 5.5 (dotted line), and the Weingartner & Draine (2001) models for RV = 5.5, case B (dashed line) for the corresponding wavelengths. All extinction laws are normalized to AH/AKs = 1.55. The references are as follows: (1) Lutz (1999); (2) Bertoldi et al. (1999) and Bertoldi et al. (1999); (3–5) Indebetouw et al. (2005) for RCW49; l = 284°; l = 42°; (6–10) Flaherty et al. (2007) for 2024/2023; 2068/2071; Serpens; Orion; Ophiuchus; (11–12) McClure (2009) for AKs < 1 mag; AKs > 1 mag; (13–16) Zasowski et al. (2009) for 10° < |l| < 15°; 30° < |l| < 40°; 50° < |l| < 60°; | l| > 90°; (17) Nishiyama et al. (2009); (18–21) Chapman et al. (2009) for 0 < AKs ≤ 0.5; 0.5 < AKs ≤ 1; 1 < AKs ≤ 2; AKs ≥ 2 mag; (22-25) Chapman & Mundy (2009) for 0 < AKs ≤ 0.5; 0.5 < AKs ≤ 1; AKs > 1 mag; regions with outflows; (26) Gao et al. (2009); (27) Fritz et al. (2011); (28–29) Olofsson & Olofsson (2011) for low and high column densities; (30–31) Cambrésy et al. (2011) for AV < 15 mag; AV > 20 mag; (32–33) This work for B59 and FeSt. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


