| Issue |
A&A
Volume 549, January 2013
|
|
|---|---|---|
| Article Number | A77 | |
| Number of page(s) | 12 | |
| Section | Stellar structure and evolution | |
| DOI | https://doi.org/10.1051/0004-6361/201220099 | |
| Published online | 21 December 2012 | |
The accretion disk in the post period-minimum cataclysmic variable SDSS J080434.20 + 510349.2⋆
Instituto de Astronomía, Universidad Nacional Autonoma de Mexico, Apdo. Postal 877, Ensenada, Baja California, 22800 Mexico, Mexico
e-mail: zhar@astrosen.unam.mx
Received: 24 July 2012
Accepted: 27 October 2012
Aims. This study of SDSS J080434.20+510349.2 is primarily concerned with the double-hump shape in the light curve and its connection with the accretion disk in this bounce-back system.
Methods. Time-resolved photometric and spectroscopic observations were obtained to analyze the behavior of the system between superoutbursts. A qualitative geometric model of a binary system containing a disk with two outer annuli spiral density waves was applied to explain the light curve and the Doppler tomography.
Results. Observations were carried out during 2008−2009, after the object’s magnitude decreased to V ~ 17.7 ± 0.1 from the March 2006 eruption. The light curve clearly shows a sinusoid-like variability with a 0.07 mag amplitude and a 42.48 min periodicity, which is half of the orbital period of the system. In September 2010, the system underwent yet another superoutburst and returned to its quiescent level by the beginning of 2012. This light curve once again showed a double-hump-shape, but with a significantly smaller (~0.01 mag) amplitude. Other types of variability like a “mini-outburst” or SDSS1238-like features were not detected. Doppler tomograms, obtained from spectroscopic data during the same period of time, show a large accretion disk with uneven brightness, implying the presence of spiral waves.
Conclusions. We constructed a geometric model of a bounce-back system containing two spiral density waves in the outer annuli of the disk to reproduce the observed light curves. The Doppler tomograms and the double-hump-shape light curves in quiescence can be explained by a model system containing a massive ≥0.7 M⊙ white dwarf with a surface temperature of ~12 000 K, a late-type brown dwarf, and an accretion disk with two outer annuli spirals. According to this model, the accretion disk should be large, extending to the 2:1 resonance radius, and cool (~2500 K). The inner parts of the disk should be optically thin in the continuum or totally void.
Key words: novae, cataclysmic variables / stars: dwarf novae / stars: individual: SDSS J080434.20+510349.2
Photometry and reduced spectra are only available at the CDS via anonymous ftp to cdsarc.u-strasbg.fr (130.79.128.5) or via http://cdsarc.u-strasbg.fr/viz-bin/qcat?J/A+A/549/A77
© ESO, 2012
1. Introduction
A widely accepted evolutionary theory of cataclysmic variables (CVs), as presented in Kolb & Baraffe (1999, and references therein), predicts a significant accumulation of systems around the orbital period minimum (Paczynski 1981). It also envisions that ~70% of the current CV population has evolved past the orbital period minimum and formed so-called bounce-back systems that contain a brown dwarf as a secondary (Patterson 2011). According to the calculations, the orbital period of a bounce-back system should be slightly longer than before reaching the period minimum. Bounce-back systems are expected to float within the 80–90 min orbital period range. However, neither a peak in the period distribution nor any past period-minimum systems were observed prior to the Sloan Digital Sky Serve (SDSS). The SDSS has identified more than a hundred new faint CV systems with accurately measured orbital periods (Gänsicke et al. 2009). A significant portion of the new CVs have periods clustered at the lower end of the orbital period distribution and some of them are good bounce-back system candidates. SDSS J103533.03+055158.4 (hereafter SDSS1035) was proposed by Littlefair et al. (2008) as a solid example of a bounce-back system based upon the system parameters found using a parametrized model of an eclipse observed in its light curve. Aviles et al. (2010) included SDSS J123813.73-033933.0 (hereafter SDSS1238) in the list of bounce-back CVs using a direct IR broad band photometry of the secondary and modeling the spectral energy distribution of the system.
The subject of this paper is SDSS J080434.20+510349.2 (hereafter SDSS0804), which has a very peculiar light curve (Szkody et al. 2006). A similar light curve has only been observed in one other system of SDSS1238. Hence, SDSS0804 is considered a twin to SDSS1238. Since its discovery, SDSS0804 underwent two superoutbursts, confirming its membership as a WZ Sge-type. Zharikov et al. (2008) included it in the list of bounce-back candidates based upon its orbital period and mass ratio estimates. SDSS0804 exhibits some phenomena (“brightenings” and “mini-outbursts”) that are not common in other CVs (Zharikov et al. 2008). Its superoutburst in September 2010 (Pavlenko et al. 2012), which was only about four years after the previous superoutburst, was unexpected. A general description of the characteristics and observational features of SDSS0804 can be found in Szkody et al. (2006), Pavlenko et al. (2007), Zharikov et al. (2008), Kato et al. (2009), and Pavlenko et al. (2012).
In this paper we report the results of monitoring SDSS0804 in 2008–2009 and 2012, during periods when the object almost retuned to its pre-superoutburst, quiescent level. The main aim of this study is to investigate the system’s behavior to determine the structure of the accretion disk during the quiescence.
In Sect. 2, we describe our observations and the data reduction. The light curve analysis and results of infrared and spectral observations are presented in Sects. 3 and 4. A discussion of the accretion disk structure of this bounce-back system is given in Sects. 6 and 7. The light curve simulation of bounce-back systems is described in Sect. 8, and our conclusions are given in Sect. 9.
Log of the time-resolved photometric observations of SDSS J080434.20+510349.2.
2. Observations and data reduction
Time-resolved photometry of SDSS 0804 was obtained using the direct CCD image mode at the 1.5 m and 0.84 m telescopes of the Observatorio Astronómico Nacional at San Pedro Mártir (OAN SPM1) in Mexico. The log of photometric observations is given in Table 1. Photometric data were calibrated using Landolt’s standard stars. The errors of photometry were calculated from the dispersion of the magnitude of the comparison stars in the object field. The errors ranged from 0.01 to 0.05 mag.
Log of the time-resolved spectroscopic observations of SDSS J080434.20+510349.2.
 |
Fig. 1 Light curves of SDSS0804 are shown from 2005 to 2012 in the V band. The plot is based on a combination of data obtained by us, including those published in Zharikov et al. (2008), and data accumulated by the AAVSO. |
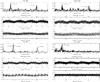 |
Fig. 2 Power spectra (top panel) of SDSS0804 is shown for different observational runs; the corresponding light curves are folded with the orbital period (upper axis of the middle panels). The half orbital period (bottom axis of the middle panels) and the 12.6 min period (lower panels) are also shown. |
Long-slit observations were obtained with the Boller & Chivens spectrograph and the 2.1-m telescope of OAN SPM. The spectra span from 4000 to 7100 Å with a resolution of 3.03 Å pixel-1. To improve the signal-to-noise ratio, we obtained a series of phase-locked spectra: ten spectra were taken at equal phase intervals over a single orbital period (Porb = 80.5 min). This sequence of spectra was repeated at exactly the same phase intervals for subsequent periods and on subsequent nights. This allowed us to calculate the phase-averaged spectra by summing up spectra at the same orbital phase obtained during several cycles without decreasing the time resolution. The log of the spectral observations is given in Table 2. There is a small difference in the exposure times at different epochs because different CCDs were used, and each CCD has its own readout time.
The J band photometry of SDSS0804 was obtained in October 2009 with the “CAMILA” IR CCD camera attached to the 0.84 m telescope of OAN SPM. The data were reduced by the standard way and were calibrated using IR standards observed before and after the object.
3. Light curve variability
The light curve of SDSS0804 during 2005–2012 is shown in Fig. 1. Before the March 2006 superoutburst the brightness of the system was V ~ 17.9 and the object displayed SDSS1238-like long-term variability (Szkody et al. 2006; Zharikov et al. 2006, 2008). On March 4, 2006, a superoutburst commenced, exhibiting all attributes of WZ Sge-type: a large amplitude >6 mag, superhumps, and 11 echoes (Pavlenko et al. 2006). The maximum brightness during the superoutburst reached about V ~ 12 mag. Based upon the superhump period (Kato et al. 2009), the mass ratio of the system was estimated to be q ≈ 0.05 (Zharikov et al. 2008), which is a typical value for bounce-back systems.
About eight months after the first superoutburst, the brightness decreased to 17.1 mag. Variability at different time-scales was detected: a rapid modulation with a period of P1 = 12.6 min and amplitude of ~0.05 mag was interpreted as a strong nonradial pulsation of the cooling (i.e., after the outburst) white dwarf, that entered the instability strip (Pavlenko et al. 2006); significant short-term variations with periods P2 = 21.7 min, P3 = 14.1 min, and P4 = 4.28 min that may be additional pulsation modes (Pavlenko et al. 2012); and the superhumps were replaced with orbital double-hump-shape light variations (Zharikov et al. 2008; Pavlenko et al. 2007). In addition to these, the object also showed a new phenomenon – recurring (~32 day) “mini-outbursts” that lasted approximately four days and increased the brightness to up to ~0.6 mag (Zharikov et al. 2008).
Given the diversity of the variability displayed by SDSS0804 , we continued monitoring the system with an aim to find any systematics in its behavior. In the three years after the 2006 superoutburst, the V-band magnitude of the object decreased to about 17.7 mag. However, the object never reached the pre-superoutburst level of March 2006 because in September 2010 SDSS0804 suddenly underwent another superoutburst (Pavlenko et al. 2012), only ~4.5 years after the previous one. This short recess between superoutbursts is atypical for WZ Sge-type systems. The amplitude of this superoutburst was similar to the previous, but the shape of the light curve was different: the brightness decreased faster and fewer echoes were detected (Pavlenko et al. 2012). By December 2011, more than a year after this superoutburst, the brightness of the system fell practically to the quiescence level. From December 2011 to January 2012 we obtained a new set of photometric and spectroscopic data at quiescence to compare with our previous observations.
The photometric data were analyzed for periodicities using a discrete Fourier transformation code (Deeming 1975). The power spectra for different observational runs are given in Figs. 2 and 3. The power spectra clearly show double orbital frequency in all observational runs. The amplitude of the double-hump-shape light curve decreases with brightness (from ~0.07 mag at HJD 2 454 110, ~0.02 mag at HJD 245 456 to only ~0.01 at HJD 2 455 953). The 12.6 min period, attributed to WD pulsations, was only detected in the February–March 2008 and January 2009 runs. This period disappeared afterwards (Figs. 2 and 3). The light curves folded by the 42.5 min and 12.6 min periods are shown along with their corresponding power spectra in Figs. 2 and 3. The long-term SDSS1238-like variability and mini-outburst phenomena were not detected during our monitoring of the system between superoutbursts and after the last superoutburst (HJD 2 454 500–HJD 2 456 000).
4. Infrared data
Kato et al. (2009) performed infrared photometry of SDSS0804 using OAO/ISLE in March 2007, about one year after the superoutburst. The IR magnitudes were estimated to be J = 17.29(5), H = 16.97(5), and K = 16.41(6). During these observations the object was ~17.1 in the visual band, about 0.7–0.8 mag above the pre-outburst quiescence level. Our IR observations were made in the J band in October, 2009. The object magnitudes was J = 17.3(1) (see Fig. 4). Hence, the object did not change significantly in the J band although it was still cooling and becoming fainter in the optical. We assume that the brightness of the object in the IR, as measured by Kato et al. (2009), corresponds to the quiescence state. On timescales comparable to the orbital period, the system is expected to show some variability in the near-IR due to the elliptical shape of the Roche-lobe-filling secondary. The ellipsoidal variability of the secondary can be calculated and it has been taken into account as an additional error of about 0.15 mag in the following considerations of spectral energy distribution.
5. Spectral energy distribution
The optical spectrum of SDSS0804 shows a blue continuum with broad absorption lines (caused by the white dwarf) that surrounds the double-peaked Balmer emission lines (caused by the accretion disk). The spectrum undergoes some changes throughout the outburst cycle. The flux-calibrated spectra of SDSS0804, which cover a period of more than two years prior to the 2006 superoutburst until one year after the 2010 superoutburst, are shown in the upper panel of Fig. 5. As already mentioned above, during the 2008–2009 the object was about 0.3 mag brighter than before the superoutburst. But in January 2012, the object brightness returned to the pre-outburst level of March 2006. The continuum of the post-outburst spectra is bluer, Balmer absorption lines are deeper, and emission lines are weaker than in the pre-superoutburst spectrum. The equivalent width of Hα, for example, changed from ≈−90 to ≈−15 in 2004 and 2008. In January 2012, the equivalent width of the Hα line increased to up to ≈ − 70, about four times larger than values obtained between superoutbursts. However, the value does not reach the level seen in 2004 (see Fig. 6) because the object never reached the same quiescent state prior to the first superoutburst.
 |
Fig. 3 Power spectra (top panel) of SDSS0804 using the 2012 data and the corresponding light curves folded with the orbital period (upper axis of the lower panel) and the half orbital period (bottom axis of the lower panel) are shown. |
 |
Fig. 4 J band image obtained in October 2009 using Camila at the 0.84 m telescope of the OAN SPM. |
 |
Fig. 5 Flux-calibrated time-averaged spectra of SDSS0804 obtained in different epochs. |
We fit the spectral energy distribution (SED) of SDSS0804 in quiescence with the model described in detail by Aviles et al. (2010) using a combination of the SDSS spectrum obtained in 2004 with the IR data of Kato et al. (2009). Following Aviles et al. (2010), we assumed that the total flux, F∗(λ), is the sum of the radiation from a hydrogen WD (DA type) FWD(Teff,λ), an accretion disk with FAD ~ λΓ, and a red/brown dwarf with FBD(λ): 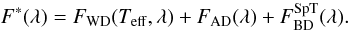 (1)Brown dwarf fluxes were taken from the literature (McLean et al. 2003, 2007) and online sources2. The white dwarf radii were calculated using the mass-radius relation
(1)Brown dwarf fluxes were taken from the literature (McLean et al. 2003, 2007) and online sources2. The white dwarf radii were calculated using the mass-radius relation
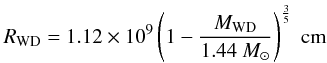 from Nauenberg (1972) for an MWD = 0.6 − 1.1 M⊙ range, with steps of a 0.1 M⊙. Spectra of WDs with pure hydrogen atmosphere in the 4000–25 000 Å spectral interval were obtained using ATLAS9 (Kurucz 1993) and SYNTH (Piskunov 1992) codes for the appropriate range of temperatures. The calculations were performed with a 1000 K step in a temperature range from Teff = 10 000 to 18 000 K and with a surface gravity
from Nauenberg (1972) for an MWD = 0.6 − 1.1 M⊙ range, with steps of a 0.1 M⊙. Spectra of WDs with pure hydrogen atmosphere in the 4000–25 000 Å spectral interval were obtained using ATLAS9 (Kurucz 1993) and SYNTH (Piskunov 1992) codes for the appropriate range of temperatures. The calculations were performed with a 1000 K step in a temperature range from Teff = 10 000 to 18 000 K and with a surface gravity 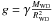 . The spectra were normalized to λ0 = 5500 Å and the contribution of the WD is
. The spectra were normalized to λ0 = 5500 Å and the contribution of the WD is
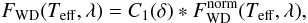 where
where 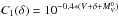 , V = 17.9 is the object’s brightness in quiescence, and δ is a parameter that determines the contribution of the flux from the WD to the total flux in the V band. Finally,
, V = 17.9 is the object’s brightness in quiescence, and δ is a parameter that determines the contribution of the flux from the WD to the total flux in the V band. Finally, 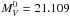 is a constant to convert magnitude into flux (in erg/cm2/s/Å) in the V band. The spectra of the accretion disk was assumed to be a simple power law
is a constant to convert magnitude into flux (in erg/cm2/s/Å) in the V band. The spectra of the accretion disk was assumed to be a simple power law
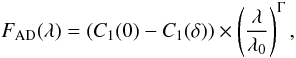 where (C1(0) − C1(δ)) determines the contribution from the accretion disk in the V band, assuming that the WD and the accretion disk are the only sources in that wavelength because the only other contributor is the brown dwarf, which has an only negligible flux in the V band. Γ is the slope of the accretion disk’s power-law spectrum.
where (C1(0) − C1(δ)) determines the contribution from the accretion disk in the V band, assuming that the WD and the accretion disk are the only sources in that wavelength because the only other contributor is the brown dwarf, which has an only negligible flux in the V band. Γ is the slope of the accretion disk’s power-law spectrum.
 |
Fig. 6 Hα line profile of the object at different epochs is shown. The continuum is subtracted. |
 |
Fig. 7 Spectral energy distribution of SDSS0804 is plotted with the components of the best-fit models. The tiny black line is the observed quiescent optical spectrum, red dots are JHK IR measurements. Overplotted with a thick black line is the sum of all components that comprise the close binary. The green line is the WD spectral model, the blue line corresponds to the accretion disk contribution, and the maroon line represents the brown dwarf spectrum. The top figure shows the solution corresponding the χ2 minimum in which the accretion disk dominates in the IR. The bottom figure presents the solution with the standard spectral index of Γ = Γ0 ≡ −7/3 ≅ −2.33 and the secondary dominating in the IR. |
The distance to the object is estimated to be
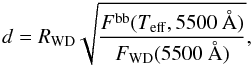 where Fbb(Teff;5500 Å) is the black body flux at λ = 5500 Å with an effective temperature Teff. Observed SEDs of red/brown dwarfs with spectral types between M6 to L5, normalized to fit the observed flux in the J band, were used. The bolometric correction to the J magnitude for each spectral type was taken from Tinney et al. (2003).
where Fbb(Teff;5500 Å) is the black body flux at λ = 5500 Å with an effective temperature Teff. Observed SEDs of red/brown dwarfs with spectral types between M6 to L5, normalized to fit the observed flux in the J band, were used. The bolometric correction to the J magnitude for each spectral type was taken from Tinney et al. (2003).
The free parameters of this three-component model are the white dwarf effective temperature Teff, the mass of the white dwarf MWD, the spectral type of the secondary star SpT, the ratio δ of WD-to-accretion disk contribution in the V band, and the slope of the accretion disk spectrum Γ.
Results of the fitting are presented in Figs. 7 and 8. A marked minimum in χ2 occurs at Γ = −1.93 (see the vertical dash-dotted line in Fig. 8). This solution implies an MWD = 0.7 ± 0.1 M⊙ white dwarf with TWD = 12 000 ± 1000 K temperature, a ~L5 ± 2 brown dwarf, and an accretion disk with a 50% contribution in the optical spectrum that dominates in the infrared. The system will be located at a distance of about ~200 pc. Indeed, this solution works for a range of −2.2 ≲ Γ ≲ −1.8 where the χ2 variation is weak.
If constraints on χ2 are relaxed even more, another solution becomes viable for the spectral slope of −2.75 ≲ Γ ≲ −2.2 and − 1.8 ≲ Γ ≲ − 1.3, which includes the standard spectral index of Γ = Γ0 ≡ − 7/3 ≅ − 2.33 Lynden-Bell (1969, see the dashed line in Fig. 8). The fit parameters for solutions in these Γ ranges correspond to a system formed by a more massive MWD = 1.0 ± 0.1 M⊙ white dwarf with the same temperature, a brown dwarf of slightly earlier spectral type ~L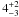 , and an accretion disk whose contribution is only ~30 ± 10% in the optical spectrum dominated by the white dwarf. In the infrared the contribution of the accretion disk is comparable to the secondary star. Accordingly, the system would be located at a distance of about 120–130 pc.
, and an accretion disk whose contribution is only ~30 ± 10% in the optical spectrum dominated by the white dwarf. In the infrared the contribution of the accretion disk is comparable to the secondary star. Accordingly, the system would be located at a distance of about 120–130 pc.
 |
Fig. 8 Relations of distance, white dwarf temperature, spectral type of the secondary, mass of the primary, contribution of the accretion disk, and χ2 (from the top to the bottom) vs. the slope of the power law spectrum of the accretion disk. The two models presented in Fig. 7 are marked by vertical lines. |
The difference between these two solutions arises from the different contribution of the accretion disk in the infrared. In the model with the lowest χ2 the spectrum of the accretion disk is flatter compared to the standard model, as expected for an optically thin disk in the continuum (Idan et al. 2008). It also means more contribution from the cooler outskirts of the disk in the infrared. Therefore, if the disk dominates in the IR, the distance estimate to the system increases, which leads to a less massive white dwarf with a larger radius and higher luminosity. However, there is evidence that short period CVs tend to contain massive (~0.9 M⊙) white dwarfs (Littlefair et al. 2008). It is difficult to choose the right solution based on quality of the available data and the uncertainties in applied models, but it is beyond doubt that the contribution of the accretion disk in the continuum of bounce-back systems is far less than in ordinary CVs. Additional ultraviolet and infrared spectroscopy would be necessary to determine fractions of fluxes from the stellar components and separate the spectrum of the accretion disk.
Additionally, we calculated models for spectra obtained immediately after the superoutburst. The infrared values of the system were kept the same (within the error range) as in quiescence. The temperature inferred for the best-fit model is TWD = 15 000 ± 1000 K. This value is not surprising because an increase of white dwarf surface temperature during superoutburst has been observed recently in a number of other CVs (Godon et al. 2004; Sion et al. 1996). In the case of SDSS0804 the appearance of WD pulsations after the superoutburst and their subsequent disappearance is also good evidence of temperature change (Pavlenko 2009).
 |
Fig. 9 Trailed spectra around the Hα line folded with the orbital period of the system and the corresponding Doppler maps. The center of mass, both stellar components, the stream of mass transfer, and the circle corresponding to the 2:1 resonance radius of the accretion disk are marked on the tomograms. |
6. Doppler tomography
We used Doppler tomography (Marsh & Horne 1988) to study the structure of the accretion disk of SDSS0804. We generated Doppler maps from our time-resolved spectra of the object using the maximum entropy method as implemented by Spruit (1998)3. Trailed spectra around the Hα line and their corresponding Doppler maps are shown in Fig. 9. The orbital period of Porb = 0.059 days, a white dwarf mass of MWD = 1.0 M⊙, and mass ratio of q = 0.05 are used to overlay positions of the stellar components and the stream on the Doppler maps4. The inclination angle i = 70° is arbitrarily chosen as a compromise between strong double-peaked emission lines in the spectra and absence of obvious eclipses in the light curve. A possible presence of weak eclipses during the superoutburst, as reported by Kato et al. (2009), supports the idea of a high-inclination system. Trailed spectra folded with the orbital period of the system clearly show an S-wave emanating from the bright spot created by the impact of the stream with the accretion disk. The Doppler maps show not only the bright spot, but also two distinctive bright regions on the ring, indicative of an accretion disk. The bright regions repeat from epoch to epoch. The brighter one is located, as expected, where the mass transfer stream hits the accretion disk. This bright region is commonly seen in most CVs, but here it looks extended along the mass transfer stream line. The other bright region is extended and is located completely on the opposite side of the disk at V ≈ 750 km s-1. This bright region is not common for accretion disk systems but is a feature shared by the bounce-back candidates SDSS1238 (Aviles et al. 2010) and SDSS1035 (Southworth et al. 2006) in quiescence. This latter bright region was also detected in Doppler maps of WZ Sge during its superoutburst in 2001 (Baba et al. 2002; Howell et al. 2003). We assume that the most probable interpretation of these tomograms is two spiral waves in the outer annuli, formed by the 2:1 resonance in the extended accretion disk (Lin & Papaloizou 1979).
 |
Fig. 10 Same as shown in Fig. 7 but for the Hβ line and only the 2012 data. |
In January 2012, the intensity of the S-wave in the trailed spectra of the Hα line was somewhat fainter compared the total flux from the accretion disk. However, the distribution of matter in the accretion disk did not change overall. This observation is also confirmed by the Hβ map obtained at the same time (see Fig. 10).
 |
Fig. 11 Plots of the mass ratio and the mass transfer rate vs. the orbital period of CVs. In the schema (left panel), locations of different CV types are marked along with the 3:1 and 2:1 resonance radii. The lower box in that panel corresponds to the location of bounce-back systems, as labeled. In the right panel observed systems with known parameters are plotted with the mass ratio axes marked on the left and estimated mass transfer rates on the right axes. The bounce-back candidates are enclosed in a dash-dotted box. |
Parameters of bounce-back candidates.
7. Accretion disk structure of bounce-back systems
Figure 11 illustrates the current concept of CV evolution at the orbital period turn-around point and displays the position of the bounce-back candidates on the mass-transfer rate and mass-ratio to orbital period diagrams. Some CV classifications are are labeled on the mass transfer rate to orbital period diagram. The classification in astronomy is often phenomenological: CVs with orbital periods close to the 80 min orbital period minimum that undergo infrequent (years to decades) superoutbursts are called WZ Sge-type stars. Objects with short periods that have not been observed in outburst or superoutburst but have spectral characteristics similar to WZ Sge (i.e., a mildly blue continuum with relatively weak Balmer emission lines from the accretion disk embedded in a broad absorptions formed in the atmosphere of the white dwarf) are listed as WZ Sge-type candidates. Bounce-back systems are spectroscopically similar to these, but not every WZ Sge-type object has necessarily passed through the turning point. The parameters of bounce-back systems (i.e. objects that would fall into the box in the right panel of Fig. 11) are listed in Table 3.
 |
Fig. 12 Size of a typical bounce-back system and its components in solar units compared with the size of Jupiter and the sun. The 2:1 and 3:1 resonance radii are also shown. |
To separate the bounce-back systems from the others, the mass of the secondary or the mass ratio is needed. Direct measurement of the mass of either stellar component in CVs is an extremely difficult task. But the mass ratio can be estimated from the period of the superhumps that may be seen in the light curves during superoutbursts. Four objects (V455 And, AL Com, SDSS0804 and EG Cnc) produced WZ Sge-type superoutbursts in the near past. Estimates of the system parameters often show the presence of a massive white dwarf (M1 ≳ 0.9 M⊙) and an extremely low mass ratio q ≲ 0.06, which assumes that the secondary is a Jupiter-sized brown dwarf (see Fig. 12). A q this low implies that the Roche lobe of the primary is huge and the accretion disk could extend to the 2:1 resonance radius and beyond. If that is the case, the disk will develop two spiral density waves in the outer annuli as shown by Kunze & Speith (2005). The two waves will cause the appearance of the double hump-shape per orbital period in the light curves, especially in high-inclination systems. Thus, one way of separating bounce-back systems from other WZ Sge objects is to detect the spiral structure in the accretion disk in quiescence. WZ Sge usually exhibits double-humps only during the early stages of the superoutburst, when the disk expands. In the left panel of Fig. 11, the mass ratio leading to the 2:1 resonance disk radius is indicated by a tiny dotted line, which clearly separates bounce-back systems from the rest.
We aim to determine the conditions in bounce-back systems that enable detection of these two spiral waves in the outer annuli. The accretion disk structure of bounce-back candidates is analyzed here primarily based on our spectral and IR photometric observations of SDSS1238 (Aviles et al. 2010) and SDSS0804 in quiescence. The conditions of the disk are inferred from the Doppler tomography maps and from the analysis of the SEDs of these systems. The SED modeling requires a low contribution from the accretion disk to the total flux. The main uncertainty of the SED model is the slope of the accretion disk continuum. The shape of a standard spectrum (Fλ ~ λ − 7/3) of the accretion disk is based on a blackbody approximation of a disk element flux intensity and the relation Teff(r) ≈ T∗(r/R1) − 3/4 for the radial temperature structure of a steady-state accretion disk (Warner 1995). However, an optically thick accretion disk emitting as a blackbody of this size will totally dominate the radiation of the system. Because observations show that the white dwarf radiation dominates in the optical range and the secondary’s radiation dominates the JHK bands in SDSS0804 and SDSS1238, the “standard accretion disk model” (Frank et al. 2002) does not apply to bounce-back systems.
It is known that accretion disks in CVs develop optically thin outer regions for mass transfer rates below about 10-8 M⊙ yr-1 (Williams 1980). Tylenda (1981) confirmed this and added that an increase in the radius of the α-model disk (Shakura & Sunyaev 1973) always increases the role of the thin region. For α ≤ 1 the thin part of the disk is rather cool ( ≤ 6000 K). Because a large part of the accretion disk is optical thin in continuum (i.e., in the non-LTE regime and for α < 0.1), the disk temperature can drop below 5000 K (Dumont et al. 1991). Cannizzo & Wheeler (1984) studied the vertical structure of a steady-state, α-model thin-accretion disk for an accreting object of 1 M⊙. They found that, for low accretion rates, the disk structure is optically thin. For 0.01 < α < 1, the solution of disk Eqs. (1)–(3) (Cannizzo & Wheeler 1984) can be double-valued with high- (~5000 K) and low- (~2000 K) temperature branches. For α > 0.1 a warm solution is possible in the inner region of the accretion disk, but disk annuli at larger radii will be in a cold state with T < 2000 K. Only the low-temperature solution exists for α ≈ 0.1. As α decreases with temperature, the tendency to develop cold solutions in quiescence is enhanced. Until now, models of disk emission spectra for these cool disks have not been calculated, the nearest approach is a flat spectrum in the range 3000–10 000 Å for the model of the cool (T = 5000 K, α = 0.03) accretion disk (Idan et al. 2008). The next important aspect regarding accretion disks of bounce-backers is the non-uniform structure inferred from the Doppler tomograms and optical light curves alike. As already mentioned, the non-uniform structure was interpreted as spiral arms in the accretion disks (Aviles et al. 2010, see Doppler maps discussion and references therein). The inner part of the accretion disk in a standard model is usually optically thick and forms a continuum of the disk spectrum (Cannizzo & Wheeler 1984, and references therein). However, for WZ-Sge-type systems, various authors have supported the idea that the inner part of the disk is void during quiescence (see Kuulkers et al. 2011; Mennickent et al. 2001, and reference therein). This void is assumed to explain the long recurrence time for superoutbursts and the absence of normal outbursts. The missing inner part of the accretion disk may be caused by evaporation (Meyer & Meyer-Hofmeister 1994) or/and by magnetic field of the primary WD (Matthews et al. 2006). According to the equation 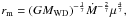 where
where 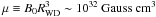 (Kluźniak & Rappaport 2007, and references therein), the size of the magnetosphere will increase with the decrease of mass transfer rate (see Fig. 13). A relatively faint ( ≤ 1 MGauss) magnetic field is enough to form a cavity in the inner part of the accretion disk. Magnetic fields of about 0.5 MG and stronger are detected in magnetic CVs from the white dwarf spin modulation observed in optical light or X-rays. V455 And is a proven intermediate polar. In SDSS0804 a number of high-frequency periods were detected (Pavlenko et al. 2012), but none was identified as a spin period so far. X-ray observations are needed to probe the magnetic properties of the white dwarfs in bounce-back candidates to verify the intermediate polar hypothesis. A typical system with parameters corresponding to a bounce-back system may look like the sketch in Fig. 14 (top panel). The simulated disk is thin in the inner regions and thick along the spiral density waves, which are located in the outer annuli.
(Kluźniak & Rappaport 2007, and references therein), the size of the magnetosphere will increase with the decrease of mass transfer rate (see Fig. 13). A relatively faint ( ≤ 1 MGauss) magnetic field is enough to form a cavity in the inner part of the accretion disk. Magnetic fields of about 0.5 MG and stronger are detected in magnetic CVs from the white dwarf spin modulation observed in optical light or X-rays. V455 And is a proven intermediate polar. In SDSS0804 a number of high-frequency periods were detected (Pavlenko et al. 2012), but none was identified as a spin period so far. X-ray observations are needed to probe the magnetic properties of the white dwarfs in bounce-back candidates to verify the intermediate polar hypothesis. A typical system with parameters corresponding to a bounce-back system may look like the sketch in Fig. 14 (top panel). The simulated disk is thin in the inner regions and thick along the spiral density waves, which are located in the outer annuli.
 |
Fig. 13 Primary’s magnetosphere radius for different mass transfer rates (in solar mass per year) vs. the primary’s magnetic field. |
 |
Fig. 14 Top panel: model configuration used to calculate the light curves of bounce-back systems. The bottom panel shows the vertical thickness of the accretion disk (left) and the temperature distribution (right) of the model. |
8. Light curve simulation
An eye-catching double-hump-shape per orbital period in quiescent light curves is a common feature of objects proposed to be bounce-back candidates. We developed a geometric model of CV disks with two spiral density waves in the outer annuli of a thin accretion disk to model light curves of bounce-back systems. The top panel of Fig. 14 presents a snapshot of this model. The system is comprised of a primary white dwarf, a secondary brown dwarf star, a stream of accretion matter, and an accretion disk. The white dwarf is a sphere defined by the mass-radii relation (2.83b) from Warner (1995). The secondary is assumed to fill its Roche lobe, and the Roche lobe shape is calculated directly using Eq. (2.2) from Warner (1995) for equipotential Φ(L1). The temperature of the primary and the secondary are defined as initial parameters. Although illumination of the secondary by the primary in these systems is low, this illumination is also included. A moderate temperature gradient T(r) ~ T(rin) × r − 3/4 between the inner and outer edges of the disk and T ~ T(r) × (1 + θ × z(r)) from the spiral density waves (see Fig. 14) was assumed. Here, T(rin) is the temperature of the internal radius of the disk, which depends on the mass ratio (see Eqs. (2.35) and (2.36) in Warner 1995), and θ is a free parameter that defines the temperature gradient in the spiral density waves. The model takes into account the positions of the bright structures in the Doppler maps, the large size of accretion disk, and the description of the spiral density waves in Hachisu et al. (2004). Figure 14 presents the geometry used in the model (top panel) and grayscale images present the height of the disk (bottom left) and the temperature distribution (bottom right) of the accretion disk.
We calculated a variety of models using the typical average parameters of bounce-back systems presented in Table 3. In Fig. 15 four representative models corresponding to the entries of Table 4 are plotted along with the observed, averaged light curves of AL Com, SDSS0804, SDSS1610, and V455 And. The main difference between the models is the choice of parameters, which influences the spiral density wave structures in the disk. In the second model (N2), the spiral density waves are hotter and thus the amplitude is higher than in the model N1 (Table 4). To show the dependence on system inclination from the orbital plane and the radius of inner disk in the models, we plot three curves for each model in the lower panels of Fig. 15. Obviously, the inclination varies in the N1 model and the inner disk radius varies in the N2 model. For models N3 and N4, a significantly smaller θ is used for the MWD = 0.9 M⊙, i = 75° and MWD = 0.7 M⊙, i = 80° cases, respectively. Clearly, the double-hump-shape light curve is easily reproduced by these models. From our models, we find that the shape and amplitude of the variability depends on the parameters chosen for the two spiral density waves, the disk temperature distribution, the size of the inner cavity, and the outer radius of the disk. We also find that the amplitude of the double-humped variability decreases with decreasing temperature gradient in the spiral density waves and/or the decline of the system’s inclination. We note that changing the primary’s mass has no effect on the shape of the light curve. However, as noted previously, a low-mass primary will not allow the disk to reach the 2:1 resonance radius, which results in the spiral structures in the outer annuli of the accretion disk.
 |
Fig. 15 Light curves of AL Com, V455 And, SDSS0804, and SDSS1610 folded with their orbital periods are shown in the upper four panels. Simulated light curves from our models are shown in the lower four panels (see Table 4). |
Parameters used for V- band light curve modeling.
The number of free parameters of the light curve model is large. Using a χ2 minimization to fit each light curve precisely would be a very complicated task and is not the aim of this study. The simple models used in this work validate previously reported ideas on the disk structure in WZ Sge systems – a large, cool, mostly optically thin accretion disk containing two dense/hot spirals. We add that these models offer a reasonable explanation for the observed characteristics of bounce-back systems.
9. Conclusion
We here continued our study of SDSS J080434.20+510349.2 focusing on the nature of double humps in the light curve and their relation to the structure of the accretion disk.
The object exhibited ≈ 0.07 mag variability with 42.48 min period, exactly half the orbital period of the system, during 2008–2009 when it almost retuned to quiescent level after the March 2006 superoutburst. In September 2010, the system underwent yet another superoutburst and approached its quiescent level by the beginning of 2012. The light curve once again showed double humps, but with a significantly smaller (~0.01 mag) amplitude. No long-term SDSS1238-like variability and mini-outburst phenomena were detected.
The SED of SDSS0804 in quiescence was fitted by the three-component model, which requires a massive ≥ 0.7 M⊙ white dwarf with a surface temperature of ~12 000 K, a late-type brown dwarf, and an accretion disk with a weak contribution to the total flux.
Hα and Hβ Doppler maps obtained in quiescence from time-resolved spectroscopy persistently show excess emission from two opposing sides of the accretion disk. This pattern is a common characteristic that SDSS0804 shares with SDSS1238 and other bounce-back candidates.
We constructed a geometric model of a bounce-back system to reproduce the observed light curves. The double-humped light curves in quiescence can be generated by the model in which the accretion disk extends to the 2:1 resonance radius, is cool (~2500 K) and contains two spiral density waves in the outer annuli of the disk. The spirals should be denser and hotter than the rest of the disk. The inner parts of the disk should be optically thin in the continuum or be totally void. A synthetic Doppler map constructed using this model of the accretion disk can also reproduce the observed maps, as was recently shown in Aviles et al. (2010, Fig. 4).
Acknowledgments
The authors greatly appreciate discussions with Michele Montgomery and her suggestions, which helped to improve the manuscript significantly. We are also thankful to the anonymous referee for constructive comments. S.Z. and G.T. acknowledge PAPIIT grants IN-109209/IN-103912 and CONACyT grants 34521-E; 151858 for resources provided towards this research.
References
- Araujo-Betancor, S., Gänsicke, B. T., Hagen, H.-J., et al. 2005, A&A, 430, 629 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Aviles, A., Zharikov, S., Tovmassian, G., et al. 2010, ApJ, 711, 389 [NASA ADS] [CrossRef] [Google Scholar]
- Baba, H., Sadakane, K., Norimoto, Y., et al. 2002, PASJ, 54, L7 [NASA ADS] [CrossRef] [Google Scholar]
- Cannizzo, J. K., & Wheeler, J. C. 1984, ApJS, 55, 367 [NASA ADS] [CrossRef] [Google Scholar]
- Deeming, T. J. 1975, Ap&SS, 36, 137 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- Dumont, A. M., Lasota, J. P., Collin-Souffrin, S., & King, A. R. 1991, A&A, 242, 503 [NASA ADS] [Google Scholar]
- Frank, J., King, A., & Raine, D. J. 2002, Accretion Power in Astrophysics, eds. J. Frank, & A. King, & D. Raine (Cambridge, UK: Cambridge University Press) [Google Scholar]
- Gänsicke, B. T., Dillon, M., Southworth, J., et al. 2009, MNRAS, 397, 2170 [NASA ADS] [CrossRef] [Google Scholar]
- Godon, P., Sion, E. M., Cheng, F., et al. 2004, ApJ, 602, 336 [NASA ADS] [CrossRef] [Google Scholar]
- Hachisu, I., Kato, M., & Kato, T. 2004, ApJ, 606, L139 [NASA ADS] [CrossRef] [Google Scholar]
- Howell, S. B., Adamson, A., & Steeghs, D. 2003, A&A, 399, 219 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Idan, I., Lasota, J.-P., Hameury, J.-M., & Shaviv, G. 2008, New A Rev., 51, 759 [NASA ADS] [CrossRef] [Google Scholar]
- Kato, T., Pavlenko, E. P., Maehara, H., et al. 2009, PASJ, 61, 601 [NASA ADS] [Google Scholar]
- Kolb, U., & Baraffe, I. 1999, MNRAS, 309, 1034 [NASA ADS] [CrossRef] [Google Scholar]
- Kluźniak, W., & Rappaport, S. 2007, ApJ, 671, 1990 [NASA ADS] [CrossRef] [Google Scholar]
- Kunze, S., & Speith, R. 2005, ASPC, 330, 389 [NASA ADS] [Google Scholar]
- Kurucz, R. 1993, ATLAS9 Stellar Atmosphere Programs and 2 km s-1 grid. Kurucz CD-ROM No. 13, Cambridge, Mass.: Smithsonian Astrophysical Observatory [Google Scholar]
- Kuulkers, E., Henden, A. A., Honeycutt, R. K., et al. 2011, A&A, 528, A152 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lin, D. N. C., & Papaloizou, J. 1979, MNRAS, 186, 799 [NASA ADS] [CrossRef] [Google Scholar]
- Littlefair, S. P., Dhillon, V. S., Marsh, T. R., et al. 2008, MNRAS, 388, 1582 [NASA ADS] [CrossRef] [Google Scholar]
- Lynden-Bell, D. 1969, Nature, 223, 690 [NASA ADS] [CrossRef] [Google Scholar]
- Marsh, T. R., & Horne, K. 1988, MNRAS, 235, 269 [NASA ADS] [CrossRef] [Google Scholar]
- Matthews, O. M., Wheatley, P. J., Wynn, G. A., & Truss, M. R. 2006, MNRAS, 372, 1593 [NASA ADS] [CrossRef] [Google Scholar]
- McLean, I. S., McGovern, M. R., Burgasser, A. J., et al. 2003, ApJ, 596, 561 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- McLean, I. S., Prato, L., McGovern, M. R., et al. 2007, ApJ, 658, 1217 [NASA ADS] [CrossRef] [Google Scholar]
- Mennickent, R. E., Diaz, M., Skidmore, W., & Sterken, C. 2001, A&A, 376, 448 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Meyer, F., & Meyer-Hofmeister, E. 1994, A&A, 288, 175 [NASA ADS] [Google Scholar]
- Mukadam, A. S., Townsley, D. M., Gänsicke, B. T., et al. 2010, ApJ, 714, 1702 [NASA ADS] [CrossRef] [Google Scholar]
- Nauenberg, M. 1972, ApJ, 175, 417 [NASA ADS] [CrossRef] [Google Scholar]
- Paczynski, B. 1981, Acta Astron., 31, 1 [NASA ADS] [Google Scholar]
- Patterson, J. 2011, MNRAS, 411, 2695 [NASA ADS] [CrossRef] [Google Scholar]
- Patterson, J., Augusteijn, T., Harvey, D. A., et al. 1996, PASP, 108, 748 [NASA ADS] [CrossRef] [Google Scholar]
- Patterson, J., Kemp, J., Skillman, D. R., et al. 1998, PASP, 110, 1290 [NASA ADS] [CrossRef] [Google Scholar]
- Patterson, J., Thorstensen, J. R., & Kemp, J. 2005, PASP, 117, 427 [NASA ADS] [CrossRef] [Google Scholar]
- Pavlenko, E. 2009, J. Phys. Conf. Ser., 172, 012071 [NASA ADS] [CrossRef] [Google Scholar]
- Pavlenko, E., & Golovin, A. 2006, Binary Stars as Critical Tools and Tests in Contemporary Astrophysics, International Astronomical Union, Symp., 240, held 22–25 August, Prague, Czech Republic, 89 [Google Scholar]
- Pavlenko, E., Shugarov, S., Yu., & Katysheva, N. A., 2007, 15th European Workshop on White Dwarfs, 372, 511 [Google Scholar]
- Pavlenko, E., Malanushenko, V., Tovmassian, G., et al. 2012, Mem. Soc. Astron. It., 83, 520 [NASA ADS] [Google Scholar]
- Piskunov, N. E. 1992, Stellar Magnetism, eds. Yu. V. Glagolevskij, & I. I. Romanyuk (Sankt Petersburg: Nauka, Sankt Petersburg branch), 92 [Google Scholar]
- Shakura, N. I., & Sunyaev, R. A. 1973, A&A, 24, 337 [NASA ADS] [Google Scholar]
- Sion, E. M., Cheng, F.-H., Huang, M., Hubeny, I., & Szkody, P. 1996, ApJ, 471, L41 [Google Scholar]
- Spruit, H. C. 1998 [arXiv:astro-ph/9806141] [Google Scholar]
- Southworth, J., Gänsicke, B. T., Marsh, T. R., et al. 2006, MNRAS, 373, 687 [NASA ADS] [CrossRef] [Google Scholar]
- Szkody, P., Fraser, O., Silvestri, N., et al. 2003, AJ, 126, 1499 [NASA ADS] [CrossRef] [Google Scholar]
- Szkody, P., Henden, A., Agüeros, M., et al. 2006, AJ, 131, 973 [NASA ADS] [CrossRef] [Google Scholar]
- Tinney, C. G., Burgasser, A. J., & Kirkpatrick, J. D. 2003, AJ, 126, 975 [NASA ADS] [CrossRef] [Google Scholar]
- Tylenda, R. 1981, Acta Astron., 31, 127 [NASA ADS] [Google Scholar]
- Unda-Sanzana, E., Marsh, T. R., Gänsicke, B. T., et al. 2008, MNRAS, 388, 889 [NASA ADS] [CrossRef] [Google Scholar]
- van Spaandonk, L., Steeghs, D., Marsh, T. R., & Parsons, S. G. 2010, ApJ, 715, L109 [NASA ADS] [CrossRef] [Google Scholar]
- Warner, B. 1995, Cataclysmic Variable Stars (Cambridge: Cambridge Univ. Press), Cambridge Astrophys. Ser., 28 [Google Scholar]
- Williams, R. E. 1980, ApJ, 235, 939 [NASA ADS] [CrossRef] [Google Scholar]
- Zharikov, S. V., Tovmassian, G. H., Napiwotzki, R., Michel, R., & Neustroev, V. 2006, A&A, 449, 645 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Zharikov, S. V., Tovmassian, G. H., Neustroev, V. V., et al. 2008, A&A, 486, 505 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Zharikov, S., Tovmassian, G., Aviles, A., Tapia, M., & Roth, M. 2010 [arXiv:1010.0008] [Google Scholar]
All Tables
All Figures
 |
Fig. 1 Light curves of SDSS0804 are shown from 2005 to 2012 in the V band. The plot is based on a combination of data obtained by us, including those published in Zharikov et al. (2008), and data accumulated by the AAVSO. |
| In the text | |
 |
Fig. 2 Power spectra (top panel) of SDSS0804 is shown for different observational runs; the corresponding light curves are folded with the orbital period (upper axis of the middle panels). The half orbital period (bottom axis of the middle panels) and the 12.6 min period (lower panels) are also shown. |
| In the text | |
 |
Fig. 3 Power spectra (top panel) of SDSS0804 using the 2012 data and the corresponding light curves folded with the orbital period (upper axis of the lower panel) and the half orbital period (bottom axis of the lower panel) are shown. |
| In the text | |
 |
Fig. 4 J band image obtained in October 2009 using Camila at the 0.84 m telescope of the OAN SPM. |
| In the text | |
 |
Fig. 5 Flux-calibrated time-averaged spectra of SDSS0804 obtained in different epochs. |
| In the text | |
 |
Fig. 6 Hα line profile of the object at different epochs is shown. The continuum is subtracted. |
| In the text | |
 |
Fig. 7 Spectral energy distribution of SDSS0804 is plotted with the components of the best-fit models. The tiny black line is the observed quiescent optical spectrum, red dots are JHK IR measurements. Overplotted with a thick black line is the sum of all components that comprise the close binary. The green line is the WD spectral model, the blue line corresponds to the accretion disk contribution, and the maroon line represents the brown dwarf spectrum. The top figure shows the solution corresponding the χ2 minimum in which the accretion disk dominates in the IR. The bottom figure presents the solution with the standard spectral index of Γ = Γ0 ≡ −7/3 ≅ −2.33 and the secondary dominating in the IR. |
| In the text | |
 |
Fig. 8 Relations of distance, white dwarf temperature, spectral type of the secondary, mass of the primary, contribution of the accretion disk, and χ2 (from the top to the bottom) vs. the slope of the power law spectrum of the accretion disk. The two models presented in Fig. 7 are marked by vertical lines. |
| In the text | |
 |
Fig. 9 Trailed spectra around the Hα line folded with the orbital period of the system and the corresponding Doppler maps. The center of mass, both stellar components, the stream of mass transfer, and the circle corresponding to the 2:1 resonance radius of the accretion disk are marked on the tomograms. |
| In the text | |
 |
Fig. 10 Same as shown in Fig. 7 but for the Hβ line and only the 2012 data. |
| In the text | |
 |
Fig. 11 Plots of the mass ratio and the mass transfer rate vs. the orbital period of CVs. In the schema (left panel), locations of different CV types are marked along with the 3:1 and 2:1 resonance radii. The lower box in that panel corresponds to the location of bounce-back systems, as labeled. In the right panel observed systems with known parameters are plotted with the mass ratio axes marked on the left and estimated mass transfer rates on the right axes. The bounce-back candidates are enclosed in a dash-dotted box. |
| In the text | |
 |
Fig. 12 Size of a typical bounce-back system and its components in solar units compared with the size of Jupiter and the sun. The 2:1 and 3:1 resonance radii are also shown. |
| In the text | |
 |
Fig. 13 Primary’s magnetosphere radius for different mass transfer rates (in solar mass per year) vs. the primary’s magnetic field. |
| In the text | |
 |
Fig. 14 Top panel: model configuration used to calculate the light curves of bounce-back systems. The bottom panel shows the vertical thickness of the accretion disk (left) and the temperature distribution (right) of the model. |
| In the text | |
 |
Fig. 15 Light curves of AL Com, V455 And, SDSS0804, and SDSS1610 folded with their orbital periods are shown in the upper four panels. Simulated light curves from our models are shown in the lower four panels (see Table 4). |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


