| Issue |
A&A
Volume 549, January 2013
|
|
|---|---|---|
| Article Number | A50 | |
| Number of page(s) | 16 | |
| Section | Stellar structure and evolution | |
| DOI | https://doi.org/10.1051/0004-6361/201220069 | |
| Published online | 18 December 2012 | |
Cumulative physical uncertainty in modern stellar models
I. The case of low-mass stars⋆
1
Dipartimento di Fisica “Enrico Fermi”Università di Pisa,
largo Pontecorvo 3,
56127
Pisa,
Italy
e-mail: valle@df.unipi.it
2
INFN, Sezione di Pisa, Largo B. Pontecorvo 3,
56127
Pisa,
Italy
Received:
20
July
2012
Accepted:
26
October
2012
Context. Theoretical stellar evolutionary models are still affected by not negligible uncertainties due to the errors in the adopted physical inputs.
Aims. In this paper, using our updated stellar evolutionary code, we quantitatively evaluate the effects of the uncertainties in the main physical inputs on the evolutionary characteristics of low mass stars, and thus of old stellar clusters, from the main sequence to the zero age horizontal branch (ZAHB). To this aim we calculated more than 3000 stellar tracks and isochrones, with updated solar mixture, by changing the following physical inputs within their current range of uncertainty: 1H(p, νe+)2H, 14N(p,γ)15O, and triple-α reaction rates, radiative and conductive opacities, neutrino energy losses, and microscopic diffusion velocities.
Methods. The analysis was conducted performing a systematic variation on a fixed grid, in a way to obtain a full crossing of the perturbed input values. The effect of the variations of the chosen physical inputs on relevant stellar evolutionary features, such as the turn-off luminosity, the central hydrogen exhaustion time, the red-giant branch tip luminosity, the helium core mass, and the ZAHB luminosity in the RR Lyrae region are analyzed in a statistical way.
Results. We find that, for a 0.9 M⊙ model, the cumulative uncertainty on the turn-off, the red-giant branch tip, and the ZAHB luminosities accounts for ±0.02 dex, ±0.03 dex, and ±0.045 dex respectively, while the central hydrogen exhaustion time varies of about ±0.7 Gyr. For all examined features the most relevant effect is due to the radiative opacities uncertainty; for the later evolutionary stages the second most important effect is due to the triple-α reaction rate uncertainty. For an isochrone of 12 Gyr, we find that the isochrone turn-off log luminosity varies of ±0.013 dex, the mass at the isochrone turn-off varies of ±0.015 M⊙, and the difference between ZAHB and turn-off log-luminosity varies of ±0.05 dex. The effect of the physical uncertainty affecting the age inferred from turn-off luminosity and from the vertical method are of ±0.375 Gyr and ±1.25 Gyr, respectively.
Key words: methods: statistical / stars: evolution / stars: horizontal-branch / stars: interiors / stars: low-mass / Hertzsprung-Russell and C-M diagrams
Appendices are available in electronic form at http://www.aanda.org
© ESO, 2012
1. Introduction
An evaluation of the global uncertainty in stellar models due to the micro-physical inputs is essential for understanding the actual significance of the application of these models when deriving quantitatively fundamental stellar, and even cosmological, parameters. In fact, theoretical models for the structure and evolution of stars are indispensable tools in many astronomical research areas. Much fundamental information on resolved stellar populations otherwise inaccessible, as for example the age, is obtained by comparing observational data and theoretical predictions. Furthermore, evolutionary models play a crucial role also in the studies of unresolved stellar populations, since they are a fundamental ingredient for the required stellar population synthesis tools. As such, in the last decades a huge effort has been focused on refining the accuracy and reliability of evolutionary predictions. As a result, stellar evolution theory has become one of the most robust area of astrophysical research allowing a firm understanding of the main stellar population characteristics.
However, the current generation of stellar models are still affected by not negligible uncertainties, as proved by the discrepancies among the stellar tracks and isochrones computed by different authors adopting different input physics and/or prescriptions for the treatment of processes occurring in stars. These models are in fact the result of complex calculations relying on many physical assumptions (i.e. equation of state, radiative and conductive opacities, nuclear reaction cross sections, neutrino emission rates, etc.), algorithms describing physical processes (i.e. convective transport, rotation, etc.), and input parameters (i.e. initial metallicity, initial helium abundance, heavy-element mixture, etc.), each affected by uncertainties.
A first estimate of the uncertainty in stellar models can be obtained by comparing the results provided by different authors and codes (see e.g. Bertelli et al. 2009; Dotter et al. 2007; Pietrinferni et al. 2006). However, this kind of approach does not allow to disentangle and quantify the contributions of the various uncertainty sources.
A more suitable approach consists in changing a given input physics at a time keeping all the other inputs and parameters fixed. For hydrogen-burning models of metal poor low-mass stars, an early example of this technique is provided by Chaboyer et al. (1995) and subsequently extended to more advanced evolutionary phases by various authors such as Cassisi et al. (1998); Brocato et al. (1998); Castellani & Degl’Innocenti (1999), and for white dwarf cooling models by Prada Moroni & Straniero (2002). Many other papers followed this approach focusing on different mass ranges and/or evolutionary phases (see e.g. Castellani et al. 2000; Imbriani et al. 2001; Salaris et al. 2002; Imbriani et al. 2004; Weiss et al. 2005; Prada Moroni & Straniero 2007; Valle et al. 2009; Tognelli et al. 2011).
However, the previous method does not allow to quantify the possible interactions among the different input physics. A more systematic and exhaustive analysis consists in varying simultaneously all the main input physics adopting either a Monte Carlo technique (see e.g. Chaboyer et al. 1996, 1998; Chaboyer & Krauss 2002; Krauss & Chaboyer 2003; Bjork & Chaboyer 2006) or a systematic variation of the inputs in a fixed grid. These kind of studies are clearly much more time consuming than the previous ones, since they require the computation of a huge number of stellar models. This is the reason why a thorough analysis of this kind is still lacking.
In the present paper we begin to fill this gap focusing only on the impact on stellar models of low-mass stars, from the main sequence (MS) to the zero age horizontal branch (ZAHB), of the uncertainties affecting some of main physical inputs adopted in modern stellar evolution codes.
The aim is twofold: first, to give an estimate of the cumulative effect of physical uncertainties on the tracks, isochrones and on the main stellar quantities; second, to break down such a global variability, evidencing the effects of the single physical inputs on different stages of stellar evolution.
Relying on the computation of a large number of stellar models (i.e. 3159 stellar tracks and 567 isochrones), we performed a rigorous statistical analysis of the effects of the variations of the chosen physical inputs on relevant stellar evolutionary features, such as the turn-off luminosity, the central hydrogen exhaustion time, the luminosity and helium-core mass at the Red Giant Branch (RGB) tip, and the ZAHB luminosity in the RR Lyrae region at log Teff = 3.83.
Section 2 is devoted to a description of the method employed for the calculations and of the physical inputs relevant to the calculations and of their current uncertainty. Sections 3 and 4 present and analyze the results on the global uncertainty of our reference model due to all the variations of the chosen inputs within their estimated uncertainty. In Sects. 5 and 6 we report the corresponding uncertainty on the isochrones. Some concluding remarks are given in Sect. 7.
2. Description of the method
For the present analysis we are only interested in quantifying the theoretical uncertainty
affecting low-mass stellar models due to the cumulative effects of the uncertainties in the
main input physics. We focus on the typical member of an old stellar population, choosing
for reference a M = 0.90 M⊙ model with
initial metallicity Z = 0.006 – suitable for metal-rich galactic globular
clusters and in the Magellanic Clouds – with heavy elements solar mixture by Asplund et al. (2009). The initial helium abundance,
Y = 0.26, was obtained following the often adopted linear helium-to-metal
enrichment law given by: 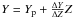 , with
cosmological 4He abundance Yp = 0.2485 (Cyburt et al. 2004; Steigman 2006; Peimbert et al. 2007a,b). In this work we assume
ΔY/ΔZ = 2, a typical value for this quantity, still
affected by several important sources of uncertainty (Pagel
& Portinari 1998; Jimenez et al.
2003; Flynn 2004; Gennaro et al. 2010).
, with
cosmological 4He abundance Yp = 0.2485 (Cyburt et al. 2004; Steigman 2006; Peimbert et al. 2007a,b). In this work we assume
ΔY/ΔZ = 2, a typical value for this quantity, still
affected by several important sources of uncertainty (Pagel
& Portinari 1998; Jimenez et al.
2003; Flynn 2004; Gennaro et al. 2010).
The adopted stellar evolutionary code, FRANEC, has been extensively described in previous papers (Cariulo et al. 2004; Degl’Innocenti et al. 2008, and references therein). A detailed discussion of the recent updates of the physical inputs can be found in Valle et al. (2009) and Tognelli et al. (2011). The code adopted here is the same used for the construction of the Pisa Stellar Evolution Data Base1 for low-mass stars, as illustrated in Dell’Omodarme et al. (2012), where a detailed description of the inputs of the stellar evolutionary code and of the ZAHB2 construction technique can be found.
The mixing length formalism (Böhm-Vitense 1958) is used to treat the convective transport in superadiabatic regions. In such a scheme the convection efficiency depends on the mixing length parameter l = αmlHp, where Hp is the local pressure scale height and αml a free parameter to be calibrated.
The treatment of the superadiabatic convective transport is one of the weakest aspect in current generation of stellar evolution codes and consequently one of the main sources of theoretical uncertainty, which, however, mainly affects effective temperature predictions while luminosity evaluations are affected in very much less extent. Such an uncertainty should be considered as systematic and due to an oversimplified treatment of a very complex phenomenon, whose precise physical description is not yet available. Since we are interested only in evaluating the cumulative effect of the main input physics uncertainties, we did not take into account the effect of the large error in the efficiency of the superadiabatic convective transport, i.e. on the αml value. For this reason, all the models computed in the present analysis adopt αml = 1.90. However, a change of the αml value chosen in the computations might in principle affect the estimate of the extent of the cumulative uncertainties in stellar predictions. For this reason, as shown in detail in Appendix C, we computed additional sets of models with two different mixing-length parameter values, namely αml = 1.70 and 1.80, checking the robustness of the results presented in the paper for a reasonable change in the mixing-length value.
2.1. Input physics uncertainties
The computation of stellar models relies on the detailed knowledge of matter and radiation behavior in the temperature and density regimes typical of stellar interiors. These input physics include: radiative and conductive opacities, equation-of-state (EOS), nuclear reaction cross sections, neutrino emission rates (i.e. plasma, photo, pair, and bremsstrahlung processes).
In this subsection, we briefly summarize the uncertainty on the up to date input physics, focusing only on those which play a relevant role in the structure and evolution of the reference case, with the notable exception of the EOS. In fact, in spite of its importance in modeling stellar interiors, a detailed and rigorous evaluation of the propagation of the EOS uncertainties into the final model is a difficult task. The reason is that the main thermodynamic quantities required for computing stellar models (i.e. pressure, temperature, density, specific heat, adiabatic gradient, etc.) are available only in the form of numeric tables, where the values of the various quantities are given without the associated uncertainty. Furthermore, those thermodynamic quantities are related in a not trivial way. Thus, we preferred to fix the EOS as it was without errors rather than adopting a too crude treatment.
Present calculations used the most recent version of the OPAL EOS3, namely the 2006 release (Rogers et al. 1996; Rogers & Nayfonov 2002).
Anyway, an estimate of the impact of two different choices of EOS is presented in Appendix D, where we evaluate the differences in the evolutionary features computed with OPAL and FreeEOS (Irwin 2004).
Nuclear reaction rates.
Regarding the nuclear reactions relevant for hydrogen and helium burning phases, we adopted the same cross sections detailed in Dell’Omodarme et al. (2012). In order to avoid the huge and useless explosion of computational time that would result taking into account the uncertainty in the cross sections of all the nuclear reactions belonging to the hydrogen and helium burning networks, we limited the analysis only to the three main reactions, namely the 1H(p, νe+)2H, 14N(p,γ)15O, and triple-α. In fact the 1H(p, νe+)2H and 14N(p,γ)15O have the lowest cross sections which thus drive, respectively, the efficiency of the proton-proton chain and the CNO cycle, while the triple-α cross section influences both the core helium flash and the ZAHB luminosity.
Experimental measurements of the 1H(p, νe+)2H cross section are not available, thus one has to rely only on theoretical models. The uncertainty in the Spp(0) factor is on the order of 1% (Kamionkowski & Bahcall 1994; Adelberger et al. 1998, 2011). However, the current version of the FRANEC, as many other evolutionary codes, calculates the 1H(p, νe+)2H reaction rate following the analytical approximation provided by the NACRE compilation (Angulo et al. 1999), whose accuracy with respect to the tabulated rates is better than 3%. This is the value of uncertainty we adopted as it is the dominant source of error in the rate calculations.
For 14N(p,γ)15O reaction rate we used the recent estimate by Imbriani et al. (2005). The uncertainty on the analytical fit given in that paper is about 8 ÷ 10% in the range of temperature [106−108] K. In the calculations we assumed an uncertainty of 10%.
Fynbo et al. (2005) reported new measurements for the triple-α rate: however, in the temperature range of interest, the differences with respect to the most widely adopted rate (NACRE, Angulo et al. 1999) are within the uncertainty evaluated in the NACRE compilation, reaching a maximum of ≈20% at temperatures of about 108 K (see e.g. Weiss et al. 2005). For this reason we decided to take the error quoted by NACRE (20%), in the temperature range of interest, as an estimate of the uncertainty on the triple-α reaction rate.
 |
Fig. 1 Contour plots of the difference between OPAL and OP calculations for different
hydrogen abundance X and metallicity Z = 0.004.
The temperature T is in K, while R is in
g cm-3 K-3. The colored scale marks the values of the
relative difference |
Radiative opacity.
The radiative opacity is one the most important input for stellar model calculations. As described in Dell’Omodarme et al. (2012), we implemented in our code the opacity tables provided in 2005 by OPAL4 (see e.g. Iglesias & Rogers 1996) for log T(K) > 4.5 and by Ferguson et al. (2005) for lower temperatures. Both opacity tables have been computed adopting the solar heavy-element mixture by Asplund et al. (2009).
In spite of the crucial importance of radiative opacity in the computation of stellar
models, the quoted tables do not contain the uncertainty associated to the single
Rosseland mean opacity coefficients. Furthermore, neither Iglesias & Rogers (1996) nor Ferguson et al. (2005) provide even a rough estimate of the accuracy of the
results. The same occurs for the radiative opacity tables made available by the Opacity
Project (OP; Seaton & Badnell 2004; Badnell et al. 2005). Given such a situation, a first
idea of the accuracy level of the current radiative opacity generations can be achieved
by comparing the results provided by different and independent groups. Rose (2001) performed this kind of analysis for a
plasma mixture very similar in composition, temperature, and density to that in the
Sun’s center finding an agreement between Rosseland mean opacity coefficients provided
by different codes at the level of 5%. The agreement gets worse at different plasma
conditions, as shown by comparing the results provided by OPAL and OP (hereafter
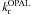 and
and
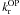 ) over their
whole validity domain, which are in agreement within about 10–15% (Seaton & Badnell 2004; Badnell
et al. 2005).
) over their
whole validity domain, which are in agreement within about 10–15% (Seaton & Badnell 2004; Badnell
et al. 2005).
To further extend the investigation, we evaluated the differences in the
(log T, log R) plane between OPAL and OP radiative
opacities computed for Asplund et al. (2009) solar
elements mixture. As in OPAL and OP works, we used here the variable
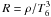 , where
ρ is the mass density and
T6 = 10-6 × T
with T in K. Figure 1 shows the
values of
, where
ρ is the mass density and
T6 = 10-6 × T
with T in K. Figure 1 shows the
values of 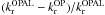 in
four contour plots, for different hydrogen abundances (i.e. X = 0.8,
0.5, 0.2, and 0.0) and metallicity Z = 0.004. Notice that we did not
plot the comparison for the same metallicity of our reference track, i.e.
Z = 0.006, because the corresponding tables are not available neither
in OPAL nor OP calculations, thus we preferred to use the nearest value of the
metallicity for which both groups provide the opacity tables, i.e.
Z = 0.004, rather than interpolate. The computed evolution of the
standard stellar model with M = 0.90 M⊙,
Z = 0.006, Y = 0.26 is superimposed to each panel.
To give an indication of the region spanned in the plane by the whole stellar structure,
we showed the path of four different mass fractions of the structure, from the center to
the outer layers, corresponding to the 0.99974 mass fraction (labels from 0.00 to 1.00
in Fig. 1, respectively).
in
four contour plots, for different hydrogen abundances (i.e. X = 0.8,
0.5, 0.2, and 0.0) and metallicity Z = 0.004. Notice that we did not
plot the comparison for the same metallicity of our reference track, i.e.
Z = 0.006, because the corresponding tables are not available neither
in OPAL nor OP calculations, thus we preferred to use the nearest value of the
metallicity for which both groups provide the opacity tables, i.e.
Z = 0.004, rather than interpolate. The computed evolution of the
standard stellar model with M = 0.90 M⊙,
Z = 0.006, Y = 0.26 is superimposed to each panel.
To give an indication of the region spanned in the plane by the whole stellar structure,
we showed the path of four different mass fractions of the structure, from the center to
the outer layers, corresponding to the 0.99974 mass fraction (labels from 0.00 to 1.00
in Fig. 1, respectively).
Looking at the panels of Fig. 1 we see that, for the selected model, a 5% uncertainty on the values of radiative opacities is adequate, so we adopted this value in the calculations. We assumed the same uncertainty also for the low-temperature radiative opacity coefficients computed by Ferguson et al. (2005).
Conductive opacity.
In regions of stellar interiors characterized by electron degeneracy, as in the helium core of low-mass red giant stars, thermal electron conduction, elsewhere inefficient, contributes significantly to the energy transport. Thus, in these regimes it becomes an important input which affects the stellar model.
For the electron conduction opacities kc, we adopted the results by Cassisi et al. (2007), which improved the conductive opacities by Potekhin (1999). In the mildly degenerate, weakly or moderately coupled plasmas, typical of the red giant helium cores, the dynamical plasma screening may be non-negligible. This effect was studied by Lampe (1968), but it was not included in either Hubbard & Lampe (1969) or in Cassisi et al. (2007) calculations. Using an estimate for the correction due to the dynamical plasma screening, Potekhin suggested (2011, priv. comm.) that Cassisi et al. (2007) opacities are uncertain by 5% at the center and few ten percent in the outer regions of the helium core. However, in our case the uncertainty is lower than the 10% in about the 80% of the He-core mass, which roughly corresponds to the zone dominated by electron conductivity. So we adopted a 5% uncertainty as sensible choice for conductive opacity.
Neutrino emission rates.
At high temperature and density, several processes of neutrino emission are efficient (i.e. plasma, photo, pair, and bremsstrahlung processes), which provide additional and relevant energy loss channels in stellar interiors, with the consequent significant effect on stellar structures. During the red giant phase for the chosen reference case, in the dense and not extremely hot helium core, neutrino losses are dominated by the plasma neutrino emission process, whose efficiency affects important quantities of red giant evolution, such as the helium core mass and the stellar luminosity at the helium-flash onset.
We followed the fitting formulae given in Haft et al. (1994) to compute the plasma neutrino emission rate. As reported in literature (Itoh et al. 1996; Haft et al. 1994), the accuracy of that approximation is better than 4% for almost every value of temperature and density and better than 5% everywhere. In the calculations, we adopted an uncertainty of 4%.
Helium and heavy elements diffusion velocities.
The computation of the diffusion velocities of helium and heavy elements in our code is performed by the routine developed by Thoul et al. (1994; for more details see e.g. Castellani et al. 1997; Dell’Omodarme et al. 2012). These diffusion velocities are generally thought to be accurate at 10 ÷ 15% (see e.g. Thoul et al. 1994), thus, in the present computations we adopted a conservative uncertainty of 15%.
The selected physical inputs and their assumed uncertainty are listed in Table 1.
2.2. Method to evaluate the cumulative uncertainties
The complexity of stellar evolution calculations hampers an analytical evaluation of the impact of the variation of the chosen inputs on stellar models calculation, so that the problem must be addressed by direct computation of perturbed stellar models, i.e. models adopting physical inputs perturbed within the uncertainties.
Several choices are available for the design of the sample to investigate. As already discussed in the introduction, the widely followed approach is to allow for the variation of one parameter at a time, making possible the quantification of the separate effect of the studied inputs. This approach is, however, vulnerable in presence of interactions among the inputs, since it does not allow to detect a possible synergyc effect due to the variation of several inputs at a time.
To avoid this weakness, we employ a more robust, even if much more computationally expensive, technique namely a systematic variation of the inputs on a fixed grid. For each physical input, we introduced a three-values multiplier pi with value 1.00 for the reference case and values 1.00 ± Δpi for perturbed cases (Δpi is the uncertainty listed in Table 1), which defines the range of variations. For each stellar track calculation, a set of multiplier values (i.e. p1,...,p7 for the seven input physics allowed to vary) is chosen and kept constant during the evolution of the stellar structure. To cover the whole parameters space, calculations of stellar tracks were performed for a full crossing, i.e. each parameter value pi was crossed with all the values of the other parameters pj, with j ≠ i. In this way, we computed stellar models for all the possible sets of multiplier values. A total of 37 = 2187 tracks were then computed, with same mass, chemical composition and αml.
Physical inputs perturbed in the calculations and their assumed uncertainty.
The technique allows the exploration of the edge of the variability region, and it is robust in presence of interaction among the inputs of the calculations, since it does not assume physical independence of the individual processes.
An alternative approach to the problem would require the use of Monte Carlo simulations (see e.g. Chaboyer et al. 1996, 1998; Chaboyer & Krauss 2002; Krauss & Chaboyer 2003; Bjork & Chaboyer 2006): this technique allows the construction of probabilistic confidence intervals for the most interesting evolutionary features.
The grid technique employed is distribution-free, i.e. it needs only the specification of a sensible range of variation for each physical input, and it does not rely on explicit specification of the parent distributions of the physical parameters that we varied. The simpler grid variation technique has the additional advantage to be less computationally expensive than a Monte Carlo. In fact a key value to evaluate for a Monte Carlo simulation is the number of runs N to perform in order to have an acceptable coverage of the input parameter hyperspace. As an example, dividing the range of variation of all the parameters in 4 zones according to quartiles, the hyperspace of parameters will consist on n = 47 = 16 384 hypercells. In the hypothesis that all the parameters have uniform distribution, the probability of having k hit of a cell during the Monte Carlo simulations is given by Poisson density function with mean N/n: P(k,N/n) = kN/n/(N/n) ! e−k. If we require a probability α that a cell has zero hit – i.e. it is unexplored during the simulations – we have: P(0,N/n) = α. Solving for α = 0.15, an acceptable compromise between coverage of the hyperspace and accuracy of the output, it results N ≈ 31 000 run, which is an order of magnitude bigger than our sample size.
3. Global physical uncertainty in stellar models
The availability of a large set of stellar models covering all the possible combinations of simultaneously perturbed input physics allow us to quantify the cumulative physical uncertainty in stellar models.
The combined effect in the theoretical plane (log Teff, log L/L⊙) of the variation of all the seven physical inputs (i.e. p1,...,p7 in Table 1) selected for the calculations is displayed in Fig. 2, where the track computed with the standard inputs is enveloped by an error stripe constructed by considering the region of the plane spanned by the perturbed stellar models. To the best of our knowledge, this is the first time that an error stripe is computed and plotted for theoretical stellar tracks. A detailed description of the technique employed for the construction of the stripe is given in Appendix A.
The considerable narrowing of the error stripe in the RGB is due to the fact that the perturbed stellar models are disposed along the tracks itself and do not imply the vanishing of the uncertainty. This effect is best evidenced in left panel of Fig. 3 which displays the range in Δlog L/L⊙, computed with respect to the standard track, from ZAMS to helium flash. To perform the comparison, the raw tracks were reduced to a set of tracks with the same number of homologous points. Details about the reduction procedure are reported in Appendix A. We note that the error stripe has a nearly constant width of about 0.05 dex until the central hydrogen exhaustion, while the error grows to about 0.07 dex in the final part of RGB, from the RGB bump to helium flash.
To compare this uncertainty with the one due to a variation in the initial chemical composition, Fig. 3 also shows stellar models computed with standard physical input but different Z and Y. We trace a variation in [Fe/H] of ±0.07 – a typical value of uncertainty for a cluster of metallicity similar to our reference case – with unchanged ΔY/ΔZ = 2, resulting in two sets: the first one with Z = 0.005, Y = 0.258 and the second one with Z = 0.007, Y = 0.262. As one can see in the figure, the impact of the quoted chemical variation on the predicted stellar luminosity is essentially the same of the input physics uncertainties until the central hydrogen exhaustion. At later evolutionary stages the former effect prevails, becoming the dominant by approximately 20% after RGB bump.
As for evolutionary time, in the right panel of Fig. 3 we show the evolution of the central hydrogen abundance Xc as a function of time (Gyr). In this case the effect of the variation of the physical inputs is larger than the one due to the quoted changes in chemical abundances. For instance, the range for the Xc exhaustion time due to physics variation is [9.83–11.26] Gyr, while the one due to chemical variation is [10.03–11.00] Gyr.
 |
Fig. 2 Left panel: Hertzsprung-Russell (HR) diagram showing the error stripe due to the variation of all the seven analyzed physical inputs (i.e. p1,...,p7 in Table 1) on the stellar track with M = 0.9 M⊙, Z = 0.006, Y = 0.26 from pre-main sequence to helium flash. The narrowing of the error stripe in the RGB is due to the fact that the perturbed stellar models are disposed along the tracks itself. See text for details. Right panel: as in the left panel, but for the ZAHB. |
 |
Fig. 3 Left panel: Δlog L/L⊙ with respect to the track computed with standard inputs from ZAMS to helium flash. The comparison was performed on a set of reduced tracks with the same number of homologous points. Right panel: central hydrogen abundance Xc vs. time (Gyr). In both panels, the red solid and green dashed lines show for comparison the output of models with standard physical inputs and Z = 0.005, 0.007 respectively. |
The radius is another quantity worth to be discussed, whose accurate determination is important also in determining the properties of any orbiting exoplanet. Regarding the impact of the perturbed physical inputs on the predicted stellar radius, in Fig. 4 we show the range in ΔR/R, computed with respect to the standard track, from ZAMS to helium flash. The error stripe has an increasing width from about 0.02 at the ZAMS to about 0.04 at the central hydrogen exhaustion, while the width grows to about 0.09 in the final part of RGB.
We quantified also the global physical uncertainty in the theoretical predictions of
various stellar quantities of common interest, namely the turn-off luminosity, the central
hydrogen exhaustion time tH, the luminosity
Ltip and the helium core mass
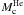 at the RGB tip, and
the ZAHB luminosity in the RR Lyrae region LHB. In the case of
turn-off luminosity we chose to investigate the luminosity of a point brighter and 100 K
lower than the turn-off (hereafter BTO), adopting a technique similar to the one proposed by
Chaboyer et al. (1996) for isochrones in the
(B − V,V) plane. This method has the advantage of
reducing the intrinsic luminosity variation of the canonical turn-off, whose position is
difficult to accurately identify both in observed Hertzsprung-Russell (HR) diagrams and in
theoretical tracks/isochrones, as a consequence of the almost vertical slope (i.e. large
luminosity variation at essentially the same effective temperature). Then, a small
fluctuation in the effective temperature determination could have a large effect in the
determination of the turn-off luminosity.
at the RGB tip, and
the ZAHB luminosity in the RR Lyrae region LHB. In the case of
turn-off luminosity we chose to investigate the luminosity of a point brighter and 100 K
lower than the turn-off (hereafter BTO), adopting a technique similar to the one proposed by
Chaboyer et al. (1996) for isochrones in the
(B − V,V) plane. This method has the advantage of
reducing the intrinsic luminosity variation of the canonical turn-off, whose position is
difficult to accurately identify both in observed Hertzsprung-Russell (HR) diagrams and in
theoretical tracks/isochrones, as a consequence of the almost vertical slope (i.e. large
luminosity variation at essentially the same effective temperature). Then, a small
fluctuation in the effective temperature determination could have a large effect in the
determination of the turn-off luminosity.
Total range of variation and range half-width of the theoretical predictions for the selected quantities for our reference case, i.e. M = 0.90 M⊙ with Z = 0.006 and Y = 0.26, due to input physics uncertainties.
Table 2 lists the total range of variation in
predictions of the selected quantities for our reference stellar track due to current input
physics uncertainties. The turn-off log luminosity log LBTO
varies in the range [0.334–0.376] dex (range half-width 0.021 dex, ≈6% of the value
obtained with unperturbed physical inputs). The total range of variation of the predicted
central hydrogen exhaustion time tH is [9.83–11.26] Gyr
(0.72 Gyr, ≈6.5%). The RGB tip log Ltip and ZAHB
log LHB log luminosities vary, respectively, in the ranges
[3.38–3.44] dex (0.03 dex, ≈1%) and [1.52–1.61] dex (0.045 dex, ≈3%). Finally, the
helium core mass at the RGB tip 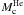 varies in the
range [0.4796–0.4879] M⊙
(0.0042 M⊙, ≈0.85%).
varies in the
range [0.4796–0.4879] M⊙
(0.0042 M⊙, ≈0.85%).
4. Statistical analysis of physical uncertainty in stellar models
The large set of computed stellar models is suitable for an accurate statistical analysis of the effect of the variation of the chosen physical inputs on relevant stellar evolutionary features. Beside the quantification of the whole range of uncertainty performed in the previous section, it is possible to disentangle the effects of the different physical inputs on the above selected stellar quantities.
The dependence of the aforementioned evolutionary quantities on physical inputs was
explored by means of linear regression models. These models were constructed extracting the
values of the chosen dependent variable in study (i.e. LBTO,
tH, Ltip,
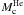 , and
LHB) from the computed stellar tracks and regressing it
against the independent variables (more properly defined as predictor variables or
covariates), in our case the values of the
parameter pi.
, and
LHB) from the computed stellar tracks and regressing it
against the independent variables (more properly defined as predictor variables or
covariates), in our case the values of the
parameter pi.
The regression model construction started from models linear in the physical inputs, since a priori we do not anticipate the need of higher power of the inputs. Similarly, at first no interaction among the covariates were considered. These choices were supported by the detailed a posteriori analysis of each regression model: it results in fact that the insertion of higher power of the predictors or explicit interaction among them is not needed, because the aforementioned linear models capture almost the whole variation of the data. These models included as covariates only the physical inputs which can have an influence on the studied evolutionary feature: for LBTO and tH only the first four parameters of Table 1, while for later evolutionary stages all the parameters were used. The models were fitted to the data with a least-squares method using the software R 2.14.1 (R Development Core Team 2011). Results of the statistical analyses were considered statistical significant for p-value < 0.05.
For the BTO log-luminosity log LBTO and
tH the regression models were:
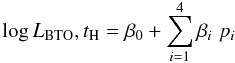 (1)where
β0,...,β4
were the regression coefficients to be estimated by the fit and
p1,...,p4
respectively the perturbation multipliers (see Table 1) for 1H(p, νe+)2H and
14N(p, γ)15O reaction rates, radiative opacity
kr, and microscopic diffusion velocities.
(1)where
β0,...,β4
were the regression coefficients to be estimated by the fit and
p1,...,p4
respectively the perturbation multipliers (see Table 1) for 1H(p, νe+)2H and
14N(p, γ)15O reaction rates, radiative opacity
kr, and microscopic diffusion velocities.
Fit of BTO log-luminosity (dex).
Fit of central hydrogen exhaustion time (Gyr).
 |
Fig. 4 ΔR/R with respect to the track computed with standard inputs from ZAMS to helium flash. |
 |
Fig. 5 Boxplot of the impact of the variation of the most important physical inputs on log LBTO and on tH. The black thick lines show the median of the data set, while the box marks the interquartile range, i.e. it extends form the 25th to the 75th percentile of data. The whiskers extend from the box until the extreme data. For each parameter pi, the labels low, std and high refer to the values 1.00−Δpi, 1.00, and 1.00 + Δpi. |
The regression model coefficients, along with their statistical significance, are listed in
Tables 3 and 4. In the first two columns of the tables we report the least-squares estimates of
the regression coefficients and their errors; in the third column we report the
t-statistic for the tests of the statistical significance of the
covariates. In the last row of the tables we report the residual standard error of the
fit σ and the value of the squared multiple correlation coefficient
R2, i.e. the fraction of the variance of the data explained by
the model, defined as: 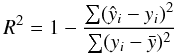 (2)where
yi are the values of the dependent variable,
(2)where
yi are the values of the dependent variable,
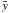 their mean value, and ŷi the values predicted
by the linear model.
their mean value, and ŷi the values predicted
by the linear model.
All the tests reach a very high statistical significance (p-values <2 × 10-16). The physical relevance of the different covariates can be assessed by looking at Fig. 5 where we show the boxplots highlighting the influence of the variation of the inputs among the three values chosen for the calculations. For each parameter pi the boxplots are a convenient way to summarize the variability of the data subsetted according to the three values of pi (1.00−Δpi, 1.00, and 1.00 + Δpi, labeled as low, std, and high in the plots). The black thick lines show the median of the data set, while the box marks the interquartile range, i.e. it extends form the 25th to the 75th percentile of data. The whiskers extend from the box until the extreme data, the bottom whisker ranges from the sample minimum to the first quartile while the top whisker from the third quartile to the sample maximum. While the position of the medians are related to the effect of the parameter in study in each plot, the extension of the box and whiskers are due to the variation of all the other parameters. The larger the separation of the medians with respect to the dimension of the boxes and the greater the importance of a given parameter.
The figures show that the radiative opacity uncertainty largely dominates for both LBTO and tH. For LBTO the impact of an increase of 5% in kr is Δlog LBTO/L⊙ = 0.05 × (− 0.276) = −0.0138 dex, while the impact of the variation of the second most important input – i.e. 14N(p, γ)15O reaction rate – is only Δlog LBTO/L⊙ = −0.0028 dex. The sum of the effects in the statistical models does not account for the whole variation of the data, due to the presence of the random variation extracted in the residuals of the statistical models.
In the case of tH the dominance of kr is even larger since its variation accounts for ΔtH = 0.579 Gyr, and the second most important input, the microscopic diffusion velocities, for ΔtH = 0.065 Gyr.
Fit of RGB tip log-luminosity (dex).
Fit of helium core mass 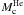 (M⊙).
(M⊙).
Fit of the ZAHB log-luminosity log LHB (dex) at log Teff = 3.83.
In the cases of log Ltip, log LHB
and 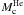 the linear
models were:
the linear
models were: 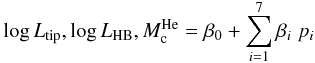 (3)where
the three additional physical inputs considered are respectively the
triple-α reaction rate, the neutrino emission rate, and the conductive
opacity kc (see Table 1).
The regression model coefficients, along with their statistical significance, are listed in
Tables 5–7.
The boxplots of the influence of the various inputs on the calculations are presented in
Figs. 6–8.
(3)where
the three additional physical inputs considered are respectively the
triple-α reaction rate, the neutrino emission rate, and the conductive
opacity kc (see Table 1).
The regression model coefficients, along with their statistical significance, are listed in
Tables 5–7.
The boxplots of the influence of the various inputs on the calculations are presented in
Figs. 6–8.
For log Ltip and log LHB the most important factor is again the radiative opacity kr, although its impact is not as dominant as in the previous cases. For instance, in the case of Ltip, the impact of an increase of 5% in kr is Δlog Ltip/L⊙ = −0.0149 dex, while the variation of the second most important input, the triple-α reaction rate, accounts for Δlog Ltip/L⊙ = −0.0061 dex, i.e. about 40% of the kr effect.
For LHB the effect of the variation of kr is Δlog LHB/L⊙ = −0.0216 dex, while the one of triple-α is Δlog LHB/L⊙ = −0.0115 dex, i.e. about 55% of the previous one.
Regarding the helium core mass, the main variation is due to triple-α
reaction rate: an increase of 20% of this value accounts for
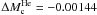 M⊙;
the effect due to the uncertainty on neutrino emission rate, radiative and conductive
opacities are all of the same order, i.e. about 45% of the triple-α one
each, while 14N(p, γ)15O reaction rate uncertainty
accounts for about 35% of the triple-α effect.
M⊙;
the effect due to the uncertainty on neutrino emission rate, radiative and conductive
opacities are all of the same order, i.e. about 45% of the triple-α one
each, while 14N(p, γ)15O reaction rate uncertainty
accounts for about 35% of the triple-α effect.
 |
Fig. 6 Boxplot of the impact of the variation of the most important physical inputs on Ltip. |
 |
Fig. 7 Boxplot of the impact of the variation of the most important physical inputs on
|
 |
Fig. 8 Boxplot of the impact of the variation of the most important physical inputs on LHB. |
The statistical models presented in this section rely on the assumption of the linearity of the output of the calculations with respect to the perturbations of the physical inputs. As a check of this hypothesis, we made some additional runs varying only one parameter at a time, in a set of 9 points spanning the assumed range of uncertainty. The procedure is fully justified by the lack of interaction among physical inputs in the linear models presented in Tables 3–7. In fact in presence of a relevant interaction, the values of the multiple correlation coefficient R2 of the fits would be much smaller than the ones found in the models, which had a minimum value of 0.997 for LBTO, i.e. the 99.7% of the variance of the data are explained by the model.
In Fig. 9 we present a graphic test of linearity. The four panels show, for each evolutionary feature studied in the section, the results of the calculations for the variation of the two most important physical inputs with superimposed the linear fit of the different trends. In all the cases the assumption of linearity is respected with high accuracy.
Since the hypotheses of linearity in the inputs and their independence hold, the statistical models presented in this section can be safely used to interpolate the effect of a perturbation of the physical inputs in the assumed range.
In the case of the central hydrogen exhaustion time (i.e. Xc = 0), the effect of the radiative opacity variation will equate the one due to the second most important contribution, namely that due to the microscopic velocity variation, for a perturbation estimated as the product of assumed perturbation by the ratio of the effect of the two inputs as resulted by the model, i.e. 0.05 × 0.065/0.58 = 0.0056. This means that in order to reduce the uncertainty in the predicted main sequence lifetime due to the radiative opacity at the level of the second largest contribution, the uncertainty affecting the Rosseland mean opacity should decrease from the currently adopted 5% down to 0.56%. For the turn-off LBTO and ZAHB LHB luminosities, the radiative opacity remains the most important uncertainty source for assumed perturbation greater or equal to 0.05 × 0.0028/0.014 = 0.01 and 0.05 × 0.012/0.022 = 0.027, respectively. Thus, in order to reduce the uncertainty in the turn-off luminosity caused by the radiative opacity to the same order of that caused by the second most important contribution, i.e. the 14N(p, γ)15O reaction rate, the uncertainty of the former should be decreased from 5% to 1%. Finally, the radiative opacity should be known with a precision better than about 2.7% to lead a variation in the predicted ZAHB luminosity lower than the second largest contribution, i.e. the triple-α reaction rate.
5. Global physical uncertainty in stellar isochrones
The direct theoretical counterparts of the observed color-magnitude diagrams of simple stellar populations are isochrones rather than tracks with fixed mass. For this reason, we extended the previous statistical analysis of the physical uncertainties affecting stellar models to isochrones with age in the range 8–14 Gyr, suitable for galactic globular clusters, with time steps of 1.0 Gyr.
Since we were interested mainly in studying the variation near the turn-off region, we performed calculations varying only the four physical inputs p1, ..., p4 that can influence the evolution until this phase, as shown in the previous section. Thus, for each set of perturbed input physics, i.e. for each set of multipliers values p1, ..., p4, we computed a grid of stellar tracks with different masses, for a total of 34 = 81 grids. Each grid contains 12 stellar models with mass values chosen to accurately reconstruct the zone near the BTO, namely M = 0.40, 0.50, 0.60, 0.70, 0.80, 0.85, 0.87, 0.90, 0.92, 0.95, 1.00, 1.10 M⊙. Then we computed 972 stellar tracks and 567 isochrones with fixed chemical composition (Z = 0.006, Y = 0.26) and mixing-length parameter (αml = 1.90).
The global effect of the combined variation of the four selected inputs on the 12.0 Gyr isochrone in the (log Teff, log L/L⊙) plane is displayed in Fig. 10. The stripe around the isochrone computed with standard inputs represents the region of the plane spanned by the perturbed stellar models.
Figure 11 shows the boxplots of three selected
quantities as a function of the isochrone age, namely the turn-off luminosity
(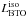 ) and mass
(
) and mass
(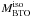 ), and the
differences between log LHB and
), and the
differences between log LHB and
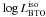 . The last one
is the theoretical counterpart of the ΔV(TO−HB), i.e. the visual
magnitude difference between turn-off and horizontal branch regions, used as age indicator
in the vertical method technique.
. The last one
is the theoretical counterpart of the ΔV(TO−HB), i.e. the visual
magnitude difference between turn-off and horizontal branch regions, used as age indicator
in the vertical method technique.
Table 8 lists the half-width of the variation range
in predictions of the selected quantities for our reference stellar isochrone of 12 Gyr due
to current input physics uncertainties. The turn-off log luminosity
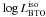 and mass
and mass
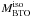 vary of
±0.013 dex and ±0.015 M⊙, respectively, while the
vary of
±0.013 dex and ±0.015 M⊙, respectively, while the
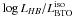 vary of
±0.05 dex.
vary of
±0.05 dex.
 |
Fig. 9 Study of the linearity of the outputs of the calculations with respect to the variation of the physical inputs in their range of uncertainty. The symbols are the results of the calculations, while the lines are the linear fit of each set of values. Only the two most important inputs are shown in each panel. |
6. Statistical analysis of physical uncertainty in stellar isochrones
To explore the influence of the physical inputs variation on the reconstructed turn-off
log-luminosity 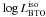 and mass
and mass
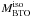 , we chose to pool
the results for different ages removing the trend due to the age, increasing the possibility
to detect the effect of the perturbations due to a larger statistic. The removal of the age
trend was done by adapting a linear model to either
, we chose to pool
the results for different ages removing the trend due to the age, increasing the possibility
to detect the effect of the perturbations due to a larger statistic. The removal of the age
trend was done by adapting a linear model to either 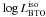 and
and
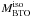 using as covariate
a categorical variable, i.e. a variable which assumes different values for each age. The
variable is then used as in a classical ANOVA (i.e. analysis of variance) model to filter
out the variation due to the different isochrones ages. The residuals of the models were
then regressed with respect to
p1,...,p4.
The procedure guarantees the removal of the mean trend from the data, i.e. every set of
residuals for each age has mean value of zero. The technique assumes that the effect of
pi are the same at different ages in the
studied time interval, i.e. 8–14 Gyr. As a rapid check of the hypothesis, we performed two
Bartlett tests of homogeneity of variances of residuals among ages (Snedecor & Cochran 1989). The tests did not suggest any problem
(
using as covariate
a categorical variable, i.e. a variable which assumes different values for each age. The
variable is then used as in a classical ANOVA (i.e. analysis of variance) model to filter
out the variation due to the different isochrones ages. The residuals of the models were
then regressed with respect to
p1,...,p4.
The procedure guarantees the removal of the mean trend from the data, i.e. every set of
residuals for each age has mean value of zero. The technique assumes that the effect of
pi are the same at different ages in the
studied time interval, i.e. 8–14 Gyr. As a rapid check of the hypothesis, we performed two
Bartlett tests of homogeneity of variances of residuals among ages (Snedecor & Cochran 1989). The tests did not suggest any problem
(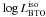 p-value = 0.16,
p-value = 0.16,
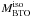 p-value = 0.26).
p-value = 0.26).
The results of the linear models for 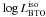 and
and
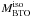 are in Tables 9 and 10,
respectively. In Figs. 12 and 13 we present the boxplots which evidence the influence of the variation
of the physical inputs among the three values chosen for the calculations. For the turn-off
mass
are in Tables 9 and 10,
respectively. In Figs. 12 and 13 we present the boxplots which evidence the influence of the variation
of the physical inputs among the three values chosen for the calculations. For the turn-off
mass 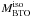 , the effect of the
variation of the radiative opacity is largely dominant. An increase of 5% in
kr produces a variation of
ΔM = 0.05 × 0.270 = 0.0135 M⊙, while the
impact of the variation of the second most important input – i.e. microscopic diffusion
velocities – is only ΔM = −0.0014 M⊙. The
total range of variation of
, the effect of the
variation of the radiative opacity is largely dominant. An increase of 5% in
kr produces a variation of
ΔM = 0.05 × 0.270 = 0.0135 M⊙, while the
impact of the variation of the second most important input – i.e. microscopic diffusion
velocities – is only ΔM = −0.0014 M⊙. The
total range of variation of 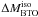 is
[–0.0184–0.0180] M⊙.
is
[–0.0184–0.0180] M⊙.
For the luminosity of the turn-off 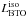 , no physical
input definitely dominates on the others. The most important factor turned out to be
radiative opacity with a variation
Δlog L/L⊙ = 0.0042 dex,
followed by 1H(p, νe+)2H reaction rate
with a variation
Δlog L/L⊙ = 0.0031 dex,
14N(p, γ)15O reaction rate with
Δlog L/L⊙ = −0.0029 dex,
and microscopic diffusion velocities with
Δlog L/L⊙ = −0.0026 dex.
The total range of variation of
, no physical
input definitely dominates on the others. The most important factor turned out to be
radiative opacity with a variation
Δlog L/L⊙ = 0.0042 dex,
followed by 1H(p, νe+)2H reaction rate
with a variation
Δlog L/L⊙ = 0.0031 dex,
14N(p, γ)15O reaction rate with
Δlog L/L⊙ = −0.0029 dex,
and microscopic diffusion velocities with
Δlog L/L⊙ = −0.0026 dex.
The total range of variation of 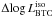 is
[–0.0142–0.0135] dex, about 2/3 of the one found in Sect. 3 for the turn-off luminosity log LBTO of the
reference track. This lower uncertainty in the isochrones with respect to the tracks used to
build them is due to the fact that isochrones of the same age but computed with different
sets of
multipliers p1,...,p4
values have turn-off regions populated by different masses
is
[–0.0142–0.0135] dex, about 2/3 of the one found in Sect. 3 for the turn-off luminosity log LBTO of the
reference track. This lower uncertainty in the isochrones with respect to the tracks used to
build them is due to the fact that isochrones of the same age but computed with different
sets of
multipliers p1,...,p4
values have turn-off regions populated by different masses
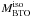 . As already shown,
the variation of kr splits the mass at BTO in three separate
sets for each value of the parameter (see Fig. 13).
The higher the value of kr, the more massive are the stellar
models at BTO. The luminosity of these models, which are intrinsically higher, are depleted
by the high value of the radiative opacity, as in the third panel of first row in Fig. 5. The opposite behavior was evidenced for low value of
kr. The net effect is a shrinkage of the luminosity range
spanned by the models.
. As already shown,
the variation of kr splits the mass at BTO in three separate
sets for each value of the parameter (see Fig. 13).
The higher the value of kr, the more massive are the stellar
models at BTO. The luminosity of these models, which are intrinsically higher, are depleted
by the high value of the radiative opacity, as in the third panel of first row in Fig. 5. The opposite behavior was evidenced for low value of
kr. The net effect is a shrinkage of the luminosity range
spanned by the models.
 |
Fig. 10 HR diagram showing the error stripe due to the variation of the physical inputs for a 12.0 Gyr isochrone (zoom of the TO region). |
 |
Fig. 11 Left panel: boxplots for BTO luminosity due to the variation of the selected physical inputs as a function of the isochrone age in Gyr. Central panel: same plot for mass at BTO. Right panel: same plot for difference of HB and BTO log luminosity. |
The most important and common application of theoretical isochrones is the age estimate of
stellar clusters. As such, it would be of primary importance to evaluate the current
uncertainty affecting the age inferred from the comparison between observed and predicted
turn-off luminosity, in addition to the uncertainty in the BTO luminosity at a given age
analyzed above. The computed isochrones can be used for such purpose, even if a special care
is needed. In fact a direct modeling of the age with respect to
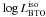 is not
feasible, since the age is used in the calculation as a parameter with null uncertainty and
it cannot be viewed as random variable, as required for a linear model dependent variable.
Therefore we proceed in the following way. We found that the relation between
is not
feasible, since the age is used in the calculation as a parameter with null uncertainty and
it cannot be viewed as random variable, as required for a linear model dependent variable.
Therefore we proceed in the following way. We found that the relation between
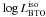 and the age
is well described by the following linear model:
and the age
is well described by the following linear model:
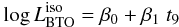 (4)where
t9 = log t, with t the age
of the isochrone in Gyr. The parameters of the model are:
β0 = 1.2871, β1 = −0.8771, with
σ = 0.0056 dex. Since we do include explicitly the contribution of the
parameter
p1,...,p4,
they contribute to the inflation of the residual standard error of the model, reflecting our
global uncertainty. This model can be used to perform a reverse inference on the value of
the age, given
(4)where
t9 = log t, with t the age
of the isochrone in Gyr. The parameters of the model are:
β0 = 1.2871, β1 = −0.8771, with
σ = 0.0056 dex. Since we do include explicitly the contribution of the
parameter
p1,...,p4,
they contribute to the inflation of the residual standard error of the model, reflecting our
global uncertainty. This model can be used to perform a reverse inference on the value of
the age, given 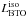 . As described in
detail in Appendix B, in the explored range
[8–14] Gyr, a typical uncertainty in the age is about ±375 Myr.
. As described in
detail in Appendix B, in the explored range
[8–14] Gyr, a typical uncertainty in the age is about ±375 Myr.
With an analysis like the one described in the previous paragraph for
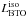 , we can obtain a
reverse inference of the uncertainty on age given the value of
, we can obtain a
reverse inference of the uncertainty on age given the value of
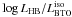 . The linear model
adapted to data is:
. The linear model
adapted to data is: 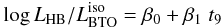 (5)where
t9 = log t, with t the age
of the isochrone in Gyr. The parameters of the model are:
β0 = 0.2779, β1 = 0.8771, with
σ = 0.024 dex. As a result of the large value of σ, a
typical uncertainty in age, given
(5)where
t9 = log t, with t the age
of the isochrone in Gyr. The parameters of the model are:
β0 = 0.2779, β1 = 0.8771, with
σ = 0.024 dex. As a result of the large value of σ, a
typical uncertainty in age, given 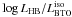 , is on the order
of ±1.25 Gyr.
, is on the order
of ±1.25 Gyr.
7. Conclusions
In this paper we addressed the problem of a quantitative and systematic evaluation of the cumulative propagation of physical uncertainties in current generation of stellar models of low mass stars from the main sequence to the zero age horizontal branch. At variance with several previous work (see e.g. Chaboyer et al. 1995; Cassisi et al. 1998; Castellani & Degl’Innocenti 1999; Castellani et al. 2000; Imbriani et al. 2001; Prada Moroni & Straniero 2002; Salaris et al. 2002; Imbriani et al. 2004; Weiss et al. 2005; Prada Moroni & Straniero 2007; Valle et al. 2009; Tognelli et al. 2011), where a single input physics was changed at a time, we performed a systematic and simultaneous variation on a fixed grid within their current range of uncertainty, in a way to obtain a full crossing of the perturbed input values, of the main physical inputs adopted in stellar codes (i.e. 1H(p, νe+)2H, 14N(p,γ)15O, and triple-α reaction rates, radiative and conductive opacities, neutrino energy losses, and microscopic diffusion velocities).
Although very expensive from the computational point of view, such an approach has the important advantage with respect to the previous one to be more robust against possible interactions among the varied input physics, as any a priori independence among them is assumed.
Relying on a set of stellar models fully covering all the possible combinations of simultaneously perturbed input physics, we were able to compute the error stripe associated to our reference stellar track, i.e. M = 0.90 M⊙ with initial metallicity Z = 0.006 and helium abundance Y = 0.26, from the pre-main sequence up to the RGB tip, in different planes (i.e. log L vs. log Teff, Xc vs. age, Δlog L vs. model, and Δlog R vs. model). We built also the error stripe associated to the ZAHB locus resulting from the evolution of a progenitor of M = 0.90 M⊙. As far as we know, this is the first time that an error stripe is computed and plotted for stellar tracks (see Appendix A for a detailed description of the error stripe construction method).
Range half-width of variation in theoretical predictions of selected quantities for our reference isochrone of 12 Gyr, with Z = 0.006 and Y = 0.26, due to input physics uncertainties.
Furthermore, we quantified the extension of the global variability regions (i.e. due to the
cumulative effect of all physical uncertainties) for some relevant stellar quantities,
without any assumption on the parent distributions of the varied physical inputs. In
particular, we focused on the turn-off luminosity LBTO, the
central hydrogen exhaustion time tH, the luminosity
Ltip and the helium core mass
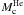 at the RGB tip, and
the ZAHB luminosity in the RR Lyrae region LHB, were computed,
too (see e.g. Table 2). We found that the turn-off
log luminosity log LBTO varies of ±0.021 dex, while the RGB
tip log Ltip and ZAHB log LHB ones
of ±0.03 dex and ±0.045 dex, respectively. Thus, uncertainties on the order of
±0.075 mag and ±0.10 mag should be taken into account in distance modulo estimates
obtained by theoretically calibrated RGB tip and ZAHB luminosities. The predicted central
hydrogen exhaustion time tH varies of ±0.72 Gyr, whereas the
helium core mass at the RGB tip
at the RGB tip, and
the ZAHB luminosity in the RR Lyrae region LHB, were computed,
too (see e.g. Table 2). We found that the turn-off
log luminosity log LBTO varies of ±0.021 dex, while the RGB
tip log Ltip and ZAHB log LHB ones
of ±0.03 dex and ±0.045 dex, respectively. Thus, uncertainties on the order of
±0.075 mag and ±0.10 mag should be taken into account in distance modulo estimates
obtained by theoretically calibrated RGB tip and ZAHB luminosities. The predicted central
hydrogen exhaustion time tH varies of ±0.72 Gyr, whereas the
helium core mass at the RGB tip 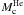 of ±0.0042 M⊙.
of ±0.0042 M⊙.
Fit of the isochrones BTO log-luminosity (dex).
Fit of mass at BTO (M⊙).
This large computational effort (i.e. 3159 stellar tracks) made possible a thorough and rigorous statistical analysis of the effects of the variations of the quoted physical inputs on the chosen relevant stellar evolutionary features, allowing to disentangle the contributions of the different inputs physics.
 |
Fig. 12 Boxplot of the impact of the variation of the chosen physical inputs on the isochrone
turn-off luminosity |
The results of our extended statistical analysis show that the radiative opacity is, by
far, the dominant source of physical uncertainty in almost all of the examined stellar
evolutionary features, with the exception of the helium core mass
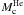 at the RGB tip which
is affected mainly by the uncertainty in the triple-α reaction rate. As an
example, for the turn-off log luminosity log LBTO, in order to
reduce the impact of the radiative opacity variation to the level of the second most
important input, i.e. the 14N(p, γ)15O reaction rate,
the uncertainty of the former should decrease from the current 5% down to 1%. For the
central hydrogen exhaustion time tH, the prevalence of the
radiative opacity is even larger, as for reducing its effect at the level of the second most
important input physics, i.e. the microscopic diffusion velocities, its uncertainty should
be decreased at the 0.56% level. Notice that the 5% uncertainty in radiative opacity assumed
in our calculations is probably an underestimate, at least in some regions of the
temperature-density plane of interest for stellar models.
at the RGB tip which
is affected mainly by the uncertainty in the triple-α reaction rate. As an
example, for the turn-off log luminosity log LBTO, in order to
reduce the impact of the radiative opacity variation to the level of the second most
important input, i.e. the 14N(p, γ)15O reaction rate,
the uncertainty of the former should decrease from the current 5% down to 1%. For the
central hydrogen exhaustion time tH, the prevalence of the
radiative opacity is even larger, as for reducing its effect at the level of the second most
important input physics, i.e. the microscopic diffusion velocities, its uncertainty should
be decreased at the 0.56% level. Notice that the 5% uncertainty in radiative opacity assumed
in our calculations is probably an underestimate, at least in some regions of the
temperature-density plane of interest for stellar models.
Beside this analysis of the cumulative uncertainty in a stellar track of fixed mass and
chemical composition, we extended the previous analysis of the cumulative uncertainty due to
the main input physics to theoretical isochrones in the age range 8–14 Gyr. We focused in
particular on the turn off luminosity 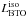 and mass
and mass
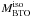 , and
, and
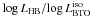 , which is
the theoretical counterpart of the visual magnitude difference between turn-off and
horizontal branch regions (i.e. ΔV(TO−HB) used as age indicator in the
“vertical method”). For an age of 12 Gyr, we found that the isochrone turn-off log
luminosity
, which is
the theoretical counterpart of the visual magnitude difference between turn-off and
horizontal branch regions (i.e. ΔV(TO−HB) used as age indicator in the
“vertical method”). For an age of 12 Gyr, we found that the isochrone turn-off log
luminosity 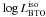 varies of
±0.013 dex, about 2/3 of the value found for the turn-off luminosity
LBTO of the reference stellar track. For the same age, the
mass at the isochrone turn-off varies of ±0.015 M⊙ and
varies of
±0.013 dex, about 2/3 of the value found for the turn-off luminosity
LBTO of the reference stellar track. For the same age, the
mass at the isochrone turn-off varies of ±0.015 M⊙ and
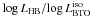 of
±0.05 dex. The large set of perturbed isochrones allowed us to perform the same kind of
statistical analysis previously applied to tracks of fixed mass, with the aim to evaluate
the effects of the single varied input physics.
of
±0.05 dex. The large set of perturbed isochrones allowed us to perform the same kind of
statistical analysis previously applied to tracks of fixed mass, with the aim to evaluate
the effects of the single varied input physics.
 |
Fig. 13 Boxplot of the impact of the variation of the chosen physical inputs on the isochrone
turn-off mass |
Finally, the availability of isochrones computed by varying simultaneously all the main
input physics made possible to evaluate the physical uncertainty affecting the age inferred
from two of the most used cosmic clocks, namely the turn-off luminosity and the vertical
method. For given 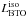 and
and
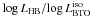 values, the
inferred age varies in a of about ±0.375 Gyr and ±1.25 Gyr, respectively.
values, the
inferred age varies in a of about ±0.375 Gyr and ±1.25 Gyr, respectively.
An equally systematic approach is provided by Monte Carlo simulations as those presented by Chaboyer and collaborators (Chaboyer et al. 1996, 1998; Chaboyer & Krauss 2002; Krauss & Chaboyer 2003; Bjork & Chaboyer 2006). However, a direct comparison with their results is difficult since the studies address different questions about the global uncertainty. The main problem is due to the fact that we focus on the uncertainty of evolutionary features different from the one studied in those papers. The only possible feature we can compare is the change in the evolutionary age due to the variation of radiative opacity. In Chaboyer & Krauss (2002) a 2% change in radiative opacity accounts for a 2.6% variation (i.e. 6.5% for a variation of radiative opacity of 5%) of the age of a Sub-Giant Branch star. As proxy of this quantity, we found that a 5% increase in radiative opacity account for a change of the time of central hydrogen exhaustion of 5.5%, i.e. 1% lower to the equivalent variation quoted above. The small difference can be in principle due to the different sampling schema for the radiative opacity adopted in Chaboyer & Krauss (2002), and to the different chemical inputs and solar mixture employed in the calculations.
Although the present paper addresses some fundamental topics about the uncertainty of modern stellar models, many other questions remain open and need further investigations. The first problem concerns the possibility to extend the results of our analysis – performed at fixed values of metallicity and initial helium abundance – to different values of the chemical inputs. In the lack of the very huge set of computations required to specifically address this topic, the extrapolation of the results presented in this paper to values of Z and Y very different from the ones employed in the computations is to be considered with care. Some cautions should also be adopted for “borderline” stellar models which can develop a different structure – such as the development of a convective core – due to a perturbation of a physical input. In these few cases the evaluation of the uncertainty can not be inferred but has to be performed with direct computations.
A second question concerns the possibility to extend the results presented here to the computations performed with other stellar evolutionary codes. This point could be addressed only with the replication with other codes, with the very same inputs and configurations, of the computations presented here. The availability of such calculations by different groups of the stellar evolution community would be of invaluable importance. In fact in this way could be assessed not only the uncertainty due to the variations of the physical inputs, but also quantified the impact of another source of uncertainty, i.e. the possible systematic difference among various codes due to different implementations of physical mechanisms and to the algorithms used in the computations.
Online material
Appendix A: Tracks reduction and error stripe construction on the theoretical plane
The first step of the construction of the stellar track uncertainty stripe on the theoretical plane is the reduction of the raw tracks to a set of tracks with the same number n of homologous points. The reduction is based upon the identification of some keystone evolutionary points on the raw track and subsequent deployment of the same number of points – obtained by interpolation – on all the tracks.
 |
Fig. B.1 Left panel: reverse inference on the isochrone age given the BTO
log luminosity. The solid line represents the best fit model, the dashed lines
define the 95% confidence interval on the prediction of the model. The dotted
lines show the uncertainty on age given a value of BTO log luminosity.
Right panel: same for |
As reference points we adopted the following:
-
1.
PMS1: the point for which gravitational luminosity reaches0.996 times the surface luminosity.
-
2.
PMS2: the point for which the gravitational luminosity decreases of 0.05 from the value at PMS1.
-
3.
ZAMS: the point for which the central hydrogen abundance drops below 99% of its initial value.
-
4.
MS1: the point for which the central hydrogen abundance drops below 7%.
-
5.
MS2: the point for which the central hydrogen abundance drops below 1%.
-
6.
MS3: the point for which the central hydrogen abundance drops below 0.1%.
-
7.
HC: the point for which the central hydrogen is exhausted.
-
8.
RGB1, or RGB start: the point on the track at maximum distance from the line connecting the HC and the RGB2 point.
-
9.
RGB2, or RGB bump: the point for which the luminosity of RGB start decreasing.
-
10.
RGB3, or He-flash: the point for which the He burning luminosity reaches 100 times the surface luminosity.
The ZAHB models have been computed through a synthetic method where the starting models were obtained by accreting envelopes of different mass extensions onto the He-core left at the tip of the RGB. Then, full evolutionary calculations were started again as thermal relaxed models in the central He burning phase; ZAHB point corresponds to the model in which the equilibrium abundance of CNO burning secondary elements is reached, after about 1 Myr.
Let { Ti } ,
i = 1,...,N be the
set of the N reduced tracks and let
Ti(j) be the
jth point on the ith reduced track. Let’s define:
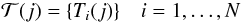 (A.1)\vadjust{\eject\vspace*{7.70cm}}the
set of the jth points over the whole set of reduced tracks. Let
Hc(X) be the convex hull of a generic
set X. We define:
(A.1)\vadjust{\eject\vspace*{7.70cm}}the
set of the jth points over the whole set of reduced tracks. Let
Hc(X) be the convex hull of a generic
set X. We define:
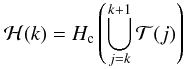 (A.2)the
convex hull of the set composed by the kth and
(k + 1)th points of the reduced tracks.
(A.2)the
convex hull of the set composed by the kth and
(k + 1)th points of the reduced tracks.
The full stripe is then given by:
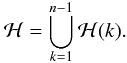 (A.3)The required
computations were carried out using R 2.14.1 (R Development Core Team 2011).
(A.3)The required
computations were carried out using R 2.14.1 (R Development Core Team 2011).
Appendix B: Reverse inference on the age of a isochrone given the TO luminosity
Let us consider a simple linear model:
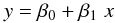 (B.1)the 95% confidence
interval (y1, y2) on a future
observation y given x, is (see e.g. Faraway 2004):
(B.1)the 95% confidence
interval (y1, y2) on a future
observation y given x, is (see e.g. Faraway 2004):
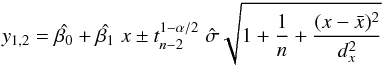 (B.2)where
(B.2)where
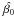 ,
,
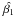 ,
,
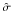 are the least-squares estimates of the model parameters, α is the
required confidence level (in our case, α = 0.05), n
is the number of points in the model,
are the least-squares estimates of the model parameters, α is the
required confidence level (in our case, α = 0.05), n
is the number of points in the model, 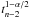 is
the 1 − α/2 quantile of the Student
t distribution with n − 2 degrees of freedom,
is
the 1 − α/2 quantile of the Student
t distribution with n − 2 degrees of freedom,
 is the sample mean value of x,
is the sample mean value of x, 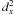 is the
sample deviance of x.
is the
sample deviance of x.
In our case we have: 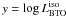 and
x = log T, with T the age of the
isochrone in Gyr. The boundaries of the 95% confidence interval are displayed along with
the best fit line in Fig. B.1, where we show the
construction of the range of uncertainty on age, given the value of BTO log luminosity.
As an example, for
and
x = log T, with T the age of the
isochrone in Gyr. The boundaries of the 95% confidence interval are displayed along with
the best fit line in Fig. B.1, where we show the
construction of the range of uncertainty on age, given the value of BTO log luminosity.
As an example, for 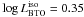 dex the estimated ages
from the models lie in the range [11.37–12.05] Gyr.
dex the estimated ages
from the models lie in the range [11.37–12.05] Gyr.
Appendix C: On the mixing-length influence
The results quoted in the present paper are computed for a fixed value of mixing-length parameter, i.e. αml = 1.90. The possibility to extend them to different values of this parameter must be checked by computing stellar models with different αml.
In presence of an effect due to the mixing-length, we expect a difference in the regression coefficients for the models summarized in Tables 3–7 when they are computed from stellar model with different αml. The computation of the huge sets of stellar models for different mixing-length values is not fully needed since in the linear models presented in Sect. 4 is shown that the various physical inputs do not interact. Therefore a subset of stellar models carefully selected can suffice to assess the presence of a mixing-length effect of distortion on the regression coefficients.
To perform the analysis we computed, for the two values of the mixing-length parameter αml = 1.70, 1.80 (αml = 1.74 is the solar-calibrated value of the mixing-length parameter), 81 stellar models each. The models to be computed were randomly selected using a latin hypercube sampling design, which is an extension of latin square to higher dimensions and has optimal property in reducing the variance of the estimators obtained from the linear models (Stein 1987). The random selection was performed using the R library lhs (Carnell 2012). The corresponding 81 models for αml = 1.90 were extracted from the 2187 original calculations and these 243 stellar models are used for establishing the influence of αml.
The analysis is performed by adapting to data linear models of the form:
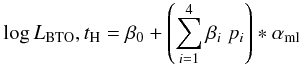 (C.1)or:
(C.1)or:
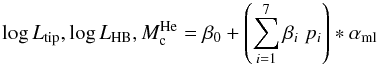 (C.2)where,
for convenience, we adopted the operator “*” defined as
A ∗ B ≡ A + B + A·B.
The effect of distortion of the regression coefficients due to the presence of the
mixing-length parameter is represented by the interaction between each multiplier
pi and αml.
The statistical significance of these coefficients is of limited importance, since it
can be arbitrarily increased by selecting a larger subsample thus reducing the standard
error estimate of the coefficients. A more useful indicator is the physical impact of
the introduction of the interaction in the linear models. As explained in the text the
impact of a perturbation Δpi on a parameter
pi which enters a linear model can be
evaluated as
Δpi·βi,
where βi is the estimate of the regression
coefficient. In presence of the interaction the impact of the same perturbation
Δpi combined with a variation of
Δαml can be estimated as
Δpi·Δαml·βj
where βj is the regression coefficient of
the interaction term under analysis. In Table C.1 we report the impact of the interaction terms in the various models for
Δαml = 0.1. In all cases the physical impact of the
interaction is negligible, so we can
(C.2)where,
for convenience, we adopted the operator “*” defined as
A ∗ B ≡ A + B + A·B.
The effect of distortion of the regression coefficients due to the presence of the
mixing-length parameter is represented by the interaction between each multiplier
pi and αml.
The statistical significance of these coefficients is of limited importance, since it
can be arbitrarily increased by selecting a larger subsample thus reducing the standard
error estimate of the coefficients. A more useful indicator is the physical impact of
the introduction of the interaction in the linear models. As explained in the text the
impact of a perturbation Δpi on a parameter
pi which enters a linear model can be
evaluated as
Δpi·βi,
where βi is the estimate of the regression
coefficient. In presence of the interaction the impact of the same perturbation
Δpi combined with a variation of
Δαml can be estimated as
Δpi·Δαml·βj
where βj is the regression coefficient of
the interaction term under analysis. In Table C.1 we report the impact of the interaction terms in the various models for
Δαml = 0.1. In all cases the physical impact of the
interaction is negligible, so we can
conclude that the regression presented in Sect. 4 are robust for an acceptable change in αml.
Appendix D: On the EOS influence
The assessment of the EOS influence on the stellar models can not be done in the same way of the other physical inputs, given the available information. As discussed in the text, the thermodynamic quantities required for computing stellar models and provided by EOS are related together in a not trivial way, hampering a simple parametrization of the uncertainty associated with them.
Nevertheless, a rough estimate of the impact due to the present uncertainty on EOS can be computed in an alternative way. For this purpose, in this appendix we provide the output of the stellar models computed with two different and widely adopted choices for equation-of-state: OPAL EOS and FreeEOS (Irwin 2004).
Impact of equation of state change from OPAL to FreeEOS for the examined evolutionary features.
Table D.1 reports – for each evolutionary feature – the values obtained using the two different EOS and, in the last column, the impact of the EOS change. By comparing them with the values in the last column of Table 2, one sees that the EOS change accounts for about 1/7–1/8 of the total variation due to all the other physical inputs. The only exception is the He core mass, for which the EOS change accounts for 1/3 of the total variation.
Unlike the other analysis performed in the paper, in this case it is not possible to identify which of the varied thermodynal quantities mainly affects the total result. One also should be aware that a given thermodynamical quantity can have different influences in different evolutionary phases.
Tables available at http://rdc.llnl.gov/EOS_2005/
The OPAL radiative opacity can be found at the URL: http://opalopacity.llnl.gov/new.html
Acknowledgments
We warmly thank Alexander Potekhin for providing us an estimate of the uncertainty affecting the electron conduction opacity coefficients. We thank Dario Andrea Bini for enlightening suggestions about the error stripe construction and Steven N. Shore for carefully reading the paper and for useful comments. We are grateful to our anonymous referee for many stimulating suggestions that helped in clarify and improve the paper. This work has been supported by PRIN-INAF 2011 (Tracing the formation and evolution of the Galactic Halo with VST, PI M. Marconi).
References
- Adelberger, E. G., Austin, S. M., Bahcall, J. N., et al. 1998, Rev. Mod. Phys., 70, 1265 [NASA ADS] [CrossRef] [Google Scholar]
- Adelberger, E. G., García, A., Robertson, R. G. H., et al. 2011, Rev. Mod. Phys., 83, 195 [NASA ADS] [CrossRef] [Google Scholar]
- Angulo, C., Arnould, M., Rayet, M., et al. 1999, Nucl. Phys. A, 656, 3 [NASA ADS] [CrossRef] [Google Scholar]
- Asplund, M., Grevesse, N., Sauval, A. J., & Scott, P. 2009, ARA&A, 47, 481 [NASA ADS] [CrossRef] [Google Scholar]
- Badnell, N. R., Bautista, M. A., Butler, K., et al. 2005, MNRAS, 360, 458 [NASA ADS] [CrossRef] [Google Scholar]
- Bertelli, G., Nasi, E., Girardi, L., & Marigo, P. 2009, A&A, 508, 355 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bjork, S. R., & Chaboyer, B. 2006, ApJ, 641, 1102 [NASA ADS] [CrossRef] [Google Scholar]
- Böhm-Vitense, E. 1958, ZAp, 46, 108 [NASA ADS] [Google Scholar]
- Brocato, E., Castellani, V., & Villante, F. L. 1998, MNRAS, 298, 557 [NASA ADS] [CrossRef] [Google Scholar]
- Cariulo, P., Degl’Innocenti, S., & Castellani, V. 2004, A&A, 421, 1121 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Carnell, R. 2012, lhs: Latin Hypercube Samples, r package version 0.10 [Google Scholar]
- Cassisi, S., Castellani, V., Degl’Innocenti, S., & Weiss, A. 1998, A&AS, 129, 267 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Cassisi, S., Potekhin, A. Y., Pietrinferni, A., Catelan, M., & Salaris, M. 2007, ApJ, 661, 1094 [NASA ADS] [CrossRef] [Google Scholar]
- Castellani, V., & Degl’Innocenti, S. 1999, A&A, 344, 97 [NASA ADS] [Google Scholar]
- Castellani, V., Ciacio, F., Degl’Innocenti, S., & Fiorentini, G. 1997, A&A, 322, 801 [NASA ADS] [Google Scholar]
- Castellani, V., Degl’Innocenti, S., Girardi, L., et al. 2000, A&A, 354, 150 [NASA ADS] [Google Scholar]
- Chaboyer, B., & Krauss, L. M. 2002, ApJ, 567, L45 [NASA ADS] [CrossRef] [Google Scholar]
- Chaboyer, B., Kernan, P. J., Krauss, L. M., & Demarque, P. 1995, in BAAS 27, AAS Meeting Abstracts, 1292 [Google Scholar]
- Chaboyer, B., Demarque, P., Kernan, P. J., Krauss, L. M., & Sarajedini, A. 1996, MNRAS, 283, 683 [NASA ADS] [Google Scholar]
- Chaboyer, B., Demarque, P., Kernan, P. J., & Krauss, L. M. 1998, ApJ, 494, 96 [NASA ADS] [CrossRef] [Google Scholar]
- Cyburt, R. H., Fields, B. D., & Olive, K. A. 2004, Phys. Rev. D, 69, 123519 [NASA ADS] [CrossRef] [Google Scholar]
- Degl’Innocenti, S., Pra da Moroni, P. G., Marconi, M., & Ruoppo, A. 2008, Ap&SS, 316, 25 [NASA ADS] [CrossRef] [Google Scholar]
- Dell’Omodarme, M., Valle, G., Degl’Innocenti, S., & Pra da Moroni, P. G. 2012, A&A, 540, A26 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Dotter, A., Chaboyer, B., Jevremović, D., et al. 2007, AJ, 134, 376 [NASA ADS] [CrossRef] [Google Scholar]
- Faraway, J. J. 2004, Linear Models with R (Chapman & Hall/CRC) [Google Scholar]
- Ferguson, J. W., Alexander, D. R., Allard, F., et al. 2005, ApJ, 623, 585 [NASA ADS] [CrossRef] [Google Scholar]
- Flynn, C. 2004, PASA, 21, 126 [NASA ADS] [CrossRef] [Google Scholar]
- Fynbo, H. O. U., Diget, C. A., Bergmann, U. C., et al. 2005, Nature, 433, 136 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Gennaro, M., Prada Moroni, P. G., & Degl’Innocenti, S. 2010, A&A, 518, A13 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Haft, M., Raffelt, G., & Weiss, A. 1994, ApJ, 425, 222 [NASA ADS] [CrossRef] [Google Scholar]
- Hubbard, W. B., & Lampe, M. 1969, ApJS, 18, 297 [NASA ADS] [CrossRef] [Google Scholar]
- Iglesias, C. A., & Rogers, F. J. 1996, ApJ, 464, 943 [NASA ADS] [CrossRef] [Google Scholar]
- Imbriani, G., Limongi, M., Gialanella, L., et al. 2001, ApJ, 558, 903 [NASA ADS] [CrossRef] [Google Scholar]
- Imbriani, G., Costantini, H., Formicola, A., et al. 2004, A&A, 420, 625 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Imbriani, G., Costantini, H., Formicola, A., et al. 2005, Eur. Phys. J. A, 25, 455 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Irwin, A. W. 2004, http://freeeos.sourceforge.net/documentation.html [Google Scholar]
- Itoh, N., Hayashi, H., Nishikawa, A., & Kohyama, Y. 1996, ApJS, 102, 411 [NASA ADS] [CrossRef] [Google Scholar]
- Jimenez, R., Flynn, C., MacDonald, J., & Gibson, B. K. 2003, Science, 299, 1552 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Kamionkowski, M., & Bahcall, J. N. 1994, ApJ, 420, 884 [NASA ADS] [CrossRef] [Google Scholar]
- Krauss, L. M., & Chaboyer, B. 2003, Science, 299, 65 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Lampe, M. 1968, Phys. Rev., 170, 306 [NASA ADS] [CrossRef] [Google Scholar]
- Pagel, B. E. J., & Portinari, L. 1998, MNRAS, 298, 747 [NASA ADS] [CrossRef] [Google Scholar]
- Peimbert, M., Luridiana, V., & Peimbert, A. 2007a, ApJ, 666, 636 [NASA ADS] [CrossRef] [Google Scholar]
- Peimbert, M., Luridiana, V., Peimbert, A., & Carigi, L. 2007b, in From Stars to Galaxies: Building the Pieces to Build Up the Universe, eds. A. Vallenari, R. Tantalo, L. Portinari, & A. Moretti, ASP Conf. Ser., 374, 81 [Google Scholar]
- Pietrinferni, A., Cassisi, S., Salaris, M., & Castelli, F. 2006, ApJ, 642, 797 [NASA ADS] [CrossRef] [Google Scholar]
- Potekhin, A. Y. 1999, A&A, 351, 787 [NASA ADS] [Google Scholar]
- Prada Moroni, P. G., & Straniero, O. 2002, ApJ, 581, 585 [NASA ADS] [CrossRef] [Google Scholar]
- Prada Moroni, P. G., & Straniero, O. 2007, A&A, 466, 1043 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- R Development Core Team 2011, R: A Language and Environment for Statistical Computing, R Foundation for Statistical Computing, Vienna, Austria, ISBN 3-900051-07-0 [Google Scholar]
- Rogers, F. J., & Nayfonov, A. 2002, ApJ, 576, 1064 [Google Scholar]
- Rogers, F. J., Swenson, F. J., & Iglesias, C. A. 1996, ApJ, 456, 902 [NASA ADS] [CrossRef] [Google Scholar]
- Rose, S. J. 2001, J. Quant. Spec. Radiat. Transf., 71, 635 [Google Scholar]
- Salaris, M., Cassisi, S., & Weiss, A. 2002, PASP, 114, 375 [NASA ADS] [CrossRef] [Google Scholar]
- Seaton, M. J., & Badnell, N. R. 2004, MNRAS, 354, 457 [NASA ADS] [CrossRef] [Google Scholar]
- Snedecor, G., & Cochran, W. 1989, Statistical methods, Statistical Methods No. v. 276 (Iowa State University Press) [Google Scholar]
- Steigman, G. 2006, Int. J. Mod. Phys. E, 15, 1 [Google Scholar]
- Stein, M. 1987, Technometrics, 29, 143 [CrossRef] [Google Scholar]
- Thoul, A. A., Bahcall, J. N., & Loeb, A. 1994, ApJ, 421, 828 [NASA ADS] [CrossRef] [Google Scholar]
- Tognelli, E., Prada Moroni, P. G., & Degl’Innocenti, S. 2011, A&A, 533, A109 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Valle, G., Marconi, M., Degl’Innocenti, S., & Pra da Moroni, P. G. 2009, A&A, 507, 1541 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Weiss, A., Serenelli, A., Kitsikis, A., Schlattl, H., & Christensen-Dalsgaard, J. 2005, A&A, 441, 1129 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
All Tables
Total range of variation and range half-width of the theoretical predictions for the selected quantities for our reference case, i.e. M = 0.90 M⊙ with Z = 0.006 and Y = 0.26, due to input physics uncertainties.
Range half-width of variation in theoretical predictions of selected quantities for our reference isochrone of 12 Gyr, with Z = 0.006 and Y = 0.26, due to input physics uncertainties.
Impact of equation of state change from OPAL to FreeEOS for the examined evolutionary features.
All Figures
 |
Fig. 1 Contour plots of the difference between OPAL and OP calculations for different
hydrogen abundance X and metallicity Z = 0.004.
The temperature T is in K, while R is in
g cm-3 K-3. The colored scale marks the values of the
relative difference |
| In the text | |
 |
Fig. 2 Left panel: Hertzsprung-Russell (HR) diagram showing the error stripe due to the variation of all the seven analyzed physical inputs (i.e. p1,...,p7 in Table 1) on the stellar track with M = 0.9 M⊙, Z = 0.006, Y = 0.26 from pre-main sequence to helium flash. The narrowing of the error stripe in the RGB is due to the fact that the perturbed stellar models are disposed along the tracks itself. See text for details. Right panel: as in the left panel, but for the ZAHB. |
| In the text | |
 |
Fig. 3 Left panel: Δlog L/L⊙ with respect to the track computed with standard inputs from ZAMS to helium flash. The comparison was performed on a set of reduced tracks with the same number of homologous points. Right panel: central hydrogen abundance Xc vs. time (Gyr). In both panels, the red solid and green dashed lines show for comparison the output of models with standard physical inputs and Z = 0.005, 0.007 respectively. |
| In the text | |
 |
Fig. 4 ΔR/R with respect to the track computed with standard inputs from ZAMS to helium flash. |
| In the text | |
 |
Fig. 5 Boxplot of the impact of the variation of the most important physical inputs on log LBTO and on tH. The black thick lines show the median of the data set, while the box marks the interquartile range, i.e. it extends form the 25th to the 75th percentile of data. The whiskers extend from the box until the extreme data. For each parameter pi, the labels low, std and high refer to the values 1.00−Δpi, 1.00, and 1.00 + Δpi. |
| In the text | |
 |
Fig. 6 Boxplot of the impact of the variation of the most important physical inputs on Ltip. |
| In the text | |
 |
Fig. 7 Boxplot of the impact of the variation of the most important physical inputs on
|
| In the text | |
 |
Fig. 8 Boxplot of the impact of the variation of the most important physical inputs on LHB. |
| In the text | |
 |
Fig. 9 Study of the linearity of the outputs of the calculations with respect to the variation of the physical inputs in their range of uncertainty. The symbols are the results of the calculations, while the lines are the linear fit of each set of values. Only the two most important inputs are shown in each panel. |
| In the text | |
 |
Fig. 10 HR diagram showing the error stripe due to the variation of the physical inputs for a 12.0 Gyr isochrone (zoom of the TO region). |
| In the text | |
 |
Fig. 11 Left panel: boxplots for BTO luminosity due to the variation of the selected physical inputs as a function of the isochrone age in Gyr. Central panel: same plot for mass at BTO. Right panel: same plot for difference of HB and BTO log luminosity. |
| In the text | |
 |
Fig. 12 Boxplot of the impact of the variation of the chosen physical inputs on the isochrone
turn-off luminosity |
| In the text | |
 |
Fig. 13 Boxplot of the impact of the variation of the chosen physical inputs on the isochrone
turn-off mass |
| In the text | |
 |
Fig. B.1 Left panel: reverse inference on the isochrone age given the BTO
log luminosity. The solid line represents the best fit model, the dashed lines
define the 95% confidence interval on the prediction of the model. The dotted
lines show the uncertainty on age given a value of BTO log luminosity.
Right panel: same for |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


