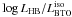| Issue |
A&A
Volume 549, January 2013
|
|
|---|---|---|
| Article Number | A50 | |
| Number of page(s) | 16 | |
| Section | Stellar structure and evolution | |
| DOI | https://doi.org/10.1051/0004-6361/201220069 | |
| Published online | 18 December 2012 | |
Online material
Appendix A: Tracks reduction and error stripe construction on the theoretical plane
The first step of the construction of the stellar track uncertainty stripe on the theoretical plane is the reduction of the raw tracks to a set of tracks with the same number n of homologous points. The reduction is based upon the identification of some keystone evolutionary points on the raw track and subsequent deployment of the same number of points – obtained by interpolation – on all the tracks.
 |
Fig. B.1
Left panel: reverse inference on the isochrone age given the BTO
log luminosity. The solid line represents the best fit model, the dashed lines
define the 95% confidence interval on the prediction of the model. The dotted
lines show the uncertainty on age given a value of BTO log luminosity.
Right panel: same for |
| Open with DEXTER | |
As reference points we adopted the following:
-
1.
PMS1: the point for which gravitational luminosity reaches0.996 times the surface luminosity.
-
2.
PMS2: the point for which the gravitational luminosity decreases of 0.05 from the value at PMS1.
-
3.
ZAMS: the point for which the central hydrogen abundance drops below 99% of its initial value.
-
4.
MS1: the point for which the central hydrogen abundance drops below 7%.
-
5.
MS2: the point for which the central hydrogen abundance drops below 1%.
-
6.
MS3: the point for which the central hydrogen abundance drops below 0.1%.
-
7.
HC: the point for which the central hydrogen is exhausted.
-
8.
RGB1, or RGB start: the point on the track at maximum distance from the line connecting the HC and the RGB2 point.
-
9.
RGB2, or RGB bump: the point for which the luminosity of RGB start decreasing.
-
10.
RGB3, or He-flash: the point for which the He burning luminosity reaches 100 times the surface luminosity.
The ZAHB models have been computed through a synthetic method where the starting models were obtained by accreting envelopes of different mass extensions onto the He-core left at the tip of the RGB. Then, full evolutionary calculations were started again as thermal relaxed models in the central He burning phase; ZAHB point corresponds to the model in which the equilibrium abundance of CNO burning secondary elements is reached, after about 1 Myr.
Let { Ti } ,
i = 1,...,N be the
set of the N reduced tracks and let
Ti(j) be the
jth point on the ith reduced track. Let’s define:
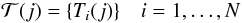 (A.1)\vadjust{\eject\vspace*{7.70cm}}the
set of the jth points over the whole set of reduced tracks. Let
Hc(X) be the convex hull of a generic
set X. We define:
(A.1)\vadjust{\eject\vspace*{7.70cm}}the
set of the jth points over the whole set of reduced tracks. Let
Hc(X) be the convex hull of a generic
set X. We define:
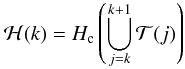 (A.2)the
convex hull of the set composed by the kth and
(k + 1)th points of the reduced tracks.
(A.2)the
convex hull of the set composed by the kth and
(k + 1)th points of the reduced tracks.
The full stripe is then given by:
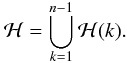 (A.3)The required
computations were carried out using R 2.14.1 (R Development Core Team 2011).
(A.3)The required
computations were carried out using R 2.14.1 (R Development Core Team 2011).
Appendix B: Reverse inference on the age of a isochrone given the TO luminosity
Let us consider a simple linear model:
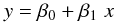 (B.1)the 95% confidence
interval (y1, y2) on a future
observation y given x, is (see e.g. Faraway 2004):
(B.1)the 95% confidence
interval (y1, y2) on a future
observation y given x, is (see e.g. Faraway 2004):
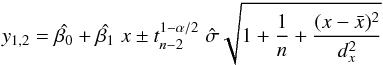 (B.2)where
(B.2)where
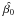 ,
,
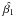 ,
,
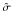 are the least-squares estimates of the model parameters, α is the
required confidence level (in our case, α = 0.05), n
is the number of points in the model,
are the least-squares estimates of the model parameters, α is the
required confidence level (in our case, α = 0.05), n
is the number of points in the model, 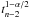 is
the 1 − α/2 quantile of the Student
t distribution with n − 2 degrees of freedom,
is
the 1 − α/2 quantile of the Student
t distribution with n − 2 degrees of freedom,
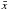 is the sample mean value of x,
is the sample mean value of x, 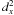 is the
sample deviance of x.
is the
sample deviance of x.
In our case we have: 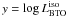 and
x = log T, with T the age of the
isochrone in Gyr. The boundaries of the 95% confidence interval are displayed along with
the best fit line in Fig. B.1, where we show the
construction of the range of uncertainty on age, given the value of BTO log luminosity.
As an example, for
and
x = log T, with T the age of the
isochrone in Gyr. The boundaries of the 95% confidence interval are displayed along with
the best fit line in Fig. B.1, where we show the
construction of the range of uncertainty on age, given the value of BTO log luminosity.
As an example, for 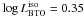 dex the estimated ages
from the models lie in the range [11.37–12.05] Gyr.
dex the estimated ages
from the models lie in the range [11.37–12.05] Gyr.
Appendix C: On the mixing-length influence
The results quoted in the present paper are computed for a fixed value of mixing-length parameter, i.e. αml = 1.90. The possibility to extend them to different values of this parameter must be checked by computing stellar models with different αml.
In presence of an effect due to the mixing-length, we expect a difference in the regression coefficients for the models summarized in Tables 3–7 when they are computed from stellar model with different αml. The computation of the huge sets of stellar models for different mixing-length values is not fully needed since in the linear models presented in Sect. 4 is shown that the various physical inputs do not interact. Therefore a subset of stellar models carefully selected can suffice to assess the presence of a mixing-length effect of distortion on the regression coefficients.
To perform the analysis we computed, for the two values of the mixing-length parameter αml = 1.70, 1.80 (αml = 1.74 is the solar-calibrated value of the mixing-length parameter), 81 stellar models each. The models to be computed were randomly selected using a latin hypercube sampling design, which is an extension of latin square to higher dimensions and has optimal property in reducing the variance of the estimators obtained from the linear models (Stein 1987). The random selection was performed using the R library lhs (Carnell 2012). The corresponding 81 models for αml = 1.90 were extracted from the 2187 original calculations and these 243 stellar models are used for establishing the influence of αml.
The analysis is performed by adapting to data linear models of the form:
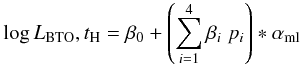 (C.1)or:
(C.1)or:
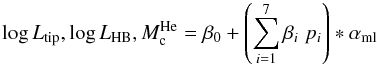 (C.2)where,
for convenience, we adopted the operator “*” defined as
A ∗ B ≡ A + B + A·B.
The effect of distortion of the regression coefficients due to the presence of the
mixing-length parameter is represented by the interaction between each multiplier
pi and αml.
The statistical significance of these coefficients is of limited importance, since it
can be arbitrarily increased by selecting a larger subsample thus reducing the standard
error estimate of the coefficients. A more useful indicator is the physical impact of
the introduction of the interaction in the linear models. As explained in the text the
impact of a perturbation Δpi on a parameter
pi which enters a linear model can be
evaluated as
Δpi·βi,
where βi is the estimate of the regression
coefficient. In presence of the interaction the impact of the same perturbation
Δpi combined with a variation of
Δαml can be estimated as
Δpi·Δαml·βj
where βj is the regression coefficient of
the interaction term under analysis. In Table C.1 we report the impact of the interaction terms in the various models for
Δαml = 0.1. In all cases the physical impact of the
interaction is negligible, so we can
(C.2)where,
for convenience, we adopted the operator “*” defined as
A ∗ B ≡ A + B + A·B.
The effect of distortion of the regression coefficients due to the presence of the
mixing-length parameter is represented by the interaction between each multiplier
pi and αml.
The statistical significance of these coefficients is of limited importance, since it
can be arbitrarily increased by selecting a larger subsample thus reducing the standard
error estimate of the coefficients. A more useful indicator is the physical impact of
the introduction of the interaction in the linear models. As explained in the text the
impact of a perturbation Δpi on a parameter
pi which enters a linear model can be
evaluated as
Δpi·βi,
where βi is the estimate of the regression
coefficient. In presence of the interaction the impact of the same perturbation
Δpi combined with a variation of
Δαml can be estimated as
Δpi·Δαml·βj
where βj is the regression coefficient of
the interaction term under analysis. In Table C.1 we report the impact of the interaction terms in the various models for
Δαml = 0.1. In all cases the physical impact of the
interaction is negligible, so we can
conclude that the regression presented in Sect. 4 are robust for an acceptable change in αml.
Appendix D: On the EOS influence
The assessment of the EOS influence on the stellar models can not be done in the same way of the other physical inputs, given the available information. As discussed in the text, the thermodynamic quantities required for computing stellar models and provided by EOS are related together in a not trivial way, hampering a simple parametrization of the uncertainty associated with them.
Nevertheless, a rough estimate of the impact due to the present uncertainty on EOS can be computed in an alternative way. For this purpose, in this appendix we provide the output of the stellar models computed with two different and widely adopted choices for equation-of-state: OPAL EOS and FreeEOS (Irwin 2004).
Impact of equation of state change from OPAL to FreeEOS for the examined evolutionary features.
Table D.1 reports – for each evolutionary feature – the values obtained using the two different EOS and, in the last column, the impact of the EOS change. By comparing them with the values in the last column of Table 2, one sees that the EOS change accounts for about 1/7–1/8 of the total variation due to all the other physical inputs. The only exception is the He core mass, for which the EOS change accounts for 1/3 of the total variation.
Unlike the other analysis performed in the paper, in this case it is not possible to identify which of the varied thermodynal quantities mainly affects the total result. One also should be aware that a given thermodynamical quantity can have different influences in different evolutionary phases.
© ESO, 2012
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.