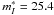| Issue |
A&A
Volume 549, January 2013
|
|
|---|---|---|
| Article Number | A136 | |
| Number of page(s) | 9 | |
| Section | Extragalactic astronomy | |
| DOI | https://doi.org/10.1051/0004-6361/201219671 | |
| Published online | 15 January 2013 | |
The luminosity of supernovae of type Ia from tip of the red-giant branch distances and the value of H0
Department of Physics and Astronomy, University of Basel, Klingelbergstrasse 82, 4056 Basel, Switzerland
e-mail: g-a.tammann@unibas.ch
Received: 24 May 2012
Accepted: 7 October 2012
Distances from the tip of the red-giant branch (TRGB) in the halo population of galaxies – calibrated through RR Lyr stars as well as tied to Hipparcos parallaxes and further supported by stellar models – are used to determine the luminosity of six nearby type Ia supernovae (SN 2011fe, 2007sr, 1998bu, 1989B, 1972E, and 1937C). The result is ⟨ McorrV ⟩ = -19.41 ± 0.05. If this value is applied to 62 SNe Ia with 3000 < v < 20,000 km s-1 a large-scale value of the Hubble constant follows of H0 = 64.0 ± 1.6 ± 2.0. The SN HST Project gave H0 = 62.3 ± 1.3 ± 5.0 from ten Cepheid-calibrated SNe Ia. The near agreement of young Population I (Cepheids) and old, metal-poor Population II (TRGB) distance indicators is satisfactory. The combined weighted result is H0 = 63.7 ± 2.3 (i.e. ± 3.6%). The value will be helpful to constrain models of the early Universe.
Key words: cosmological parameters / distance scale / galaxies: distances and redshifts / galaxies: clusters: individual: M101 / supernovae: general
© ESO, 2013
1. Introduction
The observational determination of the precise large-scale value of the Hubble constant (H0) is decisive for understanding the nature of dark energy and for determining the equation of state ω and other cosmological parameters (e.g. Suyu et al. 2012). The most direct route to achieve this goal is through the Hubble diagram of supernovae of type Ia (SNe Ia) which are the tightest standard candles known and trace the linearity of the cosmic expansion out to z > 1. But for the numerical value of H0 the intrinsic luminosity of SNe Ia is also needed. So far their mean luminosity has been derived from a few SNe Ia in nearby Population I parent galaxies whose distances can be derived from the period-luminosity relation of Cepheids. Present results from calibrated SNe Ia, however, diverge considerably giving, e.g., H0 = 71 ± 6 using only SNe Ia from the Hubble Space Telescope (HST) Project for H0 (Freedman et al. 2001), 62.3 ± 5.2 from the SN HST Project (Sandage et al. 2006), and 73.8 ± 2.4 (Riess et al. 2011). The divergence is almost entirely caused by different Cepheid distances: of the ten Cepheid distances used for the calibration of SNe Ia by Sandage et al. (2006) six are also in the list of Freedman et al. (2001) and four (out of 8) are in the list of Riess et al. (2011). The distances of the two latter samples are shorter on average by 0.41 ± 0.10 and 0.32 ± 0.08mag, respectively, than those by Saha et al. (2006). The reason for these differences, that perpetuate of course into all Cepheid-calibrated distance indicators, are different interpretations of metallicity effects on the shape and the zero point of the period-color relation and the period-luminosity relation and the related question of internal absorption; these points are further discussed by Tammann & Reindl (2012, and references therein).
The unsatisfactory situation with Cepheid-calibrated SNe Ia calls for an independent calibration. Therefore an alternative SN Ia calibration is pursued here using tip of the red-giant branch (TRGB) distances. The two routes to H0 are truly independent because Cepheids belong to the young Population I whereas the TRGB is a feature of the old Population II.
Over the last 70 years the TRGB of the old, metal-poor Population has developed into a powerful distance indicator. By now it fulfills the long-standing hope for a large-scale distance scale based on only Population II objects because the inherent disadvantage of the TRGB, i.e. its limited range, can be overcome with the first SNe Ia with known TRGB distances. Thus the TRGB will provide an independent check on the Population I distance scale that relies so far almost entirely on Cepheids.
The TRGB has several advantages. It is physically well understood and empirically exceptionally well calibrated. It needs fewer observations than variable stars, the problem of absorption in the halo of the host galaxy is minimal, and within the relevant metallicity range its luminosity is nearly independent of color. The observation of the TRGB in the galaxian halos obliterate the danger of blends, a much debated problem in case of Cepheids. Moreover the determination of the TRGB – that is defined as a cutoff magnitude – is immune against selection effects (Malmquist bias), a problem that has severely hampered the application of distance indicators with substantial internal dispersion.
In the following all magnitudes are corrected for Galactic absorption (Schlegel et al. 1998) with RB = 4.1, RV = 3.1, and RI = 1.8. Reduced values of 3.65, 2.65, and 1.35, respectively, are adopted for the absorption of the SNe Ia in their host galaxies as further discussed in Sect. 3. The SN magnitudes refer to the maxima in B, V, and I, respectively, if not otherwise stated. The colors (B − V)max are defined as (Bmax − Vmax).
The method of the TRGB is discussed in Sect. 2. The TRGB distances and optical luminosities of six SNe Ia are derived in Sect. 3. In Sect. 4 the calibrated SN Ia luminosity is applied to distant SNe Ia leading to the value of H0. JHKs luminosities are briefly discussed in Sect. 5. The discussion and conclusions follow in Sect. 6.
2. The tip of the red-giant branch (TRGB)
The TRGB was first observed by Baade (1944a,b). He noticed on red-sensitive plates that in several nearby Population II galaxies the resolution into stars suddenly sets in at a fixed luminosity. He explained what later became known as “Baade’s sheet” as the top of the red-giant branch which was then already known in globular clusters. The full power of the TRGB became apparent only with the inclusion of I-colors (Mould & Kristian 1986; Da Costa & Armandroff 1990). The use of the TRGB as an extragalactic distance indicator has been specifically addressed by Lee et al. (1993); Madore et al. (1997), and many others.
The physical explanation of the TRGB is due to Hoyle & Schwarzschild (1955) who showed that the maximum luminosity an old, metal-poor star can reach on the red-giant branch is sharply bounded – independent of mass in first approximation – by the Helium flash that occurs once the star has developed an electron-degenerate core. The physics of the TRGB was further elucidated by Thomas (1967), Rood (1972), Sweigart & Gross (1978). After the flash low-mass stars settle on the Horizontal Branch and more massive stars in the Red Clump (Faulkner 1966). Later models predict the TRGB luminosity to be nearly constant for masses below about 1.8 solar masses and [Fe/H] < −0.7. This holds particularly in the I-band where a tip luminosity of 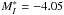 is predicted by the models and where the dependence on the tip color (B − V) ∗ is minimal (Salaris 2012, and references therein).
is predicted by the models and where the dependence on the tip color (B − V) ∗ is minimal (Salaris 2012, and references therein).
2.1. The empirical calibration of the TRGB
The absolute magnitude of 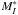 of the TRGB is empirically well determined for the color range 1.40 < (V − I) ∗ ≤ 1.75. Lee et al. (1993) adopted
of the TRGB is empirically well determined for the color range 1.40 < (V − I) ∗ ≤ 1.75. Lee et al. (1993) adopted  from four globular clusters with RR Lyr star distances. Rizzi et al. (2007) have fitted the Horizontal Branches (HB) of five galaxies to the Hipparcos-based HB of Carretta et al. (2000) allowing for metallicity effects; their result of
from four globular clusters with RR Lyr star distances. Rizzi et al. (2007) have fitted the Horizontal Branches (HB) of five galaxies to the Hipparcos-based HB of Carretta et al. (2000) allowing for metallicity effects; their result of 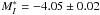 is independent of RR Lyr stars. It is therefore independent of a calibration of the TRGB luminosity from 20 galaxies with known RR Lyr distances, on the zero point of Sandage & Tammann (2006), that yields in perfect agreement
is independent of RR Lyr stars. It is therefore independent of a calibration of the TRGB luminosity from 20 galaxies with known RR Lyr distances, on the zero point of Sandage & Tammann (2006), that yields in perfect agreement 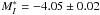 (Tammann et al. 2008a). The individual calibrators of Rizzi et al. and Tammann et al. do not show a significant color dependence in the indicated color range, corresponding roughly to a metallicity range of − 2.0 < [Fe/H] < − 1.1 in the system of Carretta & Gratton (1997).
(Tammann et al. 2008a). The individual calibrators of Rizzi et al. and Tammann et al. do not show a significant color dependence in the indicated color range, corresponding roughly to a metallicity range of − 2.0 < [Fe/H] < − 1.1 in the system of Carretta & Gratton (1997).
The agreement of the TRGB luminosity from model calculations and observations is so good that the zero-point error is likely to be ≤ 0.05mag. The dispersion between RR Lyr and TRGB distances of 20 galaxies is only 0.08mag. Allowing for a random error of RR Lyr distances of 0.05mag leaves a random error for the TRGB distances of only 0.06mag.
2.2. The TRGB in mixed populations
The most severe problem of the TRGB as a distance indicator, as pointed out already by Freedman (1989), are very red stars like supergiants, evolved AGB and carbon stars, that can become brighter than and as red as the TRGB in dense fields of mixed populations. In that case the TRGB may get drowned by contaminating stars. This always leads to an underestimate of the distance. The problem can be illustrated by the following cases.
In case of M101 Sakai et al. (2004) have found, plotting the red part of the CMD in I versus (V − I), the clearly visible TRGB in the outermost chips WF3 and WF4 of an outlying WFPC2 field (Fig.1 left). They applied a Sobel edge-detection kernel (Lee et al. 1993) and adopt 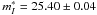 (corrected for Galactic absorption) for its position. The CMD of the entire WFPC2 field, reaching deeper into the disc population, is swamped with an admixture of evolved AGB stars and supergiants such that the TRGB becomes invisible to the eye and also the edge detection spectrum becomes much noisier (Fig.1 right). Rizzi et al. (2007) have remeasured the field of Sakai et al. (2004) and found
(corrected for Galactic absorption) for its position. The CMD of the entire WFPC2 field, reaching deeper into the disc population, is swamped with an admixture of evolved AGB stars and supergiants such that the TRGB becomes invisible to the eye and also the edge detection spectrum becomes much noisier (Fig.1 right). Rizzi et al. (2007) have remeasured the field of Sakai et al. (2004) and found 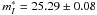 . The mean of
. The mean of 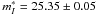 is adopted here. Shappee & Stanek (2011) have suggested
is adopted here. Shappee & Stanek (2011) have suggested 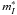 to lie at 24.98 ± 0.06 for a reference color of (V − I) ∗ = 1.6, yet the magnitude is clearly too bright. The value is measured in two inner fields of M101. The authors have taken the precaution to exclude the stars within 4′75 from the center, but in spite of this the field contains a mixture of old and young stars. Clearly some of the latter are very bright and red and hide the true TRGB. The authors’ edge detection function shows also a weaker maximum at
to lie at 24.98 ± 0.06 for a reference color of (V − I) ∗ = 1.6, yet the magnitude is clearly too bright. The value is measured in two inner fields of M101. The authors have taken the precaution to exclude the stars within 4′75 from the center, but in spite of this the field contains a mixture of old and young stars. Clearly some of the latter are very bright and red and hide the true TRGB. The authors’ edge detection function shows also a weaker maximum at 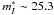 which presumably is the signature of the true TRGB in agreement with Sakai et al. (2004) and Rizzi et al. (2007).
which presumably is the signature of the true TRGB in agreement with Sakai et al. (2004) and Rizzi et al. (2007).
 |
Fig. 1 Color–magnitude diagrams in I versus (V − I) of an outlying WFPC2 field in M101 from Sakai et al. (2004, Fig. 11; note that the figure legend confuses M101 with NGC 3621). Left: only the stars in the outermost chips WF3 & WF4 with a prevailing halo population are shown. The TRGB is clearly visible at |
The situation in NGC 3621 is similar to M101. Sakai et al. (2004, Fig. 10) have shown that the TRGB is definitely detected in an outlying WFPC2 field (chip WF2), whereas the entire WFPC2 field contains so many equally red, but brighter stars that the TRGB becomes undetectable.
An additional illustration is provided by the interacting galaxy NGC 4038. Saviane et al. (2008), considering an ACS HST field containing clear tracers of a young population, found in the quadrant most distant of the star-forming tidal tail two discontinuities along the red-giant branch, the one at 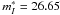 and the other one at ~27.5. The authors identified the brighter one with the TRGB. However, Schweizer et al. (2008) applied a Sobel edge-detection kernel to the whole ACS field and convincingly showed the TRGB to lie at
and the other one at ~27.5. The authors identified the brighter one with the TRGB. However, Schweizer et al. (2008) applied a Sobel edge-detection kernel to the whole ACS field and convincingly showed the TRGB to lie at 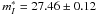 ; it is the faintest TRGB so far measured.
; it is the faintest TRGB so far measured.
The galaxies NGC 3368 and NGC 3627 are bona fide members of the Leo I group (e.g. Humason et al. 1956; Huchra & Geller 1982), yet their published 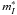 magnitudes of 25.61 (Mould & Sakai 2009a) and 25.82 (Mould & Sakai 2009b), respectively, are brighter by ~ 0.6mag than the mean TRGB magnitude
magnitudes of 25.61 (Mould & Sakai 2009a) and 25.82 (Mould & Sakai 2009b), respectively, are brighter by ~ 0.6mag than the mean TRGB magnitude 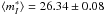 of four unquestioned group members (NGC 3351, 3377, 3379, and 3384; see Sakai et al. 2004; Rizzi et al. 2007; Mould & Sakai 2009a,b). The proposed tip of NGC 3368 is based on (too) few stars, and the genuine tip of NGC 3627 may well be buried in a dense cloud of stars. The edge detection functions of both galaxies show secondary peaks at
of four unquestioned group members (NGC 3351, 3377, 3379, and 3384; see Sakai et al. 2004; Rizzi et al. 2007; Mould & Sakai 2009a,b). The proposed tip of NGC 3368 is based on (too) few stars, and the genuine tip of NGC 3627 may well be buried in a dense cloud of stars. The edge detection functions of both galaxies show secondary peaks at 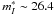 that presumably reflect the true TRGBs. Also the velocities of v220 = 720 and 428 km s-1 (v220 is the velocity corrected for a self-consistent Virgocentric infall model with a local infall 220 km s-1) of NGC 3368 and NGC 3627 compared with the mean velocity of ⟨ v220 ⟩ = 497 km s-1 (σ = 159 km s-1) from 8 bright group members make it unlikely that they could be foreground galaxies. Moreover, we note that the Cepheid distances of NGC 3368 and NGC 3627 of (m − M) = 30.34 and (m − M) = 30.50 (Saha et al. 2006) are in very good agreement with the adopted mean TRGB distance of the Leo I group of ⟨ m − M ⟩ = 30.39 ± 0.08. Finally convincing evidence for the group membership comes from the HI maps of the Leo I group (Stierwalt et al. 2009, Figs. 3 and 4). For these arguments NGC 3368 and 3627 are unquestionable members of the Leo I group; as such they are treated in the following.
that presumably reflect the true TRGBs. Also the velocities of v220 = 720 and 428 km s-1 (v220 is the velocity corrected for a self-consistent Virgocentric infall model with a local infall 220 km s-1) of NGC 3368 and NGC 3627 compared with the mean velocity of ⟨ v220 ⟩ = 497 km s-1 (σ = 159 km s-1) from 8 bright group members make it unlikely that they could be foreground galaxies. Moreover, we note that the Cepheid distances of NGC 3368 and NGC 3627 of (m − M) = 30.34 and (m − M) = 30.50 (Saha et al. 2006) are in very good agreement with the adopted mean TRGB distance of the Leo I group of ⟨ m − M ⟩ = 30.39 ± 0.08. Finally convincing evidence for the group membership comes from the HI maps of the Leo I group (Stierwalt et al. 2009, Figs. 3 and 4). For these arguments NGC 3368 and 3627 are unquestionable members of the Leo I group; as such they are treated in the following.
At present about 200 TRGB magnitudes of nearby galaxies have been determined by many observers (for a compilation see e.g. Tammann et al. 2008b, in the following TSR08b). First attempts to calibrate SNe Ia with TRGBs have already been made (Tammann et al. 2008a; Mould & Sakai 2009b).
3. The six calibrating SNe Ia with TRGB distances
SNe Ia develop their full power as standard candles only once they are fully corrected for absorption and standardized to a fixed decline rate (or some other light curve characteristics). The calibrating SNe Ia as well as the distant SNe Ia, that need in addition z-dependent time dilation and K-corrections, are here homogenized following Reindl et al. (2005, in the following RTS05) because the resulting magnitudes define the Hubble diagram with a particularly small dispersion of 0.14mag; even the dispersion of 0.13mag in the H band is hardly smaller (Kattner et al. 2012). Other standardization systems have been applied, but the magnitudes from different systems should not be mixed because they do not necessarily have the same zero point. In particular, different assumptions on the intrinsic color of SNe Ia and on the absorption-to-reddening ratio R lead to different corrections for internal absorption and hence to different corrected magnitudes. However the choice of the intrinsic color and the value of R becomes irrelevant as long as nearby calibrators and distant SNe Ia are treated consistently.
RTS05 have corrected the SN magnitudes in B, V and I for Galactic absorption following Schlegel et al. (1998) and for internal absorption. The internal absorption AV is RV × E(B − V) where RV = 2.65 is adopted. Several investigations indicate that such a low value is appropriate for SNe Ia (e.g. Branch & Tammann 1992; Riess et al. 1996; Tripp 1998; Krisciunas et al. 2000; Altavilla et al. 2004; RTS05; Wang et al. 2006; Jha et al. 2007). The observed colors are defined as 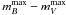 and
and 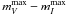 ; the color (B − V)35, 35 days after B maximum is also used because the colors (Lira 1995; Phillips et al. 1999) and spectra (Filippenko 1997) of SNe Ia with different decline rates are quite similar at that epoch (see also Jha et al. 2007). The reddenings are the differences between the observed colors and the intrinsic colors. The intrinsic colors (B − V)max, (B − V)35, and (V − I) were derived in function of the decline rate Δm15 from 34 unreddened SNe Ia in E/S0 galaxies and from outlying SNe Ia in spirals. The resulting excesses E(B − V)35 and E(V − I) are converted into values of E(B − V) at maximum, using empirical relations (RTS05, Eqs. (9) and (12)), and then averaged. Finally the magnitudes were standardized to a fiducial decline rate of Δm15 = 1.1 (RTS05, Fig. 12). The magnitudes, fully corrected for Galactic and host absorption and standardized to Δm15 = 1.1, are denoted mcorr.
; the color (B − V)35, 35 days after B maximum is also used because the colors (Lira 1995; Phillips et al. 1999) and spectra (Filippenko 1997) of SNe Ia with different decline rates are quite similar at that epoch (see also Jha et al. 2007). The reddenings are the differences between the observed colors and the intrinsic colors. The intrinsic colors (B − V)max, (B − V)35, and (V − I) were derived in function of the decline rate Δm15 from 34 unreddened SNe Ia in E/S0 galaxies and from outlying SNe Ia in spirals. The resulting excesses E(B − V)35 and E(V − I) are converted into values of E(B − V) at maximum, using empirical relations (RTS05, Eqs. (9) and (12)), and then averaged. Finally the magnitudes were standardized to a fiducial decline rate of Δm15 = 1.1 (RTS05, Fig. 12). The magnitudes, fully corrected for Galactic and host absorption and standardized to Δm15 = 1.1, are denoted mcorr.
 |
Fig. 2 Light curve of SN Ia 2011fe in M101 in B (blue), V (green), and I (red) from AAVSO data (small open dots) and Richmond & Smith (2012) (large open dots). The well fitting, mean standard light curves in B and V of SNe Ia with Δm15 = 1.1 are overplotted; they are taken from Leibundgut (1988); in I the light curve of SN 1992al (Hamuy et al. 1996) is shown for comparison (for details see text). The maximum epochs and those 15 and 35 days after B maximum are marked. The light curves in V and I are shifted by −1 and −2 mag, respectively. |
 |
Fig. 3 Light curve of SN Ia 2007sr in NGC 4038 in B (blue), V (green), and I (red) from different sources. The full lines are the light curves of SN 2011fe (Fig. 2) which has closely the same decline rate of Δm15 = 1.10; the poorly fitting tail of the B light curve is shown as a dashed line. The maximum epochs and those 15 and 35 days after B maximum are marked. The light curves in V and I are shifted by − 1 and − 2mag, respectively. |
3.1. The SN 2011fe in M101
The supernova 2011fe was discovered in M101 by the Transient Palomar Factory on August 24, 2011, and classified as a normal type Ia (Nugent et al. 2011) that had exploded two days before. The American Association of Variable Star Observers (AAVSO) had collected by November 10, 2011, 190 B, 4143 V, and 252 I magnitudes from 48 different sources. Subsequently published, extensive UBVRI CCD photometry, starting 16.4 days before B maximum, was provided by Richmond & Smith (2012) and proves the excellent quality of the AAVSO data. In addition the Las Cumbres Observatory Global Telescope Network (LCOGT) will provide daily multi-wavelength photometry of SN 2011fe including observations only hours after the explosion by the Palomar Transient Factory (Bianco et al. 2012); pre-publication maximum magnitudes and Δm15 were kindly made available by Bianco (priv. comm.). The three sources agree very well, giving Bmax = 9.93 ± 0.01, Vmax = 9.93 ± 0.01, Imax = 10.18 ± 0.03, and Δm15 = 1.10 ± 0.06. The BVI photometry of Richmond & Smith (2012) and of the AAVSO are plotted in Fig. 2 as well as a templet light curve for Δm15 = 1.10 (Leibundgut 1988; Hamuy et al. 1996) for comparison. The rising branch of these light curves is drawn here through the observations of SN 2011fe itself, and in addition the V light-curve is slightly lowered around the epoch of 40 days after B maximum to better fit the observations.
The mean color excess from E(B − V), E(B − V)35, and E(V − I) gives, after appropriate transformation, ⟨ E(B − V) ⟩ = 0.01 ± 0.02; this is so close to zero that it is assumed that the internal absorption of SN 2011fe is zero. Note that any absorption correction could make the intrinsic luminosity of SN 2011fe only brighter. – Since SN 2011fe has closely the fiducial decline rate of Δm15 = 1.10 the correction for the decline rate is δΔm15 = 0.00 ± 0.04.
The mean TRGB magnitude of M101 is well determined in an outer halo field by Sakai et al. (2004) and Rizzi et al. (2007) to be 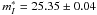 (see Sect. 2.2). This with the above TRGB calibration gives a distance modulus of (m − M) = 29.40 ± 0.06. With
(see Sect. 2.2). This with the above TRGB calibration gives a distance modulus of (m − M) = 29.40 ± 0.06. With 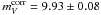 follows an absolute magnitude of SN 2011fe of
follows an absolute magnitude of SN 2011fe of 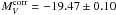 . The relevant parameters of SN 2011fe are listed in Table 1.
. The relevant parameters of SN 2011fe are listed in Table 1.
SNe Ia with TRGB distances and their luminosities.
3.2. The SN 2007sr in NGC 4038
The supernova 2007sr was discovered as a transient object on the southern tail of the interacting galaxy NGC 4038 on December 12, 2007 (Drake et al. 2007). It was identified as a SN Ia by Naito et al. (2007) and Umbriaco et al. (2007, see also Silverman et al. (2012). The photometry of the object in the BVI bands is here collected; the data, including the three earliest observations of Pojmanski et al. (2008) are plotted in Fig. 3, where also the sources are identified. The data are over-plotted with the light curves of SN 2011fe (Fig. 2). They fit the observations well in B and V, except the tail in B. The good fit in B at earlier epochs implies Δm15 = 1.10 ± 0.05. The data meander in I about the light curve of SN 2011fe which is not unusual for this passband. The adopted BVI maximum magnitudes in Table 1 agree within the errors with those of Ganeshalingam et al. (2010), that are based on fewer observations. The maximum value in B is the same as in Neill et al. (2009).
The mean color excess is ⟨ E(B − V) ⟩ = 0.13 ± 0.05 from E(B − V) at maximum and 35days after B maximum. The I maximum is too uncertain to be helpful for the determination of the reddening. The internal absorption becomes then AV = 0.34 ± 0.13 for the adopted value of RV = 2.65.
With the TRGB distance of (m − M) = 31.51 ± 0.12 of Schweizer et al. (2008, see Sect. 2.2 and with 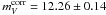 the absolute magnitude of SN 2007sr becomes
the absolute magnitude of SN 2007sr becomes 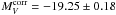 . SN 2007sr is the most distant calibrator of the present sample. Its light curve parameters of interest are compiled in Table 1.
. SN 2007sr is the most distant calibrator of the present sample. Its light curve parameters of interest are compiled in Table 1.
3.3. The SN 1998bu in NGC 3368
The supernova was confirmed to be of type Ia by Silverman et al. (2012). The relevant BVI light curve parameters, based on very extensive photometry by Suntzeff et al. (1999); Jha et al. (1999); Hernandez et al. (2000), were derived in RTS05 and are listed in Table 1. Wang et al. (2006) and Hicken et al. (2009) have determined the same ( ± 0.02mag) maxima in B and V from an independent templet fitting method. The large reddening is well determined to be ⟨ E(B − V) ⟩ = 0.28 ± 0.04 from E(B − V) proper, E(V − I), and E(B − V)35; this yields AV = 0.74 ± 0.11. The decline rate Δm15 = 1.1 5 ± 0.05 is close to the standard value of 1.10 and requires a luminosity correction of only − 0.03 ± 0.03mag.
The resulting value of 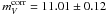 gives – together with the mean TRGB distance of the Leo I group, of which NGC 3368 is a bona fide member (see Sect. 2.2), of (m − M) = 30.39 ± 0.10 – an absolute magnitude of
gives – together with the mean TRGB distance of the Leo I group, of which NGC 3368 is a bona fide member (see Sect. 2.2), of (m − M) = 30.39 ± 0.10 – an absolute magnitude of 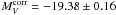 .
.
3.4. The SN 1989B in NGC 3627
The supernova was confirmed to be a Branch-normal SN Ia by Silverman et al. (2012). The BVI light curve parameters are mainly based on CCD photometry of Wells et al. (1994) and compiled in RTS05. The maximum magnitudes agree within 0.02mag with independent templet fits by Wang et al. (2006) and in B and V also by Altavilla et al. (2004) and Hicken et al. (2009). The mean value of ⟨ E(B − V) ⟩ = 0.31 ± 0.03 from E(B − V), E(V − I) and E(B − V)35 is reliable and corresponds to AV = 0.82 ± 0.08. The SN was relatively fast (Δm15 = 1.35) and requires a correction of the V magnitude of − 0.13 ± 0.03mag.
As shown in Table 1 the corrected apparent magnitude becomes 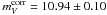 . For reasons given in Sect. 2.2 NGC 3627 is assumed to be at the mean TRGB distance of the Leo I group of (m − M) = 30.39 ± 0.10. This then gives an absolute magnitude of
. For reasons given in Sect. 2.2 NGC 3627 is assumed to be at the mean TRGB distance of the Leo I group of (m − M) = 30.39 ± 0.10. This then gives an absolute magnitude of 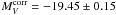 of SN 1989B.
of SN 1989B.
3.5. The SN 1972E in NGC 5253
The supernova is the prototypical Ia SN (Branch et al. 1993). The well determined photoelectric BVI light curve parameters in Table 1 were derived by RTS05 from the published photometry (Lee et al. 1972; Cousins 1972; Ardeberg & de Groot 1973). The I photometry of van Genderen (1975) sets in too late to determine a reliable value of Imax. The negative mean color excess ⟨ E(B − V) ⟩ is based therefore on only E(B − V) measured at maximum and 35 days thereafter. Anyhow the assumption of zero internal absorption seems secure for this far outlying SN. The standardization of Δm15 = 1.05 ± 0.05 to the fiducial decline rate of Δm15 = 1.10 requires a V magnitude correction of only + 0.03 ± 0.06mag. This leads to 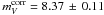 which we adopt. – The templet fitting of Wang et al. (2006) yields somewhat brighter magnitudes and a slower decline rate (Bmax = 8.11 ± 0.10, Vmax = 8.17 ± 0.09, and Δm15 = 0.87 ± 0.10). The two effects nearly compensate and decrease
which we adopt. – The templet fitting of Wang et al. (2006) yields somewhat brighter magnitudes and a slower decline rate (Bmax = 8.11 ± 0.10, Vmax = 8.17 ± 0.09, and Δm15 = 0.87 ± 0.10). The two effects nearly compensate and decrease 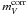 by only 0.03mag.
by only 0.03mag.
The adopted value of 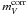 and the TRGB distance of NGC 5253 of 27.79 ± 0.10 (Sakai et al. 2004; Rizzi et al. 2007) lead to a luminosity of SN 1972E of
and the TRGB distance of NGC 5253 of 27.79 ± 0.10 (Sakai et al. 2004; Rizzi et al. 2007) lead to a luminosity of SN 1972E of 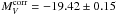 .
.
3.6. The SN 1937C in IC 4182
The supernova was the subject of Baade & Zwicky’s (1938) seminal paper and was for a long time the prototype SN I (Minkowski 1940). It was later classified as a Branch-normal SN Ia (Branch et al. 1993). The various contemporary photometry is difficult to transform into a modern system. Two sets of BV light curve parameters have been derived (Schaefer 1994, 1996; Pierce & Jacoby 1995; Jacoby & Pierce 1996), they disagree dependent mainly on the weight given to the photometry at early and at late phases. Average light curve parameters are adopted here as shown in Table 1; they agree reasonably well with those of Wang et al. (2006). The assigned large errors comprise either set of parameters. There is no doubt that SN 1937C was quite blue at maximum; the absorption in the host galaxy is therefore negligible. The somewhat slow decline of Δm15 = 0.96 ± 0.10 requires a V magnitude correction of 0.09 ± 0.06mag.
With 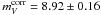 and a TRGB distance of (m − M) = 28.21 (Sakai et al. 2004; Rizzi et al. 2007) the absolute magnitude of SN 1937C becomes
and a TRGB distance of (m − M) = 28.21 (Sakai et al. 2004; Rizzi et al. 2007) the absolute magnitude of SN 1937C becomes 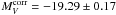 .
.
The parameters of the six SNe Ia are collected together with their TRGB distances and corresponding absolute magnitudes in Table 1. Columns 3 − 5 give the apparent BVI magnitudes corrected for Galactic absorption. The color excesses in Col. 6 are the mean of E(B − V), E(B − V)35, and E(V − I), the latter two reduced to the value of E(B − V) at maximum. The absorption AV in Col. 7 is based on RV = 2.65. Columns 8 and 9 give the decline rate Δm15 and the correction δ(Δm15) for the standardization to Δm15 = 1.10. The values 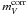 in Col. 10 are the apparent V magnitudes corrected for internal absorption and for δ(Δm15). The adopted TRGB moduli and their sources are in Cols. 11 and 12. Column 13 lists the final absolute V magnitudes
in Col. 10 are the apparent V magnitudes corrected for internal absorption and for δ(Δm15). The adopted TRGB moduli and their sources are in Cols. 11 and 12. Column 13 lists the final absolute V magnitudes 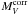 . The statistical errors of the various entries are shown in parentheses in units of 0.01mag.
. The statistical errors of the various entries are shown in parentheses in units of 0.01mag.
The mean luminosity of the six SNe Ia is 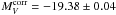 . The dispersion of σ = 0.09mag is even smaller than that of the distant SNe Ia (0.14mag). The small dispersion suggests that the random errors assigned to the individual SNe Ia are rather overestimated. The weighted mean luminosity is
. The dispersion of σ = 0.09mag is even smaller than that of the distant SNe Ia (0.14mag). The small dispersion suggests that the random errors assigned to the individual SNe Ia are rather overestimated. The weighted mean luminosity is 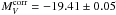 which we adopt.
which we adopt.
JHKs luminosities of three SNe Ia with TRGB distances.
4. The calibration of H0
The log cz – apparent-magnitude relations of a ΛCDM model for the case ΩM = 0.3 and ΩΛ = 0.7 is given here (Carroll et al. 1992) 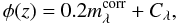 (1)where
(1)where ![\begin{equation} \phi(z) = \log c\left(1+z_{1}\right)\int_{0}^{z_{1}}\left[(1+z)^{2}(1+0.3z)-0.7z(2+z)\right]^{-1/2}{\rm d}z, \label{eq:hubble:02} \end{equation}](/articles/aa/full_html/2013/01/aa19671-12/aa19671-12-eq239.png) (2)and where the intercept is given by
(2)and where the intercept is given by 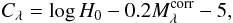 (3)from which follows
(3)from which follows 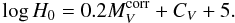 (4)The intercept CV of the Hubble line was determined by 62 standardized SNe Ia with 3000 < v < 20 000 km s-1 to be CV = 0.688 ± 0.004 (RTS05, Table 9). Inserting this value and the weighted mean absolute magnitude
(4)The intercept CV of the Hubble line was determined by 62 standardized SNe Ia with 3000 < v < 20 000 km s-1 to be CV = 0.688 ± 0.004 (RTS05, Table 9). Inserting this value and the weighted mean absolute magnitude 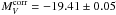 of the six SNe Ia from Table 1 gives
of the six SNe Ia from Table 1 gives 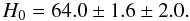 (5)The random error is small (2.5%). Systematic errors are due to errors of the photometry (±0.05 mag), to the zero-point error of the adopted TRGB ( ± 0.05), to the error of the corrections for internal absorption, and to errors of the standardization to Δm15. For the internal absorption the value of RV was assumed to be 2.65 throughout. The average reddening of the calibrating SNe Ia is E(B − V) = 0.12 and of the distant SNe Ia defining the Hubble line E(B − V) = 0.06. Only the difference of these average reddenings multiplied with the error of R enter the systematic error. Even for a wide range of 2.1 < R < 3.2 the systematic error is therefore only 0.04mag. The mean Δm15 values of the six SNe Ia in Table 1 and of the 62 distant SNe Ia are 1.11 ± 0.05 and 1.22 ± 0.03, respectively. The difference of 0.11 ± 0.06 multiplied with the error of the slope of the Deltam15 correction (0.07) enters as a systematic error which in this case is confined to 0.01mag. The compounded systematic error is therefore 0.064mag (3.2%).
(5)The random error is small (2.5%). Systematic errors are due to errors of the photometry (±0.05 mag), to the zero-point error of the adopted TRGB ( ± 0.05), to the error of the corrections for internal absorption, and to errors of the standardization to Δm15. For the internal absorption the value of RV was assumed to be 2.65 throughout. The average reddening of the calibrating SNe Ia is E(B − V) = 0.12 and of the distant SNe Ia defining the Hubble line E(B − V) = 0.06. Only the difference of these average reddenings multiplied with the error of R enter the systematic error. Even for a wide range of 2.1 < R < 3.2 the systematic error is therefore only 0.04mag. The mean Δm15 values of the six SNe Ia in Table 1 and of the 62 distant SNe Ia are 1.11 ± 0.05 and 1.22 ± 0.03, respectively. The difference of 0.11 ± 0.06 multiplied with the error of the slope of the Deltam15 correction (0.07) enters as a systematic error which in this case is confined to 0.01mag. The compounded systematic error is therefore 0.064mag (3.2%).
The solution in Eq. (5) is stable against the selection of the SNe Ia in Table 1. The exclusion of any two or any three SNe Ia yields mean values of H0 between 62.8 and 67.3. The three SNe Ia with relatively large internal-absorption corrections and those with zero internal-absorption corrections yield the same mean value of H0 within 2%. Even under the devious assumption of zero internal absorption for all six SNe Ia their mean luminosity decreases by only 0.11mag, increasing H0 by 6%.
Moreover, the effect of the adopted cosmological model on H0 is small because the distant SN sample is confined to ≤ 20 000 km s-1. Replacing the ΛCDM model used here with a Euclidean model gives an intercept of the Hubble line of CV = 0.679 and decreases H0 by only 1.3 units.
Summarizing the random and systematic errors added in quadrature gives a safe upper limit for the total error of H0 of 5%.
5. A note on the JHKs luminosities of SNe Ia
For three of the SNe Ia in Table 1 also near-infrared maximum magnitudes in J and H are available, for SN 2011fe and SN 1998bu also in Ks. The data are compiled in Table 2 where also the TRGB distances are repeated from Table 1 and the ensuing absolute magnitudes are given. The absolute magnitudes of the two last-mentioned SNe Ia agree in JHKs to within 0.05 ± 0.12, 0.15 ± 0.12, and 0.21 ± 0.12, respectively. Yet any correction for internal absorption, one wants to apply, can only increase these differences, because SN 2011fe is nearly absorption-free whereas SN 1998bu has a color excess of E(B − V) = 0.28 (Sect. 3.3).
Folatelli et al. (2010) have calculated the mean absolute maximum JHKs magnitudes of a set of SNe Ia from their velocity distances assuming H0 = 72 and applying no correction for internal absorption. If their result is scaled to the above value of H0 = 64.0 one obtains MJ = − 18.69 ± 0.07, MH = − 18.68 ± 0.06, and MKs = − 18.73 ± 0.12. This is slightly fainter (1 − 2σ) than the mean magnitude of SN 2011fe and SN 2007sr (MJ = − 18.87 ± 0.06, MH = − 18.73 ± 0.06, and MKs = − 18.87 ± 0.07) and would suggest that H0 should be further reduced by a modest amount. But it would be imprudent to attempt an infrared luminosity calibration of SNe Ia with only two objects.
As seen in Table 2 SN 2007sr appears to be less luminous in J and H by as much as ~0.7mag on the basis of the published maximum magnitudes (Schweizer et al. 2008) than the two preceding SNe. This is surprising since it is spectroscopically a normal SNIa with B,V light curves quite similar to SN 2011fe and other SNe Ia. It can hardly be the effect of internal absorption because its optical color excess is intermediate (E(B − V) = 0.13; Sect. 3.2). However the J and H observations set in only 5 days after B maximum and hence roughly 10 days after the expected infrared maxima; for the true J and H maxima remains therefore a considerable margin.
6. Discussion
SNe Ia play a special role for the determination of the cosmic value of H0 because no other (relative) distance indicators trace the cosmic expansion field with so small dispersion well beyond all possible local effect. The next best route is offered by galaxy clusters with multiple I-band Tully-Fisher distances, although this method has large intrinsic dispersion and is therefore particularly susceptible to selection bias. The group of Giovanelli has determined such distances for 28 clusters with 26 cluster members per cluster on average (Masters et al. 2006). After a very careful and complex correction for various selection effects they define the slope of the galaxy-type-dependent mI − log (line width) relation. The ensuing relative cluster distances define the Hubble line with a surprisingly small scatter of only 0.15mag over a velocity range from 2000 to just 10 000 km s-1. However the three nearest clusters with v < 2000 km s-1 lie 0.4mag below the Hubble line (Tammann et al. 2008a, Fig. 8) implying a 20% decrease of H0 around 2000 km s-1, which is impossible in view of the linearity of the Hubble flow (e.g. Sandage et al. 2010). The discontinuity of H0 is a clear indication that the objective definition of cluster samples could not be maintained in nearby clusters. Masters et al. (2006) have zero-pointed their relative cluster distances by means of 15 nearby field galaxies with Cepheid distances from Freedman et al. (2001) and of two additional galaxies from other sources. (Their Cepheid moduli carry a special metallicity correction and are larger on average than those given by Freedman et al. 2001 by 0.10mag; they are still smaller than those given by Saha et al. 2006 by 0.15mag on average). In this way they derived a value of H0 = 74 ± 2. However, we strongly object to the calibration procedure: the objectively homogenized cluster sample cannot be compared with the sample of nearby calibrators that are chosen for the sole reason that Cepheid distances and suitable line width data are available for them.
Hislop et al. (2011) have used the data for 15 clusters from Masters et al. (2006), but their I-band Tully-Fisher relation is calibrated with 13 local field galaxies with available TRGB distances. Six of these calibrators (NGC 247, 3351, 3368, 3621, 3627, and 4826) are questionable because the respective TRGB distances published by Mould & Sakai (2008, 2009a,b) and Sakai et al. (2004) are larger by 0.34mag on average. But this is of minor importance compared with the principal objection that – as in the case of Masters et al. (2006) – the samples of calibrators and cluster galaxies constitute entirely differently selected samples. If anything, the situation is here even worse, because Hislop et al. use only 30% of the available cluster members thereby questioning the corrections for selection bias derived by Masters et al. (2006). For these reasons the value of H0 = 79 ± 2 of Hislop et al. (2011) should be given low weight.
To support the present solution it is noted that for the six galaxies in Table 1 also Cepheid distances are available. The corresponding data are set out in the self-explanatory Table 3. The resulting mean Cepheid-calibrated luminosity of the six SNe Ia is 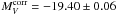 with a dispersion of 0.15mag (i.e. larger than in case of the TRGB calibration). Hence the calibration through the TRGB distances and the adopted Cepheid distances yields – in fortuitous agreement – the same mean luminosity of SNe Ia to within 0.01mag.
with a dispersion of 0.15mag (i.e. larger than in case of the TRGB calibration). Hence the calibration through the TRGB distances and the adopted Cepheid distances yields – in fortuitous agreement – the same mean luminosity of SNe Ia to within 0.01mag.
Luminosity of six calibrating SNe Ia from Cepheid distances.
It is also noted that the TRGB distances of 78 field galaxies with v220 > 280 km s-1 give a local value of H0 = 62.9 ± 1.6 (TSR08b). A slightly augmented sample of Saha et al. (2006), comprising now 29 Cepheid distances with 280 < v220 < 1600 km s-1, yields 63.4 ± 1.8 (TSR08b). The large-scale value from the summary paper of the HST Supernova Project, based on ten SNe Ia with Cepheid distances and a total of 62 standardized SNe Ia with 2000 < v < 20 000 km s-1, that resulted in H0 = 62.3 ± 1.3 ± 5.0 (Sandage et al. 2006), has been mentioned before.
Additional support for a rather low value of H0 comes from Reid et al. (2010) who have derived – on the assumption of a ΛCDM model, without using H0 as a prior – a value of H0 = 65.6 ± 2.5 by combining the 5-year WMAP data (Dunkley et al. 2009) with the Hubble diagram of the SN Ia Union Sample (Kowalski et al. 2008) and with a sample of over 110 000 luminous red galaxies (LRG) from the Sloan Digital Sky Survey DR7.
A new prospect to directly measure H0 at cosmological relevant distances comes from water maser distances of galaxies beyond ~3000 km s-1; the first two galaxies, UGC 3789 and NGC 6264 yield a mean value of H0 = 67 with a still large error of ± 6 (Braatz et al. 2010; Kuo 2011; Henkel et al. 2012). Further progress along this novel route is to be expected. – Present results from strongly lensed quasars (e.g. Vuissoz et al. 2008) and from the Sunyaev-Zeldovich effect (Holanda et al. 2012) give even larger error margins on H0.
The main conclusion is that the TRGB distances of six SNe Ia require a large-scale value of the Hubble constant of H0 = 64.0 ± 2.6 (including random and systematic errors). Suggested values as high as H0 > 70 are unlikely in the light of the TRGB. If the present result is combined with the independent value of H0 = 62.3 ± 5.2 from ten Cepheid-calibrated SNe Ia (Sandage et al. 2006) one obtains a weighted mean of H0 = 63.7 ± 2.3, which is our best estimate. The result is in good agreement with local determinations of H0 and the linearity of the expansion field (Sandage et al. 2010).
The present result will be further improved by future TRGB distances of galaxies that have produced a standard SN Ia. It is desirable that the search for the TRGB in NGC 3368 and 3627 in the Leo I group will be repeated in some uncontaminated halo fields to definitely prove their group membership. The next easiest targets at present are the Branch normal SN Ia in the Virgo cluster galaxies NGC 4419, 4501 (with the highly absorbed SN 1999cl), 4526, and 4639 (yet on the far side of Virgo); the two rather old SNe Ia in NGC 4496A and 4536 in the W-cloud are less attractive. Somewhat more difficult are the Fornax cluster galaxies NGC 1316 with five SNe Ia of which three are Branch-normal (1980N, 1981D, and 2006dd; Stritzinger et al. 2010), and the galaxies NGC 1380 and NGC 1448 with one SN Ia each; SN 2007on in NGC 1404 is as a fast decliner (Kattner et al. 2012) unreliable for calibration purposes. The Virgo and Fornax galaxies will probably be easier and more difficult, respectively, by a few 0.1mag than NGC 4038 where Schweizer et al. (2008) have demonstrated that the TRGB can be reached.
It is foreseeable that the route to a precision value of H0 through TRGB-calibrated SNe Ia will become highly competitive with any Cepheid-based distance scale.
Acknowledgments
We thank Dr. Shoko Sakai for valuable information and Dr. Federica Bianco for pre-publication data. We have made extensive use of the excellent data for SN 2011fe of the AAVSO.
References
- Altavilla, G., Fiorentino, G., Marconi, M., et al. 2004, MNRAS, 349, 1344 [NASA ADS] [CrossRef] [Google Scholar]
- Ardeberg, A., & de Groot, M. 1973, A&A, 28, 295 [NASA ADS] [Google Scholar]
- Baade, W. 1944a, ApJ, 100, 137 [NASA ADS] [CrossRef] [Google Scholar]
- Baade, W. 1944b, ApJ, 100, 147 [NASA ADS] [CrossRef] [Google Scholar]
- Baade, W., & Zwicky, F. 1938, ApJ, 88, 411 [NASA ADS] [CrossRef] [Google Scholar]
- Bianco, F., Fulton, B., Dilday, B., et al. 2012, BAAS, 219, 224.23 [Google Scholar]
- Braatz, J. A., Reid, M. J., Humphreys, E. M. L., et al. 2010, ApJ, 718, 657 [NASA ADS] [CrossRef] [Google Scholar]
- Branch, D., & Tammann, G. A. 1992, ARA&A, 30, 359 [NASA ADS] [CrossRef] [Google Scholar]
- Branch, D., Fisher, A., & Nugent, P. 1993, AJ, 106, 2383 [NASA ADS] [CrossRef] [Google Scholar]
- Carretta, E., & Gratton, R. G. 1997, A&AS, 121, 95 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Carretta, E., Gratton, R. G., Clementini, G., & Fusi Pecci, F. 2000, ApJ, 533, 215 [NASA ADS] [CrossRef] [Google Scholar]
- Carroll, S. M., Press, W. H., & Turner, E. L. 1992, ARA&A, 30, 499 [NASA ADS] [CrossRef] [Google Scholar]
- Cousins, A. W. J. 1972, IBVS, 700, 1 [NASA ADS] [Google Scholar]
- Da Costa, G. S., & Armandroff, T. E. 1990, AJ, 100, 162 [NASA ADS] [CrossRef] [Google Scholar]
- Drake, A. J., Djorgovski, S. G., Williams, R., et al. 2007, CBET, 1172 [Google Scholar]
- Dunkley, J., Komatsu, E., Nolta, M. R., et al. 2009, ApJS, 180, 306 [NASA ADS] [CrossRef] [Google Scholar]
- Faulkner, J. 1966, ApJ, 144, 978 [NASA ADS] [CrossRef] [Google Scholar]
- Filippenko, A. V. 1997, ARA&A, 35, 309 [NASA ADS] [CrossRef] [Google Scholar]
- Folatelli, G., Phillips, M. M., Burns, C. R., et al. 2010, AJ, 139, 120 [NASA ADS] [CrossRef] [Google Scholar]
- Freedman, W. L. 1989, AJ, 98, 1285 [NASA ADS] [CrossRef] [Google Scholar]
- Freedman, W. L., Madore, B. F., Gibson, B. K., et al. 2001, ApJ, 553, 47 [NASA ADS] [CrossRef] [Google Scholar]
- Ganeshalingam, M., Li, W., Filippenko, A. V., et al. 2010, ApJS, 190, 418 [NASA ADS] [CrossRef] [Google Scholar]
- Hamuy, M., Phillips, M. M., Suntzeff, N. B., et al. 1996, AJ, 112, 2438 [NASA ADS] [CrossRef] [Google Scholar]
- Henkel, C., Braatz, J. A., Reid, M. J., et al. 2012, in Cosmic masers – from OH to H0 (Cambridge: Cambridge Univ. Press), IAU Symp., 287, 301 [NASA ADS] [CrossRef] [Google Scholar]
- Hernandez, M., Meikle, W. P. S., Aparicio, A., et al. 2000, MNRAS, 319, 223 [NASA ADS] [CrossRef] [Google Scholar]
- Hicken, M., Wood-Vasey, W. M., Blondin, S., et al. 2009, ApJ, 700, 1097 [NASA ADS] [CrossRef] [Google Scholar]
- Hislop, L., Mould, J., Schmidt, B., et al. 2011, ApJ, 733, 75 [NASA ADS] [CrossRef] [Google Scholar]
- Holanda, R. F. L., Cunha, J. V., Marassi, L., & Lima, J. A. S. 2012, JCAP, 2, 35 [NASA ADS] [CrossRef] [Google Scholar]
- Hoyle, F., & Schwarzschild, M. 1955, ApJS, 2, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Huchra, J. P., & Geller, M. J. 1982, ApJ, 257, 423 [NASA ADS] [CrossRef] [Google Scholar]
- Humason, M. L., Mayall, N. U., & Sandage, A. R. 1956, AJ, 61, 97 [NASA ADS] [CrossRef] [Google Scholar]
- Jacoby, G. H., & Pierce, M. J. 1996, AJ, 112, 723 [NASA ADS] [CrossRef] [Google Scholar]
- Jha, S., Garnavich, P. M., Kirshner, R. P., et al. 1999, ApJS, 125, 73 [NASA ADS] [CrossRef] [Google Scholar]
- Jha, S., Riess, A. G., & Kirshner, R. P. 2007, ApJ, 659, 122 [NASA ADS] [CrossRef] [Google Scholar]
- Kattner, S., Leonard, D. C., Burns, C. R., et al. 2012, PASP, 124, 114 [NASA ADS] [CrossRef] [Google Scholar]
- Kowalski, M., Rubin, D., Aldering, G., et al. 2008, ApJ, 686, 749 [NASA ADS] [CrossRef] [Google Scholar]
- Krisciunas, K., Hastings, N. C., Loomis, K., et al. 2000, ApJ, 539, 658 [NASA ADS] [CrossRef] [Google Scholar]
- Kuo, C. Y. 2011, Ph.D. Thesis, Univ. of Virginia, Charlottesville [Google Scholar]
- Lee, M. G., Freedman, W. L., & Madore, B. F. 1993, ApJ, 417, 553 [Google Scholar]
- Lee, T. A., Wamsteker, W., Wisniewski, W. Z., & Wdowiak, T. J. 1972, ApJ, 177, L59 [NASA ADS] [CrossRef] [Google Scholar]
- Leibundgut, B. 1988, Ph.D. Thesis, Univ. Basel [Google Scholar]
- Lira, P. 1995, Masters thesis, Univ. Chile [Google Scholar]
- Madore, B. F., Freedman, W. L., & Sakai, S. 1997, in The Extragalactic Distance Scale, eds. M. Livio, M. Donahue, & N. Panagia (Cambridge: Cambridge Univ. Press), 239 [Google Scholar]
- Masters, K. L., Springob, C. M., Haynes, M. P., & Giovanelli, R. 2006, ApJ, 653, 861 [NASA ADS] [CrossRef] [Google Scholar]
- Matheson, T., Joyce, R. R., Allen, L. E., et al. 2012, ApJ, 754, 19 [NASA ADS] [CrossRef] [Google Scholar]
- Milne, P. A., Brown, P. J., Roming, P. W. A., et al. 2010, ApJ, 721, 1627 [NASA ADS] [CrossRef] [Google Scholar]
- Minkowski, R. 1940, PASP, 52, 206 [NASA ADS] [CrossRef] [Google Scholar]
- Mould, J., & Kristian, J. 1986, ApJ, 305, 591 [NASA ADS] [CrossRef] [Google Scholar]
- Mould, J., & Sakai, S. 2008, ApJ, 686, 75 [Google Scholar]
- Mould, J., & Sakai, S. 2009a, ApJ, 694, 1331 [NASA ADS] [CrossRef] [Google Scholar]
- Mould, J., & Sakai, S. 2009b, ApJ, 697, 996 [NASA ADS] [CrossRef] [Google Scholar]
- Naito, H., Sakane, Y., Anan, T., Kouzuma, S., & Yamaoka, H. 2007, CBET, 1173 [Google Scholar]
- Neill, J. D., Sullivan, M., Howell, D. A., et al. 2009, ApJ, 707, 1449 [NASA ADS] [CrossRef] [Google Scholar]
- Nugent, P. E., Sullivan, M., Cenko, S. B., et al. 2011, Nature, 480, 344 [NASA ADS] [CrossRef] [Google Scholar]
- Phillips, M. M., Lira, P., Suntzeff, N. B., Schommer, R. A., Hamuy, M., & Maza, J. 1999, AJ, 118, 1766 [NASA ADS] [CrossRef] [Google Scholar]
- Pierce, M. J., & Jacoby, G. H. 1995, AJ, 110, 2885 [NASA ADS] [CrossRef] [Google Scholar]
- Pojmanski, G., Prieto, J. L., Stanek, K. Z., & Beacom, J. F. 2008, CBET 1213 [Google Scholar]
- Reid, B. A., Percival, W. J., Eisenstein, D. J., et al. 2010, MNRAS, 404, 60 [NASA ADS] [CrossRef] [Google Scholar]
- Reindl, B., Tammann, G. A., Sandage, A., & Saha, A. 2005, ApJ, 624, 532 (RTS05) [NASA ADS] [CrossRef] [Google Scholar]
- Riess, A. G., Press, W. H., & Kirshner, R. P. 1996, ApJ, 473, 88 [NASA ADS] [CrossRef] [Google Scholar]
- Riess, A. G., Macri, L., Casertano, S., et al. 2011, ApJ, 730, 119 [NASA ADS] [CrossRef] [Google Scholar]
- Richmond, M. W., & Smith, H. A. 2012, J. Am. Assoc. Var. Star Obs., accepted [arXiv:1203.4013] [Google Scholar]
- Rizzi, L., Tully, R. B., Makarov, D., et al. 2007, ApJ, 661, 815 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- Rood, R. T. 1972, ApJ, 177, 681 [NASA ADS] [CrossRef] [Google Scholar]
- Saha, A., Thim, F., Tammann, G. A., Reindl, B., & Sandage, A. 2006, ApJS, 165, 108 [NASA ADS] [CrossRef] [Google Scholar]
- Sakai, S., Ferrarese, L., Kennicutt, R. C., & Saha, A. 2004, ApJ, 608, 42 [NASA ADS] [CrossRef] [Google Scholar]
- Salaris, M. 2012, Ap&SS, 341, 65 [Google Scholar]
- Sandage, A., & Tammann, G. A. 2006, ARA&A, 44, 93 [NASA ADS] [CrossRef] [Google Scholar]
- Sandage, A., Tammann, G. A., Saha, A., Reindl, B., Macchetto, F. D., & Panagia, N. 2006, ApJ, 653, 843 [NASA ADS] [CrossRef] [Google Scholar]
- Sandage, A., Reindl, B., & Tammann, G. A. 2010 ApJ, 714, 1441 [Google Scholar]
- Saviane, I., Momany, Y., da Costa, G. S., Rich, R. M., & Hibbard, J. E. 2008, ApJ, 678, 179 [NASA ADS] [CrossRef] [Google Scholar]
- Schaefer, B. E. 1994, ApJ, 426, 493 [NASA ADS] [CrossRef] [Google Scholar]
- Schaefer, B. E. 1996, AJ, 111, 1668 [NASA ADS] [CrossRef] [Google Scholar]
- Schlegel, D., Finkbeiner, D., & Davis, M. 1998, ApJ, 500, 525 [NASA ADS] [CrossRef] [Google Scholar]
- Schweizer, F., Burns, C. R., Madore, B. F., et al. 2008, AJ, 136, 1482 [NASA ADS] [CrossRef] [Google Scholar]
- Shappee, B. J., & Stanek, K. Z. 2011, ApJ, 733, 124 [NASA ADS] [CrossRef] [Google Scholar]
- Silverman, J. M., Foley, R. J., Filippenko, A. V., et al. 2012, MNRAS, 425, 1789 [NASA ADS] [CrossRef] [Google Scholar]
- Stierwalt, S., Haynes, M. P., Giovanelli, R., et al. 2009, AJ, 138, 338 [NASA ADS] [CrossRef] [Google Scholar]
- Stritzinger, M., Burns, C. R., Phillips, M. M., et al. 2010, AJ, 140, 2036 [NASA ADS] [CrossRef] [Google Scholar]
- Suntzeff, N. B., Phillips, M. M., Covarrubias, R., et al. 1999, AJ, 117, 1175 [NASA ADS] [CrossRef] [Google Scholar]
- Suyu, S. H., Treu, T., Blandford, R. D., et al. 2012 [arXiv:1202.4459] [Google Scholar]
- Sweigart, A. V., & Gross, P. G. 1978, ApJS, 36, 405 [NASA ADS] [CrossRef] [Google Scholar]
- Tammann, G. A., & Reindl, B. 2012, Ap&SS, 341, 3 [NASA ADS] [CrossRef] [Google Scholar]
- Tammann, G. A., Sandage, A., & Reindl, B. 2008a, ApJ, 679, 52 [NASA ADS] [CrossRef] [Google Scholar]
- Tammann, G. A., Sandage, A., & Reindl, B. 2008b, A&ARv, 15, 289 (TSR08b) [NASA ADS] [Google Scholar]
- Thomas, H.-C. 1967, ZfA, 67, 420 [Google Scholar]
- Tripp, R. 1998, A&A, 331, 815 [NASA ADS] [Google Scholar]
- Umbriaco, G., Pietrogrande, T., di Mille, F., Agnoletto, I., Harutyunyan, A., & Benetti, S. 2007, CBET 1174 [Google Scholar]
- van Genderen, A. M. 1975, A&A, 45, 429 [NASA ADS] [Google Scholar]
- Vuissoz, C., Courbin, F., Sluse, D., et al. 2008, A&A, 488, 481 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Wang, X., Wang, L., Pain, R., Zhou, X., & Li, Z. 2006, ApJ, 645, 488 [NASA ADS] [CrossRef] [Google Scholar]
- Wells, L. A., Phillips, M. M., Suntzeff, B., et al. 1994, AJ, 108, 2233 [NASA ADS] [CrossRef] [Google Scholar]
- Wood-Vasey, W. M., Friedman, A. S., Bloom, J. S., et al. 2008, ApJ, 689, 377 [NASA ADS] [CrossRef] [Google Scholar]
All Tables
All Figures
 |
Fig. 1 Color–magnitude diagrams in I versus (V − I) of an outlying WFPC2 field in M101 from Sakai et al. (2004, Fig. 11; note that the figure legend confuses M101 with NGC 3621). Left: only the stars in the outermost chips WF3 & WF4 with a prevailing halo population are shown. The TRGB is clearly visible at |
| In the text | |
 |
Fig. 2 Light curve of SN Ia 2011fe in M101 in B (blue), V (green), and I (red) from AAVSO data (small open dots) and Richmond & Smith (2012) (large open dots). The well fitting, mean standard light curves in B and V of SNe Ia with Δm15 = 1.1 are overplotted; they are taken from Leibundgut (1988); in I the light curve of SN 1992al (Hamuy et al. 1996) is shown for comparison (for details see text). The maximum epochs and those 15 and 35 days after B maximum are marked. The light curves in V and I are shifted by −1 and −2 mag, respectively. |
| In the text | |
 |
Fig. 3 Light curve of SN Ia 2007sr in NGC 4038 in B (blue), V (green), and I (red) from different sources. The full lines are the light curves of SN 2011fe (Fig. 2) which has closely the same decline rate of Δm15 = 1.10; the poorly fitting tail of the B light curve is shown as a dashed line. The maximum epochs and those 15 and 35 days after B maximum are marked. The light curves in V and I are shifted by − 1 and − 2mag, respectively. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.