| Issue |
A&A
Volume 549, January 2013
|
|
|---|---|---|
| Article Number | A130 | |
| Number of page(s) | 8 | |
| Section | Stellar structure and evolution | |
| DOI | https://doi.org/10.1051/0004-6361/201219570 | |
| Published online | 11 January 2013 | |
An analysis of star formation with Herschel in the Hi-GAL survey
I. The science demonstration phase fields⋆
1
Infrared Processing and Analysis Center, California Institute of
Technology,
Pasadena,
CA
91125,
USA
e-mail: marcella.veneziani@ipac.caltech.edu
2
INAF-IFSI - Via Fosso del Cavaliere, 100, Rome, Italy
3
School of Physics, Astronomy and Mathematics, University of
Hertfordshire, College
Lane, Hatfield,
AL10 9AB,
UK
4
Dipartimento di Fisica, Universita di Roma “La
Sapienza”, P.le Aldo Moro
2, 00185
Rome,
Italy
Received: 9 May 2012
Accepted: 14 November 2012
Aims. The Herschel survey of the Galactic plane (Hi-GAL) provides a unique opportunity to study star formation over large areas of the sky and different environments in the Milky Way. We use the best-studied Hi-GAL fields to date, two 2°·2° tiles centered on (ℓ, b) = (30°, 0°) and (ℓ, b) = (59°, 0°), to study the star formation activity in these regions of the sky using a large sample of well-selected young stellar objects (YSOs).
Methods. We used the science demonstration phase Hi-GAL fields, where a tremendous effort has been made to identify the newly formed stars and to derive their properties as accurately as possible, e.g. distance, bolometric luminosity, envelope mass, and stage of evolution. We estimated the star formation rate (SFR) for these fields using the number of candidate YSOs and their average time scale to reach the zero age main sequence, and compared it with the rate estimated using their integrated luminosity at 70 μm, combined with an extragalactic star formation indicator.
Results. We measure an SFR of (9.5 ± 4.3) × 10-4 M⊙/yr and (1.6 ± 0.7) × 10-4 M⊙/yr with the source counting method, in ℓ = 30° and ℓ = 59°, respectively. Results with the 70 μm estimator are (2.4 ± 0.4) × 10-4 M⊙/yr and (2.6 ± 1.1) × 10-6 M⊙/yr. Since the 70 μm indicator is derived from averaging extragalactic star forming complexes, we extrapolated of these values to the whole Milky Way and obtain SFRMW = (0.71 ± 0.13) M⊙/yr from l = 30° and SFRMW = (0.10 ± 0.04) M⊙/yr from ℓ = 59°. The estimates in ℓ = 30° agree with the most recent results for Galactic star formation activity.
Conclusions. The source-counting method gives results that are only valid for the particular region under consideration. In contrast, the construction of the IR indicator leads to results that can be extrapolated to the whole Galaxy. In particular, when it is applied to the ℓ = 30° field, it provides an SFR that is consistent with previous estimates, indicating that the characteristics of this field are very likely close to those of the star formation-dominated galaxies used for its derivation. Since the sky coverage is limited, this analysis will improve when the full Hi-GAL survey is available. It will cover the whole Galactic plane, sampling almost the totality of Galactic star forming complexes. By means of the candidate YSO-counting method, it will then be possible to calibrate an SFR Galactic indicator and to test the validity of the extragalactic estimators.
Key words: stars: formation / stars: pre-main sequence / stars: massive / stars: evolution / surveys
A machine-readable version of the full Table 1 is only available in electronic form at the CDS via anonymous ftp to cdsarc.u-strasbg.fr (130.79.128.5) or via http://cdsarc.u-strasbg.fr/viz-bin/qcat?J/A+A/549/A130
© ESO, 2013
1. Introduction
The current estimates of the star formation rate (SFR) of the Milky Way (MW) are uncertain mainly because we lack general knowledge of the structure of our Galaxy. The most recent data suggest it is a two-armed, barred spiral with several secondary arms but the actual number and position of the arms is still unclear (Dame et al. 2001; Dame & Thaddeus 2011). Moreover, the location of the solar system in the Galactic plane makes the definition of the overall Galactic structure, hence the heliocentric distance determination of star forming regions, even more difficult. Observations through the Galactic plane are affected by source overlap along the line of sight, and the optical and UV radiation emitted by young stars is absorbed or scattered by the interstellar medium (ISM) through the extinction process.
Many SFR values have been measured during the years using different datasets and techniques, such as infrared (IR) photometry (Robitaille & Whitney 2010), which measures the light from young stars reemitted by the ISM in the IR; free-free emission (Murray & Rahman 2010), which measures the amount of photons required to produce the observed ionization of the HII regions; or high-mass star counts (Reed 2005). The values range from 1 M⊙/yr (Robitaille & Whitney 2010) to 10 M⊙/yr (Güsten & Mezger 1982). Recently Chomiuk & Povich (2011) have observed that, when normalizing all these measurements to the same initial mass function (IMF), they converge to 1.9 M⊙/yr.
In recent years, a lot of progress has been made in identifying the position of many star forming regions (Russeil 2003; Benjamin et al. 2005; Russeil et al. 2011), thereby improving our knowledge of the structure of the Galaxy. This has been made possible mostly by combining the information from line tracers with IR surveys, such as GLIMPSE (Galactic Legacy Infrared Mid-Plane Survey Extraordinaire, Benjamin et al. 2003), MIPSGAL (A 24 and 70 Micron Survey of the Inner Galactic Disk with MIPS, Carey et al. 2009), and Hi-GAL (Herschel Infrared Galactic Plane Survey, Molinari et al. 2010a,b), which provide a wealth of data in the domain where the dust surrounding young stellar objects (YSOs) peaks. In these bands it is therefore possible to study the quantity of young stars through the UV and optical light of the protostar that is absorbed, processed, and reemitted by dust in the IR domain. In particular, Hi-GAL mapped the Galactic plane in |ℓ| < 60° and |b| < 1° with the Photodetector Array Camera and Spectrometer (PACS; Poglitsch et al. 2010) and Spectral and Photometric Imaging Receiver (SPIRE; Griffin et al. 2010) instruments in parallel mode, in the 70, 160, 250, 350, and 500 μm bands. Given its spectral range and sky coverage, it provides a unique opportunity to study collapsing dust clouds and protostars, i.e., the early stages of star formation. Moreover, the survey is particularly sensitive to high-mass stars (OB, M > 8 M⊙), which regulate the ecology of our Galaxy as a whole.
In this paper, we estimate the SFR in the sky regions mapped during the Herschel science demonstration phase (SDP), i.e., two 2°·2° tiles centered on the Galactic plane in ℓ = 30° and ℓ = 59°. The ℓ = 30° field observes the Sagittarium and Perseus arms, while ℓ = 59° is centered on an interarm region (Russeil et al. 2011). Owing to its location, the ℓ = 30° field is expected to be more active in terms of star formation than the ℓ = 59° field. A higher number of YSOs and HII regions are located in the ℓ = 30° area, including the W43 complex (Bally et al. 1999), a massive star forming region with an associated giant HII region. This gives us the opportunity to study the star formation processes both in a very active and in a quiescent environment.
Owing to the aforementioned difficulties in estimating the SFR of the MW, we do not have a reliable far IR star formation indicator. Many indicators have been calibrated on extragalactic star forming complexes and then applied to Galactic observations (see for example Kennicutt 1998; Calzetti et al. 2007; Kennicutt et al. 2007). Since one of the main goals of Galactic star formation studies is to derive an SFR estimator of the MW, hence test the validity of estimators calibrated on other galaxies, we make use both of an extragalactic indicator (Li et al. 2010) and of a star-counting method to estimate the SFR in the two Hi-GAL SDP tiles, and then compare the results. This way, we both study the star formation activity in the two Hi-GAL fields and test the method in order to apply it to a larger sample when the whole Hi-GAL survey has been completed. The paper is organized as follow: Sect. 2 describes the dataset; Sect. 3 outlines the spectral energy distribution (SED) fitting, the sample selection criteria, and the estimate of the candidate YSOs physical parameters such as temperatures and masses; in Sect. 4 we estimate the SFR with the extragalactic estimator and count the young stars. The approximation adopted in this procedure and the quantifiable errors are discussed in Sect. 5. Conclusions are summarized in Sect. 6.
2. The dataset
The starting point of this study is the catalog of sources in the two Hi-GAL SDP fields (Elia et al. 2010). A new version of this catalog has recently been released to the Hi-GAL consortium, obtained with updated data cleaning procedures, mapmaking, calibration factors, extraction, and photometry in the PACS and SPIRE bands. For more information about the Hi-GAL pipeline from raw data to map production we refer the reader to Traficante et al. (2011). The algorithm used for the source detection is CuTEX (Curvature Thresholding EXtractor) (Molinari et al. 2011) which double-differentiates the sky image and studies the variation in the curvature above a given threshold. The identified source profiles are then fitted with a 2D elliptical Gaussian plus an underlying inclined planar plateau. This allows us to detect sources in the presence of a variable background, like the one in the Galactic plane, and to select not only point-like sources but also compact objects. These two conditions are crucial for us because we are interested in studying YSOs emitting in the PACS and SPIRE bands, which are still embedded. The considered sources have known kinematic distances (Russeil et al. 2011) and are detected in at least three contiguous Herschel bands. This last condition is required to exclude spurious detections. After these conditions have been applied, we have a total of 681 sources in ℓ = 30° and 316 in ℓ = 59°. To sample the SEDs better and constrain the evolutionary stage, the 24 μm flux from MIPSGAL (Carey et al. 2009) is also measured at the same position of the 70 μm band. For more information about the source extraction and distance determination, we refer the reader to Elia et al. (2010) and Russeil et al. (2011).
3. SED fitting
The physical parameters of the sources with at least three positive fluxes (Sλ) are estimated through a modified black body fit. The emission at wavelength λ can be modeled as 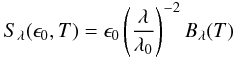 (1)where T is the source temperature, ϵ0 the emissivity at the reference wavelength λ0 = 100 μm, the emissivity spectral index is set to 2, and Bλ(T) is the blackbody at temperature T. The emissivity can be rewritten as
(1)where T is the source temperature, ϵ0 the emissivity at the reference wavelength λ0 = 100 μm, the emissivity spectral index is set to 2, and Bλ(T) is the blackbody at temperature T. The emissivity can be rewritten as 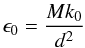 (2)where M is the total mass of the source, k0 the mass opacity at wavelength λ0 per unit mass, and d is the heliocentric distance.
(2)where M is the total mass of the source, k0 the mass opacity at wavelength λ0 per unit mass, and d is the heliocentric distance.
We perform the fit using a Monte Carlo Markov chain algorithm (MCMC Lewis & Bridle 2002) and estimate the temperatures and the total masses. We do not fit the SEDs with the grid of models from Robitaille et al. (2006), as was done with the previous version of this catalog, because almost all the sources peak at wavelength 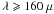 m, which is the threshold identified by Elia et al. (2010) as the one above which the Robitaille models do not apply anymore. The fit is performed including only Herschel PACS and SPIRE bands. The associated error bars come mainly from calibration uncertainties and background removal. Since we are not analyzing point-like objects but embedded sources we make use of the calibration errors measured on extended emission, which amount to 20% of the total flux for PACS and 15% of the flux for SPIRE. We also include a 10% statistical error coming from the background fluctuations. The two errors are added in quadrature and associated to the fluxes. In the present analysis we chose not to include the 24 μm flux in the fit since we are interested in the envelope emission. The 24 μm flux samples the internal source, and this would require a two-component model, one for the envelope and one for the central star. We do not probe sources with T < 7 K in our analysis, because in that temperature regime, the assumption of an optically thin regime implicit in the modified black body fitting breaks down. We would need a full radiative transfer model to account for optical depth effects, and this goes beyond the scope of the present paper. The average temperature in the two fields are ⟨ Tl30 ⟩ = 17.5 K and ⟨ Tℓ59 ⟩ = 14.3 K. The ℓ = 59° tile is colder on average, consistent with its being an interarm field, and star formation is not very active.
m, which is the threshold identified by Elia et al. (2010) as the one above which the Robitaille models do not apply anymore. The fit is performed including only Herschel PACS and SPIRE bands. The associated error bars come mainly from calibration uncertainties and background removal. Since we are not analyzing point-like objects but embedded sources we make use of the calibration errors measured on extended emission, which amount to 20% of the total flux for PACS and 15% of the flux for SPIRE. We also include a 10% statistical error coming from the background fluctuations. The two errors are added in quadrature and associated to the fluxes. In the present analysis we chose not to include the 24 μm flux in the fit since we are interested in the envelope emission. The 24 μm flux samples the internal source, and this would require a two-component model, one for the envelope and one for the central star. We do not probe sources with T < 7 K in our analysis, because in that temperature regime, the assumption of an optically thin regime implicit in the modified black body fitting breaks down. We would need a full radiative transfer model to account for optical depth effects, and this goes beyond the scope of the present paper. The average temperature in the two fields are ⟨ Tl30 ⟩ = 17.5 K and ⟨ Tℓ59 ⟩ = 14.3 K. The ℓ = 59° tile is colder on average, consistent with its being an interarm field, and star formation is not very active.
To estimate envelope masses, we put ourselves in the Rayleigh-Jeans (RJ) regime which is optically thin. Since the 500 μm band has a low resolution and is affected by problems with source multiplicity, the 350 μm band is then the best compromise, so we estimate masses according to the formula 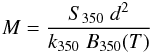 (3)where S350 is the flux at 350 μm, d the kinematic distance, k350 = 0.07 cm2 g-1 the mass opacity coefficient at 350 μm per unit mass (Preibisch et al. 1993), and T the temperature estimated by means of Eq. (1). The measured masses range between 1 and 105 M⊙ in ℓ = 30° and between 0.1 and 104 M⊙ in ℓ = 59°, with median values of 454 M⊙ in ℓ = 30° and 48 M⊙ in ℓ = 59°.
(3)where S350 is the flux at 350 μm, d the kinematic distance, k350 = 0.07 cm2 g-1 the mass opacity coefficient at 350 μm per unit mass (Preibisch et al. 1993), and T the temperature estimated by means of Eq. (1). The measured masses range between 1 and 105 M⊙ in ℓ = 30° and between 0.1 and 104 M⊙ in ℓ = 59°, with median values of 454 M⊙ in ℓ = 30° and 48 M⊙ in ℓ = 59°.
3.1. Selection criteria
Once we have fluxes, temperatures, and masses for the whole sample of sources, we perform a further selection to ensure we only collect YSOs for the SFR estimate. First, we remove sources with a negligible emission in the PACS 70 μm band. Second, we identify and remove AGB stars using color–color criteria.
The presence of a 70 μm counterpart has been demonstrated to be correlated with the internal luminosity of a protostar (Dunham et al. 2008) and, moreover, we do not expect our survey to detect a 70 μm flux of diffuse ISM just heated by the interstellar radiation field. For these reasons, we consider all those sources without a detection at 70 μm as starless.
One of the most challenging steps in cleaning our catalog is to make certain not to include AGB sources in our sample. Around 30% to 50% of the mid-infrared sources are estimated to be AGBs by Robitaille et al. (2008) using the GLIMPSE survey. AGB sources also emit in the IR and can be disentangled from YSOs by applying color–color criteria. We make use of the criteria developed by Martinavarro et al. (in perp.) in the Herschel bands. According to these authors, AGBs are located in the color–color diagram where the following is verified: 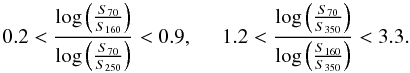 (4)The percentage of AGBs among sources detected at 70 μm is 47% in ℓ = 30° and 52% in ℓ = 59°, which is consistent with what was found in the GLIMPSE survey. All the sources satisfying these color criteria are removed from the sample.
(4)The percentage of AGBs among sources detected at 70 μm is 47% in ℓ = 30° and 52% in ℓ = 59°, which is consistent with what was found in the GLIMPSE survey. All the sources satisfying these color criteria are removed from the sample.
To identify starless objects that are gravitationally bound, i.e. prestellar sources, we applied the method used by Giannini et al. (2012) on the Vela-C molecular cloud. Instead of the virial mass, they make use of the Bonnor-Ebert mass, MBE ~ 2.4RBEa2/G, where RBE is the Bonnor-Ebert radius, which can be approximated by the actual radius of the source, RBE = δ/2 where δ is the diameter, G the gravitational constant, and 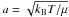 . Here, kB is the Boltzmann constant, T the source temperature, and μ is the mean molecular weight. The source diameters (δ) are shown in Fig. 1. They are estimated from the 250 μm map by approximating the ellipse provided by CuTEX as a circle with the same area and deconvolving it with the instrumental beam. The choice of the 250 μm was made because all sources are detected in this band. In both tiles the majority of sources have δ > 0.1 pc, meaning that they are essentially clumps (see e.g. Kauffmann et al. 2010, and references therein), as is also confirmed by their mass distribution. Following the criteria in Giannini et al. (2012) we identify sources with
. Here, kB is the Boltzmann constant, T the source temperature, and μ is the mean molecular weight. The source diameters (δ) are shown in Fig. 1. They are estimated from the 250 μm map by approximating the ellipse provided by CuTEX as a circle with the same area and deconvolving it with the instrumental beam. The choice of the 250 μm was made because all sources are detected in this band. In both tiles the majority of sources have δ > 0.1 pc, meaning that they are essentially clumps (see e.g. Kauffmann et al. 2010, and references therein), as is also confirmed by their mass distribution. Following the criteria in Giannini et al. (2012) we identify sources with 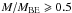 as gravitationally bound.
as gravitationally bound.
 |
Fig. 1 Diameter distribution of all sources detected in three adjacent Herschel bands, estimated from the 250 μm map. |
The temperature distribution of the prestellar and protostellar sources is reported in Fig. 2. This figure clearly shows two populations of objects, a cold one (red histogram), mostly prestellar, which peaks around 11 K; and a warm one (blue histogram), mostly protostellar, which peaks around 20 K. The protostellar sources constitute the final sample used in the following analysis.
 |
Fig. 2 Temperature distribution of the considered YSO candidates and prestellar cores estimated by means of a modified black body fit from 70 μm to 500 μm. |
Two recent papers (Battersby et al. 2011; Paradis et al. 2010) have measured the temperature of these fields on a pixel-by-pixel basis, smoothing the signal of all wavelengths to 35.6′′, i.e. the resolution of the Herschel 500 μm band. Their results do not show the same bimodal distribution as ours because we keep the original resolution of each band, and therefore, we identify and collect compacts objects and are sensitive to the temperature variations on these smaller scales. After applying those criteria, the number of identified candidate YSOs is 235 in ℓ = 30° and 50 in ℓ = 59°. Table 1 gives the coordinates, fluxes, and distances of the 285 selected sources.
List of candidate YSOs in the SDP fields with their MIPS and Hi-GAL photometry and distances.
The distance distribution of the selected sources is shown in Fig. 3. In ℓ = 30° (left panel), most of the sources cluster, as expected, in the Scutum spiral arm, which crosses the line of sight twice (at d ~ 5.5 kpc (near) and d ~ 9 kpc (far)) and in the Sagittarius arm (at d ~ 3.5 kpc (near) and d ~ 11 kpc (far)). The peak centered on d ~ 13 kpc corresponds to sources located in the Perseus arm. In ℓ = 59° (right panel) the line of sight is tangential to the Sagittarius arm (d ~ 3−7 kpc) where most of the sources are located. For more information about the Galactic distribution of Hi-GAL sources in the SDP fields and for a distance derivation we refer the reader to Russeil et al. (2011).
 |
Fig. 3 Distance distribution of the selected candidate YSOs in SDP fields. |
The color–color plots of the final sample are shown in Fig. 4. Each axis of these figures reports the magnitude difference between the two bands according to the formula ![\hbox{$[\lambda_1 - \lambda_0] = m_1 - m_0 = -2.5\log(\frac{S(\lambda_1)}{S(\lambda_0)})$}](/articles/aa/full_html/2013/01/aa19570-12/aa19570-12-eq78.png) where S(λ) is the flux at the band λ and m its magnitude. The left hand panel shows a subsample of the right panel because some of the protostellar sources are detected at 70 μm but not at 24 μm.
where S(λ) is the flux at the band λ and m its magnitude. The left hand panel shows a subsample of the right panel because some of the protostellar sources are detected at 70 μm but not at 24 μm.
 |
Fig. 4 Color–color diagrams for all the protostellar sources in the ℓ = 30° (black squares) and ℓ = 59° (red diamonds) fields. The color distribution is consistent with embedded sources that can only be fitted with a modified black body and not with an embedded ZAMS model (Molinari et al. 2008). |
4. SFR estimate
The SFR in the SDP fields is estimated using two independent techniques, one based on an IR extragalactic estimator and the other on source counting. Results for the tiles as a whole are reported in Table 2.
SFR estimates.
4.1. Source counts
Starting from fluxes and distances we estimate the bolometric luminosities (Lbol) of our sources according to the formula 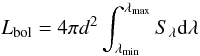 (5)where λmin = 24 μm, λmax = 500 μm, d is the heliocentric distance, and Sλ is the source flux at the wavelength λ. The prestellar and protostellar source distributions of the Lbol in the Galaxy towards the two considered tiles is shown in Fig. 5.
(5)where λmin = 24 μm, λmax = 500 μm, d is the heliocentric distance, and Sλ is the source flux at the wavelength λ. The prestellar and protostellar source distributions of the Lbol in the Galaxy towards the two considered tiles is shown in Fig. 5.
 |
Fig. 5 Bolometric luminosity of prestellar (red squares) and protostellar (blue circles) sources in the SDP fields as a function of the heliocentric distance. |
We then build the Menv − Lbol diagram where Menv is the envelope mass. This kind of diagram provides information on the evolutionary stage of the source and a prescription of both when it will join the zero age main sequence (ZAMS hereafter) and with which final mass (Molinari et al. 2008). The source evolves along defined tracks according to the chosen evolutionary model. We adopt the model of collapse in turbulence-supported dust cores (McKee & Tan 2003). According to this model, the evolution of high-mass YSOs has two main phases. In a first phase, as soon as the initial cloud starts collapsing, the luminosity of the embedded star increases in an accelerated fashion and the initial mass envelope decreases because part of the material feeds the central core and part is expelled through molecular outflows. The path followed by the protostar in the Menv − Lbol diagram is almost vertical. At the end of this phase, the star reaches the ZAMS, or is very close to it, and is surrounded by an HII region. The average time of this phase is 2.7 × 105 yr for an initial envelope mass of 13.5 M⊙ (Molinari et al. 2008). In the second phase, after the end of the accelerating accretion, the remaining envelope mass is partially drained by other objects forming in the same clump and part of it is expelled through molecular outflows. An accretion disk is also present, so part of the initial cloud still keeps feeding the central star. The envelope clean-up phase ends when the object is visible in the optical band and the initial cloud has completely disappeared. Since the luminosity in this phase remains almost constant, this results in a horizontal track in the diagram. The total average evolutionary time for the entire path is 3.5 × 106 yr for an initial envelope mass of 13.5 M⊙. For more detailed information about the evolutionary model we refer the reader to McKee & Tan (2003) and Molinari et al. (2008).
Since the sources we are considering are still deeply embedded, we can assume that M corresponds to the Menv derived in Sect. 3. The Menv − Lbol diagrams for the two tiles are shown in Fig. 6. The solid black line is the best log-log fit of the high-mass counterpart of the low-mass Class I regime (Molinari et al. 2008), while the dashed black line is the high-mass counterpart of the best log-log fit of the low-mass Class 0 regime. In the high-mass domain, the subdivision of young stars in classes is a conventional extrapolation from low-mass stars. Since high-mass clumps contain unresolved structures that might fragment into more than one high-mass star, and continue to accrete even after entering the main sequence, one has to be careful about this subdivision. The majority of the sources in our sample are below this line, meaning that these objects are still in an early evolutionary phase as already argued from the color–color plots in Fig. 4. The average uncertainties on luminosities and masses in ℓ = 30° are ⟨ σL/L ⟩ = 0.2 and ⟨ σM/M ⟩ = 0.4, while in ℓ = 59° they are ⟨ σL/L ⟩ = 0.4 and ⟨ σM/M ⟩ = 0.7. These values have been estimated through the error propagation of fluxes and distances.
 |
Fig. 6 Menv − Lbol diagram of the sources in the ℓ = 30° (left panel) and ℓ = 59° (right panel) fields for the prestellar and protostellar cores shown in Fig. 2. The solid black line and the dashed black line are the best log-log fit of the high-mass counterparts of the Class I and Class 0 sources, respectively, in the low-mass regime, as found in Molinari et al. (2008). |
To estimate the SFR from the evolutionary tracks provided by McKee & Tan (2003), we bin these diagrams into two-dimensional histograms. Each bin has an associated formation time that depends on the source stage and mass. Since high-mass objects keep accreting even after they join the ZAMS, the formation timescales used in our analysis cover the entire evolutionary path, from the beginning of the accelerating accretion phase to the end of the envelope clean-up phase, i.e. when the envelope has disappeared and the object is visible in the optical bands. They are tf = (2.1,2.7,3.5,4.8,4.5) × 106 yr for sources with initial envelope masses in the bins (80, 140, 350, 700, 2000) M⊙, respectively (Molinari et al. 2008). Owing to Hi-GAL sensitivity limits, we are not confident in the detection of objects with Menv < 10 M⊙. These sources are then excluded from further analysis, and the missing contribution to the SFR, coming from the low-mass regime, is estimated in Sect. 5.
The SFR from candidate high-mass YSOs in each tile is obtained by summing up the final masses and by dividing them by the associated formation time: 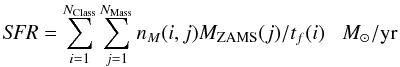 (6)where NClass = 3 (counterparts of low-mass Class 0, I, II), NMass = 5 are the number of classes and of initial masses, respectively. Here, nM(i,j) is the number of sources of Class i with envelope mass j and MZAMS(j) is the expected final mass of sources of initial envelope mass j, when they reach the ZAMS. The SFR obtained with this method is (9.5 ± 4.3) × 10-4 M⊙/yr in ℓ = 30° and (1.6 ± 0.7) × 10-4 M⊙/yr in ℓ = 59°. We have not extrapolated these estimates to the whole MW because they were calculated through a counting procedure, so are very local values. Since YSOs generally join the ZAMS when the accelerating accretion phase has been completed, we also report the SFR estimated at the end of this phase, so with shorter evolutionary timescales, in order to provide an upper limit to the estimates. The average evolutionary timescales of the main accretion phase for the mass bins mentioned before are tf = (4.5,3.7,2.7,2.1,1.5) × 105 yr, and the corresponding SFR would be (1.6 ± 0.7) × 10-2 M⊙/yr in ℓ = 30° and (7.9 ± 3.6) × 10-4 M⊙/yr in ℓ = 59°.
(6)where NClass = 3 (counterparts of low-mass Class 0, I, II), NMass = 5 are the number of classes and of initial masses, respectively. Here, nM(i,j) is the number of sources of Class i with envelope mass j and MZAMS(j) is the expected final mass of sources of initial envelope mass j, when they reach the ZAMS. The SFR obtained with this method is (9.5 ± 4.3) × 10-4 M⊙/yr in ℓ = 30° and (1.6 ± 0.7) × 10-4 M⊙/yr in ℓ = 59°. We have not extrapolated these estimates to the whole MW because they were calculated through a counting procedure, so are very local values. Since YSOs generally join the ZAMS when the accelerating accretion phase has been completed, we also report the SFR estimated at the end of this phase, so with shorter evolutionary timescales, in order to provide an upper limit to the estimates. The average evolutionary timescales of the main accretion phase for the mass bins mentioned before are tf = (4.5,3.7,2.7,2.1,1.5) × 105 yr, and the corresponding SFR would be (1.6 ± 0.7) × 10-2 M⊙/yr in ℓ = 30° and (7.9 ± 3.6) × 10-4 M⊙/yr in ℓ = 59°.
4.2. Monochromatic estimator at 70 μm
Another way to study the SFR of a sample of sources with known infrared luminosities is to make use of an extragalactic estimator. Dust surrounding the forming stars absorbs UV radiation and radiates it again in the IR. Therefore, optical/UV based indicators are not reliable in the MW because of the high extinction generated by interstellar dust along the line of sight. In contrast, IR emission is a reliable tracer of the photons produced by the forming source. Lawton et al. (2010) finds that, among all the IR bands, the 70 μm band is the most reliable indicator of star formation because it is able to account for IR emission from HII regions (see for example Tibbs et al. 2012; Faimali et al. 2012).
We then consider the 70 μm monochromatic estimator developed by Li et al. (2010). They measure the 70 μm luminosities of extragalactic star forming regions and calibrate them on their previous SFR estimator based on 24 μm and H(α) luminosities (Calzetti et al. 2007). The conversion factor between total luminosity at 70 μm and the SFR is 1.067 × 1043 erg/s. The SFR obtained with this method is (2.4 ± 0.4) × 10-4 M⊙/yr in ℓ = 30° and (2.6 ± 1.1) × 10-6 M⊙/yr in ℓ = 59°.
Since the estimator is built by averaging extragalactic star forming complexes, we extrapolate these values to the whole Galaxy and model it as a disk in which sources are uniformly distributed within the volume. The observed fields are then slices of this volume, with the vertex centered on the Sun and an aperture angle of 2°, i.e. the dimension of the tiles. The SFR value of the single tiles is then extrapolated to the whole MW through the equation 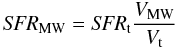 (7)where
(7)where 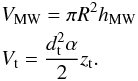 (8)\arraycolsep1.75ptIn the previous equations, Vt and VMW are the volumes of the tile and of the whole MW, respectively, hMW = 0.3 kpc is the thickness of the Galactic disk, R = 15 kpc is its radius, dt is the average heliocentric distance of the candidate YSOs in the tile (7.6 kpc in ℓ = 30° and 3.3 kpc in ℓ = 59°), α = 2° is the aperture angle, and zt is the distance of the sources from the Galactic plane. Following Paladini et al. (2004), we estimate zt by means of a Gaussian fit of the z = dsin(b) distribution of the sources, where b is their Galactic latitude. The FWHM of the fitted Gaussian curve is the zt value we assume for all the protostars in the same tile. The fits are shown in Fig. 7. We obtain zℓ30 = 71.9 pc and zℓ59 = 27.6 pc. These values agree with the distribution of 456 Galactic HII regions reported in Paladini et al. (2004).
(8)\arraycolsep1.75ptIn the previous equations, Vt and VMW are the volumes of the tile and of the whole MW, respectively, hMW = 0.3 kpc is the thickness of the Galactic disk, R = 15 kpc is its radius, dt is the average heliocentric distance of the candidate YSOs in the tile (7.6 kpc in ℓ = 30° and 3.3 kpc in ℓ = 59°), α = 2° is the aperture angle, and zt is the distance of the sources from the Galactic plane. Following Paladini et al. (2004), we estimate zt by means of a Gaussian fit of the z = dsin(b) distribution of the sources, where b is their Galactic latitude. The FWHM of the fitted Gaussian curve is the zt value we assume for all the protostars in the same tile. The fits are shown in Fig. 7. We obtain zℓ30 = 71.9 pc and zℓ59 = 27.6 pc. These values agree with the distribution of 456 Galactic HII regions reported in Paladini et al. (2004).
 |
Fig. 7 z distribution of the Hi-GAL protostars in the ℓ = 30° and ℓ = 59° fields. The z value adopted to estimate the tile volumes is the FWHM of the Gaussian fit. The second peak at z ~ 60 pc in ℓ = 59° is due to a concentration of YSOs in the Vulpecula OB association (Billot et al. 2010). |
We obtain an SFRMW = 0.71 ± 0.13 M⊙/yr in ℓ = 30° and SFRMW = 0.10 ± 0.04 M⊙/yr in ℓ = 59°. As expected, the extrapolation from ℓ = 30° gives more reasonable results since it is an area with active star forming regions, and therefore, it has characteristics similar to the star-formation-dominated galaxies used to calibrate the estimator. In fact, the value of SFRMW from ℓ = 30° is in good agreement with previous results in the MW obtained using different estimators and datasets (Chomiuk & Povich 2011), and it falls in the range measured by Robitaille & Whitney (2010) using the Spitzer/IRAC GLIMPSE survey (0.68−1.45 M⊙/yr). In the previous extrapolation of the local SFR to the whole Galaxy, we set the overall tile distance dt (Eq. (8)) to the average distance of the sources in the considered tile. When we set dt to the distance of the farther source in the tile (dt = 14.4 kpc in ℓ = 30° and dt = 7 kpc in ℓ = 59°), i.e. the distance in which we assume our sample to be complete, we obtain SFRMW = 0.20 ± 0.04 M⊙/yr in ℓ = 30° and SFRMW = 0.02 ± 0.01 M⊙/yr in ℓ = 59°.
5. Catalog completeness
The catalog completeness provides us with the information about how many sources we can miss with fluxes fainter than a given threshold. This translates into how much mass and luminosity we are missing when calculating the SFR. Since the masses were estimated from the 350 μm flux (Eq. (3)), we studied the distribution of the fluxes in this band to identify the lower detection threshold.
 |
Fig. 8 Distribution of the candidate YSOs 70 μm, 160 μm, and 350 μm fluxes in the SDP fields. These bands are particularly important because the 70 μm fluxes are used to indicate star formation activity, the 160 μm is located in the peak of the SED, and the 350 μm fluxes determine the masses through Eq. (3). The vertical red-dashed lines in the bottom panels indicate the sensitivity limit used to calculate the completeness of our sample. They correspond to 1.5 and 0.7 Jy in ℓ = 30° and ℓ = 59°, respectively. |
In Fig. 8 we show a zoom of the 70 μm (top line), 160 μm (central line), and 350 μm flux distributions (bottom line) of the candidate YSOs in the two tiles. We can see that below a given flux value fewer and fewer sources are detected and that this threshold is lower in ℓ = 59° than in ℓ = 30°. The threshold value depends mostly on the instrumental sensitivity, on the detection algorithm, and on the observed field. The more the field is populated, as in the ℓ = 30° case, with bright sources and variable background, the more difficult it is for the detection algorithm to detect faint objects. We chose as a flux sensitivity threshold at 350 μm the values right before the first peak of sources. These limit fluxes are 1.5 Jy and 0.7 Jy for ℓ = 30° and ℓ = 59°, respectively. These values are very similar to the ones estimated by Molinari et al. (2010a) through synthetic source experiments in the old version of the catalog.
To translate those values into the amount of missing mass, we estimate the mass corresponding to those limit fluxes using Eq. (3) where we assign, as distance, the median distance detected in the field and, as temperature, the average temperature of protostars in that field. The conservative choice of the median distance associated to the limit flux allows us to even include the faintest objects in the estimate of missing mass. The envelope masses corresponding to the limit flux then turn out to be 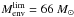 in ℓ = 30° and
in ℓ = 30° and 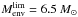 in ℓ = 59°. According to Molinari et al. (2008) and Saraceno et al. (1996), this translates into a final stellar mass of
in ℓ = 59°. According to Molinari et al. (2008) and Saraceno et al. (1996), this translates into a final stellar mass of 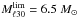 and
and 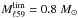 . The number of sources expected with M < Mlim is estimated with the Kroupa (2001) initial mass function (IMF). The IMF is normalized to the counts in the bin of lowest envelope masses (80 M⊙ < ΔM0 < 140 M⊙) where our detection is complete, according to the formula
. The number of sources expected with M < Mlim is estimated with the Kroupa (2001) initial mass function (IMF). The IMF is normalized to the counts in the bin of lowest envelope masses (80 M⊙ < ΔM0 < 140 M⊙) where our detection is complete, according to the formula 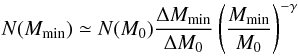 (9)where N(Mmin) is the number of stars in the bin ΔMmin = [0.1,0.5] M⊙, N(M0) the number of stars in the bin ΔM0, M0 the limit mass of the final star Mlim in each tile, γ = 2.3 for M > 0.5 M⊙, and γ = 1.3 for 0.1 M⊙ < M < 0.5 M⊙. We then calculate the number of missing stars until Mmin = 0.1 M⊙, which we assume to be the minimum value for a YSO mass.
(9)where N(Mmin) is the number of stars in the bin ΔMmin = [0.1,0.5] M⊙, N(M0) the number of stars in the bin ΔM0, M0 the limit mass of the final star Mlim in each tile, γ = 2.3 for M > 0.5 M⊙, and γ = 1.3 for 0.1 M⊙ < M < 0.5 M⊙. We then calculate the number of missing stars until Mmin = 0.1 M⊙, which we assume to be the minimum value for a YSO mass.
By means of this procedure we estimate that, considering 0.1 M⊙ as the lower limit for a final star mass, we are not detecting ~55% of the total number of sources in ℓ = 30° and ~3% in ℓ = 59°. The average timescale for a low-mass YSO population is τ ~ 2 Myr (see for example Evans et al. 2009; Covey et al. 2010; Lada et al. 2010). By using again the star count method, we can then calculate the amount of missing SFR as SFRM < M(lim) = Mmin·N(Mmin)/τ. We obtain SFRM < M(lim) = 1.0 × 10-5 M⊙/yr in ℓ = 30° and SFRM < M(lim) = 3.9 × 10-8 M⊙/yr in ℓ = 59°. Those values are negligible with respect to the estimates of the SFR obtained with both methods.
6. Summary and conclusions
We estimated the SFR in the two best-studied Hi-GAL fields, making use of the most updated version of the source catalog. Owing to the spectral range, sensitivity, and sky coverage of our dataset and because of the extraction algorithm, we were particularly sensitive to the very early stages of high-mass star formation. Moreover, the two Hi-GAL fields in this study cover both Galactic arms and interarm regions, and this gave us the chance to study the SFR both in a very active and in a more quiescent field. Color–color criteria and the knowledge of heliocentric distances enabled us to remove AGBs stars, keeping only the protostellar sources.
In this work we have made use both of an extragalactic monochromatic estimator at 70 μm and of a source-counting procedure for comparing the results. The SFR estimates for the two tiles are (9.5 ± 4.3) × 10-4 M⊙/yr and (1.6 ± 0.7) × 10-5 M⊙/yr with the star-counting method in ℓ = 30° and ℓ = 59°, respectively. Results with the IR estimator are (2.4 ± 0.4) × 10-4 M⊙/yr and (2.6 ± 1.1) × 10-6 M⊙/yr in ℓ = 30° and ℓ = 59°, respectively. Those values are in good agreement in ℓ = 30°, which is an active field.
We also estimated that our catalog is complete at ~45% in ℓ = 30° and ~97% in ℓ = 59°. Because of the instrument characteristics, in ℓ = 30° we miss a large population of low-mass stars, while the ℓ = 59° field is closer and less populated, so the sampling is more complete. The contribution to the Galactic star forming activity coming from nondetected low-mass stars is estimated to be at least more than one order of magnitude lower than the SFR from high-mass objects obtained using both methods.
The extragalactic indicator is, thanks to its construction, an average value of extragalactic star forming regions, so it provides SFR estimates that are meant to be calculated on whole galaxies. Therefore, it makes sense to extrapolate the local results of the tiles to the whole MW. When applying this method to the ℓ = 30° tile, which has similar star formation activity to the galaxies on which the indicator has been calibrated, we get results in agreement with previous studies (SFRMW ~ 0.71 ± 0.13 M⊙/yr) and the two methods provide consistent results. This means that, when applied to areas with characteristics similar to the extragalatic star forming regions used to calibrate it, the IR estimator gives reliable results even in the MW. In contrast, the SFR from the source-counting method is not meant to be extrapolated because it is based on the local population of YSOs, so it would provide very different results depending on the observed area.
Both methods are dominated by model errors that are not quantifiable. The evolutionary star model, the IR indicator, and the Galactic extrapolation are subject to assumptions that might be negligible for the averages of large numbers, but might be significant when a limited sample is available. It will therefore be important to expand the analysis described in this work to the whole Hi-GAL survey, which will cover the entire Galactic plane and, with it, the vast majority of the star formation complexes. The use of a significantly larger sample of YSOs distributed across the Galaxy will also allow us to derive an effective Galactic SFR indicator.
Acknowledgments
The authors acknowledge an anonymous referee for helpful comments. The activity of D.E., M.P. and E.S. has been possible thanks to generous support from the Italian Space Agency via contract I/038/080/0.
References
- Bally, J., Anderson, L. D., Battersby, C., et al. 2010, A&A, 518, L90 [Google Scholar]
- Battersby, C., Bally, J., Ginsburg, A., et al. 2011, A&A, 535, A128 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Benjamin, R. A., Churchwell, E., Babler, B. L., et al. 2003, PASP, 115, 953 [NASA ADS] [CrossRef] [Google Scholar]
- Benjamin, R. A., Churchwell, E., et al. 2005, ApJ, 630, L149 [NASA ADS] [CrossRef] [Google Scholar]
- Billot, N., Noriega-Crespo, A., Carey, S., et al. 2010, ApJ, 712, 797 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Calzetti, D., Kennicutt, R. C., Engelbracht, C. W., et al. 2007, ApJ, 666, 870 [NASA ADS] [CrossRef] [Google Scholar]
- Carey, S. J., Noriega-Crespo, A., Mizuno, D. R., et al. 2009, PASP, 121, 76 [NASA ADS] [CrossRef] [Google Scholar]
- Chomiuk, L., & Povich, M. S. 2011, AJ, 142, 197 [NASA ADS] [CrossRef] [Google Scholar]
- Covey, K. R., Lada, C. J., Román-Zúñiga, C., et al. 2010, ApJ, 722, 971 [NASA ADS] [CrossRef] [Google Scholar]
- Dame, T. M., & Thaddeus, P. 2011, ApJ, 734, L24 [NASA ADS] [CrossRef] [Google Scholar]
- Dame, T. M., Hartmann, D., & Thaddeus, P. 2001, ApJ, 547, 792 [NASA ADS] [CrossRef] [Google Scholar]
- Dunham, M. M., Crapsi, A., Evans, II, N. J., et al. 2008, ApJ, 179, 249 [NASA ADS] [Google Scholar]
- Elia, D., Schisano, E., Molinari, S., et al. 2010, A&A, 518, L97 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Evans, II, N. J., Dunham, M. M., Jørgensen, J. K., et al. 2009, ApJS, 181, 321 [NASA ADS] [CrossRef] [Google Scholar]
- Faimali, A., Thompson, M. A., Hindson, L., et al. 2012, MNRAS, 426, 402 [NASA ADS] [CrossRef] [Google Scholar]
- Giannini, T., Elia, D., Lorenzetti, D., et al. 2012, A&A, 539, A156 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Griffin, M. J., Abergel, A., Abreu, A., et al. 2010, A&A, 518, L3 [Google Scholar]
- Güsten, R., & Mezger, P. G. 1982, Vistas Astron., 26, 159 [NASA ADS] [CrossRef] [Google Scholar]
- Kauffmann, J., Pillai, T., Shetty, R., et al. 2010, ApJ, 716, 433 [NASA ADS] [CrossRef] [Google Scholar]
- Kennicutt, R. C. 1998, ARA&A, 36, 189 [Google Scholar]
- Kennicutt, R. C., Calzetti, D., Walter, F., et al. 2007, ApJ, 671, 333 [NASA ADS] [CrossRef] [Google Scholar]
- Kroupa, P. 2001, MNRAS, 322, 231 [NASA ADS] [CrossRef] [Google Scholar]
- Lada, C. J., Lombardi, M., & Alves, J. F. 2010, ApJ, 724, 687 [NASA ADS] [CrossRef] [Google Scholar]
- Lawton, B., Gordon, K. D., Babler, B., et al. 2010, ApJ, 716, 453 [NASA ADS] [CrossRef] [Google Scholar]
- Lewis, A., & Bridle, S. 2002, Phys. Rev., 66, 103511 [Google Scholar]
- Li, Y., Calzetti, D., Kennicutt, R., et al. 2010, ApJ, 725, 667 [Google Scholar]
- McKee, C. F., & Tan, J. C. 2003, ApJ, 585, 850 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- Molinari, S., Pezzuto, S., Cesaroni, R., et al. 2008, A&A, 481, 345 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Molinari, S., Swinyard, B., Bally, J., et al. 2010a, PASP, 122, 314 [NASA ADS] [CrossRef] [Google Scholar]
- Molinari, S., Swinyard, B., Bally, J., et al. 2010b, A&A, 518, L100 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Molinari, S., Schisano, E., Faustini, F., et al. 2011, A&A, 530, A133 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Murray, N., & Rahman, M. 2010, ApJ, 709, 424 [NASA ADS] [CrossRef] [Google Scholar]
- Paladini, R., Davies, R. D., & De Zotti, G. 2004, MNRAS, 347, 237 [NASA ADS] [CrossRef] [Google Scholar]
- Paradis, D., Veneziani, M., Noriega-Crespo, A., et al. 2010, A&A, 520, L8 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Pilbratt, G. L., Riedinger, J. R., Passvogel, T., et al. 2010, A&A, 518, L1 [CrossRef] [EDP Sciences] [Google Scholar]
- Poglitsch, A., Waelkens, C., Geis, N., et al. 2010, A&A, 518, L2 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Preibisch, T., Ossenkopf, V., Yorke, H. W., & Henning, T. 1993, A&A, 279, 577 [NASA ADS] [Google Scholar]
- Reed, B. C. 2005, AJ, 130, 1652 [NASA ADS] [CrossRef] [Google Scholar]
- Robitaille, T. P., & Whitney, B. A. 2010, ApJ, 710, L11 [NASA ADS] [CrossRef] [Google Scholar]
- Robitaille, T. P., Whitney, B. A., Indebetouw, R., Wood, K., & Denzmore, P. 2006, ApJS, 167, 256 [NASA ADS] [CrossRef] [Google Scholar]
- Robitaille, T. P., Meade, M. R., Babler, B. L., et al. 2008, AJ, 136, 2413 [NASA ADS] [CrossRef] [Google Scholar]
- Russeil, D. 2003, A&A, 397, 133 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Russeil, D., Pestalozzi, M., Mottram, J. C., et al. 2011, A&A, 526, A151 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Saraceno, P., Andre, Ph., Ceccarelli, C., et al. 1996, A&A, 309, 827 [NASA ADS] [Google Scholar]
- Tibbs, C., Paladini, R., Compiegne, M., et al. 2012, ApJ, 754, 94 [NASA ADS] [CrossRef] [Google Scholar]
- Traficante, A., Calzoletti, L., Veneziani, M., et al. 2011, MNRAS, 416, 2932 [NASA ADS] [CrossRef] [Google Scholar]
All Tables
List of candidate YSOs in the SDP fields with their MIPS and Hi-GAL photometry and distances.
All Figures
 |
Fig. 1 Diameter distribution of all sources detected in three adjacent Herschel bands, estimated from the 250 μm map. |
| In the text | |
 |
Fig. 2 Temperature distribution of the considered YSO candidates and prestellar cores estimated by means of a modified black body fit from 70 μm to 500 μm. |
| In the text | |
 |
Fig. 3 Distance distribution of the selected candidate YSOs in SDP fields. |
| In the text | |
 |
Fig. 4 Color–color diagrams for all the protostellar sources in the ℓ = 30° (black squares) and ℓ = 59° (red diamonds) fields. The color distribution is consistent with embedded sources that can only be fitted with a modified black body and not with an embedded ZAMS model (Molinari et al. 2008). |
| In the text | |
 |
Fig. 5 Bolometric luminosity of prestellar (red squares) and protostellar (blue circles) sources in the SDP fields as a function of the heliocentric distance. |
| In the text | |
 |
Fig. 6 Menv − Lbol diagram of the sources in the ℓ = 30° (left panel) and ℓ = 59° (right panel) fields for the prestellar and protostellar cores shown in Fig. 2. The solid black line and the dashed black line are the best log-log fit of the high-mass counterparts of the Class I and Class 0 sources, respectively, in the low-mass regime, as found in Molinari et al. (2008). |
| In the text | |
 |
Fig. 7 z distribution of the Hi-GAL protostars in the ℓ = 30° and ℓ = 59° fields. The z value adopted to estimate the tile volumes is the FWHM of the Gaussian fit. The second peak at z ~ 60 pc in ℓ = 59° is due to a concentration of YSOs in the Vulpecula OB association (Billot et al. 2010). |
| In the text | |
 |
Fig. 8 Distribution of the candidate YSOs 70 μm, 160 μm, and 350 μm fluxes in the SDP fields. These bands are particularly important because the 70 μm fluxes are used to indicate star formation activity, the 160 μm is located in the peak of the SED, and the 350 μm fluxes determine the masses through Eq. (3). The vertical red-dashed lines in the bottom panels indicate the sensitivity limit used to calculate the completeness of our sample. They correspond to 1.5 and 0.7 Jy in ℓ = 30° and ℓ = 59°, respectively. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


