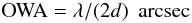| Issue |
A&A
Volume 549, January 2013
|
|
|---|---|---|
| Article Number | A52 | |
| Number of page(s) | 11 | |
| Section | Planets and planetary systems | |
| DOI | https://doi.org/10.1051/0004-6361/201219212 | |
| Published online | 18 December 2012 | |
LBT observations of the HR 8799 planetary system⋆
First detection of HR 8799e in H band
1
INAF – Osservatorio Astrofisico di Arcetri L.go E. Fermi 5,
50125
Firenze,
Italy
e-mail: esposito@arcetri.astro.it
2
INAF – Osservatorio Astronomico di Padova, Vicolo
dell’Osservatorio 5, 35122
Padova,
Italy
3
Steward Observatory, Department of Astronomy, University of
Arizona, Tucson,
AZ
85721,
USA
4
INAF – Osservatorio Astronomico di Bologna, via Ranzani 1,
40127
Bologna,
Italy
5
Dipartimento di Fisica e Astronomia – Universitá di Padova,
via Marzolo 8,
Padova,
Italy
6
LBT Observatory, Univ. of Arizona, 933 North Cherry Ave.,
Tucson, AZ
85721,
USA
7
INAF – Osservatorio Astronomico di Roma,
via Frascati 33, 00040
Monteporzio ( RM), Italy
8
Minnesota Institute of Astrophysics, University of Minnesota,
Minneapolis,
MN
5455,
USA
Received:
12
March
2012
Accepted:
1
August
2012
We have performed H and KS band observations of the planetary system around HR 8799 using the new AO system at the Large Binocular Telescope and the PISCES Camera. The excellent instrument performance (Strehl ratios up to 80% in H band) enabled the detection of the innermost planet, HR 8799e, at H band for the first time. The H and KS magnitudes of HR 8799e are similar to those of planets c and d, with planet e being slightly brighter. Therefore, HR 8799e is likely slightly more massive than c and d. We also explored possible orbital configurations and their orbital stability. We confirm that the orbits of planets b, c and e are consistent with being circular and coplanar; planet d should have either an orbital eccentricity of about 0.1 or be non-coplanar with respect to b and c. Planet e can not be in circular and coplanar orbit in a 4:2:1 mean motion resonances with c and d, while coplanar and circular orbits are allowed for a 5:2 resonance. The analysis of dynamical stability shows that the system is highly unstable or chaotic when planetary masses of about 5 MJ for b and 7 MJ for the other planets are adopted. Significant regions of dynamical stability for timescales of tens of Myr are found when adopting planetary masses of about 3.5, 5, 5, and 5 MJ for HR 8799b, c, d, and e respectively. These masses are below the current estimates based on the stellar age (30 Myr) and theoretical models of substellar objects.
Key words: stars: individual: HR 8799 / planetary systems / instrumentation: adaptive optics / techniques: high angular resolution / planets and satellites: dynamical evolution and stability / planets and satellites: physical evolution
The LBT is an international collaboration among institutions in the United States, Italy and Germany. LBT Corporation partners are: The University of Arizona on behalf of the Arizona university system; Istituto Nazionale di Astrofisica, Italy; LBT Beteiligungsgesellschaft, Germany, representing the Max-Planck Society, the Astrophysical Institute Potsdam, and Heidelberg University; The Ohio State University, and The Research Corporation, on behalf of The University of Notre Dame, University of Minnesota and University of Virginia.
© ESO, 2012
1. Introduction
The planetary system around HR 8799 represents a unique laboratory to constrain the physical properties of massive giant planets, to study the architecture of a crowded planetary system, and the link between planets and debris belts.
Three planets (HR 8799b, c and d) were discovered by Marois et al. (2008), at a projected separation of about 24, 38, and 68 AU, followed by the detection of an inner planet (HR 8799e) at about 15 AU (Marois et al. 2010). The system is completed by three debris disk components: a belt of warm dust (T ~ 150 K) between about 6 to 10 AU, a broad belt of cold dust (T ~ 45 K) between 90 to 300 AU, whose inner edge is probably defined by the interactions with the outer planet, and an extended halo of small grains up to 1000 AU (Su et al. 2009). The belt of cold dust at ~100 AU has been spatially resolved at 70 μm using Spitzer (Su et al. 2009). The central star is an A5 star located at 39.4 pc from the Sun (van Leeuwen 2007), characterized by λ Boo-like abundances anomalies and γ Doradus pulsations (Gray & Kaye 1999).
The architecture of the HR 8799 system, with its four giant planets and two belts, resembles that of our Solar system, especially when the two systems are plotted against the equilibrium temperature at various distances from the central star, taking the higher luminosity of HR 8799 compared to the Sun into account (Marois et al. 2010). However, the planets around HR 8799 are much more massive than those in the Solar System.
The discovery of this planetary system prompted several investigations focused mostly on the physical properties of the planets (e.g. Bowler et al. 2010; Currie et al. 2011) and the dynamical stability of the planetary system (e.g. Goździewski & Migaszewski 2009; Fabrycky & Murray-Clay 2010).
The masses of the planets have not been determined dynamically and estimates are therefore derived from the stellar age of HR 8799 and theoretical models. Marois et al. (2008) estimated age limits between 30 to 160 Myr, from the position of HR 8799 on HR diagram. Marois et al. (2010) narrowed the plausible age range to 30–60 Myr (with preference for the younger value) by classifying HR 8799 as a probable member of the Columba moving group (Torres et al. 2008). The association of HR 8799 with Columba was questioned by Hinz et al. (2010), who noted that the closest approach to the centroid of Columba moving group was ~58 pc 27 Myr ago (this was considered too large for a direct link) and that the size of this and other young groups might be too large to have a common origin. Furthermore, available models of substellar objects suffer from significant uncertainties, especially at young ages (Baraffe et al. 2002), leaving some ambiguity on the planet masses as derived from magnitudes or colors even at a fixed age.
On the other hand, studies of dynamical stability of the system showed that, for masses above 20 MJ, it is basically impossible to find orbital configurations compatible with the astrometric data that are also stable for the age of the system (Moro-Martín et al. 2010). The packed configuration of the system then favours the lowest planetary masses (corresponding to the youngest ages for the system), i.e. about 5 MJ for the outer planet and 7 MJ for the other three. Most of these studies were based on a 3-planet system architecture and should be extended to include the fourth planet. Continued astrometric monitoring, including improved reanalysis of past data (Soummer et al. 2011) is expected to provide tighter constraints on both the planetary orbits and masses.
The development of new instrumentation for imaging giant planets at small separation is crucial for a further understanding of the system. Enhanced Strehl ratios allow us to detect the inner planets at additional wavelengths, which in turn allows us to better characterize their physical properties. In addition they provide improved astrometric and photometric measurements thanks to the reduced speckle noise and the enhanced contrast of the planet PSF.
The new adaptive optics system (FLAO) of the Large Binocular Telescope (LBT) has achieved, since its commissioning, unprecedented performance with Strehl Ratios higher than 80% in H band (Esposito et al. 2010). Images of HR 8799 system with such instrumentation allowed us to detect, for the first time, the innermost planet (HR 8799e) in H band, enabling a more robust characterization of this planetary system. The present paper describes the instrumentation, observations and data analysis as well as a discussion of the physical characterization and dynamical architecture of the system. A companion paper, Skemer et al. (2012), presents 3.3 μm photometry of the HR 8799 system obtained using the Large Binocular Telescope Interferometer (LBTI) and the FLAO system, together with the independent analysis of the H band data discussed here and a comparison of the spectral energy distributions of the four planets with a variety of models including a new set of mixed-cloud models.
2. Observations
2.1. The LBT Adaptive Optics system
The Large Binocular Telescope (LBT) is a unique telescope featuring two co-mounted optical trains with 8.4 m primary mirrors (Hill 2010). The First-Light Adaptive Optics system (FLAO) of the LBT takes advantage of two innovative key components, namely an adaptive secondary mirror with 672 actuators and a high-order pyramid wave-front sensor with a maximum pupil sampling of 30 × 30 subapertures (Esposito et al. 2010). FLAO system #1 is located on the right telescope bent Gregorian focal station and controls the right secondary mirror. The WFS is mounted on a rotator that compensates for sky-rotation. A dichroic mirror reflects the visible light to the WFS and transmits the infrared light to the scientific instrument (in our case, PISCES). The commissioning of the instrument was completed in the winter of 2011, and included a period of science demonstration time (SDT) during which time a corrected wavefront was delivered to the PISCES imaging near-infrared (NIR) camera (McCarthy et al. 2001). The full adaptive optics imaging and spectroscopic channel will be completed when the LUCIFER (Mandel et al. 2000) instrument is installed on the NIR focal plane corrected by the FLAO#1.
Since the initial phases of the on-sky commissioning, the FLAO#1 system reached performances never achieved before on large ground-based optical telescopes. Images with 40 mas resolution and Strehl Ratios higher than 80% were obtained in H band (1.6 μm). The images show a ratio between the intensity at 0.4 arcsec and the central peak larger than 10-4 (Esposito et al. 2011).
2.2. PISCES Camera
The observations presented here used the 1–2.5 μm camera PISCES (McCarthy et al. 2001) at a bent-Gregorian focus of one 8.4 m primary mirror of the LBT. Internal optics, cooled to 77 K, reimaged the f/15 focal plane onto a HAWAII-1 detector (1024 pixel square) at f/23.5, yielding a scale of 19.31 ± 0.03 mas/px with a field-of-view of 19.7 arcsec on a side (Close et al. 2012). This scale critically samples the diffraction-limit in the H-band (λ/D = 40.5 mas). A cold pupil stop, nearly conjugated to the adaptive secondary mirror, shielded unwanted background radiation. A dichroic beamsplitter located in the converging beam ahead of the camera directed visible light (<0.95 μm) onto the wavefront sensor unit. Images from PISCES are obtained from double-correlated sampling with a read-noise of 20 electrons. Further details on the performances of the PISCES camera coupled with the LBT AO system are described in Guerra et al. (2012).
2.3. Observing strategy
Our observations of HR 8799 were obtained with the LBT in two different filters: H band on 2011 October 16 UT, within the LBT PISCES+AO science verification time (SV), and in Ks band on 2011 November 09 UT during the Science Demonstration Time (SDT). The summary of the observing setup and of the observing conditions for these two epochs is reported in Table 1.
The camera rotator was stopped to enable angular differential imaging (Marois et al. 2006). In order to minimize the dynamic effect of quasi-static speckles, we concentrated the H-band observations close to the meridian passage of the star achieving the largest angular coverage in the small time frame available. However, this strategy was not used during the observation in Ks band because observations started slightly after the meridian passage due to technical problems. The seeing was measured with the LBT-DIMM pointing to the same direction of the scientific target on sky.
We observed HR 8799 saturating the inner region in both runs (i.e. in both filters H and Ks) at radii closer to 160 mas. At radii larger than 160 mas, the planets were observed with the stellar halo within the linear regime of the camera (that is below 8000–10 000 counts). We collected calibration images to compute differential sky flat-field at the sunset and at the sunrise of the observing night.
3. Data analysis procedure
Initial image processing corrects all raw images for electronic cross-talk between the quadrants in the detector using Corquad, an IRAF1 task developed for this purpose2. The cross-talk coefficients were updated after final electronic set-up at the LBT as described in Guerra et al. (2012). After this, data analysis aiming to achieve the best possible contrast was performed using two independent pipelines and data-reduction strategies, hereafter called “A” and “B” developed at the Padova Observatory and Steward Observatory respectively. The pipelines achieved consistent results.
Summary of the observing setup and the observing conditions for HR 8799.
3.1. Pipeline A
The data analysis is composed of different steps that were implemented using IDL routines prepared for this purpose. The adopted procedure represents an optimization of data analysis routines prepared for similar datasets obtained with NACO at VLT (Chauvin & The Naco Large Programme For Giant Planets Imaging Collaboration 2010). The first step, which is critical because of heavy saturation, concerns the identification of the center of the star in each image. Accurate frame-to-frame relative positions were obtained by performing a cross-correlation (CC) between one image chosen as reference (the first image in the dataset) and all the other ones. The peak of the CC represents the shift between the center position of the two images. The position of the maximum was obtained by fitting a 2D Gaussian to this peak. This was found to be more precise than a Gaussian fit of the image itself. It is much more difficult to derive the position of the center of the star, with respect to that of faint planet images, that are not detectable in individual images. We proceeded as follows. First, the absolute position was obtained by finding the center of the stellar image after heavily smoothing using a 2D Gaussian fit. This procedure was repeated for every image. The results were then corrected for the relative frame-to-frame positions determined above, and then averaged. We found that on average the centers have an offset of about 0.5 pixels in both coordinates with respect to the value determined from the first image. We apply this correction to our star center position. The rms scatter for individual images is 0.31 pixels in both coordinates. Assuming that errors in the individual determinations are independent, a very small error of 0.01 pixels (~0.2 mas) is derived for the H-band data, and about twice this value for those in the K-band. However, systematic errors due to asymmetries of the PSF’s are likely much larger. A rough estimate can be obtained by determining the star center in a slightly different way. Rather than heavily smoothing the profiles, we replaced pixel values in the saturated region with a constant value close to the maximum of the unsaturated pixels. The resulting center positions differ systematically by 0.116 ± 0.005 pixels with respect to the adopted ones. Since both procedures look fairly legitimate, we conclude that our star position may have systematic errors on the order of 0.1 pixels and likely more, as both procedures take into account only the outer regions of the PSF, and may underestimate asymmetries of these with respect to the core of the PSF, which is the only part that can be detected for the planets. Therefore, conservatively we adopt a larger error of 0.5 pixels in our discussion.
In the second step, a 2D stellar profile is subtracted from each individual image. The aim is to reduce the strong signal gradients present in the image, improving the effectiveness of the following filtering procedures. This was done for each pixel by subtracting the median of the counts in annuli one pixel wide at different separations from the stellar center. After this, a low-pass filter was applied to each image to eliminate bad and hot pixels. The next step was a high-pass filter of the images. This was done by subtracting, from each pixel, the median of a sub-image composed by n × n pixels around it. The value of n changes according to the distance from the center of the star and it can be optimized in such a way to obtain the best final result. However, to reduce the possibility of self-subtracting a possible companion, the median was performed without considering the central pixels of the sub-image.
Finally, we implemented our version of the angular differential imaging (ADI) method (Marois et al. 2006). We first located the center of the star in each image. Then, for each image, we selected a sub-sample of images in such a way that their rotation with respect to the reference image was not too small, to avoid to self-subtracting possible companion objects, and not too large, otherwise the speckle pattern would change too much. The best criteria for image selection are different at different separations from the central star, so we repeated this part of the procedure using different sets of images optimized for different separations. We then evaluated a median image for each sub-sample of images giving larger weights to images taken at shorter time lapses and the resulting image was then subtracted from the reference one. This subtracted image was then rotated by the appropriate value, given by the parallactic angle as reported in the image header. To this angle, however, we had to add a further rotation to obtain a proper absolute orientation of each image. The calibration of this position angle is preliminary. However, an a posteriori test of the accuracy of the zero point correction to true north is given by the consistency of our astrometry with the predictions of the orbit of planet b by Soummer et al. (2011). This test indicates that the zero point is correct to within 0.3 degrees, in agreement with the error in the position of the true north by Close et al. (2012). This procedure is repeated for each image of the datacube. After this, the companion objects were in the same position in every image. We searched for such companions on the median of this datacube.
For the H-band data, the best result (in terms of S/N on HR 8799e) is achieved using only the frames taken closest to meridian passage (216 frames corresponding to ± 15°, for a total integration time of 7 min). This is due to a better subtraction of speckles given by large angular velocity and short time baseline compared to the full dataset. At larger separation, where speckle noise is less critical, the use of a larger dataset provides a slightly better S/N due to the greater fractional error due to photon noise. The results presented in Sect. 4 are based on the subset of the 216 images taken close to meridian passage.
For the case of the KS band we used all the images (apart from three of very poor quality) because it was not possible to observe the star during meridian transit due to technical problems.
3.2. Pipeline B
The H-band data were independently reduced with a LOCI-based pipeline (Locally Optimized Combination of Images; Lafrenière et al. 2007b), which is hereafter referred to as Pipeline B. Pipeline B begins by flat/dark/distortion correcting the first 500 images (rather than 216 images for pipeline A), before the natural seeing worsened. Processed images were aligned by cross-correlation. The stellar profile was subtracted from each image, using an azimuthal average, and quasi-static speckles were suppressed by subtracting the median of the full set of images from each image. Through this step, pipeline A and pipeline B are mostly similar, other than the fact that pipeline B uses more data frames, and pipeline A includes an additional high-pass/low-pass filter (they are also independent implementations). After these (fairly standard) ADI steps, pipeline B uses LOCI to further suppress the noise of quasi-static speckle residuals. Pipeline B’s results are statistically consistent with the results of Pipeline A. An in-depth description of Pipeline B, and its photometric results are presented in a companion paper, Skemer et al. (2012). In the context of this work, it is important to highlight that independent pipelines have produced similar results given that they are being used with a new instrumental setup. Some discrepancies are present in astrometric results between the two pipelines. This probably arises from the different image centering procedures that, as said in the previous paragraph, are probably the more tricky step of our data reduction procedures.
 |
Fig. 1 Final image obtained from the H band data. |
3.3. Astrometric calibration and distortion correction
A laser cut sieve mask was used in laboratory to derive the distortion correction for the PISCES camera (Guerra et al. 2012). The coefficients of the polynomial computed in this way, reported in Appendix A, have a 0.6-pixel accuracy in one σ error. This error does not affect the data reduction since it produces negligible correction (less than 0.1 pixels) on distances of the order of the separation of HR 8799 planets.
The absolute plate scale (19.274 mas/pix) was taken from Close et al. (2012) observations of the Orion Trapezium field. Preliminary analysis of on sky observations of galactic Globular Cluster compared to HST calibrated ones further give support to the adopted value. Following Close et al. (2012) we also adopted a true north correction of 0.9 ± 0.3°.
4. Results
In Figs. 1 and 2 we display the final best ADI image obtained using the H- and K-band data, respectively3. In both figures the four planets are clearly visible; for best identification we marked their position with red circles. The FWHM of the planetary images are about 2.9 pixels, slightly larger than expected value of diffraction peaks.
 |
Fig. 2 Final image obtained from the KS band data. |
Astrometry (measured with respect to the centroid of the star HR 8799) obtained from the H-band data (epoch 2011.79).
Astrometry (measured with respect to the centroid of the star HR 8799) obtained from the Ks-band data (epoch 2011.86).
We measure both the position and the brightness of the four detected planets as follows.
4.1. Astrometry
In Tables 2 and 3 we report our astrometric measurements for the four planets around HR 8799 in the H-band and Ks-band respectively. Table 4 gives the astrometric error budget. We considered several sources of errors: stellar centroid, image orientation (true north), scale distortion and planet centering errors (photometric errors). These last two were evaluated by comparing the measured positions of a number of simulated planets, inserted into the original images, with their original values. Since these fake planets were inserted into the original images, these errors include artefacts due to data reduction and ADI, as well as the impact of speckles.
Astrometric error budgets (in mas) for the four HR 8799 planets.
Final errors in our astrometry were obtained by quadratically combining uncertainties concerning star position, true north, scale, distortion and statistical error in photometry. The dominant term is star centering. Uncertainties in the image orientation contribute significantly to the astrometric error of planet b, while photometry is the dominant source of error for planet e.
4.2. Photometry
Because the central star is saturated in all of our images, we can not use the star magnitude as a reference to evaluate the planet ones. For this reason we assume, the magnitude of HR 8799b from Marois et al. (2008) and we calculate the magnitude of the other planets by the ratio of planets counts. Pixels with separation ≤ 1 from the position of each planet were used for the relative aperture photometry. We then repeated the same procedure assuming the same thing for HR 8799c and we averaged the two results to obtain the final result. Given that HR 8799b and HR 8799c are located at quite large distances from the center of the star (1.72 and 0.97 arcsec respectively), this assumption is reasonable because the images of the planets are weakly affected by speckles. Table 5 reports the absolute magnitude of the four exo-planets as well as the associated errors. The magnitudes are corrected for the self-subtraction effect introduced by the ADI procedure. A set of errors (photometric errors, error due to the self-subtraction of the PSF of the star and errors due to the filtering data-reduction procedure) were evaluated by inserting into the original images ~10 template planets with the same counts and at the same separation of each of the four planets. The same data analysis procedure was then performed on these latter images. The standard deviation of the counts for planets at the same separation was then taken as the uncertainty on the photometry of each planet. Our H band photometry is on average about 0.20 mag fainter than that of Skemer et al. (2012), with a dispersion of 0.13 mag. This offset is primarily due to different choices for reference magnitude adopted for the outer planets, Marois et al. (2008) in our case and Metchev et al. (2009) for Skemer et al. (2012), which implies a systematic difference of 0.21 mag.
Beside the agreement with the photometry by Marois et al. (2008, 2010) for planets b and c, which is expected considering our normalization procedure, we note that the photometry of HR 8799e is also fully consistent with Marois et al. (2010) measurements. HR 8799d results instead about 0.6 mag fainter in Ks band and 0.4 mag in H band. The discrepancy is however only marginally significant (about 2σ) as HR 8799d happens to be projected close to the AO outer working angle in our images (see below). Therefore photometry of planet d is affected by larger errors (0.25 mag in Ks band). Further observations are necessary to confirm the reality and physical nature of this variation.
Photometry (absolute magnitudes) obtained from the H-band and the KS-band data with the corresponding errors.
4.3. Detection limits
To calculate the detection limit as a function of angular separation from the central star, we proceeded as follows. Along the radial direction, we calculated the standard deviation of the intensity over a d × d pixel box (with d equal to the FWHM of the PSF i.e. 3 pixels for FLAO and PISCES) in one pixels step (Masciadri et al. 2005). Values are then averaged over the azimuthal direction and the 5σ contrast versus separation is calculated taking into account the flux losses due to the application of ADI. Figures 3 and 4 show the contrast obtained in H and KS bands. The location of the four planets is marked with red triangles. For comparison, the position of the planets as determined by Marois et al. (2008) are showed using green squares. In Figs. 3 and 4 the noise peak due to the outer working angle of the AO system (which is expected to be at 0.49 arcsec for H and 0.65 arcsec for KS4) is clearly seen. Such a feature is not usually present in contrast curves created by typical AO systems on 6−10 m class telescopes that achieve a much lower Strehl ratio than that delivered by the LBT FLAO system (Masciadri et al. 2005; Lafrenière et al. 2007a; Biller et al. 2007; Chauvin et al. 2010).
 |
Fig. 3 5σ contrast plot expressed in magnitudes for the H-band data. Overplotted are our own measurements for the four HR 8799 planets (red triangles) and the corresponding measurements from Marois et al. (2008) as green squares. |
5. Physical properties of planets around HR 8799
We compared the near-IR properties of the four HR 8799 planets with those of other substellar objects in order to investigate systematic differences due to various physical properties such as mass and age. First we compared the H and Ks magnitude observed for HR 8799 planets with those obtained by Leggett et al. (2010) for field brown dwarfs (BDs). We then collected literature data for other low mass companions with direct imaging observations in the same photometric bands (Table 6). All of these objects, together with the HR 8799 planets, are plotted in an H − Ks color–magnitude diagram (Fig. 5).
Photometry of others small mass companions adopted by literature.
Three planets of HR 8799 (cde) have colors roughly consistent with the L and T BDs sequences. HR 8799c and HR 8799d are slightly underluminous with respect to the brown dwarfs, with HR 8799d being redder than the colors of T BDs. We also recall that our Ks photometry of d has rather large error and is 0.6 fainter than the Marois et al. (2008) photometry (see Sect. 4). Marois et al. (2008)’s photometry would imply a redder color, and a position slightly outside the field BD sequence. HR 8799b has redder colors than the other HR 8799 planets, and it is manifestly under luminous with respect not only to the L-T sequence of BDs but also with respect to the other planets of the HR 8799 system (regardless of the systematic uncertainties in the photometry). A similar but even more extreme anomaly is that of 2M1207b. To explain these locations in the color–magnitude phase space various ad-hoc hypothesis were proposed, such as an occulting edge-on circumplanetary disk (Mohanty et al. 2007) or a collision afterglow (Mamajek & Meyer 2007). The similar discrepancies occurring for HR 8799b and 2M1207b (Barman et al. 2011b) and specific inconsistencies (see Skemer et al. 2011, for details) argue against such ad-hoc explanations suggesting a more general feature linked to cloud properties in low-gravity atmospheres.
 |
Fig. 4 5σ contrast plot expressed in magnitudes for the Ks-band data. Overplotted are our own measurements for the four HR 8799 planets (red triangles) and the corresponding measurements from Marois et al. (2008) as green squares. |
 |
Fig. 5 H/H − K color magnitude diagram comparing the observed magnitudes of HR 8799 planets with other cool objects in the field and known low mass companion. Three planets of the HR 8799 system (c, d, e) are quite consistent with the observed L and T spectral type BDs. HR 8799b is manifestly redder and fainter than L and T spectral type BDs separation. |
In summary, we can confirm the faintness and red NIR colors of HR 8799b. When considering only the H/H − K color–magnitude diagram, the positions of HR 8799c, d, and e are close to the field brown dwarf sequence, especially for the brightest planet e. Including information from other wavelengths clearly suggests the HR 8799c, d, and e show significant differences. This is likely due to the presence of thick cloud layers and non equilibrium chemistry in their atmospheres (Currie et al. 2011; Barman et al. 2011a; Skemer et al. 2012). A more extensive discussion is given in the companion paper (Skemer et al. 2012).
6. The architecture of the HR 8799 planetary system
6.1. Orbital fit
Since the planet discovery papers (Marois et al. 2008, 2010), it has been shown that all the planets in the HR 8799 system orbit the star in the same direction and that their orbits are roughly compatible with nearly pole-on circular orbits. The cumulation of additional observational data (Bergfors et al. 2011) and the detection of the some of the planets in older, reprocessed images (Soummer et al. 2011; Fukagawa et al. 2009; Lafrenière et al. 2009) has allowed an extended time baseline.
The time coverage from 1998 to present epoch represents only a minor fraction of the orbital periods. Nevertheless some indications of the actual orbits are emerging from the accumulated data. The orbits of planets b and c are compatible with circular orbits seen nearly but not exactly pole-on. Instead the orbit of planet d is eccentric and/or seen at a different inclination (Bergfors et al. 2011).
A recent study of the configuration of the outer part of the HR 8799 system was presented by Soummer et al. (2011), taking advantage of the detection of the three outer planets in HST images taken in 1998. They consider as the most likely solution a coplanar system in 4:2:1 mean motion resonance, with HR 8799d in a slightly eccentric orbit (e = 0.1), as suggested in the dynamical stability analysis by Fabrycky & Murray-Clay (2010).
The increase of the time baseline of 1 yr is not decisive for a major revision of these results. However, Soummer et al. (2011) consider only the outer three planets and they restricted to coplanar orbits. Furthermore, evaluation of dynamical stability of the proposed configuration was not performed.
Figure 6 shows the relative astrometry of the HR 8799 planets, as compiled by Bergfors et al. (2011) plus the inclusion of data from Galicher et al. (2011), Soummer et al. (2011) and our own measurements (Tables 2 and 3). Overplotted are the Soummer et al. (2011) orbital solutions for the three outer planets and our own solution for the inner planet (see below for the fitting procedure).
 |
Fig. 6 Relative astrometry of HR 8799 planets. Overline are the Soummer et al. (2011) orbital solution for the outer planets and a coplanar circular orbital solution in 5:2 resonance for the inner planet (blue lines, Case A in Table 7). For HR 8799e, the dotted line shows the circular and coplanar orbital solution for 2:1 mean motion resonance with planet d, which does not fit the observations. Filled circles: literature results. Filled squares: data from the present paper. Red lines connect the predicted and observed position for all the data points. |
New data are consistent with those of previous works and follow the best-fit orbit derived in Soummer et al. (2011) for the three outer planets. If we adopt the Soummer et al. (2011) orbital solution, planet e cannot be in a circular and coplanar orbit with a 2:1 mean motion resonance with d. Instead, a 5:2 resonance represents a satisfactory fit to the data, when assuming circular orbit and coplanarity with the other planets (Fig. 6, Case A in Table 7).
This orbital solution represents only one of the possible ones fitting the observational data. Unique determination of orbital parameters is not yet possible as the observations cover only a minor fraction of the orbital periods. To somewhat complement the Soummer et al. (2011) study, that assumes coplanarity between the three outer planets, we focused our attention here on non-coplanar configurations. We restrict our analysis to circular orbits to reduce the number of parameters. However, this approximation is likely not realistic considering that secular perturbations among planets causes some eccentricity pumping, with average values of about 0.03–0.05. We also considered only a stellar mass of 1.56 M⊙, the preferred value in Soummer et al. (2011). Our analysis of possible orbital solutions was performed in two steps:
-
Monte Carlo simulations for a broad exploration ofthe orbital solutions compatible with the data andcorrelations between the orbital parameters(Fig. 8). This allows us to identifythe possible ranges to bound the least-squareorbital fitting and to identify appropriate initialguesses.
-
A best-fit least-squares orbital solution for the four planets simultaneously using the Levenberg-Marquard minimization algorithm as implemented in the IDL routine MPFIT. The program allows users to fix some of the parameters (e.g. impose null eccentricity) or to tie parameters of one planet to those of another planet (e.g. for coplanar orbits or for imposing orbital resonances).
When forcing all consecutive planets to be involved in 2:1 resonances (8:4:2:1 resonance involving all the known planets) we found orbital solutions that nicely fit the available data. The formal best-fit case is listed as case B in Table 7. A notable property of this orbit is the strong deviation from coplanarity involving the inner planet e, larger than 50° with respect to planet d (when including both i and Ω into account). Forcing planets bcd to be in a 4:2:1 resonance, planets de to be in a 5:2 resonance, and assuming all orbits are circular yields the orbital parameters labeled as case C in Table 7. In this case the deviations from coplanarity are on the order of 10−20° and can become much smaller when allowing for some eccentricity of the orbits (see Case A). Such differences in the orientation of HR 8799e orbit, depending on the chosen resonance with d, are independent on the orbit of planet b. We found a similar behaviour when adopting an outer orbit for b, outside 2:1 resonance with c following Sudol & Haghighipour (2012).
Orbital solution considered in this paper.
Additional constraints on the orientation of the components of the HR 8799 system are available for the central star, for which Wright et al. (2011) derived i ≥ 40° from asteroseismology, and for the outer debris disk, for which Su et al. (2009) found i ≤ 25°. The best-fit solutions listed in Table 7 show that the outer three planets have intermediate values, with hints of a trend in inclination from b to d toward more pole-on orientations inside (cases B and C). The relative inclination of e instead depends critically on the adopted orbital period, as discussed above. The two orbital solutions (B and C) will diverge significantly within 2–3 years.
6.2. Dynamical stability
After these explorations based only on observational data, we consider the additional clues that can be derived from the dynamical stability of the system.
Previous dynamical studies considering the three planet system (without planet e), found that only a minor fraction of the orbital solutions compatible with the astrometric observations are dynamically stable. Stability is favoured by the occurrence of a 2:1 mean motion orbital resonance between each couple of consecutive planets, low eccentricity of their orbits and by planetary masses at the low end of the plausible values derived from their luminosity and stellar age (Goździewski & Migaszewski 2009; Reidemeister et al. 2009; Fabrycky & Murray-Clay 2010).
Recently, Sudol & Haghighipour (2012) presented a study of the dynamical stability of the 4-planet system. They found that the system is strongly unstable with a few solutions that barely survive for ages comparable to the age of the system. Planet e is marginally fit by these stable solutions, and Sudol & Haghighipour (2012) proposed that HR 8799e astrometry is systematically biased toward larger separations. Additional, more limited, dynamical studies of the 4-planet system were performed in the discovery paper by Marois et al. (2010) and in Currie et al. (2011) with similar results.
 |
Fig. 7 Residuals in x and y coordinates vs. time for each of the planets with respect to the orbital solution plotted in Fig. 6 (Case A in Table 7). |
 |
Fig. 8 Reduced χ2 surfaces for orbital period, inclination and longitude of node for HR 8799 planets assuming circular orbits. Each plot row refers to one of the planets, starting from b (top) to e (down). The plotted levels refer to reduced χ values in step of 0.20 starting from 2.0, with darker area correspinding to lower χ values. |
 |
Fig. 9 Relative astrometry of HR 8799 planets available in literature. Blue lines show the adopted orbital solution (Case B in Table 7, non coplanar circular orbits). Red lines connect the predicted and observed position for all the data points. For HR 8799e, the dotted line shows the orbital solution for 5:2 mean motion resonance with planet d (Case C in Table 7). |
 |
Fig. 10 Residuals in x and y coordinates vs. time for each of the planets with respect to the orbital solution plotted in Fig. 9 (Case B in Table 7). |
We numerically integrated the orbits of the planets around the star in a full 5 body problem using the numerical integrator RADAU (Everhart 1985). The timespan of the integration was fixed to 25 Myr and the computed orbital elements were used to estimate the stability properties using the frequency map analysis (FMA) technique as in Marzari et al. (2005). We studied the shift in frequency of the perihelion longitude of the middle planet as a stability indicator. The phase space of a four planet system is wide so we devised the following strategy. We set the two middle planets in a 2:1 resonance while the outer planet is moved from the 2:1 to the 7:3 resonances with the third planet. Planet e is started with random orbital elements close to its expected orbit for a 2:1 and 5:2 mean motion resonances with planet d. The orbital elements are sampled randomly around this initial configuration looking for solutions which may be stable for long timespans.
Assuming stellar mass of 1.56 M⊙ (Soummer et al. 2011) and planetary masses of 9,10,10,7 MJ for e,d,c,b, respectively, and by numerically integrating the orbits, we find highly chaotic solutions that survive on orbits similar to the observed ones for a few Myrs only. This is not compatible with the stellar age even assuming that the primordial gas disk damped the eccentricities of the planets granting stability. The disk lifetime can be no longer than ~20 × 106 years. This is a conservative assumption as, according to observations, the presence of gas in the inner regions of the disk is observed only for timescales shorter than 107 years (see the review by Williams & Cieza 2011). Of course, due to the chaotic nature of the orbits, it may be possible to find orbits surviving for longer timescales, as those found by Sudol & Haghighipour (2012), but a different choice of the numerical integrator gives already different solutions undergoing close encounters after a few Myrs. As already noted by Fabrycky & Murray-Clay (2010), reducing the planetary masses leads to longer timespans before the onset of a “Jumping Jupiter” phase. By reducing all masses by 30% and setting the outer planet in a 7:3 resonance with the third planet and planet e in a 5:2 resonance with the second planet, we find the most stable solutions to the system, according to the FMA analysis. They are still chaotic but they survive at least over the estimated stellar age. However, these solutions are not fully compatible with the observational data. If the masses of the planets are reduced to 50% of the original values, the phase space area where orbits survive for at least 30 Myr becomes significant and even solutions with all four planets in mutual 2:1 resonance become stable over a longer timespan.
While a 30% reduction of the planetary masses is still compatible with the stellar age and theoretical models, a reduction of 50% (about 3.5, 5, 5, and 5 MJ for HR 8799b, c, d, e respectively) is below the current estimates. Using Baraffe et al. (2003) models, a stellar age of 15–20 Myr would be required to be compatible with such low masses for the planet, which is below the youngest age derived by Marois et al. (2010) from membership to Columba association (nominal age 30 Myr) and only marginally compatible with the youngest age estimate (20 Myr) by Moór et al. (2006). However, Torres et al. (2008) quoted a significant age uncertainty for Columba association. Furthermore, some age dispersion within the association or a small age difference between the star and the planets might help to reconciliate evolutionary model predictions and constraints from dynamical stability of the system. The 3σ lower limits of the model atmospheres fit by Madhusudhan et al. (2011) are 2, 6, and 3 MJ and ages of 10, 20 and 10 Myr for planets b, c, and d, respectively.
Our explorative analysis cannot be considered completed. For example, we did not explored the possible impact of varying the stellar mass within the rather broad errorbars (± 0.3 M⊙) allowed by Gray & Kaye (1999) study. A full analysis is postponed to a forthcoming paper.
7. Conclusion
We have performed H and Ks band observations using the new AO system at the LBT and the PISCES camera. Analyses performed independently by different members of our team using two different pipelines yielded consistent results. The excellent instrument performance (Strehl ratios up to 80% in H band) enabled detection of the inner planet HR 8799e for the first time in the H band. The H and Ks magnitudes of HR 8799e are similar to those of planets c and d, with planet e being slightly brighter. Therefore, the innermost planet should have similar masses to c and d, being likely slightly more massive. When considering only H/H − K and K/H − K color–magnitude diagrams, the positions of HR 8799c, d, and e are close to the field brown dwarf sequence, especially for the brightest planet e. Planet b is significantly fainter than the other HR 8799 planets, as already discussed in the literature. The occurrence of some systematic differences at 0.2 mag level between photometric measurement of the HR 8799 planets from different sources have some impact on these conclusions and should be further investigated.
We also collected the available astrometric measurements of the HR 8799 planets, exploring possible orbital configurations and orbital stability. We confirm that the orbits of planets b, c and e are consistent with being circular and coplanar; planet d should have either an orbital eccentricity of about 0.1 or be non-coplanar with respect to b and c. We found that planet e can not be in a circular and coplanar orbit with the other planets and in a 4:2:1 mean motion resonances with planets c and d. These resonances require significant deviations from coplanarity or eccentricity. A coplanar and circular orbit with 5:2 resonance between d and e is instead compatible with the observational data.
Distortion coefficients for the PISCES camera.
We found the system to be highly unstable or chaotic when the nominal planetary masses are adopted. Significant regions of dynamical stability for timescales of tens of Myr are found only when adopting planetary masses of about 3.5, 5, 5, and 5 MJ for HR 8799b, c, d, and e respectively. These masses are below the current estimates based on stellar age (30 Myr) and theoretical models of substellar objects. A more complete exploration of the parameter space will be performed in a forthcoming study to identify possible system configurations that are compatible with the observations and dynamically stable. In any case it is more difficult to find dynamically stable solutions for the 4-planet system than for the 3-planet case considered in most of the literature studies. This implies smaller upper limits on planetary masses from dynamical stability constraints. These results will be relevant to place clues on the physical models of planet structure and atmospheres.
On the observational side, the continuation of the astrometric monitoring is mandatory for a better characterization of the system. With an orbital period of about 50 yr for HR 8799e, a few more years of observations will allow significant refinement of the constraints we can put on the orbital parameters. New observations should pay specific attention to achieve the best astrometric accuracy (optimization of the observing procedure and instrument set-up, dedicated astrometric calibrations, etc.).
Following Riccardi et al. (2010) the outer working angle (OWA) is computed as
where d is the effective
inter-actuator distance considering the number of correcting modes and the actuator pitch
projected to the primary mirror, which is 27 cm. Hence,
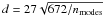 .
When nmodes = 400 (which is the value in general used in
FLAO), d = 35 cm. Hence we obtain OWA = 0.49 arcsec
(H band, 1.65 μm) and 0.65 arcsec (K
band, 2.2 μm) It is important to mention that the extension of this
halo spans about ± 0.06 arcsec from the OWA values reported above (Fig. 17 in Riccardi et al. 2010). These values agree very well
with the position of the secondary maxima in the contrast vs. separation curves.
.
When nmodes = 400 (which is the value in general used in
FLAO), d = 35 cm. Hence we obtain OWA = 0.49 arcsec
(H band, 1.65 μm) and 0.65 arcsec (K
band, 2.2 μm) It is important to mention that the extension of this
halo spans about ± 0.06 arcsec from the OWA values reported above (Fig. 17 in Riccardi et al. 2010). These values agree very well
with the position of the secondary maxima in the contrast vs. separation curves.
Acknowledgments
This research has made use of the SIMBAD database, operated at CDS, Strasbourg, France. D.M., R.C., S.D., F.M. ackowledge support by INAF through PRIN-INAF 2010 “Planetary systems at young ages”. We thank Piero Salinari for his insight, leadership and persistence which made the developement of the LBT adaptive secondaries possible. We are grateful to Mr. Elliott Solheid, the lead mechanical engineer on the adaptation of the PISCES camera to LBT AO system. Mr. Roland Sarlot and Mr. Andrew Rakich provided support in optical design and engineering, respectively. We warmly thank the anonymous referee for the helpful report.
References
- Baraffe, I., Chabrier, G., Allard, F., & Hauschildt, P. H. 2002, A&A, 382, 563 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Baraffe, I., Chabrier, G., Barman, T. S., Allard, F., & Hauschildt, P. H. 2003, A&A, 402, 701 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Barman, T. S., Macintosh, B., Konopacky, Q. M., & Marois, C. 2011a, ApJ, 733, 65 [NASA ADS] [CrossRef] [Google Scholar]
- Barman, T. S., Macintosh, B., Konopacky, Q. M., & Marois, C. 2011b, ApJ, 735, L39 [Google Scholar]
- Bergfors, C., Brandner, W., Janson, M., Köhler, R., & Henning, T. 2011, A&A, 528, A134 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Biller, B. A., Close, L. M., Masciadri, E., et al. 2007, ApJS, 173, 143 [NASA ADS] [CrossRef] [Google Scholar]
- Bowler, B. P., Liu, M. C., Dupuy, T. J., & Cushing, M. C. 2010, ApJ, 723, 850 [NASA ADS] [CrossRef] [Google Scholar]
- Burningham, B., Leggett, S. K., Homeier, D., et al. 2011, MNRAS, 414, 3590 [NASA ADS] [CrossRef] [Google Scholar]
- Chauvin, G., & The Naco Large Programme For Giant Planets Imaging Collaboration. 2010, in In the Spirit of Lyot 2010 [Google Scholar]
- Chauvin, G., Lagrange, A.-M., Dumas, C., et al. 2004, A&A, 425, L29 [NASA ADS] [CrossRef] [EDP Sciences] [MathSciNet] [Google Scholar]
- Chauvin, G., Lagrange, A.-M., Zuckerman, B., et al. 2005, A&A, 438, L29 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Chauvin, G., Lagrange, A.-M., Bonavita, M., et al. 2010, A&A, 509, A52 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Close, L. M., Puglisi, A., Males, J. R., et al. 2012, ApJ, 749, 180 [NASA ADS] [CrossRef] [Google Scholar]
- Currie, T., Burrows, A., Itoh, Y., et al. 2011, ApJ, 729, 128 [NASA ADS] [CrossRef] [Google Scholar]
- Esposito, S., Riccardi, A., Quirós-Pacheco, F., et al. 2010, Appl. Opt., 49, 174 [Google Scholar]
- Esposito, S., Riccardi, A., Pinna, E., et al. 2011, in SPIE Conf. Ser., 8149 [Google Scholar]
- Everhart, E. 1985, in Dynamics of Comets: Their Origin and Evolution, Proceedings of IAU Colloq. 83, held in Rome, Italy, June 11–15, 1984, eds. A. Carusi, & G. B. Valsecchi (Dordrecht: Reidel, Astrophysics and Space Science Library), 115, 185 [Google Scholar]
- Fabrycky, D. C., & Murray-Clay, R. A. 2010, ApJ, 710, 1408 [NASA ADS] [CrossRef] [Google Scholar]
- Fukagawa, M., Itoh, Y., Tamura, M., et al. 2009, ApJ, 696, L1 [Google Scholar]
- Galicher, R., Marois, C., Macintosh, B., Barman, T., & Konopacky, Q. 2011, ApJ, 739, L41 [Google Scholar]
- Goździewski, K., & Migaszewski, C. 2009, MNRAS, 397, L16 [NASA ADS] [CrossRef] [Google Scholar]
- Gray, R. O., & Kaye, A. B. 1999, AJ, 118, 2993 [NASA ADS] [CrossRef] [Google Scholar]
- Guerra, J., Boutsia, K., Rakich, A., et al. 2012, PISCES Technical Report [Google Scholar]
- Hill, J. M. 2010, Appl. Opt., 49, D115 [CrossRef] [Google Scholar]
- Hinz, P. M., Rodigas, T. J., Kenworthy, M. A., et al. 2010, ApJ, 716, 417 [NASA ADS] [CrossRef] [Google Scholar]
- Ireland, M. J., Kraus, A., Martinache, F., Law, N., & Hillenbrand, L. A. 2011, ApJ, 726, 113 [NASA ADS] [CrossRef] [Google Scholar]
- Itoh, Y., Hayashi, M., Tamura, M., et al. 2005, ApJ, 620, 984 [NASA ADS] [CrossRef] [Google Scholar]
- Kuzuhara, M., Tamura, M., Ishii, M., et al. 2011, AJ, 141, 119 [NASA ADS] [CrossRef] [Google Scholar]
- Lafrenière, D., Doyon, R., Marois, C., et al. 2007a, ApJ, 670, 1367 [NASA ADS] [CrossRef] [Google Scholar]
- Lafrenière, D., Marois, C., Doyon, R., Nadeau, D., & Artigau, É. 2007b, ApJ, 660, 770 [NASA ADS] [CrossRef] [Google Scholar]
- Lafrenière, D., Jayawardhana, R., & van Kerkwijk, M. H. 2008, ApJ, 689, L153 [NASA ADS] [CrossRef] [Google Scholar]
- Lafrenière, D., Marois, C., Doyon, R., & Barman, T. 2009, ApJ, 694, L148 [NASA ADS] [CrossRef] [Google Scholar]
- Lafrenière, D., Jayawardhana, R., Janson, M., et al. 2011, ApJ, 730, 42 [NASA ADS] [CrossRef] [Google Scholar]
- Leggett, S. K., Burningham, B., Saumon, D., et al. 2010, ApJ, 710, 1627 [NASA ADS] [CrossRef] [Google Scholar]
- Liu, M. C., Delorme, P., Dupuy, T. J., et al. 2011, ApJ, 740, 108 [NASA ADS] [CrossRef] [Google Scholar]
- Luhman, K. L., Patten, B. M., Marengo, M., et al. 2007, ApJ, 654, 570 [NASA ADS] [CrossRef] [Google Scholar]
- Madhusudhan, N., Burrows, A., & Currie, T. 2011, ApJ, 737, 34 [Google Scholar]
- Mamajek, E. E., & Meyer, M. R. 2007, ApJ, 668, L175 [NASA ADS] [CrossRef] [Google Scholar]
- Mandel, H., Appenzeller, I., Bomans, D., et al. 2000, in SPIE Conf. Ser. 4008, eds. M. Iye, & A. F. Moorwood, 767 [Google Scholar]
- Marois, C., Lafrenière, D., Doyon, R., Macintosh, B., & Nadeau, D. 2006, ApJ, 641, 556 [Google Scholar]
- Marois, C., Macintosh, B., Barman, T., et al. 2008, Science, 322, 1348 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Marois, C., Zuckerman, B., Konopacky, Q. M., Macintosh, B., & Barman, T. 2010, Nature, 468, 1080 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Marzari, F., Scholl, H., & Tricarico, P. 2005, A&A, 442, 359 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Masciadri, E., Mundt, R., Henning, T., Alvarez, C., & Barrado y Navascués, D. 2005, ApJ, 625, 1004 [NASA ADS] [CrossRef] [Google Scholar]
- McCarthy, Jr., D. W., Ge, J., Hinz, J. L., Finn, R. A., & de Jong, R. S. 2001, PASP, 113, 353 [NASA ADS] [CrossRef] [Google Scholar]
- Metchev, S. A., & Hillenbrand, L. A. 2006, ApJ, 651, 1166 [NASA ADS] [CrossRef] [Google Scholar]
- Metchev, S., Marois, C., & Zuckerman, B. 2009, ApJ, 705, L204 [NASA ADS] [CrossRef] [Google Scholar]
- Mohanty, S., Jayawardhana, R., Huélamo, N., & Mamajek, E. 2007, ApJ, 657, 1064 [NASA ADS] [CrossRef] [Google Scholar]
- Moór, A., Ábrahám, P., Derekas, A., et al. 2006, ApJ, 644, 525 [NASA ADS] [CrossRef] [Google Scholar]
- Moro-Martín, A., Rieke, G. H., & Su, K. Y. L. 2010, ApJ, 721, L199 [NASA ADS] [CrossRef] [Google Scholar]
- Reidemeister, M., Krivov, A. V., Schmidt, T. O. B., et al. 2009, A&A, 503, 247 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Riccardi, A., Xompero, M., Briguglio, R., et al. 2010, in SPIE Conf. Ser., 7736 [Google Scholar]
- Skemer, A. J., Close, L. M., Szűcs, L., et al. 2011, ApJ, 732, 107 [NASA ADS] [CrossRef] [Google Scholar]
- Skemer, A. J., Hinz, P. M., Esposito, S., et al. 2012, ApJ, 753, 14 [NASA ADS] [CrossRef] [Google Scholar]
- Soummer, R., Brendan Hagan, J., Pueyo, L., et al. 2011, ApJ, 741, 55 [NASA ADS] [CrossRef] [Google Scholar]
- Su, K. Y. L., Rieke, G. H., Stapelfeldt, K. R., et al. 2009, ApJ, 705, 314 [NASA ADS] [CrossRef] [Google Scholar]
- Sudol, J. J., & Haghighipour, N. 2012, ApJ, 755, 38 [NASA ADS] [CrossRef] [Google Scholar]
- Todorov, K., Luhman, K. L., & McLeod, K. K. 2010, ApJ, 714, L84 [NASA ADS] [CrossRef] [Google Scholar]
- Torres, C. A. O., Quast, G. R., Melo, C. H. F., & Sterzik, M. F. 2008, Young Nearby Loose Associations, ed. B. Reipurth, 757 [Google Scholar]
- van Leeuwen, F. 2007, A&A, 474, 653 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Wahhaj, Z., Liu, M. C., Biller, B. A., et al. 2011, ApJ, 729, 139 [NASA ADS] [CrossRef] [Google Scholar]
- Williams, J. P., & Cieza, L. A. 2011, ARA&A, 49, 67 [NASA ADS] [CrossRef] [Google Scholar]
- Wright, D. J., Chené, A.-N., De Cat, P., et al. 2011, ApJ, 728, L20 [NASA ADS] [CrossRef] [Google Scholar]
Appendix A: Distortion correction coefficients
Drizzle coefficients for PISCES distortion and plate scale determination were obtained
for drizzled and un-drizzled PISCES images from the sieve mask data. For what concerns the
fitted Drizzle coefficients, let us assume
x′,y′ are
corrected centroid values in pixels, x,y are raw data centroid values, in
pixels. Then x0,y0 translate the distortion equation to
an appropriate centre for the distortion equation: 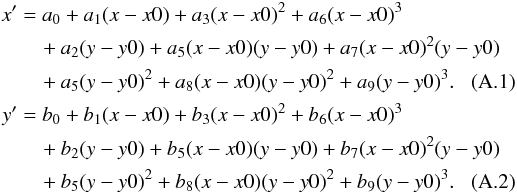 The
values of the ai and
bi coefficients are listed in the
Table A.1.
The
values of the ai and
bi coefficients are listed in the
Table A.1.
All Tables
Astrometry (measured with respect to the centroid of the star HR 8799) obtained from the H-band data (epoch 2011.79).
Astrometry (measured with respect to the centroid of the star HR 8799) obtained from the Ks-band data (epoch 2011.86).
Photometry (absolute magnitudes) obtained from the H-band and the KS-band data with the corresponding errors.
All Figures
 |
Fig. 1 Final image obtained from the H band data. |
| In the text | |
 |
Fig. 2 Final image obtained from the KS band data. |
| In the text | |
 |
Fig. 3 5σ contrast plot expressed in magnitudes for the H-band data. Overplotted are our own measurements for the four HR 8799 planets (red triangles) and the corresponding measurements from Marois et al. (2008) as green squares. |
| In the text | |
 |
Fig. 4 5σ contrast plot expressed in magnitudes for the Ks-band data. Overplotted are our own measurements for the four HR 8799 planets (red triangles) and the corresponding measurements from Marois et al. (2008) as green squares. |
| In the text | |
 |
Fig. 5 H/H − K color magnitude diagram comparing the observed magnitudes of HR 8799 planets with other cool objects in the field and known low mass companion. Three planets of the HR 8799 system (c, d, e) are quite consistent with the observed L and T spectral type BDs. HR 8799b is manifestly redder and fainter than L and T spectral type BDs separation. |
| In the text | |
 |
Fig. 6 Relative astrometry of HR 8799 planets. Overline are the Soummer et al. (2011) orbital solution for the outer planets and a coplanar circular orbital solution in 5:2 resonance for the inner planet (blue lines, Case A in Table 7). For HR 8799e, the dotted line shows the circular and coplanar orbital solution for 2:1 mean motion resonance with planet d, which does not fit the observations. Filled circles: literature results. Filled squares: data from the present paper. Red lines connect the predicted and observed position for all the data points. |
| In the text | |
 |
Fig. 7 Residuals in x and y coordinates vs. time for each of the planets with respect to the orbital solution plotted in Fig. 6 (Case A in Table 7). |
| In the text | |
 |
Fig. 8 Reduced χ2 surfaces for orbital period, inclination and longitude of node for HR 8799 planets assuming circular orbits. Each plot row refers to one of the planets, starting from b (top) to e (down). The plotted levels refer to reduced χ values in step of 0.20 starting from 2.0, with darker area correspinding to lower χ values. |
| In the text | |
 |
Fig. 9 Relative astrometry of HR 8799 planets available in literature. Blue lines show the adopted orbital solution (Case B in Table 7, non coplanar circular orbits). Red lines connect the predicted and observed position for all the data points. For HR 8799e, the dotted line shows the orbital solution for 5:2 mean motion resonance with planet d (Case C in Table 7). |
| In the text | |
 |
Fig. 10 Residuals in x and y coordinates vs. time for each of the planets with respect to the orbital solution plotted in Fig. 9 (Case B in Table 7). |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.