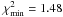| Issue |
A&A
Volume 548, December 2012
|
|
|---|---|---|
| Article Number | A20 | |
| Number of page(s) | 22 | |
| Section | Extragalactic astronomy | |
| DOI | https://doi.org/10.1051/0004-6361/201219818 | |
| Published online | 13 November 2012 | |
The nature of the interstellar medium of the starburst low-metallicity galaxy Haro 11: a multi-phase model of the infrared emission⋆
1
Laboratoire AIM, CEA/DSM – CNRS – Université Paris Diderot,
Irfu/Service d’Astrophysique, CEA Saclay, 91191
Gif-sur-Yvette,
France
e-mail: diane.cormier@cea.fr
2
University of Cincinnati, Clermont College, Batavia, OH, 45103,
USA
3
Sterrenkundig Observatorium, Universiteit Gent,
Krijgslaan 281 S9, 9000
Gent,
Belgium
4
Department of Physics & Astronomy, University of
California, Irvine,
CA
92697,
USA
5
Institute of Astronomy, University of Cambridge,
Madingley Road, Cambridge, CB3 0HA, UK
6
Department of Physics and Astronomy, University College
London, Gower
Street, London
WC1E 6BT,
UK
7
Dept. of Physics & Astronomy, McMaster
University, Hamilton,
Ontario, L8S 4M1, Canada
8
Istituto di Fisica dello Spazio Interplanetario, INAF, via del
Fosso del Cavaliere 100, 00133
Roma,
Italy
Received: 14 June 2012
Accepted: 28 August 2012
Context. The low-metallicity interstellar medium (ISM) is profoundly different from that of normal systems, being clumpy with low dust abundance and little CO-traced molecular gas. Yet many dwarf galaxies in the nearby universe are actively forming stars. As the complex ISM phases are spatially mixed with each other, detailed modeling is needed to understand the gas emission and subsequent composition and structure of the ISM.
Aims. Our goal is to describe the multi-phase ISM of the infrared bright low-metallicity galaxy Haro 11, dissecting the photoionised and photodissociated gas components.
Methods. We present observations of the mid-infrared and far-infrared fine-structure cooling lines obtained with the Spitzer/IRS and Herschel/PACS spectrometers. We use the spectral synthesis code Cloudy to methodically model the ionised and neutral gas from which these lines originate.
Results. We find that the mid- and far-infrared lines account for ~1% of the total infrared luminosity LTIR, acting as major coolants of the gas. Haro 11 is undergoing a phase of intense star formation, as traced by the brightest line, [O iii] 88 μm, with L [O III] /LTIR ~ 0.3%, and high ratios of [Ne iii]/[Ne ii] and [S iv]/[S iii]. Due to their different origins, the observed lines require a multi-phase modeling comprising: a compact H ii region, dense fragmented photodissociation regions (PDRs), a diffuse extended low-ionisation/neutral gas which has a volume filling factor of at least 90%, and porous warm dust in proximity to the stellar source. For a more realistic picture of the ISM of Haro 11 we would need to model the clumpy source and gas structures. We combine these 4 model components to explain the emission of 17 spectral lines, investigate the global energy balance of the galaxy through its spectral energy distribution, and establish a phase mass inventory. While the ionic emission lines of Haro 11 essentially originate from the dense H ii region component, a diffuse low-ionisation gas is needed to explain the [Ne ii], [N ii], and [C ii] line intensities. The [O iii] 88 μm line intensity is not fully reproduced by our model, hinting towards the possible presence of yet another low-density high-ionisation medium. The [O i] emission is consistent with a dense PDR of low covering factor, and we find no evidence for an X-ray dominated component. The PDR component accounts for only 10% of the [C ii] emission. Magnetic fields, known to be strong in star-forming regions, may dominate the pressure in the PDR. For example, for field strengths of the order of 100 μG, up to 50% of the [C ii] emission may come from the PDR.
Key words: galaxies: ISM / galaxies: individual: Haro11 / ISM: lines and bands / ISM: structure / techniques: spectroscopic / radiative transfer
© ESO, 2012
1. Introduction
Star formation in the most pristine environments of the early universe is poorly understood. The closest analogs to chemically unevolved systems are the low-metallicity dwarf galaxies of our local universe. But even those well-studied nearby galaxies continue to plague us with fundamental questions on what triggers and regulates star formation in metal-poor gas-rich conditions. Certainly, from an observational point of view, at all wavelengths, local universe low-metallicity dwarf galaxies show dramatic differences compared to their more metal-rich counterparts (Kunth & Östlin 2000, for a review), in the mid-infrared (MIR), far-infrared (FIR), and submillimeter (submm) wavelength regimes. These include the dearth of polycyclic aromatic hydrocarbons (PAHs), prominent hot MIR-emitting dust, submm excess, and enhanced [C ii] 157 μm/CO(1−0) ratios (e.g. Madden 2008; Madden et al. 2012).
What physical properties, local as well as global, within the dwarf galaxies are we witnessing with these observational signatures? How do we turn these signatures into a realistic view of star formation under early universe conditions? How do basic local parameters, such as radiation field, density, compactness, filling factors, metallicity, etc. figure in the picture we have of star-forming dwarf galaxies? Much of the ambiguity surrounding these questions is due to the lack of understanding the precise role of critical diagnostics and of spatial resolution in the most nearby objects, especially in the FIR/submm, resulting in a mixture of different interstellar medium (ISM) phases in the integrated view of galaxies.
Low-metallicity star-forming dwarf galaxies host young massive stellar clusters (e.g. Turner et al. 2000; Beck et al. 2000; Johnson & Kobulnicky 2003) which produce ultraviolet (UV) photons.The low abundance and prevailing hard radiation field can explain most of the differences observed in dwarf galaxies in destroying large grains and PAHs, in favor of smaller dust grains. The UV photons also photodissociate molecules such as CO, which are unable to adequately self-shield, thus reducing the CO abundance in metal-poor gas (e.g. Wolfire et al. 2010; Narayanan et al. 2012).Thus UV photons play an important role in the heating and the chemistry of the ISM, controlling the structure of H ii regions and photodissociation regions (PDRs). While the heating of the gas is mainly due to photoionisation and gas-grain collisions in the H ii regions and to the photoelectric effect and cosmic rays in the neutral phase, the cooling is normally dominated by radiative de-excitation of fine-structure lines, readily observed in the MIR and FIR/submm. The behavior of these tracers and their relationship to the star formation properties, have been extensively studied to access physical parameters in terms of the gas temperature, density, and the radiation field (e.g. Malhotra et al. 2001; Hunter et al. 2001; Brauher et al. 2008). These sudies make use of photoionisation and PDR models at the scale of individual clouds (Kaufman et al. 1999; Wolfire et al. 1990; Ferland et al. 1998; Abel et al. 2005; Röllig et al. 2006; Tielens & Hollenbach 1985).
The [C ii] 157 μm line is an important FIR diagnostic often put forward as a star formation tracer (Stacey et al. 2010; Boselli et al. 2002; de Looze et al. 2011). It has been observed in many different object types, including dense star-forming regions (Stacey et al. 1991), diffuse ionised and atomic regions (Madden et al. 1993), and high-redshift galaxies (Maiolino et al. 2009; Stacey et al. 2010). Since the [C ii] line is well-correlated with the 12CO(1−0) line and the FIR luminosity (e.g. Stacey et al. 1991; Pierini et al. 2003), it is generally considered that the [C ii] line traces massive star formation within the PDR paradigm. [C ii] is normally the brightest FIR cooling line, being much brighter than CO, and carrying about 0.1 to ~0.5% of the FIR luminosity in metal-rich star-forming galaxies. In low-metallicity dwarf galaxies, where CO(1−0) is not easily detectedbecause of photodissociation(e.g. Schruba et al. 2012; Leroy et al. 2011), [C ii] can be as high as 1% of the LFIR and often 5 to 10 times brighter relative to CO than in dustier starburst galaxies (e.g. Poglitsch et al. 1995; Madden et al. 1995; Madden 2000; Hunter et al. 2001; Cormier et al. 2010). The high [C ii]/CO(1−0) ratio in low-metallicity systems may be alerting us to the fact that the morphology of their PDRs and H ii regions and the relative filling factors of the various phases of dwarf galaxies differ from those of more metal-rich objects (e.g. Madden 2000; Kaufman et al. 2006; Röllig et al. 2006). Even in the nearest neighboring dwarf galaxies, the picture of star formation – and what controls this star formation – is enigmatic.
However, using [C ii] alone can lead to ambiguous interpretation, particularly on the origin of the C+ emission, which can arise from the ionised as well as neutral phases of the ISM. To employ the [C ii] line as a valuable star formation tracer, it is necessary to model the different phases on galaxy-wide scales. The challenge rests on the unavoidable fact that on the scale of galaxies, aside from the closest dwarf galaxies such as the LMC (50 kpc, 1/2 Z⊙), SMC (60 kpc, 1/5 Z⊙), NGC 6822 (500 kpc, 1/4 Z⊙), or IC 10 (800 kpc, 1/3 Z⊙), the phases of the ISM are mixed together in single telescope beams. When using a limited number of diagnostic lines, only a single galactic component can be modeled and average conditions derived, which is otherwise an ensemble of individual PDRs, ionised regions, etc. This requires modeling a comprehensive suite of tracers covering a range of critical densities and excitation potentials to characterise the dense H ii regions, the diffuse H ii regions, PDRs, etc. self-consistently. This approach allow us to grapple with degeneracies and ambiguities in the interpretation of these tracers. In this way, valuable observational diagnostics can be turned into a more accurate description of the multi-phase configuration of a full galaxy.
The Herschel Space Observatory (Pilbratt et al. 2010) has brought the opportunity to obtain a wide range of valuable FIR fine-structure diagnostics never observed before in dwarf galaxies. The Dwarf Galaxy Survey (DGS; P.I. Madden) is surveying the dust and gas of a wide range of low metallicity galaxies in the local universe (Cormier et al. 2010; Galametz et al. 2010; O’Halloran et al. 2010; Madden et al., in prep.; Rémy et al., in prep.) using PACS (Poglitsch et al. 2010) and SPIRE (Griffin & et al. 2010). The brightest low-metallicity galaxy of the DGS observed with the PACS spectrometer is Haro 11, an infrared-luminous starburst galaxy with metallicity Z = 1/3 Z⊙. Haro 11 has the largest dataset obtained with PACS with observations of 7 FIR fine-structure lines: [C ii] 157, [O iii] 88, [O i] 63, [O i] 145, [N iii] 57, [N ii] 122, and [N ii] 205 μm. It has also been observed with the IRS spectrograph onboard Spitzer. Unresolved in the IR, Haro 11 is an ideal candidate to conduct a study modeling an exhaustive set of gas tracers to retrieve information about the structure of the multi-phase low-metallicity ISM.
In this paper, we propose a systematic approach to model the multi-phase ISM of Haro 11, focusing on the gas properties of the ionised and neutral ISM phases. We consider a set of 17 Herschel and Spitzer MIR and FIR ionic and atomic fine-structure cooling lines which trace a wide range of environmental conditions, spanning excitation potentials from 8 to 55 eV. With the spectral synthesis code Cloudy (Ferland et al. 1998), we create a self-consistent model of the dominant ISM components from which these lines originate in order to understand the prevailing mechanisms and physical conditions. In Sect. 2, we present spectroscopic data from the Spitzer and Herschel observatories. Section 3 explains the modeling strategy and assumed initial parameters. Sections 4–6 report the model results and conditions of the ISM components. This study establishes an encompassing picture of the dominant ISM phases in Haro 11 and describes the mass budget of the various phases in our model (Sect. 7).
1.1. Studies of Haro 11
Several studies of Haro 11 have highlighted its peculiarity as a galaxy and challenged our understanding of star formation. Haro 11 – also know as ESO 350-IG38 – is a blue compact dwarf (BCD) galaxy located at 84 Mpc, with MB = −20.3, and metallicity Z ~ 1/3 Z⊙ (Guseva et al. 2012). It is composed of 3 main star-forming regions, or knots, described in Vader et al. (1993) and Kunth et al. (2003), with a morphology presumably resulting from a merger event (Östlin et al. 2001). The starbursting nature of Haro 11 is visible in Fig. 1 with a dominant bright stellar component and dust lanes in front of knot B. These knots host hundreds of young star clusters and ~60 super star clusters (SSC) with ages between 1 and 100 Myr peaking at 3 Myr, and constituting a total stellar mass of 1010 M⊙ (Adamo et al. 2010). An older stellar population is also present, primarily in knots A and C, as seen in the red colors of the V-K bands, modeled in Micheva et al. (2010) by a metal-poor (Z = 0.001) stellar population of age around 14 Gyr with standard Salpeter IMF, indicating that the galaxy is not undergoing its first star formation event. Lyα emission (Kunth et al. 1998) and Lyman continuum leakage were investigated using UV and X-ray observations in Bergvall et al. (2006), Hayes et al. (2007), Grimes et al. (2007), and Leitet et al. (2011). In Leitet et al. (2011), they estimated the leakage to be 3%. In particular, the discrepant location of Lyα and Hα emission, originating in the ionised gas surrounding the star-forming regions, may be explained by a diffuse ionised ISM in the halo of the galaxy with internal resonant scattering at the surface of clumpy dense neutral clouds (Kunth et al. 2003; Hayes et al. 2007). These properties have resulted in its popularity as a local analogue of the high-redshift Lyman-break galaxies (Overzier et al. 2008), and therefore a must-study case to link nearby star formation to the distant universe and galaxy evolution.
 |
Fig. 1 HST/ACS 3-color image of Haro 11 with labels for the 3 star-forming knots (blue: F435, green: F550, red: FR656N/Hα). Images were downloaded from the Hubble Legacy Archive. (This figure is available in color in electronic form.) |
In the IR, Haro 11 is extremely bright compared to other nearby dwarf galaxies. IRAS measurements yielded a FIR luminosity LFIR of 1 × 1011 L⊙ (Sanders et al. 2003a) from 40 to 400 μm using the Lonsdale et al. (1985) prescription. Its spectral energy distribution (SED) shows a peculiar behavior. It peaks around 40 μm, indicating the prevalence of warm dust, and shows an excess of emission in the submm, as unveiled by APEX/LABOCA and Herschel, which is often seen in low-metallicity starbursting dwarf galaxies (Galliano et al. 2003, 2005; Galametz et al. 2009, 2011; Rémy et al., in prep.). The origin of the excess is not well determined and several hypotheses described in Galametz et al. (2011), including a change of dust emissivity, spinning dust grains, or a cold dust component, are invoked in current dust models to explain the submm excess. Galametz et al. (2009) present a detailed dust modeling of Haro 11 in which they derive a total dust mass of 6×106 M⊙ if the submm excess is ignored, and of 2×107 M⊙ if the submm excess is interpreted as cold dust. Assuming the excess as cold dust (T ~ 10 K) is however difficult to reconcile with the observed dust and gas mass budgets, and the expected lower dust-to-gas mass ratios (DGR; Galametz et al. 2011). Integrating the SED from 3 to 1100 μm, the total IR luminosity LTIR is 1.4 × 1011 L⊙ (Galametz et al. 2009). We will use this value of LTIR throughout this paper.
General properties of Haro 11.
Spectroscopic observations show bright lines in the FIR with ISO/LWS, while both the H i 21-cm line, and the CO (J = 1−0) line, the most common tracer of molecular gas in galaxies, are undetected (Bergvall et al. 2000). A detailed study of the neutral gas of the ISM of Haro 11 by Bergvall et al. (2000) investigated the mass budget of the different ISM phases. They establish masses for each phase: M(H i) < 108 M⊙, with an upper limit on the atomic H i; M(PDR) of 2 × 108 M⊙ using the LWS [C ii] observations, the PDR mass being larger than the H i mass; and M(H2) ~ 108 M⊙ for the molecular gas, using both a scaling of the PDR mass and the CO upper limit converted to H2 column density through the CO/H2 conversion factor (XCO). They used a Galactic value for XCO (Strong et al. 1988): XCO,gal = 2.3×1020 cm-2 (K km s-1)-1. Therefore they describe the ISM structure as: very extended PDRs, in which the H i mass resides; a small fraction of the total ISM gas is left in atomic form; and the bulk of the gas, that is normally in neutral state, is ionised by the starburst. Bergvall & Östlin (2002) derive M(H ii) ~ 109 M⊙ from Hα observations for the ionised gas. These masses are lower than the total stellar mass of 1010 M⊙ derived in Adamo et al. (2010).
However, important questions remain, particularly on the state of the ionised, neutral atomic, and molecular gas. While evidence for young massive stellar populations and SSCs exist from the optical and IR point of view, evidence for any substantial reservoir of neutral gas, in the form of either atomic or molecular, is non-existent to date. Where is the fuel for the vigorous star formation observed in Haro 11? What is the state of the gas reservoirs in Haro 11, residing in the ionised, neutral, and molecular form? This study, using a wide variety of tracers of neutral and ionised gas, aims for a more complete description of the enigmatic nature of the ISM of Haro 11.
2. Observations
2.1. Spitzer data
Haro 11 was observed with the Infrared Spectrograph (IRS; Houck et al. 2004) on board the Spitzer Space Telescope (Werner et al. 2004), on the 17th of July 2004 (P.I.: J. R. Houck). The 4 modules were used, i.e., the 2 high-resolution modules: Short-High SH (≈10−20 μm) and Long-High LH (≈19−37 μm) with R ~ 600, and the 2 low-resolution modules: Short-Low SL (≈5−14 μm) and Long-Low LL (≈14−37 μm) with R ~ 60−120. Observations were done in staring mode (AORKey 9007104). Figure 2 shows the slits of the high-resolution module on the sky.
 |
Fig. 2 Hα image of Haro 11 from the Hubble Legacy Archive. The Spitzer/IRS high-resolution slits are overlaid in green and the Herschel/PACS array in red. The PACS beamsize at 150 μm is 11.5″. The IRS low-resolution slits are not shown. (This figure is available in color in electronic form.) |
The low-resolution spectra were retrieved from the CASSIS Atlas1 (Lebouteiller et al. 2011), with a tapered spatial window that scales with wavelength to account for the broader PSF at longer wavelengths. The high-resolution spectra were obtained with SMART v8.2.2 (Lebouteiller et al. 2010; Higdon et al. 2004) from the full-slit extraction of SH and LH and assuming a point-like source calibration. The SL and SH spectra were stitched to LL and LH by applying the same factor 1.13, which is due to the fact that the source is slightly extended for the SL and SH apertures (3.7″ and 4.7″ height respectively), while it is point-like for the LL and LH apertures (≈11″). Another factor of 1.15 was applied to the low-resolution spectra to match the continuum of the high-resolution. The final rest-frame spectrum is displayed in Fig. 3 (top), with a zoom on individual spectral lines (bottom). With a spectral resolution ≥500 km s-1, the lines are not spectrally resolved.
Line fitting and flux measurements were also done in SMART. A Gaussian and second order polynomial function were fitted to the line and continuum. For total uncertainties, we added 10% of the line flux due to calibration uncertainties. The resulting fluxes and uncertainties of the most prominent lines are listed in Table 2. The fluxes agree within the uncertainties to those of Wu et al. (2006). The [Ne iii] line at 36.0 μm was not observed as it falls out of the IRS spectral range.
 |
Fig. 3 Top: Spitzer/IRS spectrum of Haro 11 in the rest wavelength frame (z = 0.0206), SL in green, SH in blue, and LH in red. Emission lines are labeled on top. The IRAC and MIPS photometry is also overlaid (fluxes in Table 3). Bottom: zoom on the individual spectral lines. Fluxes and upper limits are reported in Table 2. (This figure is available in color in electronic form.) |
2.2. Herschel data
Haro 11 was observed with the PACS spectrometer (Poglitsch et al. 2010) on the 27th of June 2010, OD 409 of the Herschel mission (Pilbratt et al. 2010) as part of the Guaranteed Time Key Program, the Dwarf Galaxy Survey (P.I.: S. C. Madden). The PACS array is composed of 5 × 5 spatial pixels each 9.4″ square, covering a total field-of-view of 47″. Haro 11 was mapped with 2 × 2 rasters separated by 4.5″ in the 7 following fine-structure spectral lines: [C ii] 157 μm, [O iii] 88 μm, [O i] 145 μm (OBSID 1342199236), [O i] 63 μm, [N iii] 57 μm, [N ii] 122 μm (OBSID 1342199237), and [N ii] 205 μm (OBSID 1342199238), for a total of 7.2 h. The [N ii] 205 μm line was also re-observed on OD 942 for 1.6 h with a single pointing (OBSID 1342234063). The observations were done in chop-nod mode with a chop throw of 6′ off the source. The chopped position is free of emission. The beam size is 9.5″ at 60 μm, and 11.5″ at 150 μm (diffraction limited above ~100 μm). The spectral resolution is ~90 km s-1 at 60 μm, 125 km s-1 at 90 μm, 295 km s-1 at 120 μm, and 250 km s-1 at 150 μm (PACS Observer’s Manual 20112).
The data were reduced with the Herschel Interactive Processing Environment (HIPE) v7.0.1935 (Ott 2010). We used standard scripts of the PACS spectrometer pipeline. The line fitting and map making were done using the software PACSman (Lebouteiller et al. 2012). The signal from each spatial position of the PACS array is fitted with a second order polynomial plus Gaussian for the baseline and line. For total uncertainties, we add 30% of the line flux due to calibration uncertainties (Poglitsch et al. 2010). The rasters are combined by drizzling to produce final reduced maps with pixel size of 3″.
With Herschel, all of the lines are well detected, at least in the central pixel of the PACS array, except the [N ii] 205 μm line. The [N ii] 205 μm line is located at the edge of the first grating order of the spectrometer and affected by spectral leakage, due to overlapping of the grating orders. It is contaminated by signal from the second grating order around 100 μm, and is therefore difficult to observe and to calibrate. The line profiles are displayed in Fig. 4. The line centers range between −30 and +70 km s-1 within the maps of all observed lines, and indicate a rotation around the north-south axis of both the ionised and neutral gas components, slightly tilted compared to the velocity structure of Hα analysed in Östlin et al. (1999). All lines display broad profiles, with a broadening up to 300 km s-1, which suggests that both the neutral and ionised gas are coming from several components with different velocities. However, with spectral resolution >100 km s-1, the lines are well fitted by a single Gaussian and we cannot separate the different velocity components in the spectra. This suggested complex velocity structure is corroborated by studies of optical lines that show broad profiles as well (Kunth et al. 1998; Östlin et al. 1999), and where the neutral gas is shifted compared to the ionised gas, expanding over few kpcs (Kunth et al. 2003). FUSE spectra in Grimes et al. (2007) show absorption lines of the ISM with FWHM 300 km s-1 and blueshifted by 80 km s-1. The higher ionisation lines can be stronger in galactic outflows (Contursi et al. 2012).
 |
Fig. 4 Herschel/PACS line profiles from an individual spatial pixel (9.4″) centered on the galaxy. |
The [C ii] line shows a marginally extended emission at 157 μm, peaking at a signal-to-noise ratio of 50 in the center and dropping below detection at the edge of the map. The emission of the other lines is rather compact. The shape of the PACS spectrometer beam is not known well enough to measure an accurate source size if the source were slightly extended. Hence we cannot recover spatial information. To derive total line intensities, we integrated the fluxes over a circular aperture of diameter 30″ to encompass all the emission. The line intensities are listed in Table 2. Observations of the [O iii], [C ii], and [O i] 63 and 145 μm lines were also performed with the LWS instrument onboard ISO (Bergvall et al. 2000; Brauher et al. 2008; Vasta et al. 2010). The PACS intensities of the [O i] 63 μm and [O iii] lines agree within 40% with the LWS observations, although they are found to be lower with PACS. This may be attributed to a beam effect, the LWS beam size being ~80″. However, we find that the [C ii] intensity is two times brighter with PACS compared to LWS. To understand this discrepancy, we have reduced the PACS data with different flat-field corrections, as well as with background normalisation (PACS Data Reduction Guide). All these methods give the same final [C ii] flux as quoted in Table 2 within 10%, ruling out a mis-calibration from PACS. Therefore we attribute the difference between the PACS and LWS fluxes to a calibration problem from the LWS instrument.
Spitzer and Herschel line fluxes.
2.3. Spectral line description
The IRS and PACS spectra probe the ionised and neutral media. The IRS spectrum shows a wealth of MIR fine-structure lines, the brightest being (in order) [Ne iii] 15.6 μm, [Si ii] 34.8 μm, [S iii] 18.7 and 33.5 μm, [S iv] 10.5 μm, and [Ne ii] 12.8 μm. PAH features at 6.2, 7.7, 8.6, 11.2, and 12.8 μm are also present. The PACS spectrum also shows bright FIR lines, especially [O iii], [C ii], [O i] 63 μm, and [N iii]. The [O iii] line is the brightest of all, with [O iii]/[C ii] = 2.4. While [C ii] is the brightest FIR fine-structure line in normal and dusty starburst galaxies (Brauher et al. 2008), we find that this is often not the case in low-metallicity dwarf galaxies (Hunter et al. 2001; Cormier et al. 2010; Madden et al., in prep.; Cormier et al., in prep.).
The young star-forming nature of this galaxy also agrees with intense [Ne iii] (41.0 eV), [O iii] (35.1 eV), [S iv] (34.8 eV), and [N iii] (29.6 eV) lines observed, arising from relatively highly ionised regions. [O iv] (54.9 eV) at 25.9 μm, which requires a relatively hard radiation field (Sect. 6.3), is also detected. The [Ne iii]/[Ne ii] ratio is 3.5, [S iv]/[S iii] is 0.9, and [N iii]/[N ii] is 8. These ratios are indicative of a hard radiation field typical of BCDs (Thornley et al. 2000; Madden et al. 2006). While [C ii] can come from both the diffuse ionised phase and the neutral phase, [O i] traces only the neutral phase. The [O i] 63 μm/[C ii] ratio is 0.9, similar to that found in other dwarf galaxies and dustier galaxies (Hunter et al. 2001; Brauher et al. 2008). Table 2 lists the ionisation energies of the observed lines, as well as the excitation temperatures and critical densities (ncrit) of the transitions with collisions with H and/or e−.
Comparing line luminosities to the TIR luminosity, we find L [C II] /LTIR = 0.1%, L [O III] /LTIR = 0.3%, and L [O I] /LTIR = 0.1%. Altogether, the FIR lines represent 0.6% of the TIR luminosity; and when adding the MIR lines, they represent 1.2% of LTIR. Together these lines are responsible for most of the gas cooling of the ISM. Such line-to-TIR ratios are typical of star-forming galaxies (Malhotra et al. 2001; Brauher et al. 2008)3. Similar L [C II] /LTIR ratios are found in several high-redshift galaxies (Maiolino et al. 2009; Stacey et al. 2010). Croxall et al. (2012) find L [C II] /LTIR ~ 0.5% and L [O I] /LTIR ~ 0.1% in spatially resolved regions of the nearby spiral galaxy NGC 4559. There is observational evidence that L [C II] /LTIR tends to decrease in galaxies with warmer FIR-color, fν(60 μm)/fν(100 μm). Among other effects, this may be attributed to a less efficient photoelectric heating due to charged grains (Malhotra et al. 2001; Croxall et al. 2012), or to a UV-photon screening from large amounts of dust as in ultra-luminous IR galaxies (ULIRGs) (Abel et al. 2009; Graciá-Carpio et al. 2011). With observed FIR-color ~1, Haro 11 falls within the large spread of L [C II] /LTIR values and is not particularly [C ii] deficient nor [C ii] excessive, as often seen in low-metallicity galaxies (Madden et al., in prep.).
2.4. Photometry data
For the discussion on the SED of Haro 11 in Sect. 7.1, we use broad-band data available from the X-ray to the radio regime, to assess how the models perform in reproducing the continuum emission. The photometry is taken from NED. In addition, we use the Spitzer/MIPS photometry from Bendo et al. (2012), the Herschel/PACS and SPIRE photometry from Rémy et al. (in prep.), and the Spitzer/IRAC and LABOCA 870 μm photometry from Galametz et al. (2009). All fluxes are summarized in Table 3.
Photometry data.
3. Modeling strategy
3.1. Identification of the model components
We aim to model the IR emission from all 17 detected lines (except the MIR H2 lines which will be modeled in a coming paper) listed in Table 2 to understand the conditions of the various media and the dominant processes at work in this low-metallicity starburst. The ISM is very heterogeneous, and over the scale of a galaxy, various phases with a wide range of conditions are mixed together.
In our spectral dataset, we notice that Haro 11 is typified by very intense [Ne iii], [Ne ii], [S iii], [S iv], [O iii], and [N iii] lines. These high-excitation lines require a hard radiation field which is naturally encountered in a compact H ii region.Stars in compact H ii regions are young, hence their UV radiation is harder, and SSCs are likely to contain massive stars which contribute to the production of hard photons.Moreover, the high critical densities of these lines (except the [O iii] line) favor their origin at the same location. Therefore, the intensity of these lines demonstrates the importance of the dense H ii region in the global spectrum of Haro 11. Moreover, the Herschel observations show bright [O i] and [C ii] lines, which are usual tracers of the neutral gas. In particular, the intensity of the [O i] lines indicates the presence of dense PDRs. These two dense (ionised and neutral) phases will be investigated first since they account for the emission of most of the spectral lines. Derived physical conditions are presented in Sect. 4.
With low critical density (~300 cm-3) and low ionisation potential (14.5 eV), the [N ii] 122 μm line is a tracer of low-excitation diffuse gas rather than the dense H ii region. The intensity of [N ii] demonstrates the need for an additional diffuse low-ionisation component that is investigated in Sect. 5. Our subsequent modeling also shows that this diffuse phase is the main contributor to the [Ne ii] and [C ii] lines.
Therefore, the three main phases that we identify as necessary model components to account for the observed emission lines are: 1) a dense ionised phase (Sect. 4.1), 2) PDR (Sect. 4.2), 3) a diffuse low-ionisation medium (Sect. 5).
In addition, we discuss the possible presence of other model components that may influence the line predictions. The detection of the high-excitation [O iv] line is the driver of a discussion on the role of X-rays and XDRs in Sect. 6.3. The [O iii] line, which is the brighest of all MIR-FIR lines, has high excitation potential (35.1 eV) and low critical density (~500 cm-3). Although it is accounted for by the dense H ii model, it may originate as well from diffuse high-excitation medium that we do not model but briefly discuss in Sect. 6.2. Finally, we investigate the influence of magnetic fields on the cloud density profile and their impact on the PDR predictions in Sect. 6.1.
3.2. Method
We use the 1D spectral synthesis code Cloudy v10.00, last described by Ferland et al. (1998), which includes photoionisation and photodissociation treatment (Abel et al. 2005), to model the multiple phases from which the emission lines originate. Since Haro 11 is not resolved in most of the Spitzer and Herschel bands, we have no spatial constraints. Thus, the model is reduced to a central source of energy surrounded by a spherical cloud. In the case of Haro 11, this central source is a starburst. The dense ionised gas that is closest to the central source with respect to the other phases that we model separately will yield the best constraints on the properties of the stellar cluster that is powering the model. Therefore we first derive the best fit model concentrating on the dense H ii region diagnostics, which are the [Ne ii] 12.8 μm, [Ne iii] 15.6 μm, [S iv] 10.5 μm, [S iii] 18.7 μm and 33.5 μm, and [N iii] 57 μm lines. Moreover, the interpretation of these ionic lines is less ambiguous than, for example, the [C ii] line. Following this step, we will assess what this model predicts for the PDR phase.
The starburst ionises the inner edge of the cloud, where the H ii region begins, and the radiative transfer is computed step by step progressively into the cloud. The distance from the source to the inner edge of the cloud is the inner radius (rin). Depending on where the calculation is stopped, the ionised, atomic, and molecular phases can be treated as the model is computed within one Cloudy model. Here we stop the models until the molecular fraction H2/H reaches 50% such that both the ionised and PDR phases are computed within the same model. We opt to impose pressure equilibrium throughout the models. This is particularly important for the density profile between different phases. We will come back to this assumption in Sect. 4.2.
3.2.1. Parameter grid of the dense H II region
We vary the following 3 physical parameters in order to calculate our model grid: the age of the burst (Aburst), the initial hydrogen density at the inner edge of the cloud (nH), and rin, where the calculation starts (see Fig. 5 for an illustration). The age is varied from 2.4 to 5.0 Myr (Sect. 4.1.2), rin from 1020.0 to 1022.0 cm (or 30 pc to 3 kpc, Sect. 4.1.3), and nH from 101 to 104 cm-3 (Sect. 4.1.1). The step size for Aburst is 0.2 Myr (linear step), and for rin and nH, we use 0.2 step sizes on a logarithmic scale.
 |
Fig. 5 Geometry of the Cloudy model with the three free parameter that we vary in the grid: the age of the burst (Aburst), inner radius (rin), and initial hydrogen density (nH). Parameter boundaries and step sizes are also indicated. |
3.2.2. χ2 evaluation
In order to find a solution for this ionised phase, we aim first to reproduce as best as possible the intensities of the ionic lines. For each individual model, the goodness of the fit is evaluated by computing the reduced χ2. The χ2 is measured from a set of selected lines. The lines we consider to constrain the fit are the following: [Ne ii] 12.8 μm, [Ne iii] 15.6 μm, [S iv] 10.5 μm, [S iii] 18.7 μm, and 33.5 μm, because they are the brightest and relatively well understood, as well as the [N iii] 57 μm line from PACS which is also bright and expected to arise from the same medium. With 6 observations and 3 free parameters to fit, the degree of freedom is N = nobs − nparam = 3. Best fit models are determined by minimising the reduced χ2. There are several lines that originate in part from the dense ionised gas that we do not consider when calculating the χ2, although we do discuss how the model predictions of these lines compare to the observations. We do not consider the high-excitation [O iv] line because it is faint and can be excited by several mechanisms (see Sect. 6.3). We do not include the [O iii] and [N ii] lines here as constraints for the dense H ii region because our subsequent modeling shows that a fraction of these lines arises from a low density ionised medium which we consider in a later step (see Sect. 5).
3.3. Setting the input fixed parameters
3.3.1. Incident radiation field
We use Starburst99 v6.0.2 (Leitherer et al. 2010) to reproduce the incident, wavelength-dependent radiation field density of Haro 11. Following the UV-optical studies by Hayes et al. (2007) and Grimes et al. (2007), we assume a Salpeter IMF from 0.1 to 100 M⊙ and stellar tracks from Padova AGB with metallicity Z = 0.004. According to Adamo et al. (2010), the stellar population of Haro 11 is very young. The present starburst started less than 40 Myr ago, and shows a formation peak at about 3.5 Myr. Knot B is dominated by a young starburst of 3.5 Myr, and knot C contains an older starburst of 9.5 Myr (Fig. 1). Therefore, we select the stellar spectrum of an instantaneous burst of a few Myr, letting the age of the burst be a free parameter, varying from 2.4 to 5.0 Myr. We also add to this the spectrum of an instantaneous burst of 9.5 Myr to account for the slightly older stellar population. We keep this age fixed since the ionising part of the stellar spectrum does not vary significantly for ages larger than 5 Myr, and will therefore not significantly affect the model predictions of the ionised gas. This starburst spectrum dictates the shape of the input energy source in Cloudy. The incident radiation field on the cloud is shown in purple in Fig. 12. For the input luminosity of the central source, we take the total observed infrared luminosity of Haro 11: LTIR = 1.4×1011 L⊙. This approximation assumes an energy balance between the UV and IR domains, i.e. that all of the UV photons are reprocessed in the IR by the gas and the dust. The emergent SED (bottom panel of Fig. 12) shows that this approximation is reasonable since only 20% of the total emergent luminosity is emitted in the UV-optical, and 80% in the IR. We discuss in more details the energy balance in Sect. 7.1.
Haro 11 is detected in X-rays (e.g. Grimes et al. 2007). Previous studies on X-ray observations indicate the presence of soft (L0.5−2 kev = 1.9×108 L⊙) and hard (L2−10 kev = 2.6×108 L⊙) X-rays. Therefore we add to the input SED an X-ray component that reproduces the shape of the observed X-ray spectrum and of total luminosity 5×108 L⊙. The effects of the X-rays in the models are discussed in Sect. 6.3.
3.3.2. Elemental abundances
The elemental abundances directly impact on the predicted line intensities. To match the observed abundances in Haro 11 as closely as possible, we use the abundances in the literature. Abundances of oxygen, nitrogen, neon, sulphur, and argon were obtained in knots B and C of Haro 11 by Guseva et al. (2012) using VLT/X-shooter observations in the optical. In particular, they find an oxygen abundance 12 + log(O/H) of 8.1 in knot B and 8.3 in knot C, giving a O/H twice as large as the value 12 + log(O/H) = 7.9 previously found by Bergvall & Östlin (2002), altering the determination of the metallicity from ~1/6 to 1/3 Z⊙. We use the abundances in Guseva et al. (2012), averaged over the two knots, which have similar luminosities, for our calculations. Uncertainties on these abundances are 10%. For neon and sulphur, Guseva et al. (2012) find similar values to those found in Wu et al. (2008), derived from Spitzer data. The relatively high neon abundance is typical of BCDs (Izotov & Thuan 1999). For nitrogen, such high abundance is observed in a few BCDs (e.g. Thuan et al. 1996; Izotov & Thuan 1998; Pustilnik et al. 2004), and can be explained by the presence of Wolf-Rayet stars (Bergvall & Östlin 2002), which inject matter enriched in N and C into the ISM. For the other elements, we use gas-phase relative abundances typical of H ii regions, based on an average of the abundances in the Orion Nebula determined by Baldwin et al. (1991), Rubin et al. (1991), Osterbrock et al. (1992), Rubin et al. (1993), and scaling them to the metallicity of Haro 11. The resulting carbon abundance is log (C/O) = −0.15, which is relatively high compared to Izotov & Thuan (1999), where log (C/O) ~ −0.5. However, Bergvall et al. (2006) find that the ratio of C and O column densities is ~−0.3 (log) from the analysis of absorption lines in IUE and FUSE data. Such high value may indicate an enrichment in C and agrees with our adopted carbon abundance (assuming Orion-like C/O) within the uncertainties. For silicon, its abundance Si/O is low in the Orion abundance set compared to that usually found in BCDs, therefore we use the average abundance of log (Si/O) = −1.5 from Izotov & Thuan (1999). We consider the uncertainty on these theoretical abundances to be of a factor of 2. Table 4 summarizes the elemental abundances (and uncertainties) we use in Cloudy. The lack of measured abundances for the other elements limits their use to constrain the models (e.g. Fe, Si).
Elemental abundances set in Cloudy.
3.3.3. Dust properties
It is important to accurately set the dust properties for two reasons: (1) dust plays an important role in heating the gas through the photoelectric effect, which depends on the dust abundance and grain size distribution, and (2) the radiative transfer is strongly influenced by the properties of the grains. We first tried using the standard MRN grain size distribution (Mathis et al. 1977), which failed to reproduce the observed dust emission in the MIR, falling below the photometry data by more than an order of magnitude. The MRN distribution underpredicts the number of small grains (minimum grain radius of 5 nm) and is usually not appropriate for modeling the MIR emission in galaxies. Standard dust models such as Draine & Li (2001) and Zubko et al. (2004) do include more small grains than the standard MRN model. Dust modeling of dwarf galaxies (e.g. Galliano et al. 2003, 2005; Galametz et al. 2011) also demonstrates the need for an increased abundance of smaller grains. Therefore, in Cloudy, we use the MRN distribution extended down to 1.1 nm to account for the very small grains.Other grain size distributions have been used to model the IR emission of galaxies, such as grain shattering distributions (Dopita et al. 2005), that we discuss in Sect. 7.1.2.We also use PAHs as described in Abel et al. (2008). Both grains and PAH abundances are scaled to the metallicity of Haro 11 (1/3 Z⊙), fixing the dust-to-gas mass ratio (D/G) to 2.64 × 10-3 (~1/400, the Galactic D/G is ~1/150). This yields a ratio of visual extinction to hydrogen column density, AV/N(H), of 10-22 mag cm-2.
3.4. Limitations of the approach
Our first limitation lies on the geometry of our modeling that we aim to constrain as much as possible with diagnostics from a large set of spectral lines. Some of the derived parameters of the compact H ii region are strongly dependent on the (simple) geometry we impose on the model, which we will see is a recurring theme throughout the paper. The parameters that are best constrained, irrespective of the geometry, are the electron density, temperature and mass of ionised gas. As found in Sect. 4.1.3, the geometrically thin ionised gas shell, in combination with the large inner radius (~1 kpc) that describes the model solution of the dense H ii region, seems physically implausible. Despite the geometry of the model, we refer to it with the term “compact” since this model component represents what is observationally described as a compact H ii region. This is a direct result of assuming a single region with a single central source. Although we are aware that the knots B and C of Haro 11 are spatially separated in the optical, we do not have the spatial resolution in the Spitzer and Herschel observations to treat them separately. If, for example, we were to construct a model as the sum of several regions – as seems reasonable when perusing the optical images – the inner radius of each region would have to decrease in order to obtain a similar effective U parameter, while the shell thickness would increase in order to obtain the same gas mass, thus evolving towards a model with a more geometrically thick layout. It is impossible to obtain reliable and reproducible results using such a complex model, without better observational constraints on the actual source distribution, i.e. spatially resolved spectroscopy. In this paper we focus on the derived parameters that are least sensitive on the actual assumed geometry. In Sect. 7.1, we discuss the spectral energy distribution resulting from the combination of models of the various phases in terms of energy balance, but we do not pretend to accurately fit the total SED because of these geometry issues.
Our second limitation lies in the evalutation of the goodness of the fits. It is mainly weighted by the elemental abundance uncertainties, which can be up to a factor of 2, and by the observational uncertainties (up to 40%). Therefore, when comparing the model predictions to observed intensities, we aim for a match within a factor of 2.
4. A model of the H II region and PDR: C
4.1. The compact H II region
The results of the computed grid are displayed in Fig. 6. It shows the intensity predictions of the compact model labeled C for each ionic line as a function of density, nH, and inner radius, rin, for a starburst age of 3.7 Myr (age of the best fit model, see Sect. 4.1.2). In this section, we discuss the influence of each grid parameter on the model predictions and possible solution values. These parameters are linked via the quantity U, which is the ionisation parameter, defined as the dimensionless ratio of the incident ionising photon surface density to the hydrogen density nH: 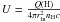 , where Q(H) is the rate of hydrogen-ionising photons striking the illuminated face and c is the velocity of light. U describes how many ionising photons arrive per atom.
, where Q(H) is the rate of hydrogen-ionising photons striking the illuminated face and c is the velocity of light. U describes how many ionising photons arrive per atom.
 |
Fig. 6 Predicted intensities for model C (Imodel) normalised by their observed value (Iobs) for all ionic lines considered, as a function of nH and rin for a given starburst age (of 3.7 Myr). The vertical dashed line shows the best fit model density nH = 102.8 cm-3, and the vertical dotted line the critical density of the ionic specie, if within the range displayed. The best fit inner radius is rin = 1021.4 cm (green symbols). (This figure is available in color in electronic form.) |
4.1.1. The density of the gas
In general terms the predicted line intensities are dependent on the gas density through both the critical density of each atom, and the ionisation parameter, U. Line intensities increase with increasing gas density until the critical density of a fine-structure line is reached. Above such critical density, the de-excitation process is dominated by collisions rather than radiative decay. Therefore the maximum gas density is well determined by the critical density of the brightest line tracers. The gas density also plays an important role in determining the population of the different ionisation stages. The ionisation parameter, U, is inversely proportional to the density (bottom right panel of Fig. 6).
We find that the minimum χ2 occurs for a solution with a density around 102.8 cm-3 (dashed vertical line in Fig. 6). This derived gas density compares well with density diagnostics proposed in the literature, for example, based on the ratio of the [S iii] lines at 18.7 and 33.5 μm (Houck et al. 1984). This ratio is sensitive to the density since these lines originate from the same ion but with significantly different critical densities (Table 2). From Abel et al. (2005) and requiring ![\hbox{$\mathrm{\frac{[S~III]~18~\mu\,m}{[S~III]~33~\mu\,m}\sim1.0}$}](/articles/aa/full_html/2012/12/aa19818-12/aa19818-12-eq148.png) , we obtain a density of the ionised gas of nH = 102.7 cm-3. The value of the electron density predicted by the diagnostic plot in Houck et al. (1984) is also around 102.8 cm-3. Following the method from Kingsburgh & Barlow (1992, 1994) who use the programs EQUIB and RATIO (developed at UCL by Howarth and modified by Adams), we also find nH ~ 102.8 cm-3.
, we obtain a density of the ionised gas of nH = 102.7 cm-3. The value of the electron density predicted by the diagnostic plot in Houck et al. (1984) is also around 102.8 cm-3. Following the method from Kingsburgh & Barlow (1992, 1994) who use the programs EQUIB and RATIO (developed at UCL by Howarth and modified by Adams), we also find nH ~ 102.8 cm-3.
4.1.2. The age of the burst
The spectrum of the starburst (intensity and shape) changes drastically with time in the age range considered here. The age of the burst sets the hardness of the incident radiation field. Figure 7 shows line ratios of [Ne iii]/[Ne ii], [O iv]/[Ne iii], [O iii]/[N iii], [O iii]/[S iv], and [S iv]/[S iii] 18.7 μm as a function of burst age. The observed ratios agree with an age of burst of 3.5−5 Myr. These values are also in agreement with the age of 3.5 Myr for the brightest knot B and 9 Myr for knot C, and a mixture of very young and older bursts, found in Adamo et al. (2010). After 5 Myr, the ionising part of the burst spectrum decreases, the high ionisation lines start to disappear, and in particular the [Ne iii]/[Ne ii] ratio drops off (bottom panel of Fig. 7). This is why we do not compute models with Aburst > 5 Myr in our grid. The best fit on the neon lines favours a relatively young burst, of about 3 Myr. However, the emission of the highest excitation potential [O iv] line (54.9 eV) is rather favoured by models with ages between 3.7 and 4.7 Myr. Indeed this time frame corresponds to the time needed for the onset of Wolf-Rayet stars. A burst age of 4.7 Myr is also a good match to the [Ne iii]/[Ne ii] ratio, although it does not agree with the intensity of the [S iv] line, which is one of the lines that has the highest weight in the χ2. The best single solution model in that case has an age of burst of 3.7 Myr.
 |
Fig. 7 Model predicted intensity ratios as a function of burst age Aburst, for a hydrogen density of 102.8 cm-3, and inner radius of 1021.4 cm. The true burst age of these models is an average of Aburst and the older stellar population of 9.5 Myr, although the latter has a negligible influence on the high-ionisation lines considered here. The horizontal solid lines represent the observed ratios and the dashed lines the uncertainties on the ratios. The vertical dashed line shows the solution burst age of 3.7 Myr, and the vertical dotted lines the age of 3 Myr and 4.7 Myr that would better match the [Ne iii]/[Ne ii] ratio. (This figure is available in color in electronic form.) |
4.1.3. The inner radius
All lines are sensitive to the inner radius rin. Its choice has no direct influence on the hardness of the radiation field, but rather on its intensity. With increasing radius, the total input luminosity is distributed over a larger surface, decreasing the number of ionising photons per surface area, and therefore the ionisation rate. U decreases as the inverse square of the radius. Intensities of species with a high ionisation potential, such as [O iv], decrease with increasing rin, and the inverse is observed for low ionisation species such as [N ii]. For rin < 1021.0 cm, atoms are preferably present in high ionisation states. Models with such small rin often predict too much [O iv] and [S iv], and not enough [Ne ii] and [S iii]. [Ne iii] and [S iv] intensities are constant at low rin and then drop with increasing rin. [S iii], [N iii] and [O iii] intensities increase with low rin (<1021.5 cm) because of an ionisation balance between S2+, N2+, O2+ and S3+, N3+, O3+. Then their intensities drop with increasing rin. The opposite effect is observed for the lower ionisation state species such as [Ne ii] and [N ii] which increase with rin.
 |
Fig. 8 Contour plots of the χ2 values of the 3D grid (log scale). The parameters are given in logarithmic values. Units are cm-3 for the density, yr for the burst age, and cm for the inner radius. The minimum reduced χ2 found for CHII is |
The observations are best matched for an inner radius of 1021.4 cm (800 pc). At that distance, the model cloud is a very thin shell of large radius, at the center of which resides the central starburst. The resulting geometry is plane-parallel. This is not a realistic geometry, as discussed in Sect. 3.4, but we do not aim to model the spatial structures in Haro 11.
4.1.4. Parameters of the best fit model CHII
We have minimised the χ2 to find the parameters of the best fit model for the compact H ii region described above. Figure 8 shows contour plots of the reduced χ2 computed for our grid of models. Contour levels at 1-σ, 3-σ, and 5-σ from the minimum χ2 are displayed in orange. The intensities of the spectral lines included in the fit are best reproduced with the parameters: nH = 102.8 cm-3, Aburst = 3.7 Myr, and rin = 1021.4 cm. The ionisation parameter is U = 10-2.5. The reduced χ2 of this model solution, which has the minimum χ2, is 1.48. This value is close to 1, indicating that this model describes the data well, with a probability of ~70%. For clarity throughout the following sections, we will refer to this model solution of the compact H ii region as CHII.
With CHII, the strongest MIR line, [Ne iii], is reproduced within 15%, as well as the [O iv] line. The two [S iii] lines are achieved within 5% and their ratio within 1%. The modeled [S iv] and [Ar iii] lines deviate by 20%. The [N iii] line is reproduced within 40%. The [Ne ii] line, however, is under-predicted by a factor of 5 by CHII.
We then compare the line intensities predicted by CHII to the PACS lines, [O iii] and [N ii] 122 μm, which were not used to constrain the model fit since they can originate from less dense ionised gas. We find that [O iii] is under-predicted by a factor of 2, which is within our expectations, while the [N ii] 122 μm is under-predicted by a factor of 4. The dense H ii region is not the primary source of [N ii]. The prediction for the [N ii] 205 μm line falls below its derived upper limit.
We discuss the origin of the [Ne ii] and [N ii] lines from diffuse low-ionisation gas in Sect. 5 and the possible origin of the [O iii] emission from diffuse high-ionisation gas in Sect. 5.
We also find that CHII contributes very little to the [O i] emission (3%), as expected since the atomic oxygen is a tracer of the neutral gas. CHII shows very little contribution to the [C ii] (<1%) and [Si ii] (11%) lines as well. The energy required to create C++ ions is 24.4 eV, close to that of S++, therefore when the radiation field is sufficiently hard, as is the case inside the H ii region, C is doubly rather than singly ionised.
4.2. The dense photodissociation regions: CPDR
We subsequently investigate the properties of the neutral gas and compare model predictions to the [C ii] and [O i] 63 and 145 μm lines. To this end, we extend CHII into the atomic phase and the outer envelope of the molecular phase, until the molecular fraction H2/H reaches 99%. The modeled shell is fully covered by the gas. The ionised cloud, with average density of 102.8 cm-3, transitions from the H ii region into a dense PDR, which is where the [O i] originates. This transition between these two phases in a constant pressure model translates into a jump of the gas density at the ionisation front. With this model, the average density of the PDR is 105.1 cm-3. The radiation field striking the PDR is: G0 = 3.5×103 Habing unit (1.6×10-3 erg cm-2 s-1). The heating of the gas in the PDR is dominated by grain photoelectric heating (85%), and there is a second order contribution from collisions with H0, He, and H2. The cooling is done by radiative de-excitation mainly of the [O i] 63 μm (65%), [Si ii] (20%), [C ii] 157 μm and [O i] 145 μm (<7% each) lines. At such low Av < 1, the [O i] lines are optically thin.
The [O i] 63 and 145 μm absolute intensities are over-estimated by a factor of 10, while their ratio is reproduced within 15% by this dense PDR component. Along with the [O i] 63 μm line, [C ii] 157 μm and [Si ii] 35 μm are the brightest PDR lines. While the [Si ii] line intensity is over-predicted by a factor of 2 by the dense model, the [C ii] line agrees with the observation within 10%.
The consistent over-prediction of the two [O i] lines may be explained by the fact that, in reality, the dense PDR does not cover the full dense H ii region. Assuming that all of the [O i] arises from a single dense phase (and not the diffuse gas, see Sect. 5.3), we reduce the covering factor of the dense PDR to only 10%, which is a proxy for dense clumps (Hunter et al. 2001; Groves et al. 2008). The PDR model with a covering factor of 1/10 matches the observed [O i] emission, but under-estimates the [C ii] emission by an order of magnitude. The main conclusion from this is that the dense PDR component cannot account for the bulk of the [C ii] emission observed in Haro 11, but only for 10%. This mismatch for the [C ii] is due to the relatively low critical density of [C ii] (2×103 cm-3) compared to the high density reached in the PDR (nPDR = 105.1 cm-3), generated by the pressure equilibrium and the drop of gas temperature between the ionised and neutral phases. Indeed, Cloudy PDR models with constant densities of ~103.5 cm-3 and a covering factor of unity would reproduce the absolute intensity of the two [O i] lines simultaneously, and yet under-predict the [C ii] by a factor of 2. Moreover, the H i mass of such models would exceed the upper limit of 108 M⊙ found by Bergvall et al. (2000).
The small fraction of [C ii] that originates from the dense PDR is at odds with the finding of Bergvall et al. (2000), who estimate that more than 80% of the observed [C ii] in Haro 11 comes from the neutral gas. They use stellar clusters of Teff ~ 35 000−40 000 K to account for the [O iii] 88 μm emission, which contributes less than 20% to the [C ii] emission, and they assume that the rest of the [C ii] (>80%) is associated with PDRs. Then, they find nPDR = 2×103 cm-3 using the Kaufman et al. (1999) model, which assumes a constant density. The much higher density that we find is compatible with the findings of Vasta et al. (2010) who analysed ISO observations with PDR models for several dwarf galaxies, including Haro 11, and find PDR densities between 104 and 9×104 cm-3, and G0 between 60 and 8×102 Habing. They also estimate that 10 to 60% of [C ii] comes from the ionised gas, which is in agreement with the diffuse ionised model contribution to the [C ii] line that we discuss in Sect. 5.3.
We have also explored the influence of cloud geometry on the line predictions by using the PDR model Kosma-τ (Röllig et al. 2006), in which the illumination of the cloud is external, simulating a spherical cloud structure. At corresponding values of nH (105.1 cm-3) and G0 (3.5×103 Habing) found with Cloudy, Kosma-τ predicts ratios of [O i] 145 μm/[C ii] ~ 1 and [O i] 145/63 μm ~ 0.05. The [O i] 145 μm/[C ii] model ratios are over-predicted, as found with Cloudy, compared to our observed value of 0.08. However, if we attribute only 10% of the [C ii] emission to the PDR, then [O i] 145 μm/[C ii]PDR ~ 0.1 from Kosma-τ, which is in line with our observations. The spherical geometry affects both [O i] and [C ii] lines similarly to first order, and is not the primary reason for the discrepancy between observed and predicted [C ii] intensities.
We prefer to impose the pressure equilibrium between the compact H ii region and the dense PDR, because this gives physical insight into the presence of dense but fragmented PDRs (e.g. Hunter et al. 2001). Although the pressure equilibrium assumption is not valid on large scales (nor is the assumption of a constant density) and, in particular, is expected to break in molecular clouds, here we do not model the molecular phase. We are interested in the interface between the dense H ii region and the PDR, the presence for which there is observational evidence. This model solution of the dense PDR with covering factor of 10% is noted CPDR. Next, we will discuss possible ways to lower the density in the PDR to account for the [C ii] emission, by either combining a high density with a low density model (Sect. 5.3), representative of the multi-phase ISM of galaxies, or by including a magnetic field (Sect. 6.1).
5. A model for the diffuse medium: D
5.1. Need for a softer radiation field
The major discrepancies between observations and model predictions in the ionised gas are seen for the [Ne ii] 12.6 μm and [N ii] 122 μm lines, which are both under-predicted by a factor of ~5 in the dense H ii region model CHII, which is not unexpected. With excitation potentials of 14.5 and 21.6 eV respectively, emission of N+ and Ne+ originates only from the ionised gas, from both the dense H ii region and the diffuse medium. For [N ii] 122 μm, CHII does not reproduce the observed value even when varying the 3 free parameters. Only rin > 1021.8 cm may agree (bottom left panel of Fig. 6). The contribution of the compact H ii region to this line is thus marginal; mostly because the radiation field produced by the young starburst is too hard and favors the ionisation of N++ rather than N+. For the [Ne ii] line, a small change in the age of the burst would impact on its prediction, as discussed in Sect. 4.1.2. For the same values of density and inner radius, a model of age 3 Myr (instead of 3.7 Myr) would agree better with the observed intensity of [Ne ii]. For a burst age of 3.7 Myr, higher densities (nH > 103 cm-3) and inner radii (rin > 1021.6 cm) are required to reproduce the observed [Ne ii] (top right panel of Fig. 6). However, such values of nH and rin would no longer agree with the other ionic lines. In order to reconcile the modeled [Ne ii] and [N ii] with their observations, a component with softer radiation field is required. This highlights the fact that one component is not enough the account for the emission of all the observed lines due to the presence of several phases in the ISM of galaxies with different properties.Our physical picture of the ISM of dwarf galaxies is of a highly permeable medium, where some of the ionising photons from the central starburst escape the H ii region and travel large distances. This means that in dwarf galaxies, larger effective volumes can be maintained in an ionised state, compared to those of dusty starbursts.
To model this additional ionised component we have tried three different methods: (1) set the cloud further away (higher rin) under the same starburst conditions, and allowing the density to be a free parameter; (2) stop CHII before it reaches the ionisation front and take the output spectrum as the input spectrum of a lower density medium; (3) opt for a softer radiation field by including a scaled local interstellar radiation field. However, all of these methods fail to reproduce the observed line intensities. Either the radiation is still too hard (case (1) and (2) when stopping too early), or too soft (case (3) and (2) when stopping too close to the ionisation front).
The radiation field that works best to explain the observed [Ne ii] and [N ii] lines is a representative stellar SED from the Kurucz library of relatively low temperature (see the next section). This is supported by the fact that more evolved stars producing low energy photons are present in Haro 11 (Micheva et al. 2010) but not accounted for in the compact model C (CHII + CPDR). This older population affects mainly the emission of [N ii], [Ne ii], and to a lesser extent [S iii].
5.2. Properties of the model D
We ran constant density models of diffuse ionised gas, stopped at the ionisation front, with stellar temperature between 20 000 and 40 000 K. The best fit to the [N ii] 122 μm and [Ne ii] emission is obtained for a stellar temperature of 35 000 K. Figure 9 shows how the [N ii], [Ne ii], [S iii], and [C ii] lines vary with density for several values of rin. We refer the reader to Sects. 4.1.1 and 4.1.3 for an interpretation of the behavior of the lines. The range of possible solutions for the [N ii] 122 μm emission are densities below 103 cm-3 and rin higher than 1021.0 cm. [Ne ii] also agrees well with these conditions. At Teff of 35 000 K, [S iii] also emits, but remains below its observed value. Very little [N iii], [Ne iii], [O iii], and [S iv] are produced in this diffuse component, and no [O iv]. Although [N ii] 122 μm has a relatively low critical density, the density of the N+ emitting medium is usually well constrained by the [N ii] 205 μm line. Unfortunately, the [N ii] 205 μm line is difficult to observe with PACS because of spectral leakage (see Sect. 2.2). The upper limit on the [N ii] 205 μm line sets an upper limit on the ratio [N ii] 205/122 μm of 0.75 which corresponds to a lower limit on the density of the “diffuse” gas component of 10 cm-3 (e.g. Rubin et al. 1994; Oberst et al. 2006). The [N ii] 122 μm line critical density sets an upper limit of 103 cm-3. Models with densities between 10 and 103 cm-3 work equally well for the “diffuse” medium in accounting for the [N ii] 122 μm and [Ne ii] emission.
 |
Fig. 9 Predictions for the model D of the [Ne ii], [C ii], [N ii], and [S iii] line intensities (Imodel), normalised by their observed value (Iobs) as a function of density nH. Models are for a diffuse ionised/neutral gas, with constant density, stellar temperature of 35 000 K, and are stopped when molecules start to form. The [S iii], [Ne ii] and [N ii] lines emit in the ionised phase. The contribution of the ionised phase to the [C ii] line is indicated with open circles. The vertical dashed lines indicate density values of the diffuse models Dl (nH = 10 cm-3) and Dh (nH = 103 cm-3) defined in Sect. 5.3. (This figure is available in color in electronic form.) |
5.3. [C II] contribution from the model D
Since CPDR predicts very little [C ii] 157 μm, we expect a significant contribution of the diffuse medium to the C+ emission. C+ is usually found in the surface layers of far-UV illuminated PDRs (Stacey et al. 1991; Negishi et al. 2001), but it can also come from the ionised gas, with a contribution up to 50% (Madden et al. 1993; Carral et al. 1994; Heiles 1994; Abel et al. 2005). With ionisation potentials lower than that of hydrogen, both C+ and Si+ can be produced by low energy photons or excited by collisions with electrons or hydrogen atoms, depending on the degree of ionisation from the emitting medium.
Figure 9 shows the predicted [C ii] line intensities from the diffuse medium with a stellar temperature of 35 000 K, as a function of gas density. The contribution of the diffuse phase (ionised+neutral) is in filled circles, and the contribution of the ionised phase only shown by open circles. Calculations are stopped when molecules start to form and the fraction of H2/H reaches 10%. At low nH, the empty and filled circles are very close: a large fraction of the [C ii] can arise from the ionised phase, until [C ii] is collisionally de-excited by e− (ncrit = 50 cm-3), and emits mostly in the neutral phase, its intensity then increasing with density. At rin = 1022.2 cm, the [C ii] predictions decrease for nH > 102 cm-3, because the atomic phase is very thin as the material is cold and enters quickly into the molecular phase where the models stop. We disregard these models which do not predict enough [C ii]. The range of possible solutions for the [C ii] 157 μm emission are rin higher than 1021.4 cm, and are degenerate in nH. We can set a low-density case where nH = 10 cm-3 – for example. Then rin = 1021.8 cm is the best fit, and [C ii] comes mostly from the ionised phase, accounting for ~45% of the observed value. We also consider a high-density case where nH = 103 cm-3, and rin = 1021.8 cm. In this case, [C ii] is mostly emitted in the neutral phase, accounting for ~40% of the observed value. Both models fill a larger volume than the compact model C.
5.3.1. Constraint from the H I 21-cm line
The H i 21-cm mass upper limit of 108 M⊙ from Bergvall et al. (2000) is an important gas diagnostic of the diffuse atomic gas and brings a strong constraint that we can use to differentiate between the low-density and high-density case models. The H i mass from CPDR is 107 M⊙. While the models from Fig. 9 were stopped at a fraction of H2/H reaching 10% to compute entirely the ionised and atomic phases, most of those models exceed the H i mass upper limit. By stopping those models when the upper limit on the H i mass is reached, we find that the low-density case model contribution to the [C ii] line is unchanged since it comes from the ionised phase, while the high-density case model contributes to only ~20% of the [C ii] line intensity, since the atomic phase is stopped at lower AV than previously computed.
For the rest of this study, we refer to the low-density case model as Dl, and to the high-density case model as Dh. We cannot exclude the presence of a diffuse neutral gas, but in all cases, there is a prominent contribution to the [C ii] from the ionised gas. We estimate that ~40% originates in Dl; the rest coming from CPDR and little from Dh. Moreover, the diffuse models do not contribute more than 15% to the [O i] lines, which are reliable tracers of the PDR.
6. Influence from other possible components
6.1. Magnetic fields
Magnetic fields impact the model solution, dominating the pressure deep into the cloud, and they are expected to be important in star-forming regions (Shaw et al. 2009). Robishaw et al. (2008) found magnetic fields on the order of a few mG in ULIRGs, from OH Zeeman splitting. In local dwarf irregular galaxies, magnetic fields are found to be weak, of a few μG to 50 μG in more extreme cases (e.g. NGC 1569, NGC 4214; Chyży et al. 2011; Kepley et al. 2010, 2011). No study on magnetic fields has been conducted for Haro 11, so we did not include them in our grid calculation. Nevertheless, in view of the fact that we have found that the density of the dense PDR plays a determining role in the predicted line fluxes, we investigate the influence of adding a magnetic field Bmag of strength 1 μG to 3 mG to the solution model C described in Sect 4.
The magnetic field (Bmag) is expressed as a pressure term (Pmag) through the cloud by the following equation: 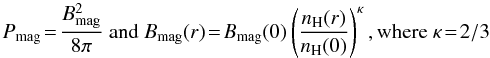 (1)where r is the depth of the cloud, Bmag(0) and nH(0) are the initial values of the magnetic field and hydrogen density. This density-magnetic field relationship from Crutcher (1999) corresponds to the case where gravity dominates over magnetic support in the cloud collapse, and the magnetic flux is conserved.Figure 10 shows the predicted [C ii] and [O i] intensities with increasing Bmag. For low values of Bmag, thermal pressure, expressed as Pgas ∝ nH Tgas, dominates and the densities in the PDR are high, with strong emission of [O i], as seen previously. With increasing Bmag, magnetic pressure starts to dominate over gas pressure and the transition into the PDR is smooth, resulting in lower densities in the PDR, and less emission of [O i]. The [C ii]/[O i] ratio increases with increasing Bmag. The [C ii] prediction falls between a factor of 0.5 and 1 of its observed value for all models. Values of Bmag up to 10-3.75 G predict enough [O i] emission. For Bmag > 10-3.75 G, the models under-predict the intensity of the PDR lines, which would require extra input power, although we are still within the errors (factor of 2).
(1)where r is the depth of the cloud, Bmag(0) and nH(0) are the initial values of the magnetic field and hydrogen density. This density-magnetic field relationship from Crutcher (1999) corresponds to the case where gravity dominates over magnetic support in the cloud collapse, and the magnetic flux is conserved.Figure 10 shows the predicted [C ii] and [O i] intensities with increasing Bmag. For low values of Bmag, thermal pressure, expressed as Pgas ∝ nH Tgas, dominates and the densities in the PDR are high, with strong emission of [O i], as seen previously. With increasing Bmag, magnetic pressure starts to dominate over gas pressure and the transition into the PDR is smooth, resulting in lower densities in the PDR, and less emission of [O i]. The [C ii]/[O i] ratio increases with increasing Bmag. The [C ii] prediction falls between a factor of 0.5 and 1 of its observed value for all models. Values of Bmag up to 10-3.75 G predict enough [O i] emission. For Bmag > 10-3.75 G, the models under-predict the intensity of the PDR lines, which would require extra input power, although we are still within the errors (factor of 2).
However, when lowering the density, the size of the PDR layer increases, and the H i mass as well. With no magnetic field, we find M(H i) = 107 M⊙ with a covering factor of ~10%. For Bmag > 10-4 G, we find M(H i) > 2×108 M⊙ for a covering factor of unity. By increasing the magnetic field strength, we go from a picture of small dense clumps to a more diffuse extended medium, which again does not agree with the observed upper limit on the H i mass. Moreover, high field strengths (>100 μG) may be found in the cores of star formation, but are unlikely to hold on galaxy-wide scales. Models with Bmag > 10-4 G are therefore discarded and appear in the shaded grey area in Fig. 10. The model with Bmag of 10-4 G is noted CB. Then, if we consider that all of the [O i] 145 μm emission originates in the PDR, we can consequently scale the [C ii] intensity and we estimate the contribution of the PDR to the [C ii] line to be from 10% up to at most 50% in strong magnetic field cases.
 |
Fig. 10 Influence of the magnetic field on the PDR lines. Top: model predictions of the [C ii] and [O i] intensities (Imodel) normalised by their observed value (Iobs) as a function of magnetic strength Bmag. The effective density in the PDR is indicated for each Bmag value. Bottom: fraction of [C ii] coming from the PDR, scaled to the [O i] 145 μm prediction, assuming that all of it originates in the PDR. Models in the shaded area are not valid with respect to the upper limit on the H i column density. (This figure is available in color in electronic form.) |
6.2. Origin of the [O III] 88 μm line
Although emission from the [O iii] 88 μm line is expected in starburst galaxies, recent Herschel observations show that it is exceptionally bright in dwarf galaxies (Madden et al., in prep.). In Haro 11, it is the brightest of all MIR and FIR lines. With excitation potential of 35.1 eV and critical density, ncrit = 5×102 cm-3, this line is expected to originate from a high ionisation and relatively low density medium. Effective temperatures, Teff > 40 000 K, are usually needed to explain the bright [O iii] emission in star-forming irregular galaxies (Hunter et al. 2001). When considering both models CHII and D, we find a good match between model predictions and observations for all ionic lines considered, although the [O iii] 88 μm line is under-predicted by the models by a factor of ~2. CHII accounts for 60% of the [O iii] 88 μm emission, and D does not predict any [O iii] emission; the ionising photons are not energetic enough. This factor of 2 is within the uncertainties of this study, however we discuss the possible origin of the [O iii] 88 μm line from a highly ionised more diffuse medium. Although the [O iii] emission is explained by CHII in the extreme case of Haro 11, this may not be the case in other metal-poor dwarf galaxies.
In the star-forming region N11-B of the Large Magellanic Cloud, Lebouteiller et al. (2012) find bright [O iii] 88 μm emission that originates from spatially extended high-excitation diffuse ionised gas, and can be modeled by O stars distributed across the region. In the case of Haro 11, the density in CHII is too high to fully reproduce the observed [O iii] 88 μm emission. As shown in Fig. 6, lowering the density in CHII to densities ≤ 102 cm-3 would better reproduce the observed [O iii] 88 μm intensity.
Given the two components that we have modeled CHII and D, we may consider a picture in which CHII does not have a covering factor of unity, but is actually porous. This would allow some fraction of the ionising photons to escape the compact H ii region and travel further away in a lower density medium. Such a configuration could explain the [O iii] 88 μm emission, but would also lead to over-predicting several lines. In particular, in our case, predicted intensities of the [S iv], [O iv], and [N iii] lines would be a factor of ~2 higher than their observed values.
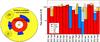 |
Fig. 11 Left: multi-phase build-up of the ISM of Haro 11, composed of a compact H ii region (CHII) in red, a dense fragmented PDR (CPDR) in blue, a diffuse medium of lower ionisation (D) in yellow, and warm dust in the inner region (represented as dots close to the starburst). Right: diagram of the contribution of each individual ISM phase to the global emission of the MIR and FIR lines. Red color corresponds to CHII, blue to CPDR, with possible enhancement in the [C ii] (and [Si ii]) lines when considering magnetic fields (hashed blue, CB), and yellow from the diffuse ionised medium (Dl), also with possible contribution from a diffuse neutral phase (hashed yellow, Dh). (This figure is available in color in electronic form.) |
6.3. Origin of the [O IV] line and X-rays
With an ionisation potential of 54.9 eV, [O iv] can only be excited by high energy sources. Its origin has been discussed in Lutz et al. (1998) or Schaerer & Stasińska (1999). It can come from AGN activity (X-rays), very hot sources or shocks. In this Section, we explore the role of X-ray photons and/or shocks. In dwarf starbursting galaxies, a hot and young stellar population is usually responsible for the [O iv] emission. This has been confirmed by ISO observations of the dwarf galaxies II Zw 40 and NGC 5253 (Schaerer & Stasińska 1999). Signatures of Wolf-Rayet stars in the optical and P Cygni profiles in the far-UV (O vi lines), revealing the presence of O supergiants and a very young burst in Haro 11, were reported by Bergvall et al. (2006) and Grimes et al. (2007). In the case of Haro 11, we find that the young starburst containing Wolf-Rayet stars can indeed account for the [O iv] 25.9 μm line intensity. The luminosity of the [O iv] line is ~0.006% of LTIR. Spinoglio et al. (2012) have compared the IR/submm emission lines to the IR luminosity in local samples of AGNs and starburst galaxies. They showed that the [O iv] line is weaker in starburst galaxies, about one order of magnitude less intense than in AGNs, and that starbursts follow the relation L [O IV] ~ 10-4 LTIR in the high IR luminosity range, which is consistent with that observed in Haro 11. The [Ne v] (97.1 eV) at 14.3 μm is not detected in the Spitzer/IRS spectrum. The upper limit in Table 2 is consistent with our model prediction. Its absence confirms the fact that there is no AGN activity nor intense hard X-ray emission in Haro 11. The X-ray component discussed in Sect. 3.3.1 in our model has little effect on the intensities of the ionic lines. Around the parameters of CHII, adding X-rays to the radiation field increases the intensity of the [O iv] 25.9 μm line by only ~1%. In the PDR, the X-rays have a moderate effect. They contribute up to 5% to the [C ii] intensity, and ~10% to the [O i] intensities. X-rays play a second order role and the physics of the neutral gas is dominated by the FUV photons (PDR), not the X-rays (XDR).
Shocks are also not our prefered explanation for the [O iv] emission. O’Halloran et al. (2008) find that the emission of the [Fe ii] 26.0 μm line in low-metallicity BCDs may be shock-derived or can result from a larger abundance of iron in the gas-phase as it is less depleted onto dust grains at low metallicity. However, the [Fe ii] 26.0 μm line is barely detected in Haro 11. The observed ratio of [Fe iii]/[Fe ii] is ~0.005, which also tends to rule out shocks as a major heating process here.
7. Multi-phase build-up of Haro 11
We summarize the contributions of the different ISM phases that, when put together, account for the global MIR and FIR fine-structure line emission observed in Haro 11 (Fig. 11). The panel on the left is an illustration of this multi-phase build-up: the central starburst is surrounded by our main model C composed of a compact H ii region CHII (red), with adjacent dense PDRs CPDR (blue). The volume around this compact nucleus is filled by diffuse ionised/neutral gas D (yellow). We also add a low filling factor component of warm dust close to the starburst (black dots), the need for which we discuss in Sect. 7.1. This scheme is the global picture (not to scale) that results from this modeling study. We remind the reader that the models C and D were computed separately. The panel on the right is a histogram indicating the contribution of each model to the line intensities, with identical color-coding. All 17 lines considered are reproduced by the 3 models CHII, CPDR, and D within a factor of 2. The model parameters of these phases and line predictions are also listed in Table 5. In view of the results from Sects. 5.3 and 6.1, in which the upper limit on the H i mass limits the contribution from the diffuse neutral medium and from magnetic fields, the models Dh and CB are not taken into account for our final build-up of the ISM of Haro 11. The models we combine are:
-
a compact H ii region that dominates theemission of the ionic lines,CHII;
-
a dense PDR of coverage ~10%, CPDR;
-
a diffuse low-ionisation medium, Dl.
We analyse results from this build-up in terms of dust emission, extinction, and mass budget.
Model parameters and line predictions.
7.1. The global SED
The proposed geometry also implies a prediction for the dust emission coming from the different ISM phases of Haro 11. We compare the predicted SED of the multi-phase build-up with the observations of Haro 11 in Fig. 12. The goal here is not to fit in detail the dust emission but rather to reproduce the global shape of the SED because it is sensitive to the temperature of the dust, which is one of the main predictions of the multi-phase model. The SED of the compact model C (both CHII and CPDR) peaks at ~40 μm (Fig. 12), as in the observed SED. In particular, CPDR is too dense to explain the FIR shape of the SED, which corroborates the presence of a more diffuse component. Indeed, the diffuse component Dl matches the temperature of Haro 11 in the FIR, although the longest wavelengths, beyond 250 μm, are still under-predicted. Perhaps the most surprising result is that the multi-phase model fails completely to reproduce the UV-optical extinction and the MIR emission, despite the choice of a lower cut in the grain sizes (Sect. 3.3.3). We discuss these two points in Sects. 7.1.1 and 7.1.2.
7.1.1. Energy balance
In the UV-optical wavelength range, the total outward luminosity (Fig. 12: bottom panel, black line) is 80% greater than the observed luminosity. Has the input energy in the UV-optical wavelength range been over-estimated? We are confident about the shape of the input starburst spectrum since the spectral line ratios depend on the hardness of the radiation field and are well fitted by our models. Additional confidence draws from the right amount of input energy as the level of the NIR photometry, unaffected by the little extinction present in Haro 11, is well matched.
The SED reflects the global energy balance of Haro 11 and shows that a fraction of the total input energy injected in the UV-optical wavelength range is not absorbed. The models CHII and Dl are responsible for the over-prediction in the UV-optical. We find the average extinction of the model to be AV = 0.15 mag. The spectrum is dominated by emission from the ionised model components: CHII, of which 90% of the radiation escapes since the PDR covers only 10%, and Dl. These models are computed separately and work as MIR-FIR emission line diagnostics, very little affected by dust attenuation, but we neglect their interaction. We can estimate the reddening needed to match the level of the model spectrum to the observed data points. Using the extinction law of Calzetti et al. (2000), with RV = 3.3 set by the model, we find AV = 0.9 mag, hence AB = 1.2 mag and E(B − V) = 0.3 mag. The reddened spectrum appears in dashed dark line in Fig. 12 (bottom). From UV continuum measurements and Hα/Hβ ratio, Bergvall & Östlin (2002) estimate AB = 0.7 mag. The optical image (Fig. 1) shows a dust lane passing in front of knot B, where the extinction is known to be higher (Adamo et al. 2010; Guseva et al. 2012). Adamo et al. (2010) find that E(B − V) is 0.4 towards knot B and 0.1 towards knot C.
 |
Fig. 12 Top: spectral energy distribution (SED) of the incident radiation field striking the cloud and outward radiation from each component modeled by Cloudy. The dark spectrum is the total outward radiation resulting from multi-phase build-up, and arriving to the observer. Photometry data from NED, Bendo et al. (2012), Galametz et al. (2009), and Rémy et al. (in prep.), and the IRS spectrum are overlaid in grey. Bottom: spectral energy distribution of the total outward radiation field and the reddened outward radiation field in dashed dark line. (This figure is available in color in electronic form.) |
On the contrary, in the MIR (5 to 40 μm), the predicted luminosity is two times lower than the observed luminosity. This emission in the MIR can be attributed to warm dust that we model in the following section.
This suggests an interpretation in terms of geometry of the galaxy, in which a large number of ionising photons can travel far, but in the end, the different media (compact and diffuse) are well mixed together, yielding a significant dust column along most lines of sight. In particular, the warm dust component that we add close to the central starburst and emits in the MIR is likely responsible for the absorption of the UV-optical part of the CHII spectrum which is the primary contributor to the total spectrum in this range.
7.1.2. Warm dust component
To account for the observed warm dust that our models do not produce in the MIR range (Fig. 12, top panel), we have examined two possible solutions that do not change the intrinsic properties of the dust grains (which are little known):
-
1)
change the dust distribution for a postshock distribution(Jones et al. 1996), where grainsare affected by shocks, with preferential destruction of largegrains, resulting in an enhancement of small grains with re-spect to large grains. This grain shattering results in a distri-bution with steeper slope and lower cut-off sizes. This distri-bution is successfully applied to model IR SEDs of LIRGs inDopita et al. (2011).Gallianoet al. (2003) used this distribution,that may have been generated by supernova shocks, to modelthe dust in the dwarf galaxy NGC 1569. Howeverwe have been unable to satisfactorily fit the SED by changing thegrain properties;
-
2)
add a warm dust component close to the central starburst. In this way we add to our picture a porous layer of dust particles close to the central starburst, which is not inconceivable for compact H ii regions. Models from Groves et al. (2008) show that the observed warm dust emission arises from hot dust embedded within the H ii region. This is also supported by spatially resolved observations of nearby galaxies. Calzetti et al. (2005) find that the 8 μm and 24 μm emission originate within the H ii regions.
This warm dust model matches the continuum level in the NIR-MIR, but produces a silicate feature in emission at 9.7 μm, which is not seen in the Spitzer/IRS spectrum. This discrepancy is likely due to the fact that we have modeled the compact and diffuse phases of the ISM independently. Foreground dust from the other components may in turn extinguish the silicate seen in emission. Another factor at play is the adopted abundance of silicate grains. Quantitative surveys with Spitzer of AGB carbon and silicate dust production rates in the Magellanic Clouds find that carbon dust injection rates dominate over those of silicate (Matsuura et al. 2009; Boyer et al. 2012). There may be a small effect from foreground cold dust from the molecular phase of Haro 11 that we do not model, which would have low filling factor and high AV.
7.1.3. FIR-mm wavelength range
The mismatch between the observed and predicted SED beyond 250 μm (Fig. 12) may be attributed to colder dust in the molecular phase. With no molecular gas constraint, we cannot include a cold molecular phase in our modeling. However, as a first approximation on the required dust properties, we can continue CPDR to higher AV and stop the model when it matches the submm temperature. This way, we estimate that the missing emission requires high AV ~ 40 mag and agrees with a grain temperature of ~25 K, which would fit the SPIRE data to 500 μm but still under-predict the LABOCA 870 μm data (see Fig. A.1 in Appendix A). The latter is rather related to the submm excess introduced in Sect. 1.1. This excess is modeled by a cold dust component in Galametz et al. (2009).
7.2. Optical lines
Several optical lines, including Hα, Hβ, [O iii] 5007 Å, have been observed towards the central visual peak in Bergvall & Östlin (2002). Because of the small aperture of the observations, 4″×4″, an absolute flux comparison cannot be made, except for Hα which was fully mapped in Östlin et al. (1999) with the ESO 3.6 m telescope. More recent observations were also performed with the VLT/X-shooter, in the wavelength range 3000−24 000 Å, by Guseva et al. (2012). In particular, they observed, in a slit of size ~1″×11″, the Hα, Hβ, [O ii] 3727 Å, [O iii] 4959 and 5007 Å, [S ii] 6716 and 6731 Å, [S iii] 9069 and 9535 Å lines, in both knots B and C of Haro 11. From these observations, they determined the metallicity of Haro 11 and elemental abundances. Optical lines are affected by dust extinction, and comparison of the model predictions to the observations is very dependent on the adopted geometry. With Cloudy, we can compare the intrinsic emission predicted by our model to the extinction-corrected observations.
The ratio of the optical lines listed above to Hβ are all well reproduced by our Cloudy models, within 40%, with contribution from both the H ii region and the diffuse medium (Table 6). The only line which poses a problem is [S ii], which is over-estimated by a factor of 3 at 6716 Å, and 1.5 at 6731 Å. The Cloudy ratio of the two [S ii] lines is thus 0.9. The Cloudy models of Guseva et al. (2012) also over-predict the [S ii] lines by a factor of 2, but reproduce their observed ratio of 1.5. This ratio is sensitive to the electron density of the medium probed, which in their case is a density of 10 cm-3. We find that our diffuse ionised model with density 10 cm-3 does predict a [S ii] line ratio of 1.5. Concerning Hα, we compare its absolute flux and find that it emits from both the H ii region and the diffuse medium, with a total predicted luminosity of 7×108 L⊙, close to the observed value of Östlin et al. (1999), LHα = 8×108 L⊙.
Optical line predictions.
7.3. Mass budget
The gas mass of each ISM component can be calculated using the density profile in the cloud and integrating over the volume of each slice inside the cloud. We then multiply the gas mass by 1.36 to account for helium, and use the D/G mass ratio of the model (2.64×10-3) to derive the dust mass. The masses of each component are summarized in Table 7. We find a mass of ionised gas (CHII+Dl) of 5.8×108 M⊙, and a mass of neutral gas (CPDR+Dl) of 2.4×108 M⊙. This neutral gas mass accounts for the H i mass as well as the mass of H2 formed in PDR envelopes before the CO formation. This H2 layer not traced by CO is referred as the “dark gas” (Wolfire et al. 2010). The PDR-H2 mass is ~108 M⊙ and comes from CPDR, while the H i mass comes essentially from the diffuse model Dl with M(H i) ~ 108 M⊙ fixed by its upper limit. As expected, the ionised phase is dominant in Haro 11. The ionised gas and PDR masses are similar to that of Bergvall et al. (2000). We derive a total dust mass of 2.1×106 M⊙, comparable to the value 6×106 M⊙ of Galametz et al. (2009).
These dust and gas mass inventories do not include modeling of the cold CO-cloud. The missing FIR emission discussed in Sect. 7.1.3 results in a dust mass of ~2×106 M⊙, which does not include the observed submm excess. When modeling the dust submm excess as cold dust, Galametz et al. (2009) find a total dust mass of 2×107 M⊙, which would result in a higher D/G mass ratio (~1/50) compared to our current gas modeling. A significant fraction of ISM mass would therefore not be accounted for by our models, part of which should sit in the molecular phase that we have not modeled. CO(1−0) is to date undetected (Bergvall et al. 2000). The state of a reservoir of warm molecular gas is addressed in a forthcoming paper (Cormier et al., in prep.). We would like to emphasize that the determination of the cold dust mass is very sensitive to the model and geometry adopted. Both the cool dust interpretation of the submm excess and the model accounting for the missing FIR emission (Sect. 7.1.3) are, without further constraints on the cold phase, ad hoc means to fit the dust SED. In particular, the cold dust interpretation of the submm excess has little physical support as it is unlikely to encounter such very large columns of (cold shielded) dust in dwarf galaxies, and because the submm excess does not seem to correlate spatially with the densest ISM phases (Galliano et al. 2011).
Mass budget in solar mass M⊙.
8. Conclusion
We have presented Spitzer/IRS and Herschel/PACS spectroscopic observations of the MIR-FIR fine-structure cooling lines in the starburst low-metallicity galaxy Haro 11. Investigating the nature of the different gas phases in this galaxy, we have modeled the ISM phases of Haro 11 step by step with the spectral synthesis code Cloudy. The main results can be summarized as follows:
-
1.
The IRS and PACS spectra show very bright MIR and FIR fine-structure cooling lines, the brightest of all being the [O iii] 88 μm line. The galaxy is undergoing young active star formation, as traced by the [O iii] 88 μm line (35.1 eV), which is about 3 times brighter than the classical neutral gas tracers [C ii] 157 μm and [O i] 63 μm. High line ratios of [Ne iii]/[Ne ii], [S iv]/[S iii], and [N iii]/[N ii] also trace the hard radiation field. We find L [C II] /LTIR = 0.1%, (L [C II] + L [O I] )/LTIR = 0.2%, and altogether, the MIR and FIR lines represent 1.2% of LTIR.
-
2.
We model our exhaustive dataset of 17 fine-structure lines with Cloudy and find the need to describe Haro 11 with these component phases:
-
a dense H ii region, illuminated by a young starburst; from which most of the ionic lines originate;
-
adjacent dense PDR of low (~10%) covering factor;
-
an extended diffuse low-ionised/neutral medium;
-
a porous warm dust component close to the stars that accounts for the elevated MIR continuum.
-
-
3.
Emission from the [N ii] 122 μm and [Ne ii] lines cannot be reconciled with the compact H ii region but are rather associated with a more diffuse low-ionisation medium.
-
4.
We find that 10% of the [C ii] emission is associated with the dense PDR, and up to 50% when lowering the density. About 50% of the [C ii] arises from a more diffuse ionised medium. The low extinction and low metallicity of Haro 11 make its ISM more leaky, and the emitting region of [C ii] larger. The [O i] emission is fully associated with the PDR. The observed [C ii] luminosity is comparable to that of the [O i] 63 μm line. In the dense component we derive L [C II] /LTIR ~ 0.05% and (L [C II] + L [O I] )/LTIR ~ 1%, which is a common measure of the gas heating efficiency in the neutral gas, and in the diffuse component we find L [C II] /LTIR ~ 0.1%.
-
5.
The only line that we do not completely reconcile with our model is the [O iii] 88 μm. Our compact H ii region model accounts for 50% of the emission of [O iii]. Our prefered explanation for the intense [O iii] emission is the presence of yet another additional diffuse component, filling the volume around the porous H ii region, and where the gas is heated by escaping UV photons.
-
6.
We estimate the mass from each modeled phase. We find a mass of ionised gas of 6×108 M⊙, a PDR mass of 2×108 M⊙, and a dust mass (without submm constraints, because of the submm excess) of 2×106 M⊙. The ionised gas mass is larger than the atomic gas mass.
-
7.
Finally, in terms of structure, the ISM of Haro 11 appears to be mostly filled with extended diffuse gas. Our simple picture can reproduce the observations by a galaxy with a filling factor of diffuse neutral and ionised gas of at least 90%, a dense H ii region component of filling factor ~0.2%, and a PDR component of filling factor <0.01%. A radiative transfer model which takes into account clumpy source and gas structures would provide a more realistic picture of Haro 11.
 |
Fig. A.1 Same as Fig. 12 (top panel) except that the PDR component is continued to higher AV in the molecular regime to match the observed submm photometry data. The covering factor of this molecular component is of ~5%. (This figure is available in color in electronic form.) |
Available at http://herschel.esac.esa.int/Docs/PACS/html/pacs_om.html
Note that they use LFIR, determined from IRAS fluxes with the Helou et al. (1988) formula, and that LTIR estimated as 2×LFIR (Hunter et al. 2001) can be different from the true LTIR when including submm observations.
Acknowledgments
The authors would like to thank Albrecht Poglitsch and Alessandra Contursi for their help with the PACS data. Part of this work has been made possible by financial support from the CNRS/INSU programme PCMI. PACS has been developed by a consortium of institutes led by MPE (Germany) and including UVIE (Austria); KU Leuven, CSL, IMEC (Belgium); CEA, LAM (France); MPIA (Germany); INAF-IFSI/OAA/OAP/OAT, LENS, SISSA (Italy); IAC (Spain). This development has been supported by the funding agencies BMVIT (Austria), ESA-PRODEX (Belgium), CEA/CNES (France), DLR (Germany), ASI/INAF (Italy), and CICYT/MCYT (Spain). This research has made use of the NASA/IPAC Extragalactic Database (NED) which is operated by the Jet Propulsion Laboratory, California Institute of Technology, under contract with the National Aeronautics and Space Administration. Based on observations made with the NASA/ESA Hubble Space Telescope, and obtained from the Hubble Legacy Archive, which is a collaboration between the Space Telescope Science Institute (STScI/NASA), the Space Telescope European Coordinating Facility (ST-ECF/ESA) and the Canadian Astronomy Data Centre (CADC/NRC/CSA).
References
- Abel, N. P., Ferland, G. J., Shaw, G., & van Hoof, P. A. M. 2005, ApJS, 161, 65 [NASA ADS] [CrossRef] [Google Scholar]
- Abel, N. P., van Hoof, P. A. M., Shaw, G., Ferland, G. J., & Elwert, T. 2008, ApJ, 686, 1125 [Google Scholar]
- Abel, N. P., Dudley, C., Fischer, J., Satyapal, S., & van Hoof, P. A. M. 2009, ApJ, 701, 1147 [NASA ADS] [CrossRef] [Google Scholar]
- Adamo, A., Östlin, G., Zackrisson, E., et al. 2010, MNRAS, 407, 870 [NASA ADS] [CrossRef] [Google Scholar]
- Baldwin, J. A., Ferland, G. J., Martin, P. G., et al. 1991, ApJ, 374, 580 [NASA ADS] [CrossRef] [Google Scholar]
- Beck, S. C., Turner, J. L., & Kovo, O. 2000, AJ, 120, 244 [NASA ADS] [CrossRef] [Google Scholar]
- Bendo, G. J., Galliano, F., & Madden, S. C. 2012, MNRAS, 423, 197 [NASA ADS] [CrossRef] [Google Scholar]
- Bergvall, N., & Östlin, G. 2002, A&A, 390, 891 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bergvall, N., Masegosa, J., Östlin, G., & Cernicharo, J. 2000, A&A, 359, 41 [NASA ADS] [Google Scholar]
- Bergvall, N., Zackrisson, E., Andersson, B.-G., et al. 2006, A&A, 448, 513 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Boselli, A., Gavazzi, G., Lequeux, J., & Pierini, D. 2002, A&A, 385, 454 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Boyer, M. L., Srinivasan, S., Riebel, D., et al. 2012, ApJ, 748, 40 [NASA ADS] [CrossRef] [Google Scholar]
- Brauher, J. R., Dale, D. A., & Helou, G. 2008, ApJS, 178, 280 [NASA ADS] [CrossRef] [Google Scholar]
- Calzetti, D., Armus, L., Bohlin, R. C., et al. 2000, ApJ, 533, 682 [NASA ADS] [CrossRef] [Google Scholar]
- Calzetti, D., Kennicutt, Jr., R. C.,Bianchi, L., et al. 2005, ApJ, 633, 871 [NASA ADS] [CrossRef] [Google Scholar]
- Carral, P., Hollenbach, D. J., Lord, S. D., et al. 1994, ApJ, 423, 223 [NASA ADS] [CrossRef] [Google Scholar]
- Chyży, K. T., Weżgowiec, M., Beck, R., & Bomans, D. J. 2011, A&A, 529, A94 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Contursi, A., et al. 2012, A&A, accepted [arXiv:1210.3496] [Google Scholar]
- Cormier, D., Madden, S. C., Hony, S., et al. 2010, A&A, 518, L57 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Croxall, K. V., Smith, J. D., Wolfire, M. G., et al. 2012, ApJ, 747, 81 [NASA ADS] [CrossRef] [Google Scholar]
- Crutcher, R. M. 1999, ApJ, 520, 706 [NASA ADS] [CrossRef] [Google Scholar]
- de Looze, I., Baes, M., Bendo, G. J., Cortese, L., & Fritz, J. 2011, MNRAS, 416, 2712 [Google Scholar]
- Dopita, M. A., Groves, B. A., Sutherland, R. S., & Kewley, L. J. 2003, ApJ, 583, 727 [NASA ADS] [CrossRef] [Google Scholar]
- Dopita, M. A., Groves, B. A., Fischera, J., et al. 2005, ApJ, 619, 755 [NASA ADS] [CrossRef] [Google Scholar]
- Dopita, M. A., Armus, L., Kewley, L. J., et al. 2011, Ap&SS, 333, 225 [NASA ADS] [CrossRef] [Google Scholar]
- Draine, B. T., & Li, A. 2001, ApJ, 551, 807 [NASA ADS] [CrossRef] [Google Scholar]
- Ferland, G. J., Korista, K. T., Verner, D. A., et al. 1998, PASP, 110, 761 [Google Scholar]
- Galametz, M., Madden, S., Galliano, F., et al. 2009, A&A, 508, 645 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Galametz, M., Madden, S. C., Galliano, F., et al. 2010, A&A, 518, L55 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Galametz, M., Madden, S. C., Galliano, F., et al. 2011, A&A, 532, A56 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Galliano, F., Madden, S. C., Jones, A. P., et al. 2003, A&A, 407, 159 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Galliano, F., Madden, S. C., Jones, A. P., Wilson, C. D., & Bernard, J.-P. 2005, A&A, 434, 867 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Galliano, F., Hony, S., Bernard, J.-P., et al. 2011, A&A, 536, A88 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Giveon, U., Sternberg, A., Lutz, D., Feuchtgruber, H., & Pauldrach, A. W. A. 2002, ApJ, 566, 880 [NASA ADS] [CrossRef] [Google Scholar]
- Graciá-Carpio, J., Sturm, E., Hailey-Dunsheath, S., et al. 2011, ApJ, 728, L7 [NASA ADS] [CrossRef] [Google Scholar]
- Griffin, M. J., Abergel, A., Abreu, A., et al. 2010, A&A, 518, L3 [Google Scholar]
- Grimes, J. P., Heckman, T., Strickland, D., et al. 2007, ApJ, 668, 891 [NASA ADS] [CrossRef] [Google Scholar]
- Grimes, J. P., Heckman, T., Aloisi, A., et al. 2009, ApJS, 181, 272 [NASA ADS] [CrossRef] [Google Scholar]
- Groves, B., Dopita, M. A., Sutherland, R. S., et al. 2008, ApJS, 176, 438 [NASA ADS] [CrossRef] [Google Scholar]
- Guseva, N. G., Izotov, Y. I., Fricke, K. J., & Henkel, C. 2012, A&A, 541, A115 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hayes, M., Östlin, G., Atek, H., et al. 2007, MNRAS, 382, 1465 [NASA ADS] [Google Scholar]
- Heiles, C. 1994, ApJ, 436, 720 [NASA ADS] [CrossRef] [Google Scholar]
- Helou, G., Khan, I. R., Malek, L., & Boehmer, L. 1988, ApJS, 68, 151 [NASA ADS] [CrossRef] [Google Scholar]
- Higdon, S. J. U., Devost, D., Higdon, J. L., et al. 2004, PASP, 116, 975 [NASA ADS] [CrossRef] [Google Scholar]
- Houck, J. R., Shure, M. A., Gull, G. E., & Herter, T. 1984, ApJ, 287, L11 [NASA ADS] [CrossRef] [Google Scholar]
- Houck, J. R., Roellig, T. L., Van Cleve, J., et al. 2004, in SPIE Conf. Ser., 5487, ed. J. C. Mather, 62 [Google Scholar]
- Hunter, D. A., Kaufman, M., Hollenbach, D. J., et al. 2001, ApJ, 553, 121 [NASA ADS] [CrossRef] [Google Scholar]
- Iglesias-Páramo, J., Buat, V., Takeuchi, T. T., et al. 2006, ApJS, 164, 38 [NASA ADS] [CrossRef] [Google Scholar]
- Izotov, Y. I., & Thuan, T. X. 1998, ApJ, 500, 188 [NASA ADS] [CrossRef] [Google Scholar]
- Izotov, Y. I., & Thuan, T. X. 1999, ApJ, 511, 639 [NASA ADS] [CrossRef] [Google Scholar]
- Jarrett, T. H., Chester, T., Cutri, R., et al. 2000, AJ, 119, 2498 [NASA ADS] [CrossRef] [Google Scholar]
- Johnson, K. E., & Kobulnicky, H. A. 2003, ApJ, 597, 923 [NASA ADS] [CrossRef] [Google Scholar]
- Jones, A. P., Tielens, A. G. G. M., & Hollenbach, D. J. 1996, ApJ, 469, 740 [NASA ADS] [CrossRef] [Google Scholar]
- Kaufman, M. J., Wolfire, M. G., Hollenbach, D. J., & Luhman, M. L. 1999, ApJ, 527, 795 [NASA ADS] [CrossRef] [Google Scholar]
- Kaufman, M. J., Wolfire, M. G., & Hollenbach, D. J. 2006, ApJ, 644, 283 [NASA ADS] [CrossRef] [Google Scholar]
- Kepley, A. A., Mühle, S., Everett, J., et al. 2010, ApJ, 712, 536 [NASA ADS] [CrossRef] [Google Scholar]
- Kepley, A. A., Zweibel, E. G., Wilcots, E. M., Johnson, K. E., & Robishaw, T. 2011, ApJ, 736, 139 [NASA ADS] [CrossRef] [Google Scholar]
- Kingsburgh, R. L., & Barlow, M. J. 1992, MNRAS, 257, 317 [NASA ADS] [Google Scholar]
- Kingsburgh, R. L., & Barlow, M. J. 1994, MNRAS, 271, 257 [NASA ADS] [CrossRef] [Google Scholar]
- Kunth, D., & Östlin, G. 2000, A&ARv, 10, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Kunth, D., Mas-Hesse, J. M., Terlevich, E., et al. 1998, A&A, 334, 11 [NASA ADS] [Google Scholar]
- Kunth, D., Leitherer, C., Mas-Hesse, J. M., Östlin, G., & Petrosian, A. 2003, ApJ, 597, 263 [NASA ADS] [CrossRef] [Google Scholar]
- Lauberts, A., & Valentijn, E. A. 1989, The surface photometry catalogue of the ESO-Uppsala galaxies [Google Scholar]
- Lebouteiller, V., Bernard-Salas, J., Sloan, G. C., & Barry, D. J. 2010, PASP, 122, 231 [NASA ADS] [CrossRef] [Google Scholar]
- Lebouteiller, V., Barry, D. J., Spoon, H. W. W., et al. 2011, ApJS, 196, 8 [NASA ADS] [CrossRef] [Google Scholar]
- Lebouteiller, V., et al. 2012, A&A, submitted [Google Scholar]
- Leitet, E., Bergvall, N., Piskunov, N., & Andersson, B.-G. 2011, A&A, 532, A107 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Leitherer, C., Ortiz Otálvaro, P. A., Bresolin, F., et al. 2010, ApJS, 189, 309 [NASA ADS] [CrossRef] [Google Scholar]
- Leroy, A. K., Bolatto, A., Gordon, K., et al. 2011, ApJ, 737, 12 [NASA ADS] [CrossRef] [Google Scholar]
- Lonsdale, C. J., Helou, G., Good, J. C., & Rice, W. L. 1985 [Google Scholar]
- Lutz, D., Kunze, D., Spoon, H. W. W., & Thornley, M. D. 1998, A&A, 333, L75 [NASA ADS] [Google Scholar]
- Madden, S. C. 2000, New Astron. Rev., 44, 249 [NASA ADS] [CrossRef] [Google Scholar]
- Madden, S. C. 2008, in EAS Pub. Ser. 31, eds. C. Kramer, S. Aalto, & R. Simon, 123 [Google Scholar]
- Madden, S. C., Geis, N., Genzel, R., et al. 1993, ApJ, 407, 579 [NASA ADS] [CrossRef] [Google Scholar]
- Madden, S. C., Geis, N., Townes, C. H., et al. 1995, in From Gas to Stars to Dust, eds. M. R. Haas, J. A. Davidson, & E. F. Erickson, ASP Conf. Ser., 73, 181 [Google Scholar]
- Madden, S. C., Galliano, F., Jones, A. P., & Sauvage, M. 2006, A&A, 446, 877 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Madden, S. C., Remy, A., Galliano, F., et al. 2012, in The Spectral Energy Distribution of Galaxies, Proceeding of the International Astronomical Union, IAU Symp., 284, 141 [Google Scholar]
- Maiolino, R., Caselli, P., Nagao, T., et al. 2009, A&A, 500, L1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Malhotra, S., Kaufman, M. J., Hollenbach, D., et al. 2001, ApJ, 561, 766 [Google Scholar]
- Mathis, J. S., Rumpl, W., & Nordsieck, K. H. 1977, ApJ, 217, 425 [NASA ADS] [CrossRef] [Google Scholar]
- Matsuura, M., Barlow, M. J., Zijlstra, A. A., et al. 2009, MNRAS, 396, 918 [NASA ADS] [CrossRef] [Google Scholar]
- Micheva, G., Zackrisson, E., Östlin, G., Bergvall, N., & Pursimo, T. 2010, MNRAS, 405, 1203 [NASA ADS] [Google Scholar]
- Narayanan, D., Krumholz, M. R., Ostriker, E. C., & Hernquist, L. 2012, MNRAS, 421, 3127 [NASA ADS] [CrossRef] [Google Scholar]
- Negishi, T., Onaka, T., Chan, K., & Roellig, T. L. 2001, A&A, 375, 566 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Oberst, T. E., Parshley, S. C., Stacey, G. J., et al. 2006, ApJ, 652, L125 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- O’Halloran, B., Madden, S. C., & Abel, N. P. 2008, ApJ, 681, 1205 [NASA ADS] [CrossRef] [Google Scholar]
- O’Halloran, B., Galametz, M., Madden, S. C., et al. 2010, A&A, 518, L58 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Osterbrock, D. E., Tran, H. D., & Veilleux, S. 1992, ApJ, 389, 305 [NASA ADS] [CrossRef] [Google Scholar]
- Östlin, G., Amram, P., Masegosa, J., Bergvall, N., & Boulesteix, J. 1999, A&AS, 137, 419 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Östlin, G., Amram, P., Bergvall, N., et al. 2001, A&A, 374, 800 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ott, S. 2010, in Astronomical Data Analysis Software and Systems XIX, eds. Y. Mizumoto, K.-I. Morita, & M. Ohishi, ASP Conf. Ser., 434, 139 [Google Scholar]
- Overzier, R. A., Heckman, T. M., Kauffmann, G., et al. 2008, ApJ, 677, 37 [NASA ADS] [CrossRef] [Google Scholar]
- Pierini, D., Leech, K. J., & Völk, H. J. 2003, A&A, 397, 871 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Pilbratt, G. L., Riedinger, J. R., Passvogel, T., et al. 2010, A&A, 518, L1 [CrossRef] [EDP Sciences] [Google Scholar]
- Poglitsch, A., Krabbe, A., Madden, S. C., et al. 1995, ApJ, 454, 293 [NASA ADS] [CrossRef] [Google Scholar]
- Poglitsch, A., Waelkens, C., Geis, N., et al. 2010, A&A, 518, L2 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Pustilnik, S., Kniazev, A., Pramskij, A., et al. 2004, A&A, 419, 469 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Robishaw, T., Quataert, E., & Heiles, C. 2008, ApJ, 680, 981 [NASA ADS] [CrossRef] [Google Scholar]
- Röllig, M., Ossenkopf, V., Jeyakumar, S., Stutzki, J., & Sternberg, A. 2006, A&A, 451, 917 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Rubin, R. H., Simpson, J. P., Haas, M. R., & Erickson, E. F. 1991, ApJ, 374, 564 [NASA ADS] [CrossRef] [Google Scholar]
- Rubin, R. H., Dufour, R. J., & Walter, D. K. 1993, ApJ, 413, 242 [NASA ADS] [CrossRef] [Google Scholar]
- Rubin, R. H., Simpson, J. P., Lord, S. D., et al. 1994, ApJ, 420, 772 [NASA ADS] [CrossRef] [Google Scholar]
- Sanders, D. B., Mazzarella, J. M., Kim, D., Surace, J. A., & Soifer, B. T. 2003a, AJ, 126, 1607 [Google Scholar]
- Sanders, D. B., Mazzarella, J. M., Kim, D.-C., Surace, J. A., & Soifer, B. T. 2003b, AJ, 126, 1607 [Google Scholar]
- Schaerer, D., & Stasińska, G. 1999, A&A, 345, L17 [NASA ADS] [Google Scholar]
- Schruba, A., Leroy, A. K., Walter, F., et al. 2012, AJ, 143, 138 [NASA ADS] [CrossRef] [Google Scholar]
- Shaw, G., Ferland, G. J., Henney, W. J., et al. 2009, ApJ, 701, 677 [NASA ADS] [CrossRef] [Google Scholar]
- Siebenmorgen, R., & Krügel, E. 2007, A&A, 461, 445 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Spinoglio, L., Dasyra, K. M., Franceschini, A., et al. 2012, ApJ, 745, 171 [NASA ADS] [CrossRef] [Google Scholar]
- Stacey, G. J., Geis, N., Genzel, R., et al. 1991, ApJ, 373, 423 [NASA ADS] [CrossRef] [Google Scholar]
- Stacey, G. J., Hailey-Dunsheath, S., Ferkinhoff, C., et al. 2010, ApJ, 724, 957 [NASA ADS] [CrossRef] [Google Scholar]
- Strong, A. W., Bloemen, J. B. G. M., Dame, T. M., et al. 1988, A&A, 207, 1 [NASA ADS] [Google Scholar]
- Tajer, M., Trinchieri, G., Wolter, A., et al. 2005, A&A, 435, 799 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Thornley, M. D., Schreiber, N. M. F., Lutz, D., et al. 2000, ApJ, 539, 641 [NASA ADS] [CrossRef] [Google Scholar]
- Thuan, T. X., Izotov, Y. I., & Lipovetsky, V. A. 1996, ApJ, 463, 120 [NASA ADS] [CrossRef] [Google Scholar]
- Tielens, A. G. G. M., & Hollenbach, D. 1985, ApJ, 291, 722 [NASA ADS] [CrossRef] [Google Scholar]
- Turner, J. L., Beck, S. C., & Ho, P. T. P. 2000, ApJ, 532, L109 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Vader, J. P., Frogel, J. A., Terndrup, D. M., & Heisler, C. A. 1993, AJ, 106, 1743 [NASA ADS] [CrossRef] [Google Scholar]
- Vasta, M., Barlow, M. J., Viti, S., Yates, J. A., & Bell, T. A. 2010, MNRAS, 404, 1910 [NASA ADS] [Google Scholar]
- Werner, M. W., Roellig, T. L., Low, F. J., et al. 2004, ApJS, 154, 1 [Google Scholar]
- Wolfire, M. G., Tielens, A. G. G. M., & Hollenbach, D. 1990, ApJ, 358, 116 [NASA ADS] [CrossRef] [Google Scholar]
- Wolfire, M. G., Hollenbach, D., & McKee, C. F. 2010, ApJ, 716, 1191 [NASA ADS] [CrossRef] [Google Scholar]
- Wu, Y., Charmandaris, V., Hao, L., et al. 2006, ApJ, 639, 157 [NASA ADS] [CrossRef] [Google Scholar]
- Wu, Y., Bernard-Salas, J., Charmandaris, V., et al. 2008, ApJ, 673, 193 [NASA ADS] [CrossRef] [Google Scholar]
- Zubko, V., Dwek, E., & Arendt, R. G. 2004, ApJS, 152, 211 [NASA ADS] [CrossRef] [Google Scholar]
Appendix A: SED including the cold molecular component
We model the SED beyond 250 μm by stopping the dense PDR model CPDR at larger AV so that it predicts cold dust emission and matches the Herschel/SPIRE observations (as discussed in Sect. 7.1.3). The resulting SED is shown in Fig. A.1.
All Tables
All Figures
 |
Fig. 1 HST/ACS 3-color image of Haro 11 with labels for the 3 star-forming knots (blue: F435, green: F550, red: FR656N/Hα). Images were downloaded from the Hubble Legacy Archive. (This figure is available in color in electronic form.) |
| In the text | |
 |
Fig. 2 Hα image of Haro 11 from the Hubble Legacy Archive. The Spitzer/IRS high-resolution slits are overlaid in green and the Herschel/PACS array in red. The PACS beamsize at 150 μm is 11.5″. The IRS low-resolution slits are not shown. (This figure is available in color in electronic form.) |
| In the text | |
 |
Fig. 3 Top: Spitzer/IRS spectrum of Haro 11 in the rest wavelength frame (z = 0.0206), SL in green, SH in blue, and LH in red. Emission lines are labeled on top. The IRAC and MIPS photometry is also overlaid (fluxes in Table 3). Bottom: zoom on the individual spectral lines. Fluxes and upper limits are reported in Table 2. (This figure is available in color in electronic form.) |
| In the text | |
 |
Fig. 4 Herschel/PACS line profiles from an individual spatial pixel (9.4″) centered on the galaxy. |
| In the text | |
 |
Fig. 5 Geometry of the Cloudy model with the three free parameter that we vary in the grid: the age of the burst (Aburst), inner radius (rin), and initial hydrogen density (nH). Parameter boundaries and step sizes are also indicated. |
| In the text | |
 |
Fig. 6 Predicted intensities for model C (Imodel) normalised by their observed value (Iobs) for all ionic lines considered, as a function of nH and rin for a given starburst age (of 3.7 Myr). The vertical dashed line shows the best fit model density nH = 102.8 cm-3, and the vertical dotted line the critical density of the ionic specie, if within the range displayed. The best fit inner radius is rin = 1021.4 cm (green symbols). (This figure is available in color in electronic form.) |
| In the text | |
 |
Fig. 7 Model predicted intensity ratios as a function of burst age Aburst, for a hydrogen density of 102.8 cm-3, and inner radius of 1021.4 cm. The true burst age of these models is an average of Aburst and the older stellar population of 9.5 Myr, although the latter has a negligible influence on the high-ionisation lines considered here. The horizontal solid lines represent the observed ratios and the dashed lines the uncertainties on the ratios. The vertical dashed line shows the solution burst age of 3.7 Myr, and the vertical dotted lines the age of 3 Myr and 4.7 Myr that would better match the [Ne iii]/[Ne ii] ratio. (This figure is available in color in electronic form.) |
| In the text | |
 |
Fig. 8 Contour plots of the χ2 values of the 3D grid (log scale). The parameters are given in logarithmic values. Units are cm-3 for the density, yr for the burst age, and cm for the inner radius. The minimum reduced χ2 found for CHII is |
| In the text | |
 |
Fig. 9 Predictions for the model D of the [Ne ii], [C ii], [N ii], and [S iii] line intensities (Imodel), normalised by their observed value (Iobs) as a function of density nH. Models are for a diffuse ionised/neutral gas, with constant density, stellar temperature of 35 000 K, and are stopped when molecules start to form. The [S iii], [Ne ii] and [N ii] lines emit in the ionised phase. The contribution of the ionised phase to the [C ii] line is indicated with open circles. The vertical dashed lines indicate density values of the diffuse models Dl (nH = 10 cm-3) and Dh (nH = 103 cm-3) defined in Sect. 5.3. (This figure is available in color in electronic form.) |
| In the text | |
 |
Fig. 10 Influence of the magnetic field on the PDR lines. Top: model predictions of the [C ii] and [O i] intensities (Imodel) normalised by their observed value (Iobs) as a function of magnetic strength Bmag. The effective density in the PDR is indicated for each Bmag value. Bottom: fraction of [C ii] coming from the PDR, scaled to the [O i] 145 μm prediction, assuming that all of it originates in the PDR. Models in the shaded area are not valid with respect to the upper limit on the H i column density. (This figure is available in color in electronic form.) |
| In the text | |
 |
Fig. 11 Left: multi-phase build-up of the ISM of Haro 11, composed of a compact H ii region (CHII) in red, a dense fragmented PDR (CPDR) in blue, a diffuse medium of lower ionisation (D) in yellow, and warm dust in the inner region (represented as dots close to the starburst). Right: diagram of the contribution of each individual ISM phase to the global emission of the MIR and FIR lines. Red color corresponds to CHII, blue to CPDR, with possible enhancement in the [C ii] (and [Si ii]) lines when considering magnetic fields (hashed blue, CB), and yellow from the diffuse ionised medium (Dl), also with possible contribution from a diffuse neutral phase (hashed yellow, Dh). (This figure is available in color in electronic form.) |
| In the text | |
 |
Fig. 12 Top: spectral energy distribution (SED) of the incident radiation field striking the cloud and outward radiation from each component modeled by Cloudy. The dark spectrum is the total outward radiation resulting from multi-phase build-up, and arriving to the observer. Photometry data from NED, Bendo et al. (2012), Galametz et al. (2009), and Rémy et al. (in prep.), and the IRS spectrum are overlaid in grey. Bottom: spectral energy distribution of the total outward radiation field and the reddened outward radiation field in dashed dark line. (This figure is available in color in electronic form.) |
| In the text | |
 |
Fig. A.1 Same as Fig. 12 (top panel) except that the PDR component is continued to higher AV in the molecular regime to match the observed submm photometry data. The covering factor of this molecular component is of ~5%. (This figure is available in color in electronic form.) |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.