EDP Sciences logo
Subscriber Authentication Point
Search
Menu
Home All issues Volume 548 (December 2012) A&A, 548 (2012) L1 Full HTML
Free Access
Issue
A&A
Volume 548, December 2012
Article Number L1
Number of page(s) 8
Section Letters
DOI https://doi.org/10.1051/0004-6361/201219791
Published online 16 November 2012

© ESO, 2012

1. Introduction

For the first time in modern astrophysics, two space missions, Kepler and CoRoT, are providing accurate observations of solar-like oscillations for hundreds of main-sequence stars and thousands of red giant stars (Baglin et al. 2006; Borucki et al. 2009). CoRoT observes in the direction of the intersection between the equator and the Galactic plane. In each of these fields, CoRoT has identified many solar-type dwarf stars (Baglin et al. 2006). Another abundant class observed by CoRoT are giant stars. Intermediate between these two groups are the subgiants, a known rare class of objects. They have been accepted as an explicit stellar group in 1930 (Strömberg 1930). Until the 1950s they were not understood in terms of stellar evolution theory. An interesting review of the subgiant history can be found in Sandage et al. (2003). Theoretically, when stars exhaust their hydrogen in the core (turn-off), they leave the main sequence (MS), pass through the subgiant phase and become red giants. Studying subgiants is interesting for several reasons: they are particularly appropriate for dating purposes (Thorén et al. 2004), are associated with rotation periods (Prot), and can be useful in stellar gyrochronology. F-type subgiants are important for studying solar-like oscillations (Barban & Michel 2006). As stars evolve through the subgiant branch, their surface convection zone becomes deeper. The matter that resided below the surface convection zone at the MS is then exposed. From the subgiant phase to the red giant branch, the stellar radius increases at the same time that the convection zone deepens. It is the first dredge-up.

The rotation period of subgiant stars could constrain the interior angular momentum distribution and mixing in low-mass stars. Subgiant Prot measurements can teach us about the rotation of low-mass stars and by implication about the solar rotation as well. Subgiants are more evolved and slightly more luminous than the Sun. They are expected to rotate with Prot greater than the 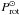Prot⊙\hbox{$P_{\mathrm {rot}}^{\odot} $}. Many of them have a convective core. The deepening of the convective layers has a major influence on the chemical abundance and chromospheric activity in this phase (do Nascimento et al. 2000, 2003, and references therein). Studies show that lithium abundance in subgiants agrees well with dilution predictions and reflects the well-known dilution process that occurs when the convective envelope deepens after turn-off (Iben 1967; do Nascimento et al. 2000). On the other hand, more massive cool subgiant stars show lithium depletion by up to two orders of magnitude before the start of dilution. The de Medeiros et al. (1997); Lèbre et al. (1999); do Nascimento et al. (2000) and Palacios et al. (2003) results agree with the findings by Balachandran (1990) and Burkhart & Coupry (1991) about a few slightly evolved field subgiants that originate from the hot side of the dip and show significant lithium depletion. As suggested by Vauclair (1991) and Charbonnel & Vauclair (1992), the additional lithium depletion from rotationally induced mixing (Charbonnel & Vauclair 1992; Charbonnel & Talon 1999) occurs early inside these stars when they are on the MS, even if its signature does not appear at the stellar surface at the age of the Hyades. This extra-mixing process is linked to rotation. If the Sun rotates as a solid body, it should have a Prot greater than 90 d when it will become a subgiant. The Pinsonneault et al. (1989) non standard models for subgiants imply a Prot of 50 d for subgiants. Clearly, a directly measured rotation period is needed to decide in this matter. Until now, the only available Prot for subgiants were inferred from chromospheric activity calibrations (Noyes et al. 1984) and are a matter of debate. We aim to give a quantitative answer based on direct measurements of Prot for selected CoRoT subgiants.

In this study we measured Prot for a sample of subgiants and present updated evolutionary models with an internal distribution of angular momentum to probe the expected Prot for the subgiant branch. We organize the paper as follows: we describe the observational sample and the Prot determination in Sect. 2. The models are presented in Sect. 3. The results are discussed in Sect. 4. We summarize our conclusions in Sect. 5.

2. Stellar sample and time series analysis

The focus of our study is a first analysis of the Prot for selected subgiants observed by CoRoT. For the instrument description and its operation readers are referred to Auvergne et al. (2009). We used the available public data level 2 (N2) light curves that are ready for scientific analysis. These light curves were delivered by the CoRoT pipeline after nominal corrections (Samadi et al. 2006). In the present analysis we used stars classified as subgiants by Gazzano et al. (2010). We chose only light curves with  ~150 d with a low contamination factor and high-quality photometry without systematic errors. Eventual discontinuities and long-term trends were corrected following a similar procedure as in Affer et al. (2012).

2.1. Time series analysis

To achieve the largest possible sample of subgiants with determined Prot, stars analyzed by Gazzano et al. (2010) that are in the CoRoT Exo-Dat database were checked for periodic modulation. To determine the rotational periods for our sample of subgiants, we used a combination of two procedures, the Lomb-Scargle (LS) algorithm (Scargle 1982), and the Plavchan periodogram (Plavchan et al. 2008). For time series in which the sampling is not uniformly distributed, the LS periodogram analysis is particularly suitable. The LS algorithm identifies sinusoidal periodic signals in time series such as pulsating variable stars. The Plavchan algorithm is a variant of the phase dispersion minimization (PDM) algorithm (Stellingwerf 1978) that does not use phase bins. It competently detects periodic time series shapes that are poorly described by the assumptions of other algorithms. This procedure is more computationally demanding than the LS analysis.

For each star, we applied the two procedures and then isolated the most significant periods of each method. For the LS algorithm, we computed the normalized power as a function of periods and then searched for peaks in the function. To decide whether there is a significant signal from a certain period in the power spectrum, the power at that period was linked to the false-alarm probability (FAP). This is the probability that a peak with a power z equal to, or higher than, the highest peak observed in the periodogram would appear anywhere in the considered frequency range in the presence of pure noise. We derived the FAP for all detected periods and only those with an FAP  < 0.000001 were considered as significant peaks. The FAP is given by FAP = 1− [1−exp(− z)] Ni, where Ni = −6.362 + 1.193N + 0.00098N2 is the number of independent frequencies, N is the number of data points and z the height of the peak (e.g., Horne & Baliunas 1986). For clumped data, Scholz & Eislöffel (2004) used Ni = N/2 for their first estimation of an FAP. These two different approaches do not result in a significant change of the FAP. The light curve coverage allows us to detect periods longer than 2 d and shorter than 100 d with a relevant FAP  <  0.000001. The uncertainties in Prot are determined by the frequency resolution in the power spectrum and the sampling error. The error of our measurement is defined by the probable error, which in turn is defined as 0.2865 FWHM (full-width at half-maximum of the peak), assuming a Gaussian statistics around the LS peak. The most significant periods are compared with models presented in Sect. 3. Our final work sample is composed of 30 subgiant stars. The derived periods and their respective errors are presented in Table A.1. In Fig. 2 we show the Lomb-Scargle periodogram (top), the phased curve (middle), and the Plavchan periodogram (bottom) for CoRoT ID 100570829. This is a representative subgiant star classified as a K0IV in the Exo-Dat (Deleuil et al. 2006, 2009; Meunier et al. 2007) andGazzano et al. (2010). The data we used were obtained during the CoRoT first long run (LRc01 and LRa01). The rotation periods for this target were derived from Lomb-Scargle and Plavchan periodograms analysis of the light curve, giving Prot = 84.2    ± 15.8 d with a FWHM of 55 d. The Prot uncertainty comes mainly from the time series limitation.

3. Evolutionary models

Our models1 were computed with the Toulouse-Geneva stellar evolution code (Hui-Bon-Hoa 2008). More details of the physics used in the models can be found in Richard et al. (1996, 2004), Hui-Bon-Hoa (2008), and do Nascimento et al. (2009) as well as in Appendix A. The initial composition follows the Grevesse & Noels (1993) mixture. The convection was treated according to the Böhm-Vitense (1958) formalism of the mixing length theory with a mixing length parameter α = l/Hp, where l is the mixing length and Hp the pressure height scale. The rotation-induced mixing due to meridional circulation and the transport of angular momentum due to rotationally induced instabilities are computed as described by Zahn (1992) and Talon & Zahn (1997) and takes into account differential rotation. The angular momentum distribution at a given time is a function of its previous history. As underlined by Pinsonneault et al. (1989), the initial conditions are critical for rotating models. The angular momentum loss from the disk-locking process is linked with stellar magnetic fields and remains poorly understood. The evolution of the angular momentum is computed with the Kawaler  (1988) prescription as in Eq. (A.1). Our solar model is calibrated to match the observed solar effective temperature, luminosity, and rotation at the solar age. The calibration is based on the Richard et al. (1996) prescription. For a 1.0 M⊙ star, we adjusted the mixing-length parameter α and the initial helium abundance Yini to reproduce the observed solar luminosity, and the radius at the solar age: L⊙ = 3.8515 ± 0.0055 × 1033  erg   s-1, R⊙ = 6.95749 ± 0.00241 × 1010  cm, and t⊙ = 4.57 ± 0.02  Gyr (Richard et al. 2004). For the best-fit solar model, we obtained L = 3.8514 × 1033  erg   s-1 and R = 6.95750 × 1010  cm at an age t = 4.576  Gyr, with Yini = 0.277 and α = 1.72. The free parameters of the rotation-induced mixing determine the efficiency of the turbulent motions and are adjusted to produce a mixing that satisfies both the helium gradient below the surface convective zone, which improves the agreement between the model and seismic sound speed profiles, and the absence of beryllium destruction (see Appendix A for details). We used the initial angular momentum inferred by Pinsonneault et al. (1989) for the Sun J0 = 1.63 × 1050   g   cm2   s-1 and calibrated the angular momentum loss by requiring that the solar model has the solar rotation rate at the solar age. We obtained the solar surface rotation velocity v = 2.2   km   s-1 at the solar age. The models of 0.8, 1.0, 1.2, 1.5, and 1.8 solar masses (Fig. 1) were computed from the zero-age main sequence (ZAMS) to the top of the red giant branch (RGB) with the same calibration values as for the solar model. In these diagrams the asterisk indicates the evolutionary region where the subgiant branch starts, this point corresponds to the age of hydrogen exhaustion in stellar central regions. From Alonso et al. (1999) we calibrated Teff as function of (J − H) color index. For the selected objects we obtained (J − H) 2MASS photometry from CoRoT Exo-Dat and applied the pseudo-colors C3 reddening correction as described by Catelan et al. (2011) to obtain the reddening-free index (J − H)C3.

thumbnail Fig. 1

Log(g) − Teff diagram. Evolutionary models for [Fe/H] = 0.0 and for 0.8, 1.0, 1.2, 1.5, and 1.8 solar masses. The color pallet denotes the evolution of rotation period for each model. The Sun is flagged and the beginning of the subgiant branch (turn-off point) is marked with an asterisk.

thumbnail Fig. 2

CoRoT ID 100570829. In the top panel we show the LS periodogram with the Prot = 84.2 d derived with the LS algorithm. In the middle panel we show the phased curve for this Prot. In the bottom panel we show the Plavchan periodogram.

thumbnail Fig. 3

Rotation period evolution from the main sequence to the giant branch as a function of (J − H)C3 index. The models are shown for [Fe/H] = 0 and different stellar masses computed with differential rotation. Filled circles stand for rotational periods determined as described in Sect. 2. The beginning of the subgiant branch (turn-off point) is flagged with an asterisk.

4. Results

The Prot measured from light curves for subgiants are shown in Fig. 3. These Prot measurements indicate the range of 30 to 100 d for subgiants in agreement with expected Prot from models. The Prot for subgiants with M < 1.8   M⊙ increases slightly until the bottom of the RGB. Figure 4 compares the expected Prot from a 1.0 M⊙ model rotating as a solid body with a 1.0 M⊙ rotating differentially. Open circles represent Prot for subgiants determined by Lovis et al. (2011). Our models follow the same prescription for the angular momentum loss as Pinsonneault et al. (1989) and an updated physics (opacities, equation of state, meridional circulation, and shear instabilities). The metallicity effect on the evolution of the rotational period for models with [Fe/H] =  ±0.3 dex is lower than the LS intrinsical error. On the subgiant branch, the separations of solid-body rotation models and models with internal angular momentum distribution are satisfactorily distinguished by the measured rotation periods from CoRoT light curves. Thus, we emphasize that this range of rotation periods for subgiants reinforces the scene of a strong radial differential rotation in depth at the main sequence or a fast core rotating in the subgiant branch. The Prot in the subgiant phase is driven by the deepening of the convective zone, which extracts angular momentum from the radial differential rotation reservoir. From the angular momentum conservation, this extraction compensates for the increase of the momentum of inertia due to the stellar radius enhancement. It causes the difference between the two models shown in Fig. 4. Another interesting fact is that subgiants present a chromospheric activity lower than main-sequence stars with the same mass (Lovis et al. 2011), even if its convective zone is deeper than their progenitor. This scenario contrasts with the suggestion of the magnetic breaking as the root cause of the low rotation of subgiants (Gray & Nagar 1985).

thumbnail Fig. 4

Rotation period evolution from the main sequence to the giant branch as a function of the (J − H)C3 index. The models are shown for [Fe/H] = 0 and 1 M⊙. The dashed line represents the rotation period evolution for a solid-body model. The solid line represents the computed model with differential rotation. Open circles represent subgiants with masses of about one solar mass and rotational periods determined from the rotation-activity relation by Lovis et al. (2011). Asterisk as in Fig. 3.

5. Conclusion

We have reported Prot for 30 subgiants observed by CoRoT. These Prot combined with evolutionary models helped us to more tightly constrain the angular momentum evolution for evolved stars, which is inaccessible to direct observations. Our Prot agree well with the range of periods determined from the activity modulation studies of subgiants. We showed that subgiants present Prot ranging from 30 to 100 d in the mass range from 0.8 to 1.8 solar masses. This work presents a first step in addressing the study of the Prot of the subgiants. Our models agree with rotational period measurements for subgiant stars. The rotation period range for subgiants reinforces the scene of a differential

rotation in depth or a fast-core rotating. This result also agrees with the findings by Mosser et al. (2012), who observed that rotational splittings and core rotation significantly slows down during the RGB.

Online material

Appendix A: Description of the physics adopted for the transport of internal angular momentum

In addition to the input described in Sect. 3., we provide here more details on the physics adopted for the transport of internal angular momentum for the present modeling. We used the same approach as Pinsonneault et al. (1989) after updating the treatment of the instabilities relevant to the transport of angular momentum according to Zahn (1992) and Talon & Zahn (1997).

Initial conditions: The rotational properties are strongly influenced by the pre-main-sequence phase. Kawaler (1987) determined the initial angular momentum for the Sun as J0 = 1.63 × 1050  g   cm2   s-1.

Angular momentum loss: Kawaler  (1988) described the angular momentum loss for stars with an outer convective envelope as 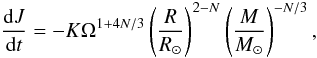dJdt=−KΩ1+4N/3(RR⊙)2−N(MM⊙)−N/3,\appendix \setcounter{section}{1} \begin{equation} \frac{{\rm d}J}{{\rm d}t} = -K \Omega^{1+4N/3} \left(\frac{R}{R_{\odot}}\right)^{2-N} \left(\frac{M}{M_{\odot}}\right)^{-N/3}, % \label{equ:kawaler} \end{equation}(A.1)with Ω the angular velocity and K a constant that combines scale factors for the wind velocity and magnetic field strength. This is adjusted to give the solar surface rotation velocity at the solar age. N denotes the wind index and is a measure of the magnetic geometry. N = 3/2 for the Sun. The mass loss dependence rate is very weak, and we assumed the rate Ṁ to be 10-14  M⊙   yr-1.

Transport of matter and angular momentum: The redistribution of matter and angular momentum is carried out by dynamical instabilities (convection and dynamical shear mainly) that occur on a time scale much shorter than the evolutionary time scale, and also by secular instabilities (Eddington circulation and secular shear) with a similar or longer time scale. The Eddington meridional circulation (Eddington 1926), is a large-scale mass motion due to thermic gradients caused by rotation. The vertical velocity Ur of this circulation is related to the divergence of the radiation flux (Eddington 1925; Sweet 1950; Zahn 1987). In a uniformly rotating star, Ur has the following analytical form: 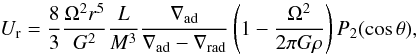Ur=83Ω2r5G2LM3∇ad∇ad−∇rad(1−Ω22πGρ)P2(cosθ),\appendix \setcounter{section}{1} \begin{equation} U_{\rm r} = \frac{8}{3} \frac{\Omega^2 r^5}{G^2} \frac{L}{M^3} \frac{\nabla_{\mathrm{ad}}}{\nabla_{\mathrm{ad}} - \nabla_{\mathrm{rad}}} \left( 1 - \frac{\Omega^2}{2 \pi G \rho} \right) P_2 (\cos \theta), \end{equation}(A.2)where Ω is the angular velocity, r the mean radius, and ρ the density of the considered equipotential, L and M are the luminosity and the mass at this location, G is the gravitational constant, ∇ad and ∇rad are the adiabatic and radiative gradients; P2(cosθ) is the second-order Legendre polynomial in which θ is the colatitude. This flow advects angular momentum and thereby induces differential rotation.

The rotation state is then a result from the balance between meridional advection and turbulent stresses. Shear instabilities ensure that the angular velocity is constant in equipotential surfaces. The turbulent viscosity is assumed to be anisotropic and dominant in the horizontal over the vertical direction. Horizontal turbulent motions work against the advection of chemicals by the meridian flow, which homogenizes horizontal layers. The vertical transport of matter is accordingly treated as a diffusion process: 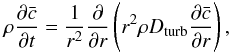ρ∂c̅∂t=1r2∂∂r(r2ρDturb∂c̅∂r),\appendix \setcounter{section}{1} \begin{equation} \rho \frac{\partial \bar{c}}{\partial t} = \frac{1}{r^{2}} \frac{\partial}{\partial r} \left( r^{2} \rho D_{\rm turb} \frac{\partial \bar{c}}{\partial r} \right) , \end{equation}(A.3)with ρ being the density, r the radial coordinate, 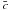\hbox{$\bar{c}$} the mean concentration diffusing vertically, and

Dturb=Dv+[rUr(r)]230Dh$$D_{\rm turb} = D_{\rm v} + \frac{[r U_{\rm r} (r)]^{2}}{30 D_{\rm h}}$$the turbulent diffusion coefficient expressed from the vertical and horizontal diffusion coefficients, valid when Dh ≫ DvUr(r) is the amplitude of the vertical component of the circulation velocity. If we assume that the meridional velocity and the turbulent diffusion coefficients are correlated (Zahn 1992), we have

The free parameters αturb and Ch are adjusted in our models to reproduce the solar proprieties affected by rotation-induced mixing. The values found in the calibration presented in Sect. 3 are αturb = 1 and Ch = 9000.

The transport of angular momentum is governed by an advection/diffusion equation: ∂∂t[ρr2Ω]=15r2∂∂r[ρr4ΩUr]+1r2∂∂r[ρνvr4∂Ω∂r],\appendix \setcounter{section}{1} \begin{equation} \frac{\partial}{\partial t} \left[ \rho r^{2} \Omega \right] = \frac{1}{5r^{2}} \frac{\partial}{\partial r} \left[ \rho r^{4} \Omega U_{\rm r} \right] + \frac{1}{r^{2}} \frac{\partial}{\partial r} \left[ \rho \nu_v r^{4} \frac{\partial \Omega}{\partial r} \right], \end{equation}(A.4)with Ω the angular velocity and νv the vertical turbulent viscosity. 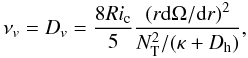We use the prescription given by Talon & Zahn (1997): νv=Dv=8Ric5(rdΩ/dr)2NT2/(κ+Dh),\appendix \setcounter{section}{1} \begin{equation} \nu_v = D_v = \frac{8 Ri_{\rm c}}{5} \frac{(r {\rm d} \Omega/{\rm d}r)^{2}}{N_{\rm T}^{2}/(\kappa+D_{\rm h})}, \end{equation}(A.5)taking into account the homogenizing effect of the horizontal diffusion (Dh) on the restoring force caused by the gradient of molecular weight. 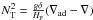NT2=gδHP(∇ad−∇)\hbox{$N_{\rm T}^{2} = \frac{g \delta}{H_{\rm P}} (\nabla_{\rm ad} - \nabla)$} is the Brunt-Väisälä frequency, κ the radiative diffusivity, and Ric ~ 1/4 is the critical Richardson number (see Talon et al. 1997). The horizontal shear is sustained by the advection of momentum: Dh=rUrCh[13dlnρr2Urdlnr−12dlnρr2Ωdlnr]·\appendix \setcounter{section}{1} \begin{equation} D_{\rm h} = \frac{rU_{\rm r}}{C_{\rm h}} \left[ \frac{1}{3} \frac{{\rm d}\! \ln \rho r^{2} U_{\rm r}}{{\rm d}\! \ln r} - \frac{1}{2} \frac{{\rm d} \!\ln \rho r^{2} \Omega}{{\rm d} \!\ln r} \right]\cdot \end{equation}(A.6)

Table A.1

Subgiant sample.

thumbnail Fig. A.1

Plot of selected light curves before and after the removal of the discontinuities and/or long-term trends.

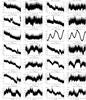thumbnail Fig. A.2

Plot of selected light curves before and after the removal of the discontinuities and/or long-term trends.

Acknowledgments

We would like to thank the Exo-Dat staff. This work has been supported by the CNPq Brazilian Agency CNPq/PQ fellowship. J.D.N.Jr. dedicates this work to his children, Malu and Léo. An anonymous referee is acknowledged for helpful suggestions.

References

  1. Affer, L., Micela, G., Favata, F., & Flaccomio, E. 2012, MNRAS, 424, 11 [NASA ADS] [CrossRef] [Google Scholar]
  2. Alonso, A., Arribas, S., & Martínez-Roger, C. 1999, Ap&SS, 140, 261 [Google Scholar]
  3. Auvergne, M., Bodin, P., Boisnard, L., et al. 2009, A&A, 506, 411 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  4. Baglin, A., Auvergne, M., Barge, P., et al. 2006, in ESA SP 1306, eds. M. Fridlund, A. Baglin, J. Lochard, & L. Conroy, 33 [Google Scholar]
  5. Balachandran, S. 1990, ApJ, 354, 310 [NASA ADS] [CrossRef] [Google Scholar]
  6. Barban, C., & Michel, E. 2000, The Third MONS Workshop, mons.proc, 33 [Google Scholar]
  7. Böhm-Vitense, E. 1958, ZAp, 46, 108 [NASA ADS] [Google Scholar]
  8. Borucki, W. J., Koch, D., Jenkins, J., et al. 2009, Science, 325, 709 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
  9. Burkhart, C., & Coupry, M. F. 1991, A&A, 249, 205 [NASA ADS] [Google Scholar]
  10. Catelan, M., Minniti, D., Lucas, P., et al. 2011, in Carnegie O. Astrop. Series, 5, 145 [Google Scholar]
  11. Charbonnel, C., & Talon, S. 1999, A&A, 351, 635 [NASA ADS] [Google Scholar]
  12. Charbonnel, C., & Vauclair, S. 1992, A&A, 265, 55 [NASA ADS] [Google Scholar]
  13. Deleuil, M., Bouret, J. C., Lecavelier Des Etangs, A., et al. 2006, ASPC, 348, 297 [NASA ADS] [Google Scholar]
  14. Deleuil, M., Meunier, J.-C., Moutou, C., et al. 2009, AJ, 138, 649 [NASA ADS] [CrossRef] [Google Scholar]
  15. De Medeiros, J. R., do Nascimento, J. D., Jr., & Mayor, M. 1997, A&A, 317, 701 [NASA ADS] [Google Scholar]
  16. do Nascimento, J. D., Jr.,Charbonnel, C., Lèbre, A., et al. 2000, A&A, 357, 931 [NASA ADS] [Google Scholar]
  17. do Nascimento, J. D., Jr., Canto Martins, B. L., Melo, C. H. F., et al. 2003, A&A, 405, 723 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  18. do Nascimento, J. D., Jr.,Castro, M., Meléndez, J., et al. 2009, A&A, 501, 687 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  19. Eddington, A. S. 1925, Observatory, 48, 78 [Google Scholar]
  20. Eddington, A. S. 1926, in The Int. Const. of the Stars (1959 New York: Dover) [Google Scholar]
  21. Gazzano, J. C., de Laverny, P., Deleuil, M., et al. 2010, A&A, 523, 91 [Google Scholar]
  22. Gray, D. F., & Nagar, P. 1985, ApJ, 298, 756 [NASA ADS] [CrossRef] [Google Scholar]
  23. Grevesse, N., & Noels, A. 1993, Origin and Evolution of the Elements, eds. N. Prantzos, E. Vangioni-Flam, & M. Cassé (Cambridge Univ. Press), 15 [Google Scholar]
  24. Horne, J. H., & Baliunas, S. L. 1986, ApJ, 302, 757 [NASA ADS] [CrossRef] [Google Scholar]
  25. Hui-Bon-Hoa, A. 2008, Ap&SS, 316, 55 [NASA ADS] [CrossRef] [Google Scholar]
  26. Iben I. Jr. 1967, ApJ, 147, 624 [NASA ADS] [CrossRef] [Google Scholar]
  27. Kawaler, S. D. 1987, Pub. A.S.P, 99, 1322 [Google Scholar]
  28. Kawaler, S. D. 1988, ApJ, 333, 236 [NASA ADS] [CrossRef] [Google Scholar]
  29. Lèbre, A., de Laverny, P., de Medeiros, J. R., et al. 1999, A&A, 345, 936 [NASA ADS] [Google Scholar]
  30. Lovis, C., Dumusque, X., Santos, N. C., et al. 2011, A&A, submitted [arXiv:1107.5325] [Google Scholar]
  31. Meunier, J.-C., Deleuil, M., Moutou, C., et al. 2007, in Astron. Data A. Soft. and Sys. XVI, eds. R. A. Shaw, F. Hill, & D. J. Bell, ASP Conf. Ser., 376, 339 [Google Scholar]
  32. Mosser, B., Goupil, M. J., Belkacem, K., et al. 2012, A&A, 548, A10 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  33. Noyes, R. W., Hartmann, L. W., Baliunas, S. L., et al. 1984, ApJ, 279, 763 [NASA ADS] [CrossRef] [Google Scholar]
  34. Palacios, A., Talon, S., Charbonnel, C., et al. 2003, ApJ, 399, 603 [Google Scholar]
  35. Pinsonneault, M. H., Kawaler, S. D., Sofia, S., et al. 1989, ApJ, 338, 424 [NASA ADS] [CrossRef] [Google Scholar]
  36. Plavchan, P., Jura, M., Kirkpatrick, J. D., et al. 2008, ApJS, 175, 191 [NASA ADS] [CrossRef] [Google Scholar]
  37. Richard, O., Vauclair, S., Charbonnel, C., et al. 1996, A&A, 312, 1000 [NASA ADS] [Google Scholar]
  38. Richard, O., Théado, S., & Vauclair, S. 2004, Sol. Phys., 220, 243 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
  39. Samadi, R., Fialho, F., Costa, J. E. S., et al. 2006, ESA SP, 1306, 317 [Google Scholar]
  40. Sandage, A., Lubin, L. M., & VandenBerg, D. A. 2003, PASP, 151, 187 [Google Scholar]
  41. Scargle, J. D. 1982, ApJ, 263, 835 [NASA ADS] [CrossRef] [Google Scholar]
  42. Scholz, A., & Eislöffel, J. 2004, A&A, 419, 249 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  43. Stellingwerf, R. F. 1978, ApJ, 224, 953 [NASA ADS] [CrossRef] [Google Scholar]
  44. Strömberg, G. 1930, ApJ, 71, 175 [NASA ADS] [CrossRef] [Google Scholar]
  45. Sweet, P. A. 1950, MNRAS, 110, 548 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
  46. Talon, S., & Zahn, J.-P. 1997, A&A, 317, 749 [Google Scholar]
  47. Talon, S., Zahn, J.-P., Maeder, A., & Meynet, G. 1997, A&A, 322, 209 [NASA ADS] [Google Scholar]
  48. Thorén, P., Edvardsson, B., & Gustafsson, B. 2004, A&A, 425, 187 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  49. Vauclair, S. 1991, IAUS, 145, 327V [NASA ADS] [Google Scholar]
  50. Zahn, J.-P. 1987, in Summer School in Astrophysics Fluid Dynamics (Les Houches: Elsevier Sci. Publ.) [Google Scholar]
  51. Zahn, J.-P. 1992, A&A, 265, 115 [NASA ADS] [Google Scholar]

All Tables

Table A.1

Subgiant sample.

In the text

All Figures

thumbnail Fig. 1

Log(g) − Teff diagram. Evolutionary models for [Fe/H] = 0.0 and for 0.8, 1.0, 1.2, 1.5, and 1.8 solar masses. The color pallet denotes the evolution of rotation period for each model. The Sun is flagged and the beginning of the subgiant branch (turn-off point) is marked with an asterisk.
In the text
thumbnail Fig. 2

CoRoT ID 100570829. In the top panel we show the LS periodogram with the Prot = 84.2 d derived with the LS algorithm. In the middle panel we show the phased curve for this Prot. In the bottom panel we show the Plavchan periodogram.
In the text
thumbnail Fig. 3

Rotation period evolution from the main sequence to the giant branch as a function of (J − H)C3 index. The models are shown for [Fe/H] = 0 and different stellar masses computed with differential rotation. Filled circles stand for rotational periods determined as described in Sect. 2. The beginning of the subgiant branch (turn-off point) is flagged with an asterisk.
In the text
thumbnail Fig. 4

Rotation period evolution from the main sequence to the giant branch as a function of the (J − H)C3 index. The models are shown for [Fe/H] = 0 and 1 M⊙. The dashed line represents the rotation period evolution for a solid-body model. The solid line represents the computed model with differential rotation. Open circles represent subgiants with masses of about one solar mass and rotational periods determined from the rotation-activity relation by Lovis et al. (2011). Asterisk as in Fig. 3.
In the text
thumbnail Fig. A.1

Plot of selected light curves before and after the removal of the discontinuities and/or long-term trends.
In the text
thumbnail Fig. A.2

Plot of selected light curves before and after the removal of the discontinuities and/or long-term trends.
In the text

Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.

Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.

Initial download of the metrics may take a while.