| Issue |
A&A
Volume 548, December 2012
|
|
|---|---|---|
| Article Number | L1 | |
| Number of page(s) | 8 | |
| Section | Letters | |
| DOI | https://doi.org/10.1051/0004-6361/201219791 | |
| Published online | 16 November 2012 | |
Online material
Appendix A: Description of the physics adopted for the transport of internal angular momentum
In addition to the input described in Sect. 3., we provide here more details on the physics adopted for the transport of internal angular momentum for the present modeling. We used the same approach as Pinsonneault et al. (1989) after updating the treatment of the instabilities relevant to the transport of angular momentum according to Zahn (1992) and Talon & Zahn (1997).
Initial conditions: The rotational properties are strongly influenced by the pre-main-sequence phase. Kawaler (1987) determined the initial angular momentum for the Sun as J0 = 1.63 × 1050 g cm2 s-1.
Angular momentum loss: Kawaler (1988) described the angular momentum loss for stars with an outer convective envelope as 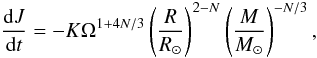 (A.1)with Ω the angular velocity and K a constant that combines scale factors for the wind velocity and magnetic field strength. This is adjusted to give the solar surface rotation velocity at the solar age. N denotes the wind index and is a measure of the magnetic geometry. N = 3/2 for the Sun. The mass loss dependence rate is very weak, and we assumed the rate Ṁ to be 10-14 M⊙ yr-1.
(A.1)with Ω the angular velocity and K a constant that combines scale factors for the wind velocity and magnetic field strength. This is adjusted to give the solar surface rotation velocity at the solar age. N denotes the wind index and is a measure of the magnetic geometry. N = 3/2 for the Sun. The mass loss dependence rate is very weak, and we assumed the rate Ṁ to be 10-14 M⊙ yr-1.
Transport of matter and angular momentum: The redistribution of matter and angular momentum is carried out by dynamical instabilities (convection and dynamical shear mainly) that occur on a time scale much shorter than the evolutionary time scale, and also by secular instabilities (Eddington circulation and secular shear) with a similar or longer time scale. The Eddington meridional circulation (Eddington 1926), is a large-scale mass motion due to thermic gradients caused by rotation. The vertical velocity Ur of this circulation is related to the divergence of the radiation flux (Eddington 1925; Sweet 1950; Zahn 1987). In a uniformly rotating star, Ur has the following analytical form: 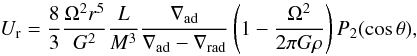 (A.2)where Ω is the angular velocity, r the mean radius, and ρ the density of the considered equipotential, L and M are the luminosity and the mass at this location, G is the gravitational constant, ∇ad and ∇rad are the adiabatic and radiative gradients; P2(cosθ) is the second-order Legendre polynomial in which θ is the colatitude. This flow advects angular momentum and thereby induces differential rotation.
(A.2)where Ω is the angular velocity, r the mean radius, and ρ the density of the considered equipotential, L and M are the luminosity and the mass at this location, G is the gravitational constant, ∇ad and ∇rad are the adiabatic and radiative gradients; P2(cosθ) is the second-order Legendre polynomial in which θ is the colatitude. This flow advects angular momentum and thereby induces differential rotation.
The rotation state is then a result from the balance between meridional advection and turbulent stresses. Shear instabilities ensure that the angular velocity is constant in equipotential surfaces. The turbulent viscosity is assumed to be anisotropic and dominant in the horizontal over the vertical direction. Horizontal turbulent motions work against the advection of chemicals by the meridian flow, which homogenizes horizontal layers. The vertical transport of matter is accordingly treated as a diffusion process: 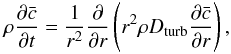 (A.3)with ρ being the density, r the radial coordinate,
(A.3)with ρ being the density, r the radial coordinate, 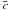 the mean concentration diffusing vertically, and
the mean concentration diffusing vertically, and
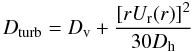 the turbulent diffusion coefficient expressed from the vertical and horizontal diffusion coefficients, valid when Dh ≫ DvUr(r) is the amplitude of the vertical component of the circulation velocity. If we assume that the meridional velocity and the turbulent diffusion coefficients are correlated (Zahn 1992), we have
the turbulent diffusion coefficient expressed from the vertical and horizontal diffusion coefficients, valid when Dh ≫ DvUr(r) is the amplitude of the vertical component of the circulation velocity. If we assume that the meridional velocity and the turbulent diffusion coefficients are correlated (Zahn 1992), we have
The free parameters αturb and Ch are adjusted in our models to reproduce the solar proprieties affected by rotation-induced mixing. The values found in the calibration presented in Sect. 3 are αturb = 1 and Ch = 9000.
The transport of angular momentum is governed by an advection/diffusion equation: 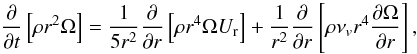 (A.4)with Ω the angular velocity and νv the vertical turbulent viscosity. We use the prescription given by Talon & Zahn (1997):
(A.4)with Ω the angular velocity and νv the vertical turbulent viscosity. We use the prescription given by Talon & Zahn (1997): 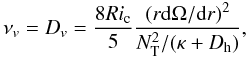 (A.5)taking into account the homogenizing effect of the horizontal diffusion (Dh) on the restoring force caused by the gradient of molecular weight.
(A.5)taking into account the homogenizing effect of the horizontal diffusion (Dh) on the restoring force caused by the gradient of molecular weight. 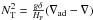 is the Brunt-Väisälä frequency, κ the radiative diffusivity, and Ric ~ 1/4 is the critical Richardson number (see Talon et al. 1997). The horizontal shear is sustained by the advection of momentum:
is the Brunt-Väisälä frequency, κ the radiative diffusivity, and Ric ~ 1/4 is the critical Richardson number (see Talon et al. 1997). The horizontal shear is sustained by the advection of momentum: 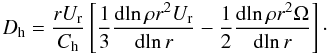 (A.6)
(A.6)
Subgiant sample.
 |
Fig. A.1
Plot of selected light curves before and after the removal of the discontinuities and/or long-term trends. |
| Open with DEXTER | |
 |
Fig. A.2
Plot of selected light curves before and after the removal of the discontinuities and/or long-term trends. |
| Open with DEXTER | |
© ESO, 2012
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


