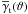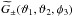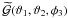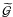| Issue |
A&A
Volume 548, December 2012
|
|
|---|---|---|
| Article Number | A102 | |
| Number of page(s) | 14 | |
| Section | Cosmology (including clusters of galaxies) | |
| DOI | https://doi.org/10.1051/0004-6361/201218993 | |
| Published online | 30 November 2012 | |
Towards an understanding of third-order galaxy-galaxy lensing
Argelander-Institut für Astronomie, Universität Bonn, Auf dem Hügel 71, 53121 Bonn, Germany
e-mail: psimon@astro.uni-bonn.de
Received: 8 February 2012
Accepted: 17 October 2012
Context. Third-order galaxy-galaxy lensing (G3L) is a next generation galaxy-galaxy lensing (GGL) technique that either measures the excess shear about lens pairs or the excess shear-shear correlations about lenses. From their definition it is clear that these statistics assess the three-point correlations between galaxy positions and projected matter density.
Aims. For future applications of these novel statistics, we aim at a more intuitive understanding of G3L to isolate the main features that possibly can be measured.
Methods. We construct a toy model (“isolated lens model”; ILM) for the distribution of galaxies and associated matter to determine the measured quantities of the two G3L correlation functions and traditional GGL in a simplified context. The ILM presumes single lens galaxies to be embedded inside arbitrary matter haloes that, however, are statistically independent (“isolated”) from any other halo or lens position. Clusters of galaxies and their common cluster matter haloes are a consequence of clustering smaller haloes. In particular, the average mass-to-galaxy number ratio of clusters of any size cannot change in the ILM.
Results. GGL and galaxy clustering alone cannot distinguish an ILM from any more complex scenario. The lens-lens-shear correlator in combination with second-order statistics enables us to detect deviations from a ILM, though. This can be quantified by a difference signal defined in the paper. We demonstrate with the ILM that this correlator picks up the excess matter distribution about galaxy pairs inside clusters, whereas pairs with lenses well separated in redshift only suppress the overall amplitude of the correlator. The amplitude suppression can be normalised. The lens-lens-shear correlator is sensitive to variations among matter haloes. In principle, it could be devised to constrain the ellipticities of haloes, without the need for luminous tracers, or maybe even random halo substructure.
Key words: gravitational lensing: weak / galaxies: halos / large-scale structure of Universe
© ESO, 2012
1. Introduction
Gravitational lensing (Schneider 2006, for a recent review) has established itself as valuable tool for cosmology to investigate the large-scale distribution of matter and its relation to visible tracers such as galaxies. In the currently favoured standard model of cosmology (e.g., Peebles 1993; Dodelson 2003), the major fraction of matter is a non-baryonic cold dark matter component, i.e., matter with non-relativistic velocities during the epoch of cosmic structure formation. In this situation, gravitational lensing is an excellent probe as it is sensitive to all matter as long as it interacts gravitationally.
The main observable in lensing is the distortion of shapes of galaxy images, in the weak lensing regime mainly “shear”, by the intervening inhomogeneous gravitational potential that is traversed by light bundles from the galaxy. Over the course of the past decade, applications of the gravitational lensing effect have come of age. To name a few results (Bartelmann 2010, and references therein), it was used to map the dark matter distribution, to study the matter density profiles in galaxy clusters and to determine their masses, to measure the relation between the galaxy and dark matter distribution (the so-called galaxy bias), to constrain the total matter density of the Universe and its fluctuation power spectrum, and very recently to gather independent evidence for the overall accelerated expansion of the cosmos (Schrabback et al. 2010).
Of particular interest for this paper is the so-called galaxy-galaxy lensing (GGL) technique where positions of foreground galaxies (“lenses”) are correlated with the (weak lensing) shear on background galaxy images (“sources”). Thereby, statistical information on the projected matter distribution around lens galaxies can be extracted. Since the first attempt by Tyson et al. (1984) and the first detection (Brainerd et al. 1996; Griffiths et al. 1996) of this effect, GGL nowadays is a widely applied robust method to study the galaxy-matter connection (Fischer et al. 2000; McKay et al. 2001; Guzik & Seljak 2002; Hoekstra et al. 2002, 2004; Pen et al. 2003; Seljak & Warren 2004; Sheldon et al. 2004; Mandelbaum et al. 2005; Kleinheinrich et al. 2005; Mandelbaum et al. 2006b,a; Simon et al. 2007; Parker et al. 2007; van Uitert et al. 2011). The traditional and hitherto mainly employed approach (GGL hereafter) is to correlate the position of one lens with the shear of one source galaxy.
Schneider & Watts (2005, SW05 hereafter) advanced the traditional GGL by considering a new set of three-point correlation functions that either involves two lenses and one source (“correlator  ”) or two sources and one lens (“correlator G±”). Both correlators are tools to directly study higher-order correlations between galaxies and the surrounding matter field. In the literature, this technique is termed 3rd-order galaxy-galaxy lensing or galaxy-galaxy-galaxy lensing (G3L). There are alternative but mathematically equivalent ways to express these statistics, e.g., the aperture statistics
”) or two sources and one lens (“correlator G±”). Both correlators are tools to directly study higher-order correlations between galaxies and the surrounding matter field. In the literature, this technique is termed 3rd-order galaxy-galaxy lensing or galaxy-galaxy-galaxy lensing (G3L). There are alternative but mathematically equivalent ways to express these statistics, e.g., the aperture statistics 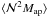 and
and 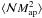 instead of the three-point correlation functions G± and
instead of the three-point correlation functions G± and  (SW05, Simon et al. 2008). In practical measurements usually the aperture statistics are preferred, as they automatically remove unconnected 2nd-order contributions in estimators of the statistics and allow one to separate E-modes from B-modes or parity modes, of which the latter two cannot be generated by gravitational lensing as leading order effect. In this paper, we focus on the E-modes in the correlators
(SW05, Simon et al. 2008). In practical measurements usually the aperture statistics are preferred, as they automatically remove unconnected 2nd-order contributions in estimators of the statistics and allow one to separate E-modes from B-modes or parity modes, of which the latter two cannot be generated by gravitational lensing as leading order effect. In this paper, we focus on the E-modes in the correlators  and G±.
and G±.
G3L has already been measured in contemporary lensing surveys, such as the Red-Sequence Cluster Survey (Simon et al. 2008), and will therefore presumably be routinely measured with ongoing surveys such as KiDS1, Pan-STARRS2, DES3, or in the future surveys Euclid4 and LSST5. The prospects of learning more on the galaxy-matter relation or new observational tests for theoretical galaxy models (e.g. Weinberg et al. 2004; Bower et al. 2006; De Lucia et al. 2007) with G3L are thus quite promising.
The main obstacle for exploiting the new G3L statistics is their physical interpretation. It is clear from the definition that  quantifies the shear signal (or projected matter density) in excess of purely randomly distributed lenses, picking up only signal from clustered lens pairs (e.g., Johnston 2006), and that G± is a two-point correlation function of shear associated with matter physically close to lenses. It is unclear, however, what physical information this translates to and what new feature may be contained in G3L that may be missing or is degenerate in traditional GGL. To elucidate these new statistics and to pave the way for new applications of G3L, we conceive here a simplistic model for the distribution of lenses and matter: the ILM. Then G3L is flashed out in the light of this model. For the definition of quantities relevant for weak gravitational lensing, we refer the reader to Bartelmann & Schneider (2001). The mathematical machinery of a halo model expansion devised in the calculations is very similar to Scherrer & Bertschinger (1991), although used in a different physical context.
quantifies the shear signal (or projected matter density) in excess of purely randomly distributed lenses, picking up only signal from clustered lens pairs (e.g., Johnston 2006), and that G± is a two-point correlation function of shear associated with matter physically close to lenses. It is unclear, however, what physical information this translates to and what new feature may be contained in G3L that may be missing or is degenerate in traditional GGL. To elucidate these new statistics and to pave the way for new applications of G3L, we conceive here a simplistic model for the distribution of lenses and matter: the ILM. Then G3L is flashed out in the light of this model. For the definition of quantities relevant for weak gravitational lensing, we refer the reader to Bartelmann & Schneider (2001). The mathematical machinery of a halo model expansion devised in the calculations is very similar to Scherrer & Bertschinger (1991), although used in a different physical context.
The structure of the paper lays out as follows. Section 2 introduces our model and derives the tangential shear about a lens, the GGL signal, expected from this description. Section 3 moves on to calculate the lens-lens-shear or  correlator for this specific scenario. Section 4 does the same for the lens-lens-shear or G± correlator. The final Sect. 5 summarises the main conclusions drawn in the preceding sections. In the following sections, we are introducing a number of symbols that are listed in Table 1 for clarity.
correlator for this specific scenario. Section 4 does the same for the lens-lens-shear or G± correlator. The final Sect. 5 summarises the main conclusions drawn in the preceding sections. In the following sections, we are introducing a number of symbols that are listed in Table 1 for clarity.
2. The isolated lens model and galaxy-galaxy lensing
List of symbols used in the paper and their meaning.
Here we lay out a simple model for the distribution of matter and galaxies inside it. This model is founded on the assumption that lenses are embedded inside a matter halo that generates the shear profile γh(θ;α) acting upon a background source, where θ is the separation vector from the centroid of the galaxy, and α denotes a set of intrinsic halo parameters that control the matter density profile of the halo. Importantly, the intrinsic parameters are statistically independent of the intrinsic halo parameters of any other halo or the separations of other lenses. We hence coin lenses and their host haloes in this scenario “isolated”. In this sense, this is a very crude halo model representation (Cooray & Sheth 2002) of the lens and matter distribution, assuming for simplicity that every halo is occupied by exactly one (lens) galaxy. Notice that matter which is statistically independent of the lenses does not need to be accounted for, as this would not contribute to a galaxy-matter cross-correlation function, although it certainly would affect the noise in a measurement.
In the following, 2D positions on the flat sky are, for convenience, denoted by complex numbers θ = θ1 + iθ2 where θ1 (θ2) is the position in direction of the x(y)-axis. By 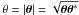 we denote the modulus of θ. Likewise the Cartesian shear 2-spinor γc = γ1 + iγ2 is denoted as complex number. We define the tangential, γt, and cross, γ × , shear of γc(θ) relative to the origin by
we denote the modulus of θ. Likewise the Cartesian shear 2-spinor γc = γ1 + iγ2 is denoted as complex number. We define the tangential, γt, and cross, γ × , shear of γc(θ) relative to the origin by 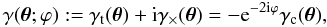 (1)where ϕ is the polar angle of θ.
(1)where ϕ is the polar angle of θ.
 |
Fig. 1 Illustration of the isolated lens model. Galaxies are depicted by black pixels, their matter haloes as red disks. For simplicity all haloes are identical in this visualisation. Left panel: lenses are distributed randomly on the sky. Right panel: lenses cluster to produce clumps with a common matter envelope, yet still described as sums of individual haloes. On the statistical level, this clumping is quantified by non-vanishing 2nd-order and 33d-order correlation functions ω and Ω, respectively. |
2.1. Isolated lens model
Within the isolated lens model (ILM), the number density distribution of lenses on the (flat) sky with area A is 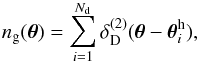 (2)where
(2)where 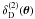 is the Dirac delta function, and the resulting shear field is
is the Dirac delta function, and the resulting shear field is 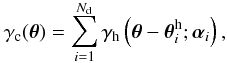 (3)sticking a shear profile to every of the Nd lens position
(3)sticking a shear profile to every of the Nd lens position 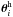 . The shear profile is directly related to the projected matter density about the lens. In the following we will use the lens number density contrast
. The shear profile is directly related to the projected matter density about the lens. In the following we will use the lens number density contrast 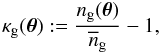 (4)where
(4)where 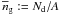 is the mean number density of lenses within the area A. For the 2nd-order angular clustering correlation function of lenses on the sky (e.g. Peebles 1980), we employ the function
is the mean number density of lenses within the area A. For the 2nd-order angular clustering correlation function of lenses on the sky (e.g. Peebles 1980), we employ the function 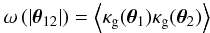 (5)with θij: = θi − θj being the separation vector of two positions. A value ω(θ12) > 0 expresses an excess of galaxy pairs at separation θ12 compared to a purely random distribution.
(5)with θij: = θi − θj being the separation vector of two positions. A value ω(θ12) > 0 expresses an excess of galaxy pairs at separation θ12 compared to a purely random distribution.
The ILM is a more general description than may appear at first sight: Galaxy clumps with joint matter envelopes (“galaxy clusters”) are not explicitly excluded, although every individual halo does host only one lens. To form matter haloes of whole clusters, we can always stick together and overlap matter haloes, changing the clustering correlation functions in consequence. The difference between the left and right panel of Fig. 1 lies therefore in the choice of the clustering correlation functions, which will enter the following calculations. Hence, the ILM expands larger matter haloes as sums of individual matter haloes of clustered galaxies. Crucially, however, the ILM is incapable to implement clumps of N galaxies that contain on average more mass than N isolated galaxies; the mean matter-to-lens-number ratio has to be constant throughout. To form a clump with a higher mass-to-lens number ratio would require to increase the mass of all individual haloes simultaneously, i.e., to change the internal halo parameters of all lenses inside the clump in a similar fashion. This is not allowed, except by chance, however, since internal parameters are statistically independent. A generalisation of the ILM in this direction could be achieved in a full-scale halo model with matter haloes hosting more than one galaxy. Note that the luminosity of a lens can also be seen as an internal parameter. Therefore, a constant mass-to-lens number ratio plus statistical independence of internal parameters amounts also to a constant mass-to-light ratio of all clumps in the model.
2.2. Galaxy-galaxy lensing
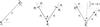 |
Fig. 2 Left panel: illustration of the parametrisation of the GGL correlator |
Before we embark on 3rd-order statistics, we start with the more familiar 2nd-order GGL (Bartelmann & Schneider 2001). These statistics are the mean tangential shear 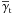 about a lens at separation ϑ = | θ2 − θ1 | (Fig. 2), defined by the correlator
about a lens at separation ϑ = | θ2 − θ1 | (Fig. 2), defined by the correlator 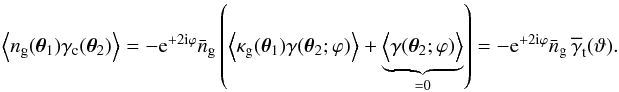 (6)Owing to isotropy, the mean tangential shear
(6)Owing to isotropy, the mean tangential shear 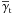 is only a function of separation ϑ and independent of the polar angle ϕ. The bracket ⟨ ... ⟩ denotes the ensemble average over lens number densities and shear configurations. The underbraced term has to vanish due to the statistical isotropy and homogeneity.
is only a function of separation ϑ and independent of the polar angle ϕ. The bracket ⟨ ... ⟩ denotes the ensemble average over lens number densities and shear configurations. The underbraced term has to vanish due to the statistical isotropy and homogeneity.
As lens number densities and shear configurations are expanded in terms of haloes in the ILM, we consider the correlator as ensemble average over all possible lens positions and internal halo parameters, 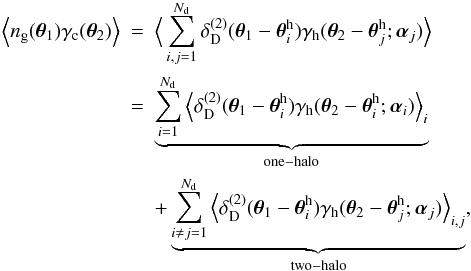 (7)which splits into two separate sums with ensemble averages over all halo parameters of one halo (one-halo term)
(7)which splits into two separate sums with ensemble averages over all halo parameters of one halo (one-halo term) 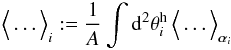 (8)or two haloes (two-halo term)
(8)or two haloes (two-halo term) 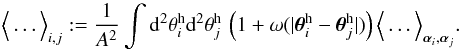 (9)The statistical independence of halo positions
(9)The statistical independence of halo positions 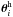 and internal halo parameters αi is explicitly used here; ⟨ ... ⟩ αi and ⟨ ... ⟩ αi,αj are the averages over internal halo parameters of a single halo or jointly for two haloes, respectively. For the latter, we stress again that we will assume statistical independence of αi and αj.
and internal halo parameters αi is explicitly used here; ⟨ ... ⟩ αi and ⟨ ... ⟩ αi,αj are the averages over internal halo parameters of a single halo or jointly for two haloes, respectively. For the latter, we stress again that we will assume statistical independence of αi and αj.
In the following, we will need the average halo shear profile 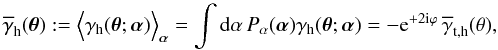 (10)Pα(α) is the probability density distribution function (p.d.f.) of the internal halo parameters α. The tangential halo shear profile
(10)Pα(α) is the probability density distribution function (p.d.f.) of the internal halo parameters α. The tangential halo shear profile 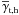 is not to be confused with
is not to be confused with 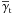 in Eq. (6) that describes the total mean tangential shear about a lens including contributions from the lens halo and haloes of clustering neighbouring lenses. Due to rotational symmetry, the average profile
in Eq. (6) that describes the total mean tangential shear about a lens including contributions from the lens halo and haloes of clustering neighbouring lenses. Due to rotational symmetry, the average profile 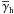 has a vanishing cross shear component, for which reason we can express it in terms of the tangential halo shear function
has a vanishing cross shear component, for which reason we can express it in terms of the tangential halo shear function 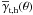 , which is only a function of the separation θ.
, which is only a function of the separation θ.
Utilising this definition, we arrive for the GGL correlator at ![\begin{eqnarray} \Ave{n_{\rm g}(\vec{\theta}_1)\gamma_{\rm c}(\vec{\theta}_2)} &=& \sum_{i=1}^{N_{\rm d}}\frac{1}{A} \Ave{\gamma_{\rm h}(\vec{\theta}_{21};\vec{\alpha})}_{\vec{\alpha}} + \sum_{i\ne j=1}^{N_{\rm d}}\frac{1}{A^2} \int\d^2\theta^\prime\left[1+\omega(|\vec{\theta}^\prime-\vec{\theta}_{21}|)\right] \Ave{\gamma_{\rm h}(\vec{\theta}^\prime;\vec{\alpha})}_{\vec{\alpha}}\\ &\approx&\nonumber \bar{n}_{\rm g} \overline{\gamma}_{\rm h}(\vec{\theta}_{21})+ \bar{n}^2_{\rm g} \int\d^2\theta^\prime\omega(|\vec{\theta}^\prime-\vec{\theta}_{21}|) \overline{\gamma}_{\rm h}(\vec{\theta}^\prime)+ \underbrace{\bar{n}_{\rm g}^2\int\d^2\theta^\prime\overline{\gamma}_{\rm h}(\vec{\theta}^\prime)}_{=0}. \end{eqnarray}](/articles/aa/full_html/2012/12/aa18993-12/aa18993-12-eq75.png) (11)The underbraced term must vanish due to radial symmetry. Inside the sums all terms become independent of individual lens positions
(11)The underbraced term must vanish due to radial symmetry. Inside the sums all terms become independent of individual lens positions 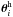 and halo parameters αi due to the averaging. The last step assumes that the number of haloes is large, i.e., Nd ≫ 1, in particular
and halo parameters αi due to the averaging. The last step assumes that the number of haloes is large, i.e., Nd ≫ 1, in particular 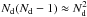 . This will also be assumed for all following calculations.
. This will also be assumed for all following calculations.
Employing (6) and (10), we finally find 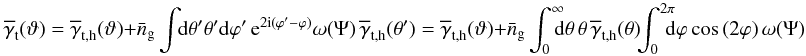 (12)with the expression
(12)with the expression 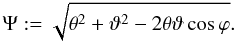 (13)The last step in (12) exploits that ω(θ) has vanishing imaginary part. In the specific ILM description, the average shear is expanded in terms of two components: the first term in Eq. (12) is the one-halo term, dominating at small separations, whereas the second term is the two-halo term due to the clustering of haloes. Importantly, GGL is only sensitive to the average lens halo
(13)The last step in (12) exploits that ω(θ) has vanishing imaginary part. In the specific ILM description, the average shear is expanded in terms of two components: the first term in Eq. (12) is the one-halo term, dominating at small separations, whereas the second term is the two-halo term due to the clustering of haloes. Importantly, GGL is only sensitive to the average lens halo 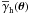 but insensitive to deviations of γh(θ;α) from
but insensitive to deviations of γh(θ;α) from 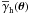 in the actual halo population, which are explicitly allowed within the ILM.
in the actual halo population, which are explicitly allowed within the ILM.
3. Lens-lens-shear correlator
We now turn to G3L, starting with the constellation of two lenses and one source as depicted in the right panel of Fig. 2. The correlator considers a cross-correlation between lens number densities at two positions θ1 and θ2 and the shear at θ3,  (14)Statistical homogeneity and isotropy implies that we can extract a correlation function
(14)Statistical homogeneity and isotropy implies that we can extract a correlation function 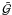 from the correlator that is solely a function of lens and source separations, ϑ1 and ϑ2, and the opening angle φ3. This function is split into an unconnected,
from the correlator that is solely a function of lens and source separations, ϑ1 and ϑ2, and the opening angle φ3. This function is split into an unconnected, 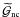 , and a connected part
, and a connected part 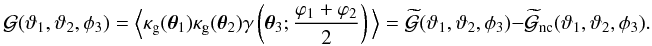 (15)The connected part vanishes for unclustered lenses, while the unconnected part can be shown to be generally (SW05)
(15)The connected part vanishes for unclustered lenses, while the unconnected part can be shown to be generally (SW05) 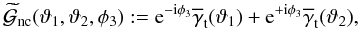 (16)which is just the sum of the GGL shear profile around each lens. Therefore,
(16)which is just the sum of the GGL shear profile around each lens. Therefore,  encodes the shear in excess of what is expected from unclustered lenses with the average shear profile
encodes the shear in excess of what is expected from unclustered lenses with the average shear profile 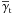 around them, or: it quantifies the shear signal about clustered lens pairs. Note that the unconnected terms do not contribute to the aperture statistics
around them, or: it quantifies the shear signal about clustered lens pairs. Note that the unconnected terms do not contribute to the aperture statistics 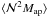 and are thus not the primary quantity measured with G3L.
and are thus not the primary quantity measured with G3L.
3.1. Derivation
For  within the ILM, we need to evaluate the connected terms of the correlator ⟨ ng(θ1)ng(θ2)γc(θ3) ⟩ with the model specifics Eqs. (2) and (3),
within the ILM, we need to evaluate the connected terms of the correlator ⟨ ng(θ1)ng(θ2)γc(θ3) ⟩ with the model specifics Eqs. (2) and (3), 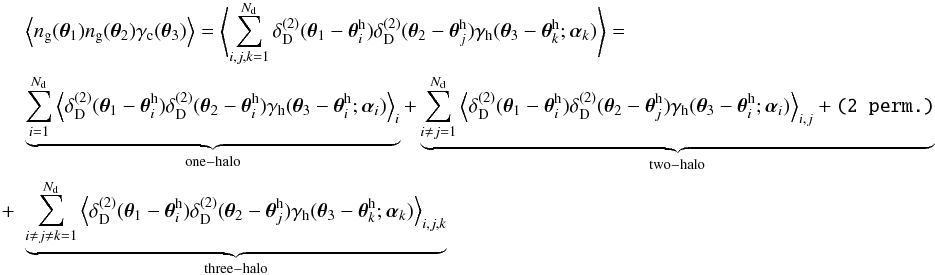 (17)where
(17)where ![\begin{equation} \Ave{\ldots}_{i,j,k}:= \frac{1}{A^3}\int\d^2\theta^{\rm h}_i\d^2\theta^{\rm h}_j\d^2\theta^{\rm h}_k\, \big[ \underbrace{1+\omega(\theta^{\rm h}_{ij})+ \omega(\theta^{\rm h}_{ik})+ \omega(\theta^{\rm h}_{jk})}_{\rm unconnected}+ \Omega(\theta^{\rm h}_{ik},\theta^{\rm h}_{jk},\theta^{\rm h}_{ij})\big] \Ave{\ldots}_{\vec{\alpha}_i,\vec{\alpha}_j,\vec{\alpha}_k} \end{equation}](/articles/aa/full_html/2012/12/aa18993-12/aa18993-12-eq92.png) (18)is the ensemble average over three haloes (three-halo term). By
(18)is the ensemble average over three haloes (three-halo term). By 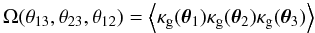 (19)we denote the (connected) 3rd-order angular clustering correlation function of the lenses that only depends on relative galaxy separations. The sum (17) hence decays into a one-halo term (first sum), two-halo (next sum plus two identical sums apart from permutations of the indices i and j) and the three-halo term (last sum). The one-halo term vanishes for θ1 ≠ θ2, i.e., distinct lens positions, owing to the Delta functions. For the connected terms, in the halo correlators ⟨ ... ⟩ i,j or ⟨ ... ⟩ i,j,k only the summands with the leading order clustering correlation functions are relevant, i.e., only the terms with Ω in the correlator ⟨ ... ⟩ i,j,k, while terms with ω or 1 are part of the unconnected terms (underbraced). They belong to the unconnected part of the 3rd-order lens clustering. Similarly, in ⟨ ... ⟩ i,j only terms associated with ω are of relevance, the terms generated by 1, the unconnected part of the 2nd-order lens clustering, will go into
(19)we denote the (connected) 3rd-order angular clustering correlation function of the lenses that only depends on relative galaxy separations. The sum (17) hence decays into a one-halo term (first sum), two-halo (next sum plus two identical sums apart from permutations of the indices i and j) and the three-halo term (last sum). The one-halo term vanishes for θ1 ≠ θ2, i.e., distinct lens positions, owing to the Delta functions. For the connected terms, in the halo correlators ⟨ ... ⟩ i,j or ⟨ ... ⟩ i,j,k only the summands with the leading order clustering correlation functions are relevant, i.e., only the terms with Ω in the correlator ⟨ ... ⟩ i,j,k, while terms with ω or 1 are part of the unconnected terms (underbraced). They belong to the unconnected part of the 3rd-order lens clustering. Similarly, in ⟨ ... ⟩ i,j only terms associated with ω are of relevance, the terms generated by 1, the unconnected part of the 2nd-order lens clustering, will go into  .
.
By evaluation of all these ensemble averages one thereby obtains for θ1 ≠ θ2 ≠ θ3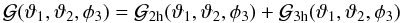 (20)with the two-halo terms (we utilise the relation
(20)with the two-halo terms (we utilise the relation 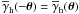 following from Eq. (10))
following from Eq. (10)) 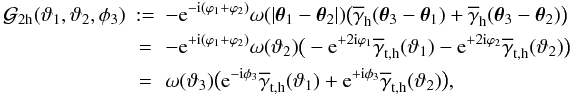 (21)the lens-lens separation
(21)the lens-lens separation 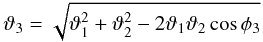 (22)and the three-halo term
(22)and the three-halo term 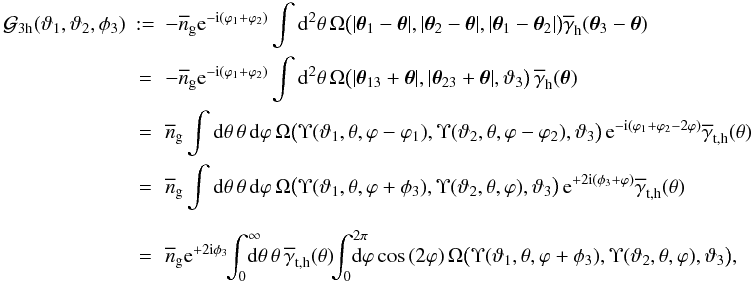 (23)for which we have introduced the auxiliary function
(23)for which we have introduced the auxiliary function 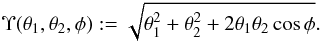 (24)The transformations in (23) use φ3 = ϕ2 − ϕ1 and a change of the integral variables ϕ → ϕ + ϕ2 and θ → θ + θ3. The last step utilises that Ω(...) has a vanishing imaginary part.
(24)The transformations in (23) use φ3 = ϕ2 − ϕ1 and a change of the integral variables ϕ → ϕ + ϕ2 and θ → θ + θ3. The last step utilises that Ω(...) has a vanishing imaginary part.
 |
Fig. 3 Right panels: excess mass around lens pairs with fixed separation; squares indicate the lens positions inside the maps. Left panels: excerpts of the underlying ILM mock data: lenses, shown as little dots, are either clustered (top left) or randomly distributed on the sky (bottom left). For simplicity, every lens has the same individual matter halo with a Gaussian lensing convergence profile (rms size is 20 pixel) sticked to it. The clustered lens haloes produces the joint matter halo of galaxy clusters in this model. The intensity scale in the left panels depicts the combined lensing convergence of all lenses; this is probed as shear by a sample of source galaxies. Note that the angular scale or the shear amplitude are of no particular interest here. The bottom right panel is the actual measurement of the bottom left scenario with the colour scale of thetop right panel. |
3.2. Interpretation
In the context of  , we can define a excess mass map in the following way. The function
, we can define a excess mass map in the following way. The function  can, for lens pairs of fixed separation ϑ3, be mapped as excess shear field at position θ3 with Cartesian shear value
can, for lens pairs of fixed separation ϑ3, be mapped as excess shear field at position θ3 with Cartesian shear value 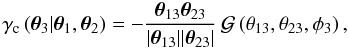 (25)where φ3 is defined as angle spanned by θ23 and θ13. In this map, we fix the lens positions at θ1 = + ϑ3/2 and θ2 = −ϑ3/2 on the x-axis. This shear map can be converted into a convergence map (e.g. Kaiser & Squires 1993), as for example done in Simon et al. (2008). The excess mass from the two-halo term of the ILM is just the halo mass about each lens at θ1 and θ2, weighed with the clustering strength ω(ϑ3) of the pair. This is exactly the mass we would anticipate around a pair of lenses, after one has subtracted the mass around unclustered pairs (Eq. (21) with ω(ϑ3) ≡ 1) and if one ignored the effect of third haloes. The excess mass stemming from a third halo, clustering around the lens pair, is described by the three-halo term.
(25)where φ3 is defined as angle spanned by θ23 and θ13. In this map, we fix the lens positions at θ1 = + ϑ3/2 and θ2 = −ϑ3/2 on the x-axis. This shear map can be converted into a convergence map (e.g. Kaiser & Squires 1993), as for example done in Simon et al. (2008). The excess mass from the two-halo term of the ILM is just the halo mass about each lens at θ1 and θ2, weighed with the clustering strength ω(ϑ3) of the pair. This is exactly the mass we would anticipate around a pair of lenses, after one has subtracted the mass around unclustered pairs (Eq. (21) with ω(ϑ3) ≡ 1) and if one ignored the effect of third haloes. The excess mass stemming from a third halo, clustering around the lens pair, is described by the three-halo term.
That the excess shear or mass originates from galaxy clusters can be argued from the ILM (Fig. 3). In the ILM, the excess shear is expressed in terms of the 2nd- and 3rd-order lens clustering correlation functions on the sky. We have no signal, if lenses are unclustered, i.e., ω = Ω = 0, or simply if we have no galaxy clusters. Unclustered lenses with statistically independent matter haloes cannot produce any excess mass. On the other hand, they still may generate a GGL signal (12) if 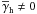 . If lenses cluster, i.e., ω ≠ 0 or Ω ≠ 0, we will get automatically non-vanishing contributions to
. If lenses cluster, i.e., ω ≠ 0 or Ω ≠ 0, we will get automatically non-vanishing contributions to  . For lens-lens separations comparable or smaller than the typical angular size of a cluster, most lens pairs will inhabit clusters and contribute mostly to the excess mass. Therefore, those pairs probe essentially the matter environment of clusters, provided they are at similar redshift. We do not expect relevant contribution to
. For lens-lens separations comparable or smaller than the typical angular size of a cluster, most lens pairs will inhabit clusters and contribute mostly to the excess mass. Therefore, those pairs probe essentially the matter environment of clusters, provided they are at similar redshift. We do not expect relevant contribution to  from pairs of lenses with distinct redshifts (apparent pairs), though. Imagine a catalogue of lenses in which all galaxies are clearly separated in radial distance. On the sky, these lenses are (a) unclustered and (b) their matter environments are mutually statistically independent owing to the large physical distances between lenses. This exactly covers the aforementioned situation as reflected in a ILM with vanishing ω and Ω:
from pairs of lenses with distinct redshifts (apparent pairs), though. Imagine a catalogue of lenses in which all galaxies are clearly separated in radial distance. On the sky, these lenses are (a) unclustered and (b) their matter environments are mutually statistically independent owing to the large physical distances between lenses. This exactly covers the aforementioned situation as reflected in a ILM with vanishing ω and Ω:  from this lens catalogue vanishes. In comparison with a sample of galaxies all at similar radial distance, a survey with radial spread in the lens distribution will have a larger fraction of apparent pairs, a reduced angular clustering of lenses and hence a overall suppressed amplitude of
from this lens catalogue vanishes. In comparison with a sample of galaxies all at similar radial distance, a survey with radial spread in the lens distribution will have a larger fraction of apparent pairs, a reduced angular clustering of lenses and hence a overall suppressed amplitude of  . This suppression can be corrected for, if the radial distribution of lenses is specified (Appendix A).
. This suppression can be corrected for, if the radial distribution of lenses is specified (Appendix A).
The ILM is only an approximation for the clustering of galaxies and matter since a change of the matter-to-light ratio with size of structures is not possible. Every structure can only be a sum of individual haloes with no correlation to each other. Contrary to GGL this limitation is relevant for G3L, as discussed in the following. We first notice that in comparison with GGL, the lens-lens-shear correlator under ILM assumptions seemingly does not provide any fundamentally new information about the lens-matter connection. To clarify this, the clustering correlation functions (ω,Ω) can be determined by the observable lens angular distribution without exploiting the gravitational lensing effect. Then, by utilising ω and the observed mean tangential shear 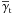 , the average halo shear profile
, the average halo shear profile 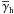 can be constrained from Eq. (12) so that all essential ingredients for predicting
can be constrained from Eq. (12) so that all essential ingredients for predicting  , Eq. (20), are already fixed. In particular,
, Eq. (20), are already fixed. In particular,  appears to be only sensitive to the average halo shear profile as GGL is. Seen this way, G3L can at most complement constraints on the mean shear profile
appears to be only sensitive to the average halo shear profile as GGL is. Seen this way, G3L can at most complement constraints on the mean shear profile 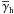 . In a scenario more complex than the ILM, however, this differs. Imagine throwing in a few completely different matter haloes into a ILM, hosting several galaxies simultaneously, that cannot be described as sums of individual haloes. Conventional GGL would be unable to detect a difference to a ILM scenario, as we can still use the clustering correlation function ω and the GGL signal
. In a scenario more complex than the ILM, however, this differs. Imagine throwing in a few completely different matter haloes into a ILM, hosting several galaxies simultaneously, that cannot be described as sums of individual haloes. Conventional GGL would be unable to detect a difference to a ILM scenario, as we can still use the clustering correlation function ω and the GGL signal 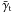 with (12) to define an average lens shear profile
with (12) to define an average lens shear profile 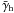 . Therefore the ILM is always, even when falsely presumed, sufficient to consistently describe the GGL signal and the lens clustering. On the other hand, when then combined with
. Therefore the ILM is always, even when falsely presumed, sufficient to consistently describe the GGL signal and the lens clustering. On the other hand, when then combined with  , we would observe inconsistencies, as we fail to correctly explain
, we would observe inconsistencies, as we fail to correctly explain  with Eq. (20). In fact, the new haloes with more than one galaxy would produce a one-halo term (Appendix B), which is missing in the ILM description. From this we conclude that
with Eq. (20). In fact, the new haloes with more than one galaxy would produce a one-halo term (Appendix B), which is missing in the ILM description. From this we conclude that  , in combination with GGL, enables us to detect whether a ILM sufficiently explains the data or whether a more advanced description is required.
, in combination with GGL, enables us to detect whether a ILM sufficiently explains the data or whether a more advanced description is required.
With the ILM as reference scenario we suggest to construct a test for the applicability of the ILM with the excess signal 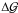 constructed as follows:
constructed as follows:
-
1.
use GGL, lens clustering statistics and numbers to obtain the ILM parameter set
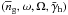 via Eq. (12);
via Eq. (12); -
2.
define the ILM excess signal by
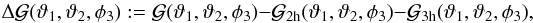 (26)where the last two terms on the r.h.s. are the two- and three-halo term, Eqs. (21) and (23), from the ILM description.
(26)where the last two terms on the r.h.s. are the two- and three-halo term, Eqs. (21) and (23), from the ILM description.
A vanishing 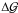 tests the validity of a ILM description for the data or expresses the deviation from it.
tests the validity of a ILM description for the data or expresses the deviation from it.
4. Lens-lens-shear correlator
Here we predict a measurement for the second G3L correlator 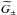 , given through the correlation of two shears and one lens number density
, given through the correlation of two shears and one lens number density 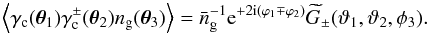 (27)The geometry of the correlator is depicted in the middle panel of Fig. 2. Here and in the following equations, a superscript “ ± ” as in
(27)The geometry of the correlator is depicted in the middle panel of Fig. 2. Here and in the following equations, a superscript “ ± ” as in 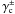 means γc for
means γc for 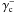 and
and 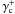 for the complex conjugate
for the complex conjugate 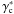 . This correlator measures the shear-shear correlations as function of lens separation. As before with
. This correlator measures the shear-shear correlations as function of lens separation. As before with  , symmetries demand that the correlator depends only on relative separations and angles given by the triangle defined by lens and source positions. It contains an unconnected part that describes the shear-shear correlations for randomly distributed lenses with no correlation to the shear field, namely (SW05)
, symmetries demand that the correlator depends only on relative separations and angles given by the triangle defined by lens and source positions. It contains an unconnected part that describes the shear-shear correlations for randomly distributed lenses with no correlation to the shear field, namely (SW05) 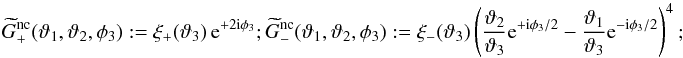 (28)ϑ3 denotes the source-source separation. As before, the unconnected terms do not contribute to the aperture statistics, here
(28)ϑ3 denotes the source-source separation. As before, the unconnected terms do not contribute to the aperture statistics, here 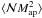 , and are thus of no particular interest for G3L. Subtracting the unconnected terms leaves us with the relevant excess shear-shear correlations about lenses, formally (cf. Eq. (1))
, and are thus of no particular interest for G3L. Subtracting the unconnected terms leaves us with the relevant excess shear-shear correlations about lenses, formally (cf. Eq. (1)) 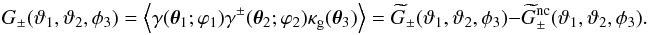 (29)
(29)
4.1. Derivation
The evaluation of G± for the ILM boils down to evaluating the connected terms of the triple correlator ![\begin{eqnarray} \label{eq:gpmcalc} \lefteqn{\Ave{ \gamma_{\rm c}(\vec{\theta}_1) \gamma^\pm_{\rm c}(\vec{\theta}_2) n_{\rm g}(\vec{\theta}_3)}=} \\[-0.5mm] &&\nonumber \underbrace{\sum_{i}^{N_{\rm d}} \Ave{\delta_{\rm D}^{(2)}(\vec{\theta}_3-\vec{\theta}^{\rm h}_i) \gamma_{\rm h}(\vec{\theta}_1-\vec{\theta}^{\rm h}_i;\vec{\alpha}_i) \gamma^\pm_{\rm h}(\vec{\theta}_2-\vec{\theta}^{\rm h}_i;\vec{\alpha}_i)}_i}_{\rm one-halo} + \underbrace{\sum_{i\ne j \ne k}^{N_{\rm d}} \Ave{\delta_{\rm D}^{(2)}(\vec{\theta}_3-\vec{\theta}^{\rm h}_i) \gamma_{\rm h}(\vec{\theta}_1-\vec{\theta}^{\rm h}_j;\vec{\alpha}_j) \gamma^\pm_{\rm h}(\vec{\theta}_2-\vec{\theta}^{\rm h}_k;\vec{\alpha}_k)}_{i,j,k}}_{\rm three-halo}\\[-0.5mm] &+&\nonumber \underbrace{\sum_{i\ne j}^{N_{\rm d}} \Ave{\delta_{\rm D}^{(2)}(\vec{\theta}_3-\vec{\theta}^{\rm h}_i) \gamma_{\rm h}(\vec{\theta}_1-\vec{\theta}^{\rm h}_j;\vec{\alpha}_j) \gamma^\pm_{\rm h}(\vec{\theta}_2-\vec{\theta}^{\rm h}_i;\vec{\alpha}_i)}_{i,j} + \sum_{i\ne j}^{N_{\rm d}} \Ave{\delta_{\rm D}^{(2)}(\vec{\theta}_3-\vec{\theta}^{\rm h}_i) \gamma_{\rm h}(\vec{\theta}_1-\vec{\theta}^{\rm h}_i;\vec{\alpha}_i) \gamma^\pm_{\rm h}(\vec{\theta}_2-\vec{\theta}^{\rm h}_j;\vec{\alpha}_j)}_{i,j}}_{\rm two-halo-2}\\[-0.5mm] &+&\nonumber \underbrace{\sum_{i\ne j}^{N_{\rm d}} \Ave{\delta_{\rm D}^{(2)}(\vec{\theta}_3-\vec{\theta}^{\rm h}_j) \gamma_{\rm h}(\vec{\theta}_1-\vec{\theta}^{\rm h}_i;\vec{\alpha}_i) \gamma^\pm_{\rm h}(\vec{\theta}_2-\vec{\theta}^{\rm h}_i;\vec{\alpha}_i)}_{i,j}}_{\rm two-halo-1}, \end{eqnarray}](/articles/aa/full_html/2012/12/aa18993-12/aa18993-12-eq141.png) (30)which now contains a one-halo term, two-halo terms and a three-halo term. We distinguish two categories of two-halo terms: in “two-halo-1”, the two shear signals are associated with the same halo, while in “two-halo-2” the shear signals originate from the lens halo and a different neighbouring halo. In analogy to the calculations for the correlator
(30)which now contains a one-halo term, two-halo terms and a three-halo term. We distinguish two categories of two-halo terms: in “two-halo-1”, the two shear signals are associated with the same halo, while in “two-halo-2” the shear signals originate from the lens halo and a different neighbouring halo. In analogy to the calculations for the correlator  , only terms associated with the leading order clustering correlation functions in the halo correlators ⟨ ... ⟩ i,j (terms with ω) and ⟨ ... ⟩ i,j,k (terms with Ω) are of interest for the connected terms; for ⟨ ... ⟩ i all terms are connected. Going through the averages step by step and collecting the connected terms, yields as final result for θ1 ≠ θ2 ≠ θ3
, only terms associated with the leading order clustering correlation functions in the halo correlators ⟨ ... ⟩ i,j (terms with ω) and ⟨ ... ⟩ i,j,k (terms with Ω) are of interest for the connected terms; for ⟨ ... ⟩ i all terms are connected. Going through the averages step by step and collecting the connected terms, yields as final result for θ1 ≠ θ2 ≠ θ3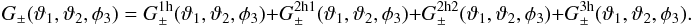 (31)We start with the three-halo term, which is after performing the integral variable transformations θ → θ + θ3 and θ′ → θ′ + θ3
(31)We start with the three-halo term, which is after performing the integral variable transformations θ → θ + θ3 and θ′ → θ′ + θ3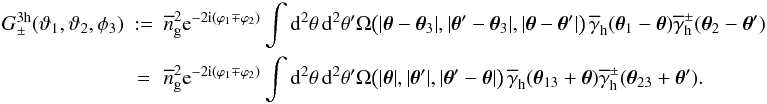 (32)To cast this into a form that no longer explicitly contains any ϕi, we need to do a few more transformations. We first note that for a shifted tangential shear one has
(32)To cast this into a form that no longer explicitly contains any ϕi, we need to do a few more transformations. We first note that for a shifted tangential shear one has 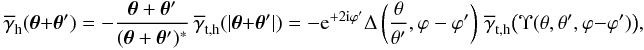 (33)where
(33)where 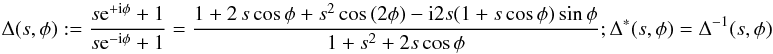 (34)is an additional phase factor; ϕ and ϕ′ are the polar angles of θ and θ′, respectively; Υ is given by the previous Eq. (24). Then this allows us to rewrite the previous equation for
(34)is an additional phase factor; ϕ and ϕ′ are the polar angles of θ and θ′, respectively; Υ is given by the previous Eq. (24). Then this allows us to rewrite the previous equation for 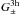 as
as 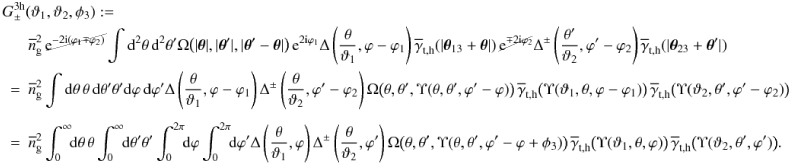 (35)The (connected) two-halo terms can be split into two sub-groups. One group is insensitive to shape variations of the lens halo, as it only contains the mean halo shear profile
(35)The (connected) two-halo terms can be split into two sub-groups. One group is insensitive to shape variations of the lens halo, as it only contains the mean halo shear profile 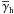 ,
, 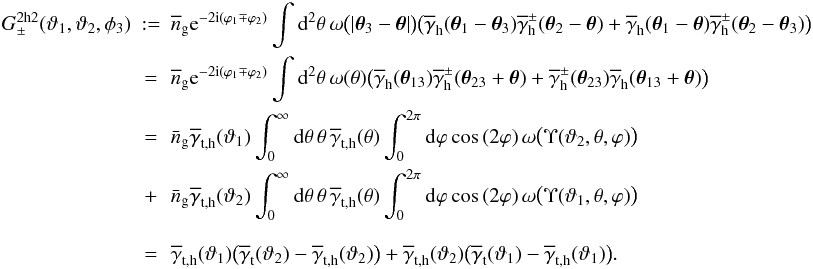 (36)The last step exploits the two-halo term of our previous result (12) for GGL. The terms inside the brackets express the excess tangential shear due to haloes clustering around the lens halo. The steps in the calculation of
(36)The last step exploits the two-halo term of our previous result (12) for GGL. The terms inside the brackets express the excess tangential shear due to haloes clustering around the lens halo. The steps in the calculation of 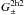 are by and large identical to the steps undertaken in Sect. 2.2.
are by and large identical to the steps undertaken in Sect. 2.2.
The remaining terms in (31) are special, as they are indeed sensitive to halo variations, which sets them clearly apart from all aforementioned correlation functions. The (connected) one-halo term is 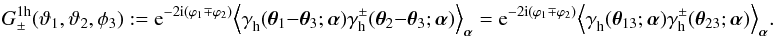 (37)If we write the halo shear as sum of the mean shear profile and some fluctuation δγh(θ;α) about it, i.e.,
(37)If we write the halo shear as sum of the mean shear profile and some fluctuation δγh(θ;α) about it, i.e., 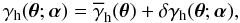 (38)with ⟨ δγh(θ;α) ⟩ α = 0, then the one-halo term becomes
(38)with ⟨ δγh(θ;α) ⟩ α = 0, then the one-halo term becomes 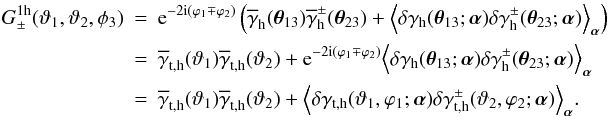 (39)In the last equation, we employed
(39)In the last equation, we employed 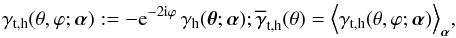 (40)where ϕ is the polar angle of θ; an equivalent definition is employed for the fluctuations δγt,h. Owing to statistical isotropy of the shear field, the model halo shear profile γh(θ;α) has to have a random orientation. Therefore, the correlator in the previous equation must be invariant with respect to any rotation φ, or
(40)where ϕ is the polar angle of θ; an equivalent definition is employed for the fluctuations δγt,h. Owing to statistical isotropy of the shear field, the model halo shear profile γh(θ;α) has to have a random orientation. Therefore, the correlator in the previous equation must be invariant with respect to any rotation φ, or 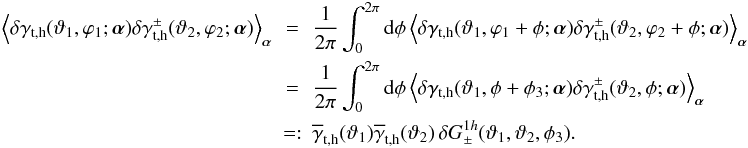 (41)The remaining two-halo term in (31) is similar to the one-halo term, actually an integral over
(41)The remaining two-halo term in (31) is similar to the one-halo term, actually an integral over 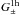 ,
, 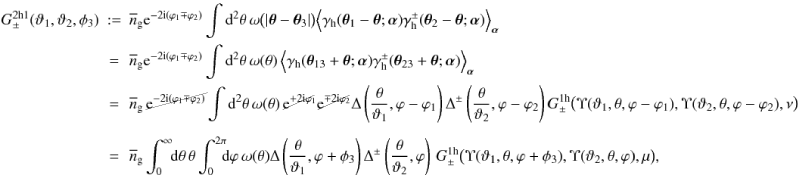 (42)where the angle ν spanned by θ23 + θ and θ13 + θ and the corresponding angle μ for a θ rotated by ϕ2 are implicitly given by
(42)where the angle ν spanned by θ23 + θ and θ13 + θ and the corresponding angle μ for a θ rotated by ϕ2 are implicitly given by 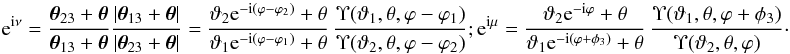 (43)
(43)
4.2. Interpretation
The resulting G± is the lowest-order galaxy-galaxy lensing correlation function that, at least within the framework of the ILM, is sensitive to variations among shear profiles of haloes. Nevertheless, we also have a G± signal when all halo shear profiles are identical, i.e., δγt,h = 0, which is generated by the tangential shear of the lens halo and the excess tangential shear of clustering neighbouring haloes. Only (39) and (42), which both contain the correlator δG1h, are affected by a scatter in halo matter profiles. The one-halo term of G± remains unchanged, even if we allow for general correlations between halo parameters α of distinct haloes or for correlations between lens positions and α, since a statistical independence of haloes has not been used for this term. Therefore, we expect the behaviour of G± on small angular scales to be described generally by 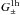 , not just within the ILM.
, not just within the ILM.
In the simplest case that all halo shear profiles are exactly identical, 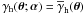 , we find
, we find 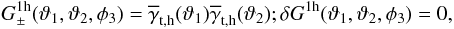 (44)i.e., the one-halo term has no explicit dependence on the opening angle φ3. Note that
(44)i.e., the one-halo term has no explicit dependence on the opening angle φ3. Note that 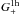 and
and 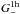 are identical. As illustration of the impact of variance in halo shear profiles, consider a singular isothermal ellipsoid (SIE) profile with ellipticity ϵh and random orientation φ (Mandelbaum et al. 2006a)
are identical. As illustration of the impact of variance in halo shear profiles, consider a singular isothermal ellipsoid (SIE) profile with ellipticity ϵh and random orientation φ (Mandelbaum et al. 2006a) 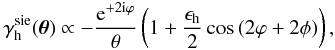 (45)ϕ is the polar angle of θ. The absolute amplitude of the shear profile is not of interest here. The tangential shear profile of the SIE is
(45)ϕ is the polar angle of θ. The absolute amplitude of the shear profile is not of interest here. The tangential shear profile of the SIE is 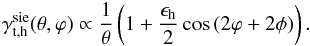 (46)In this case, we find by marginalising over all orientations φ,
(46)In this case, we find by marginalising over all orientations φ, ![\begin{equation} G^{\rm 1h}_\pm(\vartheta_1,\vartheta_2,\phi_3)= \frac{1}{2\pi}\int_0^{2\pi}\d\phi\, \gamma_{\rm t,h}^{\rm sie}(\vartheta_1,\phi_3) \left[\gamma_{\rm t,h}^{\rm sie}(\vartheta_2,0)\right]^\pm \propto \overline{\gamma}_{\rm t,h}(\vartheta_1) \overline{\gamma}_{\rm t,h}(\vartheta_2) \left(1+\frac{\epsilon_{\rm h}^2}{8}\cos{(2\phi_3)}\right); \overline{\gamma}_{\rm t,h}(\vartheta)\propto\frac{1}{\vartheta}, \end{equation}](/articles/aa/full_html/2012/12/aa18993-12/aa18993-12-eq183.png) (47)thus similar to the previous result but now with an additional φ3-dependent term, or
(47)thus similar to the previous result but now with an additional φ3-dependent term, or  (48)The result becomes somewhat more complicated for general slopes δ (Appendix C) and will reveal a difference between
(48)The result becomes somewhat more complicated for general slopes δ (Appendix C) and will reveal a difference between 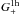 and
and 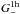 when δ ≠ 1 (not SIE) and ϵh ≠ 0 (elliptical). Moreover, the correlator (41) will exhibit no φ3-dependence, if the lens haloes are always axially symmetric, even though their radial matter density profile or their mass may scatter as to be expected in reality. Therefore, we conclude that G± may in principle be used to constrain the shape or, more specifically, the mean second-moment of the projected halo matter density profiles. In addition to that, fluctuations δγt,h in the halo shear profile due to halo substructure also add to the variance dependent one- and two-halo term of G±. As with the foregoing
when δ ≠ 1 (not SIE) and ϵh ≠ 0 (elliptical). Moreover, the correlator (41) will exhibit no φ3-dependence, if the lens haloes are always axially symmetric, even though their radial matter density profile or their mass may scatter as to be expected in reality. Therefore, we conclude that G± may in principle be used to constrain the shape or, more specifically, the mean second-moment of the projected halo matter density profiles. In addition to that, fluctuations δγt,h in the halo shear profile due to halo substructure also add to the variance dependent one- and two-halo term of G±. As with the foregoing  , it may be useful to define an excess ΔG±, obtained by subtracting off the G±-signal as anticipated from the ILM with parameters from lens clustering and GGL. In the ILM regime, the excess signal ΔG± exactly vanishes, if there is no scatter in the (projected) matter density profiles.
, it may be useful to define an excess ΔG±, obtained by subtracting off the G±-signal as anticipated from the ILM with parameters from lens clustering and GGL. In the ILM regime, the excess signal ΔG± exactly vanishes, if there is no scatter in the (projected) matter density profiles.
5. Conclusions
In order to gain a better understanding of G3L, we conceived a toy model, the “isolated lens model” (ILM), for the distribution of galaxies and matter about galaxies. In this picture, “isolated” galaxies are surrounded by their own matter envelope (halo). Variations in the halo matter density profile are explicitly allowed, albeit statistically independent to variations of other matter envelopes or to positions of other lenses. Consequently, the matter environment of clusters is herein the superposition of independent haloes produced by clustering galaxies. The average independent matter halo is described by the mean tangential shear around lenses and the clustering of the lenses (GGL), Eq. (12). The foregoing calculations evaluate what would be measured by G3L (Eqs. (20) and (31)) under the ILM assumptions and discuss the results. Here we summarise our main conclusions.
5.1. Excess shear about lens pairs
The lens-lens-shear correlation function  basically stacks the shear field about clustered lens pairs as opposed to GGL, which stacks the shear field about individual lenses. “Clustered lens pairs” refers to the fact that the connected part of the lens-lens-shear correlator
basically stacks the shear field about clustered lens pairs as opposed to GGL, which stacks the shear field about individual lenses. “Clustered lens pairs” refers to the fact that the connected part of the lens-lens-shear correlator  does not include the expected shear pattern around pairs formed by randomly distributed lenses6. “Excess mass” refers to the convergence map that corresponds to the excess shear of lens pairs. Our conclusions are:
does not include the expected shear pattern around pairs formed by randomly distributed lenses6. “Excess mass” refers to the convergence map that corresponds to the excess shear of lens pairs. Our conclusions are:
-
Unclustered lenses do not generate any
 signal, although they may exhibit a GGL signal.
signal, although they may exhibit a GGL signal.  is a probe for the matter environment of clusters (or groups), probed by lens pairs inhabiting the cluster.
is a probe for the matter environment of clusters (or groups), probed by lens pairs inhabiting the cluster. -
Apparent lens pairs formed by lenses well separated in redshift, overall diminish the signal and add noise. The signal-to-noise of
 can thus probably be improved by exploiting lens redshift information and by giving more weight to lenses that are close in redshift. The susceptibility of the
can thus probably be improved by exploiting lens redshift information and by giving more weight to lenses that are close in redshift. The susceptibility of the  amplitude as to the radial distribution of lenses can be normalised (Appendix A).
amplitude as to the radial distribution of lenses can be normalised (Appendix A). -
In the ILM, the excess mass constituents are the haloes about the clustered lens pairs (two-halo term; Eq. (21)) and a third halo clustering about the clustered lens pair (three-halo term; Eq. (23)). In a more elaborate model incorporating haloes hosting more than one galaxy at a time, we expect also one-halo terms adding to the excess mass (Appendix B), especially at small scales.
-
If the ILM is a fair description, then
 does not provide any new information on the galaxy-matter connection compared to GGL combined with 2nd-order galaxy clustering.
does not provide any new information on the galaxy-matter connection compared to GGL combined with 2nd-order galaxy clustering.  can at most complement the information on the mean halo shear profile.
can at most complement the information on the mean halo shear profile. -
G3L in combination with GGL and lens clustering can probe whether the matter environments of clusters could be expanded as sums of independent haloes, as in the ILM. In particular, a sum of independent haloes would be unable to change the mass-to-light ratio compared to that of field galaxies.
-
Moreover, the ILM can be employed as reference to quantify the deviation
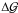 from the ILM picture in the real matter distribution around galaxies. This can be devised as practical test for a more advanced halo-model picture that naturally presumes the possibility of genuine joint matter haloes of galaxies that are fundamentally different to sums of matter haloes about isolated lenses. In analogy to
from the ILM picture in the real matter distribution around galaxies. This can be devised as practical test for a more advanced halo-model picture that naturally presumes the possibility of genuine joint matter haloes of galaxies that are fundamentally different to sums of matter haloes about isolated lenses. In analogy to  ,
, 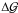 can be visualised as mass map about lens pairs or as aperture statistics.
can be visualised as mass map about lens pairs or as aperture statistics.
5.2. Excess shear-shear correlations about lenses
Unlike GGL and  , which both stack shear about lenses, G± measures the excess shear-shear correlations relative to a lens position. “Excess” means in this context shear-shear correlations in contrast to randomly distributed lenses, which would have a vanishing
, which both stack shear about lenses, G± measures the excess shear-shear correlations relative to a lens position. “Excess” means in this context shear-shear correlations in contrast to randomly distributed lenses, which would have a vanishing
GGL or  signal. In this respect, G± more resembles the shear-shear correlation function ξ± utilised in cosmic shear studies (e.g. Schneider 2006) rather than GGL. Our conclusions are:
signal. In this respect, G± more resembles the shear-shear correlation function ξ± utilised in cosmic shear studies (e.g. Schneider 2006) rather than GGL. Our conclusions are:
-
In the ILM, or more generally in a full halo model picture, the excess shear-shear correlations have two basic contributors: (i) the host halo of a lens (one-halo term; Eq. (39)); and (ii) neighbouring haloes clustering about the lens (two-halo terms: Eqs. (42) and (36); three-halo term: Eq. (35)).
-
G± is the lowest-order galaxy-galaxy lensing correlation function that is sensitive to variations in the (projected) density profiles of matter around lenses. Traditional GGL and
 are only functions of the mean, stacked shear profiles.
are only functions of the mean, stacked shear profiles. -
In particular is G± sensitive to variations due to elliptical haloes with random orientations. Therefore, the correlator is principally sensitive to the shape of matter haloes and could be exploited as such to measure halo shapes without the need of luminous tracers of presumed alignment to the halo. An elliptical halo generates an extra φ3-modulation in G±, where φ3 is the opening angle between the two lens-source directions. The one-halo term of G± does not exhibit a φ3-modulation for spherical haloes.
-
Halo substructure, i.e., random fluctuations about a smooth halo profile, also contribute to the one- and two-halo term of G±. Therefore, G± is in principle also sensitive to halo substructure.
-
The one-halo term of G± is unchanged, if we generally allow for statistical dependences of the lens haloes within the framework of a general model. Therefore, the ellipticity and substructure effect will also be present to some extend, if we have strong deviations from the ILM assumptions. However, it is unclear at this point how strong the effects are, even within the ILM, and what possible degeneracies are. We defer a thorough study of these effects to a future paper.
http://sci.esa.int/euclid, see also Laureijs et al. (2011).
Acknowledgments
This work has been supported by the Deutsche Forschungsgemeinschaft in the framework of the Collaborative Research Center TR33 “The Dark Universe”. Patrick Simon also acknowledges supported by the European DUEL Research-Training Network (MRTN-CT-2006-036133).
References
- Bartelmann, M. 2010, Rev. Mod. Phys., 82, 331 [NASA ADS] [CrossRef] [Google Scholar]
- Bartelmann, M., & Schneider, P. 2001, Phys. Rep., 340, 291 [NASA ADS] [CrossRef] [Google Scholar]
- Bower, R. G., Benson, A. J., Malbon, R., et al. 2006, MNRAS, 370, 645 [NASA ADS] [CrossRef] [Google Scholar]
- Brainerd, T. G., Blandford, R. D., & Smail, I. 1996, ApJ, 466, 623 [NASA ADS] [CrossRef] [Google Scholar]
- Cooray, A., & Sheth, R. 2002, Phys. Rep., 372, 1 [NASA ADS] [CrossRef] [Google Scholar]
- De Lucia, G., Poggianti, B. M., Aragón-Salamanca, A., et al. 2007, MNRAS, 374, 809 [NASA ADS] [CrossRef] [Google Scholar]
- Dodelson, S. 2003, Modern cosmology (Academic Press) 2003, XIII + 440 p. [Google Scholar]
- Fischer, P., McKay, T. A., Sheldon, E., et al. 2000, AJ, 120, 1198 [NASA ADS] [CrossRef] [Google Scholar]
- Griffiths, R. E., Casertano, S., Im, M., & Ratnatunga, K. U. 1996, MNRAS, 282, 1159 [Google Scholar]
- Guzik, J., & Seljak, U. 2002, MNRAS, 335, 311 [NASA ADS] [CrossRef] [Google Scholar]
- Hoekstra, H., Van Waerbeke, L., & Gladders, M. D. 2002, ApJ, 577, 604 [NASA ADS] [CrossRef] [Google Scholar]
- Hoekstra, H., Yee, H. K. C., & Gladders, M. D. 2004, ApJ, 606, 67 [NASA ADS] [CrossRef] [Google Scholar]
- Johnston, D. E. 2006, MNRAS, 367, 1222 [NASA ADS] [CrossRef] [Google Scholar]
- Kaiser, N., & Squires, G. 1993, ApJ, 404, 441 [NASA ADS] [CrossRef] [Google Scholar]
- Kleinheinrich, M., Rix, H.-W., Erben, T., et al. 2005, A&A, 439, 513 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Laureijs, R., Amiaux, J., Arduini, S., et al. 2011 [arXiv:1110.3193] [Google Scholar]
- Mandelbaum, R., Tasitsiomi, A., Seljak, U., Kravtsov, A. V., & Wechsler, R. H. 2005, MNRAS, 362, 1451 [NASA ADS] [CrossRef] [Google Scholar]
- Mandelbaum, R., Hirata, C. M., Broderick, T., Seljak, U., & Brinkmann, J. 2006a, MNRAS, 370, 1008 [NASA ADS] [CrossRef] [Google Scholar]
- Mandelbaum, R., Seljak, U., Kauffmann, G., Hirata, C. M., & Brinkmann, J. 2006b, MNRAS, 368, 715 [Google Scholar]
- McKay, T. A., Sheldon, E. S., Racusin, J., et al. 2001, unpublished [arXiv:0108013] [Google Scholar]
- Parker, L. C., Hoekstra, H., Hudson, M. J., van Waerbeke, L., & Mellier, Y. 2007, ApJ, 669, 21 [Google Scholar]
- Peebles, P. J. E. 1980, The large-scale structure of the universe (USA: Princeton University Press) [Google Scholar]
- Peebles, P. J. E. 1993, Principles of physical cosmology (Princeton University Press) [Google Scholar]
- Pen, U.-L., Lu, T., van Waerbeke, L., & Mellier, Y. 2003, MNRAS, 346, 994 [NASA ADS] [CrossRef] [Google Scholar]
- Scherrer, R. J., & Bertschinger, E. 1991, ApJ, 381, 349 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- Schneider, P. 2006, in Saas-Fee Advanced Course 33: Gravitational Lensing: Strong, Weak and Micro, eds. G. Meylan, P. Jetzer, P. North, P. Schneider, C. S. Kochanek, & J. Wambsganss, 269 [Google Scholar]
- Schneider, P., & Watts, P. 2005, A&A, 432, 783 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Schrabback, T., Hartlap, J., & Joachimi, B. 2010, A&A, 516, A63 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Seljak, U., & Warren, M. S. 2004, MNRAS, 355, 129 [NASA ADS] [CrossRef] [Google Scholar]
- Sheldon, E. S., Johnston, D. E., Frieman, J. A., et al. 2004, AJ, 127, 2544 [NASA ADS] [CrossRef] [Google Scholar]
- Simon, P., Hetterscheidt, M., Schirmer, M., et al. 2007, A&A, 461, 861 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Simon, P., Watts, P., Schneider, P., et al. 2008, A&A, 479, 655 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Tyson, J. A., Valdes, F., Jarvis, J. F., & Mills, Jr., A. P. 1984, ApJ, 281, L59 [NASA ADS] [CrossRef] [Google Scholar]
- van Uitert, E., Hoekstra, H., Velander, M., et al. 2011, A&A, 534, A14 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Weinberg, D. H., Davé, R., Katz, N., & Hernquist, L. 2004, ApJ, 601, 1 [NASA ADS] [CrossRef] [Google Scholar]
Appendix A: Normalisation scheme
Let 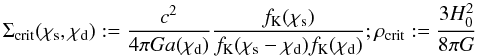 (A.1)be the critical surface matter density for lenses at comoving distance χd and sources at χs, and the critical density of the Universe, respectively; fK(χ) denotes the angular diameter distance. Using Limber’s equation for projecting the 3D bispectrum to the angular 2D bispectrum, SW05 showed for
(A.1)be the critical surface matter density for lenses at comoving distance χd and sources at χs, and the critical density of the Universe, respectively; fK(χ) denotes the angular diameter distance. Using Limber’s equation for projecting the 3D bispectrum to the angular 2D bispectrum, SW05 showed for ![\appendix \setcounter{section}{1} \begin{equation} |k|^2:=k_1^2+k_2^2-2 k_1k_2\cos{\psi}; A^2:= k_1^2R_1^2+ k_2^2R_2^2-2 k_1 k_2R_1R_2\cos{(\psi_3-\psi)}; \e^{2\i\nu}:=\frac{1}{A^2} \left[2 k_1 k_2 R_1 R_2+(k_1 R_1)^2 \e^{\i(\phi_3-\psi)}+(k_2 R_2)^2 \e^{\i(\phi_3-\psi)}\right] \end{equation}](/articles/aa/full_html/2012/12/aa18993-12/aa18993-12-eq194.png) (A.2)that
(A.2)that 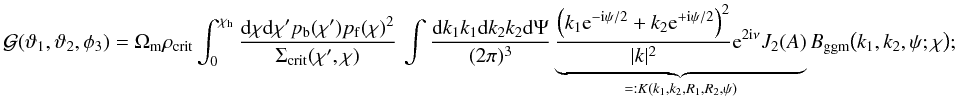 (A.3)pf(χ) and pb(χ) are the radial lens and source distribution; Bggm(k1,k2,ψ;χ) is the galaxy-galaxy-matter bispectrum at comoving radial distance χ; the wave numbers ki are also in comoving units. Note that we here, inside the integral, transformed angular separations ϑi to the projected comoving distance at lens plane distance χ, Ri: = fK(χ)ϑi. We recast this equation into
(A.3)pf(χ) and pb(χ) are the radial lens and source distribution; Bggm(k1,k2,ψ;χ) is the galaxy-galaxy-matter bispectrum at comoving radial distance χ; the wave numbers ki are also in comoving units. Note that we here, inside the integral, transformed angular separations ϑi to the projected comoving distance at lens plane distance χ, Ri: = fK(χ)ϑi. We recast this equation into 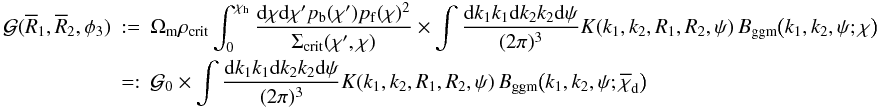 (A.4)where
(A.4)where 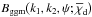 is the bispectrum at effective lens plane distance
is the bispectrum at effective lens plane distance 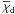 defined by
defined by 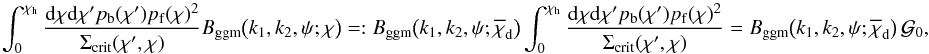 (A.5)and
(A.5)and 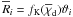 is the projected comoving distance of angular separation ϑi at the effective lens plane distance. Therefore, normalising
is the projected comoving distance of angular separation ϑi at the effective lens plane distance. Therefore, normalising  by
by 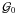 corrects the correlator for the amplitude reduction due to lens pairs with lenses at distinct redshifts, encoded in pf(χ), and removes lensing related quantities, yielding a bispectrum at an effective distance
corrects the correlator for the amplitude reduction due to lens pairs with lenses at distinct redshifts, encoded in pf(χ), and removes lensing related quantities, yielding a bispectrum at an effective distance 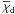 projected onto the lens plane by kernel K(...).
projected onto the lens plane by kernel K(...).
Similarly, we find for the lens-lens-shear correlator 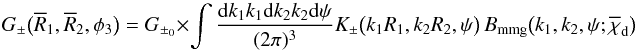 (A.6)with
(A.6)with 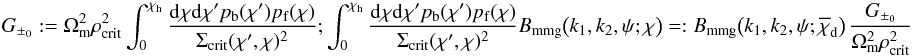 (A.7)and the integral kernels
(A.7)and the integral kernels 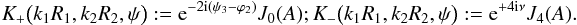 (A.8)
(A.8)
Appendix B: One-halo term for 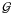 in a more complex model
in a more complex model
The ILM does not have any one-halo terms for  since haloes are hosting only one lens at a time. Matter haloes of clusters have to be represented as sums of independent haloes. In a more realistic situation beyond the ILM, we can imagine genuinely new haloes, hosting more than one galaxy, that cannot be expanded as sum of independent haloes. For simplicity, for this new type of haloes we here assume round haloes with shear profile
since haloes are hosting only one lens at a time. Matter haloes of clusters have to be represented as sums of independent haloes. In a more realistic situation beyond the ILM, we can imagine genuinely new haloes, hosting more than one galaxy, that cannot be expanded as sum of independent haloes. For simplicity, for this new type of haloes we here assume round haloes with shear profile 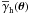 ; θ = 0 is the centre of the halo. Every halo hosts the same number of Ng galaxies. Galaxies belonging to the ith halo are scattered throughout the halo with a separation Δθij relative to the halo centre
; θ = 0 is the centre of the halo. Every halo hosts the same number of Ng galaxies. Galaxies belonging to the ith halo are scattered throughout the halo with a separation Δθij relative to the halo centre 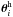 . Now the number density of galaxies on the sky and the (relevant) shear field associated with the new halo type are
. Now the number density of galaxies on the sky and the (relevant) shear field associated with the new halo type are 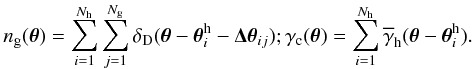 (B.1)In the following, we will focus on the connected one-halo terms of the lens-lens-shear correlator only,
(B.1)In the following, we will focus on the connected one-halo terms of the lens-lens-shear correlator only, 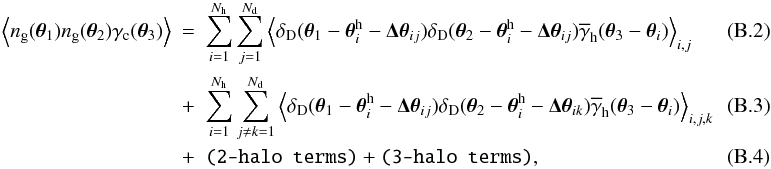 where we have the ensemble averages
where we have the ensemble averages ![\appendix \setcounter{section}{2} \begin{equation} \Ave{\ldots}_{i,j}:= \frac{1}{A}\int\d^2\theta_i\,\d^2\Delta\theta_{ij}\, P_\Delta(|\vec{\Delta\theta}_{ij}|)\big[\ldots\big]; \Ave{\ldots}_{i,j,k}:= \frac{1}{A}\int\d^2\theta_i\,\d^2\Delta\theta_{ij}\,\d^2\Delta\theta_{ik}\, P_\Delta(|\vec{\Delta\theta}_{ij}|,|\vec{\Delta\theta}_{ik}|, |\vec{\Delta\theta}_{ij}-\vec{\Delta\theta}_{ik}|) \big[\ldots\big]. \end{equation}](/articles/aa/full_html/2012/12/aa18993-12/aa18993-12-eq219.png) (B.5)By PΔ(Δθ) we denote the p.d.f. of a single relative galaxy position inside a halo, whereas by PΔ(Δθ,Δθ′, | Δθ − Δθ′ | ) we denote the joint p.d.f. of two galaxy positions. Owing to isotropy, the former can only be a function of the modulus of Δθ, the latter only a function of the relative separations | Δθ | , | Δθ′ | and | Δθ − Δθ′ | . The mean number density of galaxies populating the new haloes is NhNg/A. If the new halo type is mixed with other haloes, such as ILM haloes, the total number density of galaxies,
(B.5)By PΔ(Δθ) we denote the p.d.f. of a single relative galaxy position inside a halo, whereas by PΔ(Δθ,Δθ′, | Δθ − Δθ′ | ) we denote the joint p.d.f. of two galaxy positions. Owing to isotropy, the former can only be a function of the modulus of Δθ, the latter only a function of the relative separations | Δθ | , | Δθ′ | and | Δθ − Δθ′ | . The mean number density of galaxies populating the new haloes is NhNg/A. If the new halo type is mixed with other haloes, such as ILM haloes, the total number density of galaxies, 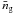 , may be different. The one halo term is not affected by the presence of the other haloes apart from
, may be different. The one halo term is not affected by the presence of the other haloes apart from 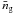 .
.
The sum (B.2) vanishes for θ1 ≠ θ2 so that the only relevant contribution to the one-halo terms of  is, after exploiting the Dirac delta functions,
is, after exploiting the Dirac delta functions, 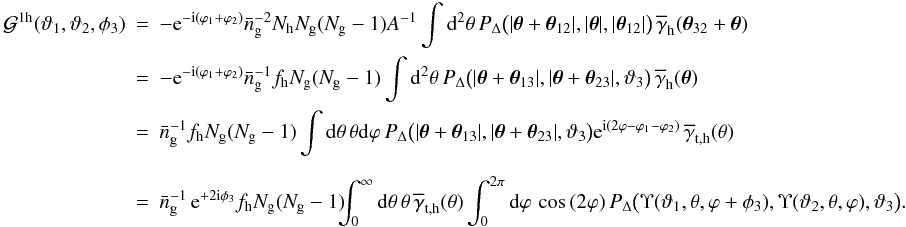 (B.6)We used (24) for the definition of Υ. By
(B.6)We used (24) for the definition of Υ. By 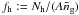 we mean the ratio of new type haloes to the total number of galaxies; as usual,
we mean the ratio of new type haloes to the total number of galaxies; as usual, 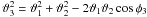 is the separation of the lenses. If we add more haloes with, say, different shear profiles or numbers of galaxies Ng, we will obtain a sum of one-halo terms of the previous kind, all weighed with (i) their halo fractions fh and (ii) number of galaxy pairs Ng(Ng − 1). ILM haloes have trivially Ng = 1, thus vanishing one-halo terms due to the absence of galaxy pairs. Moreover, if galaxies are unclustered inside their host haloes, PΔ ~ const., one will also have a vanishing one-halo term. When the host haloes are not clustered as well, there will be no contribution to
is the separation of the lenses. If we add more haloes with, say, different shear profiles or numbers of galaxies Ng, we will obtain a sum of one-halo terms of the previous kind, all weighed with (i) their halo fractions fh and (ii) number of galaxy pairs Ng(Ng − 1). ILM haloes have trivially Ng = 1, thus vanishing one-halo terms due to the absence of galaxy pairs. Moreover, if galaxies are unclustered inside their host haloes, PΔ ~ const., one will also have a vanishing one-halo term. When the host haloes are not clustered as well, there will be no contribution to  at all.
at all.
Appendix C: General elliptical matter haloes and G±
We consider a projected halo matter density profile with constant power law slope when averaged over annuli. The profiles have an elliptical shape with ellipticity ϵh = (a2 − b2)/(a2 + b2); a,b are the sizes of the major and minor axis, respectively. Mandelbaum et al. (2006a) find for the shear profile corresponding to this matter density profile 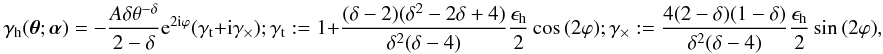 (C.1)where we denote by ϕ the polar angle of θ and by A the amplitude of the shear. For simplicity, we work with the assumption that all haloes have the same ellipticity, power law index and amplitude. As the orientation of a halo is a-priori not known, we have to marginalise over the random orientation angle of the halo for correlator (41),
(C.1)where we denote by ϕ the polar angle of θ and by A the amplitude of the shear. For simplicity, we work with the assumption that all haloes have the same ellipticity, power law index and amplitude. As the orientation of a halo is a-priori not known, we have to marginalise over the random orientation angle of the halo for correlator (41), 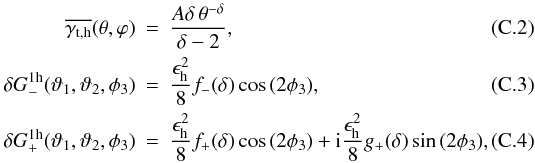 with the auxiliary functions
with the auxiliary functions 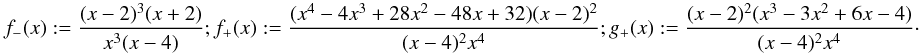 (C.5)One has f + (δ) = f − (δ) = 1 and g + (δ) = 0 for a SIE (δ = 1).
(C.5)One has f + (δ) = f − (δ) = 1 and g + (δ) = 0 for a SIE (δ = 1).
All Tables
All Figures
 |
Fig. 1 Illustration of the isolated lens model. Galaxies are depicted by black pixels, their matter haloes as red disks. For simplicity all haloes are identical in this visualisation. Left panel: lenses are distributed randomly on the sky. Right panel: lenses cluster to produce clumps with a common matter envelope, yet still described as sums of individual haloes. On the statistical level, this clumping is quantified by non-vanishing 2nd-order and 33d-order correlation functions ω and Ω, respectively. |
| In the text | |
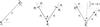 |
Fig. 2 Left panel: illustration of the parametrisation of the GGL correlator |
| In the text | |
 |
Fig. 3 Right panels: excess mass around lens pairs with fixed separation; squares indicate the lens positions inside the maps. Left panels: excerpts of the underlying ILM mock data: lenses, shown as little dots, are either clustered (top left) or randomly distributed on the sky (bottom left). For simplicity, every lens has the same individual matter halo with a Gaussian lensing convergence profile (rms size is 20 pixel) sticked to it. The clustered lens haloes produces the joint matter halo of galaxy clusters in this model. The intensity scale in the left panels depicts the combined lensing convergence of all lenses; this is probed as shear by a sample of source galaxies. Note that the angular scale or the shear amplitude are of no particular interest here. The bottom right panel is the actual measurement of the bottom left scenario with the colour scale of thetop right panel. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.