| Issue |
A&A
Volume 547, November 2012
|
|
|---|---|---|
| Article Number | A25 | |
| Number of page(s) | 11 | |
| Section | The Sun | |
| DOI | https://doi.org/10.1051/0004-6361/201219812 | |
| Published online | 22 October 2012 | |
SDO AIA and EVE observations and modelling of solar flare loops
1
DAMTP, Centre for Mathematical Sciences, University of
Cambridge,
Wilberforce Road,
Cambridge
CB3 0WA,
UK
e-mail: P.Petkaki@damtp.cam.ac.uk
2
Department of Physics and Astronomy, Rice
University, Houston,
TX
77005,
USA
Received: 13 June 2012
Accepted: 27 September 2012
We present imaging and spectroscopic observations of an isolated C1-class solar flare, obtained with the Atmospheric Imaging Assembly (AIA) and Extreme ultraviolet Variability Experiment (EVE) on the Solar Dynamics Observatory (SDO). We obtain excellent agreement between the peak flare temperatures estimated using the EVE spectra with those obtained from GOES and, most importantly, from the ratio of the 94 Å and 131 Å AIA channels, which are found to be dominated by Fe xviii and Fe xxi. These results confirm that these two AIA bands can be reliably used to provide temperature diagnostics for the peak and gradual phases of solar flares. The flare kernels, probable sources of chromospheric evaporation, are seen as strong localised emission in the AIA bands at the footpoints of flare loops. The flare loops are close to isothermal during the gradual phase. We have run several hydrodynamic simulations (using the HYDRAD code) to study the cooling of the flare loops. We find good overall agreement between observed and predicted electron temperatures and densities when a gradual increase and decrease of the heating is assumed.
Key words: Sun: flares / Sun: corona / techniques: spectroscopic / techniques: image processing
© ESO, 2012
1. Introduction
Despite several decades of observations, we still know very little about the physical mechanisms which trigger solar flares, accelerate particles to X-ray producing energies and heat the solar coronal plasma during a flare. In most models of solar flares the release of energy in the corona drives chromospheric evaporation and leads to the formation of hot dense loops. According to standard flare models, magnetic reconnection in the corona generates high energy particles (see e.g. Burge et al. 2012; Petkaki & MacKinnon 2011; Gordovskyy et al. 2010) that are carried along magnetic field lines down to the chromosphere. High energy electron beams cause chromospheric evaporation when the beam energy is high enough so that the chromosphere cannot radiate away energy fast enough and hence expands at high velocities into the corona (Fisher et al. 1985). Direct spectroscopic and spatially resolved measurements of the main heating events during the impulsive phase are very difficult to obtain, however there are a number of observations that can provide important insights into two aspects, the chromospheric evaporation and the gradual phase (when flare plasma cools back to coronal (non-flaring) temperatures).
Recent observations with the Hinode EUV Imaging Spectrometer, EIS (Culhane et al. 2007) have provided some important insights into the flare heating mechanisms (e.g. Watanabe et al. 2010; Graham et al. 2011). New important characteristics of the chromospheric evaporation during the impulsive phase of a small B-class flare were discovered in Del Zanna et al. (2011a) using Hinode EUV Imaging Spectrometer (EIS) observations. The kernels of the loop footpoint were found to have high densities, and the profiles of lines formed around 3 MK were found to be strongly blue-shifted. The old Skylab X-ray observations of X-ray kernels (Kahler et al. 1975, 1976; Mason et al. 1984) were revisited, suggesting that those kernels were due to high densities at 6−8 MK (Fe xvii) caused by the chromospheric evaporation process.
The plasma response during the gradual phase was also studied by Del Zanna et al. (2011a) with a non-equilibrium hydrodynamic numerical simulation using the HYDRAD (Bradshaw & Mason 2003a; Bradshaw & Mason 2003b) code. Overall agreement between predicted temperatures and densities was found. However, detailed comparisons could not be carried out given the cadence of the Hinode/EIS spectroscopic rasters for this study (4 min).
The Solar Dynamics Observatory (SDO) Atmospheric Imaging Assembly (AIA, see Lemen et al. 2012) has been producing stunning extreme-ultraviolet (EUV) images of the Sun since May 2010, revolutionising our view of the solar corona. The AIA data, with their 12 s cadence and 1′′ spatial resolution provide a new opportunity to investigate the dynamics of solar flares on the Sun.
The AIA on SDO consists of four independent normal incidence, multi-layer telescopes, each with two channels. Each channel images the full Sun. The 304 Å and 94 Å bands share the same telescope, as is the case for the 131 Å and 335 Å bands, the 193 Å and 211 Å bands, and the 171-Å band pass and broad UV band (Lemen et al. 2012). Particularly interesting for flares are the two “new” bands in the soft X-rays, centred at 94 and 131 Å. However, their diagnostic use has been questioned in previous studies. Various authors have found large discrepancies between observed and predicted count rates in the 94 Å. For example, Aschwanden & Boerner (2011) suggested a correction factor of 6 to the AIA calibration of this band. Another issue on the interpretation of AIA data is related to the completeness and accuracy of the atomic data such as provided within the CHIANTI atomic database (Dere et al. 1997; Landi et al. 2012). For example, shortcomings in the atomic data for the analysis of “cool” 1 MK plasmas in active regions were discussed in Del Zanna et al. (2011b; see also Testa et al. 2012). One of the aims of our work was therefore an assessment of the reliability of these two bands for flare diagnostics.
Other powerful diagnostic possibilities come from the soft X-ray full-Sun (irradiance) spectra of the SDO Extreme ultraviolet Variability Experiment (EVE) (Woods et al. 2012). EVE observes the same spectral regions as the AIA bands, and has the advantage over any imaging instrument (e.g. SDO AIA) that individual spectral lines can be resolved. EVE spectrographs measure the solar extreme ultraviolet spectrum from 60 to 1050 Å with a resolution of approximately 1 Å and a cadence of 10 s.
Of particular importance is the 94−140 Å wavelength region, where strong flare lines from a range of Fe ions is present. These lines were observed for the first (and only) time by OSO 5, as described by Kastner et al. (1974). They provide a range of diagnostic possibilities, mostly to measure temperatures and densities of the flare plasma (Mason et al. 1984).
In this paper we bring together spatially resolved SDO/AIA observations, SDO/EVE spectra and modelling with the hydrodynamic code HYDRAD (Bradshaw & Mason 2003a; Bradshaw & Mason 2003b) in order to study a small solar flare. The paper is organised as follows. In Sect. 2 we present observations of a C1 class solar flare on the solar disk. In Sect. 3 we present a model for the cooling of the flaring loops and in Sect. 4 we discuss the results and their implications.
2. Observations and analysis
We performed an extensive search over the first two years of the SDO mission to look for suitable candidate datasets, following a series of criteria. First, we looked for small flares where the AIA detectors did not saturate (a common problem). Then we searched for single events occurring in an isolated active region on the Sun, to avoid any contamination to the EVE datasets. We then considered only events with a simple morphology, i.e. where the flaring loops were composed of simple structures. We found a few events. We looked for B or C class flares in EVE and AIA data and then identified the active region they came from, looking at the AIA images (http://www.helioviewer.org). We looked for events where the loop structure was clear and the rise and fall of the emission as seen in the EVE 133 and 94 Å wavelengths was smooth. The small solar flare which we selected for further analysis was a C1.2 class flare which took place on 03/03/2011 starting 19:25 UT in active region NOAA 11164.
2.1. GOES observations
Figure 1 shows both GOES light curves (black for 1−8 Å, red for 0.5−4 Å) of the flare on a logarithmic scale. Pre-flare emission begins shortly after 19:15 UT, while the main phase of the C1.2 -class flare starts around 19:25 UT, peaks at about 19:45 UT, and is over by 20:00 UT. The temperature derived from GOES data using the goes.pro software in SolarSoft (White et al. 2005) is shown in Fig. 2. We adopted photospheric abundances and CHIANTI 7.0. For estimating the temperature from GOES, we used the standard GOES software which uses a set of tables based on CHIANTI v.7.0. No uncertainties in the calculation of the temperature are provided by the software.
The event peak temperature is close to 11 MK (12 MK when coronal abundances are used). To obtain the temperature from GOES data we have subtracted the background using the GOES measurements in both bands from 19:08 to 19:14 UT. The plot shows 30 point smoothed data (the GOES cadence is 2 s). In Fig. 2 we have overplotted temperature calculations using the GOES software (for photospheric abundances) for two further choices of background. The dotted line shows the results for the background taken in the interval 19:52−20:05 UT. The dashed line shows the results for the background taken in the interval 19:01−19:14 UT. We have no other way to estimate uncertainties to the GOES temperature, however we have found that a major uncertainty is associated to the choice of the background. This uncertainty is higher than that associated to the choice of elemental abundances, which at most is about 10% (assuming coronal abundances of low-FIP elements four times higher than photospheric).
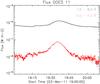 |
Fig. 1 GOES light curves on 2011 Mar 03 (black for 1−8 Å red for 0.5−4 Å). |
 |
Fig. 2 Temperature evolution derived from GOES for the C1.2 flare on 2011 Mar. 03. The full line shows the event temperature with the background taken from 19:08 to 19:14 UT. The dotted line shows the temperature for the background taken in the interval 19:52−20:05 UT. The dashed line shows the temperature for the background taken in the interval 19:01−19:14 UT. |
 |
Fig. 3 EVE spectra during the flare on 2011 Mar. 03 after subtracting a pre-flare emission, (in W m-2 nm-1). Overplotted as dotted lines are the following iron lines: Fe xviii 93.93 Å, Fe xviii 103.97 Å, Fe xix 108.37 Å, Fe xxii 117.17 Å, Fe xx 118.88 Å, Fe xx 121.845 Å, Fe xxi 128.7 Å, Fe xxiii 132.8 Å, Fe xxii 135.755 Å. The AIA 94 (dashed-dotted) and 131 (dashed) Å channel responses are indicated on each graph. |
2.2. EVE spectra
The EVE flare lines for small flares are weak and blended with cooler lines (emitting from the whole Sun), so it was necessary to rebin the data and subtract the pre-flare spectrum. We rebinned the data to a 1 min resolution using the frebin.pro function of SolarSoft. We averaged the spectra in the time interval 19:10 to 19:19 UT and used this as an estimate for the pre-flare “background” emission. We then subtracted this background from the spectra at later times in order to clearly show the flare emission. Figure 3 shows the EVE spectra in the range 80 to 142 Å at four different times during the evolution of the flare, at 19:30, 19:34, 19:40, and 19:45 UT, after subtracting the background (pre-flare) emission. Superposed on the first and the last graph are dashed lines for the wavelengths of the following iron ions: Fe xviii 93.93 Å, Fe xviii 103.97 Å, Fe xix 108.37 Å, Fe xxii 117.17 Å, Fe xx 118.88 Å, Fe xx 121.845 Å, Fe xxi 128.7 Å, Fe xxiii 132.8 Å, Fe xxii 135.755 Å.
We note that once the background emission has been subtracted these EVE flare lines are relatively unblended, with the exception of the resonance Fe xxiii 132.8 Å line, which is blended with a strong Fe xx transition. Indeed during the later phase, when the Fe xxiii decreases, the Fe xx emission becomes the dominant one in the blend.
The AIA effective areas available through SSWIDL (aia_get_response.pro) were published by Boerner et al. (2012). The AIA effective areas for the 94 Å and 131 Å channels are shown in Fig. 3 overplotted in each graph, and renormalised to a maximum value 4.5 × 10-6 cm-2 DN phot-1. Figure 3 shows that the dominant emission during the flare in the 94 Å band is indeed the Fe xviii at 93.93 Å line, as expected. On the other hand, the 131 Å band is dominated by a mixture of Fe xx, Fe xxi, and Fe xxiii, with Fe xxiii showing the strongest emission, as suggested by O’Dwyer et al. (2010). However the AIA 131 Å channel is dominated by Fe xxi 128.7 Å since it is close to the peak of the effective area. This can be verified by taking the ratio of the line Fe xxi 128.7 Å to the Fe xxiii 132.8 Å (ratio = 0.6) and comparing this ratio to the ratio of the AIA response function at the same wavelengths (ratio = 26.4).
 |
Fig. 4 Irradiance (W m-2) evolution in a selection of EVE spectral lines during the 2011 Mar. 03 flare. The overplotted line indicates the start time of the flare. |
The intensities of the EVE lines were obtained with Gaussian fitting, subtracting a constant bias. We have obtained the intensities of several lines including: Fe xxiii 132.8 Å, Fe xxii 135.755 Å, Fe xxi 128.7 Å, Fe xx 121.845 Å, Fe xix 108.37 Å, Fe xviii 93.93 Å. In Fig. 4 we plot the time evolution of these spectral lines. The time evolution of the lines shows the cooling of the loop from hot temperatures where Fe xxiii is emitting (12 MK) to temperatures of the order of 6 MK. The Fe xxiii 132.8 Å line starts rising first, followed closely by the Fe xxi 128.7 Å line. This indicates the presence of hot plasma well above 10 MK. By 19:35 the Fe xviii 93.93 Å line is rising, indicating that the plasma has now started to cool down to 6 MK, the formation temperature of Fe xviii. This is a good example of where heating and cooling are observed throughout the flare in all the ionisation stages of iron, from Fe xxiii to Fe xviii.
 |
Fig. 5 EVE derived temperatures on 2011 Mar. 03 in the interval 19:30 to 19:50 from the following line ratios (1) deblended Fe xxiii/Fe xxi; (2) Fe xxi/Fe xix; (3) Fe xxi/Fe xviii. We used the following Iron lines, Fe xviii 93.93 Å, Fe xix 108.37 Å, Fe xx 121.845 Å, Fe xxi 128.7 Å, Fe xxiii 132.8 Å. Overplotted are: 1) dashed line for Te = 11 MK; and 2) dashed line for Te = 6 MK and 3) an estimate of the uncertainties in the derived temperature is shown with diamond symbols (± 20% uncertainty in the line intensities). |
The intensity of the Fe xx 132.84 Å line is estimated from theory (Witthoeft et al. 2007, and CHIANTI 7) to be 1.38 × I(Fe xx 121.845 Å). We have therefore subtracted the Fe xx contribution to the 132 Å line measuring the Fe xx 121.845 Å intensity and assuming that the latter is not blended.
We have then used the EVE irradiances to obtain measurements of the electron temperature during the flare. The list of lines used to estimate electron temperatures is shown in Table 1 Using CHIANTI v.7 and assuming isothermal plasma we obtained temperatures from the following line ratios: (1) I(Fe xxiii (132.8 Å))/I(Fe xxi (128.7 Å)); (2) deblended I(Fe xxiii (132.8 Å))–1.38 I(Fe xx (121.845 Å))/I(Fe xxi (128.7 Å)), (3) I(Fe xxi)/I(Fe xix); (4) I(Fe xxi)/I(Fe xviii); (5) I(Fe xx)/I(Fe xviii); (6) I(Fe xix)/I(Fe xviii). In Fig. 5 we plot the derived temperatures of the flare as a function of time from 19:30 UT for three of these ratios. We estimated the plasma temperature only for the times where the intensities of the lines were above noise level. All the ratios produced similar temperatures indicating that the plasma was nearly isothermal during the event. Only the ratios involving the de-blended Fe xxiii produced higher values as shown in the figure. This could be due to incorrect deblending, or to a real higher-temperature component in the flare plasma.
List of EVE lines used to estimate temperatures.
The overplotted lines in Fig. 5 indicate temperatures of 6 MK and 11 MK. Also overplotted in each panel and in diamond symbol is an estimate of the uncertainties in the calculation of the temperature, based on a ± 20% uncertainty in the line intensities. The temperature estimates using EVE spectra are comparable to the ones from GOES (Fig. 2), giving a peak temperature close to 11 MK, which cools down temperature of 6 MK close to 19:45 UT.
2.3. AIA observations
The AIA coronal EUV channels were designed to include solar radiation in and around strong emission lines from the following ions: 304 Å (includes emission from He ii, formed around T = 0.05 MK), 171 Å (Fe ix formed in the range T = 0.63−1.1 MK), 211 Å (Fe xiv formed around T = 2.0 MK), 335 Å (Fe xvi formed around T = 2.7 MK), 94 Å (Fe xviii formed around T = 7.0 MK), 193 Å (Fe xii formed around T = 1.6 MK, and Fe xxiv around T = 19 MK), and 131 Å (Fe viii around T = 0.4 MK, Fe xx around T = 10.0 MK, Fe xxi around T = 11 MK, and Fe xxiii formed around T = 15 MK). For a detailed discussion of the predicted contributions to each AIA channel see O’Dwyer et al. (2010), Martínez-Sykora et al. (2011).
Del Zanna et al. (2011b) performed a detailed comparison of AIA active region observations with spectroscopic measurements with EIS, and found that the 94 Å band is dominated by Fe x, but has significant residual emission at lower and hotter temperatures. When active regions flare, the dominant emission becomes Fe xviii (Del Zanna 2006). Part of the lower temperature emission is to be ascribed to Fe viii and Fe ix emission (see O’Dwyer et al. 2012; Foster & Testa 2011) for which CHIANTI did not have reliable atomic data. As shown in Del Zanna et al. (2012), the CHIANTI atomic data for Fe x are also incorrect. In summary, the 94 Å band can only reliably be used when the Fe xviii emission is dominating the band (see also Testa & Reale 2012; Teriaca et al. 2012).
Del Zanna et al. (2011b) found very good agreement between predicted and observed AIA count rates for the 131 Å band, that is dominated by strong Fe viii transitions. The Fe viii atomic data discussed in Del Zanna (2009) were used for that study. This suggests that this band could be reliably be used for diagnostic purposes. Testa et al. (2012) on the other hand used stellar spectra from Procyon to show that some atomic data are still missing for this band. As we have seen, during flares this band is dominated by Fe xxi.
We analysed AIA data taken simultaneously with the EVE observations. Figure 6 shows AIA images of NOAA 11164 on 2011 Mar. 03, with a field-of-view (FOV) of 61″ × 38″. The images are plotted using the same intensity scale. We plot images for three AIA channels at five instances in the time interval 19:30 to 20.00 UT. Hot loops appear first in the 131 Å AIA channel, and a few (about 6) minutes later they have cooled down enough to become very bright in the 94 Å channel. Around 20:00 UT, the flare loops become very bright in the 171 band. This band is dominated by Fe ix, which is formed over a broad temperature range centred around 0.8 MK. The flare loops also brighten in the 131 band. A large emission measure for Fe ix implies a large one for Fe viii, if the emission is from plasma below 1 MK. Given that the Fe viii lines are the dominant features in the 131 band (when flare temperatures are not present), it is likely that the bulk of the observed 131 emission comes from Fe viii (see also O’Dwyer et al. 2010). We will be able to know for sure when more accurate and complete atomic data for this band will be available.
Small kernels of high intensities in the flare footpoint regions are evident in all the bands. As suggested by Del Zanna et al. (2011a), we interpret them as the high-density heated regions where chromospheric evaporation is taking place. The footpoints of the flare loops appear very clearly in the 171 Å channel. The location and appearance of the kernels, together with the high-resolution AIA images, indicate that the flare emission is located within an ensemble of loops (at least 4−5), which are activated at nearly the same time. The fact that the apparent lengths of these loops are about the same, as well as the overall evolution, allows us to make some simple comparisons with a 1-D hydrodynamic model of a single loop, described below.
 |
Fig. 6 AIA channels emission on 2011 Mar. 03, [2−63] arcsec West [454−492] arcseconds North, at five instances in the time interval 19:30 to 20:00 UT from the following bands (1) 131 Å, (2) 94 Å, (3) 171 Å. |
 |
Fig. 7 AIA channels average emission on 2011 Mar. 03 in the interval 19:30 to 20:00 UT from the following AIA channels (1) 131 Å (full black line); (2) 94 Å (red dotted line); (3) 335 Å (orange dashed line); (4) 211 Å (green dashed-dotted line); (5) 193 Å (dark green dashed-triple dotted line); (6) 171 Å (blue long-dashed line). Each averaged emission is normalised to its maximum in the time interval shown in the plot. |
In Fig. 7 we plot the average intensity of the field of view emission for each AIA channel: (1) 131 Å (full black line); (2) 94 Å (red dotted line); (3) 335 Å (orange dashed line); (4) 211 Å (green dashed-dotted line); (5) 193 Å (dark green dashed-triple dotted line), (6) 171 Å (blue long-dashed line). Each averaged emission is normalised to its maximum in the time interval shown in the plot. Interestingly, the emission in the 131 Å channel shows secondary peaks at the same time as 171 Å channel at 19:53 and 20:00 UT, indicating the presence of strong emission from Fe viii. The time evolution of the emission in the AIA channels also indicates the cooling of the loop from hot temperatures where Fe xxi is emitting (131 Å ~ 11 MK) to temperatures of the order of 1 MK where Fe viii (131 Å) and Fe ix (171 Å) are emitting at the end of the flare.
The intensity I of an AIA band can be expressed as: 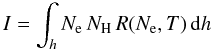 (1)where R(Ne,T) is the response function of the band, Ne,NH are the electron and hydrogen number densities, and the integral is along the line-of-sight h. The AIA temperature responses were calculated following the procedure outlined in the appendix of Del Zanna et al. (2011b), i.e. using directly the latest AIA effective areas and the CHIANTI v.7 data, CHIANTI v.6 ion abundances, constant pressure (1015) and “photospheric” chemical abundances from Asplund et al. (2009). The column emission measure is defined as EMh ≡ ∫hNeNHdh. If the plasma is isothermal (say T = T0), EMh = I/(R(Ne,T0)). Hence, the loci of the I/(R(Ne,T0)) curves represent the upper limits to the emission measure. The emission measure plots allow an estimate of the electron temperatures and densities (from the EMh values) during the flare assuming ionisation equilibrium.
(1)where R(Ne,T) is the response function of the band, Ne,NH are the electron and hydrogen number densities, and the integral is along the line-of-sight h. The AIA temperature responses were calculated following the procedure outlined in the appendix of Del Zanna et al. (2011b), i.e. using directly the latest AIA effective areas and the CHIANTI v.7 data, CHIANTI v.6 ion abundances, constant pressure (1015) and “photospheric” chemical abundances from Asplund et al. (2009). The column emission measure is defined as EMh ≡ ∫hNeNHdh. If the plasma is isothermal (say T = T0), EMh = I/(R(Ne,T0)). Hence, the loci of the I/(R(Ne,T0)) curves represent the upper limits to the emission measure. The emission measure plots allow an estimate of the electron temperatures and densities (from the EMh values) during the flare assuming ionisation equilibrium.
 |
Fig. 8 Emission measure loci from the flare loop top region at 19:32 UT obtained from the responses and the intensities of the 94 Å and the 131 Å channels. |
We have produced emission measure (EM) loci plots for various regions at various times during the flare. In Fig. 8 we see a EM Loci plot for 94 Å and 131 Å from the the main loop top region at 19:32. We have also included in the EM loci analysis the 193 Å band and have found relatively good agreement.
To assess the reliability of using the AIA 94 Å and 131 Å channels to measure temperatures, we have looked at the evolution of the isothermal temperature obtained from the ratio of these two bands and CHIANTI v.7 data (Landi et al. 2012), over the whole active region. The temperature evolution is in very good agreement with that one obtained from the EVE data. For example, considering the EVE line ratios of Fe xxi/Fe xix and Fe xxi/Fe xviii (see Fig. 5), we find that: at 19:32 UT 9.5 MK from AIA and 9.8 MK from EVE; at 19:38 UT, 9 MK from both instruments. This agreement suggests that: 1) the absolute calibration of the 94, 131 Å bands is correct; 2) the relevant atomic data for these channels are also correct for solar flares.
 |
Fig. 9 AIA channels temperature estimation on 2011 Mar. 03 at three instances, 19:30:09, 19:37:45 and 19:42:09 obtained from the ratio of 94 Å to the 131 Å channel. The colorbar shows Log (Te). Overplotted are contours of the 131 Å channel intensity. |
Having established confidence in the method, we can now study the spatial distribution of the derived temperatures. To calculate temperatures maps we first subtracted a background, which we took to be that at the time frame (19:17:38 UT), which has the lowest total emission for the 94 and 131 Å AIA channels for this event. In Fig. 9 we plot the map of the temperature of the event at three times during the evolution of the flaring loop. These are the same as in the first three rows of images in Fig. 6. The temperature maps are obtained by dividing the intensity in the 94 Å AIA channel to the intensity in the 131 Å AIA channel. Overplotted on each map is the corresponding emission in the 94 Å AIA channel shown in intensity levels (contours). In the time sequence we see the cooling of the flaring loop from temperatures in the approximate range of 12−14 MK at 19:31:02 UT at the loop top location, down to 7 MK at 19:41:02 at the same location.
The top panel in Fig. 10 shows the evolution of the temperature at the loop top and the top panel in Fig. 11 at one footpoint. The exact locations are indicated in black dotted lines in the top left-hand panel of Fig. 6. The evolution of the loop top (apex) temperature is in good agreement with the estimates made using EVE data. Specifically we estimate that the highest temperature on the loop top is 11 MK at 19:32 UT and it is 10 MK near 19:38 UT. We believe that temperatures in the 6−12 MK range are reliable, however blending and issues with the atomic data make any measurements of lower temperatures progressively less reliable.
We can also use the AIA images to infer a lower limit to the average electron density at the loop top, by assuming that the absolute calibration of the AIA channels is correct, and that the plasma is uniformly distributed along the line of sight (a filling factor of one). Since NH = 0.83Ne in a fully ionised gas with relative helium abundance A(He) = 0.1, and using the formula EM ≈ 0.83 ⟨ Ne ⟩ 2Δh, where Δh is the depth along the line of sight of the emission layer, we can estimate the averaged density of the plasma. We assume that the depth of the structures is the same as their width, and we measured the width of the flare plasma using AIA 94 Å images. We obtained estimates in the range 4.8, 6.0 and 8.4′′and used this range of widths (~3.4 to ~5.9 × 108 cm) in the estimate of the electron density. The time evolution of the density estimation is shown in the lower panel of Fig. 10. Assuming photospheric abundances, we obtain a maximum density of ~2 × 1010 cm-3 (ranging from 1.7 to 2.2 × 1010 cm-3) at the loop top (keep in mind that we are inferring a lower limit to the average electron density), similar to that obtained for a flaring loop with spectroscopic measurements by Del Zanna et al. (2011b) for another flare. We estimate the temperature of the footpoints of the main group of loops shown in Fig. 11, and of a relatively isolated loop at the left of the main group to peak at ~10 MK. Using the emission measure loci and assuming the width of the emitting footpoints to be 0.5, 1.0 and 2.0′′, we estimate the (lower limit) electron number density the loop footpoints to be in the range 8 to 4 × 1010 cm-3, shown in the lower panel of Fig. 11. We would like also to point out that the one of the main uncertainties in the EMh estimate is the elemental abundances.
 |
Fig. 10 Top panel: AIA temperature estimation on 2011 Mar. 03 starting on 19:25 UT at the loop top of the main set of loops as a function of time, obtained from the ratio of 94 Å to the 131 Å channel. Lower panel: density estimation as a function of time. Overplotted dotted lines at 19:31 and 19:38 UT provide comparison with the simulation results in Sect. 3. |
 |
Fig. 11 Top panel: AIA temperature estimation on 2011 Mar. 03 starting on 19:25 UT at the foot of the main set of loops as a function of time, obtained from the ratio of 94 Å to the 131 Å channel. Lower panel: density estimation as a function of time. Overplotted dotted lines at 19:31 and 19:38 UT provide comparison with the simulation results in Sect. 3. |
We adopted one of the latest set of “standard” photospheric abundances, however we would like to point out that the temperatures we obtain are completely independent of the choice of abundances, since iron lines are dominating the 94 and 131 Å bands. The choice of abundance does, however have a direct effect on the densities estimated from the emission measures. If we adopt standard “coronal” abundances (cf. Feldman 1992), where the iron abundance is increased by a factor of 4, we obtain lower emission measures and a factor of 2 lower densities. As regards to which coronal abundances might be more appropriate for flares, we note that a large variety of measurements can be found in the literature. For example, in a recent measurement of the iron abundance in flares, Phillips (2012) found an increased abundance (compared to the photospheric value) of about a factor of 2. This is a factor of 2 lower than previous measurements from the same author.
3. Hydrodynamic modeling of flare loops
We use the 1D hydrodynamic code HYDRAD to simulate the evolution of a flaring loop. HYDRAD solves the one dimensional hydrodynamic equations in the field-aligned direction and adopts a multi-species approach by treating electrons and ions as separate fluids, coupled via Coulomb collisions, assuming quasi-neutrality and current free conditions. The equations solved are formulated in terms of the conservation of mass, momentum and energy. The terms of the equations include transport and compression, viscous stress, gravitational acceleration and potential energy, Coulomb collisions, thermal conduction, optically-thin radiation (for equilibrium and non-equilibrium ionisation), and an external energy input (heating). Collisions between like-species are frequent enough that the electron and ion equations of state are given by pe = kBnTe and pi = kBnTi, and only the thermal component of the electron energy and the thermal plus kinetic components of the ion energy are considered. The HYDRAD code (Bradshaw & Mason 2003a; Bradshaw & Mason 2003b; Bradshaw & Klimchuk 2011) is used to solve these equations for the evolution of the flare. Written exclusively in C++, HYDRAD is fast, robust and models an entire loop strand (foot-point to foot-point for any geometry via an analytical equation, or look-up table, for gravity). An adaptive grid is employed to ensure that adequate spatial resolution is achieved at all times during the flare and this is important for capturing the particularly steep gradients that arise during the impulsive phase. HYDRAD is easily configurable via a Java-developed graphical user interface and can therefore be adapted to a wide variety of scenarios.
We have run various numerical simulations using HYDRAD. The properties of the flaring loop (e.g. loop length, apex temperature) were determined from the observations and we aimed to match them as closely as possible in the simulation. We estimated the loop length of the flaring loop to be 4 × 109 cm assuming a semicircular loop. We assumed that the loop initially had a uniform temperature of 0.02 MK, and an apex density of 1.5 × 109 cm-3. We would like to note that the initial temperature and density in the simulation do not affect the thermodynamic evolution of the flare. The total energy released in the heating event is orders of magnitude greater than the total energy of the preheated loop. Thus, the input energy from heating effectively governs its thermal properties thereafter. The initially hydrostatic loop (gravitationally stratified) was subject to uniform heating everywhere along its length for a period of 13 min with a rate of 0.5 erg cm-3 s-1. The rate of heating increased from zero to the maximum of 0.5 erg cm-3 s-1 in the first 4 min. The rate of heating decreased in the last 80 s of the 13 min. The energy deposited into the loop was chosen such that the loop of chosen length could be heated up to the observed peak temperature. In Fig. 12 we plot the results of this HYDRAD simulation. The top panel shows the time evolution of the electron temperature at the apex of the simulated loop while the lower panel shows the apex electron density. The flare started at 19:25 UT, so the time axis in the two plots reflects this. The maximum temperature was reached maximum at 19:31 UT and then declined. The apex temperature is 11 MK, comparable to the one we derived from observations. The density increases as material is evaporated from the chromosphere. The electron number density reaches 3.5 × 1010 cm-3, a value close to our measured lower limit (which was obtained by assuming a filling factor of one).
 |
Fig. 12 HYDRAD apex temperature (top panel) and apex density (lower panel) of flaring loop plasma assuming that the start of the simulation corresponds to 19:25 UT. The vertical lines at 19:31 and 19:38 UT are overplotted to compare with observational results in Sect. 2.3 at the same times. |
When the heating is switched off, the flare loop starts to cool, and the evaporated material after 19:40 UT begins to drain, as can be seen in the lower plot of Fig. 12. The extremely rapid initial cooling is due to highly efficient thermal conduction, which is clear because material continues to be evaporated into the corona after the heating is switched off. After 25 min at 19:50 the simulation plasma has cooled down to 1 MK. Looking at Fig. 7, we see that there is a first peak in the 171 Å channel emission just after 19:51, indicating the presence of plasma around the 1 MK range of temperature. This is in good agreement with the result of our simulations.
We have run a number of simulations using the HYDRAD code. We have kept the size of the loop fixed and varied the location of heating, the heating time and the heating rate. For uniform loop heating, the simulations have shown that the apex temperature and density of the loop is larger for higher heating rates. The simulations for loop top heating have also shown a similar dependence. Lower total energy is needed to heat the loop to the same apex temperature, when loop top heating is assumed.
4. Summary and conclusions
In this paper we have studied a small, isolated C1.2 class flare on 03/03/2011. We have presented a direct comparison of flare temperatures estimated using EVE spectra, the SDO/AIA imaging bands and GOES 1−8 Å and 0.5−4 Å. We believe that this is the first analysis of this nature. The EVE spectra provide an exciting opportunity for studying solar flares in 80−150 Å band, which we have not had since OSO-5, almost 40 years ago. The AIA 94 Å and 131 Å channels cover the wavelength ranges where emission from Fe XVIII and Fe XXI dominate respectively (for hot flaring plasma, close to 10MK). The peak temperature we obtained from SDO/AIA, EVE and GOES was consistent and around 11MK. We conclude that the ratio of intensities from the AIA 94 Å and 131 Å channels can be reliably used to provide temperature diagnostics for solar flares (during the peak of soft X-ray emission, when high temperature plasma dominates). During the impulsive phase, Fe XVIII emission is weak. It is only when the flare reaches the peak phase that Fe XVIII starts to increase and reliable temperatures can be obtained. These SDO/AIA bands also include spectral lines from lower temperature emission (around 1 MK, which is not understood yet) so great care must be taken in deriving temperatures from the ratios of these bands when hot plasma (10 MK) does not dominate.
In standard models of solar flares the release of magnetic energy in the corona heats coronal magnetic loops and drives chromospheric evaporation, which leads to the formation of hot dense loops in active regions. In the small flare event presented here, the main group of flaring loops appear to heat-up to temperatures of around 11 MK, perhaps even higher. This seems a reasonable temperature for a C class flare (cf. Feldman et al. 1996). A detailed analysis of the SDO/AIA observations shows regions close to the loop top with electron temperature (Te) up to 14 MK. We estimate the temperature of the footpoints of the main group of loops to peak around 10 MK. We estimate the (lower limit) of electron number density of the loop apex to be 2 × 1010 cm-3 and the loop footpoints to be 8 × 1010 cm-3 assuming a filling factor of one.
In order to see how well our observations can be reproduced by theory, we have run numerical simulations using the hydrodynamic code HYDRAD to model the gradual phase of the flare. We obtained good agreement between theory and observations for the apex electron temperature and density. This is particularly pleasing considering that we are modelling a single loop, and in the event the AIA resolution shows the presence of 4 or 5 distinct loops. The heating duration consistent with the C1 class flare that we studied appears to be around 13 min. Knowing the temperature, the evolution timescale and estimating the flare size and volume (from SDO/AIA) allowed us to make a reasonable estimate of the total energy input (heating rate of 0.5 erg cm-3 s-1) to drive the flare (confirmed by later good agreement obtained by using this input energy in a hydrodynamic model). The hot 10 MK loop structures cool quickly, showing enhanced emission in progressively lower temperature iron lines. The cooling process is in broad agreement with the HYDRAD numerical simulations.
With regard to the driving mechanism behind the possible evaporation of material from the chromosphere, we are unable to assess the relative importance of heating by a beam of non-thermal electrons or thermal conduction (due to a lack of observations from RHESSI, Lin et al. 2002). In addition the EVE spectra are full Sun, and the spectral resolution does not allow us to measure any blue-shifts (upflows). In the HYDRAD numerical simulation, the chromospheric evaporation is being driven solely by thermal conduction. Further studies with, for example the addition of data from Hinode/EIS (EUV Imaging Spectrometer, Culhane et al. 2007) might provide further insights into the nature of chromospheric evaporation.
An important result from our analysis comes from comparing the time of peak apex temperature (19:31) and peak apex density (19:40) in the observations with the hydrodynamic model. In the model, the peak temperature is at (19:31), by design, but the peak density is also just about at 19:40 (lower panels in Figs. 10 and 12). Getting the time delay between the peak temperature and peak density correct provides evidence that the model is getting the physics of ablation right. Since this is a thermal conduction driven flare model then this evidence suggests that this particular flare is indeed driven by thermal conduction. So, the physics of the flare in this case is consistent with ablation driven by thermal conduction, suggesting that no significant heating occurs during the cooling phase.
In conclusion, the strength of combining spectroscopic (EVE) and imaging (SDO/AIA) observations has been demonstrated in this paper. Comparing the physical parameters derived with a theoretical model (HYDRAD) has provided useful insights into the heating and dominant physical processes in small solar flares. Further detailed forward-modelling of other flare events are in progress, to compare timings, densities, temperatures and flare line emission with observations from SDO AIA and EVE (in addition if possible to RHESSI and Hinode/EIS observations).
Acknowledgments
P.P. and H.E.M. acknowledge support from STFC. G.D.Z. acknowledges support from STFC (UK) via the Advanced Fellowship programme. The AIA data used here are courtesy of SDO (NASA) and the AIA consortium. CHIANTI is a collaborative project involving researchers at the Universities of Cambridge (UK), George Mason, and Michigan (USA). We would like to thank the referee for useful comments and suggestions, and Dr. Stephen White (UMD) for comments on the GOES temperature calculations.
References
- Aschwanden, M. J., & Boerner, P. 2011, ApJ, 732, 81 [NASA ADS] [CrossRef] [Google Scholar]
- Asplund, M., Grevesse, N., Sauval, A. J., & Scott, P. 2009, ARA&A, 47, 481 [NASA ADS] [CrossRef] [Google Scholar]
- Boerner, P., Edwards, C., Lemen, J., et al. 2012, Sol. Phys., 275, 41 [NASA ADS] [CrossRef] [Google Scholar]
- Bradshaw, S. J., & Klimchuk, J. A. 2011, ApJS, 194, 26 [NASA ADS] [CrossRef] [Google Scholar]
- Bradshaw, S. J., & Mason, H. E. 2003a, A&A, 401, 699 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bradshaw, S. J., & Mason, H. E. 2003b, A&A, 407, 1127 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Burge, C. A., Petkaki, P., & MacKinnon, A. L. 2012, Sol. Phys., 65 [Google Scholar]
- Culhane, J. L., Harra, L. K., James, A. M., et al. 2007, Sol. Phys., 243, 19 [Google Scholar]
- Del Zanna, G. 2006, A&A, 459, 307 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Del Zanna, G. 2009, A&A, 508, 513 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Del Zanna, G., Mitra-Kraev, U., Bradshaw, S. J., Mason, H. E., & Asai, A. 2011a, A&A, 526, A1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Del Zanna, G., O’Dwyer, B., & Mason, H. E. 2011b, A&A, 535, A46 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Del Zanna, G., Storey, P. J., Badnell, N. R., & Mason, H. E. 2012, A&A, 541, A90 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Dere, K. P., Landi, E., Mason, H. E., Monsignori Fossi, B. C., & Young, P. R. 1997, A&AS, 125, 149 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Feldman, U. 1992, Phys. Scr., 46, 202 [CrossRef] [Google Scholar]
- Feldman, U., Doschek, G. A., Behring, W. E., & Phillips, K. J. H. 1996, ApJ, 460, 1034 [NASA ADS] [CrossRef] [Google Scholar]
- Fisher, G. H., Canfield, R. C., & McClymont, A. N. 1985, ApJ, 289, 425 [NASA ADS] [CrossRef] [Google Scholar]
- Foster, A. R., & Testa, P. 2011, ApJ, 740, L52 [NASA ADS] [CrossRef] [Google Scholar]
- Gordovskyy, M., Browning, P. K., & Vekstein, G. E. 2010, A&A, 519, A21 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Graham, D. R., Fletcher, L., & Hannah, I. G. 2011, A&A, 532, A27 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kahler, S. W., Krieger, A. S., & Vaiana, G. S. 1975, ApJ, 199, L57 [NASA ADS] [CrossRef] [Google Scholar]
- Kahler, S. W., Petrasso, R. D., & Kane, S. R. 1976, Sol. Phys., 50, 179 [NASA ADS] [CrossRef] [Google Scholar]
- Kastner, S. O., Rothe, E. D., & Neupert, W. M. 1974, A&A, 37, 339 [NASA ADS] [Google Scholar]
- Landi, E., Del Zanna, G., Young, P. R., Dere, K. P., & Mason, H. E. 2012, ApJ, 744, 99 [NASA ADS] [CrossRef] [Google Scholar]
- Lemen, J., Title, A., Akin, D., et al. 2012, Sol. Phys., 275, 17 [NASA ADS] [CrossRef] [Google Scholar]
- Lin, R. P., Dennis, B. R., Hurford, G. J., et al. 2002, Sol. Phys., 210, 3 [Google Scholar]
- Martínez-Sykora, J., De Pontieu, B., Testa, P., & Hansteen, V. 2011, ApJ, 743, 23 [NASA ADS] [CrossRef] [Google Scholar]
- Mason, H. E., Bhatia, A. K., Kastner, S. O., Neupert, W. M., & Swartz, M. 1984, Sol. Phys., 92, 199 [NASA ADS] [CrossRef] [Google Scholar]
- O’Dwyer, B., Del Zanna, G., Mason, H. E., Weber, M. A., & Tripathi, D. 2010, A&A, 521, A21 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- O’Dwyer, B., Del Zanna, G., Badnell, N. R., Mason, H. E., & Storey, P. J. 2012, A&A, 537, A22 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Petkaki, P., & MacKinnon, A. L. 2011, Adv. Sp. Res., 48, 884 [Google Scholar]
- Phillips, K. J. H. 2012, MNRAS, 421, 1757 [NASA ADS] [CrossRef] [Google Scholar]
- Teriaca, L., Warren, H. P., & Curdt, W. 2012, ApJ, 754, L40 [NASA ADS] [CrossRef] [Google Scholar]
- Testa, P., & Reale, F. 2012, ApJ, 750, L10 [NASA ADS] [CrossRef] [Google Scholar]
- Testa, P., Drake, J. J., & Landi, E. 2012, ApJ, 745, 111 [NASA ADS] [CrossRef] [Google Scholar]
- Watanabe, T., Hara, H., Sterling, A. C., & Harra, L. K. 2010, ApJ, 719, 213 [NASA ADS] [CrossRef] [Google Scholar]
- White, S. M., Thomas, R. J., & Schwartz, R. A. 2005, Sol. Phys., 227, 231 [NASA ADS] [CrossRef] [Google Scholar]
- Witthoeft, M. C., Del Zanna, G., & Badnell, N. R. 2007, A&A, 466, 763 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Woods, T. N., Eparvier, F. G., Hock, R., et al. 2012, Sol. Phys., 275, 115 [Google Scholar]
All Tables
All Figures
 |
Fig. 1 GOES light curves on 2011 Mar 03 (black for 1−8 Å red for 0.5−4 Å). |
| In the text | |
 |
Fig. 2 Temperature evolution derived from GOES for the C1.2 flare on 2011 Mar. 03. The full line shows the event temperature with the background taken from 19:08 to 19:14 UT. The dotted line shows the temperature for the background taken in the interval 19:52−20:05 UT. The dashed line shows the temperature for the background taken in the interval 19:01−19:14 UT. |
| In the text | |
 |
Fig. 3 EVE spectra during the flare on 2011 Mar. 03 after subtracting a pre-flare emission, (in W m-2 nm-1). Overplotted as dotted lines are the following iron lines: Fe xviii 93.93 Å, Fe xviii 103.97 Å, Fe xix 108.37 Å, Fe xxii 117.17 Å, Fe xx 118.88 Å, Fe xx 121.845 Å, Fe xxi 128.7 Å, Fe xxiii 132.8 Å, Fe xxii 135.755 Å. The AIA 94 (dashed-dotted) and 131 (dashed) Å channel responses are indicated on each graph. |
| In the text | |
 |
Fig. 4 Irradiance (W m-2) evolution in a selection of EVE spectral lines during the 2011 Mar. 03 flare. The overplotted line indicates the start time of the flare. |
| In the text | |
 |
Fig. 5 EVE derived temperatures on 2011 Mar. 03 in the interval 19:30 to 19:50 from the following line ratios (1) deblended Fe xxiii/Fe xxi; (2) Fe xxi/Fe xix; (3) Fe xxi/Fe xviii. We used the following Iron lines, Fe xviii 93.93 Å, Fe xix 108.37 Å, Fe xx 121.845 Å, Fe xxi 128.7 Å, Fe xxiii 132.8 Å. Overplotted are: 1) dashed line for Te = 11 MK; and 2) dashed line for Te = 6 MK and 3) an estimate of the uncertainties in the derived temperature is shown with diamond symbols (± 20% uncertainty in the line intensities). |
| In the text | |
 |
Fig. 6 AIA channels emission on 2011 Mar. 03, [2−63] arcsec West [454−492] arcseconds North, at five instances in the time interval 19:30 to 20:00 UT from the following bands (1) 131 Å, (2) 94 Å, (3) 171 Å. |
| In the text | |
 |
Fig. 7 AIA channels average emission on 2011 Mar. 03 in the interval 19:30 to 20:00 UT from the following AIA channels (1) 131 Å (full black line); (2) 94 Å (red dotted line); (3) 335 Å (orange dashed line); (4) 211 Å (green dashed-dotted line); (5) 193 Å (dark green dashed-triple dotted line); (6) 171 Å (blue long-dashed line). Each averaged emission is normalised to its maximum in the time interval shown in the plot. |
| In the text | |
 |
Fig. 8 Emission measure loci from the flare loop top region at 19:32 UT obtained from the responses and the intensities of the 94 Å and the 131 Å channels. |
| In the text | |
 |
Fig. 9 AIA channels temperature estimation on 2011 Mar. 03 at three instances, 19:30:09, 19:37:45 and 19:42:09 obtained from the ratio of 94 Å to the 131 Å channel. The colorbar shows Log (Te). Overplotted are contours of the 131 Å channel intensity. |
| In the text | |
 |
Fig. 10 Top panel: AIA temperature estimation on 2011 Mar. 03 starting on 19:25 UT at the loop top of the main set of loops as a function of time, obtained from the ratio of 94 Å to the 131 Å channel. Lower panel: density estimation as a function of time. Overplotted dotted lines at 19:31 and 19:38 UT provide comparison with the simulation results in Sect. 3. |
| In the text | |
 |
Fig. 11 Top panel: AIA temperature estimation on 2011 Mar. 03 starting on 19:25 UT at the foot of the main set of loops as a function of time, obtained from the ratio of 94 Å to the 131 Å channel. Lower panel: density estimation as a function of time. Overplotted dotted lines at 19:31 and 19:38 UT provide comparison with the simulation results in Sect. 3. |
| In the text | |
 |
Fig. 12 HYDRAD apex temperature (top panel) and apex density (lower panel) of flaring loop plasma assuming that the start of the simulation corresponds to 19:25 UT. The vertical lines at 19:31 and 19:38 UT are overplotted to compare with observational results in Sect. 2.3 at the same times. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


