| Issue |
A&A
Volume 546, October 2012
|
|
|---|---|---|
| Article Number | A13 | |
| Number of page(s) | 8 | |
| Section | Numerical methods and codes | |
| DOI | https://doi.org/10.1051/0004-6361/201219755 | |
| Published online | 28 September 2012 | |
Photometric redshifts with the quasi Newton algorithm (MLPQNA) Results in the PHAT1 contest
1 Department of Physics, Federico II University, via Cinthia 6, 80126 Napoli, Italy
e-mail: cavuoti@na.infn.it
2 INAF – Astronomical Observatory of Capodimonte, via Moiariello 16, 80131 Napoli, Italy
3 Visiting associate – Department of Astronomy, California Institute of Technology, CA 90125, USA
Received: 5 June 2012
Accepted: 7 August 2012
Context. Since the advent of modern multiband digital sky surveys, photometric redshifts (photo-z’s) have become relevant if not crucial to many fields of observational cosmology, such as the characterization of cosmic structures and the weak and strong lensing.
Aims. We describe an application to an astrophysical context, namely the evaluation of photometric redshifts, of MLPQNA, which is a machine-learning method based on the quasi Newton algorithm.
Methods. Theoretical methods for photo-z evaluation are based on the interpolation of a priori knowledge (spectroscopic redshifts or SED templates), and they represent an ideal comparison ground for neural network-based methods. The MultiLayer Perceptron with quasi Newton learning rule (MLPQNA) described here is an effective computing implementation of neural networks exploited for the first time to solve regression problems in the astrophysical context. It is offered to the community through the DAMEWARE (DAta Mining & Exploration Web Application REsource) infrastructure.
Results. The PHAT contest (Hildebrandt et al. 2010, A&A, 523, A31) provides a standard dataset to test old and new methods for photometric redshift evaluation and with a set of statistical indicators that allow a straightforward comparison among different methods. The MLPQNA model has been applied on the whole PHAT1 dataset of 1984 objects after an optimization of the model performed with the 515 available spectroscopic redshifts as training set. When applied to the PHAT1 dataset, MLPQNA obtains the best bias accuracy (0.0006) and very competitive accuracies in terms of scatter (0.056) and outlier percentage (16.3%), scoring as the second most effective empirical method among those that have so far participated in the contest. MLPQNA shows better generalization capabilities than most other empirical methods especially in the presence of underpopulated regions of the knowledge base.
Key words: techniques: photometric / galaxies: distances and redshifts / galaxies: photometry / cosmology: observations / methods: data analysis
© ESO, 2012
1. Introduction
Estimating redshifts of celestial objects is one of the most pressing technological issues in observational astronomy and, since the advent of modern multiband digital sky surveys, photometric redshifts (photo-z) have become fundamental when it is necessary to know the distances of million of objects over large cosmological volumes. Photo-z’s provide redshift estimates for objects fainter than the spectroscopic limit and turn out to be much more efficient in terms of the number of objects per telescope time with respect to spectroscopic ones (spec-z). For these reasons, after the advent of modern panchromatic digital surveys, photo-z’s have become crucial. For instance, they are essential in constraining dark matter and dark energy studies by means of weak gravitational lensing for the identification of galaxy clusters and groups (e.g. Capozzi et al. 2009), for type Ia supernovae, and for the study of the mass function of galaxy clusters (Albrecht et al. 2006; Peacock et al. 2006; Keiichi et al. 2012).
The need for fast and reliable methods of photo-z evaluation will become even greater in the near future for exploiting ongoing and planned surveys. In fact, future large-field public imaging projects, such as KiDS (Kilo-Degree Survey1), DES (Dark Energy Survey2), LSST (Large Synoptic Survey Telescope3), and Euclid (Euclid Red Book 2011), require extremely accurate photo-z’s to obtain accurate measurements that do not compromise the survey’s scientific goals. This explains the very rapid growth in the number of methods that can be more or less effectively used to derive photo-z estimates and in the efforts made to better understand and characterize their biases and systematics. The possibility of achieving a very low level of residual systematics (Huterer et al. 2006; D’Abrusco et al. 2007; Laurino et al. 2011) is in fact strongly influenced by many factors: the observing strategy, the accuracy of the photometric calibration, the different point spread function in different bands, the adopted de-reddening procedures, etc.
The evaluation of photo-z’s is made possible by the existence of a rather complex correlation existing between the fluxes, as measured in broad band photometry, the morphological types of the galaxies, and their distance. The search for such a correlation (a nonlinear mapping between the photometric parameter space and the redshift values) is particularly suited to data mining methods. Existing methods can be broadly divided into two large groups: theoretical and empirical. Theoretical methods use templates, such as libraries of either observed galaxy spectra or model spectral energy distributions (SEDs). These templates can be shifted to any redshift and then convolved with the transmission curves of the filters used in the photometric survey to create the template set for the redshift estimators (e.g. Koo 1999; Massarotti et al. 2001a,b; Csabai et al. 2003). However, for datasets in which accurate and multiband photometry for a large number of objects are complemented by spectroscopic redshifts, and for a statistically significant subsample of the same objects, the empirical methods offer greater accuracy, as well as being far more efficient. These methods use the subsample of the photometric survey with spectroscopically-measured redshifts as a training set to constrain the fit of a polynomial function mapping the photometric data as redshift estimators.
Several template-based methods have been developed to derive photometric redshifts with increasingly high precision such as BPZ4, HyperZ5, Kcorrect6, Le PHARE7, ZEBRA8, LRT Libraries9, EAzY10, and Z-PEG11. Moreover there are also training-based methods, such as AnnZ12 and RFPhotoZ13. The variety of methods and approaches and their application to different types of datasets, as well as the adoption of different and often not comparable statistical indicators, make it difficult to evaluate and compare performances in an unambiguous and homogeneous way. Blind tests of photo-z’s that one useful but limited in scope have been performed in Hogg et al. (1998) on spectroscopic data from the Keck telescope on the Hubble Deep Field (HDF), in Hildebrandt et al. (2008) on spectroscopic data from the VIMOS VLT Deep Survey (VVDS; Le Févre et al. 2004) and the FORS Deep Field (FDF; Noll et al. 2004, and in Abdalla et al. 2011) on the sample of luminous red galaxies from the SDSS-DR6.
A significant advance in comparing different methods has been introduced by Hildebrandt and collaborators (Hildebrandt et al. 2010), with the so-called PHAT (PHoto-z Accuracy Testing) contest, which adopts a black-box approach that is typical of benchmarking. Instead of insisting on the subtleties of the data structure, they performed a homogeneous comparison of the performances, concentrating the analysis on the last link in the chain: the photo-z’s methods themselves.
As pointed out by the authors, in fact, “it is clear that the two regimes – data and method – cannot be separated cleanly because there are connections between the two. For example, it is highly likely that one method of photo-z estimation will perform better than a second method on one particular dataset while the situation may well be reversed on a different data set.” (cf. Hildebrandt et al. 2010).
Considering that empirical methods are trained on real data and do not require assumptions on the physics of the formation and evolution of stellar populations, neural networks (NNs) are excellent tools for interpolating data and extracting patterns and trends (cf. the standard textbook by Bishop 2006). In this paper we show the application in the PHAT1 contest of the multi layer perceptron (MLP) implemented with a quasi Newton algorithm (QNA) as a learning rule that has been employed for the first time to interpolate the photometric redshifts.
The present work follows the same path, by having the testing and probing of the accuracy of the quasi Newton based Neural Model (MLPQNA) as its aim for deriving of photometric redshifts. The application of MLPQNA to the photometric redshift estimation of QSO will be presented in Brescia et al. (in prep.).
In Sect. 2 we shortly describe the PHAT contest and the PHAT1 data made available to the contestants and used for the present work. In Sect. 3 we describe the MLPQNA method that was implemented by us and used for the contest, while in Sect. 4 we describe the experiments performed, and in Sect. 5 we present the results derived for us by the PHAT board. Summary and conclusions are wrapped up in Sect. 6.
2. The PHAT dataset
First results from the PHAT contest were presented in Hildebrandt et al. (2010), but the contest still continues on the project’s web site. PHAT provides a standardized test environment that consists of simulated and observed photometric catalogs complemented by additional materials like filter curves convolved with transmission curves, SED templates, and training sets. The PHAT project has been conceived as a blind contest, still open to host new participants who want to test their own regression method performances, as in our case, since we developed our model in the past two years. However, the subsets used to evaluate the performances are still kept secret in order to provide a more reliable comparison of the various methods. Two different datasets are available (see Hildebrandt et al. 2010, for more details).
The first one, indicated as PHAT0, is based on a very limited template set and a long-wavelength baseline (from UV to mid-IR). It is composed of a noise-free catalog with accurate synthetic colors and a catalog with a low level of additional noise. PHAT0 represents an easy case for testing the most basic elements of photo-z estimation and identifying possible low-level discrepancies between the methods.
The second one, which is the one used in the present work, is the PHAT1 dataset, which is based on real data originating in the Great Observatories Origins Deep Survey Northern field (GOODS-North; Giavalisco et al. 2004). According to Hildebrandt et al. (2010), it represents a much more complex environment to test methods to estimate photo-z’s, pushing codes to their limits and revealing more systematic difficulties. Both PHAT test datasets are made publicly available through the PHAT website14, while in Hildebrandt et al. (2010) there is a detailed description of the statistical indicators used for comparing the results provided by the 21 participants who have so far participated by submitting results obtained with 17 different photo-z codes.
The PHAT1 dataset consists of photometric observations, both from ground and space instruments, presented in Giavalisco et al. (2004), complemented by additional data in other bands derived from Capak et al. (2004). The final dataset covers the full UV-IR range and includes 18 bands: U (from KPNO), B, V, R, I, Z (from Subaru), F435W, F606W, F775W, F850LP (from HST-ACS), J, H (from ULBCAM), HK (from QUIRC), K (from WIRC), and 3.6, 4.5, 5.8, and 8.0 μ (from IRAC Spitzer).
The photometric dataset was then cross correlated with spectroscopic data from Cowie et al. (2004), Wirth et al. (2004), Treu et al. (2005), and Reddy et al. (2006). Therefore, the final PHAT1 dataset consists of 1984 objects with 18-band photometry and accurate spectroscopic redshifts. In the publicly available dataset a little more than one quarter of the objects comes with spectroscopic redshifts and can be used as the knowledge base (KB) for training empirical methods. In this contest, in fact, only 515 objects were made available with the corresponding spectroscopic redshift, while for the remaining 1469 objects the related spectroscopic redshift has been hidden from all participants. The immediate consequence is that any empirical method exploited in the contest was constrained to using the 515 objects as training set (knowledge base) and the 1469 objects as the test set, to be delivered to PHAT contest board in order to receive the statistical evaluation results back. While it is clear that the limited amount of objects in the knowledge base is not enough to ensure the best performances of most empirical methods, the fact that all methods must cope with similar difficulties makes the comparison consistent.
3. The MLPQNA regression model
MLPQNA stands for the traditional neural network model named Multi Layer Perceptron (MLP; cf. Bishop 2006) implemented with a QNA as learning rule. This particular implementation of the traditional MLP’s has already been described in Brescia et al. (2012a), and we refer to that paper for a more detailed description in the classification problem context. MLPQNA is made available to the community through the DAMEWARE (DAta Mining and Exploration Web Application REsource; Brescia et al. 2011, 2012a,b). In the text we also provide the details and the parameter settings for the best performing MLPQNA model so that anyone can easily reproduce the results using the web application. User manuals are available on the DAMEWARE web site15. A complete mathematical description of the MLPQNA model is available on the DAME web site16. Feed-forward neural networks provide a general framework for representing nonlinear functional mappings between a set of input variables and a set of output variables (Bishop 2006). One can achieve this goal by representing the nonlinear function of many variables by a composition of nonlinear activation functions of one variable, which formally describes the mathematical representation of a feed-forward neural network with two computational layers (Eq. (1)): 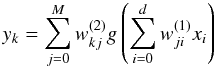 (1)A multi-layer perceptron may be also represented by a graph, as also shown in Fig. 1: the input layer (xi) is made of a number of perceptrons equal to the number of input variables (d); the output layer, on the other hand, will have as many neurons as the output variables (K). The network may have an arbitrary number of hidden layers (in most cases one), which in turn may have an arbitrary number of perceptrons (M). In a fully connected feed-forward network, each node of a layer is connected to all the nodes in the adjacent layers.
(1)A multi-layer perceptron may be also represented by a graph, as also shown in Fig. 1: the input layer (xi) is made of a number of perceptrons equal to the number of input variables (d); the output layer, on the other hand, will have as many neurons as the output variables (K). The network may have an arbitrary number of hidden layers (in most cases one), which in turn may have an arbitrary number of perceptrons (M). In a fully connected feed-forward network, each node of a layer is connected to all the nodes in the adjacent layers.
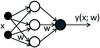 |
Fig. 1 The classical feed-forward architecture of a multi layer perceptron represented as a graph. There are three layers, respectively, input with black nodes, hidden with white nodes and the output represented by a single gray node. At each layer, its nodes are fully connected with each node of the next layer. Each connection is identified by a numerical value called weight, usually a real number normalized in the range [ − 1, + 1] . |
Each connection is represented by an adaptive weight, which represents the strength of the synaptic connection between neurons (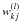 ). The response of each perceptron to the inputs is represented by a nonlinear function g, referred to as the activation function. The above equation assumes a linear activation function for neurons in the output layer. We refer to the topology of an MLP and to the weights matrix of its connections as to the model. To find the model that fits the data best, one has to provide the network with a set of examples: the training phase thus requires the KB, i.e. the training set. The learning rule of our MLP is the QNA, which differs from the Newton algorithm in terms of the calculation of the Hessian of the error function. In fact Newtonian models are variable metric methods used to find local maxima and minima of functions (Davidon 1968) and, in the case of MLPs, they can be used to find the stationary (i.e. the zero gradient) point of the learning function and are the general basis for a whole family of so-called quasi Newton methods.
). The response of each perceptron to the inputs is represented by a nonlinear function g, referred to as the activation function. The above equation assumes a linear activation function for neurons in the output layer. We refer to the topology of an MLP and to the weights matrix of its connections as to the model. To find the model that fits the data best, one has to provide the network with a set of examples: the training phase thus requires the KB, i.e. the training set. The learning rule of our MLP is the QNA, which differs from the Newton algorithm in terms of the calculation of the Hessian of the error function. In fact Newtonian models are variable metric methods used to find local maxima and minima of functions (Davidon 1968) and, in the case of MLPs, they can be used to find the stationary (i.e. the zero gradient) point of the learning function and are the general basis for a whole family of so-called quasi Newton methods.
The traditional Newton method uses the Hessian of a function to find the stationary point of a quadratic form. The Hessian of a function is not always available and in many cases it is far too complex to be computed. More often we can only calculate the function gradient, which can be used to derive the Hessian via N consequent gradient calculations.
The gradient in every point w is in fact given by 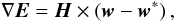 (2)where w corresponds to the minimum of the error function, which satisfies the condition
(2)where w corresponds to the minimum of the error function, which satisfies the condition 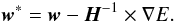 (3)The vector − H-1 × ∇E is known as Newton direction and it is the traditional base for a variety of optimization strategies,
(3)The vector − H-1 × ∇E is known as Newton direction and it is the traditional base for a variety of optimization strategies,
The step of this traditional method is thus defined as the product of an inverse Hessian matrix and a function gradient. If the function is a positive definite quadratic form, the minimum can be reached in just one step, while for an indefinite quadratic form (which has no minimum), we will reach either the maximum or a saddle point. To solve this problem, quasi Newton methods proceed with a positive definite Hessian approximation. So far, if the Hessian is definitely positive, we take the step using the Newton method. If, instead it is indefinite, we first modify it to make it definitely positive, and then perform a step using the Newton method, which is always calculated in the direction of the function decrement.
In practice, QNA is an optimization of learning rule based on a statistical approximation of the Hessian by cyclic gradient calculation, which, as already mentioned, is the basis of the classical back propagation (BP; Bishop 2006) method.
Instead of calculating the H matrix and then its inverse, the QNA uses a series of intermediate steps of lower computational cost to generate a sequence of matrices that are more and more accurate approximations of H-1. During the exploration of the parameter space and in order to find the minimum error direction, QNA starts in the wrong direction. This direction is chosen because at the first step the method has to follow the error gradient, so it takes the direction of steepest descent. However, in subsequent steps, it incorporates information from the gradient. By using the second derivatives, QNA is able to avoid local minima and to follow the error function trend more precisely, revealing a “natural” capability to find the absolute minimum error of the optimization problem.
However, this last feature could be a downside of the model, especially when the signal-to-noise ratio of data is very poor. But with “clean” data, such as in the presence of high-quality spectroscopic redshifts, used for model training, the QNA performances result extremely precise.
The experiment described in Sect. 4 consists of a supervised regression based on the MLP neural network trained by the quasi Newton learning rule. As already described, the MLP is a network model composed of input and two computational layers of neurons (see Eq. (1)), which propagate submitted data from the input to the output layer. Each neuron of a hidden layer is represented by a nonlinear activation function (in our case hyperbolic tangent) of the sum of inputs from all previous layer neurons, multiplied by weights (normalized values in [− 1, +1] representing the connections between neurons, see Fig. 1). After propagating the input data, at the final (output) layer, the learning error is evaluated (in our case by means of the mean square error, MSE, between calculated vs desired outputs), and then the backward phase is started, in which a learning rule is applied, by adapting the neuron connection weights in such a way that the error function is minimized. Then the input data are submitted again and a new cycle of learning is achieved. The algorithm stops after a chosen number of iterations or if the error becomes less than a chosen threshold. The error is calculated at each iteration by comparing the calculated value (on all input data) against the desired (a priori known) target value. This is the typical approach called “supervised”. When the learning phase is stopped, the trained network is used like a simple function. Input data not used for training, or a mix in case of learning validation, can be submitted to the network, which, if trained well, is able to provide correct output (generalization capability). By looking at the local squared approximation of the error function, it is possible to obtain an expression of minimum position. It is in fact known that the gradient in every point w of the error surface is given by Eq. (2). The network is trained in order to learn to calculate the correct photometric redshift given the input features for each object (see Sect. 4). This is indeed a typical supervised regression problem.
In terms of computational cost, the implementation of QNA can be problematic. In fact, to approximate the inverse Hessian matrix, it requires generating and storing N × N approximations, where N is the number of variables, hence the number of gradients involved in the calculation. So far, given nI the number of iterations chosen by the user, the total computational cost is about nI ∗ N2 floating point per second (flops). For this reason a family of quasi-Newton optimization methods exists that allow the complexity of the algorithm to be improved. In particular, in our implementation, we use the limited-memory BFGS (L-BFGS; Byrd et al. 1994; Broyden 1970; Fletcher 1970; Goldfarb 1970; Shanno 1970), where BFGS is the acronym composed of the names of the four inventors.
L-BFGS never stores the full N approximations of the Hessian matrix, but only the last M steps (with M ≪ N). As a result, given M the stored approximation steps, the computational cost could be reduced to about nI ∗ (N ∗ M) flops, which in practice trasforms the total cost of the algorithm from an exponential form to a polynomial one. Moreover, to give a complete computational complexity evaluation for implementing the MLPQNA model, it remains to analyze the feed-forward part of the algorithm, for instance the computational flow of input patterns throughout the MLP network, up to the calculation of the network error (as said the MSE between the desired spectroscopic redshift and the one calculated by the network), at each training iteration after a complete submission of all input patterns.
The feed-forward phase involves the flow of each input pattern throughout the network, from the input to the output layer, passing through the hidden layer. This phase can be described by the following processing steps (Mizutani & Dreyfus 2001):
-
Process 1 (P1): network node input computation;
-
Process 2 (P2): network node activation function computation;
-
Process 3 (P3): error evaluation.
The computational cost, in terms of needed flops, for the above three processing steps, can be summarized as follows: Given d the number of training data, Nw the number of network weights, Af and Nn respectively, the flops needed to execute the activation function (strongly depending on the hosting computer capabilities) and number of nodes present in the hidden plus output layers, On the number of output nodes, we obtain ![\begin{eqnarray} P1 &\cong& d \times N_{\rm w} \label{PHAT:eq4} \\[1mm] P2& \cong& d \times A_{\rm f} \times N_{\rm n} \label{PHAT:eq5} \\[1mm] P3& \cong& d \times O_{\rm n}. \label{PHAT:eq6} \end{eqnarray}](/articles/aa/full_html/2012/10/aa19755-12/aa19755-12-eq26.png) In conclusion, the computational cost of the feed-forward phase of the MLPQNA algorithm has a polynomial form of about nI ∗ d × [Nw + (Af × Nn) + On] . The total complexity of MLPQNA implementation is thus obtained by the polynomial expansion of Eq. (7), as the sum of feed-forward and backward phases multiplied by the number of training iterations.
In conclusion, the computational cost of the feed-forward phase of the MLPQNA algorithm has a polynomial form of about nI ∗ d × [Nw + (Af × Nn) + On] . The total complexity of MLPQNA implementation is thus obtained by the polynomial expansion of Eq. (7), as the sum of feed-forward and backward phases multiplied by the number of training iterations. ![\begin{equation} flops \cong nI*[(d \times (N_{\rm w}+(A_{\rm f} \times N_{\rm n})+O_{\rm n}))+(N*M)]. \label{PHAT:eq7} \end{equation}](/articles/aa/full_html/2012/10/aa19755-12/aa19755-12-eq28.png) (7)Considering our training experiment described in Sect. 4.3 and using parameters reported in Table 2, from Eq. (7) we obtain about 1200 Gflops, which corresponds to about 15 min of execution time.
(7)Considering our training experiment described in Sect. 4.3 and using parameters reported in Table 2, from Eq. (7) we obtain about 1200 Gflops, which corresponds to about 15 min of execution time.
Percentages of Not a Number (NaN) in the whole dataset (Col. 3), with 1984 objects and in the trainset (Col. 4) with 515 objects, for each band.
4. The experiment workflow
In this section we describe the details of the sequence of concatenated computational steps performed in order to determine photometric redshifts. This is what we intended as a workflow, whick can be seen also as the description of the procedure building blocks. The MLPQNA method was applied by following the standard machine learning (ML) workflow (Bishop 2006), which is summarized here: i) extraction of the KB by using the 515 available spectroscopic redshifts; ii) determination of the “optimal” model parameter setup, including pruning of data features and training/test with the available KB; iii) application of the tuned model to measure photometric redshifts on the whole PHAT1 dataset of N = 1984 objects, by including also the re-training on the extended KB. We also follow the rules of the PHAT1 contest by applying the new method in two different ways, first to the whole set of 18 bands and then only to the 14 non-IRAC bands. In order to better clarify what is discussed more in the next sections, it is important to stress that the 515 objects, the publicly available spectroscopic redshifts, have been used to tune our model. In practice, 400 objects have been used as a training set and the remaining 115 as a test/validation set (steps i) and ii) of the workflow, see Sects. 4.1 and 4.2). After having tuned our model, we performed a full training on all 515 objects, in order to exploit all the available knowledge base (see Sect. 4.3).
4.1. Extraction of the knowledge base
For supervised methods it is common praxis to split the KB into at least three disjoint subsets: one (training set) to be used for training purposes, i.e. to teach the method how to perform the regression; the second one (validation set) to check against loss of generalization capabilities (also known as overfitting); and the third one (test set) to evaluate the performances of the model. As a rule of thumb, these sets should be populated with 60%, 20% and 20% of the objects in the KB. In order to ensure a proper coverage of the parameter space (PS), objects in the KB are divided up among the three datasets by random extraction, and usually this process is iterated several times to minimize the biases introduced by fluctuations in the coverage of the PS.
In the case of MLPQNA described here, we used cross-validation (cf. Geisser 1975) to minimize the size of the validation set ( ~ 10%). Training and validation were therefore performed together using ~ 80% of the objects as a training set and the remaining ~ 20% as test set (in practice 400 records in the training set and 115 in the test set). To ensure proper coverage of the PS, we checked that the randomly extracted populations had a spec-z distribution that is compatible with that of the whole KB. The automatized process of the cross-validation was done by performing ten different training runs with the following procedure: (i) we split the training set into ten random subsets, each one composed of 10% of the dataset; (ii) at each training run we apply the 90% of the dataset for training and the excluded 10% for validation. This procedure is able to avoid overfitting on the training set (Bishop 2006). There are several variants of cross validation methods (Sylvain & Celisse 2010). We have chosen the k-fold cross validation in particular, because it is particularly suitable in the presence of a scarcity of known data samples (Geisser 1975). Since Eq. (7) refers to a single training run, for application of the k-fold cross validation procedure, the execution time could be estimated by multiplying the Eq. (7) by the factor k − 1, where k is the total number of runs.
Description of the best experiments for the 18 bands (Exp. n. 37) and the 14 bands datasets (Exp. n. 26).
4.2. Model optimization
As is known, supervised machine learning models are powerful methods for learning the hidden correlation between input and output features from training data. Of course, their generalization and prediction capabilities strongly depend on the intrinsic quality of data (signal-to-noise ratio), level of correlation inside of the PS, and the amount of missing data present in the dataset. Among the factors that affect performances, the most relevant is that most ML methods are very sensitive to the presence of Not a Number (NaN) in the dataset to be analyzed (Vashist & Garg 2012). This is especially relevant in astronomical dataset where NaNs may either be nondetections (i.e. objects observed in a given band but not detected since they are below the detection threshold) or related to patches of the sky that have not been observed. The presence of features with a large fraction of NaNs can seriously affect the performances of a given model and lower the accuracy or the generalization capabilities of a specific model. It is therefore good praxis to analyze the performance of a specific model in presence of features with large fractions of NaNs. This procedure is strictly related to the so called feature selection or “pruning of the features” phase which consists in evaluating the significance of individual features to the solution of a specific problem. In what follows we briefly discuss the outcome of the “pruning” performed on the PHAT1 dataset.
4.2.1. Pruning of features
It is also necessary to underline that especially in the presence of small datasets, there is a need for compromise. On the one hand, it is necessary to minimize the effects of NaNs; on the other, it is not possible to simply remove each record containing NaNs, because otherwise too much information would be lost.
In Table 1 we list the percentage of NaNs in each photometric band, both in the training and the full datasets. Poor features, namely the fluxes in the K and m5.8 bands, were not used for the subsequent analysis. As shown this difference remains always under 3%, demonstrating that the two datasets are congruent in terms of NaN quantity.
The pruning was performed separately on the two PHAT1 datasets (18-bands and 14-bands). A total of 37 experiments was run on the two datasets, with the various experiments differing in the groups of features removed. We started by considering all features (bands), removing the two worst bands, for instance K and m5.8, whose outlier quantity was over the 15% of patterns. Then a series of experiments was performed by removing one band at a time, by considering the NaNs percentage shown in Table 1.
Comparison of the performances of our MLPQNA (here labeled as QNA) method against all other empirical methods analyzed by PHAT board.
4.2.2. Performance metrics
The performances of the various experiments were evaluated (as done in the PHAT contest) in terms of
-
scatter: the rms of Δz
-
bias: the mean of Δz
-
fraction of outliers: where outliers are defined by the condition: |Δz| > 0.15,
where 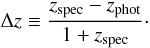 (8)At the end of this process, we obtained the best results, reported in Table 2.
(8)At the end of this process, we obtained the best results, reported in Table 2.
4.3. Application to the PHAT1 dataset
We performed a series of experiments in order to fine tune the model parameters, whose best values are MLP network topology parameters (see Table 2):
-
feat: 14 (12) input neurons (corresponding to the pruned numberof input band magnitudes listed in Table 1),
-
hid: 29 (25) hidden neurons,
-
1 output neuron.
QNA training rule parameters (see Table 2):
-
step: 0.0001 (one of the two stopping criteria. The algorithm stopsif the approximation error step size is less than this value. A stepvalue equal to zero means to use the parameter MxIt as the uniquestopping criterion.);
-
res: 30 (number of restarts of Hessian approximation from random positions, performed at each iteration);
-
dec: 0.1 (regularization factor for weight decay. The term dec ∗ | | networkweights | | 2 is added to the error function, where networkweights is the total number of weights in the network. When properly chosen, the generalization error of the network is highly improved);
-
MxIt: 3000 (max number of iterations of Hessian approximation. If zero the step parameter is used as stopping criterion);
-
CV: 10 (k-fold cross validation, with k = 10. This parameter is described in Sect. 4.1).
With these parameters, we obtained the statistical results (in terms of scatter, bias, and outlier percentage) as reported in the last three columns of Table 2.
Once the model optimization described above had been determined, the MLPQNA was re-trained on the whole KB (515 objects) and applied to the whole PHAT1 dataset (1984 objects), which was then submitted to the PHAT contest for final evaluation (see below).
Details of the experiments can be found on the DAME web site17, while the parameter settings and the results for the best models are summarized in Table 3.
5. The PHAT1 results and comparison with other models
With the model trained as described in the above section, we calculated photometric redshifts for the entire PHAT1 dataset, i.e. also for the remaining 1469 objects, for which the corresponding spectroscopic redshift was hidden to the contest participants, obtaining a final photometric catalog of 1984 objects. This output catalog has finally been delivered to the PHAT contest board, receiving the statistical results (scatter, bias and outlier’s percentage) as feedback coming from the comparison between spectroscopic and photometric information, in both cases (18 and 14 bands).
So far, the statistical results and plots have referred to the whole data sample, which is kept secret from all participants as required by the PHAT contest, were provided by Hildebrandt and also reported in the PHAT Contest wiki site 18. So far, the results obtained by analyzing the photometric redshifts calculated by MLPQNA, are shown in Table 3.
The most significant results can be summarized as follows:
-
i)
18-band experiment: 324 outliers with |Δz| > 0.15, corresponding to a relative fraction of 16.33%. For the remaining 1660 objects bias and rms are 0.000604251 ± 0.0562278;
-
ii)
14-band experiment: 384 outliers with |Δz| > 0.15, corresponding to a relative fraction of 19.35%; 1600 objects with bias and variance 0.00277721 ± 0.0626341.
A more detailed characterization of the results can be found in the first line of parts A, B, and C in Table 3, while Fig. 2, provided by Hildebrandt, gives the scatter plots (spec-z’s vs. photo-z’s) for the 18 and 14 bands.
 |
Fig. 2 Results obtained by our model and provided by the PHAT contest board in terms of direct comparison between our photometric and blind spectroscopic information. The a) panel plots the photometric vs. spectroscopic redshifts for the whole dataset using 10 photometric bands (Experiment 37). In panel b) the same but using only 14 photometric bands (Experiment 26). (Courtesy of H. Hildebrandt). |
To compare our results with other models, we also report in Table 3 the statistical indicators for the other empirical methods that competed in the PHAT1 contest. The methods are
-
AN-e: ANNz, artificial neural network, an empirical photo-zcode based on artificial neural networks (Collister &Lahav 2004);
-
EC-e: Empirical χ2, a subclass of kernel regression methods; which mimics a template-based technique with the main difference that an empirical dataset is used in place of the template grid (Wolf 2009);
-
PO-e: Polynomial fit, a “nearest neighbor” empirical photo-z method based on a polynomial fit so that the galaxy redshift is expressed as the sum of its magnitudes and colors (Li & Yee 2008);
-
RT-e: Regression Trees, based on random forests which are an empirical, non-parametric regression technique (Carliles et al. 2010).
More details can be found in the quoted references and in Hildebrandt et al. (2010).
For each of the datasets (18 and 14 bands), statistics in Table 3 refer to several regimes: the first one (A) defines all objects having |Δz| > 0.15 as outliers and it is divided into two sections: the left hand side includes all objects, while the right hand side includes objects brighter than R = 24; the second one (B) defines objects having |Δz| > 0.50 as outliers; the third one (C) defines as outliers objects having |Δz| > 0.50 and divided into a left side, for objects with z ≤ 1.5 and a right side having z > 1.5.
By analyzing the MLPQNA performance in the different regimes, we obtained:
All objects: in the 18 bands experiment, QNA scores the best results in term of bias, and gives comparable results with PO-e in terms of scatter and number of outliers. In fact, while the scatter is slightly larger in Part A than those of PO-e method (0.052 against 0.056), the number of outliers is lower (18.0% against 16.3%), and in Part. B is the viceversa (0.124 against 0.114 and 3.1% against 3.8%). In the 14-band experiment QNA obtains values slightly higher than PO-e in terms of scatter (0.051 against 0.063) and than EC-e in terms of bias (0.002 against 0.0028). For the fraction of outliers, QNA scores turn out to be larger than PO-e and EC-e (13.7% and 16.7% against 19.3%).
Bright objects: for bright objects (R < 24), the QNA resulting bias is again the best within the different empirical methods, while for scatter and number of outliers, QNA obtains slightly higher values than PO-e in both the 18 (0.047 against 0.053 and 10.7% against 11.7%) and the 14 band datasets (0.046 against 0.060 and 7.1% against 13.7%).
Distant vs. near objects: in the distant sample (zsp > 1.5) QNA scores as first in terms of bias, scatter, and number of outliers for 18 bands. In the 14-band dataset case, it is the best method in terms of scatter, but with a bias (0.015 against 0.0222) and number of outliers (29.5% against 35.0%) higher than EC-e. In the near sample (zsp < 1.5) QNA is the best in terms of bias. The scatter is slightly higher than PO-e’s for both 18 (0.049 against 0.053) and 14 bands (0.047 against 0.061). For outliers, PO-e performs better at 18 bands (12.6% against 14.6%), while PO-e and EC-e perform better at 14 bands (9.4% and 14.5% against 16.6%).
6. Summary and conclusions
For the first time the MultiLayer Perceptron with quasi Newton learning rule described here has been exploited to solve regression problems in the astrophysical context. This method was applied on the whole PHAT1 dataset of N = 1984 objects Hildebrandt et al. (2010) to determine photometric redshifts after an optimization of the model performed by using the 515 available spectroscopic redshifts as a training set.
The statistics obtained by the PHAT board, by analyzing the photometric redshifts derived with MLPQNA, and the comparison with other empirical models are reported in Table 3. From a quick inspection of Table 3, no empirical method exists that can be regarded as the best in terms of all the indicators (e.g. bias, scatter, and number of outliers) and that EC-e (Empirical χ2 method), PO-e (Polynomial Fit method), and MLPQNA produce comparable results. However, the MLPQNA method, on average, gives the best result in terms of bias in any regime.
By considering the dataset with 18 bands reported in Parts A and B of Table 3, MLPQNA obtains results for the scatter comparable to the PO-e method. In fact, in Part A, PO-e’s scatter is better than MLPQNA, but with more outliers, while the trend is reversed in Part B. In the other cases both the scatter and number of outliers are slightly worse than with PO-e and EC-e methods.
In general, MLPQNA seems to have better generalization capabilities than most other empirical methods especially in the presence of underpopulated regions of the knowledge base. In fact, ~ 500 objects with spectroscopic redshifts spread over such a large redshift interval are by far not sufficient to train most other empirical codes on the data. This has also been pointed out by Hildebrandt et al. (2010), who noticed that the high fraction of outliers produced by empirical methods is on average higher than what is currently found in the literature ( ~ 7.5%) and explained it as an effect of the small size of the training sample, which poorly maps the very wide range in redshifts and does not include enough objects with peculiar SED’s.
In this respect we wish to stress that, as already shown in another application (cf. Brescia et al. 2012a) and as will be more extensively discussed in a forthcoming paper, MLPQNA enjoys the very rare prerogative of being able to obtain good performances, also when the KB is small and thus undersampled (Brescia et al., in prep.).
Acknowledgments
The authors wish to thank the anonymous referee for useful comments that improved the paper. The authors also wish to thank H. Hildebrandt for the courtesy of providing statistical results and plots, all present and former members of the DAME collaboration, and in particular R. D’Abrusco for useful discussions. DAME has been funded through several grants, which are mentioned on the collaboration website. We acknowledge the use of TOPCAT and of other Virtual Observatory tools during some steps in the procedure. G.L. wishes to thank the California Institute of Technology for the kind hospitality. A.M. and M.B. wish to acknowledge the financial support of PRIN-INAF 2010, “Architecture and Tomography of Galaxy Clusters”.
References
- Abdalla, F. B., Banerji, M., Lahav, O., & Rashkov, V. 2011, MNRAS, 417, 1891 [NASA ADS] [CrossRef] [Google Scholar]
- Albrecht, A., Bernstein, G., Cahn, R., et al. 2006, Report of the Dark Energy Task Force [arXiv:astro-ph/0609591] [Google Scholar]
- Bishop, C. M., Pattern Recognition and Machine Learning 2006 (Springer) [Google Scholar]
- Brescia, M., Cavuoti, S., D’Abrusco, R., Laurino, O., & Longo, G. 2011, V International Workshop on Distributed Cooperative Laboratories: Instrumenting the Grid, in Remote Instrumentation for eScience and Related Aspects, 2011, eds. F. Davoli, et al. (New York: Springer) [Google Scholar]
- Brescia, M., Cavuoti, S., Paolillo, M., Longo, G., & Puzia, T. 2012a, MNRAS, 421, 1155 [NASA ADS] [CrossRef] [Google Scholar]
- Brescia, M., Longo, G., Castellani, M., et al. 2012b, Mem. SAIt Suppl., 19, 324 [Google Scholar]
- Broyden, C. G. 1970, J. Inst. Math. Appl., 6, 76 [Google Scholar]
- Byrd, R. H., Nocedal, J., & Schnabel, R. B. 1994, Math. Progr., 63, 129 [Google Scholar]
- Capak, P., Cowie, L. L., Hu, E. M., et al. 2004, AJ, 127, 180 [NASA ADS] [CrossRef] [Google Scholar]
- Capozzi, D., De Filippis, E., Paolillo, M., D’Abrusco, R., & Longo, G. 2009, MNRAS, 396, 900 [NASA ADS] [CrossRef] [Google Scholar]
- Carliles, S., Budavári, T., Heinis, S., Priebe, C., & Szalay, A. S. 2010, ApJ, 712, 511 [NASA ADS] [CrossRef] [Google Scholar]
- Collister, A. A., & Lahav, O. 2004, PASP, 116, 345 [NASA ADS] [CrossRef] [Google Scholar]
- Cowie, L. L., Barger, A. J., Hu, E. M., Capak, P., & Songaila, A. 2004, AJ, 127, 3137 [NASA ADS] [CrossRef] [Google Scholar]
- Csabai, I., Budavári, T., Connolly, A. J., et al. 2003, AJ, 125, 580 [NASA ADS] [CrossRef] [Google Scholar]
- D’Abrusco, R., Staiano, A., Longo, G., et al. 2007, ApJ, 663, 752 [NASA ADS] [CrossRef] [Google Scholar]
- Davidon, W. C. 1968, Comput. J., 10, 406 [Google Scholar]
- Euclid Red Book, ESA Technical Document, 2011, ESA/SRE(2011)12 [arXiv:astro-ph/1110.3193] [Google Scholar]
- Fletcher, R. 1970, Comp. J., 13, 317 [Google Scholar]
- Giavalisco, M., Ferguson, H. C., Koekemoer, A. M., et al. 2004, ApJ, 600, L93 [NASA ADS] [CrossRef] [Google Scholar]
- Geisser, S. 1975, J. Am. Statist. Assoc., 70, 320 [Google Scholar]
- Goldfarb, D. 1970, Math. Comput., 24, 23 [Google Scholar]
- Hildebrandt, H., Wolf, C., & Benitez, N. 2008, A&A, 480, 703 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hildebrandt, H., Arnouts, S., Capak, P., Wolf, C., et al. 2010, A&A, 523, A31 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hogg, D. W., Cohen, J. G., Blandford, R., et al. 1998, ApJ, 115, 1418 [Google Scholar]
- Huterer, D., Takada, M., Bernstein, G., & Jain, B. 2006, MNRAS 366, 101 [Google Scholar]
- Koo, D. C. 1999, ASP Conf. Ser., 191, 3, eds. Weymann, Storrie-Lombardi, Sawicki & Brunner [NASA ADS] [Google Scholar]
- Keiichi, U., Medezinski, E., Nonino, M., et al. 2012, ApJ, 755, 56 [NASA ADS] [CrossRef] [Google Scholar]
- Laurino, O., D’Abrusco, R., Longo, G., & Riccio, G. 2011, MNRAS, 418, 2165 [NASA ADS] [CrossRef] [Google Scholar]
- Le Févre, O., Vettolani, G., Paltani, S., et al. 2004, A&A, 428, 1043 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Li, I. H., & Yee, H. K. C. 2008, AJ, 135, 809 [NASA ADS] [CrossRef] [Google Scholar]
- Massarotti, M., Iovino, A., & Buzzoni, A. 2001a, A&A, 368, 74 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Massarotti, M., Iovino, A., Buzzoni, A., & Valls-Gabaud, D. 2001b, A&A, 380, 425 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Mizutani, E., & Dreyfus, S. E. 2001, On complexity analysis of supervised MLP-learning for algorithmic comparisons. In Proceedings of the 14th INNS-IEEE International Joint Conference on Neural Networks (IJCNN) (Washington, DC, Jul.), 347, 352 [Google Scholar]
- Noll, S., Mehlert, D., Appenzeller, I., et al. 2004, A&A, 418, 885 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Peacock, J. A., Schneider, P., Efstathiou, G., et al. 2006, ESA-ESO Working Group on Fundamental Cosmology, Tech. Rep. [Google Scholar]
- Reddy, N. A., Steidel, C. C., Erb, D. K., Shapley, A. E., & Pettini, M. 2006, ApJ, 653, 1004 [Google Scholar]
- Shanno, D. F. 1970, Math. Comput., 24, 647 [Google Scholar]
- Sylvain, A., & Celisse, A. 2010, A survey of cross-validation procedures for model selection, Statistics Surveys, 4, 40 [CrossRef] [Google Scholar]
- Treu, T., Ellis, R. S., Liao, T. X., & van Dokkum, P. G. 2005, ApJ, 633, 174 [NASA ADS] [CrossRef] [Google Scholar]
- Vashist, R., & Garg, M. L. 2012, A Rough Set Approach for Generation and Validation of Rules for Missing Attribute Values of a Data Set, IJCA (0975-8887), 42, 31, 35 [CrossRef] [Google Scholar]
- Wirth, G. D., Willmer, C. N. A., Amico, P., et al. 2004, AJ, 127, 3121 [NASA ADS] [CrossRef] [Google Scholar]
- Wolf, C. 2009, MNRAS, 397, 520 [NASA ADS] [CrossRef] [Google Scholar]
All Tables
Percentages of Not a Number (NaN) in the whole dataset (Col. 3), with 1984 objects and in the trainset (Col. 4) with 515 objects, for each band.
Description of the best experiments for the 18 bands (Exp. n. 37) and the 14 bands datasets (Exp. n. 26).
Comparison of the performances of our MLPQNA (here labeled as QNA) method against all other empirical methods analyzed by PHAT board.
All Figures
 |
Fig. 1 The classical feed-forward architecture of a multi layer perceptron represented as a graph. There are three layers, respectively, input with black nodes, hidden with white nodes and the output represented by a single gray node. At each layer, its nodes are fully connected with each node of the next layer. Each connection is identified by a numerical value called weight, usually a real number normalized in the range [ − 1, + 1] . |
| In the text | |
 |
Fig. 2 Results obtained by our model and provided by the PHAT contest board in terms of direct comparison between our photometric and blind spectroscopic information. The a) panel plots the photometric vs. spectroscopic redshifts for the whole dataset using 10 photometric bands (Experiment 37). In panel b) the same but using only 14 photometric bands (Experiment 26). (Courtesy of H. Hildebrandt). |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


