| Issue |
A&A
Volume 546, October 2012
|
|
|---|---|---|
| Article Number | A42 | |
| Number of page(s) | 9 | |
| Section | Stellar structure and evolution | |
| DOI | https://doi.org/10.1051/0004-6361/201118666 | |
| Published online | 02 October 2012 | |
Mass-loss predictions for evolved very metal-poor massive stars
1 Astronomical Institute “Anton Pannekoek”, University of Amsterdam, Science Park 904, 1098 Amsterdam, The Netherlands
2 Armagh Observatory, College Hill, Armagh BT61 9DG, Northern Ireland, UK
e-mail: jsv@arm.ac.uk
3 Astronomical Institute, Utrecht University, Princetonplein 5, 3584 CC Utrecht, The Netherlands
4 Astrophysics Group, EPSAM Institute, University of Keele, Keele, ST5 5BG, UK
5 Institute for the Physics and Mathematics of the Universe, University of Tokyo, 5-1-5 Kashiwanoha, Kashiwa, 277-8583, Japan
6 Argelander-Institut für Astronomie der Universität Bonn, Auf dem Hügel 71, 53121 Bonn, Germany
Received: 16 December 2011
Accepted: 5 September 2012
Context. The first couple of stellar generations may have been massive, of order 100 M⊙, and to have played a dominant role in galaxy formation and the chemical enrichment of the early Universe. Some fraction of these objects may have died as pair-instability supernovae or gamma-ray bursts. The winds of these stars may have played an important role in determining these outcomes. As the winds are driven by radiation pressure on spectral lines, their strengths are expected to vary with metallicity. Until now, most mass-loss predictions for metal-poor O-type stars have assumed a scaled-down solar-abundance pattern. However, Population III evolutionary tracks show significant surface enrichment through rotational mixing of CNO-processed material, because even metal-poor stars switch to CNO-burning early on.
Aims. We address the question of whether the CNO surface enhanced self-enrichment in the first few generations of stars could impact their mass-loss properties.
Methods. We employ Monte Carlo simulations to establish the local line-force and solve for the momentum equation of the stellar outflow, testing whether an outflow can actually be established by assessing the net acceleration at the sonic point of the flow. Stellar evolution models of rotating metal-poor stars are used to specify the surface chemical composition, focussing on the phases of early enrichment.
Results. We find that the mass-loss rates of CNO enhanced metal-poor stars are higher than those of non-enriched stars, but they are much lower than those rates where the CNO abundance is included in the total abundance Z. Metal-poor stars hotter than ~50 000 K, in the metallicity range investigated here (with an initial metallicity Z ≲ 10-4) are found to have no wind, as the high-ionization species of the CNO elements have too few strong lines to drive an outflow. We present a heuristic formula that provides mass-loss estimates for CNO-dominated winds in relation to scaled-down solar abundances.
Conclusions. CNO-enriched or not, the winds of metal-poor stars are generally found to be too weak to contribute significantly to the overall mass loss. Population III supernovae are thus expected to be responsible for the bulk of the early nucleo-synthetic enrichment, unless additional mass-loss mechanisms such as η Carinae type eruptions or steady mass loss close to the Eddington/Omega limit is important.
Key words: stars: abundances / stars: early-type / stars: winds, outflows / stars: evolution / stars: interiors / stars: mass-loss
© ESO, 2012
1. Introduction
In the present-day Universe, massive stars lose a substantial fraction of their initial mass through stellar winds, which they experience from the moment they form to the moment they end their life as a supernova (SN). These winds are driven by radiation pressure on spectral lines, and their strengths are thus expected to be a function of chemical composition; the lower the metal content, the weaker the winds. The dependence of mass loss on metallicity, Ṁ(Z), has been studied in detail, both observationally (Puls et al. 1996, 1998; Mokiem et al. 2007) and theoretically (Vink et al. 2001; Kudritzki 2002; Krtička & Kubát 2006; Vink & de Koter 2005; Gräfener & Hamann 2008). For a recent review, see e.g., Puls et al. (2008).
Studies of star formation in the early Universe suggest that the first stars (Pop III) were typically more massive than present-day objects, with ~102 M⊙ for zero metallicity (Z) objects (Abel et al. 2002; Bromm et al. 2002; Nakamura & Umemura 2002; Bromm & Larson 2004; Loeb et al. 2008). Very massive stars (VMS) of zero metallicity are considered to be the prime candidates for the re-ionization of the universe (e.g., Haehnelt et al. 2001; Wyithe & Loeb 2003, at redshifts above six (Becker et al. 2001). Therefore, it is particularly interesting to ponder on the question of how much mass these first generations of stars might have lost through stellar winds prior to explosion.
The existence of VMS with masses up to 300 M⊙ has recently been claimed for the very luminous stars in the LMC cluster R136 (Crowther et al. 2010; Bestenlehner et al. 2011). At high metallicity, mass loss is thought to be strong enough to shed most of the initial mass, such that the objects may retain only ~30 M⊙, and are expected to die as a SN Ic (Heger et al. 2003). However, as mass loss depends on Z, below a certain threshold metallicity, VMS would be expected to retain most of their initial mass. If this is indeed the case, some, or maybe even a large number of VMS might be expected to die as pair-instability supernovae (PISNe) in the early Universe. The stellar yields of such Pop III PISNe have been computed by Heger & Woosley (2002). These yields are significantly different from those of “normal” core-collapse SNII. PISNe produce orders of magnitude more iron (up to tens of solar masses) and have a conspicuous yield pattern with abundances of even Z elements consistently higher than those of odd Z elements (the so-called odd-even effect).
Observations of carbon-rich chemically extremely metal-poor (CEMP) stars have been accumulated over the last two decades, but the specific PISN signature remains as yet elusive (Umeda & Nomoto 2005). It appears that there is a piece of the puzzle missing in our understanding of the evolution of the first stars. One possibility is that Pop III stars were born with masses either higher or lower than the range expected for PISNe (140–260 M⊙), alternatively “something else” must happen during their evolution, which would avoid the expected fate as a PISN. This could well be mass loss.
Mass loss at low Z may also have interesting implications for globular-cluster research, as globular clusters display a strong abundance scatter amongst many of the light elements (Li, C, N, O, Na, Mg, Al). One explanation for these peculiar abundance patterns involves a first generation of massive stars that polluted the cluster before the second generation of stars formed (Decressin et al. 2007). Finally, if the time-integrated loss of mass is very small, or even negligible, the Pop III stars may have left intermediate mass black holes (of masses ~102 M⊙), which could have provided the building blocks of the supermassive black holes detected in the centers of galaxies today (Kawakatu et al. 2005).
It is clear that there are many reasons to study Ṁ(Z). Kudritzki (2002) and Krtička & Kubát (2006) found that massive zero-metallicity objects may drive only very weak winds or no winds at all. Evolutionary predictions for very metal poor stars, especially if they are rapidly rotating, show the surfacing of sometimes large quantities of primary carbon, nitrogen and oxygen produced in situ (e.g., Yoon & Langer 2005; Meynet et al. 2006; Yoon et al. 2006; Hirschi 2007). One may wonder whether the surfacing of such material may cause (dramatic) changes in the mass-loss behavior of these objects. This question is the topic of this study. We present tailored mass-loss predictions for evolutionary stages of metal-poor stars in which substantial amounts of CNO processed material is expected to have surfaced. These predictions thus differ from the theoretical studies mentioned in the first paragraph, in which scaled solar metallicities are used for O-stars.
The first investigation in this direction was performed by Vink & de Koter (2005) who studied the winds of CNO-enhanced atmospheres at low iron metallicities (down to Z/Z⊙ = 10-5). The enhanced wind driving by CNO-elements discovered was the reason to study whether primary carbon or nitrogen in the atmospheres of extremely metal-poor massive stars might boost the mass-loss rates, and potentially prevent the occurrence of pair-instability supernovae (Vink 2006). Such complete stellar disruptions are hypothesized to occur for initial masses in the range M = 140 − 260 M⊙ if mass loss is negligibly small (Heger et al. 2003; Langer et al. 2007). Krtička & Kubát (2009) investigated the winds of enriched metal-free stars, describing the physics of line-driven winds following Castor et al. (1975, hereafter CAK). One interesting aspect of their work is that during the initial hot phase (>50 000 K) of the evolution of metal-poor stars with initial mass above ~30 M⊙ also CNO-enriched stars fail to produce a stellar wind. Overall, it was concluded that the surfacing of primary CNO does not produce stellar winds strong enough to have a major impact on the evolution of metal-poor massive stars.
Our predictions are based on a newly developed self-consistent dynamical treatment of stellar winds by Müller & Vink (2008) and Muijres et al. (2012) based on a description of the line force that results from a Monte Carlo simulation. In Sect. 2 we introduce this method and discuss the evolutionary tracks on which the adopted chemical compositions are based. Section 3 presents the results. These are discussed in Sect. 4, as well as compared to the results of Vink et al. (2001) – often applied in evolutionary calculations – and Krtička & Kubát (2009). We end with our conclusions.
2. Method
In this section, we present our method for predicting mass loss rates for massive stars at very low metallicity. Distinctive for these computations is that a tailored chemical composition of the surface layers is used to compute the radiative line driving. The adopted surface abundance patterns are motivated using evolutionary tracks for rotating metal-poor stars. In Sects. 2.1 and 2.2 we present and discuss our wind models. Consulted evolutionary tracks are discussed in Sect. 2.3. The adopted grid is presented in Sect. 2.4.
2.1. Wind models
To determine mass-loss rates, we use an iterative method, as developed by Müller & Vink (2008) and Muijres et al. (2012), in which isa-wind model atmospheres (de Koter et al. 1993) are used to describe the model atmosphere and mc-wind models (de Koter et al. 1997; Vink et al. 1999) to treat the wind dynamics. The latter uses a Monte Carlo approach based on the method developed by Abbott & Lucy (1985). The advantageous aspects of this approach are that multiple photon scatterings are taken into account, that excitation/ionisation changes of the gas are treated self-consistently, and that one can quite easily dissect the relative contributions of individual species to the line force. Essential aspects of the wind dynamics are summarized in Sect. 2.2. First, we briefly summarize the main assumptions of the model atmospheres. For further details we refer the reader to the above references.
We assume the wind to be homogeneous, spherically symmetric and stationary. Our model atmospheres extend from the base of the photosphere to approximately 20 stellar radii. For hydrogen, helium, carbon, nitrogen, oxygen, and silicon, we solve the ionization state and the occupation numbers of the levels in non-local thermodynamical equilibrium (NLTE). The other elements are treated using a modified nebular approximation. The radiative transfer in lines is calculated using the Sobolev method (Sobolev 1960).
To compute the line force we make a selection of the strongest lines from the line-list in Kurucz & Bell (1995). This line list is essentially complete for the ions that play an important role in driving the winds studied here. Transitions of the CNO elements of ionization species C v, N vi and O vi or higher are not considered. These ions with one or few bound electrons have only few lines in the part of the spectrum that coincides with the flux maximum of the stellar radiation. As ionization of all these species depends on the radiation field in the He ii continuum above 54.4 eV they would remain trace species in our models. Shocks in the outflows of massive stars (see Kudritzki & Puls 2000, for a discussion/review) may heat a fraction of the gas to higher temperatures and produce non-thermal emission at soft X-ray wavelength. Such effects may increase the importance of transitions of these highly ionized species, although it is unlikely that an associated increase in line force is significant. We therefore do not expect that the lack of these lines has an important impact on our mass loss predictions. Finally, we note that we miss part of the transitions of N vi. However, for similar reasons we do not think that this affects our results in any notable way.
2.2. Wind dynamics
The main challenge faced in determining the structure of a line driven stellar wind is the strong, but delicate, interaction between radiation, line force, and atmospheric structure: the radiation field and the density (or velocity) structure set the excitation/ionisation state of the gas. The line force results from the structure and the state of the gas, while, in turn, the line force sets the structure, therefore indirectly also the radiation field. We try to tackle this problem through an iterative process. By assuming a velocity law and a mass-loss rate we can determine the excitation/ionization structure. Next, the line force is calculated. Based on a fit to the line force the velocity law is re-determined. A model is considered converged once the fit parameters of the line force fit function and the mass-loss rate do not change significantly from one iteration step to the next.
The procedure followed is based on the method described by Müller & Vink (2008) and Muijres et al. (2012), that improve on the treatment developed by de Koter et al. (1997) and Vink et al. (1999), and applied by Vink et al. (e.g., 2000, 2001) Actually, the Müller & Vink and Muijres et al. studies present two approaches to deal with the equation of motion. In one solution, referred to as best-β method, the velocity law is assumed to be a β-law (Lamers & Rogerson 1978). A fit function to the line force is constructed that is used to find the most appropriate terminal velocity ν∞ and measure for the rate of acceleration in the lower part of the wind, expressed by β. In the other solution the fit function to the line force is used to numerically solve the equation of motion, referred to as the hydrodynamical method. Both methods are compared in Muijres et al. (2012), where it is found that the derived mass-loss rates do not differ more than about 25 percent and that the terminal wind velocities agree within 20 percent.
The hydrodynamical method is dynamically consistent but is sensitive to the quality of the fit to the line force at the base of the wind, and therefore less stable. In the range of parameter space investigated in this article, we anticipate this to be more problematic than for the main sequence O-stars studied by Muijres et al. (2012). For this reason we apply the best β-method from Müller & Vink (2008).
The best β-method is, strictly speaking, not dynamically consistent. This warrants caution. Muijres et al. (2012) discuss this issue in detail. They identify the solution to be physically correct only if the effective gravity geff – i.e. the Newtonian gravity corrected for forces due to continuum radiation pressure – approximately balances the line force gline at the location of the sonic point rs, i.e. 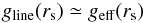 (1)the sonic point corresponds to the radial distance where the flow velocity reaches the local sound speed. We compare the line force as simulated by the Monte Carlo code to the effective gravity and conclude that if the latter differs from the line force by more than 20 percent the wind can not be driven by line radiation pressure alone. Phrased differently: in this case our model does not drive a wind.
(1)the sonic point corresponds to the radial distance where the flow velocity reaches the local sound speed. We compare the line force as simulated by the Monte Carlo code to the effective gravity and conclude that if the latter differs from the line force by more than 20 percent the wind can not be driven by line radiation pressure alone. Phrased differently: in this case our model does not drive a wind.
The condition Eq. (1) is more sophisticated than the one applied by Krtička & Kubát (2009). In their approach they apply a test to establish whether a wind is driven that does not involve solving the equation of motion, and requires specification of the wind mass-loss rate.
2.3. Evolutionary tracks
Evolutionary tracks for rotating metal-poor massive stars have been computed by Yoon & Langer (2005), Meynet et al. (2006), Yoon et al. (2006) and Hirschi (2007). The set of models by Yoon & Langer are for initially 12 to 60 M⊙ stars. They span the metallicity range Z = 10-5 to 2 × 10-3 and cover initial equatorial rotation velocities between zero and 80 percent of the Keplerian value. In these tracks, transport of angular momentum is due to Eddington-Sweet circulations, shear instability, Goldreich-Schubert-Fricke instability, and magnetic torques, and is approximated by diffusion. In most cases, magnetic torques dominate, that are described in the context of the Spruit-Tayler dynamo (Spruit 2002), as explained by Heger et al. (2005). The tracks by Hirschi (2007) are for initial masses between 20 and 85 M⊙ and cover metal fractions Z = 10-8 to 0.02 and rotational velocities from zero to 800 km s-1. Instabilities accounted for by Hirschi are meridional circulation (treated as an advective process), and secular and dynamical shear instabilities (treated as diffusion).
 |
Fig. 1 Evolutionary tracks for metal-poor stars. The green track is for Minit = 40 M⊙, Z = 10-5 and for a rotational velocity that is vrot = 555 km s-1 (Yoon et al. 2006). This model evolves homogeneously. The red track is for Minit = 85 M⊙, Z = 10-8 and vrot = 800 km s-1 (Hirschi 2007). The blue pluses denote (L, Teff) combinations for which mass-loss rates have been computed using abundance patterns that are typical for the surface composition of the evolutionary tracks. |
Typical examples of the two sets of tracks are shown in Fig. 1. Interestingly, the rapidly rotating tracks of Yoon & Langer (2005) and Yoon et al. (2006) evolve more or less along the zero age main sequence (ZAMS) toward higher luminosities. Hence, these stars remain hot and compact. The tracks of Hirschi (2007) evolve away from the ZAMS, into the cool range of the Hertzsprung-Russell diagram. This striking difference between the evolutionary tracks of the two groups is probably due to the inclusion of magnetic field in the Yoon et al. models. The different implementations of transport processes between the models might also have an impact and should be investigated properly but this is beyond the scope of this paper.
Different prescriptions are used to account for mass loss. Yoon & Langer (2005) and Yoon et al. (2006) use results by Kudritzki et al. (1989), assuming a metallicity dependence Ṁ ~ Z0.69 from Vink et al. (2001). For Wolf-Rayet phases they use results by Hamann et al. (1995), reduced by a factor 10, and a metallicity dependence as proposed by Vink & de Koter (2005). An ad hoc recipe for the effect of the increased CNO abundances on the mass loss is used. Hirschi (2007) adopt the mass-loss recipes from Nugis & Lamers (2000) for Wolf Rayet phases. For O- and B-star phases, they use Vink et al. (2001). For stars cooler than 12 500 K they use de Jager et al. (1988). An artifact of the recipe of de Jager et al. is that for luminous but cool stars (below ~10–20 kK, depending on luminosity), outside of the range of validity of the fitting function, a 20-term Chebychev polynomial, unrealistically large mass-loss rates are produced (of order 10-2 M⊙ yr-1). This rapidly strips stars of their outer envelope, causing the tracks of Hirschi (2007) to become strongly enriched in this part of the HRD. A feedback occurs, as the metallicity associated with the enriched surface causes a high mass loss once they evolve back to higher temperatures. This implies that the surface enrichment in the blue-ward tracks of Hirschi is strongly dependent on this (extreme) mass-loss history.
2.4. Grid
We limit the grid of models to the temperature range from 20 kK to 50 kK and the luminosity interval from 105.5 to 106.25 L⊙. The reason why we did not try hotter models – although predicted by Yoon et al. (2006) – is explained below. Essentially, for such high temperatures in combination with a low iron group metal content we do not find sufficient line driving to sustain a stellar wind. We encounter convergence problems of the model atmospheres for temperatures close to 10 000 K because convection is not accounted for. To avoid convection becoming an issue, we adopt 20 kK as the low end of the investigated temperature range.
For the surface abundance of carbon, nitrogen and oxygen combined, ZCNO, as well as the relative abundances of these three elements we assumed values that are typical – but, deliberately, not tailored – for the predictions of Yoon et al. (2006) and Hirschi (2007). Having said this, the abundance choices best fit the 85 M⊙, Z = 10-8 and vrot = 800 km s-1 track for the case of Hirschi and the 40 M⊙, Z = 10-5 and vrot = 555 km s-1 track for the Yoon et al. case. These are the tracks that are shown in Fig. 1. For the Hirschi case we selected two compositions, one that is characteristic for the start of the surfacing of CNO processed material by rotational mixing (termed Case 1) and one that is typical for the end of this mixing phase (termed Case 2), but before the phase of extreme mass loss as discussed in Sect. 2.3. The stars computed by Yoon et al. evolve on a chemically homogeneous track and are helium stars at the point they are enriched with hydrogen burning products. We adopt a relative CNO abundance that is typical for the start of enrichment (termed Case 4). To separate the effects of the H/He ratio from CNO abundance effects we introduce an intermediate Case 3 in which the H/He ratio was assumed to be equal to the H/He ratio from the Hirschi track. An overview of these abundance patterns is provided in Table 1.
For all these cases we adopt three values of ZCNO, i.e. 0.002, 0.02 and 0.04. For abundances of other elements, we adopt the solar values from Anders & Grevesse (1989) and scale them down to the metallicities as listed in Table 1. We note that these other elements do not contribute to the wind driving.
Adopted abundance patterns.
3. Results
3.1. Mass-loss behavior
The overall trends in the behavior of the predicted mass-loss rates are as follows: for iron-group metallicities below ~10-4 (in line with Vink et al. 2001) and no primary enrichment of the atmosphere with carbon, nitrogen and oxygen we find that we can not drive an outflow. Only for ZCNO ~ 10-3 or higher, the CNO elements can drive a stellar wind – if circumstances are favorable. For temperatures of 50 kK or higher the CNO elements are highly ionized. These ionic species – such as C v, N v and O v – have relatively simple atomic level configurations, resulting in only few lines near the flux maximum of the emergent spectrum. The cumulative radiation pressure of these lines, supplemented with a contribution by hydrogen and helium lines that is diminishing for increasing temperature, is insufficient to power a wind. Therefore, we do not predict stars hotter than ~50 kK to have a line-driven outflow.
 |
Fig. 2 Derived mass loss rates versus predictions by Vink et al. (2001) (denoted ṀV) for Z = 0.04 (top panel), Z = 0.02 (middle panel) and Z = 0.002 (bottom panel). The coefficients of the power law fits are given in Table 2. |
Table 3 presents the Ṁ, ν∞, and β predictions for our grid. For these models, characterized by a line driving that is on the brink of being sufficient to drive a wind, numerical uncertainties as well as the accuracy of the physical solution requirement Eq. (1) may play a role in whether or not a solution is found. Typical uncertainties in the (iterative) numerical method itself are 0.1–0.2 dex in the mass-loss rate and ~30% in the terminal velocity. To avoid over-interpretation of individual models, we opt to present the results in terms of their overall characteristics. Moreover, to provide a frame of reference we compare the computed mass-loss rates with predictions based on the recipe of Vink et al. (2001). These reference rates are referred to as ṀV and are also provided in Table 3.
The Vink et al. recipe has been derived for a chemical composition of all elements apart from hydrogen and helium (i.e. the metallicity in the astrophysical context) that is scaled to the solar composition as given by Anders & Grevesse (1989). We compare our mass loss Ṁ with ṀV by identifying ZCNO of the models presented here as the metallicity Z as intended by Vink et al. Clearly, as a general trend we may expect that the Vink et al. recipe predicts larger mass-loss rates compared to the values computed here, as iron-group elements are more efficient in driving the wind through the sonic point than are lines of CNO only.
The ṀV-recipe is valid for stars that are not too close to their Eddington limit. In terms of the ratio of the radiation pressure on free electrons to the Newtonian gravity, i.e. Γe = ge/gN, all ṀV predictions are for Γe ≲ 0.4. An extension of these predictions for stars close to their Eddington limit by Vink et al. (2011) shows that for Γe ≲ 0.7 the standard ṀV-recipe remains unaltered. The largest value of Γe in the computations presented in this study are Γe ~ 0.5 for models in which the luminosity log L/L⊙ = 6.25. We conclude that effects of approaching the Eddington limit do not complicate the comparison of our results to the ṀV predictions.
The outcome of the comparison is shown in Fig. 2, for the three different values of ZCNO, together with a power-law fit. The coefficients of these fits are listed in Table 2. In all cases the behavior is approximately 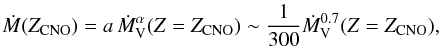 (2)where the mass-loss rates are in units of M⊙ yr-1. Note that the metallicity Z here concerns the CNO abundance, which is disjunct from the mass-loss Z relations provided by Vink & de Koter (2005) for WR stars where Z referred to the Fe abundance. We point out that the relation is only valid for the temperature range 20 kK to ~50 kK, and as long as the iron-group mass fraction is extremely low, i.e. below a few times 10-4 Z⊙, in rough agreement with the mass-loss plateau of 10-3 Z⊙ found by Vink & de Koter (2005) for late-type WC stars. The error in the relation is typically a factor of three.
(2)where the mass-loss rates are in units of M⊙ yr-1. Note that the metallicity Z here concerns the CNO abundance, which is disjunct from the mass-loss Z relations provided by Vink & de Koter (2005) for WR stars where Z referred to the Fe abundance. We point out that the relation is only valid for the temperature range 20 kK to ~50 kK, and as long as the iron-group mass fraction is extremely low, i.e. below a few times 10-4 Z⊙, in rough agreement with the mass-loss plateau of 10-3 Z⊙ found by Vink & de Koter (2005) for late-type WC stars. The error in the relation is typically a factor of three.
Fit parameters, expressing our predicted mass-loss rates for winds driven by carbon, oxygen and nitrogen lines, in terms of the mass-loss rates ṀV as predicted by Vink et al. (2001): 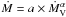 .
.
Let us appraise some aspects of Eq. (2). For a Vink et al. (2001) mass loss of 10-6 M⊙ yr-1, our models imply a mass loss that is 0.3 dex lower for ZCNO = 0.002; 0.8 dex lower for ZCNO = 0.02, and 1.0 dex lower for ZCNO = 0.04. So, for progressively higher CNO enrichments the discrepancy with ṀV increases. This reflects the fact that the driving power of the CNO lines is topped once the relevant driving lines become saturated. An increase of the iron-group metal content to high metallicities of 0.02–0.04 does not suffer from this effect as most of the iron lines that drive the wind are relatively weak. Consequently, the mass-loss rate of a wind in which the gas composition scales to the solar abundance pattern continues to rise with increasing metallicity. The fact that the main CNO driving lines are saturated in the ZCNO range explored here implies that the absolute mass-loss rates of metal-poor stars enriched with primary CNO must be essentially independent of ZCNO. Indeed, this is what we find.
3.2. Hydrogen rich versus helium rich stars
We find that overall it is more challenging for helium rich stars to drive a wind, if all other stellar parameters (notably stellar mass) remain unaltered. We identify two reasons for this. First, helium does not provide as many free electrons as hydrogen does. Therefore the contribution of the free electrons to the radiative force is less. Second, the contribution of the helium lines to the radiative force is at maximum of the order of the contribution of the hydrogen lines but in many cases less. The latter effect is most relevant for the 20 kK models, where the neutral hydrogen fraction (although small in an absolute sense) is the highest.
The mass loss is found to be independent of H/He ratio. This could, however, only be assessed for the case ZCNO = 0.002. We note that although Cases 3 and 4 are representative for the homogeneously evolving tracks of Yoon et al. (2006), they need not be representative for strongly enriched modestly rotating WNL (that may have ZN > 0.15) or WC stars (that may have ZC > 0.50). Models representative for such “classical” type of Wolf-Rayet stars have been computed by Vink & de Koter (2005).
 |
Fig. 3 Predicted terminal velocities ν∞ for all models normalized to the effective escape velocity at the stellar surface νesc. Symbols and color codings indicate temperature; black symbols represent the H-poor models. Including the outliers towards high ν∞/νesc, the average of the H-rich models increases with ZCNO, from 2.6 to 3.9 to 4.7 for ZCNO = 0.002, 0.02 and 0.04, respectively. |
3.3. Terminal velocity behavior
Figure 3 shows the ratio of the terminal velocity to the effective surface escape velocity as a function of ZCNO, for all converged models in our grid. As for the mass-loss properties we also focus on the overall trends in the terminal flow characteristics. In line-driven winds the nature of the driving lines (both in terms of chemical composition and ionization) is reflected in the ratio ν∞/νesc (see e.g., Castor et al. 1975; Kudritzki & Puls 2000), therefore we discuss our results in these terms.
Adopted model parameters and predicted wind properties.
For the H-rich stars in our grid (Cases 1 through 3) the trend is that ν∞/νesc is increasing with ZCNO. To be quantitative, the ratio increases from 2.7 ± 0.7 to 3.9 ± 1.1 to 4.7 ± 2.4 for ZCNO = 0.002, 0.02 and 0.04, respectively. We note that the scatter in ν∞/νesc is rather large for the highest metallicity, and that for this case the models of 20 000 K only yield a mean ν∞/νesc that is substantially lower, i.e. 3.5 ± 1.2.
The acceleration of the flow in the supersonic part of the wind is – as in galactic O- and early B-stars – controlled by strong lines of CNO (Vink et al. 1999; Puls et al. 2000). In galactic OB-stars the observed ratio of terminal velocity to escape velocity is ~2.6 for stars hotter than 22 000 K and about 1.3 for cooler objects (Lamers et al. 1995). Predictions of this ratio for normal O-stars by Muijres et al. (2012) for the best-β method (see Sect. 2.2) yield ν∞ values that are typically 30% higher than observed. Correcting for this, we still find higher outflows speeds. The reasons why the CNO enriched metal-poor stars produce higher terminal velocities than Galactic stars involves a combination of a lower mass-loss rate and a more efficient driving in the supersonic part of the outflow, due to the high abundances of CNO. Relative changes in the abundances of carbon, nitrogen and oxygen (as implied by Cases 1, 2 and 3) have a rather modest effect on ν∞, given the uncertainty in the predictions of the terminal velocity (~30%), this is not significant.
The converged He-rich models (Case 4) at 30 000 K tend to have higher ν∞/νesc ratios than do comparable H-rich models. In the He-rich case the continuum flux in the region where the main driving lines are located is larger, therefore these lines are more efficient, leading to larger ν∞.
4. Discussion
4.1. Comparing to other studies
Mass loss from luminous metal-free O-type stars enriched with primary CNO has been studied by Krtička & Kubát (2009), using stellar parameters from the evolutionary tracks for first stars, formed from metal-free gas clouds in the early Universe, by Marigo et al. (2001, 2003). A quantitative comparison of our results for metal-poor stars with those of Krtička & Kubát (2009) cannot be made because of the large differences in stellar parameters and surface ZCNO abundances. Yet, we provide a rough comparison for a limited number of models. Accounting for the uncertainties introduced in their model grid spacing, Krtička & Kubát found a similar Teff boundary for which stars in similar luminosity ranges can drive winds: stars must be cooler than ~60–50 kK. Accepting a ~10% difference in the stellar mass, we find similar mass-loss rates for our model with ZCNO = 0.02, Teff = 20 kK and log L/L⊙ = 5.9 (see their model M500-3): the difference is ~0.2 dex. However, we obtain a terminal velocity that is 20–40 percent lower, depending on the exact choice of chemical patterns.
We note that there are both similarities and differences in our treatment of the stellar atmosphere and wind and those by Krtička & Kubát. In both methods the state of the gas is treated in NLTE, whilst the Sobolev approximation is used to describe the transfer of radiation in spectral lines. Krtička & Kubát, however, treat the photosphere – from where the continuum radiation originates – and wind separately. They adopt an emergent flux taken from H-He model atmospheres, whereas we treat the photosphere and wind in a self-consistent, unified way. Moreover, in our Monte Carlo treatment we self-consistently account for multiple scattering effects, which are ignored in the Krtička & Kubát approach. For the type of models discussed here, these differences are not likely to cause major differences.
More important, however, is the difference pointed out in Sect. 2.2. Krtička & Kubát apply a test in order to assess whether a wind can be sustained that is much simpler than the method applied here. The advantage of their criterion is that it allows one to a priori determine whether a star can drive a wind. However, such a test does not fully capture the feedback between line driving and wind density, nor does it fulfill the requirement of dynamical consistency. For the most luminous objects, we can compare models at both 30 kK and 20 kK, again for ZCNO = 0.02 (their models M999-1 and M999-2). Here we find a mass-loss rate that is ~0.3–0.7 dex lower, while terminal velocities are lower by ~20 percent. Here it should be noted that Krtička & Kubát adopt a mass of 100 M⊙, while the tracks on which we rely suggest ~80 M⊙.
This necessarily very limited comparison suggests that we predict roughly similar mass-loss rates for stars of initially 50–75 M⊙, but that for more massive stars, in the range of 75–100 M⊙ our mass-loss rates are lower by a factor of a few.
4.2. How to apply *error*Ṁ(ZCNO)
Vink et al. (2001) point out that their recipe is valid for a scaled solar metallicities as low as 1/30 Z⊙ for luminosities less than a million solar luminosities, and 1/100 Z⊙ for more luminous objects. Their adopted solar values are from Anders & Grevesse (1989), in which Z⊙ = 0.019. In exploring the line-driving at their lowest metal contents, Vink et al. (2001) already detect an increasing relative importance of CNO. Moreover, they point out that the occurrence of the bi-stability jump at about 35 000 K at very low metal content due to the recombination of ions of a CNO element, i.e. C iv to C iii (Vink 2000). We tested whether neglecting the up-turn in mass-loss for stars cooler than 35 000 K in the present-day Universe in the ṀV-recipe improved or degraded the correlation presented in Fig. 2 and Table 2. This significantly degraded the correlation.
To provide a simple recipe to adjust the Vink et al.-recipe for models that show primary enrichment, we propose the heuristic formula: 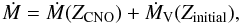 (3)where Zinitial is the initial metal content of the star and ZCNO is the primary CNO abundance. Ṁ(ZCNO) is given by Eq. (2). In the ṀV-recipe, the bi-stability jump should still be applied. Equation (3) is valid for Teff < 50 kK. For hotter temperatures and abundances below Z ~ a few 10-4 (Vink et al. 2001), we do not predict stars to lose mass in a line-driven wind. The validity of the ṀV formula extends to temperatures as low as 12 500 kK. The new ṀCNO predictions have been computed down to 20 000 kK. A modest extrapolation may be applied, although most certainly not below 15 000 kK. The highest ZCNO abundance in our computations is 0.04. Again, some extrapolation may be acceptable. However, for chemical compositions that are more typical for evolved Wolf-Rayet objects (ZCNO ≳ 0.1), we refer to Vink & de Koter (2005). The lowest ZCNO abundance in our computations is 0.002. The minimum ZCNO for which a wind may be driven is a function of luminosity, proximity to the Eddington limit, and, to a lesser extent, detailed chemical abundance pattern. However, the mass-loss rates associated with such low CNO abundances will not impact the overall mass-loss and/or angular momentum loss of these stars (see Sect. 4.3). This largely removes a practical need to define the limit below which metal-poor stars may or may not drive a wind.
(3)where Zinitial is the initial metal content of the star and ZCNO is the primary CNO abundance. Ṁ(ZCNO) is given by Eq. (2). In the ṀV-recipe, the bi-stability jump should still be applied. Equation (3) is valid for Teff < 50 kK. For hotter temperatures and abundances below Z ~ a few 10-4 (Vink et al. 2001), we do not predict stars to lose mass in a line-driven wind. The validity of the ṀV formula extends to temperatures as low as 12 500 kK. The new ṀCNO predictions have been computed down to 20 000 kK. A modest extrapolation may be applied, although most certainly not below 15 000 kK. The highest ZCNO abundance in our computations is 0.04. Again, some extrapolation may be acceptable. However, for chemical compositions that are more typical for evolved Wolf-Rayet objects (ZCNO ≳ 0.1), we refer to Vink & de Koter (2005). The lowest ZCNO abundance in our computations is 0.002. The minimum ZCNO for which a wind may be driven is a function of luminosity, proximity to the Eddington limit, and, to a lesser extent, detailed chemical abundance pattern. However, the mass-loss rates associated with such low CNO abundances will not impact the overall mass-loss and/or angular momentum loss of these stars (see Sect. 4.3). This largely removes a practical need to define the limit below which metal-poor stars may or may not drive a wind.
We point out that in terms of proximity to the Eddington limit, the stars investigated show Eddington factors Γe up to ~0.5. We therefore do not exclude that metal-poor stars very close to their Eddington limit may still drive a wind through line radiation pressure, as discussed by Kudritzki (2002); Vink & de Koter (2002, 2005); Krtička & Kubát (2006); Gräfener & Hamann (2008); Vink et al. (2011).
4.3. Implications for the evolution of metal-poor stars
Although the surfacing of CNO-cycle products may make the difference in whether or not a metal-poor star can produce a line-driven wind or not, the actual mass-loss rate such stars feature is only modest. Absolute values of Ṁ for the grid of stars presented here are in the range 10-6–10-7 M⊙ yr-1. Whilst substantial surface enrichment may only occur after a significant part of the life of metal-poor massive stars, even when simply assuming this would happen shortly after reaching the main-sequence the cumulative mass-loss is only ~1 M⊙ for a 30 M⊙ star and ~10 M⊙ for a 80 M⊙ star. So, at most a few percent of the initial mass, but likely less than that. This is similar to the conclusions reached by Vink & de Koter (2005) and Krtička & Kubát (2009).
Purely by line-driven winds, metal-poor and initially metal-free stars may inject at total of the order of 10-3 − 10-1 M⊙ of CNO processed material into their (primordial) surroundings see Hirschi (2007) (Table 3). This is substantially less than the enrichment with CNO and other metals that is to be expected in the (pair-instability) supernova that ends their lives. Still, it may be too early to conclude that a shift from a top-heavy initial mass function (IMF), predicted in simulations of the first star-forming regions (Bromm et al. 1999; Nakamura & Umemura 2002), to a Salpeter (1955) IMF, is due to dust grains formed from supernovae material. This outcome is based on the fact that a line-driven wind is the only mass-loss mechanism a metal-poor or first star may suffer. Rotation close to critical, perhaps in combination with approaching the Eddington limit (Meynet et al. 2006) and/or pulsations (Baraffe et al. 2001) may boost the mass-loss rate of these objects. Mass-loss eruptions in a post-main sequence phase, as for instance suffered by the massive star η Carinae (Humphreys & Davidson 1994), might play a role in the early Universe as well. So, far the exact nature of these eruptions eludes us (see Owocki et al. 2004), and possibly this mechanism does not depend on the chemical composition. If so, this type of mass-loss may have played a relatively important role in the Universe early-on.
5. Conclusions
We presented mass-loss calculations of metal-poor massive stars that, as a result of rotational mixing, have become enriched at their surface with products of primary CNO burning. From predictions of the evolution of such stars we adopted several characteristic CNO enriched abundance patterns, and for these chemical patterns we performed tailored computations of the mass-loss rates driven by radiation pressure on spectral lines. The formal requirement to drive a wind in this study is that the gravity balances the radiative forces at the sonic point of the flow.
The main conclusions we obtain are:
-
1.
The mass-loss predictionsṀV (Vink et al. 2001) have not been determined for massive metal-poor (Z ≲ 1/100 Z⊙) stars. Applying this formula, and equalizing the CNO enriched chemical pattern to Z, would overestimate the actual mass-loss rate.
-
2.
On the basis of our new calculations, we provide a heuristic formula to estimate the mass-loss rates of such metal poor stars, for the parameter range L ≳ 105.5 L⊙, Teff ≳ 15 000 K and Γe ≲ 0.5, and we propose to apply this formula (Eq. (3)) – expressed as a scaling to the oft-used Vink et al. (2001)-recipe – in evolutionary predictions of such objects.
-
3.
Metal-poor and surface CNO enriched massive stars hotter than 50 000 K do not feature a line-driven wind; highly ionized carbon, nitrogen and oxygen ions provide too few efficient driving lines. This result is similar to that obtained for metal-free stars by Krtička & Kubát (2009), within the uncertainties in the Teff resolution of the two grid computations. It implies that homogeneously evolving stars (which remain very hot during their entire life) do not have line-driven winds in the initial metallicity range investigated here (Z ≲ 10-4).
-
4.
In the range of ZCNO = 0.002 − 0.04, the mass-loss rate is not a strong function of the ratio of C to N to O.
-
5.
The terminal wind velocities of CNO enriched metal-poor stars are higher than those of massive stars in the present-day Universe. For ZCNO ~ 0.02–0.04 they are 25–50% higher. The reasons for this behavior are a combination of the lower mass-loss rate and a more efficient driving in the supersonic part of the outflow, due to the high abundance of CNO.
-
6.
The winds of massive very metal-poor stars (Z ≲ 10-4), whether they are CNO enriched or not, are so weak that they do not significantly impact the total mass and/or angular momentum loss during their evolution. If other mass-loss mechanisms, such as η Carinae type of mass eruptions, do not occur for such objects, their supernova explosions are expected to be responsible for the bulk of the early nucleo-synthetic enrichment.
Acknowledgments
J.S.V. acknowledges financial support from the UK Science and Technologies Facility Council (STFC). R.H. acknowledges support from the World Premier International Research Center Initiative (WPI Initiative), MEXT, Japan.
References
- Abbott, D. C., & Lucy, L. B. 1985, ApJ, 288, 679 [NASA ADS] [CrossRef] [Google Scholar]
- Abel, T., Bryan, G. L., & Norman, M. L. 2002, Science, 295, 93 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Anders, E., & Grevesse, N. 1989, Geochim. Cosmochim. Acta, 53, 197 [Google Scholar]
- Baraffe, I., Heger, A., & Woosley, S. E. 2001, ApJ, 550, 890 [NASA ADS] [CrossRef] [Google Scholar]
- Becker, R. H., Fan, X., White, R. L., et al. 2001, AJ, 122, 2850 [NASA ADS] [CrossRef] [Google Scholar]
- Bestenlehner, J. M., Vink, J. S., Gräfener, G., et al. 2011, A&A, 530, L14 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bromm, V., & Larson, R. B. 2004, ARA&A, 42, 79 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bromm, V., Coppi, P. S., & Larson, R. B. 1999, ApJ, 527, L5 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Bromm, V., Coppi, P. S., & Larson, R. B. 2002, ApJ, 564, 23 [NASA ADS] [CrossRef] [Google Scholar]
- Castor, J. I., Abbott, D. C., & Klein, R. I. 1975, ApJ, 195, 157 [NASA ADS] [CrossRef] [Google Scholar]
- Crowther, P. A., Schnurr, O., Hirschi, R., et al. 2010, MNRAS, 408, 731 [NASA ADS] [CrossRef] [Google Scholar]
- de Jager, C., Nieuwenhuijzen, H., & van der Hucht, K. A. 1988, A&AS, 72, 259 [NASA ADS] [Google Scholar]
- de Koter, A., Schmutz, W., & Lamers, H. J. G. L. M. 1993, A&A, 277, 561 [NASA ADS] [Google Scholar]
- de Koter, A., Heap, S. R., & Hubeny, I. 1997, ApJ, 477, 792 [Google Scholar]
- Decressin, T., Meynet, G., Charbonnel, C., Prantzos, N., & Ekström, S. 2007, A&A, 464, 1029 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gräfener, G., & Hamann, W. 2008, A&A, 482, 945 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Haehnelt, M. G., Madau, P., Kudritzki, R., & Haardt, F. 2001, ApJ, 549, L151 [NASA ADS] [CrossRef] [Google Scholar]
- Hamann, W., Koesterke, L., & Wessolowski, U. 1995, A&A, 299, 151 [NASA ADS] [Google Scholar]
- Heger, A., & Woosley, S. E. 2002, ApJ, 567, 532 [NASA ADS] [CrossRef] [Google Scholar]
- Heger, A., Fryer, C. L., Woosley, S. E., Langer, N., & Hartmann, D. H. 2003, ApJ, 591, 288 [NASA ADS] [CrossRef] [Google Scholar]
- Heger, A., Woosley, S. E., & Spruit, H. C. 2005, ApJ, 626, 350 [NASA ADS] [CrossRef] [Google Scholar]
- Hirschi, R. 2007, A&A, 461, 571 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Humphreys, R. M., & Davidson, K. 1994, PASP, 106, 1025 [NASA ADS] [CrossRef] [Google Scholar]
- Kawakatu, N., Saitoh, T. R., & Wada, K. 2005, ApJ, 628, 129 [NASA ADS] [CrossRef] [Google Scholar]
- Krtička, J., & Kubát, J. 2006, A&A, 446, 1039 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Krtička, J., & Kubát, J. 2009, A&A, 493, 585 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kudritzki, R. P. 2002, ApJ, 577, 389 [NASA ADS] [CrossRef] [Google Scholar]
- Kudritzki, R., & Puls, J. 2000, ARA&A, 38, 613 [NASA ADS] [CrossRef] [Google Scholar]
- Kudritzki, R. P., Pauldrach, A., Puls, J., & Abbott, D. C. 1989, A&A, 219, 205 [NASA ADS] [Google Scholar]
- Kurucz, R., & Bell, B. 1995, Atomic Line Data, eds. R. L. Kurucz, & B. Bell, Kurucz CD-ROM No. 23, Cambridge, Mass.: Smithsonian Astrophysical Observatory [Google Scholar]
- Lamers, H. J. G. L. M., & Rogerson, Jr., J. B. 1978, A&A, 66, 417 [NASA ADS] [Google Scholar]
- Lamers, H. J. G. L. M., Snow, T. P., & Lindholm, D. M. 1995, ApJ, 455, 269 [NASA ADS] [CrossRef] [Google Scholar]
- Langer, N., Norman, C. A., de Koter, A., et al. 2007, A&A, 475, L19 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Loeb, A., Ferrara, A., & Ellis, R. S. 2008, First Light in the Universe (Springer) [Google Scholar]
- Marigo, P., Girardi, L., Chiosi, C., & Wood, P. R. 2001, A&A, 371, 152 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Marigo, P., Chiosi, C., & Kudritzki, R. 2003, A&A, 399, 617 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Meynet, G., Ekström, S., & Maeder, A. 2006, A&A, 447, 623 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Mokiem, M. R., de Koter, A., Vink, J. S., et al. 2007, A&A, 473, 603 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Muijres, L., Vink, J. S., de Koter, A., Müller, P. E., & Langer, N. 2012, A&A, 537, A37 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Müller, P. E., & Vink, J. S. 2008, A&A, 492, 493 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Nakamura, F., & Umemura, M. 2002, ApJ, 569, 549 [NASA ADS] [CrossRef] [Google Scholar]
- Nugis, T., & Lamers, H. J. G. L. M. 2000, A&A, 360, 227 [NASA ADS] [Google Scholar]
- Owocki, S. P., Gayley, K. G., & Shaviv, N. J. 2004, ApJ, 616, 525 [NASA ADS] [CrossRef] [Google Scholar]
- Puls, J., Kudritzki, R., Herrero, A., et al. 1996, A&A, 305, 171 [NASA ADS] [Google Scholar]
- Puls, J., Springmann, U., & Owocki, S. P. 1998, in Cyclical Variability in Stellar Winds, eds. L. Kaper, & A. W. Fullerton, 389 [Google Scholar]
- Puls, J., Springmann, U., & Lennon, M. 2000, A&AS, 141, 23 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Puls, J., Vink, J. S., & Najarro, F. 2008, A&ARv, 16, 209 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Salpeter, E. E. 1955, ApJ, 121, 161 [Google Scholar]
- Sobolev, V. V. 1960, Moving envelopes of stars (Harvard University Press) [Google Scholar]
- Spruit, H. C. 2002, A&A, 381, 923 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Umeda, H., & Nomoto, K. 2005, ApJ, 619, 427 [NASA ADS] [CrossRef] [Google Scholar]
- Vink, J. S. 2000, Ph.D. Thesis, Universiteit Utrecht [Google Scholar]
- Vink, J. S. 2006, in Stellar Evolution at Low Metallicity: Mass Loss, Explosions, Cosmology, eds. H. J. G. L. M. Lamers, N. Langer, T. Nugis, & K. Annuk, ASP Conf. Ser., 353, 113 [Google Scholar]
- Vink, J. S., & de Koter, A. 2002, A&A, 393, 543 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Vink, J. S., & de Koter, A. 2005, A&A, 442, 587 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Vink, J. S., de Koter, A., & Lamers, H. J. G. L. M. 1999, A&A, 350, 181 [NASA ADS] [Google Scholar]
- Vink, J. S., de Koter, A., & Lamers, H. J. G. L. M. 2000, A&A, 362, 295 [NASA ADS] [Google Scholar]
- Vink, J. S., de Koter, A., & Lamers, H. J. G. L. M. 2001, A&A, 369, 574 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Vink, J. S., Muijres, L. E., Anthonisse, B., et al. 2011, A&A, 531, A132 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Wyithe, J. S. B., & Loeb, A. 2003, ApJ, 586, 693 [NASA ADS] [CrossRef] [Google Scholar]
- Yoon, S., & Langer, N. 2005, A&A, 443, 643 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Yoon, S., Langer, N., & Norman, C. 2006, A&A, 460, 199 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
All Tables
Fit parameters, expressing our predicted mass-loss rates for winds driven by carbon, oxygen and nitrogen lines, in terms of the mass-loss rates ṀV as predicted by Vink et al. (2001): 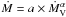 .
.
All Figures
 |
Fig. 1 Evolutionary tracks for metal-poor stars. The green track is for Minit = 40 M⊙, Z = 10-5 and for a rotational velocity that is vrot = 555 km s-1 (Yoon et al. 2006). This model evolves homogeneously. The red track is for Minit = 85 M⊙, Z = 10-8 and vrot = 800 km s-1 (Hirschi 2007). The blue pluses denote (L, Teff) combinations for which mass-loss rates have been computed using abundance patterns that are typical for the surface composition of the evolutionary tracks. |
| In the text | |
 |
Fig. 2 Derived mass loss rates versus predictions by Vink et al. (2001) (denoted ṀV) for Z = 0.04 (top panel), Z = 0.02 (middle panel) and Z = 0.002 (bottom panel). The coefficients of the power law fits are given in Table 2. |
| In the text | |
 |
Fig. 3 Predicted terminal velocities ν∞ for all models normalized to the effective escape velocity at the stellar surface νesc. Symbols and color codings indicate temperature; black symbols represent the H-poor models. Including the outliers towards high ν∞/νesc, the average of the H-rich models increases with ZCNO, from 2.6 to 3.9 to 4.7 for ZCNO = 0.002, 0.02 and 0.04, respectively. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


