EDP Sciences logo
Subscriber Authentication Point
Search
Menu
Home All issues Volume 545 (September 2012) A&A, 545 (2012) A81 Full HTML
Free Access
Issue
A&A
Volume 545, September 2012
Article Number A81
Number of page(s) 12
Section Planets and planetary systems
DOI https://doi.org/10.1051/0004-6361/201219315
Published online 11 September 2012

© ESO, 2012

1. Introduction

Circumstellar disks are the birthsites of planets. The physical conditions and the evolution of these disks control the planet formation mechanisms. An important goal is to provide theoretical models and observational constraints to understand the various stages in the evolution of gas and dust in the disk. Decrease of mass accretion rate (Sicilia-Aguilar et al. 2010; Fedele et al. 2010), and near-infrared excess with time (Hernández et al. 2007; Andrews et al. 2011b) indicate that disks have a range of lifetimes from 1 to 10 Myr.

With the advent of powerful infrared space telescopes such as Spitzer, a new class of objects has been identified, called the transition disks (e.g., Espaillat et al. 2010). Their spectral energy distribution (SED) and direct sub-millimeter (mm) imaging suggest that warm dust in the inner disk is strongly depleted compared to the outer disk. The small number of transition disks (Muzerolle et al. 2010) suggests an inside-out evolution that occurs rapidly. Various mechanisms have been proposed so far to explain the inner disk clearing: photoevaporation winds (e.g. Owen et al. 2012), grain growth (Klahr & Henning 1997; Tanaka et al. 2005) and dynamical interactions with companions (Lin & Papaloizou 1979). Transition disks are therefore excellent laboratories for planet formation models.

The clearing of a gap by a companion or planet, from a simplistic point of view, depends on the competition between the viscous torque from the disk and gravitational torques from the planet. For a laminar disk, a 1 MJup planet can clear a gap or hole. The recent discovery of a companion inside a massive disk in T Cha (Huélamo et al. 2011) supports the scenario of a dynamical clearing, at least for this object. However, models show that a single planet seems unlikely to be capable of creating the observed large holes, which require multiple systems (Zhu et al. 2011; Dodson-Robinson & Salyk 2011).

Interestingly, for most of these transition disks the inner cavity is not empty. They still present relatively high accretion rates (s10-8 M⊙ yr-1; see e.g., Calvet et al. 2005; Espaillat et al. 2007) which implies that the inner cavity is not completely empty and that some gas flows through the gap. To allow mass flowing, a limit for the planet mass can be inferred, depending on the disk viscosity (Lubow & D’Angelo 2006). In addition to the gas, some transition disks also present a strong near-infrared excess, indicating the presence of dust close to the star. Rice et al. (2006) studied the filtration of dust in the gap, considering a fixed size for the dust particles, and concluded that increasing the planet mass from e.g. 0.5 MJup to 5 MJup, the maximum particle size that sweeps into the gap decreases from ~10 μm to a few tenths of a micrometer.

Transition disks are potentially interesting laboratories to study processes related to the impact of planet formation on the disk. One of the most stubborn problems in planet formation is the so-called “meter-size barrier”. A one meter size object at 1 AU drifts towards the central star in timescales shorter than the growth timescales, impeding it to grow (see e.g., Brauer et al. 2008; Birnstiel et al. 2010a). In addition, high relative velocities lead to numerous fragmentation collisions converting a large object into smaller dust particles. The same physical process happens to the millimeter-size particles that are observed in the outer regions of the disk (e.g., Wilner et al. 2000; Ricci et al. 2010; Guilloteau et al. 2011). One possible solution to prevent the rapid inward drift and trap dust particles is to consider pressure bumps (Klahr & Henning 1997; Fromang & Nelson 2005; Brauer et al. 2008; Johansen et al. 2009; Pinilla et al. 2012). A long-lived positive pressure gradient can lead dust particles to move outwards, causing an accumulation of dust at the location of the pressure maximum. A large pressure bump is expected in protoplanetary disks as a consequence of the presence of a massive planet in a disk. In fact, when a planet carves a gap in a disk, the gas surface density shows a significant depletion, resulting in a large pressure bump at the outer edge of the gap. The dust material is trapped and piles up in this local pressure maximum where the gas motion is exactly Keplerian, and as a result there is no frictional drag between the gas and the particles. For that reason, not only do the particles not drift anymore, they also do not experience the potentially damaging high-velocity collisions due to relative radial and azimuthal drift. Under those circumstances, growth to larger-than-usual sizes is expected, possibly even a breakthrough that leads to overcome the growth barrier. However, if turbulence is still strong enough, particles may fragment due to their relative turbulent velocities. This scenario is only possible if we assume the presence of a planet, formed by another mechanism than dust agglomeration.

In this paper, our goal is to test the idea that the outer edge of a planetary gap is a particle trap. We consider the dust evolution in a disk, where the gas density profile is determined by its interaction with a massive planet. We then explore the case of LkCa 15, a transition disk (Mulders et al. 2010). The disk has been intensively observed at millimeter wavelengths (Piétu et al. 2006; Andrews et al. 2011b) with a maximum angular resolution corresponding to 28 AU (Isella et al. 2012). The dust continuum images show a ring-like structure from ~42 to ~120 AU, which is best fitted by a flat surface density profile. In addition, a ~6−15 MJup planet in circular orbit and located at 15.7 ± 2.1 AU, was claimed (Kraus & Ireland 2012), but not confirmed yet.

We describe the numerical simulations of planet-disk interactions that are considered for this work, as well as the coagulation/fragmentation model of the dust evolution in Sect. 2. Section 3 describes the results of the numerical simulations. In addition, we present observation predictions in Sect. 4. Section 5 is a discussion of the main results of our work and Sect. 6 is a summary.

2. Disk-planet interactions and dust evolution

For the disk-planet interaction process, we use the two-dimensional hydrodynamical code FARGO (Masset 2000), that solves the Navier-Stokes and continuity equations. For the dust evolution, we use the code described in Birnstiel et al. (2010a), that computes the coagulation and fragmentation of dust grains, including turbulence, gas drag and radial drift.

2.1. Codes

FARGO uses finite differences and a fixed grid in cylindrical coordinates (r,φ). Its advantage lies in the calculation of the azimuthal advection. It allows each annulus of cells to rotate at its local Keplerian velocity and at the end of each timescale, the results are stitched together. This technique speeds up the corresponding calculations. FARGO has been used for numerous studies of disk evolution (e.g., Crida et al. 2006; Zhu et al. 2011; Regály et al. 2012). We selected open inner and outer boundary conditions such that the material can leave the grid when the flow velocity at the inner or outer radial cells is pointing outwards. For this work, we only focus on the gas density profile at the outer edge of the open gap.

For the dust evolution, we consider that grains grow, crater and fragment due to radial drift, turbulent mixing and gas drag. Brownian motion, turbulence, vertical settling, radial and azimuthal drifts are taken into account to calculate the relative velocities of dust particles. For micron-sized particles, the relative velocities mainly result from Brownian motion and settling. These grains grow by coagulation as a result of van der Waals interactions. As they grow, they start to decouple from the gas, and turbulent motion as well as radial drift become the main sources for relative velocities.

When dust grains reach sizes with high enough velocities, they encounter destructive collisions. Particles above the fragmentation velocity always cause fragmentation if the impactor mass is within one order of magnitude of the target, otherwise they cause erosion. The transition from the 100% sticking probability to 100% fragmentation/erosion probability is linearly increasing between 0.2 × vf to vf, as in Birnstiel et al. (2010a).

The fragmentation velocities of the dust grains can be estimated based on laboratory experiments and theoretical work of collisions for silicates and ices (e.g., Blum & Wurm 2008; Schäfer et al. 2007; Wada et al. 2009). For silicates, they are on the order of few m s-1 (e.g., Blum & Wurm 2008), and increase with the presence of ices (Schäfer et al. 2007; Wada et al. 2009).

To characterize how well the dust particles couple to the gas, we refer to the Stokes number St, which is defined as the ratio between the turn-over time of the largest eddy (1/Ω) and the stopping time of the particle due to the friction with the gas. In the presence of a drag force, big particles are not affected by the drag and they move with their own Keplerian velocity, implying that St ≫ 1. When St ≪ 1, the particles are small enough to be well coupled to the gas and move with the gas.

In the Epstein regime, where the ratio between the mean free path of the gas molecules λmfp and the sizes of the particles a is λmfp/a ≥ 4/9, the Stokes number is at the midplane given by Birnstiel et al. (2010a), 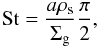(1)where ρs is the intrinsic density of the dust particles, and Σg is the gas surface density given by 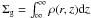, where ρ(r,z) is the total gas density.

Due to the sub-Keplerian velocity of the gas, particles that are large enough and do not move with the gas velocity experience a head wind, leading them to lose angular momentum and move inwards. The radial component of the dust velocity is the sum of a term corresponding to the frictional drag force (which opposes the motion of the dust grain) and of a term corresponding to the drift velocity, udrift, with respect to the gas, which directly depends on the radial pressure gradient ∂rP. It is given by: 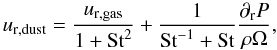(2)where ur,gas is the gas radial velocity. The first term is the dominant contribution for St ≪ 1. Equation (2) assumes low values for the dust-to-gas ratio. The drift velocity is usually negative, unless the pressure gradient is positive at a given radius. Particles with St = 1 experience the highest possible radial drift.

When particles reach certain sizes due to coagulation, they have relative velocities that may be high enough to cause fragmentation. For particles with St ~1, the maximum turbulent relative velocity is given by (Ormel & Cuzzi 2007) 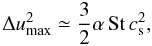(3)where α is the turbulence parameter (Shakura & Sunyaev 1973).

For dust particles with α/2 ≲ St ≲ 1 relative velocities are dominated by turbulent motion and radial drift. However, if the radial drift is reduced due to a positive pressure gradient, an approximation of the maximum size of the particles is obtained when the turbulent relative velocities are as high as the fragmentation velocity vf, therefore: 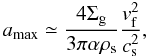(4)the dust grain distribution n(r,z,a) depends on coagulation and fragmentation collisions and is described by the Smoluchowski equation (see Birnstiel et al. 2010a, Eqs. (35) and (36)). The vertically integrated dust surface density distribution per logarithmic bin is 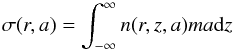(5)where m is the mass of a single particle of size a, hence the total dust surface density is: 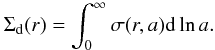(6)For the coagulation process, the midplane is the most important region, therefore the vertically integrated dust surface density distribution is a good approximation for describing the dust grain distribution. The advection-diffusion differential equation that describes the evolution of the dust surface density Σd for a single dust size, can be written in cylindrical coordinates as: (7)where Dd is the dust diffusivity and is equal to Dd = ν/(1 + St2), if the gas diffusivity is taken to be the turbulent gas viscosity ν = α cs h. Equation (7) is solved for each size using the flux-conserving donor-cell scheme (see Birnstiel et al. 2010a, Appendix A).

For a massive planet on a fixed orbit, the gap opening process reaches a quasi-steady state in timescales that are shorter (≲ 1000 orbits) than the million-years timescales of the entire process of dust evolution. For this reason, we use the gas surface density after one thousand orbits (~10-2 Myr) and take it as an input for the dust evolution models. Therefore, we assume that the gas surface density remains stationary from one thousand orbits to several million years.

We consider that after the giant planet is formed, the disk remains dust-rich and we study how the remaining dust evolves after the gap is open and has reached a quasi-steady state. We consider that the gas does not have any feedback from the dust and stays static during the dust evolution process since the dust density is always less than the gas density. In addition, since the orbital timescales are much shorter than the dust evolution timescales and there are no strong asymmetries produced by the planet, we azimuthally average the surface density for our models. With these assumptions, the dust evolution at the outer edge of the gap is computed in an accurate way.

thumbnail Fig. 1

Azimuthally averaged surface density after 1000 orbits and three different values of α-turbulence for a gap created by a planet located in a fixed orbit at 20 AU of 1 MJup in a flared disk (top-left), 9 MJup in a flared disk (top-right), 1 MJup in a wedge disk (bottom-left) and 9 MJup in a wedge disk (bottom-right). The peak of the gas surface density at the position of the planet is due to the strong gravitational effect of the massive planet on the gas of the disk.

2.2. Set-up

For our simulations, we assume a locally isothermal disk and two different radial density profiles Σ ∝ rβ. When the disk scale increases with radius as h/r ∝ r1/4 (flared disk) as suggested by modeling of T Tauri disks (D’Alessio et al. 2001), the temperature scales as T ∝ r−1/2, and β = −1. When h/r is constant (wedge disk), the temperature scales as T ∝ r-1 and β = −0.5. The α turbulence parameter is considered to have values between 10-4 to 10-2, in agreement with magnetorotational instability (MRI) of active disks (Johansen & Klahr 2005). The numerical simulations are performed with nr = 512 radial logarithmically, and nφ = 1024 azimuthal uniformly distributed grid cells.

All parameters such as the stellar properties, kinematic viscosity, disk mass, the scale height and the gas density profile of the disk are taken to be the same between the hydrodynamical gas evolution and the dust coagulation simulations.

For FARGO simulations, we use normalized units such that G = M⋆ + MP = 1 and the location of the planet is at r = 1. The simulations are performed from rin = 0.1 to rout = 7.0, such that the planet is at rp = 20 AU for a grid from 2 AU to 140 AU. The initial gas surface density Σ0 at the position of the planet is fixed Σ = Σ0(r/rp)β, such that it is around ~1−1.5 the minimum mass solar nebula (Hayashi 1981), and the disk mass is around ~0.055 M⋆. We consider a planet at a fixed orbit, with two different masses, 1 MJup and 9 MJup. The planet is introduced slowly into the smooth disk to avoid numerical issues. Planetary accretion is not taken into account since this process is still debated. We use M⋆ = 1 M⊙, and consequently, Mdisk = 55 MJup. Finally, the gravitational effect of the planet is smoothed out, such that the gravitational potential φ is softened over distances comparable to the disk scale height: 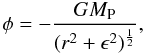(8)where ϵ is taken to be 0.6 h. The main FARGO parameters are summarized in Table 1.

Table 1

FARGO parameters.

For the dust evolution, we consider that all particles are initially 1 μm large, and a dust-to-gas ratio is 0.01, with an intrinsic volume density of ρs = 1.2 g cm-3 and a fragmentation velocity of vf = 1000 cm s-1. Two additional stellar parameters are taken into account, the stellar radius which is taken to be R⋆ = 1.7 R⊙ and the star effective temperature T⋆ = 4730 K, as typical values for T Tauri stars. The parameters of the dust evolution simulations are in Table 2.

3. Results

3.1. Gas density profile

Figure 1 shows the azimuthally averaged gas surface density after 1000 orbits in four different cases: a 1 MJup and a 9 MJup planet on a fixed orbit at 20 AU in a flared and wedge disk respectively. In each case, three different values for α turbulence parameter are considered.

Table 2

Dust model parameters.

thumbnail Fig. 2

Radial pressure gradient after 1000 orbits and three different values of α turbulence for a gap created by a planet located in a fixed orbit at 20 AU of 1 MJup and 9 MJup in a flared disk.

With a 1 MJup planet and a high value of α = 10-2, the viscous torque on the gas exceeds the gravitational torque by the planet, resulting in a much less pronounced gap than in the cases of α = 10-3 and α = 10-4. The gap is replenished easily because of the high viscosity of the disk as already predicted by different authors (e.g. de Val-Borro et al. 2006; Crida et al. 2006). However, for all α values, the width of the gap is roughly the same. It is independent of the viscosity and it depends basically on the mass and location of the planet. We notice that with low viscosity, the density waves that are produced by the planet-disk interaction at the gap edges, become more pronounced but they eventually damp with radius. Indeed, with a 1 MJup planet, these waves disappear beyond 40 AU and the disk surface density profile follows the initial power law. In this case, the main difference between the two disk geometries that we consider, is that for each value of α, the gap is slightly deeper for a wedge than for a flared disk.

With a 9 MJup planet, the gravitational torque dominates the viscous torque and the depth of the gap is almost independent of the values that we consider for α. After 1000 orbits the surface density reaches almost the same values near the planet and the width of the gap slightly changes for the different values of turbulence, when the disk is less turbulent the gap is moderately wider. The density perturbation waves are more evident in this situation than for 1 MJup, however, for α = 10-3−10-2, they again damp with radius, and at around 60 AU the gas surface density follows the initial power law. After 1000 orbits and α = 10-4, the density perturbation due to the planet is still propagating, for this reason the wiggles in the density profile are stronger than in the cases of α = 10-3−10-2. These wiggles are still present for r > 100 AU and they change slightly with the geometry of the disk.

In all four cases, it is possible to distinguish a peak in the surface density at the position of the planet, due to circumplanetary material. This is a natural consequence of the planet insertion in a smooth disk, and because the accretion onto the planet is not considered, the peak remains unaltered during the simulations.

3.2. Pressure gradient

As explained before, the rapid inward drift of the particles stops if the gradient of pressure is positive and the particles pile up in the pressure maxima. Depending on the strength of the pressure gradient, the particles can be trapped or not in the pressure bump (Pinilla et al. 2012). Figure 2 shows the radial pressure gradient considering the azimuthally averaged gas surface density after one thousand orbits, in the case of a flared disk and with an isothermal equation of state. The pressure is given by 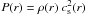, where the sound speed is defined as 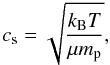(9)where kB is the Boltzmann constant, mp is the proton mass and μ is the mean molecular mass, which is μ = 2.3 in proton mass units. If the temperature is considered as a smooth decreasing function with radius, density variations induce pressure inhomogeneities. We can see that for a 1 MJup planet, there is a noticeable difference in the amplitude of the pressure gradients for α = 10-2 and α = 10-4−10-3. The pressure gradient is positive from ~22 AU to ~30 AU, and since udrift ∝ ∂rP (Eq. (2)), the dust particles have positive drift velocities and move outwards. In all cases, the zero point of the pressure gradient is located at ~10 AU (with a slight variation with viscosity) from the planet orbit and does not change with the geometry of the disk, since the density profile behaves almost the same for flared and wedge disks.

thumbnail Fig. 3

Effect of the planet mass on the radial pressure gradient after ~1000 orbits in a flared disk, α = 10-3 and five different values of the planet mass. The planet is located at 20 AU. The vertical lines indicate the locations of the pressure maximum.

For a 9 MJup planet orbiting at 20 AU, the pressure gradient on average behaves similarly for each of the α values. The wiggly profile of the gradient is due to the density waves that are produced by the interaction between the planet and the disk. For this planet mass and all values of α, the pressure gradient is positive right after the planet location and remains positive until around 48 AU, and then becomes again negative for both cases of flared and wedge disks. The influence of the planet mass on the range where the pressure gradient is positive is remarkable.

In both mass regimes, it is clear that the location of the pressure maximum differs from the outer edge radius of the gap, where the gas density again starts to increase. Therefore, if the pressure gradient is high enough to moderate the rapid inward drift, dust particles are trapped further away from the gap outer edge in the gaseous disk. This implies that the gap width for the gas is smaller than the one for the dust.

Figure 3 summarizes these findings, and shows pressure gradient curves for additional planet masses, Mp = { 1, 3, 5, 9, 15}MJup with orbital radius rp = 20 AU. The pressure gradient has its zero point at around {29.5, 33.5, 43.5, 48.5, 54.0} AU respectively.

As a comparison, we use the Hill radius rH, defined as rH = rp (Mp/3M⋆)1/3. In spite of the fact that the outer gap edge in the gas is at most 5 rH (see e.g. Dodson-Robinson & Salyk 2011), we find that the location where dust accumulates (i.e., the location of the maximum of the pressure) is at ~7 rH for 1 and 3 MJup planets, and ~10 rH for planets with Mp ≥ 5 MJup. This result will be discussed in more detail in Sect. 5.

Note that for the FARGO simulations in the case of a 15 MJup planet, we insert the planet in the disk after more orbits than in the other cases studied in Sect. 3.1, we use non-reflecting boundary conditions and a smoothing parameter of ϵ = 0.8h (see Eq. (8)) to smooth out the strong density waves produced in this scenario.

thumbnail Fig. 4

Vertically integrated dust density distribution at different times of evolution. Case of a surface density with a gap created by 1 MJup located in a fixed orbit at 20 AU in a flared disk and α = 10-2 (top panel), α = 10-3 (middle panel). Case with no planet and α = 10-3 (bottom panel). The solid white line represents the particle size corresponding to St = 1, while the blue line corresponds to the fragmentation barrier according to Eq. (4) (Brauer et al. 2008; Birnstiel et al. 2010a). The dashed line corresponds to the size for which particles drift faster than those dragged by the gas. Particles above the dashed line are perfectly trapped.

thumbnail Fig. 5

Vertically integrated dust density distribution at different times of evolution for a surface density with a gap created by 9 MJup located in a fixed orbit at 20 AU in a flared disk and α = 10-3. Lines are as in Fig. 4.

3.3. Dust size evolution

For the study of the density distribution of dust particles, we again focus on the flared disks, since this disk geometry is in good agreement with observations of T Tauri disks (D’Alessio et al. 2001). For this section, the surface density peak at the planet location was smoothed out to avoid artificial effects at this location.

Top and middle panels of Fig. 4 show the vertically integrated dust density distribution at different evolution times for a gas surface density with a gap created by a 1 MJup planet located in a fixed orbit at 20 AU, and two different values of α turbulence. As explained before the timescales of the gap opening process are much shorter than the whole dust evolution process, which allows us to take the gas surface density after ~1000 orbits and consider that it remains quasi-stable during the dust evolution. The solid white line has the shape of the gas surface density profile and is calculated when the particle size corresponds to a Stokes number of unity (Eq. (1)). The blue line is the maximum size that particles can reach before they have velocities higher than the fragmentation limit. It is important to note that the maximum size of the particles is inversely proportional to the turbulence parameter (Eq. (4)), for this reason the maximum possible grain size (blue line) differs by one order of magnitude for each α turbulent parameter considered.

The dashed line provides an approximation of the minimum size of the particles that are trapped in the pressure maximum. Particles with sizes over the dashed line are trapped and the ones below the line are dragged by the gas. This condition is found when the radial component of the dust velocity (Eq. (2)) is positive, therefore: 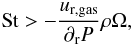(10)which in terms of the particle size and pressure gradient can be written as: 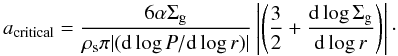(11)

3.3.1. Effect of turbulence

We notice a significant influence of the trapping of dust particles on the strength of the pressure gradient. Micron-size particles (St ≪ 1), which are easily mixed due to turbulence, are more difficult to trap, they go through the gap and finally drift towards the star. Dust grains with larger Stokes number can perfectly be trapped because they feel a tail-wind due to the fact that the gas moves with super-Keplerian velocity where the pressure gradient is positive, resulting in an outwards movement for those particles.

For α = 10-2, the pressure gradient is less steep, the turbulent mixing and drag along the accretion flow wins over the trapping, and the dust gets lost onto the star. Even when the pressure gradient is positive in a range (~22−30) AU, it is not sufficient to trap the particles in the pressure maximum. Indeed, after 3 Myr there is almost no dust remaining in the whole disk.

For α = 10-3 turbulence mixing is less strong and in the range of (~22−30) AU, the pressure gradient is greater (Fig. 2 – left panel), and is high enough to stop the rapid inward drift of the particles. The particles are quickly trapped at the location of the pressure maximum (~30 AU) and stay there after several Myr. The gap created in this case filters out all particles larger than a few μm and the particles that are inside the gap eventually drift towards the star. The gap formed by 1 MJup mass planet with α = 10-3 produces a pressure gradient high enough to create a concentration of dust particles at 10 AU from the location of the planet and the particles reach sizes of a few cm.

As we note in Fig. 2 – left panel, for 1 MJup and α = 10-4, the pressure gradient is slightly higher than in the case of α = 10-3, therefore the dust particles should be easily trapped in this case reaching even larger sizes (Eq. (4)). For comparison, we notice in the bottom panel of Fig. 4, that in the case without planet and with the same disk and stellar parameters, the dust instead of being trapped, grows, fragments, mixes and drifts to the star without forming any mm-size pebbles in the outer regions of the disk r > 20 AU.

The necessary size that particles have to reach to be trapped (Eq. (11)) is higher than the maximum sizes reached due to relative turbulent motion (Eq. (2)). The influence of turbulence for the dust dynamics is remarkable, if turbulence is not considered, particles grow enough to be decoupled from the gas and they would be trapped because of the positive pressure gradient regardless of its strength. However, we conclude that the high turbulence causes particles to go through the gap and drift finally to the star, due to the fact that they reach high relative turbulent velocities which favors fragmentation, so the mm-size particles become again micron-size grains which are not possible to trap with the strength of the pressure gradient produced with α = 10-2.

3.3.2. Effect of planet mass

In the case of a 9 MJup planet, the pressure gradient is roughly similar for each of the values of the turbulence parameter α (see Fig. 2 – right panel), hence for the dust density evolution we concentrate on the intermediate value of the viscosity, α = 10-3. Figure 5 illustrates the vertically integrated dust density distribution for the case of 9 MJup at different times of evolution. Similar to the case of 1 MJup planet and α = 10-3, the dust particles grow and due to the positive pressure gradient between ~22 and ~48 AU (Fig. 2 – right panel), the rapid inward drift is counteracted by the positive local pressure gradient and the particles are retained in a broad bump of ~20 AU width. The dust particles in the outer regions of the disk grow until mm sizes and remain there even after a few Myrs. It is important to mention that even when the pressure gradient reaches a similar value to the case of 1 MJup and α = 10-2, for which there is not particle trapping at all, the turbulent relative velocities are lower and the range of positive gradient is wider, enabling dust retention (Pinilla et al. 2012).

Comparing the dust evolution with α = 10-3 for a 1 MJup (Fig. 4 – bottom panel) and a 9 MJup (Fig. 5), we can conclude that the planet mass directly influences the position where the dust can be retained and that the dust bump is wider for the more massive planet. In addition, the pressure gradient created by the different planet masses also affects the size for which particles are trapped. For the same turbulence parameter α = 10-3 and 1 MJup, the maximum acritical is equal to ~0.70 cm, while for 9 MJup the maximum acritical is ~0.47 cm.

3.3.3. Dust to gas ratio

It is important to note that for the dust evolution models, we assume low values for the dust-to-gas ratio and we do not consider to have any feedback from the dust to the gas, since the gas density remains static. However, when the dust accumulates and grows forming a pile-up, the dust-to-gas ratio can reach values close to one. When the dust-to-gas density ratio is close to unity, the feedback from the dust to the gas is non negligible and the growth timescales can be faster than the drift timescales (Youdin & Goodman 2005), potentially leading to planetesimal formation in the absence of self-gravity. Nevertheless, these streaming instabilities are powered by the relative drift velocities between dust particles and gas, therefore in the pressure maximum where the radial drift of the dust is reduced, these instabilities are unlikely and our assumptions are still valid.

thumbnail Fig. 6

Dust-to-gas ratio for 1, 9 and 15 MJup planet, after 1 Myr of dust evolution.

thumbnail Fig. 7

Left: 1.3 mm map in the 1 MJup case, convolved with a beam of 0.1′′ × 0.1′′. Units are in Jy/beam. Right: same for 9 MJup.

Figure 6 shows the dust-to-gas ratio for each considered case of the planet mass after 1 Myr of dust evolution. The maximum value that the dust-to-gas ratio is ~{0.76, 0.36, 0.18} in the cases of 1, 9 and 15 MJup, respectively. This variation of dust to gas ratio with the planet mass can be explained considering that as the pressure bump gets wider, the dust accumulates and grows in an extended radial region. The dust-to-gas ratio is therefore higher for lower planet mass, when the pressure gradient is higher and positive in a narrower region (see Fig. 3). In addition, we can notice in Fig. 6 that for the 15 MJup mass planet, the dust-to-gas ratio reaches very low values at the location of the planet, for which the gas drag and drift is inefficient. Therefore the remaining dust in the inner region is just the initial dust that was initially in the inner part. If the initial size of the particles is taken smaller (e.g. 0.01 μm), the sub-micron size particles would go through the gap and replenish the inner part. However, for the 1 and 9 MJup cases, the micron size dust from the outer region which are not trapped, can drift and be dragged by the gas and finally move through the gap.

4. Observational predictions

4.1. Emission maps

In this section, we present continuum maps computed at a wavelength of 1.3 mm. We use the gas profiles described in Sect. 2.2 and dust size distributions determined in Sect. 3.3 and shown in Fig. 4 – middle panel and Fig. 5. We consider the same aspect ratio as in the FARGO and dust evolution simulations, and compute the volume density following: 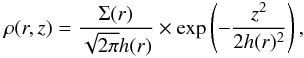(12)with Σ, the dust surface density and h(r), the scale height. After retrieving the optical constants1, we compute the opacities for silicate grains, following the Mie theory. The dust temperature is then computed self-consistently after solving the radiative transfer with the RADMC3D code2.

We consider the cases of α = 10-3, a planet with masses of 1 and 9 MJup planets and orbiting at 20 AU, after 1 Myr. We use 40° and 90°, as the disk inclination and position angle, respectively, and a distance of 140 pc. The images are convolved with a 0.10′′ × 0.10′′ beam as required for ALMA for typical sizes and distances of protoplanetary disks. As shown in Fig. 7, our model images are very similar to the transition disks observations in the (sub-)millimeter regime, that reveal a continuum emission as a resolved ring-like feature (e.g., Williams & Cieza 2011; Andrews et al. 2011a; Isella et al. 2012). In addition, after 1 Myr of dust evolution, we estimate a spectral index of ~2.7 by integrating the flux over the entire disk at wavelengths of 1 mm and 3.0 mm. This value is in agreement with recent observations (Ricci et al. 2010).

Due to the wide distribution of particles around the pressure bump (see, e.g., Fig. 5), the brightness distribution is expected to change with wavelength. This feature is also reproduced by our model, as shown in Fig. 8.

thumbnail Fig. 8

Radial surface brightness in the 9 MJup case, computed at 160 μm (crosses), 360 μm (stars) and 870 μm (diamonds).

4.2. The case of LkCa 15

In this section, we apply and discuss our model in the context of the transition disk LkCa15, for which a wealth of observational data is published. Andrews et al. (2011a) presented a 870 μm image obtained at high angular resolution (0.25′′) combining observations from the Submillimeter Array (SMA) and Plateau de Bure Interferometer (PdBI). These observations of the dust continuum emission confirms a ring-like structure at ~50 AU from the star. They compared these observations with four possible models, concluding that their best fit corresponds to a gap possibly opened by a 9 MJup companion at ~16 AU in a wedge disk, with a constant disk aspect ratio of h/r = 0.05 and constant viscosity ν = 10-5 (which corresponds to α ~ 10-3). In Sect. 3, we demonstrated that, in the case of a 9 MJup planet and α = 10-3, the pressure maximum is located around ~1.4 rp from the planet (with rp, the planet location), which implies that the pile-up of dust (up to cm-sizes) would be located at around ~38 AU. Therefore, to have an agreement with the depletion of dust opacities until ~50 AU, a bit more massive or/and further located companion is necessary to reproduce the ring-like structure as we will discuss below.

Although not confirmed, Kraus & Ireland (2012) claimed to have detected a ~6−15 MJup planet at 15.7 ± 2.1 AU in LkCa15. Considering the upper limit for the mass and the location of the planet at 20 AU, the zero point for the pressure gradient would be located ~54 AU (Fig. 3). Hence, dust would accumulate at ~54 AU distance from the star, in better agreement with the observed ring radius.

Figure 9 – top panel shows the vertically integrated dust density distribution after 1 Myr of evolution in the case of a gap opened by a 15 MJup planet, embedded in a flared disk with α = 10-3 and the same parameters given in Tables 1 and 2. Considering this dust distribution, Fig. 9 – bottom panel gives the 1.3 mm continuum map, considering a disk inclination of 51°, a disk position angle of 64.4°, a distance of 140 pc, and convolved with a beam of 0.21′′ × 0.19′′ (Isella et al. 2012). This image shares striking similarities with the ones published, with similar inner radii for the ring and similar surface brightness. We note however, that we do not reproduce the observed width of the ring, as after 1 Myr already, most of the outer disk particles are retained in a very narrow region. Nevertheless, Pinilla et al. (2012) demonstrated that the presence of long-lived pressure bumps such as results from MRI can explain the presence of mm-size grains in the regions of the disk outside 50 AU. The combination of those pressure inhomogeneities and the interaction between a massive planet with the disk may explain the radial extent.

thumbnail Fig. 9

Vertically integrated dust density distribution at 1 Myr of evolution for a surface density with a gap created by 15 MJup located in a fixed orbit at 20 AU in a flared disk and α = 10-3 (top-panel). Bottom-panel is the 1.3 mm continuum model map for LkCa15 considering the dust density distribution shown in top-panel. The map is convolved with a beam of 0.21′′ × 0.19′′, corresponding to the maximum angular resolution achieved by Isella et al. (2012) Units are in Jy/beam.

Unlike our models with an alpha-viscosity and a massive planet embedded in the disk, Isella et al. (2012) model a gas density profile which increases with radius for the inner part due to the extremely rapid increase of the viscous accretion velocity for smaller radius. They fit their CARMA 1.3 mm observations assuming no planet with the following gas surface density: (13)where the viscosity is given by ν(r) ∝ rγ. Their best fit model corresponds to γ = −2.15, rt = 60 AU and Σt ~ 10.37 g cm-2, for a disk extending from 0.2−160 AU. Their gas density profile suggests that the pressure gradient would be positive from the inner radius until the characteristic radius rt and smoothly becomes negative until the outer radius of the disk. This implies that the dust particles would have a positive drift velocity in the inner regions, and negative in the outer regions of the disk. They would therefore move outwards from the inner radius to rt, and from the outer radius inwards to rt, creating a wide concentration of dust around 60 AU.

This complementary study, that uses a prescription of the surface density based on the viscous evolution of the disk, leads to the same conclusion as our model, i.e., a pressure maximum around 60 AU. In fact, the profiles are very similar in the range of radii in which the dusty ring is observed (see Fig. 1 in Isella et al. 2012).

5. Discussion

Hydrodynamical simulations of planet/disk interactions combined with dust coagulation/fragmentation models can reproduce the ring-like emission of some transition disks.

5.1. Dust evolution

To compute the evolution of dust, one has to account for four important physical mechanisms: coagulation, fragmentation, radial drift, and turbulent mixing. Coagulation is important for grains to grow to large sizes, as inferred from millimeter observations. Fragmentation continuously replenishes the disk in small grains. If we do not consider fragmentation, in the region where the pressure gradient is positive, particles would accumulate, grow above the fragmentation barrier and reach the maximum size of ~2 m considered in our models. This would happen on timescales as short as ~0.1 Myr, and would result in a disk only made of large particles. As meter-size objects have St ≫ 1, they would therefore not be coupled with the gas anymore, move at Keplerian velocity, and would not be trapped. These grains would in addition have very low opacities, which would result in the underestimation of millimeter fluxes in the millimeter.

Radial drift is essential to distribute the grains over the disk extent. Birnstiel et al. (2010b) showed that if the radial drift is neglected, dust grains could acquire millimeter sizes, but would lead to over-predictions of mm-fluxes. In our model of LkCa15, we overcome this issue and obtain flux levels similar to the ones measured by Isella et al. (2012).

Finally, turbulent mixing provides the necessary relative velocities for grains to fragment, directly influencing the maximum particle size (Eq. (4)), and distribute the grains of various sizes all over the disk. In Sect. 3.3, we showed that the efficiency of particle trapping depends on the viscosity of the disk. For a shallow gap (see Fig. 4), we concluded that when the pressure gradient is not high enough, drag forces and diffusion do not allow particles to be trapped.

Our model can however still be refined. Recent collision experiments with silicates show that particles should also bounce as an intermediate step between sticking and fragmentation (Güttler et al. 2010). In fact, Windmark et al. (2012) showed that with the insertion of cm-sized seeds, considering mass transfer processes and bouncing, at a distance of few AU, small dust can grow to ~100 m on timescales of 1 Myr. A similar process could happen to mm-sized particles in the outer regions of the disks. However, in the presence of ices, the need to account for bouncing effects is still highly debated (e.g. Wada et al. 2011), and we do not consider it in this work.

5.2. Different gap extents in the dust and the gas

The presence of a planetary or sub-stellar companion has been suggested in many studies to explain the properties of transition disks. However, studies based on hydrodynamical simulation of gap opening in a gaseous disk have shown that a single planet could not open the large gap inferred from spatially resolved millimeter observations (e.g. Dodson-Robinson & Salyk 2011; Zhu et al. 2011). Most studies in fact consider a maximum radius for the gap of 5 Hill radii. According to the definition of the Hill radius, the increase of the planet mass does not produce a significant widening of the gap, and none of these models with a single planet can reproduce the observed characteristics of transition disks. In this study, we include for the first time the modelization of dust growth and evolution, in addition to the hydrodynamical simulations. We predict grain size distributions (and therefore brightness distributions) and show that the gap edges are different in dust and gas, and that therefore the extent of the gap due to a single planet is larger than expected based on gas simulations. We demonstrate in Sect. 3 that for a given planet, dust particles are trapped further out than the location of the edge of the gap in the gas. For example, in the specific case of a 15 MJup planet at 20 AU, the outer edge for the gas would be located at 37 AU, while the dust ring would be at 54 AU.

For Mp ≥ 5 MJup, the density waves produced by the planet are still changing with time after few thousands orbits. Kley & Dirksen (2006) showed that the disk becomes eccentric with the presence of a planet with a mass Mp > 3 MJup (for a constant viscosity given by ν = 10-5), which may cause a change in the equilibrium state. However, the disk precesses slowly enough that the eccentric pattern appears to be nearly stationary, and for a critical mass of 5 MJup, the eccentricity of the disk reaches a threshold. In fact, we demonstrated in Sect. 3.2 that for 1 and 3 MJup the dust would accumulate at 7 rH from the location of the planet rp, and at 10 rH from rP for 5, 9 and 15 MJup. We attribute this difference in the locations of the zero point of the pressure gradient to the fact that the disk becomes eccentric for planets whose mass is higher than 3 MJup. As a result, we have the pressure maximum further away for more massive planets, when the disk is eccentric, than for less massive planets.

5.3. The inner disk

Near-infrared excesses are measured in some transition disks (sometimes called pre-transition disks), and indicate the presence of dust close to the star, that can be spatially resolved in a few cases (e.g., Olofsson et al. 2011; Benisty et al. 2010; Pott et al. 2010). Besides, these objects show signs of on-going accretion (see e.g. Espaillat et al. 2007). In this paper, we do not treat the inner disk because our prescription for it is not accurate. In order to have self-consistency between gas hydrodynamical simulations and dust evolution models, we considered for the kinematic viscosity ν = α cs h. With this viscosity and the two considered assumptions for the gas density profiles, the accretion rate Ṁ = 3 π ν Σ is independent of the radius. With the disk and stellar parameters considered for the two cases (Tables 1 and 2), Ṁ is on the order of s10-9 M⊙ yr-1, about an order of magnitude lower than the measured values in some transitional disks (s10-8 M⊙ yr-1; Calvet et al. 2005; Espaillat et al. 2007). The low model value implies that even considering open boundary conditions, the gas surface density, in both inner and outer regions, only slightly decreases over the 1000 orbits (Fig. 1). In addition, the insertion of a very massive planet in the disk leads to strong density waves that may lead to unrealistic effects at the inner boundary (e.g., Crida & Morbidelli 2007). Therefore, our prescription for the inner disk is not accurate.

Besides, it is important to notice that inside the ice-line the absence of ices can change our results. In fact, according to laboratory experiments, the fragmentation velocity varies with the material properties (e.g. Gundlach et al. 2011). In the presence of ices, the fragmentation velocity reaches a value of vf ~ 1000 cm s-1, the value that we consider for the outer disk. However, this threshold decreases in the inner AUs, inside the ice-line. This directly impacts the maximum particle size (Eq. (4)).

Finally, the radial drift in our model leads to empty the inner disk in timescales that can be shorter than the age of some transition disk with NIR excess (e.g., HD 100546). Replenishment from the outer disk with small grains passing through the gap, or from planetesimal collisions (Krijt & Dominik 2011) is needed.

6. Summary and conclusions

The sub-Keplerian radial velocity of the gas in protoplanetary disks makes millimeter-size particles in the outer regions of the disk exposed to a rapid inward drift, implying that they migrate towards the star on timescales shorter than a million years. Therefore, in planet formation, rapid inward drift is one of the main issues with models to form planetesimals. The idea of the presence of pressure bumps in protoplanetary disks has been proposed as a solution to stop the rapid inward drift. With the presence of a massive planet in a disk, a pressure bump is created in the outer edge of the cleared gap. Particles may experience a positive pressure gradient and as a result, do not drift anymore and not experience the high-velocity collisions due to relative radial and azimuthal drift. Nevertheless, particles can still fragment due to turbulence motion, and the resulting micron-size particles are less easily trapped and they can finally drift inwards.

Some transition disks reveal gaps that can result from the presence of a massive planet, making them potentially interesting laboratories for studying dust growth under the favorable circumstances of having a significant pressure bump. In this paper, we combine two-dimensional hydrodynamical simulations for the gas with one-dimensional coagulation/fragmentation dust evolution models, to study how dust evolves in a disk which gas density has been disturbed by a massive planet.

We investigate the influence of the disk geometry, turbulence and planet mass on the potential trapping of particles. The disk geometry does not have a significant effect on the gap opening process. For a 1 MJup planet, there is an important influence of the α turbulence parameter on the depth of the gap and has important consequences for the trapping of particles. Unlike the case of α = 10-2, with α = 10-3, the particles are trapped at a distance of ~0.5 rp from the planet position rp. While the gas gap has a radius of ~0.35 rp (or 5 Hill radii), the dust is retained at a further distance. Without considering turbulence mixing for the dust dynamics would produce trapping of particles for certain sizes regardless of α value provided that the pressure gradient is positive. In the case of 9 MJup planet, the gap depth is independent of the turbulence and as a consequence the pressure gradient behaves similarly for all α values. The dust particles are trapped at a distance of 1.4 rp from the planet orbit rp. The planet mass strongly influences the location where the dust is retained and the width of the dust bump.

Observations at millimeter wavelengths reveal some transition disks with very wide gaps. We show that the location where the dust piles up does not coincide with the gap outer edge in the gaseous disk. This mismatch suggests that multiple planets may not necessarily be needed to account for the observed large opacity holes. We reproduce the main observed features of the disk around LkCa15, in which a companion was recently detected. Reproducing asymmetric features in the disk, such as the ones found in HD 135344B (Brown et al. 2009) is subject of future work, as they will be well detectable with ALMA.

Acknowledgments

The authors are very grateful to C. P. Dullemond for insightful suggestions, and for making RADMC3D available. We acknowledge C. Dominik and A. Natta for their enthusiasm and comments. We also thank A. Isella and S. Ataiee for useful discussions. P. Pinilla acknowledges the CPU time for running simulations in bwGRiD, member of the German D-Grid initiative, funded by the Ministry for Education and Research (Bundesministerium für Bildung und Forschung) and the Ministry for Science, Research and Arts Baden-Wuerttemberg (Ministerium für Wissenschaft, Forschung und Kunst Baden-Württemberg).

References

  1. Andrews, S. M., Rosenfeld, K. A., Wilner, D. J., & Bremer, M. 2011a, ApJ, 742, L5 [NASA ADS] [CrossRef] [Google Scholar]
  2. Andrews, S. M., Wilner, D. J., Espaillat, C., et al. 2011b, ApJ, 732, 42 [NASA ADS] [CrossRef] [Google Scholar]
  3. Benisty, M., Tatulli, E., Ménard, F., & Swain, M. R. 2010, A&A, 511, A75 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  4. Birnstiel, T., Dullemond, C. P., & Brauer, F. 2010a, A&A, 513, A79 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  5. Birnstiel, T., Ricci, L., Trotta, F., et al. 2010b, A&A, 516, L14 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  6. Blum, J., & Wurm, G. 2008, ARA&A, 46, 21 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  7. Brauer, F., Dullemond, C. P., & Henning, T. 2008, A&A, 480, 859 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  8. Brown, J. M., Blake, G. A., Qi, C., et al. 2009, ApJ, 704, 496 [NASA ADS] [CrossRef] [Google Scholar]
  9. Calvet, N., D’Alessio, P., Watson, D. M., et al. 2005, ApJ, 630, L185 [NASA ADS] [CrossRef] [Google Scholar]
  10. Crida, A., & Morbidelli, A. 2007, MNRAS, 377, 1324 [NASA ADS] [CrossRef] [Google Scholar]
  11. Crida, A., Morbidelli, A., & Masset, F. 2006, Icarus, 181, 587 [Google Scholar]
  12. D’Alessio, P., Calvet, N., & Hartmann, L. 2001, ApJ, 553, 321 [NASA ADS] [CrossRef] [Google Scholar]
  13. de Val-Borro, M., Edgar, R. G., Artymowicz, P., et al. 2006, MNRAS, 370, 529 [NASA ADS] [CrossRef] [Google Scholar]
  14. Dodson-Robinson, S. E., & Salyk, C. 2011, ApJ, 738, 131 [CrossRef] [Google Scholar]
  15. Espaillat, C., Calvet, N., D’Alessio, P., et al. 2007, ApJ, 670, L135 [NASA ADS] [CrossRef] [Google Scholar]
  16. Espaillat, C., D’Alessio, P., Hernández, J., et al. 2010, ApJ, 717, 441 [NASA ADS] [CrossRef] [Google Scholar]
  17. Fedele, D., van den Ancker, M. E., Henning, T., Jayawardhana, R., & Oliveira, J. M. 2010, A&A, 510, A72 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  18. Fromang, S., & Nelson, R. P. 2005, MNRAS, 364, L81 [NASA ADS] [CrossRef] [Google Scholar]
  19. Guilloteau, S., Dutrey, A., Piétu, V., & Boehler, Y. 2011, A&A, 529, A105 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  20. Gundlach, B., Kilias, S., Beitz, E., & Blum, J. 2011, Icarus, 214, 717 [NASA ADS] [CrossRef] [Google Scholar]
  21. Güttler, C., Blum, J., Zsom, A., Ormel, C. W., & Dullemond, C. P. 2010, A&A, 513, A56 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  22. Hayashi, C. 1981, Prog. Theor. Phys. Suppl., 70, 35 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
  23. Hernández, J., Hartmann, L., Megeath, T., et al. 2007, ApJ, 662, 1067 [NASA ADS] [CrossRef] [Google Scholar]
  24. Huélamo, N., Lacour, S., Tuthill, P., et al. 2011, A&A, 528, L7 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  25. Isella, A., Perez, L. M., & Carpenter, J. M. 2012, ApJ, 747, 136 [NASA ADS] [CrossRef] [Google Scholar]
  26. Johansen, A., & Klahr, H. 2005, ApJ, 634, 1353 [NASA ADS] [CrossRef] [Google Scholar]
  27. Johansen, A., Youdin, A., & Klahr, H. 2009, ApJ, 697, 1269 [NASA ADS] [CrossRef] [Google Scholar]
  28. Klahr, H. H., & Henning, T. 1997, Icarus, 128, 213 [NASA ADS] [CrossRef] [Google Scholar]
  29. Kley, W., & Dirksen, G. 2006, A&A, 447, 369 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  30. Kraus, A. L., & Ireland, M. J. 2012, ApJ, 745, 5 [NASA ADS] [CrossRef] [Google Scholar]
  31. Krijt, S., & Dominik, C. 2011, A&A, 531, A80 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  32. Lin, D. N. C., & Papaloizou, J. 1979, MNRAS, 186, 799 [NASA ADS] [CrossRef] [Google Scholar]
  33. Lubow, S. H., & D’Angelo, G. 2006, ApJ, 641, 526 [NASA ADS] [CrossRef] [Google Scholar]
  34. Masset, F. 2000, A&AS, 141, 165 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  35. Mulders, G. D., Dominik, C., & Min, M. 2010, A&A, 512, A11 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  36. Muzerolle, J., Allen, L. E., Megeath, S. T., Hernández, J., & Gutermuth, R. A. 2010, ApJ, 708, 1107 [NASA ADS] [CrossRef] [Google Scholar]
  37. Olofsson, J., Benisty, M., Augereau, J.-C., et al. 2011, A&A, 528, L6 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  38. Ormel, C. W., & Cuzzi, J. N. 2007, A&A, 466, 413 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  39. Owen, J. E., Clarke, C. J., & Ercolano, B. 2012, MNRAS, 422, 1880 [NASA ADS] [CrossRef] [Google Scholar]
  40. Piétu, V., Dutrey, A., Guilloteau, S., Chapillon, E., & Pety, J. 2006, A&A, 460, L43 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  41. Pinilla, P., Birnstiel, T., Ricci, L., et al. 2012, A&A, 538, A114 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  42. Pott, J.-U., Perrin, M. D., Furlan, E., et al. 2010, ApJ, 710, 265 [NASA ADS] [CrossRef] [Google Scholar]
  43. Regály, Z., Juhász, A., Sándor, Z., & Dullemond, C. P. 2012, MNRAS, 419, 1701 [NASA ADS] [CrossRef] [Google Scholar]
  44. Ricci, L., Testi, L., Natta, A., & Brooks, K. J. 2010, A&A, 521, A66 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  45. Rice, W. K. M., Armitage, P. J., Wood, K., & Lodato, G. 2006, MNRAS, 373, 1619 [NASA ADS] [CrossRef] [Google Scholar]
  46. Schäfer, C., Speith, R., & Kley, W. 2007, A&A, 470, 733 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  47. Shakura, N. I., & Sunyaev, R. A. 1973, A&A, 24, 337 [NASA ADS] [Google Scholar]
  48. Sicilia-Aguilar, A., Henning, T., & Hartmann, L. W. 2010, ApJ, 710, 597 [NASA ADS] [CrossRef] [Google Scholar]
  49. Tanaka, H., Himeno, Y., & Ida, S. 2005, ApJ, 625, 414 [NASA ADS] [CrossRef] [Google Scholar]
  50. Wada, K., Tanaka, H., Suyama, T., Kimura, H., & Yamamoto, T. 2009, ApJ, 702, 1490 [NASA ADS] [CrossRef] [Google Scholar]
  51. Wada, K., Tanaka, H., Suyama, T., Kimura, H., & Yamamoto, T. 2011, ApJ, 737, 36 [NASA ADS] [CrossRef] [Google Scholar]
  52. Williams, J. P., & Cieza, L. A. 2011, ARA&A, 49, 67 [NASA ADS] [CrossRef] [Google Scholar]
  53. Wilner, D. J., Ho, P. T. P., Kastner, J. H., & Rodríguez, L. F. 2000, ApJ, 534, L101 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
  54. Windmark, F., Birnstiel, T., Güttler, C., et al. 2012, A&A, 540, A73 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  55. Youdin, A. N., & Goodman, J. 2005, ApJ, 620, 459 [NASA ADS] [CrossRef] [Google Scholar]
  56. Zhu, Z., Nelson, R. P., Hartmann, L., Espaillat, C., & Calvet, N. 2011, ApJ, 729, 47 [NASA ADS] [CrossRef] [Google Scholar]

All Tables

Table 1

FARGO parameters.

In the text
Table 2

Dust model parameters.

In the text

All Figures

thumbnail Fig. 1

Azimuthally averaged surface density after 1000 orbits and three different values of α-turbulence for a gap created by a planet located in a fixed orbit at 20 AU of 1 MJup in a flared disk (top-left), 9 MJup in a flared disk (top-right), 1 MJup in a wedge disk (bottom-left) and 9 MJup in a wedge disk (bottom-right). The peak of the gas surface density at the position of the planet is due to the strong gravitational effect of the massive planet on the gas of the disk.
In the text
thumbnail Fig. 2

Radial pressure gradient after 1000 orbits and three different values of α turbulence for a gap created by a planet located in a fixed orbit at 20 AU of 1 MJup and 9 MJup in a flared disk.

In the text
thumbnail Fig. 3

Effect of the planet mass on the radial pressure gradient after ~1000 orbits in a flared disk, α = 10-3 and five different values of the planet mass. The planet is located at 20 AU. The vertical lines indicate the locations of the pressure maximum.
In the text
thumbnail Fig. 4

Vertically integrated dust density distribution at different times of evolution. Case of a surface density with a gap created by 1 MJup located in a fixed orbit at 20 AU in a flared disk and α = 10-2 (top panel), α = 10-3 (middle panel). Case with no planet and α = 10-3 (bottom panel). The solid white line represents the particle size corresponding to St = 1, while the blue line corresponds to the fragmentation barrier according to Eq. (4) (Brauer et al. 2008; Birnstiel et al. 2010a). The dashed line corresponds to the size for which particles drift faster than those dragged by the gas. Particles above the dashed line are perfectly trapped.
In the text
thumbnail Fig. 5

Vertically integrated dust density distribution at different times of evolution for a surface density with a gap created by 9 MJup located in a fixed orbit at 20 AU in a flared disk and α = 10-3. Lines are as in Fig. 4.
In the text
thumbnail Fig. 6

Dust-to-gas ratio for 1, 9 and 15 MJup planet, after 1 Myr of dust evolution.
In the text
thumbnail Fig. 7

Left: 1.3 mm map in the 1 MJup case, convolved with a beam of 0.1′′ × 0.1′′. Units are in Jy/beam. Right: same for 9 MJup.
In the text
thumbnail Fig. 8

Radial surface brightness in the 9 MJup case, computed at 160 μm (crosses), 360 μm (stars) and 870 μm (diamonds).
In the text
thumbnail Fig. 9

Vertically integrated dust density distribution at 1 Myr of evolution for a surface density with a gap created by 15 MJup located in a fixed orbit at 20 AU in a flared disk and α = 10-3 (top-panel). Bottom-panel is the 1.3 mm continuum model map for LkCa15 considering the dust density distribution shown in top-panel. The map is convolved with a beam of 0.21′′ × 0.19′′, corresponding to the maximum angular resolution achieved by Isella et al. (2012) Units are in Jy/beam.
In the text

Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.

Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.

Initial download of the metrics may take a while.