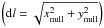| Issue |
A&A
Volume 545, September 2012
|
|
|---|---|---|
| Article Number | A78 | |
| Number of page(s) | 12 | |
| Section | The Sun | |
| DOI | https://doi.org/10.1051/0004-6361/201219281 | |
| Published online | 10 September 2012 | |
Spine-fan reconnection
The influence of temporal and spatial variation in the driver
1
School of Mathematics and Statistics, University of
Sheffield, Sheffield,
S3 7RH, UK
2
Division of Mathematics, University of Dundee,
DD1 4HN,
UK
e-mail: app09pfw@sheffield.ac.uk
Received:
26
March
2012
Accepted:
30
July
2012
Context. From observations, the atmosphere of the Sun has been shown to be highly dynamic with perturbations of the magnetic field often lacking temporal or spatial symmetry. Despite this, studies of the spine-fan reconnection mode at 3D nulls have so far focused on the very idealised case with symmetric driving of a fixed spatial extent.
Aims. We investigate the spine-fan reconnection process for less idealised cases, focusing on asymmetric driving and drivers with different length scales. We look at the initial current sheet formation and whether the scalings developed in the idealised models are robust in more realistic situations.
Methods. The investigation was carried out by numerically solving the resistive compressible 3D magnetohydrodynamic equations in a Cartesian box containing a linear null point. The spine-fan collapse was driven at the null through tangential boundary driving of the spine foot points.
Results. We find significant differences in the initial current sheet formation with asymmetric driving. Notable is the displacement of the null point position as a function of driving velocity and resistivity (η). However, the scaling relations developed in the idealised case are found to be robust (albeit at reduced amplitudes) despite this extra complexity. Lastly, the spatial variation is also shown to play an important role in the initial current sheet formation through controlling the displacement of the spine foot points.
Conclusions. We conclude that during the early stages of spine-fan reconnection both the temporal and spatial nature of the driving play important roles, with the idealised symmetrically driven case giving a “best case” for the rate of current development and connectivity change. As the most interesting eruptive events occur in relatively short time frames this work clearly shows the need for high temporal and spatial knowledge of the flows for accurate interpretation of the reconnection scenario. Lastly, since the scalings developed in the idealised case remain robust with more complex driving we can be more confident of their use in interpreting reconnection in complex magnetic field structures.
Key words: magnetic reconnection / magnetohydrodynamics (MHD) / Sun: magnetic topology / Sun: corona
© ESO, 2012
1. Introduction
In recent years, with the increasing advancement of space-based instruments, we now have a better appreciation of the three dimensional (3D) complexity and magnetic structure of the solar atmosphere. In particular it is now widely accepted that solar flares and other explosive events must involve a change in magnetic connectivity and therefore involve Magnetic Reconnection. Magnetic reconnection occurs in regions of strong magnetic shear where intense electric current sheets form. Reconnection requires that in these current sheets a non-zero electric field parallel to the magnetic field is present. Under these conditions the ideal evolution of the magnetic field lines breaks down, allowing them to change connectivity (Priest et al. 2003; Hesse & Schindler 1988). Magnetic field structures in which field lines diverge naturally develop these regions of intense current as small foot point motions at one end of the field line lead to large field line motions where the field lines strongly diverge (Lau & Finn 1990; Priest & Démoulin 1995). One such magnetic structure containing diverging magnetic field lines is a 3D magnetic null point. The field near the null is characterized by two structures. The fan plane: a surface of field lines emanating out from (in to) the null, and the spine line: a pair of field lines approaching (receding from) the null. Magnetic field lines in the vicinity of the spine/fan diverge greatly when traced toward the fan/spine (see Fig. 1) as the field line mapping is discontinuous at the null. Thus the spine line and fan plane of magnetic null points are regions of preferential current growth.
That 3D null points are important sites for magnetic reconnection is borne out by the varied scenarios in which they are inferred to be involved. Single and multiple nulls have been observed in the reconnecting current sheet in the earth’s magnetotail through in situ measurements from the cluster satellites (Xiao et al. 2006, 2007), as well as being inferred through fully 3D simulations in the polar cusp regions (Dorelli et al. 2007). Their importance has also been noted in reconnection within laboratory plasmas (Gray et al. 2010). In the solar context, with the large number of flux sources seen in MDI magnetograms the existence of 3D nulls is virtually guaranteed. Indeed, in the quiet sun the number of nulls is found to be greatest near the photosphere with a drop in number with height between an exponential (Régnier et al. 2008) and power law (Longcope & Parnell 2009). 3D nulls play a more important roll higher up in the solar atmosphere during active times of the solar cycle and have been inferred to be involved in solar jets (Pariat et al. 2009; Liu et al. 2011), flux emergence (Török et al. 2009), flare brightening (Masson et al. 2009) and fully 3D magnetic breakout (Lynch et al. 2008).
The exact nature of the reconnection process at 3D nulls has only in recent years been explored more fully. The first investigation into current sheet formation was conducted by Rickard & Titov (1996) in the zero β cold plasma approximation. These authors noted that depending on the manner of driving, current sheet formation occurs either along the spine or fan or preferentially toward the null. The twisting modes were further investigated through simulations (Pontin & Galsgaard 2007; Galsgaard et al. 2003) and kinematic analytical models (Wyper & Jain 2010; Pontin et al. 2011). Subsequently it has been shown that twisting motions about the spine/fan create a current sheet along the fan/spine leading to Torsional fan/spine respectively (Priest & Pontin 2009). Shearing motions of the spine or fan in the incompressible situation give rise to current accumulation at the fan and spine respectively (Priest & Titov 1996; Craig & Fabling 1996) known as fan and spine reconnection. When finite plasma compressibility is invoked the plasma pressure gradient is too weak within the planar current sheets of both cases to resist the Lorentz force driven spine-fan collapse and a current sheet forms at an angle to the spine and fan within which “spine-fan” reconnection takes place (Priest & Pontin 2009; Galsgaard & Pontin 2011; Pontin et al. 2007a,b).
In this study we wish to explore more deeply the initial spine-fan collapse process. From satellite images it is clear that foot point motions are unlikely to maintain any strong symmetry for any appreciable time. Therefore we investigate the dynamics of current sheet formation and connectivity change due to asymmetrically driven perturbations. In particular we will extend the work of Pontin et al. (2007a) to investigate spine-fan reconnection driven from only one boundary as well as by both boundaries with a lag period between the driving pulses. With this difference in the driver we then investigate the validity of the scaling relations developed in the idealised symmetrically driven cases already studied. Beyond the initial current sheet formation certain cases are also considered over much longer timescales with a view toward future work. Lastly we also investigate the effect that the physical displacement of the driven foot points has on the current sheet development and dynamics as in practice foot point motions may be restricted by line-tying and driving flow topology.
 |
Fig. 1 Top: the initial magnetic field configuration. The spine (in blue) lies along the x-axis and the fan (in red) lies in the x = 0 plane. Coloured arrows indicated the field direction. The black arrows show the direction of shear applied by the driver at the boundaries. Bottom: the driving profile applied to the x-boundaries with Ad = 80. (This figure is available in color in the electronic form.) |
2. Simulation setup
We use a very similar simulation setup to that used in Pontin et al. (2007a, hereafter PBG07). We start with an isolated linear null point with magnetic field B = B0(−2x,y,z) in the center of our numerical box of size [±Xl, ± Yl, ± Zl]. The plasma is initially in equilibrium with density ρ = 1 and internal energy e = 5β ∗ /2. Here β ∗ is a parameter that controls the plasma-β, the ratio of plasma pressure to magnetic pressure: P/(B2/2μ0) = 10μ0β ∗ /3B2 (where the plasma is assumed to be an ideal gas such that P = (γ − 1)e). The plasma-β is infinite at the null where B = 0, with the rate of its reduction away from the null controlled by β ∗ . We set γ = 5/3, β ∗ = 0.05 and B0 = 1 for all the simulations.
The full set of compressible resistive magnetohydrodynamic (MHD) equations are solved numerically1. The equations are non-dimensionalised by setting the magnetic permeability μ0 = 1 and the gas constant (R) equal to the mean molecular weight (M). This results in one time unit equaling the travel time of an Alfvén wave over a unit distance through a plasma with unit density and unit magnetic field (ρ = 1, |B| = 1).
At the beginning of each run the fan plane sits on the x = 0 surface and
the spine lies along the x-axis and connects with the boundaries at
[ ±Xl,0,0] (see Fig.
1). Boundary shearing is then applied in opposite
directions to the x-boundaries which advect the spine foot points. The
driven boundaries are line-tied whereas the other two are closed with a thin damping region
to reduce numerical effects there. The driver is divergence free with the stream function
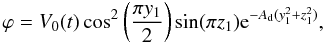 (1)where
y1 = y/Yl
and
z1 = z/Zl
and Ad controls the spatial extent of the driving patch. This
driver advects the spine in the
(1)where
y1 = y/Yl
and
z1 = z/Zl
and Ad controls the spatial extent of the driving patch. This
driver advects the spine in the 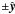 direction with return flows at a larger radius (Fig. 1). Throughout the simulations we set
Yl = Zl = 3 and
Xl = 0.5 with a resolution of 1283. The grid is
stretched to include more points near the null (δx ~ 0.005 and
δy,δz ~ 0.025) to better resolve structures there.
direction with return flows at a larger radius (Fig. 1). Throughout the simulations we set
Yl = Zl = 3 and
Xl = 0.5 with a resolution of 1283. The grid is
stretched to include more points near the null (δx ~ 0.005 and
δy,δz ~ 0.025) to better resolve structures there.
As one of the things we are interested in is the effect of driving the foot points at
different times, we choose a time variation of 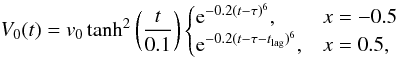 (2)when
the reconnection is driven by two pulses. The plasma velocity on the
x = −0.5 boundary is driven by a pulse that peaks in magnitude at
t = τ and drops to near zero by
t = 2τ. A second pulse is then initiated at the
x = 0.5 boundary but offset in time by tlag.
When the spine-fan collapse is driven by only one pulse we set
V0(t) = 0 on the x = 0.5
boundary. We begin by discussing the initial current sheet formation in runs with such
temporal variations.
(2)when
the reconnection is driven by two pulses. The plasma velocity on the
x = −0.5 boundary is driven by a pulse that peaks in magnitude at
t = τ and drops to near zero by
t = 2τ. A second pulse is then initiated at the
x = 0.5 boundary but offset in time by tlag.
When the spine-fan collapse is driven by only one pulse we set
V0(t) = 0 on the x = 0.5
boundary. We begin by discussing the initial current sheet formation in runs with such
temporal variations.
 |
Fig. 2 Shaded contours show |J| (scaled to the maximum of each snapshot), while the arrows depict the plasma flow. For the case of v0 = 0.01 with only one pulse. (This figure is available in color in the electronic form.) |
3. Temporal variation: one pulse vs. two simultaneous pulses
3.1. Current and plasma flow evolution
To investigate the role of temporal variation we first consider the difference between spine-fan reconnection driven by one pulse or by two pulses sent at the same time (tlag = 0). In both sets of experiments τ = 1.8, Ad = 80 and η = 5 × 10-4. When there are two pulses they both propagate essentially Alfvénically away from the boundaries at the same time. As the pulses reach the null the shear of the wavefront steepens generating strong electric currents. Near the null where the Alfvén velocity drops to zero the disturbance couples to acoustic wave modes and focuses on the null itself (for a review of the properties of MHD waves in the vicinity of magnetic nulls see McLaughlin et al. 2011). A strong current sheet then forms at the null, with the null location remaining fixed at the origin for all time. This case was described in detail in PBG07.
To clearly visualize the process when there is only one pulse it is useful to study the current evolution in the z = 0 plane (i.e. the plane of shear containing both spine and fan). Figure 2 shows a typical case when v0 = 0.01. The pulse propagates (from the x = −0.5 boundary) into the volume and follows the field lines toward the null (Fig. 2a). As there is no symmetric pulse from the opposite boundary, while the pulse arrives at the null, the position of the null point shifts in the direction of shear due to ideal and non-ideal effects (see Sect. 3.5).
In Fig. 2b the null point position (following the direction of shear) is shifting in the positive y direction. As the null point moves, connectivity change at the null changes the field line that the spine line falls along in the near static plasma in the x > 0 region (see Sect. 3.2). Thus both spine lines have plasma passing through them, with one spine line (x < 0) having it driven through by the pulse and the other because the spine itself moves through the plasma (x > 0). From the frame of reference of the null point the plasma appears to locally adopt a stagnation point flow. This shows that, even in the absence of symmetric driving, flow across the spine line and fan plane are ubiquitous to the early stages of spine-fan collapse. The system then begins to relax as the driving ceases and the null reaches its maximum displacement (Fig. 2c). The electric current sheet then slowly spreads out across the fan plane (Fig. 2d) as the system enters the relaxation phase of the process (t > 5, see Sect. 5).
Figure 3 (top panel) shows the variation of current modulus (|J|) with time for one pulse (green) and two pulses sent together (black) over the period of current sheet formation and relaxation. As in PBG07 we find the z-component (in the direction perpendicular to the shear) dominates the x and y-components of current. We see that during the formation of the current sheet (t < 5) the temporal evolution for one pulse follows closely that of the tlag = 0 case with two pulses except at a lower amplitude. This is because with only one pulse there is half the available free energy to drive spine-fan collapse. Both the curves reach their maximum at the same time, at the point where the pulses reach the null. Once the maximum is reached the current sheet spreads out across the fan plane and the null point returns toward it’s initial position.
 |
Fig. 3 Solid lines (top panel): |J| plotted against t. Solid lines (bottom panel): ∫E ∥ dl plotted against t. For the cases with two pulses the dashed lines indicate the driving amplitude of the second pulse. Black: tlag = 0, red: tlag = 0.9 and blue: tlag = 1.8. The solid green line is with only one pulse. For the case of v0 = 0.01. (This figure is available in color in the electronic form.) |
3.2. Connectivity change
It is known from previous studies that spine-fan reconnection involves reconnection of field lines across both the spine line and the fan surface. How is connectivity change affected by asymmetry in the driving? In Fig. 4 we see the connectivity change in the two cases. The gold field lines are anchored in the side boundaries and are initially connected (at t = 0) to the blue and red flux tubes, the ends of which are shifted by the boundary driving. In the symmetrically driven case as the current sheet forms at the null the two (red and blue) initial flux tubes split into four. The red and blue tubes reconnect through the spine, whereas the gold tubes reconnect through the fan. However, the four flux tubes do not rejoin perfectly on the other side. This is indicative of the continuous change in connectivity within the diffusion region leading to a non-pairwise reconnection process (Pontin et al. 2005; Priest et al. 2003).
In the case with one pulse, however, only the red flux tube foot points are driven. From Fig. 4 we see that the current sheet formation and subsequent movement of the null still gives rise to connectivity change on the undriven side. This is indicated in the figure by the spine line on the undriven side initially being a field line below the blue flux tube at t = 1 but a field line inside it by t = 5. In fact at later times the whole blue flux tube is reconnected to the other side of the spine on the undriven side.
We also note that the driven red flux tube reconnects across the spine more rapidly than the undriven blue one. This shows that the connectivity change is uneven in the asymmetric case. Again this is indicative of the continuous nature of the connectivity change within the diffusion region in three dimensions.
 |
Fig. 4 The change in connectivity with two simultaneous pulses (top) one pulse (bottom) and when v0 = 0.04, Ad = 80 and η = 5 × 10-4. The red and blue flux tubes (traced from the driving boundaries) are initially connected to the gold field lines anchored on the side boundaries. Taken at times t = 1 (left), 3 (middle) and 5 (right). (This figure is available in color in the electronic form.) |
3.3. Reconnection rate and E∥
The signature of reconnection in 3D is an electric field component parallel to the
magnetic field (E ∥ ). In the presence of a non-zero magnetic
field the reconnection rate is given by the maximum of
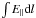 along a
field line threading the non-ideal region (Hesse &
Schindler 1988). Pontin et al. (2005)
showed in the case of a symmetric null point that, for the spine-fan reconnection mode,
the reconnection rate at the null can be found from
Ψ = ∫x = y = 0E ∥ dz.
This quantity gives the amount of flux transfered through the fan plane when the
reconnection region is localized.
along a
field line threading the non-ideal region (Hesse &
Schindler 1988). Pontin et al. (2005)
showed in the case of a symmetric null point that, for the spine-fan reconnection mode,
the reconnection rate at the null can be found from
Ψ = ∫x = y = 0E ∥ dz.
This quantity gives the amount of flux transfered through the fan plane when the
reconnection region is localized.
In the simulations with one pulse the null point position moves and so the
z-axis is no longer co-incident with the magnetic field line along
which E ∥ is maximum (see Fig. 5). In such single pulse cases we integrate along several field lines in the fan
plane near the null as far as the edge of the current sheet (i.e. where
|J| = 0). The reconnection rate is then given by the
sum of the maximum integrals for z positive and negative with an
additional term including a contribution from
E = (0,0, − ηjz)
across the null i.e. 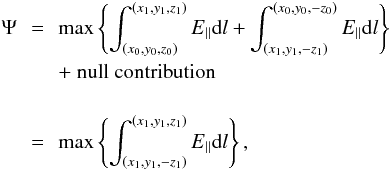 (3)where
(x0,y0, ± z0)
is the starting point near the null and
(x1,y1, ± z1)
is the edge of the current sheet. Note that
(x1,y1, ± z1)
varies from run to run and changes in time in each case as the shape of the current sheet
changes. For these runs we choose z0 = 0.05. Any smaller
choices of z0 may result in the magnetic field line being
traced increasingly inaccurately. On the other hand, for a larger choice of
z0 the null contribution becomes increasingly inaccurate.
Thus, z0 = 0.05 is chosen to reduce both these inaccuracies.
(3)where
(x0,y0, ± z0)
is the starting point near the null and
(x1,y1, ± z1)
is the edge of the current sheet. Note that
(x1,y1, ± z1)
varies from run to run and changes in time in each case as the shape of the current sheet
changes. For these runs we choose z0 = 0.05. Any smaller
choices of z0 may result in the magnetic field line being
traced increasingly inaccurately. On the other hand, for a larger choice of
z0 the null contribution becomes increasingly inaccurate.
Thus, z0 = 0.05 is chosen to reduce both these inaccuracies.
 |
Fig. 5 Top: an iso-surface (at 50% of maximum) of |E ∥ |. Bottom: a contour plot of |E ∥ | in the x = −0.005 plane (containing the null point). For the case of one pulse with v0 = 0.04 and τ = 1.8. Taken at the point where the null is most displaced from its initial position. Note the asymmetrical shape (in the y-direction) of the strong E ∥ regions near the null point. (This figure is available in color in the electronic form.) |
Figure 3 (bottom panel) shows the variation of the reconnection rate with t during the formation of the current sheet (t < 5) for one pulse (green) and two pulses sent simultaneously from opposite boundaries (black). Similar to the current density the reconnection rate for one pulse closely matches the temporal behaviour of the case of two pulses sent at the same time but at a reduced amplitude. Unlike in two dimensions, where peak current and reconnection rate occur together, we see that in 3D the reconnection rate peaks after the current. This is because the reconnection rate in 3D is the integral through the whole sheet which widens after the current peaks compensating for the reduced current at the null itself. This is an interesting aspect of the three dimensional nature of the current sheet which can allow the same amount of flux to pass through the fan plane but over a wider area.
 |
Fig. 6 Scaling of the absolute value of the driving velocity with peak current
|J|max, peak reconnection rate
|
3.4. Qualitative trends
We now compare the trends in quantitative behaviour of current sheet formation driven by only one pulse and two pulses sent together. For two pulses sent at the same time (tlag = 0) from opposite boundaries and for only one pulse we carried out runs with varied driving strength (v0) when τ = 1.8, Ad = 80 and η = 5 × 10-4. We wish to extend the results of PBG07 and so focus on the peak current (occurring at the null even when it is advected and the peak reconnection rate calculated as described earlier. Similarly we also consider the sheet dimensions in the x-, y- and z-directions (Lx,Ly and Lz respectively), measured as the full width at half maximum of the current sheet.
As the driving is not sustained we expect that the flux pileup at the onset of the current sheet does not saturate due to the finite speed of reconnection within the current layer. Therefore the peak reconnection rate and current should scale linearly with driving velocity (compared to the non-linear relations observed in the continuously driven case, Galsgaard & Pontin 2011). Indeed Fig. 6 shows that both the two pulse and one pulse driving cases increase linearly with v0 and that the gradient of the line described by the single pulse case is half that of the two pulse one. Clearly despite the non-linear movement of the null point and the differing plasma dynamics what is important is the available free energy to drive the reconnection.
The current sheet dimensions are dictated by the strength of the spine-fan collapse which increases when the current (and therefore the Lorentz force) in the sheet increases. This manifests in the increase in Lx and decrease in Ly as v0 increases (Fig. 6). Compared with the two pulse case the one pulse case creates less total stress at the fan plane. Therefore it is natural that the spine-fan collapse be reduced and that the sheet spread the stress more widely across the fan plane (reducing Lx and increasing Ly (Fig. 6)).
As with the case of tlag = 0 studied in PBG07 the interpretation of Lx and Ly varies with the changes in current sheet morphology. When the driving is very weak the current sheet is almost planar across the fan plane. When the driving strength is increased the current sheet forms an S-shape with some collapse of the spine and fan. With the driving further increased the current forms into a planar sheet spanning both spine and fan at an angle to both. In the case of only one pulse and the cases discussed in Sect. 4 where tlag ≠ 0 the current sheet becomes asymmetrical but in general the same qualitative interpretation of the sheet dimensions discussed in PGB07 for tlag = 0 applies.
Lastly we note the slight difference in magnitude of the sheet dimensions and peak values measured for the runs with tlag = 0 to those in PBG07. This is due to the slight differences in the driving, the resolution and the boundary damping between the two numerical setups. Here we wish to ascertain the qualitative trends of each parameter which in both setups are linear.
 |
Fig. 7 Arrows depict Lorentz (top left: blue) and pressure forces (top right: red) in the z = 0 plane. Bottom left: the combination of Lorentz and pressure forces (green). The solid black lines show a selection of field lines and the “+” sign indicates the null point position. Bottom right: field lines traced from around the null in 3D. Taken at t = 2.0 for the case of one pulse with v0 = 0.04, τ = 1.8, Ad = 80 and η = 5 × 10-4. (This figure is available in color in the electronic form.) |
3.5. Null displacement
We now focus on the physics behind the initial displacement of the null point in the case
of one driving pulse. There are two dominant competing effects that govern the rate of
null point movement. As the disturbance reaches the null there is an asymmetric collapse
of the spine on to the fan plane (see Fig. 7). The
balance of Lorentz and pressure forces in the two outflow regions are unequal and so the
whole non-ideal region is pulled toward the more collapsed side, taking with it the null
point. This initial local collapse is ideal, however as the collapse increases the current
in the collapsed region intensifies at which point non-ideal effects become important.
Therefore, the degree of collapse depends upon the value of resistivity which dictates the
rate at which flux is asymmetrically moved into the collapsed region by the non-ideal
stagnation point flow. As such the displacement of the null should be a function of the
resistivity. The null remains in the z = 0 plane by symmetry so we define
the displacement of the null as 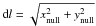 ,
where
(xnull,ynull,0)
is the displaced position of the null from the origin. Figure 8 (top panel) shows the dependency of the maximum displacement
(dlmax) with η for two values of
v0 when Ad = 80 and
τ = 1.8. For the values chosen the null displacement most closely
follows an exponential increase with a reduction in η, with relationships
given by
,
where
(xnull,ynull,0)
is the displaced position of the null from the origin. Figure 8 (top panel) shows the dependency of the maximum displacement
(dlmax) with η for two values of
v0 when Ad = 80 and
τ = 1.8. For the values chosen the null displacement most closely
follows an exponential increase with a reduction in η, with relationships
given by 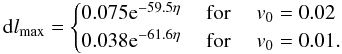 Therefore
when η is smaller the asymmetric collapse of the spine and fan is greater
and the null moves position more rapidly. In addition the reconnection rate is smaller
with reduced η, forcing less flux into the more collapsed region allowing
the null to shift position even faster. The maximum displacement of the null also depends
linearly on the driving associated with the pulse (Fig. 8: bottom panel) in agreement with the linear dependence of
|J|max in Fig. 6.
Therefore
when η is smaller the asymmetric collapse of the spine and fan is greater
and the null moves position more rapidly. In addition the reconnection rate is smaller
with reduced η, forcing less flux into the more collapsed region allowing
the null to shift position even faster. The maximum displacement of the null also depends
linearly on the driving associated with the pulse (Fig. 8: bottom panel) in agreement with the linear dependence of
|J|max in Fig. 6.
An intriguing question is does this rapid change of position of the null change the
scalings associated with the reconnection rate and current? Recently Lukin & Linton (2011) discussed reconnection at a magnetic null
moving parallel to the direction of current passing through it (compared to the null
moving perpendicular to the direction of current here). In their setup the null has the
ability to move out of the plane containing the outflow from the reconnection site which
hints at the possibility of fast reconnection not choked by the Sweet-Parker bottle neck.
In the present study will the ability of the null to move increase or decrease such a
bottleneck effect? Figure 9 shows the scalings with
η of peak reconnection rate and current density with one pulse (green
points) and two pulses (black points). We see that the trends of both quantities are in
excellent agreement, with the average power law dependencies for each quantity given by
![\begin{equation} \left[\int E_{\parallel} {\rm d}l\right]_{\max}\propto \eta^{0.15} \quad \& \quad |\vec{J}|_{\max} \propto \eta^{-0.65}. \end{equation}](/articles/aa/full_html/2012/09/aa19281-12/aa19281-12-eq86.png) (4)Therefore we
conclude that there is no evidence to suggest that the movement of the null perpendicular
to the direction of current affects the reconnection rate and current scalings. What is
important is the available free energy from the driving pulses and the value of
resistivity.
(4)Therefore we
conclude that there is no evidence to suggest that the movement of the null perpendicular
to the direction of current affects the reconnection rate and current scalings. What is
important is the available free energy from the driving pulses and the value of
resistivity.
Lastly, how do these resistive scalings compare with those of other investigations? This kind of transient driving is on the cusp between truly wave driven reconnection, which in the linear regime gives rise to oscillatory reconnection and scaling relations which depend upon log η (Craig & McClymont 1991), and driven flux pileup reconnection which scales as a power law. An initial investigation by Priest & Pontin (2009) found a power law fit for |J|max and somewhere between a power law and logarithmic scaling for reconnection rate. Here a power law appears to fit best for both. Comparing to the flux pileup regimes the power law scaling for peak current (η-0.65) is comparable with those of the dynamic incompressible fan solutions of Craig & Fabling (1998): η−3/4 and those found empirically for the continuously driven case: η-0.6 ~ η-0.8 (Galsgaard & Pontin 2011). The reconnection rate however scales slightly faster compared to the η0.25 scaling found in the other two cases. What is evident is that a highly accurate scaling analysis covering many decades of resistivity is needed to fully determine the scaling behaviour of the transient case. However, in the context of the present investigation we can confidently say that the behaviour of the idealised symmetric case at low values of resistivity will be mirrored by that of the more complex asymmetrically driven cases.
 |
Fig. 8 Case of spine-fan reconnection driven by a single pulse. Top
panel: maximum displacement |
 |
Fig. 9 Log-log plots of peak reconnection rate (top panel) and peak current (bottom panel) against η. Black points: two pulses sent at the same time (diamonds: v0 = 0.01, squares: v0 = 0.02). Green points: one pulse (asterisks: v0 = 0.01, triangles: v0 = 0.02). The lines depict the lines of best fit for two pulses sent at the same time (solid) and one pulse (dashed) in each case. (This figure is available in color in the electronic form.) |
4. Temporal variation: two pulses with a lag between
4.1. Current, reconnection rate, and plasma flow evolution
In the two preceding cases the disturbances reach the null at the same time. Therefore it should not be surprising that there are similarities in the early temporal evolutions of current or reconnection rate between the two cases. What happens, however, if we apply the second pulse at a later time? How important is the subsequent overlap to the reconnection process? To investigate this we ran two more simulations with two pulses with lag periods between them of tlag = 0.9 and tlag = 1.8 for τ = 1.8, Ad = 80 and η = 5 × 10-4.
Figure 10 shows the current evolution in the z = 0 plane (the plane containing both spine and fan) for the v0 = 0.01 and tlag = 1.8 case taken at the same times as in Fig. 2. The early evolution (Figs. 10a and b) of the system is the same as that seen in the case with one pulse. The first pulse generates an asymmetric current sheet at the null which is displaced in the direction of shear. From the point of view of the null point the flow near it is a stagnation point flow.
The second pulse (sent from the x = 0.5 boundary at tlag) then arrives and shifts the null back toward and then past its initial position (Figs. 10c and 11: top panel). This forms the current sheet into an S-shape which then stretches along the fan plane once both pulses start to dissipate (Fig. 10d). At this point the driving flow in the y-direction starts to dominate.
For the tlag = 0.9 case, the same morphology of the wavefronts and current sheet occurs but (with the second pulse arriving sooner) the null travels less distance when displaced and the shear from the first pulse is less dissipated when the second pulse arrives.
Figure 3 shows the variation of current modulus (|J|) and reconnection rate with time for the two cases (tlag = 0.9: red and 1.8: blue) compared against the symmetrically driven case (tlag = 0: black). As the lag period between the pulses increases (tlag = 0 → 1.8) the latent shear associated with the first pulse is reduced by the time the second pulse arrives. This reduces the maximum current attained which in both cases occurs shortly after the second pulse reaches the null, at which time the entire current sheet (including the null) is being advected in the direction of the shear from the second pulse.
Similar to the peak current density, the maximum reconnection rate is slightly reduced and occurs at a later time for the drivers with a longer lag between the pulses. In the case of tlag = 1.8 (see blue solid lines) we see two peaks as the second pulse arrives late enough that the flux transfer from the first pulse has started to slow down.
 |
Fig. 10 Shaded contours show |J| (scaled to the maximum of each snapshot), while the arrows depict the plasma flow. For the case of v0 = 0.01 and tlag = 1.8. (This figure is available in color in the electronic form.) |
4.2. Qualitative trends
We have shown the dynamics of current sheet formation and initial null displacement is complicated significantly by a later second pulse. Might we still expect the linear increase in peak reconnection rate and current with driving velocity that we found in the simpler cases in Sect. 3? To investigate this the above analysis was repeated for several more values of v0. Surprisingly the peak reconnection rate and current do still depend linearly upon driving velocity, despite the increased complexity of the situation (Fig. 6, red: tlag = 0.8, blue: tlag = 1.8). In fact the one pulse case and the tlag = 0 symmetric two pulse case provide upper and lower bounds for the peak current and reconnection rate within which the asynchronous two pulse simulations (when all other parameters are fixed) fall.
The spine-fan collapse (and therefore the sheet dimensions) follows the same trend as the single and symmetric double pulse cases in that they increase with driving velocity through stronger Lorentz force driven collapse (increasing Lx and decreasing Ly). The sheet dimensions themselves are measured at the time of peak current which occurs progressively later as the time between pulses increases (see Fig. 3). As such we expect the stress in the field from the first pulse to have spread out further across the fan plane by the arrival at the null of the second pulse. This is demonstrated in Fig. 6 as an increase in Ly and decrease in Lx for increasing tlag.
The naturally wider and weaker current sheets that occur as the gap between the pulses increases leads to a subtle difference between the trends in the peak values of reconnection rate and current. The peak reconnection rate is affected slightly less than the peak current (staying closer to the values obtained when tlag = 0) by the increasing gap between the two pulses (tlag = 0 → 1.8). As the reconnection rate is the integral across the whole sheet, the spread of the current sheet compensates somewhat for the reduced maximum strength of current within it.
In summary the initial current sheet morphology is further complicated by the introduction of a second pulse sent at a later time. Clearly the timing of the pulses plays an important roll in the values obtained for peak reconnection rate and current. However, the relationships developed in the symmetric case remain valid despite the extra complexity in the dynamics.
5. Temporal variation: relaxation phase
In this section we briefly comment upon the longer term behaviour of the system beyond the initial peak in current density and reconnection rate. We define this relaxation phase as beginning once the reconnection rate begins to decline. To show this phase the runs for tlag = 0,0.9,1.8 and one pulse with v0 = 0.01, η = 5 × 10-4 and Ad = 80 were carried out well beyond their peaks in reconnection rate. Once each case enters this phase of reconnection the spine-fan collapse reduces, the current sheet spreads out across the fan plane and the null point returns toward it’s initial position (in the cases where it has been displaced). However in these cases the null does not simply slowly make its way to the origin. During the null’s initial displacement the spine-fan collapse not only pulled the null forward (in y) but also upward (in x). This displacement in x gives rise to an oscillation of the null point and surrounding fan plane as the null overshoots the x = 0 plane in returning toward it (Fig. 11, bottom panel). Thus the null oscillates perpendicular to the fan plane (in x) as it slowly moves back in y toward y = 0 (Fig. 11, top panel). The amplitude of the null oscillation depends upon the timing of the pulses with the asynchronous case of tlag = 1.8 giving the largest displacement in x. In this case the second pulse acts to amplify the displacement created by the first. Clearly the timing of the second pulse is critical to producing a bigger oscillation. Also, recall that the initial displacement of the null depends upon driving velocity and resistivity (see Fig. 8) indicating that an increase/decrease in each respectively will also lead to bigger oscillations. Interestingly the period of oscillation is nearly the same in the three cases (tperiod ≈ 4 Alfvén times) suggesting that there is a unique frequency of oscillation that must depend upon the plasma parameters. An interesting avenue of investigation would be to explore this wave behaviour further and to see firstly how the oscillation period depends upon the plasma parameters and secondly whether this oscillation could be driven resonantly if the right driving period is used. Such an investigation is however beyond the current scope of this investigation which focuses on the early stages of the spine-fan process.
 |
Fig. 11 Components of the null position (xnull, ynull,0) plotted against t. Top: ynull and bottom: xnull. For one pulse (green) and two asynchronous pulses with tlag = 0.9 (red) and 1.8 (blue). Each case has v0 = 0.01, η = 5 × 10-4 and Ad = 80. (This figure is available in color in the electronic form.) |
Comparing Figs. 3 and 11 what is clear is that this induced wave-like behaviour is non-reconnective as it continues well beyond the time (t > 14) when the reconnection ceases. At this point there is still significant current in the system which slowly reduces through magnetic diffusion. Such fan plane perturbations are reminiscent of the radially symmetric non-reconnecting m = 0 spine mode of Craig & Fabling (1996) hinting that such solutions could be utilized to analyze such oscillations in the future. For much longer time frames this oscillatory motion will damp out (which we see begins to occur around t = 10 in Fig. 11, bottom panel) leaving the null back at the origin and a current sheet in force balance between plasma pressure gradient and Lorentz force with the current slowly reducing through magnetic diffusion.
Lastly we note that the current in the system perturbed by a single pulse decays more slowly than the cases perturbed by two pulses. When perturbed by two pulses (symmetric or otherwise) much of the stress applied by the first pulse to the magnetic field on one side of the fan plane is matched by the second on the other side. As the field relaxes both combine to bring the field toward a potential field configuration faster than when the stress applied is uneven as in the case of a single pulse.
In summary beyond the initial current sheet formation phase asymmetric perturbations generate oscillations of the null perpendicular to the fan plane at an apparently natural frequency to the system. Further work is needed to fully understand the details of this dynamics and will be the topic of future investigations. For the moment we continue our investigation of the early stages of spine-fan collapse.
 |
Fig. 12 Scaling of the absolute value of the driving velocity with peak current
|J|max, peak reconnection rate
|
6. Spatial variation
Due to the complex surface flow topology of the sun and the effective line-tying at the
solar photosphere, driving motions could often be constrained in size. In this section we
consider the effect that a restriction to the foot point displacement has on current growth
and reconnection rate. To achieve this we ran further simulations for varied driving patch
sizes with v0 = 0.1, τ = 1.8 and
η = 5 × 10-4. The patch length scale
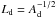 is
doubled by varying Ad from 320 to 80 (see Eq. (1)). For increased generality we also repeated
the runs with varied Ld for two pulses with temporal variation,
tlag = τ/2 and
τ and for a single driving pulse.
is
doubled by varying Ad from 320 to 80 (see Eq. (1)). For increased generality we also repeated
the runs with varied Ld for two pulses with temporal variation,
tlag = τ/2 and
τ and for a single driving pulse.
What can we expect? With a larger driving patch the spine should be displaced more during the driving and therefore the current sheet formed at the null should be stronger. We find that the relation of peak values for current and reconnection rate with Ld (and therefore spine displacement) is linear (Fig. 12) indicating that for transient driving the width over which the perturbation occurs also plays an important role in the dynamics of current sheet formation.
With an increase in current within the sheet we expect an increase in spine-fan collapse through the stronger Lorentz force. This is seen as an increase in Lx in Fig. 12. The sheet length along the direction of shear however appears to be less altered, with a variation ≈10% compared with ≈30% in Lx. The sheet is actually lengthening along the fan plane in the y-direction, however the angle that the sheet makes to the fan is also increasing, reducing Ly in the way it is measured here. Lastly out of the xy-plane with an increase in Ld (and therefore the width of the driver) we expect a linear increase in current sheet width (Lz). What we find is a near linear curve as the increase in current at the null (due to the increased spine displacement) slightly reduces the width between the half maximum points.
Finally we note that for the smallest driving patches the spine foot point may reach close to the edge of the patch (where the driving stops) within the duration of the driving time. That is, compared with larger patches the spine may be perturbed for a shorter time. To compensate for this the runs with tlag = 0 were repeated but with the driving switched off once the spine was at the same point within the patch i.e. the driving time scale τ was scaled down at the same rate as the driving spatial scale Ld. The results of changing Ld are the same as above but with a weaker dependence in peak current and reconnection rate.
7. Discussion
In this study we have explored the current sheet formation of spine-fan reconnection focusing on the importance of the driving on current sheet development and reconnection rate. We chose to investigate two important unresolved questions. Firstly, when the driving is asymmetric how does the spine-fan collapse occur and do the scaling laws developed in symmetric models apply? As transient motions in the solar atmosphere are ubiquitous this seems a pertinent question. Secondly, we might not unreasonably expect that foot point motions may be constrained in size through local flow topology. To what extent does the spatial limiting of foot point motion change the system behaviour?
In answering the first question we looked at the spine-fan collapse in response to transient asymmetric driving and found that any degree of asymmetry in the collapse produced a displacement of the null itself. This suggests that in practice a coronal null will be constantly moving. Indeed, that the displacement of the null increases with reducing η shows that at realistic coronal values a 3D null will be severely rattled around by buffeting driving flows. This rapid movement could be a potential mechanism to crash together nulls of opposite type (A or B) leading to the null cancellation observed in the null clusters that connect large scale reconnecting separators (Dorelli et al. 2007; Parnell et al. 2010; Maclean et al. 2009).
In terms of reconnection rate and current what became apparent was that the timing of when the energy of the perturbations is delivered to the null is of crucial importance for the reconnection process. This agrees with the 2D work on driven reconnection of Jain et al. (2005) and underlines the importance of understanding the timing of perturbations in the early stages of current sheet development. What is encouraging, considering the complexity of the flows in the solar atmosphere, is that despite the extra dynamical effects the scaling relationships established in the idealised cases with symmetric driving remain robust.
An interesting finding from these transiently driven cases is that unlike in the 2D wave
driven case (Craig & McClymont 1991; McLaughlin et al. 2009) we see no evidence of oscillatory
reconnection as the system relaxes once the driving ceases (i.e. no change in sign of
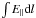 , Fig.
3). What we find instead is the generation of
oscillations of the null itself. However, if the driving is sufficiently impulsive we would
also expect to see oscillatory reconnection. It seems likely that both behaviours will occur
together in the relaxation phase of spine-fan reconnection with the type of perturbation
dictating which dominates. This is clearly an interesting avenue of future work.
, Fig.
3). What we find instead is the generation of
oscillations of the null itself. However, if the driving is sufficiently impulsive we would
also expect to see oscillatory reconnection. It seems likely that both behaviours will occur
together in the relaxation phase of spine-fan reconnection with the type of perturbation
dictating which dominates. This is clearly an interesting avenue of future work.
What we do see in our transiently driven simulations in common with those of McLaughlin et al. (2009) is a move toward a non-potential final state in force balance through plasma pressure. This final state indicates that even small perturbations of the spine or fan will lead to a non-potential fan plane magnetic field and preferential heating there. This seems in agreement with the heating observed at domed fan structures observed in solar jets (e.g. Liu et al. 2011; Török et al. 2009).
In approaching the second question we considered the current build up through transient driving with different patch sizes where we found a direct linear correlation between driving length scale and peak reconnection rate and current. Thus, in line-tied systems a limited spatial scale can have a detrimental effect on the efficiency of the reconnection process. This highlights that, although line-tied photospheric motions are often used as the catalysts for generating non-ideal regions and reconnection (e.g. magnetic breakout, Antiochos et al. 1999), depending on the magnetic topology they can also limit the ultimate reconnection rate.
It should be noted that since we have considered a linear magnetic null point our results are only applicable in the vicinity of the null where the linear nature of the magnetic field is valid. However the spine-fan mode has been shown to occur in highly non-linear setups, for example (Masson et al. 2009; Gray et al. 2010; Lynch et al. 2008) and thus our results seem likely to carry over to some extent outside of the linear region.
Lastly, we also note that varying the global plasma-β or the ratio of specific heats (γ) will change the above results. With higher values of either parameter the plasma sound speed increases. This reduces the spine-fan collapse spreading the current sheet out across the fan plane (Pontin et al. 2007b). As the null displacement depends upon the spine-fan collapse, this should mean that it is also a function of global plasma-β and γ. This would be interesting to investigate in the future.
8. Conclusion
In this work we investigated two important aspects, the timing and length scale, of boundary driving for the initial development of the spine-fan reconnection mode at a 3D magnetic null point. We find significant differences in the early dynamics for the transiently driven case when the driving deviates from the idealised scenario with one pulse sent from either side of the null at the same time. Of note is the propensity of the null to be displaced in a manner which increases with reducing resistivity. Surprisingly, we find that despite the difference in the driving pattern the scaling relationships developed for peak reconnection rate and current against driving strength and resistivity are maintained, albeit at reduced amplitudes. The linear reduction in reconnection rate and current with driving length scale also highlights the importance of the spatial element of the driving and the potentially retarding effect of line-tying.
We conclude that during the early phase of current sheet formation both the temporal and spatial nature of the driver play important roles, with the idealised symmetrically driven case giving a “best case” for the rate of current development and connectivity change. As the most interesting eruptive events occur in relatively short time frames this work clearly shows the need for high temporal and spatial knowledge of the flows for accurate interpretation of the reconnection scenario. Lastly since the scalings developed in the symmetric case remain robust to more complex driving we can be more confident of their use in interpreting reconnection in complex magnetic field structures.
Details of the scheme can be found in Galsgaard & Nordlund (1997) and on http://www.astro.ku.dk/~kg.
Acknowledgments
We thank K. Galsgaard for the use of his 3D resistive MHD code in this study. We also thank the anonymous referee for many instructive comments leading to the improvement of this work. Computational time was given by the MHD cluster of the University of St. Andrews. P.W. and R.J. also acknowledge the financial support of EPSRC.
References
- Antiochos, S. K., DeVore, C. R., & Klimchuk, J. A. 1999, ApJ, 510, 485 [Google Scholar]
- Craig, I. J. D., & Fabling, R. B. 1996, ApJ, 462, 969 [NASA ADS] [CrossRef] [Google Scholar]
- Craig, I. J. D., & Fabling, R. B. 1998, Phys. Plasmas, 5, 635 [NASA ADS] [CrossRef] [Google Scholar]
- Craig, I. J. D., & McClymont, A. N. 1991, ApJ, 371, L41 [NASA ADS] [CrossRef] [Google Scholar]
- Dorelli, J. C., Bhattacharjee, A., & Raeder, J. 2007, J. Geophys. Res., 112, A02202 [NASA ADS] [CrossRef] [Google Scholar]
- Galsgaard, K., & Nordlund, Å. 1997, J. Geophys. Res., 102, 231 [NASA ADS] [CrossRef] [Google Scholar]
- Galsgaard, K., & Pontin, D. I. 2011, A&A, 529, A20 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Galsgaard, K., Priest, E. R., & Titov, V. S. 2003, J. Geophys. Res., 108, 1042 [NASA ADS] [CrossRef] [Google Scholar]
- Gray, T., Lukin, V., Brown, M., & Cothran, C. D. 2010, Phys. Plasmas, 17, 102106 [NASA ADS] [CrossRef] [Google Scholar]
- Hesse, M., & Schindler, K. 1988, J. Geophys. Res., 93, 5559 [NASA ADS] [CrossRef] [Google Scholar]
- Jain, R., Browning, P., & Kusano, K. 2005, Phys. Plasmas, 12, 012904 [NASA ADS] [CrossRef] [Google Scholar]
- Lau, Y. T., & Finn, J. M. 1990, ApJ, 350, 672 [NASA ADS] [CrossRef] [Google Scholar]
- Liu, W., Berger, T. E., Title, A. M., Tarbell, T. D., & Low, B. C. 2011, ApJ, 728, 103 [NASA ADS] [CrossRef] [Google Scholar]
- Longcope, D. W., & Parnell, C. E. 2009, Sol. Phys., 254, 51 [NASA ADS] [CrossRef] [Google Scholar]
- Lukin, V. S., & Linton, M. G. 2011, Nonlinear Processes Geophys., 18, 871 [Google Scholar]
- Lynch, B. J., Antiochos, S. K., DeVore, C. R., Luhmann, J. G., & Zurbuchen, T. H. 2008, ApJ, 683, 1192 [NASA ADS] [CrossRef] [Google Scholar]
- Maclean, R. C., Parnell, C. E., & Galsgaard, K. 2009, Sol. Phys., 260, 299 [NASA ADS] [CrossRef] [Google Scholar]
- Masson, S., Pariat, E., Aulanier, G., & Schrijver, C. J. 2009, ApJ, 700, 559 [NASA ADS] [CrossRef] [Google Scholar]
- McLaughlin, J. A., De Moortel, I., Hood, A. W., & Brady, C. S. 2009, A&A, 493, 227 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- McLaughlin, J. A., de Moortel, I., & Hood, A. W. 2011, A&A, 527, A149 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Pariat, E., Antiochos, S. K., & DeVore, C. R. 2009, ApJ, 691, 61 [NASA ADS] [CrossRef] [Google Scholar]
- Parnell, C. E., Maclean, R. C., & Haynes, A. L. 2010, ApJ, 725, L214 [NASA ADS] [CrossRef] [Google Scholar]
- Pontin, D. I., & Galsgaard, K. 2007, J. Geophys. Res., 112, A03103 [NASA ADS] [CrossRef] [Google Scholar]
- Pontin, D. I., Hornig, G., & Priest, E. R. 2005, Geophys., Astrophys. Fluid Dyn., 99, 77 [NASA ADS] [CrossRef] [Google Scholar]
- Pontin, D. I., Bhattacharjee, A., & Galsgaard, K. 2007a, Phys. Plasmas, 14, 052106 [NASA ADS] [CrossRef] [Google Scholar]
- Pontin, D. I., Bhattacharjee, A., & Galsgaard, K. 2007b, Phys. Plasmas, 14, 052109 [NASA ADS] [CrossRef] [Google Scholar]
- Pontin, D. I., Al-Hachami, A. K., & Galsgaard, K. 2011, A&A, 533, A78 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Priest, E. R., & Démoulin, P. 1995, J. Geophys. Res., 100, 23443 [NASA ADS] [CrossRef] [Google Scholar]
- Priest, E. R., & Pontin, D. I. 2009, Phys. Plasmas, 16, 122101 [NASA ADS] [CrossRef] [Google Scholar]
- Priest, E. R., & Titov, V. S. 1996, Roy. Soc. London Proc. Ser. A, 354, 2951 [NASA ADS] [Google Scholar]
- Priest, E. R., Hornig, G., & Pontin, D. I. 2003, J. Geophys. Res., 108, 1285 [Google Scholar]
- Régnier, S., Parnell, C. E., & Haynes, A. L. 2008, A&A, 484, L47 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Rickard, G. J., & Titov, V. S. 1996, ApJ, 472, 840 [NASA ADS] [CrossRef] [Google Scholar]
- Török, T., Aulanier, G., Schmieder, B., Reeves, K. K., & Golub, L. 2009, ApJ, 704, 485 [NASA ADS] [CrossRef] [Google Scholar]
- Wyper, P. F., & Jain, R. 2010, Phys. Plasmas, 17, 092902 [NASA ADS] [CrossRef] [Google Scholar]
- Xiao, C. J., Wang, X. G., Pu, Z. Y., et al. 2006, Nat. Phys., 2, 478 [NASA ADS] [CrossRef] [Google Scholar]
- Xiao, C. J., Wang, X. G., Pu, Z. Y., et al. 2007, Nat. Phys., 3, 609 [CrossRef] [Google Scholar]
All Figures
 |
Fig. 1 Top: the initial magnetic field configuration. The spine (in blue) lies along the x-axis and the fan (in red) lies in the x = 0 plane. Coloured arrows indicated the field direction. The black arrows show the direction of shear applied by the driver at the boundaries. Bottom: the driving profile applied to the x-boundaries with Ad = 80. (This figure is available in color in the electronic form.) |
| In the text | |
 |
Fig. 2 Shaded contours show |J| (scaled to the maximum of each snapshot), while the arrows depict the plasma flow. For the case of v0 = 0.01 with only one pulse. (This figure is available in color in the electronic form.) |
| In the text | |
 |
Fig. 3 Solid lines (top panel): |J| plotted against t. Solid lines (bottom panel): ∫E ∥ dl plotted against t. For the cases with two pulses the dashed lines indicate the driving amplitude of the second pulse. Black: tlag = 0, red: tlag = 0.9 and blue: tlag = 1.8. The solid green line is with only one pulse. For the case of v0 = 0.01. (This figure is available in color in the electronic form.) |
| In the text | |
 |
Fig. 4 The change in connectivity with two simultaneous pulses (top) one pulse (bottom) and when v0 = 0.04, Ad = 80 and η = 5 × 10-4. The red and blue flux tubes (traced from the driving boundaries) are initially connected to the gold field lines anchored on the side boundaries. Taken at times t = 1 (left), 3 (middle) and 5 (right). (This figure is available in color in the electronic form.) |
| In the text | |
 |
Fig. 5 Top: an iso-surface (at 50% of maximum) of |E ∥ |. Bottom: a contour plot of |E ∥ | in the x = −0.005 plane (containing the null point). For the case of one pulse with v0 = 0.04 and τ = 1.8. Taken at the point where the null is most displaced from its initial position. Note the asymmetrical shape (in the y-direction) of the strong E ∥ regions near the null point. (This figure is available in color in the electronic form.) |
| In the text | |
 |
Fig. 6 Scaling of the absolute value of the driving velocity with peak current
|J|max, peak reconnection rate
|
| In the text | |
 |
Fig. 7 Arrows depict Lorentz (top left: blue) and pressure forces (top right: red) in the z = 0 plane. Bottom left: the combination of Lorentz and pressure forces (green). The solid black lines show a selection of field lines and the “+” sign indicates the null point position. Bottom right: field lines traced from around the null in 3D. Taken at t = 2.0 for the case of one pulse with v0 = 0.04, τ = 1.8, Ad = 80 and η = 5 × 10-4. (This figure is available in color in the electronic form.) |
| In the text | |
 |
Fig. 8 Case of spine-fan reconnection driven by a single pulse. Top
panel: maximum displacement |
| In the text | |
 |
Fig. 9 Log-log plots of peak reconnection rate (top panel) and peak current (bottom panel) against η. Black points: two pulses sent at the same time (diamonds: v0 = 0.01, squares: v0 = 0.02). Green points: one pulse (asterisks: v0 = 0.01, triangles: v0 = 0.02). The lines depict the lines of best fit for two pulses sent at the same time (solid) and one pulse (dashed) in each case. (This figure is available in color in the electronic form.) |
| In the text | |
 |
Fig. 10 Shaded contours show |J| (scaled to the maximum of each snapshot), while the arrows depict the plasma flow. For the case of v0 = 0.01 and tlag = 1.8. (This figure is available in color in the electronic form.) |
| In the text | |
 |
Fig. 11 Components of the null position (xnull, ynull,0) plotted against t. Top: ynull and bottom: xnull. For one pulse (green) and two asynchronous pulses with tlag = 0.9 (red) and 1.8 (blue). Each case has v0 = 0.01, η = 5 × 10-4 and Ad = 80. (This figure is available in color in the electronic form.) |
| In the text | |
 |
Fig. 12 Scaling of the absolute value of the driving velocity with peak current
|J|max, peak reconnection rate
|
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.