| Issue |
A&A
Volume 545, September 2012
|
|
|---|---|---|
| Article Number | A1 | |
| Number of page(s) | 8 | |
| Section | Interstellar and circumstellar matter | |
| DOI | https://doi.org/10.1051/0004-6361/201118726 | |
| Published online | 27 August 2012 | |
Two short mass-loss events that unveil the binary heart of Minkowski’s Butterfly Nebula⋆
1 Institut de Radioastronomie Millimétrique, 300 rue de la Piscine, 38406 Saint Martin d’Hères, France
e-mail: ccarrizo@iram.fr; neri@iram.fr; cox@iram.fr
2 Observatorio Astronómico Nacional, Ap 112, 28803 Alcalá de Henares, Spain
e-mail: v.bujarrabal@oan.es
3 UMR 6525 Fizeau, Univ. Nice Sophia Antipolis, CNRS, Obs. de la Côte d’Azur, Bvd. de l’Observatoire, BP 4229, 06304 Nice Cedex 4, France
e-mail: Olivier.Chesneau@oca.eu
4 Observatorio Astronómico Nacional, Alfonso XII N 3, 28014 Madrid, Spain
e-mail: r.bachiller@oan.es
Received: 23 December 2011
Accepted: 31 May 2012
Context. Studying the appearance and properties of bipolar winds is critical to understand the stellar evolution from the AGB to the planetary nebula (PN) phase. Many uncertainties exist regarding the presence and role of binary stellar systems, mainly due to the deficit of conclusive observational evidences.
Aims. We investigate the extended equatorial distribution around the early bipolar planetary nebula M 2−9 (“Minkowski’s Butterfly Nebula”) to gather new information on the mechanism of the axial ejections.
Methods. Interferometric millimeter observations of molecular emission provide the most comprehensive view of the equatorial mass distribution and kinematics in early PNe. Here we present subarcsecond angular-resolution observations of the 12CO J = 2−1 line and continuum emission with the Plateau de Bure interferometer.
Results. The data reveal two ring-shaped and eccentric structures at the equatorial basis of the two coaxial optical lobes. The two rings were formed during short mass-loss episodes (~40 yr), separated by ~500 yr. Their positional and dynamical imprints provide evidence of the presence of a binary stellar system at the center, which yields critical information on its orbital characteristics, including a mass estimate for the secondary of ≲0.2 M⊙. The presence of a stellar system with a modest-mass companion at the center of such an elongated bipolar PN strongly supports the binary-based models, because these are more easily able to explain the frequent axisymmetric ejections in PNe.
Key words: circumstellar matter / stars: AGB and post-AGB / radio lines: stars / stars: mass-loss
© ESO, 2012
1. Introduction
The appearance and shaping of bipolar winds in a stage when stars transit from the late asymptotic giant branch (AGB) to the planetary nebula (PN) phase is one of the most intriguing open questions in stellar evolution. Studying bipolar winds (Balick & Frank 2002) is critical for unraveling this late stellar transition and ultimately for understanding the formation of PNe, which often show strongly axisymmetric shapes (e.g. Sahai et al. 2007). One mechanism that is supposed to trigger the generation of bipolar winds is the presence of a binary stellar system at the nebulae’s center (Soker 2001; Frank & Blackman 2004; De Marco 2009). The direct detection of stellar companions remains an observational challenge, however. Indeed, central stars of bipolar post-AGB nebulae are rarely found to be multiple (Hrivnak et al. 2011).
M 2−9 (also known as “Minkowski’s Butterfly Nebula” or “the Twin Jet Nebula”) is a prototypical young planetary nebula that displays a very elongated bipolar structure (120″ × 12″ in size, Schwarz et al. 1997). It became very popular from the spectacular images obtained by the Hubble Space Telescope (Balick et al. 1997; Balick 1999) in the central 60′′-size region of the nebula, which show two coaxial thin outflows. In the equator, the waist of the nebula is very slim (Balick et al. 1997), and its optical image is diffuse due to a dense torus of gas and dust.
A sequence of observations of ionized gas emission obtained every 2–5 years (Doyle et al. 2000; Corradi et al. 2011) shows a pattern of changes with mirror symmetry, with respect to the equatorial plane, that rotates around the symmetry axis of the nebula. A rotating ionizing/exciting beam from the star is postulated to explain the observed increase in brightness in a line of knots along the lobe edges. These observations indicate that there is a binary stellar system at the center (Schmeja & Kimeswenger 2001; Smith & Gehrz 2005), orbiting with a period ~90 years (Doyle et al. 2000; Corradi et al. 2011; Livio & Soker 2001; Smith et al. 2005).
 |
Fig. 1 Channel maps of the 12CO J = 2−1 line emission toward M 2 − 9 (in contours) superimposed on the optical image obtained with the Hubble Space Telescope (in color scale; Balick et al. 1997). The center is given by the position of compact continuum emission, here subtracted, at the J2000 coordinates RA 17:05:37.958, Dec −10:08:32.48. The LSR velocities are specified in the top-left corner of each panel. Contours are shown from 4σ with a spacing of 5σ (where the root-mean-square noise is 7.9 mJy beam-1) in solid line, and at −4σ in dashed lines. The synthesized beam is 0 |
Several theoretical studies have addressed the possible relationship between nebular bipolarity and binarity of its nucleus, which is one of the major long-standing problems toward a better understanding of stellar evolution. Particularly, for M 2 − 9 it was proposed (Livio & Soker 2001) that a white dwarf star accretes mass from the wind of an AGB or post-AGB companion, and that a subsequent increase in magneto-centrifugal forces launches the fast bipolar jets responsible for the rotating knots. Since the core (Lykou et al. 2011; Torres-Peimbert et al. 2010) is embedded within a high-density dusty environment, there is no direct evidence of this scenario yet. On the other hand, the presence of disks in rotation in the innermost equatorial regions of several young PNe has been found to be associated to binarity (Bujarrabal et al. 2005; van Winckel 2003). Several recent works have investigated such disks using mid-IR high-resolution observations (Matsuura et al. 2006; Chesneau et al. 2007; Lykou et al. 2011; Lagadec et al. 2011).
Low-excitation rotational lines of carbon monoxide (CO) are particularly useful for probing the obscured cores at the center of evolved stars, including young PNe. They trace the mass distribution, hindered by extinction in the optical, and provide direct information on the gas kinematics (Bujarrabal et al. 2001, 1998; Zweigle et al. 1997; Bachiller et al. 1988). Zweigle et al. (1997) mapped the 12CO J = 2−1 line emission in M 2 − 9 with the Plateau de Bure Interferometer (PdBI). These maps revealed, with an angular resolution of 3′′ × 5′′, a large expanding equatorial ring in the nebula waist. Zweigle et al. (1997) estimated from 12CO J = 1−0 line emission a mass of ~0.01 M⊙. To explore the equatorial mass distribution in M 2−9 in more detail, we carried out new PdBI high angular-resolution observations. We present in this paper the results of those observations, and analyze in detail the morphology and kinematics that lead to a new understanding of the nebula shaping and the central stellar system.
2. Observations of 12CO J = 2–1 line and 1 mm continuum emission
Observations of 12CO J = 2−1 line emission (at 230.538 GHz) were performed with the Plateau de Bure interferometer in M 2−9. A track of observations was obtained in each Aq and Bq array configuration in February 2009. Channel maps were obtained with a synthetic beam (at half power) of 0 8 × 0
8 × 0 4 (PA 15°) in size. Image synthesis was performed with natural weighting and with the Hogbom cleaning algorithm. The results are presented in Fig. 1 with a channel spacing of 1 km s-1, though a detailed data inspection was performed to spectral resolutions of 0.1 km s-1. In Figs. 1 and 2 the new M 2 − 9 CO data are superimposed over the optical image obtained with the Hubble Space Telescope (Balick et al. 1997). Astrometry was performed to properly overlay millimetric and optical data.
4 (PA 15°) in size. Image synthesis was performed with natural weighting and with the Hogbom cleaning algorithm. The results are presented in Fig. 1 with a channel spacing of 1 km s-1, though a detailed data inspection was performed to spectral resolutions of 0.1 km s-1. In Figs. 1 and 2 the new M 2 − 9 CO data are superimposed over the optical image obtained with the Hubble Space Telescope (Balick et al. 1997). Astrometry was performed to properly overlay millimetric and optical data.
Simultaneously, we observed a 1.8GHz bandwidth free of line emission, which was averaged to detect unresolved 1.3 mm continuum emission of 240 ± 1 mJy in brightness. Note that this emission was subtracted in the interferometric visibilities before imaging the CO line emission presented in this paper. The measured continuum flux is compatible with a previous analysis of single-dish observations by Sánchez Contreras et al. (1998), where the central compact continuum emission was deduced to originate from a region of warm dust close to the stellar system.
In addition to the ring seen in previous studies (Zweigle et al. 1997), the new observations reveal a second tight inner ring in the waist of M 2−9. The new ring is almost three times smaller and its 12CO J = 2−1 emission is about four times weaker than that of the outer ring.
Figure 2 presents in an inset the velocity-integrated 12CO J = 2−1 line emission synthesized with a circular beam of 0 4 in size. Only the brightest CO line emission was included to better separate the closest parts of the two rings (northernmost and southernmost regions). As in Fig. 1, the inset is superimposed over the HST optical image. The continuum emission is represented with a red dot.
4 in size. Only the brightest CO line emission was included to better separate the closest parts of the two rings (northernmost and southernmost regions). As in Fig. 1, the inset is superimposed over the HST optical image. The continuum emission is represented with a red dot.
 |
Fig. 2 Velocity-integrated 12CO J = 2−1 line emission is shown in the inset, superimposed over the optical image obtained with the Hubble Space Telescope (Balick et al. 1997). Only the brightness distribution above 60 mJy beam-1 (which corresponds to ~8σ, where σ is the root-mean-square noise) was included to better separate the close projected image of the two rings. At the center the continuum emission is represented by a red dot, which traces the position of the stellar system. More details can be found in Sect. 2. |
At first we deduce that the inclination angles of the two equatorial rings coincide, and are perpendicular to the optical lobes (see further analysis in Sect. 3.1). No emission is detected in the intermediate regions down to a level of 10 mJy beam-1. The most extended molecular ring is detached by more than 1′′ from the inner one. Its outermost deprojected diameter is 7 2, and the innermost one 4
2, and the innermost one 4 2. The easternmost part of the outer ring seems to reach regions outside the external optical lobes, perhaps with some flaring, and is thicker than the westernmost part. The inner ring is 2
2. The easternmost part of the outer ring seems to reach regions outside the external optical lobes, perhaps with some flaring, and is thicker than the westernmost part. The inner ring is 2 4 in size, and its easternmost part also presents a moderate increase in brightness. From the spatial resolution and the signal-to-noise ratio, we consider our size estimates to be better than 0
4 in size, and its easternmost part also presents a moderate increase in brightness. From the spatial resolution and the signal-to-noise ratio, we consider our size estimates to be better than 0 2.
2.
Position-velocity diagrams of the 12CO J = 2 − 1 line emission in M 2 − 9 along the east-west and north-south directions are shown in Fig. 3.
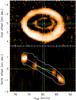 |
Fig. 3 Position-velocity diagrams of the 12CO J = 2−1 line emission in M 2−9 along the east-west (on the top) and north-south (on the bottom) directions. The green (violet) dotted lines represent the kinematical and spatial center of the inner (outer) ring. Top: integrated brightness from the whole nebula. Bottom: brightness obtained within a slit along the projected symmetry axis. With a green (violet) solid line we plot the position-velocity gradient corresponding to the entire inner (outer) ring along the north-south direction. A white contour traces the emission integrated over the complete nebula at low brightness level. Note that the (VLSR) velocity axis shows the expanding gas speed projected on the line of sight. A more detailed discussion can be found in Sect. 3.2. |
3. Data analysis
Two coaxial rings or torus-like structures have been found in 12CO J = 2−1 line emission laying on the equatorial plane of the elongated M 2−9 nebula.
3.1. Two outflows in M 2−9
The relation of the two rings and the extended optical lobes is best shown in Fig. 2. This comparison suggests that the two rings are the equatorial counterparts of the two coaxial optical lobes (the outer one being more diffuse). The shaping of the rings (or torus-like structures) and the formation of the bipolar optical outflows seem hence to result from the same two events of material ejection. The low equatorial expansion velocities measured for the two rings (Sect. 3.3) suggest that they likely originate from an increase in the mass loss when the optical lobes were formed. Note that by extrapolating the image of the innermost optical lobes, from the region where their image becomes diffuse (at ~2′′ from the equator) to the equatorial plane, we measured that the offset between the lobes and the rings in the equator must be smaller than 0 4 (the rings being outwards; this relation was investigated in young PNe by Huggins 2007).
4 (the rings being outwards; this relation was investigated in young PNe by Huggins 2007).
Assuming that the rings are circular, we estimated the inclination of their symmetry axes with respect to the plane of the sky from their projected and actual sizes (along the symmetry and perpendicular axes). For the two rings we derived a similar inclination of ~19°, with an uncertainty of ±2° due to ring asymmetries. The northern (southern) part of the ring is approaching (receding from) us. Therefore, we see the south face of the ring. Similar inclinations have been derived for the symmetry axis of the bipolar outflows seen in the optical (Solf 2000; Schwarz et al. 1997). This confirms that the rings are accurately placed in the nebula equator.
3.2. The lifetime of the nebula: its formation by means of two ejections
The position-velocity diagrams presented in Fig. 3 clearly show that both rings expand. By assuming that their expansion is isotropic, the systemic velocities corresponding to the large and small rings are 80.0 and 80.6 km s-1. The systemic velocity associated to the outer ring hence differs from that of the inner ring by ~0.6 km s-1 ( ± 0.1 km s-1).
In Figs. 1–3 we also see that the centers of both rings are shifted along the east-west axis. The inner-ring center seems to coincide with the position of the stellar system, as traced by the continuum emission, whereas the center of the larger ring is offset eastwards by ~0 3. The uncertainty in this estimate mainly comes from departures from circular symmetry, since the easternmost part of the larger ring is thicker than the westernmost part. If we only consider the regions brighter than half the maximum, we estimate that the measured offset is 0
3. The uncertainty in this estimate mainly comes from departures from circular symmetry, since the easternmost part of the larger ring is thicker than the westernmost part. If we only consider the regions brighter than half the maximum, we estimate that the measured offset is 0 34 ± 0
34 ± 0 07. Considering the weakest detected regions, the offset would be 0
07. Considering the weakest detected regions, the offset would be 0 31 ± 0
31 ± 0 09. Note that the uncertainty triggered by the interferometer position precision is considerably smaller.
09. Note that the uncertainty triggered by the interferometer position precision is considerably smaller.
These kinematical and spatial differences between the two rings strongly suggest that the velocity of the mass-losing star was different when it expelled the two rings.
The ratios between the projected sizes and expansion velocities presented in the position-velocity gradients along the north-south direction (in Fig. 3) provide the times at which the ejections occurred (multiplied by the tangent of the inclination angle of the symmetry axis with respect to the sky plane). These different gradients for the two rings (represented with solid lines in Fig. 3) would hence be another indication that the rings were formed at different epochs. For a distance of 650 pc (see Schwarz et al. 1997, and discussion in Sect. 4), we deduce that the time elapsed between the ejections of the two molecular rings is 500 yr. This value cannot be much lower (by less than 10%) considering the uncertainties in the inclinations of the rings. The first ejection, which shaped the outer ring, would have happened about 1400 yr ago. The second ejection, responsible for the inner ring, would have occurred 900 yr ago. We estimate a maximum uncertainty of 140 yr in the derived times considering all possible errors. As discussed there, sizes and times depend proportionally on the assumed distance; all other results presented in this paper are distance-independent.
We have already argued that the optical and molecular data show different parts of the same nebula components, which were formed by the same (two) events of mass ejection. This implies that the two lobes seen in the optical are not coeval, but were formed by two ejection events separated by ~500 yr, contrary to what was concluded in previous studies (Smith et al. 2005).
The measured difference between the systemic velocities of the two rings is readily explained if the star responsible for the ejections changed its velocity. This can be justified if the star orbits within a binary (or multiple) system. The very short time (~500 yr) elapsed between the two ejections compared to the life of a solar-mass type star (~109 yr) strongly suggests that the same late AGB or post-AGB star was responsible for these events. We do not consider the remote possibility of having two distinct post-AGB stars to have formed the two outflows. Moreover, the time lag between the two outflows is ~5 times longer than the binary-orbit period of ~90 yr (Doyle et al. 2000; Corradi et al. 2011; Livio & Soker 2001). This suggests that the ejections were triggered during a critical phase in the evolution of one star, such as ultimate and sudden increases in the mass-loss rate of the late AGB (or post-AGB) star. The interaction between the stars therefore would not have determined the time at which the axial ejections happened. This is supported by the kinematical offset detected between the two rings, which implies that the ejections occurred at two different relative positions within the binary orbit (Sect. 3.3).
Mass-loss variations have been observed in the envelopes around other AGB and post-AGB stars with different time scales, from ~400 yr (of ~3 × 10-6 M⊙ yr-1 for R Cas; see Schöier 2007; Castro-Carrizo et al. 2010) to ~2000 yr (of ~10-4 M⊙ yr-1 for CRL 618 and IRC +10420; Sánchez Contreras et al. 2004; Castro-Carrizo et al. 2007), some of them being also visible as arcs or rings in the circumstellar envelopes. In M 2-9, from the estimate of ejection duration (Sect. 5), we derive a mass-loss rate of ~9 × 10-5 M⊙ yr-1 for the first molecular wind. The mass-loss rate of the second wind, ejected ~500 yr later, is likely lower. However, in spite of these evidences of mass-loss variations in the late AGB or early post-AGB phase, the current small sample and significant differences prevent us from a more detailed analysis.
3.3. The nebula kinematics
The large and small rings expand with velocities of 7.8 and 3.9 km s-1 ( ± 0.1 km s-1). The expansion velocity of 7.8 km s-1 is moderate compared with that seen in most of the AGB outflows, but 3.9 km s-1 is a very low velocity compared to AGB shell velocities. Recent studies of the inner equatorial regions of some post-AGB objects, such as CRL 618 (Sánchez Contreras et al. 2004; Bujarrabal et al. 2010) and M 1–92 (Alcolea et al. 2007), show that equatorial outflows in the very late AGB (or early post-AGB) phase can expand at these very low velocities, which is also supported by our data.
There is no sign of deceleration within the rings that could indicate some interaction with a slower previously expelled halo or surrounding interstellar medium: no deceleration position-velocity gradient is detected in the rings, the outermost layers of both rings present a good circular symmetry, and the mean expansion velocity is uniform in each ring. In addition, no CO emission was detected close to the rings or to the rest of nebula, which would indicate the presence of nearby interstellar molecular gas. The good axis-symmetry of the optical nebula also supports this interpretation. No circumstellar emission is detected either between the two rings and, moreover, the innermost ring is expanding much slower than the previous one, which renders any interaction between them impossible. We interpret the data to show that the rings expand freely, and therefore conclude that times derived from the measured velocities indeed correspond to times elapsed since the mass ejections.
From the estimated binary period and assuming a stellar mass of the AGB star ≲ 1 M⊙, we deduce a binary distance ≲ 20 AU (corresponding to ~0 03 at a distance of 650 pc), which is indiscernible in the present data. The measured position offset between the ring centers of ~0
03 at a distance of 650 pc), which is indiscernible in the present data. The measured position offset between the ring centers of ~0 3 is therefore too large by a factor >10 with respect to the orbit size. Therefore the relative motion of the rings, deduced from the difference in the velocity centroids (Sect. 3.2), likely also triggers this offset. The millimeter continuum emission should correspond to the position of the binary system (Sect. 2), which seems to coincide with the center of the inner ring.
3 is therefore too large by a factor >10 with respect to the orbit size. Therefore the relative motion of the rings, deduced from the difference in the velocity centroids (Sect. 3.2), likely also triggers this offset. The millimeter continuum emission should correspond to the position of the binary system (Sect. 2), which seems to coincide with the center of the inner ring.
In Fig. 3 we see that the center of the inner ring remains very close to the binary position (from our perspective), a possible displacement in the last 900 yr being smaller than our uncertainty in the determination of the ring center, which is estimated to be ~0.06′′ due to small ring inhomogeneities (slightly larger than the position uncertainty, <0.04′′, Reid et al. 1988). Accordingly we deduce that the inner ring should be moving in a direction closer to the line of sight than 12° (independently of the distance, by adopting a binary rotation speed of 1 km s-1). The last ejection happened therefore when the star was moving in a direction very close to the light of sight, in the easternmost or the westernmost part of the orbit.
The relative offset between the two rings indicates that when the first ejection happened, the star was moving eastwards. Their systemic-velocity offset suggests that the last ejection occurred when the star was receding. However, at this point we cannot distinguish the sense of the binary rotation. If clockwise (as seen from the Earth, from the south), the first ejection would have happened in the semi-orbit that is farther from us and the last one in the westernmost part of the binary orbit. If counterclockwise, the first ejection would have occurred in the section of the orbit that is closer to us, and the last one in the easternmost part. These two scenarios are represented in Fig. 4. Corradi et al. (2011) deduced that the observed east-to-west motion of the bright nebular knots takes place in the side of the bulbs facing the Earth. This would indicate that the binary presents a clockwise orbit (upper plot in Fig. 4). Accordingly, we can determine the position of the stars when the ejections took place, as shown in Sect. 5.2. There, additional discussion supports the clockwise orbital scenario.
4. Distance
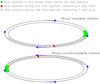 |
Fig. 4 Sketch representing the position at which the ejections occurred in the binary orbit, according to the discussion in Sect. 3.3 and the two scenarios presented in Sect. 5 regarding the first ejection. Note that at first we cannot discern the sense of the binary rotation, clock- or counterclock-wise (as seen from the Earth, from the south), and both possibilities are hence represented in this figure. A clockwise rotation is suggested by Corradi et al. (2011) and also by the position-velocity gradient detected in the southernmost part of the outer ring (see Sect. 5.2). |
 |
Fig. 5 East-west position-velocity diagrams (similar to those in Fig. 3) to compare the observations performed in 1997 (in red contours) with the new data observed in 2009 (in color scale and black contours). From left to right data are synthesized with different beams. Left: all contours and the image are synthesized with the beam corresponding to the observations obtained in 1997 (of 2 |
We adopted a distance of 650 pc, a value so far mostly considered in the literature for M 2 − 9 that reasonably agrees with the tentative ring expansion presented in this section. Recently Corradi et al. (2011) proposed a farther distance of 1300 pc.
To investigate the ring-expansion proper motions, a comparison was performed between observations obtained in 1997 (unpublished data by Neri et al.) and the new data presented in this paper. In Fig. 5 we compare the east-west position-velocity diagrams (equivalent to that in Fig. 3) for the two data sets, synthesized with different beams. A correlation analysis of the brightest parts in the outer ring clearly suggests expansion proper motion over the elapsed time. From the compared images in Fig. 5, we estimate a diameter increase that roughly ranges from 0.10′′ to 0.24′′. We have performed a similar analysis by fitting the data in the uv-plane. The two data sets were fitted at the central channel by two Gaussian functions of FWHP 1 17 and 0
17 and 0 81, for the eastern and western ring components, their positions being free fitting parameters. In this way we estimate that the ring diameter increased by 0
81, for the eastern and western ring components, their positions being free fitting parameters. In this way we estimate that the ring diameter increased by 0 25 ± 0
25 ± 0 11.
11.
From the measured expansion velocity (7.8 km s-1) and the time elapsed between the two observations (11.5 yr), we calculated the distance to M 2 − 9 with the formula d(pc) = 36.9/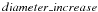 (′′). Accordingly, from the proper-motion estimates we deduce that the distance to M 2 − 9 ranges from 100 to 300 pc. By arbitrarily increasing our uncertainty to 0
(′′). Accordingly, from the proper-motion estimates we deduce that the distance to M 2 − 9 ranges from 100 to 300 pc. By arbitrarily increasing our uncertainty to 0 20, the distance would range from 80 to 800 pc. Therefore, though we cannot perform a precise distance estimate, it seems improbable that the distance is larger than 1000 pc.
20, the distance would range from 80 to 800 pc. Therefore, though we cannot perform a precise distance estimate, it seems improbable that the distance is larger than 1000 pc.
Because our detection of proper motion is only tentative, we have analyzed the uncertainty in the value derived by Corradi et al. (2011). Distances shorter than 1000 pc should not be discarded either from their analysis of the proper motions in reflected light, particularly considering the observational uncertainties and the inconsistencies in the measured offsets for the two lobes.
The choice of distance has an impact on the main known nebula characteristics. The estimated sizes and times in particular are proportional to the distance. For a distance twice larger (as proposed by Corradi et al. 2011), the total nebula extent (as mapped by Schwarz et al. 1997) would be ~2 × 1018 cm, about three times larger than usual PNe sizes (e.g. Bujarrabal et al. 1988). M 2−9 would be one of the largest known PNe. Also, the two ejections would be separated by ~1000 yr, the first one would have occurred 2800 yr ago. We note that these times are extraordinary long from what we expect in the AGB-to-PNe evolution, which is estimated to last ~500–2000 yr (Bujarrabal et al. 1988). This is particularly unexpected if we consider that M 2−9 is not thought to be a developed PN but an early PN (Castro-Carrizo et al. 2001), based on the estimate of its effective stellar temperature (Calvet & Cohen 1978; Swings & Andrillat 1979).
In view of the presented data comparison, the above discussion, and the uncertainties we have, we prefer to adopt a distance of 650 pc. This value is so far mostly adopted in the literature, and facilitates a comparison with previous results.
However, we also note that all the main results obtained in this paper are independent of the adopted distance. Regarding the velocities, they are either directly measured or derived by the ratio of sizes and times. Therefore estimated speeds, and consequently masses, are distance-independent (Sect. 5). The inclination angle of the nebula symmetry axis is also derived from angular sizes (Sect. 3.1). For the estimate of the direction along which the inner ring moves (Sect. 3.3) the distance dependence cancels out with the ejection lifetime. The angular size of the binary orbit would be smaller by adopting 1300 pc, ~0.01′′, which would make it more difficult to resolve the binary with the current data (Sect. 3.3), again supporting our interpretation.
5. Kinematics of the binary orbit
From the properties of the two rings we can estimate the modulus of the orbital velocity of the star that ejected the rings, V. For this we assume that the orbit is circular, that V remained constant during the whole mass-loss phase, and that the same star ejected both rings. We note that no time variations have been reported in the rotation pattern seen in optical observations, and associated to the orbital rotation itself. Hence, no high eccentricities are expected in the binary orbit (as concluded by Doyle et al. 2000; Corradi et al. 2011), which supports our main assumptions. Here we derive properties of the binary rotation from parameters directly measured from the observations, and the mentioned assumptions. To start, note that the speed difference between the two rings allows us to give a lower limit for the orbital velocity of 0.31 km s-1 (obtained by deprojecting the measured velocity difference, divided by two).
Below, we refer to axis x as the axis perpendicular to the east-west direction within the equatorial plane, passing through the continuum position, its projection in the sky plane being parallel to that of the nebular axis. Axis y is perpendicular to axis x within the equatorial plane, parallel to the east-west direction.
5.1. Very short mass-loss event assumption
In a first approach, we assume that the rings were ejected during phases much shorter than the orbital period. From the observations, we deduce 1) a position offset between the ring centers of 0 34 ( ± 0
34 ( ± 0 07) in axis y, which results from the relative motion of the rings; 2) the second inner ring is moving in a direction closer than 12° to that of axis x, which is an upper limit; 3) the relative velocity between the two rings has a projection in the line of sight equal to 0.60 km s-1 ( ± 0.10 km s-1). From point (2) we can assume that the last ejection took place when the star was moving in the direction of axis x, so that the velocity of the inner ring was such that
07) in axis y, which results from the relative motion of the rings; 2) the second inner ring is moving in a direction closer than 12° to that of axis x, which is an upper limit; 3) the relative velocity between the two rings has a projection in the line of sight equal to 0.60 km s-1 ( ± 0.10 km s-1). From point (2) we can assume that the last ejection took place when the star was moving in the direction of axis x, so that the velocity of the inner ring was such that 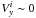 and
and 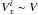 (Eq. (E1)) (where V is the modulus of the binary rotation velocity). Then, by considering item (1) the offset of 0
(Eq. (E1)) (where V is the modulus of the binary rotation velocity). Then, by considering item (1) the offset of 0 34 in axis y is only due to the velocity of the outer ring, i.e.
34 in axis y is only due to the velocity of the outer ring, i.e. 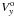 = 0
= 0 34/To = 0.74 km s-1 ( ± 0.23 km s-1) (Eq. (E2)), where To is the time from the first ejection (~0.45′′/km s-1 from the gradient shown in Fig. 3, which multiplied by the distance gives ~ 1400 yr). We hence obtain (
34/To = 0.74 km s-1 ( ± 0.23 km s-1) (Eq. (E2)), where To is the time from the first ejection (~0.45′′/km s-1 from the gradient shown in Fig. 3, which multiplied by the distance gives ~ 1400 yr). We hence obtain (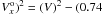 km s-1)2 (Eq. (E3)). Finally, from point (3) we deduce that
km s-1)2 (Eq. (E3)). Finally, from point (3) we deduce that 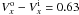 km s-1 (where 0.63 km s-1 is estimated by deprojection toward the equatorial plane of the measured 0.60 km s-1). By using Eq. (E1) we obtain
km s-1 (where 0.63 km s-1 is estimated by deprojection toward the equatorial plane of the measured 0.60 km s-1). By using Eq. (E1) we obtain 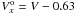 km s-1 (Eq. (E4)). From the last two Eqs. ((E3) and (E4)) we deduce that V = 0.75 km s-1 ( ± 0.50 km s-1). From
km s-1 (Eq. (E4)). From the last two Eqs. ((E3) and (E4)) we deduce that V = 0.75 km s-1 ( ± 0.50 km s-1). From 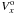 and V we also deduce that the ejection of the outer ring happened from an orbital point at 17° from the intersection with axis x. The velocity-vector direction was hence close to that of axis y, though this angle estimate is uncertain within the southern semi-orbit. We finally note that assuming ejections shorter than they actually are would lead to underestimated velocities.
and V we also deduce that the ejection of the outer ring happened from an orbital point at 17° from the intersection with axis x. The velocity-vector direction was hence close to that of axis y, though this angle estimate is uncertain within the southern semi-orbit. We finally note that assuming ejections shorter than they actually are would lead to underestimated velocities.
We can also derive the systemic velocity of the binary stellar system in M 2−9 by correcting the measured systemic velocities of the rings by the derived stellar velocity at the time of the ejections. This is particularly straightforward from the inner-ring velocity. We obtain a stellar speed of 79.8 km s-1 (±0.5 km s-1), which is slower and hence agrees better with the values recently suggested from optical observations (Torres-Peimbert et al. 2010). The fact that this value is lower than the outer-ring systemic velocity would indicate that the first ejection would have happened when the star was receding with respect to us within the binary orbit, as represented in Fig. 4, though moving close to the east-west direction.
5.2. Longer mass-loss event assumption
 |
Fig. 6 Sketch to visualize the origin of the velocity gradient expected in one side of the ring, if its shaping took place for a fraction of the binary orbit period. According to the scenario described in Sect. 5.2, in the sourthern part of the ring the outermost layers would expand faster than the innermost ones. |
Let us suppose that the first ejection happened over a longer time, during a significant fraction of the orbital period. From what is derived in Sect. 5.1, we can suppose that the oldest ring was ejected when the star was moving basically in the direction parallel to the east-west axis. The ejection happened when the star was describing an angle 2α in its orbit. The average velocity of the outer ejected ring in the y direction is then 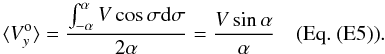 In previous estimates (Eq. (E2)) we derived that
In previous estimates (Eq. (E2)) we derived that 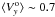 km s-1 ( ± 0.2 km s-1). Note that because of the longer mass-loss, we would expect an acceleration gradient in the ring along the perpendicular axis (x) whose extreme values would be separated by ΔVx = 2Vsinα (Eq. (E6)). This would be because the gas expelled during the first part of the ejection phase would move faster in the expansion direction (x in our case) than the gas ejected subsequently, as a consequence of the change in the
km s-1 ( ± 0.2 km s-1). Note that because of the longer mass-loss, we would expect an acceleration gradient in the ring along the perpendicular axis (x) whose extreme values would be separated by ΔVx = 2Vsinα (Eq. (E6)). This would be because the gas expelled during the first part of the ejection phase would move faster in the expansion direction (x in our case) than the gas ejected subsequently, as a consequence of the change in the 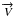 direction. This gradient should only be observed in the ring part corresponding to the same angle interval described by the star in its orbit during the ejection. Also, a compression effect should have happened at the opposite side of the ring (at 180°) due to the contrary relative movement between the different ring layers (see a descriptive sketch in Fig. 6).
direction. This gradient should only be observed in the ring part corresponding to the same angle interval described by the star in its orbit during the ejection. Also, a compression effect should have happened at the opposite side of the ring (at 180°) due to the contrary relative movement between the different ring layers (see a descriptive sketch in Fig. 6).
We did indeed detect a small acceleration position-velocity gradient along the axis x in the southernmost part of the north-south diagram, shown in Fig. 3: the outermost layers of the outer ring expand faster than the innermost layers. Indeed, similar acceleration gradients are detected in the north-south position-velocity diagrams obtained in the central east-west 3′′-size section. Considering the uncertainties we could have in our estimates of the gradient (regarding the beam size and the comparison with the northern part) and also projection effects, we estimate that ΔVx = 2 km s-1 ( ± 1 km s-1). As predicted, we detected no sign of a velocity gradient in the northernmost side of the outer ring. From Eqs. (E5) and (E6) we derive α ~ 80° ( ± 60°), the ejection takes hence place during about half of an orbital period ( ± α) and V would be ~1 km s-1 ± 1 km s-1, and therefore ranging from 0.3 (hard limit from the measured velocities; Sect. 5) to 2 km s-1.
If our interpretation on the observed relative gradient in the southern part of the outermost ring is correct, this would be an additional indication that the ejection took place when the star was somewhere in the southernmost binary semi-orbit, suggesting a binary clockwise rotation (as shown in Fig. 4). As described in Sect. 3.3, this agrees with what was already suggested by Corradi et al. (2011).
We estimate this second scenario, based on the gradient detected in the ring southern part, to be more realistic, and hence to allow a better characterization of the first ejection and of the orbital kinematics. We note, however, that a deeper analysis of this gradient is limited by the angular resolution in the north-south direction.
From the deduced orbital velocity we estimate a systemic velocity for the binary stellar system of ~79.6 km s-1, which also remains compatible with Torres-Peimbert et al. (2010, see previous discussion in Sect. 5.1. In addition, from the duration estimates we derive that the first ejection took place during ~40 yr ( ± 30 yr). For the inner ring, the determination of the ejection time is more difficult, but must anyhow be considerably shorter considering its narrowness.
5.3. Implications for the companion mass
We can estimate the mass of the companion from the derived orbital velocity. For this we assume again a circular binary orbit and an orbital period, P, of ~90 yr (Corradi et al. 2011; Livio & Soker 2001; Doyle et al. 2000). From the gravitational equations associated to the movement of two bodies we obtain that the modulus of the orbital velocity of the primary star (1: presumably the most massive and responsible for the mass ejection) is in solar units: 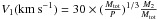 (Eq. (E7)), where Mtot is the total mass and M2 that of the secondary.
(Eq. (E7)), where Mtot is the total mass and M2 that of the secondary.
By introducing the derived V in Eq. (E7), we find that the mass of the secondary must be very small. Indeed, for a mass of the primary (late AGB) star of ~1 M⊙ the mass of the companion is M2 ~ 0.1–0.2 M⊙. If we adopt a different Mtot by a factor 2, the mass of the companion would change by ± 0.1 M⊙. Considering that the total estimated circumstellar mass is ≲0.1 M⊙ (including ionized and atomic gas, Castro-Carrizo et al. 2001), a mass for the primary much larger than 2 M⊙ does not seem very likely. However, note that if Mtot would be ~4 M⊙, the mass of the companion would be ~0.4 M⊙. In all the cases the companion would be considerably smaller than the primary star.
6. Conclusions
We presented subarcsecond-resolution mapping of 12CO J = 2−1 line emission in the proto-planetary nebula M 2 − 9. Our data show two independent expanding rings (or torus-like structures) in the nebula equator. Continuum emission has been detected, likely tracing the position of the stellar system.
The centers of the two rings are offset by 0.34′′, and their systemic velocities differ by 0.6 km s-1. This is solid evidence that there is a binary system at the center of M 2 − 9. In this scenario, the two rings were very probably ejected by one of the stars, in a very late AGB or very early post-AGB phase. The different velocities of the star in its orbit when the material shaping the rings was expelled explain the measured position and velocity offsets between the rings. At the same time, these two mass-loss events likely gave rise to the two coaxial lobes seen in infrared and optical images The first ejection happened 1400 yr ago, the second 500 yr later. We suggest that, after the material was expelled by the star, the axial lobes were shaped, accelerated, by interaction with post-AGB fast and collimated jets. The interaction effects are still visible in the bright shock-excited knots detected in the visible but did not affect the dynamics of the equatorial rings, in agreement with current theoretical ideas of PN shaping (see Sect. 1). Although most of the material in the equatorial rings and the axial lobes was probably ejected by the primary (in a late AGB or early post-AGB phase), the structure and movements of the knots indicate that the collimated exciting jets came from a compact, less bright secondary (Corradi et al. 2011).
A distance of 650 pc was adopted in this paper, which agrees better with the tentative detection of proper motion we presented here. None of our main results (except for lifetimes) depend on the adopted distance.
By analyzing the kinematics of the CO-emitting equatorial rings we estimated the positions at which the two ejections took place in the binary orbit. With some few simple assumptions, we derived an orbital velocity of ~1 km s-1. From the equations of the orbital movement of two objects, we obtained a very small mass for the secondary, ≲ 0.2 M⊙ ( ± 0.1 M⊙, by assuming that the mass of the primary star is between 0.5 and 2 M⊙). We suggested that the binary system is composed of a red giant and a dwarf. We estimated that they would be separated by 20 ± 5 AU (for the interval of total masses considered above), which is too large for the stars to have undergone a common envelope phase, or for being interacting symbiotic systems (Mikołajewska 2007; Podsiadlowski & Mohamed 2007).
The strongly axisymmetric nebula and very collimated jets around the binary system convincingly suggest that the multiple nature of the stellar component played a relevant role in the ejection and shaping of M 2 − 9. The significance of this low-mass companion to shape the extended and elongated bipolar nebula seen in M 2 − 9 has important consequences on our understanding of the mechanisms that drive the shaping of asymmetrical planetary nebulae, since the existence of companions is increasingly more probable when the requirements for their masses are relaxed.
Acknowledgments
The data here presented were reduced and analyzed entirely by using the different packages available in the GILDAS software (http://www.iram.fr/IRAMFR/GILDAS). This project has been partially supported by the Spanish MICINN, program CONSOLIDER INGENIO 2010, grant “ASTROMOL” (CSD2009-00038).
References
- Alcolea, J., Neri, R., & Bujarrabal, V. 2007, A&A, 468, L41 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bachiller, R., Gomez-Gonzalez, J., Bujarrabal, V., & Martin-Pintado, J. 1988, A&A, 196, L5 [NASA ADS] [Google Scholar]
- Balick, B. 1999, in Optical and Infrared Spectroscopy of Circumstellar Matter, eds. E. Guenther, B. Stecklum, & S. Klose, ASP Conf. Ser., 188, 241 [Google Scholar]
- Balick, B., & Frank, A. 2002, ARA&A, 40, 439 [NASA ADS] [CrossRef] [Google Scholar]
- Balick, B., Icke, V., Mellema, G., & NASA. 1997, in NASA press release, ed. NASA, NASA press release, GRIN DataBase Number: GPN–2000–000953 [Google Scholar]
- Bujarrabal, V., Gomez-Gonzalez, J., Bachiller, R., & Martin-Pintado, J. 1988, A&A, 204, 242 [NASA ADS] [Google Scholar]
- Bujarrabal, V., Alcolea, J., Sahai, R., Zamorano, J., & Zijlstra, A. A. 1998, A&A, 331, 361 [NASA ADS] [Google Scholar]
- Bujarrabal, V., Castro-Carrizo, A., Alcolea, J., & Sánchez Contreras, C. 2001, A&A, 377, 868 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bujarrabal, V., Castro-Carrizo, A., Alcolea, J., & Neri, R. 2005, A&A, 441, 1031 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bujarrabal, V., Alcolea, J., Soria-Ruiz, R., et al. 2010, A&A, 521, L3 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Calvet, N., & Cohen, M. 1978, MNRAS, 182, 687 [NASA ADS] [Google Scholar]
- Castro-Carrizo, A., Bujarrabal, V., Fong, D., et al. 2001, A&A, 367, 674 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Castro-Carrizo, A., Quintana-Lacaci, G., Bujarrabal, V., Neri, R., & Alcolea, J. 2007, A&A, 465, 457 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Castro-Carrizo, A., Quintana-Lacaci, G., Neri, R., et al. 2010, A&A, 523, A59 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Chesneau, O., Lykou, F., Balick, B., et al. 2007, A&A, 473, L29 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Corradi, R. L. M., Balick, B., & Santander-García, M. 2011, A&A, 529, A43 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- De Marco, O. 2009, PASP, 121, 316 [NASA ADS] [CrossRef] [Google Scholar]
- Doyle, S., Balick, B., Corradi, R. L. M., & Schwarz, H. E. 2000, AJ, 119, 1339 [NASA ADS] [CrossRef] [Google Scholar]
- Frank, A., & Blackman, E. G. 2004, ApJ, 614, 737 [NASA ADS] [CrossRef] [Google Scholar]
- Hrivnak, B. J., Lu, W., Bohlender, D., et al. 2011, ApJ, 734, 25 [NASA ADS] [CrossRef] [Google Scholar]
- Huggins, P. J. 2007, ApJ, 663, 342 [NASA ADS] [CrossRef] [Google Scholar]
- Lagadec, E., Verhoelst, T., Mékarnia, D., et al. 2011, MNRAS, 417, 32 [NASA ADS] [CrossRef] [Google Scholar]
- Livio, M., & Soker, N. 2001, ApJ, 552, 685 [NASA ADS] [CrossRef] [Google Scholar]
- Lykou, F., Chesneau, O., Zijlstra, A. A., et al. 2011, A&A, 527, A105 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Matsuura, M., Chesneau, O., Zijlstra, A. A., et al. 2006, ApJ, 646, L123 [NASA ADS] [CrossRef] [Google Scholar]
- Mikołajewska, J. 2007, Baltic Astron., 16, 1 [Google Scholar]
- Podsiadlowski, P., & Mohamed, S. 2007, Baltic Astron., 16, 26 [Google Scholar]
- Reid, M. J., Schneps, M. H., Moran, J. M., et al. 1988, ApJ, 330, 809 [NASA ADS] [CrossRef] [Google Scholar]
- Sahai, R., Morris, M., Sánchez Contreras, C., & Claussen, M. 2007, AJ, 134, 2200 [NASA ADS] [CrossRef] [Google Scholar]
- Sánchez Contreras, C., Alcolea, J., Bujarrabal, V., & Neri, R. 1998, A&A, 337, 233 [NASA ADS] [Google Scholar]
- Sánchez Contreras, C., Bujarrabal, V., Castro-Carrizo, A., Alcolea, J., & Sargent, A. 2004, ApJ, 617, 1142 [NASA ADS] [CrossRef] [Google Scholar]
- Schmeja, S., & Kimeswenger, S. 2001, A&A, 377, L18 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Schöier, F. L. 2007, in Why Galaxies Care About AGB Stars: Their Importance as Actors and Probes, eds. F. Kerschbaum, C. Charbonnel, & R. F. Wing, ASP Conf. Ser., 378, 216 [Google Scholar]
- Schwarz, H. E., Aspin, C., Corradi, R. L. M., & Reipurth, B. 1997, A&A, 319, 267 [NASA ADS] [Google Scholar]
- Smith, N., & Gehrz, R. D. 2005, AJ, 129, 969 [NASA ADS] [CrossRef] [Google Scholar]
- Smith, N., Balick, B., & Gehrz, R. D. 2005, AJ, 130, 853 [NASA ADS] [CrossRef] [Google Scholar]
- Soker, N. 2001, ApJ, 558, 157 [NASA ADS] [CrossRef] [Google Scholar]
- Solf, J. 2000, A&A, 354, 674 [NASA ADS] [Google Scholar]
- Swings, J. P., & Andrillat, Y. 1979, A&A, 74, 85 [NASA ADS] [Google Scholar]
- Torres-Peimbert, S., Arrieta, A., & Bautista, M. 2010, Rev. Mex. Astron. Astrofis., 46, 221 [Google Scholar]
- van Winckel, H. 2003, ARA&A, 41, 391 [NASA ADS] [CrossRef] [Google Scholar]
- Zweigle, J., Neri, R., Bachiller, R., Bujarrabal, V., & Grewing, M. 1997, A&A, 324, 624 [NASA ADS] [Google Scholar]
All Figures
 |
Fig. 1 Channel maps of the 12CO J = 2−1 line emission toward M 2 − 9 (in contours) superimposed on the optical image obtained with the Hubble Space Telescope (in color scale; Balick et al. 1997). The center is given by the position of compact continuum emission, here subtracted, at the J2000 coordinates RA 17:05:37.958, Dec −10:08:32.48. The LSR velocities are specified in the top-left corner of each panel. Contours are shown from 4σ with a spacing of 5σ (where the root-mean-square noise is 7.9 mJy beam-1) in solid line, and at −4σ in dashed lines. The synthesized beam is 0 |
| In the text | |
 |
Fig. 2 Velocity-integrated 12CO J = 2−1 line emission is shown in the inset, superimposed over the optical image obtained with the Hubble Space Telescope (Balick et al. 1997). Only the brightness distribution above 60 mJy beam-1 (which corresponds to ~8σ, where σ is the root-mean-square noise) was included to better separate the close projected image of the two rings. At the center the continuum emission is represented by a red dot, which traces the position of the stellar system. More details can be found in Sect. 2. |
| In the text | |
 |
Fig. 3 Position-velocity diagrams of the 12CO J = 2−1 line emission in M 2−9 along the east-west (on the top) and north-south (on the bottom) directions. The green (violet) dotted lines represent the kinematical and spatial center of the inner (outer) ring. Top: integrated brightness from the whole nebula. Bottom: brightness obtained within a slit along the projected symmetry axis. With a green (violet) solid line we plot the position-velocity gradient corresponding to the entire inner (outer) ring along the north-south direction. A white contour traces the emission integrated over the complete nebula at low brightness level. Note that the (VLSR) velocity axis shows the expanding gas speed projected on the line of sight. A more detailed discussion can be found in Sect. 3.2. |
| In the text | |
 |
Fig. 4 Sketch representing the position at which the ejections occurred in the binary orbit, according to the discussion in Sect. 3.3 and the two scenarios presented in Sect. 5 regarding the first ejection. Note that at first we cannot discern the sense of the binary rotation, clock- or counterclock-wise (as seen from the Earth, from the south), and both possibilities are hence represented in this figure. A clockwise rotation is suggested by Corradi et al. (2011) and also by the position-velocity gradient detected in the southernmost part of the outer ring (see Sect. 5.2). |
| In the text | |
 |
Fig. 5 East-west position-velocity diagrams (similar to those in Fig. 3) to compare the observations performed in 1997 (in red contours) with the new data observed in 2009 (in color scale and black contours). From left to right data are synthesized with different beams. Left: all contours and the image are synthesized with the beam corresponding to the observations obtained in 1997 (of 2 |
| In the text | |
 |
Fig. 6 Sketch to visualize the origin of the velocity gradient expected in one side of the ring, if its shaping took place for a fraction of the binary orbit period. According to the scenario described in Sect. 5.2, in the sourthern part of the ring the outermost layers would expand faster than the innermost ones. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


