| Issue |
A&A
Volume 543, July 2012
|
|
|---|---|---|
| Article Number | A141 | |
| Number of page(s) | 21 | |
| Section | Planets and planetary systems | |
| DOI | https://doi.org/10.1051/0004-6361/201219157 | |
| Published online | 12 July 2012 | |
Differentiation and core formation in accreting planetesimals
Deutsches Zentrum für Luft- und Raumfahrt (DLR), Institut für
Planetenforschung,
Planetenphysik, Rutherfordstr. 2,
12489
Berlin,
Germany
e-mail: wladimir.neumann@dlr.de
Received:
2
March
2012
Accepted:
29
May
2012
Aims. The compositions of meteorites and the morphologies of asteroid surfaces provide strong evidence that partial melting and differentiation were widespread among the planetesimals of the early solar system. However, it is not easily understood how planetesimals can be differentiated. To account for significantly smaller radii, masses, gravity and accretion energies early, intense heat sources are required, e.g. the short-lived nuclides 26Al and 60Fe. Here, we investigate the process of differentiation and core formation in accreting planetesimals taking into account the effects of sintering, melt heat transport via porous flow and redistribution of the radiogenic heat sources.
Methods. We use a spherically symmetric one-dimensional model of a partially molten planetesimal consisting of iron and silicates, which considers the accretion by radial growth. The common heat conduction equation has been modified to consider also melt segregation. In the initial state, the planetesimals are assumed to be highly porous and consist of a mixture of Fe,Ni-FeS and silicates consistent to an H-chondritic composition. The porosity change due to the so called hot pressing is simulated by solving a corresponding differential equation. Magma segregation of iron and silicate melt is treated according to the flow in porous media theory by using the Darcy flow equation and allowing a maximal melt fraction of 50%.
Results. We show that the differentiation in planetesimals depends strongly on the formation time, accretion duration, and accretion law and cannot be assumed as instantaneous. Iron melt segregation starts almost simultaneously with silicate segregation and lasts between 0.4 and 10 Ma. The degree of differentiation varies significantly and the most evolved structure consists of an iron core, a silicate mantle, which are covered by an undifferentiated but sintered layer and an undifferentiated and unsintered regolith – suggesting that chondrites and achondrites can originate from the same parent body.
Key words: convection / planets and satellites: formation / planets and satellites: interiors / minor planets, asteroids: general / conduction
© ESO, 2012
1. Introduction
The compositions of meteorites and the surfaces of asteroids provide strong evidence that partial melting and differentiation were ubiquitous in the planetesimals of the early solar system. It is even widely held that planets were formed by differentiated planetesimals and that the differentiation of the proto-planets was facilitated by the planetesimals being pre-differentiated (e.g. Rubie et al. 2007). However, it is not easily understood how planetesimals can be differentiated. In contrast to models of the differentiation of terrestrial planets, one must account for significantly lower gravity and significantly smaller radii. Since the latter imply much larger surface to volume ratios it must be concluded that the differentiation of planetesimals requires early, intense heat sources. These heat sources must have produced much more power than the decay of U, Th and K, the major heat source for the present-day planets.
With respect to the degree of differentiation meteorites can be divided into two classes: chondrites that originate from primitive, undifferentiated parent bodies and achondrites, iron meteorites and stony and stony-iron meteorites that originate from bodies that were apparently fractionated into (at least) a silicate mantle and a metallic core. A large variety in the degree of differentiation has been identified: metal separated partially or completely from silicates and silicates fractionated from each other, causing the composition of rock to deviate moderately to strongly from a primitive chondritic composition (see references in: Mittlefehldt 2003; Haack & McCloy 2003). Also, the surfaces of asteroids show large variations. For example, the most massive of these, Ceres and Vesta, are most complementary. Ceres has a very primitive surface characterised by water-bearing minerals. Vesta – on the contrary – has a dry, basaltic composition indicating that the body is differentiated and has been resurfaced by basaltic lava flows. It has been speculated that Vesta once had a magma ocean just like the Moon and an iron rich core (e.g. Taylor et al. 1993). Differentiation of asteroids and planetesimals (assuming that the former are surviving examples of the latter) must have occurred within the first few million years of the solar system judging from the ages of meteorites and the surfaces of asteroids. Further evidence for rapid iron-silicate differentiation, i.e. the core formation, comes from 182Hf-182W concentration variations in iron meteorites (e.g. Horan et al. 1998; Kleine et al. 2002) and for basalt formation from the concentrations of 26Al-26Mg and 53Mn-53Cr in eucrites and angrites (e.g. Srinivasan et al. 1999; Bizzarro et al. 2005).
 |
Fig. 1 Heat generation by the short-lived radionuclides 26Al and 60Fe as a function of time relative to CAI formation. The data are taken from Table 6. |
Recent analyses of some meteorites from differentiated parent bodies provided some unexpected findings and confirmed the supposed large variety of differentiation events and associated processes. Palaeomagnetic analyses of angrites, which are among the oldest known basaltic meteorites, revealed remnant magnetisation that suggests a magnetic field of the parent body at the time of magnetisation of ~10 microteslas between 4564 and at least 4558 Ma b.p. (Weiss et al. 2008). These authors suggest that this palaeofield originated from an early internal dynamo in a rapidly formed iron-rich core. The isotope chemistry of the angrites suggests rapid core formation within 4 Ma after the formation of the Ca-Al-rich inclusions (CAIs) (Kurat et al. 2004). The Fe-Ni core would have had a mass of 8 to 60% of that of the angrite parent body.
Because of their small sizes of a few hundred kilometres, rapid differentiation of planetesimals necessitates a heat source that can provide sufficient thermal energy to balance against loss through heat conduction. The radiogenic decay of the short lived nuclide 26Al has been proposed as a plausible heat source (Urey 1955). Its widespread presence in the early solar system has been identified in the CAIs and chondrules (e.g. Lee et al. 1976; MacPherson et al. 1995; Bizzarro et al. 2004). An initial 26Al/27Al abundance ratio of 5 × 10-5 is suggested at the time of CAI formation (canonical value) that is based on measurements of CAIs in meteorites (MacPherson et al. 1995). In contrast to the long-lived radioactive elements uranium, thorium and potassium, 26Al features several orders of magnitude higher specific power but a half-life time of only 0.717 Ma. Alternatively, impact energy released during the accretion of planetesimals and electromagnetic induction due to the magnetically active protosun (Sonnett et al. 1968) have been suggested as viable heat sources. However, the two latter energy sources have failed to be proven attractive because a) impact melting can only cause localised heating and melting of the planetesimals (Keil et al. 1997) and b) induction heating alone cannot explain the thermal processing of planetesimals as indicated by recent experiments (Marsh et al. 2006). Most recently revised estimates of the 60Fe/56Fe concentration ratio in the early solar system (Tachibana & Huss 2003; Mostefaoui et al. 2005) raises the possibility that the short lived nuclide 60Fe could also contribute significantly to heating and melting even in the absence of other heat sources (cf. Fig. 1 and Table 6). In particular, a redistribution of Fe with core formation makes this heat source specifically interesting for the discussion of the thermal evolution of planetesimals.
A wide range of thermal models of planetesimals with 26Al as the heat source exists in the literature (e.g. Miyamoto et al. 1981; Grimm & McSween Jr. 1993; Sahijpal et al. 1995; Bennett & McSween Jr. 1996; Ghosh & McSween Jr. 1998, 1999; Merk et al. 2002; Ghosh et al. 2003; Yoshino et al. 2003; Sahijpal & Soni 2005; Bizzarro et al. 2005; Hevey & Sanders 2006; Sahijpal et al. 2007; Moskovitz & Gaidos 2011). The aim of these works is the study of the thermal metamorphism and/or melting of asteroids and planetesimals.
For the iron-silicate differentiation, one has to distinguish between two scenarios in the literature: 1) the melt fraction of the silicates is required to be larger than about 50 vol.% for an iron core to form (e.g. Taylor 1992; Taylor et al. 1993), arguing for the presence of an early magma ocean in a planetesimal to form a core. This assumption is supported by experimental studies showing that partial melting of meteorites does not lead to metal melt migration (Takahashi 1983; Walker & Agee 1988); 2) iron segregation and possibly core formation can start already for small melt fractions of iron (Hewins & Newsom 1988) even before silicate starts to melt. This assumption is supported by the observation of Fe,Ni-FeS veins in the acapulcoite-lodranite parent body (McCoy et al. 1997) and by recent experiments suggesting an interconnected melt network for pressures below 2−3 GPa (Terasaki et al. 2008).
The first study to consider the differentiation of an asteroid, i.e., asteroid 4 Vesta, with a numerical code was presented by Ghosh & McSween Jr. (1998). These authors demonstrated that it is possible to sustain partial melt on Vesta for ~100 Ma assuming radiogenic heating by 26Al. They examined the influence of the delay time of accretion with respect to the formation time of the CAIs and assumed that accretion was instantaneously at that time. The delay time of accretion basically determined the concentration of the radioactive elements at the onset of accretion. The longer the delay time assumed, the smaller was the rate of heat production through 26Al found to be available for heating. The calculations of Ghosh & McSween Jr. (1998) showed that melting and core formation did not occur if accretion started later than 3 Ma after CAI formation. A lower limit for the accretion time of 2.8 Ma has been proposed for Vesta based on the assumption that the eucrites were generated with no more than 25% partial melting of the source region (e.g. Stolper 1977). The latter constraint has been questioned, however, for instance by Taylor et al. (1993) and Righter & Drake (1997). These authors proposed that the eucrites formed during the crystallisation of a magma ocean. Ghosh & McSween Jr. (1998) further find that an iron-rich core formed instantaneously at 4.58 ± 0.05 Ma after CAI formation. This calculation was done under the assumption that core formation requires melting of iron but not necessarily melting of the silicate matrix as proposed by Hewins & Newsom (1988).
Merk et al. (2002) criticised the assumption of instantaneous accretion and examined the influence of an extended accretion time on the thermal evolution of a spherically symmetric planetesimal. Instead, they assumed various constant accretion rates acting over times of up to one million years. They concluded that the accretion rate had to be considered in any study of short-lived nuclide heating of small planetary bodies as long as the accretion time was not much smaller than the half-live of the nuclide under study. The reason lies with the competition between heating in the interior of the planetesimal and heat loss through its surface. The latter is minimised in an instantaneous accretion model where the growth rate is infinite. With decreasing growth rate the heating decreases in effectiveness with consequences for key parameters such as the peak temperature and the extent and lifetime of completely or partially molten regions in the interior. If a fast accreting planetesimal of a given size and age may melt and differentiate, a slow accreting planetesimal of the same size and age may stay completely solid and undifferentiated.
In a more recent work, Hevey & Sanders (2006) also incorporated convection in their thermal evolution models of planetesimals assuming that mantle regions where the degree of partial melting exceeded 50%, i.e. a magma ocean (Taylor et al. 1993) would be convecting. Their model further assumes that the planetesimals were initially very porous with a low thermal conductivity (e.g. 10-4 W m-1 K-1) but that sintering would commence at a temperature of 700 K (Yomogida & Matsui 1984). The sintering would result in a shrinking radius and be accompanied by an increase of the thermal conductivity due to the loss of porosity. The assumption of initially porous planetesimals is consistent with recent accretion models. The model suggests that the parent bodies of differentiated meteorites have accreted before about 1.5 to 2 Ma after CAI and that these meteorites had formed before most chondritic parent bodies. Molten planetesimals, it was further proposed, may be a source of the chondrule melt droplets.
Sahijpal et al. (2007) performed numerical simulations of the differentiation of planetesimals undergoing a linear accretion growth with both 26Al and 60Fe as the heat sources. For one set of models (labelled A in their study) they calculated the gradual growth of an iron core due to the flow of Fe,Ni-FeS melt towards the centre of the planetesimal and of a basaltic crust for specific melt percolation velocities. They studied in particular the dependence of the growth rate of the Fe,Ni-FeS core on the onset time of planetesimal accretion (relative to CAI formation), the (constant) accretion rate, the final size of the planetesimal, and the 60Fe/56Fe initial ratio. Their thermal models predict the earliest Fe,Ni-FeS melts to appear within ~0.1 Ma of the onset of accretion if the latter occurs at CAI formation. Assuming that iron starts to segregate at 1213–1233 K (the assumed solidus and liquidus temperature of the Fe,Ni-FeS, respectively), the differentiation process is almost instantaneous for small and fast accreting bodies. However, it could have continued for several Ma depending on the accretion scenario and the initial abundances of the short-lived radioactive nuclides. In this model, the onset and the duration of core and crust formation depends mostly on the time when the melt is generated (relative to CAI) rather than on the migration velocity as melt is taken to sink or rise rapidly toward the centre or surface of the planetesimal.
Recently, Moskovitz & Gaidos (2011) studied how the migration of silicate melt and in particular the redistribution of 26Al from the interior into a crustal layer would affect the thermal evolution of a planetesimal. They conclude that this process can significantly dampen the increase of the interior temperature and strongly reduce the melting rate. In their model, core formation would require a bulk melting degree of 50%. Therefore, segregation of iron is found to occur only after the crust formed when the decay of the remaining 60Fe generates melt fractions in excess of 50% (Taylor 1992). In the model by Moskovitz & Gaidos (2011) – as before in the model by Sahijpal et al. (2007) – it is assumed that silicate melt can rise toward the surface by porous flow and form a basaltic crust. An assumption that differs from another recent model by Elkins-Tanton et al. (2011), who argue that silicate melt would not be able to reach the surface because of its higher density in comparison to that of the primordial crust. In their model, any melt that rises towards the surface would cool and crystallize as crust intrusions. Their core formation model resembles that of Moskovitz & Gaidos (2011), though.
A most recent paper Sramek et al. (2012) presented a multiphase model for differentiation of planetesimals which takes into account phase separations by compaction driven melt migration and considers accretion. As their bodies of interest have radii ≥500 km, impacts provide an additional heat source. In their model, heating by the radioactive decay (of 26Al only) and by impact heating can occur in two stages or simultaneously. Depending on the accretion rate, melting starts either in the centre, or directly under the surface, or both. Comparable to Merk et al. (2002), accretion rate is a crucial factor. To melt the centre of ≈500 km body during its runaway growth stage, it needs to be formed within a couple of million years after CAI formation.
It needs to be noted that the mentioned studies focus on the model calculation of some important process and discuss or assume the effects of other physical processes. E.g. Ghosh & McSween Jr. (1998), Merk et al. (2002), Moskovitz & Gaidos (2011), Sramek et al. (2012) do not consider sintering of an initially porous planetesimal. Similarly, accretion is not modelled in Ghosh & McSween Jr. (1998), Hevey & Sanders (2006) and Moskovitz & Gaidos (2011). Velocities of melt migration are not calculated self-consistently but are either assumed to be constant (Sahijpal et al. 2007) or do not depend on radius, i.e. the decrease of gravity towards the centre of the planetesimal is neglected (Moskovitz & Gaidos 2011). The heat loss due to the melt transport has been neglected by most studies.
In the present work, we focus on the differentiation of small planetesimals (with radii ≤120 km) for melt fractions smaller than 50% – thus we do not consider the effects of a magma ocean. We combine the calculation of conduction, accretion, sintering, melting, melt segregation by porous flow and associated approach of differentiation modelling. We use a multiple material approach where materials can occur in both solid and liquid states, take into account heating by both 26Al and 60Fe, redistribution of those nuclei with melting and melt migration and the growth of the grains associated to the solid phase via Ostwald ripening. We discuss separate and coupled effects of accretion and sintering on the thermal evolution, the importance of the magmatic heat transport associated to the porous flow, the factors the rate and timing of core formation as well as core radius and mantle thickness depend on, the differentiation scenarios arising from the modelled processes and the consequences on the thermal evolution and interior structure.
2. Model and methodology
Our model is based on the 1D heat conduction equation, which is modified to account for processes such as accretion, sintering, melting, and melt segregation. The associated equation with non-constant coefficients is solved numerically along with supplementary equations as described below using the finite difference method for non-stationary problems. We assume planetesimals to be composed of a mixture of two components, the first one referred to as “iron” and the second referred to as “silicates”. This distinction is in particular important when considering the melting process.
Assuming a solid body with a fixed radius, in which convective heat transport is neglected,
the temperature distribution can be obtained with the non-stationary heat conduction
equation for the temperature T as a function of space and time in spherical
coordinates 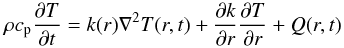 (1)where
r ≤ Rp(t) is the radial
variable, t ≥ t0 is the temporal variable,
ρ is the density, cp is the specific heat,
k is the thermal conductivity, and Q is the heat source
density. The corresponding boundary and initial conditions are chosen as follows:
(1)where
r ≤ Rp(t) is the radial
variable, t ≥ t0 is the temporal variable,
ρ is the density, cp is the specific heat,
k is the thermal conductivity, and Q is the heat source
density. The corresponding boundary and initial conditions are chosen as follows:
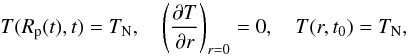 (2)implying a Dirichlet
boundary condition at the surface (constant surface temperature), a Neumann boundary
condition (no point source for heat, i.e. the heat flux
(2)implying a Dirichlet
boundary condition at the surface (constant surface temperature), a Neumann boundary
condition (no point source for heat, i.e. the heat flux
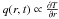 vanishes) at the centre and a homogeneous initial interior temperature distribution at some
instant of formation t0.
Rp(t) is the radius of the body
and TN is a fixed value describing the temperature of the
ambient nebula. It is set equal to 290 K in our calculations and can be assumed to be the
initial temperature of the accreting bodies in a nebula at 2.36 AU (Ghosh & McSween Jr. 1998).
vanishes) at the centre and a homogeneous initial interior temperature distribution at some
instant of formation t0.
Rp(t) is the radius of the body
and TN is a fixed value describing the temperature of the
ambient nebula. It is set equal to 290 K in our calculations and can be assumed to be the
initial temperature of the accreting bodies in a nebula at 2.36 AU (Ghosh & McSween Jr. 1998).
2.1. Accretion
To model the thermal evolution of a planetesimal, we further consider its growth with time due to accretion. In the cooling protoplanetary nebula dust settles at the mid-plane and the grains grow to become larger objects through collision and adhesion. After reaching a size of about 1 km, the accretion proceeds dominated by the mutual gravitational attraction of those bodies, growing possibly to moon-sized protoplanets at the end of the accretion. It could have taken several million years for bodies with a radius of 500 km to accrete to their final size (Weidenschilling 1988), although much shorter time scales have been discussed (Kaula 1998).
This scenario can be modelled by a radial growth of the planetesimals with time. The main
idea of the procedure is taken from Merk et al.
(2002). In that approach a moving boundary condition is introduced on the heat
transport equation by increasing the solution domain and imposing Eq. (2) at the new boundary. To avoid the moving
boundary condition, we transform the equations to a non-moving frame of reference. This is
achieved by scaling the radial variable according to 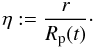 (3)Hence, the
surface radius of the body is always fixed to the value 1. This approach is also suitable
to simulate the shrinking of a planetesimal due to sintering (see below). The above
transformation changes the corresponding derivatives in the η-space, see
Merk et al. (2002). For numerical reasons all
variables are non-dimensionalised as follows (reference values are marked with the
subscript zero, non-dimensionalised variables are marked with a star; as the reference
radius we chose the terminal radius D, which will be defined further
below):
(3)Hence, the
surface radius of the body is always fixed to the value 1. This approach is also suitable
to simulate the shrinking of a planetesimal due to sintering (see below). The above
transformation changes the corresponding derivatives in the η-space, see
Merk et al. (2002). For numerical reasons all
variables are non-dimensionalised as follows (reference values are marked with the
subscript zero, non-dimensionalised variables are marked with a star; as the reference
radius we chose the terminal radius D, which will be defined further
below): 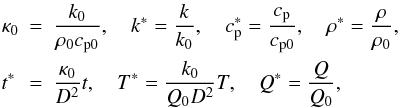 (4)which
leads to the modified heat transport equation:
(4)which
leads to the modified heat transport equation: 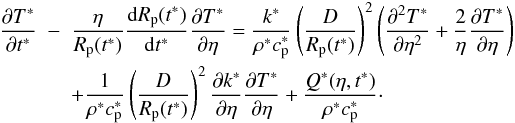 (5)To
simulate melt migration (Sect. 2.3) we will also need
the non-dimensionalised velocity
v∗ = vD/κ0.
(5)To
simulate melt migration (Sect. 2.3) we will also need
the non-dimensionalised velocity
v∗ = vD/κ0.
One advantage of the above transformation is the stability of the finite difference scheme. After transforming to a non-moving frame of reference the stability of the explicit method is ensured by the Courant criterion and there is no need to perform a linearisation as for the implicit finite difference method (Merk et al. 2002).
The growth of a planetesimal over a finite time can be considered by using any
time-dependent accretion law Rp(t). In the
present work we consider three accretion rates, i.e. a linear accretion rate 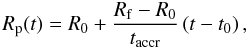 (6)an exponential
accretion rate
(6)an exponential
accretion rate 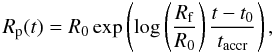 (7)and an asymptotic
accretion rate
(7)and an asymptotic
accretion rate 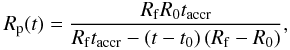 (8)with the radius of the
planetesimal Rp(t), its initial radius
R0, its final radius Rf, the
accretion duration taccr (i.e. the time of growth between
R0 and Rf) and the accretion
onset time t0 relative to CAIs.
(8)with the radius of the
planetesimal Rp(t), its initial radius
R0, its final radius Rf, the
accretion duration taccr (i.e. the time of growth between
R0 and Rf) and the accretion
onset time t0 relative to CAIs.
The linear accretion law corresponds to a constant radial growth rate
dRp(t)/dt
which is typically about 200 km Ma-1 (Encrenaz
et al. 1987). The asymptotic accretion law corresponds to a non-constant radial
growth rate. A large amount of material is added in the late stage of accretion. This is
known as the runaway accretion of the largest body within a swarm of self-interacting
planetesimals. According to Wetherill & Stewart
(1989) planetary embryos could have accreted in this way in less than 0.1 Ma. The
runaway accretion scenario is typical only for a few singular bodies in the swarm that
serve as seeds for the accretion of planets (Wetherill
& Stewart 1989). Finally, the exponential accretion law can be considered
as a mean between the two described cases. All three accretion laws can be derived from
the following equation of the evolution of planetary radius (Kortenkamp et al. 2000) 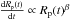 with
β = 0 for the linear, 1 for the exponential or 2 for the asymptotic
law.
with
β = 0 for the linear, 1 for the exponential or 2 for the asymptotic
law.
2.2. Sintering
In their initial state planetesimals are assumed to be highly porous as they initially
grew as aggregates of dusty and unconsolidated material of the protoplanetary discs. As
most meteorites are well-consolidated (Britt &
Consolmagno 2003), the planetesimals should have experienced some form of
sintering from the unconsolidated and highly porous to the consolidated state. The
porosity of a planetesimal changes due to the so called hot pressing, i.e. sintering. In
an idealised approach we assume the grains of the accreting dust to have spherical form
and equal initial radii of 1 μm. Furthermore, we assume hexagonal
prismatic packing of those dust grains with 8 contact points per particle, and hence the
corresponding initial porosity of 40%. Following a similar approach as Yomogida & Matsui (1984) we determine the
evolution of the volume filling factor (1 − φ) by using 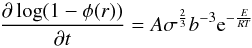 (9)with
1.6 × 10-5 ≤ A ≤ 5.4 × 10-5,
σ(φ) being the effective stress on the contact faces
of two grains, b the grain radius, E the activation
energy, T the temperature and R the universal gas
constant. This approach is based on the experimental determination of creep of prepared
pure olivine powders during hot pressing (Schwenn
& Goetze 1978). The change of the effective stress σ is
computed according to the geometric deformation theory of spheres during hot pressing of
Kakar & Chaklader (1967) and Rao & Chaklader (1972). For the constant
A we use the value 3.8 × 10-5. The value of the activation
energy E has been chosen to be
E = 60 kcal mol-1. This value lies well within the interval
given by Schwenn & Goetze (1978) and also
guarantees that sintering precedes melting and porous flow as a theory for simultaneous
treatment of sintering, melting and porous flow is lacking. Table 1 summarises the parameter values used to compute the loss of porosity
due to sintering. Note that the particles in planetesimals would have different radii and
irregular shapes. Smaller particles would fill the gaps, hence reducing the porosity but
irregular shapes of some grains would reduce the contact areas between the grains, hence
raising the porosity. Equation (9) is in a
non-transformed form. We transform the partial derivative of log (1 − φ)
according to (3) and obtain
(9)with
1.6 × 10-5 ≤ A ≤ 5.4 × 10-5,
σ(φ) being the effective stress on the contact faces
of two grains, b the grain radius, E the activation
energy, T the temperature and R the universal gas
constant. This approach is based on the experimental determination of creep of prepared
pure olivine powders during hot pressing (Schwenn
& Goetze 1978). The change of the effective stress σ is
computed according to the geometric deformation theory of spheres during hot pressing of
Kakar & Chaklader (1967) and Rao & Chaklader (1972). For the constant
A we use the value 3.8 × 10-5. The value of the activation
energy E has been chosen to be
E = 60 kcal mol-1. This value lies well within the interval
given by Schwenn & Goetze (1978) and also
guarantees that sintering precedes melting and porous flow as a theory for simultaneous
treatment of sintering, melting and porous flow is lacking. Table 1 summarises the parameter values used to compute the loss of porosity
due to sintering. Note that the particles in planetesimals would have different radii and
irregular shapes. Smaller particles would fill the gaps, hence reducing the porosity but
irregular shapes of some grains would reduce the contact areas between the grains, hence
raising the porosity. Equation (9) is in a
non-transformed form. We transform the partial derivative of log (1 − φ)
according to (3) and obtain 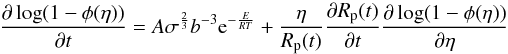 (10)which
accounts for the Lagrangian transport of porosity. Furthermore, in the numerical
calculations we prescribe the value φ = 0 in case that the porosity falls
below the value 0.001.
(10)which
accounts for the Lagrangian transport of porosity. Furthermore, in the numerical
calculations we prescribe the value φ = 0 in case that the porosity falls
below the value 0.001.
Parameter values for the computation of the porosity loss by sintering.
To obtain the effective stress σ on the contact areas between the dust
grains, we need to further calculate the internal pressure of the planetesimals. For an
idealised case of a spherically symmetric body the internal pressure is given by the
solution of the boundary value problem: 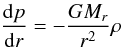 (11)with
(11)with
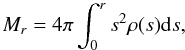 (12)and the surface
pressure
(12)and the surface
pressure 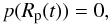 (13)where p
is the pressure, G is the gravitational constant,
Mr is the mass inside the radius
r and s is the integration variable. Here, the density
is
(13)where p
is the pressure, G is the gravitational constant,
Mr is the mass inside the radius
r and s is the integration variable. Here, the density
is 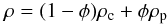 (14)with
the porosity φ, the density ρc of the compact
material (i.e. material that has no pore spaces) and the density
ρp of the pore space. In our model calculation Eq. (11) is used to obtain an adequate pressure in
the regions where porosity changes due to sintering. The internal pressure is computed in
every grid shell of the solution domain dependent on the current composition and densities
according to Eq. (11). It is used as
applied stress for the computation of the effective stress σ by following
the approach in Kakar & Chaklader (1967)
and Rao & Chaklader (1972).
(14)with
the porosity φ, the density ρc of the compact
material (i.e. material that has no pore spaces) and the density
ρp of the pore space. In our model calculation Eq. (11) is used to obtain an adequate pressure in
the regions where porosity changes due to sintering. The internal pressure is computed in
every grid shell of the solution domain dependent on the current composition and densities
according to Eq. (11). It is used as
applied stress for the computation of the effective stress σ by following
the approach in Kakar & Chaklader (1967)
and Rao & Chaklader (1972).
To obtain an estimate of a pressure at the distance r from the centre of
a planetesimal with nearly constant density (meaning homogeneous porosity in the entire
body) we can use the formula 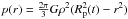 . By
setting r = 0 and ρ = 3700 kg m-3 we obtain
an estimate of the pressure in the centre:
. By
setting r = 0 and ρ = 3700 kg m-3 we obtain
an estimate of the pressure in the centre: ![\hbox{$p(r)\vert_{r=0}=1.913\times 10^{-8} \frac{\text{bar}}{\text{m}^2}\cdot R_{\rm p}^{2}(t) \text{ } \left[ \text{bar} \right]$}](/articles/aa/full_html/2012/07/aa19157-12/aa19157-12-eq99.png) . A central
pressure of more than 1 bar can be hence obtained in bodies with the above density and the
radius Rp(t) ≥ 8 km (e.g.
Rp(t) ≈ 100 km yields
p(r = 0) ≈ 191 bar).
. A central
pressure of more than 1 bar can be hence obtained in bodies with the above density and the
radius Rp(t) ≥ 8 km (e.g.
Rp(t) ≈ 100 km yields
p(r = 0) ≈ 191 bar).
In a most recent paper (Henke et al. 2012) the sintering process and modelling of sintering of H-chondritic planetesimals is described thoroughly. We refer to this work for further details considering this specific part of our model.
As sintering changes the porosity, the size of the planetesimal and thus the radius
Rp(t) are also affected. The radius is
hence modified – in addition to the accretion (Eqs. (6)–(8)) – according to:
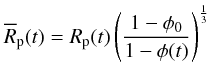 (15)with
the initial porosity φ0, the averaged porosity
φ(t) of the planetesimal at the time
t and the radius
(15)with
the initial porosity φ0, the averaged porosity
φ(t) of the planetesimal at the time
t and the radius 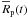 of an initially porous body,
which is simultaneously undergoing accretion and sintering. Note that
R0 and Rf in Eqs. (6)–(8) correspond to the radii of the porous planetesimal and assuming that the seed
of a planetesimal and the accreting surface layer from the protoplanetary dust have the
same initial porosity.
of an initially porous body,
which is simultaneously undergoing accretion and sintering. Note that
R0 and Rf in Eqs. (6)–(8) correspond to the radii of the porous planetesimal and assuming that the seed
of a planetesimal and the accreting surface layer from the protoplanetary dust have the
same initial porosity.
2.3. Melt generation, melt heat transport and differentiation
Melt is generated in planetesimals when the solidus temperature of the material is
reached. During the process of melting latent heat is consumed, whereas latent heat is
released during solidification – thus temperature variations are buffered in the
temperature interval between solidus and liquidus. To account for this effect, we modify
the heat capacity in the heat conduction equation by 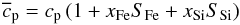 (16)where
SFe and SSi are the Stefan
numbers and xFe and xSi are the
mass fractions of the iron and silicate components of the material, respectively. In our
model
(16)where
SFe and SSi are the Stefan
numbers and xFe and xSi are the
mass fractions of the iron and silicate components of the material, respectively. In our
model 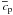 is used in the heat
conduction equation (Eqs. (1) and (5)) instead of cp.
For simplicity we write
is used in the heat
conduction equation (Eqs. (1) and (5)) instead of cp.
For simplicity we write 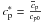 in the following. The Stefan numbers are set equal to zero in the pure solid and pure
liquid state of the respective materials and are defined as:
in the following. The Stefan numbers are set equal to zero in the pure solid and pure
liquid state of the respective materials and are defined as:
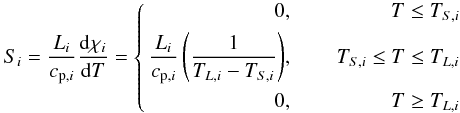 (17)where
Li is the latent heat of melting
and TL,i the liquidus
and TS,i the solidus temperature of the
species i. Note that the two species, i.e. iron and silicates (see also
Sect. 2.4) have different melting temperatures.
Equation (17) assumes that the degree of melting varies linearly
between the solidus and the liquidus and the melt fractions
χi(T) of both iron and
silicates depend on their respective solidus and liquidus temperatures
(17)where
Li is the latent heat of melting
and TL,i the liquidus
and TS,i the solidus temperature of the
species i. Note that the two species, i.e. iron and silicates (see also
Sect. 2.4) have different melting temperatures.
Equation (17) assumes that the degree of melting varies linearly
between the solidus and the liquidus and the melt fractions
χi(T) of both iron and
silicates depend on their respective solidus and liquidus temperatures 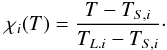 (18)In the partial melt ions
of incompatible trace elements such as the radioactive isotopes prefer to be dispersed in
the loosely structured melt and are excluded from the crystal structure of the solid phase
(Best 2002). This redistribution between melt and
matrix is formalised by a concentration ratio called the partition coefficient
Di of the element i,
defined as
(18)In the partial melt ions
of incompatible trace elements such as the radioactive isotopes prefer to be dispersed in
the loosely structured melt and are excluded from the crystal structure of the solid phase
(Best 2002). This redistribution between melt and
matrix is formalised by a concentration ratio called the partition coefficient
Di of the element i,
defined as 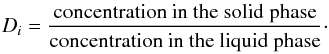 (19)Incompatible trace
elements have Di ≪ 1. Hence silicate partial
melting results in the enrichment of the incompatible trace element 26Al in the
silicate melt and its depletion of the solid phase. This is an important effect because
once the silicate melt which is enriched in 26Al starts to migrate, the
radioactive elements become redistributed in the interior. The exact value of the
partition coefficient
(19)Incompatible trace
elements have Di ≪ 1. Hence silicate partial
melting results in the enrichment of the incompatible trace element 26Al in the
silicate melt and its depletion of the solid phase. This is an important effect because
once the silicate melt which is enriched in 26Al starts to migrate, the
radioactive elements become redistributed in the interior. The exact value of the
partition coefficient 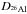 for
26Al varies with the composition of magma and that of the solid phase. Values
range between 0.003 and 0.02 (Kennedy et al. 1993;
Pack & Palme 2003) and in the light of
this obvious uncertainty we use a fixed value of 0.02. Assuming equilibrium melting, the
chemical partitioning is described by
for
26Al varies with the composition of magma and that of the solid phase. Values
range between 0.003 and 0.02 (Kennedy et al. 1993;
Pack & Palme 2003) and in the light of
this obvious uncertainty we use a fixed value of 0.02. Assuming equilibrium melting, the
chemical partitioning is described by 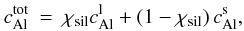 (20)with
(20)with
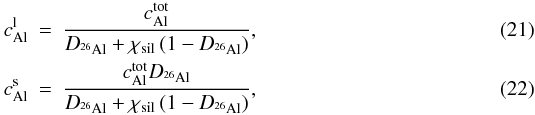 where
where
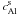 and
and
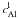 are the
concentrations of 26Al in solid and liquid phase, respectively and
χsil is the melt fraction of the silicates. The total
concentration of 26Al depends on the material transport inside a planetesimal,
which will be discussed in the following. With the occurrence of the first melt in a given
volume, a certain amount of the 26Al particles which is computed with the above
formulae partitions into the melt. Once this melt leaves the volume, the total
concentration of 26Al is computed from the particles that still reside in the
solid phase and from the particles added due to the matrix compaction. With further
melting a certain amount of those particles partitions again according to Eqs. (20)–(22).
are the
concentrations of 26Al in solid and liquid phase, respectively and
χsil is the melt fraction of the silicates. The total
concentration of 26Al depends on the material transport inside a planetesimal,
which will be discussed in the following. With the occurrence of the first melt in a given
volume, a certain amount of the 26Al particles which is computed with the above
formulae partitions into the melt. Once this melt leaves the volume, the total
concentration of 26Al is computed from the particles that still reside in the
solid phase and from the particles added due to the matrix compaction. With further
melting a certain amount of those particles partitions again according to Eqs. (20)–(22).
The separation of the molten fraction from the solid can be described by the model from McKenzie (1984, 1985): a uniform layer of material of thickness h is assumed to consist of a solid matrix with a density ρs and a melt of density ρl that occupies a volume fraction ϕ relative to the overall volume of the layer. This volume fraction is often referred to as porosity. As we already use the term porosity in the chapter describing the sintering process, the term melt fraction and the symbol ϕ will be used instead. Note that ϕ is not equal to and not the same as χ (cf. Eq. (18)). The described partially molten layer is placed above an impermeable surface. In such setting the melt can separate from the matrix if there is a density contrast between the molten and the solid material necessary to obtain melt movement due to buoyancy forces. Furthermore, an interconnected melt network is required as the melt won’t separate easily from the residual crystals if trapped in disconnected pockets. The pockets occur if the so called dihedral angle exceeds value of 60° and the melt fraction stays below a certain value termed critical melt fraction ϕc (von Bargen & Waff 1986). Thereby the dihedral angle is measured at the triple junctions of two grains and melt and is defined as the angle between the grains. If, however, the dihedral angle is smaller than 60°, then a stable interconnected network of melt channels forms at any melt fraction. In most partial melts including basic Si melts, the dihedral angle is less than 60° (Beere 1975; Waff & Bulau 1979). Thus, even if the silicate melt fraction is as small as a few percent, an interconnected network forms (Taylor et al. 1993). For iron the situation is more controversial. Early experimental studies by Takahashi (1983) and Walker & Agee (1988) shows disconnected melt pockets but more recent experiments suggest an interconnected melt network at conditions of high oxygen fugacity and pressures below 2–3 GPa (Terasaki et al. 2008) (note that even the central pressure of the planetesimals considered is significantly below these values). Furthermore, early cotectic Fe,Ni-FeS melt migration took place in acapulcoites and lodranites (McCoy et al. 1997). Even the rocks that experienced melt fractions of only about 5% are severely depleted in FeS, suggesting removal of nearly the entire volume of the Fe,Ni-FeS cotectic melt and the existence of an interconnected network at such small melt fractions. In conclusion, we consider in our model for both silicate and iron an interconnected network even for very small melt fractions.
Parameter values used to model the Darcy law.
The process of melt extraction from the matrix is directly linked to the compaction of
the matrix and both processes occur instantaneously. If the interconnectivity and the
density contrast are ensured, the partially molten material will compact and expel the
melt from the matrix. The compaction of the solid framework starts directly above the
impermeable surface, and the expelled melt moves through the veins in the upper regions
preventing their compaction (McKenzie 1984). The
ability of the matrix to compact is determined by the so called compaction length
δc and is a crucial factor for the melt percolation and
hence differentiation inside a planetesimal. The compaction length is defined as the size
of the region lying directly over the impermeable surface and undergoing compaction:
![\begin{equation} \delta_{\rm c}=\left[ \frac{\mu_{\rm b}+\frac{4}{3}\mu_{\rm s}}{\eta_{\rm l}} K_{\varphi} \right] ^{\frac{1}{2}} \label{complength} \end{equation}](/articles/aa/full_html/2012/07/aa19157-12/aa19157-12-eq145.png) (23)where
μb and μs are the effective bulk
and shear viscosities of the matrix, ηl the viscosity of the
melt and Kϕ the permeability of the matrix,
which is given by
(23)where
μb and μs are the effective bulk
and shear viscosities of the matrix, ηl the viscosity of the
melt and Kϕ the permeability of the matrix,
which is given by 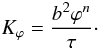 (24)Here,
b is a typical grain size after sintering, τ is a
constant which has a value that depends on n, and n is
related to the geometry of the melt. For isotropic systems the values
n = 2 and τ ≈ 1600 to 3000 have been derived numerically
(von Bargen & Waff 1986; Cheadle et al. 2004), whereas experimental data yield
n ≈ 3 and τ ≈ 10 to 270 (Wark & Watson 1998; Connolly
et al. 2009). In our calculations we use
(n,τ) = (2,1600) (von Bargen & Waff 1986) but discuss later variation of
n and τ in Sect. 3 (cp. Table 2).
(24)Here,
b is a typical grain size after sintering, τ is a
constant which has a value that depends on n, and n is
related to the geometry of the melt. For isotropic systems the values
n = 2 and τ ≈ 1600 to 3000 have been derived numerically
(von Bargen & Waff 1986; Cheadle et al. 2004), whereas experimental data yield
n ≈ 3 and τ ≈ 10 to 270 (Wark & Watson 1998; Connolly
et al. 2009). In our calculations we use
(n,τ) = (2,1600) (von Bargen & Waff 1986) but discuss later variation of
n and τ in Sect. 3 (cp. Table 2).
For the derivation of the described relations we refer to McKenzie (1984). According to this model the relative velocity of the melt that
is expelled from the compacting layer and moving through the uncompacted rest of the
matrix can be computed by the modified Darcy law if the thickness h of
the region across which melting occurred is considerably larger than the compaction length
δc. We estimate δc as a function
of the melt fraction ϕ to get a notion about the depth of the compacting
region. Using
(μb + (4/3)μs) ≈ 1018 Pa s
from McKenzie (1984) as the average viscosity of an
olivine matrix at 1570 K and ϕ = 0.15 and assuming
ηl = 1 Pa s and b = 10-4 m we
obtain ![\begin{eqnarray} \delta_{\rm c}(\varphi)_{\varphi=0.15}&=&\left[ \frac{\mu_{\rm b}+\frac{4}{3}\mu_{\rm s}}{\eta_{\rm l}} K_{\varphi} \right]_{\varphi=0.15} ^{\frac{1}{2}} = \left[ \frac{\mu_{\rm b}+\frac{4}{3}\mu_{\rm s}}{\eta_{\rm l}} \frac{b^{2} \varphi^{n}}{\tau} \right]_{\varphi=0.15} ^{\frac{1}{2}} \nonumber \\ \label{complengthnum} &\approx & \left[ 10^{18}\frac{10^{-8}\,0.15^{2}}{1600} \right] ^{\frac{1}{2}}=0.375 \text{ km}. \nonumber \end{eqnarray}](/articles/aa/full_html/2012/07/aa19157-12/aa19157-12-eq162.png) The
thickness of the melting layer will be of the same order of magnitude as the radius
Rp(t) of the planetesimal. For a body of
the radius Rp(t) = 10 km we obtain
Rp(t)/δc(0.15) ≈ 26.7
using above parameters and a melt fraction of 15%. For ϕ = 0.01 the ratio
of the radius and the compaction length is exactly 400. Both values suggest that
compaction-driven melt migration would occur easily. However, the size of the compaction
region would rise with further melting and the ratio
Rp(t)/δc(ϕ)
would approach the value 10/δc(1.0) = 4.
This indicates that with growing melt fraction the melt migration may not proceed for the
chosen radius of 10 km. For larger bodies (e.g.
Rp(t) ≥ 12.5 km) we obtain ratios ≥ 10 for
ϕ = 0.5, meaning that melt migration would proceed even at this
relatively high melt fraction. In the case that the size of the melting zone exceeds the
compaction length, the rheological properties of the matrix do not matter (McKenzie 1985) and the time needed until melt fraction
decreases by a factor of 1/e can be calculated
directly from the melt percolation velocity.
The
thickness of the melting layer will be of the same order of magnitude as the radius
Rp(t) of the planetesimal. For a body of
the radius Rp(t) = 10 km we obtain
Rp(t)/δc(0.15) ≈ 26.7
using above parameters and a melt fraction of 15%. For ϕ = 0.01 the ratio
of the radius and the compaction length is exactly 400. Both values suggest that
compaction-driven melt migration would occur easily. However, the size of the compaction
region would rise with further melting and the ratio
Rp(t)/δc(ϕ)
would approach the value 10/δc(1.0) = 4.
This indicates that with growing melt fraction the melt migration may not proceed for the
chosen radius of 10 km. For larger bodies (e.g.
Rp(t) ≥ 12.5 km) we obtain ratios ≥ 10 for
ϕ = 0.5, meaning that melt migration would proceed even at this
relatively high melt fraction. In the case that the size of the melting zone exceeds the
compaction length, the rheological properties of the matrix do not matter (McKenzie 1985) and the time needed until melt fraction
decreases by a factor of 1/e can be calculated
directly from the melt percolation velocity.
The described model treats the case of silicate melts with a smaller density than that of the matrix. However, the first melt in our model would be the cotectic Fe,Ni-FeS melt and its density would be higher than that of the solid phase. Hence, the buoyant force due to the density contrast would act downwards. In our model, we treat the process of iron melt migration in the same manner as the migration of the silicate melt (Sahijpal et al. 2007; Stevenson 1990) and assume the migration of molten metal through a mixed iron-silicate matrix by buoyant flow.
Molten iron will migrate to the centre of the body in the presence of a density contrast
between the melt and the surrounding solid matrix. We model the heat transport via magma
segregation using a flow in porous media theory (Stevenson
& Scott 1991) treating simultaneously iron and silicates in solid and
liquid states. Melt segregating from the solid mantle transports the energy of the hot
material. This transport becomes more significant with increasing melt fraction. The
segregation of melt is modelled using the modified Darcy law (McKenzie 1984): 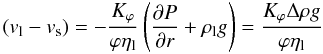 (25)where
(vl − vs) is the relative
velocity of liquid and solid phases, P is the non-hydrostatic pressure of
the melt, ϕ is the volume fraction of the melt equal to the porosity,
Δρ is the density contrast between the solid and the melt,
ηl is the viscosity of the melt (see Table 2) and ρl is the density of
the melt. The equation describes the relative motion of the melt and matrix in terms of
the pressure gradient and the buoyancy. Thereby we neglect the dynamic pressure arising
from the matrix compaction. Assuming an immobile matrix we obtain
vs = 0 and the relative velocity
Δv = (vl − vs)
is equal to the flow speed of molten material. The relative velocity Δv
is non-dimensionalised using the relation
v∗ = vD/κ0
and included into the heat conduction equation Eq. (5) as an advection term (non-dimensionalised velocity times transformed
temperature gradient) on the right-hand side.
(25)where
(vl − vs) is the relative
velocity of liquid and solid phases, P is the non-hydrostatic pressure of
the melt, ϕ is the volume fraction of the melt equal to the porosity,
Δρ is the density contrast between the solid and the melt,
ηl is the viscosity of the melt (see Table 2) and ρl is the density of
the melt. The equation describes the relative motion of the melt and matrix in terms of
the pressure gradient and the buoyancy. Thereby we neglect the dynamic pressure arising
from the matrix compaction. Assuming an immobile matrix we obtain
vs = 0 and the relative velocity
Δv = (vl − vs)
is equal to the flow speed of molten material. The relative velocity Δv
is non-dimensionalised using the relation
v∗ = vD/κ0
and included into the heat conduction equation Eq. (5) as an advection term (non-dimensionalised velocity times transformed
temperature gradient) on the right-hand side.
Once the solidus temperature of the silicates is reached, the silicate melt will migrate
toward the surface as its density is lower than the matrix density. Hence, the heat
conduction Eq. (5) is supplemented by a
second advection term, which is calculated analogously using the data for silicates:
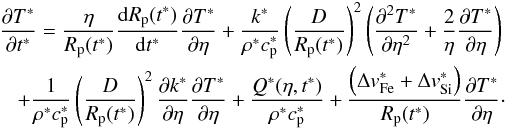 (26)The
density contrasts Δρ between the liquid phases of iron resp. silicates
and the solid matrix are computed for every time step in every discretisation shell to
account for the composition of the matrix:
(26)The
density contrasts Δρ between the liquid phases of iron resp. silicates
and the solid matrix are computed for every time step in every discretisation shell to
account for the composition of the matrix: 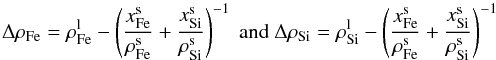 where
ΔρFe is the density contrast between liquid iron and the
matrix consisting of solid iron and solid silicates and ΔρSi
is the density contrast between liquid silicates and the matrix. Here,
where
ΔρFe is the density contrast between liquid iron and the
matrix consisting of solid iron and solid silicates and ΔρSi
is the density contrast between liquid silicates and the matrix. Here,
 and
and
 is the density of
the component i in the liquid and solid state, respectively, and
is the density of
the component i in the liquid and solid state, respectively, and
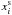 is the mass
fraction of the solid portion of the component i (with respect to the
overall amount of the solid material in a given shell). Note that the value
ΔρSi is negative emphasizing the upward movement of the
silicate melt.
is the mass
fraction of the solid portion of the component i (with respect to the
overall amount of the solid material in a given shell). Note that the value
ΔρSi is negative emphasizing the upward movement of the
silicate melt.
It should be noted that several limitations exist assuming flow in porous media in planetary bodies. For melt contents larger than about 50%, the process of magma segregation differs from the flow in porous media and we do not account for this effect. Furthermore, iron and silicate melt can occur at the same time and migrate apart, i.e. silicate rises and iron sinks. We are not aware of any work showing how this would affect the melt percolation and thus the Darcy flow equation. Here, we assume for simplicity that iron and silicate melt migrate along different grain boundaries and do not disturb each other. The porosity used to calculate the permeability of iron or silicate is then equal to the amount of melt of each species.
To calculate the melt percolation velocity, the grain size of the matrix needs to be
estimated. The best available approximation for the grain size is provided by the
undifferentiated chondrites having grain sizes ≤1 mm (Taylor et al. 1993). When melting starts, small particles dissolve, and
redeposit on the surfaces of larger crystals – the grain sizes grow with time, a process
known as Ostwald ripening. The crystal size b after time
t is given by 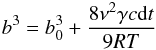 (27)with
the initial crystal size b0, molar volume of typical silicate
crystals ν, surface free energy of the crystal-liquid interface
γ, equilibrium concentration of solute c and diffusion
coefficient d (Greenwood 1969).
The values used in our model are listed in Table 3.
With those values and assuming 1500 K, crystals originally 0.1 mm in radius will coarsen
to 1.1 mm after 104 a, 2.5 mm after 105 a and 5.4 mm after
106 a. Note that b is an averaged value and that grains of
different sizes are present in a partially molten system. However, in general, the
permeability increases when the average grain size increases (Chilingarian & Wolf 1976; Al-Homadhi 2001).
(27)with
the initial crystal size b0, molar volume of typical silicate
crystals ν, surface free energy of the crystal-liquid interface
γ, equilibrium concentration of solute c and diffusion
coefficient d (Greenwood 1969).
The values used in our model are listed in Table 3.
With those values and assuming 1500 K, crystals originally 0.1 mm in radius will coarsen
to 1.1 mm after 104 a, 2.5 mm after 105 a and 5.4 mm after
106 a. Note that b is an averaged value and that grains of
different sizes are present in a partially molten system. However, in general, the
permeability increases when the average grain size increases (Chilingarian & Wolf 1976; Al-Homadhi 2001).
Parameter values used to calculate the Ostwald ripening.
To model the actual melt movement and thus the redistribution of iron and silicates inside a body, we use the melt velocity and calculate the time needed for the melt to travel over a certain distance Δr by using Δt = Δr/Δv. Assuming a fixed discretisation of the solution domain and a fixed planetesimal radius the distance Δr is constant. As soon as the velocity reaches the value that is high enough for the melt to travel over Δr, the respective melt migrates from one shell to the other. If the radius Rp(t) varies, i.e. if accretion and sintering take place, both Δr and Δv are adjusted to the new distance between the grid points and new melt fraction by using Eq. (3). To ensure the volume conservation a part of the solid (iron and silicate) matrix from the lower shells replaces the migrated iron melt from the upper shells in the case of iron melt migration, and a part of the solid matrix from the upper shells replaces the migrated silicate melt from the lower shells in the case of silicate melt migration. After each melt movement we calculate the new concentration of the 26Al and 60Fe from the current concentrations in the involved shells and the fractions of the interchanged material.
2.4. Composition, density and melting temperatures
We assume the planetesimals to consist of a mixture of iron, silicates and the pore
spaces to be filled with gas or vacuum. The dependence of the density on the porosity is
described by Eq. (14). Assuming the pore
density ρp to be negligible,
ρ = (1 − φ)ρc is given. To
calculate the density ρc of the compact material in the solid
state, the densities ρi of the pure
components are weighted with their mass fractions
xi: 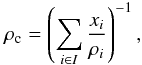 (28)where
I = { solid iron, solid silicates } . The metallic fraction is a mixture
of Fe, Ni and FeS and its density is computed using the same formula as above. Chondritic
materials (H and L chondrites) consist typically of about 20 wt.% iron where Fe is present
as free iron, iron sulphide and iron oxide. We use the average mass fractions of Fe, Ni
and FeS of 0.1512, 0.0168 and 0.051, respectively, reported by Keil (1962) for the H-chondritic composition. Additional iron in the
form of fayalite and ferrosilite is contained in the olivine, orthopyroxene and
clinopyroxene and is considered as a fraction of the silicates. The silicates represent
the remaining mass of the planetesimal. The mass fractions and densities used in our model
are taken for the most part from Yomogida & Matsui
(1983). The densities of the solid and liquid states and initial abundances of
the pure components are listed in Table 4. We
assume the compound iron(II) sulfide (FeS) that exists in several forms (pyrrhotite,
troilite, mackinawite etc.) to be represented by the troilite. The average density
4610 kg m-3 of troilite is used as the density of FeS in the solid state. The
value of 3920 kg m-3 for the density of FeS in the liquid state is extrapolated
from Fig. 3 of Byerley & Takebe (1970) and
is consistent with the value from Nagamori (1969).
The density of the iron component in our model is computed from the values of Fe, Ni and
FeS. The volume fraction of the Fe,Ni-FeS mixture and hence the maximal possible volume
fraction of the core after the differentiation is completed is about 10%.
(28)where
I = { solid iron, solid silicates } . The metallic fraction is a mixture
of Fe, Ni and FeS and its density is computed using the same formula as above. Chondritic
materials (H and L chondrites) consist typically of about 20 wt.% iron where Fe is present
as free iron, iron sulphide and iron oxide. We use the average mass fractions of Fe, Ni
and FeS of 0.1512, 0.0168 and 0.051, respectively, reported by Keil (1962) for the H-chondritic composition. Additional iron in the
form of fayalite and ferrosilite is contained in the olivine, orthopyroxene and
clinopyroxene and is considered as a fraction of the silicates. The silicates represent
the remaining mass of the planetesimal. The mass fractions and densities used in our model
are taken for the most part from Yomogida & Matsui
(1983). The densities of the solid and liquid states and initial abundances of
the pure components are listed in Table 4. We
assume the compound iron(II) sulfide (FeS) that exists in several forms (pyrrhotite,
troilite, mackinawite etc.) to be represented by the troilite. The average density
4610 kg m-3 of troilite is used as the density of FeS in the solid state. The
value of 3920 kg m-3 for the density of FeS in the liquid state is extrapolated
from Fig. 3 of Byerley & Takebe (1970) and
is consistent with the value from Nagamori (1969).
The density of the iron component in our model is computed from the values of Fe, Ni and
FeS. The volume fraction of the Fe,Ni-FeS mixture and hence the maximal possible volume
fraction of the core after the differentiation is completed is about 10%.
Species, initial mass fractions and densities for an H-chondritic composition.
Once the eutectic temperature of the Fe,Ni-FeS mixture (1213 K) in a sintered
planetesimal is reached, iron melting starts and melt of eutectic composition is
generated. The densities of iron and silicates from Eq. (28) are calculated as follows: 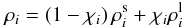 (29)with the
densities
(29)with the
densities 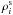 and
and
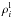 of the solid and
liquid state, respectively, and the melt fractions
χi of the compound i
relative to the volume of the fraction i. While we assume a constant
value for the density of molten silicates the density of the liquid iron is considered as
a function of the iron melt fraction. The first partial unfractionated iron melt would
consist of 76.7 wt% Fe,Ni and 23.3 wt% FeS (cp. Table 4). However, the first partial melt at the eutecticum 1213 K is sulfur-rich and
would consist of about 15 wt% Fe, Ni and 85 wt% FeS (Kullerud 1963). Its density hence would be lower than that of the Fe, Ni and FeS
mixture in the complete molten state at higher temperatures. We approximate the enrichment
of sulfur in the eutectic melt as follows. We use the density 4200 kg m-3 for
the eutectic melt at 1213 K and the value 5940 kg m-3 for temperatures above
the liquidus of the iron. Between the solidus and the liquidus temperature a linear
dependence of the density on the iron melt fraction is assumed.
of the solid and
liquid state, respectively, and the melt fractions
χi of the compound i
relative to the volume of the fraction i. While we assume a constant
value for the density of molten silicates the density of the liquid iron is considered as
a function of the iron melt fraction. The first partial unfractionated iron melt would
consist of 76.7 wt% Fe,Ni and 23.3 wt% FeS (cp. Table 4). However, the first partial melt at the eutecticum 1213 K is sulfur-rich and
would consist of about 15 wt% Fe, Ni and 85 wt% FeS (Kullerud 1963). Its density hence would be lower than that of the Fe, Ni and FeS
mixture in the complete molten state at higher temperatures. We approximate the enrichment
of sulfur in the eutectic melt as follows. We use the density 4200 kg m-3 for
the eutectic melt at 1213 K and the value 5940 kg m-3 for temperatures above
the liquidus of the iron. Between the solidus and the liquidus temperature a linear
dependence of the density on the iron melt fraction is assumed.
Parameter values used to simulate melting.
For the melting temperature of iron and silicates we assume the values listed in Table 5. Various authors fix the liquidus temperature of the Fe,Ni-FeS system at the value of 1233 K (e.g. Sahijpal et al. 2007; Ghosh & McSween Jr. 1999) reducing the temperature range for complete iron melting to only 20 K. Such restriction would be true only for extreme sulfur rich compositions. At low concentrations of sulphur higher liquidus temperatures are required to melt Fe,Ni-FeS systems. Appropriate values of the liquidus temperature for the iron melt are 1630 K for LL chondrites and 1700 K for H chondrites (Taylor 1992). The respective percentages of Fe, Ni and FeS in our model correspond to those in H chondrites, hence we chose TL,Fe = 1700 K for our standard model. In additional calculation, we also test the influence of a low liquidus temperature for iron on the differentiation of planetesimals for a better comparison to previous models.
2.5. Thermal conductivity and heat capacities
In the initial state the material of the planetesimal is in a powder-like form,
suggesting a much lower thermal conductivity by lattice vibration (phonon conduction) than
that of the compacted material because in a high porous body the dust grains have only a
few contact points or small contact areas to the neighbouring particles. However, if a
planetesimal experiences sintering, the material compacts and the thermal conductivity
rises. We use the approximation of Krause et al.
(2011): 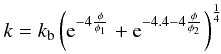 (30)where
kb = 4.56 W m-1 K-1,
φ1 = 0.08 and φ2 = 0.17. This
equation is a smooth approximation of the fits to the data obtained by Krause et al. (2011) from laboratory experiments and
numerical simulations (second term, φ ≥ 0.4) and to the experimental
results for ordinary chondrites by Yomogida &
Matsui (1983) (first term, φ ≤ 0.2). The resulting thermal
conductivity varies exponentially by two orders of magnitude between
≈0.017kb at φ = 0.5 and
kb at φ = 0. The term
kb estimates the mean thermal conductivity of the
composition from Table 4 and is calculated using
the geometric mean model (Beardsmore & Cull
2001). In this model several components of known conductivity are randomly
orientated and distributed within a mixture; a distribution that is appropriate for
planetesimals. The geometric mean of a n-component system is the product
(30)where
kb = 4.56 W m-1 K-1,
φ1 = 0.08 and φ2 = 0.17. This
equation is a smooth approximation of the fits to the data obtained by Krause et al. (2011) from laboratory experiments and
numerical simulations (second term, φ ≥ 0.4) and to the experimental
results for ordinary chondrites by Yomogida &
Matsui (1983) (first term, φ ≤ 0.2). The resulting thermal
conductivity varies exponentially by two orders of magnitude between
≈0.017kb at φ = 0.5 and
kb at φ = 0. The term
kb estimates the mean thermal conductivity of the
composition from Table 4 and is calculated using
the geometric mean model (Beardsmore & Cull
2001). In this model several components of known conductivity are randomly
orientated and distributed within a mixture; a distribution that is appropriate for
planetesimals. The geometric mean of a n-component system is the product 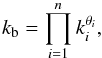 (31)where
θi are the volume fractions and
ki are the known thermal conductivities of
the involved minerals. The pure mineral thermal conductivities are taken from Yomogida & Matsui (1983) and have the values
4.3 W m-1 K-1 for olivine, 3.9 W m-1 K-1 for
orthopyroxene, 4.6 W m-1 K-1 for clinopyroxene,
1.9 W m-1 K-1 for plagioclase, 4.6 W m-1 K-1
for troilite and 21 W m-1 K-1 for the Fe-Ni mixture. The first four
values form the bulk conductivity of the silicate component and the latter two that of the
iron component, both according to Eq. (31). From the resulting two values and from the volume fractions of iron and
silicates during and after the differentiation, the conductivity in a given volume is
calculated using (31). Once a protocore is
formed, the relatively high conductivity of the Fe,Ni-FeS system results in a flat
temperature profile throughout the core, whereas in the mantle the temperature
equalisation proceeds rather slowly. We neglect the energy transport by radiation between
grains of the porous material. This kind of heat transport occurs at the starting stage of
the thermal evolution. Yet, in Henke et al. (2012)
the laboratory measurements of Fountain & West
(1970) of radiative heat conduction are discussed and the resulting thermal
conductivity is found to be approximately one order of magnitude lower than the above fit
(30).
(31)where
θi are the volume fractions and
ki are the known thermal conductivities of
the involved minerals. The pure mineral thermal conductivities are taken from Yomogida & Matsui (1983) and have the values
4.3 W m-1 K-1 for olivine, 3.9 W m-1 K-1 for
orthopyroxene, 4.6 W m-1 K-1 for clinopyroxene,
1.9 W m-1 K-1 for plagioclase, 4.6 W m-1 K-1
for troilite and 21 W m-1 K-1 for the Fe-Ni mixture. The first four
values form the bulk conductivity of the silicate component and the latter two that of the
iron component, both according to Eq. (31). From the resulting two values and from the volume fractions of iron and
silicates during and after the differentiation, the conductivity in a given volume is
calculated using (31). Once a protocore is
formed, the relatively high conductivity of the Fe,Ni-FeS system results in a flat
temperature profile throughout the core, whereas in the mantle the temperature
equalisation proceeds rather slowly. We neglect the energy transport by radiation between
grains of the porous material. This kind of heat transport occurs at the starting stage of
the thermal evolution. Yet, in Henke et al. (2012)
the laboratory measurements of Fountain & West
(1970) of radiative heat conduction are discussed and the resulting thermal
conductivity is found to be approximately one order of magnitude lower than the above fit
(30).
The specific heat capacity of the iron and silicate mixture depends on the temperature
and on the composition according to 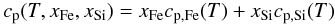 (32)with
cp,Si(T) and
cp,Fe(T) the temperature
dependent heat capacity of silicate and iron, respectively. For the temperature dependent
heat capacity of the iron phase, we use an approximation on the fit from Wilthan (2002) (90% iron, 10% nickel):
(32)with
cp,Si(T) and
cp,Fe(T) the temperature
dependent heat capacity of silicate and iron, respectively. For the temperature dependent
heat capacity of the iron phase, we use an approximation on the fit from Wilthan (2002) (90% iron, 10% nickel): 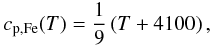 (33)where the structural
transition of iron at the Curie-temperature of 1042 K is neglected. We calculate
cp,Si(T) by assuming for
the heat capacity of the non-differentiated bulk chondritic material the analytic fit of
Yomogida & Matsui (1984):
(33)where the structural
transition of iron at the Curie-temperature of 1042 K is neglected. We calculate
cp,Si(T) by assuming for
the heat capacity of the non-differentiated bulk chondritic material the analytic fit of
Yomogida & Matsui (1984): 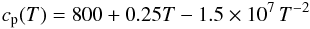 (34)and
using Eq. (32) with
(34)and
using Eq. (32) with
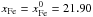 and
and
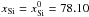 (
(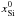 and
and
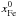 are initial
mass fractions, see Table 4) and Eq. (33). Having
cp,Fe(T) and
cp,Si(T), the specific
heat capacity can be computed for any mass fractions of iron and silicates from Eq. (32). At the temperatures of e.g. 500 K, 1000 K
and 1500 K we obtain the values 511, 567 and 622 for
cp,Fe(T), 964, 1166 and
1321 for cp,Si(T), and 865,
1035 and 1168 J kg-1 K-1 for
are initial
mass fractions, see Table 4) and Eq. (33). Having
cp,Fe(T) and
cp,Si(T), the specific
heat capacity can be computed for any mass fractions of iron and silicates from Eq. (32). At the temperatures of e.g. 500 K, 1000 K
and 1500 K we obtain the values 511, 567 and 622 for
cp,Fe(T), 964, 1166 and
1321 for cp,Si(T), and 865,
1035 and 1168 J kg-1 K-1 for 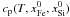 , respectively. For all possible
mass fractions xFe and xSi and the
above temperature range, the
values ρFecp,Fe,
ρSicp,Si and
ρcp vary between 3.0 × 106 and
4.3 × 106 J K-1 m-3 meaning that the sensible heat is
nearly constant across the different compositions and temperatures.
, respectively. For all possible
mass fractions xFe and xSi and the
above temperature range, the
values ρFecp,Fe,
ρSicp,Si and
ρcp vary between 3.0 × 106 and
4.3 × 106 J K-1 m-3 meaning that the sensible heat is
nearly constant across the different compositions and temperatures.
Parameter values used to model the radioactive heat production.
List of models presented in the figures including the varied input parameters.
2.6. Radiogenic heat sources
The heat source distribution depends on volume fractions of Fe,Ni-FeS and silicates and
is calculated from ![\begin{eqnarray} Q(r,t)=\left( 1-\phi(r) \right) \left( v_{\rm Si}(r)f_{\rm Al}\left[ \frac{\rm ^{26}Al}{\rm ^{27}Al} \right] \frac{E_{\rm Al}}{\tau_{\rm Al}}{\rm e}^{-\frac{t+t_{0}}{\tau_{\rm Al}}} \right. \nonumber \\ \left. + v_{\rm Fe}(r)f_{\rm Fe}\left[ \frac{\rm ^{60}Fe}{\rm ^{56}Fe} \right] \frac{E_{\rm Fe}}{\tau_{\rm Fe}}{\rm e}^{-\frac{t+t_{0}}{\tau_{\rm Fe}}} \right) \label{sources} \end{eqnarray}](/articles/aa/full_html/2012/07/aa19157-12/aa19157-12-eq346.png) (35)where
fi is the chondritic abundance,
Ei the decay energy per atom,
τi the mean life,
[i/i] the initial abundance of
the nuclide i and t0 the delay time of
accretion with respect to the formation time of the CAIs (i.e. the time passed between the
formation of the CAIs and the beginning of the growth of the planetesimals). The
pre-factor vi is given by the equation
(35)where
fi is the chondritic abundance,
Ei the decay energy per atom,
τi the mean life,
[i/i] the initial abundance of
the nuclide i and t0 the delay time of
accretion with respect to the formation time of the CAIs (i.e. the time passed between the
formation of the CAIs and the beginning of the growth of the planetesimals). The
pre-factor vi is given by the equation
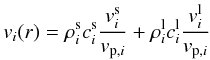 (36)with
the volume fractions
(36)with
the volume fractions 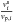 and
and 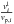 of liquid resp. solid phase (with respect to the volume
vp,i of the species i in
a given discretisation shell at the instance t assuming a primordial
composition of this shell) and the corresponding concentrations
of liquid resp. solid phase (with respect to the volume
vp,i of the species i in
a given discretisation shell at the instance t assuming a primordial
composition of this shell) and the corresponding concentrations
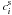 and
and 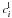 of the species
i in those phases. At the beginning of a simulation the heat producing
nuclei are distributed homogeneously, although later this may change due to the melting
and subsequent chemical differentiation. Note that we neglect that some of the
60Fe is contained in the silicates and would migrate with them. Compared to
the overall heat production heating by this portion of nuclides is considered as
negligible. The used parameter values are listed in Table 6.
of the species
i in those phases. At the beginning of a simulation the heat producing
nuclei are distributed homogeneously, although later this may change due to the melting
and subsequent chemical differentiation. Note that we neglect that some of the
60Fe is contained in the silicates and would migrate with them. Compared to
the overall heat production heating by this portion of nuclides is considered as
negligible. The used parameter values are listed in Table 6.
 |
Fig. 2 The volume filling factor as a function of time and radius of the planetesimal. Left panel: an instantaneously accreted body with the terminal radius D = 10 km (Rp(t0) = 11.9 km) and the accretion time t0 = 1.61 Ma. Right panel: an asymptotically accreted body with the initial radius R0 = 1.2 km, the terminal radius D = 10 km (Rp(t0 + taccr) = 11.9 km), the onset time of accretion t0 = 1.61 Ma and the accretion duration taccr = 0.5 Ma. |
3. Results
We first study bodies in which heat is transported by conduction only, i.e. the internal temperatures remain below the melting temperatures (cf. Table 7, first 14 cases FI-TLP), to investigate the change of porosity with time due to sintering. We study the differences between instantaneous and continuous accretion and vary the onset time of accretion, the duration taccr of the accretion as well as the accretion law (cases PI-PA). The effect of the initial porosity on the thermal evolution have been examined in the models TS–TLP.
Next we consider bodies that undergo melting and study the effects of heat transport due to melt migration, material transport and redistribution of radiogenic heat sources (cf. Table 7, cases A1–A4). To determine the evolution of the interior structure, e.g. the onset time of differentiation, the duration of iron-silicate and silicate-silicate separation, and constrain the parameter range for which a planetesimal undergoes melting and differentiation, we investigate two different compositions of the Fe,Ni-FeS system: a sulfur-poor composition with 5.1 wt% FeS (corresponding to 23 wt% of the iron phase, cf. Table 4) is chosen, representative for H chondrites (cases P1–P4) and a sulfur-rich composition with 15.33 wt% FeS (corresponding to 70 wt% of the iron phase) (cases PL1–PL4). We further examine the influence of the initial grain size b0 and the Ostwald ripening (cases G1–G3) and the effects of accretion and different accretion laws (cases L1–L3 and R1–R3) on the differentiation of the planetesimals. Table 7 provides an overview on the simulations that were performed for the current study and the parameters corresponding to the respective simulation.
The considered planetesimals accrete as porous bodies and undergo sintering due to
increasing temperature and pressure. We show that the thermal evolution depends on the
accretion onset time t0, the accretion duration
taccr, the accretion law and the terminal radius
D. The latter corresponds to a body with the porosity equal to zero and
is prescribed at the beginning of a simulation. The initial radius
Rp(t0) at the accretion onset
time t0 is calculated using the prescribed uniform initial
porosity φ0. In the case of instantaneous formation the initial
radius is larger than the terminal radius and is given by 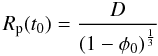 (37)the
radius changes with time due to sintering but the terminal radius D will
not be reached as discussed below. If the accretion is not instantaneous the initial radius
of the planetesimal (without porosity) is chosen to be 1 km; thus using Eq. (37) and 1 km instead of D the
initial radius is 1.2 km assuming an initial porosity of 0.4. This value corresponds to the
hexagonal prismatic packing of dust particles, consistent to the computation of the
effective stress (Eq. (9)). The initial
temperature and the boundary temperature are set to TN = 290 K.
(37)the
radius changes with time due to sintering but the terminal radius D will
not be reached as discussed below. If the accretion is not instantaneous the initial radius
of the planetesimal (without porosity) is chosen to be 1 km; thus using Eq. (37) and 1 km instead of D the
initial radius is 1.2 km assuming an initial porosity of 0.4. This value corresponds to the
hexagonal prismatic packing of dust particles, consistent to the computation of the
effective stress (Eq. (9)). The initial
temperature and the boundary temperature are set to TN = 290 K.
3.1. Thermal evolution of accreting planetesimals without melting
 |
Fig. 3 Porosity φ as a function of radius for bodies that accrete at t0 = 1.44 from Rp(t0) = 1.2 km to Rp(t0 + taccr) = 11.9 km with the initial porosity of φ = 0.4 (D = 10 km). Left panel: linear accretion with varying accretion duration taccr. Right panel: varying accretion law with fixed accretion duration taccr = 1.0 Ma. |
 |
Fig. 4 Effects of the porosity, accretion law and accretion duration on the evolution of the central temperature. Left panel: planetesimal with the terminal radius D = 1 km that accretes instantaneously at t0 = 0 Ma and φ equal to either zero (solid line), or 0.4 (dashed line). In the subplot of the left panel: instantaneously accreting planetesimal with D = 100 km and t0 = 2.51 Ma. Middle panel: linear accretion from R0 = 1.2 km to D = 10 km at t0 = 1.44 Ma with varying accretion duration taccr. Right panel: non-instantaneous accretion within 1 Ma with t0 = 1.44 Ma, R0 = 1.2 km and D = 10 km in comparison to an instantaneously accreting planetesimal assuming the same parameters (solid line). |
During the early evolution the interior of the planetesimals is heated by the decay of the radioactive elements. Sintering starts at a threshold temperature that depends on the activation energy (Eq. (9)) and the pressure (radius) of the body. For a pressure of 0.341 bar (e.g. central pressure for an H-chondritic planetesimal with a radius of about 4.2 km) and the chosen activation energy of E = 60 kcal mol-1 sintering starts at a temperature of about 600 K – with decreasing pressure the threshold temperature increases, consistent with the results of Yomogida & Matsui (1984).
As in the early stages of the thermal evolution the peak temperature is attained in centre of the planetesimal, it compacts from the inside out. For planetesimals with larger radii a porosity of zero can be reached almost in the entire body. Only in the uppermost layers the temperature conditions necessary for sintering are not reached due to the cooling through the surface and low pressure. Thus, the surface retains its porosity during the entire evolution and serves as an insulating layer. The loss of porosity is accompanied by the shrinkage of the radius. As the upper layers remain porous, the final radius is in any case larger than the terminal radius D but smaller than Rp(t0 + taccr). The shrinkage results in a larger surface-to-volume ratio and hence in a more effective cooling of the sintered body – in addition to the higher thermal conductivity of the compacted material in comparison to the low conductivity of the porous material.
In the following, we focus on the effects of a non-instantaneous accretion of a body on its thermal evolution. For a detailed discussion of the thermal evolution of instantaneously formed porous bodies that undergo sintering by hot pressing we refer to Henke et al. (2012). In Fig. 2 the evolution of the volume filling factor is compared between an instantaneously accreted body with D = 10 km (corresponding to Rp(t0) = 11.9 km) and t0 = 1.61 Ma and an asymptotically accreted body with D = 10 km, t0 = 1.61 Ma and taccr = 0.5 Ma. The instantaneous accreting planetesimal starts as a porous 11.9 m sized body that heats up due to the decay of 26Al and 60Fe. Sintering then leads to the shrinkage of the body with a final radius of 10.2717 km. The non-instantaneous accreting body starts from a 1.2 km sized seed and accretes to 11.9 km. During accretion the central regions reach the threshold temperature for sintering and begin to compact. Because accretion and sintering proceed simultaneously, the latter does not result in the shrinkage, but in a slightly dampened growth of the radius. The loss of porosity continues during the growth of the body – the already accreted surface material gets covered by the new layers, heats up and gets exposed to higher temperatures and pressures. As a consequence, the planetesimal does not reach the radius Rp(t0 + taccr) = 11.856 km that would follow from the prescribed terminal radius D = 10 km and φ = 0.4 and grows only to the size of 11.811 km. Once accretion is finished, sintering leads to the actual shrinkage of the body to the final radius of 10.3825 km, which is larger by 0.110 km than in the case of instantaneous accretion. Thus, planetesimals with the same mass differ in their final size dependent on the accretion time and – as we will show later – on the accretion law.
The difference in size can be explained by the difference in the thermal evolution. In the case of non-instantaneous accretion the threshold temperature for sintering is reached at later times, if at all. After accretion and sintering, this results in a smaller sintered region and a thicker porous layer in contrast to an instantaneously accreting body. A simple relationship can be deduced between the accretion duration and the amount of sintering. The longer it takes for a body to accrete to the same terminal radius (abiding by the same accretion law), the lower is the central temperature and the average temperature at any time t, leading to a thicker regolith layer. When a planetesimal cools down and the temperature drops below the critical sintering temperature, no further changes of the porosity due to the hot pressing are possible.
Figure 3 (left panel) shows final porosity profiles of cooled bodies that accreted in the same manner but with different taccr. In the presented case the thickness of the porous layer increases from about 2 km for instantaneous accretion to about 5 km assuming an accretion time of 1.5 Ma. Similarly, for a fixed accretion duration taccr and fixed terminal radius, linearly accreting bodies will sinter more efficient than exponentially accreting ones, and those, again, more efficient than the asymptotically accreting cases (Fig. 3, right panel). However, the differences in the final porosity profiles of those three cases are almost negligible.
In addition to differences in the final radius and the thickness of the outer porous layer, sintering in combination with accretion influences the central peak temperatures of the planetesimals. The peak temperature depends on several factors: the radius of the planetesimal determines the surface-to-volume ratio and hence controls the efficiency of the heat loss. The accretion onset time influences the radiogenic heat source density. The accretion law controls the change of the radius during the evolution. The accretion duration either catalyses or inhibits the change of the radius and finally, the presence of porous material influences the heat conductivity.
 |
Fig. 5 The evolution of the central temperature (left panel) and the radial temperature distribution at the instance of the maximum temperature (right panel) in a body that accreted instantaneously to D = 35 km at t0 = 1.6 Ma. Consideration of both the heat transport by melt and the redistribution of radioactive elements (solid line), consideration of the heat transport by melt and neglection of the redistribution of radioactive elements (dashed line), consideration of the redistribution of radioactive elements and neglection of the heat transport by melt (dot-dashed line), neglection of both the heat transport by melt and the redistribution of radioactive elements (dotted line). |
In Fig. 4 (left panel) the evolution of the central temperature of two bodies with D = 1 km and t0 = 0 Ma (main plot) and D = 100 km and t0 = 2.51 Ma (subplot) for φ0 = 0 and φ0 = 0.4 with subsequent sintering have been compared. Note that the evolution of the peak temperature for the 100 km sized body is similar for both the initially compact and the initially porous state; the peak temperatures differ by about 12%. For the small planetesimal with D = 1 km the situation is different. The initially compact body remains cold (<350 K), whereas the initially porous body of equal size heats up to over 1100 K – the peak temperatures differ by a factor of 3.1.
Figure 4 (middle panel) shows the dependence of the central temperature on the accretion duration for the linear accretion law and Fig. 4 (right panel) shows the dependence on the accretion law for a fixed accretion duration of 1 Ma. An instantaneously formed body heats up to its peak central temperature and cools down with the reduction of the concentration of 26Al and 60Fe. The sintering takes place in the beginning of the evolution and influences only the increase of the temperature before it reaches the maximum, see Fig. 4, middle and right panels. The thermal evolution of non-instantaneously accreting bodies is associated with the interplay of heating, sintering and accretion. Under favourable conditions (e.g. D ≥ 1 km at t0 = 0) the planetesimal heats up to the threshold temperature for sintering in the centre. Regions around the centre lose their porosity and the heat loss by conduction becomes more efficient. As the accretion continues, the higher surface to volume ratio dampens the temperature increase. The longer the accretion the stronger is the dampening and may even result in a decrease of the temperature. Later, after the accretion, the temperature can rise again leading to a second maximum. Note that although non-instantaneously accreting bodies have lower peak temperature, they cool down significantly slower (Fig. 4, middle and right panels).
It can be concluded that the central peak temperature in initially highly porous planetesimals is significantly higher than assuming initially compact planetesimals. The temperature difference is in particular large for small sized planetesimals of less than a few km, consistent with the results of Henke et al. (2012). Accretion dampens the temperature increase and thus the sintering process compared to the instantaneous formation – the longer the accretion the less efficient is the sintering and thus the porosity loss. This influence of accretion on the porosity loss differs, however, between very small bodies that will not sinter at all due to the unsufficient pressure and those with larger final radii and higher pressures that will compact and reach higher thermal conductivity. In the first case, prolonged accretion does not alter the peak temperature significantly, whereas in the second case the temperature increase depends on taccr and the accretion law.
3.2. Thermal evolution including the effect of melt migration
In the following we discuss the effects of melting on the chemical composition, internal structure and thermal evolution of planetesimals. We study in particular the influence of accretion (duration and accretion law), the liquidus temperature of iron and the grain size, which is an important parameter constraining the flow velocities of melt.
3.2.1. Heat transport due to the melt migration and redistribution of radioactive elements
To demonstrate the influence of the magmatic heat transport due to the migration of iron and silicate melts and the associated redistribution of radioactive elements on the thermal evolution, we compare the evolution of the central temperature in an instantaneously formed body at t0 = 1.6 Ma and D = 35 km for four cases (Fig. 5). Case A1 neglects the heat transport of melt and the redistribution of radioactive elements. Case A2 considers the heat transport of melt but neglects the redistribution of radioactive elements. Case A3 considers the redistribution of the radiogenic heat sources due to melt migration but neglects the heat transport of melt. Finally, case A4 considers both the heat transport of melt and the redistribution of radioactive elements. Figure 5 (right panel) shows the temperature profiles at the instant when the maximal (peak) temperature in the planetesimal is reached. These temperatures and the associated times are given in Table 8. Note that TFe,L = 1233 K has been chosen for those simulations to emphasize the effects of the heat transport by melt.
Peak temperatures and instances of peak temperatures for the simulations A1–A4.
The temperature increase in the centre is slightly buffered due to sintering after about 1.8 Ma (Fig. 5). Then, at the temperature interval between 1213 and 1233 K, i.e. when iron melts, the temperature increase is strongly reduced due to the loss of the latent heat of melting. After melting of the iron, the temperature rises rapidly again for the cases A1 and A2 (neglection of the transport of radioactive elements) until the silicates start to melt. For the cases A3 and A4 the iron melt sinking to the centre displaces the 26Al-enriched compacted matrix. Thus, the heat source density is strongly reduced in the centre and the phase of a constant central temperature lasts longer, until heating from above causes a further temperature increase (cf. Fig. 5).
The consideration of both the heat transport by melt and the redistribution of radioactive elements leads to a dampening of the temperature in the region around the centre and to relative higher temperature in the upper layers (e.g. the mantle is superheated by ΔT ≈ 160 K, see Fig. 5, right panel). The peak temperature is about 100 K lower when considering the effect of the heat transport by melt and redistribution of the heat sources and occurs at about 1.6 Ma earlier as compared to model A1 (cf. Table 7). Neglecting both effects results in a “typical” onion-shell temperature distribution with the maximum temperature in the centre and decreasing temperatures toward the surface. The dampening of the central temperature is relatively strong if we assume TFe,L = 1233 K and would be less pronounced for TFe,L = 1700 K. This is due to the fact that for the lower liquidus temperature of 1233 the melt fraction χ of iron is equal to 1 and the advection term is larger than that at the respective temperatures but for TFe,L = 1700 K. Apart from the amount of melting, the magnitude of dampening depends also on the assumed Darcy exponent, the Darcy coefficient and on the grain size, which will be discussed below.
3.2.2. Evolution of the interior structure
The melt migration of iron and silicates is also associated with the differentiation and thus a change of the interior structure of the planetesimal with time. We distinguish in particular between the iron-silicate separation associated with core formation and the silicate-silicate separation.
We consider four exemplary bodies starting as porous objects with the radii of 9.5, 41.5, 83.0 and 118.6 km that correspond to a terminal radius of D = 8, 35, 70 and 100 km, respectively. The formation times are t0 = 0, 2.25, 2.5 and 2.75 half lifes of 26Al, respectively, and have been chosen to keep the maximal melt fraction below 50%. The iron liquidus temperature is either 1700 K (P1–P4) or 1233 K (PL1–PL4). Table 9 lists the time of the first iron melt movement t1, the time of the last iron melt movement into the core t2, the duration of core formation Δt = t2 − t1 and the time of last silicate melt movement in a silicate matrix t3. Furthermore, the relative radius is given at which the first melt starts to migrate as well as the relative size and volume of the obtained reservoirs, i.e. the iron core, and silicate mantle and the thickness of the regolith layer.
The melt velocity depends in addition to the melt fraction (and hence temperature) also on the gravity. Thus, the location of the first melt movement is not at the centre, where g equals to zero. In all cases for TL,Fe = 1700 K the melt migration begins for a peak temperature higher than 1425 K, i.e. when the solidus temperature of the silicates is exceeded and both components, iron and silicates, start to migrate at some temperatures which are higher than TL,Si = 1425 K. At the temperature of e.g. 1425 K the melt fraction of iron (with respect to the total amount of iron in a given volume) χFe is equal to about 50%, but the overall melt fraction (with respect to all of the material in a given volume) ϕ is only about 6%. Hence, no extensive melt migration is expected to occur at temperatures below the silicate solidus. For TL,Fe = 1233 K iron melt starts to migrate earlier, at lower temperatures and at higher relative radii than in the respective cases with TL,Fe = 1700 K (cf. Table 9). This is due to the considerably lower liquidus temperature and the associated higher degree of melting and larger partially molten zone causing higher migration velocities of the iron melt.
Formation times and extent of the different reservoirs for planetesimals assuming the liquidus temperature of iron equal to 1700 K (a) and the liquidus temperature of iron equal to 1233 K (b).
 |
Fig. 6 Volume fractions (horizontal axis) of solid iron (black), liquid iron (red), solid silicates (green) and liquid silicates (yellow) as function of the relative radius r/Rp(t) (vertical axis). Plotted data show the internal structures at the time when the core formation is completed, i.e. no more iron separation from a matrix with silicates (in the case P1, for which no core forms, the final structure is shown at 15 Ma). Note also that after iron melt percolates downwards and a core forms, some of the iron recrystallises again with decreasing temperature. From left to right the panels correspond to the cases P1–P4 with TL,Fe = 1700 K and PL1–PL4 with TL,Fe = 1233 K. See Table 9 for further information. |
Depending on the prescribed liquidus temperature of the iron material in planetesimals, we can distinguish between two differentiation scenarios. In the first scenario that corresponds to TL,Fe = 1233 K high iron melt fractions are available at relative low temperatures. Downward movement of the iron melt starts from above the distance halfway from the centre. Molten iron sinks to the centre moving the compacted silicate matrix upwards. Depending on the specific case (cp. PL1–PL4) the iron-silicate separation ends either before silicates start to melt or at almost negligible silicate melt fractions. In the second scenario that corresponds to TL,Fe = 1700 K the fraction of iron magma available to trigger migration is too low until silicates start to melt. In this case both iron and silicate melts migrate simultaneously, assuming migration along separate veins.
Independently on the liquidus temperatures (except case P1, for which no iron core is formed), the first differentiated layer is located about halfway between the centre and the surface. The following final structure develops: a high density core consisting of a mixture of Fe, Ni and FeS with a radius less than about 0.4 times the radius of the planetesimal, a low density silicate mantle of about the same thickness, an undifferentiated but sintered layer and an undifferentiated and unsintered regolith layer at the surface. The larger the planetesimal the thinner is the regolith layer for the chosen cases. Lower iron liquidus temperature results in larger core, thicker mantle and smaller undifferentiated volume (see Table 9). The thickness of the regolith that is controlled by the temperature and the pressure does not change significantly. This layer serves as an insulating blanket that inhibits the heat loss through the surface.
Figure 6 shows the volume fractions of solid (black) and liquid (red) iron and solid (green) and liquid (yellow) silicates as functions of the relative radius for the cases P1–P4 and L1–PL4. The interior structure is depicted at the time when a planetesimal cools below the iron solidus and no further differentiation is possible or at the time t2 when iron melt migration ceases although molten iron is still present. The migration of silicate melt from the silicate matrix exceeds that time but changes the interior structure only minor. The silicate melt is not able to penetrate the upper layers, it freezes at depth before reaching the surface – no basaltic crustal layer can form. Note that sintered and unsintered regions are not indicated in this figure.
Influence of the grain size on the differentiation process.
The duration of the core formation, i.e. the difference Δt = t2 − t1 depends on the assumed core composition and thus on liquidus temperature TL,Fe of the iron component. In the cases PL1–PL4, i.e. for TL,Fe = 1233 K, Δt varies between 0.16 and 0.75 Ma (cp. Table 9 (b)) and stays below 1 Ma. This coincides with the findings of Sahijpal et al. (2007) and estimates of Taylor et al. (1993) and results from the small temperature interval of only 20 K for the melting of iron. In the simulations with the liquidus temperature TL,Fe = 1700 K suggested for H chondrites, the duration of core formation is much longer and Δt varies between 0.4 Ma and 9.96 Ma (cp. Tables 9–11).
Influence of the accretion duration and accretion law on the differentiation process.
Although the metal-silicate separation ends at the time t2, some melt migration still occurs in the partially molten mantle. The density contrast of the molten silicate to the silicate matrix is about 370 kg m-3 and therefore smaller than for the iron melt relative to the solid matrix. For the latter a density contrast between 510 and 2680 kg m-3 is given depending on the composition of the iron melt and of the solid matrix. The silicate-silicate separation is thus less efficient than the metal-silicate separation. Silicate melt rises to the colder upper mantle and solidifies subsequently. The time of the last silicate melt migration inside a pure silicate matrix coincides roughly with the time when the temperature in the mantle falls below the silicate solidus temperature (cp. Tables 9–11). Typically, the silicate-silicate separation exceeds the separation of iron by a factor of two to three and can last up to 20 Ma after CAI formation.
The differentiation of the planetesimals and thus the interior structure depends also strongly on the formation time (Fig. 7). Assuming instantaneous accretion, a formation time simultaneously with the CAIs and an H-chondritic composition, planetesimals larger than about 6 km can be partly differentiated and those larger than 8 km can even form a core. Note that in the region between the dashed and solid line, melt segregation is only minor and a pure iron core cannot be formed. With increasing radius the melt segregation and thus differentiation is more efficient resulting in a larger final core radius. For later formation times, the occurrence of differentiated planetesimal is shifted to larger planetesimals and a formation time of about 3.5 Ma after the CAIs suggests that the planetesimal remains undifferentiated. In Fig. 7 white arrow indicates that differentiation would be more efficient and relative core radii would be larger for early accreting and large bodies. Note that in the most part of the dark grey differentiation field melt fractions surpass 50% and in this region our model most likely underestimates the duration of the core formation.
 |
Fig. 7 The degree of differentiation is shown as a function of the formation time t0 (assuming instantaneous accretion) and the terminal radius D. The light grey area indicates the parameter range for which no melting occurs. This region is separated (dashed line) to the small region where melting occurs but only partial differentiation, i.e. no core forms. The dark grey region indicates the parameter range for which the planetesimals is differentiated into an iron core and silicate mantle. The sizes of the core and the mantle increase with increasing terminal radius and decreasing accretion time (white arrow). |
 |
Fig. 8 Volume fractions (horizontal axis) of solid iron (black), liquid iron (red), solid silicates (green) and liquid silicates (yellow) as functions of the relative radius r/Rp(t) (vertical axis). Plotted data show the internal structures at the time when the core formation is completed, i.e. no more iron separation from a matrix with silicates (case G2 and G3) and for the model without core formation at the time 30 Ma (case G1). Left panel corresponds to the case G1, middle panel to G2 and right panel to G3. |
3.2.3. Variation of the grain size
The relative velocity Δv corresponding to the migration velocity, depends on the assumed grain size of the material (Eq. (25)). To demonstrate the dependence of the efficiency of differentiation on the grain size we compare three cases. In the first case (G1) the grain size b is set to b = 0.01 cm and does not change. In the second case (G2 equivalent to P3) the initial grain size is b = 0.01 cm and the grains grow via Ostwald ripening (our standard approach). In the third case (G3) b is equal to 1 cm and does not change. The considered planetesimal with the terminal radius of D = 70 km forms instantaneously at t0 = 1.79 Ma.
Figure 8 shows the fractions of solid iron (black), liquid iron (red), solid silicates (green) and liquid silicates (yellow) for cases G1, G2 and G3. A straightforward relationship can be identified between the grain size and the efficiency of the differentiation by porous flow. The body with b = 0.01 cm does only partly differentiate. In the centre the iron fraction increases and dominates, whereas the mid-depth layers consist almost entirely of the silicate material. However, no pure iron or silicate layer forms. This is the result of some small scale melt migration which takes more than 10 Ma (see Table 10). Imposing Ostwald ripening on the same initial grain size leads to larger grains during melting and consequently to larger melt migration velocities. Hence, the case G2 differentiates into an iron core, a silicate mantle and a relatively thick (around one fourth of the radius) undifferentiated outer layer. Note that in this case the grains do not grow to 1 cm, as there is not enough melting. The most efficient differentiation is obtained for case G3. Due to large grains and hence high melt migration velocities the body differentiates as in the second case but has a larger core, a thicker mantle and a thinner undifferentiated layer. The onset of the melt migration and the duration of the differentiation also correlates with the grain size. Small grains lead to low velocities and later onset of melt migration. The melt movement proceeds in G1 for over 10 Ma but does not lead to a pure iron core or silicate mantle layer. For G2 the core formation time decreases to 2.95 Ma and for G3 to 1.86 Ma (Table 10).
3.2.4. Effects of the accretion on the differentiation
 |
Fig. 9 Volume fractions (horizontal axis) of solid iron (black), liquid iron (red), solid silicates (green) and liquid silicates (yellow) as functions of the relative radius r/Rp(t) (vertical axis). Plotted data show the internal structures at the time when the core formation is completed, i.e. no more iron separation from a matrix with silicates (L1, L2, L3, R1) and for the models without core formation at the time 20 Ma (R2, R3). From left to right the panels correspond to the cases L1, L2, L3, R1, R2 and R3. See Table 11 for further data. |
The planetesimals investigated in the cases P1–P4 accreted instantaneously. As the accretion dampens the temperatures in a planetesimal compared to the instantaneous formation (see Fig. 4), it will also influence the efficiency of differentiation. For a comparison, we have performed simulations analogous to P3 with non-constant radii. We assume both linear and asymptotical accretion from R0 = 1.2 km to D = 70 km, within 0.2, 0.5 and 1.0 Ma. Those cases are referred to as L1, L2, L3 for linear accretion and R1, R2, R3 for the late runaway accretion, which is represented by the asymptotic law. Apart from the accretion law and varying accretion duration all parameters are identical to those of the case P3 including the iron liquidus temperature of 1700 K.
Any kind of accretion as well as a prolonged accretion duration seems to inhibit the differentiation (see Fig. 9 and Table 11). The radius of the core and the thickness of the mantle decrease with the accretion duration and the inefficiency of differentiation is even more pronounced for the late runaway accretion scenario, where no differentiation took place for taccr ≥ 0.5 Ma.
Compared to the instantaneous accretion (case P3, see Table 9, Figs. 6 and 8) the onset of melt migration is delayed by 0.21 to 5.28 Ma in linearly accreting and asymptotically accreting bodies for the considered parameter values. This correlates with the influence of the accretion on the thermal evolution, i.e. the decrease of the peak temperature with accretion. A relationship between the accretion mode and the duration of the core formation is not that straightforward – although the tendency shows a longer duration of core formation for the accreting planetesimals between 2.78 and 9.96 Ma as compared to 2.95 Ma for an instantaneously accreting body. In fast accreting bodies even shallow layers can melt and prolong the melt migration. Those layers do not melt in slowly accreting bodies and this leads to faster differentiation but smaller cores – if existent at all – of the latter (compare L1, R1 and R2).
3.2.5. Thermal evolution after differentiation
 |
Fig. 10 Temporal evolution of the radial distribution of the temperature and of the non-dimensionalised heat source density Q∗. Upper panel: temperature in the cases P3 (left panel), L1 (middle panel) and R1 (right panel). Lower panel: temperature in the cases PL3 (left panel) and L2 (middle panel) and heat source density in the case PL3 (right panel). |
During the differentiation process the radiogenic heat sources are redistributed in the interior. The iron core becomes enriched in 60Fe and entirely depleted in 26Al while the silicate mantle becomes enriched in 26Al and entirely depleted in 60Fe. Thus, during the early evolution (t < 4 Ma) when the heat production by 26Al is stronger than the heat production by 60Fe (see Fig. 1), a temperature increase from the core towards the silicate mantle, i.e. a super-heated mantle, is possible.
Figure 10 depicts the evolution of the radial temperature distribution and the non-dimensionalised heat source density distribution for a planetesimal with a terminal radius of 70 km but varying accretion duration and accretion law. On the top middle and top right panels the radius increases during 0.2 Ma and on the bottom middle panel during 0.5 Ma after t0 due to the accretion. In the other shown cases the planetesimal accretes instantaneously. After the accretion is completed the radius decreases due to sintering. Simultaneously the heat source density per volume increases (see Fig. 10, bottom right panel). In the early stage the temperature profiles are very flat in the interior with the maximal temperature in the centre and display a steep gradient near the surface. Later, as soon as differentiation begins, the profiles attain their maxima off the centre in the silicate mantle. This is due to the radiogenic heating associated with the migrated 26Al (note the larger concentration of Q∗ for 3 ≲ t ≲ 5 Ma in the region between ≈30 and ≈65 km from the centre compared to the region around the centre on the bottom right panel of Fig. 10). The enrichment of 26Al in the silicate melt leads to the depletion of the lower mantle and enrichment of the middle and upper mantle in 26Al. In most cases the maximal enrichment of the upper layers is attained after several million years, when heating by 26Al is much weaker than the heat production by 60Fe and the effect on the temperature distribution is only minor. Note, though, that we used an upper limit value D26Al = 0.02 for the partition coefficient of 26Al. Adoption of smaller values would enhance the partitioning of 26Al into the silicate melt and most probably influence the distribution of 26Al and the temperature structure in a differentiated planetesimal.
For a late runaway accretion the onset of differentiation in the case R1 is shifted to ≈4 Ma; thus, the heat production rate in the iron core is similar (and later even higher) to that in the silicate mantle. Hence, a super-heated mantle occurs in that case (top right panel) only at about 5 Ma with a relative small temperature difference. Similar to the early purely conductive stage the profile displays a steep gradient towards the surface due to the cooling through the surface. Note that if a body accretes slowly but is large enough to differentiate after t ≈ 4 Ma, the temperature profiles would differ from the above scheme – the maximal temperature remains in the core. This is due to the faster decay of 26Al in comparison to 60Fe, the crossover at which the heat production of 60Fe dominates over 26Al is after 4 Ma relative to the CAIs (see Fig. 1). This scenario is shown on the bottom middle panel of Fig. 10.
In case of a super-heated mantle, the heat flux at the core-mantle boundary would be negative. In the subsequent evolution with the dominance of 60Fe as heat producing element, the temperature peak in the mantle becomes less prominent and moves towards the centre until a monotonous profile is established again (notice the higher value of Q∗ from ≈5 Ma on around the centre on the bottom right panel of Fig. 10). Note that for TL,Fe = 1233 the differentiation is more effective (see Fig. 6 and Table 9 (b)) and the described effects are more pronounced (see Fig. 10, bottom left panel). In such a case, the temperature peak would still move from the mantle to the centre with time, yet it is possible, that the central temperature never reaches the maximum value attained in the mantle.
4. Summary and discussion
In the present study, we examine the thermal evolution and differentiation of accreting planetesimals that do not exceed a degree of melting larger than about 50%. We assume an H-chondritic composition but vary the sulfur concentration in the Fe,Ni-FeS system between sulfur-rich (15.33 wt% FeS) and sulfur-poor (5.1 wt% FeS). We further consider sintering due to hot pressing as well as the heat transport and redistribution of radioactive elements via magma segregation. For the melt transport of molten iron or silicates we assume porous flow by Darcy law and calculate the subsequent separation of iron and silicates resulting in a differentiated planetesimal. The general findings can be summarised as follows:
The heat production by the short-lived radioactive elements 26Al and 60Fe in an initially porous planetesimal that undergoes sintering suffices to achieve melting even in a small body with the radius of ~2 km similar to the findings of previous studies (e.g. Hevey & Sanders 2006; Moskovitz & Gaidos 2011; Henke et al. 2012). The later the onset time of accretion the larger must be the planetesimals for melting to occur. For instantaneously accreting planetesimals and onset times larger than about 3.5 Ma after CAI formation, melt generation and differentiation is unlikely. This threshold time can be even shorter considering non-instantaneous accretion due to lower peak temperatures. Generally, melt generation and the efficiency of differentiation increase with decreasing onset time of accretion relative to CAIs, increasing size of the planetesimal, and decreasing duration of accretion.
The interior structure of the planetesimals that do not experience melting, i.e. small or late accreted bodies, either consists of an entirely porous interior for which the temperatures remain below the pressure dependent threshold temperature for sintering or of a sintered interior and a porous outer shell. The parameter range for the first case are e.g. D ≲ 1 km at t0 ≥ 0 Ma, D ≲ 50 km at t0 ≥ 4 Ma or D ≲ 100 km at t0 ≥ 4.3 Ma. In the latter case, sintering starts in the centre where the material looses porosity and compacts. The temperature distribution in an undifferentiated but sintered planetesimal shows a typical onion-shell thermal structure for which the temperature decreases from the centre toward the surface. The coupling of accretion and sintering, however, leads to an episodic evolution of the temperatures around the centre with at least two heating phases during the first few Ma – an effect that needs to be considered when interpreting the metallographic cooling rates of meteorites. The heating by the long-lived isotopes of U, Th and K becomes significant only after ≈8 Ma after CAIs. These nuclides do not provide an effective heat source because in asteroid-sized bodies their heat generation rate is of the same magnitude as the rate of heat loss through the surface (Yomogida & Matsui 1984).
The interior structure of planetesimals that experience melting and differentiation varies
strongly with the degree of differentiation. For a small degree of differentiation the
structure consists of a layered interior (alternating iron and silicate enriched layers), a
non-differentiated but sintered middle shell and a porous regolith layer. For a high degree
of differentiation an iron core and a silicate mantle can form that are enclosed by an
undifferentiated but sintered layer and an undifferentiated and porous regolith. For the
considered parameter range the outer layer always remains primordial. Similar layered
structures have been also obtained for accreting bodies larger than 500 km (Sramek et al. 2012). It is expected that the upper layer
of the planetesimals considered remains unmelted and thus primordial even when considering
impacts. The impact energy for planetesimals smaller than D ≈ 1000 km is
expected to be too small to produce an outer molten layer (Sramek et al. 2012). Furthermore, for a Vesta-sized body that accretes within 1 Ma
and an impactor velocity of 100 m s-1 the impact heating power is smaller
than 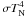 (where
σ is the Stefan-Boltzmann constant) by about three orders of magnitude
(Squyres et al. 1988; Merk et al. 2002). The existence of an unmelted upper layer further
suggests that the maximal possible core radius, which depends on the iron fraction and can
only be obtained for an entirely molten planetesimal, is never reached. In contrast to the
assumption of Hevey & Sanders (2006) that the
parent bodies of differentiated meteorites formed prior to the accretion of the most
chondritic parent bodies, our results indicate that both chondritic meteorites and
differentiated meteorites can originate from one and the same parent body. This finding is
consistent to the results of Weiss et al. (2010) and
Elkins-Tanton et al. (2011), where a differentiated
interior is covered with undifferentiated crust to explain the remanent magnetisation of the
CV meteorite Allende.
(where
σ is the Stefan-Boltzmann constant) by about three orders of magnitude
(Squyres et al. 1988; Merk et al. 2002). The existence of an unmelted upper layer further
suggests that the maximal possible core radius, which depends on the iron fraction and can
only be obtained for an entirely molten planetesimal, is never reached. In contrast to the
assumption of Hevey & Sanders (2006) that the
parent bodies of differentiated meteorites formed prior to the accretion of the most
chondritic parent bodies, our results indicate that both chondritic meteorites and
differentiated meteorites can originate from one and the same parent body. This finding is
consistent to the results of Weiss et al. (2010) and
Elkins-Tanton et al. (2011), where a differentiated
interior is covered with undifferentiated crust to explain the remanent magnetisation of the
CV meteorite Allende.
The redistribution of 26Al (enrichment in the mantle) and of 60Fe (enrichment in the core) as a consequence of melt migration influences the temperature structure. If core formation takes place before about 5 Ma after the CAIs, the temperature profiles show a peak in the mantle and decrease towards the centre and towards the surface. The superheated partially molten mantle heats the cooler partially molten core from above and with time the peak moves to the centre of the body. If a core formes later than about 5 Ma after the CAIs, the heat production by 60Fe dominates and the temperature structure remains unchanged from the onion-like thermal structure with decreasing temperature from the centre toward the surface.
Our findings suggest that the core formation in planetesimals (H chondrites), in which the total degree of melting is less than 50%, is for most cases slower than 2 Ma and can take up to 10 Ma. The iron-silicate differentiation starts only during the melting of silicates. The degree of silicate melting ranges locally between 3% and 42% across the melting zone. Those values are significantly smaller than expected by Taylor et al. (1993), who argued that a minimum silicate melt fraction of 50% is required for core formation. Our obtained duration times for core formation are also longer in comparison to models (labelled A) by Sahijpal et al. (2007). For these models the authors assumed a high content of FeS, i.e. the core formation takes place prior to silicate melting at temperatures below ≈1425 K, and a constant percolation velocity of 30–300 m a-1, which is at least two orders of magnitude higher than obtained in our study. The segregation time of silicate melt exceeds in most cases the segregation of iron melt by a factor of 2 to 3 and silicate melt migration can last up to 20 Ma after CAI formation. Kleine et al. (2002) concludes from the Hf-W chronometry that silicate-iron separation in the asteroid (4) Vesta must have taken place at 4.2 ± 1.3 Ma after CAI formation. Combining this with the result from Horan et al. (1998), who pointed out that metal segregation in all of the iron meteorite parent bodies took place within 5 Ma of each other, we arrive at a possible upper bound of ≈10 Ma after the formation of the CAIs for the core formation in H-chondritic planetesimals. In almost all of our models (except L3) core formation ends before 10 Ma (cp. Tables 9–11) consistent with these findings.
The heat transport by melt dampens the heating in a planetesimal by about a few tens to hundred K (cp. Fig. 5). The efficiency of this heat transport depends on the amount of melting, and is proportional to the permeability of the matrix, the density difference between melt and matrix and the gravity (size of the planetesimal) and inversely proportional to the viscosity of the melt. Melt migration starts and is most efficient at about half radius of the planetesimal as a consequence of an increase in the Darcy velocity with gravity g (radius). Thus, in the most cases the first pure silicate layer is located around the half radius and the differentiation continues downwards.
Silicate melt is not able to reach the surface via porous flow as the melt freezes on its way to the surface, consistent to Elkins-Tanton et al. (2011) who argue that buoyancy alone does not suffice to cause silicate eruption in small bodies with cool crusts. The migration velocities obtained in our model calculation are not high enough to prevent freezing in the narrow interconnected pores. This finding is in contrast to Moskovitz & Gaidos (2011), who argue that melt can rise toward the surface via porous flow and form a basaltic crust. However, these authors assume that the heat loss due to conduction is negligible relative to heating and melt migration. Furthermore, they do not consider the change of gravity with depth and assume a constant density contrast between melt and matrix, thereby overestimating the migration velocities.
Eruptive magma transport requires most likely fractures and dykes and is possibly not very common for small bodies. This may also explain why there are in addition to Vesta only two other meteorites, i.e. 1459 Magnya and 1904 Massevitch, with a radius larger than 8 km that show spectroscopically basaltic surfaces. Eruptive magma transport is for instance possible if the heating of gas and production of silicate partial melts with substantially lower density than the matrix causes volume expansion and hence excess pressures in the mixtures of gas and melt (Muenow et al. 1992). These pressures may cause the formation of fractures and dikes. The dikes would provide an additional mechanism for the melt migration and enhance the transport of the melt to the surface. For high content of volatiles this may result in pyroclastical eruptions and loss of melt into the space (Taylor et al. 1993). The consequence is a more efficient cooling of the interior and possibly less efficient core formation.
The used Darcy law for porous flow Eq. (25) simplifies the flow in a partially molten system and is valid if the pressure difference between the solid matrix and the melt and the surface tension force due to interface curvature either balance each other or are both zero (Bercovici et al. 2001). Models by two-phase flow consider these contributions to the melt velocity (e.g. Bercovici et al. 2001). Such a model is presented in Sramek et al. (2012) for planetesimals with a size of 500 km and larger. To validate our model approach we compared the evolution and differentiation of one of the bodies presented in Sramek et al. (2012). For this comparison we deactivated the porosity dependence, the sintering and the grain growth via Ostwald ripening in our model – these effects have been neglected by Sramek et al. (2012) – and used the same parameters as Sramek et al. (2012). We compared the differentiation for a body with the initial radius of 5 km that accreted linearly to 500 km within 3 Ma (cf. Fig. 8 in Sramek et al. 2012) and obtained almost identical internal structures at respective times. This comparison makes us confident that the simplified approach via the Darcy law can be used for the differentiation of planetesimals.
In the present approach we consider for simplicity that iron and silicate melt segregate along separate networks. Consideration of a mix of both melts in a single vein would necessitate a theory of a simultaneous interactions between the melts themselves and between the single melts and the matrix. One can expect that a higher density contrast between the molten iron and the molten silicates would act towards faster separation. However, opposite movement directions may slow down the separation.
We have further tested the results assuming that a threshold melt fraction is required for an interconnected network to exist. For a threshold fraction of less than 5 vol.%, the results are unaffected whereas for larger threshold melt fractions the onset time for core formation is overestimated in our models.
During the melting changes in the geometry of the matrix may occur, e.g. by the coalescence
of small veins into larger ones (Wilson et al. 2008).
This would necessitate adjustments of the Darcy exponent n and the Darcy
coefficient τ that control the permeability. Due to the lack of theory we
keep in the present study both parameters constant assuming
(n,τ) = (2,1600) (von Bargen & Waff 1986). The permeability and hence the percolation
velocity is inversely proportional to τ. Assuming a fixed value of
n, increasing τ would inhibit and decreasing
τ would catalyse the migration velocities. Similarly, increasing Darcy
exponent n for a fixed value of τ would yield a smaller
ϕn and decreasing n a larger
ϕn (as ϕ ≤ 1), inhibiting
and catalysing the migration velocities, respectively. If n and
τ change both then the velocities are influenced by the ratio
ϕn/τ. As
it has been pointed out in Sect. 2.3 a variety of
values has been derived for both n and τ, e.g.
(n,τ) = (2,1600) (von Bargen & Waff 1986), (n,τ) = (3,200)
(Wark & Watson 1998). Assuming two pairs
(n1,τ1) (case 1)
and (n2,τ2) (case
2) and the identity 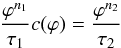 (38)we
obtain
(38)we
obtain 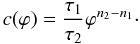 (39)The permeabilities
and hence the velocities in both cases will be equal for a critical melt fraction
ϕ0 if c(ϕ0) = 1,
i.e. if
(39)The permeabilities
and hence the velocities in both cases will be equal for a critical melt fraction
ϕ0 if c(ϕ0) = 1,
i.e. if 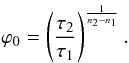 (40)If the melt fraction is
below ϕ0, then case 1 would yield a higher velocity than case 2
and for melt fractions above ϕ0 velocity from case 2 is higher
than in case 1 by the factor c(ϕ). For the two afore
mentioned parameter pairs the critical melt fraction ϕ0 is equal
to 12.5 vol% and c(ϕ) = 8ϕ. Hence, for 1
vol% melting the velocities for (n,τ) = (2,1600) are
higher than for (n,τ) = (3,200) by a factor of 12.5 and
for 50 vol% melting the case (3,200) yields higher velocities than the case
(2,1600) by the factor of 4. Although the exact timing of melt
segregation might slightly differ with known variations of n and
τ from the literature (e.g. von Bargen
& Waff 1986; Wark & Watson
1998; Cheadle et al. 2004; Connolly et al. 2009), the general findings of our model
are robust.
(40)If the melt fraction is
below ϕ0, then case 1 would yield a higher velocity than case 2
and for melt fractions above ϕ0 velocity from case 2 is higher
than in case 1 by the factor c(ϕ). For the two afore
mentioned parameter pairs the critical melt fraction ϕ0 is equal
to 12.5 vol% and c(ϕ) = 8ϕ. Hence, for 1
vol% melting the velocities for (n,τ) = (2,1600) are
higher than for (n,τ) = (3,200) by a factor of 12.5 and
for 50 vol% melting the case (3,200) yields higher velocities than the case
(2,1600) by the factor of 4. Although the exact timing of melt
segregation might slightly differ with known variations of n and
τ from the literature (e.g. von Bargen
& Waff 1986; Wark & Watson
1998; Cheadle et al. 2004; Connolly et al. 2009), the general findings of our model
are robust.
In our model the viscosity of both the silicate and the iron melt is chosen to be 1 Pa s, similar to e.g. Sramek et al. (2012), although smaller viscosities for the iron melt (ηFe = 0.015 Pa s) have been suggested (de Wijs et al. 1998). We have tested the influence of a variation in the iron melt viscosity. With ηFe = 0.015 Pa s the onset of the differentiation is shifted to slightly earlier times, yet the duration of core formation remains similar. The adoption of ηSi = 1 Pa s is reasonable as the viscosities of basaltic melts derived from chondritic precursors (the latter having silica contents of less than 50% according to Mittlefehldt et al. 1998) range from 1 to 100 Pa s (Giordano et al. 2008).
For the proposed differentiation scenarios in this study the melt content is always smaller than about 50%. It is, however, possible that the planetesimals experience more melting in particular if they accrete very early with respect to the CAIs. In that case the process of gravitational settling of molten spherules of metal through a mixture of silicate melt and matrix could contribute to the core formation (Stevenson 1990; Taylor 1992). Globules of molten metal and sulfide could form and sink through the matrix at a velocity given by Stoke’s law. At that stage of the thermal evolution the silicate-iron separation might be rather rapid. The influence of a strongly molten interior on the thermo-chemical evolution of planetesimals will be examined in a following study.
Acknowledgments
We thank the reviewer Y. Ricard for the constructive and helpful comments on the paper. This work was supported by the Deutsche Forschungsgemeinschaft (DFG) Priority Programme 1385 “The First 10 Million Years of the Solar System – a Planetary Materials Approach” and by the Helmholtz Association through the research alliance “Planetary Evolution and Life”.
References
- Al-Homadhi, E. S. 2001, J. King Saud Univ., 14, 95 [Google Scholar]
- Audi, G., Bersillon, O., Blachot, J., & Wapstra, A. H. 2003, Nucl. Phys. A, 729, 3 [NASA ADS] [CrossRef] [Google Scholar]
- Beardsmore, G. R., & Cull, J. P. 2001, Crustal heat flow: a guide to measurement and modelling (Cambridge University Press) [Google Scholar]
- Beere, W. 1975, Acta Metal., 23, 131 [CrossRef] [Google Scholar]
- Bennett, M. E. I., & McSween Jr., H. Y. 1996, Meteor. Planet. Sci., 31, 783 [Google Scholar]
- Bercovici, D., Ricard, Y., & Schubert, G. 2001, J. Geophys. Res., 106, 8887 [NASA ADS] [CrossRef] [Google Scholar]
- Best, M. G. 2002, Igneous and Metamorphic Petrology, 2nd edn. (Wiley-Blackwell) [Google Scholar]
- Bizzarro, M., Baker, J. A., & Haack, H. 2004, Nature, 431, 275 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Bizzarro, M., Baker, J. A., Haack, H., & Lundgaard, K. L. 2005, ApJ, 632, L41 [NASA ADS] [CrossRef] [Google Scholar]
- Britt, D., & Consolmagno, S. 2003, Meteorit. Planet. Sci., 38, 1161 [NASA ADS] [CrossRef] [Google Scholar]
- Byerley, J. J., & Takebe, N. 1970, Metall. Mater. Trans. B, 2, 1107 [NASA ADS] [CrossRef] [Google Scholar]
- Cheadle, M. J., Elliott, M. T., & McKenzie, D. 2004, Geology, 32, 757 [NASA ADS] [CrossRef] [Google Scholar]
- Chilingarian, G. V., & Wolf, K. H. 1976, Compaction of Coarse-grained Sediments II, Development in Sedimentology, 18B (Elsevier Scientific Publishing Company) [Google Scholar]
- Connolly, J., Schmidt, M., Solferino, G., & Bagdassarov, N. 2009, Nature, 462, 209 [NASA ADS] [CrossRef] [Google Scholar]
- de Wijs, G. A., Kresse, G., Vocadlo, L., et al. 1998, Nature, 392, 805 [NASA ADS] [CrossRef] [Google Scholar]
- Elkins-Tanton, L. T., Weiss, B. P., & Zuber, M. T. 2011, Earth Planet. Sci. Lett., 305, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Encrenaz, T., Bibring, J.-P., & Blanc, M. 1987, The Solar System (Berlin: Springer) [Google Scholar]
- Fountain, J. A., & West, E. A. 1970, J. Geophys. Res., 75, 4063 [NASA ADS] [CrossRef] [Google Scholar]
- Ghosh, A., & McSween Jr., H. 1998, Icarus, 134, 187 [NASA ADS] [CrossRef] [Google Scholar]
- Ghosh, A., & McSween Jr., H. 1999, Meteorit. Planet. Sci., 34, 121 [NASA ADS] [CrossRef] [Google Scholar]
- Ghosh, A., Weidenschilling, S., & McSween Jr., H. 2003, Meteorit. Planet. Sci., 38, 711 [NASA ADS] [CrossRef] [Google Scholar]
- Giordano, D., Russell, J. K., & Dingwell, D. B. 2008, Earth Planet. Sci. Lett., 271, 123 [NASA ADS] [CrossRef] [Google Scholar]
- Greenwood, G. W. 1969, in The Mechanism of Phase Transformations in Crystalline Solids, Monograph and Report Series, No. 33 (London, UK: Institute of Metals, University of Manchester), 103 [Google Scholar]
- Grimm, R. E., & McSween Jr., H. Y. 1993, Icarus, 82, 244 [Google Scholar]
- Haack, H., & McCloy, T. J. 2003, in Treatise on Geochemistry, ed. A. W. Davis (Oxford: Elsevier, Pergamon), 1 [Google Scholar]
- Henke, S., Gail, H.-P., Trieloff, M., Schwarz, W. H., & Kleine, T. 2012, A&A, 537, A45 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hevey, P., & Sanders, I. 2006, Meteorit. Planet. Sci., 41, 95 [Google Scholar]
- Hewins, M. F., & Newsom, H. E. 1988, in Meteorites and the early Solar system, eds. J. F. Kerridge, & M. S. Matthews (Tucson, Arizona: The University of Arizona Press) [Google Scholar]
- Horan, M. F., Smoliar, M. I., & Walker, R. J. 1998, Geochim. Cosmochim. Acta, 62, 545 [NASA ADS] [CrossRef] [Google Scholar]
- Kakar, A. K., & Chaklader, A. C. D. 1967, J. Appl. Phys., 38, 3223 [NASA ADS] [CrossRef] [Google Scholar]
- Kaula, W. M. 1998, Formation of the terrestrial planets in Planetary Systems, the Long View, eds. L. M. Celnikier, & J. Tran Thanh Van (Paris: Edition Frontieres) [Google Scholar]
- Keil, K. 1962, J. Geophys. Res., 67, 4055 [NASA ADS] [CrossRef] [Google Scholar]
- Keil, K., Stoeffler, D., Love, S. G., & Scott, E. R. D. 1997, Meteoritics, 32, 349 [NASA ADS] [CrossRef] [Google Scholar]
- Kennedy, A., Lofgren, G., & Wasserburg, G. 1993, Earth Planet. Sci. Lett., 115, 177 [NASA ADS] [CrossRef] [Google Scholar]
- Kleine, T., Munker, C., Mezger, K., & Palme, H. 2002, Nature, 418, 952 [NASA ADS] [CrossRef] [Google Scholar]
- Kortenkamp, S. J., Kokubo, E., & Weidenschilling, S. 2000, in Origin of the Earth and Moon, eds. R. M. Canup, & K. Righter (Tucson, Arizona: The University of Arizona Press) [Google Scholar]
- Krause, M., Henke, S., Gail, H.-P., et al. 2011, Lunar Planet. Sci. Conf. Lett., 42, 2696 [NASA ADS] [Google Scholar]
- Kullerud, G. 1963, Ann. Rep. Geophys. Lab., 1412, 175 [Google Scholar]
- Kurat, G., Varela, M. E., Brandstaetter, F., et al. 2004, Geochim. Cosmochim. Acta, 68, 1901 [NASA ADS] [CrossRef] [Google Scholar]
- Larimer, J. W. 1995, Meteoritics, 30, 533 [NASA ADS] [Google Scholar]
- Lee, T., Papanastassiou, D., & Wasserburg, G. 1976, Geophys. Res. Lett., 3, 41 [NASA ADS] [CrossRef] [Google Scholar]
- Lide, D. R. 2004, CRC handbook of chemistry and physics: a ready-reference book of chemical and physical data, ed. D. R. Lide (Boca Raton: CRC Press) [Google Scholar]
- MacPherson, G., Davis, A., & Zinner, E. 1995, Meteorit. Planet. Sci., 30, 365 [Google Scholar]
- Marsh, C. A., Della-Giustina, D. N., Giacalone, J., & Lauretta, D. S. 2006, in 37th Annual Lunar and Planetary Science Conference, 2078 [Google Scholar]
- McCoy, T. J., Keil, K., Muenow, D. W., & Wilson, L. 1997, Geochim. Cosmochim. Acta, 61, 639 [NASA ADS] [CrossRef] [Google Scholar]
- McKenzie, D. 1984, J. Petrol., 25, 713 [NASA ADS] [CrossRef] [Google Scholar]
- McKenzie, D. 1985, Earth Planet. Sci. Lett., 74, 81 [NASA ADS] [CrossRef] [Google Scholar]
- Merk, R., Breuer, D., & Spohn, T. 2002, Icarus, 159, 183 [NASA ADS] [CrossRef] [Google Scholar]
- Mittlefehldt, D. W. 2003, in Treatise on Geochemistry, ed. A. W. Davis (Oxford: Elsevier, Pergamon), 1 [Google Scholar]
- Mittlefehldt, D., McCoy, T., Goodrich, C., & Kracher, A. 1998, Rev. Mineral. Planet. Mater., 36, 4.01 [Google Scholar]
- Miyamoto, M., Fujii, N., & Takeda, H. 1981, Proc. Lunar Planet. Sci. Conf., 12B, 1145 [NASA ADS] [Google Scholar]
- Moore, W. B. 2001, Icarus, 154, 548 [NASA ADS] [CrossRef] [Google Scholar]
- Moskovitz, N., & Gaidos, E. 2011, Meteorit. Planet. Sci., 46, 903 [Google Scholar]
- Mostefaoui, S., Lugmair, G. W., & Hoppe, P. 2005, ApJ, 625, 271 [NASA ADS] [CrossRef] [Google Scholar]
- Muenow, D. W., Keil, K., & Wilson, L. 1992, Geochim. Cosmochim. Acta, 56, 4267 [NASA ADS] [CrossRef] [Google Scholar]
- Nagamori, M. 1969, Trans. Metall. Soc. AIME, 245, 1897 [Google Scholar]
- Pack, A., & Palme, H. 2003, Meteorit. Planet. Sci., 38, 1263 [NASA ADS] [CrossRef] [Google Scholar]
- Rao, A. S., & Chaklader, A. C. D. 1972, J. Am. Ceram. Soc., 55, 596 [CrossRef] [Google Scholar]
- Righter, K., & Drake, M. J. 1997, Meteorit. Planet. Sci., 32, 929 [Google Scholar]
- Rubie, D. C., Nimmo, F., & Melosh, H. J. 2007, in Treatise on Geophysics: The Core, Chap. 9, ed. D. J. Stevenson (Elsevier) [Google Scholar]
- Rugel, G., Faestermann, T., Knie, K., et al. 2009, Phys. Rev. Lett., 103, 072502 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Sahijpal, S., & Soni, P. 2005, Lun. Planet. Sci. Conf. Lett., 36, 1296 [NASA ADS] [Google Scholar]
- Sahijpal, S., Ivanova, M. A., Kashkarov, L. L., et al. 1995, Earth Planet. Sci. Lett., 104, 555 [Google Scholar]
- Sahijpal, S., Soni, P., & Gupta, G. 2007, Meteorit. Planet. Sci., 42, 1529 [Google Scholar]
- Schwenn, M. B., & Goetze, C. 1978, Tectonophysics, 48, 41 [NASA ADS] [CrossRef] [Google Scholar]
- Sonnett, C. P., Colburn, D. S., & Schwartz, K. 1968, Nature, 219, 924 [NASA ADS] [CrossRef] [Google Scholar]
- Squyres, S. W., Reynolds, R. T., & Summers, A. L. 1988, J. Geophys. Res., 93, 87798794 [NASA ADS] [CrossRef] [Google Scholar]
- Sramek, O., Milelli, L., Ricard, Y., & Labrosse, S. 2012, Icarus, 217, 339 [NASA ADS] [CrossRef] [Google Scholar]
- Srinivasan, G., Goswami, J. N., & Bhandari, N. 1999, Science, 284, 1348 [NASA ADS] [CrossRef] [Google Scholar]
- Stevenson, D. J. 1990, in Origin of the Earth, eds., eds. H. E. Newsom, & J. H. Jones (New York: Oxford Univ. Press) [Google Scholar]
- Stevenson, D. J., & Scott, D. R. 1991, Ann. Rev. Fluid Mech., 23, 305 [NASA ADS] [CrossRef] [Google Scholar]
- Stolper, E. 1977, Geochim. Cosmochim. Acta, 41, 587 [NASA ADS] [CrossRef] [Google Scholar]
- Tachibana, S., & Huss, G. R. 2003, ApJ, 588, L41 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- Takahashi, E. 1983, in National Institute of Polar Research, Memoirs, Special Issue, ISSN 0386-0744, No. 30 [Google Scholar]
- Taylor, G. 1992, J. Geophys. Res., 97, 14717 [NASA ADS] [CrossRef] [Google Scholar]
- Taylor, G. J., Keil, K., McCoy, T., Haack, H., & Scott, E. R. D. 1993, Meteoritics, 28, 34 [NASA ADS] [CrossRef] [Google Scholar]
- Terasaki, H., Frost, D. J., Rubie, D. C., & Langenhorst, F. 2008, Earth Planet. Sci. Lett., 273, 132 [NASA ADS] [CrossRef] [Google Scholar]
- Urey, H. 1955, Proc. Natl. Acad. Sci., 41, 127 [Google Scholar]
- von Bargen, N., & Waff, H. S. 1986, J. Geophys. Res., 91, 9261 [NASA ADS] [CrossRef] [Google Scholar]
- Waff, H. S., & Bulau, J. R. 1979, J. Geophys. Res., 84, 6109 [NASA ADS] [CrossRef] [Google Scholar]
- Walker, D., & Agee, C. B. 1988, Meteoritics, 23, 81 [NASA ADS] [CrossRef] [Google Scholar]
- Wark, D. A., & Watson, E. B. 1998, Earth Planet. Sci. Lett., 164, 591 [NASA ADS] [CrossRef] [Google Scholar]
- Weidenschilling, S. J. 1988, in Meteorites and the Early Solar System, eds. J. F. Kerridge, & M. S. Matthews (Tucson: University of Arizona Press) [Google Scholar]
- Weiss, B., Berdahl, J., Elkins-Tanton, L., et al. 2008, Science, 332, 713 [NASA ADS] [CrossRef] [Google Scholar]
- Weiss, B. P., Gattacceca, J., Stanley, S., Rochette, P., & Christensen, U. R. 2010, Space Sci. Rev., 152, 341 [NASA ADS] [CrossRef] [Google Scholar]
- Wetherill, G. W., & Stewart, G. R. 1989, Icarus, 77, 330 [NASA ADS] [CrossRef] [Google Scholar]
- Wilson, L., Goodrich, C. A., & Van Orman, J. A. 2008, Geochim. Cosmochim. Acta, 72, 6154 [NASA ADS] [CrossRef] [Google Scholar]
- Wilthan, B. 2002, Master’s Thesis, Tecnical University Graz [Google Scholar]
- Yomogida, K., & Matsui, T. 1983, J. Geophys. Res., 88, 9513 [Google Scholar]
- Yomogida, K., & Matsui, T. 1984, Earth Planet. Sci. Lett., 68, 34 [NASA ADS] [CrossRef] [Google Scholar]
- Yoshino, T., Walter, M. J., & Kasura, T. 2003, Nature, 422, 154 [NASA ADS] [CrossRef] [Google Scholar]
All Tables
Formation times and extent of the different reservoirs for planetesimals assuming the liquidus temperature of iron equal to 1700 K (a) and the liquidus temperature of iron equal to 1233 K (b).
Influence of the accretion duration and accretion law on the differentiation process.
All Figures
 |
Fig. 1 Heat generation by the short-lived radionuclides 26Al and 60Fe as a function of time relative to CAI formation. The data are taken from Table 6. |
| In the text | |
 |
Fig. 2 The volume filling factor as a function of time and radius of the planetesimal. Left panel: an instantaneously accreted body with the terminal radius D = 10 km (Rp(t0) = 11.9 km) and the accretion time t0 = 1.61 Ma. Right panel: an asymptotically accreted body with the initial radius R0 = 1.2 km, the terminal radius D = 10 km (Rp(t0 + taccr) = 11.9 km), the onset time of accretion t0 = 1.61 Ma and the accretion duration taccr = 0.5 Ma. |
| In the text | |
 |
Fig. 3 Porosity φ as a function of radius for bodies that accrete at t0 = 1.44 from Rp(t0) = 1.2 km to Rp(t0 + taccr) = 11.9 km with the initial porosity of φ = 0.4 (D = 10 km). Left panel: linear accretion with varying accretion duration taccr. Right panel: varying accretion law with fixed accretion duration taccr = 1.0 Ma. |
| In the text | |
 |
Fig. 4 Effects of the porosity, accretion law and accretion duration on the evolution of the central temperature. Left panel: planetesimal with the terminal radius D = 1 km that accretes instantaneously at t0 = 0 Ma and φ equal to either zero (solid line), or 0.4 (dashed line). In the subplot of the left panel: instantaneously accreting planetesimal with D = 100 km and t0 = 2.51 Ma. Middle panel: linear accretion from R0 = 1.2 km to D = 10 km at t0 = 1.44 Ma with varying accretion duration taccr. Right panel: non-instantaneous accretion within 1 Ma with t0 = 1.44 Ma, R0 = 1.2 km and D = 10 km in comparison to an instantaneously accreting planetesimal assuming the same parameters (solid line). |
| In the text | |
 |
Fig. 5 The evolution of the central temperature (left panel) and the radial temperature distribution at the instance of the maximum temperature (right panel) in a body that accreted instantaneously to D = 35 km at t0 = 1.6 Ma. Consideration of both the heat transport by melt and the redistribution of radioactive elements (solid line), consideration of the heat transport by melt and neglection of the redistribution of radioactive elements (dashed line), consideration of the redistribution of radioactive elements and neglection of the heat transport by melt (dot-dashed line), neglection of both the heat transport by melt and the redistribution of radioactive elements (dotted line). |
| In the text | |
 |
Fig. 6 Volume fractions (horizontal axis) of solid iron (black), liquid iron (red), solid silicates (green) and liquid silicates (yellow) as function of the relative radius r/Rp(t) (vertical axis). Plotted data show the internal structures at the time when the core formation is completed, i.e. no more iron separation from a matrix with silicates (in the case P1, for which no core forms, the final structure is shown at 15 Ma). Note also that after iron melt percolates downwards and a core forms, some of the iron recrystallises again with decreasing temperature. From left to right the panels correspond to the cases P1–P4 with TL,Fe = 1700 K and PL1–PL4 with TL,Fe = 1233 K. See Table 9 for further information. |
| In the text | |
 |
Fig. 7 The degree of differentiation is shown as a function of the formation time t0 (assuming instantaneous accretion) and the terminal radius D. The light grey area indicates the parameter range for which no melting occurs. This region is separated (dashed line) to the small region where melting occurs but only partial differentiation, i.e. no core forms. The dark grey region indicates the parameter range for which the planetesimals is differentiated into an iron core and silicate mantle. The sizes of the core and the mantle increase with increasing terminal radius and decreasing accretion time (white arrow). |
| In the text | |
 |
Fig. 8 Volume fractions (horizontal axis) of solid iron (black), liquid iron (red), solid silicates (green) and liquid silicates (yellow) as functions of the relative radius r/Rp(t) (vertical axis). Plotted data show the internal structures at the time when the core formation is completed, i.e. no more iron separation from a matrix with silicates (case G2 and G3) and for the model without core formation at the time 30 Ma (case G1). Left panel corresponds to the case G1, middle panel to G2 and right panel to G3. |
| In the text | |
 |
Fig. 9 Volume fractions (horizontal axis) of solid iron (black), liquid iron (red), solid silicates (green) and liquid silicates (yellow) as functions of the relative radius r/Rp(t) (vertical axis). Plotted data show the internal structures at the time when the core formation is completed, i.e. no more iron separation from a matrix with silicates (L1, L2, L3, R1) and for the models without core formation at the time 20 Ma (R2, R3). From left to right the panels correspond to the cases L1, L2, L3, R1, R2 and R3. See Table 11 for further data. |
| In the text | |
 |
Fig. 10 Temporal evolution of the radial distribution of the temperature and of the non-dimensionalised heat source density Q∗. Upper panel: temperature in the cases P3 (left panel), L1 (middle panel) and R1 (right panel). Lower panel: temperature in the cases PL3 (left panel) and L2 (middle panel) and heat source density in the case PL3 (right panel). |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


