| Issue |
A&A
Volume 543, July 2012
|
|
|---|---|---|
| Article Number | A36 | |
| Number of page(s) | 13 | |
| Section | Interstellar and circumstellar matter | |
| DOI | https://doi.org/10.1051/0004-6361/201218965 | |
| Published online | 25 June 2012 | |
An extension of the DUSTY radiative transfer code and an application to OH 26.5 and TT Cygni⋆
Koninklijke Sterrenwacht van België, Ringlaan 3, 1180 Brussel, Belgium
e-mail: marting@oma.be
Received: 6 February 2012
Accepted: 2 May 2012
For the best-studied nearby Galactic asymptotic giant branch (AGB) stars a wealth of observational data is typically available in the form of photometry, often extending into the sub-mm, spectra covering a wide wavelength range, and often also visibility curves. Almost 100 AGB stars and red super giants have been imaged as part of the MESS Herschel guaranteed time key program. This does not only add photometry points between 60 and 500 micron, but also intensity profiles at these wavelengths. Dust radiative transfer models are often used to analyse these types of datasets, but there are very many input parameters and therefore it is not straightforward how to derive a best fit. In order to facilitate this, the publicly available one-dimensional (1D) dust radiative transfer code DUSTY was modified and extended, and included as a subroutine in a minimazation code. The code allows a certain parameter set (typically luminosity, dust optical depth, dust temperature at the inner radius and slope of the density law) to be minimised against photometric and spectroscopic data, visibility curves and 1D intensity profiles as constraints. The code is described and first results are presented on the MESS targets OH 26.5 and TT Cyg. For OH26.5 previous findings regarding a two-component wind are confirmed, but with a smaller drop in mass loss (a factor of 5) than previously suggested. For TT Cyg it proved difficult to fit the Herschel intensity profiles and spectral energy distribution simultaneously. The best fits are obtained for density profiles that deviate strongly from r-2 and are more like r + 3 − + 3.5. This is qualitatively consistent with hydrodynamical models that simulate the interaction of the stellar wind with the interstellar medium.
Key words: stars: AGB and post-AGB / circumstellar matter / stars: individual: OH 26.5 / stars: individual: TT Cyg
Appendices are available in electronic form at http://www.aanda.org
© ESO, 2012
1. Introduction
Mass loss is the dominating factor in the post-main sequence evolution of almost all stars. For low and intermediate mass stars (initial mass ≲8 M⊙) this takes place mainly on the thermally pulsing asymptotic giant branch (AGB) in a slow (typically 5–25 km s-1) dust-driven wind with high mass-loss rates (up to 10-4 M⊙ yr-1, see the contributions in the book edited by Habing & Olofsson 2003).
Information on the dust formation and mass-loss process is encoded in various observables, e.g. the spectral energy distribution (SED) that is sensitive to the density distribution of the dust in the circumstellar envelope (CSE) and the dust optical depth and spectra, especially in the 10–30 μm region, which contain information on the type of dust that is present, high-angular resolution data that probe the inner part of the dust shell, and intensity profiles that are sensitive to the density distribution.
Over the past 25 years, numerous studies have used dust radiative transfer (RT) models to infer properties of the dust, the dust formation process and mass-loss rates typically from SEDs and near infrared (NIR) spectra. Examples of these studies that considered samples of stars are Rowan-Robinson & Harris (1983a,b), Schutte & Tielens (1989), Chan & Kwok (1990), Justtanont & Tielens (1992), Groenewegen (1995), Le Bertre (1997), Groenewegen et al. (1998), and Lorenz-Martins et al. (2001) for Galactic stars, and van Loon et al. (1999), and Groenewegen et al. (2007, 2009) for samples in the Magellanic Clouds.
Interferometric data for larger samples of AGB stars have been obtained since the 1980s, e.g. Dyck et al. (1984), Danchi et al. (1994), Sudol et al. (1999), Monnier et al. (2004). In some cases these were combined with relatively simple RT modelling to interpret these data. On the other hand, large datasets of interferometric data were obtained for a few well-known stars, e.g. OH 26.5, AFGL 3116, o Cet, or most notably, CW Leo (see the analysis in Groenewegen 1997; Men’shchikov et al. 2001, 2002), and, as a very recent example, R Scl (Sacuto et al. 2011).
Intensity profiles have not been used much as constraints (except when derived from visibility measurements) probably because the angular resolution with direct imaging was not sufficient. However, in the FIR and sub-mm where the dust shells should be the most extended and with sufficient sensitivity and spatial resolution it should be possible to resolve the shell. A recent example is Ladjal et al. (2010), who used the LABOCA bolometer array at 870 μm (with a full width at half maximum – FWHM – beam size of about 20′′) to map the CSE of a few AGB stars and resolved the shells around CW Leo, π Gru, WX Psc and o Cet. Even more can be expected from the PACS (Poglitsch et al. 2010) instrument on board Herschel (Pilbratt et al. 2010) with FWHM beam sizes of 5.6, 6.8 and 11.4′′ (at 60, 110, 170 μm), and to a lesser extent SPIRE (Griffin et al. 2010) with FWHM beam sizes of 18, 25, 36′′ (at 250, 350, 550 μm).
With the increasing availability of several kinds of datasets and the number of parameters that are involved in the RT modelling, there is a need to obtain a best fit by a minimisation procedure and also to obtain a quantitative measure of the goodness of a fit.
With this objective in mind, the publicly available one-dimensional (1D) dust RT model DUSTY was adapted to suit this need. The modified code determines a set of parameters (typically luminosity, dust optical depth, and temperature at the inner dust radius) by minimising a χ2. Constraints can be photometry, spectra, visibility data, and intensity curves.
Section 2 describes the modifications to the DUSTY code. Section 3 describes the results of the RT modelling for two stars. Section 4 concludes this paper. In the appendices technical details on the modification of DUSTY are described, and additional models for OH 26.5 and TT Cyg are presented.
2. The model: a modified version of DUSTY
2.1. Modifications to DUSTY
DUSTY is a publicly available1 1D dust RT code (Ivezić et al. 1999) that is widely used in astronomy. The mathematical formulation was described in Ivezić & Elitzur (1997) and DUSTY is its implementation.
First the high-level modifications and extensions that were made to DUSTY are described; additional technical details are given in Appendix A. The modified code, including the minimisation part described below, will be referred to as MoD (More of DUSTY). The core of MoD is DUSTY version 2.01, and the changes described below and in the appendix are w.r.t. that version. MoD has already been used in fitting the SEDs of AGB stars in the Large Magellanic Cloud (Gullieuszik et al. 2012) and in investigating possible mass loss in nearby RGB stars (Groenewegen 2012).
-
In DUSTY it is possible to calculate in-tensity profiles. From an observational point, however,one would prefer intensity profiles convolved with thebeam of the instrument/telescope. Indeed, this optionwas already present in DUSTY, but not described in theDUSTY user manual. The calculation re-quires parameters for the convolution (described belowwhen discussing the input to the code), but also the angulardiameter of the inner dust shell. In DUSTY thisnumber was simply an input parameter, independent ofany observational parameter (luminosity, effective tem-perature, dust condensation temperature, which basicallyset this value) because DUSTY is scale-freeand hence does not require the luminosity as input. InMoD the angular diameter of the inner dustshell must be calculated self-consistently. To achieve this, thecall to the subroutines that calculate the convolved intensityprofiles (and visibilities as well) had to be moved to a differentlocation in DUSTY.
-
A more general form of the piecewise power law (density type = 1) for the density structure η was implemented in DUSTY,
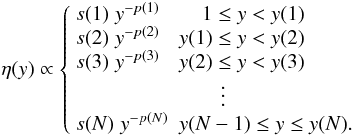 (1)With this density structure it is possible to model sudden changes in the mass-loss rate. This implementation required modification in some subroutines (see Appendix A).
(1)With this density structure it is possible to model sudden changes in the mass-loss rate. This implementation required modification in some subroutines (see Appendix A).
2.2. The minimisation part
The modified DUSTY code is included as a subroutine in a minimisation code using the mrqmin routine (using the Levenberg-Marquardt method from Press et al. 1992).
In principle any combination of parameters that can appear in a standard DUSTY input file can be minimised, but here two obvious examples are presented. First a standard case, where the parameters that are fitted in the minimisation process are the luminosity (L), the dust optical depth (τ), the dust temperature at the inner radius (Tc), and the slope of the density law (parameter p(1) in Eq. (1)). Second, the case that is next in complexity, with a second shell. In that case y(1) (the location of the second shell), s(2) (the density contrast), and p(2) (the slope of the density law in the second shell) are three additional free parameters. All these parameters may also be fixed. The fitting of τ, L, Tc (and y(1) and s(2)) is actually performed on the logarithm of these values to fit parameters that are on the order of unity. Derivatives that are needed in the minimisation process are calculated numerically by varying the parameters by 0.01 unit.
The quality of the fit is based on a χ2 analysis 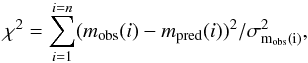 (2)with m the observed or predicted magnitude (for the broadband photometry) or flux (for the spectrum) or visibility at a spatial frequency or normalised intensity at a radial offset, with error bar σmobs and n is the total number of measurements. In practice, Eq. (2) is calculated for all four types of observations separately, so that it is possible to compare the contribution of all photometry, spectra, visibility data and intensity curves to the total χ2. Because it it possible to scale the error bars of any given observational dataset (see below), the user has the choice to, e.g., weigh all four types of observations equally. Moreover the reduced χ2 is defined:
(2)with m the observed or predicted magnitude (for the broadband photometry) or flux (for the spectrum) or visibility at a spatial frequency or normalised intensity at a radial offset, with error bar σmobs and n is the total number of measurements. In practice, Eq. (2) is calculated for all four types of observations separately, so that it is possible to compare the contribution of all photometry, spectra, visibility data and intensity curves to the total χ2. Because it it possible to scale the error bars of any given observational dataset (see below), the user has the choice to, e.g., weigh all four types of observations equally. Moreover the reduced χ2 is defined: 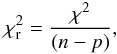 (3)with p the number of free parameters, and the quantity
(3)with p the number of free parameters, and the quantity 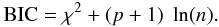 (4)This is based on the Bayesian information criterion (Schwarz 1978). In this way it is possible, for example, to compare models with fitted and fixed Tc, and by comparing the values of BIC to decide whether adding free parameters leads to a statistically significant reduction in χ2.
(4)This is based on the Bayesian information criterion (Schwarz 1978). In this way it is possible, for example, to compare models with fitted and fixed Tc, and by comparing the values of BIC to decide whether adding free parameters leads to a statistically significant reduction in χ2.
2.3. Input and output
Input to MoD is a master input file that contains: the interstellar reddening AV, the assumed distance (d), the path to the file containing the absorption and scattering coefficients of the dust, the path to the file containing the spectrum of the central star, the effective temperature, and (see Eq. (1)) the number of shells, the outer radius (radii), y(N), of these shells, the exponents of the density law, p(N), of these shells (note that p(1) is one of the fit parameters in the current version of the code), and the scaling factors, s(N) (s(1) is set to 1). Finally, initial guesses of the fit parameters are given, and a code whether these parameters should be varied or fixed.
Target list and basic information.
For the central star spectra MARCS2 model atmospheres (Gustafsson et al. 2008) were used for the oxygen-rich stars, and models by Aringer et al. (2009) for the carbon stars, for the examples discussed in Sect. 3. The central star spectra are user input and are not part of MoD. The very high resolution MARCS models were first convolved with a Gaussian of width 200 km s-1, then extended beyond 20 μm based on a blackbody (BB) using the effective temperature of the model and the average flux in 19.5–20 μm region, and finally re-binned on a wavelength grid. The Aringer et al. models are already at a sufficiently low resolution, and were only extended to longer wavelength and re-binned.
MoD then generates the standard format input file3 expected by the DUSTY subroutine, and the standard output files of DUSTY are generated.
The next crucial ingredient is to take these output files, and link them to observational data to calculate the χ2 and proceed with the minimisation of the free parameters.
The scale-free flux distribution is put on an absolute scale using L and d and reddened using the input value of AV. The adopted reddening law is that of Cardelli et al. (1989) with the improvement by O’Donnell (1994) from the UV to the NIR. For λ > 1.5 μm the local interstellar medium (ISM) model of Chiar & Tielens (2006) is used (with AV/AK = 0.118 to bring it on the same scale as in the optical), and extrapolated for λ > 27 μm by Aλ ~ λ-2.1.
The reddened spectrum is folded with the filter response curves of almost 100 different filters to produce magnitudes to compare to the observations (see Groenewegen 2006 for details).
Additional input to MoD are the observational data that are used as constraints. For photometric data this would be a file that contains the filter names, magnitudes and errors in the magnitudes. For spectroscopic data this would be a master file with the number of observational spectra, and per dataset the path to the file containing the spectrum, a scaling factor of the overall flux level and a scaling factor for the error in each flux point, and the possibility to exclude certain wavelength regions from the fitting. For visibility data this would be a master file with the number of visibility datasets, and per dataset the path to the file with the visibility data, the effective wavelength of the observation, a scaling factor for the error bar in each visibility point, and also an angular radius (the field-of-view, FoV) corresponding to the largest scale that the interferometric observation was sensitive to.
This last requires some explanation. The visibility V is related to the intensity I in the spherical case as 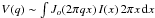 , where J0 is Bessell function of zeroth order, q the spatial frequency and where the integral runs from 0 to ∞ in theory and in practice, in DUSTY, to the outer radius of the dust shell as defined by the user. However, the emission region may have been resolved already with a single telescope of a multi-telescope interferometer. In the code the integration is extended to the outer radius of the dust shell, or and the FoV, whichever is smallest.
, where J0 is Bessell function of zeroth order, q the spatial frequency and where the integral runs from 0 to ∞ in theory and in practice, in DUSTY, to the outer radius of the dust shell as defined by the user. However, the emission region may have been resolved already with a single telescope of a multi-telescope interferometer. In the code the integration is extended to the outer radius of the dust shell, or and the FoV, whichever is smallest.
For intensity profiles this would be a master file with the number of intensity profiles, and per dataset the path to the file with the intensity profile, the effective wavelength of the observation, a scaling factor for the error bar in each intensity point, the FWHM of a Gaussian to convolve the theoretical intensity profile with (corresponding to the FWHM of the observation), and also the pixel scale on which the object was imaged. The latter parameter allows one to integrate the convolved intensity profile over a square pixel to achieve a more direct comparison to observations, because the convolved intensity profile is smeared due to the finite pixel scale.
3. Radiative transfer modelling
In this section the results of the RT modelling are presented. Two well-known stars were selected from the Herschel MESS (Mass-loss of Evolved StarS) programme (Groenewegen et al. 2011), OH 26.5 and TT Cyg, for which PACS aperture photometry is available (Groenewegen et al. 2011; Cox et al. 2012). Along the same lines as described in those papers the azimuthally averaged 1D intensity profiles were determined.
Table 1 lists the adopted distance with the reference. The interstellar reddening was calculated using several 3D reddening models available in the literature (Drimmel et al. 2003; Marshall et al. 2006), for details see Groenewegen (2008). The table also includes references to the photometry used. The spectroscopic data used as constraints are ISO SWS spectra for both stars (Sloan et al. 2003), and for OH 26.5 the ISO LWS spectrum from Sylvester et al. (1999). The visibility data for OH 26.5 is discussed in the subsection below.
Models for OH 26.5 and TT Cyg.
3.1. OH 26.5
3.1.1. Previous work
Suh et al. (1990) presented a pulsation phase-dependent model. The dust condensation temperature Tc was set at 1000 K. The density structure followed from the pulsation model and the authors adopted a r-3 dependence for radii smaller than three condensation radii (which they state is about six stellar radii) and r-2 beyond that. For their model at minimum light, which has a luminosity of 10 000 L⊙, they adopted a stellar effective temperature of 2000 K (although not stated explicitly, this is probably a BB).
Justtanont et al. (1996, J96) presented a model of the dust and gas outflow. Constraints were a ground-based spectrum in the 10 and 20 μm window, photometry up to 100 μm (IRAS), visibility data from Fix & Cobb (1988), and line profiles in the CO J = 2–1, 3–2 and 4–3 transitions. The extinction coefficients were calculated as described in Justtanont & Tielens (1992) and were manually tuned in the 10 μm region for OH 26.5, and assumed a far-IR extinction efficiency of λ-1. The dust condensation temperature Tc was set at 1000 K. The inner radius is then 4.5 × 1014 cm, or 7.5 stellar radii for the adopted effective temperature of 2200 K (probably a BB). A luminosity of 15 700 L⊙ is derived (for a distance of 1.37 kpc). Their best model consisted of an superwind-AGB two-component model where the mass-loss rate drops by a factor of about 550 at about 18 condensation radii.
This model was refined in Fong et al. (2002), where OH 26.5 was mapped in the CO J = 1–0 line with the BIMA interferometer, and where the ISO SWS and LWS spectrum were used as well to constrain the SED modelling. Pure silicate grains and silicate core water-ice mantle grains were used. The conclusions of the 1996 paper were largely confirmed in that the best-fit model consisted of a superwind (Ṁ = 5.5 × 10-4 M⊙ yr-1) out to about 130 R ⋆ where the mass-loss rate drops by a factor of about 530. The distance of about 1016 cm where the superwind ends combined with a expansion velocity of 15.4 km s-1 corresponds to a flow timescale of about 200 years.
Driebe et al. (2005) presented speckle interferometry at 2.2 μm. They found no evidence for deviations from spherical symmetry in their data. The visibility data and SED were fitted with DUSTY using the optical properties of silicate dust from Suh (1999). Driebe et al. adopted a temperature at the inner boundary of 800 K. Depending on the pulsation phase they adopted effective temperatures between 2000 and 3000 K. The density was calculated from a radiation-driven wind approach (i.e. density type 3 or 4 in DUSTY). No two-component mass loss was required, and the authors derived mass-loss rates between 0.3 and 1.2 × 10-4 M⊙ yr-1 (depending on the pulsation phase).
Chesneau et al. (2005) presented spectrally dispersed interferometric data between 8 and 13.5 μm with MIDI. In addition an acquisition image at 8.7 μm resolved the object and showed an asymmetry, with an axial ratio of 0.75 and a FWHM of the major and minor axis of 286 and 214 mas (after deconvolution). The MIDI spectrum and the SWS and LWS spectrum were modelled based on the two-component model of J96. Adopted were pure amorphous olivine grains (MgFeSiO4 from Dorschner et al. 1995) and metallic iron (Henning & Stognienko 1996) using CDE and in a ratio of 97:3 in mass and with a size of 0.1 μm (Verhoelst, priv. comm.). At minimum light (~8900 L⊙) J96 adopted an effective temperature of 2200 K. The dust temperature at the inner radius was 650 K (Verhoelst, priv. comm.). In their model the location of the transition of superwind to AGB wind was at the same distance as found by J96 and Fong et al. (2002), but the drop in mass loss was 10 times smaller at about a factor of 40. Notwithstanding the indications from their acquisition image that there may be an asymmetry, Chesneau et al. concluded that their fit to the SED is compatible with the 1D model they used. Driebe et al. (2005) found no evidence for deviations from spherical symmetry in their data. A 1D model is used here, acknowledging however that the geometry of the environment around OH 26.5 may be more complex.
3.1.2. This work
The LWS spectrum in the ISO archive has an apparent problem with the background subtraction, and the LWS spectrum presented in Sylvester et al. (1999) was used. The SWS below 3 μm was excluded from the fitting because of the presence of water ice, which is not considered here.
The following visibility data were considered in the fitting: interferometric data at 2.2 μm (Driebe et al. 2005), 4.9 and 10 μm (Cobb & Fix 1987), and 8.7 and 9.8 μm (Fix & Cobb 1988).
Another independent constraint (because the models are not optimised to fit this), is the size determined by Chesneau et al. (2005) at 8.7 μm from direct imaging. The observed mean value is 240 ± 14 mas. In the model, the intensity curve is first convolved with a FWHM of 152 mas (Chesneau et al. 2005, Table 2) and then the FWHM of the result can be compared to the observed value.
The coolest available MARCS model of 2600 K was adopted. The dust temperature at the inner radius was fixed to 700 K, and the outer radius was set to 2600 times the inner radius in the standard model, where the dust temperature reaches approximately 20 K. The parameters of the standard model are listed in Table 2, and the fits to the photometry and spectra, intensity and visibility curves are shown in Figs. 1–3. The errors quoted are the internal errors scaled to a reduced χ2 of 1. The fit to the intensity curve is particularly poor in the PACS blue filter at about 8′′ and to a lesser extent in the PACS red filter at about 15′′. This is because at a low flux level a tri-lobe structure in the PSF is visible (see Fig. B.1 in Groenewegen et al. 2011), which is explained by Herschel’s secondary mirror support structure, see Pilbratt et al. (2010) and Poglitsch et al. (2010), and therefore the PSF is not well represented by a Gaussian at those radial offsets. Details may be found in the instrument observer’s manuals4.
 |
Fig. 1 Fit to the SED of OH 26.5 for the standard model. |
 |
Fig. 2 Fit to the visibility data of OH 26.5 for the standard model. The wavelength is listed in the top right corner of each panel. References to the data are given in the text. Error bars are plotted throughout but are sometimes smaller than the plot symbol. |
 |
Fig. 3 Fit to the azimuthally averaged PACS intensity distributions of OH 26.5 for the standard model. The wavelength is listed in the top right corner of each panel. The inset shows the outer low-intensity part in more detail. |
Sources for the optical constants used in this paper.
The fitted grain size is a = 0.2 μm, and the finally adopted dust is a mix of Mg4.5Fe4.5AlSi9O28.5:FeO:Fe3O4 = 100:2:1, calculated using DHS (distribution of hollow spheres; Min et al. 2003) with a maximum volume fraction of a vacuum core of fmax = 0.7. The references to the optical constants used in this paper are listed in Table 3.
The visibility curve at 2.2 μm allows one to derive the grain size with good precision. With this particular dust mix, and allowing only single-sized grains, radii of <0.15 or >0.25 μm can be excluded (see Appendix B).
The dust mix in the standard model is a mix of aluminasilicate and iron-oxides. The adopted aluminasilicate clearly fits better than olivine (MgFeSiO4), especially in the 13–16 μm region (see Appendix). The addition of iron-oxides is also required to obtain the overall best fit, but the exact composition is less constrained. Using Mg0.6Fe0.4O instead of FeO, and/or metallic iron instead of magnetite, with the sum of the two components in the range 3–5%, results in almost identical fits.
At 8.7 μm a FWHM of 261 mas is found in excellent agreement with the observed value of 240 ± 14 mas.
The best model converges to a density distribution steeper than r-2. Models with a fixed r-2 distribution are considered in in more detail in the appendix, but fit all constraints less well.
To illustrate the potential of MoD more complicated models with two shells were considered to investigate the previous findings of an AGB and a superwind phase. The density distributions were fixed to r-2 in both shells, and the two additional free parameters are the drop in the mass-loss and the location of the drop. Several starting values were tried, and the best fit (which is better than that of the standard model) converges to a drop of 0.2 located at 102 stellar radii (3.4 condensation radii, or 0.18′′). The fits are shown in Figs. 4–6. The location of the second shell agrees reasonably with previous determinations. The drop in mass loss is also confirmed but seems even less than found by Chesneau et al. (2005).
 |
Fig. 4 Fit to the SED of OH 26.5 for the best model with two shells. |
 |
Fig. 5 Fit to the visibility data of OH 26.5 for the best model with two shells. |
 |
Fig. 6 Fit to the azimuthally averaged PACS intensity distributions of OH 26.5 for the best model with two shells. |
3.2. TT Cyg
3.2.1. Previous work
TT Cyg is one of a handful AGB stars known to have detached shells. Originally discovered as having an excess at 60 μm in IRAS data (Willems & de Jong 1988), TT Cyg was subsequently observed in molecular CO by single-dish (Olofsson et al. 1996) and radio interferometers (Olofsson et al. 1998, 2000). These observations revealed a very thin almost perfectly round shell of width ~2.5′′ located at ~35′′ from the central star, consistent with an expanding spherically symmetric shell.
Schöier et al. (2005) modelled the interferometric CO data and the SED and found a current (gas) mass-loss rate of 3.2 × 10-8 M⊙ yr-1, and for the detached shell, from the dust modelling of the SED (no spatial information was available at the time), a dust mass of (4.3 ± 3.7) × 10-4 M⊙ with a characteristic temperature of (39 ± 10) K located at (75 ± 45)′′, and from the gas modelling a gas mass of (4.0 ± 1.0) × 10-3 M⊙ with a characteristic gas temperature above 200 K, located at 35.1′′ (no error bar given).
Kerschbaum et al. (2010) presented Herschel/PACS 70 and 160 μm imaging data. The detached shell was clearly present, located at about 33′′. The SED and intensity distribution were modelled “by eye” with DUSTY.
Precisely because DUSTY cannot handle non-continuous density distributions, the flux of the SED was approximated by using the flux at the outer radius of a model of star plus shell as the inner boundary to another DUSTY run to model a second shell, etc. This ignores back-warming effects, but as pointed out in Kerschbaum et al., the approximation is valid in the optically thin limit. A model with five shells (assuming an r-2 law in each of them) fitted the intensity curve at 70 μm almost perfectly, but underestimated the maximum intensity of the outer shell at 160 μm, and also provided a poor fit to the SED, in particular the total flux in the IRAS 60 and 100 μm and PACS 70 μm bands (see Figs. 2 and 4 in Kerschbaum et al.).
3.2.2. This work
In all models a distance of 510 pc was adopted (as in Kerschbaum et al., and consistent with the parallax of 1.78 ± 0.51 mas of van Leeuwen 2007), and the temperature at the inner dust radius was fixed at 1000 K. The outer radius was set to 6000 times the inner radius. The dust composition was a mix of 95% amorphous carbon and 5% silicon carbide.
First, the detached shell was not considered (that is, the IRAS 60 and 100 μm data and Herschel data were excluded from the fit) and all photospheric models with solar metallicity from the Aringer et al. (2009) set were fitted to determine the best stellar parameters. The model that was chosen has Teff = 3200 K, log g = −0.4 and C/O = 1.10, and this agrees well with Jörgensen et al. (2000), who give Teff = 2900 K (with log g = −1, and C/O in the range 1.3–1.5) or Teff = 3000 K (with log g = 0, and C/O in the range 1.2–1.5). Another effective temperature often adopted in the literature is Teff = 2825 K by Bergeat & Chevallier (2005), and Kerschbaum et al. adopted the closest temperature in the Aringer et al. (2009) model grid, Teff = 2800 K. The predicted angular diameter for the best-fit atmosphere model is 3.08 mas, with an error of about 0.13 mas, assuming an error of 70 K in effective temperature. The observed value taken from the CHARM2 catalogue (Richichi et al. 2005; Gerard van Belle, priv. comm.) is a uniform disk model value of 3.30 ± 0.07 mas, which multiplied with 1.022 (Dyck et al. 1996) gives a limb-darkened value of 3.37 mas. The agreement is satisfactory, considering the fact that the star is variable as well. A slightly lower effective temperature would improve the agreement but, see Appendix C, can be excluded from the fit to the SWS spectrum. From this fit, and for the adopted distance, a luminosity of L = 2735 ± 4 L⊙ is derived (internal error bar), which is now fixed in all subsequent models.
For this model atmosphere and luminosity, models with a detached shell were calculated.
Figures 7 and 8 show the SED and intensity distribution in the classical case that the density law has p(1) = p(2) = 2, that is, constant mass loss and velocity. The optical depth, the contrast (s(2)) and the location of the outer shell are free parameters (to obtain a reasonable fit the thickness of the shell was fixed to about 8′′); its fitted values are τ = 0.08, s(2) = 480, respectively, and the shell starts at 30.7′′ (see Table 2). However, the fit is very poor, in particular there is much more emission interior to the detached shell
 |
Fig. 7 Fit to the SED of TT Cyg for the model with r-2 density distributions. The bluest two photometric points (the crosses) are excluded from the fitting. |
 |
Fig. 8 Fit to the azimuthally averaged PACS intensity distributions of TT Cyg for the model with r-2 density distributions. The wavelength is listed in the top right corner of each panel. The inset shows the outer low-intensity part in more detail. |
Figure 9 shows a model where p(1) and p(2) are also allowed to vary. The results indicate much steeper distributions in both shells with p(1) = 1.2 and p(2) = −3.0. The fit is looks better (although the BIC is actually slightly worse) but certainly not perfect, in particular the balance between the PACS blue and red filter is incorrect, and this could be related to the temperature in the shell. The contrast in this model is only s(2) = 9.7.
 |
Fig. 9 Fit to the azimuthally averaged PACS intensity distributions of TT Cyg for the model where the slopes of the density distributions are allowed to vary. The wavelength is listed in the top right corner of each panel. The inset shows the outer low-intensity part in more detail. |
The dust temperature at the inner radius of the detached shell is 52.0 K, and varies as r-0.4. As a test, the dust temperatures in the shell were manually overwritten as T0·r-0.4, and several temperatures were tested. Figure 10 shows the best fit with T0 = 46 K. The balance between the 70 and 160 μm distributions is much improved, although the clear peak seen at 70 μm is not well reproduced. The implications of these results are given in Sect. 4.
 |
Fig. 10 Fit to the azimuthally averaged PACS intensity distributions of TT Cyg for the model where the temperature in the detached shell is 46·r-0.4. The wavelength is listed in the top right corner of each panel. The inset shows the outer low-intensity part in more detail. |
4. Conclusions
MoD, a modified and extended version of the well-known 1D dust radiative transfer code DUSTY was presented, which allowed one to calculate in a flexible way the parameters that best fit a set of photometric, spectroscopic, interferometric data and intensity profiles. MoD is available through collaboration with its author.
For OH 26.5 the modelling of the available intensity curves, interferometric, spectroscopic, and photometric data allowed us to confirm previous findings of a two-component wind, where the mass-loss rate dropped by a significant amount. The location of the drop at about 100 stellar radii corresponds to a time scale of about 80 years assuming an expansion velocity of 16 km s-1 (Kemper et al. 2003). The best-fit parameters, dust properties and expansion velocity translate into a current mass-loss rate (for an assumed dust-to-gas ratio of 0.005) of 4.0 × 10-4 M⊙ yr-1, which agrees well with literature determinations.
For TT Cyg it proved difficult to fit intensity curves and SED simultaneously. The best fit was obtained when the density distribution in the shell close to the star and in the detached shell depart significantly from r-2, and when the dust temperature in the detached shell was lower than predicted from radiative equilibrium.
The departure from r-2 likely happends because the stellar winds are interacting with each other and/or the ISM. The MESS program has revealed new cases of detached shells around carbon stars, as well as many cases of wind-ISM interaction (Kerschbaum et al. 2010; Cox et al. 2012). Schöier et al. (2005) investigated the properties of the detached shells around the known carbon stars with detached shells and concluded that these shells show clear signs of interaction with a surrounding medium, whereby the shell is sweeping up material from a surrounding medium. Using hydrodynamical simulations, Steffen & Schönberner (2000) showed that the interaction of a faster inner wind running into a slower outer wind also results in a thin shell. Libert et al. (2007) presented an analytical model of the shell around Y CVn consisting of a freely expanding wind and a detached shell. They showed the resulting density profile (their Fig. 7), and in the detached shell I found that this can be approximated, assuming a power law, as r + 6. This is qualitatively consistent with the r + 3 − + 3.5 derived here for TT Cyg.
Although the good spatial resolution of the Herschel/PACS and SPIRE instruments allowed the detection of interesting phenomena in the far-IR around many AGB stars, even better spatial resolution appears required to make definitive statements about the exact origin of the detached shells. ALMA can provide these observations both in spectral lines and in the (dust) continuum. Especially for the dust it would be important to verify whether the inner wind is as smooth as suggested by the Herschel/PACS observations, or if there is additional substructure due to additional, or more complicated, wind-wind interaction, and to verify if the dust distribution in the detached shell is clumpy (as has been suggested for the CO, e.g. Olofsson et al. 2000). These types of observations would also clarify to which extent 1D dust modelling is still a valid approach.
Online material
Appendix A: Modifications to DUSTY
In this appendix some technical aspects are described of the modifications and extensions that were made to DUSTY. Some familarity with DUSTY and its manual is assumed. The modified code will be referred to as MoD (More of DUSTY). The core of MoD is DUSTY version 2.01, and the changes described below are w.r.t. that version.
-
In the process of developing MoD, one bug was found and corrected, namely in subroutine visi2d where the loop over the radial positions ran from 1 to Nin, but should run to (Nin-1).
-
The 2D array Elems, which has dimensions (25, npL). The second dimension was increased to npP.
-
In DUSTY it is possible to calculate intensity profiles (the *.itb files). From an observational point one would prefer intensity profiles convolved with the beam of the instrument/ telescope. In fact, this option was already present in DUSTY (subroutines Convolve and Conv2D ), but not described in the DUSTY user manual. The calculation requires parameters for the convolution, but also the angular diameter of the inner dust shell. In DUSTY this number is simply an input parameter, independent of any observational parameter (luminosity, effective temperature, dust condensation temperature, which basically set this value) because DUSTY is scale-free and hence does not require the luminosity as input. In MoD the angular diameter of the inner dust shell must be calculated self-consistently. In order to achieve this, the call to the subroutines that calculate the convolved intensity profiles (and visibilities as well) had to be moved to a different location in DUSTY.
-
A more general form of the piecewise power law for the density structure (density type = 1) was implemented in DUSTY, see Eq. (1) in the main text. With this density structure it is possible to model steps in the mass-loss rate. This implementation required modification in subroutine Ygrid to better resolve the different regions, and a change in subroutines ETA and Product. The parameter EtaRat, which is a control parameter on how much the normalized density profile may change between two radial gridpoints, was set to a high value.
Appendix B: OH 26.5
The best-fit model presented in Figs. 1–3 has grains of size a = 0.2 μm, and the finally adopted dust is a mix of Mg4.5Fe4.5AlSi9O28.5:FeO:Fe3O4 = 100:2:1, calculated using DHS with fmax = 0.7.
For this mix, Figs B.1, B.2 show the visibility data for grains of size 0.15 and 0.25 μm, respectively. The visibility curve at the shortest wavelength is very sensitive to the adopted grain size, likely due to the effect of scattering. At 2.1 μm, Qabs/a is almost constant with values of 0.28, 0.30, 0.32 μm-1 for a = 0.15, 0.20, 0.25 μm, respectively, but Qsca/Qabs is 0.27, 0.58, 0.97, respectively. The effect is smaller at longer wavelengths; already at 4.9 μm the ratio of scattering to absorption is a factor of 2 lower.
 |
Fig. B.1 Standard model for OH 26.5 but with a = 0.15 μm. |
 |
Fig. B.2 Standard model for OH 26.5 but with a = 0.25 μm. |
 |
Fig. B.3 Standard model for OH 26.5 but with olivine instead of aluminosilicate. |
Figure B.3 shows the best fit with pure olivine instead of the aluminosilicate. The best fit to the K-band visibility curve (not shown) is for a = 0.l8 μm. The fit is clearly poorer, and adding iron(-oxides) does not significantly improve the fit.
 |
Fig. B.4 Model for OH 26.5 with r-2 density distribution and Rout = 5. |
The standard model converged to a r-2.55 density distribution. The outer radius in this model is set to 1600 condensation radii where the dust temperature reached 20 K, corresponding to about 1.5′.
Non-standard models are now considered where the density distribution is fixed to r-2, as adopted in somestudies mentioned in Sect. 3.1.1. The dust is fixed to 100% aluminasilicates. It turns out that the outer radius has to be decreased significantly to obtain even an approximately good fit. Figures B.4–B.6 show the results for an outer radius of five condensation radii. Although the fit to the SWS spectrum is even slightly better than for the standard model, the fit to the intensity curves and visibility curves is worse. Such a small outer radius can in fact be excluded. Fong et al. (2002) mapped CO and detected it to 7 × 1017 cm correspoding to about 3.3′′. This should correspond to the CO photodissociation radius, and the outer radius of the dust should extent beyond this.
Appendix C: TT Cyg
 |
Fig. C.1 Best fit to the optical and NIR photometry and SWS spectrum of TT Cyg, with Teff = 3200 K, log g = −0.4, C/O = 1.10. The top panel shows the full SED, while the middle and lower panel show details of the SWS spectrum. The C3 feature near 5.4 μm is not well fitted in any of the Aringer et al. (2009) models and is excluded from the fit (as indictated by the line between 4.4 and 6.1 μm). This is likely related to the issue discussed in Jörgensen et al. (2000) about the parameter Kp(C3) that expresses the equilibrium between atomic carbon, C2 and C3 and that is not well known. |
In this section the influence of the different stellar parameters is illustrated. Figure C.1 shows the best-fit model from the
Aringer et al. (2009) set with solar metallicity, which has Teff = 3200 K, log g = −0.4, and C/O = 1.10 as parameters. Figures C.2–C.4 show models where one parameter is varied to Teff = 3000 K, log g = −0.0, and C/O = 2.0, respectively. Gravity is almost unconstrained by the SWS spectrum, but the strength of the 3.1 μm feature (due to HCN and C2H2) and 7.5 μm feature (mainly CS) strongly depend on effective temperature and C/O ratio (see Jörgensen et al. 2000). Based on these results error bars of 50 K in effective temperature and 0.15 in C/O are estimated.
 |
Fig. C.2 Fit with Teff = 3100 K. |
 |
Fig. C.3 Fit with log g = 0.0. |
 |
Fig. C.4 Fit with C/O = 1.4. |
Acknowledgments
M.G. acknowledges support by ESA-Prodex grant C90371, and would like to thank Franz Kerschbaum and Z˘eljko Ivezić for reading a draft version of this paper.
References
- Aringer, B., Girardi, L., Nowotny, W., Marigo, P., & Lederer, M. T. 2009, A&A, 503, 913 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bagnulo, S., Doyle, J. G., & Andretta, V. 1998, MNRAS, 296, 545 [NASA ADS] [CrossRef] [Google Scholar]
- Bergeat, J., & Chevallier, L. 2005, A&A, 429, 235 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Beichman, C. A., Neugebauer, G., Habing, H. J., Clegg, P. E., & Chester, T. J. 1985, IRAS Point source Catalogue (Pasadena: JPL) [Google Scholar]
- Cardelli, J. A., Clayton, G. C., & Mathis, J. S. 1989, ApJ, 345, 245 [NASA ADS] [CrossRef] [Google Scholar]
- Chesneau, O., Verhoelst, T., Lopez, B., et al. 2005, A&A, 43, 563 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Chan, S. J., & Kwok, S. 1990, A&A, 237, 354 [NASA ADS] [Google Scholar]
- Chiar, J. E., & Tielens, A. G. G. M. 2006, ApJ, 637, 774 [NASA ADS] [CrossRef] [Google Scholar]
- Cobb, M. L., & Fix, J. D. 1987, ApJ, 315, 325 [NASA ADS] [CrossRef] [Google Scholar]
- Cox, N. L. J., Kerschbaum, F., van Marle, A.-J., et al. 2012, A&A, 537, A35 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Cutri, R. M., Skrutskie, M. F., Van Dyk, S., et al. 2003, Explanatory Supplement to the 2MASS All-Sky Data Release [Google Scholar]
- Danchi, W. C., Bester, M., Degiacomi, C. G., Greenhill, L. J., & Townes, C. H. 1994, AJ, 107, 1469 [NASA ADS] [CrossRef] [Google Scholar]
- Dorschner, J., Begemann, B., Henning, Th., Jäger, C., & Mutschke, H. 1995, A&A, 300, 503 [Google Scholar]
- Driebe, T., Riechers, D., Balega, Y., et al. 2005, AN, 326, 648 [Google Scholar]
- Drimmel, R., Cabrera-Lavers, A., & López-Corredoira, M. 2003, A&A, 409, 205 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Dyck, H. M., Zuckerman, B., Leinert, Ch., & Beckwith, S. 1984, ApJ, 287, 801 [NASA ADS] [CrossRef] [Google Scholar]
- Dyck, H. M., Benson, J. A., van Belle, G. T., & Ridgway, S. T. 1996, AJ, 111, 1705 [NASA ADS] [CrossRef] [Google Scholar]
- ESA 1997, in The Hipparcos Catalogue, ESA SP, 1200 (viZier catalog I/239) [Google Scholar]
- Fix, J. D., & Cobb, M. L. 1988, ApJ, 329, 290 [NASA ADS] [CrossRef] [Google Scholar]
- Fong, D., Justtanont, K., Meixner, M., & Campbell, M. T. 2002, A&A, 396, 581 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Griffin, M. J., Abergel, A., Ade, P. A. R., et al. 2010, A&A, 518, L3 [Google Scholar]
- Groenewegen, M. A. T. 1995, A&A, 293, 463 [NASA ADS] [Google Scholar]
- Groenewegen, M. A. T. 1997, A&A, 317, 503 [NASA ADS] [Google Scholar]
- Groenewegen, M. A. T. 2006, A&A, 448, 181 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Groenewegen, M. A. T. 2008, A&A, 488, 935 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Groenewegen, M. A. T. 2012, A&A, 540, A32 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Groenewegen, M. A. T., Whitelock, P. A., Smith, C. H., & Kerschbaum, F. 1998, MNRAS, 298, 13 [Google Scholar]
- Groenewegen, M. A. T., Wood, P. R., Sloan, G. C., et al. 2007, MNRAS, 367, 313 [NASA ADS] [CrossRef] [Google Scholar]
- Groenewegen, M. A. T., Sloan, G. C., Soszyński, I., & Petersen, E. A. 2009, A&A, 506, 1277 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Groenewegen, M. A. T., Waelkens, C., Barlow, M. J., et al. 2011, A&A, 526, A162 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gullieuszik, M., Groenewegen, M. A. T., Cioni, M.-R. L., et al. 2012, A&A, 537, A105 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gustafsson, B., Edvardsson, B., Eriksson, K., et al. 2008, A&A, 486, 951 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Habing, H. J., & Olofsson, H. 2003, in Asymptotic Giant Branch Stars (New York: Springer-Verlag) [Google Scholar]
- Henning, Th., & Mutschke, H. 1997, A&A, 327, 743 [Google Scholar]
- Henning, T., & Stognienko, R. 1996, A&A, 311, 291 [NASA ADS] [Google Scholar]
- Henning, Th., Begemann, B., Mutschke, H., & Dorschner, J. 1995, A&AS, 112, 143 [NASA ADS] [Google Scholar]
- Ivezić, Ž., & Elitzur, M. 1997, MNRAS, 287, 799 [NASA ADS] [CrossRef] [Google Scholar]
- Ivezić, Ž., Nenkova, M., & Elitzur M. 1999, DUSTY user manual, University of Kentucky internal report [Google Scholar]
- Jörgensen, U., Hron, J., & Loidl, R. 2000, A&A, 356, 253 [NASA ADS] [Google Scholar]
- Justtanont, K., & Tielens, A. G. G. M. 1992, ApJ, 389, 400 [CrossRef] [Google Scholar]
- Justtanont, K., Skinner, C. J., Tielens, A. G. G. M., Meixner, M., & Baas, F. 1996, ApJ, 456, 337 (J96) [NASA ADS] [CrossRef] [Google Scholar]
- Kemper, F., Stark, R., Justtanont, K., et al. 2003, A&A, 407, 609 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kerschbaum, F., & Hron, J. 1994, A&AS, 106, 397 [NASA ADS] [Google Scholar]
- Kerschbaum, F., Ladjal, D., Ottensamer, R., et al. 2010, A&A, 518, L140 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kharchenko, N. V., & Roeser, S. 2009, Kinematika i Fizika Nebesnykh Tel, 17, 409 (viZier catalog I/280B) [Google Scholar]
- Ladjal, D., Justtanont, K., Groenewegen, M. A. T., et al. 2010, A&A, 513, A53 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Le Bertre, Th. 1993, A&AS, 97, 729 [NASA ADS] [Google Scholar]
- Le Bertre, Th. 1997, A&A, 324, 1059 [NASA ADS] [Google Scholar]
- Libert, Y., Gérard, E., & Le Bertre, T. 2007, MNRAS, 380, L1161 [NASA ADS] [CrossRef] [Google Scholar]
- López, J. M., & Hiriart, D. 2011, AJ, 142, 11 [NASA ADS] [CrossRef] [Google Scholar]
- Lorenz-Martins, S., De Araujo, F. X., Codina-Landaberry, S. J., De Almeida, W. G., & De Nader, R. V. 2001, A&A, 367, 189 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Marshall, D. J., Robin, A. C., Reylé, C., Schultheis, M., & Picaud, S. 2006, A&A, 453, 635 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Mathis, J. S., Rumpl, W., & Nordsieck, K. H. 1977, ApJ, 217, 425 [NASA ADS] [CrossRef] [Google Scholar]
- Men’shchikov, A. B., Balega, Y., Blöcker, T., Osterbart, R., & Weigelt, G. 2001, A&A, 368, 497 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Men’shchikov, A. B., Hofmann, K.-H., & Weigelt, G. 2002, A&A, 392, 921 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Min, M., Hovenier, J. W., & de Koter, A. 2003, A&A, 404, 35 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Monnier, J. D., Millan-Gabet, R., Tuthill, P. G., et al. 2004, ApJ, 605, 436 [NASA ADS] [CrossRef] [Google Scholar]
- Mutschke, H., Begemann, B., Dorschner, J., et al. 1998, A&A, 333, 188 [NASA ADS] [Google Scholar]
- Noguchi, K., Kawara, K., Kobayashi, Y., et al. 1981, PASJ, 33, 373 [NASA ADS] [Google Scholar]
- Nyman, L.-A., Hall, P. J., & Le Bertre, T. 1993, A&A, 280, 551 [NASA ADS] [Google Scholar]
- O’Donnell, J. E. 1994, ApJ, 422, 158 [NASA ADS] [CrossRef] [Google Scholar]
- Olofsson, H., Bergman, P., Eriksson, K., & Gustafsson, B. 1996, A&A, 311, 587 [NASA ADS] [Google Scholar]
- Olofsson, H., Bergman, P., Lucas, R., et al. 1998, A&A, 330, L1 [NASA ADS] [Google Scholar]
- Olofsson, H., Bergman, P., Lucas, R., et al. 2000, A&A, 353, 583 [NASA ADS] [Google Scholar]
- Press, W. H., Teukolsky, S. A., Vetterling, W. T., & Flannery, B. P. 1992, in Numerical Recipes in Fortran 77 (Cambridge U.P.) [Google Scholar]
- Pilbratt, G. L., Riedinger, J. R., Passvogel, T., et al. 2010, A&A, 518, L1 [CrossRef] [EDP Sciences] [Google Scholar]
- Pitman, K. M., Hofmeister, A. M., Corman, A. B., & Speck, A. K. 2008, A&A, 483, 661 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Poglitsch, A., Waelkens, C., Geis, N., et al. 2010, A&A, 518, L2 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Pollack, J. B., Hollenback, D., Beckwith, S., et al. 1994, ApJ, 421, 615 [NASA ADS] [CrossRef] [Google Scholar]
- Richichi, A., Percheron, I., & Khristoforova, M. 2005, A&A, 431, 773 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Rouleau, F., & Martin, P. G. 1991, ApJ, 377, 526 [NASA ADS] [CrossRef] [Google Scholar]
- Rowan-Robinson, M., & Harris, S. 1983a, MNRAS, 202, 767 [NASA ADS] [CrossRef] [Google Scholar]
- Rowan-Robinson, M., & Harris, S. 1983b, MNRAS, 202, 797 [Google Scholar]
- Sacuto, S., Aringer, B., Hron, J., et al. 2011, A&A, 525, A42 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Schöier, F. I., Lindqvist, M., & Olofsson, H. 2005, A&A, 436, 633 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Schutte, W. A., & Tielens, A. G. G. M. 1989, ApJ, 343, 369 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Schwarz, G. 1978, Ann. Stat., 6, 461 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- Sloan, G. C., Kraemer, K. E., Price, S. D., & Shipman, R. F. 2003, ApJS, 147, 379 [NASA ADS] [CrossRef] [Google Scholar]
- Steffen, M., & Schönberner, D. 2000, A&A, 357, 180 [NASA ADS] [Google Scholar]
- Sudol, J. J., Dyck, H. M., Stencel, R. E., Klebe, D. I., & Creech-Eakman, M. J. 1999, AJ, 117, 1609 [NASA ADS] [CrossRef] [Google Scholar]
- Suh, K.-W. 1999, MNRAS, 304, 389 [NASA ADS] [CrossRef] [Google Scholar]
- Suh, K.-W., Jones, T. J., & Bowen, G. H. 1990, ApJ, 358, 588 [NASA ADS] [CrossRef] [Google Scholar]
- Sylvester, R. J., Kemper, F., Barlow, M. J., et al. 1999, A&A, 352, 587 [NASA ADS] [Google Scholar]
- van der Veen, W. E. C. J., Omont, A., Habing, H. J., & Matthews, H. E. 1995, A&A, 295, 445 [NASA ADS] [Google Scholar]
- van Langevelde, H. J., van der Heiden, R., & van Schooneveld, C. 1990, A&A, 239, 193 [NASA ADS] [Google Scholar]
- van Leeuwen, F. 2007, in Hipparcos, the new reduction of the raw data (New York: Springer) [Google Scholar]
- van Loon, J. Th., Groenewegen, M. A. T., de Koter, A., et al. 1999, A&A, 351, 559 [NASA ADS] [Google Scholar]
- Walmsley, C. M., Chini, R., Kreysa, E., et al. 1991, A&A, 248, 555 [NASA ADS] [Google Scholar]
- Willems, F. J., & de Jong, T. 1988, A&A, 196, 173 [NASA ADS] [Google Scholar]
- Xiong, G. Z., Chen, P. S., & Gao, H. 1994 A&AS, 108, 661 [Google Scholar]
- Yamamura, I., Makiuti, S., Ikeda, N., et al. 2010, ISAS/JAXA (viZier catalog II/298) [Google Scholar]
All Tables
All Figures
 |
Fig. 1 Fit to the SED of OH 26.5 for the standard model. |
| In the text | |
 |
Fig. 2 Fit to the visibility data of OH 26.5 for the standard model. The wavelength is listed in the top right corner of each panel. References to the data are given in the text. Error bars are plotted throughout but are sometimes smaller than the plot symbol. |
| In the text | |
 |
Fig. 3 Fit to the azimuthally averaged PACS intensity distributions of OH 26.5 for the standard model. The wavelength is listed in the top right corner of each panel. The inset shows the outer low-intensity part in more detail. |
| In the text | |
 |
Fig. 4 Fit to the SED of OH 26.5 for the best model with two shells. |
| In the text | |
 |
Fig. 5 Fit to the visibility data of OH 26.5 for the best model with two shells. |
| In the text | |
 |
Fig. 6 Fit to the azimuthally averaged PACS intensity distributions of OH 26.5 for the best model with two shells. |
| In the text | |
 |
Fig. 7 Fit to the SED of TT Cyg for the model with r-2 density distributions. The bluest two photometric points (the crosses) are excluded from the fitting. |
| In the text | |
 |
Fig. 8 Fit to the azimuthally averaged PACS intensity distributions of TT Cyg for the model with r-2 density distributions. The wavelength is listed in the top right corner of each panel. The inset shows the outer low-intensity part in more detail. |
| In the text | |
 |
Fig. 9 Fit to the azimuthally averaged PACS intensity distributions of TT Cyg for the model where the slopes of the density distributions are allowed to vary. The wavelength is listed in the top right corner of each panel. The inset shows the outer low-intensity part in more detail. |
| In the text | |
 |
Fig. 10 Fit to the azimuthally averaged PACS intensity distributions of TT Cyg for the model where the temperature in the detached shell is 46·r-0.4. The wavelength is listed in the top right corner of each panel. The inset shows the outer low-intensity part in more detail. |
| In the text | |
 |
Fig. B.1 Standard model for OH 26.5 but with a = 0.15 μm. |
| In the text | |
 |
Fig. B.2 Standard model for OH 26.5 but with a = 0.25 μm. |
| In the text | |
 |
Fig. B.3 Standard model for OH 26.5 but with olivine instead of aluminosilicate. |
| In the text | |
 |
Fig. B.4 Model for OH 26.5 with r-2 density distribution and Rout = 5. |
| In the text | |
 |
Fig. B.5 Visibility curves for the model in Fig. B.4. |
| In the text | |
 |
Fig. B.6 Intensity curves for the model in Fig. B.4. |
| In the text | |
 |
Fig. C.1 Best fit to the optical and NIR photometry and SWS spectrum of TT Cyg, with Teff = 3200 K, log g = −0.4, C/O = 1.10. The top panel shows the full SED, while the middle and lower panel show details of the SWS spectrum. The C3 feature near 5.4 μm is not well fitted in any of the Aringer et al. (2009) models and is excluded from the fit (as indictated by the line between 4.4 and 6.1 μm). This is likely related to the issue discussed in Jörgensen et al. (2000) about the parameter Kp(C3) that expresses the equilibrium between atomic carbon, C2 and C3 and that is not well known. |
| In the text | |
 |
Fig. C.2 Fit with Teff = 3100 K. |
| In the text | |
 |
Fig. C.3 Fit with log g = 0.0. |
| In the text | |
 |
Fig. C.4 Fit with C/O = 1.4. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


