EDP Sciences logo
Subscriber Authentication Point
Search
Menu
Home All issues Volume 542 (June 2012) A&A, 542 (2012) A87 Full HTML
Free Access
Issue
A&A
Volume 542, June 2012
Article Number A87
Number of page(s) 12
Section Galactic structure, stellar clusters and populations
DOI https://doi.org/10.1051/0004-6361/201219004
Published online 12 June 2012

© ESO, 2012

1. Introduction

The Galactic halo contains some of the oldest stars in the Milky Way, and understanding its formation and evolution is one of the necessary steps to understand the Galaxy as a whole. Our ideas evolved in time, from the classical “monolithic collapse” scenario (Eggen et al. 1962), through the “chaotic” scenario (Searle & Zinn 1978) to the realisation that the halo has had a complex history and that both collapse and merging have contributed to its shaping (for a review see Helmi 2008, and references therein).

A milestone in the field was certainly the in situ study of the north Galactic pole by Majewski (1992) who showed that the halo appears to be counter-rotating. The panoramic view offered by modern wide-field surveys has allowed us to identify significant sub-structure in the halo, often referred to as the “field of streams” (Belokurov et al. 2006). From the theoretical point of view, modern simulations predict that it is a general expectation that halos of spiral galaxies are built by a combination of in situ star formation and accretion from satellite dwarf galaxies (Zolotov et al. 2009; Font et al. 2011).

Exploiting the data of the Sloan Digital Sky Survey (SDSS and SEGUE York et al. 2000; Yanny et al. 2009), Carollo et al. (2007, 2010) showed that the Galactic stellar halo is composed of at least two components with distinct kinematics and metallicity distribution, the more distant halo being more metal-poor. This analysis was based on relatively bright stars in SDSS, for which accurate proper motions could be derived. The SDSS catalogue contains spectra and photometry down to g = 20, suggesting that an in situ study of the distant halo is indeed possible.

With this in mind we began in 2006 to work on the analysis of SDSS spectra with two main goals: 1) retrieve from SDSS candidate stars of extremely low metallicity for high-resolution follow-up; 2) determine the metal-weak tail of the halo metallicity distribution function directly from the SDSS spectra.

The first goal was motivated to see if there is indeed a metallicity threshold for the formation of low-metallicity stars, as suggested by some theories of star formation at low metallicity (Schneider et al. 2003; Bromm & Loeb 2003; Salvadori et al. 2007), and to check the hypothesis that at very low abundances of iron only stars with strong enhancements of C and O can be found (Bromm & Loeb 2003; Frebel et al. 2007).

The second goal is straightforward. The metallicity distribution function (MDF) provides a strong constraint on the theories of galaxy formation and evolution, especially at the low-metallicity end. The current versions of the MDF are based on a limited number of stars (Ryan & Norris 1991; Schörck et al. 2009; Li et al. 2010), a few thousands at most. The SDSS has the potentiality of doing this for a sample of stars that is two orders of magnitudes larger. For this to be possible, though, two steps are necessary: 1) the abundance estimated from the low-resolution SDSS spectra must be confidently calibrated against abundances derived from high-resolution spectra; 2) the selection biases in the SDSS sample must be understood.

It is clear that our goals require that extremely metal-poor (EMP) candidates extracted from the SDSS should be observed at higher resolution. To this end we carried out several observational campaigns at the European Southern Observatory with the UVES (Dekker et al. 2000) and X-Shooter (D’Odorico et al. 2006) spectrographs. Over the years we have made three progress reports (Ludwig et al. 2008; Bonifacio et al. 2010; Sbordone et al. 2010b) on this programme. The abundances of three C-enhanced dwarf stars, observed with UVES, have been reported in Behara et al. (2010), and the abundances for two stars observed with X-Shooter in Bonifacio et al. (2011). In this paper we report the abundances for 16 stars of typical magnitude g ~ 17, observed with UVES in the course of ESO periods 78 and 81. In an accompanying papers (Caffau et al. 2011b) we reported the abundances of five stars observed with X-Shooter. Finally, in Caffau et al. (2011c, 2012) we described the most metal-poor star found in the sample, observed with both X-Shooter and UVES.

2. Target selection

The programme stars were selected from the SDSS Data Releases 5 (Adelman-McCarthy et al. 2007) and 6 (Adelman-McCarthy et al. 2008). Names, coordinates, and g magnitudes are provided in Table 4. To obtain spectra of good quality in a limited amount of time with UVES, based on the exposure time calculator and on our personal experience with this instrument, we restricted the sample to g ≤ 17.5. We decided to focus on turn-off (TO) stars, for several reasons. In the first place the surface gravity can be confidently fixed at log g = 4.0 for these stars, a minor contaminant being Horizontal Branch stars of higher luminosity. According to the Padova isochrone of metallicity –2.0 and age of 13 Gyr (Marigo et al. 2008), the absolute g magnitude of TO stars ranges between 3.0 and 3.6. This implies, if one neglects interstellar extinction, a distance range between roughly 6 kpc and 8 kpc, these objects are thus capable to probe the outer halo. In this phase of the project we aimed to avoid the complication of discriminating between K dwarfs and K giants, although in the future we do intend to tackle cooler stars, because K giants allow one to probe considerably greater distances. Another reason is that the SDSS spectroscopic sample is very rich in TO-colour objects. There are two factors that contributed to boost their number: metal-poor F dwarfs were often observed as suitable flux-calibration standards, and the SDSS QSO selection algorithm (Richards et al. 2002) also selects very metal-poor TO stars.

To select the TO stars we relied on the (g − z)0 colour, which we calibrated against Teff (Ludwig et al. 2008), our initial selection was −0.3 ≤ (g − z)0 ≤ 0.7, which, in terms of Teff, corresponds to: 5500 ≤  Teff  ≤ 8000 K. Our initial sample consisted of about 34 000 stars. The motivation for including these high effective temperatures was to be able to capture the EMP stars with C-enhanced composition predicted by the isochrones of Piau et al. (2006).

The raw metallicity distribution function is shown in Fig. 3 of Ludwig et al. (2008). The almost flat behaviour at metallicities below −4.0 is clearly suspicious. It should be emphasized that at these low metallicities the only metallic line measurable on SDSS spectra for TO stars is the Ca ii K line. Visual inspection of all SDSS spectra of the sample, with estimated metallicity below −3.0 showed that in fact the low-metallicity sample was dominated by white dwarfs, some of which do show a measurable Ca ii K line in the SDSS spectra. At this stage we also realised that the vast majority of the white dwarfs could indeed be excluded by a simple cut on the (u − g)0 colour: (u − g)0 > 0.70. The cleaned sample with a more restrictive temperature cut 0.18 ≤ (g − z)0 ≤ 0.70 consisted of about 26 000 stars. The metallicity distribution function was presented in Bonifacio et al. (2010) and shows no flattening at low metallicity. We have already used these cuts on data of SDSS Data Release 7 (see Caffau et al. 2011b) and we will use it on SDSS Data Release 8. These more restricted colour cuts will not be able to select the stars predicted by Piau et al. (2006), if they exist. We point out that finding these objects among the white dwarfs of similar colours is fairly challenging.

The final selection of the targets to be observed with UVES had to take into account the observability conditions from Paranal (δ ≤ +28) and was made by visual inspection of all stars with [Fe/H]SDSS ≤ −3.0. It was not our purpose to observe a sample of stars with a well-defined selection function, but rather to observe a sample of true EMP stars. The three stars reported in Behara et al. (2010) were already recognized at this stage as C-enhanced stars.

For the reader’s convenience an excerpt of the SDSS photometry for our programme stars is provided in Table 3. Full information is available on the SDSS site www.sdss.org.

3. UVES observations and data reduction

The observations were obtained in the course of two ESO periods, both programmes had Ludwig as PI. In period 78 we were allocated 29 h in service mode, in period 81 we were allocated three nights in visitor mode. A log of the observations, including the slit width and CCD binning is given in Table 1, more details on each observation are available through the ESO archive1. We only remark that in the visitor run of April 2008 (observer L. Sbordone) we lost almost half of the time, due to strong northern wind, which prohibited pointing of our targets. The run of August 2008 (observer Ludwig) was instead quite succesful. The instrumental set-up was similar for the service and the visitor-mode observations. In both cases we used the dichroic #1 390+580 nm setting. In the service mode we used a 1.″\hbox{$\farcs$}4 wide slit and 2  ×  2 on-chip binning. This was made to collect as many photons as possible for these faint stars, however, if the seeing was less than the slit width, the actual resolution was set by the seeing. In the visitor observations, the same philosphy was employed, but if the observer noticed that the seeing was much smaller than the slit width he had the opportunity of narrowing the slit width and, if the chosen slit width was less than, or equal to 0.″\hbox{$\farcs$}8, also to change the binning to 1  ×  1 binning. The data of period 78 were retrieved reduced from the ESO archive, we reduced the observations of period 81 using the UVES pipeline.

thumbnail Fig. 1

The signal-to-noise ratio as a function of wavelength in the blue-arm spectra. This is a by-product of MyGIsFOS, which calculates it in all the continuum regions.

thumbnail Fig. 2

Portion of the spectrum of SDSS J122935+262445, one of the lowest S/N spectra in our sample. The boxes show the wavelength intervals used to fit the lines (blue for Fe i lines, green the Si i line, red the Ti ii line), when they are shaded it means that MyGIsFOS has rejected the line. Two boxes showing continuum regions are also shown (grey boxes). Horizontal dashed and dotted lines indicate the local 1σ and 3σ estimated noise ranges. Vertical magenta continuous and dashed lines (in the top part of the plot) indicate by how much every single line has been shifted in radial velocity by MyGIsFOS to achieve an optimal fit.

For each star we had several spectra of slightly different resolution. To combine the spectra, we estimated the actual resolution from a number of unblended lines and then convolved each spectrum with a Gaussian so that the final resolution was either 13.9  km s-1 or 12  km s-1.

Two stars, SDSS J002113–005005 and SDSS J004029+ 160416 were observed both in period 78 and period 81. We decided to analyse the two sets of spectra independently to obtain a consistency check.

The signal-to-noise ratios obtained are shown in Fig. 1 for the blue arm, where this ratio is lowest.

Star SDSS J153110+095255 was observed in ESO period 81, a preliminary analysis confirms that its metallicity is about −3.0, yet the star is double-lined spectroscopic binary. This star was excluded from the present sample and will be analysed when more spectra are available.

4. Abundance analysis

The analysis was performed with the MyGIsFOS code (Sbordone et al. 2010b; Sbordone et al., in prep.). The code evolved from the code of Bonifacio & Caffau (2003), and was entirely re-coded in fortran 90 with several improvements. Briefly: this program compares the observed spectrum to a grid of synthetic spectra and performs χ2 fitting. The most noticeable improvement is a loop to determine the surface gravity from the iron ionisation equilibrium. The grid of synthetic spectra was computed from a grid of ATLAS 12 (Kurucz 2005; Castelli 2005; Sbordone et al. 2004; Sbordone 2005) model atmospheres. Convection was treated in the mixing-length approximation with αMLT = 1.25. The grid covers the effective temperatures 5400–7000 K at steps of 200 K, logarithmic surface gravities 3.5–4.5 (cgs units) at steps of 0.5 dex, logaritmic metallicities in the range −4.0 to −2.0, at steps of 0.5 dex, [α/Fe] = 0.0, +0.4 and microturbulent velocities of 1,2,3  km s-1.

The effective temperature was considered a prior and was derived from the (g − z)0 colour using the calibration presented in Ludwig et al. (2008). We checked the effective temperatures also with fits of the wings of Hα based on CO5BOLD models, as in Sbordone et al. (2010a), these provide temperature that are hotter, on average, by 116 K. In five cases the fits required extrapolation beyond the range of the CIFIST grid (Ludwig et al. 2009). We decided to keep the photometric temperatures, to make the comparison of the metallicities with those derived from the SDSS spectra straightforward. The surface gravity was determined from the iron ionisation equilibrium. If no Fe ii lines were retained in the analysis, then the surface gravity was held fixed at the starting value, log g = 4.0. The ratio [α/Fe] was determined from the Mg and Ca lines. The solar abundances adopted are given in Table 2, Fe is from Caffau et al. (2011a), the other elements are from Lodders et al. (2009).

thumbnail Fig. 3

Same as Fig. 2, but for SDSS J004029+160416 observed in period 81, probably the best spectrum of the sample. In this case none of the lines is rejected.

Table 2

Adopted solar abundances.

Table 3

Sloan photometry for the programme stars.

Two examples of fits performed by MyGIsFOS are shown in Figs. 2 and 3, illustrating the capability of MyGIsFOS to reject poor fits. That we recovered the same abundances, within errors, for the two stars for which we analysed the spectra observed in period 78 and 81 independently, reassures us about the robustness and reproducibility of MyGIsFOS.

The resulting chemical abundances are provided in Tables 5 and 6. For chemical species for which several lines are measurable, we provide the standard deviation of the abundances derived from the different lines (line-to-line scatter). This can be assumed to be a reasonable estimate of the error on the provided abundance or abundance ratio. The different quality (S/N ratio) of the spectra is immediately reflected in the line-to-line scatter of a species with many lines available, such as Fe i. This is indeed illustrated in Fig. 4. For species for which only one line is available the error could be estimated from the S/N in the spectrum at the wavelength of the line. With the spectra at hand this should be in the range 0.1–0.2 dex.

The systematic error caused by the uncertainty in atmospheric parameters has been treated in many papers. For an estimate we refer the readers to Table 4 of Bonifacio et al. (2009), the systematic errors in our analysis are essentially the same.

Table 4

Coordinates and atmospheric parameters for the programme stars.

thumbnail Fig. 4

Line-to-line scatter in the Fe i abundances as a function of the S/N ratio at 420 nm. There is a clear correlation between the two.

For lithium we did not use MyGIsFOS, but we measured the equivalent widths by fitting synthetic profiles, as described in Bonifacio et al. (2002) and then determined the lithium abundances by using the fitting formula of Sbordone et al. (2010a), based on CO5BOLD 3D models (Freytag et al. 2002; Wedemeyer et al. 2004; Freytag et al. 2012) and NLTE treatment of line transfer. For the stars for which we could not detect the Li doublet we estimated the upper limit at 3σ by using the Cayrel formula (Cayrel 1988). The results are provided in Table 7.

Star SDSS J090733+024608 is in common between us and Caffau et al. (2011b), the abundances derived by us from the UVES spectrum of this star agree excellently with those derived by Caffau et al. (2011b) from the X-Shooter spectrum.

Table 5

Abundances of the α elements and strontium.

Table 6

Abundances of the iron peak elements.

5. Distances

Using the SDSS photometry and theoretical isochrones, it is possible to estimate the distances of our sample of stars. We used the Padova isochrone (Girardi et al. 2002) with Z = 0.0001 and an age of 13.5 Gyr. To read the absolute magnitude from the isochrone it is necessary to decide whether a star is above or below the turn-off. For any set of atmospheric parameters we assumed the star is on the Main Sequence (MS, i.e. it is below the TO) if log g  ≥ 4.18 and on the sub giant branch (SG, i.e. is above the TO) if log g  < 4.18. This distinction is based on the estimated surface gravity of the TO from the theoretical isochrone. In Table 8 we provide the distances, d, from the Sun derived in this way, averaged over the five SDSS bands, in kpc. In the column σd we provide the standard deviation of the distances derived from the different bands. This should not be used as an estimate for the errors on our distances, but only as a sanity check of the consistency of the photometry in the different bands. For star SDSS J090733+024608Caffau et al. (2011b) estimate a distance that is about 1 kpc larger, becasue they chose a different isochrone. This difference can be taken as an estimate of the uncertainty on our distances.

We also provide the distances from the Galactic centre, computed as 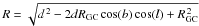R=d 2−2dRGCcos(b)cos(l)+RGC 2\hbox{$R = \sqrt { d^{\,2} - 2 d R_{\rm GC}\cos(b)\cos(l) + R_{\rm GC}^{\,2} }$} where RGC is the Sun-Galactic centre distance, taken to be 8.5 Kpc, l,b are Galactic longitude and latitude. As expected from their faintness, the stars are distant.

In the last column of Table 8 we also provide the barycentric radial velocities, computed by cross-correlation of the blue spectra against a synthetic template, after masking out the Balmer lines. For the stars for which we have multiple observations the standard deviation of the different radial velocities never exceeds 0.6  km s-1, thus none of the stars shows any radial velocity variations. The radial velocity accuracy is dominated by the systematics, and mainly by the centering of the star in the slit. The plate scale of the UVES blue arm (0.″\hbox{$\farcs$}215 or 0.0019 nm in the dispersion direction) implies that an error of 0.″\hbox{$\farcs$}2 in centering, corresponds to 1.3  km s-1, this can be taken as an estimate of the absolute error on radial velocities. Our measured radial velocity for SDSS J090733+024608 agrees excellently with the measurement of Caffau et al. (2011b) from their X-Shooter spectrum.

Table 7

Abundances of lithium in the programme stars.

Bonifacio et al. (2009) did not estimate distances for their sample of stars, and it is beyond the purpose of the present paper to provide such estimates for those stars. Suffice it to say that the V magnitudes of the Bonifacio et al. (2009) sample range from 13 to 15.2, while most of the stars in the present sample have g magnitudes between 16 and 17.5. Given that V and g magnitudes are fairly similar for stars of these spectral types, we expect the stars of the present sample to be on average four times more distant2.

6. Discussion

The first thing to remark is the quite good performance of the [Fe/H] estimates obtained from the SDSS spectra, down to about [Fe/H]  = −3.5. Owing to the few objects at lowest metallicity no definite conclusion can be drawn whether the metallicity estimates based on SDSS spectra are biased. However, the low metallicity of SDSS J102915+172927 (Caffau et al. 2011c) indicates that this is not very likely.

The fact that at low metallicity the estimate based on SDSS spectra relies essentially on the Ca ii K line implies that the method is prone to underestimate the abundances of stars that are not enhanced in α elements, as discussed in Bonifacio et al. (2011).

Considering the results of the present paper, of Caffau et al. (2011b) and Caffau et al. (2011c, 2012) together allows us to conclude that the metallicities estimated from the SDSS spectra are reliable, in a statistical sense, at least down to [Fe/H] = −5. The study of the halo metallicity distribution based on the SDSS spectra will be adressed in a future paper.

The results on the chemical composition of the present sample of stars suggests that, by and large, they are “typical” halo stars compared to the sample of Bonifacio et al. (2009), as we did in Figs. 6 to 9. Below we remark on the groups of elements.

thumbnail Fig. 5

Difference between the [Fe/H] derived from the UVES spectra and that derived from the SDSS spectra as a function of [Fe/H]SDSS. Evidently down to [Fe/H]  ~ −3.5 is accurate to about 0.2 dex, but rapidly increases below. The open symbols are the stars observed with X-Shooter by Caffau et al. (2011b). The star symbol is SDSS J102915+172927 (Caffau et al. 2011c).

thumbnail Fig. 6

Ratios of alpha elemements to iron for our programme stars (filled circles) compared to those of the stars of Bonifacio et al. (2009) (open circles). The spectra of SDSS J004029+160416 and SDSS J002113-005005 observed in periods 78 and 81 were treated independently and the points referring to the derived abundances are connected by a line. The one referring to the two measures of SDSS J004029+160416 is not visible, since the two points are indistinguishable at the resolution of the plot.

thumbnail Fig. 7

Ratios of even iron-peak elemements to iron for our programme stars (filled circles) compared to those of the stars of Bonifacio et al. (2009) (open circles). In the lower panel the two measures of Cr ii lines are shown as  ×  symbols.

thumbnail Fig. 8

Ratios of odd iron-peak elemements to iron for our programme stars (filled circles) compared to those of the stars of Bonifacio et al. (2009) (open circles).

thumbnail Fig. 9

Ratios of strontium to iron for our programme stars (filled circles) compared to those of the stars of Bonifacio et al. (2009) (open circles).

thumbnail Fig. 10

Mn i 403 nm resonance triplet plotted for star SDSS J144640+ 124917 (above) and SDSS J004029+160416. The spectra are normalized, and the continuum for star SDSS J004029+160416 was shifted down to 0.75 for readibility. The wavelengths of the three Mn lines are marked. Star SDSS J004029+160416 is 280 K warmer and about 0.1 dex more metal-poor. Gravity is almost the same. [Mn/Fe] = −0.08 in SDSS J144640+124917 and −0.67 in SDSS J004029+160416.

thumbnail Fig. 11

Lithium abundance as a function of [Fe/H] for our sample of stars (filled hexagons), together with the stars of Sbordone et al. (2010a, open hexagons), the two components of the binary system CS 22876-32 (González Hernández et al. 2008, crosses), the three Li-depleted stars G 122-69, G 139-8, G 186-26 from Norris et al. (1997, asterisks), star SDSS J102915+172927, from Caffau et al. (2011c, star symbol) and star HE 1327-2326 from Frebel et al. (2008, crossed square).

thumbnail Fig. 12

Lithium abundance as a function of Teff, the symbols are the same as in Fig. 11.

6.1. α elements

In Fig. 6 we compare the present results with those of Bonifacio et al. (2009), which were rescaled to the solar abundances here adopted. The abundance ratios of our stars show a larger scatter than those of Bonifacio et al. (2009) and we interpret this result as caused by the lower S/N ratio of our spectra. The [Ca/Fe] ratio in the figure is the straight average of the abundance derived from Ca i lines and the Ca ii 370.6024 nm, when both are available, although in several cases there is a sizeable difference in the two abundances, this could arise from an incorrect gravity. The most striking case is that of SDSS J144640+124917, for which the Ca i 445.4779 nm line provides [Ca/Fe] = +0.51, while the Ca ii 370.6024 nm, provides [Ca/Fe] = −0.26. The current version of MyGIsFOSadjusts the gravity only on the iron ionisation equilibrium, use of other elements is possible in future implementations. Two stars, SDSS J082521+040334 and SDSS J154246+054426 show a negative [Ca/Fe], based only on the Ca ii 370.6024 nm line, remarkably, they also show a negative [Ti/Fe], although both have standard enhancement of Si and Mg.

SDSS J130017+263238 ([Fe/H] = −3.65) shows a value of [Si/Fe], [Mg/Fe] and [Ca/Fe], which is higher than the mean value of the sample, but this is not the case for [Ti/Fe].

The two spectra of SDSS J004029+160416 provide very similar abundances, so that they are not distinguishable in the plot. Instead the two spectra of SDSS J002113-005005 imply a difference of 0.1 dex in [Fe/H]; to identify that the two points refer to the same star we connected them with a line in Fig. 6 and all subsequent plots.

6.2. Even iron peak elements

The abundances of Ni and Cr behave as expected, the decrease of the [Cr/Fe] is probably driven by NLTE effects, as testified by the two measurements of Cr ii lines and discussed in Bonifacio et al. (2009) and Bergemann & Cescutti (2010). There is one star, SDSS J082521+040334, which has a remarkably high [Ni/Fe] = +0.48, note that this star also has low [Ca/Fe] and [Ti/Fe]. Three more stars have [Ni/Fe]  ~ +0.3, SDSS J113528+010848, SDSS J154246+054426 and SDSS J230814–085526. Considering the errors, all these are compatible with [Ni/Fe]  ~ 0 at 2σ. The straight mean of all values is  ⟨  [Ni/Fe]  ⟩  = 0.13  ±  0.16, again compatible with zero.

Table 8

Galactic coordinates, distances from the Sun and from the Galactic centre, and barycentric radial velocities, for the programme stars.

6.3. Odd iron peak elements

The elements Sc and Co show a behaviour that totally agrees with that found by Bonifacio et al. (2009). Only Mn is higher on average and a few stars show a [Mn/Fe] that is almost solar, while others show [Mn/Fe] as low as −0.5 dex or lower. Both in the present paper and in Bonifacio et al. (2009) the abundances are derived from the Mn i resonance triplet at 403 nm. In the plots we did not adopt the correction of +0.4 dex suggested by Bonifacio et al. (2009), based on the offset found in giant stars between resonance and high excitiation lines. Bergemann & Gehren (2008) have computed Mn abundances for a sample of metal-poor dwarfs, and for their model closest to the parameters of our stars (Teff = 6000, log g = 4.0, [M/H] = −3.0) they found a sizeable NLTE correction of about 0.6 dex for the resonance triplet, but their computations do not show strong variations of the NLTE corrections with either temperature, metallicity, or gravity. Although a wider set of computations would be desirable, it does seem unlikely that the scatter we observe in Mn abundances is caused by differential NLTE effects. In Fig. 10 we compare two stars whose [Mn/Fe] ratios differ by 0.5 dex, clearly the difference of almost 300 K in effective temperature between the two stars cannot justify the obvious difference in line strength. It is possible that there is some real scatter in Mn abundances, and one should keep in mind that also in the sample of Bonifacio et al. (2009) there are at least two stars with relatively high [Mn/Fe], although at slightly higher metallicities.

6.4. Strontium

Strontium is the only neutron capture element that we are able to measure in this sample of stars. It shows a large scatter in [Sr/Fe] ratios, as expected (Burris et al. 2000; Barklem et al. 2005; François et al. 2007), and is compatible with the results of Bonifacio et al. (2009).

6.5. Lithium

We measured lithium abundances for 12 stars and provide four upper limits. In Figs. 11 and 12 we show the lithium abundances in our stars. We also added to the plot the stars of Sbordone et al. (2010a) and the two components of the binary system CS 22876-32 (González Hernández et al. 2008, crosses), the three Li-depleted stars G 122-69, G 139-8, G 186-26 from Norris et al. (1997, asterisks), star SDSS J102915+172927 from Caffau et al. (2011c, star symbol) and star HE 1327-2326 from Frebel et al. (2008, crossed square).

Our measured equivalent width of the Li i doublet for star SDSS J090733+024608, agrees excellently with that of Caffau et al. (2011b). This is the only star for which they could measure lithium from the X-Shooter spectra.

The present results reinforce the existence of the meltdown of the Spite plateau at low metallicities, found by Aoki et al. (2009) and Sbordone et al. (2010a). In particular the upper limits, which are quite stringent, call for strong depletions. However, in spite of the evident meltdown it is remarkable that two of the lowest metallicity stars of the sample, SDSS J130017+263238, and SDSS J090733+024608, stay on the Spite plateau, implying that the meltdown is not a mere increase of Li depletion with decreasing metallicity.

It is intriguing that the two most iron-poor objects in the plot, HE 1327-2326 and SDSS J102915+172927, display no lithium. In Figs. 11 and 12 we plot the upper limits as provided by Frebel et al. (2008) and Caffau et al. (2011c), respectively, although in the first case it is a 3σ upper limit, while in the latter it is a 5σ upper limit, by adopting the same criterion the two upper limits would lie roughly at the same level. Caffau et al. (2011c) have pointed out that given the peculiar chemical composition of HE 1327-2326, there is little connection between its iron abundance and its metallicity Z. By plotting the lithium abundances as a function of carbon abundance, rather than of iron abundance, HE 1327-2326 occupies the same region in the diagram as the well-known Li-depleted stars G 122-69, G 139-8 and G 186-26. The known Li-depleted stars are a handful and at [Fe/H]  > −3.0 they are only a few percent of the warm halo stars. The fact that in a very limited sample, like ours, we find three new Li-depleted stars suggests that these stars are more frequently found at low [Fe/H]. There is no widely accepted explanation of the Li-depleted stars. Probably the most promising hypothesis is that of Ryan et al. (2002), who measured sizeable rotational velocities in some of the Li-depleted stars and suggested that they are “blue stragglers to be”, i.e. although they have colours that are currently compatible with the halo turn-off, in the future, as the TO stars evolve to redder colours, they will remain in their current position in the colour–magnitude diagram. Although it is well known that blue stragglers display no lithium (Glaspey et al. 1994), the reasons for this, or for the blue stragglers phenomenon, for that matter, are not well understood. Although promising, the Ryan et al. (2002) hypothesis does not readily provide any argument that could explain a higher frequency of these objects at low [Fe/H].

There are many mechanisms that can destroy lithium, all of which imply that the material is processed at temperatures exceeding two million degrees. In the present state of affairs it is difficult to argue that one and the same mechanism is responsible for all the Li-depleted stars. At the same time it is not clear if Li-depleted stars are related to the Spite plateau meltdown.

Figure 12 shows that Li-depleted stars are not confined to a particular range in Teff. The hottest Li-depleted star has an effective temperature of 6400 K.

7. Conclusions

Thanks to a very efficient technique of selecting EMP stars from the Sloan Digital Sky Survey, we have considerably increased the sample of stars at the lowest metallicities for which detailed chemical abundances were measured. Note that while in the sample of Bonifacio et al. (2009) there was only one dwarf star with [Fe/H]  < −3.4, the present sample comprises six such stars. The agreement between the metallicities estimated from the SDSS spectra and those derived from the UVES spectra suggests that the former are reliable, at least in a statistical sense, for investigating the metallicity distribution of the halo.

The chemical composition of the sample of stars presented here is consistent with that of the sample of Bonifacio et al. (2009), suggesting that the halo was well mixed at all probed metallicities. The only possible exception is a sizeable scatter in Mn abundances. This indication should be taken with caution however, given the lower S/N ratio of the present data compared to that of Bonifacio et al. (2009), and because there are still only few observed stars.

The relatively high S/N ratios in the red part of the spectra allowed us to increase the sample of dwarf stars with measured lithium abundance at metallicities below –3.0. The meltdown of the Spite plateau is confirmed and the three upper limits show the occurance of strong lithium depletions, at least in some cases. On the other hand, the presence at the lowest metallicities of non-depleted stars on the Spite plateau implies that the meltdown depends on some other parameter besides metallicity.

Online material

Table 1

Log of the observations.

2

If two stars have the same absolute magnitude and different apparent magnitudes m1 and m2, the ratios of their distances is log (d1/d2) = (m1 − m2)/5. Thus if m1 − m2 = 3, then d1 ≈ 4d2.

Acknowledgments

We acknowledge support from the Programme National de Physique Stellaire (PNPS) and the Programme National de Cosmologie et Galaxies (PNCG) of the Institut National de Sciences de l’Universe of CNRS. H.G.L. acknowledges financial support by the Sonderforschungsbereich SFB 881 “The Milky Way System” (subproject A4) of the German Research Foundation (DFG).

References

  1. Adelman-McCarthy, J. K., Agüeros, M. A., Allam, S. S., et al. 2007, ApJS, 172, 634 [NASA ADS] [CrossRef] [Google Scholar]
  2. Adelman-McCarthy, J. K., Agüeros, M. A., Allam, S. S., et al. 2008, ApJS, 175, 297 [NASA ADS] [CrossRef] [Google Scholar]
  3. Aoki, W., Barklem, P. S., Beers, T. C., et al. 2009, ApJ, 698, 1803 [NASA ADS] [CrossRef] [Google Scholar]
  4. Barklem, P. S., Christlieb, N., Beers, T. C., et al. 2005, A&A, 439, 129 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  5. Behara, N. T., Bonifacio, P., Ludwig, H.-G., et al. 2010, A&A, 513, A72 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  6. Belokurov, V., Zucker, D. B., Evans, N. W., et al. 2006, ApJ, 642, L137 [NASA ADS] [CrossRef] [Google Scholar]
  7. Bergemann, M., & Cescutti, G. 2010, A&A, 522, A9 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  8. Bergemann, M., & Gehren, T. 2008, A&A, 492, 823 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  9. Bonifacio, P., & Caffau, E. 2003, A&A, 399, 1183 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  10. Bonifacio, P., Pasquini, L., Spite, F., et al. 2002, A&A, 390, 91 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  11. Bonifacio, P., Spite, M., Cayrel, R., et al. 2009, A&A, 501, 519 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  12. Bonifacio, P., Caffau E., Ludwig, H.-G., et al. 2010, IAU XVII General Assembly, Joint Discussion 5, ed. J. Binney [Google Scholar]
  13. Bonifacio, P., Caffau, E., François, P., et al. 2011, Astron. Nachr., 332, 251 [NASA ADS] [CrossRef] [Google Scholar]
  14. Bromm, V., & Loeb, A. 2003, Nature, 425, 812 [NASA ADS] [CrossRef] [EDP Sciences] [PubMed] [Google Scholar]
  15. Burris, D. L., Pilachowski, C. A., Armandroff, T. E., et al. 2000, ApJ, 544, 302 [NASA ADS] [CrossRef] [Google Scholar]
  16. Caffau, E., Ludwig, H.-G., Steffen, M., Freytag, B., & Bonifacio, P. 2011a, Sol. Phys., 268, 255 [NASA ADS] [CrossRef] [Google Scholar]
  17. Caffau, E., Bonifacio, P., François, P., et al. 2011b, A&A, 534, A4 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  18. Caffau, E., Bonifacio, P., François, P., et al. 2011c, Nature, 477, 67 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
  19. Caffau, E., Bonifacio, P., François, P., et al. 2012, A&A, 542, A51 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  20. Carollo, D., Beers, T. C., Lee, Young, S., et al. 2007, Nature, 450, 1020 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
  21. Carollo, D., Beers, T. C., Chiba, M., et al. 2010, ApJ, 712, 692 [NASA ADS] [CrossRef] [Google Scholar]
  22. Castelli, F. 2005, Mem. Soc. Astron. Ital. Supp., 8, 25 [Google Scholar]
  23. Cayrel, R. 1988, in The Impact of Very High S/N Spectroscopy on Stellar Physics, ed. G. Cayrel de Strobel, & M. Spite, IAU Symp., 132, 345 [Google Scholar]
  24. Dekker, H., D’Odorico, S., Kaufer, A., Delabre, B., & Kotzlowski, H. 2000, Proc. SPIE, 4008, 534 [Google Scholar]
  25. D’Odorico, S., Dekker, H., Mazzoleni, R., et al. 2006, Proc. SPIE, 6269, [Google Scholar]
  26. Eggen, O. J., Lynden-Bell, D., & Sandage, A. R. 1962, ApJ, 136, 748 [NASA ADS] [CrossRef] [Google Scholar]
  27. Font, A. S., McCarthy, I. G., Crain, R. A., et al. 2011, MNRAS, 416, 2802 [NASA ADS] [CrossRef] [Google Scholar]
  28. François, P., Depagne, E., Hill, V., et al. 2007, A&A, 476, 935 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  29. Frebel, A., Johnson, J. L., & Bromm, V. 2007, MNRAS, 380, L40 [NASA ADS] [CrossRef] [Google Scholar]
  30. Frebel, A., Collet, R., Eriksson, K., Christlieb, N., & Aoki, W. 2008, ApJ, 684, 588 [NASA ADS] [CrossRef] [Google Scholar]
  31. Freytag, B., Steffen, M., & Dorch, B. 2002, Astron. Nachr., 323, 213 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  32. Freytag, B., Steffen, M., Ludwig, H.-G., et al. 2012, J. Comp. Phys., 231, 919 [Google Scholar]
  33. Girardi, L., Bertelli, G., Bressan, A., et al. 2002, A&A, 391, 195 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  34. Glaspey, J. W., Pritchet, C. J., & Stetson, P. B. 1994, AJ, 108, 271 [NASA ADS] [CrossRef] [Google Scholar]
  35. González Hernández, J. I., Bonifacio, P., Ludwig, H.-G., et al. 2008, A&A, 480, 233 [NASA ADS] [CrossRef] [EDP Sciences] [MathSciNet] [Google Scholar]
  36. Helmi, A. 2008, A&ARv, 15, 145 [CrossRef] [Google Scholar]
  37. Kurucz, R. 1993, SYNTHE Spectrum Synthesis Programs and Line Data, Kurucz CD-ROM No. 18 (Cambridge, Mass.: Smithsonian Astrophysical Observatory) [Google Scholar]
  38. Kurucz, R. L. 2005, Mem. Soc. Astron. Ital. Supp., 8, 14 [Google Scholar]
  39. Li, H. N., Christlieb, N., Schörck, T., et al. 2010, A&A, 521, A10 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  40. Lodders, K., Palme, H., & Gail, H.-P. 2009, in Landolt-Börnstein – Group VI Astronomy and Astrophysics Numerical Data and Functional Relationships in Science and Technology, Vol. 4B, Solar System, ed. J. E. Trümper, 44 [Google Scholar]
  41. Ludwig, H.-G., Bonifacio, P., Caffau, E., et al. 2008, Phys. Scr. T, 133, 014037 [Google Scholar]
  42. Ludwig, H.-G., Caffau, E., Steffen, M., et al. 2009, Mem. Soc. Astron. Italiana, 80, 711 [Google Scholar]
  43. Majewski, S. R. 1992, ApJS, 78, 87 [NASA ADS] [CrossRef] [Google Scholar]
  44. Marigo, P., Girardi, L., Bressan, A., et al. 2008, A&A, 482, 88 [Google Scholar]
  45. Mashonkina, L., Korn, A. J., & Przybilla, N. 2007, A&A, 461, 261 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  46. Norris, J. E., Ryan, S. G., Beers, T. C., & Deliyannis, C. P. 1997, ApJ, 485, 370 [NASA ADS] [CrossRef] [Google Scholar]
  47. Piau, L., Beers, T. C., Balsara, D. S., et al. 2006, ApJ, 653, 300 [NASA ADS] [CrossRef] [Google Scholar]
  48. Richards, G. T., Fan, X., Newberg, H. J., et al. 2002, AJ, 123, 2945 [NASA ADS] [CrossRef] [Google Scholar]
  49. Ryan, S. G., & Norris, J. E. 1991, AJ, 101, 1865 [NASA ADS] [CrossRef] [Google Scholar]
  50. Ryan, S. G., Gregory, S. G., Kolb, U., Beers, T. C., & Kajino, T. 2002, ApJ, 571, 501 [NASA ADS] [CrossRef] [Google Scholar]
  51. Salvadori, S., Schneider, R., & Ferrara, A. 2007, MNRAS, 381, 647 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
  52. Sbordone, L. 2005, Mem. Soc. Astron. Ital. Supp., 8, 61 [Google Scholar]
  53. Sbordone, L., Bonifacio, P., Castelli, F., & Kurucz, R. L. 2004, Mem. Soc. Astron. Ital. Supp., 5, 93 [Google Scholar]
  54. Sbordone, L., Bonifacio, P., Caffau, E., et al. 2010a, A&A, 522, A26 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  55. Sbordone, L., Bonifacio, P., Caffau, E., & Ludwig, H.-G. 2010b [arXiv:1009.5210] [Google Scholar]
  56. Schneider, R., Ferrara, A., Salvaterra, R., Omukai, K., & Bromm, V. 2003, Nature, 422, 869 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
  57. Schörck, T., Christlieb, N., Cohen, J. G., et al. 2009, A&A, 507, 817 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  58. Searle, L., & Zinn, R. 1978, ApJ, 225, 357 [NASA ADS] [CrossRef] [Google Scholar]
  59. Wedemeyer, S., Freytag, B., Steffen, M., Ludwig, H.-G., & Holweger, H. 2004, A&A, 414, 1121 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  60. Yanny, B., Rockosi, C., Newberg, H. J., et al. 2009, AJ, 137, 4377 [NASA ADS] [CrossRef] [Google Scholar]
  61. York, D. G., Adelman, J., Anderson, J. E., Jr., et al. 2000, AJ, 120, 1579 [Google Scholar]
  62. Zolotov, A., Willman, B., Brooks, A. M., et al. 2009, ApJ, 702, 1058 [NASA ADS] [CrossRef] [Google Scholar]

All Tables

Table 2

Adopted solar abundances.

In the text
Table 3

Sloan photometry for the programme stars.

In the text
Table 4

Coordinates and atmospheric parameters for the programme stars.

In the text
Table 5

Abundances of the α elements and strontium.

In the text
Table 6

Abundances of the iron peak elements.

In the text
Table 7

Abundances of lithium in the programme stars.

In the text
Table 8

Galactic coordinates, distances from the Sun and from the Galactic centre, and barycentric radial velocities, for the programme stars.

In the text
Table 1

Log of the observations.

In the text

All Figures

thumbnail Fig. 1

The signal-to-noise ratio as a function of wavelength in the blue-arm spectra. This is a by-product of MyGIsFOS, which calculates it in all the continuum regions.
In the text
thumbnail Fig. 2

Portion of the spectrum of SDSS J122935+262445, one of the lowest S/N spectra in our sample. The boxes show the wavelength intervals used to fit the lines (blue for Fe i lines, green the Si i line, red the Ti ii line), when they are shaded it means that MyGIsFOS has rejected the line. Two boxes showing continuum regions are also shown (grey boxes). Horizontal dashed and dotted lines indicate the local 1σ and 3σ estimated noise ranges. Vertical magenta continuous and dashed lines (in the top part of the plot) indicate by how much every single line has been shifted in radial velocity by MyGIsFOS to achieve an optimal fit.
In the text
thumbnail Fig. 3

Same as Fig. 2, but for SDSS J004029+160416 observed in period 81, probably the best spectrum of the sample. In this case none of the lines is rejected.
In the text
thumbnail Fig. 4

Line-to-line scatter in the Fe i abundances as a function of the S/N ratio at 420 nm. There is a clear correlation between the two.
In the text
thumbnail Fig. 5

Difference between the [Fe/H] derived from the UVES spectra and that derived from the SDSS spectra as a function of [Fe/H]SDSS. Evidently down to [Fe/H]  ~ −3.5 is accurate to about 0.2 dex, but rapidly increases below. The open symbols are the stars observed with X-Shooter by Caffau et al. (2011b). The star symbol is SDSS J102915+172927 (Caffau et al. 2011c).
In the text
thumbnail Fig. 6

Ratios of alpha elemements to iron for our programme stars (filled circles) compared to those of the stars of Bonifacio et al. (2009) (open circles). The spectra of SDSS J004029+160416 and SDSS J002113-005005 observed in periods 78 and 81 were treated independently and the points referring to the derived abundances are connected by a line. The one referring to the two measures of SDSS J004029+160416 is not visible, since the two points are indistinguishable at the resolution of the plot.
In the text
thumbnail Fig. 7

Ratios of even iron-peak elemements to iron for our programme stars (filled circles) compared to those of the stars of Bonifacio et al. (2009) (open circles). In the lower panel the two measures of Cr ii lines are shown as  ×  symbols.
In the text
thumbnail Fig. 8

Ratios of odd iron-peak elemements to iron for our programme stars (filled circles) compared to those of the stars of Bonifacio et al. (2009) (open circles).

In the text
thumbnail Fig. 9

Ratios of strontium to iron for our programme stars (filled circles) compared to those of the stars of Bonifacio et al. (2009) (open circles).

In the text
thumbnail Fig. 10

Mn i 403 nm resonance triplet plotted for star SDSS J144640+ 124917 (above) and SDSS J004029+160416. The spectra are normalized, and the continuum for star SDSS J004029+160416 was shifted down to 0.75 for readibility. The wavelengths of the three Mn lines are marked. Star SDSS J004029+160416 is 280 K warmer and about 0.1 dex more metal-poor. Gravity is almost the same. [Mn/Fe] = −0.08 in SDSS J144640+124917 and −0.67 in SDSS J004029+160416.

In the text
thumbnail Fig. 11

Lithium abundance as a function of [Fe/H] for our sample of stars (filled hexagons), together with the stars of Sbordone et al. (2010a, open hexagons), the two components of the binary system CS 22876-32 (González Hernández et al. 2008, crosses), the three Li-depleted stars G 122-69, G 139-8, G 186-26 from Norris et al. (1997, asterisks), star SDSS J102915+172927, from Caffau et al. (2011c, star symbol) and star HE 1327-2326 from Frebel et al. (2008, crossed square).
In the text
thumbnail Fig. 12

Lithium abundance as a function of Teff, the symbols are the same as in Fig. 11.
In the text

Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.

Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.

Initial download of the metrics may take a while.