| Issue |
A&A
Volume 542, June 2012
|
|
|---|---|---|
| Article Number | A9 | |
| Number of page(s) | 8 | |
| Section | Planets and planetary systems | |
| DOI | https://doi.org/10.1051/0004-6361/201118500 | |
| Published online | 25 May 2012 | |
Formation and long-term evolution of 3D vortices in protoplanetary discs
1
Physikalisches Institut & Center for Space and Habitability,
Universität Bern,
3012
Bern,
Switzerland
e-mail: meheut@space.unibe.ch
2
Centre for Plasma Astrophysics, Department of Mathematics,
KU Leuven, Celestijnenlaan
200B, 3001
Heverlee,
Belgium
3
AstroParticule et Cosmologie (APC), Université Paris Diderot,
10 rue A. Domon et L.
Duquet, 75205
Paris Cedex 13,
France
Received: 22 November 2011
Accepted: 13 April 2012
Context. In the context of planet formation, anticyclonic vortices have recently received much attention for the role they can play in planetesimal formation. Radial migration of intermediate-size solids towards the central star may prevent them from growing to larger solid grains. On the other hand, vortices can trap the dust and accelerate this growth, counteracting fast radial transport. Several effects have been shown to affect this scenario, such as vortex migration or decay.
Aims. We aim to study the formation of vortices by the Rossby wave instability and their long-term evolution in a full three-dimensional (3D) protoplanetary disc.
Methods. We used a robust numerical scheme combined with adaptive mesh refinement in cylindrical coordinates, which allowed us to affordably compute long-term 3D evolutions. We considered a full disc radially and vertically stratified, in which vortices can be formed by the Rossby wave instability.
Results. We show that the 3D Rossby vortices grow and survive over hundreds of years without migration. The localised overdensity that initiated the instability and vortex formation survives the growth of the Rossby wave instability for very long times. When the vortices are no longer sustained by the Rossby wave instability, their shape changes towards more elliptical vortices. This allows them to survive shear-driven destruction, but they may be prone to elliptical instability and slow decay.
Conclusions. When the conditions for growing Rossby-wave-related instabilities are maintained in the disc, large-scale vortices can survive over very long timescales and may be able to concentrate solids.
Key words: planets and satellites: formation / protoplanetary disks / hydrodynamics / instabilities / accretion, accretion disks
© ESO, 2012
1. Introduction
The origin of kilometer-sized planetesimals is still an open question of planet formation theory. The growth of micron-size solids towards centimetre or metre blocks is predicted by coagulation models (Dominik 2009), but collisions usually lead to the destruction of these solids (Benz 2000). These collisions arise because the pressure-supported gas moves at sub-Keplerian speed and the solid bodies experience a head wind from the gas because of the drag forces. The consequence is a loss of angular momentum and a radial drift of solids spiraling towards the central star. This can occur on a timescale as short as a hundred years for metre sized blocks at one astronomical unit (Weidenschilling 1977). These timescales are far too short to explain the subsequent growth into larger particles that are unaffected by the head wind.
To overcome these difficulties, anticyclonic vortices, where the velocity streamlines rotate in the opposite direction to the Keplerian flow (Marcus 1990), may be a good environment for planetesimal growth. They induce a drag force towards the centre of the structures, and are therefore proposed as possible nurseries for intermediate-size blocks, concentrating the solids and accelerating the planetesimal formation processes (Barge & Sommeria 1995; Tanga et al. 1996; Bracco et al. 1999; Godon & Livio 1999, 2000; Johansen et al. 2004; Heng & Kenyon 2010). As mentioned by Armitage (2011), vortices can also be important for mechanisms that require an increase in the dust-to-gas ratio, such as the streaming instability (Johansen et al. 2009). Furthermore, Klahr & Bodenheimer (2006) argued that anticyclonic vortices are regions with lower turbulence. Fragmentation is less likely to occur if lower velocity fluctuations prevail.
One of the main difficulties with this scenario is the question of vortice formation. Different instabilities have been proposed for the vortex generation, such as the baroclinic instability (Klahr & Bodenheimer 2003; Klahr 2004) in which interest has been recently revived (Lesur & Papaloizou 2010; Lyra & Klahr 2011), or potentially the magneto-rotational instability (Fromang & Nelson 2005). In this paper we will study the Rossby wave instability (RWI), which may form vortices with unusual elongated shape in regions of particular interest for the long-term survival of those structures. It has recently been pointed out that the survival of the vortices on a sufficient timescale may be a problem. The elliptical instability may destroy three dimensional (3D) elliptical vortices (Lesur & Papaloizou 2009). Moreover, Paardekooper et al. (2010) have shown that vortices can be subject to radial migration towards the disc centre on short timescales.
In this paper, we investigate the generation, the 3D structure and the long-term evolution of vortices formed by the RWI within a protoplanetary disc. This follows the work presented in Meheut et al. (2010), revisited with a new code that allows us to handle long-term simulations. The numerical and physical setup is described in the next section. The results are presented in Sect. 3, followed by a detailed discussion including comparisons with previous works.
2. Methods and setup
2.1. Rossby wave instability
The RWI (Lovelace et al. 1999; Li et al. 2000, 2001) has been studied and discussed in various situations of differentially rotating discs, from galactic discs (Lovelace & Hohlfeld 1978; Sellwood & Kahn 1991) to microquasar and protoplanetary discs (Papaloizou & Pringle 1985; Lovelace et al. 1999). It can be seen as the form that the Kelvin-Helmholtz instability takes in differentially rotating discs, and has a similar instability criterion: it requires an extremum in a vorticity-related quantity, defined in a non-magnetised thin disc as (Li et al. 2000) 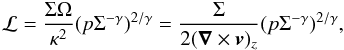 (1)where Σ is the surface density, p the pressure, v is the velocity of the fluid, γ the adiabatic index, Ω the rotation frequency and κ2 = 4Ω2 + 2rΩΩ′ the squared epicyclic frequency (so that κ2/2Ω is the vorticity). Here the prime denotes a radial derivative. For the isentropic discs we consider here, this criterium is reduced to an extremum of
(1)where Σ is the surface density, p the pressure, v is the velocity of the fluid, γ the adiabatic index, Ω the rotation frequency and κ2 = 4Ω2 + 2rΩΩ′ the squared epicyclic frequency (so that κ2/2Ω is the vorticity). Here the prime denotes a radial derivative. For the isentropic discs we consider here, this criterium is reduced to an extremum of 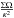 . This quantity is directly related to vortensity defined as the ratio of vorticity to surface density.
. This quantity is directly related to vortensity defined as the ratio of vorticity to surface density.
2.2. Equations
We work in cylindrical coordinates (r,z,ϕ) with the 3D Euler equations 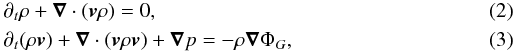 where ρ is the mass density of the fluid, v its velocity, and p its pressure.
where ρ is the mass density of the fluid, v its velocity, and p its pressure. 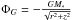 is the gravity potential of the central object with G the gravitational constant and M ∗ the mass of the star. We consider a barotropic flow, i.e. the entropy is constant in the entire system. The pressure is then p = Sργ, with the adiabatic index γ = 5/3 and the constant S related to entropy. The sound speed is given by
is the gravity potential of the central object with G the gravitational constant and M ∗ the mass of the star. We consider a barotropic flow, i.e. the entropy is constant in the entire system. The pressure is then p = Sργ, with the adiabatic index γ = 5/3 and the constant S related to entropy. The sound speed is given by  and the temperature by T ~ p/ρ = Sργ − 1. The temperature is normalised to the temperature at 1 AU.
and the temperature by T ~ p/ρ = Sργ − 1. The temperature is normalised to the temperature at 1 AU.
2.3. Numerics
The numerical methods used for these simulations are inspired by those of Meheut et al. (2010). We used the message passing interface-adaptive mesh refinement versatile advection code (MPI-AMRVAC) developed by Keppens and Meliani (Keppens et al. 2012). The use of a code that allows the mesh to adapt during the simulation has many advantages. One aim is to reach higher resolution in the vortex regions, as well as to have a better resolution in the upper region of the disc, where the gas density decreases abruptly forming a “corona”. The AMR offers flexibility to enforce a lower resolution in this physically irrelevant, but computationally challenging region. Since low-density material can easily be accelerated, which in turn enforces shorter timesteps to maintain numerical stability in explicit time stepping schemes, handling the corona at low resolution is computationally advantageous. The current AMR approach can therefore model the unstable disc on long timescales with similar computing resources as the short timescale run performed earlier. Also, by better numerically representing the disc-corona interface, combined with a sharper limiter function, we have a more robust numerical treatment of the governing equations.
The numerical scheme is the same for all refinement levels, namely the total variation diminishing Lax-Friedrich scheme (see Tóth & Odstrčil 1996) with a third-order accurate Koren limiter (Koren 1993) on the primitive variables. We used a cylindrical grid with r ϵ [1,6] AU, z ϵ [0,0.5] AU and the full azimuthal direction ϕ ϵ [0,2π] . The simulations consider only the upper half of the disc, because the disc mid-plane appeared to be a symmetry plane for the instability in our earlier full vertical simulations (Meheut et al. 2010). If not specified, the length is given in AU and the code unit time corresponds to 1/(2π) yr. The resolution of the base level is (64,32,32). Up to three levels of refinement are allowed, corresponding to an effective resolution of (256,128,128). In the region of the density bump where the instability is expected to grow, the resolution is fixed to the higher level during the whole simulation. The initial grid is presented in Fig. 2, and then evolves to follow the growth of the instability. Because the refinement criterion is the density variation, the grid follows the growth of the spiral density waves propagating radially. At the end of the simulation ~70% of the grid volume is at the highest resolution level. In the beginning, it is only about ~26%, as is shown in Fig. 2. Since refinement happens in all directions, each grid block handled at the base resolution level represents a gain factor of 64 in computational cost compared to a uniform high-resolution run. This gain is even more dramatic when memory issues are considered as well. During the entire run, the corona region is maintained at this lowest resolution, dramatically impacting stability, memory, and wall-clock time.
The boundary conditions are transparent at inner and outer radius, we considered the mid-plane as a symmetry plane and transparent boundary conditions were applied at the upper boundary, while the azimuthal direction is periodic.
2.4. Initial conditions
The initial conditions for the simulations are chosen to represent a protoplanetary disc in radial and vertical equilibrium. We considered that an overdensity is formed at some radius (rbump) of the disc. This bump could have been formed by various effects.
-
1.
The presence of a dead zone in the protoplanetarydisc, corresponding to a region of lower ionisation andresistivity, leads to a lower accretion rate in this region(Gammie 1996). This can induce the forma-tion of an overdensity at the edges of this region (Varnière& Tagger 2006; Lyraet al. 2008; Kretkeet al. 2009), which can inturn trigger the RWI. The initial density bump used in thispaper is a Gaussian fit to the one obtained in Varnière &Tagger (2006), when the instability started togrow.
-
2.
The ice sublimation front (“snow line”) can also be responsible for the formation of an overdensity (Kretke & Lin 2007). One can note that an extremum of entropy should be located in this region, which may also trigger the RWI (Lovelace et al. 1999).
-
3.
It has also been shown that the RWI grows at the edge of planet gaps (Koller et al. 2003; Lin & Papaloizou 2011).
The radial positions of these regions depend on the physical characteristics of the disc (such as accretion rate and temperature) or the position of the planets. We have chosen to place the bump at a distance of 3 AU, which is a plausible region for these different effects.
The initial mid-plane density is given by 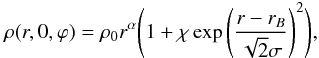 (4)with ρ0 = 3 × 10-9 g cm-3 the density at r = 1 AU, and α = −1.5 the power law index of the underlying density. This value for the alpha parameter gives a surface density varying approximately as Σ ~ r−1/2 if there is no bump. Parameters rB = 3 AU, χ = 1, and σ = 0.1 AU are the radius, amplitude, and width of the Gaussian bump.
(4)with ρ0 = 3 × 10-9 g cm-3 the density at r = 1 AU, and α = −1.5 the power law index of the underlying density. This value for the alpha parameter gives a surface density varying approximately as Σ ~ r−1/2 if there is no bump. Parameters rB = 3 AU, χ = 1, and σ = 0.1 AU are the radius, amplitude, and width of the Gaussian bump.
The vertical and radial force equilibria give the initial vertical structure in density and azimuthal velocity, respectively. The pressure is calculated with constant entropy, with S = 10-3. The mid-plane and vertical density profile chosen as initial condition are shown in Figs. 1 and 2.
The azimuthal velocity is close to Keplerian where the deviation from Keplerian rotation is due to the pressure gradient. In most of the disc, except in the inner part of the bump, the gas is then sub-Keplerian. There is initially no vertical velocity, while a very low radial velocity perturbation is added to the equilibrium as a seed for the instability. These are random perturbations, meaning that all the spatial frequencies in the three directions are present in the seed.
3. Results
The evolution of the pressure bump in a protoplanetary disc was followed over more than 600 years (tmax = 4000). This timescale corresponds to ~123 rotations of the overdensity and ~43 rotations at the outer edge of the grid. This configuration allows the development of the Rossby wave instability, and we present here the characteristics of the 3D flow under this instability and its non-linear evolution.
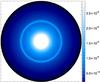 |
Fig. 1 Mid-plane density of the gas in g cm-3. The density bump is placed at 3 AU. |
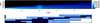 |
Fig. 2 Initial gas density in the disc in g cm-3 (up) and AMR grid (down). The three levels are plotted in white, blue and dark blue from lower to higher resolution. The highest resolution is reached in the overdensity region and at the interface between the disc and corona. |
 |
Fig. 3 Density (left), density perturbations and velocity streamlines (centre), perturbed vortensity defined as ζ − ⟨ ζ ⟩ ϕ with ζ = (∇ × v)z/ρ (right) at t = 100,300,800 from top to bottom. |
3.1. Growth of the RWI
The RWI is characterised by vortex waves in the region of the pressure bump and spiral density waves propagating on each side of the bump. These features can be seen in Fig. 3 where the vortex waves can be identified by the vortensity extrema or the velocity streamlines characteristic for these waves. In the upper plot, the inner and outer Rossby waves are visible. Spiral density waves are emitted from each vortex inwards and outwards (e.g. at t = 300). The growth of the instability is quantified in Figs. 4 and 5. The linear phase of the instability corresponds to the exponential growth of the perturbations until t ~ 300 when the density perturbation reaches ~20% of the initial density. The straight line corresponds to a linear fit of the amplitude growth of the density perturbation in logarithmic scale. This fit gives a growth rate of γ = 0.033Ω0 in code units, which corresponds to 0.17Ω(rB) or 0.21 yr-1. We have also plotted the amplitude evolution of selected azimuthal modes, out of the Fourier transform of the density 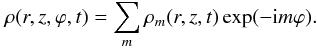 (5)The most unstable mode during the exponential growth has azimuthal mode number m = 5, but lower azimuthal mode numbers are then excited by the m = 5 mode, leading to their growth, with m = 1 and m = 2 shown in the figure. The mode number corresponds, in Fig. 3 to the number of anticyclonic vortices, which are those counter-rotating the Keplerian rotation. They correspond to high pressure and negative vortensity regions. Very many anticyclonic vortices result from the initial random perturbations, which rapidly decrease to 5.
(5)The most unstable mode during the exponential growth has azimuthal mode number m = 5, but lower azimuthal mode numbers are then excited by the m = 5 mode, leading to their growth, with m = 1 and m = 2 shown in the figure. The mode number corresponds, in Fig. 3 to the number of anticyclonic vortices, which are those counter-rotating the Keplerian rotation. They correspond to high pressure and negative vortensity regions. Very many anticyclonic vortices result from the initial random perturbations, which rapidly decrease to 5.
 |
Fig. 4 Time evolution of the amplitudes of the density perturbations in a logarithmic scale. The time is given in code units (lower axis) and in years (upper axis). We also show the amplitude of some of the modes with low mode number. The upper figure is a zoom on the exponential growth where we have added a linear fit for the dominant mode, whose growth rate is 0.033 in code units. |
 |
Fig. 5 Time evolution of the enstrophy in a logarithmic scale. The time is given in code units (lower axis) and in years (upper axis). |
3.2. Saturation of the RWI
 |
Fig. 6 Comparison of the amplitude of the first 10 azimuthal modes between t = 0 and t = 400 (left) and over the whole simulation (right). The instability is dominated by the mode m = 5 but both lower and higher azimuthal modes are excited during the growth phase. The decaying phase shows a shift to lower azimuthal mode number. |
After the exponential growth, the instability reaches saturation owing to non-linearities that induce mode mixing. Figure 6 shows the amplitude of the modes at saturation. The fifth mode clearly dominates for quite some time, and modes with high azimuthal mode number are less prominent, but very low and intermediate azimuthal mode numbers are non-linearly excited by the prevailing mode. However, one can see in Fig. 3 that later on (t = 800) m = 2 dominates, and then m = 1 until the end of the simulation (see Fig. 6). On the other hand, the higher mode numbers (5 < m < 10) are not dominant after saturation. Accordingly, the general sketch of the instability is first the linear growth of the fifth mode, then saturation is reached and the higher wavelength modes (lower mode number) dominate with a transfer towards larger scales. This evolution diminishes the number of vortices through merging, as described in Godon & Livio (1999). This is similar to the 2D simulations of Baty et al. (2003), where planar shear layers were studied in high-resolution Cartesian settings. Baty and coworkers found that the pairing/merging of vortices in Kelvin-Helmholtz unstable shear layers, studied from hydro to magnetized cases, is controlled by the growth of subharmonic modes and the phase differences between them. In the present 3D cylindrical configurations, their results represent local box evolutions, performed in the frame rotating at the local Keplerian speed. This pairing/merging trend to large scale structure is then predominantly a 2D process known from planar hydrodynamical evolutions. Because the RWI is closely related to the Kelvin-Helmholtz instability, the merging of vortices seen in our 3D thin-disc simulations is consistent with Baty et al.’s findings.
 |
Fig. 7 Vertical structure in density of the dominant fifth azimuthal mode. The amplitude of the mode is normalised to its value in z = 0, so its structure at different times and positions can be compared. |
3.3. Decay of the vortices
The simulation was run over more than 600 years to investigate the long-term evolution of the vortices. After the growing phase, the vortices survive during hundreds of years but then start to decrease and have disappeared at the end of the simulation. After a few hundreds of inner rotations, the dominant azimuthal mode does not change anymore, and has a global m = 1 value. This corresponds to the largest possible scale. One can see in Fig. 7 that during the decaying phase (after about 100–150 years), perturbations on the vertical structure appear in the m = 5 mode. These perturbations are present inside the vortex (r = 3), but not in the outer region (r = 3.5).
 |
Fig. 8 Accretion as a function of radius during the exponential growth (solid line) and at the end of the simulation (dashed line). The accretion rate is defined as |
One can notice that the spiral density waves disappear after the growing phase when the vortices survive. This implies that the Rossby wave instability is not active anymore because of the weakening of the bump by the instability itself, and no angular momentum is transferred radially. This is quantified in Fig. 8, where the radial accretion rate is plotted: the bump stops to decrease due to radial accretion. When the Rossby vortices are no longer sustained by the RWI, they should be very efficiently destroyed by differential rotation (Tagger 2001), but the shape of the streamlines changes to become more similar to closed elliptical streamlines, as presented in Fig. 9. The vortex streamlines are not directly linked to the shearing sub-Keplerian streamlines, and can survive over more than one rotation time. By the end of the simulation, the vortices have been completely destroyed. This will be discussed in the following section.
 |
Fig. 9 Vortex streamline at t = 300 and t = 1000: the shape of the vortex evolves during the simulation. The radial extent of the vortices is constant and fixed by the radial extent of the density bump, while their azimuthal extent increases when the m mode number decreases. In the right figure, the streamlines become elliptic and an aspect ratio can be estimated (~6 here, but each vortex has a different aspect ratio, as can be seen in Fig. 3). |
 |
Fig. 10 Some streamlines that pass next to the centre of the anticyclone (upper figure) and cyclone (lower figure) at t = 300 are plotted in 3D. The direction of the flow is given by the colours: the flow moves from the blue part to the red part. The cyclone is a downward flow, contrary to the upward anticyclonic flow. The vortices have a coherent structure over the whole height of the disc. The radial extent of this figure corresponds approximately to half of of Fig. 9: only the inner parts of the vortices are shown here. |
4. Discussion
4.1. Comparison with previous 3D simulations
From a numerical point of view, the main difference with the previous simulations of Meheut et al. (2010) is the use of an AMR grid. This allowed us to increase the resolution at the interface between the disc and the corona above it and to avoid numerical difficulties caused by the dynamics in this low-density region. Our current simulation uses an improved limiter and benefits from grid adaptivity, allowing us to robustly compute and follow the growth of the instability over longer times. The limit in time is now related to computational resources. We tested simulations of the initial growth of the RWI with and without AMR, and obtained near-identical results.
The simulations presented in this paper show that the most unstable mode of the RWI in the current disc equilibrium has an azimuthal mode number m = 5. In Meheut et al. (2010) we stressed the global m = 1 mode. There, only one mode was present in the seed perturbation, while we now chose to use random perturbations that included all modes. For confirmation, we have run the simulation of Meheut et al. (2010) with random initial perturbations, and the instability was dominated by the m = 5 mode. The difference with our earlier work is therefore not due to disparity in initial equilibrium or numerical approach. This result is also coherent with the linear calculations of Meheut et al. (2012).
The unusual 3D structure of the Rossby vortices with an non-negligible vertical velocity is confirmed by these higher resolution simulations, as can be seen in Fig. 10. We selected some streamlines that pass next to the centre of the vortices, they show the “eye” of the vortices and the larger basis. The direction of the flow in the eye of the vortices differs between the cyclones (downward flow) and anticyclones (upward flow). In the outskirts of the vortices, the flows have opposite directions.
4.2. Vortex migration
 |
Fig. 11 Mean azimuthal density in the mid-plane of the bump region, initially and at t = 1000. The bump has survived the growth of the RWI. |
We see no migration of the vortices in our simulation over more than 600 years. This result is expected, since the growth mechanism of these vortices is localised in the bump region. Vortex migration is oriented in the direction of the positive density gradient, and as a consequence the density maximum at the location of the vortices locks their radial position. One can see in Fig. 11 that the overdensity is diminished by the Rossby wave instability, but it survives the growth of the RWI. The vortices are then indefinitely blocked in this region.
4.3. Elliptical instability
The elliptical instability is a purely 3D instability that is caused by resonances between the vortex turnover frequency and an inertial wave frequency (Kerswell 2002). Lesur & Papaloizou (2009) have shown that 3D elliptical vortices are vulnerable to this instability, and can destroy them. In our simulation, the elliptical instability does not prevent the emergence of vortices by the RWI and their survival over hundreds of years. This was expected because closed velocity streamlines are needed for the turnover frequency to be properly defined and the elliptical instability to grow. Some streamlines of the (non-steady) Rossby vortices can be seen in Fig. 9 (see also Fig. 10). After saturation of the RWI, the streamlines tend to close; on the one hand this allows them to survive against shearing, but on the other hand, they become subject to the elliptical instability. This may be the reason for the decay of the vortices. The growth of this instability can explain the appearance of smaller-scale vertical perturbations (as those plotted in Fig. 7) while the azimuthal scale is fixed. Indeed, in contrast to the RWI, the elliptical instability is a local instability without any interaction between the vortices, it cannot change their number, but affects only their structure. The detailed study of the decay of the vortices through the elliptical instability, including elongated vortices or short wavelengths, needs a very high resolution, as has been performed by Lesur & Papaloizou (2009). These authors studied the effects of the aspect ratio, the ratio of semi-major to semi-minor axis of elliptical streamlines, and showed that elliptical vortices are always unstable. However, the elliptical instability becomes weak for high aspect ratios (i.e. elongated vortices, as is the case in Fig. 9). Therefore, the low azimuthal mode number vortices are expected to survive longer, as observed in our simulations. As pointed out by Godon & Livio (1999), we must caution that the inherently higher numerical dissipation of our finite volume method compared to a spectral method also induces vortex decay. The elliptical instability is also present in the vortices formed when the disc is radially buoyant, e.g. subject to a subcritical baroclinic instability, and Lesur & Papaloizou (2010) have shown with higher resolution simulations that this secondary instability does not fully destroy the vortices (see also Lyra & Klahr 2011).
4.4. Outlooks
We have shown that Rossby vortices can emerge in a 3D protoplanetary disc with an overdensity, and that they can survive for hundreds of years without migrating. When they are not sustained anymore by the RWI, the structure of the vortices will evolve to previously studied vortices in isolation (Godon & Livio 1999; Lesur & Papaloizou 2009). They are then expected to be destroyed and may be prone to the elliptical instability and viscous decay. However, our simulations show that the Rossby vortices can survive for long timescales, if they keep being sustained by the RWI and their unusual structure is preserved. That would be the case if the mechanism that forms the overdensity and launches the RWI is permanent, as for instance in a disc with both active and dead zone regions.
A point to explore is the study of this instability when the active zone is also considered. On the one hand we would expect the viscosity to decrease the growth rate of the instability and eventually to destroy the vortices. On the other hand, if a dead zone is included, a density bump arises that will in turn sustain the instability. A full MHD simulation could allow us to study jointly the bump formation process and its decay due to the RWI, in combination with magneto-rotational driven accretion.
The results presented here are especially interesting in the context of planetesimal formation. Future work should also study the joint evolution of the gas and dust particles to question the influence of the dust particles on the growth of the RWI and their concentration in Rossby vortices. Previous studies have proposed a bi-dimensional approach (Chang & Oishi 2010; Johansen et al. 2004; Wolf & Klahr 2005), but a full 3D study, as the one presented here including solid particles, will be necessary to handle both vertical stratification and vortex concentration. With this intent, a module of MPI-AMRVAC has been developed and was recently used for circumstellar wind modelling (van Marle et al. 2011).
From an analytical point of view, the first work that deals with the RWI in 3D is the one by Umurhan (2010). The vertical structure of the modes has recently be studied in more detail (Meheut et al. 2012; Lin 2012) with dedicated tools as those presented in Zhang & Lai (2006).
Acknowledgments
This work was partially supported by the Tournesol program of the PHC (Partenariat Hubert Curien) and by the Swiss National Science Foundation.
References
- Armitage, P. J. 2011, ARA&A, 49, 195 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Barge, P., & Sommeria, J. 1995, A&A, 295, L1 [NASA ADS] [Google Scholar]
- Baty, H., Keppens, R., & Comte, P. 2003, Phys. Plasmas, 10, 4661 [NASA ADS] [CrossRef] [Google Scholar]
- Benz, W. 2000, Space Sci. Rev., 92, 279 [NASA ADS] [CrossRef] [Google Scholar]
- Bracco, A., Chavanis, P. H., Provenzale, A., & Spiegel, E. A. 1999, Phys. Fluids, 11, 2280 [NASA ADS] [CrossRef] [Google Scholar]
- Chang, P., & Oishi, J. S. 2010, ApJ, 721, 1593 [NASA ADS] [CrossRef] [Google Scholar]
- Dominik, C. 2009, in Cosmic Dust – Near and Far, ed. T. Henning, E. Grün, & J. Steinacker, ASP Conf. Ser., 414, 494 [Google Scholar]
- Fromang, S., & Nelson, R. P. 2005, MNRAS, 364, L81 [NASA ADS] [CrossRef] [Google Scholar]
- Gammie, C. F. 1996, ApJ, 457, 355 [NASA ADS] [CrossRef] [Google Scholar]
- Godon, P., & Livio, M. 1999, ApJ, 523, 350 [NASA ADS] [CrossRef] [Google Scholar]
- Godon, P., & Livio, M. 2000, ApJ, 537, 396 [NASA ADS] [CrossRef] [Google Scholar]
- Heng, K., & Kenyon, S. J. 2010, MNRAS, 408, 1476 [NASA ADS] [CrossRef] [Google Scholar]
- Johansen, A., Andersen, A. C., & Brandenburg, A. 2004, A&A, 417, 361 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Johansen, A., Youdin, A., & Mac Low, M.-M. 2009, ApJ, 704, L75 [NASA ADS] [CrossRef] [Google Scholar]
- Keppens, R., Meliani, Z., van Marle, A., et al. 2012, J. Comput. Phys., 231, 718 [Google Scholar]
- Kerswell, R. R. 2002, Ann. Rev. Fluid Mech., 34, 83 [Google Scholar]
- Klahr, H. 2004, ApJ, 606, 1070 [NASA ADS] [CrossRef] [Google Scholar]
- Klahr, H., & Bodenheimer, P. 2006, ApJ, 639, 432 [NASA ADS] [CrossRef] [Google Scholar]
- Klahr, H. H., & Bodenheimer, P. 2003, ApJ, 582, 869 [NASA ADS] [CrossRef] [Google Scholar]
- Koller, J., Li, H., & Lin, D. N. C. 2003, ApJ, 596, L91 [NASA ADS] [CrossRef] [Google Scholar]
- Koren, B. 1993, A robust upwind discretization method for advection, diffusion and source terms, Notes on numerical fluid mechanics, ed. C. B. Vreugdenhil, & B. Koren, 45, 117 [Google Scholar]
- Kretke, K. A., & Lin, D. N. C. 2007, ApJ, 664, L55 [NASA ADS] [CrossRef] [Google Scholar]
- Kretke, K. A., Lin, D. N. C., Garaud, P., & Turner, N. J. 2009, ApJ, 690, 407 [NASA ADS] [CrossRef] [Google Scholar]
- Lesur, G., & Papaloizou, J. C. B. 2009, A&A, 498, 1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lesur, G., & Papaloizou, J. C. B. 2010, A&A, 513, A60 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Li, H., Finn, J. M., Lovelace, R. V. E., & Colgate, S. A. 2000, ApJ, 533, 1023 [NASA ADS] [CrossRef] [Google Scholar]
- Li, H., Colgate, S. A., Wendroff, B., & Liska, R. 2001, ApJ, 551, 874 [NASA ADS] [CrossRef] [Google Scholar]
- Lin, M.-K. 2012, ApJ, accepted [arXiv:1203.2630] [Google Scholar]
- Lin, M.-K., & Papaloizou, J. C. B. 2011, MNRAS, 415, 1426 [NASA ADS] [CrossRef] [Google Scholar]
- Lovelace, R. V. E., & Hohlfeld, R. G. 1978, ApJ, 221, 51 [NASA ADS] [CrossRef] [Google Scholar]
- Lovelace, R. V. E., Li, H., Colgate, S. A., & Nelson, A. F. 1999, ApJ, 513, 805 [NASA ADS] [CrossRef] [Google Scholar]
- Lyra, W., & Klahr, H. 2011, A&A, 527, A138 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lyra, W., Johansen, A., Klahr, H., & Piskunov, N. 2008, A&A, 491, L41 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Marcus, P. S. 1990, J. Fluid Mech., 215, 393 [Google Scholar]
- Meheut, H., Casse, F., Varniere, P., & Tagger, M. 2010, A&A, 516, A31 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Meheut, H., Yu, C., & Lai, D. 2012, MNRAS, 2748 [Google Scholar]
- Paardekooper, S., Lesur, G., & Papaloizou, J. C. B. 2010, ApJ, 725, 146 [NASA ADS] [CrossRef] [Google Scholar]
- Papaloizou, J. C. B., & Pringle, J. E. 1985, MNRAS, 213, 799 [NASA ADS] [Google Scholar]
- Sellwood, J. A., & Kahn, F. D. 1991, MNRAS, 250, 278 [NASA ADS] [Google Scholar]
- Tagger, M. 2001, A&A, 380, 750 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Tanga, P., Babiano, A., Dubrulle, B., & Provenzale, A. 1996, Icarus, 121, 158 [NASA ADS] [CrossRef] [Google Scholar]
- Tóth, G., & Odstrčil, D. 1996, J. Comput. Phys., 128, 82 [Google Scholar]
- Umurhan, O. M. 2010, A&A, 521, A25 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- van Marle, A. J., Meliani, Z., Keppens, R., & Decin, L. 2011, ApJ, 734, L26 [NASA ADS] [CrossRef] [Google Scholar]
- Varnière, P., & Tagger, M. 2006, A&A, 446, L13 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Weidenschilling, S. J. 1977, MNRAS, 180, 57 [NASA ADS] [CrossRef] [Google Scholar]
- Wolf, S., & Klahr, H. 2005, in ESA SP 577, ed. A. Wilson, 473 [Google Scholar]
- Zhang, H., & Lai, D. 2006, MNRAS, 368, 917 [NASA ADS] [CrossRef] [Google Scholar]
All Figures
 |
Fig. 1 Mid-plane density of the gas in g cm-3. The density bump is placed at 3 AU. |
| In the text | |
 |
Fig. 2 Initial gas density in the disc in g cm-3 (up) and AMR grid (down). The three levels are plotted in white, blue and dark blue from lower to higher resolution. The highest resolution is reached in the overdensity region and at the interface between the disc and corona. |
| In the text | |
 |
Fig. 3 Density (left), density perturbations and velocity streamlines (centre), perturbed vortensity defined as ζ − ⟨ ζ ⟩ ϕ with ζ = (∇ × v)z/ρ (right) at t = 100,300,800 from top to bottom. |
| In the text | |
 |
Fig. 4 Time evolution of the amplitudes of the density perturbations in a logarithmic scale. The time is given in code units (lower axis) and in years (upper axis). We also show the amplitude of some of the modes with low mode number. The upper figure is a zoom on the exponential growth where we have added a linear fit for the dominant mode, whose growth rate is 0.033 in code units. |
| In the text | |
 |
Fig. 5 Time evolution of the enstrophy in a logarithmic scale. The time is given in code units (lower axis) and in years (upper axis). |
| In the text | |
 |
Fig. 6 Comparison of the amplitude of the first 10 azimuthal modes between t = 0 and t = 400 (left) and over the whole simulation (right). The instability is dominated by the mode m = 5 but both lower and higher azimuthal modes are excited during the growth phase. The decaying phase shows a shift to lower azimuthal mode number. |
| In the text | |
 |
Fig. 7 Vertical structure in density of the dominant fifth azimuthal mode. The amplitude of the mode is normalised to its value in z = 0, so its structure at different times and positions can be compared. |
| In the text | |
 |
Fig. 8 Accretion as a function of radius during the exponential growth (solid line) and at the end of the simulation (dashed line). The accretion rate is defined as |
| In the text | |
 |
Fig. 9 Vortex streamline at t = 300 and t = 1000: the shape of the vortex evolves during the simulation. The radial extent of the vortices is constant and fixed by the radial extent of the density bump, while their azimuthal extent increases when the m mode number decreases. In the right figure, the streamlines become elliptic and an aspect ratio can be estimated (~6 here, but each vortex has a different aspect ratio, as can be seen in Fig. 3). |
| In the text | |
 |
Fig. 10 Some streamlines that pass next to the centre of the anticyclone (upper figure) and cyclone (lower figure) at t = 300 are plotted in 3D. The direction of the flow is given by the colours: the flow moves from the blue part to the red part. The cyclone is a downward flow, contrary to the upward anticyclonic flow. The vortices have a coherent structure over the whole height of the disc. The radial extent of this figure corresponds approximately to half of of Fig. 9: only the inner parts of the vortices are shown here. |
| In the text | |
 |
Fig. 11 Mean azimuthal density in the mid-plane of the bump region, initially and at t = 1000. The bump has survived the growth of the RWI. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.