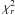| Issue |
A&A
Volume 542, June 2012
|
|
|---|---|---|
| Article Number | A41 | |
| Number of page(s) | 9 | |
| Section | Planets and planetary systems | |
| DOI | https://doi.org/10.1051/0004-6361/201118346 | |
| Published online | 04 June 2012 | |
Orbital characterization of the β Pictoris b giant planet⋆,⋆⋆
1 UJF-Grenoble 1 / CNRS-INSU, Institut de Planétologie et d’Astrophysique de Grenoble (IPAG) UMR 5274, 38041 Grenoble, France
2 Max Planck Institute for Astronomy, Königstuhl 17, 69117 Heidelberg, Germany
3 LESIA, Observatoire de Paris Meudon, 5 pl. J. Janssen, 92195 Meudon, France
4 Department of Astronomy and Department of Planetary Sciences, The University of Arizona, 933 N Cherry Avenue, Tucson, AZ 85718, USA
5 Centre de Recherche Astronomique de Lyon, 46 allée d’Italie, 69364 Lyon Cedex 7, France
6 European Southern Observatory, Casilla 19001, Santiago 19, Chile
Received: 27 October 2011
Accepted: 16 January 2012
Context. In June 2010, we confirmed the existence of a giant planet in the disk of the young star βPictoris located between 8 AU and 15 AU from the star. This young planet offers the rare opportunity to monitor a large fraction of the orbit using the imaging technique over a reasonably short timescale. It also offers the opportunity to study its atmospheric properties using spectroscopy and multi-band photometry, and possibly derive its dynamical mass by combining imaging with radial velocity data to set tight constraints on giant planet formation theories.
Aims. We aim to measure the evolution of the planet’s position relative to the star βPictoris to determine the planetary orbital properties. Our ultimate goal is to relate both the planetary orbital configuration and physical properties to either the disk structure or the cometary activity observed for decades in the βPictoris system.
Methods. Using the NAOS-CONICA adaptive-optics instrument (NACO) at the Very Large Telescope (VLT), we obtained repeated follow-up images of the βPictoris system in the Ks and L′ filters at four new epochs in 2010 and 2011. Complementing these data with previous measurements, we conduct a homogeneous analysis, which covers more than eight yrs, to accurately monitor the βPictoris b position relative to the star. We then carefully consider the various sources of uncertainties that may affect the orbital parameter determination.
Results. On the basis of the evolution of the planet’s relative position with time, we derive the best-fit orbital solutions for our measurements using two fitting methods, a least squares Levenberg-Marquardt algorithm and a Markov-chain Monte Carlo approach. More reliable results are found with the second approach as our measurements do not cover the complete planetary orbit, and are biased toward the most recent epochs since the planet recovery. The solutions favor a low-eccentricity orbit e ≲ 0.17, with semi-major axis in the range 8–9 AU corresponding to orbital periods of 17–21 yrs. Our solutions favor a highly inclined solution with a peak around i = 88.5 ± 1.7°, and a longitude of ascending node tightly constrained at Ω = −147.5 ± 1.5°. These results indicate that the orbital plane of the planet is likely to be above the midplane of the main disk, and compatible with the warp component of the disk being tilted between 3.5 deg and 4.0 deg. This suggests that the planet plays a key role in the origin of the inner warped-disk morphology of the β Pic disk. Finally, these orbital parameters are consistent with the hypothesis that the planet is responsible for the transit-like event observed in November 1981, and also linked to the cometary activity observed in the β Pic system.
Key words: instrumentation: adaptive optics / techniques: high angular resolution / astrometry / planetary systems
Based on observations collected at the European Southern Observatory, Chile (ESO programmes 072.C-0624, 384.C-0207, 084.C-0739, 284.C-5057, 385.C-0132, 086.C-0341).
Appendices are available in electronic form at http://www.aanda.org
© ESO, 2012
1. Introduction
 |
Fig. 1 Left: astrometric positions of β Pic b relative from A used in the present work to characterize the orbital parameters of the β Pic b planet. The predictions for the β Pic b in case of a background source are reported in gray from November 10, 2003 to March 26, 2011. Two linear fits, passing through the origin (Δα,Δδ) = (0,0), for the 2003 NE data points (at 34.25 deg) and the 2009, 2010 and 2011 SW measurements (at 211.15 deg) are indicated by the two blue dashed lines. A zoomed view of the most recent astrometric observations over 2010 and 2011 is presented on the right. |
In the context of exoplanetary science, the direct imaging technique offers a unique observing window to explore the frequency and the properties of the extrasolar giant planet (EGP) population in large orbits ( ≥ 5 AU). The recent discoveries of massive planetary mass companions around stars and brown dwarfs (Chauvin et al. 2004, 2005; Lafrenière et al. 2008; Kalas et al. 2008; Marois et al. 2008; Lagrange et al. 2009; Marois et al. 2010) have shown that core-accretion alone cannot explain the formation of all imaged giant planets, because the core-accretion timescales become too long and the disk surface density too low. Disk or core fragmentation are alternative mechanisms that could even operate in wide orbits, leading to different physical and orbital distributions (Boley 2009; Dodson-Robinson et al. 2009; Vorobyov 2010). Additional mechanisms such as inward/outward migrations or planet-planet interactions might also modify the EGP orbital properties (Crida et al. 2009). Consequently, there is a real need to characterize the orbital properties of recently imaged EGPs, to determine the planetary system architectures and dynamical stabilities, and to obtain additional constraints on their formation and evolution mechanisms. Follow-up astrometric studies have been conducted on the HR 8799 multiple exoplanetary system (Lafrenière et al. 2009; Marois et al. 2010; Bergfors et al. 2011; Soummer et al. 2011). Inclined orbital solutions for the b and d planets, and a 1:2:4 resonance for the planets c, d, and e, confirm stable configurations supported by dynamical simulations (Reidemeister et al. 2009; Fabrycky & Murray-Clay 2010). Owing to its even smaller semi-major axis, the planet βPictoris b (hereafter β Pic b) offers a rare opportunity to constrain both the planetary orbital and physical properties (Lagrange et al. 2010; Currie et al. 2011). This massive giant planet orbits at 8–15 AU around the young star β Pictoris (A5V, 19.44 ± 0.05 pc,  Myr), which has been studied for almost three decades because of its emblematic debris disk (see Vidal-Madjar et al. 1998, for a review). So-called hot start theoretical models predict a mass of 9 ± 3 MJup and Teff = 1700 ± 300 K (Quanz et al. 2010; Bonnefoy et al. 2011). Characterizing the planetary properties offers a rare opportunity to directly investigate the planet-disk interactions, particularly the role played by the planet in the formation of the the inner warped component of the β Pic circumstellar disk (Mouillet et al. 1997; Augereau et al. 2001; Dawson et al. 2011).
Myr), which has been studied for almost three decades because of its emblematic debris disk (see Vidal-Madjar et al. 1998, for a review). So-called hot start theoretical models predict a mass of 9 ± 3 MJup and Teff = 1700 ± 300 K (Quanz et al. 2010; Bonnefoy et al. 2011). Characterizing the planetary properties offers a rare opportunity to directly investigate the planet-disk interactions, particularly the role played by the planet in the formation of the the inner warped component of the β Pic circumstellar disk (Mouillet et al. 1997; Augereau et al. 2001; Dawson et al. 2011).
Since the recovery of β Pic b (i.e. its re-discovery after its passage behind the star), we have performed an astrometric monitoring campaign, using NACO at the VLT. In Sect. 2, we describe observations aquired in the years 2010 and 2011. In Sect. 3, we present the data analysis of these new data together with previous measurements including available astrometric calibrations (Lagrange et al. 2009, 2010; Bonnefoy et al. 2011). Our main objective is to homogeneously analyze the astrometric position of β Pic b relative to the central star to accurately constrain its orbital properties. In Sect. 4, we report the most probable solutions for the planet’s orbit that best fits our astrometric measurements, using two orbital fitting methods, a least-square Levenberg-Marquardt algorithm and a Markov-chain Monte Carlo approach. Finally, in Sect. 5, we discuss the consequences of our results in the context of previous astrometric studies, and their implications for a possible connection with the past transiting event observed in 1981, the disk structures, and the cometary activity of the β Pic system.
2. Observations
To monitor the β Pic b astrometry, we used the NACO high contrast adaptive optics (AO) imager of the VLT, equipped with the NAOS AO system (Rousset et al. 2003), and the near-infrared imaging camera CONICA (Lenzen et al. 2003). The follow-up observations were obtained at five different epochs between September 2010 and March 2011, using the angular differential imaging (ADI) mode of NACO. For accurate astrometry, two observing set-ups were used, the L′ filter with the L27 camera and the Ks filter with the S27 camera. The NACO detector cube mode was in addition used for frame selection. A classical dithering sequence was used with the repetition of five offset positions to properly remove the sky contribution. In the end, the typical observing sequence represented a total of 200–250 cubes, i.e. a total integration time of 35–50 min for an observing sequence of 1–1.5 h on target. The parallactic angles at the start and the end of our observations are reported in Table 1, together with the exposure time (DIT), the number of frame per cube (NDIT), and the number of cubes (Nexp) for each epoch. Typical exposure times of 0.15 s and 0.2 s were used in the Ks and L′-filters, respectively, to saturate the point spread function (PSF) core by a factor of 100 (a few pixels in radius) to improve the dynamics of our images. The observing sequences were executed to optimize both the field rotation and the position of the secondary mirror diffraction spikes relative to the companion, except in March 26, 2011 when the data were obtained in service observing mode. Two sequences of non-saturated PSFs were acquired using a neutral density filter at the beginning and the end of each observing sequence to monitor the image quality. These data also served for the calibration of the relative photometric and astrometric measurements of β Pic b. During the different observing sequences obtained in visitor and service queue modes at ESO, the atmospheric conditions were stable, with seeing and coherence times of 0.6–1.0′′ and 3–6 ms, respectively. The same astrometric field was observed within a week of each follow-up observation of β Pic (see below).
Obs log of new 2010–2011 VLT/NACO observations.
3. Data analysis
For the present study, we processed the data of the new observations of β Pic b obtained in September 28, 2010, November 16, 2010, November 17, 2010, February 1st, 2011, and March 26, 2011. Previously archived data including available astrometric calibrations, obtained between November 2003 and April 2010, were also re-processed (see Table 2 and Fig. 1). The most robust astrometric measurements (in terms of observing conditions and stability) were selected at each epoch. Data obtained on November 16, 2010 and November 17, 2010 were both reduced to check the consistency of astrometric results obtained in the setups L′/L27 and Ks/S27 at a given epoch, as both setups were used for the astrometric analysis. The VLT/NACO M ′ data of Currie et al. (2011) could not be considered owing to a lack of information about the NACO rotator offset position during the observation that could not be recovered from the ESO keywords, and that may affect the final absolute angular position. All data were homogeneously flat-fielded, cleaned from bad and hot pixels, and sky-subtracted. Sub-frames of 200 × 200 pixels were extracted to reduce the computing time of the data processing. The frames were recentered based on a registration of the central star position measured by a Moffat fitting of the non-saturated part of the stellar PSF wing, that was a threshold equal to at 1% of the detector linearity (i.e. about 60% of the saturation limit). We also automatically decided to reject open-loop and poor-AO correction images, using a PSF encircled energy criterion.
For PSF-subtraction of the field-tracking data of November 11, 2003 and October 25, 2009, a reference star matching the β Pic observations in terms of parallactic angles was used to minimize the residuals in the final images (see Lagrange et al. 2009). For ADI data, three different ADI-algorithms were applied to the PSF-subtraction, to verify the consistency of the solutions obtained using the classical ADI, smart ADI, and LOCI algorithms (see Lagrange et al. 2010; Lafrenière et al. 2007, for more details on the algorithms). For smart ADI, we considered a separation criteria of 1.0 and 1.5 × FWHM, at the companion separation (ranging from 11 to 16 pixels), and ten images to compute each individual PSF. For LOCI, we considered optimization regions of NA = 300 × FWHM, the radial-to-azimuthal width ratio g = 1, the radial width Δr = 2 × FWHM, and a separation criteria of 1.0 and 1.5 × FWHM. Only smart ADI results were finally considered owing the the ability of that method to reduce the companion self-subtraction, optimize the temporal PSF selection, and minimize the algorithm complexity when testing the photometric and astrometric systematics induced by the algorithm itself. We always found consistent results within the measurement uncertainty, which are detailed below, when using the classical ADI and LOCI algorithms.
The main difficulty in deriving the planet’s position relative to the primary star was to accurately estimate the position of a central star with a saturated core, and the position of the low signal-to-noise planet affected by the stellar residuals. To determine the central star position, as for the frames recentering, a Moffat fitting of the non-saturated part of the stellar PSF wing (with a similar threshold) was used. For the planet position and flux, we used a grid of 5000 negative fake planets scanning a three-dimensional parameter space in (X, Y) positions (sampling of 0.02 pixels) and flux (sampling of 10 ADU), injected one-by-one in the datacubes before PSF-subtraction. The datacubes were then reprocessed to derive the best-fit solution minimizing the residuals in the final subtracted-image, considering a region covering the companion ADI signature. The positions of the companion relative to the primary star were finally transformed into sky coordinates using the θ1 Ori C field observed with HST by McCaughrean & Stauffer (1994) (with the same set of stars TCC058, 057, 054, 034, and 026). For ADI data, the NACO rotator offset at the start of each ADI sequence was also calibrated and taken into account, using an astrometric binary observed in both field-tracking and pupil-tracking mode to estimate this offset.
The results are given in Table 2 and reported in Fig. 1. The main contributors to the uncertainty in our astrometric measurements are listed below. Errors 2/ and 3/ were added quadratically, then linearly added to the systematic error in our measurement error 1/. The errors 4/ were neglected. We know consider the four types of error:
-
1.
The first contributor is the systematic error related to the de-termination of the (saturated) star center position, which isestimated from the fit to the PSF wings. We used non-saturatedimages to explore this effect given the saturation factor and theMoffat fitting threshold. If the PSF were centro-symmetric, thecenter estimate based on either the PSF wings or the PSF corewould perfectly match. Tests on non-saturated data show thatit does not. It induces a bias of 0.2–0.4 pixels (i.e.6–12 mas). This asymmetry is variable such thatthis offset cannot be securely calibrated and subtracted. We notethat, for consistency purposes, we re-analyzed the 2003 datawith exactly the same method. Owing to the minor modificationof the fitting pattern, this leads to slightly different values (of0.5 pixels) from Lagrange et al. (2009).
-
2.
A second source of error is the uncertainty in the companion position. Twelve negative fake planets of similar flux and separation at various position angles were then inserted to test the effect of both the stellar residuals in our measurements, and the measurement procedure itself. The two non-saturated PSFs were used to take into account their influence on the final result. The typical error found was about 0.1–0.2 pixels (3–6 mas).
-
3.
We then considered the errors related to the platescale and true north orientation (see Table 2), as well as the uncertainty in the NACO rotator offset for ADI measurements (the error of 0.10 deg in the rotator angular accuracy). We note that an accurate absolute angular calibration of the NACO detector is difficult to achieve at mas precision. The two main limitations are the significant variation of the NACO detector true north with time, and the uncertainty associated with the calibrators themselves. Comparing data from different authors using different calibrators may then be risky in the end. A first solution is then to observe the same astrometric references at each epoch to ensure an accurate relative astrometry (as done here). A residual angular systematic cannot be totally excluded but does similarly affect all measurements and the orbital solution (see discussion below).
-
4.
Finally, we neglected the errors related to the distortion correction, detector non-linearity, differential tilt jitter, Strehl ratio variation, or differential refraction which were estimated smaller than 1–2 mas (see Fritz et al. 2010).
4. Orbital fit
Our astrometric measurements reported in Table 2 show that the position angles are almost consistent with an edge-on orbital configuration, and are roughly consistent with the position angle of the β Pic circumstellar disk, which is reported to be 30.1 deg and 211.4 deg by Kalas & Jewitt (1995) for the NE and SW sides respectively, but with no error bars for these values). To derive the best-fit solution for our measurements, we considered the planet’s inclination as a free parameter. We assumed a Keplerian orbit described in a referential frame OXYZ, where, as usual, the XOY plane corresponds to the plane of the sky and the Z-axis points towards the Earth. In this formalism, the astrometric position of the planet relative to the star is given by: 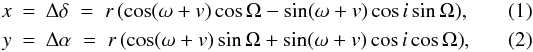 where Ω is the longitude of the ascending node (measured from North), ω is the argument of periastron, i is the inclination, v is the true anomaly, and r = a(1 − e2)/(1 + ecosv), where a represents for the semi-major axis and e the eccentricity.
where Ω is the longitude of the ascending node (measured from North), ω is the argument of periastron, i is the inclination, v is the true anomaly, and r = a(1 − e2)/(1 + ecosv), where a represents for the semi-major axis and e the eccentricity.
 |
Fig. 2 Plots ot the orbit of Table 3 with their orientation with respect to the line of sight. The larger orbit is the best LSLM χ2 model and the smaller one is an example of the highly probable orbit obtained with the MCMC approach. In each case, the dashed line shows the location of the periastron. The position of the planet at different observation epochs is shown as black dots along the orbit (projected error bars in the astrometric measurements are smaller than the symbol size), and predictions for the upcoming years are shown in gray. |
A Keplerian model was then fitted to our (Δδ,Δα) results of Table 2, to derive the orbital period P (or equivalently the semi-major axis a, using the stellar mass M∗ = 1.75 M⊙; Crifo et al. 1997), the e, i, Ω, ω, and the time for periastron passage tp. To constrain the β Pic b’s orbit, we used two complementary fitting methods: a least squares Levenberg-Marquardt (LSLM) algorithm (Press et al. 1992) to search for the model with the minimal reduced χ2, and a more robust statistical approach using the Markov-chain Monte Carlo (MCMC) Bayesian analysis technique (Ford 2005, 2006). The details of the MCMC analysis, which was adapted to this astrometric characterization, are reported in Appendix A. The best-fit LSLM solution found, and a typical example of a “highly probable orbit” according to the result of the MCMC study, are given in Table 3. These orbits are plotted in Fig. 2, in a plane containing the line of sight, as well as the positions of the planet at various observing dates. The results of both orbital fitting methods are also shown for the five orbital elements (a,e,i,Ω,ω) in Fig. 3. In that figure, we also display the 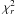 distribution obtained for both analyses (considering a degree of freedom N − P = 12, where N is our number of measurements, here 18, and P the number of parameters in our orbital model, here 6). Additional figures illustrating the goodness of both orbital fits are given in Appendix B.
distribution obtained for both analyses (considering a degree of freedom N − P = 12, where N is our number of measurements, here 18, and P the number of parameters in our orbital model, here 6). Additional figures illustrating the goodness of both orbital fits are given in Appendix B.
 |
Fig. 3 Results of the MCMC fit of the astrometric data of β Pic b: statistical distribution of the orbital elements a (top left), e (top middle), i (top right), Ω (bottom left) and ω (bottom middle). We also show the distribution of |
When comparing the results of the best-fit LSLM solution with our MCMC distributions, our first striking result is that they do not match. The best-fit LSLM solution has a relatively good 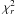 compared to the
compared to the 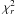 distribution of the MCMC. However, this discrepancy seems to illustrate that our astrometric measurements are still too sparse to derive a deep LSLM
distribution of the MCMC. However, this discrepancy seems to illustrate that our astrometric measurements are still too sparse to derive a deep LSLM 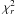 mininum, as the region of probable orbits is probably fairly flat. Consequently, our confidence in the LSLM approach is low, and a robust determination of the orbital parameters of β Pic b is currently impossible with this fitting method. In contrast, we appear to have more success with the statistical MCMC approach, which produces the probable ranges of orbital elements of β Pic b, enabling us to explore the significance of each orbital solution.
mininum, as the region of probable orbits is probably fairly flat. Consequently, our confidence in the LSLM approach is low, and a robust determination of the orbital parameters of β Pic b is currently impossible with this fitting method. In contrast, we appear to have more success with the statistical MCMC approach, which produces the probable ranges of orbital elements of β Pic b, enabling us to explore the significance of each orbital solution.
The results of our MCMC analysis, reported in Fig. 3, are distributions of the orbital parameters that are far from gaussian, except for the inclination, and the longitude of ascending node. The semi-major axis distribution peaks at 8.0–9.0 AU, and most eccentricities are given by e ≤ 0.17. The inclination appears to be extremely concentrated close to 90°, but with a peak at i = 88.5 ± 1.7° (considering a confidence level at 1σ). This is indicative of a ~ 1.5° tilt with respect to a strict edge-on configuration. The longitude of ascending node is also fairly well-constrained at Ω = −147.5 ± 1.5° (Ω + 180 = 32.6 ± 1.5°, with a 1σ error). Finally, the statistical distribution of the argument of periastron ω is more erratic, and does not appear to have clear solutions, which is not unsurprising owing to the low values of the eccentricity distribution. Currie et al. (2011) performed a similar analysis, but on a smaller dataset that had not been homogeneously processed, thus with presumably larger systematics (different data processing, and possible lack of NACO rotator offset calibration). With the same dataset, we found similar results to Currie et al. (2011), using our own MCMC code. The results of both studies, with four epochs (Table 1 from Currie et al. 2011) and eight epochs (Table 2, this work), are compared in Fig. 3. To a first order, they give similar results, although we note some differences. The peak of our semi-major axis distribution is shifted by about 1 AU to larger values. Our eccentricity distribution has a sharper cutoff that excludes a larger fraction of high eccentricity solutions, thanks to our most recent observations in 2010 and 2011. Our distributions of inclination, and longitude of ascending node are also shifted by respectively − 1.0 and 1.5°. Finally, the distribution of 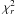 is better constrained in our case (
is better constrained in our case (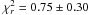 , respectively to
, respectively to 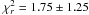 ), corroborating a more concentrated and robust set of orbital solutions. A peak value lower than unity however indicates that our uncertainty estimates are probably conservative. Further astrometric monitoring of β Pic b, during the next quadrature, will be mandatory to improve the planetary orbital characterization.
), corroborating a more concentrated and robust set of orbital solutions. A peak value lower than unity however indicates that our uncertainty estimates are probably conservative. Further astrometric monitoring of β Pic b, during the next quadrature, will be mandatory to improve the planetary orbital characterization.
5. Discussion
From our orbital fit analysis, four important outcomes arise: the semi-major axis of β Pic b falls in the probable range of 8–9.0 AU, the eccentricity distribution is concentrated at e ≲ 0.17, and the longitude of ascending node is fairly well-constrained at −147.5 ± 1.5°, as is the inclination distribution which peaks at 88.5 ± 1.7°. The existence of a giant planet orbiting β Pic has been proposed by various studies during the past few decades (e.g. Freistetter et al. 2007). The main indirect indicators are (i) the inner warped component of the β Pic circumstellar disk, together with additional asymmetries observed in the outer part (Mouillet et al. 1997; Kalas & Jewitt 1995); (ii) the photometric transit-like event observed in 1981 (Lecavelier des Etangs et al. 1997); and (iii) the cometary activity observed in the absorption spectrum of β Pic (Ferlet et al. 1987; Lagrange et al. 1996; Vidal-Madjar et al. 1998; Petterson & Tobin 1999). We discuss below how each of these observational findings may be related to both the existence and the orbital and physical properties of β Pic b.
5.1. Disk-planet configuration
Dedicated scattered-light studies have accurately mapped the morphology of the β Pic disk (Kalas & Jewitt 1995; Heap et al. 2000; Golimowski et al. 2006). They revealed mainly a nearly edge-on disk composed of a main disk observed beyond 80 AU, and an inner warped component (at less than 80 AU), inclined by 2 − 5° with respect to the main disk position angle. The simulations of Mouillet et al. (1997), Augereau et al. (2001), and more recently Dawson et al. (2011) demonstrated that the presence of a planet orbiting the star at 10 AU, misaligned with the main disk, could actually form and sustain the β Pic inner warped disk. The observing challenge is then to test wether β Pic b might be this perturbating planet, that hence has with a significantly inclined orbit with respect to the main disk midplane. Currie et al. (2011) presented evidence of a misalignment between the planet and the inner warped disk of β Pic concluding that the planet was orbiting inside the main disk’s orbital plane. We, however, do not confirm these results based on simultaneous measurements of the planet, and the main disk positions. This work, detailed in Lagrange et al. (2012), and using our Ks/S27 measurements of November 16, 2010 with a dedicated analysis for the disk orientation, shows that the current location of β Pic b is above the midplane of the main disk (which has a position angle of PAmain − disk = 209.0 ± 0.3 deg in the south west direction). This position is more compatible with the warp component orientation tilted by 3.5–4.0 deg (i.e. with PAwarped − disk = 212.5 − 213.0 deg). Moreover, the current distribution of longitude of ascending node Ω, which peaks at −147.5 ± 1.5° (and would correspond to a position angle of 32.5 or 212.5°), can also be directly compared with the main disk and the warp orientations. This distribution currently supports an orbital plane for β Pic b that does not coincide with the main disk midplane, but more probably with the warp component. The hypothesis that the β Pic b planet is the one responsible for the inner warped morphology of the β Pic disk, without evoking any planetary inclination damping (an alternative scenario proposed by Dawson et al. 2011), remains valid. We may therefore still conclude that the β Pic b planet continues to excite the disk of planetisimals, forcing them to precess about its misaligned orbit.
5.2. 1981 Transiting event
Lecavelier des Etangs et al. (1995) reported significant photometric variations in November 1981 with a peculiar transit-like event on November 10, 1981. Lecavelier des Etangs et al. (1997) showed that a planet with 2–4 times the radius of Jupiter, orbiting at ~9 AU at most could well be responsible for the photometric variations they reported. Lecavelier des Etangs & Vidal-Madjar (2009) investigated this issue on the sole basis of the 2003 detection (Lagrange et al. 2009) of β Pic b. They found that a transit of β Pic b in November 1981 could be compatible with a quadrature position in November 2003, assuming a semi-major axis in the range [7.6–8.7] AU. They also predicted that if the planet detected in 2003 on the NE side of the disk matched the one they predicted, it should reappear on the SW side in 2009 roughly where it was reobserved. We reinvestigate this prediction based on our MCMC orbital fit, considering both that we find a peak for the inclination distribution at 88.5 ± 1.7°, and the transit dates predicted in our set of orbital solutions. A tilt larger than 0.1 deg with respect to strictly edge-on configuration would simply exclude the possibility that β Pic b is transiting along the line of sight. However, the sphere of influence of β Pic b with a Hill radius of about 1 AU (angular extension of about 7 deg at 8–9 AU) would still cross the line of sight (even considering all MCMC solutions), and therefore influence the β Pic photometry (if filled with absorbing or scattering material). Assuming this hypothesis, we can still compare the date of the transit-like event of November 1981 with the predicted transit dates of the sphere of influence of β Pic b between 1960 and 2030 obtained by our MCMC analysis (see Fig. 4). The MCMC distribution of transit dates show that the parameters of the most recent (~1999) and next (~2018) transits are somewhat well-constrained. The peak is broader in ~1980. The suggested transit date of November 1981 falls to the right edge of that peak (although not at the center) and remains compatible with the current set of orbital properties obtained from our MCMC analysis.
5.3. The β Pic cometary activity
Transient redshifted spectral events have been regularly monitored in the absorption spectrum of β Pic (Ferlet et al. 1987; Lagrange et al. 1996; Vidal-Madjar et al. 1998; Petterson & Tobin 1999), and attributed to the sublimation of numerous star-grazing planetesimals crossing the line of sight, which are referred to the falling evaporating bodies (FEBs) phenomenon. Their origin has been tentatively related to mean-motion resonances with a Jovian planet orbiting the star (Beust & Morbidelli 1996, 2000; Thébault & Beust 2001; Beust & Valiron 2007). Several constraints have been deduced from dynamical studies of the FEBs scenario, suggesting that:
-
1.
the planet responsible for the phenomenon is massive enough (~jovian) to allow numerous bodies to be trapped in mean-motion resonances;
-
2.
its orbit is slightly eccentric (e ≳ 0.05 − 0.1) to allow bodies trapped in the resonances to see their eccentricity pumped up (Beust & Morbidelli 1996, 2000);
-
3.
the longitude of periastron ϖ of the planet with respect to the line of sight is ~−70° ± 20° (Thébault & Beust 2001), to enable the statistics of the Doppler velocities of the FEB spectral signatures to match the observed ones which are largely strongly biased towards redshifts;
-
4.
finally, the planet location is no further away than ~20 AU, otherwise the FEBs would hardly be able to get into the dust sublimation zone.
The β Pic b planet obviously has orbital and physical properties compatible with constraints 1/ and 4/. The situation is less straighforward for the constraints 2/ and 3/. Eccentricities higher than ~0.05–0.1 are indeed fully compatible with our fit, but circular orbits cannot not excluded. Finally, the longitude of perisatron ϖ measured from the line of sight is related to the argument of periastron ω in our fit. The parameter ω is measured from the XOY plane of our reference frame, i.e., the plane of the sky. Assuming an edge-on orientation of the disk, we then have ω = ϖ + π/2. Thus, ϖ ≃ −70° ± 20° means that ω ≃ 20° ± 20°. Unfortunately, our constraint on ω remains too low to state whether condition 3/ is fulfilled or not, partly due to our upper limit on the eccentricity distribution at e ≲ 0.17). Further measurements are needed to yield conclusive results.
 |
Fig. 4 MCMC fit to the transit dates of β Pic b in front of the line of sight. The plotting conventions are the same as in Fig. 3. In addition, the date of the transiting event observed by Lecavelier des Etangs et al. (1997) is indicated by a thick vertical line. |
6. Conclusion
We have reported the results of our analysis of follow-up observations of the astrometric positions of β Pic b relative to β Pic. Together with previously archived data including available astrometric calibrations, we have homogeneously reprocessed all relevant astrometric measurements of β Pic b at nine different observing epochs. We have taken into account the various contributors to the uncertainty in our astrometric analysis, including the determination of the star position in the low-flux part of the saturated PSF, the influence of the PSF residuals on the companion position, and the errors related to the detector calibration, and the NACO Nasmyth-rotator position. We then used orbital-fitting techniques to derive the most probable orbital solutions for the β Pic b planet: a least squares Levenberg-Marquardt algorithm and a Markov-chain Monte Carlo Bayesian analysis. As our measurements do not cover the complete planetary orbit, and are biased towards the most recent epochs since the planet recovery, the Markov-chain Monte Carlo approach provides more robust and reliable orbital solutions for β Pic b. The most probable ones favor a low-eccentricity orbit e ≲ 0.17, with a semi-major axis of 8–9 AU corresponding to orbital periods of 17–21 yrs, an inclination that peaks at 88.5 ± 1.7°, and a longitude of ascending node fairly well-constrained at − 147.5 ± 1.5°. Our results support the previous astrometric studies of Lagrange et al. (2010) and Currie et al. (2011), although our present study have indeed provided a more robust set of orbital solutions. Our conclusions support the idea that the planet is not in the midplane of the main disk. The planet’s position is more compatible with the warped component orientation, thus corroborating the idea that β Pic b is responsible for the inner warped disk morphology. The current orbital solution of β Pic b is still consistent with the sphere of influence of the planet being responsible for the 1981 transiting event, although a deviation of more than 0.1 deg from an edge-on configuration would exclude a planetary transit. Finally, the planet’s predicted mass, eccentricity, semi-major axis, and longitude of periastron also imply that β Pic b is likely to be the origin of the cometary activity observed in the β Pic system. Further deep imaging characterization should help us to more tightly constrain the orbital parameter space, once the planet has passed the quadrature (most probably in 2013). Further spectroscopic or multi-photometric observations should also help us to determine the underlying physics of this giant planet in the framework of current planetary atmosphere studies (Bonnefoy et al. 2010; Janson et al. 2010; Skemer et al. 2011; Madhusudhan et al. 2011; Barman et al. 2011a, b). Therefore, much is to be expected from future extreme-AO instruments SCExAO/Subaru (Guyon 2010), GPI/Gemini (Macintosh et al. 2008), SPHERE/VLT (Beuzit et al. 2008) in the coming years.
Online material
Appendix A: Convention and Markov-chain Monte Carlo adapted for astrometry
The astrometric position of the planet relative to the star is described by Eqs. (1) and (2). Fo any orbital solution, Ω and ω changed to Ω + π, ω + π, v + π respectively yields the same astrometric data. In the context of Ω, the difference between Ω and Ω + π actually resides in the z-motion (along the line of sight). If we consider a nearly edge-on orbit, we expect the longitude of the ascending node Ω to match the PA of the astrometric data (here, Ω ≃ 34° or Ω ≃ 211 = −149° if we consider an edge-on orbit for β Pic b). By convention, Ω must thus corresponds to the PA when the z-coordinate grows, i.e., when the planet is moving towards the observer. In the context of β Pic, the rotation sense of the gaseous disk was determined by Olofsson et al. (2001): the NE branch is receding from us while the SW branch is approaching. If we assume that the planet is moving in the same sense as the disk, then β Pic b was receding in the 2003 observations and is approching now, and it passed behind the star in between. This means that the ascending node is located towards the SW branch of the orbit, or that Ω ≃ − 149°. We will use this property to distinguish between solutions that yield the same astrometric data. Note that this determination occurs in any case after the fitting procedure. In both approaches, we fit ω + Ω and ω − Ω. Equations (1) and (2) can be rewritten unambiguously as a function of ω + Ω and ω − Ω).
In the context of the Markov-chain Monte Carlo, let us briefly recall the detail of that technique that we here adapted for β Pic b. Let us call x the model parameters vector we want to constrain and d the data vector. We want to determine the posterior distribution p(x | d), i.e., the probability function of the parameter vector x given the data vector d and its error vector. This requires the knowledge of a prior probability function p0(x) for x. A Markov chain is a sequence of successive set of trial values xi (i ≥ 1) for x. The Metropolis-Hastings (M-H) algorithm (Ford 2005) is used to derive xi + 1 from xi via a transition probability. After convergence, the equilibrium distribution of the chain equals the posterior distribution p(x | d). Ford (2006) suggests several assumptions for MCMC adapted to the search of exoplanets by radial velocity, depending on the kind of orbit we are looking for. We adapt here his recommendations to our astrometric fit. Following Ford (2006), we assume the prior distribution p0(x) to be uniform in x = (log P,e,cosi,Ω + ω,ω − Ω,tp). However, the work is done on the parameter vector u(x).
Our main motivation in using u as a variable instead of x was to improve the convergence of the Markov chains, as suggested by Ford (2006). A good way to achieve this is to avoid singularities. For instance, using ecos(ω + Ω) and esin(ω + Ω) instead of ω and Ω removes the non-regularity at e = 0 (Ω is not defined); using ω + Ω causes these variable to be still well defined even if i = 0, which is not the case for ω and Ω individually. Finally, dividing by 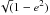 avoids to test non-physical values at large eccentricities.
avoids to test non-physical values at large eccentricities.
The following equation is then used: ![\appendix \setcounter{section}{1} \begin{eqnarray} \vec{u}(x) & = & \left(\frac{\cos(\omega+\Omega+v_0)}{P}, \frac{\sin(\omega+\Omega+v_0)}{P},\frac{e\cos(\omega+\Omega)}{\sqrt{1-e^2}}, \right.\nonumber\\[-0.5mm] &&\frac{e\sin(\omega+\Omega)}{\sqrt{1-e^2}}, (1-e^2)^{1/4}\sin\frac{i}{2}\cos(\omega-\Omega),\nonumber\\[-0.5mm] &&\left.(1-e^2)^{1/4}\sin\frac{i}{2}\sin(\omega-\Omega)\right) \end{eqnarray}](/articles/aa/full_html/2012/06/aa18346-11/aa18346-11-eq179.png) (A.1)where v0 is the true anomaly of the planet at a specific better constraining date t0. Here we fix t0 to be the date of the 2003 observation (Nov. 13, 2003). We run 10 chains in parallel and use the Gelman-Rubin statistics as convergence criterion (see details in Ford 2006). The results of the MCMC runs are reported in the context of β Pic b in Figs. 3 and 4.
(A.1)where v0 is the true anomaly of the planet at a specific better constraining date t0. Here we fix t0 to be the date of the 2003 observation (Nov. 13, 2003). We run 10 chains in parallel and use the Gelman-Rubin statistics as convergence criterion (see details in Ford 2006). The results of the MCMC runs are reported in the context of β Pic b in Figs. 3 and 4.
Appendix B: Orbital fit material
You will find below the astrometric data of β Pic b (with their error bars from Table 2), together with the results of the orbital fit for: 1/ the best LSLM solution, and 2/ the “highly probable orbit” according to the MCMC approach. The details of the orbital parameters of both solutions are given in Table 3. Figure B.1 gives the results of the orbital fit on the projected sky plane. Figures B.2 and B.3 give the evolution of the relative astrometric values of Δα and Δδ as a function of time.
 |
Fig. B.1 Measured astrometric positions of β Pic b relative from A on the plane of sky used in the present work to characterize the orbital parameters of the β Pic b planet. Together with the observed measurements are overplotted the orbital solution the best LSLM χ2 model and the highly probable orbit obtained with the MCMC approach. |
 |
Fig. B.2 Measured astrometric positions of β Pic b relative from A in Δα as a function of time. Both orbital solutions of the best LSLM χ2 model and the highly probable orbit obtained with the MCMC approach are overplotted. |
 |
Fig. B.3 Measured astrometric positions of β Pic b relative from A in Δδ as a function of time. Both orbital solutions of the best LSLM χ2 model and the highly probable orbit obtained with the MCMC approach are overplotted. |
Acknowledgments
We would like to thank the staff of ESO-VLT for their support at the telescope. This publication has made use of the SIMBAD and VizieR database operated at CDS, Strasbourg, France. Finally, we acknowledge support from the French National Research Agency (ANR) through project grant ANR10-BLANC0504-01 and the Programmes Nationaux de Planétologie et de Physique Stellaire (PNP & PNPS), in France.
References
- Augereau, J.-C., Nelson, R. P., Lagrange, A.-M., Papaloizou, J. C. B., & Mouillet, D. 2001, A&A, 370, 447 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Barman, T. S., Macintosh, B., Konopacky, Q. M., et al. 2011a, ApJ, 733, 65 [NASA ADS] [CrossRef] [Google Scholar]
- Barman, T. S., Macintosh, B., Konopacky, Q. M., et al. 2011b, ApJ, 735, L39 [Google Scholar]
- Bergfors, C., Brandner, W., Janson, M., Khler, R., & Henning, T. 2011, A&A, 528, A134 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Beust, H., & Morbidelli, A. 1996, Icarus, 120, 358 [NASA ADS] [CrossRef] [Google Scholar]
- Beust, H., & Morbidelli, A. 2000, Icarus, 143, 170 [NASA ADS] [CrossRef] [Google Scholar]
- Beust, H., & Valiron, P. 2007, A&A, 466, 201 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Beuzit, J.-L., Feldt, M., Dohlen, K., et al. 2008, SPIE, 7014, 41 [NASA ADS] [Google Scholar]
- Boley, A. C. 2009, ApJ, 695, L53 [NASA ADS] [CrossRef] [Google Scholar]
- Bonnefoy, M., Chauvin, G., Rojo, P., et al. 2010, A&A, 512, A52 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bonnefoy, M., Lagrange, A.-M., Boccaletti, A., et al. 2011, A&A, 528, A15 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Chauvin, G., Lagrange, A.-M., Dumas, C., et al. 2004, A&A, 425, L25 [Google Scholar]
- Chauvin, G., Lagrange, A.-M., Zuckerman, B., et al. 2005, A&A, 438, L29 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Crida, A., Masset, F., & Morbidelli, A. 2009, ApJ, 705, L148 [NASA ADS] [CrossRef] [Google Scholar]
- Crifo, F., Vidal-Madjar, A., Lallement, R., Ferlet, R., & Gerbaldi, M. 1997, A&A, 320, L29 [NASA ADS] [Google Scholar]
- Currie, T., Thalmann, C., Matsumura, S., et al. 2011, ApJ, 756, L33 [NASA ADS] [CrossRef] [Google Scholar]
- Dawson, R. I., Murray-Clay, R. A., & Fabrycky, D. C. 2011, ApJ, 743, L17 [NASA ADS] [CrossRef] [Google Scholar]
- Dodson-Robinson, S. E., Veras, D., Ford, E. B., & Beichman, C. A. 2009, ApJ, 707, 79 [NASA ADS] [CrossRef] [Google Scholar]
- Fabrycky, D. C., & Murray-Clay, R. A. 2010, ApJ, 710, 1408 [NASA ADS] [CrossRef] [Google Scholar]
- Ferlet, R., Hobbs, L. M., & Vidal-Madjar, A. 1987, A&A, 185, 267 [NASA ADS] [Google Scholar]
- Ford, E. B. 2005, AJ, 129, 1706 [Google Scholar]
- Ford, E. B. 2006, ApJ, 642, 505 [NASA ADS] [CrossRef] [Google Scholar]
- Freistetter, F., Krivov, A. V., & Lhne, T. 2007, A&A, 466, 389 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Fritz, T., Gillessen, S., Trippe, S., et al. 2010, MNRAS, 401, 1177 [NASA ADS] [CrossRef] [Google Scholar]
- Golimowski, D. A., Ardila, D. R., Krist, J. E., et al. 2006, AJ, 131, 3109 [NASA ADS] [CrossRef] [Google Scholar]
- Guyon, O., Martinache, F., Garrel, V., et al. 2010, SPIE, 7736, 71 [NASA ADS] [Google Scholar]
- Heap, S. R., Lindler, D. J., Lanz, T. M., et al. 2000, ApJ, 539, 435 [Google Scholar]
- Janson, M., Bergfors, C., Goto, M., Brandner, W., & Lafreniére, D. 2010, ApJ, 710, 35 [Google Scholar]
- Kalas, P., & Jewitt, D. 1995, AJ, 110, 794 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Kalas, P., Graham, J. R., Chiang, E., et al. 2008, Science, 322, 1345 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Lafrenière, D., Marois, C., Doyon, R., et al. 2007, ApJ, 660, 770 [NASA ADS] [CrossRef] [Google Scholar]
- Lafrenière, D., Jayawardhana, R., van Kerkwijk, M. H., et al. 2008, ApJ, 689, 153 [Google Scholar]
- Lafrenière, D., Marois, C., Doyon, R., & Barman, T. 2009, ApJ, 694, L148 [NASA ADS] [CrossRef] [Google Scholar]
- Lagrange, A.-M., Plazy, F., Beust, H., et al. 1996, A&A, 310, 547 [NASA ADS] [Google Scholar]
- Lagrange, A.-M., Gratadour, D., & Chauvin, G. 2009, A&A, 493, L21 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lagrange, A.-M., Bonnefoy, M., Chauvin, G., et al. 2010, Science, 329, 57 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Lagrange, A.-M., Boccaletti, A., Milli, J., et al. 2012, A&A, 542, A40 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lecavelier des Etangs, A., Deleuil, M., Vidal-Madjar, A., et al. 1995, A&A, 299, 557 [NASA ADS] [Google Scholar]
- Lecavelier des Etangs, A., Vidal-Madjar, A., Burki, G., et al. 1997, A&A, 328, 311 [NASA ADS] [Google Scholar]
- Lecavelier des Etangs, A., & Vidal-Madjar, A. 2009, A&A, 497, 557 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lenzen, R., Hartung, M., Brandner, et al. 2003, SPIE, 4841, 944 [Google Scholar]
- Macintosh, B., Graham, J. R., Palmer, D., et al. 2008, SPIE, 7015, 31 [NASA ADS] [Google Scholar]
- Madhusudhan, N., Burrow, A., & Currie, T. 2011, ApJ, 737, 34 [Google Scholar]
- Marois, C., Macintosh, B., Barman, T., et al. 2008, Science, 322, 1348 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Marois, C., Zuckerman, B., Konopacky, Q. M., Macinosh, B., & Barman, T. 2010, Nature, 468, 1080 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- McCaughrean, M. J., & Stauffer, J. R. 1994, AJ, 108, 1382 [NASA ADS] [CrossRef] [Google Scholar]
- Mouillet, D., Larwood, J. D., Papaloizou, J. C. B., & Lagrange, A.-M. 1997, MNRAS, 292, 896 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Olofsson, G., Liseau, R., & Brandeker, A. 2001, ApJ, 563, 77 [Google Scholar]
- Petterson, O. K. L., & Tobin, W. 1999, MNRAS, 304, 733 [NASA ADS] [CrossRef] [Google Scholar]
- Press, W. H., Teukolsky, S. A., Vetterling, W. T., & Flannery, B. P. 1992, Numerical Recipes (Cambridge, Univ. Press.) [Google Scholar]
- Quanz, S. P., Meyer, M. R., Kenworthy, M., et al. 2010, ApJ, 722, L49 [NASA ADS] [CrossRef] [Google Scholar]
- Reidemeister, M., Krivov, A. V., Schmidt, T. O. B., et al. 2009, A&A, 503, 247 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Rousset, G., Lacombe, F., Puget, P., et al. 2003, SPIE, 4839, 140 [Google Scholar]
- Skemer, A. J., Close, L. M., Szücs, L., et al. 2011, ApJ, 732, 107 [NASA ADS] [CrossRef] [Google Scholar]
- Soummer, R., Hagan, J. B., Pueyo, L., et al. 2011, ApJ, 741, 55 [NASA ADS] [CrossRef] [Google Scholar]
- Thébault, P., & Beust, H. 2001, A&A, 376, 621 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Vidal-Madjar, A., Lecavelier des Etangs, A., & Ferlet, R. 1998, P&SS, 46, 629 [NASA ADS] [CrossRef] [Google Scholar]
- Vorobyov, E., & Basu, S. 2010, ApJ, 714, 133 [Google Scholar]
All Tables
All Figures
 |
Fig. 1 Left: astrometric positions of β Pic b relative from A used in the present work to characterize the orbital parameters of the β Pic b planet. The predictions for the β Pic b in case of a background source are reported in gray from November 10, 2003 to March 26, 2011. Two linear fits, passing through the origin (Δα,Δδ) = (0,0), for the 2003 NE data points (at 34.25 deg) and the 2009, 2010 and 2011 SW measurements (at 211.15 deg) are indicated by the two blue dashed lines. A zoomed view of the most recent astrometric observations over 2010 and 2011 is presented on the right. |
| In the text | |
 |
Fig. 2 Plots ot the orbit of Table 3 with their orientation with respect to the line of sight. The larger orbit is the best LSLM χ2 model and the smaller one is an example of the highly probable orbit obtained with the MCMC approach. In each case, the dashed line shows the location of the periastron. The position of the planet at different observation epochs is shown as black dots along the orbit (projected error bars in the astrometric measurements are smaller than the symbol size), and predictions for the upcoming years are shown in gray. |
| In the text | |
 |
Fig. 3 Results of the MCMC fit of the astrometric data of β Pic b: statistical distribution of the orbital elements a (top left), e (top middle), i (top right), Ω (bottom left) and ω (bottom middle). We also show the distribution of |
| In the text | |
 |
Fig. 4 MCMC fit to the transit dates of β Pic b in front of the line of sight. The plotting conventions are the same as in Fig. 3. In addition, the date of the transiting event observed by Lecavelier des Etangs et al. (1997) is indicated by a thick vertical line. |
| In the text | |
 |
Fig. B.1 Measured astrometric positions of β Pic b relative from A on the plane of sky used in the present work to characterize the orbital parameters of the β Pic b planet. Together with the observed measurements are overplotted the orbital solution the best LSLM χ2 model and the highly probable orbit obtained with the MCMC approach. |
| In the text | |
 |
Fig. B.2 Measured astrometric positions of β Pic b relative from A in Δα as a function of time. Both orbital solutions of the best LSLM χ2 model and the highly probable orbit obtained with the MCMC approach are overplotted. |
| In the text | |
 |
Fig. B.3 Measured astrometric positions of β Pic b relative from A in Δδ as a function of time. Both orbital solutions of the best LSLM χ2 model and the highly probable orbit obtained with the MCMC approach are overplotted. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.