| Issue |
A&A
Volume 542, June 2012
|
|
|---|---|---|
| Article Number | A41 | |
| Number of page(s) | 9 | |
| Section | Planets and planetary systems | |
| DOI | https://doi.org/10.1051/0004-6361/201118346 | |
| Published online | 04 June 2012 | |
Online material
Appendix A: Convention and Markov-chain Monte Carlo adapted for astrometry
The astrometric position of the planet relative to the star is described by Eqs. (1) and (2). Fo any orbital solution, Ω and ω changed to Ω + π, ω + π, v + π respectively yields the same astrometric data. In the context of Ω, the difference between Ω and Ω + π actually resides in the z-motion (along the line of sight). If we consider a nearly edge-on orbit, we expect the longitude of the ascending node Ω to match the PA of the astrometric data (here, Ω ≃ 34° or Ω ≃ 211 = −149° if we consider an edge-on orbit for β Pic b). By convention, Ω must thus corresponds to the PA when the z-coordinate grows, i.e., when the planet is moving towards the observer. In the context of β Pic, the rotation sense of the gaseous disk was determined by Olofsson et al. (2001): the NE branch is receding from us while the SW branch is approaching. If we assume that the planet is moving in the same sense as the disk, then β Pic b was receding in the 2003 observations and is approching now, and it passed behind the star in between. This means that the ascending node is located towards the SW branch of the orbit, or that Ω ≃ − 149°. We will use this property to distinguish between solutions that yield the same astrometric data. Note that this determination occurs in any case after the fitting procedure. In both approaches, we fit ω + Ω and ω − Ω. Equations (1) and (2) can be rewritten unambiguously as a function of ω + Ω and ω − Ω).
In the context of the Markov-chain Monte Carlo, let us briefly recall the detail of that technique that we here adapted for β Pic b. Let us call x the model parameters vector we want to constrain and d the data vector. We want to determine the posterior distribution p(x | d), i.e., the probability function of the parameter vector x given the data vector d and its error vector. This requires the knowledge of a prior probability function p0(x) for x. A Markov chain is a sequence of successive set of trial values xi (i ≥ 1) for x. The Metropolis-Hastings (M-H) algorithm (Ford 2005) is used to derive xi + 1 from xi via a transition probability. After convergence, the equilibrium distribution of the chain equals the posterior distribution p(x | d). Ford (2006) suggests several assumptions for MCMC adapted to the search of exoplanets by radial velocity, depending on the kind of orbit we are looking for. We adapt here his recommendations to our astrometric fit. Following Ford (2006), we assume the prior distribution p0(x) to be uniform in x = (log P,e,cosi,Ω + ω,ω − Ω,tp). However, the work is done on the parameter vector u(x).
Our main motivation in using u as a variable instead of x was to improve the convergence of the Markov chains, as suggested by Ford (2006). A good way to achieve this is to avoid singularities. For instance, using ecos(ω + Ω) and esin(ω + Ω) instead of ω and Ω removes the non-regularity at e = 0 (Ω is not defined); using ω + Ω causes these variable to be still well defined even if i = 0, which is not the case for ω and Ω individually. Finally, dividing by 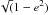 avoids to test non-physical values at large eccentricities.
avoids to test non-physical values at large eccentricities.
The following equation is then used: 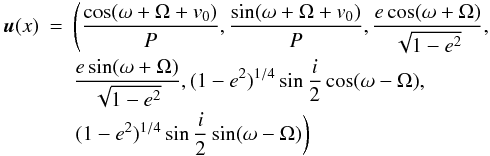 (A.1)where v0 is the true anomaly of the planet at a specific better constraining date t0. Here we fix t0 to be the date of the 2003 observation (Nov. 13, 2003). We run 10 chains in parallel and use the Gelman-Rubin statistics as convergence criterion (see details in Ford 2006). The results of the MCMC runs are reported in the context of β Pic b in Figs. 3 and 4.
(A.1)where v0 is the true anomaly of the planet at a specific better constraining date t0. Here we fix t0 to be the date of the 2003 observation (Nov. 13, 2003). We run 10 chains in parallel and use the Gelman-Rubin statistics as convergence criterion (see details in Ford 2006). The results of the MCMC runs are reported in the context of β Pic b in Figs. 3 and 4.
Appendix B: Orbital fit material
You will find below the astrometric data of β Pic b (with their error bars from Table 2), together with the results of the orbital fit for: 1/ the best LSLM solution, and 2/ the “highly probable orbit” according to the MCMC approach. The details of the orbital parameters of both solutions are given in Table 3. Figure B.1 gives the results of the orbital fit on the projected sky plane. Figures B.2 and B.3 give the evolution of the relative astrometric values of Δα and Δδ as a function of time.
 |
Fig. B.1
Measured astrometric positions of β Pic b relative from A on the plane of sky used in the present work to characterize the orbital parameters of the β Pic b planet. Together with the observed measurements are overplotted the orbital solution the best LSLM χ2 model and the highly probable orbit obtained with the MCMC approach. |
| Open with DEXTER | |
 |
Fig. B.2
Measured astrometric positions of β Pic b relative from A in Δα as a function of time. Both orbital solutions of the best LSLM χ2 model and the highly probable orbit obtained with the MCMC approach are overplotted. |
| Open with DEXTER | |
 |
Fig. B.3
Measured astrometric positions of β Pic b relative from A in Δδ as a function of time. Both orbital solutions of the best LSLM χ2 model and the highly probable orbit obtained with the MCMC approach are overplotted. |
| Open with DEXTER | |
© ESO, 2012
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


