| Issue |
A&A
Volume 542, June 2012
|
|
|---|---|---|
| Article Number | A59 | |
| Number of page(s) | 14 | |
| Section | Cosmology (including clusters of galaxies) | |
| DOI | https://doi.org/10.1051/0004-6361/201118284 | |
| Published online | 06 June 2012 | |
Limits on the extragalactic background light in the Fermi era
1 Institut für Experimentalphysik, University of Hamburg, Luruper Chaussee 149, 22761 Hamburg, Germany
e-mail: manuel.meyer@physik.uni-hamburg.de
2 Institut de Fisica d’Altes Energies (IFAE), Edifici Cn. Universitat Autonoma de Barcelona, 08193 Bellaterra, Spain
Received: 17 October 2011
Accepted: 3 February 2012
Very high energy (VHE, energy E ≲ 100 GeV) γ-rays from cosmological sources are attenuated due to the interaction with photons of the extragalactic background light (EBL) in the ultraviolet to infrared wavelength band. The EBL, thus, leaves an imprint on the observed energy spectra of these objects. In the last four years, the number of extragalactic VHE sources discovered with imaging atmospheric Cherenkov telescopes (IACTs), such as MAGIC, H.E.S.S., and VERITAS, has doubled. Furthermore, the measurements of the Fermi satellite brought new insights into the intrinsic spectra of the sources at GeV energies. In this paper, upper limits on the EBL intensity are derived by considering the most extensive VHE source sample ever used in this context. This is accomplished by constructing a large number of generic EBL shapes and combining spectral informations from Fermi and IACTs together with minimal assumptions about the source physics at high and very high γ-ray energies. The evolution of the EBL with redshift is accounted for and the possibility of the formation of an electromagnetic cascade and the implications on the upper limits are explored. The EBL density at z = 0 is constrained over a broad wavelength range between 0.4 and 100 μm. At optical wavelengths, the EBL density is constrained below 24 nW m-2 sr-1 and below 5 nW m-2 sr-1 between 8 μm and 31 μm.
Key words: diffuse radiation / BL Lacertae objects: general / galaxies: active / infrared: diffuse background
© ESO, 2012
1. Introduction
The extragalactic background light (EBL) is the diffuse and isotropic radiation field from ultraviolet to far infrared wavelengths (see e.g. Hauser & Dwek 2001; Kashlinsky 2005, for a review). It originates from the starlight integrated over all epochs and starlight emission reprocessed by interstellar dust. These two distinct components lead to two maxima in the spectral energy distribution (SED) of the EBL, the first at ~1 μm (starlight) and the second at ~100 μm (dust). Narrow spectral features like absorption lines are smeared out in the integration over redshift leading to a smooth shape of the EBL at z = 0. Further contributions may come from diffuse emission from galaxy clusters (Chelouche et al. 2007), unresolved active galactic nuclei (Matute et al. 2006), Population III stars (e.g. Santos et al. 2002; Raue et al. 2009), or exotic sources like dark matter powered stars in the early universe (Maurer et al. 2011). The SED of the EBL at z = 0 comprises information about the star and galaxy formation rates and the dust content of galaxies. Direct measurements of the EBL are, however, impeded, especially in the infrared, by foreground emission such as the zodiacal light (Hauser et al. 1998). Therefore, upper and lower limits are often the only available information about the EBL density. Lower limits are derived from integrated galaxy number counts e.g. by the Hubble Space Telescope in the optical (Madau & Pozzetti 2000) and the Spitzer telescope in the infrared (Fazio et al. 2004). Several authors have modeled the EBL in the past (e.g. Primack et al. 2005; Stecker et al. 2006; Franceschini et al. 2008; Kneiske & Dole 2010; Domínguez et al. 2011). Although the approaches forecast different EBL densities at z = 0, the most recent models more or less agree on the overall EBL shape.
The observations of very high energy (energy E ≲ 100 GeV; VHE) γ-rays from extragalactic sources with imaging atmospheric Cherenkov telescopes (IACTs) has opened a new window to constrain the EBL density. Most of the extragalactic γ-ray sources are active galactic nuclei (AGN), especially blazars (see e.g. Urry & Padovani 1995). The γ-rays from these objects are attenuated by the pair production mechanism: γVHE + γEBL → e+ + e− (Nikishov 1962; Jelley 1966; Gould & Schréder 1967). If assumptions are made about the properties of the intrinsic blazar spectrum, a comparison with the observed spectrum allows to place upper limits on the EBL intensity (e.g. Stecker et al. 1992). In this context, the spectra of Markarian (Mkn) 501 during an extraordinary flare (Aharonian et al. 1999) and of the distant blazar H 1426+482 (Aharonian et al. 2003a) resulted in the first constraints of the EBL density from mid to far infrared (MIR and FIR) wavelengths. With the new generation of IACTs, limits were derived from the spectra of 1ES 1101-232 and H 2356-309 (Aharonian et al. 2006) and 1ES 0229+200 (Aharonian et al. 2007a) in the near infrared (NIR), and in the optical from the MAGIC observation of 3C 279 (Albert et al. 2008). Mazin & Raue (2007, henceforth MR07) use a sample of all at that time known blazars and test a large number of different EBL shapes to derive robust constraints over a large wavelength range. The authors exclude EBL densities that produce VHE spectra, characterized by dN/dE ∝ E−Γ, with Γ < Γlimit (being Γlimit = 1.5 for realistic and Γlimit = 2/3 for extreme scenarios) or an exponential pile up at highest energies.
With the advent of the large area telescope (LAT) on board the Fermi satellite (Atwood et al. 2009) and its unprecedented sensitivity at high energies (100 MeV ≲ E ≲ 100 GeV; HE), further possibilities arose to confine the EBL density. Bounds can be derived either by considering solely Fermi-LAT observations of AGN and gamma-ray bursts (Abdo et al. 2010b; Raue 2010) or by combining HE with VHE spectra (e.g. Georganopoulos et al. 2010; Orr et al. 2011). It has also been proposed that the Fermi-LAT can, in principle, measure the EBL photons upscattered by electrons in lobes of radio galaxies directly (Georganopoulos et al. 2008). Attenuation limits can also be estimated by modeling the entire blazar SED in order to forecast the intrinsic VHE emission (Krawczynski et al. 2002; Mankuzhiyil et al. 2010).
In this paper, results from the recently published Fermi two year catalog (Fermi-LAT Collaboration 2012, henceforth 2FGL) together with a comprehensive VHE spectra sample are used to place upper limits on the EBL density. This approach relies on minimal assumptions about the intrinsic spectra. The VHE sample is composed of spectra measured with different instruments, thereby ensuring that the results are not influenced by the possible systematic bias of an individual instrument or observation.
The article is organized as follows. In Sect. 2 the calculation of the attenuation is presented in order to correct the observed spectra for absorption. The resulting intrinsic spectra are subsequently described with analytical functions. Section 3 outlines in detail the different approaches to constrain the EBL before the selection of VHE spectra is addressed in Sect. 4. The combination of VHE and HE spectra of variable sources will also be discussed. The results are presented in Sect. 5 before concluding in Sect. 6. Throughout this work a standard ΛCDM cosmology is assumed with Ωm = 0.3, ΩΛ = 0.7, and h = 0.72.
2. Intrinsic VHE gamma-ray spectra
The intrinsic energy spectrum dNint/dE of a source at redshift z0 at the measured energy E differs from the observed spectrum dNobs/dE due to the interaction of source photons with the photons of the EBL which is most commonly expressed as ![\begin{equation} \Diff{N_\mathrm{obs}}{E} = \Diff{N_\mathrm{int}}{E} \times \exp\left[-\tau_\gamma(E,z_0)\right]\label{eqn:abs}. \end{equation}](/articles/aa/full_html/2012/06/aa18284-11/aa18284-11-eq22.png) (1)The strength of the attenuation at energy E is given by the optical depth τγ: a threefold integral over the distance ℓ, the cosine μ of the angle between the photon momenta, and the energy ϵ of the EBL photons (e.g. Dwek & Krennrich 2005),
(1)The strength of the attenuation at energy E is given by the optical depth τγ: a threefold integral over the distance ℓ, the cosine μ of the angle between the photon momenta, and the energy ϵ of the EBL photons (e.g. Dwek & Krennrich 2005), 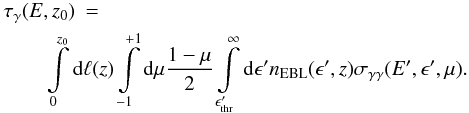 (2)The primed values correspond to the redshifted energies and nEBL(ϵ′,z) denotes the comoving EBL photon number density. The threshold energy for pair production is given by
(2)The primed values correspond to the redshifted energies and nEBL(ϵ′,z) denotes the comoving EBL photon number density. The threshold energy for pair production is given by 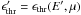 with E′ = E(1 + z). The cross section for pair production, σγγ, is strongly peaked at a wavelength (e.g. Guy et al. 2000)
with E′ = E(1 + z). The cross section for pair production, σγγ, is strongly peaked at a wavelength (e.g. Guy et al. 2000) 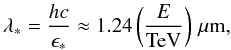 (3)and, therefore, VHE γ-rays predominantly interact with EBL photons from optical to FIR wavelengths.
(3)and, therefore, VHE γ-rays predominantly interact with EBL photons from optical to FIR wavelengths.
The comoving EBL photon density is described here by splines constructed from a grid in (λ, νIν)-plane (see MR07 for further details). This ensures independence of EBL model assumptions and allows for a great variety of EBL shapes to be tested. Furthermore, the usage of splines drastically reduces the effort to compute the complete threefold integral of Eq. (2) numerically as shown in MR07.
Each spline is defined by the choice of knot points and weights from the grid in the (λ, νIν)-plane. The grid is bound by a minimum and a maximum shape, shown in Fig. 1. The setup of grid points is taken from MR07. The minimum shape tested is set to reproduce the lower limits from the galaxy number counts from Spitzer (Fazio et al. 2004) while the maximum shape roughly follows the upper limits derived from measurements. To reduce the computational costs, the extreme cases considered by MR07 of the EBL density in the optical and near infrared (NIR) are not tested. Moreover, with current VHE spectra the EBL intensity is only testable up to a wavelength λ ≈ 100 μm so no additional grid points beyond this wavelength are used. In total this range of knots and weights allows for 1 920 000 different EBL shapes. A much smaller spacing of the grid points is not meaningful as small structures are smeared out in the calculation of τγ and the EBL can be understood as a superposition of black bodies that are not arbitrarily narrow in wavelength (MR07, Raue 2007).
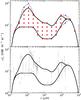 |
Fig. 1 Upper panel: grid in wavelength versus the energy density of the EBL used to construct the EBL shapes for testing (red bullets). Also shown are the minimum and maximum shape tested (solid lines) and the same for the grid of MR07 (blue triangles; dashed lines). Lower panel: minimum and maximum EBL shape tested versus EBL limits and measurements (light gray symbols, see Raue & Mazin 2011, and references therein). |
In most previous studies, no EBL evolution with redshift is assumed when computing EBL upper limits using VHE γ-ray observations. Neglecting the evolution leads to an overestimation of the optical depth between 10% (z = 0.2) and 35% (z = 0.5) (Raue & Mazin 2008) and, consequently, too rigid upper limits (see Appendix A). In this study, the z evolution is accounted for by a phenomenological ansatz (e.g. Raue & Mazin 2008): the effective cosmological photon number density scaling is changed from nEBL ∝ (1 + z)3 to nEBL ∝ (1 + z)3 − fevo. For a value of fevo = 1.2 a good agreement is found between this simplified approach and complete EBL model calculations for redshifts z ≲ 0.7 (Raue & Mazin 2008). Including the redshift evolution of the EBL in general decreases the attenuation compared to the no-evolution case and, therefore, weaker EBL limits are expected.
The intrinsic γ-ray spectrum for a given EBL shape and measured γ-ray spectrum is reconstructed by solving Eq. (1) for dNint/dE. For a spectrum with n energy bins the relation reads ![\begin{equation} \left(\Diff{N_\mathrm{int}}{E}\right)_i = \left(\Diff{N_\mathrm{obs}}{E}\right)_i \times \exp\left[{\tau_\gamma(E_i,z_0)}\label{eqn:deabs}\right], \quad i = 1,\ldots,n, \end{equation}](/articles/aa/full_html/2012/06/aa18284-11/aa18284-11-eq43.png) (4)where the energy of the logarithmic bin center is denoted by Ei. A systematic error is introduced by using τγ calculated for the energy at the bin center since, on the one hand, the attenuation can change dramatically within relatively wide energy bins and, on the other hand, the mean attenuation actually depends on the intrinsic spectral shape in the energy bin (Stecker & Scully 2009). The introduced error is studied by comparing τγ with an averaged value of the optical depth over the highest energy bin for the spectra that are attenuated most. These spectra are described with an analytical function f(E) (a power or broken power law, cf. Table 2) and the averaged optical depth ⟨ τγ ⟩ is found to be
(4)where the energy of the logarithmic bin center is denoted by Ei. A systematic error is introduced by using τγ calculated for the energy at the bin center since, on the one hand, the attenuation can change dramatically within relatively wide energy bins and, on the other hand, the mean attenuation actually depends on the intrinsic spectral shape in the energy bin (Stecker & Scully 2009). The introduced error is studied by comparing τγ with an averaged value of the optical depth over the highest energy bin for the spectra that are attenuated most. These spectra are described with an analytical function f(E) (a power or broken power law, cf. Table 2) and the averaged optical depth ⟨ τγ ⟩ is found to be 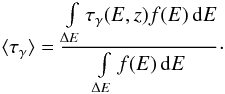 (5)The results are summarized in Table 1. The ratios ⟨ τγ ⟩ /τγ are close to, but always smaller than, one and the optical depth is overestimated by <5%. Thus, the simplified approach adds marginally to the uncertainties of the upper limits.
(5)The results are summarized in Table 1. The ratios ⟨ τγ ⟩ /τγ are close to, but always smaller than, one and the optical depth is overestimated by <5%. Thus, the simplified approach adds marginally to the uncertainties of the upper limits.
Comparison between the optical depth at the logarithmic bin center of the highest energy bin and the averaged value over the bin width.
The intrinsic spectra obtained by means of Eq. (4) will be described by analytical functions in order to test the fit parameters for their physical feasibility. An analytical description of the spectrum is determined by fitting a series of functions listed in Table 2. A χ2-minimization algorithm (utilizing the MINUIT package routines, see James 1998) is employed, starting with the first function of the table, a simple power law. The fit is not considered valid if the corresponding probability is Pfit(χ2) < 0.05. In this case the next function with more model parameters from Table 2 is evaluated. For a given energy spectrum of n data points, only functions are examined with n − 1 > 0 degrees of freedom. If more than one fit results in an acceptable fit probability, an F-Test is used to determine the preferred hypothesis. The parameters of the model with more fit parameters are examined if the test results in a 95% probability that description of the data has improved.
Analytical functions fitted to the deabsorbed spectra.
3. Exclusion criteria for the EBL shapes
In the following, arguments to exclude EBL shapes will be presented. While the first criteria are based on the expected concavity of the intrinsic VHE spectra, the second set of criteria relies on the integral of the intrinsic VHE emission.
3.1. Concavity
Observations have led to the commonly accepted picture that particles are accelerated in jets of AGN thereby producing non-thermal radiation. The SED of these objects is dominated by two components. The first low-energy component from infrared to X-ray energies is due to synchrotron radiation from a distribution of relativistic electrons. The second component responsible for HE and VHE emission can be explained by several different emission models. In leptonic blazar models, photons are upscattered by the inverse Compton (IC) process. The involved photon fields originate from synchrotron emission (e.g. Bloom & Marscher 1996), the accretion disk (Dermer & Schlickeiser 1993), or the broad line region (e.g. Sikora et al. 1994). In hadronic blazar models, on the other hand, γ-ray emission is produced either by proton synchrotron radiation (e.g. Mücke & Protheroe 2001) or photon pion production (e.g. Mücke et al. 2003). These simple emission models which commonly describe the measured data satisfactorily, do not predict a spectral hardening in the transition from HE to VHE nor within the VHE band. This is also confirmed by observations of nearby sources. On the contrary, the spectral slope is thought to become softer with energy, either due to Klein-Nishina effects in leptonic scenarios and/or a cut off in the spectrum of accelerated particles.
However, in more specific scenarios a spectral hardening is possible. If mechanisms like, e.g., second order IC scattering, internal photon absorption (e.g. Aharonian et al. 2008b), comptonization of low frequency radiation by a cold ultra-relativistic wind of particles (Aharonian et al. 2002), or multiple HE and VHE γ-ray emitting regions in the source (Lefa et al. 2011a) contribute significantly to the overall spectrum, convex curvature or an exponential pile can indeed occur. Nevertheless, neither of these features has been observed with certainty in nearby sources. Furthermore, it would imply serious fine tuning if such components appeared in all examined sources in the transition from the optical thin, i.e. τγ < 1, to optical thick regime, τγ ≥ 1. This seems unlikely, considering the large number of EBL shapes tested. Consequently, EBL shapes leading to an intrinsic VHE spectrum which is not concave will be excluded. This expectation is formulated through three test criteria:
(i) Fermi-LAT spectrum as an upper limit.
With the launch of the Fermi satellite and the current generation of IACTs, there is an increasing number of broad-band AGN energy spectra measured in the HE and VHE domains. Thus, the least model dependent approach is to test spectra against a convex curvature in the transition from HE to VHE by regarding the spectral index measured by Fermi, ΓHE, as a limit on the reconstructed intrinsic index at VHE, Γ. Hence, the intrinsic VHE spectrum is regarded as unphysical if the following condition is met, 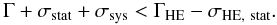 (6)The statistical error σstat is estimated from the fit of an analytical function to the intrinsic spectrum whereas the systematic uncertainty σsys is used that is estimated by the respective instrumental team. The statistical uncertainty σHE, stat of the Fermi-LAT spectral index is given by the 2FGL or the corresponding publication, see Sect. 4. This exclusion criterion will be referred to as VHE-HEIndex criterion in the following. Note that this is not the same criterion as used by Orr et al. (2011). They assume that the VHE index should be equal to the index measured with the Fermi-LAT.
(6)The statistical error σstat is estimated from the fit of an analytical function to the intrinsic spectrum whereas the systematic uncertainty σsys is used that is estimated by the respective instrumental team. The statistical uncertainty σHE, stat of the Fermi-LAT spectral index is given by the 2FGL or the corresponding publication, see Sect. 4. This exclusion criterion will be referred to as VHE-HEIndex criterion in the following. Note that this is not the same criterion as used by Orr et al. (2011). They assume that the VHE index should be equal to the index measured with the Fermi-LAT.
(ii) Super exponential pile up.
Furthermore, shapes will be excluded that lead to an intrinsic VHE spectrum that piles up super exponentially at highest energies. This is the case if it is best described by the analytical functions abbreviated SEBPL or SEDBPL, see Table 2, and the pile-up energy is positive within a 1σ confidence, 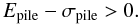 (7)This additional independent exclusion criterion relies solely on VHE observations which are subject to the attenuation in contrast to Fermi-LAT observations. It will be denoted as PileUp criterion throughout this study.
(7)This additional independent exclusion criterion relies solely on VHE observations which are subject to the attenuation in contrast to Fermi-LAT observations. It will be denoted as PileUp criterion throughout this study.
(iii) VHE concavity.
In the case that the intrinsic spectrum is best described by either a BPL or a DBPL, it is considered as convex if the following inequalities are not fulfilled, 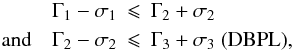 (8)and the corresponding EBL shape will be rejected. Again, 1σ uncertainties of the fitting procedure are used. This criterion will be referred to as VHEConcavity. It is very similar to the argument formulated in (ii) as intrinsic spectra that show an exponential rise may often be equally well described by a BPL or DBPL. However, with the VHEConcavity criterion also intrinsic spectra can be excluded that show only mild convexity, i.e. no exponential pile up.
(8)and the corresponding EBL shape will be rejected. Again, 1σ uncertainties of the fitting procedure are used. This criterion will be referred to as VHEConcavity. It is very similar to the argument formulated in (ii) as intrinsic spectra that show an exponential rise may often be equally well described by a BPL or DBPL. However, with the VHEConcavity criterion also intrinsic spectra can be excluded that show only mild convexity, i.e. no exponential pile up.
3.2. Cascade emission and energy budget
In this section two new approaches are introduced that are based on the integrated intrinsic emission. These methods rely on a number of parameters, whose values are, so far, not accurately determined by observations or for which only upper and lower limits exist. Therefore, the following two criteria have to be regarded as a theoretical motivated possibility to constrain the EBL in the future. As it will be shown in Sect. 5, the final upper limits are not improved by these criteria and are, thus, independent of the model parameters chosen here.
3.2.1. Cascade emission
EBL photons that interact with VHE γ-rays produce e + e − pairs. These secondary pairs can generate HE radiation by upscattering cosmic microwave background (CMB) photons by means of the IC process. This initiates an electromagnetic cascade as these photons can again undergo pair production (e.g. Svensson 1987; Aharonian et al. 1994; Dai et al. 2002; Dolag et al. 2009; Kachelriess et al. 2012). The amount of cascade radiation, that points back to the source, depends on the field strength BIGMF of the intergalactic magnetic field and its correlation length λB. The values of BIGMF and λB are unknown and only upper and lower limits exist (see e.g. Neronov & Semikoz 2009, for a compilation of limits). If the field strength is large (see Eq. (9)) or if the correlation length is small compared to the cooling length ctcool of the e + e − pairs for IC scattering, the pairs are quickly isotropized and extended halos of γ-ray emission form around the initial source (e.g Aharonian et al. 1994; Dai et al. 2002; Elyiv et al. 2009; Dolag et al. 2009). Furthermore, the time delay of the cascade emission compared to the primary emission depends on BIGMF and λB. VHE γ-rays need to be produced for a sufficiently long period so that the reprocessed radiation is observable (e.g. Dermer et al. 2011).
The cascade emission has been used to place lower limits on BIGMF and λB by assuming a certain EBL model (Neronov & Vovk 2010; Tavecchio et al. 2010, 2011; Dermer et al. 2011; Dolag et al. 2011; Taylor et al. 2011; Huan et al. 2011). Conversely, one can place upper limits on the EBL density under the assumption of a certain magnetic field strength. This novel approach is followed here whereas, in previous studies, the cascade emission is neglected when deriving upper limits on the EBL density. A higher EBL density leads to a higher production of e + e − pairs and thus to a higher cascade emission that is potentially detectable with the Fermi-LAT. If the predicted cascade radiation exceeds the observations of the Fermi-LAT, the corresponding EBL shape can be excluded. Conservative upper limits are derived if the following assumptions are made: (i) the HE emission of the source is entirely due to the cascade; (ii) the observed VHE spectrum is fitted with a power law with a super exponential cut off at the highest measured energy of the spectrum. This minimizes the reprocessed emission and allows to consider only the first generation of the cascade; (iii) the e+e− pairs are isotropized in the intergalactic magnetic field, minimizing the reprocessed emission. This condition is equal to the demand that the deflection angle ϑ of the particles in the magnetic field is ≈ π. Assuming λB ≫ ctcool, the deflection angle for electrons with an energy γmc2 ≈ E/2, where E is the energy of the primary γ ray, can be approximated by (Tavecchio et al. 2010; Neronov & Vovk 2010) 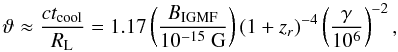 (9)with zr the redshift where the IC scattering occurs and RL the Larmor radius. The IC scattered e + e − pairs give rise to γ-rays with energy ϵ ≈ γ2hνCMB ≈ 0.63(E/TeV)2 GeV, with hνCMB = 634 μeV the peak energy of the CMB. The γ factor in Eq. (9) can be eliminated in favor of ϵ, and, solving for BIGMF, the pairs are isotropized if BIGMF ≈ 4.2 × 10-15 (1 + zr)4(ϵ/GeV) G ≈ 5 × 10-13 G for ϵ = 100 GeV, the maximum energy measured with the Fermi-LAT considered here and the maximum redshift where the IC scattering can occur, i.e. the redshift of the source1. This value of BIGMF is in accordance with all experimental bounds (see e.g. Neronov & Semikoz 2009, especially Figs. 1 and 2) For correlation lengths λB ≫ ctcool ≈ 0.65(E/TeV)-1(1 + zr)-4 Mpc
(9)with zr the redshift where the IC scattering occurs and RL the Larmor radius. The IC scattered e + e − pairs give rise to γ-rays with energy ϵ ≈ γ2hνCMB ≈ 0.63(E/TeV)2 GeV, with hνCMB = 634 μeV the peak energy of the CMB. The γ factor in Eq. (9) can be eliminated in favor of ϵ, and, solving for BIGMF, the pairs are isotropized if BIGMF ≈ 4.2 × 10-15 (1 + zr)4(ϵ/GeV) G ≈ 5 × 10-13 G for ϵ = 100 GeV, the maximum energy measured with the Fermi-LAT considered here and the maximum redshift where the IC scattering can occur, i.e. the redshift of the source1. This value of BIGMF is in accordance with all experimental bounds (see e.g. Neronov & Semikoz 2009, especially Figs. 1 and 2) For correlation lengths λB ≫ ctcool ≈ 0.65(E/TeV)-1(1 + zr)-4 Mpc 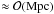 the most stringent constraints come from Faraday rotation measurements (Kronberg & Simard-Normandin 1976; Blasi et al. 1999) which limit BIGMF ≲ 10-9 G. Furthermore, the adopted value cannot be excluded neither with possible observations of deflections of ultra-high energy cosmic rays (Lee et al. 1995) nor with constrained simulations of magnetic fields in galaxy clusters, both setting an upper limit on BIGMF ≲ 10-12 G (Dolag et al. 2005; Donnert et al. 2009).
the most stringent constraints come from Faraday rotation measurements (Kronberg & Simard-Normandin 1976; Blasi et al. 1999) which limit BIGMF ≲ 10-9 G. Furthermore, the adopted value cannot be excluded neither with possible observations of deflections of ultra-high energy cosmic rays (Lee et al. 1995) nor with constrained simulations of magnetic fields in galaxy clusters, both setting an upper limit on BIGMF ≲ 10-12 G (Dolag et al. 2005; Donnert et al. 2009).
For this value of BIGMF, the cascade emission is detectable if a steady γ-ray emission of the source for the last Δt ≈ 106 years is assumed (see e.g. Dermer et al. 2011; Tavecchio et al. 2011). Other energy loss channels apart from IC scattering like synchrotron radiation or plasma instabilities (Broderick et al. 2012) are neglected. However, if the latter are present, the field strength is even higher, or the lifetime of the VHE source is shorter, no significant cascade emission is produced or it has not reached earth so far.
The cascade emission F(ϵ) is calculated with Eq. (B.3) in Appendix B following Tavecchio et al. (2011) and Dermer et al. (2011). For isotropy, the observed cascade emission has to be further modified with the solid angle 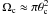 into which the intrinsic blazar emission is collimated where θc is the semi-aperture of the irradiated cone. For blazars one has θc ~ 1/ΓL where ΓL is the bulk Lorentz factor of the plasma of the jet. The observed emission is then found to be (Tavecchio et al. 2011)
into which the intrinsic blazar emission is collimated where θc is the semi-aperture of the irradiated cone. For blazars one has θc ~ 1/ΓL where ΓL is the bulk Lorentz factor of the plasma of the jet. The observed emission is then found to be (Tavecchio et al. 2011) 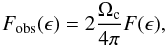 (10)where the factor of two accounts for the contribution of both jets in the isotropic case. The exclusion criterion for an EBL shape at the 2σ level reads
(10)where the factor of two accounts for the contribution of both jets in the isotropic case. The exclusion criterion for an EBL shape at the 2σ level reads 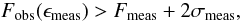 (11)where ϵmeas, Fmeas, σmeas are the measured energy, flux and statistical uncertainty reported in the 2FGL, respectively. In the case that the source is not detected Fmeas = 0 and σmeas represents the 1σ upper limit on the flux. As an example, Fig. 2 shows the observed and intrinsic VHE spectrum for a specific EBL shape of the blazar 1ES 0229+200 together with the Fermi upper limits (Tavecchio et al. 2010). The different model curves demonstrate the degeneracy between the different parameters entering the calculation. The EBL shape used to calculate the intrinsic VHE spectrum is not excluded in the isotropic case since the emission does not overproduce the Fermi upper limits. This is contrary to the case of BIGMF = 10-20 G and Δt = 3 years where the predicted cascade flux exceeds the Fermi-LAT upper limits in the 1–10 GeV range. To obtain conservative upper limits of the EBL, only the isotropic case is assumed in the following, i.e. BIGMF = 5 × 10-13 G which implies that the source has to be steady for a lifetime of Δt ≲ 106 years. Furthermore, a Lorentz factor of ΓL = 10 is generically assumed for all sources.
(11)where ϵmeas, Fmeas, σmeas are the measured energy, flux and statistical uncertainty reported in the 2FGL, respectively. In the case that the source is not detected Fmeas = 0 and σmeas represents the 1σ upper limit on the flux. As an example, Fig. 2 shows the observed and intrinsic VHE spectrum for a specific EBL shape of the blazar 1ES 0229+200 together with the Fermi upper limits (Tavecchio et al. 2010). The different model curves demonstrate the degeneracy between the different parameters entering the calculation. The EBL shape used to calculate the intrinsic VHE spectrum is not excluded in the isotropic case since the emission does not overproduce the Fermi upper limits. This is contrary to the case of BIGMF = 10-20 G and Δt = 3 years where the predicted cascade flux exceeds the Fermi-LAT upper limits in the 1–10 GeV range. To obtain conservative upper limits of the EBL, only the isotropic case is assumed in the following, i.e. BIGMF = 5 × 10-13 G which implies that the source has to be steady for a lifetime of Δt ≲ 106 years. Furthermore, a Lorentz factor of ΓL = 10 is generically assumed for all sources.
 |
Fig. 2 Cascade emission for a certain EBL shape and the VHE spectrum of 1ES 0229+200 (Aharonian et al. 2007a). The observed spectrum (dark red points and line) is fitted with a power law with an exponential cut off and corrected for the EBL absorption (dark blue dashed line and points). The green lines show the cascade emission resulting from the reprocessed flux (light gray shaded area) for a constant emission over the last three years and different magnetic field strengths. The red dotted line shows the reprocessed emission if the e+e− pairs are isotropized. The latter does not overproduce the Fermi upper limits (black diamonds Tavecchio et al. 2010) and hence the corresponding EBL shape is not excluded. The light and dark gray area together are equal to the integrated flux that is compared to the Eddington luminosity (see Sect. 3.2.2). |
3.2.2. Total energy budget
The jets of AGN, the production sites for HE/VHE emission, are powered by the accretion of matter onto a central black hole (e.g. Urry & Padovani 1995). If the radiation escapes isotropically from the black hole, the balancing of the gravitational and radiation force leads to the maximum possible luminosity due to accretion, the Eddington luminosity, (e.g. Dermer & Menon 2009) 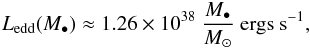 (12)where M• is the black-hole mass normalized to the mass of the sun, M⊙. Assuming that the total emission of an AGN is not super-Eddington, the Eddington luminosity is the maximum power available for the two jets, Pjet ≤ Ledd/2, which is a sum of several contributions which all can be represented as (e.g. Celotti & Fabian 1993; Bonnoli et al. 2011)
(12)where M• is the black-hole mass normalized to the mass of the sun, M⊙. Assuming that the total emission of an AGN is not super-Eddington, the Eddington luminosity is the maximum power available for the two jets, Pjet ≤ Ledd/2, which is a sum of several contributions which all can be represented as (e.g. Celotti & Fabian 1993; Bonnoli et al. 2011) 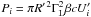 , in the case that the radiation is emitted by an isotropically radiating relativistic plasma blob in the comoving frame. The blob of radius R′ in the comoving frame moves with a bulk Lorentz factor ΓL and corresponding speed βc,
, in the case that the radiation is emitted by an isotropically radiating relativistic plasma blob in the comoving frame. The blob of radius R′ in the comoving frame moves with a bulk Lorentz factor ΓL and corresponding speed βc, 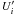 is the comoving energy density. The energy density of the produced radiation is
is the comoving energy density. The energy density of the produced radiation is 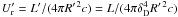 . The last equality connects the comoving luminosity with the luminosity in the lab frame via the Doppler factor
. The last equality connects the comoving luminosity with the luminosity in the lab frame via the Doppler factor ![\hbox{$\delta_\mathrm{D} = [(1+z)\Gamma_\mathrm{L}(1-\beta\cos\theta)]^{-1} \approx 2\Gamma_\mathrm{L}/[(1+z)(1 + \theta^2\Gamma_\mathrm{L}^2)] $}](/articles/aa/full_html/2012/06/aa18284-11/aa18284-11-eq123.png) where θ is the angle between the jet axis and the line of sight. The approximation holds for θ ≪ 1 and ΓL ≫ 1. Assuming θ ≈ θc, the Doppler factor and the bulk Lorentz factor are equal up to the redshift factor 1 + z, δD ≈ ΓL. The power produced in radiation is a robust lower limit for the entire power of the jet (e.g. Bonnoli et al. 2011),
where θ is the angle between the jet axis and the line of sight. The approximation holds for θ ≪ 1 and ΓL ≫ 1. Assuming θ ≈ θc, the Doppler factor and the bulk Lorentz factor are equal up to the redshift factor 1 + z, δD ≈ ΓL. The power produced in radiation is a robust lower limit for the entire power of the jet (e.g. Bonnoli et al. 2011), 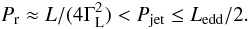 (13)Solving the inequality for the observed luminosity, one arrives at an additional exclusion criterion for EBL shapes, namely, if the intrinsic energy flux at VHE is larger than the associated Eddington energy flux,
(13)Solving the inequality for the observed luminosity, one arrives at an additional exclusion criterion for EBL shapes, namely, if the intrinsic energy flux at VHE is larger than the associated Eddington energy flux, 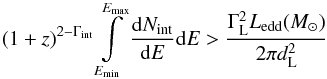 (14)where Emin and Emax are the minimum and maximum energy of the intrinsic VHE spectrum which is described with a power law with index Γint. The the factor (1 + z)2 − Γint accounts for the K-correction and dL is the luminosity distance given by
(14)where Emin and Emax are the minimum and maximum energy of the intrinsic VHE spectrum which is described with a power law with index Γint. The the factor (1 + z)2 − Γint accounts for the K-correction and dL is the luminosity distance given by 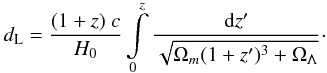 (15)For a conservative estimate, M• + σM• is used in the calculation of Ledd. The assumption of a non super-Eddington luminosity is, however, somewhat speculative as super-Eddington emission has been observed e.g. in the variable source 3C 454.3 (Abdo et al. 2011b). In Sect. 5, it will be shown that the capability of the Eddington criterion to exclude EBL shapes is extremely limited. For this reason, only steady sources (listed in Table 4) will be considered for this criterion. Here, it is only emphasized that it is in principle possible to constrain the EBL with this argument.
(15)For a conservative estimate, M• + σM• is used in the calculation of Ledd. The assumption of a non super-Eddington luminosity is, however, somewhat speculative as super-Eddington emission has been observed e.g. in the variable source 3C 454.3 (Abdo et al. 2011b). In Sect. 5, it will be shown that the capability of the Eddington criterion to exclude EBL shapes is extremely limited. For this reason, only steady sources (listed in Table 4) will be considered for this criterion. Here, it is only emphasized that it is in principle possible to constrain the EBL with this argument.
Excluding EBL shapes with cascade emission (Eq. (11)) and the total energy budget of the source (Eq. (14)), will be referred to as the IntVHELumi (short for intrinsic VHE luminosity) criterion.
VHE AGN spectra used in this study.
4. VHE AGN sample
In the past four years, the number of discovered VHE emitting AGN has doubled. In this section samples of VHE spectra are defined that are evaluated with the VHE-HEIndex, PileUp and VHEConcavity criteria (Sect. 4.1) and with the IntVHELumi criterion (Sect. 4.2).
4.1. Sample tested against concavity criteria
For this part of the analysis, 22 VHE spectra from 19 different sources are used. AGN are included in the sample only if their redshift is known, there is no confusion with other sources, and they are detected with the Fermi-LAT. This excludes the known VHE sources 3C 66A and 3C 66B, 1ES 0229+200, PG 1553+113, and S 50716+714. Two spectra from the same source are only considered if they cover different energy ranges. Furthermore, the radio galaxies Centaurus A and M 87 are not included since they are too close and measured at energies that are too low to yield any constraints of the EBL density. Spectra that are a combination of several instruments are not included due to possible systematic uncertainties. If two or more spectra are available for a variable source, the VHE spectrum is chosen that is measured simultaneously with Fermi-LAT observations. If the Fermi spectrum is best described with a logarithmic parabola, the spectral index determined at the pivot energy is used for the comparison with the intrinsic VHE spectra. The entire AGN sample is listed in Table 3 together with the redshift, the energy range, the spectral index at VHE energies, the index measured with the Fermi-LAT, the variability index given in the 2FGL, and the corresponding references.
AGN are known to be variable sources both in overall flux and spectral index. This poses a problem for the VHE-HEIndex criterion as it relies on the comparison of Fermi-LAT and IACT spectra. To address this issue, one can roughly divide the overall source sample into three categories:
-
1.
Steady sources in the Fermi-LAT energy band. In this category, all sources are assembled that show a variability index < 41.64 in the 2FGL which corresponds to a likelihood fit probability of more than 1% that the source is steady (Fermi-LAT Collaboration 2012). For these sources simultaneous measurements are not required regardless if they are steady (like 1ES 1101-232, Aharonian et al. 2007b) or variable (like H 1426+428, see below) at VHE. This does not affect the upper limits derived here because the Fermi index remains valid as a lower limit independent of the VHE index. These sources are marked as “steady” in the last column of Table 3.
-
2.
Variable sources with simultaneous measurements. Some of the variable sources were observed simultaneously with the Fermi-LAT and IACTs in multiwavelength campaigns, namely PKS 2155-304 with HESS (Aharonian et al. 2009), and PKS 1222+21 with MAGIC (Aleksić et al. 2011). Instead of the spectral slopes given in the 2FGL, the Fermi-LAT spectra from these particular observations are used to test the EBL shapes. These sources are marked as “simul” in the last column in Table 3. Note, however, that the observation times might not be equal for the individual instruments since the sensitivities for the Fermi-LAT and IACTs are different. Nevertheless, the arising systematic uncertainty is negligible for the sources under consideration. In the case of PKS 2155-304, the source was observed in a quiescent state where no fast flux variability is expected. PKS 1222+21, on the other hand, was observed in a HE flaring state and Fermi-LAT observations are not available the 30 min of MAGIC observations. Instead, Aleksić et al. (2011) derive the Fermi spectrum from 2.5 h of data encompassing these 30 min. This is justified, since the source remained in this high flux state for several days with little spectral variations (cf. Fig. 2 in Tanaka et al. 2011). Accordingly, the maximum time lag allowed for observations to be considered as simultaneous is of the order of an hour.
Table 4Sources used to exclude EBL shapes with the IntVHELumi criterion.
-
3.
Variable sources not simultaneously measured. For some variable sources, no simultaneous data are available, namely, 1ES 1011+496, 1ES 1959+650, 3C 279, BL Lacertae, the flare spectra of Mkn 501 and Mkn 421, and PKS 2005-489 (see Table 3 for the references). In these cases, the literature was examined for dedicated Fermi-LAT analyses of the corresponding sources in order to find hardest spectral index published. In the cases of 1ES 1011+496, 1ES 1959+650, PKS 2005-489 and Mkn 421 the indices reported in the 2FGL are the hardest published so far. The hardest indices for BL Lacertae and Mkn 501 are obtained by Abdo et al. (2010a) and Abdo et al. (2011a), respectively, see Table 3 for the corresponding values. The distant quasar 3C 279 was observed with the Fermi-LAT during a γ-ray flare in 2009 and the measured spectral indices vary between ~2 and ~2.5 (compare Fig. 1 in Abdo et al. 2010c). Thus, the catalog index of 2.22 ± 0.02 is appropriate to use. Table 3 refers to all the spectra discussed here as “hardest index” in the last column.
Additional uncertainties are introduced for the VHE observation with a maximum time lag between the measurement and the launch of the Fermi satellite, which is the case for Mkn 501 and H 1426+428. In the case of H 1426+428, no detection has been reported after the HEGRA measurement in 2002 at VHE which might suggest that the source is now in a quiescent state. The 2002 spectrum with an observed spectral index of Γ = 1.93 ± 0.47 is used in this study. The hard spectrum promises stronger limits with the VHE-HEIndex criterion than the 2000 spectrum which has a spectral slope of Γ = 2.79 ± 0.33. The source showed a change in flux by a factor of 2.5 between the 1999/2000 and 2002 observation runs but the spectral slope remained constant (Aharonian et al. 2003a). Additionally, the Fermi index of 1.32 ± 0.12 is the hardest of the entire sample and, in summary, it is chosen to include the source in the study. As for Mkn 501, the spectrum of the major outbreak was measured up to 21 TeV and, consequently, it is a promising VHE spectrum to constrain the EBL density at FIR wavelengths. As it turns out, it excludes most shapes due to the PileUp and VHEConcavity criteria. These criteria are independent of the Fermi index and, therefore, not affected by the difference in observation time.
 |
Fig. 3 Histogram of the fraction of excluded shapes of the different VHE spectra. The columns show the total fraction of rejected shapes as well as the fraction excluded by the different criteria. The column labeled “Curvature” combines the VHEConcavity and PileUp criteria. Spectra that allow more than 90% of all shapes are not shown. |
4.2. Sample tested against intrinsic VHE luminosity
For the integral criterion presented in Sects. 3.2.1 and 3.2.2, only spectra from steady sources are used in order to avoid systematic uncertainties introduced by variability. Only spectra are examined which suffer from large attenuations and are measured at energies beyond several TeV. These spectra are the most promising candidates for constraints as they show the highest values of integrated intrinsic emission. On the other hand, the spectrum of 1ES 0229+200 which has been reanalyzed by Tavecchio et al. (2010) can be tested against the IntVHELumi condition as upper limits on the HE flux suffice and no spectral information is required for this criterion. Otherwise, the same selection criteria apply as for the sample tested against concavity (known redshift, etc.). The VHE spectra evaluated with the IntVHELumi criterion together with the central black-hole masses of the corresponding sources are summarized in Table 4.
5. Results
The upper limits on the EBL density are derived by calculating the envelope shape of all allowed EBL shapes. The influence of the different exclusion criteria is examined by inspecting the envelope shape due to the VHE-HEIndex argument alone and successively adding the other criteria and reevaluating the resulting upper limits. Furthermore, the impact of the VHE spectra responsible for the most stringent limits in the optical, MIR and FIR will be investigated by excluding these spectra from the sample and inspect the change in the upper limits.
Figure 3 shows a histogram of the fractions of rejected shapes by each VHE spectrum, where the different colors represent the different criteria that lead to the exclusion of an EBL shape. It should be noted that individual shapes can be rejected by several criteria at the same time, and, therefore, the different columns may add up to a number larger than indicated by the total column. Results for spectra that exclude no (BL Lacertae, 1ES 2344+514, and Mkn 180) or less than 10% of all EBL shapes (the MAGIC spectrum of 1ES 1959+650, the HESS spectra of RGB J0152+017 and Mkn 421, as well as the HEGRA spectrum of 1ES 1959+650) are not shown. Most EBL shapes are excluded by the VHE spectra of H 1426+428, 1ES 1101-232, and Mkn 501. The influence of H 1426+428, and Mkn 501 on the limits in the MIR and FIR and of 3C 279 together with PKS 1222+21 in the optical will be examined by excluding these spectra from the sample. These sources provide strong constraints in the respective wavelength bands. Note that removing 1ES 1101-232 from the source sample does not change the upper limits since a number of spectra of sources with comparable redshifts (cf. Table 3) exclude the same EBL shapes as 1ES 1101-232, e.g. 1ES 0414+009, the VERITAS spectrum of 1ES 1218+304, H 2356-309, and PKS 2005-489.
 |
Fig. 4 Limits on the EBL density for different exclusion criteria. The solid line is the envelope shape of all allowed shapes from the combination of all VHE spectra whereas the dashed curve shows the envelope shape without considering the VHE spectrum of 3C 279. The dashed dotted line is the envelope shape without H 1426+428 and the dotted line displays the upper limits without Mkn 501. |
Different combinations of exclusion criteria are shown in the panels of Fig. 4. Each panel depicts the limits for the complete spectrum sample and, additionally, the resulting EBL constraints if the spectra discussed above are omitted. By itself, the VHE-HEIndex criterion gives strong upper limits in the optical and MIR on the EBL density if all spectra are included (upper left panel of Fig. 4). In the optical, the limits are dominated by the spectra of 3C 279 and PKS 1222+21, so, consequently, the restrictions are significantly weaker without these spectra (dashed line in Fig. 4). The spectra are influenced most by changes of the EBL density in the optical which is inferred from the maximum energies of 480 GeV and 350 GeV for 3C 279 and PKS 1222+21, respectively. They translate into maximum cross sections for pair production at 0.6 μm (3C 279) and 0.43 μm (PKS 1222+21), see Eq. (3). The constraints are almost unaltered if only one of these spectra is excluded from the sample. In the MIR, the spectrum of H 1426+428 provides firm limits on the EBL density whereas scarcely any EBL shape is rejected due to the spectrum of Mkn 501 with the VHE-HEIndex criterion.
 |
Fig. 5 Upper panel: example of an EBL shape excluded by Mkn 501 with the VHEConcavity criterion. Lower panel: the spectra of Mkn 501 and Mkn 421 corrected with this particular EBL shape. The flux of the latter is scaled by 10-3 for better visibility. For Mkn 501, a double broken power law provides the best description with a spectral index Γ3 = −35 at highest energies, the maximum value tested in the fitting procedure. In the case of Mkn 421, a simple power law suffices. |
The combination of the VHE-HEIndex and VHEConcavity criterion strengthens the upper limits between 2 μm and 10 μm, as shown in the upper right panel of Fig. 4. Convex intrinsic spectra are the result of an EBL density with a positive gradient between lower and higher wavelengths and, thus, a combination with the VHE-HEIndex criterion is necessary to exclude shapes with a high EBL density that are rather constant in wavelength. Therefore, on their own, neither the PileUp nor the VHEConcavity criterion provide strong upper limits. Combining the PileUp and VHE-HEIndex arguments results in very similar limits as the combination of the VHE-HEIndex and VHEConcavity criterion. This degeneracy between the PileUp and VHEConcavity criterion is also demonstrated in Fig. 5. The spectrum of Mkn 501 corrected with a certain EBL shape shows a strong exponential rise at highest energies but is best described with a double broken power law. The combination of the PileUp and VHEConcavity together with the VHE-HEIndex criterion yields robust upper limits in the FIR as displayed in the lower right panel of Fig. 4. The constraints in the FIR are entirely due to the spectrum of Mkn 501 although the spectrum of Mkn 421 is also measured beyond 20 TeV and both sources have a comparable redshift. However, the spectrum of Mkn 421 rejects far less shapes than Mkn 501. Indeed, an exponential rise is observed in intrinsic spectra of Mkn 421 for certain EBL realizations (e.g. the corrected Mkn 421 spectrum in Fig. 5) but a power law is found to be the best description of the spectrum.
Compared to the VHE-HEIndex criterion alone, the combination with the IntVHELumi criterion leads to improved upper limits only if H 1426+428 is discarded from the sample (lower left panel of Fig. 4). Most shapes are rejected by the VHE spectrum of 1ES 0229+200 which is also the sole spectrum which excludes a very limited number of shapes with the Eddington luminosity argument. Remarkably, the spectrum excludes more than 60% of all shapes. The IntVHELumi criterion has the most substantial effect in the infrared part of the EBL density as the highest energies of the spectrum of 1ES 0229+200 contribute most to the integral flux. The maximum energy measured in the spectrum is 11.45 TeV and thus the limits are most sensitive to changes in the EBL around 14 μm. The influence of the choice of the bulk Lorentz factor ΓL (and hence of the Doppler factor δD since ΓL ≈ δD is assumed) on the envelope shape can be seen from Fig. 6, where the upper limits are shown for ΓL = 5, 10, and 50. As ΓL enters quadratically into the calculation of the flux (cf. Eq. (10)) and for the Eddington luminosity (Eq. (14)) the choice of the value of ΓL is critical for the number of rejected EBL shapes. The bulk Lorentz factor is unknown for the sources tested with IntVHELumi and for the combination with the other criteria ΓL = 10 is generically chosen. However, even with this oversimplified choice of ΓL, the IntVHELumi criterion does not lead to improvements of the upper limits compared to the combination of the VHE-HEIndex, VHEConcavity and PileUp criteria. Conversely, this implies that the final upper limits will not depend on the specific choice of model parameters and assumptions that enter the evaluation of the IntVHELumi criterion.
The final result for the upper limits is the combination of all criteria and all VHE spectra, shown in Fig. 7. It is the envelope shape of all allowed EBL realizations, cf. Fig. 7a, which itself is excluded by several VHE spectra and it should, thus, not be regarded as a possible level of the EBL density. For the maximum energy of all VHE spectra of 23.1 TeV, the cross section for pair production peaks at a wavelength of the EBL photons of λ∗ ≈ 29 μm. More than half of the interactions occur in a narrow interval Δλ = (1 ± 1/2)λ∗ around the peak wavelength (e.g. Aharonian et al. 2006) and hence the constraints are not extended beyond 100 μm. Albeit including the evolution of the EBL with redshift, the derived upper limits are below 5 nW m-2 sr-1 in the range from 8 μm to 31 μm. A comparison of the constraints with previous works is shown in Fig. 7b. Above 30 μm, the constraints are consistent with those derived in MR07. For wavelengths between 1 μm and 4 μm the limits are in accordance with the results of Aharonian et al. (2006, 2007a) and Albert et al. (2008). The strong limits of Albert et al. (2008) who utilized the spectrum of 3C 279 are not reproduced. Note, however, that these limits are derived by changing certain free parameters (e.g. fraction of UV emission escaping the galaxies) of the EBL model of Kneiske et al. (2002) while the current approach allows for generic EBL shapes. Consequently, an EBL shape with a high density at UV/optical wavelengths followed by a steep decline towards optical and NIR wavelengths produces a soft intrinsic spectrum of 3C 279 that cannot be excluded by any criterion. Furthermore, an inspection of the spectrum of 3C 279 shows that the fit will be dominated by the first two energy bins due to the smaller error bars. Thus, a convex spectrum is often still sufficiently described with a soft power law. In general, it should be underlined that all of the above limits from recent studies use a theoretically motivated bound on the intrinsic spectral slope of Γ = 1.5.
 |
Fig. 6 Upper limits solely due to the IntVHELumi criterion for different values of the bulk Lorentz factor ΓL and the Doppler factor δD of the emitting region. With increasing Lorentz and Doppler factor, respectively, the limits become worse (see Eqs. (10) and (14)). |
The upper limits derived here are not in conflict with the EBL model calculations of Franceschini et al. (2008), Kneiske & Dole (2010) and Domínguez et al. (2011) and are compatible with the lower limit galaxy number counts derived from Spitzer measurements (Fazio et al. 2004, see Fig. 7c). In the FIR, the models of Franceschini et al. (2008) and Domínguez et al. (2011) lie above the derived upper limits, though one should note that the EBL limit at these wavelengths relies on a single spectrum (Mkn 501). Between ~1 μm and ~14 μm there is, however, a convergence between the upper limits and model calculations and at 13.4 μm the EBL is constrained below 2.7 nW m-2 sr-1, just above the EBL models. This leaves not much room for additional components such as Population III stars and implies that the direct measurements of Matsumoto et al. (2005) are foreground dominated as discussed in Dwek et al. (2005). The EBL models, the upper limits from previous works, and the results derived here are shown together in Fig. 8.
 |
Fig. 7 Upper limits derived in this study. a) The envelope shape (upper limits) of all allowed shapes (dark gray lines). Also shown are the grid points as light gray bullets. b) The constraints compared to the the upper limits of MR07, Aharonian et al. (2006, 2007a), and Albert et al. (2008). c) Upper limits of this study together with three EBL models (Franceschini et al. 2008; Kneiske & Dole 2010; Domínguez et al. 2011). d) Upper limits requiring different minimum numbers of VHE spectra that exclude an EBL shape. |
 |
Fig. 8 Upper limits of this work together with previous limits and EBL models. |
In general, most of the tested EBL shapes are excluded by more than one spectrum (Fig. 9). While 0.23% of all EBL shapes are excluded by only one of the spectra in the sample, the majority of shapes (93%) is rejected by five spectra or more. Figure 7d shows the limits for different minimum numbers of VHE spectra that rule out an EBL shape. From NIR to MIR wavelengths, the limits are only slightly worsened if at least two spectra are required to exclude EBL shapes. If at least five spectra are ought to reject an EBL shape, the EBL density remains confined below 40 nW sr-1 m-2 in the optical. Thus, from optical to MIR wavelengths, the limits are robust against individual spectra that possibly have a peculiar intrinsic shape due to one of the mechanisms discussed in Sect. 3.1. Especially in the MIR and FIR, however, the limits are weakened as they mainly depend on two spectra, H 1426+428 and Mkn 501. This underlines the need for more spectra measured beyond several TeV in order to draw conclusions about the EBL density in the MIR and FIR from VHE blazar measurements.
Given the similarities in procedures used, the systematic uncertainties of the limits derived in this study are similar to the ones derived in MR07 and Raue (2007). They have been estimated to be 31% in optical to near infrared and 32–55% in mid to far infrared wavelengths, mainly from the grid spacing and the uncertainties on the absolute energy scale of ground based VHE instruments which is taken to be 15%. Note that Meyer et al. (2010) achieved a cross-calibration using the broadband SED of the Crab Nebula between the Fermi-LAT and IACTs by shifting the IACT measurements by ~5% in energy. As it turns out, additional uncertainties arise from the phenomenological description of the EBL evolution (<4% for a redshift z = 0.2 and < 10% for z = 0.5, Raue & Mazin 2008). Uncertainties in the calculation of the cascade emission are caused by the choice of the model parameters which are, however, difficult to quantify. The same applies for the assumption that steady sources do not show super-Eddington luminosities. Since the most stringent limits do not rely on these exclusion criteria, these uncertainties do not affect the final results of the upper limits.
Additionally, the measurement capabilities of the Fermi-LAT affect the VHE-HEIndex criterion and hence the upper limits. While the 2FGL does not quote the systematic errors on the individual spectral indices, it gives a number of sources of systematic errors: the effective area, the diffuse emission model, and the handling of front and back converted events. The systematic error on the effective area is estimated to be between 5% and 10%, while the errors on the diffuse emission model mainly affect sources inside the galactic plane. Furthermore, the isotropic emission for front and back converted events is assumed to be equal. This leads to underestimation of the flux below 400 MeV and might produce harder source spectra. As harder spectra in the Fermi-LAT band weaken the upper limits, the results derived here can, again, be regarded as conservative.
6. Summary and conclusions
In this paper, new upper limits on EBL density over a wide wavelength range from the optical to the far infrared are derived, utilizing the EBL attenuation of HE and VHE γ-rays from distant AGN. A large number of possible EBL realization is investigated, allowing for possible features from, e.g., the first stars. Evolution of the EBL density with redshift is taken into account in the calculations using a phenomenological prescription (see e.g. Raue & Mazin 2008). A large sample of VHE spectra consisting of 23 spectra from 20 different sources with redshifts ranging from z = 0.031 to 0.536 is used in the analysis. The VHE spectra are corrected for absorption and subsequently investigated for their physical feasibility. Two basic criteria are examined: (1) concavity of the high energy part of the spectrum spanning from HE to VHE and (2) total integral flux in the VHE, a novel way to probe the EBL density. For the former criterion, spectra from the Fermi-LAT at HE are used as a conservative upper limit, combined with criteria on the overall VHE concavity. This is a more conservative argument than a theoretically motivated bound on the intrinsic spectral index at VHE of, say, Γ = 1.5. This value, used in previous studies, is somewhat under debate as a harder index can be possible, for instance, if the underlying population of relativistic electrons is very narrow (Katarzyński et al. 2006; Tavecchio et al. 2009; Lefa et al. 2011b), particles are accelerated at relativistic shocks (e.g. Stecker et al. 2007), in the case of internal photon absorption (Aharonian et al. 2008b), or in proton-synchrotron models (e.g. Aharonian 2000; Zacharopoulou et al. 2011). For the latter criterion, the expected cascade emission is investigated and, additionally, the total intrinsic luminosity is compared to the Eddington luminosity of the AGN. Limits on the EBL density are derived using each of the criteria individually and for combinations of the criteria. In addition, the influence of individual data sets is tested. The obtained constraints reach from 0.4 μm to 100 μm and are below 5 nW m-2 sr-1 between 8 μm and 31 μm even though more conservative criteria are applied and the evolution of the EBL with redshift is accounted for. In the optical, the EBL density is limited below 24 nW m-2 sr-1.
 |
Fig. 9 Percentage of all shapes excluded by at least a certain number of spectra. The majority of rejected shapes is not allowed by more than five spectra. |
The limits forecast a low level of the EBL density from near to far infrared wavelengths also predicted by the models of Kneiske & Dole (2010) and Domínguez et al. (2011) which is in accordance with MR07. Furthermore, the constraints exclude the direct measurements of Matsumoto et al. (2005). Certain mechanisms, however, are discussed in the literature that effectively reduce the the attenuation of γ-rays due to pair production. For instance, if cosmic rays produced in AGN are not deflected strongly in the intergalactic magnetic field they could interact with the EBL and form VHE γ-rays that contribute to the VHE spectrum (Essey & Kusenko 2010; Essey et al. 2010, 2011). Other suggestions are more exotic as they invoke the conversion of photons into axion like particles (e.g de Angelis et al. 2009; Mirizzi & Montanino 2009) or the violation of Lorentz invariance (e.g. Jacob & Piran 2008).
Future simultaneous observations of extragalactic blazars with the Fermi-LAT and IACTs have the potential to further constrain the EBL density.
Acknowledgments
M.M. would like to thank the state excellence cluster “Connecting Particles with the Cosmos” at the university of Hamburg. The authors would also like to thank the anonymous referee for helpful comments improving the manuscript.
References
- Abdo, A. A., Ackermann, M., Agudo, I., et al. 2010a, ApJ, 716, 30 [NASA ADS] [CrossRef] [Google Scholar]
- Abdo, A. A., Ackermann, M., Ajello, M., et al. 2010b, ApJ, 723, 1082 [NASA ADS] [CrossRef] [Google Scholar]
- Abdo, A. A., Ackermann, M., Ajello, M., et al. 2010c, Nature, 463, 919 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Abdo, A. A., Ackermann, M., Ajello, M., et al. 2011a, ApJ, 727, 129 [NASA ADS] [CrossRef] [Google Scholar]
- Abdo, A. A., Ackermann, M., Ajello, M., et al. 2011b, ApJ, 733, L26 [NASA ADS] [CrossRef] [Google Scholar]
- Acciari, V., Aliu, E., Arlen, T., et al. 2009a, ApJ, 690, L126 [NASA ADS] [CrossRef] [Google Scholar]
- Acciari, V. A., Aliu, E., Arlen, T., et al. 2009b, ApJ, 695, 1370 [NASA ADS] [CrossRef] [Google Scholar]
- Acciari, V. A., Aliu, E., Arlen, T., et al. 2010, ApJ, 715, L49 [NASA ADS] [CrossRef] [Google Scholar]
- Aharonian, F. A. 2000, New A, 5, 377 [NASA ADS] [CrossRef] [Google Scholar]
- Aharonian, F. A., Coppi, P. S., & Voelk, H. J. 1994, ApJ, 423, L5 [NASA ADS] [CrossRef] [Google Scholar]
- Aharonian, F. A., Akhperjanian, A. G., Barrio, J. A., et al. 1999, A&A, 349, 11 [NASA ADS] [Google Scholar]
- Aharonian, F. A., Timokhin, A. N., & Plyasheshnikov, A. V. 2002, A&A, 384, 834 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Aharonian, F., Akhperjanian, A., Beilicke, M., et al. 2003a, A&A, 403, 523 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Aharonian, F., Akhperjanian, A., Beilicke, M., et al. 2003b, A&A, 406, L9 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Aharonian, F., Akhperjanian, A. G., Bazer-Bachi, A. R., et al. 2006, Nature, 440, 1018 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Aharonian, F., Akhperjanian, A. G., Barres de Almeida, U., et al. 2007a, A&A, 475, L9 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Aharonian, F., Akhperjanian, A. G., Bazer-Bachi, A. R., et al. 2007b, A&A, 470, 475 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Aharonian, F., Akhperjanian, A. G., Barres de Almeida, U., et al. 2008a, A&A, 481, L103 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Aharonian, F. A., Khangulyan, D., & Costamante, L. 2008b, MNRAS, 387, 1206 [NASA ADS] [CrossRef] [Google Scholar]
- Aharonian, F., Akhperjanian, A. G., Anton, G., et al. 2009, ApJ, 696, L150 [NASA ADS] [CrossRef] [Google Scholar]
- Albert, J., Aliu, E., Anderhub, H., et al. 2006a, ApJ, 642, L119 [NASA ADS] [CrossRef] [Google Scholar]
- Albert, J., Aliu, E., Anderhub, H., et al. 2006b, ApJ, 648, L105 [NASA ADS] [CrossRef] [Google Scholar]
- Albert, J., Aliu, E., Anderhub, H., et al. 2007a, ApJ, 662, 892 [NASA ADS] [CrossRef] [Google Scholar]
- Albert, J., Aliu, E., Anderhub, H., et al. 2007b, ApJ, 666, L17 [NASA ADS] [CrossRef] [Google Scholar]
- Albert, J., Aliu, E., Anderhub, H., et al. 2007c, ApJ, 667, L21 [NASA ADS] [CrossRef] [Google Scholar]
- Albert, J., Aliu, E., Anderhub, H., et al. 2008, Science, 320, 1752 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Aleksić, J., Antonelli, L. A., Antoranz, P., et al. 2011, ApJ, 730, L8 [NASA ADS] [CrossRef] [Google Scholar]
- Atwood, W. B., Abdo, A. A., Ackermann, M., et al. 2009, ApJ, 697, 1071 [NASA ADS] [CrossRef] [Google Scholar]
- Blasi, P., Burles, S., & Olinto, A. V. 1999, ApJ, 514, L79 [NASA ADS] [CrossRef] [Google Scholar]
- Bloom, S. D., & Marscher, A. P. 1996, ApJ, 461, 657 [NASA ADS] [CrossRef] [Google Scholar]
- Blumenthal, G. R., & Gould, R. J. 1970, Rev. Mod. Phys., 42, 237 [NASA ADS] [CrossRef] [Google Scholar]
- Bonnoli, G., Ghisellini, G., Foschini, L., Tavecchio, F., & Ghirlanda, G. 2011, MNRAS, 410, 368 [NASA ADS] [CrossRef] [Google Scholar]
- Broderick, A. E., Chang, P., & Pfrommer, C. 2012, ApJ, 752, 22 [NASA ADS] [CrossRef] [Google Scholar]
- Celotti, A., & Fabian, A. C. 1993, MNRAS, 264, 228 [Google Scholar]
- Chelouche, D., Koester, B. P., & Bowen, D. V. 2007, ApJ, 671, L97 [NASA ADS] [CrossRef] [Google Scholar]
- Dai, Z. G., Zhang, B., Gou, L. J., Mészáros, P., & Waxman, E. 2002, ApJ, 580, L7 [NASA ADS] [CrossRef] [Google Scholar]
- de Angelis, A., Mansutti, O., Persic, M., & Roncadelli, M. 2009, MNRAS, 394, L21 [NASA ADS] [CrossRef] [Google Scholar]
- Dermer, C. D., & Menon, G. 2009, High Energy Radiation from Black Holes: Gamma Rays, Cosmic Rays, and Neutrinos [Google Scholar]
- Dermer, C. D., & Schlickeiser, R. 1993, ApJ, 416, 458 [NASA ADS] [CrossRef] [Google Scholar]
- Dermer, C. D., Cavadini, M., Razzaque, S., et al. 2011, ApJ, 733, L21 [NASA ADS] [CrossRef] [Google Scholar]
- Dolag, K., Grasso, D., Springel, V., & Tkachev, I. 2005, J. Cosmol. Astropart. Phys., 1, 9 [Google Scholar]
- Dolag, K., Kachelrieß, M., Ostapchenko, S., & Tomàs, R. 2009, ApJ, 703, 1078 [NASA ADS] [CrossRef] [Google Scholar]
- Dolag, K., Kachelriess, M., Ostapchenko, S., & Tomàs, R. 2011, ApJ, 727, L4 [NASA ADS] [CrossRef] [Google Scholar]
- Domínguez, A., Primack, J. R., Rosario, D. J., et al. 2011, MNRAS, 410, 2556 [NASA ADS] [CrossRef] [Google Scholar]
- Donnert, J., Dolag, K., Lesch, H., & Müller, E. 2009, MNRAS, 392, 1008 [NASA ADS] [CrossRef] [Google Scholar]
- Dwek, E., & Krennrich, F. 2005, ApJ, 618, 657 [NASA ADS] [CrossRef] [Google Scholar]
- Dwek, E., Arendt, R. G., & Krennrich, F. 2005, ApJ, 635, 784 [NASA ADS] [CrossRef] [Google Scholar]
- Elyiv, A., Neronov, A., & Semikoz, D. V. 2009, Phys. Rev. D, 80, 023010 [NASA ADS] [CrossRef] [Google Scholar]
- Essey, W., & Kusenko, A. 2010, Astropart. Phys., 33, 81 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Essey, W., Kalashev, O. E., Kusenko, A., & Beacom, J. F. 2010, Phys. Rev. Lett., 104, 141102 [NASA ADS] [CrossRef] [Google Scholar]
- Essey, W., Kalashev, O., Kusenko, A., & Beacom, J. F. 2011, ApJ, 731, 51 [NASA ADS] [CrossRef] [Google Scholar]
- Fazio, G. G., Ashby, M. L. N., Barmby, P., et al. 2004, ApJS, 154, 39 [NASA ADS] [CrossRef] [Google Scholar]
- Fermi-LAT collaboration 2012, ApJ, in press [arXiv:1108.1420] [Google Scholar]
- Franceschini, A., Rodighiero, G., & Vaccari, M. 2008, A&A, 487, 837 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Georganopoulos, M., Sambruna, R. M., Kazanas, D., et al. 2008, ApJ, 686, L5 [NASA ADS] [CrossRef] [Google Scholar]
- Georganopoulos, M., Finke, J. D., & Reyes, L. C. 2010, ApJ, 714, L157 [NASA ADS] [CrossRef] [Google Scholar]
- Gould, R. J., & Schréder, G. P. 1967, Phys. Rev., 155, 1404 [NASA ADS] [CrossRef] [Google Scholar]
- Guy, J., Renault, C., Aharonian, F. A., Rivoal, M., & Tavernet, J.-P. 2000, A&A, 359, 419 [NASA ADS] [Google Scholar]
- Hauser, M. G., & Dwek, E. 2001, ARA&A, 39, 249 [NASA ADS] [CrossRef] [Google Scholar]
- Hauser, M. G., Arendt, R. G., Kelsall, T., et al. 1998, ApJ, 508, 25 [NASA ADS] [CrossRef] [Google Scholar]
- HESS Collaboration, Abramowski, A., Acero, F., et al. 2010a, A&A, 516, A56 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- HESS Collaboration, Acero, F., Aharonian, F., et al. 2010b, A&A, 511, A52 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- HESS Collaboration, Abramowski, A., Acero, F., et al. 2012, A&A, 538, A103 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Huan, H., Weisgarber, T., Arlen, T., & Wakely, S. P. 2011, ApJ, 735, L28 [NASA ADS] [CrossRef] [Google Scholar]
- Jacob, U., & Piran, T. 2008, Phys. Rev. D, 78, 124010 [NASA ADS] [CrossRef] [Google Scholar]
- James, F. 1998, MINUIT Reference Manual, CERN Program Library Long Writeup D506 [Google Scholar]
- Jelley, J. V. 1966, Phys. Rev. Lett., 16, 479 [NASA ADS] [CrossRef] [Google Scholar]
- Kachelriess, M., Ostapchenko, S., & Tomas, R. 2012, Comp. Phys. Commun., 183, 1036 [Google Scholar]
- Kashlinsky, A. 2005, Phys. Rep., 409, 361 [NASA ADS] [CrossRef] [Google Scholar]
- Katarzyński, K., Ghisellini, G., Tavecchio, F., Gracia, J., & Maraschi, L. 2006, MNRAS, 368, L52 [NASA ADS] [CrossRef] [Google Scholar]
- Kneiske, T. M., & Dole, H. 2010, A&A, 515, A19 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kneiske, T. M., Mannheim, K., & Hartmann, D. H. 2002, A&A, 386, 1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Krawczynski, H., Coppi, P. S., & Aharonian, F. 2002, MNRAS, 336, 721 [NASA ADS] [CrossRef] [Google Scholar]
- Kronberg, P. P., & Simard-Normandin, M. 1976, Nature, 263, 653 [NASA ADS] [CrossRef] [Google Scholar]
- Lee, S., Olinto, A. V., & Sigl, G. 1995, ApJ, 455, L21 [NASA ADS] [CrossRef] [Google Scholar]
- Lefa, E., Aharonian, F. A., & Rieger, F. M. 2011a, ApJ, 743, L19 [NASA ADS] [CrossRef] [Google Scholar]
- Lefa, E., Rieger, F. M., & Aharonian, F. 2011b, ApJ, 740, 64 [NASA ADS] [CrossRef] [Google Scholar]
- Madau, P., & Pozzetti, L. 2000, MNRAS, 312, L9 [NASA ADS] [CrossRef] [Google Scholar]
- Mankuzhiyil, N., Persic, M., & Tavecchio, F. 2010, ApJ, 715, L16 [NASA ADS] [CrossRef] [Google Scholar]
- Matsumoto, T., Matsuura, S., Murakami, H., et al. 2005, ApJ, 626, 31 [NASA ADS] [CrossRef] [Google Scholar]
- Matute, I., La Franca, F., Pozzi, F., et al. 2006, A&A, 451, 443 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Maurer, A., Raue, M., Kneiske, T., et al. 2011, ApJ, submitted [Google Scholar]
- Mazin, D., & Raue, M. 2007, A&A, 471, 439 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Meyer, M., Horns, D., & Zechlin, H.-S. 2010, A&A, 523, A2 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Mirizzi, A., & Montanino, D. 2009, J. Cosmol. Astropart. Phys., 12, 4 [NASA ADS] [CrossRef] [Google Scholar]
- Mücke, A., & Protheroe, R. J. 2001, Astropart. Phys., 15, 121 [NASA ADS] [CrossRef] [Google Scholar]
- Mücke, A., Protheroe, R. J., Engel, R., Rachen, J. P., & Stanev, T. 2003, Astropart. Phys., 18, 593 [NASA ADS] [CrossRef] [Google Scholar]
- Neronov, A., & Semikoz, D. V. 2009, Phys. Rev. D, 80, 123012 [NASA ADS] [CrossRef] [Google Scholar]
- Neronov, A., & Vovk, I. 2010, Science, 328, 73 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Nikishov, A. I. 1962, Sov. Phys. JETP, 393, 14 [Google Scholar]
- Orr, M. R., Krennrich, F., & Dwek, E. 2011, ApJ, 733, 77 [NASA ADS] [CrossRef] [Google Scholar]
- Primack, J. R., Bullock, J. S., & Somerville, R. S. 2005, in High Energy Gamma-Ray Astronomy, ed. F. A. Aharonian, H. J. Völk, & D. Horns, AIP Conf. Ser., 745, 23 [Google Scholar]
- Raue, M. 2007, Ph.D. Thesis, University of Hamburg [Google Scholar]
- Raue, M. 2010, A&A, 520, A34 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Raue, M., & Mazin, D. 2008, Int. J. Mod. Phys. D, 17, 1515 [NASA ADS] [CrossRef] [Google Scholar]
- Raue, M., & Mazin, D. 2011, Il Nuovo Cimento C 34 03 [arXiv:1106:4384] [Google Scholar]
- Raue, M., Kneiske, T., & Mazin, D. 2009, A&A, 498, 25 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Santos, M. R., Bromm, V., & Kamionkowski, M. 2002, MNRAS, 336, 1082 [NASA ADS] [CrossRef] [Google Scholar]
- Sikora, M., Begelman, M. C., & Rees, M. J. 1994, ApJ, 421, 153 [NASA ADS] [CrossRef] [Google Scholar]
- Stecker, F. W., & Scully, S. T. 2009, ApJ, 691, L91 [NASA ADS] [CrossRef] [Google Scholar]
- Stecker, F. W., Baring, M. G., & Summerlin, E. J. 2007, ApJ, 667, L29 [NASA ADS] [CrossRef] [Google Scholar]
- Stecker, F. W., de Jager, O. C., & Salamon, M. H. 1992, ApJ, 390, L49 [NASA ADS] [CrossRef] [Google Scholar]
- Stecker, F. W., Malkan, M. A., & Scully, S. T. 2006, ApJ, 648, 774 [NASA ADS] [CrossRef] [Google Scholar]
- Svensson, R. 1987, MNRAS, 227, 403 [NASA ADS] [Google Scholar]
- Tagliaferri, G., Foschini, L., Ghisellini, G., et al. 2008, ApJ, 679, 1029 [NASA ADS] [CrossRef] [Google Scholar]
- Tanaka, Y. T., Stawarz, Ł., Thompson, D. J., et al. 2011, ApJ, 733, 19 [NASA ADS] [CrossRef] [Google Scholar]
- Tavecchio, F., Ghisellini, G., Ghirlanda, G., Costamante, L., & Franceschini, A. 2009, MNRAS, 399, L59 [NASA ADS] [CrossRef] [Google Scholar]
- Tavecchio, F., Ghisellini, G., Foschini, L., et al. 2010, MNRAS, 406, L70 [NASA ADS] [Google Scholar]
- Tavecchio, F., Ghisellini, G., Bonnoli, G., & Foschini, L. 2011, MNRAS, 414, 3566 [NASA ADS] [CrossRef] [Google Scholar]
- Taylor, A. M., Vovk, I., & Neronov, A. 2011, A&A, 529, A144 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Tluczykont, M. 2011 [arXiv:1106.1035] [Google Scholar]
- Urry, C. M., & Padovani, P. 1995, PASP, 107, 803 [NASA ADS] [CrossRef] [Google Scholar]
- Urry, C. M., Scarpa, R., O’Dowd, M., et al. 2000, ApJ, 532, 816 [NASA ADS] [CrossRef] [Google Scholar]
- Wagner, R. M. 2008, MNRAS, 385, 119 [NASA ADS] [CrossRef] [Google Scholar]
- Woo, J.-H., Urry, C. M., van der Marel, R. P., Lira, P., & Maza, J. 2005, ApJ, 631, 762 [NASA ADS] [CrossRef] [Google Scholar]
- Zacharopoulou, O., Khangulyan, D., Aharonian, F. A., & Costamante, L. 2011, ApJ, 738, 157 [NASA ADS] [CrossRef] [Google Scholar]
Appendix A: Evolution of the EBL with redshift
In this Appendix the influence of the evolution with redshift of the EBL density on the upper limits is investigated. For this purpose, the limits are calculated for four VHE spectra, namely 1ES 1101-232, H 1426+428, Mkn 501, and 3C 279 which is the source with the largest redshift of z = 0.536 in the sample. The evolution is included with a phenomenological ansatz (e.g. Raue & Mazin 2008). The four spectra are tested against the VHE-HEIndex, PileUp and VHEConcavity criteria and the envelope shape is determined with and without the evolution with redshift. Not surprisingly, the EBL density is less confined if the evolution is accounted for, as seen from Fig. A.1. The differences are most pronounced in the optical, where the influence of 3C 279 is the strongest (light blue shaded region in Fig. A.1). Without taking the evolution into account, the limits are overestimated by up to 40% at 0.6 μm. At higher wavelengths, the difference is not as distinct as in the optical. This outcome emphasizes that the evolution of the EBL density with redshift has a non-negligible effect on upper limits derived from VHE AGN spectra, especially for sources with a large redshift.
 |
Fig. A.1 Upper limits with and without evolution for four VHE spectra. The individual spectra have the strongest influence in the correspondingly shaded regions. |
Appendix B: Cascade emission formulae
The electron spectrum due to the interaction of VHE photons with the EBL is obtained by solving the corresponding kinetic equation for the electron distribution N(γ) in the steady state limit (Tavecchio et al. 2011), 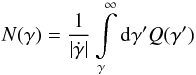 (B.1)where
(B.1)where 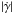 is the energy loss due to IC scattering with CMB photons in the Thomson regime with an injection rate
is the energy loss due to IC scattering with CMB photons in the Thomson regime with an injection rate 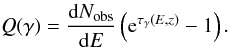 (B.2)The approximation E = 2mec2γ is used, with me the mass of the electron. The cascade spectrum for scattered photons with energy ϵ off the e + e − pairs is then readily calculated to be (Blumenthal & Gould 1970)
(B.2)The approximation E = 2mec2γ is used, with me the mass of the electron. The cascade spectrum for scattered photons with energy ϵ off the e + e − pairs is then readily calculated to be (Blumenthal & Gould 1970) ![\appendix \setcounter{section}{2} \begin{eqnarray} F(\epsilon) &=&\frac{9}{64} \frac{\epsilon~m_{\rm e}c^2}{u_{\mathrm{CMB}}(z = 0)} \nonumber \\ &{}&\times\int\limits_{\mathrm{max}\left[\sqrt{\epsilon / 4\epsilon_\mathrm{CMB}},\gamma_\mathrm{dfl}, \gamma_\mathrm{eng}\right]}^\infty \hskip-10pt \frac{\mathrm d\gamma}{\gamma^6} \int\limits_{2m_{\rm e}c^2\gamma}^\infty \mathrm d E \Diff{N_\mathrm{obs}}{E}\left({\rm e}^{\tau_\gamma(E,z)} - 1\right) \nonumber \\ &{}&\times\int\limits_0^\infty \mathrm d \epsilon^\prime \frac{n_\mathrm{CMB}(\epsilon^\prime, z = 0)}{\epsilon^{\prime\,2}} F_\mathrm{T}^\mathrm{IC}(\epsilon,\epsilon^\prime,\gamma), \label{eqn:cascade_full} \end{eqnarray}](/articles/aa/full_html/2012/06/aa18284-11/aa18284-11-eq234.png) (B.3)where uCMB(z = 0) = 0.26 eV cm-3, ϵCMB(z = 0) = 634 μeV and nCMB(ϵ′,z) denote the energy density, mean energy and differential photon number density of the CMB, respectively. The inverse Compton kernel for scattering on an isotropic photon field in the Thomson regime (Klein-Nishina effects can be neglected for the energies of the primary photons considered here) is
(B.3)where uCMB(z = 0) = 0.26 eV cm-3, ϵCMB(z = 0) = 634 μeV and nCMB(ϵ′,z) denote the energy density, mean energy and differential photon number density of the CMB, respectively. The inverse Compton kernel for scattering on an isotropic photon field in the Thomson regime (Klein-Nishina effects can be neglected for the energies of the primary photons considered here) is 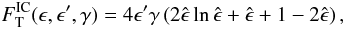 (B.4)with
(B.4)with 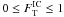 and
and 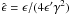 . The lower limit for the integration over γ is the maximum of three different constraints on γ. The first one stems from kinematic constraints of Compton scattering. The second denotes the γ-factor for which the electrons are deflected outside the opening cone of the blazar jet with an opening angle θc ~ 1/ΓL, with ΓL the bulk Lorentz factor of the plasma of the jet. And finally, the third factor gives the minimum possible Lorentz factor if the source is active for a certain time (see Dermer et al. 2011, for further details). However, γdfl and γeng are calculated by Dermer et al. (2011) under the approximation of small deflection and observing angles. In the case of isotropic emission, i.e. BIGMF ≈ 10-13 G and a lifetime of the source of Δt ≲ 106 years, this approximation does not longer hold and the lower integration bound is replaced by
. The lower limit for the integration over γ is the maximum of three different constraints on γ. The first one stems from kinematic constraints of Compton scattering. The second denotes the γ-factor for which the electrons are deflected outside the opening cone of the blazar jet with an opening angle θc ~ 1/ΓL, with ΓL the bulk Lorentz factor of the plasma of the jet. And finally, the third factor gives the minimum possible Lorentz factor if the source is active for a certain time (see Dermer et al. 2011, for further details). However, γdfl and γeng are calculated by Dermer et al. (2011) under the approximation of small deflection and observing angles. In the case of isotropic emission, i.e. BIGMF ≈ 10-13 G and a lifetime of the source of Δt ≲ 106 years, this approximation does not longer hold and the lower integration bound is replaced by 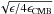 .
.
All Tables
Comparison between the optical depth at the logarithmic bin center of the highest energy bin and the averaged value over the bin width.
All Figures
 |
Fig. 1 Upper panel: grid in wavelength versus the energy density of the EBL used to construct the EBL shapes for testing (red bullets). Also shown are the minimum and maximum shape tested (solid lines) and the same for the grid of MR07 (blue triangles; dashed lines). Lower panel: minimum and maximum EBL shape tested versus EBL limits and measurements (light gray symbols, see Raue & Mazin 2011, and references therein). |
| In the text | |
 |
Fig. 2 Cascade emission for a certain EBL shape and the VHE spectrum of 1ES 0229+200 (Aharonian et al. 2007a). The observed spectrum (dark red points and line) is fitted with a power law with an exponential cut off and corrected for the EBL absorption (dark blue dashed line and points). The green lines show the cascade emission resulting from the reprocessed flux (light gray shaded area) for a constant emission over the last three years and different magnetic field strengths. The red dotted line shows the reprocessed emission if the e+e− pairs are isotropized. The latter does not overproduce the Fermi upper limits (black diamonds Tavecchio et al. 2010) and hence the corresponding EBL shape is not excluded. The light and dark gray area together are equal to the integrated flux that is compared to the Eddington luminosity (see Sect. 3.2.2). |
| In the text | |
 |
Fig. 3 Histogram of the fraction of excluded shapes of the different VHE spectra. The columns show the total fraction of rejected shapes as well as the fraction excluded by the different criteria. The column labeled “Curvature” combines the VHEConcavity and PileUp criteria. Spectra that allow more than 90% of all shapes are not shown. |
| In the text | |
 |
Fig. 4 Limits on the EBL density for different exclusion criteria. The solid line is the envelope shape of all allowed shapes from the combination of all VHE spectra whereas the dashed curve shows the envelope shape without considering the VHE spectrum of 3C 279. The dashed dotted line is the envelope shape without H 1426+428 and the dotted line displays the upper limits without Mkn 501. |
| In the text | |
 |
Fig. 5 Upper panel: example of an EBL shape excluded by Mkn 501 with the VHEConcavity criterion. Lower panel: the spectra of Mkn 501 and Mkn 421 corrected with this particular EBL shape. The flux of the latter is scaled by 10-3 for better visibility. For Mkn 501, a double broken power law provides the best description with a spectral index Γ3 = −35 at highest energies, the maximum value tested in the fitting procedure. In the case of Mkn 421, a simple power law suffices. |
| In the text | |
 |
Fig. 6 Upper limits solely due to the IntVHELumi criterion for different values of the bulk Lorentz factor ΓL and the Doppler factor δD of the emitting region. With increasing Lorentz and Doppler factor, respectively, the limits become worse (see Eqs. (10) and (14)). |
| In the text | |
 |
Fig. 7 Upper limits derived in this study. a) The envelope shape (upper limits) of all allowed shapes (dark gray lines). Also shown are the grid points as light gray bullets. b) The constraints compared to the the upper limits of MR07, Aharonian et al. (2006, 2007a), and Albert et al. (2008). c) Upper limits of this study together with three EBL models (Franceschini et al. 2008; Kneiske & Dole 2010; Domínguez et al. 2011). d) Upper limits requiring different minimum numbers of VHE spectra that exclude an EBL shape. |
| In the text | |
 |
Fig. 8 Upper limits of this work together with previous limits and EBL models. |
| In the text | |
 |
Fig. 9 Percentage of all shapes excluded by at least a certain number of spectra. The majority of rejected shapes is not allowed by more than five spectra. |
| In the text | |
 |
Fig. A.1 Upper limits with and without evolution for four VHE spectra. The individual spectra have the strongest influence in the correspondingly shaded regions. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


