| Issue |
A&A
Volume 540, April 2012
|
|
|---|---|---|
| Article Number | A15 | |
| Number of page(s) | 11 | |
| Section | Stellar structure and evolution | |
| DOI | https://doi.org/10.1051/0004-6361/201118508 | |
| Published online | 16 March 2012 | |
Cycles in the cataclysmic variable V795 Herculis⋆
1 Astronomical Institute, Academy of Sciences of the Czech Republic, 251 65 Ondřejov, Czech Republic
e-mail: simon@asu.cas.cz
2 Czech Technical University in Prague, Faculty of Electrical Engineering, Department of Radioelectronics, Technická 2, 166 27 Praha 6, Czech Republic
Received: 23 November 2011
Accepted: 27 December 2011
Aims. We investigate the photometric activity of the cataclysmic variable (CV) V795 Her. We pay attention to the time evolution of the length of its superhump cycle Psh. We investigate how well the superhump profile is reproduced in the individual phases Φsh of Psh. We also analyze the mutual relation of the intensity of the superhump light and the superimposed rapid intensity variations.
Methods. We used the photometric V-band CCD observations obtained between 2008 and 2010. The observing run on a given night consisted of a dense series of V-band images (exp. time of 20 s), which enabled us to investigate the superhump profile and the superimposed rapid changes.
Results. We identified several time segments characterized by a relatively stable Psh and mean intensity level. We find that inside such a segment, the smoothed profile of the intensity curve folded with Psh displays the largest scatter of the residuals of the mean profile in Φsh of the peak intensity and during the decay from this peak. A zone of quiescence occurs at Φsh ≈ 0.6−0.7. The profile of these residuals can be explained if the strength and luminosity of the spiral arms undergo large variations on a timescale much shorter than the segment’s duration, as predicted in a previously developed model, while the conditions for the disk precession remain much more stable. The formation of these arms is considerably faster than their fading. We find that the emission of the superimposed short cycle (~0.01–0.02 d) in this CV depends on Φsh. We conclude that it does not come from pulsations of the white dwarf or, generally, from the close vicinity of this accretor. We argue that it is flickering with the site in the disk region that produces the superhump. This flickering is not located in the impact of the stream on the disk. V795 Her is a borderline case in the sense that its disk is close to the switch to the cool state. We explain the suppression of the thermal-viscous instability of the disk in V795 Her as caused by the tidal force that is also the reason for the superhumps. This tidal heating can also help to keep the accretion disks in other permanent superhumpers in the hot state.
Key words: novae, cataclysmic variables / accretion, accretion disks / binaries: close / stars: individual: V795 Herculis / circumstellar matter
The data are only available at the CDS via anonymous ftp to cdsarc.u-strasbg.fr (130.79.128.5) or via http://cdsarc.u-strasbg.fr/viz-bin/qcat?J/A+A/540/A15
© ESO, 2012
1. Introduction
The cataclysmic variable (CV) V795 Her (PG 1711+336) was discovered in the Palomar Green (PG) survey by Green et al. (1982). It is an SW Sex-type system (Casares et al. 1996) and a hard X-ray source 2RXP J171256.0+333121 (Rosen et al. 1995). Dickinson et al. (1997) suggested a magnetic white dwarf (WD) and a gas stream overflowing the outer accretion disk and re-impacting on the inner disk regions as a possible explanation for the components of this system. An orbital period Porb of 2.6 h was found in the radial velocities of the emission lines by Shafter et al. (1990).
V795 Her displays complicated brightness variations in the optical band. Their period is significantly different from the spectroscopic one. The ~ 2.8 h modulation in the optical light curve, thought to be a superhump arising from the precession of the disk, is not stable in terms of periodicity, amplitude, and phase (Patterson & Skillman 1994; Papadaki et al. 2006). Hereafter, we will abbreviate this period as Psh. Variations of the color indices during the night were observed by Kaluzny (1989). This system was classified as a member of the group of permanent superhumpers (Retter & Naylor 2000).
In addition to the superhumps, flickering (Rosen et al. 1989) and QPO-like activity (Rosen et al. 1995; Patterson & Skillman 1994; Papadaki et al. 2006) are also observed in V795 Her. Zhang et al. (1991) found that rapid variations have a preferred time scale of 10–20 min and may be quasiperiodic. The coherence time of these variations was found to be on the order of 10 cycles. In addition, Zwitter et al. (1994) found a pronounced preferred time-scale of 0.48 hours.
An analysis of the photographic plates taken between 1934 and 1988 by Wenzel et al. (1988) showed that the longterm light curve is characterized by a superposition of a very slow variation (typical timescale of 20 000 days, peak-to-peak amplitude of 0.9 mag) and shallow waves (2000 days, 0.2 mag). The mass transfer of V795 Her therefore appears to display only small variations on the timescale of years.
Fitting the UV band spectrum of V795 Her by Mizusawa et al. (2010) for the adopted distance d of 159 pc led to a mass WD MWD = 0.8 M⊙, an inclination angle i = 41°, and an accretion rate ṁ = 1 × 10-10 M⊙ yr-1. Although no concurrent optical data are available, the long-term observations by Wenzel et al. (1988) enable us to conclude that the UV level used by Mizusawa et al. (2010) for the determination of the parameters of accretion is representative for the level of the optical brightness found by Wenzel et al. (1988). Definitely, the value of ṁ determined by Mizusawa et al. (2010) is higher than the one expected for the low state of a novalike CV (see e.g. Szkody & Downes 1982).
2. Observations
Dense series of photometric observations were obtained with the D50 telescope. It is a robotic, 500/1975 mm Newtonian telescope, located at the Astronomical Institute, Academy of Sciences of the Czech Republic (AI AS CR), in Ondřejov. It is equipped with a CCD camera FLI IMG 4710 (CCD chip E2V 47-10, mid-band coating, 1024 × 1024 pixels), focuser FLI DF-2, and field corrector TeleVue Paracorr PSB-1100. It is controlled by RTS2 software (Kubánek et al. 2006) and uses astrometric code by Lang et al. (2010). The field of view is 20 × 20 arcmin. Exposure time of each CCD image was 20 s. Heliocentric correction was applied to all data.
Each observing run on a given night consisted of a dense series of the V-band images. A typical standard deviation of a single measurement of the magnitude of V795 Her on a given CCD frame was about 0.01 mag. GSC 02595–00575 (GSC2.3 N3JJ000148) was used as the comparison star (abbreviated as C) while GSC 02595–00718 served as the check star (abbreviated as C1).
3. Data analysis
3.1. Overview
The brightness stability of the comparison star, hence the reliability of the observed variations of V795 Her in the V band, can be assessed from the difference between the magnitudes of the comparison (C) and check (C1) stars (Fig. 1a). The standard deviation of the magnitude difference of these two stars is about 0.01–0.02 mag(V) on a given night.
 |
Fig. 1 Time evolution of the activity of V795 Her. a) The difference between the magnitudes of the comparison and check stars. b) Relative magnitude of V795 Her with respect to the comparison star. c) Relative intensity of V795 Her. The individual segments are abbreviated as S1 to S6. See Sect. 3.1 for details. |
The whole light curve of V795 Her, showing the time evolution of its activity in the V band during the mapped time segment, is displayed in Fig. 1b. Both the intranight and longterm variations are clearly present in our data. The mean brightness tended to decrease. V795 Her definitely reached the brightest level in 2008, which is at the beginning of our observing. In 2009, its brightness variations were dominated by the intranight activity. In 2010, it reached the faintest level. Nevertheless, this episode was definitely surrounded by the brighter states, with their mean levels comparable to that in 2009.
Since we are interested in the time evolution of various emission components that contribute to the resulting light curve, it is advantageous to use this curve in intensity units. The relative intensity of V795 Her is displayed in Fig. 1c. It was calculated as follows. The relative intensity was set to unity in the arithmetic mean of the V-band magnitudes observed in 2008. The mean V-band magnitude of V795 Her with respect to the comparison star was Δmag(V) = 2.06. The intensity was set equal to unity for this mean magnitude. The intensity in all V-band data was then calculated with respect to this level. Nevertheless, we note that a precise setting of this intensity level does not alter our results.
Given the complex behavior of V795 Her, it proved necessary to divide the measurements into several time segments that can be regarded as representative for a given state of activity. The seasonal gaps were the natural division lines for separating the data into segments. Furthermore, even a mapping of a given season of observability of V795 Her was not quite uniform. The season was therefore subdivided into several segments. Each segment contains a sufficient amount of data to make a meaningful period analysis. The individual segments investigated in this paper are abbreviated as S1 to S6 in Fig. 1c. The observing log of each segment is given in Table 1.
Observing log of the individual segments.
3.2. Superhump period and profile
We searched for the cycle-lengths in the V-band intensity curve of V795 Her with the code Peranso1. To fold the data with Psh, the period search was carried out using the phase dispersion minimization (PDM) code (Stellingwerf 1978), included in Peranso. This method evaluates the significance of a trial period by the parameter Θ. This parameter attains the values between 0 and 1; the closer to zero, the more significant the period. The resulting frequency vs. Θ diagrams for segments S1 to S6 are displayed in Fig. 2. The spectral window, marked for each periodogram in Fig. 2, indicates possible false periods.
 |
Fig. 2 Frequency vs. Θ diagrams of the intensity variations of V795 Her determined by the PDM method (Stellingwerf 1978) for the individual segments abbreviated as S1 to S6 in Fig. 1c. The closer the value of Θ to zero, the more significant the frequency (i.e. period). The spectral window is marked by a dashed line. The arrow marks the best frequency attributed to fsh (hence to 1/Psh) in the top panel. See Sect. 3.2 for details. (This figure is available in color in electronic form.) |
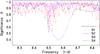 |
Fig. 3 Detail of the frequency vs. Θ diagram of the intensity variations of V795 Her. It was determined with the PDM method (Stellingwerf 1978) for segments S1, S2, S3, and S4 in Fig. 1c. See Sect. 3.2 for details. (This figure is available in color in electronic form.) |
In the top periodogram (S1) in Fig. 2a, the best frequency with Θ = 0.40 is attributed to the frequency of the superhump, fsh (i.e. 1/Psh). The neighboring minima of Θ are the aliases of this frequency: they differ by ± 1 from fsh. This pattern of the periodogram remains very similar also for S2, S3, and S4 (Figs. 2b–d). We note that the best period detected in S1 is also clearly present in the periodogram for S2, although it is only the second-best one. It is therefore desirable to compare the patterns of the periodograms for the individual segments, not only the values of the best periods (frequencies).
On the other hand, the periodogram for S5 looks quite different from the previous ones (Fig. 2e). We admit that segment S5 contains part of the intensity curve that shows large longterm variations of the mean level of intensity, which lowers the significance of Psh. The best evidence of a period change is therefore given by the periodogram for S6 (Fig. 2f). It shows that the period previously dominant in S1, S2, S3, and S4 and its aliases vanished or, at least, its significance considerably weakened. The periodogram shows a pattern clearly shifted toward longer periods (i.e. lower frequencies) now, although it is not clear which one is the true Psh (fsh) and which ones are its aliases.
Although fsh is quite similar for S1 to S4, a detail of the frequency vs. Θ diagram for segments S1, S2, S3, and S4 shows its instability (Fig. 3). The length of Psh can therefore be regarded to be characteristic only for a given segment. It increased in the sequence of S1–S4. We note that the uncertainties of fsh have to be taken with caution. The reason is that the “primary” minima of the Θ curve have different widths for the individual segments in Fig. 3 (compare e.g. S1 and S4). This “primary” minimum is often surrounded by several closely spaced “secondary” minima (this is quite clear in the minima of all segments except S1 in Fig. 3). This cluster of minima obtained for a given segment can be explained by the fact that fsh undergoes some small variations even within the segment.
The resulting ephemerides of the clearly identified superhumps in the individual segments are listed in Table 2. The time of the peak intensity, Tmax, was determined from the HEC13 fit to the intensity curve of the bump (see Sect. 4.2 for details of this fitting). This bump consisted of both a gradual intensity change and superimposed real, rapid variations. This makes the determination of the standard deviation time of this peak very difficult. The uncertainty of Tmax was therefore estimated as follows. The standard deviation of the residuals of the HEC13 fit to the intensity curve of the given night series was calculated. This standard deviation was subtracted from the peak intensity of the bump in the HEC13 fit; this yielded the quantity Is. The quantity T1, that is, the time when the HEC13 fit was crossing Is on the rising branch, was then determined. The uncertainty of Tmax was estimated as Tmax − T1. However, the uncertainty in determining a precise value of Tmax does not influence our results significantly because, as we will show, the intensity variations with the phase Φsh of Psh are gradual. The standard deviation of Psh was determined using the method of Schwarzenberg-Czerny (1991). We note that it has to be taken with caution because of the reason mentioned above. The standard deviation of Psh refers to the minimum with the smallest Θ in the cluster.
The importance of dividing the intensity curve into segments and the justification of this approach are shown in Fig. 4. Using a specific ephemeris valid for a given segment (S4 in our case) led to quite unsatisfactory results for the other segments. Notice the strong instability of Psh and Tmax, which prevents us from determining an ephemeris for the whole data set. In addition, significant changes of the mean intensity level are clearly visible.
The V-band intensity curves of V795 Her in segments S1, S3, and S4 folded with Psh are displayed in Figs. 5a,d,g. The ephemerides valid for the given segments come from Table 2. The scatter of each of these curves is substantial, especially at some Φsh. This scatter is not caused by the observing errors. Both a variable profile of the superhump in the individual nights and rapid variations on the timescale of several minutes contribute to this scatter. To determine the mean intensity profile, these folded data were smoothed by the two-sided moving averages for various values of the filter half-width Q (in units of Φsh): 0.08, 0.12, 0.16. These averages are shown in Figs. 5a,d,g; they rapidly converge to a common and well-determined smooth curve as Q decreases in each panel. The residuals of these averages were again smoothed by the moving averages (the same value of Q as for the parent intensity curve was used). This yielded the σresF curve shown in Figs. 5b,e,h. The number of data included in the calculation of each mean, displayed in Figs. 5c,f,i, shows that the data are spread in all Φsh. The σresF curve is a measure of the degree to which the intensity curve in a given Φsh is reproduced for the individual epochs. Notice that the σresF curve does not follow the intensity curve closely. A broad minimum of σresF at Φsh close to 0.6 roughly coincides with the minimum of the intensity curve, although it is exceptionally broad in S3. The rise of the σresF curve from its minimum to its maximum is steeper than the return. The maximum of the intensity curve at Φsh ≈ 0.0 occurs close to the global maximum of each σresF curve in Fig. 5. A small dip in the σresF curve close to Φsh ≈ 0.0 is present only for Q of 0.08 and 0.12Φsh in Fig. 5h. It is already absent for Q = 0.16Φsh. We ascribe this feature to an artifact – please note that the number of data points in Fig. 5i displays the lowest value at this Φsh. Nevertheless, this does not influence our main results.
 |
Fig. 4 V-band intensity curve of V795 Her in segments S1, S3, and S4 folded according to the ephemeris for S4 in Table 2. Notice the strong instability of the mean intensity level, Psh, and Tmax. See Sect. 3.2 for details. (This figure is available in color in electronic form.) |
Ephemerides of the superhumps.
 |
Fig. 5 a), d), g) V-band intensity curve of V795 Her in segments S1, S3, and S4 folded with Psh according to the ephemerides in Table 2. The folded data were smoothed by the two-sided moving averages for various Q (in units of Φsh; see the legend). b), e), h) Smoothed residuals σresF of the fits. c), f), i) The number of data included in the calculation of each mean. See Sect. 3.2 for details. (This figure is available in color in electronic form.) |
 |
Fig. 6 Simulation of the effect of a very unstable Psh in evaluating the scatter of intensity in various Φsh. a) The intensity curve artificially shifted in Φsh. The folded data were smoothed by the two-sided moving averages for various Q (in units of Φsh) (see the legend). b) Smoothed residuals σresSim of the fits. c) The number of data included in calculation of each mean. d) Dependence of the relative intensity and σresSim for the simulated data. They were smoothed by the moving averages with various Q. The observed data for S1 are included, too. Some Φsh are marked. See Sect. 3.2 for details. (This figure is available in color in electronic form.) |
 |
Fig. 7 Dependence of the relative intensity and σresF for segments S1, S3, and S4. These data were smoothed by the moving averages with Q = 0.16Φsh. See Sect. 3.2 for details. (This figure is available in color in electronic form.) |
As shown above, the length of Psh of V795 Her varies in time. It is therefore necessary to assess how its instability can influence the profiles of the intensity and σresF curves. This testing was carried out in the following way. A simulation of the effect of the unstable Psh in evaluating the scatter of intensity in various Φsh used the smoothed intensity curve for Q = 0.16Φsh from S1 (see Fig. 5a). This curve was artificially shifted in Φsh in steps of 0.03Φsh. An intensity curve with a very large resulting scatter of 0.3 Psh was thus obtained. This big scatter would be immediately noticed in the observed intensity curves (especially in their rising branches) in Fig. 5. The generated data were then smoothed by the two-sided moving averages for various Q (Fig. 6a). Although the smoothed residuals σresSim of the fits (Fig. 6b) display variations with phase, their profile is quite discordant with that in Figs. 5b,e,h. In any case, it cannot explain why the biggest scatter is observed at Φsh = 0.0 in V795 Her. A dependence of σresSim on intensity tells us even more (Fig. 6d). The shift of the simulated data makes a crescent, which is a shape quite different from that of the observed data. The amplitude of this shift is also significantly higher for the observed than for the simulated data.
A comparison of the dependence of σresF on the intensity observed for segments S1, S3, and S4 in displayed in Fig. 7. These data were smoothed by the moving averages with Q = 0.16Φsh. Generally, the value of σresF increases with the increasing intensity. However, the shifts in the individual halves are not identical for a given segment. This suggests that the scatter is not the same when the rising and decaying branches of the superhump are compared.
3.3. Superimposed rapid intensity changes
The properties of the intensity variations in the individual night series were investigated in the following way. Five series with a long coverage were chosen. To emphasize the slowly varying component during the night, to pick out the profile of the curve, and to investigate the evolution of the residuals, the data were fitted by the code HEC13 written by P. Harmanec. This code is based on the method of Vondrák (1969, 1977), who improved the original method of Whittaker (Whittaker & Robinson 1946). The method is based on minimizing the value Q = F + λ2S, where 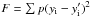 denotes the degree of smoothing (y being the smoothed and y′ the observed value of the variable), S = ∑ (Δ3yi)2 is the measure of roughness of the curve, λ2 is a constant to be selected and defines by how much the curve will be smoothed. A full description of the method can be found in Vondrák (1969). This method can fit a smooth curve to the nonequidistant data regardless of their profile. HEC13 makes use of two input parameters, ϵ (in dimensionless units) and ΔT. The quantity ϵ = 1/λ2 determines how “tight” the fit will be, that is, if only the main profile or also the high-frequency variations are to be reproduced. The quantity ΔT is the interval over which the data are binned before smoothing. The resulting fit consists of the mean points, calculated to the individual observed points of the curve. A set of fits to the data with the different ϵ and ΔT was generated and submitted for inspection. It was found that the fit with ϵ = 1014, ΔT = 0.001 d reproduces the main features of the profile of the intensity curve and suppresses rapid fluctuations. This method enables us to find a compromise between a curve running through all observed values and an ideal smooth curve. These fits are displayed in Figs. 8a,d,g,j,m. Their residuals abbreviated as RIS (relative intensity scatter) are shown in Figs. 8b,e,h,k,n. They only fluctuate around RIS = 0 without any remaining trend. The superhump profile was therefore well fitted by HEC13.
denotes the degree of smoothing (y being the smoothed and y′ the observed value of the variable), S = ∑ (Δ3yi)2 is the measure of roughness of the curve, λ2 is a constant to be selected and defines by how much the curve will be smoothed. A full description of the method can be found in Vondrák (1969). This method can fit a smooth curve to the nonequidistant data regardless of their profile. HEC13 makes use of two input parameters, ϵ (in dimensionless units) and ΔT. The quantity ϵ = 1/λ2 determines how “tight” the fit will be, that is, if only the main profile or also the high-frequency variations are to be reproduced. The quantity ΔT is the interval over which the data are binned before smoothing. The resulting fit consists of the mean points, calculated to the individual observed points of the curve. A set of fits to the data with the different ϵ and ΔT was generated and submitted for inspection. It was found that the fit with ϵ = 1014, ΔT = 0.001 d reproduces the main features of the profile of the intensity curve and suppresses rapid fluctuations. This method enables us to find a compromise between a curve running through all observed values and an ideal smooth curve. These fits are displayed in Figs. 8a,d,g,j,m. Their residuals abbreviated as RIS (relative intensity scatter) are shown in Figs. 8b,e,h,k,n. They only fluctuate around RIS = 0 without any remaining trend. The superhump profile was therefore well fitted by HEC13.
The profile of the superhump intensity curve for the individual epochs mainly varies in the vicinity of Φsh = 0. Figs. 8a,d,g,j,m show that this curve can display a sharp peak as well as a broad plateau. This change can happen during at most several nights and even when the intensity of the global minimum of intensity at Φsh ≈ 0.7 remains roughly constant.
It is important to know whether and how the standard deviations of the residuals of the HEC13 fits, σIR, change during a given night, hence with Φsh. The residuals of these fits were therefore fitted by the two-sided moving averages. A set of moving averages with different Q was generated and submitted to inspection. It was found that Q = 0.015 days yields the smoothed curve that satisfies the general profile of the observed curve but, at the same time, it averages through most rapid variations (Figs. 8c,f,i,l,o). The minimum observed value of σIR is about 0.015 in each night. This minimum occurs between Φsh of 0.5 and 0.8, that is, near Φsh of the minimum intensity. The value of σIR than rapidly grows toward Φsh = 1.0.
The series in Fig. 8m shows a very nice example of the evolution of rapid changes with Φsh. The global maxima of σIR coincide with the peak of the superhump intensity. The secondary maximum of σIR is located close to Φsh = 0.45. The evolution of RIS shows several well-defined peaks of rapid fluctuations in the vicinity of this phase. This local maximum of σIR can therefore be attributed to a smoothing of these fluctuations in time. A global minimum of σIR is situated at Φsh ≈ 0.7, close to the time of the minimum intensity of the superhump, as observed in other nights plotted in Fig. 8.
A search for the cycle-lengths in the residuals of the HEC13 fits in Fig. 8 was carried out with the Lomb-Scargle method (Lomb 1976). The result can be seen in Fig. 9. The frequency range of the observed rapid intensity variations is much broader than the widths of spectral windows. This suggests that only a cycle-length is found but not strict periodicity.
3.4. Comparison of V795 Her to other superhumpers
The absolute V-band magnitude MV of V795 Her was determined for the extrema of its brightness (apparent mag (V) = 13.07 and 13.97) in Fig. 1b. The distance of 159 pc (Mizusawa et al. 2010) and the apparent V-band magnitude of the comparison star in GSC2.3 catalog (V = 11.27) were used. The resulting MV served comparing V795 Her to other superhumpers in the MV − Porb plane in Fig. 10.
We used CVs classified as permanent superhumpers with positive superhums by Patterson (1998) and Patterson et al. (2005) for this comparison. Additional systems like these contained in The Big List of SW Sextantis Stars (Hoard et al. 2003)2 were included, too. The period gap of CVs (e.g. Warner 1995) is marked in Fig. 10. MV of dwarf novae in outburst and in quiescence according to Warner (1995) are also shown. To shed more light on the conditions in the accretion disks of permanent superhumpers, the individual phases of the 2001 superoutburst of the remarkable dwarf nova WZ Sge observed by Patterson et al. (2002) are included as well. Three phases of this event are distinguished: the phase of a slow decline of brightness from the outburst peak (lasting for ~23 days), finished by a steep decline of brightness by ~2 mag; the phase of a series of the echo outbursts (lasting for ~28 days); the final, very slow decay (FD) or a plateau lasting for ~25 d after the series of echo outbursts. The distribution of Porb of SW Sex systems (data of Hoard et al. 2003), plotted in Fig. 10, extends into the period gap. This finding will help us in the discussion of V795 Her. The position of V795 Her in Fig. 10 indicates that the accretion disk of this CV is close to the border of the thermally stable and unstable states.
 |
Fig. 8 Individual night series of V795 Her in relative intensity units. For each night, the upper panel represents the observed V-band data (panels a), d), g), j), m)). A solid line represents the HEC13 fit. Residuals of this fit, RIS, are given in the middle panel of that night (panels b), e), h), k), n)). Moving averages of the standard deviation of these residuals, σIR, are plotted in the bottom panel of the night (panels c), f), i), l), o)). The vertical dashed and dotted lines mark Φsh = 0.0 and Φsh = 0.5. The ephemeris for S3 (Table 2) was used for panels m), n), o). The quantities Φsh in the remaining panels were calculated according to the ephemeris for S1 (Table 2). See Sect. 4.2 for details. |
Following Warner (1995), the dependence of the effective temperature Teff of a thermally stable accretion disk on the distance r from the WD was determined using Eq. (1). ![\begin{equation} T_{\rm eff} = \left(\frac{3 G M_{\rm WD} \dot m}{8 \pi \sigma R_{\rm WD}^{3}}\right)^{1/4} \left(\frac{r}{R_{\rm WD}}\right)^{-3/4} \left[1 - \left(\frac{R_{\rm WD}}{r}\right)^{1/2} \right]^{1/4}\cdot \label{eq1} \end{equation}](/articles/aa/full_html/2012/04/aa18508-11/aa18508-11-eq77.png) (1)The gravity constant is G while the Stephan-Boltzmann constant is σ. The quantity MWD = 0.8 M⊙ (Mizusawa et al. 2010) was used. The radius of the WD, RWD, turned out to be ~0.01 R⊙ for the relation between RWD and MWD for the WD with the mass between 0.7 and 1.3 M⊙ given by Warner (1995). Three values of ṁ in M⊙ yr-1 are assumed in Fig. 11. The lowest one corresponds to the value determined by Mizusawa et al. (2010). Evidently, Teff is below the critical temperature for hydrogen ionization, Tcrit, in the outer disk region even for the value of ṁ by an order of magnitude higher than found by Mizusawa et al. (2010).
(1)The gravity constant is G while the Stephan-Boltzmann constant is σ. The quantity MWD = 0.8 M⊙ (Mizusawa et al. 2010) was used. The radius of the WD, RWD, turned out to be ~0.01 R⊙ for the relation between RWD and MWD for the WD with the mass between 0.7 and 1.3 M⊙ given by Warner (1995). Three values of ṁ in M⊙ yr-1 are assumed in Fig. 11. The lowest one corresponds to the value determined by Mizusawa et al. (2010). Evidently, Teff is below the critical temperature for hydrogen ionization, Tcrit, in the outer disk region even for the value of ṁ by an order of magnitude higher than found by Mizusawa et al. (2010).
4. Discussion
We report new findings concerning the properties of the photometric activity in the novalike system V795 Her. We paid special attention to the optical emission of the superhump and its time evolution. We determined how well the superhump profile is reproduced in the individual Φsh. We also investigated the relation of variations of the superhump profile and superimposed rapid changes on the timescale of 0.01–0.02 d.
4.1. (In)stability of the superhump emission in time
Our observations of V795 Her enable us to investigate how the superhumps vary with ṁ in a given CV. The optical brightness averaged over Psh decreased by about 0.5 mag between S1 and S6 (Fig. 1). Using the absolute magnitude corrections of steady-state disks by Retter & Leibowitz (1998), this corresponds to a decrease of ṁ by about 30 percent (from ṁ ≈ 3.1 × 1016 g s-1 in S1 to 2.4 × 1016 g s-1 in S6).
In determining Psh in V795 Her, we overcame the problem of aliases by comparing the patterns of the periodograms for the individual time segments, not only the lengths of the best periods. We thus conclude that Psh underwent only small variations with ΔPsh/Psh of about 0.73 percent between segments S1 and S4 in spite of a decrease of ṁ by about 15 percent; a significant shift toward longer periods was observed only later, in S6, which coincides with another decrease of ṁ. We find that its Psh slightly increased already in the sequence of S1–S4. Because the mean level of intensity varied much less than the amplitude of the superhump in the given time segment, this suggests a stable mean value of ṁ.
The stability of Psh in V795 Her resembles stage B in the superoutburst plateaux of SU UMa systems in the systematics of Kato et al. (2009). A system like this was observed to display variations of ΔPsh/Psh ≈ 1 percent during this phase of superoutburst, but this value tended to diminish for CVs with the longer Psh. This Psh/Psh is similar to V795 Her, although we conclude that the length of its Psh can be regarded as characteristic only for a given time segment. Relating the time evolution Psh and the superhump profile is important for the subsequent assessment of the state of the disk. The superhump profile in SU UMa systems is usually of a roughly triangular shape with sharp maxima and minima (e.g. Warner 1995; Kato et al. 2009; see also model of Smith et al. 2007) and the amplitude evolves gradually during stage B. In contrast, in V795 Her some profiles largely deviated from this scheme even during the neighboring nights within a given time segment.
The changes of the superhump profile in V795 Her cannot be attributed to a variable amplitude of the superimposed rapid variations discussed in Sect. 4.2 because of the following reason. The moving averages of σIR, that is, of rapid changes, are less than 0.025–0.03 (Fig. 8). On the other hand, the moving averages of σresF achieve significantly higher values, up to 0.06 (Fig. 5). Consequently, real, strong changes in generating the superhump emission at a given Φsh occurring on a timescale much shorter than the duration of the time segment must be involved.
We found new properties of the superhump emission in V795 Her that are hidden in the intensity curve and that emerge only for a proper statistical analysis of the data set covering many epochs of Psh. This approach enabled us to resolve the regularities in the variations of the intensity curve profile within a given time segment. Specifically, the smoothed profile of the intensity curve folded with Psh displays the largest scatter of the residuals of the mean profile in Φsh of the peak intensity and during the decay from this peak, but the rising and decaying branches are not identical. We found by testing that the instability of Psh within a given segment cannot lead to these observed variations of the intensity and σresF curves even when a very large scatter of 0.3Psh was included.
Applying the model of Smith et al. (2007), our analysis shows that the strength and optical luminosity of the spiral arms of the precessing disk largely vary at a given Φsh for different epochs of the superhump cycle within a given time segment in V795 Her. A zone of quiescence at Φsh ≈ 0.6−0.7 can be identified with the phase of the missing arms and the lowest disk eccentricity. The steep rise of σresF toward the peak at Φsh ≈ 0 (which coincides with the peak superhump intensity), often followed by a slow decrease, can be explained if the formation of the spiral arms is faster than their subsequent fading. This strong variability of the outer disk region must co-exist with the stability of the conditions for the disk precession (even the inner disk precesses). The reason is that a series of independent episodes of generation of the eccentricity of various disk regions would hardly enable us to obtain an intensity curve with a well-defined Psh and phasing representative of the given segment.
The fraction of the superhump luminosity in the total optical luminosity output of the disk undergoes a complicated evolution on long timescales in V795 Her. Although the intensity averaged over the superhump cycle was lower by about 15 percents in S3 and S4 compared with S1, the amplitude of the superhump did not follow it. It even peaked at a higher level in S3 than in S1 (Fig. 7). The superhump light thus contributed more to the optical luminosity output of the disk when ṁ decreased. The role of the tidal heating that helped keep the disk on the hot branch of the S-curve increased accordingly (see Sect. 4.4 for more). A detailed description of the S-curve can be found e.g. in Smak (1984).
 |
Fig. 9 Periodogram of rapid intensity variations in V795 Her. Residuals of the HEC13 fit in Fig. 8 were investigated with the Lomb-Scargle method. The spectral window is marked by a dashed line. See Sect. 4.2 for details. |
 |
Fig. 10 Comparison of V795 Her with other superhumpers. Open circles denote permanent superhumpers with positive superhumps. Circled asterisks represent SW Sex systems with positive superhumps. The individual phases of the 2001 superpotburst of WZ Sge (data from Patterson et al. 2002) are also shown; FD is the final decay. The period gap is marked by the vertical lines. The dashed and dot-dashed curves denote the absolute magnitudes of dwarf novae in outburst and in quiescence according to Warner (1995). A histogram shows the distribution of Porb of SW Sex systems (not only of the superhumping ones). See Sect. 3.4 for details. (This figure is available in color in electronic form.) |
 |
Fig. 11 Dependence of Teff on a thermally stable accretion disk on the distance r from the WD. The parameters of V795 Her were used. Three values of ṁ expressed in M⊙ yr-1 are assumed. The critical temperature for hydrogen ionization is abbreviated as Tcrit. Two values of the disk radius Rd in units of the WD lobe are marked. See Sect. 3.4 for details. |
Our findings of the changes of the superhump profile can also be used to shed more light on the difference between the evolution of the superhump emission in V795 Her and in superoutbursts of SU UMa systems. The processes that mainly influence the outer disk region play a dominant role here. Both the disk in superoutburst in stage B (Kato et al. 2009) and in permanent superhumpers including V795 Her lay on the hot branch of the S-curve (see Sect. 4.4 for more). In a permanent superhumper, the entire accreting matter is directly supplied to the disk by the donor. In superoutbursts, two sources of accretion of matter operate: (1) the matter accumulated in the disk in quiescence, (2) the matter directly supplied to the disk by the donor because of an increase of matter outflow from this star during superoutburst (Smak 2004). Although the mass of the stream can therefore be comparable in both CV types, the stream-disk interactions can differ, e.g. in the size of the cross-section of the stream or the efficiency of cooling (see models of Armitage & Livio 1996, 1998). This interaction, especially if the inflow is intermittent and proceeds in the form of blobs in the low-luminosity V795 Her (see Sect. 4.4), is a promising mechanism for affecting the outer disk region, hence the formation of the superhumps. A more detailed modeling of this interaction in a superhumping disk is needed.
4.2. The nature and site of rapid intensity changes
In principle, several mechanisms with different sites can lead to the observed rapid intensity changes superimposed on the superhump modulation in V795 Her. An important guideline is that their amplitude was variable with Φsh (Fig. 8, but this effect also partly contributes in Fig. 5). Because we observed that the strength of rapid changes can increase more than once during Psh, it is necessary to consider the possibility of several its sites. This relation helps us find the proper mechanism and site of rapid changes.
Spin modulation of the magnetized WD cannot explain rapid variations in our case because of the following reasons. The intensity fluctuations occur on the timescale of ~0.01 to ~0.02 d, which is much broader than those of spectral windows (Fig. 9). This suggests that only a cycle-length, but no strict periodicity, is present. This behavior is consistent with that observed e.g. by Zhang et al. (1991). Furthermore, the peak-to-peak amplitude of the individual spikes of rapid changes is often highest close to Φsh of the superhump’s peak intensity (Fig. 8). The outer about 40 percent of the disk radius are most influenced by the tidal forces producing the superhump light (see model of Smith et al. 2007). The viscous timescale of the disk is much longer than Psh (see Sect. 4.3 for more), which implies that it is not possible to obtain the physically related behavior of emissions from the outer disk region and the close vicinity of the WD. Spin modulation could consequently contribute in at most some segments of Φsh outside the phase of the peak intensity.
Oscillations of the WD in V795 Her might explain the period changes, for example if several periods were present simultaneously. Szkody et al. (2010) observed such oscillations with the period of 679 s in PQ And. However, the coincidence of the strongest rapid variation phase and the most intense superhump light precludes these oscillations in V795 Her. Moreover, the luminosity of the WD in V795 Her appears to be too low, and the light of the accretion disk dominates. The reason is that even in the far-UV where the contribution of the WD peaks, the spectrum can be fitted purely by disk emission (Mizusawa et al. 2010). Therefore not even some of the rapid changes in our data come from the WD in V795 Her.
Flickering of the accretion disk appears to be the best explanation for V795 Her. Generally, understanding of the site of flickering in the accretion disk of CV is difficult because the situation differs from system to system. Bruch (2000) argued that flickering can originate in two regions. One site is the innermost accretion disk region with the boundary layer and the WD surface. The other site is the region of impact of the matter transferring stream upon the accretion disk. Baptista & Bortoletto (2008) interpreted low- and high-frequency flickering from two asymmetric arcs as manifestations of a tidally induced spiral shock wave in the outer disk regions in the novalike UU Aqr.
We can exclude the impact of the stream as the site of flickering in V795 Her since the observed variations of the amplitude of flickering depend on the phase of Psh, not on Porb. If the site of flickering were located in the inner parts of the disk in V795 Her, the amplitude of flickering would decrease during Φsh of the peak superhump intensity. This behavior would have to be repeated during each superhump cycle. However, this scenario contradicts our observations. We find that the amplitude of flickering measured by σIR often reaches a minimum at Φsh of the minimum superhump intensity, and then increases during the rising branch of the superhump (Fig. 8). The peak value of σIR often occurs close to the peak of the intensity curve. Later on, the time evolution of this flickering is divergent for the individual nights. As modeled by Smith et al. (2007), the strongest spiral arms and the highest eccentricity of the particle motion occurs in the outer half of the superhumping disk. Strong spiral arms are formed during Φsh of the peak intensity. In this scenario, they are also the site of flickering in V795 Her. Our observations suggest that when this spiral arm begins to grow during the superhump cycle, this event is initially connected with a transient suppression of flickering. This supports a scenario where the site of flickering is closely related to the outer half of the disk that produces the superhump. The group of systems with unexpected location of flickering therefore increases considerably.
4.3. The effective-temperature profile of the disk
The quantity Teff of the accretion disk in V795 Her definitely turns out to fall below Tcrit in the outer region if we use ṁ = 1 × 10-10 M⊙ yr-1, determined by Mizusawa et al. (2010) (or even by a factor of 10 higher), and the radial profile of Teff of steady-state disk (Fig. 11). Taking this at face value, the whole disk should switch to the cool branch of the S-curve. The radial profile of Teff should therefore be flat and the absolute magnitude of this system should be compatible with those of the quiescent dwarf novae. However, Fig. 10 shows that this is not the case. Also as shown in Sect. 1, the value of ṁ determined for V795 Her by Mizusawa et al. (2010) exceeds that expected for the low state. Its MV is close to that of WZ Sge at the end of the slow decline of brightness from the superoutburst peak. Although the lobe of the WD in V795 Her is more extended by 88 percent than in WZ Sge (assuming the parameters by Smak 1993), the accretion disk in V795 Her is still in the hot state.
This discrepancy can be reconciled in several ways. Outflow of matter from the inner disk region, suggested by the wind features in the optical spectrum of Casares et al. (1996), can decrease the mass accretion rate in the inner disk region (radiating mainly in UV), while ṁ can be higher in the outer disk. If the true d to V795 Her is higher than 159 pc used by Mizusawa et al. (2010), the disk is more luminous, hence Teff of the outer disk is higher. If the true i is higher, then a more luminous, hence a hotter disk is the result. Also, diminishing the disk radius with respect to its lobe at least partly removes the problem. However, it cannot be smaller than the minimum radius for an inviscid disk (Lubow & Shu 1975). Such a small radius is unrealistic in our case because of the presence of superhumps. Flattening of the radial profile of Teff in the outer disk region, as in Z Cha observed during its normal outburst by Horne & Cook (1985), can also help to solve the problem. In any case, the disk in V795 Her in steady-state approximation displays a very significant discrepancy between the mass flow determined for the optical and far-UV spectral regions.
The tidal force that gives rise to the superhumps is a promising candidate for flattening the radial profile of Teff. In V795 Her, we need to increase Teff of the outer disk region from roughly 3500 K to about 7000 K (Fig. 11). We have shown in Sects. 4.1 and 4.2 that the amplitude of the superhump did not follow the decrease of the overall intensity averaged over Psh. The contribution of the superhump intensity caused by the tidal force to the total optical intensity thus increased. Heating of the outer disk region of V795 Her by a tidal instability, especially by the spiral arms, can thus keep the disk on the hot branch of the S-curve even when ṁ is lowered.
4.4. V795 Her in the group of permanent superhumpers
The position of V795 Her in the MV − Porb plane (Fig. 10) shows that this system is one of very few active CVs with accretion disks observed within the period gap (Shafter et al. 1995). V795 Her is a borderline case in the sense that its disk is close to the switch to the cool branch of the S-curve. As argued above, this switching can be prevented by the tidal force. This results in locating V795 Her about 2 mag above the line of quiescent dwarf novae. The quantities MV of the individual permanent superhumpers with Porb on both sides of the period gap display a large scatter independent of Porb. In the optical band, V795 Her is among the faintest of these systems. This scatter of MV is mainly caused by ṁ specific for each of these systems in Fig. 10. In principle, ṁ of these permanent superhumpers can reside at any value ensuring that the disk is on the hot branch of the S-curve. This means that the SX Sex phenomenon and permanent superhumps are not the result of a very high or a specific ṁ. Although CVs with the disk seen under a large i are dimmer than those seen almost face-on, this effect cannot account for the existence of SW Sex systems with MV differing by about 4 mag at similar Porb (Fig. 10) (compare e.g. the considerably different MV of two systems with similar i: V795 Her (i = 41°, Mizusawa et al. 2010) and TT Ari (i = 26° ± 6°, Wu et al. 2002).
A relatively recent (several decades ago) explosion of classical nova is a solution for the high ṁ in at least some CVs in Fig. 10, especially in those with quite short Porb. Irradiation of the disk by the WD, which remains very hot after the explosion, keeps this disk in the hot state (see model by Schreiber et al. 2000). V1974 Cyg=Nova Cyg 1992 (Collins et al. 1992) (the brightest system in Fig. 10) and CP Pup=Nova Pup 1942 (Stoy 1942) have Porb below the period gap and quite bright MV. Both of them are novalike CVs that were observed to explode as classical novae. Also two novalike CVs close to the long-period border of the gap, RR Pic=Nova Pic 1925 (Pingsdorf 1927; Spencer Jones 1933) and V603 Aql = Nova Aql 1918 (Maggini 1918) are recent classical novae. However, V795 Her was not observed to explode as a classical nova and it is improbable that this explosion would have passed unnoticed during the last about 100 years (i.e. during an interval about as long as the one which elapsed since the explosion of the still luminous V603 Aql). It would have had to be a very bright naked-eye nova with the peak magnitude of about +2 given the relation of Della Valle (1991).
It is interesting to note that superhumpers in Fig. 10 classified as SW Sex systems are not known to be classical novae and vice versa. Consequently, several mechanisms that enable one to keep a high ṁ must exist to explain Fig. 10. In this regard, it is important that the distribution of Porb of SW Sex systems is roughly Gaussian and extends into the period gap (Fig. 10). V795 Her is a member of this class, too (Casares et al. 1996); it lies on the wing of this distribution and its position is neither extreme nor isolated. Tidal heating like that in V795 Her can help keep the accretion disks in the hot state.
See D. W. Hoard’s Big List of SW Sextantis Stars at http://web.ipac.caltech.edu/staff/hoard/cvtools/swsex/biglist.html (Hoard et al. 2003).
Acknowledgments
Support by the grant 205/08/1207 and 102/09/0997 of the Grant Agency of the Czech Republic, and the project PECS 98023 is acknowledged. We thank Prof. P. Harmanec for providing us with the code HEC13. The Fortran source version, compiled version and brief instructions how to use the program can be obtained via http://astro.troja.mff.cuni.cz/ftp/hec/HEC13/.
References
- Araujo-Betancor, S., Knigge, C., Long, K. S., et al. 2003, ApJ, 583, 437 [NASA ADS] [CrossRef] [Google Scholar]
- Armitage, P. J., & Livio, M. 1996, ApJ, 470, 1024 [NASA ADS] [CrossRef] [Google Scholar]
- Armitage, P. J., & Livio, M. 1998, ApJ, 493, 898 [NASA ADS] [CrossRef] [Google Scholar]
- Baptista, R., & Bortoletto, A. 2008, ApJ, 676, 1240 [NASA ADS] [CrossRef] [Google Scholar]
- Baptista, R., Steiner, J. E., Horne, K. 1996, MNRAS, 282, 99 [NASA ADS] [CrossRef] [Google Scholar]
- Bruch, A. 2000, A&A, 359, 998 [NASA ADS] [Google Scholar]
- Casares, J., Martinez-Pais, I. G., Marsh, T. R., et al. 1996, MNRAS, 278, 219 [NASA ADS] [CrossRef] [Google Scholar]
- Chochol, D., Grygar, J., Pribulla, T., et al. 1997, A&A, 318, 908 [NASA ADS] [Google Scholar]
- Collins, P., Skiff, B. A., Bus, S. J., et al. 1992, IAUC, 5454, 1 [NASA ADS] [Google Scholar]
- della Valle, M. 1991, A&A, 252, L9 [NASA ADS] [Google Scholar]
- Dickinson, R. J., Prinja, R. K., Rosen, S. R., et al. 1997, MNRAS, 286, 447 [NASA ADS] [CrossRef] [Google Scholar]
- Gänsicke, B. T., & Koester, D. 1999, A&A, 346, 151 [NASA ADS] [Google Scholar]
- Gänsicke, B. T., Sion, E. M., Beuermann, K., et al. 1999, A&A, 347, 178 [NASA ADS] [Google Scholar]
- Gill, C. D., & O’Brien, T. J. 1998, MNRAS, 300, 221 [NASA ADS] [CrossRef] [Google Scholar]
- Godon, P., Sion, E. M., Barrett, P. E., et al. 2008, ApJ, 687, 532 [NASA ADS] [CrossRef] [Google Scholar]
- Green, R. F., Ferguson, D. H., Liebert, J., et al. 1982, PASP, 94, 560 [NASA ADS] [CrossRef] [Google Scholar]
- Haefner, R., & Betzenbichler, W. 1991, IBVS, 3665, 1 [NASA ADS] [Google Scholar]
- Hoard, D. W., Szkody, P., Froning, C. S., et al. 2003, AJ, 126, 2473 [NASA ADS] [CrossRef] [Google Scholar]
- Hoard, D. W., Kafka, S., Wachter, S., et al. 2009, ApJ, 693, 236 [NASA ADS] [CrossRef] [Google Scholar]
- Horne, K., & Cook, M. C. 1985, MNRAS, 214, 307 [NASA ADS] [Google Scholar]
- Hubble, E., & Duncan, J. C. 1927, ApJ, 66, 59 [NASA ADS] [CrossRef] [Google Scholar]
- Kaluzny, J. 1989, AcA, 39, 235 [NASA ADS] [Google Scholar]
- Kato, T., Imada, A., Uemura, M., et al. 2009, PASJ, 61, S395 [NASA ADS] [Google Scholar]
- Knigge, C., Araujo-Betancor, S., Gänsicke, B. T., et al. 2004, ApJ, 615, L129 [NASA ADS] [CrossRef] [Google Scholar]
- Kubánek, P., Jelínek, M., Vítek, S., et al. 2006, SPIE, 6274, 59 [Google Scholar]
- Lang, D., Hogg, D. W., Mierle, K., et al. 2010, AJ, 139, 1782 [Google Scholar]
- Lomb, N. R. 1976, Ap&SS, 39, 447 [NASA ADS] [CrossRef] [Google Scholar]
- Lubow, S. H., & Shu, F. H. 1975, ApJ, 198, 383 [NASA ADS] [CrossRef] [Google Scholar]
- Maggini, M. 1918, ApJ, 48, 303 [NASA ADS] [CrossRef] [Google Scholar]
- Mironov, A. V., Moshkalev, V. G., & Shugarov, S.Yu. 1983, IBVS, 2438, 1 [NASA ADS] [Google Scholar]
- Mizusawa, T., Merritt, J., Ballouz, R.-L., et al. 2010, PASP, 122, 299 [NASA ADS] [CrossRef] [Google Scholar]
- Mukai, K., & Orio, M. 2005, ApJ, 622, 602 [NASA ADS] [CrossRef] [Google Scholar]
- O’Donoghue, D., Warner, B., Wargau, W., et al. 1989, MNRAS, 240, 41 [NASA ADS] [CrossRef] [Google Scholar]
- Papadaki, C., Boffin, H. M. J., Sterken, C., et al. 2006, A&A, 456, 599 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Patterson, J. 1995, PASP, 107, 657 [NASA ADS] [CrossRef] [Google Scholar]
- Patterson, J. 1998, PASP, 110, 1132 [NASA ADS] [CrossRef] [Google Scholar]
- Patterson, J., & Skillman, D. R. 1994, PASP, 106, 1141 [NASA ADS] [CrossRef] [Google Scholar]
- Patterson, J., & Warner, B. 1998, PASP, 110, 1026 [NASA ADS] [CrossRef] [Google Scholar]
- Patterson, J., Kemp, J., Saad, J., et al. 1997, PASP, 109, 468 [NASA ADS] [CrossRef] [Google Scholar]
- Patterson, J., Richman, H., Kemp, J., et al. 1998, PASP, 110, 403 [NASA ADS] [CrossRef] [Google Scholar]
- Patterson, J., Masi, G., Richmond, M. W., et al. 2002, PASP, 114, 721 [NASA ADS] [CrossRef] [Google Scholar]
- Patterson, J., Kemp, J., Harvey, D. A., et al. 2005, PASP, 117, 1204 [NASA ADS] [CrossRef] [Google Scholar]
- Pingsdorf, F. 1927, AN, 230, 235 [NASA ADS] [Google Scholar]
- Retter, A., & Leibowitz, E. M. 1998, MNRAS, 296, L37 [NASA ADS] [CrossRef] [Google Scholar]
- Retter, A., & Naylor, T. 2000, MNRAS, 319, 510 [NASA ADS] [CrossRef] [Google Scholar]
- Retter, A., Leibowitz, E. M., Ofek, E. O. 1997, MNRAS, 286, 745 [NASA ADS] [CrossRef] [Google Scholar]
- Ringwald, F. A., Thorstensen, J. R., Honeycutt, R. K., et al. 1996, MNRAS, 278, 125 [NASA ADS] [Google Scholar]
- Rosen, S. R., Branduardi-Raymont, G., Mason, K. O., et al. 1989, MNRAS, 237, 1037 [NASA ADS] [CrossRef] [Google Scholar]
- Rosen, S. R., Watson, T. K., Robinson, E. L., et al. 1995, A&A, 300, 392 [NASA ADS] [Google Scholar]
- Schreiber, M. R., Gänsicke, B. T., Cannizzo, J. K. 2000, A&A, 362, 268 [NASA ADS] [Google Scholar]
- Schwarzenberg-Czerny, A. 1991, MNRAS, 253, 198 [NASA ADS] [CrossRef] [Google Scholar]
- Shafter, A. W., Robinson, E. L., Crampton, D., et al. 1990, ApJ, 354, 708 [NASA ADS] [CrossRef] [Google Scholar]
- Shafter, A. W., Misselt, K. A., Szkody, P., et al. 1995, ApJ, 448, L33 [NASA ADS] [CrossRef] [Google Scholar]
- Skillman, D. R., & Patterson, J. 1993, ApJ, 417, 298 [NASA ADS] [CrossRef] [Google Scholar]
- Skillman, D. R., Harvey, D., Patterson, J. 1997, PASP, 109, 114 [NASA ADS] [CrossRef] [Google Scholar]
- Skillman, D. R., Harvey, D. A., Patterson, J., et al. 1998, ApJ, 503, L67 [Google Scholar]
- Smak, J. 1984, Acta Astron., 34, 161 [NASA ADS] [Google Scholar]
- Smak, J. 1993, Acta Astron., 43, 101 [NASA ADS] [Google Scholar]
- Smak, J. 2004, Acta Astron., 54, 221 [Google Scholar]
- Smith, A. J., Haswell, C. A., Murray, J. R., et al. 2007, MNRAS, 378, 785 [NASA ADS] [CrossRef] [Google Scholar]
- Spencer Jones, H. 1933, MNRAS, 94, 35 [NASA ADS] [Google Scholar]
- Stellingwerf, R. F. 1978, ApJ, 224, 953 [NASA ADS] [CrossRef] [Google Scholar]
- Stoy, R. H. 1942, MNSSA, 1, 182 [NASA ADS] [Google Scholar]
- Szkody, P., & Downes, R. A. 1982, PASP, 94, 328 [NASA ADS] [CrossRef] [Google Scholar]
- Szkody, P., Mukadam, A., Gänsicke, B. T., et al. 2010, ApJ, 710, 64 [NASA ADS] [CrossRef] [Google Scholar]
- Taylor, C. J., Thorstensen, J. R., Patterson, J., et al. 1998, PASP, 110, 1148 [NASA ADS] [CrossRef] [Google Scholar]
- Thorstensen, J. R., Smak, J., & Hessman, F. V. 1985, PASP, 97, 437 [NASA ADS] [CrossRef] [Google Scholar]
- Vondrák, J. 1969, Bull. Astron. Inst. Czechosl., 20, 349 [NASA ADS] [Google Scholar]
- Vondrák, J. 1977, Bull. Astron. Inst. Czechosl., 28, 84 [NASA ADS] [Google Scholar]
- Warner, B. 1995, Cataclysmic Variable Stars (Cambridge: Cambridge Univ. Press) [Google Scholar]
- Wenzel, W., Banny, M. I., & Andronov, I. L. 1988, MitVS, 11, 141 [NASA ADS] [Google Scholar]
- Whittaker, E., & Robinson, G. 1946, The Calculus of Observations (London: Blackie & Son Ltd), 303 [Google Scholar]
- Williams, R. E. 1982, ApJ, 261, 170 [NASA ADS] [CrossRef] [Google Scholar]
- Wu, X., Li, Z., Ding, Y., et al. 2002, ApJ, 569, 418 [NASA ADS] [CrossRef] [Google Scholar]
- Zellem, R., Hollon, N., Ballouz, R.-L., et al. 2009, PASP, 121, 942 [NASA ADS] [CrossRef] [Google Scholar]
- Zhang, E., Robinson, E. L., Ramseyer, T. F., et al. 1991, ApJ, 381, 534 [NASA ADS] [CrossRef] [Google Scholar]
- Zwitter, T., Dintinjana, B., Cadez, A., et al. 1994, IBVS, 3975, 1 [NASA ADS] [Google Scholar]
All Tables
All Figures
 |
Fig. 1 Time evolution of the activity of V795 Her. a) The difference between the magnitudes of the comparison and check stars. b) Relative magnitude of V795 Her with respect to the comparison star. c) Relative intensity of V795 Her. The individual segments are abbreviated as S1 to S6. See Sect. 3.1 for details. |
| In the text | |
 |
Fig. 2 Frequency vs. Θ diagrams of the intensity variations of V795 Her determined by the PDM method (Stellingwerf 1978) for the individual segments abbreviated as S1 to S6 in Fig. 1c. The closer the value of Θ to zero, the more significant the frequency (i.e. period). The spectral window is marked by a dashed line. The arrow marks the best frequency attributed to fsh (hence to 1/Psh) in the top panel. See Sect. 3.2 for details. (This figure is available in color in electronic form.) |
| In the text | |
 |
Fig. 3 Detail of the frequency vs. Θ diagram of the intensity variations of V795 Her. It was determined with the PDM method (Stellingwerf 1978) for segments S1, S2, S3, and S4 in Fig. 1c. See Sect. 3.2 for details. (This figure is available in color in electronic form.) |
| In the text | |
 |
Fig. 4 V-band intensity curve of V795 Her in segments S1, S3, and S4 folded according to the ephemeris for S4 in Table 2. Notice the strong instability of the mean intensity level, Psh, and Tmax. See Sect. 3.2 for details. (This figure is available in color in electronic form.) |
| In the text | |
 |
Fig. 5 a), d), g) V-band intensity curve of V795 Her in segments S1, S3, and S4 folded with Psh according to the ephemerides in Table 2. The folded data were smoothed by the two-sided moving averages for various Q (in units of Φsh; see the legend). b), e), h) Smoothed residuals σresF of the fits. c), f), i) The number of data included in the calculation of each mean. See Sect. 3.2 for details. (This figure is available in color in electronic form.) |
| In the text | |
 |
Fig. 6 Simulation of the effect of a very unstable Psh in evaluating the scatter of intensity in various Φsh. a) The intensity curve artificially shifted in Φsh. The folded data were smoothed by the two-sided moving averages for various Q (in units of Φsh) (see the legend). b) Smoothed residuals σresSim of the fits. c) The number of data included in calculation of each mean. d) Dependence of the relative intensity and σresSim for the simulated data. They were smoothed by the moving averages with various Q. The observed data for S1 are included, too. Some Φsh are marked. See Sect. 3.2 for details. (This figure is available in color in electronic form.) |
| In the text | |
 |
Fig. 7 Dependence of the relative intensity and σresF for segments S1, S3, and S4. These data were smoothed by the moving averages with Q = 0.16Φsh. See Sect. 3.2 for details. (This figure is available in color in electronic form.) |
| In the text | |
 |
Fig. 8 Individual night series of V795 Her in relative intensity units. For each night, the upper panel represents the observed V-band data (panels a), d), g), j), m)). A solid line represents the HEC13 fit. Residuals of this fit, RIS, are given in the middle panel of that night (panels b), e), h), k), n)). Moving averages of the standard deviation of these residuals, σIR, are plotted in the bottom panel of the night (panels c), f), i), l), o)). The vertical dashed and dotted lines mark Φsh = 0.0 and Φsh = 0.5. The ephemeris for S3 (Table 2) was used for panels m), n), o). The quantities Φsh in the remaining panels were calculated according to the ephemeris for S1 (Table 2). See Sect. 4.2 for details. |
| In the text | |
 |
Fig. 9 Periodogram of rapid intensity variations in V795 Her. Residuals of the HEC13 fit in Fig. 8 were investigated with the Lomb-Scargle method. The spectral window is marked by a dashed line. See Sect. 4.2 for details. |
| In the text | |
 |
Fig. 10 Comparison of V795 Her with other superhumpers. Open circles denote permanent superhumpers with positive superhumps. Circled asterisks represent SW Sex systems with positive superhumps. The individual phases of the 2001 superpotburst of WZ Sge (data from Patterson et al. 2002) are also shown; FD is the final decay. The period gap is marked by the vertical lines. The dashed and dot-dashed curves denote the absolute magnitudes of dwarf novae in outburst and in quiescence according to Warner (1995). A histogram shows the distribution of Porb of SW Sex systems (not only of the superhumping ones). See Sect. 3.4 for details. (This figure is available in color in electronic form.) |
| In the text | |
 |
Fig. 11 Dependence of Teff on a thermally stable accretion disk on the distance r from the WD. The parameters of V795 Her were used. Three values of ṁ expressed in M⊙ yr-1 are assumed. The critical temperature for hydrogen ionization is abbreviated as Tcrit. Two values of the disk radius Rd in units of the WD lobe are marked. See Sect. 3.4 for details. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


