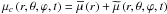| Issue |
A&A
Volume 540, April 2012
|
|
|---|---|---|
| Article Number | A37 | |
| Number of page(s) | 19 | |
| Section | Stellar structure and evolution | |
| DOI | https://doi.org/10.1051/0004-6361/201118322 | |
| Published online | 22 March 2012 | |
Low-frequency internal waves in magnetized rotating stellar radiation zones
II. Angular momentum transport with a toroidal field
1 Laboratoire AIM Paris-Saclay, CEA/DSM-CNRS-Université Paris Diderot, IRFU/SAp Centre de Saclay, 91191 Gif-sur-Yvette, France
e-mail: stephane.mathis@cea.fr
2 LESIA, Observatoire de Paris, CNRS, UPMC, Université Paris Diderot, Place Jules Janssen, 92195 Meudon, France
3 Departamento de Astronomía y Astrofísica, Universidad de Valencia, 46100 Burjassot (Valencia), Spain
Received: 22 October 2011
Accepted: 11 January 2012
Context. With the progress of observational constraints on dynamical processes in stars, it becomes necessary to understand the angular momentum and the rotation profile history. In this context, internal waves constitute an efficient transport mechanism over long distances in stellar radiation zones. Indeed, they could be one of the mechanisms responsible for the quasi-flat rotation profile of the solar radiative region up to 0.2 R⊙.
Aims. Angular momentum transport induced by internal waves depends on the properties of their excitation regions and of their dissipation during propagation. Then, the bottom of convective envelopes (the top of convective cores, respectively) are differentially rotating magnetic layers while radiation zones may host fossil magnetic fields. It is therefore necessary to understand the modification of internal wave mechanisms by both rotation and magnetic fields.
Methods. We continue our previous work by proceeding step by step. We analytically built a complete formalism that treats the angular momentum transport by internal waves while taking into account both the Coriolis acceleration and the Lorentz force in a non-perturbative way for an axisymmetric toroidal field. We assumed a uniform Alfvén frequency and a weak differential rotation to isolate the transport properties as a function of the Rossby and Elsasser numbers.
Results. We examined the different possible approximations to describe low-frequency internal waves modified by the Coriolis acceleration and the Lorentz force in a deep spherical shell. The complete structure of these waves, which become magneto-gravito-inertial waves, is given assuming the quasi-linear approximation first in the adiabatic case and then in the dissipative one. Vertical and equatorial trapping phenomena appear that favor retrograde waves. The efficiency of the induced transport as a function of the Rossby and Elsasser numbers is then obtained.
Conclusions. A complete study of the transport of angular momentum induced by magneto-gravito-inertial waves in stellar radiative regions is achieved for an axisymmetric toroidal magnetic field for a uniform Alfvén frequency and a weak differential rotation. General differential rotation, complex azimuthal magnetic fields, and poloidal and mixed fields will be examined in follow-up studies.
Key words: magnetohydrodynamics (MHD) / waves / methods: analytical / stars: rotation / stars: magnetic field / stars: evolution
© ESO, 2012
1. Introduction and context
Understanding the internal differential rotation in stars and their angular momentum history during their evolution is one of the major aim of present stellar physics (Bouvier 2009; Irwin & Bouvier 2009; Maeder 2009). Indeed, (differential) rotation modifies the stellar structure through the centrifugal acceleration that modifies its shape and through internal flows and the associated chemical mixing it generates. These mechanisms impact a star evolution and modify for example their life time, their late stages of evolution, their nucleosynthetic properties, and the associated chemical enrichment of the close interstellar medium (for complete reviews see Maeder & Meynet 2000; Zahn 2007; Talon 2008). Moreover, internal transport in stellar interiors is one of the most important components of the different exchanges of angular momentum if the studied stars are hosting a planetary system (Bouvier 2008); then, couplings with the protoplanetary disks and tidal interactions can strongly modify the star’s internal differential rotation (Matt & Pudritz 2005; Goldreich & Nicholson 1989b; Barker & Ogilvie 2009). Finally, rotation is one of the key processes that have to be taken into account to understand stellar magnetism properties and their consequences for stars and their environment (Brun 2011). This is the reason why helio and asteroseismology combined with powerful ground-based instrumentations are aimed to give tight constraints on the internal profile of angular velocity, on the rotation rate of different stellar populations in the Hertzprung-Russel diagram, and on chemical abundances anomalies on stellar surfaces, which are the product of internal mixing processes driven by rotation. First, helioseismology, with SOHO in space and GONG on the ground, has revealed the internal rotation of the Sun (Schou et al. 1998; Garcia et al. 2007; Eff-Darwich et al. 2008; Garcia et al. 2011). Next, asteroseismology gives constraints on stellar rotation and the radial differential rotation that exists between stellar cores and stellar surfaces (Aerts et al. 2003, 2008; Christensen-Dalsgaard & Thompson 2011). Finally, large spectroscopic surveys for each stellar type and evolutionnary stage give a precise picture of chemical abundance anomalies, which are the signature of transport processes in the stars’ radiation zones (Hill 2008).
We therefore have to obtain the best description of angular momentum transport mechanisms in stellar interiors. Obtained prescriptions from theoretical works and numerical simulations then have to be introduced into 1D or 2D numerical codes that allow one to study the angular velocity dynamics during stellar evolution (Decressin et al. 2009; Spada et al. 2010) that can be constrained by observations (see for example Turck-Chièze et al. 2010; Eggenberger et al. 2010). Internal waves, which are excited at the borders between convection and radiation zones, constitute an efficient process for modifying angular velocity over long distances. Therefore, they are now considered as an important ingredient in understanding the evolution of stellar rotation and are candidates, together with magnetic torques (Gough & McIntyre 2008; Brun & Zahn 2006; Garaud & Guervilly 2009; Rogers 2011; Strugarek et al. 2011), for explaining the observed quasi-flat rotation profile of the solar radiative core up to 0.2 R⊙ (Talon & Charbonnel 2005).
The properties of the transport triggered by internal waves depends on the properties of the layers at which these waves are excited and where they propagate. First, the excitation regions, for example the bottom of convective envelopes in solar-type stars or the top of convective cores in more massive stars, are the seat of dynamo action and differential rotation (Brun et al. 2005; Browning et al. 2006). Thus, if internal waves are excited at frequencies of the same order as the inertial or the Alvén frequencies by turbulent convection (and a tidal potential, if there is a close companion), the Coriolis acceleration, the shear of the differential rotation, and the Lorentz force will modify these waves’ amplitude and their spatial structure. Then, once waves are propagating in stably stratified radiative layers, their action must also be taken into account since differential rotation occurs during stellar evolution and these regions may host a fossil magnetic field of complex geometry (see for example Braithwaite 2008; Duez & Mathis 2010, and the discussion in the introduction of Mathis & de Brye 2011, hereafter Paper I). This will then modify the waves’ propagation, damping, and induced transport of angular momentum (see Kumar et al. 1999; Rogers & MacGregor 2010, 2011). In such cases, the dynamics is simultaneously driven by the buoyancy force, the Coriolis acceleration, and the Lorentz force and internal waves become magneto-gravito-inertial waves (hereafter MGI waves).
In this work, we therefore focus on the transport of angular momentum by MGI waves in deep stably stratified spherical shells. As explained in Paper I, we proceed step by step to introduce the influence of the (differential) rotation and the magnetic field because of the complexity of the problem. As in Paper I, we chose to treat a purely axisymmetric toroidal field associated to a constant Alfvén frequency and a weak differential rotation (see Mathis et al. 2008, for the hydrodynamical case) to isolate the properties of the induced transport as a function of the angular velocity value and the magnetic field amplitude. General differential rotations (Ω(r,θ); cf. Mathis 2009, in the purely hydrodynamical case) and axisymmetric toroidal fields will be treated in Paper III.
First, we study the dissipative propagation of MGI waves, since dissipation is the key ingredient with “critical layers”, to obtain a net transport of angular momentum (Booker & Bretherton 1967; Goldreich & Nicholson 1989a; Schatzman 1993b; Zahn et al. 1997). We describe the possible assumptions that can be applied to study low-frequency internal waves and we recall the results obtained in the purely adiabatic1 case (Paper I). Next, we examine dissipative processes, i.e. the action of heat, viscous, and Ohmic diffusions. We establish their hierarchy in stellar radiation zones and study the resulting damping taking into account the Coriolis acceleration and the Lorentz force. Then, the total transported fluxes of energy and angular momentum are obtained; a comparison with the non-rotating and non-magnetic case is achieved. Furthermore, we give the corresponding coupling time of the radiative region with the convective one at the border of which MGI waves are excited. Finally, we describe how MGI waves are coupled with other dynamical processes in stellar radiation zones and the consequences for the transport of angular momentum in stellar interiors.
2. Structure of low-frequency waves influenced by rotation and the toroidal magnetic field
2.1. Dynamical equations
To study the transport of angular momentum induced by internal waves, which are modified both by the Coriolis acceleration and the Lorentz force (i.e. MGI waves), we have to solve the dissipative MHD dynamical equations system. It is formed by the induction equation 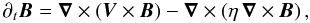 (1)the momentum equation
(1)the momentum equation ![\begin{equation} \rho\,D_{t}\vec V=-{\vec\nabla}P-\rho{\vec\nabla}\Phi\,-\vec\nabla\cdot{\overline{\overline{\mathcal D}}}+\left[\frac{1}{\mu}\left({\vec\nabla}\times{\vec B}\right)\times{\vec B}\right], \label{Eqd2} \end{equation}](/articles/aa/full_html/2012/04/aa18322-11/aa18322-11-eq5.png) (2)the continuity equation
(2)the continuity equation 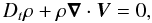 (3)the equation for the transport of heat
(3)the equation for the transport of heat ![\begin{equation} \rho T D_{t}S=\vec\nabla\cdot\left(\,\chi{\vec\nabla\,}T\right)+2\rho\nu\left[e_{ij}e_{ij}-\frac{1}{3}\left({\vec\nabla}\cdot\vec V\right)^2\right]+\mu\eta{\vec j}^{2}+\rho\epsilon, \label{Eqd4} \end{equation}](/articles/aa/full_html/2012/04/aa18322-11/aa18322-11-eq7.png) (4)where we identify the viscous, the Ohmic and the nuclear heating terms, and the Poisson equation for the gravitational potential
(4)where we identify the viscous, the Ohmic and the nuclear heating terms, and the Poisson equation for the gravitational potential 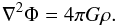 (5)Here, t is the time and r = (r,θ,ϕ) are the usual spherical coordinates with their associated unit vector basis
(5)Here, t is the time and r = (r,θ,ϕ) are the usual spherical coordinates with their associated unit vector basis 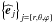 . B is the magnetic field, j = (∇ × B)/μ the current, η the magnetic diffusivity and μ the magnetic permeability of the medium. V is the macroscopic velocity field, Dt = ∂t + (V·∇) is the Lagrangian derivative, and
. B is the magnetic field, j = (∇ × B)/μ the current, η the magnetic diffusivity and μ the magnetic permeability of the medium. V is the macroscopic velocity field, Dt = ∂t + (V·∇) is the Lagrangian derivative, and ![\begin{equation} {\mathcal D}_{ij}=-2\,\rho\,\nu\left[e_{ij}-\frac{1}{3}\left(\vec\nabla\cdot\vec V\right)\delta_{i,j}\right] \end{equation}](/articles/aa/full_html/2012/04/aa18322-11/aa18322-11-eq18.png) (6)are Reynolds stresses where ν is the viscosity and
(6)are Reynolds stresses where ν is the viscosity and 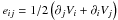 the strain rate tensor (δ is the Kronecker symbol). ρ, Φ, P, T are the density, the gravific potential, the pressure and the temperature, respectively. We define the total pressure, which is the sum of the gaseous and magnetic pressures
the strain rate tensor (δ is the Kronecker symbol). ρ, Φ, P, T are the density, the gravific potential, the pressure and the temperature, respectively. We define the total pressure, which is the sum of the gaseous and magnetic pressures 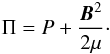 (7)S is the macroscopic entropy defined such that
(7)S is the macroscopic entropy defined such that ![\begin{equation} {\rm d}S=C_{P}\left[\frac{{\rm d}T}{T}-\nabla_{\rm ad}\frac{{\rm d}P}{P}\right], \label{defS} \end{equation}](/articles/aa/full_html/2012/04/aa18322-11/aa18322-11-eq28.png) (8)where CP and ∇ad = (∂lnT/∂lnP)ad are the heat capacity at a given pressure and the adiabatic gradient. We introduce χ the radiative conductivity, which is related to the corresponding diffusivity
(8)where CP and ∇ad = (∂lnT/∂lnP)ad are the heat capacity at a given pressure and the adiabatic gradient. We introduce χ the radiative conductivity, which is related to the corresponding diffusivity 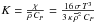 (σ and κ are the Stefan constant and the Rosseland mean opacity), and ϵ is the nuclear energy production rate per unit mass. Finally, we close the system using the general equation of state (EOS) introduced by Kippenhahn & Weigert (1990):
(σ and κ are the Stefan constant and the Rosseland mean opacity), and ϵ is the nuclear energy production rate per unit mass. Finally, we close the system using the general equation of state (EOS) introduced by Kippenhahn & Weigert (1990): 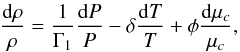 (9)where μc is the mean molecular weight, Γ1 = (∂lnP/∂lnρ)T, μc the adiabatic exponent, δ = −(∂lnρ/∂lnT)P, μc, and φ = (∂lnρ/∂lnμ)P, T. The equation for chemical element transport will be introduced when necessary to take into account the chemical stratification.
(9)where μc is the mean molecular weight, Γ1 = (∂lnP/∂lnρ)T, μc the adiabatic exponent, δ = −(∂lnρ/∂lnT)P, μc, and φ = (∂lnρ/∂lnμ)P, T. The equation for chemical element transport will be introduced when necessary to take into account the chemical stratification.
2.2. The magnetic topology and differential rotation
As in Paper I, B is chosen to be the sum of a large-scale toroidal field 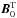 associated to a uniform Alfvén frequency ωA and of the wave-induced field b:
associated to a uniform Alfvén frequency ωA and of the wave-induced field b: 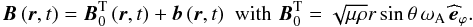 (10)Then, the velocity field V is formed by the sum of the large-scale azimuthal velocity field V0, associated to the chosen rotation law Ω, and of the wave velocity u:
(10)Then, the velocity field V is formed by the sum of the large-scale azimuthal velocity field V0, associated to the chosen rotation law Ω, and of the wave velocity u: 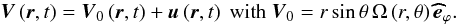 (11)Furthermore, following Unno et al. (1989), we also introduce the wave’s Lagrangian displacement, which is defined such that
(11)Furthermore, following Unno et al. (1989), we also introduce the wave’s Lagrangian displacement, which is defined such that 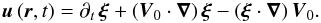 (12)Let us now consider the differential rotation law. In this first paper on transport of angular momentum by MGI waves, we consider as a first step a “shellular” rotation
(12)Let us now consider the differential rotation law. In this first paper on transport of angular momentum by MGI waves, we consider as a first step a “shellular” rotation 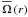 , which depends only on the radial coordinate (see Zahn 1992). Then, we split this “shellular” rotation law into a solid body rotation Ωs and a (weak) differential rotation fluctuation (
, which depends only on the radial coordinate (see Zahn 1992). Then, we split this “shellular” rotation law into a solid body rotation Ωs and a (weak) differential rotation fluctuation (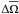 ):
): 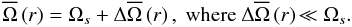 (13)This is the “weak differential rotation case”, which remains valid only for “reasonable” values of the fluctuation
(13)This is the “weak differential rotation case”, which remains valid only for “reasonable” values of the fluctuation 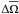 around its mean value Ωs and of the radial gradient of
around its mean value Ωs and of the radial gradient of 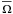 .
.
This will allow us to give a first picture of the transport of angular momentum modification by internal waves by the combined action of rotation through the Coriolis acceleration and magnetic field by the Lorentz force. Ωs will be taken into account for calculating the structure of the low-frequency adiabatic MGI waves (Sect. 2.3), and 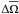 will be accounted for only in the treatment of the damping from dissipative processes (Sect. 2.5). As shown in Mathis et al. (2008) in the hydrodynamical case, this hypothesis allows us to separate the variables in the treatment of the adiabatic dynamical equations. This net variable separation becomes impossible for a general differential rotation law and azimuthal magnetic field (Ω(r,θ),
will be accounted for only in the treatment of the damping from dissipative processes (Sect. 2.5). As shown in Mathis et al. (2008) in the hydrodynamical case, this hypothesis allows us to separate the variables in the treatment of the adiabatic dynamical equations. This net variable separation becomes impossible for a general differential rotation law and azimuthal magnetic field (Ω(r,θ), 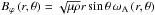 ; see Mathis 2009, for the hydrodynamical case). Then, a more subtle treatment has to be adopted, which we will provide in Paper III.
; see Mathis 2009, for the hydrodynamical case). Then, a more subtle treatment has to be adopted, which we will provide in Paper III.
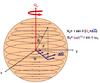 |
Fig. 1 Set-up for studying internal wave dynamics in rotating and magnetic stellar radiation zones and the associated transport of angular momentum. The Alfvén frequency |
The non-spherical character of the hydrostatic background due to the deformation associated to the centrifugal acceleration ![\hbox{$\vec\gamma_{\rm c} ({\overline\Omega} )=1/2 [{\overline\Omega}^2{\vec\nabla} (r^2\sin^2\theta ) ]$}](/articles/aa/full_html/2012/04/aa18322-11/aa18322-11-eq58.png) and to the Lorentz force associated to
and to the Lorentz force associated to 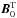 ,
, ![\hbox{${\vec F}_{\mathcal L}^{0}({\vec B}_{0}^{\rm T} )=1/\mu[ ({\vec\nabla}\times{\vec B}_{0}^{\rm T} )\times{\vec B}_{0}^{\rm T}]$}](/articles/aa/full_html/2012/04/aa18322-11/aa18322-11-eq59.png) are neglected.
are neglected.
2.3. Main assumptions
Let us now examine the assumptions that can be adopted to describe low-frequency MGI wave propagation in deep spherical shells.
As in Paper I, Eqs. (1–5) are linearised around the rotating magnetic steady-state. Indeed, each scalar field X = {ρ,P,T,μc,Φ} is expanded as the sum of its hydrostatic value, 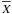 , and of the wave’s associated fluctuation,
, and of the wave’s associated fluctuation, 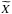 , as2
, as2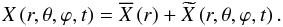 (14)Moreover,
(14)Moreover, 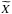 and each vectorial field x(r,t) = {u,ξ,b} are expanded in Fourier’s series in ϕ and t:
and each vectorial field x(r,t) = {u,ξ,b} are expanded in Fourier’s series in ϕ and t: 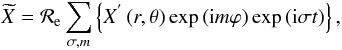 (15)
(15)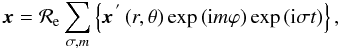 (16)σ being the wave angular velocity in an inertial frame; ℛe is the real part. Finally, we define the Doppler-shifted frequencies that we use here:
(16)σ being the wave angular velocity in an inertial frame; ℛe is the real part. Finally, we define the Doppler-shifted frequencies that we use here: 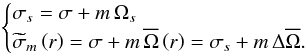 (17)The sign of m is chosen such that the prograde waves have m < 0, whereas the retrograde waves have m > 0.
(17)The sign of m is chosen such that the prograde waves have m < 0, whereas the retrograde waves have m > 0.
From now on, we fix Ωs to be the angular velocity of the layer where MGI waves are excited, i.e. the bottom of the convective envelope in a solar-type star and the top of the convective core in an intermediate or high mass star; σs is then the excited frequency.
We assume Cowling’s approximation (Cowling 1941), where the wave’s gravific potential fluctuation (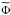 ) is neglected. Therefore, we do not solve Eq. (5).
) is neglected. Therefore, we do not solve Eq. (5).
Dimensionless numbers that characterise the internal wave propagation in rotating and magnetic stellar radiation zones.
2.3.1. The strongly stratified case: the MHD traditional approximation
In the general case, the Poincaré operator for the pressure fluctuation, which governs the spatial structure of the waves, is of mixed type (elliptic and hyperbolic) and not separable (for a detailed discussion we refer the reader to Friedlander & Siegman 1982; Dintrans et al. 1999; Ballot et al. 2010). In the hyperbolic regime, this may lead to the appearance of detached shear layers associated with the underlying singularities of the adiabatic problem, which could be crucial for transport and mixing processes in stellar radiation zones since they are the seat of strong dissipation (Stewartson & Richard 1969; Stewartson & Walton 1976; Dintrans & Rieutord 2000; Maas & Harlander 2007).
Let us first introduce the two dimensionless numbers, which compare the stratification restoring force with the Coriolis acceleration and the Lorentz force 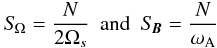 (18)(all dimensionless numbers that govern MGI waves dynamics are given in Table 1; N is the Brunt-Väisälä frequency defined in Eq. (41)). In the stellar radiation zones, we are mainly in a regime where {SΩ,SB} ≫ 1. Since we are interested in low-frequency waves for which σ ≪ N, the MHD traditional approximation (hereafter MHD TA), which consists in making an asymptotic expansion of the dynamical equations in function of SΩ and SB, then allows us to separate variables into radial and horizontal functions (see Friedlander 1987–89, Sect. 3.1 in Paper I, and Sect. 2.4). The MHD TA allows this separation of variables due to neglecting terms in the dynamical equations that changes the nature of the Poincaré operator and removes the shear layers in the hyperbolic regime. It has thus to be carefully used only in the regime for which |νM;m| < 1, where
(18)(all dimensionless numbers that govern MGI waves dynamics are given in Table 1; N is the Brunt-Väisälä frequency defined in Eq. (41)). In the stellar radiation zones, we are mainly in a regime where {SΩ,SB} ≫ 1. Since we are interested in low-frequency waves for which σ ≪ N, the MHD traditional approximation (hereafter MHD TA), which consists in making an asymptotic expansion of the dynamical equations in function of SΩ and SB, then allows us to separate variables into radial and horizontal functions (see Friedlander 1987–89, Sect. 3.1 in Paper I, and Sect. 2.4). The MHD TA allows this separation of variables due to neglecting terms in the dynamical equations that changes the nature of the Poincaré operator and removes the shear layers in the hyperbolic regime. It has thus to be carefully used only in the regime for which |νM;m| < 1, where 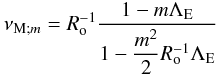 (19)is the system’s control parameter introduced in Paper I. Here, we chose to express it as a function of the wave Rossby and Elsasser numbers (see also Table 1)
(19)is the system’s control parameter introduced in Paper I. Here, we chose to express it as a function of the wave Rossby and Elsasser numbers (see also Table 1) 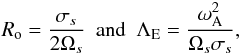 (20)which compare the Coriolis acceleration with the inertia and the magnetic force. This corresponds to the elliptic modes family (the E1 modes in Dintrans et al. 1999), which propagate in the whole sphere. In the other regime where |νM;m| ≥ 1, which corresponds to equatorially trapped hyperbolic modes (the H1 modes in Dintrans et al. 1999), the MHD TA fails to reproduce the wave behaviour rigourously and the full dynamical equation has to be solved (a detailed discussion is given in Gerkema & Shrira 2005a; Gerkema et al. 2007). For a strong stratification, which is considered here, Miles (1974) proposed an asymptotic solution to the problem, for which it is necessary to construct a boundary layer about the trapping latitude,
(20)which compare the Coriolis acceleration with the inertia and the magnetic force. This corresponds to the elliptic modes family (the E1 modes in Dintrans et al. 1999), which propagate in the whole sphere. In the other regime where |νM;m| ≥ 1, which corresponds to equatorially trapped hyperbolic modes (the H1 modes in Dintrans et al. 1999), the MHD TA fails to reproduce the wave behaviour rigourously and the full dynamical equation has to be solved (a detailed discussion is given in Gerkema & Shrira 2005a; Gerkema et al. 2007). For a strong stratification, which is considered here, Miles (1974) proposed an asymptotic solution to the problem, for which it is necessary to construct a boundary layer about the trapping latitude, 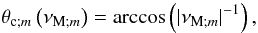 (21)the obtained solution being matched with that of the MHD TA away from it (this treatment is beyond the scope of the present paper; we also refer the reader to Fruman 2009).
(21)the obtained solution being matched with that of the MHD TA away from it (this treatment is beyond the scope of the present paper; we also refer the reader to Fruman 2009).
Here, we therefore adopted the MHD TA as a first step to give a picture of transport and mixing processes associated to MGI waves in stellar radiation zones. In Fig. 2, we show the domain where it could be applied for m = { − 2, − 1,1,2} as a function of the wave’s Rossby (Ro) and Elsasser (ΛE) numbers. Moreover, we show the domain of the space of parameters 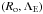 where the vertical magnetic trapping identified in Paper I and recalled in Sect. 2.4 occurs (i.e. when
where the vertical magnetic trapping identified in Paper I and recalled in Sect. 2.4 occurs (i.e. when 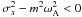 ). We also display the corresponding wave families (extending the classification by Dintrans et al. 1999, to the hydromagnetic case): the elliptic modes (E family) for which the MHD TA applies, the equatorially trapped hyperbolic modes (H family), and the vertically trapped modes (T family), for which
). We also display the corresponding wave families (extending the classification by Dintrans et al. 1999, to the hydromagnetic case): the elliptic modes (E family) for which the MHD TA applies, the equatorially trapped hyperbolic modes (H family), and the vertically trapped modes (T family), for which 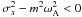 , which cannot propagate.
, which cannot propagate.
Let us now examine the consequences on wave properties using their dispersion relation. Following Kumar et al. (1999) (see also Sect. 2 in Paper I), we can obtain this relation for a stellar radiation zone where both the angular velocity and the background magnetic field are chosen to be uniform (i.e. Ω = Ωs and 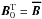 )
) ![\begin{eqnarray} \lefteqn{\sigma_s^2=\left({\widehat{\vec B}}\cdot\vec k\right)^2V_{\rm A}^{2}+ \frac{1}{2}\left\{\left(\vec N\times\widehat{\vec k}\right)^2+4\left(\vec\Omega\cdot{\widehat{\vec k}}\right)^2\right.}\nonumber\\ & &{\left.\pm\sqrt{\left[\left(\vec N\times\widehat{\vec k}\right)^2+4\left(\vec\Omega\cdot{\widehat{\vec k}}\right)^2\right]^2+16\left(\widehat{\vec B}\cdot{\vec k}\right)^2V_{\rm A}^{2}\left(\vec\Omega\cdot{\widehat{\vec k}}\right)^2}\,\right\}}. \end{eqnarray}](/articles/aa/full_html/2012/04/aa18322-11/aa18322-11-eq102.png) (22)We assumed that all perturbed quantities have a plane-wave dependence, i.e. ∝ exp[i(k·r + σt)], where k is the wave number. Furthermore, we defined
(22)We assumed that all perturbed quantities have a plane-wave dependence, i.e. ∝ exp[i(k·r + σt)], where k is the wave number. Furthermore, we defined 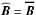 /
/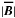 ,
, 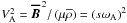 where s = rsinθ,
where s = rsinθ, 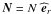 ,
, 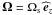 , and
, and 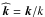 .
.
Two branches are then isolated. First, we obtain the “magnetostrophic waves” for low frequencies for which the Coriolis acceleration tries to balance the Lorentz force. Their approximate dispersion relation is given by 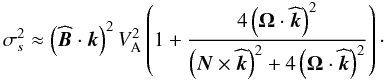 (23)In the non-rotating case, these reduce to classical Alfvén waves. Next, the high-frequency branch corresponds to MGI waves (which are also called magneto-Poincaré waves and magneto-Rossby waves for those waves that are caused by the star curvature and the associated variation of the local rotation on a tangent sphere). In this case, we obtain the following approximative dispersion relation:
(23)In the non-rotating case, these reduce to classical Alfvén waves. Next, the high-frequency branch corresponds to MGI waves (which are also called magneto-Poincaré waves and magneto-Rossby waves for those waves that are caused by the star curvature and the associated variation of the local rotation on a tangent sphere). In this case, we obtain the following approximative dispersion relation: 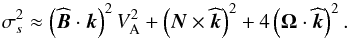 (24)Let us introduce the expansion of k both in the spherical and cylindrical coordinates:
(24)Let us introduce the expansion of k both in the spherical and cylindrical coordinates: 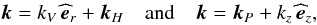 (25)where
(25)where 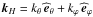 and
and 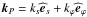 , (s,ϕ,z) are the cylindrical coordinates and
, (s,ϕ,z) are the cylindrical coordinates and 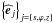 the associated unit-vector basis. Then, the dispersion relation is written
the associated unit-vector basis. Then, the dispersion relation is written ![\begin{equation} \sigma_s^{2}\approx N^2\left[\frac{k_H^2}{k^2}+\frac{1}{{S_{\Omega}}^{2}}\frac{k_z^2}{k^2}+\frac{1}{{S_{\vec B}}^{2}}\left[s\left(\widehat{\vec B}\cdot{\vec k}\right)\right]^{2}\right]. \end{equation}](/articles/aa/full_html/2012/04/aa18322-11/aa18322-11-eq120.png) (26)For highly stratified stellar radiation zones where {SΩ,SB} ≫ 1, these reduce for low-frequency waves (σ ≪ N) to
(26)For highly stratified stellar radiation zones where {SΩ,SB} ≫ 1, these reduce for low-frequency waves (σ ≪ N) to 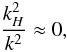 (27)which leads to the following hierarchy
(27)which leads to the following hierarchy 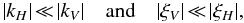 (28)because of the anelastic approximation where acoustic waves are filtered
(28)because of the anelastic approximation where acoustic waves are filtered 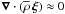 , which becomes k·ξ ≈ 0 in the local analysis case.
, which becomes k·ξ ≈ 0 in the local analysis case.
 |
Fig. 2 Top: sign of |
2.3.2. The JWKB approximation
Next, we define the Froude number (cf. Table 1) 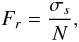 (29)which gives the ratio between the wave-inertia term and that of the stratification.
(29)which gives the ratio between the wave-inertia term and that of the stratification.
Under the assumption that Fr ≪ 1, each scalar field (X) and each component of a vector field (x) can be expanded using the JWKB approximation (see for exemple Landau & Lifschitz 1966). In this case, the vertical wave number is very high, the associated wavelength is consequently very short. Therefore, the spatial variations of the wave are very rapid compared to those of the equilibrium background (cf. compared to those of 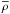 ,
, 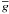 ,
, 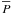 ,
, 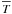 ,
, 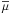 , V0,
, V0, 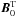 ). Then, the wave spatial structure can be described by a plane-like wave function multiplied by a slowly varying amplitude and we obtain in Eqs. (15, 16)
). Then, the wave spatial structure can be described by a plane-like wave function multiplied by a slowly varying amplitude and we obtain in Eqs. (15, 16) 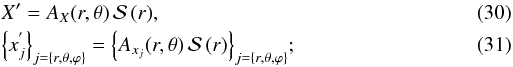 the JWKB phase function is given by
the JWKB phase function is given by ![\begin{equation} {\mathcal S}\left(r\right)=\exp\left[{\rm i}\left(\int_{r}k_{V}\left(r^{'}\right){\rm d}r^{'}\right)\right] , \end{equation}](/articles/aa/full_html/2012/04/aa18322-11/aa18322-11-eq149.png) (32)where the property of low-frequency waves given in Eq. (28) has been used to neglect kH in exp [i∫rk·dr′] .
(32)where the property of low-frequency waves given in Eq. (28) has been used to neglect kH in exp [i∫rk·dr′] .
If the JWKB approximation is adopted, this also implies that the quasi-linear approximation is assumed, where the non-linear wave-wave interactions are neglected.
Internal wave induced transport in stellar interiors was first studied by Press (1981). He emphasized the possible non-linearity of the problem of internal waves excited by turbulent convective movements. He then showed that JWKB solutions, using crude prescriptions for the wave excitation, are at the border of the linear and the non-linear regime. Furthermore, Rogers et al. (2008) obtain results where the non-linear regime develops for an excited spectrum at the convection-radiation border computed through equatorial 2D numerical simulations, which accounts for a real solar stratification. This non-linear behaviour then shows that the quasi-linear approximation has to be used carefully depending on the excited spectrum that is assumed. However, the quasi-linear approximation is relevant as long as the Froude number (Fr) is small compared to unity. This number has been computed by Rogers & Glatzmaier (2006) (cf. Fig. 4 in this paper) in the solar case using the same numerical simulations as those discussed above. The authors showed that Fr ≪ 1 in the bulk of the radiation zone, while it strongly grows in the tachocline where internal waves are excited by the turbulent convection and at the centre because of the wave’s geometrical focusing that was already identified by Press (1981); in both cases N → 0 (see also Barker & Ogilvie 2011). Therefore, it is reasonable to adopt the quasi-linear approximation (cf. Eqs. (14–16)), being aware that it has to be used with caution in the excitation region and at the centre.
In this context, it is also interesting to discuss the validity of the MHD TA and of the associated results such that the value of the critical trapping latitude θc;m given in Eq. (21). First, in the case where the quasi-linear approximation applies (i.e. when Fr ≪ 1), the MHD TA can be assumed as soon as {SΩ,SB} ≫ 1 as described in Sect. 2.3.1, which points the importance of the stratification strength given by the Brunt-Väisälä frequency (Eq. (41)) simultaneously for all the approximations. Next, if the quasi-linear approximation applies, but {SΩ,SB} do not verify the required conditions to apply the MHD TA, the expression of θc;m will be corrected by terms scaling as 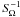 and
and 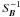 . This has been studied in the purely hydrodynamical case by Melchior (1986), Gerkema & Shrira (2005b) and Fruman (2009); furthermore, Shrira & Townsend (2010) have shown that it is then possible to describe analytically the formation of shear layers around critical latitudes such as those observed in numerical simulations by Dintrans et al. (1999). This should be generalised to our present hydromagnetic case in a near future. Finally, the derivation of the critical latitude, both in the traditional and in the non-traditional regimes, is based on the linearised MHD equations system that corresponds to the quasi-linear approximation and allows one to obtain linear partial differential equations. Furthermore, if the quasi-linear approximation fails (i.e. when N → 0), the MHD TA cannot be applied since SΩ and SB also tend to vanish. We can therefore conclude that the prediction for the critical latitude assuming the MHD TA given in Eq. (21) can be used as a first-order approximation to describe MGI wave dynamics in the bulk of radiative regions where the quasi-linear approximation applies.
. This has been studied in the purely hydrodynamical case by Melchior (1986), Gerkema & Shrira (2005b) and Fruman (2009); furthermore, Shrira & Townsend (2010) have shown that it is then possible to describe analytically the formation of shear layers around critical latitudes such as those observed in numerical simulations by Dintrans et al. (1999). This should be generalised to our present hydromagnetic case in a near future. Finally, the derivation of the critical latitude, both in the traditional and in the non-traditional regimes, is based on the linearised MHD equations system that corresponds to the quasi-linear approximation and allows one to obtain linear partial differential equations. Furthermore, if the quasi-linear approximation fails (i.e. when N → 0), the MHD TA cannot be applied since SΩ and SB also tend to vanish. We can therefore conclude that the prediction for the critical latitude assuming the MHD TA given in Eq. (21) can be used as a first-order approximation to describe MGI wave dynamics in the bulk of radiative regions where the quasi-linear approximation applies.
One can also note that here the critical latitude does not depend on the differential rotation (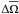 ). This is due to the choice to study in a first step the “weak differential rotation case” for which
). This is due to the choice to study in a first step the “weak differential rotation case” for which 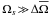 . This means that the impact of
. This means that the impact of 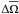 on θc;m constitutes only a small correction that does not change its main behaviour (see Mathis et al. 2008, in the hydrodynamical case). A general differential rotation in which the critical latitude explicitely depends on the angular rotation profile and on its vertical and latitudinal gradients has been studied in Mathis (2009) in the purely hydrodynamical case and will be studied in Paper III.
on θc;m constitutes only a small correction that does not change its main behaviour (see Mathis et al. 2008, in the hydrodynamical case). A general differential rotation in which the critical latitude explicitely depends on the angular rotation profile and on its vertical and latitudinal gradients has been studied in Mathis (2009) in the purely hydrodynamical case and will be studied in Paper III.
2.3.3. The anelastic approximation
From now on, we focus on low-frequency internal waves (i.e. Fr = σ/N ≪ 1), which transport angular momentum in stellar radiation zones. For these waves, we can adopt the anelastic approximation where magneto-acoustic waves are filtered out (i.e. 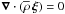 and the terms proportional to
and the terms proportional to  are neglected, where
are neglected, where 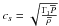 is the sound velocity).
is the sound velocity).
2.4. The adiabatic propagation
2.4.1. The adiabatic dynamical equations
Here, we recall the results obtained in the adiabatic case in Paper I for the wave velocity, magnetic and pressure fields. As in Mathis et al. (2008), we only take into account the solid-body part of the rotation law (Ωs) to derive the adiabatic wave structure, the small departure from it 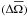 is only accounted for in the treatment of the dissipative mechanisms (Sect. 2.5). Moreover, we assume the anelastic approximation described above (Sect. 2.3.3).
is only accounted for in the treatment of the dissipative mechanisms (Sect. 2.5). Moreover, we assume the anelastic approximation described above (Sect. 2.3.3).
Then, Eq. (12) gives 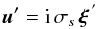 (33)while the ideal induction equation (Eq. (1)) becomes
(33)while the ideal induction equation (Eq. (1)) becomes 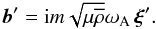 (34)The momentum equation (Eq. (2)) is written using Cowling’s approximation
(34)The momentum equation (Eq. (2)) is written using Cowling’s approximation 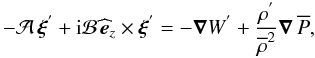 (35)where
(35)where ![\hbox{$W^{'}=\Pi^{'}/{\overline\rho}=\left[P{'}+\left({\vec B_{0}^{\rm T}\cdot{\vec b}{'}}\right)/\mu\right]/{\overline\rho}$}](/articles/aa/full_html/2012/04/aa18322-11/aa18322-11-eq169.png) and
and 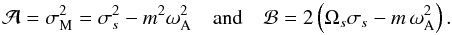 (36)Then, the continuity equation is given by
(36)Then, the continuity equation is given by ![\begin{equation} \frac{1}{r^2}\partial_{r}\left(r^2{\overline\rho}\,\xi_{r}^{'}\right)+\frac{{\overline\rho}}{r}\left[\frac{1}{\sin\theta}\partial_{\theta}\left(\sin\theta\,{\xi}_{\theta}^{'}\right)+\frac{{\rm i} m \xi_{\varphi}^{'}}{\sin\theta}\right]=0. \label{Eqd3Ad} \end{equation}](/articles/aa/full_html/2012/04/aa18322-11/aa18322-11-eq171.png) (37)Finally, using Eq. (8) and the anelastic approximation, the energy equation (Eq. (4)) is obtained in the adiabatic limit as a function of the temperature
(37)Finally, using Eq. (8) and the anelastic approximation, the energy equation (Eq. (4)) is obtained in the adiabatic limit as a function of the temperature 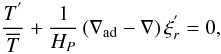 (38)where we introduce the temperature gradient
(38)where we introduce the temperature gradient 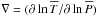 and the pressure height-scale
and the pressure height-scale 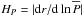 . Next, using the EOS (Eq. (9)) in the anelastic approximation to express T′ as a function of ρ′ and μ′, we obtain
. Next, using the EOS (Eq. (9)) in the anelastic approximation to express T′ as a function of ρ′ and μ′, we obtain 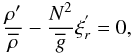 (39)where we have used the mean molecular weight conservation (Zahn et al. 1997)
(39)where we have used the mean molecular weight conservation (Zahn et al. 1997) 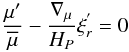 (40)with
(40)with 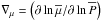 and introduced the Brunt-Väisälä frequency
and introduced the Brunt-Väisälä frequency 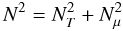 (41)with
(41)with 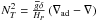 and
and 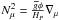 and the gravity
and the gravity 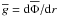 . Internal waves are only propagating if
. Internal waves are only propagating if 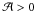 ; in the other case, they are trapped in the vertical direction (cf. Schatzman 1993a; Barnes et al. 1998) because the azimuthal magnetic field acts as a filter in the vertical direction (see in Fig. 2).
; in the other case, they are trapped in the vertical direction (cf. Schatzman 1993a; Barnes et al. 1998) because the azimuthal magnetic field acts as a filter in the vertical direction (see in Fig. 2).
2.4.2. Adiabatic wave velocity, magnetic and pressure fields
Assuming the MHD TA (see Sect. 2.2.2), the system can be separated into r and θ3. Then, scalar quantities and the displacement’s vertical component are expanded as 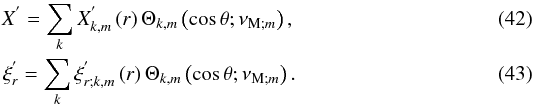 The Θk,m functions are the orthogonal Hough functions, for which
The Θk,m functions are the orthogonal Hough functions, for which 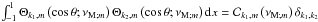 , where δi,j is the Kronecker symbol (Laplace 1799; Hough 1898; Longuet-Higgins 1968; Chapman & Lindzen 1969). These are the eigenfunctions (with the associated eigenvalues Λk,m) of the so-called “Laplace tidal equation” (hereafter LTE):
, where δi,j is the Kronecker symbol (Laplace 1799; Hough 1898; Longuet-Higgins 1968; Chapman & Lindzen 1969). These are the eigenfunctions (with the associated eigenvalues Λk,m) of the so-called “Laplace tidal equation” (hereafter LTE): ![\begin{equation} {\mathcal L}_{\nu_{{\rm M};m}}\left[\Theta_{k,m}\left(x;\nu_{{\rm M};m}\right)\right]=-\Lambda_{k,m}\left(\nu_{{\rm M};m}\right)\Theta_{k,m}\left(x;\nu_{{\rm M};m}\right), \label{Laplace} \end{equation}](/articles/aa/full_html/2012/04/aa18322-11/aa18322-11-eq192.png) (44)where we introduce x = cosθ and the Laplace tidal operator
(44)where we introduce x = cosθ and the Laplace tidal operator 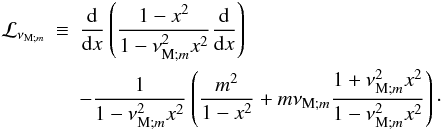 (45)The control parameter of the system νM;m, which depends on the wave Rossby and Elsasser numbers given in Eq. (20), has been defined in Eq. (19). Note that since
(45)The control parameter of the system νM;m, which depends on the wave Rossby and Elsasser numbers given in Eq. (20), has been defined in Eq. (19). Note that since 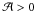 , then
, then 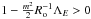 , which avoids any singularity. For a detailed discussion of the boundary conditions of the LTE, we refer the reader to Lee & Saio (1997). In the same way, we express the horizontal displacement
, which avoids any singularity. For a detailed discussion of the boundary conditions of the LTE, we refer the reader to Lee & Saio (1997). In the same way, we express the horizontal displacement 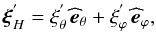 (46)where
(46)where 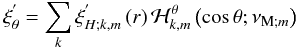 (47)and
(47)and 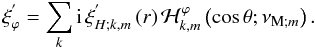 (48)Then, assuming the MHD TA, the momentum equation components along
(48)Then, assuming the MHD TA, the momentum equation components along 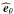 and
and 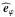 allow us to express
allow us to express 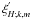 :
: 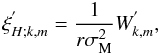 (49)where we recall that
(49)where we recall that ![\begin{eqnarray} W^{'}&=&\frac{\Pi^{'}}{\overline\rho}=\frac{1}{\overline\rho}\left[P^{'}+\frac{\left({\vec B_{0}^{\rm T}\cdot{\vec b}^{'}}\right)}{\mu}\right]\nonumber\\ &=&\sum_k W_{k,m}^{'}\left(r\right)\Theta_{k,m}\left(\cos\theta;\nu_{{\rm M};m}\right), \end{eqnarray}](/articles/aa/full_html/2012/04/aa18322-11/aa18322-11-eq204.png) (50)and the two horizontal functions
(50)and the two horizontal functions ![\begin{equation} {\mathcal H}_{k,m}^{\theta}\left(x;\nu_{{\rm M};m}\right)={\mathcal L}_{\nu_{{\rm M};m}}^{\theta}\left[\Theta_{k,m}\left(x;\nu_{{\rm M};m}\right)\right] \end{equation}](/articles/aa/full_html/2012/04/aa18322-11/aa18322-11-eq205.png) (51)and
(51)and ![\begin{equation} {\mathcal H}_{k,m}^{\varphi}\left(x;\nu_{{\rm M};m}\right)={\mathcal L}_{\nu_{{\rm M};m}}^{\varphi}\left[\Theta_{k,m}\left(x;\nu_{{\rm M};m}\right)\right] \end{equation}](/articles/aa/full_html/2012/04/aa18322-11/aa18322-11-eq206.png) (52)with
(52)with ![\begin{equation} {\mathcal L}_{\nu_{{\rm M};m}}^{\theta}\equiv\frac{1}{\left(1-\nu_{{\rm M};m}^{2}x^2\right)\sqrt{1-x^2}}\left[-\left(1-x^2\right)\frac{{\rm d}}{{\rm d}x}+m\nu_{{\rm M};m}x\right] \label{opLapTh} \end{equation}](/articles/aa/full_html/2012/04/aa18322-11/aa18322-11-eq207.png) (53)and
(53)and ![\begin{equation} {\mathcal L}_{\nu_{{\rm M};m}}^{\varphi}\equiv\frac{1}{\left(1-\nu_{{\rm M};m}^{2}x^2\right)\sqrt{1-x^2}}\left[-\nu_{{\rm M};m}x\left(1-x^2\right)\frac{{\rm d}}{{\rm d}x}+m\right]. \label{opLapPh} \end{equation}](/articles/aa/full_html/2012/04/aa18322-11/aa18322-11-eq208.png) (54)
(54)
 |
Fig. 3 Left: Hough functions Θk,m(cosθ;ν) (top) and associated latitudinal |
Moreover, the radial component of the momentum equation (Eq. (35)), the continuity equation (Eq. (37)), and the energy transport equation (Eq. (39)) become 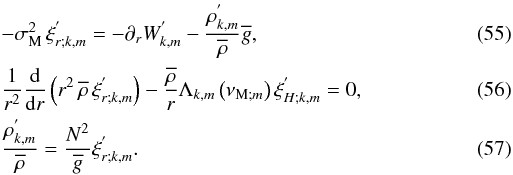 Eliminating successively
Eliminating successively 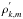 and
and 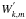 following the procedure given in Zahn (1975) and in Press (1981), we obtain the final equation for the vertical displacement
following the procedure given in Zahn (1975) and in Press (1981), we obtain the final equation for the vertical displacement ![\begin{equation} \frac{{\rm d}^{2}{\Psi}_{k,m}}{{\rm d}r^2}\!+\left[k_{V;k,m}\left(r\right)\right]^2{\Psi}_{k,m}\!=\!0, \label{PoincareAd} \end{equation}](/articles/aa/full_html/2012/04/aa18322-11/aa18322-11-eq232.png) (58)where we have introduced the adiabatic vertical wave number4.
(58)where we have introduced the adiabatic vertical wave number4.
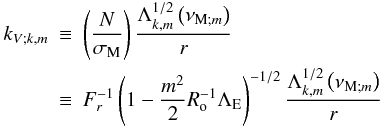 (60)and
(60)and 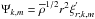 . This is a generalisation of the result obtained by Schatzman (1993b) and Zahn et al. (1997) in the non-rotating and non-magnetic case where σM and Λk,m(νM;m) replace σ and l(l + 1), l being the orbital number of the classical spherical harmonics. Since Fr = σ/N ≪ 1, the J.W.K.B. approximation can be adopted (cf. Press 1981; Schatzman 1993b; Zahn et al. 1997; Sect. 2.2.3). Applying it to Eq. (58), we obtain5
. This is a generalisation of the result obtained by Schatzman (1993b) and Zahn et al. (1997) in the non-rotating and non-magnetic case where σM and Λk,m(νM;m) replace σ and l(l + 1), l being the orbital number of the classical spherical harmonics. Since Fr = σ/N ≪ 1, the J.W.K.B. approximation can be adopted (cf. Press 1981; Schatzman 1993b; Zahn et al. 1997; Sect. 2.2.3). Applying it to Eq. (58), we obtain5![\begin{equation} {\xi}_{r;k,m}^{'}\!=\!\frac{{\mathcal E}_{k,m}\left(r\right)}{\sigma_{s}}\exp\left[{\rm i}\,\Phi_{k,m}\left(r\right)\right]\quad\hbox{with}\quad\Phi_{k,m}\left(r\right)\!=\!\int_{r}^{\,r_{c}}k_{V;k,m}\,{\rm d}r{'}, \label{JWKB1} \end{equation}](/articles/aa/full_html/2012/04/aa18322-11/aa18322-11-eq245.png) (61)where the amplitude function is given by
(61)where the amplitude function is given by 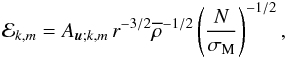 (62)Au;k,m being related to the wave-velocity amplitude at r = rc, which has to be obtained using excitation models (see for example Rogers & Glatzmaier 2006; Belkacem et al. 2009; Rogers & MacGregor 2011; Brun et al. 2011, for the stochastic turbulent excitation by convective movements and Zahn 1975; Goldreich & Nicholson 1989b; Ogilvie & Lin 2004; Ogilvie & Lin 2007, for the description of a tidal excitation). Then, we derive ξ, u, b and Π. First, we obtain
(62)Au;k,m being related to the wave-velocity amplitude at r = rc, which has to be obtained using excitation models (see for example Rogers & Glatzmaier 2006; Belkacem et al. 2009; Rogers & MacGregor 2011; Brun et al. 2011, for the stochastic turbulent excitation by convective movements and Zahn 1975; Goldreich & Nicholson 1989b; Ogilvie & Lin 2004; Ogilvie & Lin 2007, for the description of a tidal excitation). Then, we derive ξ, u, b and Π. First, we obtain ![\begin{equation} \vec\xi =\sum_{j=\left\{r,\theta,\varphi\right\}}\left[\sum_{\sigma,m,k}\xi_{j;k,m}\left(\vec r,t\right)\right]{\widehat {\vec e}}_{j}, \label{xiAd} \end{equation}](/articles/aa/full_html/2012/04/aa18322-11/aa18322-11-eq251.png) (63)where
(63)where ![\begin{equation} \xi_{j;k,m}={\mathcal R}_{\rm e}\left[{\underline\xi}_{j;k,m}\left(\vec r,t\right)\right] \end{equation}](/articles/aa/full_html/2012/04/aa18322-11/aa18322-11-eq252.png) (64)with
(64)with ![\begin{eqnarray} {\underline \xi}_{r;k,m}&=&\frac{{\mathcal E}_{k,m}\left(r\right)}{\sigma_{s}}\exp\left[{\rm i}\,\Phi_{k,m}\left(r\right)\right]\nonumber\\ & &\times\,\Theta_{k,m}\left(\cos\theta;\nu_{{\rm M};m}\right)\exp\left({\rm i}m\varphi\right)\exp\left({\rm i}\sigma t\right), \end{eqnarray}](/articles/aa/full_html/2012/04/aa18322-11/aa18322-11-eq253.png) (65)
(65)![\begin{eqnarray} {\underline\xi}_{\theta;k,m}&=&-{\rm i}\frac{r\,k_{V;k,m}}{\Lambda_{k,m}\left(\nu_{{\rm M};m}\right)}\frac{{\mathcal E}_{k,m}\left(r\right)}{\sigma_{s}}\exp\left[{\rm i}\,\Phi_{k,m}\left(r\right)\right]\nonumber\\ & &\times\,{\mathcal H}_{k,m}^{\theta}\left(\cos\theta;\nu_{{\rm M};m}\right)\exp\left({\rm i}m\varphi\right)\exp\left({\rm i}\sigma t\right), \end{eqnarray}](/articles/aa/full_html/2012/04/aa18322-11/aa18322-11-eq254.png) (66)
(66)![\begin{eqnarray} {\underline\xi}_{\varphi;k,m}&=&\frac{r\,k_{V;k,m}}{\Lambda_{k,m}\left(\nu_{{\rm M};m}\right)}\frac{{\mathcal E}_{k,m}\left(r\right)}{\sigma_{s}}\exp\left[{\rm i}\,\Phi_{k,m}\left(r\right)\right]\nonumber\\ & &\times\,{\mathcal H}_{k,m}^{\varphi}\left(\cos\theta;\nu_{{\rm M};m}\right)\exp\left({\rm i}m\varphi\right)\exp\left({\rm i}\sigma t\right). \end{eqnarray}](/articles/aa/full_html/2012/04/aa18322-11/aa18322-11-eq255.png) (67)Next, we derive from Eqs. (33, 34)
(67)Next, we derive from Eqs. (33, 34) ![\begin{equation} \vec u=\sum_{j=\left\{r,\theta,\varphi\right\}}\left[\sum_{\sigma,m,k}u_{j;k,m}\left({\vec r},t\right)\right]{\widehat {\vec e}}_{j}, \label{uAd} \end{equation}](/articles/aa/full_html/2012/04/aa18322-11/aa18322-11-eq256.png) (68)where
(68)where ![\begin{equation} u_{j;k,m}={\mathcal R}_{\rm e}\left[{\underline u}_{j;k,m}\left(\vec r,t\right)\right]={\mathcal R}_{\rm e}\left[{\rm i}\,\sigma_{s}\,{\underline\xi}_{j;k,m}\right] \end{equation}](/articles/aa/full_html/2012/04/aa18322-11/aa18322-11-eq257.png) (69)and
(69)and ![\begin{equation} \vec b=\sum_{j=\left\{r,\theta,\varphi\right\}}\left[\sum_{\sigma,m,k}b_{j;k,m}\left({\vec r},t\right)\right]{\widehat {\vec e}}_{j}, \label{bAd} \end{equation}](/articles/aa/full_html/2012/04/aa18322-11/aa18322-11-eq258.png) (70)where
(70)where ![\begin{equation} b_{j;k,m}={\mathcal R}_{\rm e}\left[{\underline b}_{j;k,m}\left(\vec r,t\right)\right]={\mathcal R}_{\rm e}\left[{\rm i}\,m\sqrt{\mu\,{\overline\rho}}\,\omega_{\rm A}\,{\underline\xi}_{j;k,m}\right]. \end{equation}](/articles/aa/full_html/2012/04/aa18322-11/aa18322-11-eq259.png) (71)Finally, we obtain using Eqs. (55) & (57) in the anelastic approximation regime
(71)Finally, we obtain using Eqs. (55) & (57) in the anelastic approximation regime 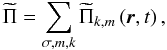 (72)where
(72)where ![\begin{equation} {\widetilde\Pi}_{k,m}={\mathcal R}_{\rm e}\left[{\widetilde{\underline\Pi}}_{k,m}\left(\vec r,t\right)\right] \end{equation}](/articles/aa/full_html/2012/04/aa18322-11/aa18322-11-eq261.png) (73)with
(73)with ![\begin{eqnarray} {\widetilde{\underline\Pi}}_{k,m}&=&-{\rm i}\,{\overline\rho}\frac{N^2}{k_{V;k,m}}\frac{{\mathcal E}_{k,m}\left(r\right)}{\sigma_s}\exp\left[{\rm i}\,\Phi_{k,m}\left(r\right)\right]\nonumber\\ &&\times\,\Theta_{k,m}\left(\cos\theta;\nu_{{\rm M};m}\right)\exp\left({\rm i} m \varphi\right)\exp\left({\rm i}\sigma t\right). \label{PiAd} \end{eqnarray}](/articles/aa/full_html/2012/04/aa18322-11/aa18322-11-eq262.png) (74)Since we have given the MGI wave structure, we have now to isolate related properties, which will modify the associated transport of angular momentum.
(74)Since we have given the MGI wave structure, we have now to isolate related properties, which will modify the associated transport of angular momentum.
2.4.3. Adiabatic wave properties
Pro- and retrograde adiabatic wave propagation
In Eqs. (45, 53, 54), we have ℒνM;m ≠ ℒνM; − m, 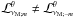 , and
, and 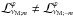 . This means that Hough functions and associated ones are different for pro- and retrograde waves, i.e. Θk,m(x;νM;m) ≠ Θk, − m(x;νM; − m),
. This means that Hough functions and associated ones are different for pro- and retrograde waves, i.e. Θk,m(x;νM;m) ≠ Θk, − m(x;νM; − m), 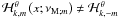 (x;νM; − m), and
(x;νM; − m), and 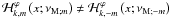 (as illustrated in Fig. 3). Moreover, we can see that where the MHD TA has to be carefully examined (i.e. when |νM;m| ≥ 1), the associated MGI wave equatorial trapping will be different for pro- and retrograde waves. Indeed, in the present case where ωA and thus ΛE are taken uniform, Eq. (21) gives θc;m ≠ θc; − m with νM;m > 0 < νM;m < 0 and thus θc;m > 0 < θc;m < 0, which means that prograde waves are more trapped than retrograde ones because of the action of the Lorentz force, as shown in Fig. 4. Therefore, the combined action of the Coriolis and the Lorentz force induces a net difference in the horizontal spatial structure of pro- and retrograde waves. The energy transmission of the excitation mechanism (i.e. the stochastic excitation by turbulent convective regions, the κ-mechanism in classical pulsators if we study the transport of angular momentum by MGI modes, and the tidal potential if there is a close companion) will be transmitted differentially as a function of the sign of m. In particular, if ΛE is constant, the Lorentz force allows a better transmission to retrograde waves. Consequences for the resulting angular momentum transport will be discussed in Sect. 3.1.
(as illustrated in Fig. 3). Moreover, we can see that where the MHD TA has to be carefully examined (i.e. when |νM;m| ≥ 1), the associated MGI wave equatorial trapping will be different for pro- and retrograde waves. Indeed, in the present case where ωA and thus ΛE are taken uniform, Eq. (21) gives θc;m ≠ θc; − m with νM;m > 0 < νM;m < 0 and thus θc;m > 0 < θc;m < 0, which means that prograde waves are more trapped than retrograde ones because of the action of the Lorentz force, as shown in Fig. 4. Therefore, the combined action of the Coriolis and the Lorentz force induces a net difference in the horizontal spatial structure of pro- and retrograde waves. The energy transmission of the excitation mechanism (i.e. the stochastic excitation by turbulent convective regions, the κ-mechanism in classical pulsators if we study the transport of angular momentum by MGI modes, and the tidal potential if there is a close companion) will be transmitted differentially as a function of the sign of m. In particular, if ΛE is constant, the Lorentz force allows a better transmission to retrograde waves. Consequences for the resulting angular momentum transport will be discussed in Sect. 3.1.
Vertical wave group and phase velocities
Next, the associated monochromatic vertical wave group velocity is given by 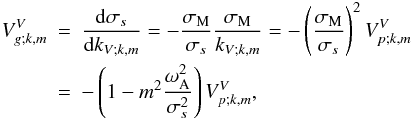 (75)where
(75)where 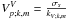 is the monochromatic wave phase velocity in solar-type stars (in massive stars, signs are inverted). First, once again we isolate the vertical trapping of MGI waves as soon as
is the monochromatic wave phase velocity in solar-type stars (in massive stars, signs are inverted). First, once again we isolate the vertical trapping of MGI waves as soon as 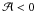 . Moreover, note that this result is the generalisation for of a deep stably stratified spherical shell as the one obtained by Kim & MacGregor (2003) for a reduced 2D Cartesian model of the solar tachocline.
. Moreover, note that this result is the generalisation for of a deep stably stratified spherical shell as the one obtained by Kim & MacGregor (2003) for a reduced 2D Cartesian model of the solar tachocline.
Wave classification under the MHD TA
Under the MHD TA (as long as |νM;m| < 1), four types of MGI waves can be identified (see Townsend 2003; Mathis et al. 2008, and references therein in the hydrodynamical case):
-
Class I waves are internal gravity waves, which exist in the non-rotating and in the non-magnetic cases, which are modified both by the Coriolis acceleration and the Lorentz force. Their eigenvalue (Λk,m), and hence their radial wave number,
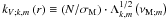 /r, are increased. These waves are also called magneto-Poincaré waves (see Zaqarashvili et al. 2009; Heng & Spitovsky 2009).
/r, are increased. These waves are also called magneto-Poincaré waves (see Zaqarashvili et al. 2009; Heng & Spitovsky 2009). -
Class II waves are purely retrograde waves (m > 0), which only exist for |νM;m| high-values. Their dynamics is driven by the conservation of the specific vorticity combined with the effects of curvature and by the Lorentz force. However, since |νM;m| ≥ 1 in this case, they cannot be treated using the MHD TA. In the hydrodynamical case, they are called “quasi-inertial” waves, which corresponds to the geophysical Rossby waves (see Provost et al. 1981). These magneto-Rossby waves have recently been studied by Zaqarashvili et al. (2007, 2009), and Heng & Spitovsky (2009) in the limit of a thin stratified layer.
-
Class III waves are mixed class I and class II waves. m ≤ 0 waves exist in the absence of rotation and of magnetic field. m > 0 appear when νM;m = m + 1 with low eigenvalues while their horizontal eigenfunctions are
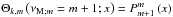 . When they appear and have low eigenvalues, they behave mostly like class II waves; m ≤ 0 and m > 0 waves with high eigenvalues behave instead like class I waves. Their eigenvalues are much lower than those of class I waves. Thus, they have a lower vertical wave number. They may be identified with the geophysical Yanai waves (Yanai & Maruyama 1966).
. When they appear and have low eigenvalues, they behave mostly like class II waves; m ≤ 0 and m > 0 waves with high eigenvalues behave instead like class I waves. Their eigenvalues are much lower than those of class I waves. Thus, they have a lower vertical wave number. They may be identified with the geophysical Yanai waves (Yanai & Maruyama 1966). -
Class IV waves are purely prograde waves (m < 0) whose characteristics change little with νM;m, their displacement in the θ direction being very small. Their dynamics is driven by the conservation of the specific vorticity combined with the stratification effects and by the Lorentz force; their eigenvalues are lower than those of both class I and class III waves. Hence, their vertical wave number is lower. In the hydrodynamical case, they may be identified with the geophysical Kelvin waves (Pedlosky 1998).
 |
Fig. 4 Top: θc;m as a function of Ro and ΛE for non-axisymmetric retrograde (m = 1) and prograde (m = −1) waves. On one hand, the corner region for which Ro ≤ ΛE/2 corresponds to the |
2.5. The dissipative propagation
2.5.1. The radiative damping
To be able to treat the net transport of angular momentum, we have now to study the dissipative propagation of internal waves (Goldreich & Nicholson 1989a). If they are modified by the Coriolis acceleration and the Lorentz force, they are subject to radiative, viscous, and Ohmic dissipations. To evaluate their relative orders of magnitude, we therefore introduce the Prandtl and Roberts numbers 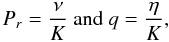 (76)which compare the heat diffusion to the viscous and the Ohmic diffusions (cf. Table 1). We recall that ν, η, and K are the viscosity and the magnetic and radiative diffusivities, respectively. From now on, we adopt the hypothesis that Pr ≪ 1 and q ≪ 1, which can be justified for example if we look at the solar radiative core case, as done by Brun & Zahn (2006); these authors showed that for the Sun Pr ∝ 10-4 and q ∝ 10-6, which justifies our assumption. Therefore, radiative damping is the dominant dissipative mechanism for MGI waves and we can neglect the viscous and the Ohmic terms in the momentum and heat transport equations (Eqs. (2–4)).
(76)which compare the heat diffusion to the viscous and the Ohmic diffusions (cf. Table 1). We recall that ν, η, and K are the viscosity and the magnetic and radiative diffusivities, respectively. From now on, we adopt the hypothesis that Pr ≪ 1 and q ≪ 1, which can be justified for example if we look at the solar radiative core case, as done by Brun & Zahn (2006); these authors showed that for the Sun Pr ∝ 10-4 and q ∝ 10-6, which justifies our assumption. Therefore, radiative damping is the dominant dissipative mechanism for MGI waves and we can neglect the viscous and the Ohmic terms in the momentum and heat transport equations (Eqs. (2–4)).
Next, as was described for the first time by Press (1981) (see also Schatzman 1993b; Zahn et al. 1997), we here assume the quasi-adiabatic approximation in which dissipative processes are only a correction of the purely adiabatic case. Then, the results obtained in the previous section concerning the geometrical structure of adiabatic MGI waves apply also to their dissipative propagation. Indeed, all scalar quantities X = {ρ,P,Φ,T,μc} and the vector fields x = {u,ξ,b} are still expanded on Hough functions Θk,m(cosθ;νM;m) and their associated functions 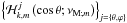 (the MHD TA is assumed) and on Fourier series in t and ϕ. Moreover, as in the end of Sect. 2.4.2, we consider low-frequency internal waves for which the Cowling, the anelastic, and the JWKB approximations can be adopted.
(the MHD TA is assumed) and on Fourier series in t and ϕ. Moreover, as in the end of Sect. 2.4.2, we consider low-frequency internal waves for which the Cowling, the anelastic, and the JWKB approximations can be adopted.
Under these assumptions, the heat equation given in Eq. (4) becomes 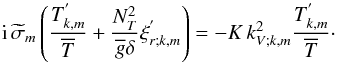 (77)Then, assuming the anelastic approximation (i.e. the term
(77)Then, assuming the anelastic approximation (i.e. the term 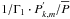 is neglected), the linearised equation of state (cf. Eq. (9)) is introduced
is neglected), the linearised equation of state (cf. Eq. (9)) is introduced 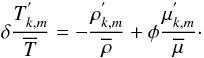 (78)Moreover, the fluctuations of the mean molecular weight are expressed following Zahn et al. (1997; see also Eq. (40))
(78)Moreover, the fluctuations of the mean molecular weight are expressed following Zahn et al. (1997; see also Eq. (40)) 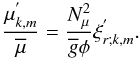 (79)Using Eqs. (78) and (79), the energy equation (Eq. (77)) is thus written in its final form
(79)Using Eqs. (78) and (79), the energy equation (Eq. (77)) is thus written in its final form 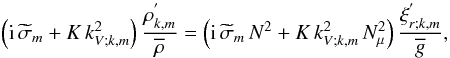 (80)where
(80)where 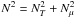 and the JWKB vertical wave number (kV;k,m) introduced in Eq. (61) is now complex because of the dissipation.
and the JWKB vertical wave number (kV;k,m) introduced in Eq. (61) is now complex because of the dissipation.
If we now introduce the continuity and vertical momentum equations in the JWKB approximation, we obtain 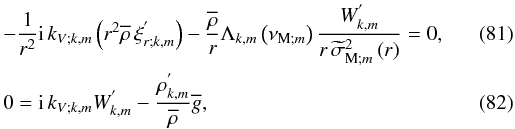 where have defined
where have defined 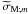 such that
such that 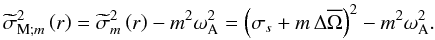 (83)Then, the following equation is obtained for {kV;k,m}
(83)Then, the following equation is obtained for {kV;k,m} 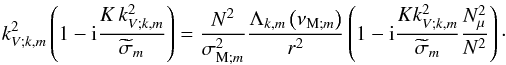 (84)Assuming, as described previously, the quasi-adiabatic approximation where the dissipation is a correction of the adiabatic case, this can be linearised and we finally obtain
(84)Assuming, as described previously, the quasi-adiabatic approximation where the dissipation is a correction of the adiabatic case, this can be linearised and we finally obtain ![\begin{equation} k_{V;k,m}=\left[\frac{N}{{\widetilde\sigma}_{{\rm M};m}}\frac{\Lambda_{k,m}^{1/2}\left(\nu_{{\rm M};m}\right)}{r}\right]+{\rm i}\left[\frac{K}{2}\frac{N_{T}^2\,N}{{\widetilde\sigma}_m\,{\widetilde\sigma}_{{\rm M};m}^3}\frac{\Lambda_{k,m}^{3/2}\left(\nu_{{\rm M};m}\right)}{r^3}\right]\cdot \label{kvDiss} \end{equation}](/articles/aa/full_html/2012/04/aa18322-11/aa18322-11-eq316.png) (85)The radiative damping rate is then defined as
(85)The radiative damping rate is then defined as 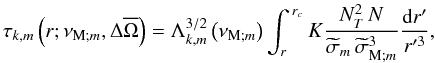 (86)with the corresponding characteristics damping length (see also Kim & MacGregor 2003)
(86)with the corresponding characteristics damping length (see also Kim & MacGregor 2003) 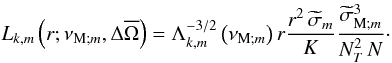 (87)
(87)
Properties of the radiative damping
Now, we can study the radiative damping properties. First, because it is proportional to 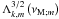 , it depends on |νM;m| as shown in Fig. 3. For class I and III waves, it grows with νM;m, which leads to a damping closer to the excitation region. Next, prograde class IV waves have a different behaviour and are able to deposit their positive angular momentum farther away from the convection zones. Moreover, it grows with the degree k and thus, as in the non-rotating non-magnetic case, high-degree waves are damped closer to the excitation region than low-degree ones. Next, we have Λk, − m(νM; − m) ≠ Λk,m(νM;m). Then, the combined action of the Coriolis acceleration and the Lorentz force creates a bias between pro- and retrograde waves that does not exist in the non-rotating and non-magnetic case. This is a direct consequence of the different geometrical properties of pro- and retrograde waves for a given k as described in Sect. 2.4.3. If we now look at the frequency dependence of the damping, we see that this varies as
, it depends on |νM;m| as shown in Fig. 3. For class I and III waves, it grows with νM;m, which leads to a damping closer to the excitation region. Next, prograde class IV waves have a different behaviour and are able to deposit their positive angular momentum farther away from the convection zones. Moreover, it grows with the degree k and thus, as in the non-rotating non-magnetic case, high-degree waves are damped closer to the excitation region than low-degree ones. Next, we have Λk, − m(νM; − m) ≠ Λk,m(νM;m). Then, the combined action of the Coriolis acceleration and the Lorentz force creates a bias between pro- and retrograde waves that does not exist in the non-rotating and non-magnetic case. This is a direct consequence of the different geometrical properties of pro- and retrograde waves for a given k as described in Sect. 2.4.3. If we now look at the frequency dependence of the damping, we see that this varies as ![\hbox{${\widetilde\sigma}_{m} \,{\widetilde\sigma}_{{\rm M};m}^3= [\sigma_{s}+m\,\Delta{\overline\Omega} ] [ (\sigma_{s}+m\, \Delta{\overline\Omega} )^2-m^2\omega_{\rm A}^2 ]^{3/2}$}](/articles/aa/full_html/2012/04/aa18322-11/aa18322-11-eq322.png) , which reduces to
, which reduces to 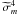 in the non-magnetic case. As we can see, the magnetic term depends on m2. Consequently, the property known in the non-magnetic case, i.e. that prograde waves are damped closer to the excitation region than retrograde ones, is unchanged because
in the non-magnetic case. As we can see, the magnetic term depends on m2. Consequently, the property known in the non-magnetic case, i.e. that prograde waves are damped closer to the excitation region than retrograde ones, is unchanged because 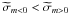 and thus
and thus 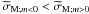 . However, if we now look at the presence and the position of critical layers (see Booker & Bretherton 1967; Barker 2011), we see that the situation becomes more complex when the magnetic field is taken into account. Indeed, if we obtain the usual critical layer for which
. However, if we now look at the presence and the position of critical layers (see Booker & Bretherton 1967; Barker 2011), we see that the situation becomes more complex when the magnetic field is taken into account. Indeed, if we obtain the usual critical layer for which 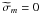 , the magnetic field leads to the onset of two supplementary ones for which
, the magnetic field leads to the onset of two supplementary ones for which 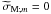 and thus
and thus 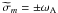 . There, internal waves also exchange energy and momentum with the medium (Rudraiah & Venkatachalappa 1972a,b,c; Barker & Lindzen 1985; MacGregor & Rogers 2011).
. There, internal waves also exchange energy and momentum with the medium (Rudraiah & Venkatachalappa 1972a,b,c; Barker & Lindzen 1985; MacGregor & Rogers 2011).
2.5.2. The quasi-adiabatic wave velocity, magnetic and pressure fields
As shown in the previous section, the vertical wave number in the JWKB approximation becomes complex in the dissipative case that allows the net transport of angular momentum by internal waves. To be able to calculate the energy and the angular momentum vertical fluxes, we therefore have to give the final form of the wave velocity, magnetic and pressure fields.
To achieve this aim we introduce the result obtained in Eq. (85) and in Eqs. (68, 74, 70) using Eq. (63). This leads to the following expression for the internal wave velocity field in the quasi-adiabatic approximation: ![\begin{equation} \vec u=\sum_{j=\left\{r,\theta,\varphi\right\}}\left[\sum_{\sigma,m,k}u_{j;k,m}\left(\vec r,t\right)\right]{\widehat {\vec e}}_{j}, \label{uDiss} \end{equation}](/articles/aa/full_html/2012/04/aa18322-11/aa18322-11-eq330.png) (88)where
(88)where ![\begin{eqnarray} u_{r;k,m}& \,=\, &-{\mathcal E}_{k,m}\left(r\right)\,\Theta_{k,m}\left(\cos\theta;\nu_{{\rm M};m}\right)\sin\left[\zeta_{k,m}\left(r,\varphi,t\right)\right]\nonumber\\ & &\times\exp\left[-\frac{\tau_{k,m}\left(r;\nu_{{\rm M};m},\Delta{\overline\Omega}\right)}{2}\right], \end{eqnarray}](/articles/aa/full_html/2012/04/aa18322-11/aa18322-11-eq331.png) (89)
(89)![\begin{eqnarray} u_{\theta;k,m}& \,=\, &\frac{r\,k_{V;k,m}}{\Lambda_{k,m}\left(\nu_{{\rm M};m}\right)}\,{\mathcal E}_{k,m}\left(r\right)\mathcal H_{k,m}^{\theta}\left(\cos\theta;\nu_{{\rm M};m}\right)\cos\left[\zeta_{k,m}\left(r,\varphi,t\right)\right]\nonumber\\ & &\times\exp\left[-\frac{\tau_{k,m}\left(r;\nu_{{\rm M};m},\Delta{\overline\Omega}\right)}{2}\right], \end{eqnarray}](/articles/aa/full_html/2012/04/aa18322-11/aa18322-11-eq332.png) (90)
(90)![\begin{eqnarray} u_{\varphi;k,m}& \,= \, &-\frac{r\,k_{V;k,m}}{\Lambda_{k,m}\left(\nu_{{\rm M};m}\right)}\,{\mathcal E}_{k,m}\left(r\right)\mathcal H_{k,m}^{\varphi}\left(\cos\theta;\nu_{{\rm M};m}\right)\sin\left[\zeta_{k,m}\left(r,\varphi,t\right)\right]\nonumber\\ & &\times\exp\left[-\frac{\tau_{k,m}\left(r;\nu_{{\rm M};m},\Delta{\overline\Omega}\right)}{2}\right] ; \end{eqnarray}](/articles/aa/full_html/2012/04/aa18322-11/aa18322-11-eq333.png) (91)ℰk,m is given in Eq. (62). Moreover, kV;k,m is the adiabatic vertical wave number (Eq. (60)) and τk,m the radiative damping (Eq. (86)). Finally, the phase function ζk,m is written
(91)ℰk,m is given in Eq. (62). Moreover, kV;k,m is the adiabatic vertical wave number (Eq. (60)) and τk,m the radiative damping (Eq. (86)). Finally, the phase function ζk,m is written 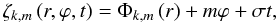 (92)where Φk,m is defined in Eq. (61).
(92)where Φk,m is defined in Eq. (61).
Then, we obtain the total pressure wave fluctuation using Eq. (74) 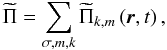 (93)where
(93)where ![\begin{eqnarray} \widetilde \Pi_{k,m}&\,=\,&{\overline\rho}\,N^2\frac{{\mathcal E}_{k,m}\left(r\right)}{\sigma_s\,k_{V;k,m}}\,\Theta_{k,m}\left(\cos\theta;\nu_{{\rm M};m}\right)\sin\left[\zeta_{k,m}\left(r,\varphi,t\right)\right]\nonumber\\ &&\times\exp\left[-\frac{\tau_{k,m}\left(r;\nu_{{\rm M};m},\Delta{\overline\Omega}\right)}{2}\right]\cdot \end{eqnarray}](/articles/aa/full_html/2012/04/aa18322-11/aa18322-11-eq340.png) (94)Finally, using Eqs. (70–68), we obtain the wave magnetic field
(94)Finally, using Eqs. (70–68), we obtain the wave magnetic field ![\begin{equation} \vec b=\sum_{j=\left\{r,\theta,\varphi\right\}}\left[\sum_{\sigma,m,k}b_{j;k,m}\left(\vec r,t\right)\right]{\widehat{\vec e}}_{j} \label{bDiss} \end{equation}](/articles/aa/full_html/2012/04/aa18322-11/aa18322-11-eq341.png) (95)with
(95)with 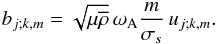 (96)We have now derived the complete expressions for the wave velocity and magnetic fields and the total pressure. It is important to summarise the main results. First, we studied the “weak differential rotation case” for which
(96)We have now derived the complete expressions for the wave velocity and magnetic fields and the total pressure. It is important to summarise the main results. First, we studied the “weak differential rotation case” for which 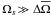 (cf. Eq. (13)). In this case, we can assume that the impact of the differential rotation (
(cf. Eq. (13)). In this case, we can assume that the impact of the differential rotation (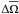 ) on the adiabatic structure of the wave and their equatorial trapping is weak and can be neglected in a first step. However, we know from the theory of angular momentum transport by internal waves that their damping depends in a crucial way on their retrograde or prograde behaviour with respect to the rotation of the excitation region (which is here Ωs) because of the Doppler effect. This is the reason why we retain
) on the adiabatic structure of the wave and their equatorial trapping is weak and can be neglected in a first step. However, we know from the theory of angular momentum transport by internal waves that their damping depends in a crucial way on their retrograde or prograde behaviour with respect to the rotation of the excitation region (which is here Ωs) because of the Doppler effect. This is the reason why we retain 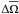 (which is therefore the differential rotation with respect to the excitation region) in the description of the radiative damping as in the hydrodynamical case described in Mathis et al. (2008). The different Doppler shift for prograde and retrograde waves, combined with their different geometrical properties, then drives the net transport of angular momentum by MGI waves.
(which is therefore the differential rotation with respect to the excitation region) in the description of the radiative damping as in the hydrodynamical case described in Mathis et al. (2008). The different Doppler shift for prograde and retrograde waves, combined with their different geometrical properties, then drives the net transport of angular momentum by MGI waves.
Since the MGI wave dynamics has been treated taking dissipative processes into account, we can now evaluate the induced transport of angular momentum and study its characteristics as a function of the value of the mean rotation rate (Ωs) and the intensity of the axisymmetric toroidal field (related to ωA).
3. The transport of angular momentum
3.1. The vertical transport of angular momentum by MGI waves
3.1.1. The monochromatic vertical transports of energy and angular momentum
Here, we follow the method that was applied for example by Kim & MacGregor (2003) to their reduced 2D Cartesian model of the magnetised solar tachocline, to derive the vertical transports of energy and angular momentum for a deep stably stratified spherical shell. First, taking the scalar product of the linearised Eulerian momentum equation with u and those of the linearised induction equation with b, we obtain the equation that rules the transport of the waves’ total energy 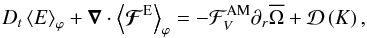 (97)where
(97)where 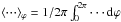 while
while 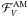 and
and 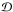 are respectively the vertical flux of angular momentum and the terms related to dissipative processes (see Grimshaw 1984). The waves’ total energy is the sum of their kinetic energy
are respectively the vertical flux of angular momentum and the terms related to dissipative processes (see Grimshaw 1984). The waves’ total energy is the sum of their kinetic energy 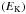 , magnetic energy
, magnetic energy 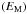 , and potential energy related to buoyancy
, and potential energy related to buoyancy 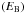
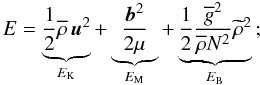 (98)moreover, we introduce the vectorial waves’ energy flux
(98)moreover, we introduce the vectorial waves’ energy flux 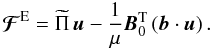 (99)From now on, we follow the general method given by Grimshaw (1975) and references therein (see also Andrews & McIntyre 1978). First, we introduce the wave action density (cf. Bretherton 1966)
(99)From now on, we follow the general method given by Grimshaw (1975) and references therein (see also Andrews & McIntyre 1978). First, we introduce the wave action density (cf. Bretherton 1966) 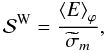 (100)which is conserved in the adiabatic case as is shown by the following conservation equation
(100)which is conserved in the adiabatic case as is shown by the following conservation equation 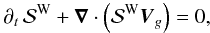 (101)with the wave group velocity:
(101)with the wave group velocity: 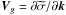 . Then, the energy flux is expressed as a function of Vg and ⟨E⟩ϕ as
. Then, the energy flux is expressed as a function of Vg and ⟨E⟩ϕ as 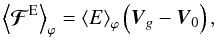 (102)where
(102)where 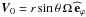 (cf. Eq. (11)). Finally, the vertical flux of angular momentum is identified as a function of the wave action density and group velocity, which gives
(cf. Eq. (11)). Finally, the vertical flux of angular momentum is identified as a function of the wave action density and group velocity, which gives 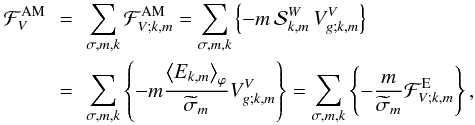 (103)where
(103)where 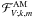 ,
, 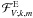 ,
, 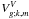 ,
, 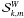 , Ek,m are the monochromatic vertical fluxes of angular momentum and energy, the vertical group velocity, the wave action, and the total energy for given degrees {k,m}, respectively.
, Ek,m are the monochromatic vertical fluxes of angular momentum and energy, the vertical group velocity, the wave action, and the total energy for given degrees {k,m}, respectively.
We are now ready to derive 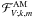 as a function of the system parameters. First, we consider the monochromatic flux of energy in the vertical direction:
as a function of the system parameters. First, we consider the monochromatic flux of energy in the vertical direction: 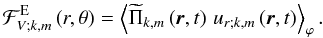 (104)Then, we define the usual monochromatic Eulerian vertical Reynolds stresses
(104)Then, we define the usual monochromatic Eulerian vertical Reynolds stresses 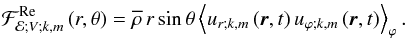 (105)Moreover, we define the monochromatical Eulerian vertical Maxwell stresses associated to the fluctuating wave magnetic field (b)
(105)Moreover, we define the monochromatical Eulerian vertical Maxwell stresses associated to the fluctuating wave magnetic field (b) 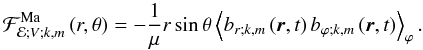 (106)Using Eq. (95), this becomes for the purely axisymmetric toroidal field
(106)Using Eq. (95), this becomes for the purely axisymmetric toroidal field ![\begin{equation} {\mathcal F}_{{\mathcal E};V;k,m}^{\rm Ma}=-m^2\frac{\omega_{\rm A}^2}{\sigma_s^2}\left[\overline\rho\,r\sin\theta\left<u_{r;k,m}u_{\varphi;k,m}\right>_{\varphi}\right]=-m^2\frac{\omega_{\rm A}^2}{\sigma_s^2}{\mathcal F}_{{\mathcal E};V;k,m}^{\rm Re}. \end{equation}](/articles/aa/full_html/2012/04/aa18322-11/aa18322-11-eq370.png) (107)Then, we can note that Maxwell stresses act against Reynolds ones with this magnetic configuration. This effect grows as
(107)Then, we can note that Maxwell stresses act against Reynolds ones with this magnetic configuration. This effect grows as 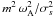 , and as was already identified previously in our discussion of the vertical group velocity and the radiative damping, we will have
, and as was already identified previously in our discussion of the vertical group velocity and the radiative damping, we will have 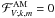 when
when 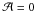 (cf. Eqs. (75, 86, 103)).
(cf. Eqs. (75, 86, 103)).
Let us now indentify the MGI wave action, which is conserved in the adiabatic case, and deduce the associated transport of angular momentum. Let us first examine the azimuthal component of the momentum equation (Eq. (35)); assuming the MHD TA, this is written 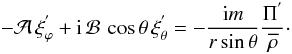 (108)Multiplying this by
(108)Multiplying this by ![\hbox{$i\,\sigma_s\,\overline\rho\,r\sin\theta \exp\left[{\rm i}m\varphi\right] \exp\left[{\rm i}\sigma t\right]$}](/articles/aa/full_html/2012/04/aa18322-11/aa18322-11-eq375.png) , we obtain for a given k
, we obtain for a given k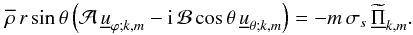 (109)Next, this is multiplied by
(109)Next, this is multiplied by 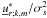 where ∗ is the complex conjugate and we identify the equation for the fluxes defined in Eqs. (104, 105, 106):
where ∗ is the complex conjugate and we identify the equation for the fluxes defined in Eqs. (104, 105, 106): 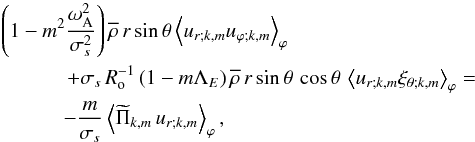 (110)which we put in its final form
(110)which we put in its final form 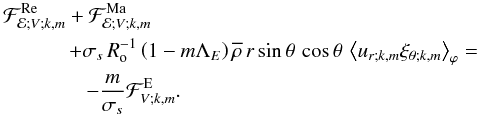 (111)Thus, we can identify the total action of angular momentum
(111)Thus, we can identify the total action of angular momentum  (112)which is conserved in the adiabatic case (see for example Goldreich & Nicholson 1989a), where
(112)which is conserved in the adiabatic case (see for example Goldreich & Nicholson 1989a), where 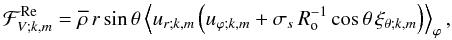 (113)and
(113)and 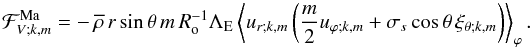 (114)In the non-magnetic case (ΛE = 0), the result obtained in Pantillon et al. (2007) and Mathis et al. (2008) is recovered.
(114)In the non-magnetic case (ΛE = 0), the result obtained in Pantillon et al. (2007) and Mathis et al. (2008) is recovered.
3.1.2. The total action (luminosity) of angular momentum
We thus obtain the total action of angular momentum transported by MGI waves in the vertical direction averaged on an isobar ![\begin{eqnarray} \overline{{\mathcal L}_{V}^{\rm AM}}\left(r\right)&\,=\,&\left<{\mathcal L}_{V}^{\rm AM}\right>_{\theta} \nonumber\\ &\,=\,&\sum_{\sigma,k,m}\overline{{\mathcal L}_{V;k,m}^{\rm AM}}\left(r_c;\nu_{{\rm M};m}\right)\exp\left[-\tau_{k,m}\left(r;\nu_{{\rm M};m},\Delta{\overline\Omega}\right)\right] ; \label{LVAMf} \end{eqnarray}](/articles/aa/full_html/2012/04/aa18322-11/aa18322-11-eq385.png) (115)its monochromatic value at the convection/radiation border is given by
(115)its monochromatic value at the convection/radiation border is given by 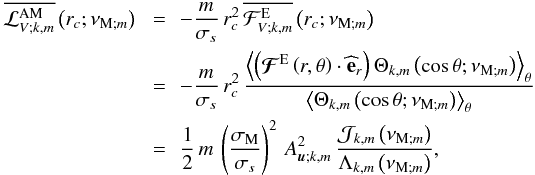 (116)where
(116)where 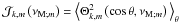 with ⟨···⟩θ = 1/2
with ⟨···⟩θ = 1/2 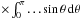 , and we recall the radiative damping expression
, and we recall the radiative damping expression 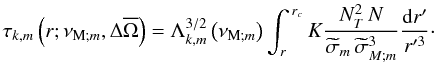 (117)MGI waves are thus excited at the convection/radiation border by the convective turbulent movements and the tidal potential if there is a close companion. At the level of this excitation region, the mean total action of angular momentum in the vertical direction has the same sign as those of the mean vertical component of the energy flux for prograde waves (m < 0), and the opposite sign for retrograde waves (m > 0). For example, for a solar-type star, prograde waves have a negative mean vertical flux of angular momentum that leads to a deposit of angular momentum in the radiative core, while we get the opposite for retrograde waves and consequently an extraction of angular momentum.
(117)MGI waves are thus excited at the convection/radiation border by the convective turbulent movements and the tidal potential if there is a close companion. At the level of this excitation region, the mean total action of angular momentum in the vertical direction has the same sign as those of the mean vertical component of the energy flux for prograde waves (m < 0), and the opposite sign for retrograde waves (m > 0). For example, for a solar-type star, prograde waves have a negative mean vertical flux of angular momentum that leads to a deposit of angular momentum in the radiative core, while we get the opposite for retrograde waves and consequently an extraction of angular momentum.
Then, two different filters act on MGI waves to modify the net amount of transported angular momentum. First, as discussed at the end of Sect. 2.5.1, the magnetic field filters internal waves for which 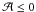 and Maxwell stresses act against Reynolds stresses as soon as the ratio
and Maxwell stresses act against Reynolds stresses as soon as the ratio  grows. Next, because of the modification of the horizontal extent of MGI waves propagation region by the Coriolis acceleration and the Lorentz force, the transmission of the excitation energy diminishes when |νM;m|, and thus θc;m, increases. Moreover, since Θk,m ≠ Θk, − m, and as a consequence θc;m ≠ θc; − m, this horizontal filter is different for prograde and retrograde waves. If we examine Fig. 4, we can see that the domain in the {Ro,ΛE} plane for which internal waves are trapped in an equatorial belt is larger for prograde waves than for retrograde waves. This is an interesting point, since this means that energy transmission will be more efficient for retrograde waves, leading to a net extraction of angular momentum in solar-type stars.
grows. Next, because of the modification of the horizontal extent of MGI waves propagation region by the Coriolis acceleration and the Lorentz force, the transmission of the excitation energy diminishes when |νM;m|, and thus θc;m, increases. Moreover, since Θk,m ≠ Θk, − m, and as a consequence θc;m ≠ θc; − m, this horizontal filter is different for prograde and retrograde waves. If we examine Fig. 4, we can see that the domain in the {Ro,ΛE} plane for which internal waves are trapped in an equatorial belt is larger for prograde waves than for retrograde waves. This is an interesting point, since this means that energy transmission will be more efficient for retrograde waves, leading to a net extraction of angular momentum in solar-type stars.
It is possible to quantify these combined actions of vertical and horizontal trappings by defining the following function ![\begin{eqnarray} {\mathcal P}_{m}\,&\,=\,&\underbrace{\left(\frac{\sigma_{\rm M}}{\sigma_{s}}\right)^{2}}_{\hbox{\small vertical trapping}}\underbrace{\left[\frac{1}{2\pi}\int_{\theta_{c;m}}^{\pi/2}\sin\theta\,{\rm d}\theta\int_{0}^{2\pi}{\rm d}\varphi\right]}_{\hbox{\small equatorial trapping}} \nonumber\\ &\,=\,&\,\left(1-\frac{m^2}{2}R_{\rm o}^{-1}\Lambda_{\rm E}\right)\left[\cos\theta_{c;m}\,{\rm H_e}\left(\vert\nu_{{\rm M};m}\vert-1\right)+{\rm H_e}\left(1-\vert\nu_{{\rm M};m}\vert\right)\right],\nonumber\\ \end{eqnarray}](/articles/aa/full_html/2012/04/aa18322-11/aa18322-11-eq395.png) (118)where He is the Heaviside function, which evaluates the surface where convective movements can transmit their energy to MGI waves for a given m. This corresponds to the spherical surface where MGI waves are propagative, normalised by the total sphere surface. This is shown in Fig. 5 for m = { − 2, − 1,1,2}. First, we see that in the non-magnetic case (ΛE = 0), we have
(118)where He is the Heaviside function, which evaluates the surface where convective movements can transmit their energy to MGI waves for a given m. This corresponds to the spherical surface where MGI waves are propagative, normalised by the total sphere surface. This is shown in Fig. 5 for m = { − 2, − 1,1,2}. First, we see that in the non-magnetic case (ΛE = 0), we have 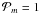 in the superinertial regime (Ro ≥ 1) while this discreases in the subinertial regime (Ro < 1) when the mean rotation rate increases. Next, we observe the combined effects of the vertical trapping and of the differential horizontal one (i.e. which depends on the sign of m, since θc;m > 0 < θc;m < 0) as soons as ΛE ≠ 0 with a stronger attenuation of
in the superinertial regime (Ro ≥ 1) while this discreases in the subinertial regime (Ro < 1) when the mean rotation rate increases. Next, we observe the combined effects of the vertical trapping and of the differential horizontal one (i.e. which depends on the sign of m, since θc;m > 0 < θc;m < 0) as soons as ΛE ≠ 0 with a stronger attenuation of 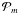 for prograde waves than for retrograde ones. Moreover, we identify the region where
for prograde waves than for retrograde ones. Moreover, we identify the region where 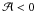 .
.
All these behaviours are summarised in Fig. 6 where the vertical magnetic trapping (identical for prograde and retrograde waves) and the equatorial one due to the Coriolis acceleration and the Lorentz force (stronger for prograde waves) are shown. The associated strength of the angular momentum transport (stronger for retrograde waves) for a same given excitation for prograde and retrograde waves is also represented.
 |
Fig. 5 Top left: |
In summary, the combined actions of the rotation and of the purely toroidal axisymmetric magnetic field modify internal waves propagation both in the vertical and in the horizontal directions and their radiative damping. Since the induced effects are not symmetric for prograde and retrograde waves, the net result on the amount of angular momentum transport 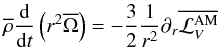 (119)is modified, as is the associated coupling time
(119)is modified, as is the associated coupling time 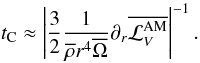 (120)The transport of angular momentum by MGI being now studied, we have to understand its couplings with the other dynamical processes in stellar radiation zones.
(120)The transport of angular momentum by MGI being now studied, we have to understand its couplings with the other dynamical processes in stellar radiation zones.
 |
Fig. 6 Synopsis of the structure and the induced transport of angular momentum in stars with an external and an internal convection zone. Convection and radiation zones are depicted in grey and orange. The short dashed blue lines represent the equatorial trapping due to the Coriolis acceleration and the Lorentz force and the purple long-dashed lines represent the vertical magnetic trapping. Finally, the vertical fluxes of energy and of angular momentum are represented by the thin dark grey arrow and the large green one. |
3.2. Secular transport in stellar interiors and the dynamical coupling of radiative and convective zones
Let us examine each step of the transport loop in radiative regions.
First, these are the seat of a large-scale flow, the so-called “meridional circulation” (Zahn 1992; Maeder & Zahn 1998; Mathis & Zahn 2004; Decressin et al. 2009), which is caused by external torques, structural adjustments during the star’s evolution, and internal Reynolds and Maxwell stresses. External torques are induced by stellar winds (magnetic for solar-type stars, radiatively-driven for massive stars) and tides, if there is a close companion close to the considered object (cf. the torque exerted on convective envelopes of solar-type stars due to the equilibrium tide; see Zahn 1966, 1989). If we consider a “shellular” rotation law, the meridional circulation is expanded in spherical harmonics as ![\begin{equation} {\vec {\mathcal U}}_{\rm M}\left(\vec r,t\right)=U_2\left(r\right)P_2\left(\cos\theta\right){\widehat {\vec e}}_r+\frac{1}{6{\overline\rho}r}\frac{{\rm d}}{{\rm d}r}\left[{\overline\rho} r^2 U_2\right]\frac{{\rm d}P_2\left(\cos\theta\right)}{{\rm d}\theta}\,{\widehat {\vec e}}_{\theta}, \end{equation}](/articles/aa/full_html/2012/04/aa18322-11/aa18322-11-eq409.png) (121)where the latitudinal component is obtained using the anelastic approximation, i.e.
(121)where the latitudinal component is obtained using the anelastic approximation, i.e. 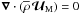 . Moreover, if we assume that the angular momentum transport is ensured by the circulation, the Reynolds stresses associated to the shear-induced turbulence due to the differential rotation, and the MGI waves Reynolds and Maxwell stresses (the torque of the large-scale axisymmetric field is not discussed here, this latter being here taken into account only as a factor that modifies internal waves propagation), we can write its evolution equation as (see Talon & Charbonnel 2005; Mathis et al. 2008):
. Moreover, if we assume that the angular momentum transport is ensured by the circulation, the Reynolds stresses associated to the shear-induced turbulence due to the differential rotation, and the MGI waves Reynolds and Maxwell stresses (the torque of the large-scale axisymmetric field is not discussed here, this latter being here taken into account only as a factor that modifies internal waves propagation), we can write its evolution equation as (see Talon & Charbonnel 2005; Mathis et al. 2008): 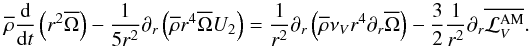 (122)We have introduced the Lagrangian operator d/dt = ∂t + ṙ∂r, which accounts for contractions and dilatations during the evolution (with a radial velocity
(122)We have introduced the Lagrangian operator d/dt = ∂t + ṙ∂r, which accounts for contractions and dilatations during the evolution (with a radial velocity  ), the vertical eddy-viscosity νV (prescriptions for this turbulent transport are discussed in Mathis et al. 2004, and references therein), and the MGI waves averaged Reynolds and Maxwell stresses computed in
), the vertical eddy-viscosity νV (prescriptions for this turbulent transport are discussed in Mathis et al. 2004, and references therein), and the MGI waves averaged Reynolds and Maxwell stresses computed in 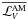 (Eq. (115)). Then, following the method given in Decressin et al. (2009), we obtain U2
(Eq. (115)). Then, following the method given in Decressin et al. (2009), we obtain U2![\begin{equation} U_2=\frac{5}{{\overline\rho}r^4{\overline\Omega}}\left[\Gamma_M\left(r\right)-{\overline\rho}\nu_V r^4 \partial_{r}\overline\Omega+\frac{3}{2}\overline{{\mathcal L}_{V}^{\rm AM}}\right], \label{U2} \end{equation}](/articles/aa/full_html/2012/04/aa18322-11/aa18322-11-eq417.png) (123)where
(123)where ![\begin{equation} \Gamma_M=\frac{1}{4\pi}\frac{\rm d}{{\rm d}t}\left[\int_{0}^{M\left(r\right)}{r'}^2{\overline\Omega}\,{\rm d}m'\right] \end{equation}](/articles/aa/full_html/2012/04/aa18322-11/aa18322-11-eq418.png) (124)is the Lagrangian variation of the angular momentum in the sphere of radius r of mass
(124)is the Lagrangian variation of the angular momentum in the sphere of radius r of mass 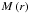 . This leads to the following boundary conditions
. This leads to the following boundary conditions
-
at the top of radiative cores (RC) of low-mass stars(
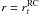 )
) ![\begin{equation} {{\rm d} \over {\rm d}t} \left[\int_{\,r_{t}^{\rm RC}}^{\,R}r^{4}\,\overline\rho\,\overline\Omega\,{\rm d}r\right]=-{1 \over 5}\,r^{4}\,{\overline\rho}\,\overline{\Omega}\,U_{2}-{\mathcal F}_{\rm W}^{\rm M}+\frac{3}{2}\overline{{\mathcal L}_{V}^{\rm AM}}\left(r_{t}^{\rm RC}\right), \end{equation}](/articles/aa/full_html/2012/04/aa18322-11/aa18322-11-eq421.png) (125)where
(125)where 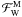 is the flux of angular momentum carried by magnetic pressure-driven stellar winds (Kawaler 1998; Matt & Pudritz 2008; Pinto et al. 2011) and ℱET is the torque of the equilibrium tide if there is a close companion (Zahn 1966–1989);
is the flux of angular momentum carried by magnetic pressure-driven stellar winds (Kawaler 1998; Matt & Pudritz 2008; Pinto et al. 2011) and ℱET is the torque of the equilibrium tide if there is a close companion (Zahn 1966–1989); -
at the top of radiative envelopes (RE) of massive stars (
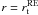 )
) 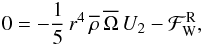 (126)where
(126)where  is the flux of angular momentum carried by radiative stellar winds (ud-Dulla et al. 2009);
is the flux of angular momentum carried by radiative stellar winds (ud-Dulla et al. 2009);
![\hbox{$t_{\rm ES}=\left[\frac{L R}{G M^2}\left(\frac{\Omega_{s}^{2}R^3}{GM}\right)\right]^{-1}$}](/articles/aa/full_html/2012/04/aa18322-11/aa18322-11-eq429.png) if external torques, internal stresses and structural adjustments vanish.
if external torques, internal stresses and structural adjustments vanish.
Then, the meridional circulation advects the mean entropy ( ) and the temperature field relaxes on the new thermal state. The induced temperature fluctuation
) and the temperature field relaxes on the new thermal state. The induced temperature fluctuation 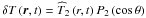 evolution is ruled by the following relaxation equation (Mathis & Zahn 2004):
evolution is ruled by the following relaxation equation (Mathis & Zahn 2004): ![\begin{equation} \underbrace{{\overline \rho}C_{p}\frac{\rm d}{{\rm d}t}{\widehat T}_2}_{{\overline\rho}{\overline T}\partial_{t}{\widetilde S}}-\left[\underbrace{{\overline \rho}\frac{L}{M}\left({\mathcal T}_{2,{\rm Th}}+{\mathcal T}_{2,{\mathcal B}}\right)}_{\vec\nabla\cdot\left(\chi\vec\nabla T\right)-\vec\nabla\cdot\vec F_{H}}\right]= \underbrace{-{\overline \rho}{\overline T}C_{p}\frac{N_{T}^{2}}{{\overline g}}U_{2}}_{{\overline\rho}{\overline T}U_{r}\partial_{r}{\overline S}}+\underbrace{{\overline \rho}\frac{L}{M}{\mathcal T}_{2,{\rm N-G}}}_{\rho\varepsilon}. \label{eqMer} \end{equation}](/articles/aa/full_html/2012/04/aa18322-11/aa18322-11-eq432.png) (128)This is an advection/diffusion equation, where the advective term associated to the meridional circulation caused by the transport of angular momentum plays the role of a source or sink of heat. The terms
(128)This is an advection/diffusion equation, where the advective term associated to the meridional circulation caused by the transport of angular momentum plays the role of a source or sink of heat. The terms  and
and  describe the usual spherical diffusion of heat and the component of the divergence of the radiative flux due to the flattening of the isobar by the centrifugal acceleration; ∇·FH is the entropy flux carried by the horizontal turbulence. Finally,
describe the usual spherical diffusion of heat and the component of the divergence of the radiative flux due to the flattening of the isobar by the centrifugal acceleration; ∇·FH is the entropy flux carried by the horizontal turbulence. Finally,  corresponds to the coupling with the nuclear energy generation. Their derivation may be found in Decressin et al. (2009) and we obtain the thermic term:
corresponds to the coupling with the nuclear energy generation. Their derivation may be found in Decressin et al. (2009) and we obtain the thermic term: ![\begin{eqnarray} {\mathcal T}_{2,{\rm Th}}=\frac{\rho_{m}}{\overline{\rho}}\left[\frac{r}{3}\partial_{r}{\cal{A}}_{2}\left(r\right) -\frac{2 H_{T}}{3 r}\left(1 + \frac{D_{H}}{K}\right)\frac{{\widehat T}_2}{\overline T}\right]\nonumber, \label{Tth} \end{eqnarray}](/articles/aa/full_html/2012/04/aa18322-11/aa18322-11-eq437.png) the barotropic term:
the barotropic term: ![\begin{eqnarray} && {\mathcal T}_{2,{\mathcal B}}= \frac{2}{3}\left[1-\frac{\overline\Omega^2}{2\pi G\overline{\rho}}-\frac{2}{3}\frac{\rho_m}{\rho}\left(\phi\frac{{\widehat\mu}_2}{\overline\mu}-\delta\frac{{\widehat T}_2}{\overline T}\right)-\frac{\left(\overline{\epsilon}+\overline{\epsilon}_{\rm grav}\right)}{\epsilon_{m}}\right]\nonumber\\&&\qquad\quad\times\overline\Omega^{2}\partial_{r}\left(\frac{r^2}{\overline g}\right) -\frac{2}{3}\frac{\rho_m}{\overline\rho}\left(\phi\frac{{\widehat\mu}_2}{\overline\mu}-\delta\frac{{\widehat T}_2}{\overline T}\right)\nonumber, \label{TB} \end{eqnarray}](/articles/aa/full_html/2012/04/aa18322-11/aa18322-11-eq438.png) the term associated with local energy sources:
the term associated with local energy sources: ![\begin{eqnarray} {\mathcal T}_{2,{\rm N-G}}&\,=\,&\frac{\left(\overline{\epsilon}+\overline{\epsilon}_{\rm grav}\right)}{\epsilon_{m}}\left[{\cal{A}}_{2}\left(r\right)+\left(f_{\epsilon}\epsilon_{T} - f_{\epsilon}\delta + \delta\right)\frac{{\widehat T}_2}{\overline T}\right.\nonumber\\ &&{\left.+\left(f_{\epsilon}\epsilon_{\mu}+f_{\epsilon}\phi - \phi\right)\frac{{\widehat\mu}_2}{\overline\mu}\right]}\nonumber, \end{eqnarray}](/articles/aa/full_html/2012/04/aa18322-11/aa18322-11-eq439.png) where
where 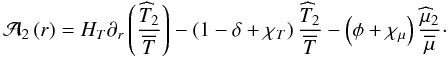 (129)L, M have their usual meaning. We have introduced the temperature scale-height
(129)L, M have their usual meaning. We have introduced the temperature scale-height 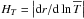 , the horizontal eddy-diffusivity DH and
, the horizontal eddy-diffusivity DH and 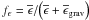 , with
, with 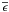 and
and 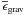 being the mean nuclear and gravitational energy release rates respectively.
being the mean nuclear and gravitational energy release rates respectively. 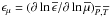 and
and 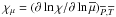 are the logarithmic derivatives of
are the logarithmic derivatives of 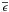 and of the radiative conductivity χ with respect to
and of the radiative conductivity χ with respect to 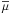 , and
, and 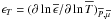 and
and 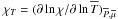 are the derivatives of these same quantities with respect to the temperature
are the derivatives of these same quantities with respect to the temperature 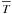 . ϵm = L/M and
. ϵm = L/M and 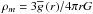 are the horizontal average of the energy production rate and the mean density inside the considered isobar. Finally, the signature of mixing induced by transport processes, i.e. the fluctuation of the mean molecular weight
are the horizontal average of the energy production rate and the mean density inside the considered isobar. Finally, the signature of mixing induced by transport processes, i.e. the fluctuation of the mean molecular weight 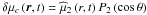 has been introduced.
has been introduced.
Next, once the temperature has relaxed, a new differential rotation is obtained through the thermal-wind equation 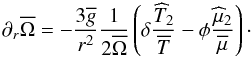 (130)
A new eddy-viscosity (νV) is thus obtained due to the modification of the vertical gradient of angular velocity. To close the loop, the meridional circulation is then substained if there are some external torques, structural adjustments, and internal stresses.
(130)
A new eddy-viscosity (νV) is thus obtained due to the modification of the vertical gradient of angular velocity. To close the loop, the meridional circulation is then substained if there are some external torques, structural adjustments, and internal stresses.
This view of the transport loop is thus the generalisation of the one given in Decressin et al. (2009) taking MGI waves into account (see Fig. 7). There, the associated Reynolds and Maxwell stresses are a source term for the transport of angular momentum and sustain the meridional circulation. However, as explained previously, contributions from waves that are excited in the neighbourhood of ωA or are strongly influenced by the Coriolis acceleration and the Lorentz force are weaker than those of other internal waves because of the strongest Maxwell stresses that act against Reynolds ones and of vertical and horizontal trappings (if 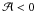 and |νM;m| ≥ 1).
and |νM;m| ≥ 1).
 |
Fig. 7 Transport loop in stellar radiation zones taking into account MGI wave action (here, in the green box). The action of (differential) rotation through the Coriolis acceleration and the Doppler shift and of the Lorentz force are represented in blue and purple. |
Moreover, we emphasize that in this work we look at the impact of a large-scale axisymmetric magnetic field on internal waves, but do not include their feed-back on the latter. This will be done in a forthcoming work, where we will evaluate the potential mean-electromotive force associated to MGI waves (Moffatt 1978; Zahn et al. 2007) to isolate a potential α-effect, as done for example by MacGregor & Rogers (2011) for these waves in Cartesian coordinates. Furthermore, to achieve a complete picture, the associated dynamics of the axisymmetric field and the corresponding couplings will be included (Mathis & Zahn 2005).
4. Conclusion and perspectives
We continued the study of the interactions between internal waves, rotation, and magnetic field in stellar radiation zones. After the work on the adiabatic propagation of regular MGI achieved in Paper I, we here focused on the properties of the transport of angular momentum by these waves. Our goal was to unravel the differences to the classical case where the modifications of internal wave properties by the action of the Coriolis acceleration and the Lorentz force are not taken into account. These modifications become important if MGI waves are excited at frequencies close to the inertial (2Ω) or the Alfvén 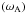 ones by turbulence and the tidal potential (if there is a close companion) at the borders with convective regions such as convective envelopes of solar-type stars or convective cores in intermediate and massive stars. As a first step, we studied the “weak differential rotation” case where a weak differential rotation
ones by turbulence and the tidal potential (if there is a close companion) at the borders with convective regions such as convective envelopes of solar-type stars or convective cores in intermediate and massive stars. As a first step, we studied the “weak differential rotation” case where a weak differential rotation 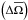 is allowed around a uniform one (Ωs), while the magnetic field is assumed to be purely axisymmetric and toroidal such that the Alvén frequency is uniform, as in Paper I. This allowed us to study the system behaviour as a function of its two control parameters, namely the wave Rossby
is allowed around a uniform one (Ωs), while the magnetic field is assumed to be purely axisymmetric and toroidal such that the Alvén frequency is uniform, as in Paper I. This allowed us to study the system behaviour as a function of its two control parameters, namely the wave Rossby 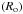 and Elsasser
and Elsasser 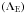 numbers. First, we recalled the properties of low-frequency adiabatic regular MGI, which could be trapped in the radial direction if
numbers. First, we recalled the properties of low-frequency adiabatic regular MGI, which could be trapped in the radial direction if 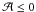 and in an equatorial belt if |νM;m| ≥ 1. Their propagation is thus modified both by rotation and magnetic field, and prograde and retrograde waves are now different. Then, we studied their dissipative propagation with particular attention to their radiative damping, which is responsible for the transport of angular momentum. The difference between prograde and retrograde waves dissipation is due to the Doppler frequency shift and now to the action of the Coriolis acceleration and the Lorentz force. For class I and III waves, it grows with νM;m, which leads to a damping closer to the excitation region; the class IV have a different behaviour and are able to deposit their positive angular momentum farther away from the convection zones. Next, we isolated the action of angular momentum, which is conserved in the adiabatic case, and showed how the wave-induced Maxwell stresses act against Reynolds stresses with an efficiency that grows with the ratio
and in an equatorial belt if |νM;m| ≥ 1. Their propagation is thus modified both by rotation and magnetic field, and prograde and retrograde waves are now different. Then, we studied their dissipative propagation with particular attention to their radiative damping, which is responsible for the transport of angular momentum. The difference between prograde and retrograde waves dissipation is due to the Doppler frequency shift and now to the action of the Coriolis acceleration and the Lorentz force. For class I and III waves, it grows with νM;m, which leads to a damping closer to the excitation region; the class IV have a different behaviour and are able to deposit their positive angular momentum farther away from the convection zones. Next, we isolated the action of angular momentum, which is conserved in the adiabatic case, and showed how the wave-induced Maxwell stresses act against Reynolds stresses with an efficiency that grows with the ratio  . Therefore, the transport of angular momentum is inhibited for waves, which are excited with a frequency close to ωA. Finally, a complete picture of transport processes in stellar radiation zones where internal waves are modified by the Coriolis acceleration and a purely axisymmetric toroidal magnetic field was discussed. Moreover, our theoretical prescriptions are ready to be implemented in a dynamical stellar evolution code aimed to follow the rotation and its profile during the life of the star, as in Talon & Charbonnel (2005).
. Therefore, the transport of angular momentum is inhibited for waves, which are excited with a frequency close to ωA. Finally, a complete picture of transport processes in stellar radiation zones where internal waves are modified by the Coriolis acceleration and a purely axisymmetric toroidal magnetic field was discussed. Moreover, our theoretical prescriptions are ready to be implemented in a dynamical stellar evolution code aimed to follow the rotation and its profile during the life of the star, as in Talon & Charbonnel (2005).
In Paper III, we will study general differential rotation, Ω(r,θ), and azimuthal field, Bϕ(r,θ), followed by purely poloidal and of twisted fields. Furthermore, the regime where the MHD TA does not apply and the critical layers phenomena have to be treated.
See Mathis et al. (2008) in the purely hydrodynamical case and Paper I for MGI.
Moreover, following Pantillon et al. (2007), we can define a horizontal wave number given by
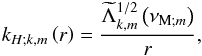 (59)where
(59)where 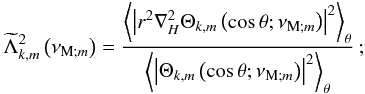
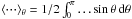 and
and 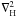 is the horizontal spherical Laplacian. Without rotation and magnetic field (νM;m = 0), we recover
is the horizontal spherical Laplacian. Without rotation and magnetic field (νM;m = 0), we recover 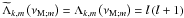
Here, we consider the case of solar-type stars for which the group velocity is negative (cf. Eq. (75)). For massive stars, where it is positive, the phase function is .
Acknowledgments
The authors thank the referee for remarks and suggestions that improved and clarified the original manuscript and A.-S. Brun, C. Charbonnel, T. Decressin, P. Eggenberger, S. Talon, S. Turck-Chièze, J.-P. Zahn, and Pr. G. Meynet for fruitful discussions during this work, which was supported in part by the Programme National de Physique Stellaire (CNRS/INSU), the CNES/GOLF grant at the Service d’Astrophysique (CEA – Saclay), and the CNRS Physique théorique et ses interfaces program. N. de Brye thanks the supports from CEA, GRISOLIA/2010/030, and ERC StG. CAMAP-259276. S. Mathis thanks Geneva Observatory for its hospitality.
References
- Aerts, C., Thoul, A., Daszyska, J., et al. 2003, Science, 300, 1926 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Aerts, C., Christensen-Dalsgaard, J., & Kurtz, D. W. 2010, Asteroseismology, Astronomy and Astrophysics Library (Berlin, Heidelberg: Springer) [Google Scholar]
- Andrews, D. G., & McIntyre, M. E. 1978, J. Fluid Mech., 89, 647 [NASA ADS] [CrossRef] [Google Scholar]
- Ballot, J., Lignières, F., Reese, D. R., & Rieutord, M. 2010, A&A, 518, A30 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Barker, A. J. 2011, MNRAS, 414, 1365 [NASA ADS] [CrossRef] [Google Scholar]
- Barker, A. J., & Ogilvie, G. I. 2009, MNRAS, 395, 2268 [NASA ADS] [CrossRef] [Google Scholar]
- Barnes, G., MacGregor, K. B., & Charbonneau, P. 1998, ApJ, 498, L169 [NASA ADS] [CrossRef] [Google Scholar]
- Belkacem, K., Samadi, R., Goupil, M. J., et al. 2009, A&A, 494, 191 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Booker, J. R., & Bretherton, F. P. 1967, J. Fluid Mech., 27, 513 [NASA ADS] [CrossRef] [Google Scholar]
- Bouvier, J. 2008, A&A, 489, L53 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bouvier, J. 2009, EAS Publ. Ser., 39, 199 [CrossRef] [EDP Sciences] [Google Scholar]
- Braithwaite, J. 2008, MNRAS, 386, 1947 [NASA ADS] [CrossRef] [Google Scholar]
- Bretherton, F. P., & Garrett, C. J. R. 1968, Proc. Roy. Soc. London A, 302, 529 [Google Scholar]
- Browning, M. K., Miesch, M. S., Brun, A.-S., & Toomre, J. 2006, ApJ, 648, L157 [Google Scholar]
- Brun, A.-S. 2011, EAS Publ. Ser., 44, 81 [Google Scholar]
- Brun, A.-S., & Zahn, J.-P. 2006, A&A, 457, 665 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Brun, A.-S., Browning, M. K., & Toomre, J. 2005, ApJ, 629, 461 [NASA ADS] [CrossRef] [Google Scholar]
- Brun, A.-S., Miesch, M. S., & Toomre, J. 2011, ApJ, 742, 79 [NASA ADS] [CrossRef] [Google Scholar]
- Busse, F. H. 1981, Geophys. Astrophys. Fluid Dyn., 17, 215 [NASA ADS] [CrossRef] [Google Scholar]
- Cowling, T. G. 1941, MNRAS, 101, 367 [NASA ADS] [Google Scholar]
- Christensen-Dalsgaard, J., & Thompson, M. J. 2011, Astrophysical Dynamics: From stars to galaxies, Proc. IAU Symp., ed. N. Brummell, A. S. Brun, M. S. Miesch, & Y. Ponty, 271, 32 [Google Scholar]
- Decressin, T., Mathis, S., Palacios, A., et al. 2009, A&A, 495, 271 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Dintrans, B., & Rieutord, M. 2000, A&A, 354, 86 [NASA ADS] [Google Scholar]
- Dintrans, B., Rieutord, M., & Valdettaro, L. 1999, J. Fluid Mech., 398, 271 [NASA ADS] [CrossRef] [Google Scholar]
- Duez, V., & Mathis, S. 2010, A&A, 517, A58 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Eff-Darwich, A., Korzennik, S. G., Jiménez-Reyes, S. J., & García, R. A. 2008, ApJ, 679, 1636 [NASA ADS] [CrossRef] [Google Scholar]
- Eggenberger, P., Meynet, G., Maeder, A., et al. 2010, A&A, 519, A116 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Friedlander, S. 1987a, Geophys. J. Roy. Astron. Soc., 89, 637 [NASA ADS] [CrossRef] [Google Scholar]
- Friedlander, S. 1987b, Geophys. Astrophys. Fluid Dyn., 39, 315 [NASA ADS] [CrossRef] [Google Scholar]
- Friedlander, S. 1989, Geophys. Astrophys. Fluid Dyn., 48, 53 [NASA ADS] [CrossRef] [Google Scholar]
- Friedlander, S., & Siegmann, W. L. 1982, Geophys. Astrophys. Fluid Dyn., 19, 267 [NASA ADS] [CrossRef] [Google Scholar]
- Fruman, M. D. 2009, J. Atmos. Sci., 66, 2937 [NASA ADS] [CrossRef] [Google Scholar]
- Garaud, P., & Guervilly, C. 2009, ApJ, 695, 799 [NASA ADS] [CrossRef] [Google Scholar]
- Garcia, R. A., Turck-Chièze, S., Jiménez-Reyes, S. J., et al. 2007, Science, 316, 1591 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Garcia, R. A., Jain, K., Salabert, D., et al. 2011, J. Phys.: Conf. Ser., 271, 012046 [NASA ADS] [CrossRef] [Google Scholar]
- Gerkema, T., & Shrira, V. I. 2005a, J. Fluid Mech., 529, 195 [NASA ADS] [CrossRef] [Google Scholar]
- Gerkema, T., & Shrira, V. I. 2005b, J. Geophys. Res., 110, C01003 [Google Scholar]
- Gerkema, T., Zimmerman, J. T. F., Mass, L. R. M., & Van Haren, H. 2008, Rev. Geophys., 46, 2004 [NASA ADS] [CrossRef] [Google Scholar]
- Goldreich, P., & Nicholson, P. D. 1989a, ApJ, 342, 1075 [NASA ADS] [CrossRef] [Google Scholar]
- Goldreich, P., & Nicholson, P. D. 1989b, ApJ, 342, 1079 [NASA ADS] [CrossRef] [Google Scholar]
- Gough, D. O., & McIntyre, M. E. 1998, Nature, 394, 755 [NASA ADS] [CrossRef] [Google Scholar]
- Grimshaw, R. 1975, J. Atmos. Sci., 32, 1779 [NASA ADS] [CrossRef] [Google Scholar]
- Grimshaw, R. 1984, Ann. Rev. Fluid Mech., 16, 11 [NASA ADS] [CrossRef] [Google Scholar]
- Heng, K., & Spitkovsky, A. 2009, ApJ, 703, 1819 [NASA ADS] [CrossRef] [Google Scholar]
- Hill, V. 2008, EAS Publ. Ser., 32, 357 [CrossRef] [EDP Sciences] [Google Scholar]
- Hough, S. S. 1898, Philos. Trans. Roy. Soc. London A, 191, 139 [Google Scholar]
- Irwin, J., & Bouvier, J. 2009, in The Ages of Stars, ed. E. E. Mamajek, D. R. Soderblom, & R. F. G. Wyse, Proc. IAU Symp., 258, 363 [Google Scholar]
- Kawaler, S. D. 1998, ApJ, 333, 236 [Google Scholar]
- Kim, E., & MacGregor, K. B. 2003, ApJ, 588, 645 [NASA ADS] [CrossRef] [Google Scholar]
- Kippenhahn, R., & Weigert, A. 1990, Stellar Structure and Evolution (Berlin, Heidelberg, New York: Springer-Verlag) [Google Scholar]
- Kumar, P., Talon, S., & Zahn, J.-P. 1999, ApJ, 520, 859 [NASA ADS] [CrossRef] [Google Scholar]
- Landau, L. D., & Lifchitz, E. M. 1966, Theoretical Physics: Quantum Mechanics (Moscow: Mir) [Google Scholar]
- Laplace, P.-S. 1799, Mécanique céleste (Paris: Bureau des Longitudes) [Google Scholar]
- Lee, U., & Saio, H. 1997, ApJ, 491, 839 [NASA ADS] [CrossRef] [Google Scholar]
- Lindzen, R. S., & Barker, J. W. 1985, J. Fluid Mech., 151, 189 [NASA ADS] [CrossRef] [Google Scholar]
- Lindzen, R. S., & Chapman, S. 1969, Space Sci. Rev., 10, 3 [NASA ADS] [CrossRef] [Google Scholar]
- Longuet-Higgins, M. S. 1968, Philos. Trans. Roy. Soc. London A, 262, 511 [Google Scholar]
- Maas, L., & Harlander, U. 2007, J. Fluid Mech., 570, 47 [NASA ADS] [CrossRef] [Google Scholar]
- MacGregor, K. B., & Rogers, T. M. 2011, Sol. Phys., 270, 417 [NASA ADS] [CrossRef] [Google Scholar]
- Maeder, A. 2009, Physics, Formation and Evolution of Rotating Stars, Astronomy and Astrophysics Library (Berlin, Heidelberg: Springer) [Google Scholar]
- Maeder, A., & Meynet, G. 2000, ARA&A, 38, 143 [NASA ADS] [CrossRef] [Google Scholar]
- Maeder, A., & Zahn, J.-P. 1998, A&A, 334, 1000 [NASA ADS] [Google Scholar]
- Mathis, S. 2009, A&A, 506, 811 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Mathis, S., & de Brye, N. 2011, A&A, 526, A65 (Paper I) [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Mathis, S., & Zahn, J.-P. 2004, A&A, 425, 229 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Mathis, S., & Zahn, J.-P. 2005, A&A, 440, 653 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Mathis, S., Palacios, A., & Zahn, J.-P. 2004, A&A, 425, 243 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Mathis, S., Talon, S., Pantillon, F.-P., & Zahn, J.-P. 2008, Sol. Phys., 251, 101 [NASA ADS] [CrossRef] [Google Scholar]
- Matt, S., & Pudritz, R. E. 2005, ApJ, 632, L135 [NASA ADS] [CrossRef] [Google Scholar]
- Matt, S., & Pudritz, R. E. 2008, ApJ, 678, 1109 [Google Scholar]
- Melchior, P. J. 1986, The physics of the Earth’s core, An introduction (Pergamon Press) [Google Scholar]
- Moffatt, H. K. 1978, Magnetic field generation in electrically conducting fluids, Monograph on Mechanics and Applied Mathematics (Cambridge University Press) [Google Scholar]
- Ogilvie, G. I., & Lin, D. N. C. 2004, ApJ, 610, 477 [NASA ADS] [CrossRef] [Google Scholar]
- Ogilvie, G. I., & Lin, D. N. C. 2007, ApJ, 661, 1180 [NASA ADS] [CrossRef] [Google Scholar]
- Pantillon, F. P., Talon, S., & Charbonnel, C. 2007, A&A, 474, 155 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Pedlosky, J. 1998, Geophysical fluid dynamics, 2nd edition (Springer) [Google Scholar]
- Pinto, R. F., Brun, A.-S., Jouve, L., & Grappin, R. 2011, ApJ, 737, 72 [Google Scholar]
- Press, W. 1981, ApJ, 245, 286 [NASA ADS] [CrossRef] [Google Scholar]
- Rieutord, M. 2006, A&A, 451, 1025 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Rogers, T. M. 2011, ApJ, 733, 12 [NASA ADS] [CrossRef] [Google Scholar]
- Rogers, T. M., & Glatzmaier, G. A. 2006, ApJ, 653, 756 [NASA ADS] [CrossRef] [Google Scholar]
- Rogers, T. M., & MacGregor, K. B. 2010, MNRAS, 401, 191 [NASA ADS] [CrossRef] [Google Scholar]
- Rogers, T. M., & MacGregor, K. B. 2011, MNRAS, 410, 946 [NASA ADS] [CrossRef] [Google Scholar]
- Rogers, T. M., MacGregor, K. B., & Glatzmaier, G. A. 2008, MNRAS, 387, 616 [NASA ADS] [CrossRef] [Google Scholar]
- Rudraiah, N., & Venkatachalappa, M. 1972a, J. Fluid Mech., 52, 193 [NASA ADS] [CrossRef] [Google Scholar]
- Rudraiah, N., & Venkatachalappa, M. 1972b, J. Fluid Mech., 54, 209 [NASA ADS] [CrossRef] [Google Scholar]
- Rudraiah, N., & Venkatachalappa, M. 1972c, J. Fluid Mech., 54, 217 [NASA ADS] [CrossRef] [Google Scholar]
- Schatzman, E. 1993a, A&A, 271, L29 [NASA ADS] [Google Scholar]
- Schatzman, E. 1993b, A&A, 279, 431 [NASA ADS] [Google Scholar]
- Schecter, D. A., Boyd, J. F., & Gilman, P. A. 2001, ApJ, 551, L185 [NASA ADS] [CrossRef] [Google Scholar]
- Shrira, V. I., & Townsend, W. A. 2010, JFM, 664, 478 [NASA ADS] [CrossRef] [Google Scholar]
- Schou, J., Antia, H. M., Basu, S., et al. 1998, ApJ, 505, 390 [NASA ADS] [CrossRef] [Google Scholar]
- Spada, F., Lanzafame, A. C., & Lanza, A. F. 2010, MNRAS, 404, 641 [NASA ADS] [CrossRef] [Google Scholar]
- Stewartson, K., & Richard, J. 1969, J. Fluid Mech., 35, 759 [NASA ADS] [CrossRef] [Google Scholar]
- Stewartson, K., & Walton, I. C. 1976, Proc. Roy. Soc. London A, 349, 141 [NASA ADS] [CrossRef] [Google Scholar]
- Strugarek, A., Brun, A.-S., & Zahn, J.-P. 2011, A&A, 532, A34 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Talon, S. 2008, EAS Publ. Ser., 32, 81 [CrossRef] [EDP Sciences] [Google Scholar]
- Talon, S., & Charbonnel, C. 2005, A&A, 440, 981 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Talon, S., Kumar, P., & Zahn, J.-P. 2002, ApJ, 574, L175 [NASA ADS] [CrossRef] [Google Scholar]
- Turck-Chièze, S., Palacios, A., Marques, J. P., & Nghiem, P. A. P. 2010, ApJ, 715, 1539 [NASA ADS] [CrossRef] [Google Scholar]
- ud-Dulla, A., Owocki, S. P., & Townsend, R. H. D. 2009, MNRAS, 392, 1022 [NASA ADS] [CrossRef] [Google Scholar]
- Unno, W., Osaki, Y., Ando, H., Saio, H., & Shibahashi, H. 1989, Non-radial oscillations of stars, second edition (Tokyo: University of Tokyo Press) [Google Scholar]
- Wood, T. S., McCaslin, J. O., & Garaud, P. 2011, ApJ, 738, Issue 1, article id. 47 [Google Scholar]
- Yanai, M., & Maruyama, T. 1966, J. Meteorol. Soc. Japan, 44, 291 [Google Scholar]
- Zahn, J.-P. 1975, A&A, 41, 329 [NASA ADS] [Google Scholar]
- Zahn, J.-P. 1992, A&A, 265, 115 [NASA ADS] [Google Scholar]
- Zahn, J.-P. 2007, EAS Publ. Ser., 26, 49 [CrossRef] [EDP Sciences] [Google Scholar]
- Zahn, J.-P., Talon, S., & Matias, J. 1997, A&A, 322, 320 [Google Scholar]
- Zahn, J.-P., Brun, A.-S., & Mathis, S. 2007, A&A, 474, 145 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Zaqarashvili, T. V., Olivier, R., Ballester, J. L., & Shergelashvili, B. M. 2007, A&A, 470, 815 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Zaqarashvili, T. V., Olivier, R., & Ballester, J. L. 2009, ApJ, 691, L41 [NASA ADS] [CrossRef] [Google Scholar]
All Tables
Dimensionless numbers that characterise the internal wave propagation in rotating and magnetic stellar radiation zones.
All Figures
 |
Fig. 1 Set-up for studying internal wave dynamics in rotating and magnetic stellar radiation zones and the associated transport of angular momentum. The Alfvén frequency |
| In the text | |
 |
Fig. 2 Top: sign of |
| In the text | |
 |
Fig. 3 Left: Hough functions Θk,m(cosθ;ν) (top) and associated latitudinal |
| In the text | |
 |
Fig. 4 Top: θc;m as a function of Ro and ΛE for non-axisymmetric retrograde (m = 1) and prograde (m = −1) waves. On one hand, the corner region for which Ro ≤ ΛE/2 corresponds to the |
| In the text | |
 |
Fig. 5 Top left: |
| In the text | |
 |
Fig. 6 Synopsis of the structure and the induced transport of angular momentum in stars with an external and an internal convection zone. Convection and radiation zones are depicted in grey and orange. The short dashed blue lines represent the equatorial trapping due to the Coriolis acceleration and the Lorentz force and the purple long-dashed lines represent the vertical magnetic trapping. Finally, the vertical fluxes of energy and of angular momentum are represented by the thin dark grey arrow and the large green one. |
| In the text | |
 |
Fig. 7 Transport loop in stellar radiation zones taking into account MGI wave action (here, in the green box). The action of (differential) rotation through the Coriolis acceleration and the Doppler shift and of the Lorentz force are represented in blue and purple. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.



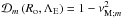
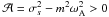
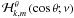
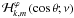
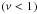
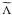
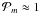
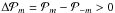
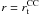
![\begin{equation} {{\rm d} \over {\rm d}t} \left[\int_{\,0}^{\,r_{\rm t}^{\rm CC}}r^{4}\,\overline\rho\,\overline\Omega\,{\rm d}r \right]=\frac{1}{5}\,r^{4}\,{\overline\rho}\,\overline{\Omega}\,U_{2}-\frac{3}{2}\overline{\mathcal{L}_{V}^{\rm AM}}\left(r_{\rm t}^{\rm CC}\right). \end{equation}](/articles/aa/full_html/2012/04/aa18322-11/aa18322-11-eq428.png)