| Issue |
A&A
Volume 540, April 2012
|
|
|---|---|---|
| Article Number | A108 | |
| Number of page(s) | 10 | |
| Section | Stellar structure and evolution | |
| DOI | https://doi.org/10.1051/0004-6361/201117817 | |
| Published online | 05 April 2012 | |
Spectroscopic monitoring of the Herbig Ae star HD 104237⋆
II. Non-radial pulsations, mode analysis, and fundamental stellar parameters
1 Université de Toulouse, UPS-OMP, IRAP, Toulouse, France
e-mail: torsten.boehm@irap.omp.eu
2 CNRS, IRAP, 14, avenue Edouard Belin, 31400 Toulouse, France
Received: 3 August 2011
Accepted: 8 March 2012
Context. Herbig Ae/Be stars are intermediate-mass pre-main sequence (PMS) stars showing signs of intense activity and strong stellar winds, whose origin is not yet understood in the frame of current theoretical models of stellar evolution for young stars. In addition, the evolutionary tracks of the earlier Herbig Ae stars cross the theoretical PMS instability strip located roughly in the same area of the HR diagram as the δ Scuti variables. Many of these stars exhibit pulsations of δ Scuti type.
Aims. Understanding the internal structure of pulsating Herbig Ae stars based on asteroseismic studies will help constraining the origin of their tremendous activity, winds, and variability. It is therefore necessary to investigate the location of the PMS instability strip and of its boundaries, and to extend the sample of observed and studied pulsating Herbig Ae stars. The aim of this work was to carry out a thorough analysis of the line profile variations of the prototype Herbig Ae star HD 104237 based on high-resolution spectroscopy and to redetermine precisely its fundamental parameters, which are the basic ingredients of a forthcoming asteroseismic modeling.
Methods. HD 104237 is a pulsating Herbig Ae star with eight detected frequencies based on the analysis of radial velocity variations. In this article, we reinvestigated an extensive high-resolution quasi-continuous spectroscopic data set in order to search for very faint indications of non-radial pulsations in the line profile by working on dynamical spectra of equivalent photospheric (LSD) profiles of HD 104237. A 2D Fourier analysis (F2D) was performed of the entire profile and the temporal variation of the central depth of the line was studied with the time-series analysis tools Period04 and SigSpec. We present the results of these analysis including the mode identification corresponding to the detected dominant frequency, as well as a new determination of its fundamental stellar parameters.
Results. The analysis of spectroscopic data set of April 22–25 obtained at SAAO in 1999 has confirmed the presence of multiple oscillation modes of low-degree ℓ in HD 104237 and led to the first direct detection of a non-radial pulsation mode in this star: the dominant mode F1 was identified by the Fourier 2D method having a degree ℓ value comprised between 1 and 2, the symmetry of the pattern variation indicating an azimuthal order of ± 1. The detailed study of the fundamental stellar parameters has provided a Teff, log g, and iron abundance of 8550 ± 150 K, 3.9 ± 0.3, and −4.38 ± 0.19 (i.e. [Fe/H] = +0.16 ± 0.19 ), respectively.
Key words: stars: pre-main-sequence / stars: oscillations / stars: individual: HD 104237 / binaries: spectroscopic / stars: fundamental parameters
© ESO, 2012
1. Introduction
Pre-main sequence (PMS) stars of intermediate mass (2 to 10 M⊙) are known as Herbig Ae/Be (hereafter HAeBe) stars, following a first classification by Herbig (1960); for a review, see Waters & Waelkens (1998). Their spectra reveal strong infrared excesses indicative of a dense circumstellar environment. Intense signs of stellar activity, variability, and winds are observed. Indeed, the frequently observed emission in Mg II h and k lines, Ca II IR triplet, Ca II H and K line, He I 5876 Å, many Fe II lines, Na I D, N V, Si IV and C IV resonance lines, imply the high temperature of a chromosphere or corona to be formed. Short-term variability of many of these lines are observed and P Cygni profiles of Hα, Hβ, Mg II h and k lines present in the spectra of some of these stars indicate the presence of strong and structured stellar winds (see e.g. Praderie et al. 1982, 1986; Catala & Talavera 1984; Catala et al. 1986a,b; Catala & Kunasz 1987; Catala 1988; Böhm & Catala 1995; Böhm et al. 1996).
A wide-spread idea consists of invoking magnetism as being responsible of these active stellar phenomena, requiring either the presence of a primordial magnetic field or a dynamo mechanism whose basic ingredients are classically convection and rotation. On one hand, recent spectropolarimetric observations of Herbig stars indicate the presence of significant magnetic fields only in a small 10% fraction of them (Wade et al. 2007), these results agree with the primordial fossil field hypothesis. On the other hand, considering a possible dynamo mechanism, the position of HAeBe stars in the HR diagram indicates that they are in the radiative phase of their quasi-static contraction toward the main sequence (Iben 1965; Gilliland 1986; Palla & Stahler 1993). Therefore, in absence of subphotospheric convection, a classical solar-type magnetic dynamo mechanism cannot be at work and the observed activity remains paradoxical. While an external origin, involving an accretion disk as invoked for explaining the activity in classical TTauri stars (Bertout et al. 1988), cannot be ruled out, growing evidence indicates that the energy needed to produce this activity is of internal stellar origin (Böhm & Catala 1995); theoretical explanations might invoke deuterium shell burning (Palla & Stahler 1990) or an alternative dynamo mecanism based on a non-convective turbulent layer (Lignieres et al. 1996). It is a major concern for testing young stellar evolutionary theory to solve this still-open question about HAeBe stellar activity by constraining the internal structure of these objects using asteroseismic techniques, i.e. the analysis and modeling of stellar pulsations, if observed.
The existence of these stellar pulsations in HAeBe stars are known since Breger (1972) discovered two pulsating candidates, V588 Mon and V589 Mon, in the young open cluster NGC 2264. Subsequently, two additional pulsating Herbig stars were detected: HR 5999 (Kurtz & Marang 1995) and HD 104237 (Donati et al. 1997). Motivated by these detections, Marconi & Palla (1998) investigated theoretically a PMS instability strip for the first three radial modes of pulsations and concluded on a topology of this instability strip, which corresponded roughly to the same area in the HR diagram as the δ Scuti variables. The study of Marconi & Palla (1998) showed that most of the Herbig Ae stars are expected to cross it for a significant fraction of their evolution to the main sequence (5 to 10% of their PMS phase). Studying the largest number of PMS pulsating stars will allow us to constrain the boundaries of the PSM instability strip and to caracterize it. The priority should be given to multiperidodic pulsators, which are the most promising candidates for an asteroseismic modeling. As of today, a significant number of Herbig Ae stars, either field stars or members of young open clusters, have indeed revealed to be pulsating at timescales typical of δ Scuti stars, i.e. with short periods (from ≈ 20 min to several hours) and low amplitudes (from mmag to few hundreths of mag in case of photometry, and less than typically 1–2 km s-1 for radial velocity studies) (for reviews see e.g. Catala 2003; Marconi & Palla 2004; Zwintz et al. 2004; Zwintz 2008). Most of them have been studied in photometry, but only very few in spectroscopy (e.g. Böhm et al. 2004, 2009). However, owing to cancellation effects, only modes of low degree are detected in photometry or radial velocity curves. For a deeper analysis high-resolution spectroscopy is necessary to study the weak variations induced by non-radial pulsations in the rotationally-broadened photospheric line profiles. It should be noted that binarity is common among HAeBe stars with approximately 60% (Baines et al. 2006). HD 104237 is also a spectroscopic binary, which tremendously complicates the analysis of its spectrum.
This article is the second of a series on the prototype Herbig Ae star HD 104237, starting with the article by Böhm et al. (2004). The first article presented the detection of multiperiodic oscillations in the radial velocity curves of the star and the analysis of its binary orbit, among others. In this present article, we describe the direct search and detection of oscillations in the line profiles, the mode identification of the dominant non-radial pulsation mode, and a fundamental stellar parameter determination by spectroscopic means. This work therefore represents the basis for the asteroseismic modeling we will present in a forthcoming article (Fumel et al., in prep.).
The article is structured as follows: in Sect. 2, we review in detail previous works on HD 104237, Sect. 3 sums up the spectroscopic observations we worked with and describes the data reduction. Section 4 presents our detection and identification of non-radial pulsations in HD 104237, Sect. 5 describes the spectral continuum determination tool we developed to obtain optimized high-quality spectra. In Sect. 6 we detail the fundamental parameter determination of HD 104237 we carried out, and finally we conclude and discuss our results in Sect. 7.
2. Previous works on HD 104237
Hu et al. (1989, 1991) derived from photometric and spectroscopic studies that HD 104237, or DX Cha, is a member of the Herbig Ae/Be group. Moreover, it is a prototype of this group of stars and a particularly suitable target because it is very bright (mv = 6.6), which allows monitoring with short exposure times in high-resolution spectroscopic mode. HD 104237 is a multiple system whose primary component (hereafter simply called HD 104237 or the “primary”) is a Herbig Ae star with several low-mass companions at separations between 1′′ and 15′′ (Feigelson et al. 2003), including a close K3 companion in an eccentric 19.9-day orbit (hereafter HD 104237b or the “secondary”). This very close component of approximate spectral class K3 forms a spectroscopic binary with the primary (Böhm et al. 2004). Indeed, K3-type spectral features (including Li I 6707 Å and Ca I 6718 Å lines) are observed in the composite spectra (Feigelson et al. 2003). As a consequence, the pollution by the secondary spectrum has to be taken into account in a precise fundamental parameter analysis.
2.1. Previous fundamental parameter determination
The strong IR excesses and the UV-extinction caused by the presence of CS dust , the emission components in many absorption lines, the P Cygni profiles observed notably in the Balmer lines, and the spectroscopic binary pollution make the determination of most fundamental stellar parameters of HD 104237 difficult. Thus, the spectral types available in the literature for HD 104237 range from A0 to A8 (implying a broad range in possible Teff values) and its bolometric luminosity from ≈20 to 60 L⊙. The most important parameters of HD 104237 (primary and secondary) found in the literature are chronologically summarized in Table 1.
Using the accurate absolute astrometric and photometric data yielded by the Hipparcos satellite, van den Ancker et al. (1997) computed new Teff, log (L⋆/L⊙), mass and age values for HD 104237, which were refined in van den Ancker et al. (1998). They should provide, as of today, the most reliable parameter determination. The uncertainties on the effective temperature (see van den Ancker et al. 1997) were estimated to correspond typically to one subclass in spectral type and were not determined in a statistical procedure.
Using evolutionary tracks and isochrones from Palla & Stahler (2001) and stellar parameters from van den Ancker et al. (1998) and Grady et al. (2004), Böhm et al. (2004) concluded on an age of 2 Myr for HD 104237, in agreement with van den Ancker et al. (1997, 1998) and Feigelson et al. (2003), Böhm and collaborators independently concluded on a value of the stellar mass M⋆ = 2.2 ± 0.1 M⊙, close to previous results. In addition, they calculated a mass ratio MP/MS of 1.29 ± 0.02, based on measures of the primary and secondary radial velocities with respect to the binary systemic velocity, which enabled them to estimate the mass of the secondary, Msec = 1.7 ± 0.1 M⊙. Assuming the same age for both components, they confirmed a K3 spectral type for the secondary and assessed a temperature of about 4750 K and a luminosity of one tenth of LP.
Stellar parameters of HD 104237.
Acke & Waelkens (2004) used the Teff and log g presented in Meeus et al. (2001, and references therein) to carry out a chemical analysis of several PMS stars including HD 104237. They measured the equivalent widths of many chemical elements and converted them into abundances using the program MOOG (Sneden 1973), but taking into account neither the binarity of this star (which adds a continuum veiling along with additional lines from the secondary) nor the asymmetries or the emission components in the line profiles. Using the solar abundances by Anders & Grevesse (1989), these authors found a solar-like global metallicity ( [M/H] = + 0.06 ± 0.05) and a solar abundance for several chemical elements including Fe ( [Fe/H] = + 0.09 ± 0.19 where ![\hbox{${\rm [Fe/H]} =\log{\left(\frac{N_{{\rm{Fe}}}}{N_{{\rm{H}}}}\right)_{{\rm{HD}}\,104237}}-\log{\left(\frac{N_{{\rm{Fe}}}}{N_{{\rm{H}}}}\right)_{\odot}}$}](/articles/aa/full_html/2012/04/aa17817-11/aa17817-11-eq51.png) ).
).
Donati et al. (1997) measured a vsini of 12 ± 2 km s-1, which suggests either that HD 104237 is viewed close to pole-on or that it is a moderate rotator. Böhm et al. (2006) detected a modulation of the Hα line profile with a period of 100 ± 5 h and suggested a rotational origin, yielding an inclination of 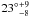 . This value of Prot was confirmed by Testa et al. (2008) in an X-ray study of the HD 104237 system.
. This value of Prot was confirmed by Testa et al. (2008) in an X-ray study of the HD 104237 system.
Concerning magnetism, Donati et al. (1997) detected a weak field of about 50 G in HD 104237, but a later survey by Wade et al. (2007) could not confirm it at this stage.
2.2. Previous pulsational analysis
Following the first discovery of pulsations in HD 104237 by Donati et al. (1997) and confirmation by Kurtz & Müller (1999), Böhm et al. (2004) obtained in 1999 and 2000 an extensive high-resolution (R ≈ 35 000) spectroscopic data set of HD 104237 at the 1.9 m Radcliffe telescope of the SAAO (see Sect. 3). The analysis of the resulting high-quality radial velocity curve allowed them to detect for the first time by spectroscopic means multi-periodic oscillations in a PMS star (eight frequencies in the 1999 data set and five in the 2000 data set). Five frequencies of 1999 were identified with frequencies of 2000, between 28.50 and 35.60 d-1. The three last frequencies of 1999 (f6 to f8) were considered as less certain. The frequency differences of the eight, respectively five frequencies detected by Böhm et al. (2004) were smaller than the estimated large separation (Δν0 ≈ 40−45 μHz), leading the authors to conclude on the nonradial nature of at least some of the pulsation modes detected in their work. More generally, no regular frequency pattern was clearly identified in the pulsational behaviour of HD 104237.
Using the results of Böhm et al. (2004), Dupret et al. (2006, 2007) found in a preliminary seismic modeling of HD 104237 that it is difficult to properly fit the observed frequencies with theoretical frequencies computed from models with Teff and log(L⋆/L⊙) presented in van den Ancker et al. (1998) and Grady et al. (2004). An important result Dupret et al.’s conclusion that HD 1043237 could in fact not be a typical δ Scuti type pulsator, because the p modes order corresponding to the observed frequencies are too high to be excited by the standard excitation mechanism of δ Scuti type variables, namely a κ-driving in the He II partial ionization zone.
3. SAAO spectroscopic observations and data reduction
The analysis presented in this article is based on parts of the data set described in Böhm et al. (2004), namely the high-resolution quasi-continuous spectroscopic observations obtained in April 1999 and April 2000 at the 1.9 m SAAO (South African Astronomical Observatory) Radcliff telescope; all data were obtained with the GIRAFFE fiber-fed echelle spectrograph (R ≈ 35 000, visible domain 430–690 nm, texp = 5 min, signal-to-noise ratio (S/N) at 550 nm of 50–70 pix-1 for each exposure). Data reduction was carried out following standard reduction procedures using the “ESPRIT” spectroscopic reduction package (Donati et al. 1997). The least-squares deconvolution (LSD) method as described in Donati et al. (1997) which uses the multiplex gain of more than 500 lines present in the spectrum of this star, allowed us to obtain high S/N equivalent photospheric profiles. High-precision radial velocity correction was achieved using the positions of more than 100 narrow telluric vapor lines. All spectra were shifted to the heliocentric rest wavelength and calibrated to a final intrinsic precision estimated to be around 100 m s-1 for this data set.
Our search for direct signatures of non-radial pulsations in the equivalent photospheric profiles was carried out based on the data collected during the nights of April 22 to 26, 1999, while the fundamental parameters were determined with data taken at the periastron night of April 12, 2000, ensuring a maximum separation of both binary components of around 60 km s-1. This avoided pollution of the primary by the much fainter HD 104237b spectrum as far as possible. The log of the observations is summarized in Table 2.
4. Direct detection and identification of non-radial pulsations
The most direct way to perform mode identification in multiperiodically oscillating stars is the analysis of line-profile variations of rotationally-broadened high-resolution photospheric profiles. The maximum attainable degree ℓ increases with the ratio vsini to the resolved spectral element (Δv = c/R), the parameters of HD 104237 and the instrumental set-up indicating a detection limit of ℓmax on the order of 3.
Each LSD profile was corrected for its radial velocity (orbital motion and centroid shifts mainly caused by radial pulsations) and a mean LSD profile, averaged over the whole run, was individually subtracted. The residuals show profile variations that are clearly indicative of non-radial stellar pulsations, with differential amplitudes on the order of 1.5% of the continuum. Also, the dynamical spectra of Fig. 1 show that beating between nearby frequencies occurs, which leads to the conclusion that there is probably more than one non radial pulsation (NRP; the night of April 26 is not represented because of shorter coverage). Figure 2 shows the differential amplitude variations at line center, extracted by taking the median value of the three central velocity bins of each spectrum, one bin corresponding to 4 km s-1.
Log of observations.
 |
Fig. 1 Line profile variations due to the non-radial pulsations of HD 104237. The deviations from the mean intensity are displayed for four different nights (top left: April 22, 1999, bottom left: April 23, 1999, top right: April 24, 1999, bottom right: April 25, 1999). Dashed lines represent the limits of the equivalent profile, an additional broadening agent generates wings reaching almost ± 2 vsini, i.e. twice the width of a pure rotational profile at continuum level. |
4.1. Central profile analysis with SigSpec and Period04
We carried out a frequency analysis of the time-series using the Period04 package (Lenz & Breger 2005) in parallel with the Sigspec package (Reegen 2007). They both use, in iterative process, combinations of discrete Fourier transform (DFT) and least-squares fitting algorithms to extract the frequencies, amplitudes and phases of multi-periodic signals in not-equally spaced data sets. To avoid at maximum low-frequency night-to-night variations, we corrected the time series by subtracting a nightly average before performing the analysis. Still, by doing so, some low frequencies persisted. The results of this analysis are shown in Table 3. As described in Böhm et al. (2004), the uncertainty in the extracted frequency value can be estimated in different ways. The most conservative approach is measuring of the FWHM of the main lobe of the spectral window function (Ripepi et al. 2003), corresponding here to Δf = 0.31 d-1. Figure 3 shows the amplitude power spectrum including all strong peaks around 29–36 d-1, the noise levels were determined after prewithening of the nine first frequencies. Figure 4 shows that even F9 has a significance level of above 99.9%, following the approach described in Breger et al. (1993) and Kuschnig et al. (1997). We arbitrarily decided to stop the iterative procedure for amplitude values below 0.1%. The verification of the results with SigSpec revealed exactly the same frequencies and amplitudes, all detected frequencies F1 to F10 having a significance level between 66.5 and 6.3, respectively. No combined frequency is present in the power spectrum, following the analysis with the Combine program by Reegen (2007). We did not consider the frequencies below approximately 5 d-1, because differential calibration problems from one night to the next might persist, i.e. this excludes F4, F7, F8, and F10. By applying the error estimate by Ripepi et al. (2003), all remaining frequencies (“F”) could be identified with the frequencies (“f”) determined by radial velocity studies on the same data set in Böhm et al. (2004). F3 is slightly outside the error bar, and the 1.0 d-1 difference between F9 and F3 indicates that we most likely deal with an alias of the same frequency. The order of the first two dominant frequencies is inverted depending on if radial velocity or central depth variations are analyzed, probably because of the prior radial velocity recentering.
4.2. Mode identification with the Fourier 2D method
A direct method of analyzing the non-radial pulsation modes present in the LSD-spectra time series is applying the Fourier 2D method on line-profile variations (Kennelly et al. 1993; Kennelly 1994; Kennelly et al. 1996). This technique analyzes the complex pattern present in the line profiles by computing a 2D Fourier transform in time and Doppler space. To do this, we performed an interpolation of each profile on a grid representing stellar longitudes, transforming velocities across the line profile into longitudes on the stellar equator using the relation Δv = vsinisinφ. Δv is here the velocity position within the LSD profile with respect to the rest wavelength of the star and φ is the stellar longitude angle of the star in spherical coordinates. In the resulting 2D Fourier spectrum, the temporal frequencies are related here mainly to the frequencies of oscillation, while the apparent azimuthal order mˆ is related to the structure of the modes present at the stellar surface, which is not identical to the usual azimuthal order m. The original work by Kennelly (1994) showed that apparent  scales as ℓ +2 for values close to zero, as ℓ +1 for values lower than 10 and as ℓ for values above 10 (ℓ being the degree of the mode). We performed this F2D computation on each night of April 22 to 25 1999. A weighted combination of the nightly F2D spectra can be seen in Fig. 5 (see Böhm et al. 2009, for details of the method) and our results confirm the presence of low-degree non-radial pulsations: a peak at the dominant frequency F1 is clearly seen with an apparent mˆ of between 2 and 4 indicating a degree ℓ of between 0 and 2. Moreover, as can be seen in Table 2.3 of Kennelly (1994) (or in simulations with available online-NRP simulators), the symmetric pattern of the dynamical residual profile as seen in Fig. 1 indicates an azimuthal order m = ± 1 for F1, implying a most likely ℓ value of 1 or 2.
scales as ℓ +2 for values close to zero, as ℓ +1 for values lower than 10 and as ℓ for values above 10 (ℓ being the degree of the mode). We performed this F2D computation on each night of April 22 to 25 1999. A weighted combination of the nightly F2D spectra can be seen in Fig. 5 (see Böhm et al. 2009, for details of the method) and our results confirm the presence of low-degree non-radial pulsations: a peak at the dominant frequency F1 is clearly seen with an apparent mˆ of between 2 and 4 indicating a degree ℓ of between 0 and 2. Moreover, as can be seen in Table 2.3 of Kennelly (1994) (or in simulations with available online-NRP simulators), the symmetric pattern of the dynamical residual profile as seen in Fig. 1 indicates an azimuthal order m = ± 1 for F1, implying a most likely ℓ value of 1 or 2.
The frequency peak in Fig. 5 between 3 and 5 d-1 is again not taken into account, because nightly calibration shifts can easily introduce such variations.
 |
Fig. 2 Amplitude variation of the central velocity bins of the residual LSD profile on the nights Apr. 22 to 26, 1999. Superimposed is a fit of the data corresponding to the result of the frequency analysis as presented in Table 3. |
Frequencies determined with Period04.
 |
Fig. 3 Periodogram of the line center variation as shown in Fig. 2, without prewithening. The large bulk of frequencies around 29-36 d-1can be seen, as well as the 3.2, 3.6 and 4.0 mean-ampitude level of the noise determined by prewithening F1 to F9, corresponding to a 90%, 99% and 99.9% significance level, respectively. |
 |
Fig. 4 Same figure as Fig. 3, but prewithened by F1 to F8. As shown, F9 is present, well above the 99.9% confidence level. |
A complementary analysis on the whole data set using the FAMIAS code (Zima et al. 2006; Zima 2008) is planned, but the highly asymmetric mean photospheric profile seen in HD 104237 adds complexity to the data analysis and cannot be taken into account in the present state of the code.
5. Optimized spectral continuum determination
Our next step, the fundamental parameter redetermination, required summing up of individual spectra obtained during a periastron night, the goal being a resulting spectrum with very high S/N. Each individual spectrum had to undergo an optimized continuum normalization as an essential prerequisite. An automatic code was developed, because the case of HD 104237 proved to be quite complicated owing to the pollution by the spectrum of its secondary companion, but also because of emission components and variability observed in numerous absorption lines. As a first step, we determined the effective continuum location within each composite spectrum. To do so, absorption line lists were extracted from the Vienna Atomic Line Database (VALD; Piskunov et al. 1995; Ryabchikova et al. 1997; Kupka et al. 1999, 2000) corresponding to the approximate fundamental parameters of each component. For each individual spectrum, these grids were shifted by the precise orbital velocities at the acquisition time. A wavelength-dependant luminosity-ratio (black-body approximation) of both components was calculated and a depth criterion applied. The rotational broadening was taken into account. Finally, the elimination of unsuited, “active” spectral line regions let us determine true continuum regions. The division by a fourth degree polynomial fitted through the remaining continuum areas of each order normalized them and was followed by their weighted concatenation, taking into account the local S/N in the overlapping regions between adjacent orders (excluding the broad Hα and Hβ line areas, which remained unnormalized). In a last step, all obtained individually normalized spectra of the night were added, weighted by their corresponding average S/N, after recentering them on their individual primary component rest velocity.
The resulting gain in S/N of our reference “periastron” spectrum (see Fig. 6) was of about a factor of 6, the S/N reaching almost 400 per resolved element at 550 nm.
 |
Fig. 5 Combined F2D analysis of HD 104237 for the nights of April 22 to 25, 1999. |
 |
Fig. 6 Individual (thin line) and summed (thick line) normalized spectrum of the periastron night around one of the selected lines (Fe I 5415.1920 Å). Synthetic spectra with Teff = 8500 K (dotted line) and Teff = 4750 K (dashed line) were overplotted (log g = 4.0, vmicro = 2 km s-1 solar abundances for both spectra), showing the location of the individual lines. The secondary’s spectrum was corrected by the local luminosity ratio. Neither fundamental parameters nor local luminosity ratios are perfectly tuned at this stage. |
6. Fundamental parameter determination
6.1. Method
Since Teff, log g, chemical abundances (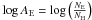 for an element E), and microturbulent velocity vmicro are interdependant and simultaneously affect the depth, width, and shape of spectral absorption lines, they have to be determined simultaneously. Numerous methods exist for this analysis, but very few of them are suitable in the particular case of HD 104237. Owing to the non-standard shape of HAeBe spectral energy distributions (IR excesses, UV depletion), classical photometric determination of Teff have to be considered with caution. Another frequently used method, the stellar parameter determination using Balmer lines had to be excluded because of core emission in the line and/or P Cygni profiles, but also on a technical side because of normalization problems for high-dispersion echelle spectra. Techniques based on line ratios for determining Teff (see e.g. Sousa et al. 2010) could not be applied owing to the too few workable lines (see Sect. 6.1.3). Photospheric lines of HD 104237 reveal additional broadening agents that are difficult to model, which led us to discard direct spectrum fitting.
for an element E), and microturbulent velocity vmicro are interdependant and simultaneously affect the depth, width, and shape of spectral absorption lines, they have to be determined simultaneously. Numerous methods exist for this analysis, but very few of them are suitable in the particular case of HD 104237. Owing to the non-standard shape of HAeBe spectral energy distributions (IR excesses, UV depletion), classical photometric determination of Teff have to be considered with caution. Another frequently used method, the stellar parameter determination using Balmer lines had to be excluded because of core emission in the line and/or P Cygni profiles, but also on a technical side because of normalization problems for high-dispersion echelle spectra. Techniques based on line ratios for determining Teff (see e.g. Sousa et al. 2010) could not be applied owing to the too few workable lines (see Sect. 6.1.3). Photospheric lines of HD 104237 reveal additional broadening agents that are difficult to model, which led us to discard direct spectrum fitting.
Our finally adopted method consists of comparing the EW of selected lines present in our reference spectrum with those extracted from a fine 3D-grid of synthetic spectra (the dimensions being Teff, log g and iron abundance). The high activity level of this HAe star (emission, variability, line asymmetry) and its binarity make a reliable determination of fundamental parameters in this case very challenging.
6.1.1. Correction of the secondary’s spectral contribution
Since our main goal was to determine the fundamental parameters of the primary component, we had to correct for the polluting spectroscopic contribution of the secondary component, HD 104237b. Indeed, although the secondary is more than 1 dex fainter than the primary component, it is also approximately 4000 K cooler and contributes with strong metallic absorption lines, leading to systematic contamination of primary lines and even lowering the continuum level in some parts of the spectrum. To free the observed spectrum from this effect, a synthetic spectrum corresponding to the secondary component’s contribution was substracted from the observed spectrum. A χ2 minimization indicated a likely secondary Teff value of 4500 K. Still, residual systematic uncertainties of the monochromatic luminosity ratio and the intrinsic stellar parameter selection of the secondary do certainly persist and are difficult to take into account.
6.1.2. Construction of a 3D-grid of synthetic spectra
Characteristics of absorption lines selected for the fundamental parameter determination.
The fundamental parameter determination method we adopted required the construction of a 3-dimensional grid (Teff, log g, log AFe) of synthetic spectra based on line catalogs provided by the VALD database as input of the SYNTH3 spectrum synthesis code (Kochukhov 2007), each spectrum covering a wavelength range from 4400 Å to 7000 Å. The SYNTH3 code assumes local thermodynamic equilibrium (LTE) and a plane-parallel hydrostatic stellar model atmosphere. For early-type stars input models are provided by the well-known Kurucz program suite. We selected solar abundance atmosphere models from the grid after checking that the effect of an input model that contains metallicities slightly different from solar is of secondary importance on the calculated synthetic spectrum.
The grid boundaries covered previously determined parameters: 7500 K ≤ Teff ≤ 9500 K and 3.5 ≤ log g ≤ 4.5. Since it is not uncommon to find HAeBe stars that simultaneously show some elements in suprasolar abundance in their spectra, whereas other ones are subsolar (see e.g. Acke & Waelkens 2004) without a particular trend in terms of global metallicity, we decided to modify only the Fe abundance in our VALD requests. log AFe values comprised between −4.84 and −4.00 seemed to be reasonable, i.e., of [Fe/H] values between –0.3 and +0.54 with respect to the solar Fe abundance given in VALD (log AFe⊙ = −4.54). Typical values of vmicro found in the literature were 2–3 km s-1(see e.g. Acke & Waelkens 2004; Guimarães et al. 2006; Catala et al. 2007). We therefore fixed a value of 2 km s-1 for the microturbulent velocity HD 104237. The resulting grid was refined by interpolating between the models that were initially spaced by steps of 250 K and 0.5 (log g).
6.1.3. Photospheric line selection and EW measurements
The photospheric absorption lines retained for our study had to satisfy several selection criteria. Only lines were kept when they existed in all line lists of our grid above a minimum threshold. We excluded blends with other than iron lines, and avoided pollution by potential residuals of the secondary spectrum. Variable and emission lines were rejected. Lines had to be strong enough with respect to local noise to minimize relative uncertainties on EW and to be able to neglect residual contribution from very faint lines of the primary’s and the secondary’s spectra, inherent to the extraction threshold of VALD requests. As a result, we kept weak and moderatly strong lines (15 mÅ ≤ EWobs ≤ 100 mÅ). Moreover, the nearby continuum of the line had to be free of emission components. We had to verify that selected lines cover a wide variety of excitation potentials, ionization stages, and wavelengths. Atomic parameters were verified, in particular log gf values (comparison with Fuhr & Wiese 2006; Meléndez & Barbuy 2009). This rigorous selection resulted in a set of only ten spectral lines (eight Fe I lines and two Fe II lines) which are listed in Table 4.
Equivalent width measurements of our selected lines were carried out using a trapezoidal integration. For consistency, the identical extraction limits were used for the integration of a given line from the observed spectrum and the synthetic spectra. To extract errors on EW values, we assumed that they mainly came from local averaged photon noise (multiplied by the line integration width).
6.2. Teff, log g, and Fe abundance determination
We then computed the degree of similarity between our observed spectrum and all synthetic spectra of our 3D-grid by means of the ten previously measured EW. A maximum-likelihood-estimation was performed by minimizing a reduced merit function Sred following Press et al. (1992).
A preliminary computation of the reduced merit function whithin the whole 3D-grid of synthetic spectra, whithout any additional constraint, yielded a Teff value of 8775 K, a log g value of 4.2, and a log AFe value of − 4.25 , i.e. [Fe/H] = + 0.29. With a confidence level of 68.3% we found the following uncertainties: 525 K on Teff, 0.7 on log g and 0.35 on log AFe. With a confidence level of 95.4% we determined the uncertainties to be 700 K on Teff and 0.48 on log AFe, the low sensitivity to log g does not allow the determination of the 95.4% confidence level for log g within our parameter space.
The lack of selected lines is responsible for the quite large uncertainties in the 3D-parameter space. Therefore we added the additional physical constraint provided by the excitation potential: if Teff is well determined, all spectral lines corresponding to a specified ion, and with a given excitation potential, should provide the same abundance determination. We therefore only kept stellar models yielding a zero ± 1σ slope regression line (through the distribution log AFe = f(χ), with χ being the excitation potential). Recalculating a minimum value of the reduced merit function Sred for this subset of models yielded significantly more precise parameters: Teff= 8550 K, log g= 3.9 and log AFe = −4.38( [Fe/H] = + 0.16). Surface gravity log g is the less accurately determined stellar parameter because of the lower sensibility of the selected lines to this parameter. The results are shown in Fig. 7 and summarized in Table 5.
 |
Fig. 7 2D-repartition of the Sred values as a function of Teff and log AFe. The white X represents the best model (Teff = 8550 K, log g = 3.9,log AFe = −4.38). Boundaries are shown for the 68.3% and 95.4% confidence intervals. Gray crosses show the parameter space investigated, after selecting models that satisfied the excitation potential criterium. |
Fundamental parameters of HD 104237 determined in this study.
7. Discussion and conclusions
We presented an in-depth analysis of the prototype Herbig Ae star HD 104237. The star was previously identified as a PMS δ Scuti pulsator, and the comprehensive line profile analysis of the extended quasi-continuous high-resolution spectroscopic time series obtained at SAAO from April 22–26, 1999 has confirmed the main frequencies that were discovered by radial velocity analysis in Böhm et al. (2004). For the first time, the less than 1.5% continuum level variations of the equivalent photospheric LSD profiles were studied and a direct confirmation of the presence of at least one non radial pulsations could be performed. Based on a Fourier 2D analysis we identified the dominant mode as an azimuthal order m = ± 1, and a most likely ℓ value of 1 or 2. Since HD 104237 is a moderate rotator with vsini of only 12 ± 2 km s-1 it will be difficult to access to additional mode identifications in the future. A potential approach would be to organize multi-site continuous observations with significantly higher resolution echelle spectrographs, ideally with R ≥ 70 000. On the mode identification aspect a modification of the FAMIAS code working with asymmetric photospheric profiles would be a great progress.
To prepare a forthcoming asteroseismic modeling of this particular star we needed to redetermine very precisely its fundamental stellar parameters. Because HD 104237 is a multiple system with a nearby spectroscopic binary companion, we decided to concentrate on the periastron night 12 of April 2000, present in our data set of spectra acquired at SAAO (and described in Böhm et al. 2004). To combine all spectra of this particular night into one high S/N reference spectrum, we developed an optimized spectral continuum determination tool. As a result, the reference spectrum had an S/N value of close to 400 per resolved element at 550 nm.
The detailed study of the fundamental stellar parameters has provided values of Teff = 8550 ± 150 K, log g = 3.9 ± 0.3 and log AFe = 4.38 ± 0.19 (i.e. [Fe/H] = + 0.16 ± 0.19), the error bars corresponding to the 68.3% confidence interval. A particular effort was made for the statistically correct determination of the associated error bars. In a review of Teff and log g determination methods, Smalley (2005) mentioned optimal error bars to be of ± 100 K for Teff, ± 0.2 for log g and on the order of 0.05 to 0.1 in abundance. Owing the high level of activity of HAeBe stars, and in the case our target star the spectroscopic binarity, it is very difficult to obtain a sufficiently large number of unpolluted, exploitable photospheric spectral lines of a given ion; the achievable uncertainties remain therefore fairly large. In addition, a wrong estimate of the contribution of the secondary, both in spectral class and in luminosity, might lead to systematic errors that are very difficult to take into account. However, we estimated these errors to be of secondary importance in our study.
Because the surface gravity was difficult to constrain in our spectroscopic approach, the associated luminosity ratio (based on the empirical mass-luminosity relation by Malkov 2007) was determined to be log (L⋆/L⊙) = 1.59 ± 0.44, a value centered on the result by van den Ancker et al. (1998), whose authors determined 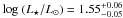 . In constrast, our spectroscopic effective temperature determination is significantly improved with Teff = 8550 ± 150 K, again centered on the central value of van den Ancker et al. (1998), whose result was Teff = 8500 ± 500 K, the latter error bars having been estimated. Our independent spectroscopic approach therefore tends to confirm the previously photometrically determined values by van den Ancker et al. (1998). Combining the two results would yield the following most likely fundamental parameters:
. In constrast, our spectroscopic effective temperature determination is significantly improved with Teff = 8550 ± 150 K, again centered on the central value of van den Ancker et al. (1998), whose result was Teff = 8500 ± 500 K, the latter error bars having been estimated. Our independent spectroscopic approach therefore tends to confirm the previously photometrically determined values by van den Ancker et al. (1998). Combining the two results would yield the following most likely fundamental parameters: 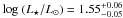 , corresponding to log g = 3.93 ± 0.09, and Teff = 8550 ± 150 K. Fig. 8 shows well the intersection between our new results and previously determined parameters from van den Ancker et al. (1998). At this stage it is important to mention that error bars by van den Ancker et al. (1998) and Grady et al. (2004) might be largely underestimated.
, corresponding to log g = 3.93 ± 0.09, and Teff = 8550 ± 150 K. Fig. 8 shows well the intersection between our new results and previously determined parameters from van den Ancker et al. (1998). At this stage it is important to mention that error bars by van den Ancker et al. (1998) and Grady et al. (2004) might be largely underestimated.
 |
Fig. 8 New fundamental stellar parameters of the primary (A) component of HD 104237, located in the HR diagram of Böhm et al. (2004). The location of the secondary component HD 104237 b (B) is also indicated. The luminosity and effective temperature pairs reported in van den Ancker et al. (1998) (VA) and Grady et al. (2004) (GR) are shown in the diagram, including their estimated error bars, along with our new parameters (FB), associated with error with an 68.3% confidence interval. Evolutionary tracks (1.5, 2.0 and 2.5 M⊙) and isochrones are by Palla & Stahler (2001). The Marconi & Palla (1998) instability strip is represented by the shaded area. |
Acke & Waelkens (2004) determined an iron abundance of [Fe/H] = +0.09 ± 0.19. Our new result of the abundance, [Fe/H]= + 0.16 ± 0.19, confirms the conclusion that HD 104237 might be slightly overabundant. Vick et al. (2011) recently calculated self-consistent stellar evolution models in this mass range including atomic diffusion; they concluded that for mass loss ranges above 10-12 M⊙ yr-1 no surface abundance anomalies are expected. HD 104237 shows a very strong Hα line with a complex profile, which tends to indicate significantly higher mass loss rates, similar to other Herbig Ae stars showing typical mass loss rates on the order of 10-7 − 10-8 M⊙ yr-1 (see e.g. Bouret & Catala 1998). Taking these new simulations into account, we conclude on a close to solar iron abundance for HD 104237, which is clearly within the error bars of both studies.
We mention at this stage that several assumptions have been made in this study, on the modeling side (LTE, plane-parrallel spectrum synthesis), on the contribution of the faint secondary (ratio of black-body fluxes), on the threshold of line selection, interpolation of models in our grid, but also the assumed photospheric line formation region of our lines of interest, among others. Although these residual errors should be negligible for our study, further improvements on line selection and analysis, such as a combined treatment of blended lines, will lead to increasingly better constrained fundamental parameters in the future.
A forthcoming article (Fumel et al., in prep.) will describe the asteroseismic modeling of the primary component of HD 104237.
Acknowledgments
The authors want to thanck N. Grevesse for interesting and fruitful discussions about stellar parameter determination and his critical advice about atomic parameters. Warm thanks also to H. Carfantan for precious discussions about the statistically meaningful use of the χ2 quantity and his advice concerning error bar determination in multiple dimension parameter spaces. Many thanks also to F. Lignières, P. Petit and P. Fouqué for their important comments on the approach we adopted. We acknowledge the Vienna Atomic Line Data base we used for our research work. Our thoughts are going to P. Reegen for his important contribution to time series analysis.
References
- Acke, B., & Waelkens, C. 2004, A&A, 427, 1009 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Anders, E., & Grevesse, N. 1989, Geochim. Cosmochim. Acta, 53, 197 [Google Scholar]
- Baines, D., Oudmaijer, R. D., Porter, J. M., & Pozzo, M. 2006, MNRAS, 367, 737 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- Bertout, C., Basri, G., & Bouvier, J. 1988, ApJ, 330, 350 [NASA ADS] [CrossRef] [Google Scholar]
- Böhm, T., & Catala, C. 1995, A&A, 301, 155 [NASA ADS] [Google Scholar]
- Böhm, T., Catala, C., Donati, J.-F., et al. 1996, A&AS, 120, 431 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Böhm, T., Catala, C., Balona, L., & Carter, B. 2004, A&A, 427, 907 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Böhm, T., Dupret., M. A., & Aynedjian, H. 2006, Mem. Soc. Astron. It., 77, 362 [NASA ADS] [Google Scholar]
- Böhm, T., Zima, W., Catala, C., et al. 2009, A&A, 497, 183 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bouret, J.-C., & Catala, C. 1998, A&A, 340, 163 [NASA ADS] [Google Scholar]
- Breger, M. 1972, ApJ, 171, 539 [NASA ADS] [CrossRef] [Google Scholar]
- Breger, M., Stich, J., Garrido, R., et al. 1993, A&A, 271, 482 [NASA ADS] [Google Scholar]
- Brown, A., Djie, H. R. E. T. A., Blondel, P. F. C., et al. 1997, in Accretion Phenomena and Related Outflows, ed. D. T. Wickramasinghe, G. V. Bicknell, & L. Ferrario, IAU Colloq. 163, ASP Conf. Ser., 121, 448 [Google Scholar]
- Catala, C. 1988, A&A, 193, 222 [NASA ADS] [Google Scholar]
- Catala, C. 2003, Ap&SS, 284, 53 [NASA ADS] [CrossRef] [Google Scholar]
- Catala, C., & Kunasz, P. B. 1987, A&A, 174, 158 [NASA ADS] [Google Scholar]
- Catala, C., & Talavera, A. 1984, A&A, 140, 421 [NASA ADS] [Google Scholar]
- Catala, C., Czarny, J., Felenbok, P., & Praderie, F. 1986a, A&A, 154, 103 [NASA ADS] [Google Scholar]
- Catala, C., Felenbok, P., Czarny, J., Talavera, A., & Boesgaard, A. M. 1986b, ApJ, 308, 791 [NASA ADS] [CrossRef] [Google Scholar]
- Catala, C., Alecian, E., Donati, J.-F., et al. 2007, A&A, 462, 293 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Donati, J., Semel, M., Carter, B. D., Rees, D. E., & Collier Cameron, A. 1997, MNRAS, 291, 658 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- Dupret, M.-A., Böhm, T., Goupil, M.-J., Catala, C., & Grigahcene, A. 2006, Commun. Asteroseismol., 147, 72 [NASA ADS] [CrossRef] [Google Scholar]
- Dupret, M.-A., Théado, S., Böhm, T., et al. 2007, Commun. Asteroseismol., 150, 59 [NASA ADS] [CrossRef] [Google Scholar]
- Feigelson, E. D., Lawson, W. A., & Garmire, G. P. 2003, ApJ, 599, 1207 [NASA ADS] [CrossRef] [Google Scholar]
- Fuhr, J. R., & Wiese, W. L. 2006, J. Phys. Chem. Ref. Data, 35, 1669 [NASA ADS] [CrossRef] [Google Scholar]
- Gilliland, R. L. 1986, ApJ, 300, 339 [NASA ADS] [CrossRef] [Google Scholar]
- Grady, C. A., Woodgate, B., Torres, C. A. O., et al. 2004, ApJ, 608, 809 [NASA ADS] [CrossRef] [Google Scholar]
- Guimarães, M. M., Alencar, S. H. P., Corradi, W. J. B., & Vieira, S. L. A. 2006, A&A, 457, 581 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Herbig, G. H. 1960, ApJS, 4, 337 [NASA ADS] [CrossRef] [Google Scholar]
- Hu, J. Y., The, P. S., & de Winter, D. 1989, A&A, 208, 213 [NASA ADS] [Google Scholar]
- Hu, J. Y., Blondel, P. F. C., The, P. S., et al. 1991, A&A, 248, 150 [NASA ADS] [Google Scholar]
- Iben, Jr., I. 1965, ApJ, 141, 993 [NASA ADS] [CrossRef] [Google Scholar]
- Iben, I., & Renzini, A. 1984, Phys. Rep., 105, 329 [NASA ADS] [CrossRef] [Google Scholar]
- Kennelly, E. J. 1994, Ph.D. Thesis, The University Of British Columbia (Canada) [Google Scholar]
- Kennelly, E. J., Walker, G. A. H., Matthews, J. M., & Merryfield, W. J. 1993, in GONG 1992, Seismic Investigation of the Sun and Stars, ed. T. M. Brown, ASP Conf. Ser., 42, 359 [Google Scholar]
- Kennelly, E. J., Walker, G. A. H., Catala, C., et al. 1996, A&A, 313, 571 [Google Scholar]
- Kochukhov, O. P. 2007, in Physics of Magnetic Stars, Proc. Int. Conf., Special Astrophysical Observatory of the Russian AS, 109 [Google Scholar]
- Kupka, F., Piskunov, N., Ryabchikova, T. A., Stempels, H. C., & Weiss, W. W. 1999, A&AS, 138, 119 [NASA ADS] [CrossRef] [EDP Sciences] [MathSciNet] [PubMed] [Google Scholar]
- Kupka, F. G., Ryabchikova, T. A., Piskunov, N. E., Stempels, H. C., & Weiss, W. W. 2000, Baltic Astron., 9, 590 [Google Scholar]
- Kurtz, D. W., & Marang, F. 1995, MNRAS, 276, 191 [NASA ADS] [Google Scholar]
- Kurtz, D. W., & Müller, M. 1999, MNRAS, 310, 1071 [NASA ADS] [CrossRef] [Google Scholar]
- Kuschnig, R., Weiss, W. W., Gruber, R., Bely, P. Y., & Jenkner, H. 1997, A&A, 328, 544 [NASA ADS] [Google Scholar]
- Lenz, P., & Breger, M. 2005, Commun. Asteroseismol., 146, 53 [NASA ADS] [CrossRef] [Google Scholar]
- Lignieres, F., Catala, C., & Mangeney, A. 1996, A&A, 314, 465 [Google Scholar]
- Luhman, K. L. 2004, ApJ, 616, 1033 [NASA ADS] [CrossRef] [Google Scholar]
- Lyo, A.-R., Lawson, W. A., & Bessell, M. S. 2008, MNRAS, 389, 1461 [NASA ADS] [CrossRef] [Google Scholar]
- Malkov, O. Y. 2007, MNRAS, 382, 1073 [NASA ADS] [CrossRef] [Google Scholar]
- Marconi, M., & Palla, F. 1998, ApJ, 507, L141 [NASA ADS] [CrossRef] [Google Scholar]
- Marconi, M., & Palla, F. 2004, in The A-Star Puzzle, ed. J. Zverko, J. Ziznovsky, S. J. Adelman, & W. W. Weiss, IAU Symp., 224, 69 [Google Scholar]
- Meeus, G., Waters, L. B. F. M., Bouwman, J., et al. 2001, A&A, 365, 476 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Meléndez, J., & Barbuy, B. 2009, A&A, 497, 611 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Palla, F., & Stahler, S. W. 1990, ApJ, 360, L47 [NASA ADS] [CrossRef] [Google Scholar]
- Palla, F., & Stahler, S. W. 1993, ApJ, 418, 414 [NASA ADS] [CrossRef] [Google Scholar]
- Palla, F., & Stahler, S. W. 1999, ApJ, 525, 772 [NASA ADS] [CrossRef] [Google Scholar]
- Palla, F., & Stahler, S. W. 2001, ApJ, 553, 299 [NASA ADS] [CrossRef] [Google Scholar]
- Piskunov, N. E., Kupka, F., Ryabchikova, T. A., Weiss, W. W., & Jeffery, C. S. 1995, A&AS, 112, 525 [NASA ADS] [Google Scholar]
- Praderie, F., Felenbok, P., Czarny, J., Talavera, A., & Boesgaard, A. M. 1982, ApJ, 254, 658 [NASA ADS] [CrossRef] [Google Scholar]
- Praderie, F., Catala, C., Simon, T., & Boesgaard, A. M. 1986, ApJ, 303, 311 [NASA ADS] [CrossRef] [Google Scholar]
- Press, W. H., Teukolsky, S. A., Vetterling, W. T., & Flannery, B. P. 1992, Numerical recipes in FORTRAN, The art of scientific computing [Google Scholar]
- Reegen, P. 2007, A&A, 467, 1353 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ripepi, V., Marconi, M., Bernabei, S., et al. 2003, A&A, 408, 1047 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ryabchikova, T. A., Piskunov, N. E., Kupka, F., & Weiss, W. W. 1997, Baltic Astron., 6, 244 [Google Scholar]
- Siess, L., Dufour, E., & Forestini, M. 2000, A&A, 358, 593 [NASA ADS] [Google Scholar]
- Smalley, B. 2005, Mem. Soc. Astron. Ital. Suppl., 8, 130 [Google Scholar]
- Sneden, C. A. 1973, Ph.D. Thesis, The University of Texas at Austin [Google Scholar]
- Sousa, S. G., Alapini, A., Israelian, G., & Santos, N. C. 2010, A&A, 512, A13 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Testa, P., Huenemoerder, D. P., Schulz, N. S., & Ishibashi, K. 2008, ApJ, 687, 579 [NASA ADS] [CrossRef] [Google Scholar]
- van den Ancker, M. E., The, P. S., Tjin A Djie, H. R. E., et al. 1997, A&A, 324, L33 [NASA ADS] [Google Scholar]
- van den Ancker, M. E., de Winter, D., & Tjin A Djie, H. R. E. 1998, A&A, 330, 145 [NASA ADS] [Google Scholar]
- Vick, M., Michaud, G., Richer, J., & Richard, O. 2011, A&A, 526, A37 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Wade, G. A., Bagnulo, S., Drouin, D., Landstreet, J. D., & Monin, D. 2007, MNRAS, 376, 1145 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- Waters, L. B. F. M., & Waelkens, C. 1998, ARA&A, 36, 233 [NASA ADS] [CrossRef] [Google Scholar]
- Zima, W. 2008, Commun. Asteroseismol., 155, 17 [Google Scholar]
- Zima, W., Wright, D., Bentley, J., et al. 2006, A&A, 455, 235 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Zwintz, K. 2008, ApJ, 673, 1088 [NASA ADS] [CrossRef] [Google Scholar]
- Zwintz, K., Marconi, M., Kallinger, T., & Weiss, W. W. 2004, in The A-Star Puzzle, ed. J. Zverko, J. Ziznovsky, S. J. Adelman, & W. W. Weiss, IAU Symp., 224, 353 [Google Scholar]
All Tables
Characteristics of absorption lines selected for the fundamental parameter determination.
All Figures
 |
Fig. 1 Line profile variations due to the non-radial pulsations of HD 104237. The deviations from the mean intensity are displayed for four different nights (top left: April 22, 1999, bottom left: April 23, 1999, top right: April 24, 1999, bottom right: April 25, 1999). Dashed lines represent the limits of the equivalent profile, an additional broadening agent generates wings reaching almost ± 2 vsini, i.e. twice the width of a pure rotational profile at continuum level. |
| In the text | |
 |
Fig. 2 Amplitude variation of the central velocity bins of the residual LSD profile on the nights Apr. 22 to 26, 1999. Superimposed is a fit of the data corresponding to the result of the frequency analysis as presented in Table 3. |
| In the text | |
 |
Fig. 3 Periodogram of the line center variation as shown in Fig. 2, without prewithening. The large bulk of frequencies around 29-36 d-1can be seen, as well as the 3.2, 3.6 and 4.0 mean-ampitude level of the noise determined by prewithening F1 to F9, corresponding to a 90%, 99% and 99.9% significance level, respectively. |
| In the text | |
 |
Fig. 4 Same figure as Fig. 3, but prewithened by F1 to F8. As shown, F9 is present, well above the 99.9% confidence level. |
| In the text | |
 |
Fig. 5 Combined F2D analysis of HD 104237 for the nights of April 22 to 25, 1999. |
| In the text | |
 |
Fig. 6 Individual (thin line) and summed (thick line) normalized spectrum of the periastron night around one of the selected lines (Fe I 5415.1920 Å). Synthetic spectra with Teff = 8500 K (dotted line) and Teff = 4750 K (dashed line) were overplotted (log g = 4.0, vmicro = 2 km s-1 solar abundances for both spectra), showing the location of the individual lines. The secondary’s spectrum was corrected by the local luminosity ratio. Neither fundamental parameters nor local luminosity ratios are perfectly tuned at this stage. |
| In the text | |
 |
Fig. 7 2D-repartition of the Sred values as a function of Teff and log AFe. The white X represents the best model (Teff = 8550 K, log g = 3.9,log AFe = −4.38). Boundaries are shown for the 68.3% and 95.4% confidence intervals. Gray crosses show the parameter space investigated, after selecting models that satisfied the excitation potential criterium. |
| In the text | |
 |
Fig. 8 New fundamental stellar parameters of the primary (A) component of HD 104237, located in the HR diagram of Böhm et al. (2004). The location of the secondary component HD 104237 b (B) is also indicated. The luminosity and effective temperature pairs reported in van den Ancker et al. (1998) (VA) and Grady et al. (2004) (GR) are shown in the diagram, including their estimated error bars, along with our new parameters (FB), associated with error with an 68.3% confidence interval. Evolutionary tracks (1.5, 2.0 and 2.5 M⊙) and isochrones are by Palla & Stahler (2001). The Marconi & Palla (1998) instability strip is represented by the shaded area. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


