| Issue |
A&A
Volume 539, March 2012
|
|
|---|---|---|
| Article Number | A76 | |
| Number of page(s) | 14 | |
| Section | Extragalactic astronomy | |
| DOI | https://doi.org/10.1051/0004-6361/201117929 | |
| Published online | 24 February 2012 | |
The fast evolution of SN 2010bh associated with XRF 100316D⋆
1 Max-Planck-Institute für extraterrestrische Physik, Giessenbachstraße 1, 85748 Garching, Germany
e-mail: foe@mpe.mpg.de
2 Thüringer Landessternwarte Tautenburg, Sternwarte 5, 07778 Tautenburg, Germany
3 Universe Cluster, Technische Universität München, Boltzmannstraße 2, 85748 Garching, Germany
4 Dark Cosmology Centre, Niels Bohr Institute, University of Copenhagen, Juliane Maries Vej 30, 2100 Copenhagen, Denmark
5 CRESST and the Observational Cosmology Laboratory, NASA/GSFC, Greenbelt, MD 20771, USA
6 Department of Astronomy, University of Maryland, College Park, MD 20742, USA
Received: 22 August 2011
Accepted: 31 October 2011
Context. The first observational evidence of a connection between supernovae (SNe) and gamma-ray bursts (GRBs) was found about a decade ago. Since then, only half a dozen spectroscopically confirmed associations have been discovered and XRF 100316D/SN 2010bh is among the latest.
Aims. We constrain the progenitor radius, the host-galaxy extinction, and the physical parameters of the explosion of XRF 100316D and its associated SN 2010bh at z = 0.059. We study the brightness and colours of SN 2010bh in the context of GRB-SNe.
Methods. We began observations 12 h after the GRB trigger and continued until 80 days after the burst. The Gamma-Ray burst Optical and Near-infrared Detector (GROND) provided excellent photometric data of XRF 100316D/SN 2010bh in six filter bands covering a wavelength range from approximately 350 to 1800 nm, significantly expanding the pre-existing data set for this event. Combining GROND and Swift data, the early broad-band spectral energy distribution (SED) is modelled with a blackbody and afterglow component attenuated by dust and gas absorption. The temperature and radius evolution of the thermal component are analysed and combined with earlier measurements available from the literature. Templates of SN 1998bw are fitted to the SN itself to directly compare the light-curve properties. Finally, a two-component parametrised model is fitted to the quasi-bolometric light curve, which delivers physical parameters of the explosion.
Results. The best-fit models to the broad-band SEDs imply moderate reddening along the line of sight through the host galaxy (AV,host = 1.2 ± 0.1 mag). Furthermore, the parameters of the blackbody component reveal a cooling envelope at an apparent initial radius of 7 × 1011 cm, which is compatible with a dense wind surrounding a Wolf-Rayet star. A multicolour comparison shows that SN 2010bh is 60–70% as bright as SN 1998bw. It proves to be the most rapidly evolving GRB-SNe to date, reaching maximum brightness at 8–9 days after the burst in the blue bands. Modelling of the quasi-bolometric light curve yields MNi = 0.21 ± 0.03 M⊙ and Mej = 2.6 ± 0.2 M⊙, typical of values within the GRB-SN population. The kinetic energy is Ek = (2.4 ± 0.7) × 1052 erg, which is making this SN the second most energetic GRB-SN after SN 1998bw.
Conclusions. This supernova has one of the earliest peaks ever recorded and thereafter fades more rapidly than other GRB-SNe, hypernovae, or typical type-Ic SNe. This implies that a thin envelope is possibly expanding at very high velocities and is, therefore, unable to retain the γ-rays that would prolong the duration of the SN event.
Key words: gamma-ray burst: general / gamma-ray burst: individual: XRF 100316D / supernovae: individual: SN 2010bh / supernovae: general
Appendix is available in electronic form at http://www.aanda.org
© ESO, 2012
1. Introduction
The core collapse of massive stars is thought to give rise to supernovae (SNe) and long-duration gamma-ray bursts (GRBs, durations larger than 2 s; Kouveliotou et al. 1993). The first clue to the connection between these events is the similarity in their kinetic-energy scale (see Woosley & Bloom 2006, for a review). Even before the discoveries of the late 90’s, a few authors discussed the possible association between high-energy outbursts and SNe (Colgate 1968; Paczyński 1986). In theory, the collapsing core of a very massive star, whose envelope has been blown away by its own stellar winds, i.e., a Wolf-Rayet (WR) star, can lead to the formation of a relativistic jet that will produce high-energy emission (Woosley 1993; Woosley & MacFadyen 1999) in the form of a GRB or an X-ray flash (XRF, softer events thought to be mainly produced by the same mechanism as GRBs; Heise et al. 2001; Kippen et al. 2004; Sakamoto et al. 2005; Heise & in ’t Zand 2001). When the jet collides with the circumstellar material, it produces a multi-wavelength afterglow (for a review, see Zhang & Mészáros 2004). Theoretically, the energy of the core collapse should also be capable of expanding the remaining envelope. However, it is unclear how this can happen, or even if there is always enough energy for a SN explosion. The kind of SN thought to be associated with GRBs are those called stripped-envelope (SE) SNe, whose hydrogen envelope have mostly been removed. Events such as these are unusually energetic stellar explosions and sometimes labelled “hypernovae” in the literature (e.g., Paczyński 1998; Hansen 1999).
To date, only type-Ic SNe have been related to GRBs. The first and most representative case was that of SN 1998bw, which was found to be associated with the soft GRB 980425 (e.g., Galama et al. 1998b; Kippen et al. 1998). A couple of days after the trigger, SN 1998bw was discovered (Galama et al. 1998a; Sadler et al. 1998) inside the 8′ error circle of GRB 980425 (Soffitta et al. 1998) in the underluminous late-type galaxy ESO184–G82 (z = 0.0085; Tinney et al. 1998). Although initially controversial (Galama et al. 1998b; Pian et al. 1998), the physical association between these objects was supported on temporal and spatial grounds by the slowly variable X-ray source at the position of the SN (Pian et al. 2000; Kouveliotou et al. 2004). As a result of this connection, both the GRB and SN research fields, which until then had both evolved more or less independently, were revolutionised by a single event.
Five years after SN 1998bw, the association between GRB 030329 and SN 2003dh came to light through a clear spectroscopic identification (Hjorth et al. 2003; Kawabata et al. 2003; Stanek et al. 2003; Matheson et al. 2003) and became the first truly solid piece of evidence in favour of the GRB-SN connection. Moreover, after 1998 there have been many other spectroscopic associations, such as the cases of GRBs 021211 (SN 2002lt; Della Valle et al. 2003), 020903 (Soderberg et al. 2005; Bersier et al. 2006), 031203 (SN 2003lw; Malesani et al. 2004), 050525A (SN 2005nc; Della Valle et al. 2006b), 060218 (SN 2006aj; Pian et al. 2006), 081007 (SN 2008hw; Della Valle et al. 2008), 091127 (SN 2009nz; Berger et al. 2011; Cobb et al. 2010; Filgas et al. 2011), and 101219B (SN 2010ma; Sparre et al. 2011) based on hypernova features in their spectra.
Furthermore, late-time bumps in the light curves of GRB afterglows have been interpreted as SN signals, e.g., GRBs 970228 (Reichart 1999; Galama et al. 2000; Reichart et al. 2000), 980326 (Castro-Tirado & Gorosabel 1999; Bloom et al. 1999), 011121 (Bloom et al. 2002; Greiner et al. 2003), 020405 (Price et al. 2003; Masetti et al. 2003), 040924 (Soderberg et al. 2006; Wiersema et al. 2008), 041006 (Stanek et al. 2005; Soderberg et al. 2006), 050824 (Sollerman et al. 2007), 060729, and 090618 (both in Cano et al. 2011a) to mention a few. These bumps show consistency in terms of colour, timing, and brightness with those expected for the GRB-SN population, but they are usually faint, which hampers the spectroscopic identification. These re-brightenings have been detected in GRB light curves out to redshifts of ~1 (Masetti et al. 2005; Della Valle et al. 2003; Bloom et al. 2009; Tanvir et al. 2010) owing to the sensitivity of current ground-based telescopes dedicated to follow-up observations. Sample studies of GRB-SNe (including bumps not spectroscopically identified) have been carried out to determine the luminosity distribution, the morphology of the light curves, and the physical parameters of the explosion such as kinetic energy, ejected mass, and 56Ni mass (Zeh et al. 2004; Ferrero et al. 2006; Richardson 2009; Thöne et al. 2011). It has been asserted that GRB-SNe are in general brighter than the local sample of SE SNe, except for cases such as SN 2010ay (Sanders et al. 2011). In contrast to the claims of Stanek et al. (2005), no correlation has been found between the brightness at maximum with the shape of the light curve (Ferrero et al. 2006).
Additional information about the explosion can be obtained from its early emission. One particular case is that of the soft XRF 060218 associated with SN 2006aj (Campana et al. 2006; Pian et al. 2006; Ferrero et al. 2006; Cobb et al. 2006; Modjaz et al. 2006; Sollerman et al. 2006; Mirabal et al. 2006). This displayed an early X-ray and UV emission, which was interpreted as thermal radiation produced by the shock breakout from the surface of the progenitor (Colgate 1974; Falk 1978; Klein & Chevalier 1978; Matzner & McKee 1999; Waxman et al. 2007; Nakar & Sari 2010). The envelope is heated up and owing to expansion it starts to adiabatically cool, which then shifts the emission to UV and optical wavelengths. From the analysis of this a signal, it is possible to constrain the afterglow component, derive both the temperature and luminosity of the thermal component, and compute the apparent radius of emission (e.g., Thöne et al. 2011). Other examples include SNe without detectable γ-ray emission that nevertheless exhibit adiabatic cooling in the UV/optical and/or X-ray observations: SN 2008D (Soderberg et al. 2008; Malesani et al. 2009; Modjaz et al. 2009; Mazzali et al. 2008), SN 2008ax (Roming et al. 2009), SNLS-04D2dc (Schawinski et al. 2008), and SN 2010aq (Gezari et al. 2010), to mention a few. As additional information, it has been claimed that high-energy emission in GRB-SNe comes from accelerated shock-breakout photons rather than highly relativistic jets (Wang et al. 2007).
Whilst no SN signature is expected for short GRBs, which are thought to be produced by the mergers of compact objects (for deep non-detections, see the cases of GRB 050509B in Hjorth et al. 2005a; and Bloom et al. 2006, and GRB 050709 in Fox et al. 2005; and Hjorth et al. 2005b), there are a few supposedly long events where an expected SN appearance was never detected. In the cases of GRBs 060505 (Fynbo et al. 2006; Ofek et al. 2007) and 060614 (Fynbo et al. 2006; Gal-Yam et al. 2006; Della Valle et al. 2006a), there are very tight constraints on the SN signature, which go down to 1% as bright as SN 1998bw. The validity of the non-detections of SNe components for these two GRBs as a classification tool is a point of controversy (e.g., Zhang et al. 2009). We refer to Kann et al. (2011) for an exhaustive discussion on GRBs 060505 and 060614, in the light of the optical luminosity of their afterglows.
We analysed the optical and near-infrared (NIR) data of XRF 100316D and its associated SN 2010bh. The paper is organised by summarising the observations, data acquisition, reduction, and analysis in Sect. 2. The main results are treated separately as three different sections. The modelling of the early broad-band spectral energy distribution (SED) provides the progenitor radius and the host-galaxy extinction and is presented in Sect. 3. The multi-wavelength light and colour curves are analysed in Sect. 4 along with comparisons with previous GRB-SN events. In Sect. 5, the quasi-bolometric light curve is analysed and the physical parameters of the explosion are derived. Finally we gather our conclusions in Sect. 6.
 |
Fig. 1 HST/WFC3 F814W, GROND i′-band, and GROND host-subtracted i′-band images of the GRB-SN field, respectively, from left to right. Images were taken at around maximum brightness. Each panel is approximately 13′′ × 13′′ in size. The HST image shows significant galaxy structure near the explosion site (marked with two lines), which is blended with the object of interest in the GROND image shown in the middle panel. GROND images in the middle and right panels are shown using the same flux scale. |
2. Observations
Gamma-ray emission from XRF 100316D triggered the Burst Alert Telescope (BAT; Barthelmy et al. 2005) on board the Swift satellite (Gehrels et al. 2004) on March 16, 2010, at t0 = 12:44:50 UT (Stamatikos et al. 2010). It turned out to show a soft γ-ray spectrum (Sakamoto et al. 2010) and a duration of at least 1300 s, one of the longest ever measured (Fan et al. 2011; Starling et al. 2011). About 15 h thereafter, a spectroscopic redshift of 0.059 was published for the host galaxy (Vergani et al. 2010a,b). Observations of the Gamma-Ray burst Optical and Near-infrared Detector (GROND; Greiner et al. 2007, 2008) confirmed that the new source became evident about 16 h after the burst (Afonso et al. 2010). The rising of the supernova was verified photometrically by Wiersema et al. (2010) only three days after the trigger. The spectroscopic confirmation of Chornock et al. (2010b) came approximately six days after the burst, which was confirmed two days later by Bufano et al. (2010a). The SN was officially named SN 2010dh eight days after the trigger (Bufano et al. 2010b; Chornock et al. 2010c). On March 26, 2010, additional GROND observations of SN 2010bh were reported along with results at the first attempts of host-galaxy subtraction (Rau et al. 2010).
2.1. GROND
The multi-channel imager GROND (Greiner et al. 2007, 2008), mounted at the MPG/ESO 2.2 m telescope on La Silla, Chile, started observations of XRF 100316D 11.7 h after the trigger, simultaneously in g′r′i′z′JHKs, with an average seeing of 1 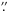 1, as soon as the astronomical night began.
1, as soon as the astronomical night began.
The GROND data were reduced using standard pyraf/IRAF1 tasks (Tody 1993), similar to the procedure described in detail by Krühler et al. (2008). A general point-spread function (PSF) model was constructed using bright field stars, from which the full width at half maximum (FWHM) was derived for each image. Aperture photometry was performed for science and calibration objects using an aperture size equal to the FWHM. The SDSS field at coordinates RA(J2000) 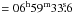 , Dec(J2000) = −17°27′00′′ was observed during photometric conditions to calibrate our images by performing relative photometry. A total of six stars in the field of XRF 100316D were employed for this purpose (see Table A.1 of the online material). The same set of stars was used to calibrate JHKs against the 2MASS catalogue. Calibration uncertainties vary in the range 0.002–0.020 mag for g′r′i′z′ and 0.02–0.12 mag for JHKs, which together with catalogue systematics are added in quadrature to the statistical error.
, Dec(J2000) = −17°27′00′′ was observed during photometric conditions to calibrate our images by performing relative photometry. A total of six stars in the field of XRF 100316D were employed for this purpose (see Table A.1 of the online material). The same set of stars was used to calibrate JHKs against the 2MASS catalogue. Calibration uncertainties vary in the range 0.002–0.020 mag for g′r′i′z′ and 0.02–0.12 mag for JHKs, which together with catalogue systematics are added in quadrature to the statistical error.
A deep host-galaxy observation was carried out on November 5, 2010. This observation resulted in images with mean seeing of 0 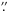 74 and was used as a reference image for the subtraction of the host contribution from the early epochs. To develop a notion of the host contamination, we refer to Fig. 1, where the position of the transient relative to the host galaxy is shown along with an F814W image of the Wield Field Camera 3 (WFC3) on board the Hubble Space Telescope (HST) as reference. In addition, the coordinates of the centre of the host galaxy, catalogue name Anon J071031–5615, were obtained from the last GROND observation: RA(J2000)
74 and was used as a reference image for the subtraction of the host contribution from the early epochs. To develop a notion of the host contamination, we refer to Fig. 1, where the position of the transient relative to the host galaxy is shown along with an F814W image of the Wield Field Camera 3 (WFC3) on board the Hubble Space Telescope (HST) as reference. In addition, the coordinates of the centre of the host galaxy, catalogue name Anon J071031–5615, were obtained from the last GROND observation: RA(J2000) 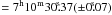 , Dec(J2000)
, Dec(J2000) 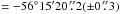 . To align the input and reference images, we use the WCSREMAP package2. For the main purpose of subtracting template from science images, the HOTPANTS package3 was employed. It matches the point spread function (PSF) and count flux of both input images. It uses Gaussian functions to model the PSF in sub-regions of the original image. Since reduced images are essentially the combination of at least four g′r′i′z′ and 24 JHKs dithered individual exposures, three and five Gaussian functions of different widths and degrees of freedom are employed for g′r′i′z′ and JHKs, respectively. Point sources define the transformation that is used to scale the template image to the flux of the science image. The routine outputs a noise map of the resulting difference image, which is employed to derive the uncertainties in the measured fluxes. The package DAOPHOT/IRAF was used to compute the magnitudes and their corresponding errors. This procedure was executed for a total of 140 individual images in a total of 20 epochs (see Fig. 1 for an example of image subtraction in the i′ band). The position of the transient is RA(J2000)
. To align the input and reference images, we use the WCSREMAP package2. For the main purpose of subtracting template from science images, the HOTPANTS package3 was employed. It matches the point spread function (PSF) and count flux of both input images. It uses Gaussian functions to model the PSF in sub-regions of the original image. Since reduced images are essentially the combination of at least four g′r′i′z′ and 24 JHKs dithered individual exposures, three and five Gaussian functions of different widths and degrees of freedom are employed for g′r′i′z′ and JHKs, respectively. Point sources define the transformation that is used to scale the template image to the flux of the science image. The routine outputs a noise map of the resulting difference image, which is employed to derive the uncertainties in the measured fluxes. The package DAOPHOT/IRAF was used to compute the magnitudes and their corresponding errors. This procedure was executed for a total of 140 individual images in a total of 20 epochs (see Fig. 1 for an example of image subtraction in the i′ band). The position of the transient is RA(J2000)  , Dec(J2000)
, Dec(J2000) 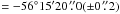 in host-subtracted optical images. The resulting photometry is tabulated in Table A.2 of the online material.
in host-subtracted optical images. The resulting photometry is tabulated in Table A.2 of the online material.
2.2. Swift/XRT and UVOT
On board the Swift satellite, the X-Ray Telescope (XRT; Burrows et al. 2005) and the UVOT (Roming et al. 2005) started observations of XRF 100316D at t0 + 2.4 min (Stamatikos et al. 2010). Whilst a bright X-ray source was detected inside the BAT error circle, initially no afterglow candidate was found by UVOT (Oates et al. 2010).
However, in deeper images taken at t0 + 33 ks in the uvw1 filter and at t0 + 63 ks in the u band, we found evidence of emission in excess of the host-galaxy contribution. To remove the contribution from the host galaxy, we requested ToO observations in the uvw1 and u filters, which were taken at t0 + 3 × 107 s (347 d after the burst), and amounted to a total exposure time of 1525 and 1369 s, respectively. We measured a host galaxy contribution within the source aperture of 25 ± 2 and 39 ± 3 μJy in the uvw1 and u bands, respectively. Subtracting this contribution from our earlier-time data gave us a 3σ detection in 1894 s of uvw1- and in 4901 s of u-band data taken at mid-times of t0 + 33 ks and t0 + 63 ks respectively. In our analysis, we include only the uvw1 detection at t0 + 33 ks, since there were no GROND data contemporaneous with the epoch of our u-band detection. All UVOT data were reduced following the procedure described in Poole et al. (2008). To minimise the contamination from the underlying host galaxy, the source flux was measured within a circular source-extraction region of a 3  5 radius. An aperture correction was then applied in order to remain compatible with the UVOT effective area calibrations, which are based on 5′′ aperture photometry (Poole et al. 2008). The background was taken from a source-free region with a 15′′ radius close to our source.
5 radius. An aperture correction was then applied in order to remain compatible with the UVOT effective area calibrations, which are based on 5′′ aperture photometry (Poole et al. 2008). The background was taken from a source-free region with a 15′′ radius close to our source.
The relatively bright X-ray afterglow (30–40 cnt s-1 between 144 and 737 s after the trigger) faded considerably at the beginning of the second XRT epoch (t0 + 33 ks; see Starling et al. 2011, for a detailed analysis). In the subsequent analysis, we employed XRT data at stages contemporaneous to GROND observations, specifically in the interval from 33 to 508 ks after the burst. These data were obtained from the public Swift archive and reduced in the standard manner using the xrtpipeline task from the HEAsoft package, with response matrices from the most recent CALDB release. All data were obtained in photon counting mode and downloaded from the XRT light curve repository (Evans et al. 2007, 2009). Spectra were grouped using the grppha task.
All the data discussed throughout the paper were corrected for the Galactic-foreground extinction of E(B − V )Gal = 0.117 mag with RV = 3.08 (Schlegel et al. 1998). All uncertainties in the following analysis are quoted at the 1σ confidence level.
3. Early broad-band SED
Using data between 33 and 54 ks (roughly from 11 to 15 h) after the burst, we compiled two early broad-band SEDs of XRF 100316D. GROND provides detections in g′r′i′z′J and upper limits in HKs, whilst the count rate of contemporaneous Swift/XRT observations is already 0.01 cnt s-1 at t0 + 33 ks and decaying. After combining data from 33 to 508 ks after the trigger, XRT provides only three bins in the X-ray energy range. As follows, XRT data are scaled to the GROND first two epochs by using a decay index of α = −1.3 ± 0.2, which is derived from the same XRT data over time. Swift/UVOT observed only in the uvw1 filter at these stages.
3.1. Modelling scheme
Early blue emission coming from the XRF position was detected by GROND. For data acquired 42.5 ks after the burst, we measured a colour g′ − r′ = −0.30 ± 0.06 mag, in contrast to the red afterglows that usually follow a GRB (photon index Γ in the range 1.2–2.5). Similar observations were made by Cano et al. (2011b), who found that this emission is incompatible with synchrotron radiation. The adiabatic cooling of the expanding atmosphere following the shock breakout gives us a reasonable explanation of the observed blue colours (e.g., Cano et al. 2011b). In this scenario, the emission from the shock breakout lasts only a few hours after the core collapse and its SED resembles a blackbody at a high temperature of the order of 106 K (or 0.1 keV equivalently; e.g., Campana et al. 2006). Thus, we interpret the blue colours in our observations as the thermal component associated with the cooling of the shock breakout, which is similar to what has been claimed for XRF 060218/SN 2006aj (Campana et al. 2006; Waxman et al. 2007) and other early-caught SNe (e.g., Soderberg et al. 2008; Modjaz et al. 2009, on SN 2008D; Roming et al. 2009, on SN 2008ax). In contrast to the idea of a thermal component producing the observed emission, there are no significant contemporaneous detections of UVOT in the uvw1 bandpass, which alludes to high reddening. On the other hand, i′ − J = 0.06 ± 0.15 mag measured at the same epoch appears to have an underlying additive red component, which is represented in this case by the GRB afterglow synchrotron emission (see Fig. 2).
 |
Fig. 2 Broad-band SED at 50 ks after trigger. The observed data are represented by black filled circles. The HKs bands provide only 3σ upper limits shown as arrows. The thick grey line shows the best-fit model able to reproduce the data: extinguished power law plus blackbody components, which are shown individually with dotted and dashed grey lines, respectively. The thin continuous grey lines show the unextinguished versions of the power law corresponding to the afterglow and the thermal component. In the lower panel, the residuals of the best fit are plotted. |
Fits to broad-band spectra constructed using GROND and Swift/XRT data.
To test this hypothesis, we modelled the SEDs at 42.5 and 50.0 ks (the latter shown in Fig. 2) using two additive components: (1) a power law for the afterglow, and (2) an ideal blackbody for the thermal component, respectively, of the forms 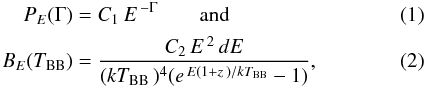 where C1 and C2 are normalisations, E is the spectral energy in units of keV, Γ is the photon index, k is the Boltzmann constant, TBB the intrinsic blackbody temperature, and z = 0.059 is the redshift (Chornock et al. 2010c). The model also accounts for host-galaxy extinction based on either Milky Way (MW; RV = 3.08), Large Magellanic Cloud (LMC; RV = 3.16), or Small Magellanic Cloud (SMC; RV = 2.98) extinction laws and soft X-ray metal absorption. The Galactic metal absorption is fixed to be N H,Gal = 7.05 × 1020 cm-2 (Kalberla et al. 2005). The model has a total of six free parameters: C1, C2, Γ, TBB, E(B − V )host, and N H,host. The luminosity of the blackbody is computed as
where C1 and C2 are normalisations, E is the spectral energy in units of keV, Γ is the photon index, k is the Boltzmann constant, TBB the intrinsic blackbody temperature, and z = 0.059 is the redshift (Chornock et al. 2010c). The model also accounts for host-galaxy extinction based on either Milky Way (MW; RV = 3.08), Large Magellanic Cloud (LMC; RV = 3.16), or Small Magellanic Cloud (SMC; RV = 2.98) extinction laws and soft X-ray metal absorption. The Galactic metal absorption is fixed to be N H,Gal = 7.05 × 1020 cm-2 (Kalberla et al. 2005). The model has a total of six free parameters: C1, C2, Γ, TBB, E(B − V )host, and N H,host. The luminosity of the blackbody is computed as 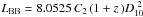 erg s-1, where D10 is the luminosity distance to the transient in units of 10 kpc. A luminosity distance of 240 ± 17 Mpc to the host galaxy of XRF 100316D is employed as computed by the NED database4 following the standard ΛCDM model, using the redshift measured by Chornock et al. (2010c), a Hubble constant of 74.2 km s-1 Mpc-1 (Riess et al. 2009), and the model of the local velocity field by Mould et al. (2000).
erg s-1, where D10 is the luminosity distance to the transient in units of 10 kpc. A luminosity distance of 240 ± 17 Mpc to the host galaxy of XRF 100316D is employed as computed by the NED database4 following the standard ΛCDM model, using the redshift measured by Chornock et al. (2010c), a Hubble constant of 74.2 km s-1 Mpc-1 (Riess et al. 2009), and the model of the local velocity field by Mould et al. (2000).
The different set of parameters are summarised in Table 1. All best-fit parameters are consistent between the two epochs within their statistical uncertainties between both epochs. The temperature TBB and luminosity LBB of the thermal component are in the range 78–81 eV and 4–7 × 1047 erg s-1 from Cols. 4 and 5 of Table 1, respectively. The afterglow power-law photon index Γ ≈ 1.8 is shown in Col. 7. The reduced χ 2 (or χμ 2 ≡ χ 2/μ, where μ is the number of degrees of freedom) improves from 16.6 for the model without extinction to 2.7 for the model extinguished by MW-like dust. The best fit to the second SED epoch is shown in Fig. 2 with a thick grey line. The UV dust feature characteristic of the MW extinction law gives the more precise results, although it is poorly constrained at the bluer end. The X-ray tail of the blackbody fits the two data bins at around 1 keV, whilst the power law fits the only data point at ≈ 3 keV; both components contain significant absorption. We note that the fitting of the X-ray data has practically no residuals, i.e., the model over-predicts the data in this energy range.
In addition to the luminosity and temperature, it is possible to compute an apparent emission radius of the thermal component (RBB) from these two measured quantities by assuming isotropic radiation from an ideal blackbody. For all our trial models, the corresponding radii were calculated as 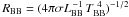 , where σ is the Stefan-Boltzmann constant (Col. 6 of Table 1). Our best-fit parameters yield a radius of 3–4 × 1013 cm, which is two orders of magnitude larger than the typical sizes of the most likely GRB progenitors (WR stars; Cappa et al. 2004).
, where σ is the Stefan-Boltzmann constant (Col. 6 of Table 1). Our best-fit parameters yield a radius of 3–4 × 1013 cm, which is two orders of magnitude larger than the typical sizes of the most likely GRB progenitors (WR stars; Cappa et al. 2004).
The amount of metal absorption (estimated based on an equivalent hydrogen column density at solar metallicity) and dust extinction required for a good fit are N H,host ≈ 4 × 1022 cm-2 and E(B − V )host = 0.2–0.4 mag, respectively. These two parameters are fitted independently and with no assumption being made about the environment gas-to-dust ratio. However, the available data is not enough to allow us to distinguish among the different extinction laws employed in the modelling procedure. Whilst the reddening is consistent with values found in previous studies (Starling et al. 2011; Cano et al. 2011b), the hydrogen column density differs significantly from the results of Starling et al. (2011). The discrepancy is due to the additional constraints provided by the optical/NIR data, which were included to derive the parameters of the blackbody contribution. With our data set it is possible to tie the thermal component at both low and high energies, which provides a more accurate value for the absorption by heavy elements because of the greater constraint on the X-ray flux.
3.2. Host-galaxy extinction
We then attempted to evaluate the constraint on the extinction value derived in the previous section. Contour plots of reddening against blackbody temperature, luminosity, and spectral index from the best fit to the data are shown in Fig. 3, respectively. The 1σ and 2σ contours show that the solution to our best-fit relation is well-defined in all three panels. In the first panel there is a second solution to our best-fit relation at the 3σ level, which is at lower temperatures and similar reddening, although its significance is rather low. In the middle panel, the contours show a slight trend of proportionality between luminosity and extinction, which is expected. At luminosities higher than 1.1 × 1048 erg s-1, there is no possible solution, because the model becomes much brighter than the X-ray data and N H,host cannot be allowed to vary and compensate for the X-ray luminosity of the model. Contours of the variations in the reddening and spectral index are shown in the lower panel, where the extinction is again restricted to high values.
 |
Fig. 3 Contour plots for the best-fit parameters from the modelling of the second epoch. From the outer- to the innermost contours, the green, red, and black lines are 3, 2, and 1σ contours, respectively. The tail at low Γ in the bottom panel is caused by numerical inaccuracies. |
Analyses of optical spectroscopy of the host galaxy have found that the line-flux ratio of Hα to Hβ in the H ii region coincident with the SN position is consistent with zero extinction (Starling et al. 2011; Levesque et al. 2011). Nevertheless, the AV,host ~ 0 estimate from the spatially resolved spectroscopy of Levesque et al. (2011) probes a much larger region ( ≈ 1.3 kpc2) than the one probed by our line of sight to the GRB-SNe. A sufficiently high dust clumpiness could explain our high extinction values along the line of sight and AV,host ~ 0 when integrated over a larger patch. The position at which the hydrogen lines are formed, i.e., the H ii region, might be located in front of the explosion site and not probe the same line of sight through the host galaxy.
Alternatively a broken power-law model was fitted to the data in Fig. 2 for which χμ 2 = 3.0, which is slightly larger than that of the model that consists of a blackbody plus power law. The broken power law provided a closer fit when we assume that there is no host-galaxy extinction, significantly different from our results for the blackbody plus power-law model. However, the low-energy spectral slope of β = + 0.5 is incompatible with synchrotron radiation ( βmax = + 1/3; e.g., Sari et al. 1998). Furthermore, the spectral break lies between the g′ and the uvw1 bands at νbreak = (8 ± 3) × 105 GHz, which is inconsistent with the self-absorption feature usually observed at radio frequencies (νa ~ 2–13 GHz; Galama et al. 1998c; Taylor et al. 1998; Granot et al. 1999; Galama et al. 2000). Given also that AV,host > 0.2 mag is derived in Sect. 3.1 and preferred by other authors (see next paragraph), the broken power-law model can be discarded with confidence.
Additional evidence of large reddening along the line of sight inside the host galaxy was found by Starling et al. (2011), E(B − V )host ≈ 0.9 mag. The reddening was derived by fitting Swift/BAT+XRT data and a u-band 3σ upper limit provided by Swift/UVOT data in the interval from 638 to 737 s after the burst. We employed a model that consists of a blackbody plus power law extinguished by SMC dust. A similar method was used here and by Campana et al. (2006), who determined E(B − V )host = 0.20 for SN 2006aj. Another attempt at dereddening SN 2010bh was carried out by Cano et al. (2011b), who found E(B − V )host = 0.18 ± 0.08 mag by assuming that the colours of SE SNe are all the same ten days after the V-band maximum brightness (Drout et al. 2011). Whilst this method is supported for the hydrogen atmospheres of type-IIP SNe by a line of physical arguments (e.g., Olivares E. et al. 2010), it is entirely empirical for SE SNe. Nevertheless, their reddening value is larger than zero with a significance of 2.3σ and consistent with our calculations for our second-epoch SED of E(B − V )host = 0.39 ± 0.03 mag at the 2.5σ confidence level.
After correcting for E(B − V )host = 0.39 ± 0.03 mag, we obtained uvw1 = 18.15 ± 0.27 and u = 19.70 ± 0.45 mag in the AB system at 33 and 63 ks after the burst, respectively. For SN 2006aj (Campana et al. 2006), these values were uvw1 = 17.73 ± 0.21 and u = 17.77 ± 0.15 mag at the same phase and redshift of SN 2010bh. If we had assumed that we should have seen a cooling envelope for SN 2010bh of comparable brightness and evolution as that shown by SN 2006aj, the host-galaxy extinction should have been higher than that estimated by our method. Nevertheless, the uncertainties are large and the comparison of the uvw1 measurements is consistent at the 1.2σ confidence level. Although in the u band the uncertainty is even larger, there is no consistency with the brightness of SN 2006aj at the 4σ confidence level and a higher host-galaxy extinction (AV,host ≈ 2.1 mag) would be required to reach the 1σ level of consistency.
In conclusion, we use the extinction value from the fit to the second-epoch broad-band SED throughout the paper, E(B − V )host = 0.39 ± 0.03 mag for MW-like dust with RV = 3.08, given that compared to the first epoch the statistical errors in the g′r′i′z′J photometry are smaller and additional uvw1 photometry is available. Moreover, when fixing the host-galaxy reddening to E(B − V )host = 0.39 mag, the quality of the fit to the first epoch is still acceptable ( χμ 2 = 1.6), whilst the fit to the second epoch using E(B − V )host = 0.21 mag from the first-epoch modelling results in χμ 2 = 3.7 and unphysical parameters. Hence, values of host-galaxy extinction including the correction for redshift (K-correction based on the spectral model) for the GROND filters and their corresponding statistical uncertainty are Ag′,host = 1.50 ± 0.12, Ar′,host = 1.10 ± 0.09, Ai′,host = 0.80 ± 0.08, Az′,host = 0.60 ± 0.06, AJ,host = 0.39 ± 0.04, AH,host = 0.22 ± 0.02, and AKs,host = 0.14 ± 0.01, all in units of magnitude.
3.3. Evolution of the thermal component
Having determined temperature, luminosity, and radius for the thermal component, it was then possible to study their evolution. Starling et al. (2011) analysed combined BAT+XRT data until 737 s after the trigger and derived blackbody temperatures, data that we used in the following analysis. Temperature and radius over time are shown in Fig. 4. The decrease in temperature and the increase in radius are both trends that are consistent with the cooling of the envelope due to expansion and, thus, with the explosive scenario.
 |
Fig. 4 Temperature and radius evolution of the blackbody component. Black data points are those derived using combined BAT+XRT data (Starling et al. 2011) plus the temperature determinations using GROND data ( ≈ 46 ks). The first data bin from Starling et al. (2011) represents the interval from − 175 to 144 s, however, due to fitting and plotting purposes, here it corresponds to 0–144 s. Solid, dashed and dotted lines are different power-law models (see main text). Best fits to temperature and radius are shown in grey and brown solid lines, respectively. Grey crosses (upper panel) and open circles (lower panel) are measurements of XRF 060218/SN 2006aj taken from Kaneko et al. (2007) and Campana et al. (2006), respectively. |
The temperature and radius of an expanding envelope that is cooling adiabatically have been theoretically shown to evolve as power laws (Waxman et al. 2007; Nakar & Sari 2010). We therefore fit power laws to the decay and rise of temperature and radius to the combined data presented here and in Starling et al. (2011). The expression TBB (t ) = Ti − κt δ was fitted to the evolving temperature (solid line in the upper panel of Fig. 4), which gave a decay index of δ = 0.3 ± 0.2 for an initial temperature of Ti = 0.17 ± 0.04 keV with χμ 2 = 0.8, where κ is the normalisation of the power law.
A model of the form RBB(t ) = R0 + υt γ was employed to fit the radius measurements. In the case of linear expansion, i.e., γ = 1, the radius grows at a mean velocity of υ ≈ 8000 km s-1 between BAT+XRT (until 737 s) and GROND observations (at 42–54 ks after the burst). When γ was allowed to vary, we obtained a growth index of γ = 1.4 ± 0.3 and an initial radius of R0 = (7.0 ± 0.9) × 1011 cm with χμ 2 = 1.1 (solid line in the lower panel of Fig. 4). The resulting radius is slightly larger than the size of WR stars (~1011 cm; Cappa et al. 2004), which are thought to be the progenitors of long-duration gamma-ray bursts and type-Ic SNe (Woosley et al. 2002). Because of this, the initial emission radius of the thermal component might indicate the position at which a preexisting dense wind surrounding the progenitor becomes optically thin (e.g., Campana et al. 2006; Soderberg et al. 2008; Balberg & Loeb 2011). From the theoretical point of view, it is γ = 0.8 (Waxman et al. 2007), although, the data do not favour this solution delivering χμ 2 = 8 (dotted line in the lower panel of Fig. 4).
For an assumption of adiabatic cooling, the luminosity must be constant and was fixed to LBB = 3.5 × 1045 erg s-1, value derived from early-time X-ray measurements (Starling et al. 2011). Assuming the best-fit model for the radius evolution from the previous paragraph, we computed the evolution of the adiabatic temperature as 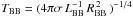 , which is shown by the dashed line in the upper panel of Fig. 4. This model is clearly inconsistent with our data set; however, it indeed shows consistency with the XRF 060218/SN 2006aj data set (grey crosses in the upper panel of Fig. 4; from Kaneko et al. 2007). Since the blackbody luminosity changes to 4–6 × 1047 erg s-1 in our late-time measurements, the assumption of a constant luminosity is invalid and inconsistent with the late-time temperature determination. This result implies that either the cooling is not strictly adiabatic for which energy injection from the inner core is needed, or TBB and LBB are overestimated by our modelling procedure, or underestimated by Starling et al. (2011).
, which is shown by the dashed line in the upper panel of Fig. 4. This model is clearly inconsistent with our data set; however, it indeed shows consistency with the XRF 060218/SN 2006aj data set (grey crosses in the upper panel of Fig. 4; from Kaneko et al. 2007). Since the blackbody luminosity changes to 4–6 × 1047 erg s-1 in our late-time measurements, the assumption of a constant luminosity is invalid and inconsistent with the late-time temperature determination. This result implies that either the cooling is not strictly adiabatic for which energy injection from the inner core is needed, or TBB and LBB are overestimated by our modelling procedure, or underestimated by Starling et al. (2011).
4. Multicolour evolution of SN 2010bh
We now present the entire GROND data set, which includes data in seven different bands covering the wavelength range from 380 to 2300 nm. Photometry was corrected for host-galaxy extinction computed at the end of Sect. 3.2. In addition, the afterglow component derived in Sect. 3.1 was subtracted from the data. Assuming a power-law decay for the optical afterglow with α = −1.3 ± 0.2 computed from the contemporaneous X-ray data, a flux and its corresponding uncertainty were derived from the power-law model fitted to the early SEDs for each epoch. We note however that typically αX ≠ αopt. The correction for the afterglow contribution is more significant at earlier times and in redder bands and it has a lower significance at around maximum brightness for all bands.
4.1. Optical and near-infrared light curves
Figure 5 shows the light curves in the optical g′r′i′z′ and the NIR JH bandpasses. The g′r′i′z′J light curves show the usual pattern of SE SNe: the redder the filter, the later and broader the peak. The H band peaks a few days earlier than J, although given the large uncertainties, the time difference is insignificant. The Ks band shows no credible detections in any of our observations down to limits in the range of 18.4–18.9 mag (AB system) despite our observations covering the expected peak of the SN (10.5–25.5 d after the burst). In the following section, we analyse our data of SN 2010bh, one of the best-observed GRB-SNe to date, and compare the light curve with those of other SNe connected to GRBs.
 |
Fig. 5 Multi-colour light curves corrected for host-galaxy extinction and afterglow-subtracted. Filled circles represent detections and arrows are upper limits. Solid lines represent the overall fits and dashed lines individual components. Fits of SN 1998bw templates are extrapolated from ≈ t0 + 60 d. For reasons of clarity, light curves were shifted along the magnitude axis and the systematical error in AV,host was not added to the error bars. |
4.2. Colour evolution
Six GROND colour curves are presented in Fig. 6 to analyse the colour evolution of SN 2010bh. Most colours show drastic evolution, where the cooling of the SN photosphere is evident as colours become redder. Non-significant variations over time are shown in r′ − i′ and J − H colours.
 |
Fig. 6 Colour curves corrected for host-galaxy extinction and afterglow-subtracted. Filled circles represent detections in both filters and arrows are upper limits derived from detections in one of the two bands. Solid lines represent the colour evolution of SN 1998bw derived from the light-curve fits in Sect. 4.3. For clarity, error bars do not include the systematic error in AV,host and for the last epoch, upper limits are not shown. |
Fits of SN 1998bw templates to SN 2010bh.
4.3. Comparison with SN 1998bw
To study the luminosity evolution of SN 2010bh to other SNe, we fit SN 1998bw templates derived from the publicly available UVBRI photometry (Galama et al. 1998b) to each of our GROND filters. The process of compiling these templates from the observed light curve of SN 1998bw is based on Zeh et al. (2004). Given their modus operandi, the NIR templates are inaccurate because they rely on an extrapolation of the UVBRI data. Therefore, the three epochs of JHKs data in Patat et al. (2001) were used to define the zero points of the flux scale. For all filters, it is assumed that the host-galaxy extinction of SN 1998bw is equal to zero (Patat et al. 2001; Clocchiatti et al. 2011). An analytical function was then employed to parametrise the SN 1998bw templates. Two of the seven template parameters represent the brightness and morphology of the light curve, the factors of luminosity k and stretch s, respectively. These were defined provided that k = 1 and s = 1 for SN 1998bw (Zeh et al. 2004). In addition, it was necessary to include a delay parameter tdelay that acts by shifting the template linearly in time, i.e., as a time offset. The delay parameters that differ from zero do not necessarily mean that the onset of the SN is out of phase.
Given that the early blue emission is inconsistent with the templates even after subtraction of the afterglow component derived in Sect. 3.1, an empirical power-law component was required (dashed in Fig. 5). The power-law slope was fixed to α = −1.3. Leaving α free did not improve the fit and different values of α only negligibly affected the stretch and luminosity factors derived for the SN component. Table 2 summarises the results of fitting the SN 1998bw templates and the empirical power-law to the GROND data. The overall fits are shown in Fig. 5 for each band using solid lines.
Luminosity factors listed in the first line of Table 2, which include the uncertainty in AV,host, reflect differences between the colours of SN 2010bh and those of SN 1998bw. The g′ band is as bright as SN 1998bw and, as a rough comparison, disagrees with the fainter B-band results from Cano et al. (2011b) at the 5σ confidence level after including the uncertainty in their extinction determination. Our r′i′ luminosity factors are also larger than previously reported from optical photometry of SN 2010bh (k ≈ 0.4–0.5; Cano et al. 2011b) mainly owing to the use of a different extinction correction. There is certainly some intrinsic blue excess in the g′ band, although the difference from the r′ band of 40% has a rather large uncertainty of 13%. Higher luminosities at bluer wavelengths indicate that the photosphere has a higher temperature at its peak luminosity than that of SN 1998bw. Given that the expanding atmospheres of SNe cool down over time and SN 2010bh peaks about a week earlier than SN 1998bw in g′, it is a natural conclusion that it must be hotter at maximum brightness. It is also possible that a g′-band peak as early as 8 d after the trigger still contains a non-negligible contribution from the cooling shock breakout. We also note that the z′-band luminosity factor is much larger than in the other bands; it is brighter than SN 1998bw at the 3σ confidence level. After inspection of the spectra around maximum light presented by Bufano et al. (2011), the Ca ii λ8579 emission line was found to contribute roughly 2–4% to the continuum flux integrated in the z′-band sensitivity range (8254–9528 Å). The contribution of this spectral feature is not enough to account for the excess of 45% in the z′ band relative to the infrared. The discrepancy is therefore attributed to the systematical uncertainties introduced when extrapolating the UBVRI data from Galama et al. (1998b) to construct the templates of SN 1998bw. In summary, the luminosity of SN 2010bh is a factor 0.5–0.7 fainter than SN 1998bw in optical r′i′ bands and 0.6–0.7 in NIR JH bands. We also note that at late times SN 2010bh fades more rapidly in the optical than SN 1998bw did, although the fluxes if the templates were extrapolated after ≈ t0 + 60 d.
The stretch factors listed in the second line of Table 2 range from 0.6 to 0.8 and are at the low end of the GRB-SNe distribution (see Fig. 5 of Ferrero et al. 2006). These are also consistent with the findings by Cano et al. (2011b) for SN 2010bh. The optical light curves are wider than the stretch factor suggests, or in other words, the stretch factor predicts later peak times for the optical light curves. To account for this, tdelay shifts the templates to earlier times by about three days in g′r′i′, which means that the optical light curves of SN 2010bh peak even earlier than the stretch factor suggests. After the inclusion of the delay parameter tdelay, the stretch factors now solely represent the width of the light curves and not the time of the maximum brightness compared to SN 1998bw. Moreover, peak times of roughly 8–9 d in the g′r′ bands (equivalent to the V in the Johnson filter system) corresponds to the earliest and fastest light curves of GRB-SNe observed to date (see Table 2 of Richardson 2009).
Offsets in peak time, in our case represented by tdelay, can be explained as the result of delayed black-hole formation (Vietri & Stella 1999). In this scenario, the XRF might be triggered by the core collapse of the progenitor to a neutron star, soon after which accretion holds. The supernova would then occur after the further collapse of the neutron star into a black hole. The delay could be of the order of months or years or perhaps as short as hours (see Zeh et al. 2004). Nevertheless, the time delay here is negative and it is much more plausible that the comparison of light-curve morphology to SN 1998bw may need more than two parameters to be accurate.
Fits of SN 1998bw templates were also employed to study the colour evolution of SN 2010bh in detail as presented in Fig. 6, where the curves are shown without the empirical afterglow component. From the first two data points, it is clear from the g′ − r′ and g′ − z′ colours that there is a blue component that cannot be modelled by the templates and is interpreted as the shock breakout in Sect. 3.1. From these two colours, it is also possible to see that SN 2010bh becomes red faster than SN 1998bw did. The r′ − i′ and J − H colours remain roughly constant, which shows that the changes occur on a broader wavelength scale. The standard colour evolution from blue to red is shown by r′ − z′ and r′ − J, which at late times evolve bluer and redder than SN 1998bw templates, respectively.
4.4. Comparison with SN 2006aj
We now compare results from optical data by Ferrero et al. (2006), who used the same technique and templates to get the luminosity and stretch factors for SN 2006aj. They computed luminosity factors in the range 0.62–0.76, which are approximately in the same range as SN 2010bh without considering the measurements in g′z′. Their stretch factors ranged from about 0.62 to 0.69, which makes the SN 2010bh optical light curves wider than those of SN 2006aj. In contrast to the definition of the stretch factor, namely that earlier peak times tend to correspond to a narrower light curve, peak times are earlier in the case of SN 2010bh. Whilst the BV photometry for SN 2006aj peaked roughly 9 and 11 d after the burst, respectively, the g′r′ photometry for SN 2010bh peaks approximately 8 and 9 d after trigger, respectively. This supports the statement that SN 2010bh has evolved more rapidly than any other GRB-SNe, given that SN 2006aj had the fastest evolution until the discovery of SN 2010bh. The JH light curves of SN 2006aj (Cobb et al. 2006; Kocevski et al. 2007) are scaled to the luminosity distance of SN 2010bh for comparison. After the host-extinction correction, SN 2010bh turns out to be as bright as SN 2006aj in the NIR as well. Hence, SN 2010bh is similar to SN 2006aj in terms of light-curve shape and luminosity.
5. Bolometric light curve
The bolometric light curves of SNe are an essential tool for examining global luminosity features and enable us to compare with other SNe and theoretical models. However, it is difficult to obtain such a light curve because of the limited information at UV, infrared, and radio wavelengths. Only a quasi-bolometric light curve can be constructed by using a broad spectral coverage to derive a total flux that is then used as a proxy of the bolometric flux. To accomplish this task, we employed the wavelength range covered by our g′r′i′z′ JH filters, i.e., from 350 to 1800 nm.
In the case of SN 2010bh, there are no UV constraints. In the following description, no attempts at correcting for the UV flux were made. By using the afterglow-subtracted g′r′i′z′ JH photometry corrected for host-galaxy extinction, monochromatic fluxes for each bandpass were derived. Sets of three bandpasses were defined to interpolate their corresponding monochromatic fluxes using the Simpson’s rule. The second-degree polynomial result of the interpolation was then integrated over frequency in the range of each set of bandpasses. Finally, the total flux in the range from 350 to 1800 nm was determined by adding up the integrated fluxes of all sets of bandpasses. The total flux is transformed to a quasi-bolometric luminosity using a distance of 240 ± 17 Mpc to the host galaxy of SN 2010bh (see Sect. 3.1 for more details). No attempts of extrapolation beyond the limits of the g′ and the H bandpasses were made. Corrections for the NIR flux at late times were found to be the most significant. The data at t0 + 30.7 d (rest frame) were corrected for the H-band non-detection by assuming that the fraction of H-band flux compared to the total bolometric flux remains constant at 8% starting from t0 + 24.1 d. Similar corrections were performed for JH non-detections at 38.6 and 78.8 d after the burst under the assumption of a constant JH flux fraction of 27% at t0 + 30.7 d. Results are shown in Fig. 7 along with quasi-bolometric light curves from SE and other GRB-SNe.
 |
Fig. 7 Quasi-bolometric light curve of SN 2010bh produced by using GROND g′r′i′z′ JH filters (black open circles) in the rest frame. For clarity, the uncertainties in the host-galaxy extinction are not included in the error bars. A single black continuous line represents the best-fit model (see Sect. 5.1). Early and late components of the model are smoothly joined at t0 + 30 d. SE and other GRB-SNe quasi-bolometric light curves have been plotted as a comparison sample: SN 2003lw (GRB 031203; Malesani et al. 2004), SN 1998bw (GRB 980425; Galama et al. 1998b), SN 2006aj (GRB 060218; Pian et al. 2006), the broad-lined Ic SN 2009bb (Pignata et al. 2011), the type-Ic SN 1994I (Richmond et al. 1996), the type Ibc SN 2008D (XRO 080109; Modjaz et al. 2009; Soderberg et al. 2008), and the type-Ic SN 2002ap (Gal-Yam et al. 2002; Foley et al. 2003; Yoshii et al. 2003). |
The analysis of the quasi-bolometric light-curve morphology yields a peak luminosity of 4.3 × 1042 erg s-1 at about 8 d after the trigger (equivalent to Mbol ≈ − 17.87), i.e., approximately two times fainter and six days sooner than for SN 1998bw. Our luminosity is 16% higher than that computed by Cano et al. (2011b), although consistent to within our 11% of uncertainty. Whilst the early peak of SN 2010bh correlates with its narrowness and low luminosity, this is the case for neither the entire GRB-SNe sample nor the local sample of SE SNe (Zeh et al. 2004; Richardson et al. 2006; Richardson 2009). The morphology of the light curve is similar to that of SN 2006aj (Pian et al. 2006), although 21% fainter. The peak time also resembles that of the type-Ic SN 1994I (Richmond et al. 1996), although SN 2010bh has a much wider light curve, which is 77% brighter at maximum. In terms of peak luminosity, SN 2010bh is similar to the broad-lined Ic SN 2009bb (Pignata et al. 2011). It also underwent the most dramatic late-time decay in the sample, which implies that its envelope became rapidly optically thin to γ-rays. The last statement is supported by the extremely high expansion velocities measured for SN 2010bh of the order of 30 000 km s-1 (Chornock et al. 2010a). Another clear feature is the sudden decrease in luminosity at around t0 + 30 d, which contrasts with the smooth decay in the comparison SNe at similar stages. This indicates either that the atmosphere becomes rapidly optically thin or that the assumption of a constant NIR contribution after ≈ t0 + 31 d underestimates the flux in the JH bands.
Physical parameters of the explosion with a varying expansion velocity.
5.1. Physical parameters of the explosion
We followed the approach described in Valenti et al. (2008) to derive the physical quantities that characterise the explosion, i.e., we modelled the early and late light curves separately. The early-time phase corresponds to the photospheric regime for which the analytical model developed by Arnett (1982) has been adopted, initially used for SNe Ia and adapted to SE SNe (e.g., Taubenberger et al. 2006; Valenti et al. 2008; Pignata et al. 2011; Benetti et al. 2011). At late stages, the atmosphere becomes nebular, i.e., optically thin, and the emitted luminosity is powered by the energy deposition of: (1) γ-rays from 56Co decay, (2) γ-rays from electron-positron annihilation, and (3) the kinetic energy of the positrons (see appendix A in Valenti et al. 2008). However, Maeda et al. (2003) noted that the two-component configuration leads to inconsistencies between the parameters derived from fitting the early and late light curves of SNe Ic, caused mainly by the model limitations in varying the γ-ray trapping over time. To enable low and high γ-ray trapping at early and late times, respectively, Maeda et al. (2003) divided the ejecta into a high-density inner region and a low-density outer region. The emission from the outer region dominates the total emission in the optically thick regime at early times, and that from the inner region, which has a higher γ-ray opacity, dominates in the nebular phase at late times. Here, we use the same procedure to model the g′r′i′z′ JH quasi-bolometric light curve of SN 2010bh.
Given the model explained above, a total of four free parameters were used to fit the quasi-bolometric light curve of SN 2010bh: the total mass of 56Ni produced in the envelope MNi, the total ejecta mass Mej, the fraction of mass in the inner component fM, and the fraction of kinetic energy in the inner component fE. The kinetic-energy-to-ejected-mass ratio of the outer region was fixed by using its correlation with photospheric velocity at peak luminosity (Arnett 1982) 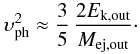 (3)This expression assumes that the density of the ejecta is homogeneous and that the inner component does not contribute to the emitted luminosity in the optically-thick regime. Since the photospheric velocity was not available directly from observations, the velocity measured by fitting P Cygni line profiles was used as a proxy of υph. However, the envelope layer where the blue-shifted absorption line forms does not necessarily coincide with the position of the photosphere, as found when measuring different expansion velocities from absorption lines of different species. The spread can amount to several hundreds km s-1 (see Jones et al. 2009, for an example of type-II SNe). For the spectra of SN 2010bh, Chornock et al. (2010a) obtained velocities of about 35 000 and 26 000 km s-1 from the Si ii λ6355 feature roughly 21 and 6 d after the burst, respectively. Since there is no measurement at the time of maximum light, which is about 8–9 d after the trigger, a range of expansion velocities was used in the modelling. Assuming that the photosphere lies at deeper layers than those where lines are formed and recedes in mass exposing deeper and slower layers, in the modelling we employed photospheric expansion velocities of 2.5, 2.8, and 3.1 × 104 km s-1. Other physical and mathematical quantities such as opacity and integration constants were chosen to be the same as in Cano et al. (2011b).
(3)This expression assumes that the density of the ejecta is homogeneous and that the inner component does not contribute to the emitted luminosity in the optically-thick regime. Since the photospheric velocity was not available directly from observations, the velocity measured by fitting P Cygni line profiles was used as a proxy of υph. However, the envelope layer where the blue-shifted absorption line forms does not necessarily coincide with the position of the photosphere, as found when measuring different expansion velocities from absorption lines of different species. The spread can amount to several hundreds km s-1 (see Jones et al. 2009, for an example of type-II SNe). For the spectra of SN 2010bh, Chornock et al. (2010a) obtained velocities of about 35 000 and 26 000 km s-1 from the Si ii λ6355 feature roughly 21 and 6 d after the burst, respectively. Since there is no measurement at the time of maximum light, which is about 8–9 d after the trigger, a range of expansion velocities was used in the modelling. Assuming that the photosphere lies at deeper layers than those where lines are formed and recedes in mass exposing deeper and slower layers, in the modelling we employed photospheric expansion velocities of 2.5, 2.8, and 3.1 × 104 km s-1. Other physical and mathematical quantities such as opacity and integration constants were chosen to be the same as in Cano et al. (2011b).
Our fitting procedure consisted of two steps. First of all, we modelled the data around maximum luminosity (5 < t − t0 ≤ 30 d) using the Arnett’s model, assuming that only the outer component contributes to the total luminosity at this stage. We then obtained MNi,out and Mej,out. Secondly, we modelled the late-time data (t − t0 > 30) using the nebular-phase components of Valenti et al. (2008) assuming that both the inner and outer regions contribute to the total emitted luminosity. Here, we fixed MNi,out and Mej,out to the values obtained in the first step of the fitting procedure and only fM and fE were allowed to vary.
From the above modelling scheme, our best-fit parameters were MNi,out = (0.135 ± 0.001) M⊙, Mej,out = 2.37–2.90 M⊙, fM = 0.36 ± 0.04, and fE = 0.11–0.15 for the three selected expansion velocities at the photosphere. All of these results combined together provided the total masses and energy of the explosion listed in Table 3 (statistical errors only). The 56Ni mass is independent of the chosen expansion velocity at the photosphere, MNi = (0.21 ± 0.03) M⊙, given that it is proportional to the luminosity. In contrast, since the ejected mass changes significantly, the weighted mean and the rms of the results of the three models in Table 3 were employed to compute a final value of Mej = (2.60 ± 0.23) M⊙. The total kinetic energy and energy fraction were derived in the same way, implying that Ek = (2.4 ± 0.7) × 1052 erg and fE = 0.12 ± 0.02.
Using comparable independent data, Cano et al. (2011b) followed a similar procedure to derive physical quantities from quasi-bolometric data. Whilst our values for Mej are consistent with those in Cano et al. (2011b) to within 1.5σ, they found that MNi = (0.10 ± 0.01) M⊙ for SN 2010bh, which is two times lower than our value. The discrepancy affects the determination of the kinetic energy as well, which is connected in Eq. (3) to υph and Mej. The causes of these inconsistencies are: (1) the host-galaxy extinction employed, which is E(B − V )host = 0.39 ± 0.03 mag in our case and 0.18 ± 0.08 mag in Cano et al. (2011b); (2) the inclusion of an inner component hidden at optically thick stages, which increases the 56Ni mass by a factor of fM; and (3) the choice of different expansion velocities of the photosphere. Furthermore, even when including the uncertainties in the host-extinction determination, which are σMNi ~ 0.02 both here and for Cano et al. (2011b), the discrepancy persisted. Nevertheless, evidence for the existence of a dense inner layer of 0.94 ± 0.15 M⊙ is provided and supported by the sub-luminous post-maximum phase of SN 2010bh, which is indicative of a high trapping of γ-rays.
The large amount of 56Ni produced is consistent with the class of SN associated with GRBs, but also matches the value derived for the highly energetic type-Ic SN 2004aw (Valenti et al. 2008), which in contrast had a much broader light curve that varied more slowly with time. Most interestingly, SN 2010bh resembles SN 2006aj in terms of light-curve shape. The 56Ni mass produced in the explosion is practically the same (Mazzali et al. 2006), whilst the ejected mass is 20% higher for SN 2010bh and the total kinetic energy is significantly different (~2 × 1051 erg in the case of SN 2006aj). This ensures that SN 2010bh is remarkable in terms of expansion velocity, which has been one of the greatest ever measured (Chornock et al. 2010a).
We note that the end of the optically-thick regime and the beginning of the nebular phase cannot be accurately defined. The rule of thumb is that the photospheric phase ends 30 d after explosion at the earliest and that the nebular phase starts 60 d after the explosion at the latest. Since Arnett’s model fits our data relatively well until day 30, it is defined as the end of the optically-thick era. Nevertheless, we are unable to clearly establish whether the period between 30 and 60 d after the burst corresponds to the nebular phase already, as the ejecta are most probably neither completely thick nor sufficiently thin.
The model reproduces the luminosity at maximum brightness and thereafter, despite underpredicting the luminosity during the rising phase. This is because the light curve is dominated by shock-breakout emission at early stages. The same is obtained in Sect. 4, when trying to fit templates of SN 1998bw to our multicolour light curve, where an extra component for the shock breakout is required. The light curves of SN 2010bh peak so early that an even more rapid evolution than observed is expected after maximum luminosity. This early-wide peak dichotomy could be explained by the 56Ni distribution in the envelope. If there were more 56Ni produced near the surface, the peak would be early and wide, i.e., the SN would rise more slowly but much earlier. In contrast, if the 56Ni were concentrated towards the centre, it would lead to a much later peak, although sharper rise, producing a narrower shape of the maximum (Bersten 2010, priv. comm.; Nomoto et al. 2010).
6. Conclusions
Spanning a time range from 12 h to 83 days after the trigger and covering from 190 to 2300 nm in wavelength (see Sect. 2), we have presented UV/optical/NIR photometric data of XRF 100316D/SN 2010bh. Given the results introduced and discussed in Sects. 3, 4, and 5, we have drawn the following conclusions:
-
Broad-band SEDs at early times demonstrate the existence of red and blue components identified as synchrotron emission from the XRF afterglow and the cooling envelope after shock breakout, respectively.
A significant amount of dust along the line of sight through the host galaxy (AV,host = 1.2 ± 0.1 mag) is consistent with the two-component SED model and agrees with the faint detections at UV wavelengths.
By comparing with earlier X-ray results from Starling et al. (2011), we have demonstrated that the temperature of the blackbody component decreases with time, which is consistent with a scenario of a cooling expanding atmosphere.
By performing an additional analysis of the thermal component and the earlier X-ray measurements we have measured expansion velocities that are consistent with SN expansion and an initial apparent emission radius of 7 × 1011 cm. This radius is slightly larger than the size of WR stars, which are the most likely GRB-SNe progenitors. If a WR star were the progenitor of XRF 100316D/SN 2010bh, then the initial radius could indicate that there was a massive dense stellar wind surrounding the progenitor.
Our multicolour light curves after host-galaxy correction and subtraction of the afterglow component, have peak r′i′ luminosities of about 0.5–0.7 times that of SN 1998bw and consistent with those of SN 2006aj. Similarly the NIR luminosity at maximum is as bright as SN 2006aj and 0.6–0.7 times that of SN 1998bw. The excess in the g′ band indicates that SN 2010bh has a hotter photosphere than that of SN 1998bw at the time of maximum brightness.
We have found that SN 2010bh is the most rapidly evolving GRB-SNe to date, reaching maximum luminosity 8–9 days after the burst in the g′r′ bands. At late times, it also fades more rapidly than SN 1998bw showing redder colours as well. This behaviour is also evident in the bolometric light curve, which decays faster than for any SN in the comparison sample.
The physical parameters of the explosion are derived by means of the quasi-bolometric light curve constructed from our g′r′i′z′ JH photometry. The modelling is performed using Arnett’s model (Arnett 1982) for data around peak and standard γ-ray deposition at later times. A high-density inner component with roughly 26% of the total mass is required to reproduce the flux ratio between maximum luminosity and tail. The total mass of 56Ni produced in the envelope is MNi = 0.21 ± 0.03 M⊙, which precisely matches the value derived for SN 2006aj, whilst the total ejecta mass of Mej = 2.6 ± 0.2 M⊙ exceeds the value for SN 2006aj by 20%. However, the kinetic energy turns out to be higher at Ek = (2.4 ± 0.7) × 1052 erg, making SN 2010bh the second most energetic GRB-SN after SN1998bw.
Online material
Appendix A: Optical and near-infrared photometry
GROND photometry of field stars used for relative photometry.
GROND photometry of XRF 100316D/SN 2010bh after image subtraction.
IRAF, the Image Reduction and Analysis Facility, is distributed by the National Optical Astronomy Observatory, which is operated by the Association of Universities for Research in Astronomy (AURA), Inc., under cooperative agreement with the National Science Foundation (NSF); see http://iraf.noao.edu.
Acknowledgments
F.O.E. thanks Ferdinando Patat for stimulating discussion as well as for accurate comments and suggestions. We thank the referee and editors for accurate comments and useful suggestions. Part of the funding for GROND (both hardware and personnel) was generously granted from the Leibniz-Prize to Prof. G. Hasinger, Deutsche Forschungsgemeinschaft (DFG) grant HA 1850/28–1. This work made use of data supplied by the UK Swift Science Data Centre at the University of Leicester. The Ph.D. studies of F.O.E. are funded by the German Deutscher Akademischer Austausch Dienst, DAAD, and the Chilean Comisión Nacional de Investigación Científica y Tecnológica, CONICYT. T.K. acknowledges support by the DFG cluster of excellence “Origin and Structure of the Universe” and by the European Commission under the Marie Curie Intra-European Fellowship Programme. The Dark Cosmology Centre is funded by the Danish National Research Foundation. S.K., A.N.G., A. Rossi, and D.A.K. acknowledge support by DFG grant Kl 766/16–1. M.N. acknowledges support by DFG grant SA 2001/2–1. P.S. acknowledges support by DFG grant SA 2001/1–1. A.C.U., A.N.G., D.A.K., and A. Rossi are grateful for travel funding support through MPE. Figure 1 is partially based on observations made with the NASA/ESA Hubble Space Telescope, obtained from the data archive at the Space Telescope Science Institute. STScI is operated by the Association of Universities for Research in Astronomy, Inc. under NASA contract NAS 5–26555. This research has made use of NASA’s Astrophysics Data System.
References
- Afonso, P., Updike, A., Nardini, M., et al. 2010, GRB Coordinates Network, Circular Service, 10514, 1 [Google Scholar]
- Arnett, W. D. 1982, ApJ, 253, 785 [NASA ADS] [CrossRef] [Google Scholar]
- Balberg, S., & Loeb, A. 2011, MNRAS, 414, 1715 [NASA ADS] [CrossRef] [Google Scholar]
- Barthelmy, S. D., Barbier, L. M., Cummings, J. R., et al. 2005, Space Sci. Rev., 120, 143 [NASA ADS] [CrossRef] [Google Scholar]
- Benetti, S., Turatto, M., Valenti, S., et al. 2011, MNRAS, 411, 2726 [NASA ADS] [CrossRef] [Google Scholar]
- Berger, E., Chornock, R., Holmes, T. R., et al. 2011, ApJ, 743, 204 [NASA ADS] [CrossRef] [Google Scholar]
- Bersier, D., Fruchter, A. S., Strolger, L. G., et al. 2006, ApJ, 643, 284 [NASA ADS] [CrossRef] [Google Scholar]
- Bloom, J. S., Kulkarni, S. R., Djorgovski, S. G., et al. 1999, Nature, 401, 453 [NASA ADS] [CrossRef] [Google Scholar]
- Bloom, J. S., Kulkarni, S. R., Price, P. A., et al. 2002, ApJ, 572, L45 [NASA ADS] [CrossRef] [Google Scholar]
- Bloom, J. S., Prochaska, J. X., Pooley, D., et al. 2006, ApJ, 638, 354 [NASA ADS] [CrossRef] [Google Scholar]
- Bloom, J. S., Perley, D. A., Li, W., et al. 2009, ApJ, 691, 723 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Bufano, F., Benetti, S., Cappellaro, E., et al. 2010a, GRB Coordinates Network, Circular Service, 10543, 1 [Google Scholar]
- Bufano, F., Benetti, S., Cappellaro, E., et al. 2010b, Central Bureau Electronic Telegrams, 2227, 1 [NASA ADS] [Google Scholar]
- Bufano, F., Benetti, S., Sollerman, J., Pian, E., & Cupani, G. 2011, Astron. Nachr., 332, 262 [NASA ADS] [CrossRef] [Google Scholar]
- Burrows, D. N., Hill, J. E., Nousek, J. A., et al. 2005, Space Sci. Rev., 120, 165 [NASA ADS] [CrossRef] [Google Scholar]
- Campana, S., Mangano, V., Blustin, A. J., et al. 2006, Nature, 442, 1008 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Cano, Z., Bersier, D., Guidorzi, C., et al. 2011a, ApJ, 740, 41 [NASA ADS] [CrossRef] [Google Scholar]
- Cano, Z., Bersier, D., Guidorzi, C., et al. 2011b, MNRAS, 413, 669 [Google Scholar]
- Cappa, C., Goss, W. M., & van der Hucht, K. A. 2004, AJ, 127, 2885 [NASA ADS] [CrossRef] [Google Scholar]
- Castro-Tirado, A. J., & Gorosabel, J. 1999, A&AS, 138, 449 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Chornock, R., Berger, E., Levesque, E. M., et al. 2010a, ApJ, submitted [arXiv:1004.2262] [Google Scholar]
- Chornock, R., Soderberg, A. M., Foley, R. J., et al. 2010b, GRB Coordinates Network, Circular Service, 10541, 1 [Google Scholar]
- Chornock, R., Soderberg, A. M., Foley, R. J., et al. 2010c, Central Bureau Electronic Telegrams, 2228, 1 [NASA ADS] [Google Scholar]
- Clocchiatti, A., Suntzeff, N. B., Covarrubias, R., & Candia, P. 2011, AJ, 141, 163 [NASA ADS] [CrossRef] [Google Scholar]
- Cobb, B. E., Bailyn, C. D., van Dokkum, P. G., & Natarajan, P. 2006, ApJ, 645, L113 [NASA ADS] [CrossRef] [Google Scholar]
- Cobb, B. E., Bloom, J. S., Perley, D. A., et al. 2010, ApJ, 718, L150 [NASA ADS] [CrossRef] [Google Scholar]
- Colgate, S. A. 1968, Canadian J. Phys., 46, 476 [Google Scholar]
- Colgate, S. A. 1974, ApJ, 187, 333 [NASA ADS] [CrossRef] [Google Scholar]
- Della Valle, M., Malesani, D., Benetti, S., et al. 2003, A&A, 406, L33 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Della Valle, M., Chincarini, G., Panagia, N., et al. 2006a, Nature, 444, 1050 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Della Valle, M., Malesani, D., Bloom, J. S., et al. 2006b, ApJ, 642, L103 [NASA ADS] [CrossRef] [Google Scholar]
- Della Valle, M., Benetti, S., Mazzali, P., et al. 2008, Central Bureau Electronic Telegrams, 1602, 1 [Google Scholar]
- Drout, M. R., Soderberg, A. M., Gal-Yam, A., et al. 2011, ApJ, 741, 97 [NASA ADS] [CrossRef] [Google Scholar]
- Evans, P. A., Beardmore, A. P., Page, K. L., et al. 2007, A&A, 469, 379 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Evans, P. A., Beardmore, A. P., Page, K. L., et al. 2009, MNRAS, 397, 1177 [NASA ADS] [CrossRef] [Google Scholar]
- Falk, S. W. 1978, ApJ, 225, L133 [NASA ADS] [CrossRef] [Google Scholar]
- Fan, Y.-Z., Zhang, B.-B., Xu, D., Liang, E.-W., & Zhang, B. 2011, ApJ, 726, 32 [NASA ADS] [CrossRef] [Google Scholar]
- Ferrero, P., Kann, D. A., Zeh, A., et al. 2006, A&A, 457, 857 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Filgas, R., Greiner, J., Schady, P., et al. 2011, A&A, 535, A57 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Foley, R. J., Papenkova, M. S., Swift, B. J., et al. 2003, PASP, 115, 1220 [NASA ADS] [CrossRef] [Google Scholar]
- Fox, D. B., Frail, D. A., Price, P. A., et al. 2005, Nature, 437, 845 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Fynbo, J. P. U., Watson, D., Thöne, C. C., et al. 2006, Nature, 444, 1047 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Gal-Yam, A., Ofek, E. O., & Shemmer, O. 2002, MNRAS, 332, L73 [NASA ADS] [CrossRef] [Google Scholar]
- Gal-Yam, A., Fox, D. B., Price, P. A., et al. 2006, Nature, 444, 1053 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Galama, T. J., Vreeswijk, P. M., Pian, E., et al. 1998a, IAU Circ., 6895, 1 [NASA ADS] [Google Scholar]
- Galama, T. J., Vreeswijk, P. M., van Paradijs, J., et al. 1998b, Nature, 395, 670 [NASA ADS] [CrossRef] [Google Scholar]
- Galama, T. J., Wijers, R. A. M. J., Bremer, M., et al. 1998c, ApJ, 500, L101 [NASA ADS] [CrossRef] [Google Scholar]
- Galama, T. J., Tanvir, N., Vreeswijk, P. M., et al. 2000, ApJ, 536, 185 [NASA ADS] [CrossRef] [Google Scholar]
- Gehrels, N., Chincarini, G., Giommi, P., et al. 2004, ApJ, 611, 1005 [NASA ADS] [CrossRef] [Google Scholar]
- Gezari, S., Rest, A., Huber, M. E., et al. 2010, ApJ, 720, L77 [NASA ADS] [CrossRef] [Google Scholar]
- Granot, J., Piran, T., & Sari, R. 1999, ApJ, 527, 236 [NASA ADS] [CrossRef] [Google Scholar]
- Greiner, J., Klose, S., Salvato, M., et al. 2003, ApJ, 599, 1223 [NASA ADS] [CrossRef] [Google Scholar]
- Greiner, J., Bornemann, W., Clemens, C., et al. 2007, The Messenger, 130, 12 [NASA ADS] [Google Scholar]
- Greiner, J., Bornemann, W., Clemens, C., et al. 2008, PASP, 120, 405 [NASA ADS] [CrossRef] [Google Scholar]
- Hansen, B. M. S. 1999, ApJ, 512, L117 [NASA ADS] [CrossRef] [Google Scholar]
- Heise, J., & in ’t Zand, J. 2001 [arXiv:astro-ph/0112353] [Google Scholar]
- Heise, J., in’t Zand, J., Kippen, R. M., & Woods, P. M. 2001, in Gamma-ray Bursts in the Afterglow Era, ed. E. Costa, F. Frontera, & J. Hjorth, ESO Astrophysics Symposia (Rome, Italy: Springer-Verlag), 16 [Google Scholar]
- Hjorth, J., Sollerman, J., Møller, P., et al. 2003, Nature, 423, 847 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Hjorth, J., Sollerman, J., Gorosabel, J., et al. 2005a, ApJ, 630, L117 [NASA ADS] [CrossRef] [Google Scholar]
- Hjorth, J., Watson, D., Fynbo, J. P. U., et al. 2005b, Nature, 437, 859 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Jones, M. I., Hamuy, M., Lira, P., et al. 2009, ApJ, 696, 1176 [NASA ADS] [CrossRef] [Google Scholar]
- Kalberla, P. M. W., Burton, W. B., Hartmann, D., et al. 2005, A&A, 440, 775 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kaneko, Y., Ramirez-Ruiz, E., Granot, J., et al. 2007, ApJ, 654, 385 [NASA ADS] [CrossRef] [Google Scholar]
- Kann, D. A., Klose, S., Zhang, B., et al. 2011, ApJ, 734, 96 [NASA ADS] [CrossRef] [Google Scholar]
- Kawabata, K. S., Deng, J., Wang, L., et al. 2003, ApJ, 593, L19 [NASA ADS] [CrossRef] [Google Scholar]
- Kippen, R. M., Briggs, M. S., Kommers, J. M., et al. 1998, ApJ, 506, L27 [NASA ADS] [CrossRef] [Google Scholar]
- Kippen, R. M., in’t Zand, J. J. M., Woods, P. M., et al. 2004, in Gamma-Ray Bursts: 30 Years of Discovery, ed. E. Fenimore, & M. Galassi (Santa Fe, NM: AIP), AIP Conf. Ser., 727, 119 [Google Scholar]
- Klein, R. I., & Chevalier, R. A. 1978, ApJ, 223, L109 [NASA ADS] [CrossRef] [Google Scholar]
- Kocevski, D., Modjaz, M., Bloom, J. S., et al. 2007, ApJ, 663, 1180 [NASA ADS] [CrossRef] [Google Scholar]
- Kouveliotou, C., Meegan, C. A., Fishman, G. J., et al. 1993, ApJ, 413, L101 [NASA ADS] [CrossRef] [Google Scholar]
- Kouveliotou, C., Woosley, S. E., Patel, S. K., et al. 2004, ApJ, 608, 872 [NASA ADS] [CrossRef] [Google Scholar]
- Krühler, T., Küpcü Yoldaş, A., Greiner, J., et al. 2008, ApJ, 685, 376 [NASA ADS] [CrossRef] [Google Scholar]
- Levesque, E. M., Berger, E., Soderberg, A. M., & Chornock, R. 2011, ApJ, 739, 23 [NASA ADS] [CrossRef] [Google Scholar]
- Maeda, K., Mazzali, P. A., Deng, J., et al. 2003, ApJ, 593, 931 [NASA ADS] [CrossRef] [Google Scholar]
- Malesani, D., Tagliaferri, G., Chincarini, G., et al. 2004, ApJ, 609, L5 [NASA ADS] [CrossRef] [Google Scholar]
- Malesani, D., Fynbo, J. P. U., Hjorth, J., et al. 2009, ApJ, 692, L84 [NASA ADS] [CrossRef] [Google Scholar]
- Masetti, N., Palazzi, E., Pian, E., et al. 2003, A&A, 404, 465 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Masetti, N., Palazzi, E., Pian, E., et al. 2005, A&A, 438, 841 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Matheson, T., Garnavich, P. M., Stanek, K. Z., et al. 2003, ApJ, 599, 394 [NASA ADS] [CrossRef] [Google Scholar]
- Matzner, C. D., & McKee, C. F. 1999, ApJ, 510, 379 [NASA ADS] [CrossRef] [Google Scholar]
- Mazzali, P. A., Deng, J., Nomoto, K., et al. 2006, Nature, 442, 1018 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Mazzali, P. A., Valenti, S., Della Valle, M., et al. 2008, Science, 321, 1185 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Mirabal, N., Halpern, J. P., An, D., Thorstensen, J. R., & Terndrup, D. M. 2006, ApJ, 643, L99 [NASA ADS] [CrossRef] [Google Scholar]
- Modjaz, M., Stanek, K. Z., Garnavich, P. M., et al. 2006, ApJ, 645, L21 [NASA ADS] [CrossRef] [Google Scholar]
- Modjaz, M., Li, W., Butler, N., et al. 2009, ApJ, 702, 226 [NASA ADS] [CrossRef] [Google Scholar]
- Mould, J. R., Huchra, J. P., Freedman, W. L., et al. 2000, ApJ, 529, 786 [NASA ADS] [CrossRef] [Google Scholar]
- Nakar, E., & Sari, R. 2010, ApJ, 725, 904 [NASA ADS] [CrossRef] [Google Scholar]
- Nomoto, K., Tanaka, M., Tominaga, N., & Maeda, K. 2010, New Astron. Rev., 54, 191 [Google Scholar]
- Oates, S. R., de Pasquale, M., & Stamatikos, M. 2010, GRB Coordinates Network, Circular Service, 10520, 1 [Google Scholar]
- Ofek, E. O., Cenko, S. B., Gal-Yam, A., et al. 2007, ApJ, 662, 1129 [NASA ADS] [CrossRef] [Google Scholar]
- Olivares, E. F., Hamuy, M., Pignata, G., et al. 2010, ApJ, 715, 833 [NASA ADS] [CrossRef] [Google Scholar]
- Paczyński, B. 1986, ApJ, 308, L43 [NASA ADS] [CrossRef] [Google Scholar]
- Paczyński, B. 1998, in Gamma-Ray Bursts: 4th Hunstville Symposium, ed. C. A. Meegan, R. D. Preece, & T. M. Koshut (Huntsville, AL: AIP), AIP Conf. Ser., 428, 783 [Google Scholar]
- Patat, F., Cappellaro, E., Danziger, J., et al. 2001, ApJ, 555, 900 [NASA ADS] [CrossRef] [Google Scholar]
- Pian, E., Antonelli, L. A., Piro, L., & Feroci, M. 1998, GRB Coordinates Network, 158, 1 [Google Scholar]
- Pian, E., Amati, L., Antonelli, L. A., et al. 2000, ApJ, 536, 778 [NASA ADS] [CrossRef] [Google Scholar]
- Pian, E., Mazzali, P. A., Masetti, N., et al. 2006, Nature, 442, 1011 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Pignata, G., Stritzinger, M., Soderberg, A., et al. 2011, ApJ, 728, 14 [NASA ADS] [CrossRef] [Google Scholar]
- Poole, T. S., Breeveld, A. A., Page, M. J., et al. 2008, MNRAS, 383, 627 [NASA ADS] [CrossRef] [Google Scholar]
- Price, P. A., Kulkarni, S. R., Berger, E., et al. 2003, ApJ, 589, 838 [NASA ADS] [CrossRef] [Google Scholar]
- Rau, A., Nardini, M., Updike, A., et al. 2010, GRB Coordinates Network, Circular Service, 10547, 1 [Google Scholar]
- Reichart, D. E. 1999, ApJ, 521, L111 [NASA ADS] [CrossRef] [Google Scholar]
- Reichart, D. E., Lamb, D. Q., & Castander, F. J. 2000, in Gamma-ray Bursts: 5th Huntsville Symposium, ed. R. M. Kippen, R. S. Mallozzi, & G. J. Fishman (Huntsville, AL: AIP), AIP Conf. Ser., 526, 414 [Google Scholar]
- Richardson, D. 2009, AJ, 137, 347 [NASA ADS] [CrossRef] [Google Scholar]
- Richardson, D., Branch, D., & Baron, E. 2006, AJ, 131, 2233 [NASA ADS] [CrossRef] [Google Scholar]
- Richmond, M. W., van Dyk, S. D., Ho, W., et al. 1996, AJ, 111, 327 [NASA ADS] [CrossRef] [Google Scholar]
- Riess, A. G., Macri, L., Casertano, S., et al. 2009, ApJ, 699, 539 [NASA ADS] [CrossRef] [Google Scholar]
- Roming, P. W. A., Kennedy, T. E., Mason, K. O., et al. 2005, Space Sci. Rev., 120, 95 [NASA ADS] [CrossRef] [Google Scholar]
- Roming, P. W. A., Pritchard, T. A., Brown, P. J., et al. 2009, ApJ, 704, L118 [NASA ADS] [CrossRef] [Google Scholar]
- Sadler, E. M., Stathakis, R. A., Boyle, B. J., & Ekers, R. D. 1998, IAU Circ., 6901, 1 [NASA ADS] [Google Scholar]
- Sakamoto, T., Lamb, D. Q., Kawai, N., et al. 2005, ApJ, 629, 311 [NASA ADS] [CrossRef] [Google Scholar]
- Sakamoto, T., Barthelmy, S. D., Baumgartner, W. H., et al. 2010, GRB Coordinates Network, Circular Service, 10511, 1 [Google Scholar]
- Sanders, N. E., Soderberg, A. M., Valenti, S., et al. 2011 [arXiv:1110.2363] [Google Scholar]
- Sari, R., Piran, T., & Narayan, R. 1998, ApJ, 497, L17 [NASA ADS] [CrossRef] [Google Scholar]
- Schawinski, K., Justham, S., Wolf, C., et al. 2008, Science, 321, 223 [NASA ADS] [CrossRef] [Google Scholar]
- Schlegel, D. J., Finkbeiner, D. P., & Davis, M. 1998, ApJ, 500, 525 [NASA ADS] [CrossRef] [Google Scholar]
- Soderberg, A. M., Kulkarni, S. R., Fox, D. B., et al. 2005, ApJ, 627, 877 [NASA ADS] [CrossRef] [Google Scholar]
- Soderberg, A. M., Kulkarni, S. R., Price, P. A., et al. 2006, ApJ, 636, 391 [NASA ADS] [CrossRef] [Google Scholar]
- Soderberg, A. M., Berger, E., Page, K. L., et al. 2008, Nature, 453, 469 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Soffitta, P., Feroci, M., Piro, L., et al. 1998, IAU Circ., 6884, 1 [NASA ADS] [Google Scholar]
- Sollerman, J., Jaunsen, A. O., Fynbo, J. P. U., et al. 2006, A&A, 454, 503 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Sollerman, J., Fynbo, J. P. U., Gorosabel, J., et al. 2007, A&A, 466, 839 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Sparre, M., Sollerman, J., Fynbo, J. P. U., et al. 2011, ApJ, 735, L24 [NASA ADS] [CrossRef] [Google Scholar]
- Stamatikos, M., Barthelmy, S. D., Baumgartner, W. H., et al. 2010, GRB Coordinates Network, Circular Service, 10496, 1 [Google Scholar]
- Stanek, K. Z., Matheson, T., Garnavich, P. M., et al. 2003, ApJ, 591, L17 [NASA ADS] [CrossRef] [Google Scholar]
- Stanek, K. Z., Garnavich, P. M., Nutzman, P. A., et al. 2005, ApJ, 626, L5 [NASA ADS] [CrossRef] [Google Scholar]
- Starling, R. L. C., Wiersema, K., Levan, A. J., et al. 2011, MNRAS, 411, 2792 [NASA ADS] [CrossRef] [Google Scholar]
- Tanvir, N. R., Rol, E., Levan, A. J., et al. 2010, ApJ, 725, 625 [NASA ADS] [CrossRef] [Google Scholar]
- Taubenberger, S., Pastorello, A., Mazzali, P. A., et al. 2006, MNRAS, 371, 1459 [NASA ADS] [CrossRef] [Google Scholar]
- Taylor, G. B., Frail, D. A., Kulkarni, S. R., et al. 1998, ApJ, 502, L115 [NASA ADS] [CrossRef] [Google Scholar]
- Thöne, C. C., de Ugarte Postigo, A., Fryer, C. L., et al. 2011, Nature, 480, 72 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Tinney, C., Stathakis, R., Cannon, R., & Galama, T. 1998, IAU Circ., 6896, 3 [Google Scholar]
- Tody, D. 1993, in Astronomical Data Analysis Software and Systems II, ed. R. J. Hanisch, R. J. V. Brissenden, & J. Barnes (San Francisco, CA: ASP), ASP Conf. Ser., 52, 173 [Google Scholar]
- Valenti, S., Benetti, S., Cappellaro, E., et al. 2008, MNRAS, 383, 1485 [NASA ADS] [CrossRef] [Google Scholar]
- Vergani, S. D., D’Avanzo, P., Levan, A. J., et al. 2010a, GRB Coordinates Network, Circular Service, 10512, 1 [Google Scholar]
- Vergani, S. D., Levan, A. J., D’Avanzo, P., et al. 2010b, GRB Coordinates Network, Circular Service, 10513, 1 [Google Scholar]
- Vietri, M., & Stella, L. 1999, ApJ, 527, L43 [NASA ADS] [CrossRef] [Google Scholar]
- Wang, X.-Y., Li, Z., Waxman, E., & Mészáros, P. 2007, ApJ, 664, 1026 [NASA ADS] [CrossRef] [Google Scholar]
- Waxman, E., Mészáros, P., & Campana, S. 2007, ApJ, 667, 351 [NASA ADS] [CrossRef] [Google Scholar]
- Wiersema, K., van der Horst, A. J., Kann, D. A., et al. 2008, A&A, 481, 319 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Wiersema, K., D’Avanzo, P., Levan, A. J., et al. 2010, GRB Coordinates Network, Circular Service, 10525, 1 [Google Scholar]
- Woosley, S. E. 1993, ApJ, 405, 273 [NASA ADS] [CrossRef] [Google Scholar]
- Woosley, S. E., & Bloom, J. S. 2006, ARA&A, 44, 507 [NASA ADS] [CrossRef] [Google Scholar]
- Woosley, S. E., & MacFadyen, A. I. 1999, A&AS, 138, 499 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Woosley, S. E., Heger, A., & Weaver, T. A. 2002, Rev. Mod. Phys., 74, 1015 [NASA ADS] [CrossRef] [Google Scholar]
- Yoshii, Y., Tomita, H., Kobayashi, Y., et al. 2003, ApJ, 592, 467 [NASA ADS] [CrossRef] [Google Scholar]
- Zeh, A., Klose, S., & Hartmann, D. H. 2004, ApJ, 609, 952 [NASA ADS] [CrossRef] [Google Scholar]
- Zhang, B., & Mészáros, P. 2004, Int. J. Mod. Phys. A, 19, 2385 [NASA ADS] [CrossRef] [Google Scholar]
- Zhang, B., Zhang, B.-B., Virgili, F. J., et al. 2009, ApJ, 703, 1696 [NASA ADS] [CrossRef] [Google Scholar]
All Tables
All Figures
 |
Fig. 1 HST/WFC3 F814W, GROND i′-band, and GROND host-subtracted i′-band images of the GRB-SN field, respectively, from left to right. Images were taken at around maximum brightness. Each panel is approximately 13′′ × 13′′ in size. The HST image shows significant galaxy structure near the explosion site (marked with two lines), which is blended with the object of interest in the GROND image shown in the middle panel. GROND images in the middle and right panels are shown using the same flux scale. |
| In the text | |
 |
Fig. 2 Broad-band SED at 50 ks after trigger. The observed data are represented by black filled circles. The HKs bands provide only 3σ upper limits shown as arrows. The thick grey line shows the best-fit model able to reproduce the data: extinguished power law plus blackbody components, which are shown individually with dotted and dashed grey lines, respectively. The thin continuous grey lines show the unextinguished versions of the power law corresponding to the afterglow and the thermal component. In the lower panel, the residuals of the best fit are plotted. |
| In the text | |
 |
Fig. 3 Contour plots for the best-fit parameters from the modelling of the second epoch. From the outer- to the innermost contours, the green, red, and black lines are 3, 2, and 1σ contours, respectively. The tail at low Γ in the bottom panel is caused by numerical inaccuracies. |
| In the text | |
 |
Fig. 4 Temperature and radius evolution of the blackbody component. Black data points are those derived using combined BAT+XRT data (Starling et al. 2011) plus the temperature determinations using GROND data ( ≈ 46 ks). The first data bin from Starling et al. (2011) represents the interval from − 175 to 144 s, however, due to fitting and plotting purposes, here it corresponds to 0–144 s. Solid, dashed and dotted lines are different power-law models (see main text). Best fits to temperature and radius are shown in grey and brown solid lines, respectively. Grey crosses (upper panel) and open circles (lower panel) are measurements of XRF 060218/SN 2006aj taken from Kaneko et al. (2007) and Campana et al. (2006), respectively. |
| In the text | |
 |
Fig. 5 Multi-colour light curves corrected for host-galaxy extinction and afterglow-subtracted. Filled circles represent detections and arrows are upper limits. Solid lines represent the overall fits and dashed lines individual components. Fits of SN 1998bw templates are extrapolated from ≈ t0 + 60 d. For reasons of clarity, light curves were shifted along the magnitude axis and the systematical error in AV,host was not added to the error bars. |
| In the text | |
 |
Fig. 6 Colour curves corrected for host-galaxy extinction and afterglow-subtracted. Filled circles represent detections in both filters and arrows are upper limits derived from detections in one of the two bands. Solid lines represent the colour evolution of SN 1998bw derived from the light-curve fits in Sect. 4.3. For clarity, error bars do not include the systematic error in AV,host and for the last epoch, upper limits are not shown. |
| In the text | |
 |
Fig. 7 Quasi-bolometric light curve of SN 2010bh produced by using GROND g′r′i′z′ JH filters (black open circles) in the rest frame. For clarity, the uncertainties in the host-galaxy extinction are not included in the error bars. A single black continuous line represents the best-fit model (see Sect. 5.1). Early and late components of the model are smoothly joined at t0 + 30 d. SE and other GRB-SNe quasi-bolometric light curves have been plotted as a comparison sample: SN 2003lw (GRB 031203; Malesani et al. 2004), SN 1998bw (GRB 980425; Galama et al. 1998b), SN 2006aj (GRB 060218; Pian et al. 2006), the broad-lined Ic SN 2009bb (Pignata et al. 2011), the type-Ic SN 1994I (Richmond et al. 1996), the type Ibc SN 2008D (XRO 080109; Modjaz et al. 2009; Soderberg et al. 2008), and the type-Ic SN 2002ap (Gal-Yam et al. 2002; Foley et al. 2003; Yoshii et al. 2003). |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


