| Issue |
A&A
Volume 538, February 2012
|
|
|---|---|---|
| Article Number | A54 | |
| Number of page(s) | 84 | |
| Section | Interstellar and circumstellar matter | |
| DOI | https://doi.org/10.1051/0004-6361/201118217 | |
| Published online | 01 February 2012 | |
Analysis of chemical abundances in planetary nebulae with [WC] central stars
I. Line intensities and physical conditions⋆,⋆⋆
1 Instituto de Astrofísica de Canarias, 38200 La Laguna, Tenerife, Spain
e-mail: jogarcia@iac.es; amd@iac.es; chris.morisset@gmail.com;
2 Departamento de Astrofísica. Universidad de La Laguna, 38205 La Laguna, Tenerife, Spain
3 Instituto de Astronomía, Universidad Nacional Autónoma de México, Apdo. Postal 70264, 04510 Méx. D. F., Mexico
e-mail: miriam@astro.unam.mx
4 Departamento de Astronomía, Universidad de Chile, Casilla 36 D, Las Condes, Santiago, Chile
e-mail: mtruiz@das.uchile.cl
Received: 6 October 2011
Accepted: 16 November 2011
Context. Planetary nebulae (PNe) around Wolf-Rayet [WR] central stars ([WR]PNe) constitute a particular photoionized nebula class that represents about 10% of the PNe with classified central stars.
Aims. We analyse deep high-resolution spectrophotometric data of 12 [WR] PNe. This sample of [WR]PNe represents the most extensive analysed so far, at such high spectral resolution. We aim to select the optimal physical conditions in the nebulae to be used in ionic abundance calculations that will be presented in a forthcoming paper.
Methods. We acquired spectra at Las Campanas Observatory with the 6.5-m telescope and the Magellan Inamori Kyocera (MIKE) spectrograph, covering a wavelength range from 3350 Å to 9400 Å. The spectra were exposed deep enough to detect, with signal-to-noise ratio higher than three, the weak optical recombination lines (ORLs) of O ii, C ii, and other species. We detect and identify about 2980 emission lines, which, to date, is the most complete set of spectrophotometric data published for this type of objects. From our deep data, numerous diagnostic line ratios for Te and ne are determined from collisionally excited lines (CELs), ORLs, and continuum measurements (H i Paschen continuum in particular).
Results. Densities are closely described by the average of all determined values for objects with ne < 104 cm-3, and by ne([Cl iii]) for the densest objects. For some objects, ne([Ar iv]) is adopted as the characteristic density of the high ionization zone. For Te, we adopt a three-zone ionization scheme, where the low ionization zone is characterised by Te([N ii]), the medium ionization zone by Te([O iii]), and the highest ionization one by Te([Ar iv]) when available. We compute Te from the H i Paschen discontinuity and from He i lines. For each object, Te(H i) is, in general, consistent with Te derived from CELs, although it has a very large error. Values of Te(He i) are systematically lower than the Te derived from CELs. When comparing Te(H i) and Te(He i) it is unclear whether the behaviour of both temperatures agrees with the predictions of the temperature fluctuations paradigm, owing to the large errors in Te(H i). We do not find any evidence of low-temperature, high-density clumps in our [WR]PNe from the analysis of faint O ii and N ii plasma diagnostics, although uncertainties dominate the observed line ratios in most objects. The behaviour of Te([O iii])/Te([N ii]), which is smaller for high ionization degrees, can be reproduced by a set of combined matter-bounded and radiation-bounded models, although, for the smallest temperature ratios, a too high metallicity seem to be required.
Key words: stars: AGB and post-AGB / ISM: abundances / planetary nebulae: general / line: identification
Full Table 3 and Fig. 3 are available in electronic form at http://www.aanda.org
© ESO, 2012
1. Introduction
Planetary nebulae (PNe) constitute the evolutionary end point of most stars in the Universe, and they play a major role in the chemical enrichment history of the interstellar medium (ISM) of galaxies. Their chemical compositions allow us to determine the abundances of some chemical elements present in the ISM when their progenitor stars were born and to analyse the contribution of these stars to galactic chemical enrichment by elements processed in the nucleus and ejected into the ISM. Planetary nebulae are produced by stars with initial masses of between ~1 M⊙ and ~8 M⊙ and a large age spread (from 0.1 to 9 Gyr, Allen et al. 1998). The central stars (CS) are evolved stars (post-AGB) in the pre-white dwarf stage. Among them, there is an interesting group that has both very intense stellar winds with mass-loss rates in the range of 10-7 − 10-5 M⊙ per year (Koesterke 2001, and references therein) and terminal velocities from several hundreds to several thousands km s-1 and a hydrogen deficient chemical composition. All these stars have been catalogued as Wolf-Rayet of the C-sequence (for a quantitative classification scheme of these stars, see Acker & Neiner 2003, and references therein). Until recently, the [WR] CSPNe were thought to represent about 5−7% of all CSPNe (Tylenda et al. 1993; Acker & Neiner 2003), but that value should be a lower limit owing to several selection effects, and the real percentage could be larger (DePew et al. 2011). Among these CSPNe, about half of them, the so-called [WC]-early stars, have very high surface temperatures from 80 kK to about 150 kK (spectral classes are [WC4-5], [WO1-3]) while the others, called [WC]-late stars (spectral classes [WC6] to [WC11]) have temperatures between 80 kK and about 30 kK (Koesterke 2001).
Object characteristics and log of observations (slit dimensions were always 1′′ × 5′′).
Many papers have been devoted to the analysis of these PNe and their CS because they can provide several clues about the processes of the chemical enrichment of both the shells and the interstellar medium with freshly made products, the processes of the shell ejection and its additional interaction with the stellar winds, etc. Several mechanisms have been proposed to explain the presence of the strong winds and the peculiar H-deficient chemical composition of [WC] stars, among them a final thermal pulse at the AGB phase (AFTP), a late thermal pulse (LTP), and a very late thermal pulse occurring in the white dwarf cooling track, (e.g., Werner & Herwig 2006, and references therein).
Recently, DePew et al. (2011) reported the discovery of several more central stars of the [WR] type, which together with the sample reported by Górny et al. (2004) have increased the number of known [WR]PNe central stars, to over a hundred.
Some years ago, we initiated a project to obtain deep high-resolution spectroscopy of PNe around [WC] stars ([WR]PNe), in order to analyse the chemical behaviour of the photoionized plasma as based on collisionally excited lines (CELs) or on optical recombination lines (ORLs). It is known that a discrepancy in the abundances of a factor of two or more is commonly found in photoionized nebulae. This discrepancy is measured through the abundance discrepancy factor, ADF, defined as: 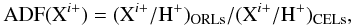 where Xi+ is the i + ionic abundance of element X and H+ is the abundance of ionized hydrogen.
where Xi+ is the i + ionic abundance of element X and H+ is the abundance of ionized hydrogen.
The presence of H-deficient inclusions is one of the mechanisms suggested to explain ADFs larger than one (see e.g., Liu et al. 2006, and references therein). Since [WR] PNe are ionized by H-deficient stars whose atmospheres are almost pure He and C (i.e., Koesterke 2001) and since they lose mass at high rates, it seems plausible that the presence of tiny H-deficient knots in the ionized plasma could cause large ADFs.
In a previous paper (García-Rojas et al. 2009), three [WR]PNe were analysed based on echelle data obtained with the same instrument as in this work: PB 8, a young nebula around an uncommon [WN]/[WC] central star (Todt et al. 2010); NGC 2867, an evolved nebula around a [WC4] star; and PB 6, a highly excited [WR]PNe around a [WO2] star. Some evidences against the presence of H-deficient metal-rich knots in the PNe coming from a late thermal pulse event were presented, based on the low (C/O)ORLs/(C/O)CELs observed in both objects with detected ORLs of C and O ions (PB 8 and NGC 2867) and the similarity between O ii and [O iii] heliocentric velocities. These results seem to argue against a “C-rich knots ejected in a late thermal pulse” scenario as the origin of the observed ADFs.
In this work, we present additional high-resolution spectrophotometric data obtained for 12 objects, where the faint O ii and C ii ORLs have been detected. The main characteristics of these nebulae are presented in Table 1 where the log of observations also can be found. An extensive catalog of lines (hundreds of lines have been detected for each analysed object). For each emission line, we provide the line identification, radial velocity, and observed and dereddened line fluxes. In the following, we describe the observations and data reduction procedures (Sect. 2), the determinations of line intensities and reddening (Sect. 3), and the analysis of the plasma physical conditions as derived from the diagnostic line ratios (Sect. 4). In Sect. 5, we discuss the results. In a forthcoming paper (García-Rojas et al., in prep., Paper II), we discuss the abundance pattern and the ADFs found for these objects.
2. Observations and data reduction
High spectral resolution data were obtained at Las Campanas Observatory (Carnegie Institution) with the Clay 6.5-m telescope and the double echelle Magellan Inamori Kyocera spectrograph (MIKE) on September 2009 and June 2010. This spectrograph operates with two arms that allow us to obtain a blue and a red spectrum simultaneously (Berstein et al. 2003). The standard set of gratings were employed, providing a wavelength coverage from 3350 Å to 5050 Å in the blue and from 4950 Å to 9400 Å in the red. Long and short exposure time observations were carried out for each object, in order to ensure an appropriate signal-to-noise ratio in the faint lines and unsaturated data in the strongest lines. The log of observations is presented in Table 1, where we list the observing date, the exposure times for each object and the averaged airmass during each set of observations. For all the observed PNe, the slit dimensions were 1′′ along the dispersion axis, and 5′′ in the spatial direction. A binning of 2 × 2 was used, obtaining a spacial scale of 0.2608′′/pix. As usual, series of bias, milky-flats and flats with the internal incandescent lamp were acquired for data reduction. A Th-Ar lamp exposure was observed after each science exposure for wavelength calibrations. The spectral resolution obtained varied from 0.14 Å to 0.17 Å (about 10.8 km s-1) in the blue, and from 0.23 Å to 0.27 Å (about 12.8 km s-1) in the red, as measured from the half-width half maximum (HWHM) of the lines of the Th-Ar comparison lamp.
As shown in Table 1, all the objects were observed at zenith distances smaller than or about 30° (as recommended by the MIKE User Manual) covering airmasses between 1.004 and 1.25, thus the atmospheric refraction was not expected to affect the spectra.
In the September 2009 run, the seeing was about 1′′−1.2′′. In the June 2010 run, the seeing was better than 1′′, being as good as 0.6−0.7′′ for some hours.
Standard data reduction procedures were performed. Two-dimensional (2D) echellograms were bias-subtracted and flat-fielded using iraf1echelle reduction packages. We used the apscatter task to substract the background-scattered light contribution in the 2D-echellograms. The spectra were extracted with an extraction window of 3 72 to fit the width of the normalized flat-field windows, and they were wavelength-calibrated using the Th-Ar exposures. The fits to the wavelength function give an rms of about 0.005, which translates into a precision of about 0.01 Å in the wavelength-calibrated spectra. The data were flux-calibrated using the spectrophotometric standard stars Feige 110, LDS 749B, and NGC 7293 (Oke 1990). For these objects, the slit width was increased to 2′′ to maximize the stellar flux entering the slit. The estimated error in the absolute flux calibration was about 5%. We estimated this error by self-calibrating the standard stars by themselves and comparing the computed flux with that obtained from the spectrophotometric data of these stars (Oke 1990). The bluest (λ < 3700 Å) flux calibration of the objects observed on June 6 (He 2-86, M 1-30, M 1-32, NGC 6369) was unreliable owing to problems deriving the stellar continuum associated with strong H i absorption lines in the blue spectrum of the selected standard star.
72 to fit the width of the normalized flat-field windows, and they were wavelength-calibrated using the Th-Ar exposures. The fits to the wavelength function give an rms of about 0.005, which translates into a precision of about 0.01 Å in the wavelength-calibrated spectra. The data were flux-calibrated using the spectrophotometric standard stars Feige 110, LDS 749B, and NGC 7293 (Oke 1990). For these objects, the slit width was increased to 2′′ to maximize the stellar flux entering the slit. The estimated error in the absolute flux calibration was about 5%. We estimated this error by self-calibrating the standard stars by themselves and comparing the computed flux with that obtained from the spectrophotometric data of these stars (Oke 1990). The bluest (λ < 3700 Å) flux calibration of the objects observed on June 6 (He 2-86, M 1-30, M 1-32, NGC 6369) was unreliable owing to problems deriving the stellar continuum associated with strong H i absorption lines in the blue spectrum of the selected standard star.
3. Line intensities and reddening correction
The splot routine of the iraf package was used to measure the line intensities. In general, as most of the lines have either a double-peak or a complex velocity structure, all the flux in the line was integrated between two given limits, over a local continuum estimated by eye. In the case of objects with a simple velocity structure showing very tight blends among nebular lines or with telluric emission lines, the analysis was performed via a multiple Gaussian fitting. In Fig. 1, we present the Hβ emission line as seen in the 2D-echellograms for all the objects in our sample, to show the spatially and spectroscopically resolved emission. The extracted spectra are also shown. It can be seen that several objects have very complicated line profiles.
 |
Fig. 1 Portion of the 2D echellograms and the extracted spectra showing the spatially resolved Hβ line for all objects in our sample. |
All the lines of a given spectrum were normalized to a particular bright emission line in the common range between both the blue and red spectrum. In the blue range we used Hβ, and in the red range we used either the [O iii] λ4959 line or the He i λ5015 line, when the [O iii] line was saturated in the long exposure. To produce a homogeneous data set of line flux ratios, all of them were rescaled to the Hβ flux by using the [O iii] λ4959/Hβ or the He i λ5015/Hβ flux ratios measured in the blue range. Some lines that were saturated in the long exposures were measured in the short ones and rescaled to the Hβ flux. Differences of up to 10% between the integrated flux of the common lines, in the blue and red ranges, were measured. These differences are probably caused by common lines (namely Hβ, [O iii] λλ4959, 5007 and He i λ5015) being at the red and blue extremes of the CCDs, where the flat-field correction might be less reliable. Nevertheless, we were always able to find a reasonable agreement between blue and red measured fluxes of [O iii] λ4959 in the short exposure, with differences amounting to a maximum of 11% in two objects (H b4 and NGC 5189), 9% in M 3-15, and remaining below or of the order of the adopted flux calibration uncertainty (5%) in the remaining objects. We do not expect the final results to be substancially affected because only line ratios are used in our analysis.
Owing to the small area covered by our slit and because our objects are extended, we were unable to extract a sky spectrum. However, taking into account the peculiar profile of the emission lines in each object, it was easy to distinguish telluric features from the nebular emission lines. The cases in which nebular emission lines were severely blended with sky telluric features are labelled in the table of line identifications (Table 3).
Extinction coefficients.
For the reddening correction we assumed the standard extinction law for the Milky Way parametrized by Seaton (1979), with Rv = 3.1. The logarithmic redddening coefficient, c(Hβ), was derived in each case by fitting the observed Balmer decrement, F(H i Balmer)/F(Hβ), and the observed F(H i Paschen)/F(Hβ) to the theoretical values computed by Storey & Hummer (1995) for an electron temperature, Te, and a density, ne, as given for each object by Girard et al. (2007). In Table 2, we present the reddening coefficient, c(Hβ), the H i lines used for deriving it, the physical conditions (Te and ne) adopted for each case, and previous determinations found in the literature. In Fig. 2, we can see that there is a good overall agreement between our derived c(Hβ) values and those reported in the literature, except for some objects of Girard et al. (2007) (red filled circles in the on-line version) and the data of Peña et al. (2001) (green stars in the on-line version) where we found significant differences in the derived c(Hβ) for most of the objects in common between both samples. These differences could be due to difficulties in separating the nebular from the stellar emission in the case of Girard et al. (2007) data, or to problems in the flux calibration in the zones of bluer H i lines in Peña et al. (2001) data.
 |
Fig. 2 Comparison between our derived c(Hβ) and those derived in the literature for common objects. Red filled circles: Girard et al. (2007); green filled stars: Peña et al. (2001); blue filled triangles: Górny et al. (2009); blue open inverse triangles: Acker & Neiner (2003). It is clear that there is a good overall agreement, except for some data (see text). |
Table 3 presents the observed and reddening corrected emission line intensities measured in all our PNe. The first column presents the adopted laboratory wavelength, λ0. The second and third columns provide the ion and multiplet number or series for each line. Column 4 lists the observed wavelength, while Col. 5 shows the heliocentric radial velocity determined for the line. Columns 6 − 8 present the observed and dereddened flux relative to Hβ and the observational 1σ error (in percentage) associated with the line flux. The uncertainties in the flux measurement, the flux calibration, and the error propagation in the reddening coefficient are included in the observational error. We provide notes in the last column.
The identification and adopted laboratory wavelength for the lines were obtained from several previous identifications in the literature (Sharpee et al. 2004; Zhang et al. 2005; García-Rojas et al. 2004; Esteban et al. 2004; Mesa-Delgado et al. 2009; Fang & Liu 2011, and references therein).
Observed and reddening corrected line ratios (F(Hβ) = 100) and line identifications.
We detected hundreds of lines in each object of our sample. The final set of detected and measured lines amounts to more than 3500 lines. Owing to the high resolution of our spectra, we were able to detect and deblend several faint lines that were partially blended with other features. In some cases, we included faint ORLs belonging to a multiplet with other clear identifications in our spectra. If the lines are brighter than 10% of the principal detected component, we then included them in our list and labelled them as blended (e.g., lines of multiplet 2 of O ii blended with other features).
Most of the lines detected in our spectra are permitted lines of H i, He i, and He ii but there also are many heavy element permitted lines, such as C i, C ii, C iii, N i, N ii, N iii, O i, O ii, O iii, Ne i, Ne ii, Si i, Si ii, S ii, S iii, Cl i, and Mg ii. Several of these lines are excited mainly by recombination and could be useful for abundance determinations (e.g., some multiplets of O i, O ii, C ii, C iii, N ii, Ne ii, and Mg ii). The analysis and discussion about these lines will be presented in Paper II.
We also detected several forbidden and semi-forbidden lines from ions such as [N i], [N ii], [O i], [O ii], [O iii], [Ne iii], [Ne iv], [Ne v], Mg i], [P ii], [S i], [S ii], [S iii], [Cl ii], [Cl iii], [Cl iv], [Ar iii], [Ar iv], [Ar v], [K iv], [Ca ii], [Cr ii], [Cr iii], [Cr iv], [Mn iv], [Mn v], [Fe ii], [Fe iii], [Fe iv], [Ni ii], [Ni iii], [Ni iv], [Se ii], [Kr iii], [Kr iv], and [Xe iii]. The abundance analysis of several of these ions will be presented in Paper II.
In Fig. 3, we show the complete spectra of our objects, from 3350 Å to 9400 Å. The flux scale is such that I(Hβ) = 100.0.
4. Plasma diagnostic: temperatures and densities
The large wavelength range covered by our spectra allows us to obtain a large number of diagnostic line ratios to determine the physical conditions (electron temperature, Te, and density, ne) in the plasma. The task temden of the package nebular (Shaw & Dufour 1995) in iraf was used to determine Te and ne. In our version of temden, the atomic parameters (transition probabilities and collisional strengths) were updated. The atomic data were taken from Table 6 of García-Rojas et al. (2009) with the exception of the collisional strengths of [S ii] lines that were updated to those computed by Tayal & Zatsarinny (2010).
In this section we describe in detail the procedures and line ratios used to determine the plasma physical properties. In the following analysis, we include the data for PB 8 and NGC 2867 by García-Rojas et al. (2009) for completeness.
4.1. Plasma diagnostics from CELs
Electron densities were inferred from the [S ii] λ6730/λ6717, [O ii] λ3726/λ3729, [Cl iii] λ5517/λ5537, and [Ar iv] λ4740/λ4711 line ratios and, for some objects, from a set of [Fe iii] lines (see discussion about this diagnostic in Sect. 5.1).
In general, we considered a three-ionization-zone scheme. First, we assumed a Te = 10 000 K and computed the densities. These densities were then used to derive Te from different diagnostic ratios. We adopted the averaged density, weighted by the errors, for the objects with a good agreement among the different density diagnostics, within the uncertainties; in the cases with large differences among the [S ii], [O ii], [Cl iii], and [Ar iv] nebular density diagnostics, we adopted ne([Cl iii]) as representative of the low-medium ionization zones (see Sect. 5). For three objects (Cn 1-5, He 2-86, and M 1-61), we adopted ne([Ar iv]) as representative of the highest ionization zone.
For the low ionization zone of each object, the representative Te was computed from the line ratios [S ii] (λλ6716+31)/ (λλ4069+76), [O ii] (λλ3726+29)/(λλ7320+30), and [N ii] (λλ6548+83)/(λ5755). For the higher ionization zone, we computed Te from [O iii] (λ4959+λ5007)/ (λ4363), [S iii] (λλ9069+530)/(λ6312), and [Ar iii] (λλ7136+751)/(λ5192) line ratios. The [Ar iv] (λλ4711+40)/(λλ7170+263) line ratio was used to compute Te([Ar iv]), which is representative of the highest ionization zones in the nebulae. These temperatures were used to compute densities and we then iterated the process until convergence.
4.1.1. The effect of recombination on some diagnostic line ratios
To obtain Te([O ii]), it is necessary to subtract the contribution to [O ii] λλ7320+7330 by recombination. Liu et al. (2000) found that this contribution can be fitted in the range 0.5 ≤ Te/104 ≤ 1.0 by 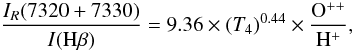 (1)where T4 = Te/104. The importance of this contribution is relative. For instance, for PB 8, by assuming the values derived for O++/H+ from ORLs and using this equation, García-Rojas et al. (2009) estimated a contribution to the observed line intensities of approximately 59% by recombination. This yielded a Te([O ii]) = 7050 K, which was 4350 K lower than those derived without taking into account this contribution. For the objects in this work, we computed the recombination contribution to the [O ii] lines by adopting the abundance derived from multiplet 1 O ii ORLs. For all of these objects, the correction of Te([O ii]) was lower than 2000 K with a median of about 500 K.
(1)where T4 = Te/104. The importance of this contribution is relative. For instance, for PB 8, by assuming the values derived for O++/H+ from ORLs and using this equation, García-Rojas et al. (2009) estimated a contribution to the observed line intensities of approximately 59% by recombination. This yielded a Te([O ii]) = 7050 K, which was 4350 K lower than those derived without taking into account this contribution. For the objects in this work, we computed the recombination contribution to the [O ii] lines by adopting the abundance derived from multiplet 1 O ii ORLs. For all of these objects, the correction of Te([O ii]) was lower than 2000 K with a median of about 500 K.
Liu et al. (2000) found that the contribution to the intensity of the λ5755 [N ii] line by recombination can also be estimated from 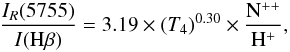 (2)in the range 0.5 ≤ T4 ≤ 2.0. We used this expression to calculate the recombination contribution to λ5755. We derived the N++/H+ abundance, to a first approximation, by assuming that N++/H+ = O++/H+ × N+/O+ where O++/H+ is the value derived from recombination lines and N+/O+ is the fraction derived from CELs. In all the objects of our sample, the correction for Te([N ii]) was smaller than 1500 K, with a median of about 550 K. The objects with the largest corrections are Hb 4 and M 3-15, whose temperature decreased by 1300 K and 1500 K, respectively. On the other hand, M 1-25, M 1-30, and M 1-32 are almost unaffected and are corrected by only about 50 − 150 K.
(2)in the range 0.5 ≤ T4 ≤ 2.0. We used this expression to calculate the recombination contribution to λ5755. We derived the N++/H+ abundance, to a first approximation, by assuming that N++/H+ = O++/H+ × N+/O+ where O++/H+ is the value derived from recombination lines and N+/O+ is the fraction derived from CELs. In all the objects of our sample, the correction for Te([N ii]) was smaller than 1500 K, with a median of about 550 K. The objects with the largest corrections are Hb 4 and M 3-15, whose temperature decreased by 1300 K and 1500 K, respectively. On the other hand, M 1-25, M 1-30, and M 1-32 are almost unaffected and are corrected by only about 50 − 150 K.
In several objects of our sample, we detected bright He ii lines. Taking into account the similarity between the ionization potentials of He++ and O3+, we expected to find a significant amount of oxygen in the form of O3+, so we had to take into account the contribution of recombination to the auroral [O iii] λ4363 line, which we estimated using Eq. (3) of Liu et al. (2000)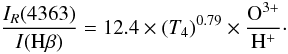 (3)We were unable to compute directly the O3+ abundance from either CELs or ORLs, but we can estimate it from helium ionic abundances using O3 + /H + = [(He/He + )2/3 − 1] × (O + /H + + O + + /H + ) (Kingsburgh & Barlow 1994). With this expression, we found that the contribution of recombination to the [O iii] λ4363 line is smaller than ~ 3% for the most ionized objects in our sample, which has negligible effects on the determination of Te([O iii]).
(3)We were unable to compute directly the O3+ abundance from either CELs or ORLs, but we can estimate it from helium ionic abundances using O3 + /H + = [(He/He + )2/3 − 1] × (O + /H + + O + + /H + ) (Kingsburgh & Barlow 1994). With this expression, we found that the contribution of recombination to the [O iii] λ4363 line is smaller than ~ 3% for the most ionized objects in our sample, which has negligible effects on the determination of Te([O iii]).
The temperatures and densities derived from the various diagnostic line ratios and their respective 1σ errors, for each object in our sample, are presented in Table 4.
Plasma diagnostics.
4.2. Plasma diagnostics from ORLs and continua
4.2.1. Electron temperatures from Paschen discontinuity
Electron temperature can be derived from the ratio of the Balmer or Paschen discontinuities to the H i lines belonging to the Balmer or Paschen series, respectively. The high resolution of our spectra allows us to measure the continuum flux in zones very close to the discontinuities. In principle, this technique would allow us to establish whether other continuum contributions apart from pure nebular processes affect the observed spectrum. However, we have to handle continuum measurements in the H i discontinuities with care, because in most of our spectra the central star was included in the slit, and [WC] CS show in their spectra prominently wide emission lines that can affect the continuum. Balmer discontinuities are indeed strongly affected by intense wide stellar He i emission lines, hence are unsuitable for computing temperatures. In the objects where this effect was negligible, the signal-to-noise ratio was too low to derive Te with any precision. In the Paschen discontinuity, the effect is smaller, but non-negligible. In Fig. 4, we show the spectral region near the Paschen limit for all our objets. The presence of strong He i λ8155.5 and λ8203.9 stellar emission lines, very close to the Paschen discontinuity, is quite clear in all of them. We attempted to compute Te from the Paschen discontinuity paying special attention to the zones where continuum flux determinations were reliable and we then made a linear fit to the blue and red continua to compute the Paschen jump (Ic(Pac)) at λ8204. This fit is overplotted in Fig. 4. Only for Cn 1-5 was it impossible to fit the red continuum owing to the presence of some quite strong wide stellar features.
The Paschen continuum temperature was derived by fitting the relation between Ic(Pac)/I(Pn) and Te for 10 ≤ n ≤ 16. The emissivities as a function of the electron temperature for the nebular continuum and the H i Paschen lines were taken from Brown & Mathews (1970) and Storey & Hummer (1995), respectively. The finally adopted value of Te(Pac) is the average of those obtained using the different H i lines, neglecting those affected by atmospheric features. Errors were computed considering the H i line uncertainties and an error of ~15% in the Paschen discontinuity determination, and propagating the error by means of an extinction correction; finally, we added quadratically the dispersion in the values obtained from different continuum-to-line ratios. Table 4 shows the Te values derived from the H i Paschen decrement. Although Te(Paschen decrement) are in relatively good agreement with Te from other diagnostics, the errors are quite large.
 |
Fig. 4 Section of the echelle spectra showing the Paschen discontinuity in all the objects of our sample. In several objects, we can clearly see the wide stellar emission line that contaminates the spectrum in the blue part of the discontinuity. |
4.2.2. Electron temperatures from helium lines
The He i recombination lines can be used as a diagnostic of electron temperature. Two approaches have been proposed for deriving Te from these lines. In the first one, Peimbert et al. (2002) claimed that in the presence of temperature fluctuations in the ionized gas, the temperature in the zone where He i is present is a function of the temperatures in the O+ and O++ zones and of the temperature fluctuation parameter, t2. These authors proposed a maximum likelihood method to obtain simultaneously the ne(He i), Te(He i), He+/H+ ratio, and the optical depth of the He i λ3889 line. In a different approach, Zhang et al. (2005) used the analytic expressions of the emissivity of He i lines given by Benjamin et al. (1999) to compute the temperature-dependent He i singlet λ7281/λ6678 line ratio. A matter of concern about this method is that there might be a departure from case B to case A for the He i singlet lines by means of the destruction of He i Lyman photons by the photoionization of neutral hydrogen and/or the absorption by dust grains (Liu et al. 2001; Fang & Liu 2011). Unfortunately, only tailored photoionization modelling constrained by multiwavelength data could quantitatively compute this effect.
In Table 4, we show Te(He i) for our objects, derived from the two methods. For the Te(He i) computed using the Peimbert et al. (2002) method, we assumed a temperature fluctuations parameter, t2, given by the ADF(O++) (see Paper II for more details about t2 determinations) and a minimum of 11 He i lines were used. In Fig. 5, we show the comparison between Te(H i) and Te(He i) derived using both methods: the open circles correspond to values using the Zhang et al. (2005) method, and the black ones are the values derived with the Peimbert et al. (2002) procedure. In this figure, we have overplotted lines representing equality (t2 = 0, solid line) and representing different values of t2 (dashed lines). It is observed that, for our objects, the Te(He i) derived from many lines (Peimbert et al. method) are in general higher (by up to 2 − 3 thousand degrees) than the values derived from Zhang et al. method. We decided to adopt the measurements obtained using the Peimbert et al. (2002) method, which, being based on the observation of several lines, more tightly constrains the temperature. It is not clear in this figure that the behaviour of our [WC]PNe corresponds to objects with a moderate t2. Most of the objects, in particular the hotter ones, have a Te(H i) that is higher than Te(He i), in some cases by up to several thousand degrees. Similar results were obtained by Zhang et al. (2005) for their PN sample, which they interpreted as evidence of H-deficient knots in the plasma. However, our large uncertainties, mainly in the derived Te(H i) for the hotter objects, cannot rule out an overall agreement with the predictions of the temperature fluctuations paradigm. We note that in our work, it is particularly difficult to properly determine Te from H i discontinuities, owing to the wide emission stellar features that are clearly present in the continuum, thus causing large uncertainties.
 |
Fig. 5 Te(He i) vs. Te(H i) diagram. Two methods for deriving Te(He i) have been used. One follows the method of Zhang et al. (2005), based on the line ratio λ7281/λ6678 (open circles). The other follows the Peimbert et al. (2002) procedure and computes Te(He i) based on several He i lines (black circles). Solid line represents equality (t2 = 0), and dotted lines show the variation in Te(H i) as a function of Te(He i) considering different t2 values. |
4.2.3. Electron temperatures and densities from O II and N II recombination lines
The intensities of the ORLs, originating from states with different orbital angular momentum, have different dependences on Te. Thus, by comparing the intensity of an O ii 3d − 4f transition to that of an O ii 3s − 3p transition, it is possible to compute the electron temperature (Tsamis et al. 2004; Wesson et al. 2003). However, this method has its difficulties: first, the dependence of the intensity ratio on the temperature is very weak, so extremely high quality spectra are required to measure accurately these faint lines; second, the relative intensities of the O ii lines can be affected by departures from the local thermodynamic equilibrium (LTE) in the fundamental recombination level of the O++ ion, 3P. Tsamis et al. (2004) argued that the intensity ratio of the λ4089.29 O ii 3d − 4f transition and the λ4649.14 O ii 3p − 3s transition (of multiplet 1) was adequate to derive Te because these lines originate from states of high total angular momentum, 3P2, and therefore must be affected in a similar way by this effect. Moreover, high densities (which is the case for most of our objects) also minimize this effect, which is negligible for ne > 104 cm-3.
The temperature-sensitive ratio I(λ4089.29)/I(4649.14) was measured for the first time by Wesson et al. (2003) for Abell 30, to determine the Te of the plasma in which O ii recombination lines arise. These authors found very low Te in two H-deficient knots in this PN. This method was later applied by several authors to other PNe, with similar results (e.g., Tsamis et al. 2004; Liu et al. 2004; Wesson et al. 2005). These results are consistent with a scenario in which there is a cold H-deficient component of the gas emitting the bulk of the O ii lines and a “normal” gas component that emits the bulk of the CELs. Independently of the origin of this cold H-deficient component which, to this day, has not been resolved, this scenario provides an explanation to the abundance discrepancy. However, García-Rojas & Esteban (2007) measured this ratio in three H ii regions with moderate ADFs, and did not find any evidence of this cold component. Our sample of [WC]PNe also have moderate values of the ADF, similar to the values found in H ii regions (see Paper II). We checked the I(λ4089.29)/I(4649.14) ratio for all our objects where the very faint O ii λ4089.29 line was detected. In Table 5, we present the values of the Te obtained from O ii ORLs for our objects. These results are discussed later.
Recently, Fang et al. (2011) computed new effective recombination coefficients for the N ii recombination spectrum, including radiative and dielectronic recombination. These authors found a set of recombination coefficients that allows us to construct density and temperature diagnostics based on the different dependences of the emissivities of different transitions on Te and ne. On the basis of their method, we computed electron temperature and density simultaneously using the loci of the recombination line ratios λ5679/λ5666 versus (vs.) λ5679/λ4041 of N ii. The results are presented in Table 5. However, prior to discussing them, we note that several authors (Grandi 1976; Escalante & Morisset 2005) have claimed that resonance fluorescence coming from both the absorption of continuum or line photons, is necessary to reproduce the observed intensities of multiplet 3 N ii lines. In particular, Grandi (1976) found that the resonance fluorescence of the 4s 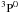 term by the recombination line He i 1s21S − 1s8p
term by the recombination line He i 1s21S − 1s8p 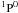 was the dominant excitation mechanism, over starlight and recombination, for several multiplets of N ii (including N ii multiplet 3, i.e., λ5666 and λ5679 lines). Escalante & Morisset (2005) found that, in the Orion nebula, recombination contributed a minor part of the observed intensities of lines from 3p and 3d levels connected to the ground state (e.g. lines of multiplet 3), but that it was the dominant mechanism producing the intensity of lines coming from 4f levels (e.g. N ii λ4041 line). These results suggest that we have to be careful when dealing with temperatures and abundances from N ii lines, especially in low ionization PNe, where the potential effects of fluorescence on these lines would be stronger2.
was the dominant excitation mechanism, over starlight and recombination, for several multiplets of N ii (including N ii multiplet 3, i.e., λ5666 and λ5679 lines). Escalante & Morisset (2005) found that, in the Orion nebula, recombination contributed a minor part of the observed intensities of lines from 3p and 3d levels connected to the ground state (e.g. lines of multiplet 3), but that it was the dominant mechanism producing the intensity of lines coming from 4f levels (e.g. N ii λ4041 line). These results suggest that we have to be careful when dealing with temperatures and abundances from N ii lines, especially in low ionization PNe, where the potential effects of fluorescence on these lines would be stronger2.
In Table 5, we show the physical conditions obtained from O ii and N ii permitted lines for the objects of our sample. In this table, objects are ordered from higher to lower ionization degree, i.e., from low to high potential influence of fluorescence in the N ii lines. Owing to the large uncertainties in the faint O ii λ4089 and N ii λ4041 line fluxes of most objects, it makes no sense to calculate the single Te and ne values obtained from the measured line ratios, because they are several times beyond the validity range of the computed diagnostics. Instead, we show the upper or lower limits given by the error boxes in the diagrams and, additionally, we show in brackets the values obtained without considering the uncertainties. However, for some objects, we can compute Te(O ii) with the corresponding uncertainties. The values obtained from O ii and N ii diagnostics seem to show that the uncertainties in the measurement of the faint O ii λ4089 and N ii λ4041 lines dominate over any other effect, real or not, so it is really hard to conclude anything about the origin of the emission of O ii and N ii permitted lines. In addition, we did not find any systematic trend to very low temperatures similar to that found in other objects (Wesson et al. 2003, 2005). To illustrate the quality of these diagnostics, in Fig. 6 we present O ii λ4089 and N ii λ4041 lines in the four PNe with the highest signal-to-noise ratios.
 |
Fig. 6 Part of the spectrum of four objects in which the faint O ii λ4089 (upper four panels) and N ii λ4041 (lower four panels) lines were most reliably measured. |
5. Discussion
The correct knowledge of chemical abundances in PNe is essential to constrain the different models of post-AGB evolution. The most accurate evaluation of these chemical abundances has several steps in which we have to make the right decisions to avoid errors that would lead us to incorrect conclusions. Adopting a correct set of plasma conditions for each ion is one of those fundamental steps that we discuss. In a forthcoming paper (Paper II), we will focus on whether ORLs or CELs are more reliable options for computing abundances and on the issue of ionization correction factors.
To obtain an overall picture of the physical conditions, we have constructed Te − ne diagnostic plots for all our objects, making use of the software pynebular (Luridiana et al. 2011), an update of the iraf package nebular, rewritten in Python. These plots are shown in Fig. 7 where all the available diagnostic ratios for Te and ne, in each object, have been included. We note in these diagrams that in general, a good average solution for Te − ne can be found for most of the objects. However, in several cases there are significant differences among the values of Te and ne derived from different diagnostic ions, which reflects the density and temperature structure inside the nebulae. We examine these differences in the following sections, to derive the most appropriate set of plasma conditions for the different nebular zones.
 |
Fig. 7 Te − ne diagnostic plots. Colors correspond to species: grey for S, blue for N, green for O, magenta for Cl, and red for Ar. Different lines indicate ions: solid for neutral ions ([N i]), dashed for once ionized ions ([N ii], [S ii] and [S ii]), dotted for two ionized ions ([O iii], [S iii], [Ar iii], and [Cl iii]), and dotted-dashed for three times ionized ions ([Ar iv]). |
5.1. The densities
We derived densities from several diagnostic ratios of [S ii], [O ii], [Cl iii], [Ar iv], and [Fe iii]. Figure 9 shows the behaviour of ne([O ii]) (blue triangles), ne([S ii]) (black circles), and ne([Ar iv]) (red stars) vs. ne([Cl iii]). A correlation is observed in all the cases. For ne([S ii]) vs. ne([Cl iii]), the slope (in logarithm) is 0.93 ± 0.05, and for ne([O ii]) the slope is about 0.69 ± 0.05. For ne([Ar iv]), the slope is 1.17 ± 0.06. We find, in general, that ne([Ar iv]) > ne([Cl iii]) > ne([S ii]) > ne([O ii]). However, the trend is not present in the objects Cn 1-5, Hb 4, NGC 5189, NGC 6369, and PC 14, for which we can adopt a density as the weighted average of all the computed density diagnostics. For the other objects, these density differences can be explained from two points of view. On the one hand, it is possible that a real and strong density stratification exists in these objects that has to be taken into account to properly compute the physical conditions and chemical abundances. On the other hand, we know that at densities higher than the critical density of the departure level, collisional de-excitation dominates over radiative de-excitation, suppressing part of the emission flux of the line; if this effect occurs for both lines of the density diagnostic, then the density derived would probably be lower than the real value. In the case of the [O ii] λ3726/λ3729 ratio, the critical density is ~3500 cm-3 and for the [S ii] λ6717/λ6731 ratio, it is about 3000 cm-3, hence, in the presence of high density clumps in the the low ionization zone, these ratios would underestimate the real density. However, the [Cl iii] λ5517/λ5537 and [Ar iv] λ4711/λ4740 line ratios are free of these effects owing to the high critical densities of the departure levels for, at least, one of the lines (>4 × 104 cm-3).
To decide which density should be adopted, other alternatives can be used. First, we could use [O ii]na and [S ii]na nebular to auroral line ratios, which in our density range are also density sensitive (see Fig. 7). However, these ratios should be treated with caution because they can be affected by telluric emisson lines in the case of [O ii] λλ 7320+30 lines, or might be blended with other emission lines, in the case of [S ii] λλ4068+76 lines (see note e in Table 4). In Table 4, we show the densities obtained from the [O ii]na and [S ii]na ratios, which were computed by assuming that Te([N ii]) is representative of the low ionization zone. The values obtained are much larger than those obtained from the nebular ratios and are, in general, consistent with the values derived from the [Cl iii] λ5517/λ5537 ratio. As said before, this suggests that the nebular [O ii] and [S ii] diagnostics are insensitive to any high density clumps in the nebula.
Second, we measured several [Fe iii] lines in our spectra, which are very useful because their ratios provide very robust density diagnostics over a wider range in electron density (Keenan et al. 2001). We derived electron densities from the analysis of [Fe iii] lines detected in several of our objects (Cn 1-5, He 2-86, M 1-25, M 1-32, M 1-61, and PC 14). In most of them, we observed at least four emission lines of the 2F and 3F multiplets, namely [Fe iii] λλ4658, 4701, 4734, and 4881. The density values of [Fe iii], ne([Fe iii]), which are presented in Table 4, were calculated by computing the minimum dispersion between the observed and theoretical ratios of the [Fe iii] lines with respect to the bright [Fe iii] λ4658 line, considering the observational errors. The theoretical emissivites were calculated by solving a 34-level model atom that uses the collision strengths of Zhang (1996), the transition probabilities of Quinet (1996), combined with the probabilities of some UV transitions estimated by Johansson et al. (2000), and adopting Te([N ii]) as the temperature of the Fe++ zone. The ne([Fe iii]) values determined from this analysis are representative of the low-medium ionization zone, though their values seems to be more consistent with those determined from high density indicators such as [Cl iii] and [Ar iv] line ratios. However, there is a clear exception to this rule: M 1-61, which has an extremely high ne([Fe iii]) of about 94 000 cm-3. We tested this value by computing the density after discarding various lines, but we reached similar values in all the cases. It is not the scope of this paper to investigate the origin of this discrepancy; however, after inspecting of the 2D echellograms (Fig. 8 upper panel) and the 1D spectra (Fig. 8 lower panel), one can easily see that the [Fe iii] line structure is completely different than that of other CELs or ORLs, which indicates that [Fe iii] emission originates from a different place in the PN than the other lines in the low and medium ionization zones. Hence, ne([Fe iii]) is no longer representative of the low-medium ionization zone of this nebula. Two [Fe iii] lines were also detected in M 1-30 and Pe 1-1, but could not be used to perform this analysis.
Therefore, in agreement with the above discussion, for each object we adopted the densities that are summarized in Table 6.
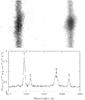 |
Fig. 8 Upper panel: portion of the 2D echellogram showing [Fe iii] λ5270 (left) and [Cl iii] λ5517 lines for M1-61. The grey scale is the same for both lines. It is clear that the [Fe iii] emission is more extended that [Cl iii] emission. Lower panel: portion of the 1D extracted spectra showing the [Fe iii] λ4658 line, compared with multiplet 1 O ii ORLs. The FWHM of the [Fe iii] line is clearly larger. |
Adopted electron densities.
 |
Fig. 9 Electron densities derived from [S ii] λλ6717/6730 (black filled circles), [O ii] λλ3726/3729 (blue triangles), and [Ar iv] λλ4711/4740 (red stars) compared to the one derived from [Cl iii] λλ5517/5537. There is a clear correlation between all quantities. The trend ne([Ar iv]) > ne([Cl iii]) > ne([S ii]) > ne([O ii]) is clear. Solid line represents the equality. Pointed, solid, and dashed lines are the fits to the ne([Ar iv]), ne([S ii]), and ne([O ii]) vs. ne([Cl iii]) data points, respectively. |
In Fig. 10, we present the behaviour of the adopted low-medium electron density vs. the [WC] spectral classification of the central star. This diagram has been constructed several times in the literature and it shows that [WC]-early stars are surrounded by lower density nebulae. Most of the [WC]-late nebulae have, in contrast, a quite high density. It can be concluded that [WC]-early PNe are more evolved objects than [WC]-late PNe, which appear younger from the point of view of the nebulae and the central star as well. This diagram and this conclusion have been used to propose that there is an evolutionary sequence from [WC]-late PNe to [WC]-early PNe (Acker & Neiner 2003). However, this sequence has been questioned from the point of view of the chemical abundances calculated for the central stars, for which it is deduced that the mean C abundance in [WC]-early stars is a factor of two lower than the C abundance in [WC]-late stars, while an evolutionary sequence would predict the opposite (Koesterke 2001; Hamann et al. 2005). In Paper II, we will discuss this point further.
 |
Fig. 10 ne as a function of the [WC] type of the central star. |
5.2. The temperatures
Given that the [O ii] λλ7320+30 and [S ii] λλ4068+76 lines are affected by telluric emission and blends with other lines, and that these ratios are also density sensitive, especially at the densities of most of the objects analysed here, we assumed that only Te([N ii]) is representative of the low ionization zone.
 |
Fig. 11 Comparison between high ionization Te diagnostics. Black dots: Te([S iii]); green stars: Te([Ar iii]). A very good correlation Te([O iii]) vs. Te([S iii]) is found. Solid line represent an equality. |
In Fig. 11, we compare the temperatures obtained from the high ionization diagnostic ratios Te([O iii]), Te([S iii]), and Te([Ar iii]). In this figure, the correlation between the [O iii] and [S iii] temperatures has a slope of 0.96 ± 0.03, which is very close the unity, and a Spearman rank correlation coefficient (SRCC) of r = 0.84. In Fig. 11, we can also see that the [Ar iii] diagnostic ratios provide somewhat lower temperatures than [O iii] ones. The slope is 0.75 ± 0.02 and the SRCC is r = 0.77. Given the similarity between these temperatures, we assumed Te([O iii]) is representative of the high ionization zone.
In general, temperatures derived from [O iii] and [N ii] diagnostics are similar, except in some cases where Te([N ii]) is higher than Te([O iii]) by as much as 3000 K. Only one object has a Te([O iii]) that is higher than Te([N ii]) by about 2000 K. In Fig. 12, we compare both temperatures, finding that they are only weakly correlated, with a slope of 0.69, but a SRCC of r = 0.61. This weak correlation is mainly due to the cases mentioned before.
 |
Fig. 12 Comparison between Te([O iii]) and Te([N ii]). Solid line represent equality. Pointed line is the fit to the data. |
 |
Fig. 13 Te([O iii])/Te([N ii]) vs. O++/O+. Black triangles: our data; red asterisks: Peña et al. (2001); blue open diamonds: Górny et al. (2004) data for bulge PNe. |
To analyse in greater depth the behaviour between the temperatures in the high and low ionization zones, we present, in Fig. 13, the electron temperature ratio Te([O iii])/Te([N ii]) vs. the ionization degree, represented by O++/O+ for our sample (filled black triangles). In general, we find two regimes in this figure: one zone in the lower ionization regime, where Te([O iii])/Te([N ii]) is about one, and a second zone where O++/O+ is larger than 10 and Te([O iii])/Te([N ii]) drops. In this zone, we find objects for which Te([N ii]) is higher than Te([O iii]). To verify that this effect (already described for the sample analysed by Peña et al. 2001) is not due to biases introduced by the incompleteness of our particular sample of [WC]PNe, we overplotted in Fig. 13 the data for [WR]PNe by Peña et al. (2001), and the data for bulge PNe by Górny et al. (2004). The trend is clear for all the samples.
This behaviour of Te([N ii]) being higher than Te([O iii]) is often found in photoionized nebulae, and is due to radiation hardening, i.e. the lower absorption probability of more energetic photons, which causes these photons to have longer mean free paths and to remain unabsorbed until the edge of the Strömgren sphere. Peña et al. (2001) found, from simple photoionization models at metallicities around solar, that the behaviour predicted by the models is mild, dependent on T ∗ , not as extreme as the one found here, and, in adition, not dependent on the excitation of the PNe. Peña et al. (2001) proposed as a possible origin of this behaviour a strong inhomogeneous structure, or additional heating by shocks and/or turbulence. Hence, to properly constrain the problem, we calculated a more complete grid of photoionization models.
 |
Fig. 14 Photoionization models computed to reproduce the observed Te([O iii])/Te([N ii]) vs. O++/O+ behaviour. Models (circles) and observational data (squares) are colored according to the O/H value. At the lower left, we show the typical error bars for the observational data. |
5.3. Photoionization modelling
A grid of photoionization models was computed using Cloudy c10.00 code (Ferland et al. 1998). The grid covers the parameter space (lower value, higher value, steps) of Teff (kK) = [50, 150, 10], log (O/H) = [− 3.5, − 3.0, 0.25], log (Rin) (cm) = [15.5, 18, 0.5], log (H-density) (cm-3) = [2.5, 4.5, 0.25], and log (L/L⊙) = [2.5, 3.5, 0.5]. A total of about 5000 models were then run, using atmosphere models from Rauch (2003) for the ionizing spectral energy distribution, constant density shells, and metal abundances following the O/H ratio. The models are radiation bounded and dust-free. The mean values of the ionic fractions and temperatures were obtained by integrating these variables over the volume of the nebula. The results of the models are presented in Fig. 14, with the observations superimposed as square symbols. The color code is related to the O/H abundance and is the same for the models and the observations. For the objects, the O/H abundance is that computed for the adopted physical conditions in each object and will be presented and discussed in Paper II.
The models, which are radiation-bounded (R), do not reach values larger than 10 for O++/O+ and do not reproduce the trend of the observed values.
We then computed matter-bounded models (M), where the geometrical size of the nebula is set to 70% of the Strömgren size for which, theoretically, we can successfully reach any high O++/O+ value, as the size of the O+ region can be reduced to values close to 0. Real nebulae may be a combination of matter- and radiation-bounded components. They can thus reach higher values of O++/O+ than the pure R nebulae shown in Fig. 14. However, for any realistic combination of M and R models, no changes in the values of Te(O++)/Te(N+) are expected relative to the R models, as the O++ temperature is the same in both models and the N+ temperature is the one from the R models (N+ is negligible in the M models). It is interesting to notice that the smallest values for Te(O++)/Te(N+) are obtained with high metallicity models (log (O/H) ~ 9.0), but the observed nebulae are not so metal-rich. We note however, that the models are relatively simple, and that, for example, for each model the density is constant within the nebula and all metal abundances follow that of oxygen. We have to bear in mind that real objects are more complex but our simple approximation seems to succesfully reproduce the observed behaviour.
6. Conclusions
We have presented deep high-resolution spectrophotometric data of 12 PNe with [WC] central star, obtained at LCO with the 6.5-m Magellan telescope and the spectrograph MIKE. Data were reduced, wavelength- and flux-calibrated and dereddened. Hundreds of lines were detected and identified for each object, and their fluxes were measured. These [WR]PNe, together with the three objects analysed by García-Rojas et al. (2009) represent the most extensive sample of this type of PNe analysed so far, at such high resolution. The spectra were exposed deep enough to detect, with a signal-to-noise ratio higher than ~3, the weak ORLs of O ii, C ii, and other species.
From our deep spectra, which cover a wide wavelength range (from 3350 Å to 9400 Å), numerous diagnostic line ratios for Te and ne were determined, from CELs and ORLs as well. In addition, H discontinuities (H Paschen discontinuity in particular) were measured for this purpose. All known recombinations effects that could perturb the CEL diagnostic ratios were careful removed. In addition, the possible mechanisms perturbing ORLs, such as fluorescence, departures from LTE and others, were considered.
Our main aim in this paper is to determine the optimal physical conditions in the nebulae, for the accurate calculation of ionic abundances. We have performed a careful analysis of all our available Te and ne and their errors to ascertain these conditions.
The conditions derived from CEL diagnostic ratios allow us to conclude the following:
-
The CEL diagnostic ratios usually used to determine ne,[S ii]λ6730/λ6717, and [O ii]λ3726/λ3729 seem to underestimate the true nebular densities owing to their low critical densities. This occurs particularly for the densest objects of our sample. Therefore, for these objects, we decided to use the density derived from the [Cl iii]λ5517/λ5537 line ratio as a representative value of the whole nebula, which agrees with density determinations using [Fe iii] lines and the densities computed from the highly density-sensitive [O ii]na and [S ii]na line ratios.
-
Temperature-sensitive CEL ratios were corrected for the effects of recombination. In some cases, these effects can severely affect (up to several thousand degrees) the Te determinations. Finally, we adopted a three-temperature scheme for the nebulae: Te([Ar iv]) is used to represent the highest ionization zone, when available, Te([O iii]) is used to represent the high ionization zone, and Te([N ii]) represent the low-ionization zone.
These physical conditions are used in Paper II to determine ionic abundances from CEL lines.
A careful analysis to determine the physical conditions from ORL diagnostic lines was also performed, with the following results:
-
Electron temperatures were derived from the Paschendiscontinuity relative to several Paschen recombination lines.Although the derived values of Te agree with Te obtained from othermechanisms, the errors are quite large because of the stellaremission lines near the Paschen jump. We also derived Te fromseveral He lines by considering two different approaches: that ofPeimbert et al. (2005) whoconsider several He i lines and at2 parameter, and that of Zhang et al. (2005), based on the ratio of two He i lines. In both cases, we found that Te(He i) appears to be lower than Te(H i), although the effect is smaller when a t2 value is considered. However, the errors are so large (for H i in particular) that no conclusive results can be extracted.
-
Electron temperatures were also computed from O ii and N ii recombination lines, as proposed in several papers in the literature (Wesson et al. 2003, 2005; Fang & Liu 2011). However, different authors have indicated that some effects, such as fluorescence and departures from LTE, could be perturbing these lines. We conclude that, despite our deep high-resolution data, the uncertainties in the measurements of these faint lines dominate over any other effect and we cannot conclude anything about the origin of these recombination lines.
Other phenomena such as the behaviour of density as a function of the [WC] spectral type and the electron temperatures as a function of the nebular ionization degree have been investigated. We have confirmed that PNe around [WC]-early stars are evolved nebulae, while those around [WC]-late stars are young, a result already reported in the literature. We have analysed the behaviour of the temperatures found by Peña et al. (2001) of an unusually small Te([O iii])/Te([N ii]) when O++/O+ is larger than 10. An ample grid of photoionization models was computed with this aim. We have found that models could reproduce this behaviour (shown in Fig. 14) if a combination of matter-bounded and radiation-bounded models are considered, but for the lowest Te(O++)/Te(N+) ratio, a too high metallicity seem required.
The second part of this work, including ADF calculations and ionic and total abundances for the nebulae, will be presented elsewhere (García-Rojas et al., in prep., Paper II).
Online material
Observed and reddening corrected line ratios (F(Hβ) = 100) and line identifications.
continued.
continued.
continued
continued.
continued.
continued.
continued.
continued.
continued.
continued.
continued.
 |
Fig. 3 Complete MIKE-echelle spectra of Cn 1-5. The most characteristic nebular emission lines have been labelled. Wide stellar WR features, generally stellar helium lines, are clearly visible in some spectral regions. |
 |
Fig. 3 Complete MIKE-echelle spectra of H b4. |
 |
Fig. 3 Complete MIKE-echelle spectra of He 2-86. |
 |
Fig. 3 Complete MIKE-echelle spectra of M 1-25. |
 |
Fig. 3 Complete MIKE-echelle spectra of M 1-30. |
 |
Fig. 3 Complete MIKE-echelle spectra of M 1-32. |
 |
Fig. 3 Complete MIKE-echelle spectra of M 1-61. |
 |
Fig. 3 Complete MIKE-echelle spectra of M 3-15. |
 |
Fig. 3 Complete MIKE-echelle spectra of NGC 5189. |
 |
Fig. 3 Complete MIKE-echelle spectra of NGC 6369. |
 |
Fig. 3 Complete MIKE-echelle spectra of PC 14. |
 |
Fig. 3 Complete MIKE-echelle spectra of Pe 1-1. |
The recombination contribution to N ii lines comes from the capture of a free electron to an excited level of N++ followed by a radiative transition, and dominates when the ionization degree is high, while the fluorescence contribution comes from the excitation of N+ by fluorescence photons followed by a radiative transition, and could be very important in relatively low ionization PNe.
Acknowledgments
This work received financial support from the Ministerio de Educación y Ciencia (MEC) Español, under project AYA2007-63030; from CONACYT-México under grant #43121 and from DGAPA-UNAM, México under grants IN118405, IN112708 and IN105511. J.G.R. acknowledges people and staff of Instituto de Astronomía at UNAM, where part of this work were done. C.M. received financial support for his Sabbatical at the IAC from the Spanish MEC. The authors want to thank Mónica Rodríguez, Grazyna Stasińska, Antonio Peimbert, Manuel Peimbert, and César Esteban for very fruitful discussions.
References
- Acker, A., & Neiner, C. 2003, A&A, 403, 659 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Allen, C., Carigi, L., & Peimbert, M. 1998, ApJ, 494, 247 [NASA ADS] [CrossRef] [Google Scholar]
- Benjamin, R. A., Skillman, E. D., & Smits, D. P. 1999, ApJ, 514, 307 [NASA ADS] [CrossRef] [Google Scholar]
- Brown, R. L., & Mathews, W. G. 1970, ApJ, 160, 939 [NASA ADS] [CrossRef] [Google Scholar]
- DePew, K., Parker, Q. A., Miszalski, B., et al. 2011, MNRAS, 414, 2812 [NASA ADS] [CrossRef] [Google Scholar]
- Escalante, V., & Morisset, C. 2005, MNRAS, 361, 813 [NASA ADS] [CrossRef] [Google Scholar]
- Esteban, C., Peimbert, M., García-Rojas, J., et al. 2004, MNRAS, 355, 229 [NASA ADS] [CrossRef] [Google Scholar]
- Fang, X., & Liu, X.-W. 2011, MNRAS, 415, 181 [NASA ADS] [CrossRef] [Google Scholar]
- Fang, X., Storey, P. J., & Liu, X.-W. 2011, A&A, 530, A18 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ferland, G. J., Korista, K. T., Verner, D. A., et al. 1998, PASP, 110, 761 [Google Scholar]
- García-Rojas, J., & Esteban, C. 2007, ApJ, 670, 457 [NASA ADS] [CrossRef] [Google Scholar]
- García-Rojas, J., Esteban, C., Peimbert, M., et al. 2004, ApJS, 153, 501 [NASA ADS] [CrossRef] [Google Scholar]
- García-Rojas, J., Peña, M., & Peimbert, A. 2009, A&A, 496, 139 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Girard, P., Köppen, J., & Acker, A. 2007, A&A, 463, 265 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Górny, S. K., Stasińska, G., Escudero, A. V., & Costa, R. D. D. 2004, A&A, 427, 231 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Górny, S. K., Chiappini, C., Stasińska, G., & Cuisinier, F. 2009, A&A, 500, 1089 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Grandi, S. A. 1976, ApJ, 206, 658 [NASA ADS] [CrossRef] [Google Scholar]
- Hamann, W.-R., Todt, H., & Gräfener, G. 2005, in Planetary Nebulae as Astronomical Tools, AIP Conf. Ser., ed. R. Szczerba, G. Stasińska, & S. K. Gorny, 804, 153 [Google Scholar]
- Johansson, S., Zethson, T., Hartman, H., et al. 2000, A&A, 361, 977 [NASA ADS] [Google Scholar]
- Keenan, F. P., Aller, L. H., Ryans, R. S. I., & Hyung, S. 2001, Proc. National Academy of Science, 98, 9476 [Google Scholar]
- Kingsburgh, R. L., & Barlow, M. J. 1994, MNRAS, 271, 257 [NASA ADS] [CrossRef] [Google Scholar]
- Koesterke, L. 2001, Ap&SS, 275, 41 [NASA ADS] [CrossRef] [Google Scholar]
- Koesterke, L., & Hamann, W.-R. 1997, in Planetary Nebulae, ed. H. J. Habing, & H. J. G. L. M. Lamers, IAU Symp., 180, 114 [Google Scholar]
- Leuenhagen, U., Hamann, W.-R., & Jeffery, C. S. 1996, A&A, 312, 167 [NASA ADS] [Google Scholar]
- Liu, X.-W., Storey, P. J., Barlow, M. J., et al. 2000, MNRAS, 312, 585 [NASA ADS] [CrossRef] [Google Scholar]
- Liu, X.-W., Luo, S.-G., Barlow, M. J., Danziger, I. J., & Storey, P. J. 2001, MNRAS, 327, 141 [NASA ADS] [CrossRef] [Google Scholar]
- Liu, Y., Liu, X.-W., Luo, S.-G., & Barlow, M. J. 2004, MNRAS, 353, 1231 [NASA ADS] [CrossRef] [Google Scholar]
- Liu, X.-W., Barlow, M. J., Zhang, Y., Bastin, R. J., & Storey, P. J. 2006, MNRAS, 368, 1959 [NASA ADS] [CrossRef] [Google Scholar]
- Luridiana, V., Shaw, R. A., & Morisset, C. 2011, in Planetary Nebulae: An Eye to the Future (Cambridge University Press), ed. A. Manchado, & L. Stanghellini, IAU Symp., 283 [Google Scholar]
- Mesa-Delgado, A., Esteban, C., García-Rojas, J., et al. 2009, MNRAS, 395, 855 [NASA ADS] [CrossRef] [Google Scholar]
- Oke, J. B. 1990, AJ, 99, 1621 [NASA ADS] [CrossRef] [Google Scholar]
- Peña, M., Stasińska, G., & Medina, S. 2001, A&A, 367, 983 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Peimbert, A., Peimbert, M., & Luridiana, V. 2002, ApJ, 565, 668 [NASA ADS] [CrossRef] [Google Scholar]
- Peimbert, A., Peimbert, M., & Ruiz, M. T. 2005, ApJ, 634, 1056 [NASA ADS] [CrossRef] [Google Scholar]
- Quinet, P. 1996, A&AS, 116, 573 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Rauch, T. 2003, A&A, 403, 709 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Seaton, M. J. 1979, MNRAS, 187, 73 [Google Scholar]
- Sharpee, B., Baldwin, J. A., & Williams, R. 2004, ApJ, 615, 323 [NASA ADS] [CrossRef] [Google Scholar]
- Shaw, R. A., & Dufour, R. J. 1995, PASP, 107, 896 [NASA ADS] [CrossRef] [Google Scholar]
- Storey, P. J., & Hummer, D. G. 1995, MNRAS, 272, 41 [NASA ADS] [CrossRef] [Google Scholar]
- Tayal, S. S., & Zatsarinny, O. 2010, ApJS, 188, 32 [NASA ADS] [CrossRef] [Google Scholar]
- Todt, H., Peña, M., Hamann, W.-R., & Gräfener, G. 2010, A&A, 515, A83 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Tsamis, Y. G., Barlow, M. J., Liu, X.-W., Storey, P. J., & Danziger, I. J. 2004, MNRAS, 353, 953 [NASA ADS] [CrossRef] [Google Scholar]
- Tylenda, R., & Stasińska, G. 1994, A&A, 288, 897 [NASA ADS] [Google Scholar]
- Tylenda, R., Acker, A., & Stenholm, B. 1993, A&AS, 102, 595 [NASA ADS] [Google Scholar]
- Werner, K., & Herwig, F. 2006, PASP, 118, 183 [NASA ADS] [CrossRef] [Google Scholar]
- Wesson, R., Liu, X.-W., & Barlow, M. J. 2003, MNRAS, 340, 253 [NASA ADS] [CrossRef] [Google Scholar]
- Wesson, R., Liu, X.-W., & Barlow, M. J. 2005, MNRAS, 362, 424 [NASA ADS] [CrossRef] [Google Scholar]
- Zhang, H. 1996, A&AS, 119, 523 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Zhang, C. Y., & Kwok, S. 1993, ApJS, 88, 137 [NASA ADS] [CrossRef] [Google Scholar]
- Zhang, Y., Liu, X.-W., Liu, Y., & Rubin, R. H. 2005, MNRAS, 358, 457 [NASA ADS] [CrossRef] [Google Scholar]
All Tables
Object characteristics and log of observations (slit dimensions were always 1′′ × 5′′).
Observed and reddening corrected line ratios (F(Hβ) = 100) and line identifications.
Observed and reddening corrected line ratios (F(Hβ) = 100) and line identifications.
All Figures
 |
Fig. 1 Portion of the 2D echellograms and the extracted spectra showing the spatially resolved Hβ line for all objects in our sample. |
| In the text | |
 |
Fig. 2 Comparison between our derived c(Hβ) and those derived in the literature for common objects. Red filled circles: Girard et al. (2007); green filled stars: Peña et al. (2001); blue filled triangles: Górny et al. (2009); blue open inverse triangles: Acker & Neiner (2003). It is clear that there is a good overall agreement, except for some data (see text). |
| In the text | |
 |
Fig. 4 Section of the echelle spectra showing the Paschen discontinuity in all the objects of our sample. In several objects, we can clearly see the wide stellar emission line that contaminates the spectrum in the blue part of the discontinuity. |
| In the text | |
 |
Fig. 5 Te(He i) vs. Te(H i) diagram. Two methods for deriving Te(He i) have been used. One follows the method of Zhang et al. (2005), based on the line ratio λ7281/λ6678 (open circles). The other follows the Peimbert et al. (2002) procedure and computes Te(He i) based on several He i lines (black circles). Solid line represents equality (t2 = 0), and dotted lines show the variation in Te(H i) as a function of Te(He i) considering different t2 values. |
| In the text | |
 |
Fig. 6 Part of the spectrum of four objects in which the faint O ii λ4089 (upper four panels) and N ii λ4041 (lower four panels) lines were most reliably measured. |
| In the text | |
 |
Fig. 7 Te − ne diagnostic plots. Colors correspond to species: grey for S, blue for N, green for O, magenta for Cl, and red for Ar. Different lines indicate ions: solid for neutral ions ([N i]), dashed for once ionized ions ([N ii], [S ii] and [S ii]), dotted for two ionized ions ([O iii], [S iii], [Ar iii], and [Cl iii]), and dotted-dashed for three times ionized ions ([Ar iv]). |
| In the text | |
 |
Fig. 8 Upper panel: portion of the 2D echellogram showing [Fe iii] λ5270 (left) and [Cl iii] λ5517 lines for M1-61. The grey scale is the same for both lines. It is clear that the [Fe iii] emission is more extended that [Cl iii] emission. Lower panel: portion of the 1D extracted spectra showing the [Fe iii] λ4658 line, compared with multiplet 1 O ii ORLs. The FWHM of the [Fe iii] line is clearly larger. |
| In the text | |
 |
Fig. 9 Electron densities derived from [S ii] λλ6717/6730 (black filled circles), [O ii] λλ3726/3729 (blue triangles), and [Ar iv] λλ4711/4740 (red stars) compared to the one derived from [Cl iii] λλ5517/5537. There is a clear correlation between all quantities. The trend ne([Ar iv]) > ne([Cl iii]) > ne([S ii]) > ne([O ii]) is clear. Solid line represents the equality. Pointed, solid, and dashed lines are the fits to the ne([Ar iv]), ne([S ii]), and ne([O ii]) vs. ne([Cl iii]) data points, respectively. |
| In the text | |
 |
Fig. 10 ne as a function of the [WC] type of the central star. |
| In the text | |
 |
Fig. 11 Comparison between high ionization Te diagnostics. Black dots: Te([S iii]); green stars: Te([Ar iii]). A very good correlation Te([O iii]) vs. Te([S iii]) is found. Solid line represent an equality. |
| In the text | |
 |
Fig. 12 Comparison between Te([O iii]) and Te([N ii]). Solid line represent equality. Pointed line is the fit to the data. |
| In the text | |
 |
Fig. 13 Te([O iii])/Te([N ii]) vs. O++/O+. Black triangles: our data; red asterisks: Peña et al. (2001); blue open diamonds: Górny et al. (2004) data for bulge PNe. |
| In the text | |
 |
Fig. 14 Photoionization models computed to reproduce the observed Te([O iii])/Te([N ii]) vs. O++/O+ behaviour. Models (circles) and observational data (squares) are colored according to the O/H value. At the lower left, we show the typical error bars for the observational data. |
| In the text | |
 |
Fig. 3 Complete MIKE-echelle spectra of Cn 1-5. The most characteristic nebular emission lines have been labelled. Wide stellar WR features, generally stellar helium lines, are clearly visible in some spectral regions. |
| In the text | |
 |
Fig. 3 Complete MIKE-echelle spectra of H b4. |
| In the text | |
 |
Fig. 3 Complete MIKE-echelle spectra of He 2-86. |
| In the text | |
 |
Fig. 3 Complete MIKE-echelle spectra of M 1-25. |
| In the text | |
 |
Fig. 3 Complete MIKE-echelle spectra of M 1-30. |
| In the text | |
 |
Fig. 3 Complete MIKE-echelle spectra of M 1-32. |
| In the text | |
 |
Fig. 3 Complete MIKE-echelle spectra of M 1-61. |
| In the text | |
 |
Fig. 3 Complete MIKE-echelle spectra of M 3-15. |
| In the text | |
 |
Fig. 3 Complete MIKE-echelle spectra of NGC 5189. |
| In the text | |
 |
Fig. 3 Complete MIKE-echelle spectra of NGC 6369. |
| In the text | |
 |
Fig. 3 Complete MIKE-echelle spectra of PC 14. |
| In the text | |
 |
Fig. 3 Complete MIKE-echelle spectra of Pe 1-1. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


