| Issue |
A&A
Volume 538, February 2012
|
|
|---|---|---|
| Article Number | A32 | |
| Number of page(s) | 14 | |
| Section | The Sun | |
| DOI | https://doi.org/10.1051/0004-6361/201118145 | |
| Published online | 30 January 2012 | |
The interplanetary magnetic structure that guides solar relativistic particles
1
LESIA, Observatoire de Paris, CNRS, UPMC, Université Paris
Diderot, 5 place Jules
Janssen, 92190
Meudon, France
e-mail: sophie.masson@nasa.gov
2
Instituto de Astronomía y Física del Espacio (CONICET-UBA) and
Departamento de Física, Facultad de Ciencias Exactas y Naturales (UBA),
Buenos Aires,
Argentina
Received: 23 September 2011
Accepted: 28 October 2011
Context. Relating in-situ measurements of relativistic solar particles to their parent activity in the corona requires understanding the magnetic structures that guide them from their acceleration site to the Earth. Relativistic particle events are observed at times of high solar activity, when transient magnetic structures such as interplanetary coronal mass ejections (ICMEs) often shape the interplanetary magnetic field (IMF). They may introduce interplanetary paths that are longer than nominal, and magnetic connections rooted far from the nominal Parker spiral.
Aims. We present a detailed study of the IMF configurations during ten relativistic solar particle events of the 23rd activity cycle to elucidate the actual IMF configuration that guides the particles to the Earth, where they are measured by neutron monitors.
Methods. We used magnetic field (MAG) and plasma parameter measurements (SWEPAM) from the ACE spacecraft and determined the interplanetary path lengths of energetic particles through a modified version of the velocity dispersion analysis based on energetic particle measurements with SoHO/ERNE.
Results. We find that the majority (7/10) of the events is detected in the vicinity of an ICME. Their interplanetary path lengths are found to be longer (1.5–2.6 AU) than those of the two events propagating in the slow solar wind (1.3 AU). The longest apparent path length is found in an event within the fast solar wind, probably caused by enhanced pitch angle scattering. The derived path lengths imply that the first energetic and relativistic protons are released at the Sun at the same time as electron beam emitting type III radio bursts.
Conclusions. The timing of the first high-energy particle arrival on Earth is mainly determined by the type of IMF in which the particles propagate. Initial arrival times are as expected from Parker’s model in the slow solar wind, and significantly longer in or near transient structures such as ICMEs.
Key words: solar-terrestrial relations / Sun: heliosphere / methods: data analysis
© ESO, 2012
1. Introduction
The solar activity has consequences for the entire inner heliosphere. In addition to high-energy photons, one can distinguish two energetic phenomena that directly affect the terrestrial environment: coronal mass ejections (CMEs), which disturb the magnetized environment, and the energetic particle events, which impact the Earth’s atmosphere and affect the ionized environment. The most energetic particles that the Sun produces are relativistic protons of up to about 10 GeV. At these relativistic energies, solar particles penetrate the magnetosphere and impact the Earth’s atmosphere. The atmospheric interaction of the GeV particles produces secondary particles through nuclear cascades that are detected at the ground level by neutron monitors (NMs). Hence, the name of ground-level enhancement or GLE. Only 70 events have been reported since 1942, which have been thoroughly studied to address the acceleration and propagation of these particles from the Sun to the Earth.
Solar energetic phenomena may accelerate particles up to relativistic energies through the coronal shock driven by the CME (Vainio & Laitinen 2007; Sandroos & Vainio 2009), or through magnetic reconnection during a flare (Arzner & Vlahos 2004; Dmitruk et al. 2004; Turkmani et al. 2005; Drake et al. 2006).
Energetic particles are guided by the interplanetary magnetic flux tube that connects the acceleration site to the Earth. Most previous studies are based on the assumption that energetic particles propagate along the nominal Parker spiral. Nevertheless, two main problems arise under this assumption. First, it implies that the parent active regions are located near 30°−80° West. However, observations show that the distribution in longitude of the parent active regions is broad, ranging from 90° East to more than 120° West (Cliver et al. 1982; Kahler et al. 1984). Second, the time measured between the radiative signatures of particle acceleration in the Sun’s corona and the in-situ measurements is longer than it should be for a propagation in the Parker spiral (Debrunner et al. 1997; Kahler et al. 2003; Tylka et al. 2003).
Several scenarios have been proposed to explain the delay and the connection problem during relativistic particle events. Indeed, the delay may be caused by a late acceleration and/or injection phase during the flare (Debrunner et al. 1997; Klein et al. 1999) or by a time-extended acceleration at the bow shock of the CME (Reames 1999; Gopalswamy 2005). Because shock acceleration supposedly injects particles over a wide angular width, which would also explain the connection problem, several studies favored the CME shock acceleration over the flare acceleration (Cliver 1982; Hudson et al. 1982; Cliver et al. 2004).
However, we have known since the early investigations of relativistic solar energetic particle events that they often occur during depressions of the galactic cosmic ray intensity. Such a depression is typically associated with a transient interplanetary magnetic field structure (see Carmichael 1962, and references therein), which is known today as an interplanetary coronal mass ejection (ICME), which is the interplanetary counter part of the CME observed in the solar corona (Wimmer-Schweingruber et al. 2006). While observed at 1 AU, ICMEs can still be connected to the Sun by one or two footpoints (e.g. Crooker et al. 2008). Therefore, relativistic particles could be detected at the Earth in ICMEs when the parent active region is far from the nominally well-connected western solar hemisphere (Debrunner et al. 1988). Detailed studies of individual events showed indeed that energetic particles can propagate within ICMEs (Richardson et al. 1991; Larson et al. 1997; Torsti et al. 2004).
Moreover, the specific magnetic topology of ICMEs modifies the interplanetary propagation of energetic particles such as the directivity of the particles flux (Krittinatham & Ruffolo 2009). This could explain peculiarities in the directional distributions of relativistic protons observed at the Earth (Bieber et al. 2002; Miroshnichenko et al. 2005; Ruffolo et al. 2006; Sáiz et al. 2008). Also, long geometrical paths in the interplanetary space inferred from velocity dispersion analysis (Larson et al. 1997) or from detailed timing comparisons (Masson et al. 2009) point to particle propagation in non-nominal interplanetary magnetic fields.
Accordingly, the relationship between solar energetic particles measured near 1 AU and the parent activity in the corona depends on a combination of processes: particle acceleration in the corona, access of the accelerated particles to open field lines, and propagation through interplanetary space along various possible magnetic field configurations.
In this paper we explore the interplanetary magnetic structures and their impact on particle propagation during the most energetic solar particle events, the GLEs (ground-level enhancements). Our analysis is based on two independent methods: the identification of the interplanetary magnetic structures using magnetic field and plasma parameters measured onboard the ACE spacecraft (Sect. 2) and the velocity dispersion analysis of the initial proton arrival times based on ERNE/SoHO and neutron monitor data (Sect. 3). This is completed by comparing the deduced solar release time of protons with the time interval of electrons as deduced from type III burst observations. We summarize and conclude in Sect. 4.
2. The interplanetary magnetic structure that guides the relativistic particles
2.1. Characteristics of interplanetary structures
The magnetic field vector at the spacecraft is conveniently characterized by the magnitude of the field, B, its orientation defined by the latitude, θB, above the ecliptic plane and the longitude, φB, with respect to the Sun-Earth axis. For the undisturbed solar wind, where the field line is a Parker spiral, the magnetic field is weak (B ~ 5nT at 1 AU) and strongly non-coherent, with angles fluctuating around typical mean values θB ≃ 0° and φB ≃ −45° or 135° (for an inward or outward sector, respectively, with GSE coordinates). When an ICME that is initially ejected from the solar corona reaches the spacecraft, B increases strongly and becomes more coherent (e.g., Burlaga 1995). The magnetic field orientation also evolves more coherently.
In the solar wind, the temperature of protons is empirically dependent on the proton
velocity (Lopez & Freeman 1986). Elliott et al. (2005) established the relation
![\begin{equation} T_{\rm exp} {\rm [K]} = 640 \times V_{\rm SW}[\rm{km\,s}^{-1}]-1.56\times 10^{5} \end{equation}](/articles/aa/full_html/2012/02/aa18145-11/aa18145-11-eq11.png) (1)
(1)
between the expected proton temperature, Texp, and the solar wind speed, VSW. A deviation from this relationship allows us to identify a transient interplanetary structure. An ICME typically has a proton temperature lower than Texp/2 (Burlaga et al. 1981; Klein & Burlaga 1982; Burlaga 1991), and this criterion is frequently used to define the extent of an ICME (Richardson & Cane 2010, and references therein). Moreover, if the magnetic field is also significantly more intense than in the solar wind and has a coherent rotation, this region defines a magnetic cloud.
Differences between solar wind and ICMEs are also expected in the proton β (ratio of proton over magnetic pressure, noted βp). Typically βp ≥ 0.4 in the solar wind, while it is generally smaller, typically in the range 0.01 ≤ βp ≤ 0.4, within an ICME or a magnetic cloud, which are cooler and have a stronger magnetic field.
When a magnetic cloud (or an ICME) moves faster than the surrounding solar wind, a sheath is formed in front with enhanced plasma density and magnetic field strength. Magnetic reconnection is typically expected between two magnetic structures when different magnetic fields are pushed against each other. In-situ evidence of this reconnection has been found recently in a magnetic cloud sheath (Chian & Muñoz 2011). More generally, reconnection between the sheath and flux rope magnetic field implies that the flux rope front can be progressively pealed, while the corresponding magnetic flux region remains at the flux rope rear (called a back region). Because of the different magnetic topologies, the back region is typically separated from the remnant flux rope by a current sheet. This back region has intermediate properties between those of the solar wind and the magnetic cloud, because it originally belongs to the flux rope, but after reconnection it is also connected to the solar wind (Dasso et al. 2006, 2007).
A priori, solar energetic particles can travel in any of the interplanetary structures summarized above. Accordingly, depending on their injection site on the Sun, or their access to the structure, energetic particles could be observed in a parkerian solar wind or in an environment associated with an ICME (e.g. in the ICME sheath, inside a magnetic cloud flux rope, in the magnetic cloud back, or in the distorted solar wind that is perturbed by the fast transient).
Summary of the studied relativistic events.
2.2. GLE selection and characterization of the interplanetary magnetic structures
We initially selected the relativistic events reported between 2000 and 2006. We did not study the GLEs with a marginal increase of the neutron monitor count rate (<5%). Our list therefore comprised 10 events (Table 1). The arrival times of the first detected protons at Earth have been already published by Moraal & McCracken (2011), and we report their results in Table 1.
Our analysis is based on measurements of the plasma and magnetic field near the L1 Lagrange point of the Sun-Earth system by the Advanced Composition Explorer (ACE) mission (Stone et al. 1998): the magnetic data were obtained from the MAG instrument (Smith et al. 1998) and the plasma data from the SWEPAM instrument (McComas et al. 1998). To be able to compare our measurements with neutron monitor measurements at 1 AU, we propagated the ACE measurements to the Earth. We performed this time correction by assuming bodily propagation of the magnetic field structures from L1 to Earth at the average solar wind proton speed Vp measured with ACE/SWEPAM during the two hours preceding the arrival of protons at Earth. This implies a time shift Δt = DL1/Vp, where DL1 is the L1-Earth distance.
The magnetic field and the plasma parameters were drawn in adjacent panels to compare their temporal evolution (e.g. Figs. 1–3). By over-plotting as a gray bar the 1-hour-time interval starting with the first arrival time of relativistic particles at the first responding neutron monitor, we characterize the magnetic structure in which the first relativistic protons arrive at the Earth.
We localized their parent active region (Col. 4 of Table 1) and the longitude of the footpoint of the Earth-connected Parker spiral field
line, given in Col. 5 of Table 1. The longitude of
the Parker spiral root on the solar source surface is at (Parker 1961) 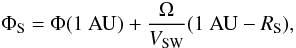 (2)where
Ω = 2.6 × 10-6 rads-1 is the angular speed of the Sun,
VSW the solar wind speed, assumed to be constant from the
Sun to the Earth, Rs = 2.5 R⊙ is
the radius of the spherical source surface, and Φ(1AU) is the longitude of the spiral at
1 AU. We selected Φ(1AU) = 0 as the reference longitude and ΦS is positive
westward from the Sun-Earth axis. Because of magnetic fluctuations, Ippolito et al. (2005) showed by a numerical study that the longitude
of the Parker spiral footpoints at the source surface cannot be estimated with an accuracy
better than 6°−10°. Moreover, coronal magnetic field extrapolations showed that an open
coronal flux tube rooted in an active region can spread by several tens of degrees in
longitude westward and eastward (Klein et al.
2008). Therefore, we consider that the parent active region is well-connected to
the Earth by the Parker spiral if its longitude is within the range
[ΦS−30°;ΦS + 30°] , otherwise we define the parent active region
as being poorly connected (Col. 7 of Table 1). The
path lengths along the nominal Parker spirals in this sample range from 1.06 AU
(VSW = 660 kms-1) to 1.15 AU
(400 km s-1), i.e. they are essentially 1.1 AU for each event.
(2)where
Ω = 2.6 × 10-6 rads-1 is the angular speed of the Sun,
VSW the solar wind speed, assumed to be constant from the
Sun to the Earth, Rs = 2.5 R⊙ is
the radius of the spherical source surface, and Φ(1AU) is the longitude of the spiral at
1 AU. We selected Φ(1AU) = 0 as the reference longitude and ΦS is positive
westward from the Sun-Earth axis. Because of magnetic fluctuations, Ippolito et al. (2005) showed by a numerical study that the longitude
of the Parker spiral footpoints at the source surface cannot be estimated with an accuracy
better than 6°−10°. Moreover, coronal magnetic field extrapolations showed that an open
coronal flux tube rooted in an active region can spread by several tens of degrees in
longitude westward and eastward (Klein et al.
2008). Therefore, we consider that the parent active region is well-connected to
the Earth by the Parker spiral if its longitude is within the range
[ΦS−30°;ΦS + 30°] , otherwise we define the parent active region
as being poorly connected (Col. 7 of Table 1). The
path lengths along the nominal Parker spirals in this sample range from 1.06 AU
(VSW = 660 kms-1) to 1.15 AU
(400 km s-1), i.e. they are essentially 1.1 AU for each event.
2.3. Magnetic configurations that guide the relativistic particles
Our analysis leads us to separate the magnetic field configurations along which relativistic particles reached the Earth into three distinct subsets (Col. 8 of Table 1): the nominal solar wind with a Parker spiral field (Sect. 2.3.1), a transient magnetic structure related to an ICME (Sect. 2.3.2), and a third category, typically a highly disturbed solar wind in the vicinity of an ICME (Sect. 2.3.3).
 |
Fig. 1 Interplanetary data around GLE 63 (Dec. 26, 2001): example of a GLE present in a typical Parker spiral. From top to bottom, panels display the magnitude of the magnetic field (nT); its latitude θB and its longitude φB (given in GSE coordinate system); then on the same panel are overplotted the temperature of protons measured by the spacecraft (black dots) and the expected temperature (gray dots), and finally the β of protons. A horizontal line is added for θB = 0, φB = −45° and βproton = 0.4 to mark characteristic values. The grayscale rectangle in the five panels corresponds to the 1-hour time interval starting at the first arrival time of relativistic protons at Earth. The time axis is as measured at Earth. The ACE measurements at the L1 Lagrangian point were shifted by the appropriate travel time (see Sect. 2.2). |
2.3.1. The Parker spiral
In our sample only three GLEs reached the Earth along a typical Parker spiral: Dec. 26, 2001 (GLE 63), Aug. 24, 2002 (GLE 64) and Dec. 13, 2006 (GLE 70).
Between 02:00–24:00 UT on Dec. 26, 2001, the magnitude of the magnetic field was fluctuating around 5−6 nT (Fig. 1). The magnetic field orientation was typical of the Parker spiral (θB ≈ 0° and φB ≈ −45°). Moreover, the expected temperature was almost the same as the observed one and 0.4 ≤ βp ≤ 1. A small magnetic cloud was possibly present between 21:00 UT on Dec. 25 and 02:00 UT on Dec. 26, but it was not listed by Richardson & Cane (2010) and ended about 4 h before the arrival of relativistic particles. Thus, the relativistic particles impacting the Earth at 05:40 UT on Dec. 26, 2001 (GLE 63), propagated along the Earth-connected Parker field line.
The two other events consistent with a propagation along the nominal Parker spiral are GLE 64 and GLE 70. The magnetic field orientation, the plasma beta and the similarity of the expected and the actually observed temperature all clearly argue in favor of this interpretation (see Sects. A.1.1, A.1.2 and Figs. A.1, A.2).
For these three events, no ICMEs have been identified several days before the particle arrival (Richardson & Cane 2010), confirming that the interplanetary medium was not disturbed. Moreover, the proximity in longitude of the parent active region and the footpoint of the nominal Parker spiral is consistent with this result (Table 1).
 |
Fig. 2 Interplanetary data around GLE 67: it is located in the back region of a magnetic cloud. Same drawing convention as Fig. 1. |
2.3.2. ICME, magnetic cloud, or back region
For the five GLEs occurring on Jul. 14, 2000 (GLE 59), on Apr. 18, 2001 (GLE 61), on Oct. 28, 2003 (GLE 65), on Oct. 29, 2003 (GLE 66), and on Nov. 2, 2003 (GLE 67), we find that particles propagate in a transient magnetic structure, such as in the sheath of an ICME, in a magnetic cloud or in the back region of a magnetic cloud.
The GLE on Nov. 2, 2003 was detected on Earth at 17:30 UT (Fig. 2). On that day, the magnetic field strength (B ≃ 5nT) and its longitude (fluctuating around φB ≃ −50°) were typical of a solar wind structured by the Parker spiral. However, θB was not aligned with the ecliptic plan (≃−50°) as one expects for a Parker spiral. Moreover, both Tobs < Texp and βp < 0.4 were inconsistent with a quiet solar wind. Indeed, an ICME was detected, starting on Oct. 31, 2003 at 2:00 UT and ending on Nov. 2, 2003 at 00:00 UT.
Within the ICME, from ≃8:00 UT on Oct. 31 to 1:00 UT on Nov. 1, both θB and φB had a relatively coherent global evolution. Moreover, Tobs < Texp/2, implying that a magnetic cloud was present. After 1:00 UT on Nov. 1, θB and φB evolved progressively away from the values found at the rear of the magnetic cloud, and their fluctuation level increases. This behavior is characteristic of the back region of a magnetic cloud that displays intermediate properties between a magnetic cloud and the solar wind (Dasso et al. 2006, 2007).
According to Richardson & Cane (2010), the ICME ends when βp shows a sharp increase. Nevertheless, even though βp increased, it remained less than 0.4 and the ratio Tobs/Texp was still less than 0.5 almost until the end of Nov. 2 (Fig. 2). In addition, both θB and φB still displayed similar mean values as at the rear of the magnetic cloud. Thus, the back region extended until the end of Nov. 2 (when Tobs ≈ Texp and βp ≈ 0.4). We conclude that the energetic particles of GLE 67 propagate up to the Earth in the extended back region of the previous magnetic cloud.
Following a similar reasoning, we identified the magnetic structures of the IMF for the other GLEs (the analysis is reported in Sect. A.2 of the Appendix). We conclude that relativistic particles related to the GLE 61 propagated in the sheath of an ICME (Sect. A.2.2). The GLE 66 occurs inside a magnetic cloud (previously studied by Mandrini et al. 2007). We remark that this magnetic cloud is related to the CME ejected from the Sun on Oct. 28, 2003 at 11:30 UT during the solar eruption that produced the GLE 65. Therefore, we conjecture that the relativistic particles produced during the flare/CME event on 29 Oct. 2003 have been injected in the footpoints of the CME launched on 28 Oct. 2003 (Sect. A.2.4). For the GLE 59 and GLE 65, the temporal evolution of magnetic field and plasma parameters of the interplanetary medium displays intermediate properties between solar wind and magnetic cloud. A detailed analysis of all variables in a four day time interval around the GLE suggests that the particles related to GLE 59 and GLE 65 propagated in the back region (see Sects. A.2.1 and A.2.3).
The four GLEs (59, 61, 65, 66) are all poorly connected to Earth by a nominal Parker spiral (Table 1). The solar eruptions associated to GLE 59, GLE 65, and GLE 66 were located near the central meridian, while the parent active region of GLE 61 was probably located behind the solar west limb. Thereby, the connection between the active region and Earth cannot have been ensured through the Parker spiral field line. According to our analysis, we conclude that particles propagated in transient magnetic structures (ICME, magnetic cloud and back region). Because the coronal roots of these transient structures extend over a wide longitudinal range, they can provide a magnetic path that connects the active region and the Earth. However, this does not imply that all GLEs associated with transient magnetic structures should be poorly connected. Indeed, the broad longitudinal extent of an ICME includes the well-connected cases. An example is GLE 67, which is well-connected by a nominal Parker spiral, while the high-energy particles are traveling in a magnetic cloud back region.
 |
Fig. 3 Interplanetary data around GLE 60: example of a GLE present in a SW disturbed by a previous ICME. Same drawing convention as Fig. 1. |
2.3.3. Disturbed solar wind
The identification of the interplanetary magnetic structure of the GLE 60 and GLE 69 indicates that particles propagate in an interplanetary medium formed by a disturbed solar wind.
We present below the case of GLE 60 in detail, which occurred on Apr. 15, 2001 (Fig. 3). The first relativistic particles impacted the Earth at 13:55 UT. Between 10:00 and 16:00 UT, even though the magnitude of the magnetic field and the plasma parameters are close to typical solar wind values, the magnetic field orientation (θB ≈ −45° and φB ≈ 0°) does not correspond to the Parker spiral. However, the fluctuations of the magnetic field around fixed values of latitude and longitude are more characteristic of a magnetic structure associated with a quiet solar wind than with an ICME. From the ICME list of Richardson & Cane (2010), the last strong magnetic perturbation was an ICME, starting the Apr. 13 at 07:34 UT and ending on Apr. 14 at 12:00 UT, while the next ICME starts about three hours after the relativistic particles reached the Earth. Therefore, we suggest that particles propagated in a solar wind strongly disturbed by the preceding ICME.
Similarly, the magnetic structure in which the relativistic particles of GLE 69 propagate is identified to be also a solar wind magnetic topology disturbed by a previous ICME (Sect. A.3.1).
Judging from their longitudes, GLE 60 (W 85) was poorly and GLE 69 (W 55) was well-connected to the Earth by the Parker spiral (Table 1). However, the apparently good connection of the active region related to the GLE 69 does not imply that the magnetic field connecting the Sun to the Earth is a Parker spiral. The anisotropy of this GLE, with the strongest and fastest rise seen by neutron monitors in Antarctica, suggests a strong out-of-the ecliptic component of the magnetic field, which is indeed observed (Sect. A.3.1).
2.4. Summary
Using ACE magnetic field and plasma parameter measurements, we identified the structure of the interplanetary magnetic field. We show that only in three events out of ten the relativistic particles possibly propagate in a solar wind structured by a Parker spiral, while in the seven other events the relativistic particles propagate in a transient IMF (ICME, magnetic cloud, back region, or disturbed solar wind). Of these seven events, five have a solar source region significantly far removed (more than 30°) from the theoretical location of the footpoint of the Parker spiral at the solar source surface.
3. The interplanetary length
Previous studies of relativistic particles, measured on Earth by neutron monitors, assume that energetic particles travel along the Earth-connected Parker spiral field line. This assumption implies that particles that are not scattered travel roughly 1.1–1.3 AU, depending on the solar wind speed. Indeed, from our above results, most GLEs do not propagate in the quiescent solar wind. Therefore, we expect that the interplanetary length traveled by energetic particles differs from that of the Parker spiral.
3.1. Velocity dispersion analysis using the rising phase method (RPM)
A commonly used estimate of interplanetary travel paths of energetic particles is the velocity dispersion analysis (VDA) of the time when the first particles arrive at the detector. The method is based on the assumption that the first energetic particles are simultaneously released from a small acceleration site in the solar corona and propagate scatter-free in the interplanetary medium. Therefore, the less energetic particles arrive on Earth later than the most energetic ones, implying a velocity-dependent time dispersion of the first particle detection. Plotting the arrival time of the first particles measured on Earth as a function of the inverse of particle speed (1/v), one predicts a linear relationship whose slope is a measure of the interplanetary distance traveled by the energetic particles, and whose intercept with the 1/v = 0 axis is the solar release time.
The main practical problem of the method is the definition of arrival times of particles at the detector. The onset time is commonly defined as the instant when the intensity exceeds a given level above background. But this value is strongly affected by fluctuations in the individual energy channels, which may introduce a distortion and produce a large error both in the slope (the length) and the intercept (the release time) of the resulting plot. This is what we experienced when applying different methods to the events under study. We therefore propose a new method, called the rising phase method (RPM). The RPM is based on the same principle as the VDA, but it compares well-defined reference times during the rise phase of the time profiles at different energies, and thereby provides an estimate of the interplanetary length that is much less sensitive to background fluctuations than the classical VDA. Practically we proceed as follows:
-
1.
The intensity profile in each energy channel is divided by thebackground intensity averaged over one hour before any evidentrise of the signal. Because the signal has a broad range of variation,we take the logarithm of this ratio, making the background levelzero.
-
2.
Depending on the energy spectrum of the event, the different energy channels reach different maximum values. To compensate for this hardness effect, we normalize the above logarithm of fractional intensity by its maximum found just after the rise phase. This normalization is realized in a time interval typically between 10 and 20 min after the rise phase, with a time-shift function of the channel energy to compensate approximately the differential arrival time in the energy channels. Thus, the logarithm of this normalized intensity increases from 0 to 1 in the rising phase of the signal. Three examples are shown in the top row of Fig. 4.
-
3.
The rising phase between the levels 0.2 and 0.8 is fitted by a straight line (assuming an exponential rise of intensity). The fit reduces the effects of the fluctuations superposed on the general increase of intensity, as seen in several curves in Fig. 4, panels a and c. We refer to the instant when the fitted straight line is at level 0.5 as the rise time at the corresponding energy. This corresponds to the maximum cross-correlation of the rising profiles.
-
4.
Finally, we plot the rising parts of intensity profiles as a function of observing time minus the rise time, and control visually how well the profiles in the different energy ranges superpose.
As the classical VDA, the RPM provides a set of times trise which depend on the energy of the channels, hence on the velocity of the detected energetic particles. Then, the slope of a linear fit of trise versus 1/v provides an estimate of the interplanetary length D (bottom row of Fig. 4). The estimation of D depends only on the relative timing of the channels.
The linear fit also provides an estimate of the solar release time, tSRT of the particles (supposed to be independent of energy) as the intercept of the straight line with the 1/v = 0 axis. We have to keep in mind that this is an upper limit, because it refers to a time during the rise of the intensity profile. We estimated the error on D and tSRT with the standard error of the fitted parameters.
We believe that the use of the rise times gives a more reliable determination of the travel path than using the onset times mainly for three reasons. As already stated, the method does not depend on the fluctuating background, because it uses the part of the signal well above it. Moreover, the fluctuations of the background and of the signal should only have a minor influence because the method cumulates the information over a finite time interval (most of the rising part of the signal). Finally, the rise time is computed in the steepest part of the rising phase of the time profile, where the timing is the most accurate. These three properties contrast with the onset time method, which relies on a local measure above the fluctuating background where the signal just starts to increase.
However, the time dispersion determined by the RPM may be affected by systematic biases, such as scattering during the propagation of particles from the Sun to the Earth. Because the mean free path increases with increasing particle energy (Dröge 2000), the lower energy particles should arrive with an extra delay compared to the arrival time that one expects. This extra delay at low energy may lead to an increase of the length obtained by the RPM. The dependance of the RPM’s results with respect to the particle scattering is hard to assess. However, we expect that one of the following three situations should apply: (1) scattering of the first arriving particles is negligible, and the slope of the onset time vs. 1/v plot gives the geometrical path, e.g. GLE 63 & GLE 64; (2) scattering dominates the propagation to the extent that the slope is mostly determined by the energy dependence of the scattering mean free path, e.g. GLE 70 ; (3) both the geometrical path and scattering shape the plot. Thereby, the RPM gives at least the apparent length travelled by energetic particles, but this apparent length may be a mix of the geometrical length and the additional length created by the scattering.
 |
Fig. 4 Example of the RPM and VDA analysis. Top row: normalized time profile of the logarithm of the intensity during the rising phase without any time shift for GLEs 64, 67 and 70, respectively, in panels a)–c) (see Sect. 3.1). The energy range (in MeV) of channels is added on the panel a). Bottom row, panels d)–f): plots of rise and onset times in function of the inverse of the proton velocity. The dark gray (or blue) points correspond to the rise times determined by RPM apply to ERNE data (Sect. 3.1), and the related linear fit is displayed by a dashed line (dark gray or blue). The linear fit related to the data set including the NM point (labeled and plotted in black or red), in addition to the previous ERNE points, is represented by a continuous line (black or red). The medium gray (or green) points correspond to the onset times of ERNE data and the related linear fit is displayed with a dashed line and the same color. The linear fit with the NM point added is shown with a continuous line and light gray (or pink). A color version is available in the electronic version. |
3.2. Application to the selected events
3.2.1. Data set and event selection
We performed the velocity dispersion analysis based on the RPM using measurements of the high energy detector (HED) of the energetic and relativistic nuclei experiment (ERNE) instrument (Torsti et al. 1995) onboard SoHO, located at the L1 Lagrangian point. The energy range covered by ERNE/HED extends from 13MeV to 130MeV. Data are provided in ten customized energy channels. The five highest energy channels, between 40−130MeV, are usually distorted during GLEs (Valtonen, priv. comm.): to prefer the detection of heavy ions, the onboard software raises the threshold for the detection of protons and He ions during large events. As a result, the proton intensities between 40−130MeV may display recurrent indentations. We corrected this artifact to recover a regular time profile to which the RPM could be applied. Identifying the start and end times of the indentations by the sudden change of intensity, we applied a correcting factor to each interval by using the measured values obtained just before and after the jump. These corrections have a negligible effect on the fitted parameters. Still, they allow us to use higher energy channels, which are closer to the NM data.
Since it is not clear a priori if the relativistic protons measured by the neutron monitors are just the high-energy extension of the solar energetic particles (SEP) spectrum measured by ERNE or a distinct population, we performed separate velocity dispersion analyses with and without the data point of the GLE as determined by Moraal & McCracken (2011). We used the mean energy of each ERNE channel to compute the velocity of energetic protons. The RPM cannot be applied to neutron monitor measurements, which respond to the integral proton spectrum above the local rigidity cutoff as determined by the geomagnetic field configuration.
Only seven of the ten GLEs have suitable ERNE observations for the RPM: there are no data for GLE 59 and for GLE 66 energetic particles of the SEP are smothered in a more time-extended energetic particles flux that is probably accelerated at the bow shock of the magnetic cloud. Finally, we were unable to use the ERNE data of the GLE 69 because the signal decreases and no bump has been detected in the time interval during which we expect the arrival of energetic particles related to the GLE.
3.2.2. Results
Figure 4 displays the results of the RPM for three GLEs selected to illustrate the three kinds of interplanetary magnetic structures previously identified. Even though the intensity profiles display significant fluctuations (top panels of Fig. 4), the RPM succeeds to derive the rise time of energetic particle fluxes in each energy channel. When these rise times are plotted as a function of 1/v (bottom panels of Fig. 4), they display a linear relation.
We report in Table 2 the interplanetary lengths resulting from our RPM with and without the NM data, respectively. We found that for five out of seven events, the difference between the two lengths computed with and without the neutron monitor data point is not larger than ≃0.05AU, which is well inside the error bars.
Path lengths and release times using RPM.
However, we emphasize that our RPM considers an instant near half maximum during the rise of the ERNE time profiles as the onset time, whereas the neutron monitor onset time is the instant when the first neutron monitor signal was detected. These times are not directly comparable. A number of the events of Table 2, for which ERNE measured well-defined onset time profiles, are associated to weak GLEs, where the time when the signal starts to exceed background is probably a rough upper estimate of the actual start, and indeed also designates a time during the rise of the GLE. It is likely that the systematic error of the neutron monitor onset time compensates the different timing definitions of the two data sets to some extent. Therefore we note that the timing is consistent, but we cannot use this finding to draw firm physical conclusions on the simultaneity of proton acceleration from tens of MeV to GeV energies.
A discrepancy between the results with and without NM data is found in GLEs 65 and 70. They display a difference comparable to the error bar sizes (Table 2 and Fig. 5). For GLE 70 the results with and without NM has a length difference of ≃0.31AU. Irrespective of the exact numerical value, both analyses lead to an interplanetary path that is significantly longer than the Parker spiral for GLE 70.
In the case of the GLE 65, we adapted the RPM. Indeed, the normalized logarithm of intensity has a temporal evolution significantly dependent of the energy channel and so has not a simple temporal shift as for other GLEs. We tested the usual normalization method, but it appears that the rising phases of the time profiles in different energy channels are not parallel. This difference in the time evolution of the channels indicates an evolution of the hardness of the spectrum during the rise phase. Indeed, one notices that a pre-increase appeared in the ERNE time profile in the high-energy channels. According to Trottet et al. (2008), the acceleration of particles during this solar eruption displays a complex temporal structure, suggesting that several episodes of acceleration occur. Thereby, the pre-increase can result from a different acceleration episode than the one accelerating the particles of the main particle flux.
To remove this effect for GLE 65, we used an earlier normalization, during the rising phase, at a time chosen such as to obtain rise time profiles in different energy channels that are parallel. We also found that the rise times are more aligned with the neutron monitor data and that the lengths computed by the RPM with and without the NM point differ by only ≃0.3AU.
3.2.3. Comparison with results of classical VDA
We compare in this section the results of the RPM with the VDA method based on the estimation of the onset time, tonset, of the first particles in each channel. Because the arrival time of the first protons is masked by the fluctuations of the background, we extrapolated the linear fit of the rise phase (see Sect. 3.1) up to the mean level of the background. This defines the onset time, tonset. The uncertainty on tonset is partly caused by the error on the linear fit of the rising phase (as for trise), but it is also increased by the extrapolation toward the background level and by the background’s fluctuations. Considering the standard deviation of the background, this extra uncertainty on tonset is typically of 3min.
Since the first particles are expected to have the highest energy, we computed 1/v from the maximum energy of each channel. Using the maximum energy, Emax, compared to the mean one, Emean introduces a systematic difference in the estimated D of a factor 1 + ΔE/(2Emean) ≈ 1.06 to the first order in ΔE/Emean (where ΔE = Emax − Emin and Emean = (Emax + Emin)/2).
We found that the results with tonset are typically much more fluctuating and incoherent with the neutron monitor data than the results with trise (Fig. 4). Moreover, the length found with the onset times is unrealistically short (below 1 AU) for some GLEs (Table 3).
Path lengths and release times using the classical VDA.
In Table 3 we also report the interplanetary length computed by Reames (2009) with a velocity dispersion analysis of the onset time of protons and heavy ions. These results are considerably different from our VDA results (Table 3). However, the Reames results are broadly consistent with our rise time results (Table 2), except mainly for three events: GLEs 63, 64, and 67. Even though the VDA has been applied to the heavy ion data (from WIND/EPACT/LEMT) to obtain a lower background level, the fluctuations of the signal before and during the rising phase, see e.g. Fig. 3 in Reames (2009), and the temporal resolution (5–10 min) introduce limits to the accuracy of the estimated lengths.
In summary, we conclude that RPM gives a more meaningful evaluation of the interplanetary length traveled by energetic particles than the VDA, whatever the data set. This conclusion is even more strengthened in the next subsection.
3.3. Comparison of the RPM results with the identification of the IMF structure
3.3.1. IMF structure and interplanetary path length
From the comparison of the interplanetary path length inferred from the RPM (Table 2) and the interplanetary structure identified in Table 1, a clear relation can be established between the magnetic field along which energetic protons propagate and the distance they traveled. Figure 5 summarizes the interplanetary lengths computed without and with NMs (Cols. 2 and 3 in Table 2) as a function of the IMF topology (Col. 8 in Table 1).
The protons in the rising phase of GLE 63 and GLE 64 that are associated to a Parker spiral magnetic structure, traveled approximately 1.3 ± 0.1 AU. These interplanetary lengths are consistent with the Parker spiral magnetic topology that has a theoretical length of ≈1.15 AU for a slow solar wind. These results differ from Reames (2009), who found a length of ≈1.6 AU and 2.2 AU (Table 3) for GLE 63 and 64, respectively. Within the error bars (±0.06), these lengths are compatible with a Parker spiral only if there is an extra delay, which means if a physical mechanism can provide it independently of the proton energy.
By contrast of GLE 63 and 64, the interplanetary lengths traveled by protons producing GLEs 60, 61, 65, and 67, are longer than 1.5 AU (see Table 2). These lengths are fully compatible with the magnetic topology of an IMF created by transient magnetic structures, such as an ICME, magnetic cloud, back region, and even a disturbed solar wind.
The two lengths obtained with and without NMs, for GLE 65 (see Table 2), are both consistent with the back region of a magnetic cloud (because a back region is formed by reconnection between the solar wind and the flux rope, see the end of Sect. 2.1). However, the longer length is supported by the results from Miroshnichenko et al. (2005). Studying this specific GLE, they showed that the delay of the proton arrival should be caused by the perturbation of the IMF and that protons should travel roughly 2 AU. In addition, they estimated that this length is consistent with a simultaneous release of relativistic protons with relativistic neutrons, estimated at 10:56 UT from the NM data (tSRT = tNM − D/v). From our RPM analysis, and for linear regression with and without NMs, the proton release occurs later (Table 2). However, the solar release time may have been overestimated because the pre-increase detected in the high-energy channels of ERNE has been ignored in the determination of the time dispersion (Sect. 3.2.2).
 |
Fig. 5 Summary of the estimated length by the RPM, with (cross symbol) and without NM (diamond symbol), in relation to the magnetic topology. |
The last relativistic event of the solar cycle 23 (GLE 70) also displays a discrepancy between the magnetic structure and the interplanetary length. Indeed, the length traveled by protons is ≈2.6−2.9 AU, while the IMF displays characteristics of the Parker spiral. We note that this is the only GLE of our sample that is detected while the Earth was in the fast solar wind. It is well known from Ulysses observations in the fast solar wind that SEP are more strongly scattered there than in the slow wind (Sanderson 2004). Since the mean free path of the particles increases with increasing energy, particles of lower energy will be more strongly delayed than if they propagated scatter-free. This may contribute to an overestimation of the interplanetary path length. Moreover, the solar source of the fast solar wind is typically farther away from active regions than the edge of the open flux region, i.e. from the source region of a GLE. Consequently, when energetic particles are detected in the fast solar wind they are expected to have been transported a long way from their acceleration site. This extra delay could contribute to the long apparent length found for GLE 70. This effect is expected to be less in ICME and slow solar wind cases because the guiding magnetic field is located closer to the GLE solar source.
Except for this complex GLE 70, the interplanetary length is consistent with the magnetic structure observed during the particle event. We conclude that the propagation of energetic protons occurs in an IMF specific to each GLE, and is frequently different from the Parker spiral often used. Moreover, this shows that the geometry of the magnetic structure affects the length traveled by particles from the Sun to the Earth.
 |
Fig. 6 Comparison of the solar release time of relativistic protons obtained from the RPM with (cross symbol) and without NM (diamond symbol), with time interval of electrons injection as deduced from type III (gray shaded bars). The onset time of type III bursts is set as the origin of the vertical axis. |
3.3.2. When are protons injected into the IMF?
The propagation of non-thermal electrons in the interplanetary medium generates radio emission in the decametric wavelength range with a characteristic drift toward lower frequencies as the electrons propagate away from the Sun, toward lower ambient densities, along open magnetic field lines. These are type III bursts. Large groups of type III bursts accompany most major SEP events (Cane et al. 2002). At 14MHz, it is generally assumed that the electromagnetic waves are emitted at ~2−3R⊙ from the solar surface. The timing of the type III bursts at this frequency gives an indication of the time of electron injection into the high corona. Although the electrons are accelerated lower in the corona, the travel time from the acceleration site to the 14 MHz source is only a few tens of seconds, so this correction of time is negligible.
We computed the time interval of the electron injection with the WIND/ WAVES (Bougeret et al. 1995) data at 14MHz and compared them to the solar release time. Figure 6 synthesizes the temporal relation of the injection of the non-thermal electrons and the relativistic protons for the seven studied events (Sect. 3.2.2).
For six of the seven events, the solar release time of energetic protons is enclosed in the time interval of electron injection (Fig. 6). For GLE 67 the solar release of energetic protons precedes that of electrons by 3−5min. This is within the uncertainty of the method (see Table 2). We therefore conclude that the first energetic protons during these events were released during the interval of the electron injection traced by the type III bursts.
This timing consistency is an additional argument that supports our results on the magnetic topology of the interplanetary medium and its role for the propagation of energetic particles. Essentially, it gives a second proxy that confirms that the interplanetary length has been well evaluated.
4. Conclusion and discussion
We performed independent studies based on different methods to define and constrain the characteristics of the interplanetary magnetic field during GLEs. The main results are summarized below.
First, in most events, relativistic protons propagate in transient magnetic structures and not along the Parker spiral field lines.
Second, the magnetic structure of the IMF is consistent with the location of the parent active region of the GLE: when the in-situ measurements show a Parker spiral, the parent active region is within ±30° of the nominal footpoint, whereas it may be farther away when the IMF has a transient configuration.
Third, the effective interplanetary length computed through our velocity dispersion analysis (rising phase method, RPM) for energetic and relativistic protons agrees with the magnetic topology of the IMF deduced from in-situ measurements. This length traveled is ≈1.3 AU when the protons travel in the slow solar wind, while it is in the range 1.5–2.6 AU for transient magnetic structures. For the only GLE whose protons travel in the fast solar wind, the effective length is much longer than expected (2.6–2.9 AU rather than 1.1 AU). This may indicate that an extra mechanism delayed the protons the more strongly, the lower their energy. Pitch angle scattering is a possible candidate, especially because it is expected to be stronger in the fast than in the slow solar wind.
Fourth, our results are consistent with the idea that the first protons that produce SEPs and GLEs are accelerated/released simultaneously into the interplanetary medium, although they do not demonstrate this. The weakness of neutron monitor signatures in a number of events where the RPM could be applied to ERNE data precludes firm conclusions. The analysis also supports the idea that the first arriving energetic protons are not significantly scattered during their travel from the Sun to the Earth.
Fifth, according to the solar release time, energetic protons are injected during the injection of non-thermal electron beam producing type III bursts, supporting the above results on the impact of the interplanetary magnetic structure on the proton transport.
The common release of relativistic protons and type III-related electrons has already been suggested in a detailed study of GLE 69 (Masson et al. 2009). The event was not studied here, because the energetic particles in-situ measurements were unreliable. But the result is fully consistent with the conclusions drawn from the seven GLEs of the present sample. Our observational study suggests that the common release of type III bursts emitting electrons and the first escaping energetic and relativistic protons is a general property of GLEs.
In addition, energetic particles related to active region poorly connected to the Earth through the Parker spiral may be connected through a transient magnetic structure. This result implies that we need to reconsider the driven-shock acceleration that is invoked to explain the detection of particles on the Earth in poorly connected SEP events.
Finally, energetic protons propagating in a transient magnetic structure travel a longer distance than they should do in the Parker spiral case. This delay, due to the geometrical length of the interplanetary magnetic field, contributes to understanding the quasi-systematic delay measured between the GLE and the first radiative signature of accelerated particles at the Sun (Cliver et al. 1982). Moreover, this longer length traveled by relativistic protons modifies the relation between the coronal radiative signatures and the detection at Earth of these protons. As an example, Li et al. (2009) assumed that relativistic protons of GLE 70 traveled 1.1 AU between the acceleration site and the Earth, leading them to conclude that particles have been flare-accelerated. However, our study clearly demonstrates that for GLE 70, one cannot consider such a short path length of the interplanetary magnetic field.
Acknowledgments
The authors gratefully acknowledge R. Wimmer-Schweingruber and A. Balogh for helpful discussions on the contents of this paper. This research has made use of NASA’s Space Physics Data Facility (SPDF). We thank the ACE instrument teams and their respective principal investigators, namely N. F. Ness (ACE/MAG) and D. J. McComas (ACE/SWEPAM). The authors acknowledge financial support from ECOS-Sud through their cooperative science program (No. A08U01). This work was partially supported by the Argentinean grants: UBACyT 20020090100264 (UBA), PIP 11220090100825/10 (CONICET), and PICT-2007-00856 (ANPCyT). S.D. acknowledges support from the Abdus Salam International Centre for Theoretical Physics (ICTP), as provided in the frame of his regular associateship. S.D. is member of the Carrera del Investigador Científico, CONICET. The work of S.M. is funded by a fellowship of Délégation Générale pour l’Armement (DGA). S.M. thank the NASA Postdoctoral Program at the Goddard Space Flight Center, administered by Oak Ridge Associated Universities through a contract with NASA for financial support. Financial support by the European Commission through the FP6 SOLAIRE Network (MTRN-CT-2006-035484) is gratefully acknowledged. We thank E. Valtonen for his very helpful assistance with the ERNE data.
References
- Arzner, K., & Vlahos, L. 2004, ApJ, 605, L69 [NASA ADS] [CrossRef] [Google Scholar]
- Belov, A. V., Eroshenko, E. A., Kryakunova, O. N., Kurt, V. G., & Yanke, V. G. 2010, Geomagnetism and Aeronomy/Geomagnetizm i Aeronomiia, 50, 21 [NASA ADS] [CrossRef] [Google Scholar]
- Bieber, J. W., Dröge, W., Evenson, P. A., et al. 2002, ApJ, 567, 622 [NASA ADS] [CrossRef] [Google Scholar]
- Bougeret, J., Kaiser, M. L., Kellogg, P. J., et al. 1995, Space Sci. Rev., 71, 231 [NASA ADS] [CrossRef] [Google Scholar]
- Burlaga, L. F. E. 1991, Magnetic Clouds, ed. R. Schwenn, & E. Marsch (Berlin, Heidelberg, New York: Springer-Verlag), 1 [Google Scholar]
- Burlaga, L. F. 1995, Interplanetary magnetohydrodynamics (New York: Oxford University Press) [Google Scholar]
- Burlaga, L., Sittler, E., Mariani, F., & Schwenn, R. 1981, J. Geophys. Res., 86, 6673 [Google Scholar]
- Cane, H. V., Erickson, W. C., & Prestage, N. P. 2002, J. Geophys. Res. (Space Physics), 107, 1315 [Google Scholar]
- Carmichael, H. 1962, Space Sci. Rev., 1, 28 [Google Scholar]
- Chian, A. C.-L., & Muñoz, P. R. 2011, ApJ, 733, L34 [NASA ADS] [CrossRef] [Google Scholar]
- Cliver, E. W. 1982, Sol. Phys., 75, 341 [NASA ADS] [CrossRef] [Google Scholar]
- Cliver, E. W., Kahler, S. W., Shea, M. A., & Smart, D. F. 1982, ApJ, 260, 362 [Google Scholar]
- Cliver, E. W., Nitta, N. V., Thompson, B. J., & Zhang, J. 2004, Sol. Phys., 225, 105 [NASA ADS] [CrossRef] [Google Scholar]
- Crooker, N. U., Kahler, S. W., Gosling, J. T., & Lepping, R. P. 2008, J. Geophys. Res., 113, A12107 [NASA ADS] [CrossRef] [Google Scholar]
- Dasso, S., Mandrini, C. H., Démoulin, P., & Luoni, M. L. 2006, A&A, 455, 349 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Dasso, S., Nakwacki, M. S., Démoulin, P., & Mandrini, C. H. 2007, Sol. Phys., 244, 115 [NASA ADS] [CrossRef] [Google Scholar]
- Debrunner, H., Flueckiger, E., Graedel, H., Lockwood, J. A., & McGuire, R. E. 1988, J. Geophys. Res., 93, 7206 [Google Scholar]
- Debrunner, H., Lockwood, J. A., Barat, C., et al. 1997, ApJ, 479, 997 [NASA ADS] [CrossRef] [Google Scholar]
- Dmitruk, P., Matthaeus, W. H., & Seenu, N. 2004, ApJ, 617, 667 [NASA ADS] [CrossRef] [Google Scholar]
- Drake, J. F., Swisdak, M., Che, H., & Shay, M. A. 2006, Nature, 443, 553 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Dröge, W. 2000, ApJ, 537, 1073 [NASA ADS] [CrossRef] [Google Scholar]
- Elliott, H. A., McComas, D. J., Schwadron, N. A., et al. 2005, J. Geophys. Res., 110, A04103 [NASA ADS] [CrossRef] [Google Scholar]
- Gopalswamy, N. E. 2005, in Int. Cosm. Ray Conf., 1, 169 [Google Scholar]
- Hudson, H. S., Lin, R. P., & Stewart, R. T. 1982, Sol. Phys., 75, 245 [NASA ADS] [CrossRef] [Google Scholar]
- Huttunen-Heikinmaa, K., Valtonen, E., & Laitinen, T. 2005, A&A, 442, 673 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ippolito, A., Pommois, P., Zimbardo, G., & Veltri, P. 2005, A&A, 438, 705 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kahler, S. W., Sheeley, Jr., N. R., Howard, R. A., et al. 1984, J. Geophys. Res., 89, 9683 [Google Scholar]
- Kahler, S. W., Simnett, G. M., & Reiner, M. J. 2003, in Int. Cosm. Ray Conf., 6, 3415 [Google Scholar]
- Klein, L. W., & Burlaga, L. F. 1982, J. Geophys. Res., 87, 613 [Google Scholar]
- Klein, K., Chupp, E. L., Trottet, G., et al. 1999, A&A, 348, 271 [NASA ADS] [Google Scholar]
- Klein, K., Krucker, S., Lointier, G., & Kerdraon, A. 2008, A&A, 486, 589 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Krittinatham, W., & Ruffolo, D. 2009, ApJ, 704, 831 [NASA ADS] [CrossRef] [Google Scholar]
- Larson, D. E., Lin, R. P., McTiernan, J. M., et al. 1997, Geophys. Res. Lett., 24, 1911 [NASA ADS] [CrossRef] [Google Scholar]
- Li, C., Dai, Y., Vial, J., et al. 2009, A&A, 503, 1013 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lopez, R. E., & Freeman, J. W. 1986, J. Geophys. Res., 91, 1701 [NASA ADS] [CrossRef] [Google Scholar]
- Mandrini, C. H., Nakwacki, M., Attrill, G., et al. 2007, Sol. Phys., 244, 25 [NASA ADS] [CrossRef] [Google Scholar]
- Masson, S., Klein, K., Bütikofer, R., et al. 2009, Sol. Phys., 257, 305 [NASA ADS] [CrossRef] [Google Scholar]
- McComas, D. J., Bame, S. J., Barker, P., et al. 1998, Space Sci. Rev., 86, 563 [NASA ADS] [CrossRef] [Google Scholar]
- Miroshnichenko, L. I., Klein, K.-L., Trottet, G., et al. 2005, J. Geophys. Res., 110, A09S08 [Google Scholar]
- Moraal, H., & McCracken, K. G. 2011, Space Sci. Rev., 99 [Google Scholar]
- Parker, E. N. 1961, The Solar Wind, Space Astrophysics (New York: McGrawHill), 157 [Google Scholar]
- Reames, D. V. 1999, Space Sci. Rev., 90, 413 [Google Scholar]
- Reames, D. V. 2009, ApJ, 706, 844 [NASA ADS] [CrossRef] [Google Scholar]
- Richardson, I. G., & Cane, H. V. 2010, Sol. Phys., 264, 189 [NASA ADS] [CrossRef] [Google Scholar]
- Richardson, I. G., Cane, H. V., & von Rosenvinge, T. T. 1991, J. Geophys. Res., 96, 7853 [Google Scholar]
- Ruffolo, D., Tooprakai, P., Rujiwarodom, M., et al. 2006, ApJ, 639, 1186 [NASA ADS] [CrossRef] [Google Scholar]
- Sáiz, A., Ruffolo, D., Bieber, J. W., Evenson, P., & Pyle, R. 2008, ApJ, 672, 650 [NASA ADS] [CrossRef] [Google Scholar]
- Sanderson, T. R. 2004, in The Sun and the Heliosphere as an Integrated System, ed. G. Poletto, & S. T. Suess, Astrophys. Space Sci. Lib., 317, 113 [Google Scholar]
- Sandroos, A., & Vainio, R. 2009, A&A, 507, L21 [CrossRef] [EDP Sciences] [Google Scholar]
- Smith, C. W., L’Heureux, J., Ness, N. F., et al. 1998, Space Sci. Rev., 86, 613 [NASA ADS] [CrossRef] [Google Scholar]
- Stone, E. C., Frandsen, A. M., Mewaldt, R. A., et al. 1998, Space Sci. Rev., 86, 1 [Google Scholar]
- Torsti, J., Valtonen, E., Lumme, M., et al. 1995, Sol. Phys., 162, 505 [NASA ADS] [CrossRef] [Google Scholar]
- Torsti, J., Riihonen, E., & Kocharov, L. 2004, ApJ, 600, L83 [NASA ADS] [CrossRef] [Google Scholar]
- Trottet, G., Krucker, S., Lüthi, T., & Magun, A. 2008, ApJ, 678, 509 [NASA ADS] [CrossRef] [Google Scholar]
- Turkmani, R., Vlahos, L., Galsgaard, K., Cargill, P. J., & Isliker, H. 2005, ApJ, 620, L59 [NASA ADS] [CrossRef] [Google Scholar]
- Tylka, A. J., Cohen, C. M. S., Dietrich, W. F., et al. 2003, in Int. Cosm. Ray Conf., 6, 3305 [Google Scholar]
- Vainio, R., & Laitinen, T. 2007, ApJ, 658, 622 [NASA ADS] [CrossRef] [Google Scholar]
- Wimmer-Schweingruber, R. F., Crooker, N. U., Balogh, A., et al. 2006, Space Sci. Rev., 123, 177 [NASA ADS] [CrossRef] [Google Scholar]
Appendix A: Interplanetary magnetic structures for other GLEs
 |
Fig. A.1 Interplanetary data around GLE 64: it is located in a Parker-like solar wind. Same drawing convention as Fig. 1. |
This appendix provides the analysis of the interplanetary structures associated with those GLEs that have not been detailed in the main text.
A.1. Solar wind
A.1.1. GLE 64 on Aug. 24, 2002
Relativistic protons of the GLE 64 arrived on Earth at 01:24 UT on Aug. 24, 2002, during the decrease of B from 12 nT to 5 nT in two days (Fig. A.1). This decrease could suggest that protons traveled in the wake of the previous ICME ending on Aug. 21, at 14:00 UT (Richardson & Cane 2010). However, the orientation of the magnetic field θB ~ 0°, φB = −45°, the criteria on the temperature, Texp ≃ Tobs, and βp ≃ 0.4, are consistent with the Parker spiral magnetic field.
 |
Fig. A.2 Interplanetary data around GLE 70: it is located in a Parker-like solar wind. Same drawing convention as Fig. 1. |
A.1.2. GLE 70 on Dec. 13, 2006
The magnetic field does not show any increase of magnitude or magnetic rotation between 00:00 UT on Dec. 12 and 24:00 UT on Dec. 13 (Fig. A.2). Indeed, the magnetic field is non-coherent and fluctuates around θB = 0° and φB = −45°, with stronger fluctuations before the GLE and weaker after that. Moreover, the expected temperature is roughly equal to the observed temperature, and 0.4βp1. The magnetic and plasma properties strongly suggest that the Parker spiral is the magnetic structure of the IMF, guiding the relativistic protons of the GLE 70, detected on the Earth at 02:50 UT on Dec. 13, 2006.
A.2. ICME, magnetic cloud, or back region
 |
Fig. A.3 Interplanetary data around GLE 59: it is located in the back region of a hot flux rope. Same drawing convention as Fig. 1. |
A.2.1. GLE 59 on Jul. 14, 2000
The magnetic field on Jul. 14, 2000 between 02:00 UT and 15:00 UT, which enclosed the arrival time of GLE 59 detected at 10:31 UT, does not display any common features of the well-defined interplanetary magnetic field (Parker spiral, ICME, or magnetic cloud, Fig. A.3). The magnetic field is weak (B ≃ 3−5nT), while the magnetic vector orientation is highly fluctuating and accordingly does not have the typical θB and φB values of the Parker spiral. The plasma parameter evolution before the GLE also displays inconsistency: Tobs ≃ 0.5Texp, like in an ICME, whereas 0.4 < βp < 1, more typical of the solar wind.
Before this time period, the magnetic field magnitude increased and its magnetic vector rotated coherently from Jul. 13, 2000 at 13:00 UT up to Jul. 14 at 02:00 UT, which is typical of a magnetic cloud with its sheath in front. Meanwhile, Tobs > Texp indicates that this is a hot flux rope. Although it is hot, it was previously classified as a magnetic cloud (Huttunen-Heikinmaa et al. 2005; Richardson & Cane 2010). These previous studies set the ICME end on Jul. 14, 2000 at 15:00 UT. The coherent rotation of the field, i.e. the flux rope ends at ≈02:00 UT. Later on the magnetic field orientation has strong fluctuations. Still, globally φB progressively evolves from its value at the rear of the flux rope (φB ≈ 250−280°) to an outward sector value. Thus, we propose that the region between 02:00 UT and 15:00 UT is the magnetic cloud back region (φB ≈ 135°). The magnetic field and plasma properties are intermediate between the solar wind and magnetic cloud. Therefore, our analysis suggests that relativistic protons of GLE 59 arrived on Earth in the back region of a hot flux rope (magnetic cloud-like).
 |
Fig. A.4 Interplanetary data around GLE 61: it is located in the sheath of an ICME. Same drawing convention as Fig. 1. |
A.2.2. GLE 61 on Apr. 18, 2001
Relativistic protons on Apr. 18, 2001 (GLE 61), reached Earth at 02:36 UT during a strong increase of the magnetic field strength (B ≃ 20−25nT, Fig. A.4). After this period, we identify an ICME (B ~ 10nT, decreasing progressively to ~5nT) from the Apr. 18 at 12:00 UT to the Apr. 20 at 11:00 UT. This temporal evolution of B is the signature of an ICME, preceded by its sheath. Our identification agrees with the boundaries determined by a composition analysis (Richardson & Cane 2010). However, this ICME is a particular case where the proton temperature was higher than the expected one and therefore βp ≃ 1 in the front part of the ICME (Fig. A.4). We conclude that the relativistic protons of GLE 61 traveled in the sheath of this ICME.
 |
Fig. A.5 Interplanetary data around GLE 65: example of a GLE present in the back of a magnetic cloud. Same drawing convention as Fig. 1. |
 |
Fig. A.6 Interplanetary data around GLE 66: it is located inside a magnetic cloud. Same drawing convention as Fig. 1. Plasma data are not available for this event. |
 |
Fig. A.7 Interplanetary data around GLE 69: it is located in a disturbed solar wind. Same drawing convention as Fig. 1. |
A.2.3. GLE 65 on Oct. 28, 2003
Figure A.5 displays the evolution of the interplanetary magnetic field and plasma parameters for the GLE 65. The increase and the temporal evolution of the magnitude of the magnetic field starting at 02:00 UT on Oct. 28, 2003, the high coherence of the magnetic field vector, the ratio of the expected and the observed temperatures approaching 2 and the low value of βp < 0.4 clearly indicate that ACE crosses an ICME. Richardson & Cane (2010) determined its end at 09:00 UT on Oct. 28. They did not classify it as a magnetic cloud probably because the magnetic field rotation is only ≈60°. This limited rotation indicates that the flux rope was crossed by the spacecraft with a large impact parameter (i.e. far from its axis). Consequently, we conclude that the in-situ data are compatible with a magnetic cloud.
Around 09:00 UT the magnetic vector had a strong discontinuity, followed by many others until 16:00 UT on Oct. 28, as well as a progressive evolution of φB. During this time interval, the observed temperature became about twice higher than the expected temperature. The evolution of the magnetic field and of plasma parameters after 09:00 UT on Oct. 28 are compatible with the mixed properties of a hot back region in the wake of the magnetic cloud (Dasso et al. 2006, 2007). However, because the impact parameter of the magnetic cloud is large, the back region was also not observed in favorable conditions for a clear identification. Finally, relativistic protons were detected at Earth at 11:12 UT, and we accordingly conclude that they propagated in this hot back region.
A.2.4. GLE 66 on Oct. 29, 2003
The interplanetary magnetic structure on Oct. 29, 2003 has already been identified as a magnetic cloud (Mandrini et al. 2007). The magnetic cloud starts at 11:25 UT on 29 Oct. and ends at 02:00 UT on 30 Oct. The relativistic particles of the GLE reached the Earth at 21:01 UT on Oct. 29, then they propagated in this well-identified magnetic cloud (Fig. A.6). In addition, this magnetic cloud was related to the CME ejected from the Sun the 28 Oct. 2003 at 11:30 UT during the solar eruption producing the GLE 65. Therefore, the relativistic protons produced during the flare/CME event the 29 Oct. 2003 have been injected in the foot-points of the CME launched the 28 Oct. 2003.
A.3. Disturbed solar wind
A.3.1. GLE 69 on Jan. 20, 2005
Before the GLE 69 on Jan. 20, 2005 at 6:49 UT, the interplanetary magnetic structure was identified as an ICME, starting on Jan. 18, at 23:00 UT and ending on Jan. 20, at 03:00 UT (Richardson & Cane 2010). During this time interval, the magnetic field had a significant strength (6–18 nT) with small fluctuations, and with a weak coherent rotation. Moreover, Tobs < 0.5Texp and βp ≃ 0.02. So all the characteristics defining a magnetic cloud, except a large rotation of the field, are present. This is a magnetic cloud-like case (Fig. A.7).
After 03:00 UT, the magnetic field and plasma parameters behavior did not correspond to the Parker spiral case because the magnetic field was nearly orthogonal to the ecliptic plane and φB is variable (so not characteristic of a solar wind sector). The rotation of the magnetic field covering a wide angular range around 03:00 UT would be an extreme case for the start of a back region, difficult to explain by the reconnection of magnetic cloud with a solar wind magnetic field, consequently we cannot identify it as belonging to a back region. Still, the field nearly orthogonal to the ecliptic plane, the increase of the temperature and the βp are consistent with a disturbed solar wind that was located in the wake of the preceding ICME. Even though no clear magnetic structure can be identified, one can at least certainly conclude that relativistic protons related to the GLE 69 propagate in a disturbed solar wind.
All Tables
All Figures
 |
Fig. 1 Interplanetary data around GLE 63 (Dec. 26, 2001): example of a GLE present in a typical Parker spiral. From top to bottom, panels display the magnitude of the magnetic field (nT); its latitude θB and its longitude φB (given in GSE coordinate system); then on the same panel are overplotted the temperature of protons measured by the spacecraft (black dots) and the expected temperature (gray dots), and finally the β of protons. A horizontal line is added for θB = 0, φB = −45° and βproton = 0.4 to mark characteristic values. The grayscale rectangle in the five panels corresponds to the 1-hour time interval starting at the first arrival time of relativistic protons at Earth. The time axis is as measured at Earth. The ACE measurements at the L1 Lagrangian point were shifted by the appropriate travel time (see Sect. 2.2). |
| In the text | |
 |
Fig. 2 Interplanetary data around GLE 67: it is located in the back region of a magnetic cloud. Same drawing convention as Fig. 1. |
| In the text | |
 |
Fig. 3 Interplanetary data around GLE 60: example of a GLE present in a SW disturbed by a previous ICME. Same drawing convention as Fig. 1. |
| In the text | |
 |
Fig. 4 Example of the RPM and VDA analysis. Top row: normalized time profile of the logarithm of the intensity during the rising phase without any time shift for GLEs 64, 67 and 70, respectively, in panels a)–c) (see Sect. 3.1). The energy range (in MeV) of channels is added on the panel a). Bottom row, panels d)–f): plots of rise and onset times in function of the inverse of the proton velocity. The dark gray (or blue) points correspond to the rise times determined by RPM apply to ERNE data (Sect. 3.1), and the related linear fit is displayed by a dashed line (dark gray or blue). The linear fit related to the data set including the NM point (labeled and plotted in black or red), in addition to the previous ERNE points, is represented by a continuous line (black or red). The medium gray (or green) points correspond to the onset times of ERNE data and the related linear fit is displayed with a dashed line and the same color. The linear fit with the NM point added is shown with a continuous line and light gray (or pink). A color version is available in the electronic version. |
| In the text | |
 |
Fig. 5 Summary of the estimated length by the RPM, with (cross symbol) and without NM (diamond symbol), in relation to the magnetic topology. |
| In the text | |
 |
Fig. 6 Comparison of the solar release time of relativistic protons obtained from the RPM with (cross symbol) and without NM (diamond symbol), with time interval of electrons injection as deduced from type III (gray shaded bars). The onset time of type III bursts is set as the origin of the vertical axis. |
| In the text | |
 |
Fig. A.1 Interplanetary data around GLE 64: it is located in a Parker-like solar wind. Same drawing convention as Fig. 1. |
| In the text | |
 |
Fig. A.2 Interplanetary data around GLE 70: it is located in a Parker-like solar wind. Same drawing convention as Fig. 1. |
| In the text | |
 |
Fig. A.3 Interplanetary data around GLE 59: it is located in the back region of a hot flux rope. Same drawing convention as Fig. 1. |
| In the text | |
 |
Fig. A.4 Interplanetary data around GLE 61: it is located in the sheath of an ICME. Same drawing convention as Fig. 1. |
| In the text | |
 |
Fig. A.5 Interplanetary data around GLE 65: example of a GLE present in the back of a magnetic cloud. Same drawing convention as Fig. 1. |
| In the text | |
 |
Fig. A.6 Interplanetary data around GLE 66: it is located inside a magnetic cloud. Same drawing convention as Fig. 1. Plasma data are not available for this event. |
| In the text | |
 |
Fig. A.7 Interplanetary data around GLE 69: it is located in a disturbed solar wind. Same drawing convention as Fig. 1. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


